三角形周长最短的动点问题

利“刃”在手亿“折”成“直”—例析坐标系中三角形周长最小值问题在近几年的各地中考中，与线段相关的最值问题频频出现，已然成为一道亮丽的风景线.而其中以平面直角坐标系为载体来设计三角形周长最小值问题，更是中考命题所关注的热点之一本文以近几年中考题为例，归纳其类型与解法，供参考.1.三角形的三个顶点中仅有一个顶点是动点例1 (2015年河南省，有改动)如图1，边长为8的正方形OABC 的两边在坐标轴上，以点C 为顶点的抛物线经过点A ，点P 是抛物线上点A 、C 间的一个动点(含端点)，过点P 作PF BC 于点F .点D 、E 的坐标分别为(0,6),(-4,0)，连接,,PD PE DE .是否存在点P ，使PDE 的周长最小?若存在，求出点P 的坐标;若不存在，请说明理由.分析存在.理由:易求抛物线的解析式为2188yx .设21(,8)8P m m(80)m ，则22222211118(8),()6(8)28888PF m m PD m mm，故2PD PF , PDE 的周长=2DE EP PD DE EP PF .如图2，过E 点作EGBC 于点G .当,,E P F 三点共线，即点P 为EG 与抛物线的交点时，EP PF 的值最小，此时214,(4)868PEPx x y ，所以PDE 周长最小时点P 的坐标为(-4,6).点评本例三角形的三个顶点中，点P 为动点，点,D E 均为定点.由于DE 的长为定值，欲使PDE 的周长最小，只需满足PDPE 的值最小即可.进而利用“点P 运动的过程中，PD 与PF 的差为定值”这一有力武器，将问题转化为“求定直线BC 上一动点F 与直线外一定点E 的距离的最小值”，最终借助“连结直线外一点与直线上各点的所有线段中，垂线段最短”确定点P 的位置.例2 (2012年XX 省，有改动)如图3，在平面直角坐标系中，抛物线223yxx 与x 轴交于A 、B 两点，与y 轴交于点C ，点D 是该抛物线的顶点.请在直线AC 上找一点M ，使BDM 的周长最小，求出M 点的坐标.分析易知(1,0),(3,0),(0,3),(1,4)A B C D ，故224,10ABACOAOC，直线AC 的解析式为33yx .如图4，作点B 关于直线AC 的对称点B ，连接BD ,交AC 于点M ，则BDM 即为符合题意的周长最小的三角形.(证明如下:不妨在直线AC 上取异于点M 的任一点M ，连接,,B M DM BM .由对称性可知:,BMB M BM B M ，于是BDM 的周长=B M ,DM BD BDM 的周长=B M DM BD .而在B DM中，B MDM B D ，即B M DM B M DM ，所以BDM 的周长大于BDM 的周长.)若BB 交AC 于点E ，则90,22cos 2cos ABECAOACO BBBEAB ABEAB ACO312241010105.过B 点作B F x 轴于点F ，则362133cos 355B x BF BB ABE ，3112sin sin 101010105B y B F BB ABE BB ACO ，故2112(,)55B ,易求直线B D 的解析式为4481313y x .联立解方程组448131333y xyx ，得93513235x y，所以M 点的坐标为9132(,)3535.点评本例三角形的三个顶点中，点M 为动点，点B 、D 均为定点，且均位于动点M所在直线AC 的同一侧.通过寻找定点B 关于动点M 所在直线AC 的对称点B ,将问题转化为“求定直线AC 上一动点M 与直线异侧两定点B ,B 的距离和的最小值”，从而可利用“三角形任意两边之和大于第三边”加似解决(当B 、M 、D 三点共线，即点M 为直线B D与直线AC 的交点时，DM BM 的值最小，此时BDM 的周长最小).2.三角形的三个顶点中有两个顶点是动点例3 (2013年湖南张家界，有改动)如图5，抛物线2(0)y axbx c a 过点(0,1)C ，顶点为(2,3)Q ，点D 在x 轴正半轴上，且OD OC .将直线CD 绕点C 逆时针方向旋转45°所得直线与抛物线相交于另一点E ，若点P 是线段QE 上的动点，点F 是线段OD 上的动点，问:在P 点和F 点移动过程中，PCF 的周长是否存在最小值?若存在，求出这个最小值;若不存在，请说明理由.分析存在.理由:如图6，分别作点C 关于直线,QE x 轴的对称点,C C ，连接C C ，交OD 于点F ，交QE 于点P ，则PCF 即为符合题意的周长最小的三角形，此时PCF的周长等于线段C C 的长.(证明如下:不妨在线段OD 上取异于点F 的任一点F ，在线段QE 上取异于点P 的任一点P ，连接,,,,CF CP F P F C P C .由轴对称的性质可知P CF 的周长=F CF PP C ，而F CF P P C 的值为折线段CPF C 的长，由两点之间线段最短可知F CF PP CC C ，即P CF 的周长大于PCF 的周长.)如图6，过点Q 作QGy 轴于点G ，过点C 作C Hy 轴于点H ，则CGOCHC，可得12CG QG CQ CH C H CC，即2212CHC H.所以4,CHC H6C H CHCC.在RtC HC 中，222246213C CC HC H.所以，在P 点和F 点移动过程中，PCF 的周长存在最小值，最小值为213.点评本例三角形的三个顶点中，点C 为定点，点P 、F 均为动点，且分别在定直线QE 、QD 上，通过寻找定点C 关于两个动点所在直线的对称点C 、C ，就得到由三条与PCF三边分别相等的线段组成的折线，然后借助“两点之间线段最短”化“折”成“直”(当C 、P 、F 、C 四点共线，即点P 、F 分别为直线QE 、QD 与直线C C 的交点时，PCF的周长最小).3.三角形的三个顶点都是动点例 4(2015年XX 沈阳，有改动)如图7，在平面直角坐标系中，抛物线224233yx x 与x 轴交于B 、C 两点(点B 在点C 的左侧)，与y 轴交于点A .若点P 是线段BC 上的动点(点P 不与点B 、C 重合)，点Q 是线段AB 上的动点(点Q 不与点A 、B 重合)点R 是线段AC 上的动点(点R 不与点A 、C 重合)，请直接写出PQR 周长的最小值.分析易求(0,2),(3,0),(1,0)A B C ，故222213,5AB OAOBAC OAOC.如图8，过点B 作BH AC 于点H ，则885,sin65565BC OA BH BHBACACBA.如图9，分别作点P 关于直线,AB AC 的对称点,P P ，连接P P ，交AB 于点Q ，交AC 于点R ，则PQR 是过点P 的ABC 的内接三角形中周长最小的三角形，且PQR的周长等于线段P P 的长.若PP 交AB 于点,D PP 交AC 于点E ，连接DE ，则90,ADPAEPDP,DP EPEP ，故2P PDE .连接AP ，取AP 的中点F ，连接EF ，则12DFEFAP ，所以⊙F 为ADP 的外接圆，且点E 在⊙F 上.延长DF 交⊙F 于点G ，连接GE ，则90,DEGBACDGE ，所以PQR的周长22sin 2sin 2sin P P DE DG DGE AP BAC AO BAC8322265656565.如图10，当点P 与点O 重合时，PQR 的周长最小，最小值为326565. 点评本例三角形的三个顶点均为动点，应采取“以退为进”的策略，即:先假设P 点的位置已经确定(即视点P 为一定点)，容易得出结论:待求三角形周长最小时，其周长等于线段P P 的长，然后继续探究点P 的位置后，发现线段P P 长度的最小值即为点A 到x 轴的距离.因为,2AP APAP P APBAC ，所以AP P 为等腰三角形，且其顶角P AP 为定值.由于本例对解答过程不作要求，也可以根据“顶角为定值的等腰三角形底边长的最小值由腰长的最小值来确定”这一经验来判定点P 的位置.然而，对该例的思考却不止于此，我们还可以再进一步探索BR 和,AC CQ 和AB 的位置关系.参考本例分析问题的方法，我们可以得出这样的结论:,,AP BR CQ 为锐角三角形ABC 的三条高，以,,P Q R 三个垂足为顶点的三角形即为周长最小的内接三角形证明留待读者自行完成.通过上述问题的探究，我们可以发现，解决此类问题通常可以采取的策略是:把已知问题转化成容易解决的问题，即关联我们熟知的几何基本模型，构造一条以动点为转折点的折线，从而为性质的运用创造条件.如:解答例1时，需分析点在运动的过程中保持不变的关系，将问题转化为“求定直线上一动点与直线外一定点的距离的最小值”问题，然后利用“垂线段最短”把折线化“折”成“直”.解答例2，例3时，则需牢牢抓住图形的几何特征，将问题转化为“求定直线上一动点与直线外两定点的距离之和的最小值”问题，借助轴对称变换使两定点与定直线的位置关系发生改变，即化“同”为“异”，最后利用“三角形任意两边之和大于第三边”或“两点之间线段最短”把折线化“折”成“直”.例4题目的背景看似复杂，但图形上似乎可以捕捉到上述两个几何基本模型的“影子”，认清了这一点，便能使复杂问题简单化，迅速找到问题的突破口.在平面几何的教学中，教师要重视几何基本模型的提炼，帮助学生深刻领悟模型的本质特征，鼓励学生尝试从不同角度拓展模型，并在应用中彰显其魅力，从而促进学生解题经验的积累和思维水平的提升，真正提高学生的数学素养和解决问题的能力.。

P、Q、R分别是△ABC三边上的动点，则△PQR周长的最小值为______在平面几何中有一类求线段和最小值问题，这类问题源自古罗马时代“将军饮马”问题。

传说亚历山大城有一位精通数学和物理的学者，名叫海伦(已知三角形三边a，b，c，求面积S可用公式S=√[p(p-a)(p-b)(p-c)]计算，其中p表示三角形的半周长，即p=(a+b+c)/2．这个公式就是海伦发现的)，一天，一位罗马将军专程去拜访他，向他请教一个百思不得其解的问题：将军每天从军营A出发，先到河边饮马，然后再去河岸同侧的B 地开会，应该怎样走才能使路程最短？从此，这个问题被称为“将军饮马”问题，在世界各地广泛流传．“将军饮马”问题，我国唐朝诗人李颀的诗《古从军行》开头两句“白日登山望烽火，黄昏饮马傍交河”与“将军饮马”情景何其相似，诗中说的是一位将军白天骑马去山上点A处巡查烽火台，黄昏时牵马到河边饮水，然后回到与河同岸的营地B宿营。

如果诗中再提出这个将军该走哪条路线使路程最短，那么这个就跟“将军饮马”问题完全相同了。

这个问题的解决并不难，据说当时海伦略加思索就解决了它．事实上，这个问题转化为数学问题就是这样一个求线段河最小值的问题：如图1，已知直线l的同侧有A、B两点，在直线l上求作一个点P，使PA+PB最小。

把P视为直线l上的动点，则问题就变成了确定动点P的位置，使得PA+PB最小。

母庸质疑，海伦解决的方法和我们今天解决的方法是一样滴，利用轴对称变换将A、B两点中的一个点变换到直线l的另一侧，比如作点A关于直线l的对称点C（这里要明白为什么要作轴对称？原因很简单，因为这样做虽然点A的位置变了，但能保证点P到A的新位置C的距离PC与原来P到A的距离PA不变，即PC=PA），此时问题变为要使PA+PB最小，只需要PC+PB最小即可。

由于不论点P在何位置，根据“两点之间，线段最短”可知总有PC+PB≥BC，当点P与B、C共线时，等号成立，PC+PB最小=BC。

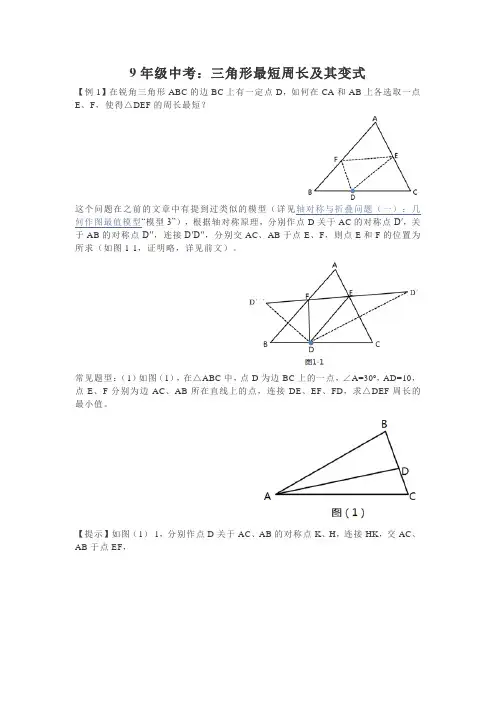
9年级中考：三角形最短周长及其变式【例1】在锐角三角形ABC的边BC上有一定点D，如何在CA和AB上各选取一点E、F，使得△DEF的周长最短？这个问题在之前的文章中有提到过类似的模型（详见轴对称与折叠问题（一）：几何作图最值模型“模型3”），根据轴对称原理，分别作点D关于AC的对称点D′，关于AB的对称点D′′，连接D′D′′，分别交AC、AB于点E、F，则点E和F的位置为所求（如图1-1，证明略，详见前文）。

常见题型：（1）如图（1），在△ABC中，点D为边BC上的一点，∠A=30º，AD=10，点E、F分别为边AC、AB所在直线上的点，连接DE、EF、FD，求△DEF周长的最小值。

【提示】如图（1）-1，分别作点D关于AC、AB的对称点K、H，连接HK，交AC、AB于点EF，则△DEF的周长为所求的最小周长；易知△AKH为等边三角形，AD=AH=HK=△DEF 的周长，故△DEF周长的最小值为10。

（2）如图（2），在△ABC中，点D为边BC上的一点，∠A=45º，点E、F分别为边AC、AB所在直线上的点，连接DE、EF、FD，已知△DEF周长的最小值为2，求AD的长。

【提示】2.【例2】在锐角三角形ABC的三边BC、CA和AB上各选取一点，连接这三点得到一个三角形，当这个三角形周长最短时，求其周长。

【解析】先假定BC边上的点D是不动点，则问题转化为【例1】中的情形（如图2-1）∵ED=ED′，FD=FD′′，∴△DEF周长=D′D′′；连接AD′，AD′′，过点A作AG⊥D′D′′于点G（如图2-2），∵AD=AD′=AD′′，∴△AD′D′′为等腰三角形，∵AG⊥D′D′′，∴D′D′′=2GD′；∵∠CAD=∠CAD′，∠BAD=∠BAD′′，∴∠D′AD′′=2∠BAC，∴∠GAD′=∠BAC；∴D′D′′=2AD′sin∠GAD′=2ADsin∠BAC.∵∠BAC为定值，∴当AD越小时，△DEF的周长越小，当AD⊥BC时，AD最小，所以点D为BC边上的高的垂足；当点D为BC边上的高的垂足时，点E和F又处于什么位置呢？下面我们来证明：点E、F也分别是AC、AB边上的高。

八年级数学动点题型归纳一、动点与三角形相关题型1. 动点在三角形边上运动求线段长度或周长题目：在等腰三角形公式中，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

当公式时，求公式的长度。

解析：过点公式作公式于点公式。

因为公式，等腰三角形三线合一，所以公式。

在公式中，根据勾股定理公式。

当公式时，公式，则公式。

在公式中，根据勾股定理公式。

2. 动点运动过程中三角形面积的变化题目：在公式中，公式，公式，公式，点公式从点公式出发，沿公式向点公式以每秒公式个单位长度的速度运动，同时点公式从点公式出发，沿公式向点公式以每秒公式个单位长度的速度运动，设运动时间为公式秒公式，求公式的面积公式与公式的函数关系式。

解析：已知公式，则公式，公式。

根据三角形面积公式公式，对于公式，底为公式，高为公式。

所以公式。

二、动点与四边形相关题型1. 动点在四边形边上运动判断四边形形状题目：在矩形公式中，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

当公式时，四边形公式是什么四边形？解析：当公式时，公式，公式。

因为四边形公式是矩形，所以公式，公式。

则公式，公式。

在四边形公式中，公式（因为公式），公式，公式（此时公式运动到公式点），公式。

因为公式且公式，所以四边形公式是梯形。

2. 动点运动过程中四边形面积的变化题目：在平行四边形公式中，公式，公式，公式，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，点公式从点公式出发沿公式向点公式运动，速度为每秒公式个单位长度，设运动时间为公式秒。

求四边形公式的面积公式与公式的函数关系式。

解析：四边形公式的面积公式。

过点公式作公式于点公式，在公式中，公式，公式，则公式，公式。

所以公式。

因为公式，则公式。

公式。

所以公式。

三、动点与函数图象相关题型1. 根据动点运动情况确定函数图象题目：如图，在边长为公式的正方形公式中，点公式以每秒公式个单位长度的速度从点公式出发，沿公式的路径运动，到点公式停止。

中考数学倒计时15：二次函数中三角形周长最小值问题
（1）直线AC的解析式不多说了；
（2）三点坐标代入，求得解析式；
（3）BD是一个定值，所以也就是求PB+PD的最小值，且必须组成三角形，
线段相加最小值，首选肯定是对称，
根据A、B、C三点的坐标，可知△ABC是直角三角形，
所以AC⊥BC，
那么我们可以作点B关于直线AC的对称点，
但是这个点怎么找呢？
直接延长BC至点B'，使CB=CB'，
相信这个B'的坐标不难求出吧？（向x轴作垂线，利用中位线求出B'坐标）
有了B'的坐标，那么PB=PB'，
所以PB'+PD的最小值就是三点共线，
连接B'D，求出B'D所在直线的解析式，
与AC相交于点P，
求出点P坐标；
这道题要善于发现ABC三点的特点，要找B或D的对称点，肯定要做垂线，所以及时发现直角的存在是非常必要的。

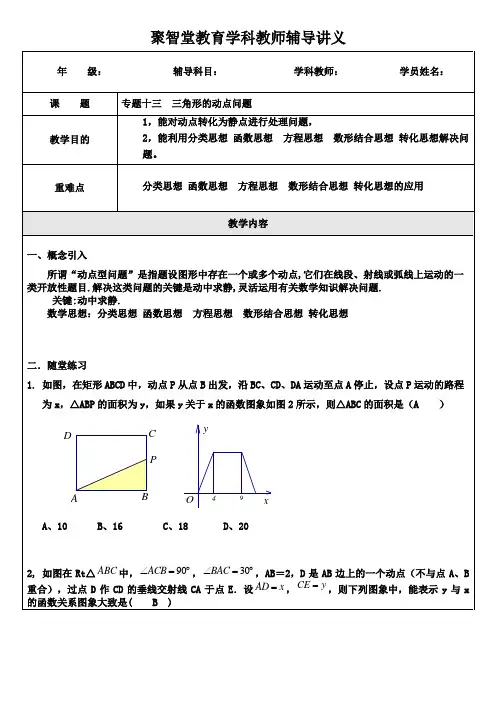
聚智堂教育学科教师辅导讲义E CAB D【答案】B【思路分析】由于D 是AB 边上的一个动点（不与点A 、B 重合），所以0<x<2，通过画图进行分析，画出的图形如图，在点D 由A 向B 移动过程中，AE 的长首先在减小如图1-图2所示，当运动到AB 的中点时CE 的长度达到最小值，当点D 再向B 移动过程中，CE 的值开始增大，离点B 越近CE 的值越大，DE 与AC 越接近平行状态。

所以此函数图象函数y 先随x 的增大而减小，然后y 先随x 的增大而增大，此题选B 。

3,平面直角坐标系中，已知点O （0,0）、A （0,2）、B （1,0.），点P 是反比例函数1y=x-图象上的一个动点，过点P 作PQ ⊥x 轴，垂足为点Q ，若以点O 、P 、Q 为顶点的三角形与 △OAB 相似，则相应的点P 共有（D)A.1个B.2个C. 3个D.4个 【答案】D【思路分析】在△OPQ 和△OAB 中，∠PQO=∠AOB=90°，如果∠POQ=∠ABO 或∠POQ=∠BAO 时，两个三角形相似，此时直线PQ 分别有2个交点，共有4个交点，即相应的点P 共有4个.4，（2013•河北）如图，梯形ABCD 中，AB ∥DC ，DE ⊥AB ，CF ⊥AB ，且AE=EF=FB=5，DE=12动点P 从点A 出发，沿折线AD-DC-CB 以每秒1个单位长的速度运动到点B 停止．设运动时间为t 秒，y=S △EPF ，则y 与t 的函数图象大致是（ A ）A ．B ．C ．D ．解：在Rt △ADE 中，AD=2213AE DE +=，在Rt △CFB 中，BC=2213BF CF +=，①点P在AD上运动：过点P作PM⊥AB于点M，则PM=APsin∠A=1213t，此时y=12EF×PM=3013t，为一次函数；②点P在DC上运动，y=12EF×DE=30；③点P在BC上运动，过点P作PN⊥AB于点N，则PN=BPsin∠B=1213（AD+CD+BC-t）=12(31)13t-，则y=12EF×PN=30(31)13t-，为一次函数．综上可得选项A的图象符合．故选A．5，（2013•荆门）如右图所示，已知等腰梯形ABCD，AD∥BC，若动直线l垂直于BC，且向右平移，设扫过的阴影部分的面积为S，BP为x，则S关于x的函数图象大致是（ A ）A．B．C． D．解：①当直线l经过BA段时，阴影部分的面积越来越大，并且增大的速度越来越快；②直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度保持不变；③直线l经过DC段时，阴影部分的面积越来越大，并且增大的速度越来越小；结合选项可得，A选项的图象符合．故选A．6，（2013•永州）如图所示，在矩形ABCD中，垂直于对角线BD的直线l，从点B开始沿着线段BD 匀速平移到D．设直线l被矩形所截线段EF的长度为y，运动时间为t，则y关于t的函数的大致图象是（ A ）A． B．C．D．7，如图所示：边长分别为1和2的两个正方形，其中一边在同一水平线上，小正方形沿该水平线自左向右匀速穿过大正方形，设穿过的时间为t，大正方形内去掉小正方形后的面积为s，那么s与t 的大致图象应为（ A ）A．B．C．D．8，（2013•衡阳）如图所示，半径为1的圆和边长为3的正方形在同一水平线上，圆沿该水平线从左向右匀速穿过正方形，设穿过时间为t，正方形除去圆部分的面积为S（阴影部分），则S与t的大致图象为（ A ）A．B．C．D．,9，如图，Rt△ABC中，∠ACB=90°，∠ABC=60°，BC=2cm，D为BC的中点，若动点E以1cm/s的速度从A点出发，沿着A→B→A的方向运动，设E点的运动时间为t秒（0≤t＜6），连接DE，当△BDE是直角三角形时，t的值为（ D ）A．2 B．2.5或3.5C．3.5或4.5 D．2或3.5或4.51．D10．图1所示矩形ABCD中，BC=x，CD=y，y与x满足的反比例函数关系如图2所示，等腰直角三角形AEF的斜边EF过C点，M为EF的中点，则下列结论正确的是（ D ）A．当x=3时，EC＜EMB．当y=9时，EC＞EMC．当x增大时，EC•CF的值增大D．当y增大时，BE•DF的值不变11，如图，将边长为4的正方形ABCD 的一边BC 与直角边分别是2和4的Rt △GEF 的一边GF 重合．正方形ABCD 以每秒1个单位长度的速度沿GE 向右匀速运动，当点A 和点E 重合时正方形停止运动．设正方形的运动时间为t 秒，正方形ABCD 与Rt △GEF 重叠部分面积为s ，则s 关于t 的函数图象为（ B ）A ．B ．C ．D ．12，如图，在平面直角坐标系xOy 中，A （0，2），B （0，6），动点C 在直线y=x 上．若以A 、B 、C 三点为顶点的三角形是等腰三角形，则点C 的个数是（ B ） A ．2 B ．3 C ．4 D ．513,如图，正方形ABCD 的边长为4，P 为正方形边上一动点，运动路线是A →D →C →B →A ，设P 点经过的路线为x ，以点A 、P 、D 为顶点的三角形的面积是y ．则下列图象能大致反映y 与x 的函数关系的是（ B ）14,如图所示，在矩形ABCD 中，垂直于对角线BD 的直线l ，从点B 开始沿着线段BD 匀速平移到D ．设直线l 被矩形所截线段EF 的长度为y ，运动时间为t ，则y 关于t 的函数的大致图象是（ A ）15，,如图（1），在R t △ABC 中，∠ACB =90°，D 为斜边AB 的中点，动点P 从B 点出发，沿B →C →A 运动，设S △DPB =y ，点P 运动的路程为x ，若y 与x 之间的函数图像如图（2）所示，则△ABC 的面积为（ B ）A ．OytBOytC ．OytD ．Oyt（第14题）第8题图A . 4B . 6C . 12D . 14【思路分析】通过图（2）可以看出，当点P 运动到点C 时，点P 运动的路程为4，即BC=4；当点P运动到点A 时，点P 运动的路程为7，即AC=3，则S △ABC =21AC ×BC=616,如图，在△ABC 中，AB =20㎝，AC =12㎝，点P 从点B 出发以每秒3㎝的速度向点A 运动，点Q 从点A 同时出发以每秒2㎝的速度向点C 运动，其中一个动点到达端点时，另一个动点也随之停止运动，当△APQ 是等腰三角形时，运动的时间是 （ D ） A ． 2.5 B ．3秒 C ．3.5秒 D ．4秒QCBPA17．（2013•丽水）如图1，在Rt △ABC 中，∠ACB=90°，点P 以每秒1cm 的速度从点A 出发，沿折线AC ﹣CB 运动，到点B 停止，过点P 作PD ⊥AB ，垂足为D ，PD 的长y （cm ）与点P 的运动时间x （秒）的函数图象如图2所示，当点P 运动5秒时，PD 的长是（ B ）A ． 1.5cmB ．1.2cm C ．1.8cmD ．2cm分析： 根据图2可判断AC=3，BC=4，则可确定t=5时BP 的值，利用sin ∠B 的值，可求出PD ． 解答： 解：由图2可得，AC=3，BC=4，当t=5时，如图所示：，此时AC+CP=5，故BP=AC+BC ﹣AC ﹣CP=2， ∵sin ∠B==，∴PD=BPsin ∠B=2×==1.2cm ．故选B ．18．（2013•莱芜）如图，等边三角形ABC 的边长为3，N 为AC 的三等分点，三角形边上的动点M 从点A 出发，沿A →B →C 的方向运动，到达点C 时停止．设点M 运动的路程为x ，MN 2=y ，则y 关于x 的函数图象大致为（ B ）A．B．CD．．考点：动点问题的函数图象．专题：压轴题．分析：注意分析y随x的变化而变化的趋势，而不一定要通过求解析式来解决．解答：解：∵等边三角形ABC的边长为3，N为AC的三等分点，∴AN=1．∴当点M位于点A处时，x=0，y=1．①当动点M从A点出发到AM=0.5的过程中，y随x的增大而减小，故排除D；②当动点M到达C点时，x=6，y=4，即此时y的值与点M在点A处时的值不相等．故排除A、C．故选B．点评：本题考查了动点问题的函数图象，解决本题应首先看清横轴和纵轴表示的量，然后根据动点的行程判断y 的变化情况．19，如图，动点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），……，按这样的运动规律，经过第2011次运动后，动点P的坐标是_（2011，2）_________．【答案】（2011，2）【思路分析】从点的坐标可以看出横坐标正好是运动的次数，所以第2011次运动后点的横坐标就是2011，纵坐标的数是1，0，2，0，1，02，0，……四个一循环，所以2011÷4=502……3，因此第2011次点的纵坐标是2，故点的坐标为（2011，2）．20，如图，在四边形ABCD中，∠A＝90°，AD＝4，连接BD，BD⊥CD，∠ADB＝∠C．若P是BC边上一动点，则DP长的最小值为 4 。

2、三角形中的动点问题例1、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点。

（1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动。

①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？例2.如图，△ABC 中，点O 为AC 边上的一个动点，过点O 作直线MN ∥BC ，设MN 交∠BCA 的外角平分线CF 于点F ，交∠ACB 内角平分线CE 于E 。

（1）试说明EO=FO ；（2）当点O 运动到何处时，四边形AECF 是矩形并证明你的结论；（3）若AC 边上存在点O ，使四边形AECF 是正方形，猜想△ABC 的形状并证明你的结论。

分析：（1）根据CE 平分∠ACB ，MN ∥BC ，找到相等的角，即∠OEC=∠ECB ，再根据等边对等角得OE=OC ，同理OC=OF ，可得EO=FO 。

（2）利用矩形的判定解答，即有一个内角是直角的平行四边形是矩形。

（3）利用已知条件及正方形的性质解答。

A Q D B练习1、在直角三角形ABC 中，BC=6，AC=8，点D 在线段AC 上从C 向A 运动。

若设CD=x ，△ABD 的面积为y 。

（1）请写出y 与x 的关系式；（2）当x 为何值时，y 有最大值，最大值是多少？此时点D 在什么位置？（3）当△ABD 的面积是△ABC 的面积的一半时，点D 在什么位置？2、直线643+-=x y 与坐标轴分别交于A 、B 两点，动点P 、Q 同时从O 点出发，同时到达A 点，运动停止。

A BCE F三角形与动点问题1、如图，在等腰△ACB中，AC＝BC＝5，AB＝8，D为底边AB上一动点（不与点A，B重合），DE⊥AC，DF⊥BC，垂足分别为E，F，则DE＋DF＝．2、在边长为2㎝的正方形ABCD中，点Q为BC边的中点，点P为对角线AC上一动点，连接PB、PQ，则△PBQ周长的最小值为____________㎝（结果不取近似值）.3、如图，将边长为1的等边△OAP按图示方式，沿x轴正方向连续翻转2011次，点P依次落在点P1，P2，P3，P4，…，P2007的位置．试写出P1，P3，P50，P2011的坐标．4、如图，在等腰Rt△ABC中，∠ACB=90°，AC=CB，F是AB边上的中点，点D、E分别在AC、BC边上运动，且始终保持AD=CE．连接DE、DF、EF．（1）求证：△ADF≌△CEF（2）试证明△DFE是等腰直角三角形5、（2009年包头）如图，已知ACB△与DFE△是两个全等的直角三角形，量得它们的斜边长为10cm，较小锐角为30°，将这两个三角形摆成如图（1）所示的形状，使点B C F D、、、在同一条直线上，且点C与点F重合，将图（1）中的ACB△绕点C顺时针方向旋转到图（2）的位置，点E在AB边上，AC交DE于点G，则线段FG的长为 cm（保留根号）．6、如图1，若△ABC 和△ADE 为等边三角形，M ，N 分别EB ，CD 的中点，易证：CD=BE ，△AMN 是等边三角形．（1）当把△ADE 绕A 点旋转到图2的位置时，CD=BE 是否仍然成立？若成立请证明，若不成立请说明理由；（2）当△ADE 绕A 点旋转到图3的位置时，△AMN 是否还是等边三角形？若是，请给出证明，并求出当AB =2AD 时，△ADE 与△ABC 及△AMN 的面积之比；若不是，请说明理由．7、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点． （1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？图1 图2 图3A EC (F ) B图（1）EA GBC (F ) D图（2）8、如图，在平面直角坐标系中，矩形AOBC 在第一象限内，E 是边OB 上的动点（不包括端点），作∠AEF = 90︒，使EF 交矩形的外角平分线BF 于点F ，设C （m ，n ）．（1）若m = n 时，如图，求证：EF = AE ；（2）若m ≠n 时，如图，试问边OB 上是否还存在点E ，使得EF = AE ？若存在，请求出点E 的坐标；若不存在，请说明理由．9.（2009年本溪）在ABC△中，AB AC =，点D 是直线BC 上一点（不与B C 、重合），以AD 为一边在AD 的右侧．．作ADE △，使AD AE DAE BAC =∠=∠，，连接CE ．（1）如图1，当点D 在线段BC 上，如果90BAC ∠=°，则BCE ∠= 度； （2）设BAC α∠=，BCE β∠=．①如图2，当点D 在线段BC 上移动，则αβ，之间有怎样的数量关系？请说明理由；②当点D 在直线BC 上移动，则αβ，之间有怎样的数量关系？请直接写出你的结论．10．如图， 直线l 与x 轴、y 轴分别交于点) 0,8 ( M ，点) 6,0 ( N ．点P 从点N 出发，以每秒1个单位长度的速度沿N →O 方向运动，点Ｑ从点O 出发，以每秒2个单位长度的速度沿O →M 的方向运动．已知点ＱP 、同时出发，当点Ｑ到达点M 时，ＱP 、两点同时停止运动， 设运动时间为t 秒．（1）设四边形．．．MNPQ 的面积为S ，求S 关于t 的函数关系式，并写出t 的取值范围．（2）当t 为何值时，ＱP 与l 平行？11.已知：等边三角形ABC 的边长为4厘米，长为1厘米的线段MN 在ABC △的边AB 上沿AB 方向以1厘米/秒的速度向B 点运动（运动开始时，点M 与点A 重合，点N 到达点B 时运动终止），过点M N 、分别作AB 边的垂线，与ABC △的其它边交于P Q 、两点，线段MN 运动的时间为t 秒．AEEAC CD BB图1 图2 AA备用图备用图ABCDE FGH KMN12345678（1）线段MN 在运动的过程中，t 为何值时，四边形MNQP 恰为矩形？并求出该矩形的面积；（2）线段MN 在运动的过程中，四边形MNQP 的面积为S ，运动的时间为t ．求四边形MNQP 的面积S 随运动时间t 变化的函数关系式，并写出自变量t 的取值范围．12.如图，AC 为正方形ABCD 的一条对角线，点E 为DA 边延长线上的一点，连接BE ，在BE 上取一点F ，使BF BC =，过点B 作BK BE ⊥于B ，交AC 于点K ，连接CF ，交AB 于点H ，交BK 于点G ． （1）求证：BG BH =； （2）求证：AE BG BE +=CPQAMN CPQBA M NCPQBA MN。

三角形周长最短的动点问题标题:三角形周长最短的动点问题(创建与此标题相符的正文并拓展)三角形周长最短的动点问题是指在一个动态环境下,寻找一个具有特定运动轨迹的动点,使得该动点的周长尽可能地短。

这个问题最初由法国数学家欧拉在18世纪提出,并被称为欧拉问题。

这个问题的数学描述如下:在一个三角形中,选取一个顶点作为动点,要求该点的邻边长度尽可能地短,且不受其他顶点的影响。

假设三角形的三个顶点分别位于三个坐标轴上,动点在x轴上运动,则其相邻边的长度可以表示为线段的长度,记为l(x)。

则动点的周长C(x)可以表示为:C(x) = 2(l(x+1) + l(x-1) + l(x-2))其中,+表示加号,-表示减号,l(x)的值域为[1,3]。

这是一个非常有趣的数学问题,具有广泛的应用价值。

在计算机图形学、物理引擎、人工智能等领域都有重要的应用。

解决该问题的方法有多种,其中一些方法需要使用高级数学知识和算法。

下面介绍几种常见的解决方法:1. 动态规划方法:该方法将问题划分为多个子问题,通过优化子问题的解来得到整个问题的解。

具体而言,可以将问题划分为三个子问题:找到x使得l(x)=2,找到x使得l(x)=3,找到x使得l(x)+l(x-1)+l(x-2)=2或3。

通过递归求解这三个子问题,可以得到最终的解。

2. 贪心算法:该方法通过贪心策略来求解问题。

具体而言,每次选取一个尽可能短的边,并不断增加相邻边的长度,直到满足周长最大或最小条件。

3. 遗传算法:该方法是一种优化算法,可以用于求解复杂的优化问题。

该算法通过模拟生物进化的过程,从多个解中随机选择一个解,并不断迭代,直到满足目标条件。

4. 粒子群算法:该方法是一种基于群体智能的优化算法,可以用于求解复杂的优化问题。

该算法将问题划分为多个子问题,每个子问题对应不同的优化目标,然后利用粒子群的思想,将问题划分为多个小组,每个小组分别求解不同的子问题,最后综合所有小组的解得到最终解。

1、如图，已知ABC △中，10AB AC ==厘米，8BC =厘米，点D 为AB 的中点． （1）如果点P 在线段BC 上以3厘米/秒的速度由B 点向C 点运动，同时，点Q 在线段CA 上由C 点向A 点运动．①若点Q 的运动速度与点P 的运动速度相等，经过1秒后，BPD △与CQP △是否全等，请说明理由；②若点Q 的运动速度与点P 的运动速度不相等，当点Q 的运动速度为多少时，能够使BPD △与CQP △全等？（2）若点Q 以②中的运动速度从点C 出发，点P 以原来的运动速度从点B 同时出发，都逆时针沿ABC △三边运动，求经过多长时间点P 与点Q 第一次在ABC △的哪条边上相遇？2.在△ABC 中，∠ACB=90°，AC=BC ，直线MN 经过点C ，且AD⊥MN 于D ，BE⊥MN 于E ． （1）当直线MN 绕点C 旋转到图1的位置时，求证：①△ADC≌△CEB；②DE=AD＋BE ； （2）当直线MN 绕点C 旋转到图2的位置时，求证：DE=AD －BE ；（3）当直线MN 绕点C 旋转到图3的位置时，试问DE 、AD 、BE 具有怎样的等量关系？请写出这个等量关系，并加以证明．3.如图A ，△ABC 和△CEF 是两个大小不等的等边三角形，且有一个公共顶点C ，连接AF 和BE ． （1）线段AF 和BE 有怎样的大小关系?请证明你的结论； （2）将图A 中的△CEF 绕点C 旋转一定的角度，得到图B ，（1）中的结论还成立吗?作出判断并说明理由；（3）若将图A 中的△ABC 绕点C 旋转一定的角度，请你画山一个变换后的图形C （草图即可），（1）中的结论还成立吗?作出判断不必说明理由； （4）根据以上证明、说理、画图，归纳你的发现．CB ED图1 NM ABCDEMN 图2 A CB EDN M图34.如图（1）△ABC为等边三角形，动点D在边CA上，动点P边BC上，若这两点分别从C、B 点同时出发，以相同的速度由C向A和由B向C运动，连接AP，BD交于点Q，两点运动过程中AP=BD成立吗？请证明你的结论；（2）如果把原题中“动点D在边CA上，动点P边BC上，”改为“动点D，P在射线CA和射线BC上运动”，其他条件不变，如图（2）所示，两点运动过程中∠BQP的大小保持不变．请你利用图（2）的情形，求证：∠BQP=60°；（3）如果把原题中“动点P在边BC上”改为“动点P在AB的延长线上运动，连接PD交BC 于E”，其他条件不变，如图（3），则动点D，P在运动过程中，DE始终等于PE吗？写出证明过程．5. 如图，已知∠AOB=120°，OM平分∠AOB，将等边三角形的一个顶点P放在射线OM上，两边分别与OA、OB（或其所在直线）交于点C、D．（1）如图①，当三角形绕点P旋转到PC⊥OA时，证明：PC=PD．（2）如图②，当三角形绕点P旋转到PC与OA不垂直时，线段PC和PD相等吗？请说明理由．（3）如图③，当三角形绕点P旋转到PC与OA所在直线相交的位置时，线段PC和PD相等吗？直接写出你的结论，不需证明．6、如图1，若△ABC和△ADE为等边三角形，M，N分别EB，CD的中点，易证：CD=BE，△AMN 是等边三角形．（1）当把△ADE绕A点旋转到图2的位置时，CD=BE是否仍然成立？若成立请证明，若不成立请说明理由；（2）当△ADE绕A点旋转到图3的位置时，△AMN是否还是等边三角形？若是，请给出证明，并求出当AB=2AD时，△ADE与△ABC的面积之比；若不是，请说明理由．7、以ABC ∆的两边AB 、AC 为腰分别向外作等腰Rt ABD ∆和等腰Rt ACE ∆，90,BAD CAE ∠=∠=︒连接DE ，M 、N 分别是BC 、DE 的中点．探究：AM 与DE 的位置关系及数量关系． （1）如图① 当ABC ∆为直角三角形时，AM 与DE 的位置关系是 ， 线段AM 与DE 的数量关系是 ；（2）将图①中的等腰Rt ABD ∆绕点A 沿逆时针方向旋转︒θ(0<θ<90)后，如图②所示，（1）问中得到的两个结论是否发生改变？并说明理由．8.已知四边形ABCD 中，AB AD ⊥，BC CD ⊥，AB BC =，120ABC =∠，60MBN =∠，MBN ∠绕B 点旋转，它的两边分别交AD DC ，（或它们的延长线）于E F ，． (1)当MBN ∠绕B 点旋转到AE CF =时（如图1），易证AE CF EF +=．(2)当MBN ∠绕B 点旋转到AE CF ≠时，在图2和图3这两种情况下，上述结论是否成立？若成立，请给予证明；若不成立，线段AE CF ，，EF 又有怎样的数量关系？请写出你的猜想，不需证明．图1 图2 图3（图1）AB CD E F MN（图2）ABCDE FMN（图3）AB CDEF MN。

「初中数学」从三角形周长的最值问题说说解题策略“问题是数学的心脏”，是思维的起点，是学生主动探索的动力。

学生在数学问题解决的过程中学习数学，提升思维。

本文意在由一组三角形周长最值问题谈在数学问题解决的过程中一些常用的解题策略。

问题1点A是∠O内一点，试在∠O的两边上分别确定点B、点C，使得△ABC周长最小分析在∠O的两边取B、C两点，构成△ABC，△ABC周长最小即AB+AC+BC最小。

由于这个问题不含任何数据，从代数角度，用参数表示出△ABC的周长几无可能，而从几何角度处理线段（和）最值问题主要有两条重要依据：① 两点之间线段距离最短；② 直线外一点到直线垂线段最短。

所以，考虑转化线段AB、AC，采用的方法是“翻折”，即做点A 关于∠O两边的对称点A1、A2，联结A1C、A2B。

根据中垂线的性质，AB=A2B，AC=A1C，将△ABC的三边转化为收尾相接的三条折线段，显然A1A2≤A2B+BC+A1C，A1A2与∠O 两边的交点即所求点，A1A2长即所求最短周长。

问题2在锐角△ABC三边AB、AC、BC取点E、F、G，若△EFG周长最小，请确定点E、F、G的位置。

分析现在点E、点F、点G的位置无一确定，怎样下手？以退为进！（可以先考虑问题的特殊情况，或先考虑问题的一部分，看清楚、想明白了再进。

退是手段、进是目的，“难的不会想简单的”是个好主意。

在具体实践中，常常是进退互化。

——罗增儒教授）假设在边BC上任取点G，在边AB、AC上确定点E、F，使得△EFG周长最短。

是否感觉回归到了“问题1”做点G关于AB、AC的对称点G1、G2，联结G1G2，交AB、AC于点E、F，则此时△GEF周长最小，其最小周长为G1G2的长度。

而接下去就要寻找G1G2的长度与点G位置之间的关系。

联结AG、因为AG1=AG=AG2，显然对于△AG1G2有以下特征：① △AG1G2是等腰三角形；② △AG1G2顶角为△ABC的内角∠BAC的两倍，是定值（所有顶角相等的等腰三角形都相似），于是要使得等腰△AG1G2的底边G1G2最短，则其要AG要最短，AG表示的是点A 到BC上点的距离，直线外一点到直线垂线段最短，所以AG要最短，则AG⊥BC！此时可以证明CE⊥AB，BF⊥AC，其实E、F、G就是△ABC三边上高的垂足，人们把这样的三角形称之为垂足三角形，又称施瓦兹三角形。

中考数学倒计时15：二次函数中三角形周长最小值问题
（1）直线AC的解析式不多说了；
（2）三点坐标代入，求得解析式；
（3）BD是一个定值，所以也就是求PB+PD的最小值，且必须组成三角形，
线段相加最小值，首选肯定是对称，
根据A、B、C三点的坐标，可知△ABC是直角三角形，
所以AC⊥BC，
那么我们可以作点B关于直线AC的对称点，
但是这个点怎么找呢？
直接延长BC至点B'，使CB=CB'，
相信这个B'的坐标不难求出吧？（向x轴作垂线，利用中位线求出B'坐标）
有了B'的坐标，那么PB=PB'，
所以PB'+PD的最小值就是三点共线，
连接B'D，求出B'D所在直线的解析式，
与AC相交于点P，
求出点P坐标；
这道题要善于发现ABC三点的特点，要找B或D的对称点，肯定要做垂线，所以及时发现直角的存在是非常必要的。

七年级动点问题三角形【最新版】目录1.引言：介绍七年级动点问题三角形的概念和意义2.动点问题的基本概念：解析动点、定点、轨迹等基本概念3.三角形的性质：详述三角形的性质及其在动点问题中的应用4.七年级动点问题三角形的解题方法：解析几何法、代数法等解题技巧5.案例分析：通过具体案例分析七年级动点问题三角形的解题思路6.总结：回顾七年级动点问题三角形的学习要点和解题技巧正文【引言】七年级动点问题三角形是初中数学中一个重要的知识点，它涉及到动点问题、几何图形和代数计算等多个方面。

掌握好七年级动点问题三角形，不仅可以提高学生的数学思维能力，还可以为以后的数学学习打下良好的基础。

本文将从动点问题的基本概念入手，详细解析七年级动点问题三角形的性质、解题方法以及具体案例分析。

【动点问题的基本概念】动点问题是指在平面直角坐标系中，已知一个点的位置随时间变化而变化，求该点的轨迹问题。

在动点问题中，有两个基本的概念，分别是解析动点和定点。

解析动点是指在平面直角坐标系中，一个点的坐标随时间变化而变化，它的轨迹是一条曲线。

而定点则是指在平面直角坐标系中，一个固定位置的点，它的坐标不随时间变化而变化。

在动点问题中，三角形也是一个重要的概念。

三角形是由三条线段组成的封闭图形，它有三个顶点和三个内角。

在动点问题中，三角形的性质和计算方法与静态几何中的三角形有很大的不同。

【三角形的性质及其在动点问题中的应用】在七年级动点问题三角形中，三角形的性质主要体现在它的三条边和三个顶点上。

三角形的三条边有长短之分，三个顶点有角度大小之分。

在动点问题中，三角形的性质主要体现在它的三条边和三个顶点的变化上。

在动点问题中，三角形的应用主要体现在求解三角形的周长、面积以及三角形的形状等。

例如，在求解一个三角形的周长时，可以利用解析几何法求解；在求解三角形的面积时，可以利用代数法求解。

【七年级动点问题三角形的解题方法】在七年级动点问题三角形中，解题方法主要有解析几何法和代数法两种。

2023年中考数学高频考点突破-三角形动点问题1．如图，长方形ABCD中，AB=10cm，AD=12cm，∠A=90°．点P从点A出发，沿射线AB的方向以5cm/秒的速度移动；同时，点Q也从点A出发，以l2cm/秒的速度沿射线AD的方向移动．设两点的运动时间为t秒．（1）当点P到达点B时，t=．（2）用含t的式子表示PQ，可以表示为．（3）试求出使△APQ的周长等于长方形ABCD周长的三分之一的t值．（4）若Q点到达D点后立刻按照原路原速返回，试求出何时△APQ为等腰三角形．2．如图，△ABC 中，△C＝90°，AB＝10cm，BC＝6cm，若动点P 从点C开始，按C→A→B→C 的路径运动，且速度为每秒1cm，设出发的时间为t 秒．（1）出发2 秒后，求△ABP 的周长．（2）当t 为几秒时，BP 平分△ABC？（3）另有一点Q，从点C 开始，按C→B→A→C 的路径运动，且速度为每秒2cm，若P、Q两点同时出发，当P、Q 中有一点到达终点时，另一点也停止运动．当t 为何值时，直线PQ 把△ABC 的周长分成相等的两部分？3．在Rt△ABC中，△ACB=90°，AC=BC=3 √2，点D是斜边AB上一动点（点D与点A、B不重合），连接CD，将CD绕点C顺时针旋转90°得到CE，连接AE，DE．（1）求△ADE的周长的最小值；（2）若CD=4，求AE的长度．4．如图，在Rt△ABC中，∠ACB=90°，AB=20cm，AC=16cm，点P从点A出发，以每秒1cm 的速度向点C运动，连接PB，设运动时间为t秒（t>0）（1）求BC的长．（2）当PA=PB时，求t的值．5．如图，在Rt△ABC中，△ABC=90°，AB=20，BC=15，点D为AC边上的动点，点D从点C出发，沿CA往A运动，当运动到点A时停止，设点D运动的时间为t秒，点D运动的速度为每秒2个单位长度。