高中数学丨外接球与内切球解题方法,8大模型

八个有趣模型一一搞定空间几何体的外接球与内切球类型一、墙角模型（三条线两个垂直，不找球心的位置即可求出球半径）解：引理：正三棱锥的对棱互垂直 。

证明如下: 如图（3）-1，取AB, BC 的中点D,E ，连接AE,CD ，AE,CD 交于H , 连接SH ,则H 是底面正三角形ABC 的中心， SH 平面ABC ,SH AB ,AC BC , AD BD , CD AB , AB 平面 SCD ,方法: 找三条两两垂直的线段，直接用公式 （2R ）2 a 2 b 2 c 2，即 2Ra 2b 2c 2，求出例1A.（1）已知各顶点都在同一球面上的正四棱柱的高为16 B • 20 C • 24体积为16，则这个球的表面积是（ • 32(2) 若三棱锥的三个侧面两垂直，且侧棱长均为 则其外接球的表面积是解: (1) V a 2h 16, a 2, 4R 2 a 22 h 24 4 16 24，S 24 ，选 C ；(2)4R 23 3 3 9, S4 R 29(3) 在正三棱锥 S ABC 中，M 、N 分别是棱 SC 、 BC 的中点，且AM MN ,若侧棱SA2、、3,则正三棱锥S ABC 外接球的表面积是363 AB SC ,同理：BC SA , AC SB ,即正三棱锥的对棱互垂直,本题图如图(3) -2 , AM MN , SB//MN ,AM SB , AC SB , SB 平面 SAC , SB SA ，SB SC ， SB SA ，BC SA ， SA 平面 SBC ，SA SC ，故三棱锥S ABC 的三棱条侧棱两两互相垂直，(2R)2 (2 3)2 (2..3)2 (2 3)2 36，即 4R 2 36，正三棱锥S ABC 外接球的表面积是36(4 ) 在四面体 S ABC 中，SA 平面ABCD .40ab 12 ac 6BAC120 ,SA AC2, AB 1,则该四面体的外接球的表面积为(D )A.11 B.7(6) (2R) b 2c 2 3 R 2 34(5)如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 ______________ (6) 已知某几何体的三视图如图所示，三视图是腰长为 何体外接球的体积为 _________________________ 1的等腰直角三角形和边长为 1的正方形，则该几解析:(4)在 ABC 中，BC 2 AC 2 AB 2 2ABBC cos120BC-7， ABC 的外接球直径为2r BCsin BAC,7 2 73 i 3，3，选D(5)三条侧棱两两生直,设三条侧棱长分别为a,b,c ( a,b,c，则bc 8 abc 24， a 3， b 4，c 2，(2R )2 b 2 29，S 4 R 2 29 ，C(2R)2 (2r)2 SA 24坐3类型二、垂面模型（一条直线垂直于一个平面）PADB图5b a 2 2R r r PP P PO O O CC AO iA A D ABB B图6图8PP P —O 2C BDO2B DOO OOiO iO i(2r)2 00, 00, 第二步：先算出小圆 0,的半径AO , r ，再算出棱锥的高 PO 1 h （也是圆锥的高）； 图7-1 图7-2 2R PA 2 (2r)2 ；②R 2 2.题设：如图6, 7, 8, P 的射影是 ABC 的外心 三棱锥P ABC 的底面 ABC 在圆锥的底上，顶点 三棱锥P ABC 的三条侧棱相等P 点也是圆锥的顶点解题步骤: 第一步：确定球心 0的位置，取 ABC 的外心01，则P,0O 三点共线; 1.题设：如图5, PA 平面ABC 解题步骤： 第一步：将 ABC 画在小圆面上， A 为小圆直径的一个端点，作小圆的直 径AD ，连接PD ，贝U PD 必过球心0 ; 第三步：利用勾股定理求三棱锥的外接球半径：① C 1 图8-2 图8-3第三步：勾股定理： 0A 2 01A 2 0102 R 2 （h R ）2 r 2，解出R 第二步: 01为 ABC 的外心，所以001 平面ABC ，算出小圆Q 的半 径01D r （三角形的外接圆直径算法：利用正弦定理，得 c 1 sinC 2r )，。

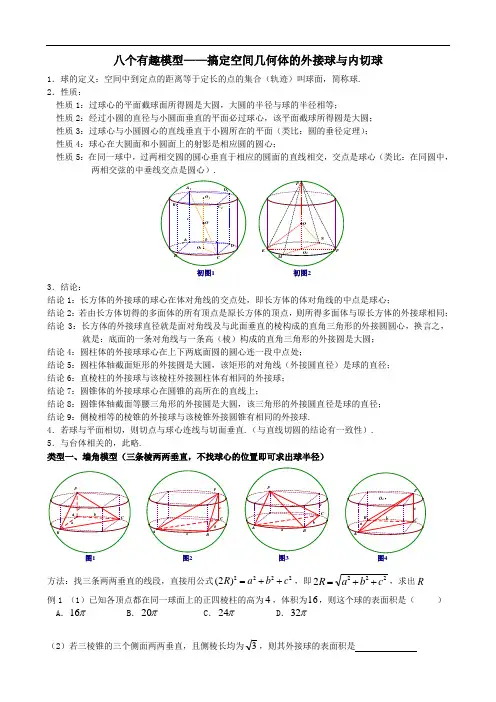
八个有趣模型——搞定空间几何体的外接球与内切球1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球. 2．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆； 性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）； 性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图2初图13．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同； 结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径； 结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球； 结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径； 结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.4．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）. 5．与台体相关的，此略.类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图2图3方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ ） A ．π16 B ．π20 C ．π24 D ．π32（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 . 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ， ∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ ）π11.A π7.B π310.C π340.D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是（6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为类型二、垂面模型（一条直线垂直于一个平面）(6)题图(3)题-1(引理）A(3)题-2（解答图）AC1．题设：如图5，⊥PA平面ABC解题步骤：第一步：将ABC∆画在小圆面上，A为小圆直径的一个端点，作小圆的直径AD，连接PD，则PD必过球心O；第二步：1O为ABC∆的外心，所以⊥1OO平面ABC，算出小圆1O的半径rDO=1（三角形的外接圆直径算法：利用正弦定理，得rCcBbAa2sinsinsin===），PAOO211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(rPAR+=⇔22)2(2rPAR+=；②2122OOrR+=⇔212OOrR+=2．题设：如图6，7，8，P的射影是ABC∆的外心⇔三棱锥ABCP-的三条侧棱相等⇔三棱锥ABCP-的底面ABC∆在圆锥的底上，顶点P点也是圆锥的顶点图6图7-1图7-2图8图8-1图8-2图8-3解题步骤：第一步：确定球心O的位置，取ABC∆的外心1O，则1,,OOP三点共线；第二步：先算出小圆1O的半径rAO=1，再算出棱锥的高hPO=1（也是圆锥的高）；第三步：勾股定理：21212OOAOOA+=⇒222)(rRhR+-=，解出R方法二：小圆直径参与构造大圆.例2 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )图5A ．π3B ．π2C ．316πD ．以上都不对类型三、切瓜模型（两个平面互相垂直）图9-1图9-2图9-3图9-41．题设：如图9-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=； 第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R2．如图9-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=3．如图9-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R4．如图9-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则 利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=例3 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 .俯视图侧视图正视图（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为 （3）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60，则该三棱锥外接球的体积为（ ） A ．π B.3π C. 4π D.43π（4）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（ ） ABCD类型四、汉堡模型（直棱柱的外接球、圆柱的外接球）图10-2题设：如图10-1，图10-2，图10-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ； 第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R例4 （1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为 （2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 .（3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π则直三棱柱111C B A ABC -的外接球的表面积为 .类型五、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图11)第一步：先画出如图所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ； 第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,； 第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+例5（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 （2）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为（3）在边长为32的菱形ABCD 中，60=∠BAD ，沿对角线BD 折成二面角C BD A --为120的四面体ABCD ，则此四面体的外接球表面积为(4)在四棱锥ABCD 中， 120=∠BDA ，150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --的平面角的大小为120，则此四面体的外接球的体积为类型六、对棱相等模型（补形为长方体） 题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =） 第一步：画出一个长方体，标出三组互为异面直线的对棱；图11第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=， 补充：abc abc abc V BCD A 31461=⨯-=- 第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R ，例如，正四面体的外接球半径可用此法，很有效.例6（1）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一 个截面如图，则图中三角形(正四面体的截面)的面积是 .（2）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）A ．433 B ．33 C ．43 D ．123（3）在三棱锥BCD A -中，,4,3,2======BD AC BC AD CD AB 则三棱锥BCD A -外接球的表面积为 .（4）如图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .（5）正四面体的各条棱长都为2，则该正面体外接球的体积为类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图12(1)题(4)题图B图13题设：90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（ ）A ．π12125 B ．π9125 C ．π6125 D ．π3125（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCD A -的外接球的表面积为 ．类型八、锥体的内切球问题1．题设：如图14，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高；第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r2．题设：如图15，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高； 第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径图14A图15D方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 棱长为a 的正四面体的内切球表面积是习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ） A.3 B.6 C.36 D.92． 三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 .3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .5． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .6． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .。

八个风趣模型——搞定空间几何体的外接球与内切球外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论 8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论 9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有同样的外接球 .3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各极点的距离均相等. （类比：与多边形的内切圆） .3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合 .5．基本方法：（1）结构三角形利用相像比和勾股定理；（2）体积切割是求内切球半径的通用做法（等体积法）.四、与台体有关的，此略.五、八大模型第一讲柱体背景的模型种类一、墙角模型（三条棱两两垂直，不找球心的地点即可求出球半径）P P Pcc cA b C C Cab bAAaB a B B图1-1图1-2图1-3PcB baAC图 1-4方法：找三条两两垂直的线段，直接用公式 (2R)2a2b2c2，即 2Ra2b2c2，求出 R例 1 （1）已知各极点都在同一球面上的正四棱柱的高为 4，体积为16，则这个球的表面积是（）A．B．C．D．16202432（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是（3）在正三棱锥S ABC中，且AM MN,若侧棱SA 2 3锥S ABC外接球的M 、N 分别是棱 SC、 BC 的中点，, 则正三棱S 表面积是.A C 解：引理：正三棱锥的对棱相互垂直 .H6取 AB,BC 的中点 D, E ，连结 AE,CD ， AE,CD 交于H，连结SH，则 H 是底面正三角形ABC 的中心，平面 ABC ， SH AB ，SH， AD BD， CD AB， AB平面 SCD ，AC BCAB SC ，同理： BC SA， AC SB，即正三S棱锥的对棱互垂直，M此题图如图（3）-2 ，AM MN ，SB// MN ，SB， AC SB ，A C AM SB平面 SAC ，N ，，，，BSASB SC SA BCSB SB SA(3)题-2（解答图）平面 SBC ， SA SC，SA故三棱锥 S ABC 的三棱条侧棱两两相互垂直，，即 4R236 ，正三棱锥S ABC外接(2R) 2(2 3)2(2 3)2(2 3)236球的表面积是36.（4）在四周体S ABC 中，SA平面 ABC ， BAC120 , SA AC 2, AB 1,则该四周体的外接球的表面积为（）1040C . D.33（5）假如三棱锥的三个侧面两两垂直，它们的面积分别为 6 、 4 、 3，那么它的外接球的表面积是（6）已知某几何体的三视图以下图，三视图是腰长为 1 的等腰直角三角形和边长为 1的正方形，则该几何体外接球的体积为种类二、对棱相等模型（补形为长方体）题设：三棱锥（即四周体）中，已知三组对棱分别相等，求外接球半径（AB CD ， AD BC ， AC BD ）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为a,b, c ，AD BC x ，AxDy y cz zxCa bB图 2-1AB CD y，AC BD z，列方程组，a 2b 2x2x2y 2z2b2c2y2(2R)2a2b2c2，c2a2z22增补：图 2-1中，V A BCD abc1 abc 41 abc .63第三步：根据墙角模型， 2R a 2b2c2x2y2z2，222222x y z，R x y z，求出R.R288例 2（1）以下列图所示三棱锥ABCD，此中AB CD 5,AC BD 6,AD BC 7,则该三棱锥外接球的表面积为.AB DC(1) 题图（2）在三棱锥A BCD中，AB CD 2， AD BC 3， AC BD 4，则三棱锥 A BCD外接球的表面积为.（3）正四周体的各条棱长都为2，则该正面体外接球的体积为（4）棱长为2的正四周体的四个极点都在同一个球面上，若过该球球心的一个截面以下列图，则图中三角形 ( 正四周体的截面 ) 的面积是.(4)题种类三、汉堡模型（直棱柱的外接球、圆柱的外接球）C1C1A1O2F A1O2B1B1OOC CA O 1E A O 1BB图 3-1图3-2C1A1FO2B1OCA O1EB图 3-3题设：如图 3-1 ，图 3-2 ，图 3-3, 直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面能够是随意三角形）第一步：确立球心O 的地点，O1是ABC的外心，则OO1平面 ABC；第二步：算出小圆 O1的半径 AO1r ，OO11AA11h（ AA1h 也是22圆柱的高）；第三步：勾股定理：2222h222h2，OA O1 A O1O R( 2)r Rr(2)解出 R.例 3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的极点都在同一个球面上，且该六棱柱的体积为9 ，底面周长为3，则8这个球的体积为（ 2）直三棱柱ABC A1 B1C1的各极点都在同一球面上，若AB AC AA12,BAC 120，则此球的表面积等于.（3）已知EAB所在的平面与矩形ABCD 所在的平面相互垂直， EA EB 3, AD 2, AEB 60 ，则多面体E ABCD 的外接球的表面积为.（ 4）在直三棱柱ABC A1 B1C1中， AB 4, AC 6, A, AA1 4 ，则直3三棱柱 ABC A1 B1C1的外接球的表面积为.第二讲锥体背景的模型种类四、切瓜模型（两个大小圆面相互垂直且交于小圆直径——正弦定理求大圆直径是通法）PPPPO O OA O1A O11A AC O C C CB B B B图 4-1图4-2图 4-3图 4-41．如图 4-1 ，平面PAC平面 ABC ，且 AB BC （即 AC 为小圆的直径），且 P 的射影是 ABC 的外心三棱锥 P ABC 的三条侧棱相等三棱 P ABC 的底面 ABC 在圆锥的底上，极点 P 点解题步骤：第一步：确立球心 O 的地点，取 ABC 的外心O1，则P,O, O1三点共线；第二步：先算出小圆 O1的半径 AO1r，再算出棱锥的高 PO1h （也是圆锥的高）；第三步：勾股定理： OA2O1 A2O1O 2R2(h R)2r2，解出R；事实上， ACP 的外接圆就是大圆，直接用正弦定理也可求解出 R.2．如图 4-2 ，平面PAC平面 ABC ，且 AB BC （即 AC 为小圆的直径），且 PA AC ，则利用勾股定理求三棱锥的外接球半径：①(2R)2PA2(2r ) 22R PA2(2r ) 2；② R2r 2OO12R r 2OO123．如图 4-3 ，平面PAC平面 ABC ，且 AB BC （即 AC 为小圆的直径）OC 2O1C 2O1O 2R 2r 2O1O 2AC 2 R2O1O 24．题设：如图 4-4 ，平面PAC平面ABC，且AB BC（即AC为小圆的直径）第一步：易知球心 O 必是 PAC 的外心，即 PAC 的外接圆是大圆，先求出小圆的直径 AC 2r ；第二步：在PAC 中，可依据正弦定理ab csin A sin B 2R ，求sin C 出 R .例 4 （1）正四棱锥的极点都在同一球面上，若该棱锥的高为 1，底面边长为 2 3 ，则该球的表面积为.（2）正四棱锥S ABCD的底面边长和各侧棱长都为2，各极点都在同一球面上，则此球体积为（3）一个正三棱锥的四个极点都在半径为1的球面上，此中底面的三个极点在该球的一个大圆上，则该正三棱锥的体积是（）A．3 3B．3C． 3D． 3 43412（4）在三棱锥P ABC 中，PA PB PC 3 ,侧棱PA与底面ABC所成的角为 60，则该三棱锥外接球的体积为（）A． B. C.43D. 43（5）已知三棱锥S ABC的全部极点都在球O的求面上, ABC是边长为1的正三角形 , SC为球O的直径 , 且SC 2 ，则此棱锥的体积为（）A．2B．3C．2 663D．22种类五、垂面模型（一条直线垂直于一个平面）1．题设：如图 5，PA平面ABC，求外接球半径 .POCA O1DB图 5解题步骤：第一步：将ABC 画在小圆面上， A 为小圆直径的一个端点，作小圆的直径 AD ，连结 PD ，则 PD 必过球心 O ；第二步： O1为ABC的外心，因此 OO1平面ABC，算出小圆 O1的半径 O1D r（三角形的外接圆直径算法：利用正弦定理，得a b c2r ）， OO11 PA；sin A sin B sin C2第三步：利用勾股定理求三棱锥的外接球半径：①(2R)2PA2(2r ) 22R PA2(2r ) 2；② R2r 2OO12Rr 2OO12.2．题设：如图 5-1至 5-8 这七个图形，P的射影是 ABC 的外心三棱锥 P ABC 的三条侧棱相等三棱锥 P ABC 的底面 ABC 在圆锥的底上，极点 P 点也是圆锥的极点 .PPPO O OC C CO1O1AO1A ABB B图 5-1图5-2图 5-3 POCA O1DB图 5-4PP PAAAO 2BCO 2O 2DBCDBO OO图 5-6图5-8解题步骤：第一步：确立球心点共线；第二步：先算出小圆（也是圆锥的高）；第三步：勾股定理：O1的半径OA2O 1 A2ABC的外心 O 1，则 P,O, O 1 三r，再算出棱锥的高 PO 1hR 2 (h R)2 r 2，解出 R方法二：小圆直径参加结构大圆，用正弦定理求大圆直径得球的直径 .例 5 一个几何体的三视图以下图，则该几何体外接球的表面积为 ( )A ． 3B ． 222 22C ．162 23正视图侧视图D ．以上都不对俯视图AO 1O 1O 2O 的地点，取 图5-7第三讲二面角背景的模型种类六、折叠模型题设：两个全等三角形或等腰三角形拼在一同，或菱形折叠(如图 6)A'OH 2DH 1A E CB图6第一步：先画出如图 6 所示的图形，将找出 BCD和 ABD的外心H1和H2；第二步：过 H 1和 H 2分别作平面BCD和平面垂线的交点即为球心 O ，连结OE , OC；第三步：解OEH 1，算出OH 1，在BCD 画在小圆上，A BD 的垂线，两222Rt OCH1 中，勾股定理：注：易知 O, H 1 , E, H 2四点共面且四点共圆，证略.17例 6（1）三棱锥P ABC中，平面PAC平面ABC，△PAC和△ABC 均为边长为 2 的正三角形，则三棱锥 P ABC 外接球的半径为.（2）在直角梯形ABCD中，AB // CD，A 90，C 45，AB AD 1，沿对角线 BD 折成四周体 A BCD ，使平面 A BD 平面 BCD ，若四周体 A BCD 的极点在同一个球面上，则该项球的表面积为（3）在四周体S ABC中，AB BC，AB BC 2 ，二面角S AC B 的余弦值为33，则四周体 S ABC 的外接球表面积为（4）在边长为2 3的菱形ABCD中，BAD 60，沿对角线BD折成二面角 A BD C 为120的四周体 ABCD ，则此四周体的外接球表面积为（5）在四棱锥ABCD中，BDA 120，BDC 150，AD BD 2，CD 3 ，二面角 A BD C 的平面角的大小为120，则此四周体的外接球的体积为种类七、两直角三角形拼接在一同 ( 斜边同样 , 也可看作矩形沿对角线折起所得三棱锥 ) 模型PBCOA图 7题设：如图 7，APB ACB 90，求三棱锥P ABC外接球半径（剖析：取公共的斜边的中点O，连结OP,OC，则OA OB OC OP 1AB ，O为三棱锥P ABC外接球球心，而后在2OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小没关，只需不是平角球半径都为定值 .例 7（1）在矩形ABCD中，AB 4，BC 3，沿AC将矩形ABCD折成一个直二面角 B AC D ，则四周体 ABCD 的外接球的体积为（）A． 125B． 125C． 125 1296 D． 1253（2）在矩形连结 AC为ABCD 中， AB 2 ，BC 3 ，沿 BD 将矩形 ABCD 折叠，，所得三棱锥 A BCD的外接球的表面积．第四讲多面体的内切球问题模型种类八、锥体的内切球问题1．题设：如图 8-1 ，三棱锥P ABC上正三棱锥，求其内切球的半径 .第一步：先现出内切球的截面图， E, H 分别是两个三角形的外心；PEOA CDHB图 8-1第二步：求DH 1 BD ，PO PH r，PD是侧面ABP的高；3第三步：由POE 相像于PDH ，成立等式：OE PO，解出rDH PDP2．题设：如图 8-2 ，四棱锥P ABC是正GO四棱锥，求其内切球的半径ADBHFC 图8-2第一步：先现出内切球的截面图，P,O, H 三点共线；第二步：求 FH1BC，PO PH r ， PF 是侧面 PCD 的高；2第三步：由POG 相像于PFH，成立等式：OG PO，解出HF PF3．题设：三棱锥P ABC是随意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面组成的四个三棱锥的体积之和相等第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r，建立等式：V P ABC V O ABC V O PAB V O PAC V O PBCV P ABC 11111r S ABC r S PAB r S PAC r S PBC r( S ABC S PAB S PAC S PBC ) 33333第三步：解出 r3V P ABCSO ABC SO PABSO PACSO PBC例 8 （1）棱长为a的正四周体的内切球表面积是（2）正四棱锥S ABCD 的底面边长为 2 ，侧棱长为 3 ，则其内切球的半径为（ 3）三棱锥 P ABC 中，底面 ABC 是边长为 2 的正三角形， PA 底面 ABC ， PA 2 ，则该三棱锥的内切球半径为习题：1．若三棱锥S ABC的三条侧棱两两垂直，且SA 2，SB SC 4，则该三棱锥的外接球半径为（）A.3B.6C.36D. 92．三棱锥S ABC中，侧棱SA平面ABC，底面ABC是边长为3的正三角形， SA 2 3 ，则该三棱锥的外接球体积等于.3．正三棱锥S ABC中，底面ABC是边长为 3 的正三角形，侧棱长为 2 ，则该三棱锥的外接球体积等于.4．三棱锥P ABC中，平面PAC平面ABC，△PAC边长为2的正三角形， AB BC，则三棱锥 P ABC外接球的半径为.5．三棱锥P ABC中，平面PAC平面ABC，AC 2，PA PC 3，AB BC，则三棱锥P ABC外接球的半径为.6．三棱锥P ABC中，平面PAC平面ABC，AC 2，PA PC，AB BC，则三棱锥P ABC外接球的半径为.。

八个有趣模型——搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章，我如获至宝.为有了教学的实施，我以付老师的文章主基石、框架，增加了我个人的理解及例题，形成此文，仍用文原名，与各位同行分享.不当之处，敬请大家批评指正.一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）. 四、与台体相关的，此略. 五、八大模型第一讲 柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ ） A ．π16 B ．π20C ．π24D ．π32 （2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 （3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1， 取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ， 则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直， 本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理）AC(3)题-2（解答图）AC（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ ）π11.A π7.B π310.C π340.D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 （6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为类型二、对棱相等模型（补形为长方体） 题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =） 第一步：画出一个长方体，标出三组互为异面直线的对棱； 第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=， 补充：图2-1中，abc abc abc V BCD A 31461=⨯-=-. 第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .(1)题图B(6)题图图2-1（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 . （3）正四面体的各条棱长都为2，则该正面体外接球的体积为（4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ； 第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R .例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为 （2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 .（3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .第二讲 锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-3图4-41．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R ；事实上，ACP ∆的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则 利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=； 第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 .（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为 （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ）A ．433 B ．33 C ．43 D ．123（4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60，则该三棱锥外接球的体积为（ ） A ．π B.3π C. 4π D.43π （5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（ ）ABD类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=； 第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=.图52．题设：如图5-1至5-8这七个图形，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( ) A ．π3 B ．π2 C ．316πD ．以上都不对俯视图侧视图正视图第三讲 二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)图6第一步：先画出如图6所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ； 第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,； 第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 .（2）在直角梯形ABCD 中，CD AB //， 90=∠A ，45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为（4）在边长为32的菱形ABCD 中，60=∠BAD ，沿对角线BD 折成二面角C BD A --为120的四面体ABCD ，则此四面体的外接球表面积为（5）在四棱锥ABCD 中， 120=∠BDA ， 150=∠BDC ，2==BD AD ，3=CD ，二面角C BD A -- 的平面角的大小为120，则此四面体的外接球的体积为类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（ ）A ．π12125 B ．π9125 C ．π6125 D ．π3125（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCD A -的外接球的表面积为 ．第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高；第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高； 第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出图8-1A图8-23．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是（2）正四棱锥ABCD S -的底面边长为2，侧棱长为3，则其内切球的半径为（3）三棱锥ABC P -中，底面ABC ∆是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则该三棱锥的内切球半径为习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ） A.3 B.6 C.36 D.9 2． 三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 . 3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .5． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 . 6． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .。

高中物理丨外接圆与内切圆解题方法,8大模型高中物理丨外接圆与内切圆解题方法，8大模型1. 解题方法在解决外接圆与内切圆相关的物理问题时，可以采用以下步骤和方法：步骤1. 阅读问题并理解题意。

2. 绘制问题所描述的图形，包括外接圆、内切圆和其他相关元素。

3. 根据已知条件，确定问题中所涉及的物理量的数值。

4. 分析问题，找出与外接圆与内切圆相关的物理原理和定律。

5. 运用物理原理和定律，建立相应的数学方程。

6. 求解方程并计算出所需的未知物理量。

7. 总结并回答问题，给出相应的解答和结论。

方法在解题过程中，可以采用以下方法：1. 几何法：利用几何关系来解决问题，例如利用相似三角形或圆上的弧长等关系。

几何法：利用几何关系来解决问题，例如利用相似三角形或圆上的弧长等关系。

2. 三角函数法：利用三角函数的性质来解决问题，例如正弦、余弦、正切等。

三角函数法：利用三角函数的性质来解决问题，例如正弦、余弦、正切等。

3. 向量法：将问题转化为向量的运算，利用向量的性质和运算来解决问题。

向量法：将问题转化为向量的运算，利用向量的性质和运算来解决问题。

4. 能量守恒法：利用能量守恒的原理，将问题转化为能量的转化和平衡问题。

能量守恒法：利用能量守恒的原理，将问题转化为能量的转化和平衡问题。

5. 牛顿定律法：利用牛顿定律和相关的力学原理来解决问题，例如受力分析、力的平衡等。

牛顿定律法：利用牛顿定律和相关的力学原理来解决问题，例如受力分析、力的平衡等。

6. 动量守恒法：利用动量守恒原理解决问题，例如碰撞问题中的动量守恒。

动量守恒法：利用动量守恒原理解决问题，例如碰撞问题中的动量守恒。

7. 电路分析法：将问题转化为电路的分析和计算，利用电路定律和电路分析方法来解决问题。

电路分析法：将问题转化为电路的分析和计算，利用电路定律和电路分析方法来解决问题。

8. 数学分析法：利用数学分析方法和相关的数学工具解决问题，例如微积分、方程求解等。

八个有趣模型——搞定空间几何体的外接球与内切球一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正弦定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）.四、与台体相关的，此略.五、八大模型第一讲 柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32 解： 162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ； （2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 π9 解：933342=++=R ，ππ942==R S ；（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1， 取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ， 则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ， ∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36.(3)题-1(引理）AC(3)题-2（解答图）AC（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D 解：在ABC ∆中，7120cos 2222=⋅⋅-+=BC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ，∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是 解：由已知得三条侧棱两两垂直，设三条侧棱长分别为c b a ,,（+∈R c b a ,,），则⎪⎩⎪⎨⎧===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ， （6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为解：3)2(2222=++=c b a R ，432=R ，23=Rπππ2383334343=⋅==R V 球，类型二、对棱相等模型（补形为长方体） 题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =） 第一步：画出一个长方体，标出三组互为异面直线的对棱； 第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=， 补充：图2-1中，abc abc abc V BCD A 31461=⨯-=-. (6)题图（6）题直观图P图2-1第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .思考：如何求棱长为a 的正四面体体积，如何求其外接球体积？例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解：对棱相等，补形为长方体，如图2-1，设长宽高分别为c b a ,,，110493625)(2222=++=++c b a ，55222=++c b a ，5542=R ，π55=S(1)题图B（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 .π229 解：如图2-1，设补形为长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ，229222=++c b a ，22942=R ，π229=S （3）正四面体的各条棱长都为2，则该正面体外接球的体积为 （3）解答题解：正四面体对棱相等的模式，放入正方体中，32=R ，23=R ，ππ2383334=⋅=V （4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解：如解答图，将正四面体放入正方体中，截面为1PCO ∆，面积是2.类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ； 第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为 解：设正六边形边长为a ，正六棱柱的高为h ，底面外接圆的半径为r ，则21=a ，正六棱柱的底面积为833)21(4362=⋅⋅=S ，89833===h Sh V 柱，∴3=h ，4)3(14222=+=R 也可1)21()23(222=+=R ），1=R ，球的体积为34π=球V ； （2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 .解：32=BC ，4120sin 322==r ，2=r ，5=R ，π20=S ； （3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .π16 解：折叠型，法一：EAB ∆的外接圆半径为31=r ，11=OO ，231=+=R ；法二：231=M O ，21322==D O r ，4413432=+=R ，2=R ，π16=表S ； 法三：补形为直三棱柱，可改变直三棱柱的放置方式为立式，算法可同上，略.换一种方式，通过算圆柱的轴截面的对角线长来求球的直径：162)32()2(222=+=R ，π16=表S ；（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解：法一：282164236162=⋅⋅⋅-+=BC ，72=BC ，37423722==r ，372=r ， 3404328)2(2122=+=+=AA r R ，π3160=表S ；法二：求圆柱的轴截面的对角线长得球直径，此略.第二讲 锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-31．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；（3）题第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R ；事实上，ACP ∆的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则 利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径） 21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=； 第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 . 解：法一：由正弦定理（用大圆求外接球直径）；法二：找球心联合勾股定理，72=R ，ππ4942==R S ；（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为 解：方法一：找球心的位置，易知1=r ，1=h ，r h =，故球心在正方形的中心ABCD 处，1=R ，34π=V 方法二：大圆是轴截面所的外接圆，即大圆是SAC ∆的外接圆，此处特殊，SAC Rt ∆的斜边是球半径，22=R ，1=R ，34π=V . （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（ ） A ．433 B ．33 C ．43 D ．123解：高1==R h ，底面外接圆的半径为1=R ，直径为22=R ，设底面边长为a ，则260sin 2==aR ，3=a ，433432==a S ，三棱锥的体积为4331==Sh V ； （4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为60，则该三棱锥外接球的体积为（ ） A ．π B.3π C. 4π D.43π 解：选D ，由线面角的知识，得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上，在圆锥中求解，1=R ； （5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（ ）AA．6 BC．3 D．2解：36)33(12221=-=-=r R OO ，362=h ，62362433131=⋅⋅==Sh V 球 类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ； 第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=； 第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=.2．题设：如图5-1至5-8这七个图形，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的 三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的 顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )C A ．π3 B ．π2 C ．316πD ．以上都不对解：选C ， 法一：（勾股定理）利用球心的位置求球半径，球心在圆锥的高线上，221)3(R R =+-,32=R ,ππ31642==R S ；法二：（大圆法求外接球直径）如图，球心在圆锥的高线上，故圆锥的轴截面三角形PMN 的外接圆是大圆，于是3460sin 22==R ，下略；第三讲 二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步：先画出如图6所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ； 第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,； 第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 . 解：如图，3460sin 22221===r r ，3221==r r ，312=H O ， 35343121222=+=+=r H O R ，315=R ； 法二：312=H O ，311=H O ，1=AH ， 352121222=++==O O H O AH AO R ，315=R ； （2）在直角梯形ABCD 中，CD AB //， 90=∠A ，45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解：如图，易知球心在BC 的中点处，π4=表S ；（1）题（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为 π6 解：如图，法一：33)2cos(cos 211-=+∠=∠πO OO B SO ， 33sin 21=∠O OO ，36cos 21=∠O OO ，22cos 21211=∠=O OO O O OO ，232112=+=R ，ππ642==R S ； 法二：延长1BO 到D 使111r BO DO ==，由余弦定理得6=SB ，2=SD ，大圆直径为62==SB R ；（4）在边长为32的菱形ABCD 中， 60=∠BAD ，沿对角线BD 折成二面角C BD A --为120的四面体ABCD ，则此四面体的外接球表面积为 π28解：如图，取BD 的中点M ，ABD ∆和CBD ∆的外接圆半径为221==r r ，ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离（弦心距）为121==d d ， 法一：四边形21MO OO 的外接圆直径2=OM ，7=R ，π28=S ；法二：31=OO ，7=R ；法三：作出CBD ∆的外接圆直径CE ,则3==CM AM ， 4=CE ，1=ME ，7=AE ，33=AC ，72147227167cos -=⋅⋅-+=∠AEC ，7233sin =∠AEC ，72723333sin 2==∠=AEC AC R ，7=R ；(4)题图(5)在四棱锥ABCD 中， 120=∠BDA ，150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --的平面角的大小为120，则此四面体的外接球的体积为 解：如图，过两小圆圆心作相应小圆所在平面的垂线确定球心，→抽象化(5)题解答图-2(5)题解答图-11B32=AB ，22=r ，弦心距32=M O ，13=BC ，131=r ，弦心距321=M O ， ∴2121=O O ，72120sin 21==O O OM ，法一：∴292222=+==OM MD OD R ，29=R ，∴329116π=球V ； 法二：2522222=-=M O OM OO ，∴29222222=+==OO r OD R ，29=R ，∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（ ）A ．π12125 B ．π9125 C ．π6125 D ．π3125解：（1）52==AC R ，25=R ，6125812534343πππ=⋅==R V ，选C（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCDA -的外接球的表面积为 ．解：BD 的中点是球心O ，132==BD R ，ππ1342==R S .第四讲 多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高；第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高； 第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等 第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是 62a π，解：设正四面体内切球的半径为r ，将正四面体放入棱长为2a的正方体中（即补形为正方体），如图，则2622313133a a V V ABCP =⋅==-正方体， 又 r a r a Sr V ABCP 223343314314=⋅⋅⋅=⋅=-，(1)题D图8-1A图8-2∴263332a r a =，62a r =，∴内切球的表面积为6422a r S ππ==表（注：还有别的方法，此略） （2）正四棱锥ABCD S -的底面边长为2，侧棱长为37解：如图，正四棱锥ABCD S -的高7=h ，正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ，正四棱锥ABCD S -的表面积为284+=表S ，正四棱锥ABCD S -的体积为r r S V ABCDS ⋅+==-328431表， ∴3743284=⋅+r ， 771427)122(7221728474-=-=+=+=r （3）三棱锥ABC P -中，底面ABC ∆是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则32解：如图，3=∆ABC S ，2==∆∆ACP ABP S S ，7=∆BCP S ，743++=表S ，三棱锥ABC P -的体积为332=-ABC P V ， 另一表达体积的方式是r r S V ABC P ⋅++==-347331表， ∴3323473=⋅++r ，∴47332++=r习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（ ） A.3 B.6 C.36 D.9 解：【A 】616164)2(2=++=R ，3=R【三棱锥有一侧棱垂直于底面，且底面是直角三角形】【共两种】2． 三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA ，则该三棱锥的外接球体积等于 .332π(2)题(3)题B解：260sin 32==r ，16124)2(2=+=R ，42=R ，2=R ，外接球体积332834ππ=⋅ 【外心法（加中垂线）找球心；正弦定理求球小圆半径】3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解：ABC ∆外接圆的半径为 ，三棱锥ABC S -的直径为3460sin 22==R ，外接球半径32=R ，或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ=⋅==R V ， 4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：PAC ∆的外接圆是大圆，3460sin 22==R ，32=R ， 5． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ，81216)97(1sin 22⋅=-=∠P ，924sin =∠P ，42922992422===R ，829=R 6． 三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .解：AC 是公共的斜边，AC 的中点是球心O ，球半径为1=R。

八个有趣模型搞定外接球内切球问题在立体几何的学习中，外接球和内切球问题常常让同学们感到头疼。

但别担心，今天我要给大家介绍八个有趣的模型，帮助大家轻松搞定这类难题！模型一：长方体模型长方体的体对角线就是其外接球的直径。

假设长方体的长宽高分别为 a、b、c，那么外接球的半径 R 就等于√（a²＋ b²＋ c²) ／ 2 。

这个模型理解起来相对简单，我们通过长方体的三条棱就能快速求出外接球的半径。

模型二：正方体模型对于正方体，外接球的直径等于正方体的体对角线。

设正方体的棱长为 a，那么外接球的半径 R 就是√3a ／ 2 。

内切球的半径 r 则等于 a／ 2 。

模型三：正四面体模型正四面体的外接球和内切球问题比较特殊。

我们先求出正四面体的棱长 a，然后外接球的半径 R 可以通过公式 R ＝√6a ／ 4 得到，内切球的半径 r ＝√6a ／ 12 。

模型四：直三棱柱模型如果直三棱柱的底面是直角三角形，且侧棱长为 l，底面直角三角形的两条直角边分别为 a、b，那么外接球的半径 R 可以通过公式 R ＝√（a²＋ b²＋ l²) ／ 2 求出。

模型五：正三棱柱模型正三棱柱的外接球问题稍微复杂一些。

我们需要先求出底面正三角形的外接圆半径 r，然后再根据侧棱长 l 来计算外接球的半径 R。

模型六：圆锥模型圆锥的外接球问题要分两种情况。

当圆锥的轴截面是等边三角形时，外接球的半径 R 可以通过一定的比例关系求出；当圆锥的轴截面不是等边三角形时，我们需要利用勾股定理来计算外接球的半径。

模型七：棱锥模型对于一般的棱锥，如果能够找到一个面是正多边形，并且这个正多边形所在的平面能够垂直于棱锥的高，那么我们就可以利用这个面的外接圆半径和棱锥的高来求出外接球的半径。

模型八：球与多面体的组合模型在这种模型中，我们要善于分析球与多面体的位置关系，找到关键的几何量，然后运用前面介绍的方法来求解外接球的半径。

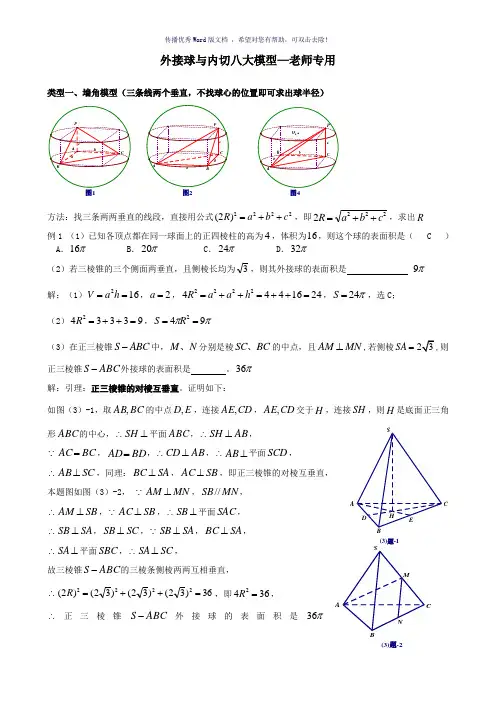
外接球与内切八大模型—老师专用类型一、墙角模型（三条线两个垂直，不找球心的位置即可求出球半径）图2方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32 （2）若三棱锥的三个侧面两垂直，且侧棱长均为3，则其外接球的表面积是 π9 解：（1）162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ； （2）933342=++=R ，ππ942==R S（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =则正三棱锥ABC S -外接球的表面积是 。

π36 解：引理：正三棱锥的对棱互垂直。

证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36(3)题-1A(3)题-2A（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是（6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为 解析：（4）在ABC ∆中，7120cos 2222=⋅⋅-+=BC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ， ∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）三条侧棱两两生直，设三条侧棱长分别为c b a ,,（+∈R c b a ,,），则⎪⎩⎪⎨⎧===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ， （6）3)2(2222=++=c b a R ，432=R ，23=Rπππ2383334343=⋅==R V ，类型二、垂面模型（一条直线垂直于一个平面） 1．题设：如图5，⊥PA 平面ABC 解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直 径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r CcB b A a 2sin sin sin ===），PA OO 211=；图5ADPO 1OCBAP第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=2．题设：如图6，7，8，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点图6PADO 1OCB图7-1PAO 1O CB图7-2PAO 1O CB图8PAO 1OCB图8-1DPOO 2ABC图8-2POO 2ABC图8-3DPOO 2AB解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）； 第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆。

十种求外接球与内切球模型【必备知识点】模型一:墙角模型墙角模型是三棱锥有一条侧棱垂直于底面且底面是直角三角形模型,用构造法(构造长方体)解决.外接球的直径等于长方体的体对角线长.使用范围:3组或3条棱两两垂直;或可在长方体中画出该图且各顶点与长方体的顶点重合推导过程:长方体的体对角线就是外接球的直径公式:找三条两两垂直的线段,直接用公式(2R)2=a2+b2+c2,即2R=a2+b2+c2,求出R.例1.四面体ABCD的每个顶点都在球O的球面上，AB,AC,AD两两垂直，且AB=3，AC=2，AD= 3，则球O的表面积为( )A.64πB.16πC.4πD.π【答案】B【详解】四面体ABCD的外接球O即为以AB,AC,AD为长、宽、高的长方体的外接球，∴球O的外接球半径R=12AB2+AC2+AD2=2，∴球O的表面积S=4πR2=16π.故选：B.例2.在边长为2的正方形ABCD中，E，F分别为线段AB，BC的中点，连接DE，DF，EF，将△ADE，△CDF，△BEF分别沿DE，DF，EF折起，使A,B,C三点重合，得到三棱锥O-DEF，则该三棱锥外接球的表面积为( )A.3πB.6πC.6πD.24π【答案】C【详解】解：在正方形ABCD中，AD⊥AE，CD⊥CF，BE⊥BF，折起后OD，OE，OF两两垂直，故该三棱锥外接球即以OD，OE，OF为棱的长方体外接球.因为OD=2，OE=1，OF=1，所以2R=OD2+OE2+OF2=6，所以R=62，所以该三棱锥外接球的表面积为S表=4πR2=6π，故选：C.例3.已知P，A，B，C为球O的球面上的四个点，若PA⊥平面ABC，AC⊥BC，PA=1，AC=BC= 2，则球O的表面积为( )A.2πB.3πC.4πD.5π【答案】D【详解】解：在三棱锥P-ABC中，PA⊥平面ABC，AC⊥BC，故可将三棱锥P-ABC补形成如图所示的长方体.若P，A，B，C为球O的球面上的四个点，则该长方体的各顶点亦在球O的球面上.设球O的半经为R，则该长方体的体对角线长为2R，即2R=PA2+AC2+BC2=5，从而有S球O=4πR2=π(2R)2=5π，故选：D.例4.如图，在矩形ABCD中，AB=2,BC=2，E为BC中点，把△ABE和△CDE分别沿AE,DE折起，使点B与点C重合于点P，若三棱锥P-ADE的四个顶点都在球O的球面上，则球O的表面积为( )A.3πB.4πC.5πD.9π【答案】C【详解】依题意，PE⊥PA,PE⊥PD，PA∩PD=P，PA,PD⊂平面PAD，则PE⊥平面PAD，又PA=PD=2,AD=2，即有PA2+PD2=AD2，则PA⊥PD，因此可将三棱锥P-ADE补形成以PE,PA,PD为相邻三条棱的长方体，若三棱锥P-ADE的四个顶点都在球O的球面上，则该长方体的各顶点亦在球O的球面上，设球O的半径为R，则该长方体的体对角线长为2R，即2R=PE2+PA2+PD2=5，所以球O的表面积为S=4πR2=π(2R)2=5π.故选：C例5.在正三棱锥S -ABC 中, 点M 是SC 的中点,且AM ⊥SB ,底面边长AB =22,则正三棱锥S -ABC 的外接球的表面积为()A.6πB.12πC.32πD.36π【答案】B【详解】因为三棱锥S -ABC 为正三棱锥, 所以SB ⊥AC ,又AM ⊥SB ,AC ∩AM =A ,AC ,AM ⊂平面SAC , 所以SB ⊥平面SAC,所以SB ⊥SA ,SB ⊥SC ,同理SA ⊥SC ,即SA ,SB ,SC 三线两两垂直,且AB =22,所以SA =SB =SC =2,所以(2R )2=3×22=12,所以球的表面积S =4πR 2=12π,故选 B .例6.将一个边长为4的正三角形ABC 沿其中线BD 折成一个直二面角，则所得三棱锥A -BCD 的外接球的体积为_________.【答案】2053π【详解】由题意得：AB =BC =4，AD =CD =2，BD ⊥AD ，CD ⊥BD ，即BD ⊥平面ADC ；∵二面角A -BD -C 为直二面角，∴AD ⊥CD ，则三棱锥A -BCD 的外接球即为以BD ,CD ,AD 为长宽高的长方体的外接球，又BD =16-4=23，∴三棱锥A -BCD 的外接球半径R =12AD 2+CD 2+BD 2=124+4+12=5，∴三棱锥A -BCD 的外接球体积V =43πR 3=2053π.故答案为：2053π.例7.在正三棱锥S -ABC 中,M ,N 分别是棱SC ,BC 的中点,且AM ⊥MN , 若侧棱SA =23,则正三棱锥S -ABC 外接球的表面积是_________.【答案】36π【详解】∵AM ⊥MN ,SB ⎳MN ,∴AM ⊥SB ,∵AC ⊥SB ,∴SB ⊥平面SAC,∴SB ⊥SA ,SB ⊥SC ,∵SB ⊥SA ,BC ⊥SA ,∴SA ⊥平面SBC ,∴SA ⊥SC ,故三棱锥S -ABC 的三棱条侧棱两两互相垂直,∴(2R )2=(23)2+(23)2+(23)2=36,即4R 2=36,∴正三棱锥S -ABC 外接球的表面积是36π.例8.在长方体ABCD -A 1B 1C 1D 1中,底面ABCD 是边长为32的正方形,AA 1=3,E 是线段A 1B 1上一点, 若二面角A -BD -E 的正切值为3,则三棱锥A -A 1D 1E 外接球的表面积为_________.【答案】35π【详解】过点E 作EF ⎳AA 1交AB 于F ,过F 作FG ⊥BD 于G ,连接EG ,则∠EGF 为二面角A -BD -E 的平面角,∵tan ∠EGF =3,∴EF FG=3,∵EF =AA 1=3,∴FG =1,则BF =2=B 1E , ∴A 1E =22,则三棱锥A -A 1D 1E 外接球的直径为8+9+18=35,因此三棱锥A -A 1D 1E 外接球的表面积S =35π.模型二:对棱相等模型使用范围:对棱相等的三棱锥推导过程:通过对棱相等,可以将其补全为长方体,补全的长方体体对角线为外接球直径,设长方体的长宽高为别为a ,b ,cAD =BC AB =CD AC =BD ⇒a 2+b 2=BC 2=λ2b 2+c 2=AC 2=μ2c 2+a 2=AB 2=k 2⇒a 2+b 2+c 2=λ2+μ2+k 22⇒R =λ2+μ2+k 28V A -BCD =abc -16abc ×4=13abc 例1.如图，在△ABC 中，AB =25,BC =210,AC=213，D ，E ，F 分别为三边中点，将△BDE,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起，使A ，B ，C 重合为点P ，则三棱锥P -DEF 的外接球表面积为( )A.72πB.7143πC.14πD.56π【答案】C【详解】由题意可知，PE =DF =10,PF =DE =13,PD =EF =5，即三棱锥P-DEF 的对棱相等，先将该三棱锥补充成长方体，如图所示：设FH =x ,HD =y ,HP =z ，则x 2+y 2=10,y 2+z 2=5,x 2+z 2=13，所以x 2+y 2+z 2=14，于是三棱锥P -DEF 的外接球直径为14，半径为142，所以该三棱锥外接球的表面积为：4π⋅1422=14π.故选：C .例2.在△ABC 中，AB =AC =2，cos A =34，将△ABC 绕BC 旋转至△BCD 的位置，使得AD =2，如图所示，则三棱锥D -ABC 外接球的体积为_____________．【答案】556π【详解】在△ABC 中，由余弦定理得BC 2=22+22-2×2×2×34=2，所以BC =2．在三棱锥D -ABC 中，AB =AC =DB =DC =2，AD =BC =2．将三棱锥D -ABC 放入长方体，设长方体的长、宽、高分别为a ，b ，c ，棱锥D -ABC 外接球的半径为R ，则a 2+b 2=4,b 2+c 2=4,a 2+c 2=2，所以a 2+b 2+c 2=5，所以R =12a 2+b 2+c 2=52，从而三棱锥D -ABC 外接球的体积V =43πR 3=556π.故答案为：556π例3.已知三棱锥P -ABC 的每条侧棱与它所对的底面边长相等，且PA =32，PB =PC =5，则该三棱锥的外接球的表面积为______．【答案】34π【详解】解：根据题意，三棱锥P -ABC 可以嵌入一个长方体内，且三棱锥的每条棱均是长方体的面对角线，设长方体交于一个顶点的三条棱长为a ，b ，c ，如图所示，则a 2+b 2=PA 2=18，a 2+c 2=PB 2=25，b 2+c 2=PC 2=25，解得a =3，b =3，c =4．所以该三棱锥的外接球的半径为R =a 2+b 2+c 22=32+32+422=342，所以该三棱锥的外接球的表面积为S =4πR 2=4π×342 2=34π．故答案为：34π例4.已知四面体ABCD 的棱长满足AB =AC =BD =CD =2，BC =AD =1，现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中，使得四面体ABCD 可以在圆锥中任意转动，则圆锥侧面积的最小值为________．【答案】274π【详解】根据题意，只需四面体ABCD 在圆锥的内切球内，下面求四面体ABCD 的外接球半径．如图所示，将四面体放入长方体中，设长方体的长宽高分别为a ,b ,c ，则a 2+b 2=4，a 2+c 2=4，b 2+c 2=1，故4R 2=a 2+b 2+c 2=92，可得四面体ABCD 的外接球半径为324．当圆锥的侧面积最小时，该圆锥的内切球即四面体ABCD 的外接球，则此时圆锥的内切球的半径为R =324，底面圆的半径为r =324×3=364，母线长为324×2=322，所以侧面积为S =π×364×362=27π4.故答案为：27π4.例5.在三棱锥P -ABC 中，PA =BC =25，PB =AC =13，AB =PC =5，则三棱锥P -ABC 的外接球的表面积是______．【答案】29π【详解】由题意，PA =BC =25，PB =AC =13，PC =AB =5，将三棱锥P -ABC 放到长方体中，可得长方体的三条面对角线分别为25，13，5，设长方体的长宽高分别为a,b ,c ,即a 2+b 2=25，c 2+b 2=13，a 2+c 2=5，解得：a =4，b =2，c =3．长方体的体对角线即为三棱锥和长方体公共外接球的直径2R ，∴(2R )2=a 2+b 2+c 2⇒4R 2=29⇒S 球=4πR 2=29π﹒故答案为：29π．例6.已知三棱锥A -BCD ,三组对棱两两相等,且AB =CD =1,AD =BC =3,若三棱雉A -BCD的外接球表面积为9π2.则AC =______．【答案】5【详解】将四面体A-BCD放置于长方体中, ∵四面体A-BCD的顶点为长方体八个顶点中的四个,∴长方体的外接球就是四面体A-BCD的外接球,∵AB=CD=1,AD=BC=3,且三组对棱两两相等,∴设AC=BD=x,得长方体的对角线长为1212+(3)2+x2=124+x2,可得外接球的直径2R=124+x2,所以 R=24+x24,∵三棱锥A-BCD的外接球表面积为9π2,∴4πR2=9π2,解得 R=32 4, 即24+x24=324,解之得x=5, 因即AC=BD=5.模型三:汉堡模型适用范围:有一条侧棱垂直于底面的柱体推导过程:如图,直三棱柱内接于球(同时直棱柱也内接于圆柱,棱柱的上下底面可以是任意三角形).第一步:确定球心O的位置,O1是ABC的外心,则OO1⊥平面ABC.第二步:算出小圆O1的半径AO1=r,OO1=12AA1=12h AA1=h也是圆柱的高).第三步:勾股定理:OA2=O1A2+O1O2⇒R2=h22+r2⇒R=r2+h2 2,求出R.公式:R=r2+h 22例1.已知某圆柱的高为42，体积为42π，则该圆柱外接球的表面积为( )A.32πB.36πC.40πD.44π【答案】B【详解】设圆柱底面圆的半径为r，则πr2×42=42π，解得r=1．设该圆柱的两底面中心分别为O1、O2，则该圆柱外接球的球心O为线段O1O2的中点，球O 的半径为R =12+422 2=3，故球O 的表面积S =4πR 2=36π．故选：B .例2.已知三棱柱的各个侧面均垂直于底面，底面为正三角形，侧棱长与底面边长之比为3：2，顶点都在一个球面上，若三棱柱的侧面积为162，则该球的表面积为( )A.120πB.129πC.129πD.180π【答案】C【详解】由题意，设球的半径为r ，底面三角形边长为2x ，因为侧棱长与底面边长之比为3：2，所以侧棱长为3x ，因为三棱柱的侧面积为162，即满足3⋅3x ⋅2x =18x 2=162，解得x =3，可知侧棱长为9，底面边长为6，如图所示，设N ，M 分别是上､下底面的中心，MN 的中点O 是三棱柱ABC -A 1B 1C 1外接球的球心，则AM =33×6=23，OM =12MN =12AA 1=92，r =OA =OM 2+AM 2=92 2+23 2=1292，所以S =4πr 2=4π×12922=129π.故选：C .例3.已知三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上，AB =AC =AA 1=2，∠BAC =120∘，则球O 的表面积是( )A.4πB.163πC.16πD.20π【答案】D【详解】由余弦定理得BC 2=AB 2+AC 2-2AB ⋅AC ⋅cos ∠BAC =22+22-2×2×2×-12 =12,∴BC =23,设△ABC 外接圆的圆心为O 1,半径为CO 1，由正弦定理得BC sin ∠BAC =2CO 1 ，即2332=2CO 1，解得CO 1=2，设外接球的半径为R =CO ,∵O 1O =12AA 1=1,∴R =CO =CO 1 2+OO 1 2=22+12=5,球O 的表面积为S =4πR 2=20π,故选：D .例4.直三棱柱ABC -A 1B 1C 1所有顶点都在球O 的表面上，且∠BAC =π6，AA 1=22，AC =3AB =3，则球O 的表面积为________．【答案】20π【详解】解：直三棱柱ABC -A 1B 1C 1的6个顶点都在球O 的表面上，且∠BAC =π6,AA 1=22，，AC =3AB =3，∴BC =AB 2+AC 2-2AB ⋅AC cos π6=3+9-2×3×3×32=3，设ΔABC 为外接圆的圆心为E ，2r =3sin π6=23，所以r =3，设外接球的球心为O ，设球的半径为R ，所以R =r 2+12AA 1 2=5，故S 球=4π⋅(5)2=20π．故答案为：20π．例5.在四面体ABCD 中，AB =CD =1，BC =2，且AB ⊥BC ，CD ⊥BC ，异面直线AB ，CD 所成角为π3，则该四面体外接球的表面积为______.【答案】16π3或8π【详解】由题意可以将四面体ABCD 补成一个如图所示的直三棱柱，因为异面直线AB ，CD 所成角为π3，所以∠ABE =π3或2π3，设△ABE 的外接圆半径为r ，当∠ABE =π3时，1sin60∘=2r ,r =33 ，当∠ABE =2π3时，AE =3 ，则3sin120∘=2r ,r =1，设四面体的外接球半径为R ，则R =r 2+BC 2 2=r 2+1 ，所以该四面体外接球的半径R =233或2，则外接球的表面积为.4πR 2=16π3或8π，故答案为：16π3或8π模型四:垂面模型适用范围:有一条棱垂直于底面的椎体推导过程:第一步:将ABC 画在小圆面上,A 为小圆直径的一个端点,作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步:O 1为ABC 的外心,所以OO 1⊥平面ABC ,算出小圆O 1的半径O 1D =r (三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=c sin C =2r ,OO 1=12PA .第三步:利用勾股定理求三棱锥的外接球半径:(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2;(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式:R 2=r 2+h 24例1.已知三棱锥P -ABC ，其中PA ⊥平面ABC ，∠BAC =120°，PA =AB =AC =2，则该三棱锥外接球的表面积为( )A.12πB.16πC.20πD.24π【答案】C【详解】根据题意设底面△ABC 的外心为G ，O 为球心，所以OG ⊥平面ABC ，因为PA ⊥平面ABC ，所以OG ⎳PA ，设D 是PA 中点，因为OP =OA ，所以DO ⊥PA ，因为PA ⊥平面ABC ，AG ⊂平面ABC ，所以AG ⊥PA ，因此OD ⎳AG ，因此四边形ODAG 是平行四边形，故OG =AD =12PA =1，由余弦定理，得BC =AB 2+AC 2-2AB ⋅AC ⋅cos120°=4+4-2×2×2×-12=23，由正弦定理，得2AG =2332⇒AG =2，所以该外接球的半径R 满足R 2=OG 2+AG 2=5⇒S =4πR 2=20π，故选：C ．例2.已知四面体ABCD 的每个顶点都在球O 的球面上，CD ⊥平面ABC ，AC =23，△ABC 是正三角形，△ACD 是等腰三角形，则球O 的体积为( )A.2053πB.86πC.2873πD.36π【答案】C【详解】∵CD ⊥平面ABC ，AC ⊂平面ABC ，∴CD ⊥AC ，又△ACD 是等腰三角形，∴CD =AC ．∵△ABC 是正三角形，∴AB =BC =AC =CD =23．设E 为△ABC 外接圆的圆心，则CE =23×32×23=2，OE =12CD =3，∴OC =OE 2+CE 2=7，∴球O 的体积V =43π×7 3=2873π.故选：C .例3.在三棱锥S -ABC 中, 侧棱SA ⊥底面ABC ,AB =5,BC =8,∠ABC =60°,SA =25, 则该三棱锥的外接球的表面积为()A.643π B.2563π C.4363π D.2048327π【答案】B【详解】 由题意知,AB =5,BC =8,∠ABC =60°,则在△ABC 中, 由余弦定理得 AC 2=AB 2+BC 2-2×AB ×BC ×cos ∠ABC ,解得AC =7,设△ABC 的外接圆半径为 r ,则△ABC 的外接圆直径2r =AC sin ∠ABC =772,∴r =73, 又∵侧棱SA ⊥底面ABC ,∴三棱锥的外接球的球心到平面ABC 的距离 h =12SA =5,则外接球的半径R =732+(5)2=643,则该三棱锥的外接球的表面积为S =4πR 2=2563π.例4.已知四棱锥P -ABCD 的五个顶点在球O 的球面上，PA ⊥底面ABCD ，PA =4，AB =AD ，BC=CD ，∠BAD =120°，且四边形ABCD 的面积为934，则球O 的表面积为___________.【答案】25π【详解】如图所示，在四边形中ABCD ，连结BD ，AC ，由AB =AD ,BC =CD ，所以△ABC ≌△ADC ，所以∠ABC =∠ADC ,∠BAC =∠DAC ，因为A ,B ,C ,D 在同一圆上，所以∠ABC =∠ADC =90°，又因为∠BAD =120°，所以∠BCD =60°，则∠BAC =∠DAC =60°，在Rt △ABC 中，可得BC =3AB ，因为底面ABCD 的面积为934，所以2×12AB ⋅3AB =934，解得AB =32，则BC =332，AC =3322+322=3，所以Rt △ABC 外接圆的半径r =32，将四棱锥P -ABCD 补成直四棱柱PEFG -ABCD ，该直棱柱的所有顶点都在球O 的球面上，设底面四边形ABCD 所在圆的圆心为O 1，连接OO 1，则OO 1⊥平面ABCD ，过OM ⊥PA ，垂足为M ,由球的对称性可知，球心O 到底面ABCD 的距离为d =OO 1=AM =12PA =2，所以球O 的半径R 满足R 2=d 2+r 2=254，所以球O 的表面积S 球O =4πR 2=25π.故答案为：25π.例5.在三棱锥P -ABC 中,PA ⊥平面ABC ,∠BAC =120°,AC =2,AB =1,设D 为BC 中点, 且直线PD 与平面ABC 所成角的余弦值为55, 则该三棱雉外接球的表面积为___________.【答案】 373π【详解】在△ABC 中,∠BAC =120°,AC =2,AB =1,由余弦定理得:BC 2=AC 2+AB 2-2AC ⋅BC ⋅cos ∠BAC ,即BC 2=22+12-2×2×1×cos120°=7,解得:BC =7. 设△ABC 的外接圆半径为r ,由正弦定理得2r =BC sin ∠BAC =7sin120°=273解得:r =73=213;且cos ∠ABC =AB 2+BC 2-AC 22AB ⋅BC =12+(7)2-222×1×7=277,又D 为BC 中点, 在△ABD 中,BD =12BC =72,AB =1,cos ∠ABD =277. 由余弦定理得:AD 2=AB 2+BD 2-2AB ⋅BD cos ∠ABD ,即:AD 2=12+722-2×1×72×277=34,解得AD =32.又因为PA ⊥平面ABC , 所以 ∠PDA 为直线PD 与平面ABC 所成角, 由cos ∠PDA =55,得 sin ∠PDA =255,tan ∠PDA =2所以在Rt △PAD 中, PA =AD ⋅tan ∠PDA =32⋅2=3. 设三棱锥P -ABC 的外接球半径为R , 所以R =PA 22+r 2=322+2132=3712,三棱锥P -ABC 外接球表面积为S =4πR 2=373π.模型五:斗笠模型使用范围:正棱雉或顶点的投影在底面的外心上推导过程:取底面的外心01, 连接顶点与外心,该线为空间几何体的高h ,在h 上取一点作为球心0,根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式:R =r 2+h 22h例1.已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1, 则球O 的表面积为()A.64πB.48πC.36πD.32π【答案】A 【详解】设⊙O 1的半径为r ,球的半径为R ,依题意,得πr 2=4π,∴r =2.由正弦定理可得ABsin60°=2r ,∴AB =2r sin60°=2 3.∴OO 1=AB =2 3.根据球的截面性质,得OO 1⊥平面ABC ,∴OO 1⊥O 1A ,R =OA =OO 21+O 1A 2=OO 21+r 2=4,∴球O 的表面积S =4πR 2=64π.故选A .例2.正四棱锥的顶点都在同一球面上, 若该棱锥的高为4 , 底面边长为2 , 则该球的表面积为()A.81π4B.16πC.9πD.27π4【答案】A 【详解】如图所示,设球半径为R ,底面中心为O 且球心为O ,∵正四棱锥P -ABCD 中 AB =2,∴AO =2,∵PO =4,∴在Rt △AOO 中, AO 2=AO ′2+OO ′2,∴R 2=(2)2+(4-R )2,解得R =94,∴该球的表面积为4πR 2=4π×942=81π4.例3.已知一个圆锥的母线长为26，侧面展开图是圆心角为23π3的扇形，则该圆锥的外接球的体积为( )A.36πB.48πC.36D.242【答案】A 【详解】设圆锥的底面半径为r ，由侧面展开图是圆心角为23π3的扇形得：2πr =23π3×26，解得：r =22.作出圆锥的轴截面如图所示：设圆锥的高为h ，则h =26 2-22 2=4.设该圆锥的外接球的球心为O ，半径为R ,则有R =h -R2+r 2，即R =4-R2+22 2，解得：R =3，所以该圆锥的外接球的体积为4πR 33=4π333=36π.故选：A .例4.在三棱锥P -ABC 中，侧棱PA =PB =PC =10，∠BAC =π4，BC =22，则此三棱锥外接球的表面积为_______．【答案】50π3【详解】因为PA =PB =PC =10，所以点P 在底面ABC 的射影为△ABC 的外心O 1，所以球心O 在直线PO 1上，设三棱锥外接球的半径为R ，因为2AO 1=22sin π4，所以AO 1=2，PO 1=6，由AO 2=OO 21+AO 21可得，R 2=6-R 2+4，解得R =56，故此三棱锥外接球的表面积为4πR 2=4π×256=503π．故答案为：50π3．例5.已知正四面体的棱长为4，则此四面体的外接球的表面积是为________.【答案】24π【详解】如图正四面体ABCD 棱长为4，AH ⊥平面BCD 于H ，则H 是△BCD 中心，BH =33×4=433，AH ⊥平面BCD ，BH ⊂平面BCD ，则AH ⊥BH ，AH =42-4332=463，设外接球球心为O ，则O 在AH ，则OA =OB =R 为外接半径，由BH 2+OH 2=BO 2得4332+463-R2=R 2，解得R =6，∴S =4πR 2=24π．故答案为：24π.例6.在三棱雉P -ABC 中,PA =PB =PC =26,AC =AB =4,且AC ⊥AB ,则该三棱锥外接球的表面积为________.【答案】36π【详解】设顶点P 在底面中的射影为O 1,由于PA =PB =PC ,所以O 1A =O 1B =O 1C ,即点O 1 是底面△ABC 的外心,又AC ⊥AB ,所以O 1为BC 的中点,因为PA =PB =PC =26,AC =AB =4,所以BC =42,AO 1=22,PO 1=4,设外接球的球心为O ,半径为R ,则O 必在PO 1上, O 1O =4-R ,在Rt △O 1OA 中, (4-R )2+(22)2=R 2, 解得R =3,所以S 2=4πR 2=36π.例7..一个圆锥恰有三条母线两两夹角为60°, 若该圆雉的侧面积为33π,则该圆雉外接球的表面积为________.【答案】27π2【详解】设∠ASB =∠BSC =∠CSA =60°,则SA =SB =SC =AB =AC =BC .设AB =x ,则底面圆的直径为2r =x sin60°=2x 3,该圆锥的侧面积为12π⋅2x3⋅x =33π,解得x =3,高OS =32-(3)2= 6.∴r =33= 3.设圆锥外接球的半径为R ,所以(6-R )2+r 2=R 2,解得R =364, 则外接球的表面积为4πR 2=27π2.类型六:切瓜模型使用范围:有两个平面互相垂直的棱雉推导过程:分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线, 两条垂线的交点即为球心0,取B C 的中点为E , 连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式:R 2=r 21+r 22-l 24例1.已知四棱锥P -ABCD 中，底面ABCD 为边长为4的正方形，侧面PAB ⊥底面ABCD ，且△PAB为等边三角形，则该四棱锥P -ABCD 外接球的表面积为( )A.112π3B.64π3C.64πD.16π【答案】A【详解】如图所示，在四棱锥P -ABCD 中，取侧面△PAB 和底面正方形ABCD 的外接圆的圆心分别为O 1,O 2，分别过O 1，O 2作两个平面的垂线交于点O ，则由外接球的性质知，点O 即为该球的球心，取线段AB 的中点E ，连O 1E ，O 2E ，O 2D ，OD ，则四边形O 1EO 2O 为矩形，在等边△PAB 中，可得PE =23，则O 1E =233，即OO 2=233，在正方形ABCD 中，因为AB =4，可得O 2D =22，在直角△OO 2D 中，可得OD 2=OO 22+O 2D 2，即R 2=OO 22+O 2D 2=283，所以四棱锥P -ABCD 外接球的表面积为S =4πR 2=112π3.故选：A .例2.已知三棱锥A -BCD 中, △ABD 与△BCD 是边长为2的等边三角形且二面角A -BD -C 为直二面角, 则三棱雉A -BCD 的外接球的表面积为()A.10π3B.5πC.6πD.20π3【答案】D 【详解】取BD 的中点M ，连接AM ,CM ,∠AMC =90°,AF :FM =2:1,CE :EM =2:1，OF ⊥AM ，OE ⊥MC ,OE ∩OF =O 连接OC ，点 O 是三棱锥A -BCD 的外接球的球心，因为棱长都是2 ，所以OE =FM =33,EC =233，所以在△OEC 中，R =OC =OE 2+EC 2=153，那么外接球的表面积是S =4πR 2=203π ，故选D .例3.已知四棱锥P -ABCD 的体积是363，底面ABCD 是正方形，△PAB 是等边三角形，平面PAB ⊥平面ABCD ，则四棱锥P -ABCD 的外接球的体积为________.【答案】2821π【详解】设正方形ABCD 的边长为2x ，在等边三角形PAB 中，过P 点作PE ⊥AB 于E ，由于平面PAB ⊥平面ABCD ，∴PE ⊥平面ABCD ．由于△PAB 是等边三角形，则PE =3x ，∴V P -ABCD =13⋅S ABCD ⋅PE =13×2x 2×3x =363，解得x =3．设四棱锥外接球的半径为R ，O 1为正方形ABCD 中心，O 2为等边三角形PAB 中心，O 为四棱锥P -ABCD 外接球球心，则易知OO 2EO 1为矩形，则OO 2=EO 1=12AD =x =3，PO 2=23PE =23⋅33=23，R =OP =OO 22+PO 22=9+12=21，∴外接球体积V =43π×(21)3=2821π．故答案为：2821π．例4.已知四面体ABCD 中，△ABD 和△BDC 是等边三角形，二面角A -BD -C 为直二面角.若AB =43，则四面体ABCD 外接球的表面积为__________________.【答案】80π【详解】如图所示：设O 1为△BCD 的中心，O 为四面体ABCD 的外接球的球心，则OO 1⊥平面BDC ．设M 为线段BD 的中点，外接球的半径为R ，连接AM ,CM ,OA ，过O 作OG ⊥AM 于点G ，易知G 为△ABD 的中心，则OO 1=OG =MO 1=MG ，因为MA =32×43=6，故MG =OG =13×6=2,GA =4，在Rt △AGO 中，GA 2+GO 2=OA 2，故22+42=R 2，则R =25．所以外接球的表面积为S =4πR 2=80π，故答案为：80π.例5.已知在三棱锥A -BCD 中，平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形，则该三棱锥的外接球体积为___________.【答案】2053π【详解】依题意，平面ABD ⊥平面BCD ,△BCD 和△ABD 均是边长为23的正三角形，设G 是BD 的中点，则AG ⊥BD ,CG ⊥BD ，由于平面ABD ⊥平面BCD 且交线为BD ，所以AG ⊥平面BCD ，CG ⊥平面ABD .设E ,F 分别是等边三角形ABD 和等边三角形BCD 的中心，则AE =CF =2GE =2GF =23CG =23×3=2,设O 是三棱锥A -BCD 外接球的球心，则OE ⊥平面ABD ，OF ⊥平面BCD .所以外接球的半径R =OF 2+CF 2=12+22=5，所以外接球的体积为4π3×5 3=2053π.故选：2053π模型七:折叠模型使用范围:两个全等三角形或等腰三角形拼在一起,或菱形折叠.推导过程:两个全等的三角形或者等腰拼在一起,或者菱形折叠,设折叠的二面角∠A EC =α,CE =A E =h .如图,作左图的二面角剖面图如右图:H 1和H 2分别为△BCD ,△A BD 外心,CH 1=r =BD2sin∠BCD,EH1=h-r,OH1=(h-r)tan α2故R2=OC2=OH21+CH21=r2+(h-r)2tan2α2.公式:R2=r2+(h-r)2tan2α2例1.已知菱形ABCD中,∠DAB=60°,AB=3,对角线AC与BD的交点为O,把菱形ABCD沿对角线BD折起, 使得∠AOC=90°,则折得的几何体的外接球的表面积为()A.15πB.15π2C.7π2D.7π【答案】A【解析】菱形ABCD中,∠DAB=60°,AB=3,三角形ABD的外接圆的半径为r=32sin60°=3,高h=332,对角线AC与BD的交点为O,使得α=∠AOC=90°,则折得的几何体的外接球的半径为:R=(3)2+332-32tan245°=152,外接球的表面积为S=4π152 2=15π, 故选 A.例2.在三棱雉P-ABC中,PA=PB=AC=BC=2,AB=23,PC=1,则三棱雉P-ABC的外接球的表面积为()A.4π3B.4πC.12πD.52π3【答案】D【解析】取AB中点D,因为PA=PB=AC=BC=2,所以PD=CD=1,又 PD⊥AB,CD⊥AB,则面PDC⊥面ABC,设△ABC的外心为O1,外接圆半径为r,三棱锥P-ABC的外接球的球心为O,则OO1⊥面ABC,∠ACB=120°,由r=AB2sin120°=2,h=1,设∠PDC=α=60°(二面角平面角),外接球的半径为 R,R=r2+(h-r)2tan2α2=(2)2+(1-2)2tan230°=133,所以三棱雉P-ABC的外接球的表面积为4πR2=52π3,故选 D.例3.在边长为23的菱形ABCD中,∠BAD=60°,沿对角线AC折成二面角B-AC-D为120°的四面体ABCD,则此四面体的外接球表面积为________.【答案】84π【解析】如图所示, 典型的全等等腰三角形共底边:ED=h=3,O2D=r=23,∠BED=α=120°,可根据几何性质知道 ∠O 2EO =60°,OO 2=EO 2tan60°=3,R =OO 22+DO 22=(3)2+(23)2=21,或者可以通过公式R =r 2+(h -r )2tan 2α2=(23)2+(3-23)2tan 260°=21,S =4πR 2=84π.模型八:已知球心或球半径模型例1.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,SC 是球O 的直径.若平面SCA ⊥平面SCB,SA =AC ,SB =BC ,三棱锥S -ABC 的体积为9,则球O 的表面积为________.【答案】36π【解析】如图, 连接AO ,OB ,∵SC 为球O 的直径,∴点O 为SC 的中点, ∵SA =AC ,SB =BC ,∴AO ⊥SC ,BO ⊥SC ,∵平面SCA ⊥平面SCB , 平面SCA ∩平面SCB =SC ,∴AO ⊥平面SCB , 设球O 的半径为R ,则OA =OB =R ,SC =2R .∴V S ⋅ABC =V A -SBC =13×S △SBC ×AO =13×12×SC ×OB ×AO , 即9=13×12×2R ×R ×R , 解得R =3,∴球O 的表面积为S =4πR 2=4π×32=36π.例2.已知三棱锥A -BCD 的所有顶点都在球O 的球面上,AB 为球O 的直径,若该三棱雉的体积为3,BC =3,BD =3,∠CBD =90°, 则球O 的体积为________.【答案】32π3【解析】设A 到平面BCD 的距离为h∵三棱锥的体积为3,BC =3,BD =3,∠CBD =90°∴13×12×3×3×h =3,∴h =2,∴球心O 到平面BCD 的距离为1.设CD 的中点为E ,连接OE ,则由球的截面性质可得OE ⊥平面CBD ,∵△BCD 外接圆的直径CD =23,∴球O 的半径OD =2,∴球O 的体积为32π3.例3.已知三棱锥S -ABC 的所有顶点都在球O 的球面上,△ABC 是边长为1的正三角形, SC 为球O的直径, 且SC =2,则此棱锥的体积为()A.26B.36C.23D.22【答案】A【解析】由于三棱锥S -ABC 与三棱锥O -ABC 底面都是△ABC ,O 是SC 的中点, 因此三棱锥S -ABC 的高是三棱锥O -ABC 高的2倍,所以三棱锥S -ABC 的体积也是三棱锥O -ABC 体积的2倍.在三棱锥O -ABC 中,其棱长都是1,S △ABC =34×AB 2=34, 高OD =12-332=63,∴V S -ABC =2V O -ABC =2×13×34×63=26. 故选 A .例4.三棱锥S -ABC 的底面各棱长均为3 , 其外接球半径为2 , 则三棱锥S -ABC 的体积最大时,点S 到平面ABC 的距离为()A.2+3B.2-3C.3D.2【答案】C【解析】如图, 设三棱锥S -ABC 底面三角形ABC 的外心为G , 三棱锥外接球的球心为O , 要使三棱锥 S -ABC 的体积最大, 则O 在SG 上,由底面三角形的边长为3,可得AG =32sin60°=3.连接OA ,在 Rt △OGA 中,由勾股定理求得OG =OA 2-GA 2=22-(3)2=1.∴点S 到平面ABC 的距离为 OS +OG =2+1=3. 故选 C .模型九:最值模型最值问题的解法有两种方法:一种是几何法,即在运动变化过䅣中得到最值,从而转化为定值问题求解.另一种是代数方法,即建立目标函数,从而求目标函数的最值.例1.在边长为6的菱形ABCD 中，∠A =π3，现将△ABD 沿BD 折起，当三棱锥A -BCD 的体积最大时，三棱锥A -BCD 的外接球的表面积为( )A.60πB.30πC.70πD.50π【答案】A 【分析】当三棱锥A -BCD 的体积最大值时，平面ABD ⊥平面BCD ，即可求出外接圆的半径，从而求出面积.【详解】当三棱锥A -BCD 的体积最大值时，平面ABD ⊥平面BCD ，如图，取BD 的中点为H ，连接AH ,CH ，则AH ⊥BD .设O 1,O 2分别为△ABD ，△BCD 外接圆的圆心，O 为三棱锥A -BCD 的外接球的球心，则O 1在AH 上，O 2在CH 上，且AO 1=2O 1H =23AH =23,且O 2H ⊥BD ,OO 1⊥平面ABD ，OO 2⊥平面BCD .∵平面ABD ⊥平面BCD ，平面ABD ∩平面BCD =BD ，AH ⊂平面ABDAH ⊥平面ABD ，AH ⎳O 2O ，同理CH ⎳O 1O ∴四边形O 1OO 2H 为平行四边形∵AH ⊥平面BCD ，O 2H ⊂平面BCD ∴AH ⊥O 2H ，即四边形O 1OO 2H 为矩形.∴OO 2=O 1H =3CO 2=23×32×6=23∴外接球半径R =OO 22+CO 22=3+12=15∴外接球的表面积为4πR 2=60π故选：A .例2.在四棱锥S -ABCD 中，侧面SAD ⊥底面ABCD ，且SA =SD ，∠ASD =90°，底面ABCD 是边长为2的正方形，设P 为该四棱锥外接球表面上的动点，则三棱锥P -SAD 的最大体积为( )A.1+2B.2+223C.2+23D.1+23【答案】D 【详解】连接AC ,BD 交于点O ，取AD 中点为M ，连接SM ,OS ，作图如下：因为AS =DS ,∠ASD =90°，又M 为AD 的中点，故M 为Rt △SAD 的外心，又平面SAD ⊥平面ABCD ，且面SAD ∩面ABCD =AD ，又OM ⊥AD ,OM ⊂面ABCD ，故可得OM ⊥面SAD ，故OA =OS =OD ；又四边形ABCD 为正方形，且O 为对角线交点，故可得OA =OB =OC =OD ，综上所述，OA =OB =OC =OD =OS ，故O 为四棱锥S -ABCD 的外接球的球心.则其外接球半径R =OD =12BD =2.又P 为该四棱锥外接球表面上的动点，若使得三棱锥P -SAD 的体积最大，则此时点P 到平面SAD 的距离h =OM +R =1+2，故其体积的最大值V =13S △SAD ×h =13×12×AD ×SM ×1+2 =13×12×2×1×1+2 =1+23.故选：D .例3.已知P ，A ，B ，C ，D 都在同一个球面上，平面PAB ⊥平面ABCD ，ABCD 是边长为2的正方形，∠APB =60°，当四棱锥P -ABCD 的体积最大时，该球的半径为______．【答案】213【分析】先求出四棱锥P -ABCD 的体积最大时，△PAB 为等边三角形，再找出外接球的球心，通过勾股定理即可求得半径.【详解】如图，过点P 作PQ ⊥AB 于Q ，平面PAB ⊥平面ABCD ，平面PAB ∩平面ABCD =AB ，∴PQ ⊥平面ABCD ，V P -ABCD =13⋅PQ ⋅S ABCD ，故四棱锥P -ABCD 的体积最大，即PQ 最大，∵AB =2，PQ 最大，即△PAB 面积最大，由∠APB =60°,S △PAB =12⋅PA ⋅PB ⋅sin ∠APB =34⋅PA ⋅PB ，得cos ∠APB =AP 2+BP 2-42AP ⋅BP=12，AP 2+BP 2=AP ⋅BP +4≥2AP ⋅BP ，得AP ⋅BP ≤4，当且仅当AP =BP =2时取等号，此时△PAB 面积最大，△PAB 为等边三角形.取△PAB 的外心为O 1，正方形ABCD 的外心为O 2，过O 1,O 2分别作所在平面的垂线，交点为O ，O 即为四棱锥P -ABCD 外接球的球心，四边形OO 2QO 1为矩形，OO 1=O 2Q =1 ，PO 1=23PQ =233，设外接球半径为R ，则R =12+2332=213.故答案为：213.例4.A ，B ，C ，D 四点均在同一球面上，∠BAC =120∘，△BCD 是边长为2的等边三角形，则△ABC 面积的最大值为__________，四面体ABCD 体积最大时球的表面积为___________．【答案】 33 20π3【分析】①由于S △ABC =12AB ⋅AC sin ∠BAC =34AB ⋅AC ，求△ABC 面积的最大值即是求AB ⋅AC 的最大值，利用余弦定理结合重要不等式即可求解②当面ABC⊥面BCD时四面体的体积最大，确定出球心后计算出球的半径即可求解【详解】①因为∠BAC=120∘所以S△ABC=12AB⋅AC sin∠BAC=34AB⋅AC又BC2=AB2+AC2-2AB⋅AC⋅cos120∘即4=AB2+AC2+AB⋅AC≥2AB⋅AC+AB⋅AC=3AB⋅AC所以AB⋅AC≤4 3所以S△ABC=34AB⋅AC≤34×43=33即△ABC面积的最大值为3 3②过A作AH⊥BC，垂足为H, S△ABC=12AH⋅BC=AH则△ABC面积的最大时，AH最大，AH的最大值为3 3，此时△ABC为等腰三角形，H为BC中点S△BCD=12×2×2×32=3，V A-BCD=13S△BCD⋅h=33h则当AH⊥平面BCD时, h最大，此时面ABC⊥面BCD如图,设O为四面体ABCD 外接球的球心, O1，O2分别为△ABC，△BCD的外接圆的圆心. OO1⊥平面ABC，OO2⊥平面BCD,在△ABC中BCsin∠BAC=433=2O2A⇒O2A=33DO1=23DH=23×32×2=233OO1=O2H=O2A-AH=33∴四面体ABCD外接球的半径R=OO21+O1D2=53外接球的表面积为4πR2=20π3模型十:内切球模型以三棱雉P-ABC为例, 求其内切球OE的半径推导过程:等体积法,三棱雉P-ABC体积等于内切球球心与四个面构成的四个三棱雉的体积之和.第一步:先求出四个表面的面积和整个雉体体积;第二步:设内切球的半径为r ,球心为O ,建立等式:V P -ABC =V O -ABC +V O -PAB +V O -PAC +V O -PBC ⇒V P -ABC =13S △ABC ⋅r +13S △PAB ⋅r +13S △PAC ⋅r +13S △PBC ⋅r =13S△ABC+S △PAB +S △PAC +S △PBC ⋅r 第三步:解出r =3V P -ABC S O -ABC +S O -PAB +S O -PAC +S O -PBC =3VS 表.公式:r =3VS 表例1.已知点O 到直三棱柱ABC -A 1B 1C 1各面的距离都相等，球O 是直三棱柱ABC -A 1B 1C 1的内切球，若球O 的表面积为16π，ABC 的周长为4，则三棱锥A 1-ABC 的体积为( )A.43B.163C.833D.1633【答案】B 【详解】解：设直三棱柱ABC -A 1B 1C 1的高为h ，AB =c ，BC =a ，AC =b ，内切球O 的半径为r ，则h =2r ，由题意可知球O 的表面积为16π=4πr 2，解得r =2，∴h =4，又△ABC 的周长为4，即a +b +c =4，∴连接OA ，OB ，OC ，OA 1,OB 1,OC 1可将直三棱柱ABC -A 1B 1C 1分成5个棱锥，即三个以原来三棱柱侧面为底面，内切球球心为顶点的四棱锥，两个以原来三棱柱底面为底面，内切球球心为顶点的的三棱锥，∴由体积相等可得直三棱柱ABC -A 1B 1C 1的体积为S △ABC h =13ahr +13bhr +13chr +2×13S △ABC r ，即4S △ABC =13(a +b +c )hr +43S △ABC ，∴S △ABC =4，∴三棱锥A 1-ABC 的体积为13S △ABC h =13×4×4=163．故选：B ．例2.在《九章算术·商功》中，将四个面都为直角三角形的四面体称为鳖臑，如图在鳖臑ABCD 中，AB ⊥平面BCD ，AB =BC =CD =1，BC ⊥CD ，则鳖臑ABCD 内切球的表面积为( )。

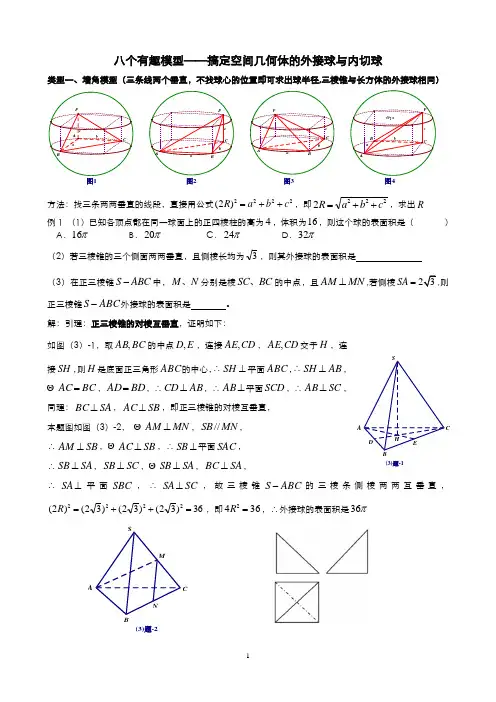
八个有趣模型——搞定空间几何体的外接球与内切球类型一、墙角模型（三条线两个垂直，不找球心的位置即可求出球半径,三棱锥与长方体的外接球相同）图2图3方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ ） A ．π16 B ．π20 C ．π24 D ．π32 （2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 （3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =则正三棱锥ABC S -外接球的表面积是 。

解：引理：正三棱锥的对棱互垂直，证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥， BC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ，∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直， 本题图如图（3）-2， MN AM ⊥，MN SB //，∴SB AM ⊥， SB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥， SA SB ⊥，SA BC ⊥，∴⊥SA 平面S B C ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互垂直，36)32()32()32()2(2222=++=R ，即3642=R ，∴外接球的表面积是π36(3)题-1A(3)题-2A（4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ ）π11.A π7.B π310.C π340.D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是（6）已知某几何体的三视图如图上右所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为类型二、垂面模型（一条直线垂直于一个平面） 1．题设：如图5，⊥PA 平面ABC 解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r CcB b A a 2sin sin sin ===），PA OO 211=； 第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；图5②2122OO r R +=⇔212OO r R +=2．题设：如图6，7，8，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔ 三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点图6图7-1图7-2图8图8-1图8-2图8-3解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线； 第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R .方法二：小圆直径参与构造大圆。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

⾼中数学掌握8⼤模型解决空间⼏何的外接球和内切球问题⼋个有趣模型——搞定空间⼏何体的外接球与内切球正三棱锥 S ABC 外接球的表⾯积是。

36 解：引理：正三棱锥的对棱互垂直。

证明如下：如图( 3)-1 ，取 AB,BC 的中点D,E ，连接 AE,CD ，AE,CD 交于 H ，连接 SH ，则 H 是底⾯正三⾓形 ABC 的中⼼， SH 平⾯ ABC ， SH AB ，AC BC ， AD BD ， CD AB ， AB 平⾯ SCD ，AB SC ，同理： BC SA ， AC SB ，即正三棱锥的对棱互垂直，本题图如图( 3)-2， AM MN ， SB// MN ，AM SB ， AC SB ， SB 平⾯ SAC ， SB SA ， SB SC ， SB SA ， BC SA ， SA 平⾯ SBC ， SA SC ，故三棱锥 S ABC 的三棱条侧棱两两互相垂直，(2R)2 (2 3)2 (2 3)2 (2 3)2 36，即 4R 2 36，正三棱锥 S ABC 外接球的表⾯积是 36类型⼀、墙⾓模型(三条线两个垂直，不找球⼼的位置即可求出球半径) 图3 图1 图2 ⽅法： a c 2 ，即 2R b 2 找三条两两垂直的线段，直接⽤公式 (2R) PcCa b 2 c 2，求出 R例1 A ．1)已知各顶点都在同⼀球⾯上的正四棱柱的⾼为 16 B ． 20 C ． 24 4，体积为 16，则这个球的表⾯积是(． 322) 若三棱锥的三个侧⾯两垂直，且侧棱长均为 3，则其外接球的表⾯积是解： 1) V a 2h 16，a 2， 4R 2 a 2 a 2h 24 4 16 24 ， S 24 ，选 C ；2) 4R 2 3 34 R 2 9 3) 在正三棱锥 S ABC中， M 、N 分别是棱 SC 、BC 的中点，且 AM MN , 若侧棱 SA 2 3 ,则CC4）在四⾯体S ABC 中，SA 平⾯ABC ，BAC 120 ,SA AC 2,AB 1, 则该四⾯体的外接5）6）解析：BC 球的表⾯积为（ D ）A.11 B.7如果三棱锥的三个侧⾯两两垂直，它们的⾯积分别为已知某⼏何体的三视图如图所⽰，三视图是腰长为何体外接球的体积为4)在ABC中，BC 2 AC22AB2 2AB7 ，ABC 的外接球直径为2rBCsin B AC5）三条侧棱两两⽣直，ab 12bc abcac6) (2R) b2V 4R333382 2 2(2R)2(2r)2SA2403S40设三条侧棱长分别为24，a 3，b2 3，R2 3，43，2，⼀条直线垂直于⼀个平⾯）10C.36、4、40D.33，那么它的外接球的表⾯积是1的等腰直⾓三⾓形和边长为1的正⽅形，则该⼏BC3，选cos12027a,b,c( a,b,c4，c 2，(2R)2R327，R），则b2 29 ，S 4 R2 29 ，类型⼆、垂⾯模型1．题设：如图5，PA 平⾯ABC 解题步骤：第⼀步：将ABC 画在⼩圆⾯上，A 为⼩圆直径的⼀个端点，作⼩圆的直径AD ，连接PD ，则PD 必过球⼼O ；第⼆步：O1为ABC的外⼼，所以OO1 平⾯ABC ，算出⼩圆O1的半O1D r （三⾓形的外接圆直径算法：利⽤正弦定理，得a sin Absin BsincC 2r )，OO1 21PA；第三步：利⽤勾股定理求三棱锥的外接球半径：①2 2 2(2R)2 PA2 (2r)2222R PA2(2r)2；2．题设：如图6，7，8，P的射影是ABC 的外⼼三棱锥P ABC的三条侧棱相等三棱锥P ABC的底⾯ABC 在圆锥的底上，顶点P点也是圆锥的顶点解题步骤：ABC的外⼼O1，则P , O, O1三点共线；第⼆步：先算出⼩圆O1 的半径AO1 r ，再算出棱锥的⾼PO1 h (也是圆锥的⾼)；第三步：勾股定理：OA2 O1A2 O1O2 R2 (h R)2 r 2，解出R ⽅法⼆：⼩圆直径参与构造⼤圆。