2021年九年级数学重庆中考22题新型函数研究专题(2)(无答案)

重庆市2021年初中学业水平暨高中招生考试数学试题（A 卷）一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号A 、B 、C 、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.1.2的相反数是A.﹣2B.2C.D. 1212-2.计算的结果是63a a ÷A.B.C.D. 63a 52a 62a 53a 3.不等式在数轴上表示正确的是2x ≤A B C D4.如图，△ABC 与△BEF 位似，点O 是它们的位似中心，其中OE=2OB ，则△ABC 与△DEF 的周长之比是A.1：2B.1:4C.1:3D.1:95.如图，四边形ABCD 内接于☉O ，若∠A=80°，则∠C 的度数是A.80° B.100° C.110° D.120°6.-A.7B.C. D. 7.如图，点B ，F ，C ，E 共线，∠B=∠E ，BF=EC ，添加一个条件，不等判断△ABC ≌△DEF 的是A.AB=DEB.∠A=∠DC.AC=DFD.AC ∥FD8.甲无人机从地面起飞，乙无人机从距离地面20m 高的楼顶起飞，两架无人机同时匀速上升10s 。

甲、乙两架无人机所在的位置距离地面的高度y （单位：m ）与无人机上升的时间x （单位：s ）之间的关系如图所示.下列说法正确的是A.5s 时，两架无人机都上升了40mB.10s 时，两架无人机的高度差为20mC.乙无人机上升的速度为8m/sD.10s 时，甲无人机距离地面的高度是60m9.如图，正方形ABCD 的对角线AC ，BD 交于点O ，M 是边AD 上一点，连接OM ，多点O 做ON ⊥OM ，交CD 于点N.若四边形MOND 的面积是1，则AB 的长为A.1 C.2 D. 10.如图，相邻两个山坡上，分别有垂直于水平面的通信基站MA 和ND.甲在山脚点C 处测得通信基站顶端M 的仰角为60°，测得点C 距离通信基站MA 的水平距离CB 为30m ；乙在另一座山脚点F处测得点F 距离通信基站ND 的水平距离FE 为50m ，测得山坡DF 的坡度i=1：1.25.若，58ND DE =点C ，B ，E ，F 在同一水平线上，则两个通信基站顶端M 与顶端N 的高度差为（参考数据：）1.73≈≈A.9.0m B.12.8m C.13.1m D.22.7m11.若关于x 的一元一次不等式组的解集为，且关于y 的分式方程()322225x x a x -≥+⎧⎪⎨-<-⎪⎩6x ≥的解是正整数，则所有满足条件的整数a 的值之和是238211y a y y y+-+=--A.5 B.8 C.12 D.1512.如图，在平面直角坐标系中，菱形ABCD 的顶点D 在第二象限，其余顶点都在第一象限，AB ∥X 轴，AO ⊥AD ，AO=AD.过点A 作AE ⊥CD,垂足为E ，DE=4CE.反比例函数的()0ky x x=>图象经过点E ，与边AB 交于点F ，连接OE ，OF ，EF.若，则k 的值为118EOF S = A. B. C.7 D. 73214212二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上.13.计算：。

重庆中考数学22题专项训练1. 若反比例函数xky =1过面积为9的正方形AMON 的顶点A ，且过点A 的直线n mx y -=2的图象与反比例函数的另一交点为B （a ,1-）（1）求出反比例函数与一次函数的解析式； （2）求∆AOB 的面积；2. 如图，反比例函数xky =的图象与一次函数b mx y +=的图象交于点(1,3)(,1).A B n -、 (1)求反比例函数与一次函数的解析式；(2)根据图象回答：当x 取何值时，反比例函数的值大于一次函数的值．3. 已知点A 与点B(-3，2)关于y 轴对称，反比例函数ky x=与一次函数y mx b =+的图象都经过点A ，xyNAM OB且点C(2，0)在一次函数y mx b =+的图象上．(1)求反比例函数和一次函数的解析式；(2)若两个函数图象的另一个交点为D ，求△AOD 的面积．4. 如图，已知反比例函数y =xm的图象经过点A （1，－3），一次函数y = kx + b 的图象经过点A 与点C （0，－4），且与反比例函数的图象相交于另一点B(3,n )．（1）试确定这两个函数的解析式； （2）求△AOB 的面积；（3）根据图形直接写出反比例函数值大于一次函数值时自变量的取值范围.5. 如图，O 是坐标原点，直线OA 与双曲线)0(≠=k xk y 在第一象限内交于点A ，过点A 作AB ⊥x 轴，垂足为B ，若OB=4，21=OB AB ． ⑴求双曲线的解析式；⑵直线AC 与y 轴交于点C （0，1），与x 轴交于点D ，求△AOD 的面积．6. 已知：如图，一次函数的图象与反比例函数的图象交于A B 、两点，过A 作x AC ⊥轴于点.C 已知,2,5AC OC OA ==且点B 的纵坐标为-3．(1)求点A 的坐标及该反比例函数的解析式； (2)求直线AB 的解析式．7. 如图，一次函数的图象与反比例函数的图象在第一象限只有—个交点A ，一次函数的图象与x 轴、y5题图轴分别交于B 、C 两点，AD 垂直平分OB ，垂足为D ，OA=5， ABAD =552. （1）求点A 的坐标及反比例函数解析式； （2）求一次函数的的解析式.8. 如图，已知反比例函数my x=的图象经过点(1,3),A -一次函数y kx b =+的图象经过点A 与点(0,4),C -且与反比例函数的图象相交于另一点(3,).B n(1)试确定这两个函数的解析式； (2)求AOB ∆的面积；(3)根据图象直接写出反比例函数值大于一次函数值时 自变量的取值范围.9. 如图，在直角坐标系中，点A 是反比例函数1ky x=的图象上一点，AB x ⊥轴的正半轴于B 点，C 是OB 的中点，一次函数2y ax b =+的图象经过A C 、两点，并交y 轴于点(0,2),D -且AOD ∆的8题图面积为4.(1)求反比例函数和一次函数的解析式；(2)请直接写出在y 轴的右侧，当12y y >时，x第9题图10. 如图，已知一次函数12y kx=+的图象与y 轴交于点,C 与反比例函数2my x=的图象相交于点,A 点A 的横坐标为1. 过A 作AD y ⊥轴于点,D 且1=CDAD(1)求这两个函数的解析式及两图象的另一交点B 的坐标；(2)观察图象，直接写出使函数值12y y ≥的自变量x11. 如图，一次函数y kx b =+的图象与反比例函数my x=的图象交于(3,1),(2,)A B n -两点，直线AB 分别交x 轴、y 轴于,D C 两点.(1)求上述反比例函数和一次函数的解析式；(2)连接,AO BO 、 求出AOB ∆的面积； (3)请由图象直接写出．．．．，当x 满足什么条件时， 一次函数的值小于反比例函数的值？12. 如图，已知一次函数1y k x b =+的图象分别与x 轴、y 轴的正半轴交于A B 、两点，且与反比例函数2k y x=交于C E 、两点，点C 在第二象限，过点C 作CD x ⊥轴于点,D 1.OA OB OD === (1)求反比例函数与一次函数的解析式； (2)求OCE ∆的面积.13. 如图，一次函数1y ax b =+的图象与反比例函数2ky x=的图象交于,A B两点，已知OA =A 点的纵坐标与横之比为1：3， 点B 的坐标为3(,).2m -(1)求反比例函数的解析式和一次函数的解析式；(2)观察图象，直接写出使函数值12y y <成立的自变量x 的取值范围12题图14. 已知如图，AOB ∆的OB 边在x 轴上，︒=∠90OAB ，23==AB OA ，反比例函数xky =1过A 点，一次函数b ax y -=2的图象过A 点且与反比例函数图象的另一交点为C ),1(m -连结OC （1）求出反比例函数与一次函数的解析式； （2）求OAC ∆的面积（3）根据图象,直接写出当21y y ≥时,x 的取值范围15、已知：如图，在平面直角坐标系xoy 中，直线AB y mx n =+与反比例函数ky x=交于A 、B 两点，过点A 作AC ⊥x 轴于C ，OA=5，OC=4，点B 的纵坐标为4- （1）求反比例函数和一次函数的解析式； （2）求AOB ∆的面积。

中考真题分类汇编（函数）----函数与几何（2）1.（2021•四川省眉山市）如图，直线y＝x+6与x轴交于点A，与y轴交于点B．直线MN∥AB，且与△AOB的外接圆⊙P相切，与双曲线y＝﹣在第二象限内的图象交于C、D两点．（1）求点A，B的坐标和⊙P的半径；（2）求直线MN所对应的函数表达式；（3）求△BCN的面积．2.（2021•四川省南充市）如图，已知抛物线y＝ax2+bx+4（a≠0）与x轴交于点A（1，0）和B，与y轴交于点C，对称轴为直线x＝．（1）求抛物线的解析式；（2）如图1，若点P是线段BC上的一个动点（不与点B，C重合），过点P作y轴的平行线交抛物线于点Q，连接OQ，当线段PQ长度最大时，判断四边形OCPQ的形状并说明理由；（3）如图2，在（2）的条件下，D是OC的中点，过点Q的直线与抛物线交于点E，且∠DQE＝2∠ODQ．在y轴上是否存在点F，得△BEF为等腰三角形？若存在，求点F的坐标；若不存在，请说明理由．3.（2021•遂宁市）如图，已知二次函数的图象与x轴交于A和B（－3，0）两点，与y轴x=-，直线y＝－2x＋m经过点A，且与y轴交于点D，交于C（0，－3），对称轴为直线1与抛物线交于点E，与对称轴交于点F．（1）求抛物线的解析式和m的值；（2）在y轴上是否存在点P，使得以D、E、P为顶点的三角形与△AOD相似，若存在，求出点P的坐标；若不存在，试说明理由；（3）直线y＝1上有M、N两点（M在N的左侧），且MN＝2，若将线段MN在直线y＝1上平移，当它移动到某一位置时，四边形MEFN的周长会达到最小，请求出周长的最小值（结果保留根号）．4. (2021•四川省自贡市) 如图，抛物线(1)()y x x a =+-（其中1a >）与x 轴交于A 、B 两点，交y 轴于点C ．（1）直接写出OCA ∠的度数和线段AB 的长（用a 表示）；（2）若点D 为ABC 的外心，且BCD △与ACO △104，求此抛物线的解析式；（3）在（2）的前提下，试探究抛物线(1)()y x x a =+-上是否存在一点P ，使得CAP DBA ∠=∠？若存在，求出点P 的坐标；若不存在，请说明理由．5. （2021•天津市）已知抛物线22y ax ax c =-+（a ，c 为常数，0a ≠）经过点()0,1C -，顶点为D ．（Ⅰ）当1a =时，求该抛物线的顶点坐标；（Ⅱ）当0a >时，点()0,1E a +，若22DE DC =，求该抛物线的解析式； （Ⅲ）当1a <-时，点()0,1F a -，过点C 作直线l 平行于x 轴，(),0M m 是x 轴上的动点，()3,1N m +-是直线l 上的动点．当a 为何值时，FM DN +的最小值为10，并求此时点M ，N 的坐标．6. 2021•湖北省恩施州）如图，在平面直角坐标系中，四边形ABCD 为正方形，点A ，B 在x 轴上，抛物线y ＝x 2+bx +c 经过点B ，D （﹣4，5）两点，且与直线DC 交于另一点E ． （1）求抛物线的解析式；（2）F 为抛物线对称轴上一点，Q 为平面直角坐标系中的一点，是否存在以点Q ，F ，E ，B为顶点的四边形是以BE为边的菱形．若存在，请求出点F的坐标；若不存在，请说明理由；（3）P为y轴上一点，过点P作抛物线对称轴的垂线，垂足为M，连接ME，BP，探究EM+MP+PB是否存在最小值．若存在，请求出这个最小值及点M的坐标；若不存在，请说明理由．7.（2021•浙江省金华市）在平面直角坐标系中，点A的坐标为（﹣，0），点B在直线l：y＝x上，过点B作AB的垂线，过原点O作直线l的垂线，两垂线相交于点C．（1）如图，点B，C分别在第三、二象限内，BC与AO相交于点D．①若BA＝BO，求证：CD＝CO．②若∠CBO＝45°，求四边形ABOC的面积．（2）是否存在点B，使得以A，B，C为顶点的三角形与△BCO相似？若存在，求OB 的长；若不存在，请说明理由．8.（2021•湖北省荆门市）如图，抛物线y＝ax2+bx+c交x轴于A（﹣1，0），B（3，0）两点，交y轴于点C（0，﹣3），点Q为线段BC上的动点．（1）求抛物线的解析式；（2）求|QO|+|QA|的最小值；（3）过点Q作PQ∥AC交抛物线的第四象限部分于点P，连接P A，PB，记△P AQ与△PBQ面积分别为S1，S2，设S＝S1+S2，求点P坐标，使得S最大，并求此最大值．9.（2021•江苏省盐城市）学习了图形的旋转之后，小明知道，将点P绕着某定点A顺时针旋转一定的角度α，能得到一个新的点P′，经过进一步探究，小明发现，当上述点P在某函数图象上运动时，点P ′也随之运动，并且点P ′的运动轨迹能形成一个新的图形． 试根据下列各题中所给的定点A 的坐标、角度α的大小来解决相关问题． 【初步感知】如图1，设A （1，1），α＝90°，点P 是一次函数y ＝kx +b 图象上的动点，已知该一次函数的图象经过点P 1（﹣1，1）．（1）点P 1旋转后，得到的点P 1′的坐标为 （1，3） ；（2）若点P ′的运动轨迹经过点P 2′（2，1），求原一次函数的表达式． 【深入感悟】如图2，设A （0，0），α＝45°，点P 是反比例函数y ＝﹣（x ＜0）的图象上的动点，过点P ′作二、四象限角平分线的垂线，垂足为M ，求△OMP ′的面积． 【灵活运用】 如图3，设A （1，﹣），α＝60°，点P 是二次函数y ＝x 2+2x +7图象上的动点，已知点B （2，0）、C （3，0），试探究△BCP ′的面积是否有最小值？若有，求出该最小值；若没有，请说明理由．10. （2021•重庆市A ）如图，在平面直角坐标系中，抛物线2y x bx c =++经过A （0，﹣1），B （4，1）．直线AB 交x 轴于点C ，P 是直线AB 下方抛物线上的一个动点．过点P 作PD ⊥AB ，垂足为D ，PE ∥x 轴，交AB 于点E ．（1）求抛物线的函数表达式；（2）当△PDE 的周长取得最大值时，求点P 的坐标和△PDE 周长的最大值；（3）把抛物线2y x bx c =++平移，使得新抛物线的顶点为（2）中求得的点P ．M 是新抛物线上一点，N 是新抛物线对称轴上一点，直接写出所有使得以点A ，B ，M ，N 为顶点的四边形是平行四边形的点M 的坐标，并把求其中一个点M 的坐标的过程写出来．11.（2021•重庆市B ）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx ﹣4（a ≠0）与x 轴交于点A （﹣1，0），B （4，0），与y 轴交于点C ． （1）求该抛物线的解析式；（2）直线l 为该抛物线的对称轴，点D 与点C 关于直线l 对称，点P 为直线AD 下方抛物线上一动点，连接P A ，PD ，求△P AD 面积的最大值．（3）在（2）的条件下，将抛物线y ＝ax 2+bx ﹣4（a ≠0）沿射线AD 平移4个单位，得到新的抛物线y 1，点E 为点P 的对应点，点F 为y 1的对称轴上任意一点，在y 1上确定一点G ，使得以点D ，E ，F ，G 为顶点的四边形是平行四边形，写出所有符合条件的点G 的坐标，并任选其中一个点的坐标，写出求解过程．12. （2021•湖北省十堰市） 已知抛物线25y ax bx =+-与x 轴交于点()1,0A -和()5,0B -，与y 轴交于点C ，顶点为P ，点N 在抛物线对称轴上且位于x 轴下方，连AN 交抛物线于M ，连AC 、CM ．（1）求抛物线的解析式；（2）如图1，当tan 2ACM ∠=时，求M 点的横坐标；（3）如图2，过点P 作x 轴的平行线l ，过M 作MD l ⊥于D ，若3MD MN =，求N 点的坐标．13. （2021•湖南省张家界市）如图，已知二次函数c bx ax y ++=2的图象经过点)3,2(-C ，且与x 轴交于原点及点)0,8(B .(1)求二次函数的表达式；(2)求顶点A 的坐标及直线AB 的表达式； （3）判断ABO 的形状，试说明理由；（4）若点P 为⊙O 上的动点，且⊙O 的半径为 22，一动点E 从点A 出发，以每秒2个单位长度的速度沿线段AP 匀速运动到点P ，再以每秒1个单位长度的速度沿线段PB 匀速运动到点B 后停止运动，求点E 的运动时间t 的最小值.14. （2021•海南省）已知抛物线y ＝ax 2+x +c 与x 轴交于A 、B 两点，与y 轴交于C 点，且点A 的坐标为（﹣1，0）、点C 的坐标为（0，3）． （1）求该抛物线的函数表达式；（2）如图1，若该抛物线的顶点为P ，求△PBC 的面积；（3）如图2，有两动点D 、E 在△COB 的边上运动，速度均为每秒1个单位长度，它们分别从点C 和点B 同时出发，点D 沿折线COB 按C →O →B 方向向终点B 运动，点E 沿线段BC 按B →C 方向向终点C 运动，当其中一个点到达终点时，另一个点也随之停止运动．设运动时间为t 秒，请解答下列问题： ①当t 为何值时，△BDE 的面积等于；②在点D 、E 运动过程中，该抛物线上存在点F ，使得依次连接AD 、DF 、FE 、EA 得到的四边形ADFE 是平行四边形，请直接写出所有符合条件的点F 的坐标．_y _x _ A_ B _ O _ C _ P15. （2021•广西玉林市）已知抛物线：234y ax ax a =--（0a >）与x 轴交点为A ，B（A 在B 的左侧），顶点为D ．（1）求点A ，B 的坐标及抛物线的对称轴； （2）若直线32y x =-与抛物线交于点M ，N ，且M ，N 关于原点对称，求抛物线的解析式；（3）如图，将（2）中抛物线向上平移，使得新的抛物线的顶点D 在直线7:8l y =上，设直线l 与y 轴的交点为O '，原抛物线上的点P 平移后的对应点为点Q ，若O P O Q ''=，求点P ，Q 的坐标．16. （2021•广西贺州市）如图，抛物线2y x bx c =++与x 轴交于A 、B 两点，且()1,0A -，对称轴为直线2x =．（1）求该抛物线的函数达式；（2）直线l 过点A 且在第一象限与抛物线交于点C ．当45CAB ∠=︒时，求点C 的坐标； （3）点D 在抛物线上与点C 关于对称轴对称，点P 是抛物线上一动点，令(,)P P P x y ，当1P x a ≤≤，15a ≤≤时，求PCD 面积的最大值（可含a 表示）．17. 2021•山东省济宁市）如图，直线y ＝﹣x +分别交x 轴、y 轴于点A ，B ，过点A 的抛物线y ＝﹣x 2+bx +c 与x 轴的另一交点为C ，与y 轴交于点D （0，3），抛物线的对称轴l 交AD 于点E ，连接OE 交AB 于点F ．（1）求抛物线的解析式；（2）求证：OE ⊥AB ；（3）P 为抛物线上的一动点，直线PO 交AD 于点M ，是否存在这样的点P ，使以A ，O ，M 为顶点的三角形与△ACD 相似？若存在，求点P 的横坐标；若不存在，请说明理由．18 . (2021•内蒙古包头市) 如图，在平面直角坐标系中，抛物线24y x x =-+经过坐标原点，与x 轴正半轴交于点A ，点(,)M m n 是抛物线上一动点．（1）如图1，当0m >，0n >，且3n m =时，①求点M 的坐标： ②若点15,4B y ⎛⎫ ⎪⎝⎭在该抛物线上，连接OM ，BM ，C 是线段BM 上一动点（点C 与点M ，B 不重合），过点C 作//CD MO ，交x 轴于点D ，线段OD 与MC 是否相等？请说明理由； （2）如图2，该抛物线的对称轴交x 轴于点K ，点7,3E x ⎛⎫ ⎪⎝⎭在对称轴上，当2m >，0n >，且直线EM 交x 轴的负半轴于点F 时，过点A 作x 轴的垂线，交直线EM 于点N ，G 为y 轴上一点，点G 的坐标为180,5⎛⎫ ⎪⎝⎭，连接GF ．若2EF NF MF +=，求证：射线FE 平分AFG ∠．19. （2021•齐齐哈尔市） 综合与探究如图，在平面直角坐标系中，抛物线2()20y ax x c a =++≠与x 轴交于点A 、B ，与y 轴交于点C ，连接BC ，1OA =，对称轴为2x =，点D 为此抛物线的顶点．（1）求抛物线的解析式；（2）抛物线上C，D两点之间的距离是__________；（3）点E是第一象限内抛物线上的动点，连接BE和CE．求BCE面积的最大值；（4）点P在抛物线对称轴上，平面内存在点Q，使以点B、C、P、Q为顶点的四边形为矩形，请直接写出点Q的坐标．20.（2021•内蒙古通辽市）如图，抛物线y＝ax2+bx+3交x轴于A（3，0），B（﹣1，0）两点，交y轴于点C，动点P在抛物线的对称轴上．（1）求抛物线的解析式；（2）当以P，B，C为顶点的三角形周长最小时，求点P的坐标及△PBC的周长；（3）若点Q是平面直角坐标系内的任意一点，是否存在点Q，使得以A，C，P，Q为顶点的四边形是菱形？若存在，请直接写出所有符合条件的点Q的坐标；若不存在，请说明理由．。

专题05 函数图像综合题1．（2021•重庆A 卷）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质及其应用的过程．以下是我们研究函数2241x y x -=+的性质及其应用的部分过程，请按要求完成下列各小题．（1）请把下表补充完整，并在给出的图中补全该函数的大致图象；x¼5-4-3-2-1-012345¼2241x y x -=+¼2126-1217-12-032432　0 ¼（2）请根据这个函数的图象，写出该函数的¨D 条性质；（3）已知函数332y x =-+的图象如图所示．根据函数图象，直接写出不等式2234321x x x --+>+的解集．（近似值保留一位小数，误差不超过0.2)【答案】见解析【详解】（1）把下表补充完整如下：x¼5-4-3-2-1-012345¼2241x y x -=+¼2126-1217-12-03243212-1217-2126¼函数2241x y x -=+的图象如图所示：（2）①该函数图象是轴对称图形，对称轴是y 轴；②该函数在自变量的取值范围内，有最大值，当0x =时，函数取得最大值4；③当0x <时，y 随x 的增大而增大：当0x >时，y 随x 的增大而减小（以上三条性质写出一条即可）；（3）由图象可知，不等式2234321x x x --+>+的解集为0.3x <-或12x <<．2．（2021•重庆B 卷）探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程．以下是我们研究函数|26|y x x m =+-++性质及其应用的部分过程，请按要求完成下列各小题．x¼2-1-012345¼y¼654a21b7¼（1）写出函数关系式中m 及表格中a ，b 的值：m =　2-　，a = ，b = ；（2）根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质： ；（3）已知函数16y x =的图象如图所示，结合你所画的函数图象，直接写出不等式16|26|x x m x+-++>的解集．【答案】见解析【详解】（1）当0x =时，|6|4m +=，解得：2m =-，即函数解析式为：|26|2y x x =+-+-，当1x =时，1|26|23a =+-+-=，当4x =时，4|246|24b =+-´+-=，故答案为：2-，3，4；（2）图象如右图，根据图象可知当3x =时函数有最小值1y =；（3）根据当|26|2y x x =+-+-的函数图象在函数16y x =的图象上方时，不等式16|26|2x x x+-+->成立，0x \<或4x >．3．（2020•重庆A 卷）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数261xy x =+性质及其应用的部分过程，请按要求完成下列各小题．（1）请把下表补充完整，并在图中补全该函数图象；x¼5-4-3-2-1-012345¼261x y x =+¼1513-2417-　95-　125-3-03125 24171513¼（2）根据函数图象，判断下列关于该函数性质的说法是否正确，正确的在答题卡上相应的括号内打“Ö”，错误的在答题卡上相应的括号内打“´”；①该函数图象是轴对称图形，它的对称轴为y 轴．②该函数在自变量的取值范围内，有最大值和最小值．当1x =时，函数取得最大值3；当1x =-时，函数取得最小值3-．③当1x <-或1x >时，y 随x 的增大而减小；当11x -<<时，y 随x 的增大而增大．（3）已知函数21y x =-的图象如图所示，结合你所画的函数图象，直接写出不等式26211xx x >-+的解集（保留1位小数，误差不超过0.2)．【答案】见解析【详解】（1）补充完整下表为：x¼5-4-3-2-1-012345¼261x y x =+¼1513-2417-95-125-3-031259524171513¼画出函数的图象如图：；（2）根据函数图象：①该函数图象是轴对称图形，它的对称轴为y 轴，说法错误；②该函数在自变量的取值范围内，有最大值和最小值．当1x =时，函数取得最大值3；当1x =-时，函数取得最小值3-，说法正确；③当1x <-或1x >时，y 随x 的增大而减小；当11x -<<时，y 随x 的增大而增大，说法正确．（3）由图象可知：不等式26211xx x >-+的解集为 1.0x <-或0.3 1.8x -<<．4．（2020•重庆B 卷）探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，请画出函数2122y x =-+的图象并探究该函数的性质．x ¼4-3-2-1-01234¼y¼23-a 2-4-b4-2-1211-23-¼（1）列表，写出表中a ，b 的值：a =　1211-　，b = ；描点、连线，在所给的平面直角坐标系中画出该函数的图象．（2）观察函数图象，判断下列关于函数性质的结论是否正确（在答题卡相应位置正确的用“Ö”作答，错误的用“´”作答）:①函数2122y x =-+的图象关于y 轴对称；②当0x =时，函数2122y x =-+有最小值，最小值为6-；③在自变量的取值范围内函数y 的值随自变量x 的增大而减小．（3）已知函数21033y x =--的图象如图所示，结合你所画的函数图象，直接写出不等式212210233x x -<--+的解集．【答案】见解析【详解】（1）3x =-、0分别代入2122y x =-+，得12129211a =-=-+，12602b =-=-+，画出函数的图象如图：故答案为：1211-，6-；（2）根据函数图象：①函数2122y x =-+的图象关于y 轴对称，说法正确；②当0x =时，函数2122y x =-+有最小值，最小值为6-，说法正确；③在自变量的取值范围内函数y 的值随自变量x 的增大而减小，说法错误．（3）由图象可知：不等式212210233x x -<--+的解集为4x <-或21x -<<．5．（2019•重庆A 卷）在初中阶段的函数学习中，我们经历了“确定函数的表达式--利用函数图象研究其性质一一运用函数解决问题“的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义(0)||(0)a a a a a ì=í-<î…．结合上面经历的学习过程，现在来解决下面的问题在函数|3|y kx b =-+中，当2x =时，4y =-；当0x =时，1y =-．（1）求这个函数的表达式；（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质；（3）已知函数132y x =-的图象如图所示，结合你所画的函数图象，直接写出不等式1|3|32kx b x -+-…的解集．【答案】见解析【详解】（1）Q 在函数|3|y kx b =-+中，当2x =时，4y =-；当0x =时，1y =-，\|23|4|3|1k b b -+=-ìí-+=-î，得324k b ì=ïíï=-î，\这个函数的表达式是3|3|42y x =--；（2）3|3|42y x =--Q ，37(2)231(2)2x x y x x ì-ïï\=íï--<ïî…，\函数372y x =-过点(2,4)-和点(4,1)-；函数312y x =--过点(0,1)-和点(2,2)-；该函数的图象如右图所示，性质是当2x >时，y 随x 的增大而增大；（3）由函数图象可得，不等式1|3|32kx b x -+-…的解集是14x ……．6．（2019•重庆B 卷）函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索．画函数2||y x =-的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数2||2y x =-+和2|2|y x =-+的图象如图所示．x¼3-2-1-0123¼y¼6-4-2-02-4-6-¼（1）观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解析式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化．写出点A ，B 的坐标和函数2|2|y x =-+的对称轴．（2）探索思考：平移函数2||y x =-的图象可以得到函数2||2y x =-+和2|2|y x =-+的图象，分别写出平移的方向和距离．（3）拓展应用：在所给的平面直角坐标系内画出函数2|3|1y x =--+的图象．若点1(x ，1)y 和2(x ，2)y 在该函数图象上，且213x x >>，比较1y ，2y 的大小．【答案】见解析【详解】（1）(0,2)A ，(2,0)B -，函数2|2|y x =-+的对称轴为2x =-；（2）将函数2||y x =-的图象向上平移2个单位得到函数2||2y x =-+的图象；将函数2||y x =-的图象向左平移2个单位得到函数2|2|y x =-+的图象；（3）将函数2||y x =-的图象向上平移1个单位，再向右平移3个单位得到函数2|3|1y x =--+的图象．所画图象如图所示，当213x x >>时，12y y >．7．（2021•沙坪坝区校级模拟）根据我们学习函数的过程与方法，对函数22|1|y x bx c x =++--的图象和性质进行探究，已知该函数图象经过(1,2)--与(2,1)两点，（1）该函数的解析式为 223|1|y x x x =-+--　，补全下表：x L 4-3-2-1-0123L yL21-2-212L（2）描点、连线，在所给的平面直角坐标系中画出该函数的图象，写出这个函数的一条性质： ．（3）结合你所画的图象与函数y x =的图象，直接写出22|1|x bx c x x ++--…的解集 ．【答案】见解析【详解】（1）Q 该函数22|1|y x bx c x =++--的图象经过(1,2)--与(2,1)两点，\21221422b cb c -=-+-ìí=++-î，\13b c =-ìí=î，223|1|y x x x \=-+--，4x =-时，2(4)423|41|1642157y =-++---=++-=，0x =时，0023|01|1y =++--=-，故答案为：223|1|y x x x =-+--，7，1-；（2）描点、连线，在所给的平面直角坐标系中画出该函数的图象，如图，由图象得这个函数的一条性质：函数有最小值，无最大值；（3）由（2）中画的图象与函数y x =的图象，22|1|x bx c x x ++--…的解集为 1.50.5x -……或1.5 3.5x ……．故答案为： 1.50.5x -……或1.5 3.5x ……．8．（2021•万州区模拟）在函数的学习中，我们经历“确定函数表达式--画函数图象--利用函数图象研究函数性质--利用图象解决问题”的学习过程，画函数图象时，我们常通过描点或平移或翻折的方法画函数图象，请根据你学到的函数知识探究函数12||(2)2(2)1x x y x x x -<ìï=-íï-î…的图象与性质并利用图象解决如下问题：列出1y 与x 的几组对应的值如表：x¼3-2-1-012345¼y¼m121n2334¼（1）根据表格中x 、y 的对应关系可得m =　1-　，n = ；（2）用你喜欢的方式画出该函数图象：根据函数图象，写出该函数的一条性质： ；（3）直接写出当函数1y 的图象与直线21y kx=+有三个交点时，k 的取值范围是 ．【答案】见解析【详解】（1）当3x =-时，231m y ==--=-，当3x =时，321312n y -===-；2（2）当02x <…时，2y x =-．当0x <时，2y x =+．当2x …时，21111x y x x -==---．如图，可得当0x …或2x …时，y 随x 增大而增大，当02x <<时，y 随x 增大而减小．故答案为：当0x …或2x …时，y 随x 增大而增大，当02x <<时，y 随x 增大而减小．（3）如图，Q 直线21y kx =+经过定点(0,1)，\当直线21y kx =+与x 轴交点在点(2,0)右侧时满足条件，即12k ->，102k -<<．29．（2021•九龙坡区校级模拟）已知函数|2|(y a x x b a =-++，b 为常数）．当3x =时，0y =，当0x =时，1y =-，请对该函数及其图象进行探究：（1）a =　　，b =　　；（2）请在给出的平面直角坐标系中画出该函数图象，并结合所画图象，写出该函数的一条性质．（3）已知函数245y x x =-++的图象如图所示，结合图象，直接写出不等式2|2|45a x x b x x -++-++…的解集．【答案】见解析【详解】（1）由题意得：|32|3021a b a b -++=ìí+=-î，解得25a b =ìí=-î，故答案为2，5-；（2）由（1）知函数的表达式为2|2|5y x x =-+-，当2x …时，2|2|539y x x x =-+-=-，当2x <时，2|2|51y x x x =-+-=--；根据函数表达式画出函数图象如下：从图象看，当2x …时，y 随x 的增大而增大，当2x <时，y 随x 的增大而减小（答案不唯一）；（3）从图象看两个函数交于点A 、(1,0)B -，联立39y x =-和245y x x =-++得：23945x x x -=-++，解得x =（负值已舍去），即点A，从函数图象看，不等式2|2|45a x x b x x -++-++…的解集为1x -…或x …．10．（2021•沙坪坝区校级模拟）学习函数时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，下面我们对函数322(0)32(0)x y x x x x -ì<ï=íï-+î…的图象和性质进行探究，请将以下探究过程补充完整：（1）选取适当的值补全表格；描点、连线，在所给的平面直角坐标系中画出函数的图象：x¼　3- ¼y¼¼（2）结合图象，写出该函数的一条性质： ；（3）结合这个函数的图象与性质，解决下列问题：①若点1(A x ，1)y ，2(B x ，2)y ，3(C x ，3)y 在这个函数的图象上，且303x <<，1210x x -<<<，请写出1y ，2y ，3y 的大小关系： （用“<”连接）．②若直线21(y a a =+是常数）与该函数图象有且只有三个交点，则a 的取值范围为 ．【答案】见解析【详解】（1）列表如下表所示：图象如图所示：（2）当0x <时，y 随x 增大而增大；当2x >时，y 随x 增大而增大（答案不唯一）；（3）①数形结合可知312y y y <<，故答案为：312y y y <<．②数形结合可知0212a <+…，解得1122a -<…，故答案为1122a -<…．11．（2021•沙坪坝区校级模拟）根据我们学习函数的过程和方法，对函数3124y x x =-的图象与性质进行探究．（1）如表是y 与x 的几组对应值：x¼ 3.5-3-2-1-0123 3.5¼y¼11932-m 274n2-3411932¼则m 的值为 ，n 的值为 ．（2）描点、连线，在所给的平面直角坐标系中画出该函数的图象，写出该函数的一条性质　　．（3）若3124x x x -…，结合图象，直接写出x 的取值范围　　．【答案】见解析【详解】（1）Q 表中各点关于原点对称，所以3x =-与3x =的值互为相反数，34m \=-，同理：74n =-，故34m =-，74n =-．（2）如图，性质为函数关于原点对称．（3）3124x x x -=，21(3)04x x -=，0x =或21304x -=，解得：0x =或x =或x =-由图得当3124x x x -…时0x -…或x …．12．（2021•沙坪坝区校级一模）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数25||4xy x =+性质及其应用的部分过程，请按要求完成下列各小题．（1）补全表：x6-5-4-　3-　2-32-1-013223 56y342529 546510 65541513 252934（2）在平面直角坐标系中，补全函数图象，根据函数图象，写出这个函数的一条性质： ；（3）已知函数512y x =-的图象如图所示，结合你所画的函数图象，直接写出关于x 的方程255||142x x x =-+的近似解（保留1位小数，误差不超过0.2)．【答案】见解析【详解】（1）分别将4x =-，3-，1，4代入25||4xy x =+，求得1y =，1513，1，3．故答案为：3-，4，1，1513，1，3；（2）补全该函数图象如图，由图象可得，函数图象是轴对称图形，对称轴是y 轴，故答案为：函数图象是轴对称图形，对称轴是y 轴；（3）观察图象可知，255||142x x x =-+的近似解为0.7x »．13．（2021•九龙坡区校级模拟）在函数学习中，我们经历了“确定函数表达式--画函数图象--利用函数图象研究函数性质的性质--利用图象解决问题”的学习过程．以下是我们研究函数212||||(2)1(26)2x a x x y bx x ì-ï=í-<ï-î……的性质及其应用的部分过程，请你按要求完成下列问题：（1）列表：如表为变量x 与1y 的几组对应数值：x¼2-1-12-0112234561y ¼4012-0012-421214-根据表格中的数据求1y 与x 的函数解析式及并写出对应的自变量x 的取值范围；（2）描点、连线：在右侧的平面直角坐标系中，画出该函数的图象，并写出该函数的一条性质　　；（3）观察函数图象：当方程11y c =+有且仅有三个不等的实数根时，根据函数图象直接写出c 的取值范围　　．【答案】见解析【详解】（1）当2x …时，212||||y x a x =-，把1x =-，10y =代入得，20a -=，2a \=，当26x <…时，112by x =--，把3x =，12y =代入得，1232b-=-，解得3b =，\212||2||(2)31(26)2x x x y x x ì-ï=í-<ï-î……；（2）如图所示即是所画的函数图象，性质：当0.5x =-或0.5时函数图象对应点最低，此时函数值最小，最小值为0.5-（答案不唯一），故答案为：当0.5x =-或0.5时函数图象对应点最低，此时函数值最小，最小值为0.5-（答案不唯一）；（3）画出直线11y c =+的图象，上下平移此图象，方程11y c =+有且仅有三个不等的实数根时，即图象1y 与直线1y c =+有且仅有三个交点，014c \<+…，得13c -<…，故答案为：13c -<…．14．（2021•九龙坡区校级模拟）在初中阶段的函数学习中，我们经历了“确定函数的表达式--利用函数图象研究其性质--运用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了所学的函数图象．同时，我们也学习了绝对值的意义(0)||(0)a a a a a ì=í-<î…．小东结合上面的学习过程，对函数31|3|522y x x =-+-的图象与性质进行了探究．（1）化简函数的表达式：当2x …时，y = ，当2x <时，y = ；（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数的图象并写出这个函数的一条性质：　　；（3）已知函数2(0)y x x =>的图象如图所示，结合你所画函数图象，直接写出312|3|522x x x-+-=的近似解　　．（精确到0.1)【答案】见解析【详解】（1）2x …时，31352822y x x x =-+-=-，2x <时，3135222y x x x =-++-=--；（2）图象如下图：性质不唯一，比如y 最小值是4-，2x …时y 随x 的增大而增大等；（3）画出图象估计交点横坐标近似值： 4.2x=．15．（2021•九龙坡区校级模拟）在画函数图象时，我们常常通过描点或平移或翻折的方法画函数图象．小明根据学到的函数知识探究函数1|4|y ax b=+-的图象与性质并利用图象解决问题．小明列出了如表1y与x 的几组对应的值：x¼5-4-3-2-1-0123¼1y¼311-3-1-1357¼（1）根据表格，直接写出a=　2　，b= ；（2）在平面直角坐标系中，画出该函数图象，并根据函数图象，写出该函数的一条性质 ；（3）当函数1y 的图象与直线21y mx =-有两个交点时，直接写出m 的取值范围．【答案】见解析【详解】（1）将(0,1)代入1|4|y ax b =+-得1|4|b =-，解得3b =，1|4|3y ax \=+-，将(1,1)--代入1|4|3y ax =+-得1|4|3a -=-+-，解得2a =或6a =，将(1,3)代入1|4|3y ax =+-得3|4|3a =+-，解得2a =或10a =-，2a \=，故答案为：2a =，3b =；（2）图象如答图1，性质不唯一，比如1y 最小值为3-，2x -…时1y 随x 的增大而增大等；（3）如答图2，直线21y mx =-过点(0,1)A -，函数1|4|y ax b =+-的图象最低点(2,3)B --，当直线21y mx =-过点(0,1)A -和(2,3)B --时，函数1y 的图象与直线21y mx =-只有一个交点，由321m -=--解得：1m =，当直线直线21y mx =-与直线27y x =--平行时，函数1y 的图象与直线21y mx =-又只有一个交点，此时2m =-，根据图象可知21m -<<时，函数1y 的图象与直线21y mx =-有两个交点，故答案为：21m -<<．16．（2021•沙坪坝区校级模拟）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数26622x y x x -=--+性质及其应用的部分过程，请按要求完成下列各小题．（1）请把下表补充完整，并在图中补全该函数图象：x¼5-4-3-2-1-012345¼26622x y x x -=--+¼363715132417　95　12533- 95-2417¼（2）观察函数图象，写出该函数的一条性质 ；（3）已知函数715y x =-+的图象如图所示，结合你所画的函数图象，直接写出不等式26671225x x x x ---+-+…的解集（保留1位小数，误差不超过0.2)．【答案】见解析【详解】（1）把下表补充完整如下：x¼5-4-3-2-1-012345¼26622x y x x -=--+¼3637151324179512533-125-95-2417¼函数26622x y x x -=--+的图象如图所示：（2）由图可知，当0x <时，y 随x 值的增大而增大，故答案为当0x <时，y 随x 值的增大而增大；（3）由图象可知，不等式26671225x x x x ---+-+…的解集为2 1.3x -……或 2.5x …．17．（2021•九龙坡区校级模拟）函数图象在探索函数的性质中有非常重要的作用，现在就一类特殊的函数展开探索：ay x x=+，探索函数图象和性质过程如下：x ¼6-4-2-1-0.5-0.51n 46¼y¼203-m4-5-172-172545203¼（1）上表是该函数y 与自变量x 的几组对应值，则a = ，m = ，n = ；（2）如图，在平面直角坐标系中，已经描出了表中部分点，请根据描出的点画出该函数图象；（3）由函数图象，写出该函数的一条性质： ；（4）请在同一个平面直角坐标系中画出函数2y x =的图象，并直接写出不等式2ax x x+…的解集： ．【答案】见解析【详解】（1）1x =-时，5y =-，15a \--=-，4a \=．\4y x x=+，令4x =-，得5m =-，令4y =，得2n =，故答案为：4；5-；2．（2）图象如图所示：（3）该函数图象关于原点对称；当2x >时，随x 的增大而增大；当2x <-时，随x 的增大而增大，（答案不唯一，写出一条即可）．（4）图象如图所示；20x -<…或2x …．解：两个函数的交点坐标为(2,4)--和(2,4)，数形结合可知不等式的解集为20x -<…或2x …．故答案为：20x -<…或2x …．18．（2021•九龙坡区校级模拟）已知|24|(y a x bx a =++，b 为常数）．当1x =时，5y =；当1x =-时，3y =．（1）a =　　，b =　　；（2）在给出的平面直角坐标系中，请用你喜欢的方法画出这个函数图象；并写出函数的一条性质：　　；（3）已知函数25|22|y x =-的图象如图所示，结合你所画的函数图象，直接写出方程25|24||22|a x bx x ++=-的近似解（精确到0.1)．【答案】见解析【详解】（1）根据题意可得，|24|5|24|3a b a b ++=ìí-+-=î，解得11a b =ìí=-î，故答案为：1；1-．（2）根据题意，当2x -…时，240x +…，244y x x x =+-=+；当0x <时，240x +<，则2434y x x x =---=--．4(2)34(2)x x y x x +-ì\=í--<-î…；由函数解析式可画出对应的函数图象，根据函数图象可得出对应函数的性质．故答案为：当2x -…时，y 随x 的增大而增大．（3）根据函数图象，交点的横坐标就是该方程的解，根据图象估算对应的解为：1 2.5x =-，2 2.8x =．19．（2021•渝中区模拟）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是张华同学研究函数()227,221,(22)x x x y x x ì--=í-+-<<î或……图象、性质及其应用的部分过程，试解答下列问题：（1）请写出下列表中m 、n 的值，并在给定的平面直角坐标系中画出该函数的图象；x ¼3-52-2-32-1-12-0121322523¼y ¼234-3-54-0341m 054-n 34-2¼（2）根据所画函数的图象，写出该函数的两条性质：① ；②　　．（3）若直线1y kx =-，(0)k >与函数()227,221,(22)x x x y x x ì--=í-+-<<î或……的图象至少有3个交点，则k 的取值范围为 ．【答案】见解析【详解】（1）当12x =时，2131144m x =-+=-+=．当2x =时，27473n x =-=-=-．如图所示：；（2）由图象可知：①函数图象关于y 轴对称；②函数有最小值3-；故答案为：函数图象关于y 轴对称；函数有最小值3-．（3）把(2,3)--代入1y kx =-得，321k -=--，解得1k =，把(2,3)-代入1y kx =-得，321k -=-，解得1k =-，根据函数图象，直线1y kx =-，(0)k >与函数()227,221,(22)x x x y x x ì--=í-+-<<î或……的图象至少有3个交点，则k 的取值范围为01k <…，故答案为01k <…．20．（2021•九龙坡区模拟）小明结合自己的学习经验，对新函数21by kx =+的解析式、图象、性质及应用进行探究：已知当0x =时，2y =；当1x =时，1y =．（1）函数解析式探究：根据给定的条件，可以确定由该函数的解析式为： ．（2）函数图象探究：①根据解析式，补全如表，则m =　　，n =　　．②根据表中数据，在如图所示的平面直角坐标系中描点，并画出函数图象．x¼4-3-2-1-12-1212n 4¼y¼2171525m8528512515217¼（3）函数性质探究：请你结合函数的解析式及所画图象，写出该函数的一条性质： ．（4）综合应用：已知函数78||1515y x =-的图象如图所示，结合你所画的函数图象，直接写出不等式278||15151bx kx -+…．【答案】见解析【详解】（1）将点(0,2)，(1,1)代入21by kx =+，得到1k =，2b =，221y x \=+，故答案为221y x =+；（2）①把1x =-代入221y x =+得，1y =，1m \=，把15y =代入221y x =+得，21251x =+，解得3x =±，3n \=，故答案为1，3:②画出函数图象如图；（3）由图可知，函数图象关于y 轴对称；故答案为函数图象关于y 轴对称；（4）观察图象，不等式278||15151bx kx -+…的解集为12x -……．21．（2021•渝中区校级二模）若一个函数当自变量在不同范围内取值时，函数表达式不同，我们称这样的函数为分段函数，下面我们参照学习函数的过程与方法，探究分段函数12(0)1|24|2(0)x y x x x ìï=-íï--+>î…的图象与性质，探究过程如下，请补充完整．（1）列表：x¼4-3-2-1-01234¼y¼0.4-0.5-m1-n0p2-¼其中，m = ，n = ，p =　　；（2）在平面直角坐标系中，描出相应的点，画出函数的图象；（3）观察函数图象，写出该函数图象的一条性质；（4）已知函数22122y x =-的图象如图所示，结合你画的函数图象，直接写出不等式12yy …的解集为 （保留一位小数，误差小于0.2)．【答案】见解析【详解】（1）当2x =-时，2213m y x ==-=--，当0x =时，221n y x==-=--，当2x =时，同理可得2y =，故答案为23-，2-，2；（2）通过描点连线绘制函数图象如下：（3）从图象看，0x …时，y 随x 的增大而减小（答案不唯一）；（4）两个函数的位置关系如下：从图象看，两个函数交点的横坐标分别为： 1.4-、0、2.4（答案不唯一），观察函数图象，12y y …的解集为 1.4x -…或 2.4x …或0.0x =，故答案为 1.4x -…或 2.4x …或0.0x =．22．（2021•沙坪坝区模拟）探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程，以下是我们研究函数2||2xy x =-的性质及其应用的部分过程，请按要求完成下列各小题：（1）请直接写出表中m ，n 的值，并在图中补全该函数图象；x¼5-4-3-2-1-013234567¼2||2x y x =-¼1074365m230266n1033145¼（2）结合函数图象，直接写出该函数的一条性质；（3）已知函数41855y x =+的图象如图所示，结合你所画的函数图象，直接写出不等式4182||552x x x +-的解集（保留1位小数，误差不超过0.2)．【答案】见解析【详解】（1）分别将2x =-，4代入2||2xy x =-，求得1y =，4．1m \=，4n =；（2）补全该函数图象如图，由图象可得，当2x >时，y 随x 的增大而减小；’（3）观察图象可知，不等式4182||552x x x +-…的解集为3 1.4x -……或3x …．23．（2021•九龙坡区模拟）在初中阶段的函数学习中，我们经历了列表、描点、连线、画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数2|2|y x x c =-+的过程．（1）已知函数过点(1,4)，则这个函数的解析式为　2|25|y x x =-+或2|23|y x x =--　；（2）在（1）的条件下，在平面直角坐标系中，若函数2|2|y x x c =-+的图象与x 轴有两个交点，请画出该函数的图象，并写出函数图象的性质：　　（写出一条即可）．（3）结合（2）中你所画的函数图象，求不等式2|2||1|x x c x -++…的解集．【答案】见解析【详解】（1）Q 函数2|2|y x x c =-+过点(1,4)，4|12|c \=-+，5c \=或3c =-，Q 这个函数的解析式为2|25|y x x =-+或2|23|y x x =--，故答案为2|25|y x x =-+或2|23|y x x =--；（2）在（1）的条件下，在平面直角坐标系中，若函数2|2|y x x c =-+的图象与x 轴有两个交点，则2|23|y x x =--，画出函数如图所示：观察图象可知，函数图象关于直线1x =对称，故答案为函数图象关于直线1x =对称．（3）根据函数图象，不等式2|2||1|x x c x -++…的解集为2x …或4x …．24．（2021•重庆模拟）在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图象，并结合图象研究函数性质的过程．以下是我们研究函数2|2|y x x ax k =+++性质及其应用的部分过程，请按要求完成下列各小题．x¼4-3-2-32-1-12-121¼y¼753121-32-1-123¼（1）如表是y 与x 的几组对应值，则a = ，k = ；（2）如图，在平面直角坐标系中，已描出了部分点并绘制了部分图象，请把该函数的图象补充完整，并写出该函数的一条性质：　　；（3）如图，在平面直角坐标系中作出了函数2y x =-+的图象，结合你所画的函数图象，直接写出不等式2|2|30x x ax x +++-…的解集（结果保留1位小数，误差不超0.2)．【答案】见解析【详解】（1）将4x =-时，7y =和3x =-时，5y =代入函数解析式，得：4|42|167a k -´-+++=，即：1615......a k +=①，3|32|95a k -´-+++=，即：98......a k +=②，由①②，得：1a =，1k =-；（2）函数图象如上图，函数y 在12x =-时，取得最小值32-，12x <-时，y 随x 的增大而减小，12x >-时，y 随x 的增大而增大；（3）由（1）知，函数的关系式为：2|2|1y x x x ¢=++-，当2x -…，即20x +…时，22(2)1221y x x x x x ¢=++-=+-，当2x <-时，222(2)12121y x x x x x x x ¢=--+-=--+-=--，即：22|2|3x x ax x +++-，2y x =¢+-，令2|2|3y x x ax x =+++-，则：当2x <-时，2(2)33y x x x x x =--++-=--，当3x =-时，0y =，当2x -…时，22(2)3233y x x x x x x =+++-=+-，对称轴34x =-，当0.69x =»时，0y =，结合（2）中的图象，可以推出2|2|3y x x ax x =+++-的图象在34x -…时，随x 的增大而减小，在34x >-时，随x 的增大而增大．\不等式2|2|30x x ax x +++-…的解集为：3x -…或0.69x …，25．（2021•沙坪坝区校级模拟）某“数学兴趣小组”根据学习函数的经验，对函数246(2)x y x -+=-的图象和性质进行了探究，探究过程如下，请补充完整：x¼3-2-1-0323456¼y¼182574109m 06-52-n98-¼（1）m =　32　，n = ；（2）同学们先找到y 与x 的几组对应值，然后在下图的平面直角坐标系xOy 中，描出各对应值为坐标的点．请你根据描出的点，画出该函数的图象；（3）根据函数图象，写出该函数的一条性质： ．（4）结合你所画的函数图象，直接写出不等式2462(2)x x x -+-+-…的解集为　　．【答案】见解析【详解】（1）把0x =代入24663(2)42x y x -+===-，把5x =代入24620614(2)99x y x -+-+===--，\32m =，149n =-，故答案为32m =，149n =-；（2）描点、连线画出函数图象如图，（3）由图象可知，当1x =时，函数有最大值为2，故答案为当1x =时，函数有最大值为2；（4）观察图象，不等式2462(2)x x x -+-+-…的解集为0.3 1.4x ……或 4.2x …，故答案为0.3 1.4x ……或 4.2x …．26．（2021•渝中区校级模拟）在初中阶段的学习中，我们经历了列表，描点，连线画出函数图象，并结合图象研究函数性质的过程．以下是我们研究函数22835x y x =-+性质及其应用的部分过程．请按要求完成下列各小题．（1）请把下表补充完整，并在图中补全该函数图象：x¼5-4-3-2-32-1-01322345¼y¼1136521157　59　1529-53- 1529-591576521113¼（2）观察该函数图象，写出该函数图象的一条性质：　　．（3）已知函数3375y x =-的图象如图所示，结合你所画的函数图象，直接写出不等式的解集： ．（保留1位小数，误差不超过【答案】见解析223383755x x x --+…0.2)【详解】（1）把代入得，，把代入得，；把代入得，，如图所示：画出函数的图象如图：；故答案为，，；（2）根据函数图象，该函数图象关于轴对称，故答案为该函数图象关于轴对称；（3）由图象可知：不等式的解集为或，故答案为或．27．（2021•渝中区校级一模）探究函数性质时，我们经历了列表，描点，连线画出函数图象，观察分析图象特征，概括函数性质的过程，结合已有的学习经验，请结合表中的数据，画图并探究该函数的性质．012342x =-22835x y x =-+59y =0x =22835x y x =-+3y =-1x =22835x y x =-+53y =-593-53-y y 223383755x x x --+... 1.1x -... 1.8x ...1.1x -... 1.8x (22)ay x =-+x¼4-3-2-1-¼。

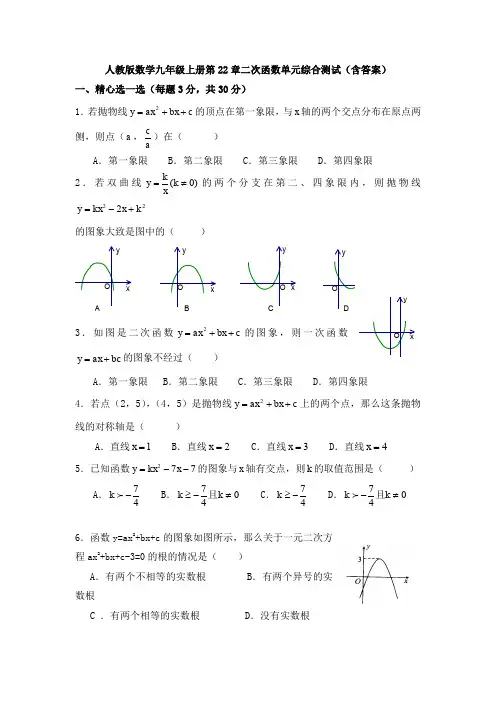
人教版数学九年级上册第22章二次函数单元综合测试（含答案） 一、精心选一选（每题3分，共30分）1．若抛物线c bx ax y ++=2的顶点在第一象限，与x 轴的两个交点分布在原点两侧，则点（a ，ac）在（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限 2．若双曲线)0(≠=k xky 的两个分支在第二、四象限内，则抛物线222k x kx y +-=的图象大致是图中的（ ）3．如图是二次函数c bx ax y ++=2的图象，则一次函数bc ax y +=的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限4．若点（2，5），（4，5）是抛物线c bx ax y ++=2上的两个点，那么这条抛物线的对称轴是（ ）A ．直线1=xB ．直线2=xC ．直线3=xD ．直线4=x 5．已知函数772--=x kx y 的图象与x 轴有交点，则k 的取值范围是（ ）A ．47- kB ．047≠-≥k k 且C ．47-≥kD ．047≠-k k 且6．函数y=ax 2+bx+c 的图象如图所示，那么关于一元二次方程ax 2+bx+c-3=0的根的情况是（ ）A ．有两个不相等的实数根B ．有两个异号的实数根C ．有两个相等的实数根D ．没有实数根xyOxyO xyO O yx DCBAOyx7．现有A ，B 两枚均匀的小立方体（立方体的每个面上分别标有数字1，2，3，4，5，6），用小莉掷A 立方体朝上的数字为x ，小明掷B 立方体朝上的数字为y 来确定点P （x ，y ），那么他们各掷一次所确定的点P 落在已知抛物线y=－x 2+4x 上的概率为（ ） A ．118 B ．112 C ．19 D ．168．已知a<－1，点（a －1，y 1），（a ，y 2），（a+1，y 2）都在函数y=x 2的图象上，则（ ）A ．y 1<y 2<y 3B ．y 1<y 3<y 2C ．y 3<y 2<y 1D ．y 2<y 1<y 3 9．已知二次函数y=ax 2+bx+c （a ≠0）的图象如图所示，给出以下结论：①a+b+c<0；②a －b+c<0；③b+2a<0；④abc>0，其中所有正确结论的序号是（ ）A ．③④B ．②③C ．①④D ．①②③ 第9题图 10. 已知二次函数y x x =++29342，当自变量x 取两个不同的值x x 12,时，函数值相等，则当自变量x 取x x 12+时的函数值与（ ）。

2021年重庆市中考二轮复习 第22题函数图像专练 专题 (一)1.已知函数y=1x 62+，请根据已学知识探究该函数的图像和性质. (1)列表，写出表中a 、b 、c 的值: a= ，b ，c .(2)描点、连线，在下面的平面直角坐标系中画出该函数的图像，并写出该函数的一条性质: . (3)已知函数y= x+2的图像如图所示，结合你所画的函数图像，直接写出不等式2x ≥1x 62++的解集: .2.小帆根据学习函数的过程与方法，对函数y=21x|ax+b| (a>0 )的图象与性质进行探究.已知该函数图象经过点(2.1)，且与x 轴的一个交点为(4，0).(1)求函数的解析式;(2)在给定的平面直角坐标系中: ①补全该函数的图象;②当2≤x ≤4时，y 随x 的增大而 (在横线上填增大或减小);③当x<4时，y=41x|ax+b|列的最大值是 ；④直线y=k 与函数y=41x|ax+b|有两个交点，则k= .3.在初中阶段的函数学习中，我们经历了列表、描点、连线画函数图像，并结合函数图像研究函数性质的过程.以下是我们研究函数的y=4x32-x 图象、性质与应用的部分过程，请按要求完成以下各小题.(1)请把下表补充完成，并根据表中数据在平面直角坐标系中描点，连线，画出该函数图象.(2)根据函数图像，判断下列关于该函数及其性质的说法是否正确，正确的请在答题卡上对应的括号内打“√”，错误的请在答题卡上对应的括号内打“×”. ①该函数的自变量的取值范围是x ≠士2; ( )②该函数图像是中心对称图形，对称中心是原点;( ) ③在自变里的取值范围内，y 随x 的增大而减小;( )(3)已知函数y=x-21的图像如如所示，结合函数圈像，请直接写出方程-=-x x 4x 3221的解; (结果保留1位小数，误差不超过0.2)4.在初中阶授的函教学习中,我们经历了列表、描点、连线画函数图象，并结合图像研究函数性质的过程，小哲根据己学的函数知识对函数y=|1-x |a的图象与性质进行了探究，其探究过程中的列表如下:(1)请写出a 和b 的值;(2根据表中数据，在如图所示的平面直角坐标系中描点,并画出该函数的图象; (3)直线y=x-1的图象图所示，结合你所画的函数图象，直接写出不等式1x |1-x |a-≥的解集.。

人教版九年级上册第二十二章二次函数单元检测（含答案）一、选择题221y ax xa=++-的图象可能是（）提示：对于122-++=axaxy的图象，对称轴是直线ax21-=，当0>a时，021<-a，则抛物线的对称轴在y轴左侧，A、B、C、D四个选项均不符合；当0<a时，021>-a，则抛物线的对称轴在y轴右侧，只有B项图象符合，故选B2．抛物线247y x x=--的顶点坐标是（）A．(211)-，B．(27)-，C．(211)，D．(23)-，提示：11)2(114474222--=-+-=--=xxxxxy所以顶点坐标为(211)-，选A3．二次函数y＝ax2＋bx＋c图象如图1所示，则点A(ac，bc)在（）．A、第一象限B、第二象限C、第三象限D、第四象限提示：由二次函数y＝ax2＋bx＋c图象可知：0,0><ca，∵对称轴0>x，在y轴右侧，即02>-ab，所以0>b，∴0,0><bcac，即点A(ac，bc)在第二象限选B4．把抛物线22y x=-向上平移1个单位，得到的抛物线是（）A．22(1)y x=-+B．22(1)y x=--C．221y x=-+D．221y x=--提示：备选答案A是向左移，备选答案B是向右移，备选答案D是向下移，所以选D5．已知二次函数)0(2≠++=acbxaxy的图象如图2所示，有下列5个结论：①0>abc；②cab+<；③024>++cba；④bc32<；⑤)(bammba+>+，（1≠m的实数）其中正确的结论有（）A. 2个B. 3个C. 4个D. 5个A B C D图2提示：由图象可知：12,0,0=-><a b c a ，即b a 21-= ∴0>b 故①不正确；由1-=x 时，0<y 得0<+-c b a ，∴c a b +>，所以②不正确；由2=x 时，0>y ，即024>++c b a ，所以③正确；由b a 21-=及0<+-c b a 得④也正确；由1=x 时y 取最大值，故⑤正确，所以选B6．已知一次函数y = ax + b 的图象过点（－2，1），则关于抛物线y = ax 2－bx + 3的三条叙述： ① 过定点（2，1）， ② 对称轴可以是x = 1，③ 当a ＜0时，其顶点的纵坐标的最小值为3．其中所有正确叙述的个数是( )A ．0B ．1C ．2D ．3提示：把(-2，1)代入b ax y +=得b a +-=21 把(-2，1)代入32+-=bx ax y 得3241++=b a ，上述两个同解，所以①成立，由对称轴1=x 得12=ab，得a b 2=，与b a +-=21矛盾，所以②不成立；由于y = ax 2－bx + 3与y 轴交于点(0，3)，所以抛物线的顶点最小值为3，③成立 ，所以选C二、填空题72＋bx ＋c 中，函数y 与自变量x 的部分对应值如下表：则m 的值为__________．提示：选择两组y x ,的值代入c bx x y ++=2得⎩⎨⎧++=-++=-c b c 12001 解得⎩⎨⎧-=-=12c b ∴122--=x x y 把2=x 代入122--=x x y 得 1144-=--=y 即1-=m8．抛物线y ＝ax 2＋2ax ＋a 2＋2的一部分如图3所示，那么该抛物线在y 轴右侧与x 轴交点的坐标是_________ 提示：抛物线y ＝ax 2＋2ax ＋a 2＋2的对称轴为122-=-=aax 由图象可知抛物线与x 轴的一个交点为(-3，0)，到直线1-=x 的距离为2，∴另一个交点为(1，0)9．将抛物线22(1)3y x =+-向右平移1个单位，再向上平移3个单位，则所得抛物线的表达式为 ．提示：将抛物线22(1)3y x =+-向右平移1个单位为322-=x y ，再向上平移3个单位得到3322+-=x y 即22x y =图310．已知二次函数22y x x m =-++的部分图象如图4所示，则关于x 的一元二次方程220x x m -++=的解为 ．提示：由图象可知抛物线对称轴为1=x ，与x 轴交点(3，0)一元二次方程220x x m -++=一、选择题221y axx a =++-的图象可能是（ ）提示：对于122-++=a x ax y 的图象，对称轴是直线a x 21-=，当0>a 时，021<-a，则抛物线的对称轴在y 轴左侧，A 、B 、C 、D 四个选项均不符合；当0<a 时，021>-a，则抛物线的对称轴在y 轴右侧，只有B 项图象符合，故选B2．抛物线247y x x =--的顶点坐标是（ ） A ．(211)-，B ．(27)-，C ．(211)，D ．(23)-，提示：11)2(114474222--=-+-=--=x x x x x y 所以顶点坐标为(211)-， 选A3． 二次函数y ＝ax 2＋bx ＋c 图象如图1所示，则点A(ac ，bc)在（ ）．A 、第一象限B 、第二象限C 、第三象限D 、第四象限提示：由二次函数y ＝ax 2＋bx ＋c 图象可知：0,0><c a ，∵对称轴0>x ，在y 轴右侧，即02>-ab ，所以0>b ，∴0,0><bc ac ，即点A(ac ，bc)在第二象限 选B4．把抛物线22y x =-向上平移1个单位，得到的抛物线是（ ）图4图5A B C DA ．22(1)y x =-+ B ．22(1)y x =-- C ．221y x =-+D ．221y x =--提示：备选答案A 是向左移，备选答案B 是向右移，备选答案D 是向下移，所以选D5．已知二次函数)0(2≠++=a c bx ax y 的图象如图2所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（ ） A. 2个 B. 3个 C. 4个D. 5个提示：由图象可知：12,0,0=-><a b c a ，即b a 21-= ∴0>b 故①不正确；由1-=x 时，0<y 得0<+-c b a ，∴c a b +>，所以②不正确；由2=x 时，0>y ，即024>++c b a ，所以③正确；由b a 21-=及0<+-c b a 得④也正确；由1=x 时y 取最大值，故⑤正确，所以选B6．已知一次函数y = ax + b 的图象过点（－2，1），则关于抛物线y = ax 2－bx + 3的三条叙述： ① 过定点（2，1）， ② 对称轴可以是x = 1，③ 当a ＜0时，其顶点的纵坐标的最小值为3．其中所有正确叙述的个数是( )A ．0B ．1C ．2D ．3提示：把(-2，1)代入b ax y +=得b a +-=21 把(-2，1)代入32+-=bx ax y 得3241++=b a ，上述两个同解，所以①成立，由对称轴1=x 得12=ab，得a b 2=，与b a +-=21矛盾，所以②不成立；由于y = ax 2－bx + 3与y 轴交于点(0，3)，所以抛物线的顶点最小值为3，③成立 ，所以选C二、填空题72则m 的值为__________．提示：选择两组y x ,的值代入c bx x y ++=2得图2⎩⎨⎧++=-++=-c b c 12001 解得⎩⎨⎧-=-=12c b ∴122--=x x y 把2=x 代入122--=x x y 得 1144-=--=y 即1-=m8．抛物线y ＝ax 2＋2ax ＋a 2＋2的一部分如图3所示，那么该抛物线在y 轴右侧与x 轴交点的坐标是_________ 提示：抛物线y ＝ax 2＋2ax ＋a 2＋2的对称轴为122-=-=aax 由图象可知抛物线与x 轴的一个交点为(-3，0)，到直线1-=x 的距离为2，∴另一个交点为(1，0)9．将抛物线22(1)3y x =+-向右平移1个单位，再向上平移3个单位，则所得抛物线的表达式为 ．提示：将抛物线22(1)3y x =+-向右平移1个单位为322-=x y ，再向上平移3个单位得到3322+-=x y 即22x y =10．已知二次函数22y x x m =-++的部分图象如图4所示，则关于x 的一元二次方程220x x m -++=的解为 ．提示：由图象可知抛物线对称轴为1=x ，与x 轴交点(3，0)一元二次方程220x x m -++=一、选择题221y ax x a =++-的图象可能是（ ）提示：对于122-++=a x ax y 的图象，对称轴是直线a x 21-=，当0>a 时，021<-a，图4 图5图3A B C D则抛物线的对称轴在y 轴左侧，A 、B 、C 、D 四个选项均不符合；当0<a 时，021>-a，则抛物线的对称轴在y 轴右侧，只有B 项图象符合，故选B 2．抛物线247y x x =--的顶点坐标是（ ） A ．(211)-，B ．(27)-，C ．(211)，D ．(23)-，提示：11)2(114474222--=-+-=--=x x x x x y 所以顶点坐标为(211)-， 选A3． 二次函数y ＝ax 2＋bx ＋c 图象如图1所示，则点A(ac ，bc)在（ ）．A 、第一象限B 、第二象限C 、第三象限D 、第四象限提示：由二次函数y ＝ax 2＋bx ＋c 图象可知：0,0><c a ，∵对称轴0>x ，在y 轴右侧，即02>-ab ，所以0>b ，∴0,0><bc ac ，即点A(ac ，bc)在第二象限 选B4．把抛物线22y x =-向上平移1个单位，得到的抛物线是（ ） A ．22(1)y x =-+ B ．22(1)y x =-- C ．221y x =-+D ．221y x =--提示：备选答案A 是向左移，备选答案B 是向右移，备选答案D 是向下移，所以选D5．已知二次函数)0(2≠++=a c bx ax y 的图象如图2所示，有下列5个结论：① 0>abc ；② c a b +<；③ 024>++c b a ；④ b c 32<；⑤ )(b am m b a +>+，（1≠m 的实数）其中正确的结论有（ ） A. 2个 B. 3个 C. 4个D. 5个提示：由图象可知：12,0,0=-><a b c a ，即b a 21-= ∴0>b 故①不正确；由1-=x 时，0<y 得0<+-c b a ，∴c a b +>，所以②不正确；由2=x 时，0>y ，即024>++c b a ，所以③正确；由b a 21-=及0<+-c b a 得④也正确；由1=x 时y 取最大值，故⑤正确，所以选B6．已知一次函数y = ax + b 的图象过点（－2，1），则关于抛物线y = ax 2－bx + 3的三条叙述： ① 过定点（2，1）， ② 对称轴可以是x = 1，③ 当a ＜0时，其顶点的纵坐标的最小值为3．其中所有正确叙述的个数是( )图2A ．0B ．1C ．2D ．3提示：把(-2，1)代入b ax y +=得b a +-=21 把(-2，1)代入32+-=bx ax y 得3241++=b a ，上述两个同解，所以①成立，由对称轴1=x 得12=ab，得a b 2=，与b a +-=21矛盾，所以②不成立；由于y = ax 2－bx + 3与y 轴交于点(0，3)，所以抛物线的顶点最小值为3，③成立 ，所以选C二、填空题72＋bx ＋c 中，函数y 与自变量x 的部分对应值如下表：则m 的值为__________．提示：选择两组y x ,的值代入c bx x y ++=2得⎩⎨⎧++=-++=-c b c 12001 解得⎩⎨⎧-=-=12c b ∴122--=x x y 把2=x 代入122--=x x y 得 1144-=--=y 即1-=m8．抛物线y ＝ax 2＋2ax ＋a 2＋2的一部分如图3所示，那么该抛物线在y 轴右侧与x 轴交点的坐标是_________ 提示：抛物线y ＝ax 2＋2ax ＋a 2＋2的对称轴为122-=-=aax 由图象可知抛物线与x 轴的一个交点为(-3，0)，到直线1-=x 的距离为2，∴另一个交点为(1，0)9．将抛物线22(1)3y x =+-向右平移1个单位，再向上平移3个单位，则所得抛物线的表达式为 ．提示：将抛物线22(1)3y x =+-向右平移1个单位为322-=x y ，再向上平移3个单位得到3322+-=x y 即22x y =10．已知二次函数22y x x m =-++的部分图象如图4所示，则关于x 的一元二次方程220x x m -++=的解为 ．图3提示：由图象可知抛物线对称轴为1=x ，与x 轴交点(3，0)一元二次方程220x x m -++=一、选择题1.下列函数中，属于二次函数的是( )A. y=2x-1B. y=x 2+C. y=x 2(x+3)D. y=x(x+1)2.若函数y ＝（3﹣m ）﹣x+1是二次函数，则m 的值为（ ）A. 3B. ﹣3C. ±3D. 9 3.二次函数 的对称轴是 A. 直线 B. 直线C. y 轴D. x轴4.二次函数y=（a ﹣1）x 2（a 为常数）的图象如图所示，则a 的取值范围为（ ）A. a ＞1B. a ＜1C. a ＞0D. a ＜05.二次函数y=（x-1）2+3图象的顶点坐标是（ ）A. (1，3)B. （1，-3)C. （-1，3）D. （-1，-3） 6.已知点A(1，y 1),B(2,y 2)在抛物线y=-(x+1)2+2上，则下列结论正确的是（ ） A. 2>y 1>y 2 B. 2>y 2 >y 1 C. y 1>y 2>2 D. y 2 >y 1>2 7.已知抛物线经过和两点，则n 的值为（ ）A. ﹣2B. ﹣4C. 2D. 4图4图58.二次函数的图象如图所示，对称轴为直线，下列结论错误的是（）A. B. 当时，顶点的坐标为C. 当时，D. 当时，y随x的增大而增大9.已知m＞0，关于x的一元二次方程（x+1）（x﹣2）﹣m＝0的解为x1，x2（x1＜x2），则下列结论正确的是（）A. x1＜﹣1＜2＜x2B. ﹣1＜x1＜2＜x2C. ﹣1＜x1＜x2＜2D. x1＜﹣1＜x2＜210.二次函数y＝ax2+bx+c的部分图象如图所示，由图象可知方程ax2+bx+c＝0的根是（）A. x1＝﹣1，x2＝5B. x1＝﹣2，x2＝4C. x1＝﹣1，x2＝2D. x1＝﹣5，x2＝511.国家实施”精准扶贫“政策以来，很多贫困人口走向了致富的道路．某地区2016年底有贫困人口9万人，通过社会各界的努力，2018年底贫困人口减少至1万人．设2016年底至2018年底该地区贫困人口的年平均下降率为，根据题意列方程得（）A. B. C.D.12.如图，利用一个直角墙角修建一个梯形储料场ABCD，其中∠C＝120°.若新建墙BC与CD 总长为12m，则该梯形储料场ABCD的最大面积是（）A. 18m2B. m2C. m2D. m2二、填空题13.某长方形的周长为24cm，其中一边长为xcm（x＞0），面积为ycm2，则y与x的关系式为________.14.已知二次函数y=x2，当x＞0时，y随x的增大而________（填“增大”或“减小”）．15.抛物线y＝3（x+2）2﹣7 的对称轴是________．16.抛物线y=-x2+15有最________值，顶点坐标是________．17.二次函数的图象如图所示，若，.则、的大小关系为________ .(填“ ”、“ ”或“ ”)18.将二次函数y＝x2﹣8x+3化为y＝a(x﹣m)2+k的形式是________.19.抛物线y＝ax2＋bx＋c经过点A(－3，0)、B(4，0)两点，则关于x的一元二次方程a(x－1)2＋c＝b－bx的解是________20.如图，抛物线y=ax2和直线y=bx+c的两个交点坐标分别为A(－2，4),B(1,1), 则关于x的方程ax2=bx+c的解为________.21.矩形的周长等于40，则此矩形面积的最大值是________．22.为了节省材料，某农场主利用围墙（围墙足够长）为一边，用总长为80m的篱笆围成了如图所示的①②③三块矩形区域，而且这三块矩形区域的面积相等，则能围成的矩形区域ABCD的面积最大值是________m2.三、解答题23.已知抛物线y＝x2﹣（2k﹣1）x+k2﹣k+1的顶点在坐标轴上，求k的值.24.如图，在平面直角坐标系xOy中，抛物线y＝﹣x2+bx+c与x轴交于点A（﹣3，0）和点B，与y轴交于点C（0，2）．（1）求抛物线的表达式，并用配方法求出顶点D的坐标；（2）若点E是点C关于抛物线对称轴的对称点，求tan∠CEB的值．25.在平面直角坐标系xOy中,抛物线y=x2-2mx+m2-m+2的顶点为D.线段AB的两个端点分别为A(-3,m),B(1,m).（1）求点D的坐标(用含m的代数式表示);（2）若该抛物线经过点B(1,m),求m的值;（3）若线段AB与该抛物线只有一个公共点,结合函数的图象,求m的取值范围.26.某百货商店服装柜在销售中发现，某品牌童装平均每天可售出20件，每件盈利40元，经市场调查发现，在进货不变的情况下，若每件童装每降价1元，日销售量将增加2件．（1）若想要这种童装销售利润每天达到1200元，同时又能让顾客得到更多的实惠，每件童装应降价多少元？（2）当每件童装降价多少元时，这种童装一天的销售利润最多？最多利润是多少？27.设二次函数的图象的顶点坐标为，且过点，求这个函数的关系式．28.如图所示，在矩形ABCD中，AB=6厘米，BC=12厘米，点P在线段AB上，P从点A开始沿AB边以1厘米/秒的速度向点B移动．点E为线段BC的中点，点Q从E点开始，沿EC 以1厘米/秒的速度向点C移动．如果P、Q同时分别从A、E出发，写出出发时间t与△BPQ 的面积S的函数关系式，求出t的取值范围．参考答案一、选择题1. D2. B3. C4. B5. A6. A7. B8. D9. A 10. A 11. B 12. C二、填空题13. 14. 增大15. x＝﹣2 16. 大；(0，15) 17. < 18. y＝(x﹣4)2﹣13 19. 或5 20. 21. 100 22. 300三、解答题23. 解：当抛物线y= x2-（2k-1）x+k2-k+1的顶点在y轴上时，=0，解得，k= ；当抛物线y= x2-（2k-1）x+k2-k+1的顶点在x轴上时，=0，解得，k=2或k=-1，由上可得，k的值是，2或-124. （1）∵抛物线y＝﹣x2+bx+c与x轴交于点A（﹣3，0）和点B，与y轴交于点C （0，2），∴，得，∴y＝﹣x2﹣x+2＝，∴抛物线顶点D的坐标为（﹣1，），即该抛物线的解析式为y＝﹣x2﹣x+2，顶点D的坐标为（﹣1，）；（2）∵y＝，∴该抛物线的对称轴为直线x＝﹣1，∵点E是点C关于抛物线对称轴的对称点，点C（0，2），∴点E的坐标为（﹣2，2），当y＝0时，0＝，得x1＝﹣3，x2＝1，∴点B的坐标为（1，0），设直线BE的函数解析式为y＝kx+n，，得，∴直线BE的函数解析式为y＝﹣+ ，当x＝0时，y＝，设直线BE与y轴交于点F，则点F的坐标为（0，），∴OF＝，∵点C（0，2），点E（﹣2，2），∴OC＝2，CE＝2，∴CF＝2﹣＝，∴tan∠CEF＝，即tan∠CEB的值是．25. （1）∵y=x2-2mx+m2-m+2=(x-m)2-m+2,∴D点的坐标为(m,-m+2). （2）∵抛物线经过点B(1,m),∴m=1-2m+m2-m+2,解得m=3或m=1.（3）根据题意,∵A点的坐标为(-3,m),B点的坐标为(1,m),∴线段AB为y=m(-3≤x≤1),与y=x2-2mx+m2-m+2联立得x2-2mx+m2-2m+2=0,令y'=x2-2mx+m2-2m+2,若抛物线y=x2-2mx+m2-m+2与线段AB只有1个公共点,即函数y'在-3≤x≤1范围内只有一个零点,当x=-3时,y'=m2+4m+11<0,∵Δ>0,∴此种情况不存在,当x=1时,y'=m2-4m+3≤0,解得1≤m≤3.26. （1）解：设要想平均每天销售这种童装盈利1200元，那么每件童装应降价x元，（40﹣x）（20+2x）＝1200，解得，x1＝10，x2＝20∵当x＝20时，卖出的多，库存比x＝10时少，∴要想平均每天销售这种童装盈利1200元，那么每件童装应降价20元；（2）解：设每件童装降价x元，利润为y元，y＝（40﹣x）（20+2x）＝﹣2（x﹣15）2+1250，∴当x＝15时，y取得最大值，此时y＝1250，即每件童装降价15元时，每天销售这种童装的利润最高，最高利润是1250元．27. 解：设这个函数的关系式为，把点代入得，解得，所以这个函数的关系式为28. 解：∵PB=6﹣t，BE+EQ=6+t，∴S= PB•BQ= PB•（BE+EQ）= （6﹣t）（6+t）=﹣t2+18，∴S=﹣t2+18（0≤t＜6）．人教新版九年级上学期第22章《二次函数》单元测试卷（含答案）(1) 一、选择题(本大题有16个小题，共42分.1～10小题各3分，11～16小题各2分．在每小题给出的四个选项中，只有一项是符合题目要求的)1.下列函数中，是反比例函数的是( )A ．y ＝3x －1B ．y ＝0.1xC ．y ＝－13 D.yx ＝22．反比例函数y ＝22x的图像在( ) A ．第一、二象限 B ．第一、三象限 C ．第二、三象限 D ．第二、四象限 3．若点A(a ，b)在反比例函数y ＝2x 的图像上，则代数式ab －4的值为( )A ．－2B ．0C ．2D ．－6 4．下列函数中，y 随x 的增大而减小的函数是( )A ．y ＝－1xB ．y ＝1xC ．y ＝－1x (x ＞0)D ．y ＝1x(x ＜0)5．某学校要种植一块面积为100 m 2的长方形草坪，要求两边长均不小于5 m ，则草坪的一边长y(单位：m)随另一边长x(单位：m)的变化而变化的图像可能是( )6．如图，在平面直角坐标系中，点A 是双曲线y ＝1x (x ＞0)上的一个动点，过点A 作x 轴的垂线，交x 轴于点B ，点A 运动过程中△AOB 的面积将会( )A ．保持不变B ．逐渐变小C ．逐渐增大D ．先增大后减小7．对于反比例函数y ＝k 2＋1x，下列说法正确的是( )A ．y 随x 的增大而减小B ．图像是中心对称图形C ．图像位于第二、四象限D ．当x ＜0时，y 随x 的增大而增大 8．已知反比例函数y ＝－9x，当1＜x ＜3时，y 的最大整数值是( )A ．－6B ．－3C ．－4D ．－19．一次函数y ＝ax －a 与反比例函数y ＝ax (a ≠0)在同一平面直角坐标系中的图像可能是( )10．已知A(－1，y 1)，B(2，y 2)两点在双曲线y ＝3＋2mx上，且y 1＞y 2，则m 的取值范围是( )A ．m ＞0B ．m ＜0C ．m ＞－32D ．m ＜－3211．一次函数y 1＝ax ＋b 与反比例函数y 2＝kx 的图像如图所示，当y 1＜y 2时，x 的取值范围是( )A ．x ＜2B ．x ＞5C ．2＜x ＜5D ．0＜x ＜2或x ＞512．在平面直角坐标系中，直线y ＝x ＋b 与双曲线y ＝－1x 只有一个公共点，则b 的值是( )A ．1B ．±1C ．±2D ．213．如图，已知双曲线y ＝kx (x ＞0)经过矩形OABC 的边AB ，BC 的中点F ，E ，且四边形OEBF的面积为2，则k 的值为( )A ．2B ．4C ．3D ．114．反比例函数y ＝mx的图像如图所示，以下结论：①常数m ＜－1；②在每个象限内，y 随x 的增大而增大；③若点A(－1，h)，B(2，k)在图像上，则h ＜k ；④若点P(x ，y)在图像上，则点P ′(－x ，－y)也在图像上．其中正确结论的个数是( ) A ．1 B ．2 C ．3 D ．415．如图，在平面直角坐标系xOy 中，菱形AOBC 的一个顶点O 在坐标原点，一边OB 在x 轴的正半轴上，sin ∠AOB ＝45，反比例函数y ＝48x 在第一象限内的图像经过点A ，与BC 交于点F ，则△AOF 的面积等于( )A ．30B ．40C ．60D ．8016．定义新运算：a ⊕b ＝⎩⎪⎨⎪⎧a b （b ＞0），－ab （b ＜0）.例如：4⊕5＝45，4⊕(－5)＝45，则函数y ＝2⊕x(x≠0)的图像大致是( )A B C D二、填空题(本大题有3个小题，共12分.17～18小题各3分；19小题有2个空，每空3分．把答案写在题中横线上)17．如图，矩形ABCD 在第一象限，AB 在x 轴的正半轴上，AB ＝3，BC ＝1，直线y ＝12x －1经过点C 交x 轴于点E ，双曲线y ＝kx经过点D ，则k 的值为 ．18．如图，过点C(2，1)作AC ∥x 轴，BC ∥y 轴，点A ，B 都在直线y ＝－x ＋6上．若双曲线y ＝kx(x ＞0)与△ABC 总有公共点，则k 的取值范围是 ．19．如图，在函数y ＝8x (x ＞0)的图像上有点P 1，P 2，P 3，…，P n ，P n ＋1，点P 1的横坐标为2，且后面每个点的横坐标与它前面相邻点的横坐标的差都是2，过点P 1，P 2，P 3，…，P n ，P n ＋1分别作x 轴、y 轴的垂线段，构成若干个矩形，如图所示，将图中阴影部分的面积从左至右依次记为S 1，S 2，S 3，…，S n ，则S 1＝ ，S n ＝ (用含n 的代数式表示)．三、解答题(本大题有7个小题，共66分．解答应写出文字说明、证明过程或演算步骤) 20．(本小题满分8分)已知反比例函数的图像过点A(－2，2)．(1)求函数的表达式；(2)y 随x 的增大而如何变化？(3)点B(－4，2)，点C(3，－43)和点D(22，－2)哪些点在图像上？21．(本小题满分9分)已知反比例函数y ＝k －1x的图像的两个分支分别位于第一、三象限． (1)求k 的取值范围；(2)若一次函数y ＝2x ＋k 的图像与该反比例函数的图像有一个交点的纵坐标是4，试确定一次函数与反比例函数的表达式，并求当x ＝－6时，反比例函数y 的值．22．(本小题满分9分)如图，一次函数y ＝kx ＋b 的图像与坐标轴分别交于A ，B 两点，与反比例函数y ＝nx 的图像在第一象限的交点为C ，CD ⊥x 轴，垂足为D.若OB ＝3，OD ＝6，△AOB的面积为3.(1)求一次函数与反比例函数的表达式； (2)直接写出当x ＞0时，kx ＋b －nx＜0的解集．解：23．(本小题满分9分)一般情况下，中学生完成数学家庭作业时，注意力指数随时间x(分钟)的变化规律如图所示(其中AB ，BC 为线段，CD 为曲线的一部分)．(1)分别求出线段AB 和曲线CD 的函数表达式；(2)若学生的注意力指数不低于40为高效时间，根据图中信息，求出一般情况下，完成一份数学家庭作业的高效时间是多少分钟？解： 24．(本小题满分10分)如图，四边形ABCD 是平行四边形，点A(1，0)，B(3，1)，C(3，3)．反比例函数y ＝mx (x ＞0)的图像经过点D ，点P 是一次函数y ＝kx ＋3－3k(k ≠0)的图像与该反比例函数图像的一个公共点．(1)直接写出D 点的坐标，并求反比例函数的表达式；(2)连接。

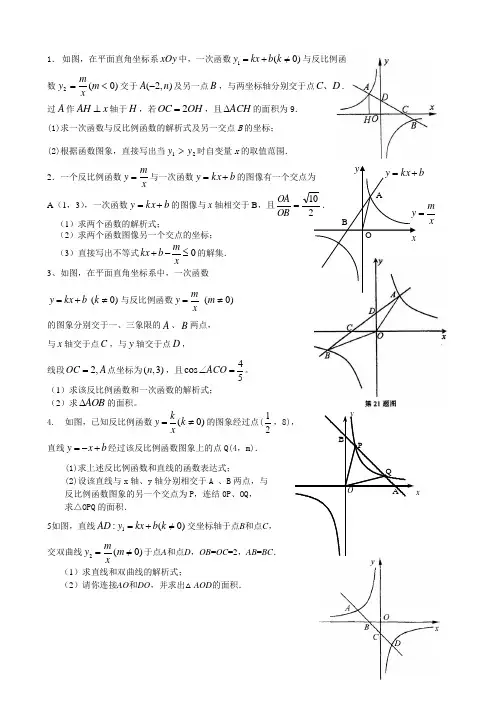
xy OABPQ1． 如图，在平面直角坐标系xOy 中，一次函数1(0)y kx b k =+=/与反比例函 数)0(2<=m xmy 交于),2(n A -及另一点B ，与两坐标轴分别交于点D C 、． 过A 作AH x ⊥轴于H ，若OH OC 2=，且ACH ∆的面积为9． (1)求一次函数与反比例函数的解析式及另一交点B 的坐标； (2)根据函数图象，直接写出当21y y >时自变量x 的取值范围．2．一个反比例函数xmy =与一次函数b kx y +=的图像有一个交点为A （1，3），一次函数b kx y +=的图像与x 轴相交于B ，且210=OB OA ． （1）求两个函数的解析式；（2）求两个函数图像另一个交点的坐标； （3）直接写出不等式0mkx b x+-≤的解集． 3、如图，在平面直角坐标系中，一次函数(0)y kx b k =+≠与反比例函数(0)my m x=≠ 的图象分别交于一、三象限的A 、B 两点， 与x 轴交于点C ，与y 轴交于点D ，线段2,OC A =点坐标为(,3)n ，且4cos 5ACO ∠=。

（1）求该反比例函数和一次函数的解析式； （2）求AOB ∆的面积。

4. 如图，已知反比例函数(0)k y k x=≠的图象经过点(12，8)，直线y x b =-+经过该反比例函数图象上的点Q(4，m)． (1)求上述反比例函数和直线的函数表达式；(2)设该直线与x 轴、y 轴分别相交于A 、B 两点，与 反比例函数图象的另一个交点为P ，连结0P 、OQ ， 求△OPQ 的面积． 5如图，直线1:(0)AD y kx b k =+=/交坐标轴于点B 和点C ， 交双曲线2(0)my m x==/于点A 和点D ，OB =OC =2，AB =BC ． （1）求直线和双曲线的解析式；（2）请你连接AO 和DO ，并求出△AOD 的面积． xyA 5 BObkx y += xm y =6．已知：如图，在平面直角坐标系xOy 中，直线AB 分别与x y 、轴交于 点B 、A ，与反比例函数的图象分别交于点C 、D ，CE x ⊥轴于点E ，2,4,55sin ===∠OE OB ABO ． （1）求该反比例函数和一次函数的解析式； （2）连接OC 、OD ，求三角形COD 的面积． 7、如图，在平面直角坐标系中，一次函数()0y kx bk =+≠的图象与反比例函数(0)m y x x=<的图象交于第二象限内的A 、B 两点，过点A 作AC x ⊥轴于点C ，5,4OA OC ==， 点B 的纵坐标为6。

人教版九年级上册第二十二章二次函数单元检测（含答案）(3)一、选择题(每小题4分，共32分)1．已知二次函数y ＝ax 2＋bx ＋1，若当x ＝1时，y ＝0；当x ＝－1时，y ＝4，则a ，b 的值分别为( )A ．a ＝1，b ＝2B ．a ＝1，b ＝－2C ．a ＝－1，b ＝2D ．a ＝－1，b ＝－22．如图，抛物线与x 轴的两个交点为A(－3，0)，B(1，0)，则由图像可知，当y ＜0时，x 的取值范围是( )A ．－3＜x ＜1B ．x ＞1C ．x ＜－3D ．0＜x ＜13．函数y ＝ax 2与y ＝－ax ＋b 的图像可能是( )A B C D4．已知点A(1，y 1)，B(2，y 2)在抛物线y ＝－(x ＋1)2＋2上，则下列结论正确的是( )A ．2＞y 1＞y 2B ．2＞y 2＞y 1C ．y 1＞y 2＞2D ．y 2＞y 1＞2 5．对于二次函数y ＝－14x 2＋x －4，下列说法正确的是( )A ．当x>0时，y 随x 的增大而增大B ．当x ＝2时，y 有最大值－3C ．图像的顶点坐标为(－2，－7)D ．图像与x 轴有两个交点6．某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y(件)与销售单价x(元/件)之间的函数关系式为y ＝－4x ＋440，要获得最大利润，该商品的售价应定为( )A ．60元B ．70元C ．80元D ．90元7．在平面直角坐标系xOy 中，四条抛物线如图所示，其表达式中的二次项系数绝对值最小的是( )A ．y 1B ．y 2C ．y 3D ．y 48．如图是二次函数y ＝ax 2＋bx ＋c (a ，b ，c 是常数，a ≠0 )图像的一部分，与x 轴的交点A 在点(2，0)和(3，0)之间，对称轴是直线x ＝1.对于下列说法：① ab<0；②2a ＋b ＝0；③3a ＋c>0；④a ＋b ≥m(am ＋b)(m 为实数)；⑤当－1<x<3时，y>0，其中正确的是( )A ．①②④B ．①②⑤C ．②③④D ．③④⑤二、填空题(每小题4分，共24分)9．二次函数y ＝－x 2＋2x 图像的顶点坐标是 ．10．当x ＝2时，二次函数y ＝a(x －h)2有最大值，且函数图像经过点(1，－3)，则该二次函数的表达式为 ．11．如图，抛物线y ＝ax 2与直线y ＝bx ＋c 的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax 2＝bx ＋c 的解是 ．12．如图是一座拱桥，当水面宽AB 为12 m 时，桥洞顶部离水面4 m ．已知桥洞的拱形是抛物线，以水平方向为x 轴，建立平面直角坐标系，若选取点A 为坐标原点时的抛物线表达式是y ＝－19(x －6)2＋4，则选取点B 为坐标原点时的抛物线的表达式是 ．13．飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数表达式是y＝60t－3t2.在飞机着陆滑行中，最后4 s滑行的距离是 .214．如图，在等腰Rt△ABC中，∠C＝90°，AB＝10，点F是AB的中点，点D，E分别在AC，BC边上运动，且始终保持DF⊥EF，则△CDE面积的最大值为．三、解答题(共44分)15．(8分)已知二次函数y＝x2＋4x＋k－1.(1)若抛物线与x轴有两个不同的交点，求k的取值范围．(2)若抛物线的顶点在x轴上，求k的值．解：16．(10分)抛物线y＝－x2＋(m－1)x＋m与y轴交于点(0，3)．(1)求出m的值，并画出这条抛物线．(2)求抛物线与x轴的交点和顶点坐标．(3)当x取什么值时，抛物线在x轴上方？(4)当x取什么值时，y的值随x的增大而减小？17．(12分)用一段长32 m的篱笆和长8 m的墙，围成一个矩形的菜园．(1)如图1，如果矩形菜园的一边靠墙AB，另三边由篱笆CDEF围成．①设DE＝x m，直接写出菜园面积y与x之间的函数关系式，并写出自变量的取值范围．②菜园的面积能不能等于110 m2？若能，求出此时x的值；若不能，请说明理由．(2)如图2，如果矩形菜园的一边由墙AB和一节篱笆BF构成，另三边由篱笆ADEF围成，求菜园面积的最大值．18．(14分)已知二次函数y＝－x2＋bx＋c的图像过点A(3，0)，C(－1，0)．(1)求二次函数的表达式．(2)点P是二次函数图像的对称轴上的一个动点，二次函数的图像与y轴交于点B，当PB＋PC最小时，求点P的坐标．(3)在第一象限内的抛物线上有一点Q，当△QAB的面积最大时，求点Q的坐标．周测(第三十章)(时间：40分钟 满分：100分)一、选择题(每小题4分，共32分)1．已知二次函数y ＝ax 2＋bx ＋1，若当x ＝1时，y ＝0；当x ＝－1时，y ＝4，则a ，b 的值分别为(B)A ．a ＝1，b ＝2B ．a ＝1，b ＝－2C ．a ＝－1，b ＝2D ．a ＝－1，b ＝－22．如图，抛物线与x 轴的两个交点为A(－3，0)，B(1，0)，则由图像可知，当y ＜0时，x 的取值范围是(A)A ．－3＜x ＜1B ．x ＞1C ．x ＜－3D ．0＜x ＜13．函数y ＝ax 2与y ＝－ax ＋b 的图像可能是(B)A B C D 4．已知点A(1，y 1)，B(2，y 2)在抛物线y ＝－(x ＋1)2＋2上，则下列结论正确的是(A)A ．2＞y 1＞y 2B ．2＞y 2＞y 1C ．y 1＞y 2＞2D ．y 2＞y 1＞2 5．对于二次函数y ＝－14x 2＋x －4，下列说法正确的是(B)A ．当x>0时，y 随x 的增大而增大B ．当x ＝2时，y 有最大值－3C ．图像的顶点坐标为(－2，－7)D ．图像与x 轴有两个交点6．某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y(件)与销售单价x(元/件)之间的函数关系式为y ＝－4x ＋440，要获得最大利润，该商品的售价应定为(C)A ．60元B ．70元C ．80元D ．90元7．在平面直角坐标系xOy 中，四条抛物线如图所示，其表达式中的二次项系数绝对值最小的是(C)A．y1 B．y2 C．y3 D．y48．如图是二次函数y＝ax2＋bx＋c (a，b，c 是常数，a≠0 )图像的一部分，与x轴的交点A在点(2，0)和(3，0)之间，对称轴是直线x＝1.对于下列说法：① ab<0；②2a＋b＝0；③3a＋c>0；④a＋b≥m(am＋b)(m为实数)；⑤当－1<x<3时，y>0，其中正确的是(A) A．①②④ B．①②⑤ C．②③④ D．③④⑤二、填空题(每小题4分，共24分)9．二次函数y＝－x2＋2x图像的顶点坐标是(1，1)．10．当x＝2时，二次函数y＝a(x－h)2有最大值，且函数图像经过点(1，－3)，则该二次函数的表达式为y＝－3(x－2)2．11．如图，抛物线y＝ax2与直线y＝bx＋c的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax2＝bx＋c的解是x1＝－2，x2＝1．12．如图是一座拱桥，当水面宽AB为12 m时，桥洞顶部离水面4 m．已知桥洞的拱形是抛物线，以水平方向为x轴，建立平面直角坐标系，若选取点A为坐标原点时的抛物线表达式是y ＝－19(x －6)2＋4，则选取点B 为坐标原点时的抛物线的表达式是y ＝－19(x ＋6)2＋4．13．飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数表达式是y ＝60t －32t 2.人教版九年级上册第二十二章二次函数单元检测（含答案）(3)一、选择题(每小题4分，共32分)1．已知二次函数y ＝ax 2＋bx ＋1，若当x ＝1时，y ＝0；当x ＝－1时，y ＝4，则a ，b 的值分别为( )A ．a ＝1，b ＝2B ．a ＝1，b ＝－2C ．a ＝－1，b ＝2D ．a ＝－1，b ＝－22．如图，抛物线与x 轴的两个交点为A(－3，0)，B(1，0)，则由图像可知，当y ＜0时，x 的取值范围是( )A ．－3＜x ＜1B ．x ＞1C ．x ＜－3D ．0＜x ＜13．函数y ＝ax 2与y ＝－ax ＋b 的图像可能是( )A B C D4．已知点A(1，y 1)，B(2，y 2)在抛物线y ＝－(x ＋1)2＋2上，则下列结论正确的是( )A ．2＞y 1＞y 2B ．2＞y 2＞y 1C ．y 1＞y 2＞2D ．y 2＞y 1＞2 5．对于二次函数y ＝－14x 2＋x －4，下列说法正确的是( )A ．当x>0时，y 随x 的增大而增大B ．当x ＝2时，y 有最大值－3C ．图像的顶点坐标为(－2，－7)D．图像与x轴有两个交点6．某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y(件)与销售单价x(元/件)之间的函数关系式为y＝－4x＋440，要获得最大利润，该商品的售价应定为( )A．60元 B．70元 C．80元 D．90元7．在平面直角坐标系xOy中，四条抛物线如图所示，其表达式中的二次项系数绝对值最小的是( )A．y1 B．y2 C．y3 D．y48．如图是二次函数y＝ax2＋bx＋c (a，b，c 是常数，a≠0 )图像的一部分，与x轴的交点A在点(2，0)和(3，0)之间，对称轴是直线x＝1.对于下列说法：① ab<0；②2a＋b＝0；③3a＋c>0；④a＋b≥m(am＋b)(m为实数)；⑤当－1<x<3时，y>0，其中正确的是( ) A．①②④ B．①②⑤ C．②③④ D．③④⑤二、填空题(每小题4分，共24分)9．二次函数y＝－x2＋2x图像的顶点坐标是．10．当x＝2时，二次函数y＝a(x－h)2有最大值，且函数图像经过点(1，－3)，则该二次函数的表达式为．11．如图，抛物线y＝ax2与直线y＝bx＋c的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax2＝bx＋c的解是．12．如图是一座拱桥，当水面宽AB 为12 m 时，桥洞顶部离水面4 m ．已知桥洞的拱形是抛物线，以水平方向为x 轴，建立平面直角坐标系，若选取点A 为坐标原点时的抛物线表达式是y ＝－19(x －6)2＋4，则选取点B 为坐标原点时的抛物线的表达式是 ．13．飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数表达式是y ＝60t －32t 2.在飞机着陆滑行中，最后4 s 滑行的距离是 .14．如图，在等腰Rt △ABC 中，∠C ＝90°，AB ＝10，点F 是AB 的中点，点D ，E 分别在AC ，BC 边上运动，且始终保持DF ⊥EF ，则△CDE 面积的最大值为 ． 三、解答题(共44分)15．(8分)已知二次函数y ＝x 2＋4x ＋k －1.(1)若抛物线与x 轴有两个不同的交点，求k 的取值范围． (2)若抛物线的顶点在x 轴上，求k 的值． 解：16．(10分)抛物线y ＝－x 2＋(m －1)x ＋m 与y 轴交于点(0，3)．(1)求出m 的值，并画出这条抛物线． (2)求抛物线与x 轴的交点和顶点坐标． (3)当x 取什么值时，抛物线在x 轴上方？ (4)当x 取什么值时，y 的值随x 的增大而减小？17．(12分)用一段长32 m的篱笆和长8 m的墙，围成一个矩形的菜园．(1)如图1，如果矩形菜园的一边靠墙AB，另三边由篱笆CDEF围成．①设DE＝x m，直接写出菜园面积y与x之间的函数关系式，并写出自变量的取值范围．②菜园的面积能不能等于110 m2？若能，求出此时x的值；若不能，请说明理由．(2)如图2，如果矩形菜园的一边由墙AB和一节篱笆BF构成，另三边由篱笆ADEF围成，求菜园面积的最大值．18．(14分)已知二次函数y＝－x2＋bx＋c的图像过点A(3，0)，C(－1，0)．(1)求二次函数的表达式．(2)点P是二次函数图像的对称轴上的一个动点，二次函数的图像与y轴交于点B，当PB＋PC最小时，求点P的坐标．(3)在第一象限内的抛物线上有一点Q，当△QAB的面积最大时，求点Q的坐标．周测(第三十章)(时间：40分钟 满分：100分)一、选择题(每小题4分，共32分)1．已知二次函数y ＝ax 2＋bx ＋1，若当x ＝1时，y ＝0；当x ＝－1时，y ＝4，则a ，b 的值分别为(B)A ．a ＝1，b ＝2B ．a ＝1，b ＝－2C ．a ＝－1，b ＝2D ．a ＝－1，b ＝－22．如图，抛物线与x 轴的两个交点为A(－3，0)，B(1，0)，则由图像可知，当y ＜0时，x 的取值范围是(A)A ．－3＜x ＜1B ．x ＞1C ．x ＜－3D ．0＜x ＜13．函数y ＝ax 2与y ＝－ax ＋b 的图像可能是(B)A B C D 4．已知点A(1，y 1)，B(2，y 2)在抛物线y ＝－(x ＋1)2＋2上，则下列结论正确的是(A)A ．2＞y 1＞y 2B ．2＞y 2＞y 1C ．y 1＞y 2＞2D ．y 2＞y 1＞2 5．对于二次函数y ＝－14x 2＋x －4，下列说法正确的是(B)A ．当x>0时，y 随x 的增大而增大B ．当x ＝2时，y 有最大值－3C ．图像的顶点坐标为(－2，－7)D．图像与x轴有两个交点6．某大学生利用课余时间在网上销售一种成本为50元/件的商品，每月的销售量y(件)与销售单价x(元/件)之间的函数关系式为y＝－4x＋440，要获得最大利润，该商品的售价应定为(C)A．60元 B．70元 C．80元 D．90元7．在平面直角坐标系xOy中，四条抛物线如图所示，其表达式中的二次项系数绝对值最小的是(C)A．y1 B．y2 C．y3 D．y48．如图是二次函数y＝ax2＋bx＋c (a，b，c 是常数，a≠0 )图像的一部分，与x轴的交点A在点(2，0)和(3，0)之间，对称轴是直线x＝1.对于下列说法：① ab<0；②2a＋b＝0；③3a＋c>0；④a＋b≥m(am＋b)(m为实数)；⑤当－1<x<3时，y>0，其中正确的是(A) A．①②④ B．①②⑤ C．②③④ D．③④⑤二、填空题(每小题4分，共24分)9．二次函数y＝－x2＋2x图像的顶点坐标是(1，1)．10．当x＝2时，二次函数y＝a(x－h)2有最大值，且函数图像经过点(1，－3)，则该二次函数的表达式为y＝－3(x－2)2．11．如图，抛物线y＝ax2与直线y＝bx＋c的两个交点坐标分别为A(－2，4)，B(1，1)，则方程ax2＝bx＋c的解是x1＝－2，x2＝1．12．如图是一座拱桥，当水面宽AB 为12 m 时，桥洞顶部离水面4 m ．已知桥洞的拱形是抛物线，以水平方向为x 轴，建立平面直角坐标系，若选取点A 为坐标原点时的抛物线表达式是y ＝－19(x －6)2＋4，则选取点B 为坐标原点时的抛物线的表达式是y ＝－19(x ＋6)2＋4．13．飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数表达式是y ＝60t －32t 2.人教版九年级上册数学第22章二次函数单元测试卷（解析版）一．选择题（共10小题，满分30分，每小题3分） 1．（3分）下列函数中，是二次函数的是（ ） A ．y ＝3x ﹣1B ．y ＝3x 3﹣x 2C ．y ＝1﹣x ﹣x 2D ．y ＝x 2+2．（3分）抛物线y ＝x 2﹣6x +24的顶点是（ ） A ．（﹣6，﹣6）B ．（﹣6，6）C ．（6，6）D ．（6，﹣6）3．（3分）由二次函数y ＝2（x ﹣3）2+1，可知正确的结论是（ ） A ．其图象的开口向下B ．其图象的对称轴为过点（﹣3，0）且与y 轴平行的直线C ．其最小值为1D ．当x ＜3时，y 随x 的增大而增大4．（3分）函数y ＝ax 2与y ＝ax ﹣a 的图象大致是（ ）A ．B ．C．D．5．（3分）二次函数y＝m2x2﹣4x+1有最小值﹣3，则m等于（）A．1B．﹣1C．±1D．±6．（3分）若y＝（m+1）是二次函数，则m＝（）A．7B．﹣1C．﹣1或7D．以上都不对7．（3分）y＝ax2+bx+c（a≠0）的图象如图所示，则下面六个代数式：abc；b2﹣4ac；a﹣b+c；a+b+c；2a﹣b；9a﹣4b，值小于0的有（）A．1个B．2个C．3个D．4个8．（3分）一名男同学推铅球时，铅球行进中离地的高度y（m）与水平距离x（m）之间的关系式是y＝﹣x2+x+，那么铅球推出后落地时距出手地的距离是（）A．m B．4 m C．8 m D．10 m9．（3分）若二次函数y＝ax2﹣x+c的图象上所有的点都在x轴下方，则a，c应满足的关系是（）A．B．C．D．10．（3分）已知函数y＝x2﹣2x+k的图象经过点（，y1），（，y2），则y1与y2的大小关系为（）A．y1＞y2B．y1＝y2C．y1＜y2D．不能确定二．填空题（共7小题，满分28分，每小题4分）11．（4分）抛物线y＝3x2+（m﹣2）x+m﹣2，当m＝时，图象顶点在y轴上，当m＝时，图象顶点在x轴上，当m＝时，图象过原点，当m＝时，图象顶点在原点．12．（4分）将二次函数y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位，所得二次函数图象的表达式为．13．（4分）抛物线上有三点（﹣2，3）、（2，﹣8）、（1，3），此抛物线的解析式为．14．（4分）周长为50cm的矩形，设其一边长为x cm，则当x＝时，矩形面积最大，为．15．（4分）若点A（3，m）是抛物线y＝﹣x2上一点，则m＝．16．（4分）抛物线y＝﹣x2+3x﹣2在y轴上的截距是，与x轴的交点坐标是．17．（4分）根据下图中的抛物线，当x时，y随x的增大而增大；当x时，y 随x的增大而减小．三．解答题（共8小题，满分62分）18．（6分）已知二次函数的图象如图所示，求它的解析式．19．（6分）已知是x的二次函数，求出它的解析式．20．（6分）画出函数y＝﹣x2+2x+3的图象，观察图象说明：当x取何值时，y＜0，当x取何值时，y＞0．21．（8分）已知二次函数y＝﹣3x2﹣6x+5．（1）求这个函数图象的顶点坐标、对称轴以及函数的最大值；（2）若另一条抛物线y＝x2﹣x﹣k与上述抛物线只有一个公共点，求k的值．22．（8分）已知二次函数y＝﹣x2+x+2．（1）求函数图象的开口方向，顶点坐标及对称轴；（2）画出函数的图象；（3）由图象回答：当x为何值时，y＜0；当x为何值时，y＞0．23．（8分）某商场销售某种品牌的纯牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40～70元之间．市场调查发现：若每箱以50元销售，平均每天可销售90箱，价格每升高1元，平均每天少销售3箱．（1）求商场平均每天销售这种牛奶的利润W（元）与每箱牛奶的售价x（元）之间的函数关系式；（每箱的利润＝售价﹣进价）（2）求出（1）中二次函数图象的顶点坐标，并当x＝40，70时W的值．在直角坐标系中画出函数图象的草图；（3）根据图象可以看出，当牛奶售价为多少时，平均每天的利润最大，最大利润是多少？24．（10分）已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣3，﹣6），并与x轴交于点B（﹣1，0）和点C，顶点为P．（1）求二次函数的解析式；（2）设点M为线段OC上一点，且∠MPC＝∠BAC，求点M的坐标；说明：若（2）你经历反复探索没有获得解题思路，请你在不改变点M的位置的情况下添加一个条件解答此题，此时（2）最高得分为3分．25．（10分）已知OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA＝10，OC＝6，（1）如图甲：在OA上选取一点D，将△COD沿CD翻折，使点O落在BC边上，记为E．求折痕CD所在直线的解析式；（2）如图乙：在OC上选取一点F，将△AOF沿AF翻折，使点O落在BC边，记为G．①求折痕AF所在直线的解析式；②再作GH∥AB交AF于点H，若抛物线过点H，求此抛物线的解析式，并判断它与直线AF的公共点的个数．（3）如图丙：一般地，在以OA、OC上选取适当的点I、J，使纸片沿IJ翻折后，点O 落在BC边上，记为K．请你猜想：①折痕IJ所在直线与第（2）题②中的抛物线会有几个公共点；②经过K作KL∥AB与IJ相交于L，则点L是否必定在抛物线上．将以上两项猜想在（l）的情形下分别进行验证．2019-2020学年九年级第22章二次函数单元测试卷参考答案一．选择题（共10小题，满分30分，每小题3分）1．（3分）下列函数中，是二次函数的是（）A．y＝3x﹣1B．y＝3x3﹣x2C．y＝1﹣x﹣x2D．y＝x2+【分析】整理成一般形式后，根据二次函数的定义判定即可．【解答】解：A、是一次函数，错误；B、最高次是3次，故错误；C、符合二次函数的一般形式y＝ax2+bx+c，正确；D、不是有关自变量的整式，故错误．故选：C．2．（3分）抛物线y＝x2﹣6x+24的顶点是（）A．（﹣6，﹣6）B．（﹣6，6）C．（6，6）D．（6，﹣6）【分析】化为顶点式表达式即可求出抛物线y＝x2﹣6x+24的顶点坐标．【解答】解：抛物线y＝x2﹣6x+24＝（x﹣6）2+6，所以抛物线y＝x2﹣6x+24的顶点是（6，6）．故选：C．3．（3分）由二次函数y＝2（x﹣3）2+1，可知正确的结论是（）A．其图象的开口向下B．其图象的对称轴为过点（﹣3，0）且与y轴平行的直线C．其最小值为1D．当x＜3时，y随x的增大而增大【分析】根据二次函数的性质对各选项进行逐一判断即可．【解答】解：A、∵二次函数y＝2（x﹣3）2+1中，a＝2＞0，∴其图象的开口向上，故本选项错误；B、∵二次函数的解析式是y＝2（x﹣3）2+1，∴其图象的对称轴是直线x＝3，故本选项错误；C、∵由函数解析式可知其顶点坐标为（3，1），∴其最小值为1，故本选项正确；D、∵二次函数的图象开口向上，对称轴是直线x＝3，∴当x＜3时，y随x的增大而减小，故本选项错误．故选：C．4．（3分）函数y＝ax2与y＝ax﹣a的图象大致是（）A．B．C．D．【分析】由抛物线的图象可知a＞0，由此可知直线y＝ax﹣a中，a＞0，﹣a＜0，再判断一次函数图象的位置．【解答】解：观察抛物线的图象可知a＞0，∴在直线y＝ax﹣a中，a＞0，﹣a＜0，直线经过一、三、四象限，故选B．5．（3分）二次函数y＝m2x2﹣4x+1有最小值﹣3，则m等于（）A．1B．﹣1C．±1D．±【分析】对二次函数y＝m2x2﹣4x+1，a＝m2＞0，存在最小值，且在顶点取得，有＝﹣3，求得m的值即可．【解答】解：在y＝m2x2﹣4x+1中，m2＞0，则在顶点处取得最小值，＝＝﹣3，解得：m＝±1．故选：C．6．（3分）若y＝（m+1）是二次函数，则m＝（）A．7B．﹣1C．﹣1或7D．以上都不对【分析】让x的指数为2，系数不为0，列出方程与不等式解答即可．【解答】解：由题意得：m2﹣6m﹣5＝2；且m+1≠0；解得m＝7或﹣1；m≠﹣1，∴m＝7，故选：A．7．（3分）y＝ax2+bx+c（a≠0）的图象如图所示，则下面六个代数式：abc；b2﹣4ac；a﹣b+c；a+b+c；2a﹣b；9a﹣4b，值小于0的有（）A．1个B．2个C．3个D．4个【分析】根据抛物线的开口方向和对称轴的位置及定顶点的位置，再结合图形可推出a ＜0，b＜0，c＜0，由此可判断各式的符号．【解答】解：①由抛物线的开口方向向下可推出a＜0；因为对称轴在y轴左侧，对称轴为x＝＜0，又因为a＜0，b＜0；由抛物线与y轴的交点在y轴的负半轴上，∴c＜0，故abc＜0；②抛物线与x轴有两个交点，b2﹣4ac＞0；③当x＝﹣1时，a﹣b+c＞0；④当x＝1时，y＝a+b+c＜0；⑤对称轴x＝﹣＝﹣1，2a＝b，2a﹣b＝0；⑥∵b＝2a，且a＜0，∴9a﹣4b＝9a﹣8a＝a＜0，则①④⑥的值小于0，故选：C．8．（3分）一名男同学推铅球时，铅球行进中离地的高度y（m）与水平距离x（m）之间的关系式是y＝﹣x2+x+，那么铅球推出后落地时距出手地的距离是（）A．m B．4 m C．8 m D．10 m【分析】铅球落地时高度y＝0，求出此时x的值，即得铅球推出后落地时距出手地的距离．【解答】解：当y＝0时，﹣x2+x+＝0，整理得：x2﹣8x﹣20＝0，解得：x＝10，x＝﹣2（不合题意，舍去），故x＝10，即铅球推出后落地时距出手地的距离是10米．故选：D．9．（3分）若二次函数y＝ax2﹣x+c的图象上所有的点都在x轴下方，则a，c应满足的关系是（）A．B．C．D．【分析】根据函数图象上所有点都在x轴下方可知，函数图象开口向下且顶点纵坐标小于0，列出不等式．【解答】解：由题意得：，解得：，故选A．10．（3分）已知函数y＝x2﹣2x+k的图象经过点（，y1），（，y2），则y1与y2的大小关系为（）A．y1＞y2B．y1＝y2C．y1＜y2D．不能确定【分析】先求得函数y＝x2﹣2x+k的对称轴为x＝1，再判断点（，y1）的对称点的坐标为（，y2），从而判断出y1＝y2．【解答】解：∵对称轴为x＝﹣＝1，∴点（，y1）的对称点的横坐标为，即称点坐标为（，y2），∴y1＝y2．故选：B．二．填空题（共7小题，满分28分，每小题4分）11．（4分）抛物线y＝3x2+（m﹣2）x+m﹣2，当m＝2时，图象顶点在y轴上，当m＝2或14时，图象顶点在x轴上，当m＝2时，图象过原点，当m＝2时，图象顶点在原点．【分析】图象顶点在y轴上，即顶点的横坐标为0，即﹣＝0；图象顶点在x轴上，即顶点的纵坐标为0，即＝0；图象过原点，则m﹣2＝0；图象顶点在原点，即顶点的横、纵坐标都为0，即m﹣2＝0，然后分别解方程求出对应的m的值．【解答】解：当﹣＝0，即m＝2时，图象顶点在y轴上；当＝0时，图象顶点在x轴上，解得m＝2或m＝14；当m﹣2＝0，即m＝2时，图象过原点；当m﹣2＝0时，图象顶点在原点．故答案为2，2或14，2，2．12．（4分）将二次函数y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位，所得二次函数图象的表达式为y＝5（x+5）2+3．【分析】利用变化规律：左加右减，上加下减进而得出答案．【解答】解：按照“左加右减，上加下减”的规律，y＝5（x+2）2﹣4的图象向左平移3个单位，再向上平移8个单位得到y＝5（x+5）2+3．故答案为：y＝5（x+5）2+3．13．（4分）抛物线上有三点（﹣2，3）、（2，﹣8）、（1，3），此抛物线的解析式为y＝﹣x2﹣x+．【分析】把点（﹣2，3）、（2，﹣8）、（1，3）代入y＝ax2+bx+c，解得a，b，c的值，即可得出抛物线的解析式．【解答】解：设此抛物线的解析式为y＝ax2+bx+c，把点（﹣2，3）、（2，﹣8）、（1，3）代入得，解得．所以此抛物线的解析式为y＝﹣x2﹣x+，故答案为：y＝﹣x2﹣x+．14．（4分）周长为50cm的矩形，设其一边长为x cm，则当x＝时，矩形面积最大，为．【分析】根据矩形的面积公式求出矩形的面积表达式，再利用配方法求出最值．【解答】解：设矩形的面积为S，则S＝x（25﹣x）＝﹣x2+25x＝﹣（x2﹣25x）＝﹣[x2﹣25x+（）2﹣（）2]＝﹣（x﹣）2+．故答案为，．15．（4分）若点A（3，m）是抛物线y＝﹣x2上一点，则m＝﹣9．【分析】将A（3，m）代入y＝﹣x2即可求解．【解答】解：当x＝3时，m＝﹣32，即m＝﹣9．16．（4分）抛物线y＝﹣x2+3x﹣2在y轴上的截距是﹣2，与x轴的交点坐标是（2，0）（1，0）．【分析】令x＝0，即可求出抛物线与y轴的交点坐标，交点纵坐标即为抛物线在y轴上的截距；令y＝0，所得关于x的一元二次方程的解即为与x轴交点的横坐标．【解答】解：当x＝0时，y＝﹣2，则抛物线在y轴上的截距为﹣2；当y＝0时，原式可化为﹣x2+3x﹣2＝0，整理得，x2﹣3x+2＝0，解得x1＝2，x2＝1，于是抛物线与x轴的交点坐标为（2，0），（1，0）．故答案为﹣2；（2，0），（1，0）．17．（4分）根据下图中的抛物线，当x＜2时，y随x的增大而增大；当x＞2时，y随x的增大而减小．【分析】已知抛物线与x轴的两交点坐标，对称轴是两交点横坐标的平均数，根据对称轴及开口方向，可判断函数的增减性．【解答】解：因为抛物线与x轴两交点坐标（﹣2，0），（6，0），所以，抛物线对称轴为x＝＝2，所以，当x＜2时，y随x的增大而增大；当x＞2时，y随x的增大而减小．三．解答题（共8小题，满分62分）18．（6分）已知二次函数的图象如图所示，求它的解析式．【分析】从图上可知道顶点坐标和与x轴的交点坐标，设成顶点式利用待定系数法求解即可．【解答】解：∵抛物线顶点坐标为（1，4），代入抛物线顶点式y＝a（x﹣h）2+k（a≠0），得：y＝a（x﹣1）2+4，∵该抛物线又过点（﹣1，0），∴4a+4＝0，解得a＝﹣1，∴y＝﹣（x﹣1）2+4＝﹣x2+2x+3．19．（6分）已知是x的二次函数，求出它的解析式．【分析】根据二次函数的定义得出有关m的方程与不等式解答即可．【解答】解：由二次函数的定义，可知m2+m≠0，即m≠0，m≠﹣1又因为m2﹣2m﹣1＝2，m2﹣2m﹣3＝0解得m＝3或m＝﹣1（不合题意，舍去）所以m＝3故y＝12x2+9．20．（6分）画出函数y＝﹣x2+2x+3的图象，观察图象说明：当x取何值时，y＜0，当x取何值时，y＞0．【分析】先把函数y＝﹣x2+2x+3化成顶点式，即可直接得出其顶点坐标，分别令x＝0，y＝0求出图象与x、y轴的交点，根据其四点可画出函数的图象，根据图象便可直接解答y＜0或y＞0时x的取值范围．【解答】解：∵y＝﹣x2+2x+3，＝﹣（x﹣1）2+4，∴开口方向向下，对称轴x＝1，顶点坐标（1，4），令x＝0得：y＝3，∴与y轴交点坐标（0，3），令y＝0得：﹣x2+2x+3＝0，∴x1＝1 x2＝3，∴与x轴交点坐标（﹣1，0），（3，0），作出函数如图所示的图象，由图象可以看出：当x＜﹣1或x＞3时，y＜0；当﹣1＜x＜3时，y＞0．21．（8分）已知二次函数y＝﹣3x2﹣6x+5．（1）求这个函数图象的顶点坐标、对称轴以及函数的最大值；（2）若另一条抛物线y＝x2﹣x﹣k与上述抛物线只有一个公共点，求k的值．【分析】（1）根据抛物线的解析式易得顶点坐标与对称轴方程，进而可得函数的最大值；（2）若两条抛物线只有一个公共点，联立两个方程可得一个一元二次方程，令△＝0可得k的值．【解答】解：（1）∵y＝﹣3x2﹣6x+5＝﹣3（x2+2x+1）+8＝﹣3（x+1）2+8，∴对称轴x＝﹣1，顶点坐标（﹣1，8），即当x＝﹣1时，函数有最大值是8．（2）∵只有一个公共点∴方程﹣3x2﹣6x+5＝x2﹣x﹣k有相等实数根，即4x2+5x﹣5﹣k＝0△＝52﹣4×4×（﹣5﹣k）＝0，∴k＝﹣．22．（8分）已知二次函数y＝﹣x2+x+2．（1）求函数图象的开口方向，顶点坐标及对称轴；（2）画出函数的图象；（3）由图象回答：当x为何值时，y＜0；当x为何值时，y＞0．【分析】（1）通过配方法求对称轴，顶点坐标，当a＞0时，开口向上，当a＜0时，开口向下；（2）可以利用描点法作图，要注意确定顶点坐标；（3）根据图象确定取值范围，当y＜0时，即为x轴下方的部分，即可确定x的取值范围，当y＞0时，即为x轴的上方部分，即可确定x的取值范围．【解答】解：（1）y＝﹣x2+x+2＝﹣（x2﹣x）+2＝﹣（x﹣）2+，∴开口向下，顶点坐标为（，），对称轴为直线x＝；（2）图象如图：（3）根据图象可知：x＜﹣1或x＞2时，y＜0；﹣1＜x＜2时，y＞0．23．（8分）某商场销售某种品牌的纯牛奶，已知进价为每箱40元，生产厂家要求每箱售价在40～70元之间．市场调查发现：若每箱以50元销售，平均每天可销售90箱，价格每升高1元，平均每天少销售3箱．（1）求商场平均每天销售这种牛奶的利润W（元）与每箱牛奶的售价x（元）之间的函数关系式；（每箱的利润＝售价﹣进价）（2）求出（1）中二次函数图象的顶点坐标，并当x＝40，70时W的值．在直角坐标系中画出函数图象的草图；（3）根据图象可以看出，当牛奶售价为多少时，平均每天的利润最大，最大利润是多少？【分析】（1）每天的利润＝每箱的利润×销售量，注意售价的范围；（2）用配方法或公式法可求顶点坐标，把x＝40、70分别代入关系式中计算求值；（3）根据图象回答问题．【解答】解：（1）当每箱牛奶售价为x元时，每箱利润为（x﹣40）元，每天售出90﹣3（x﹣50）＝240﹣3x箱，故W＝（240﹣3x）（x﹣40）＝﹣3x2+360x﹣9600；（2）W＝﹣3（x﹣60）2+1200，∴此二次函数图象的顶点坐标为（60，1200），当x＝40时，W＝﹣3（40﹣60）2+1200＝0，当x＝70时，W＝﹣3（70﹣60）2+1200＝900；（3）由图象易知：当牛奶售价为每箱60元时，平均每天利润最大，最大利润为1200元．24．（10分）已知二次函数y＝﹣x2+bx+c的图象经过点A（﹣3，﹣6），并与x轴交于点B（﹣1，0）和点C，顶点为P．（1）求二次函数的解析式；（2）设点M为线段OC上一点，且∠MPC＝∠BAC，求点M的坐标；说明：若（2）你经历反复探索没有获得解题思路，请你在不改变点M的位置的情况下添加一个条件解答此题，此时（2）最高得分为3分．【分析】（1）二次函数解析式中有两个未知数，且它的图象经过点A、B，把两点代入求解得出系数，即可求得．（2）画出二次函数图象，根据二次函数图象求解．【解答】解：把两点代入求解得：﹣3b+c＝0，b﹣c+＝0，解得：b＝1，c＝，代入原函数解析式得：y＝﹣x2+x+．（2）如图所示：M点在OC上，由题目可知∠MPC＝∠BAC，点P的坐标为（1，2），由已知个点坐标可以求得：CP＝，AC＝6，BC＝4，∠PCM＝∠ACB＝45°；由以上可以知道△PCM与△ACB相似，所以有：，解得：CM＝，所以M点的坐标为（），答：M点的坐标为（）．25．（10分）已知OABC是一张放在平面直角坐标系中的矩形纸片，O为原点，点A在x轴上，点C在y轴上，OA＝10，OC＝6，（1）如图甲：在OA上选取一点D，将△COD沿CD翻折，使点O落在BC边上，记为E．求折痕CD所在直线的解析式；（2）如图乙：在OC上选取一点F，将△AOF沿AF翻折，使点O落在BC边，记为G．①求折痕AF所在直线的解析式；②再作GH∥AB交AF于点H，若抛物线过点H，求此抛物线的解析式，并判断它与直线AF的公共点的个数．（3）如图丙：一般地，在以OA、OC上选取适当的点I、J，使纸片沿IJ翻折后，点O 落在BC边上，记为K．请你猜想：①折痕IJ所在直线与第（2）题②中的抛物线会有几个公共点；②经过K作KL∥AB与IJ相交于L，则点L是否必定在抛物线上．将以上两项猜想在（l）的情形下分别进行验证．【分析】（1）根据折叠可知四边形ODEC是正方形，由此可得知C、D点坐标，设出直线解析式，代入两点坐标即可求得；（2）借用直角△ABG和△FCG，可以求出OF、CG的长度，由此可得折痕AF所在直线的解析式，由CG的长得知G点坐标，设出H点坐标，由H在直线和抛物线上可求出抛物线的解析式，再将直线解析式代入抛物线解析式中，由根的判别式△＝0可得知仅有一个交点；（3）结合（2）得出猜想，再到图甲中找到特殊情况下，各点所对应的点，代入即可得以验证．【解答】解：（1）由折法知：四边形ODEC是正方形，∴OD＝OC＝6，∴D（6，0），C（0，6），设直线CD的解析式为y＝kx+b，则，解得，∴直线CD的解析式为y＝﹣x+6．（2）①在直角△ABG中，因AG＝AO＝10，故BG＝＝8，∴CG＝2，设OF＝m，则FG＝m，CF＝6﹣m，在直角△CFG中，m2＝（6﹣m）2+22，解得m＝，则F（0，），设直线AF为y＝k′x+，将A（10，0）代入，得k′＝﹣，∴AF所在直线的解析式为：y＝﹣x+．②∵GH∥AB，且G（2，6），可设H（2，y F），由于H在直线AF上，∴把H（2，y F）代入直线AF：y F＝﹣×2+＝，∴H（2，），又∵H在抛物线上，＝﹣×22+h，解得h＝3，∴抛物线的解析式为y＝﹣x2+3，将直线y＝﹣x+，代入到抛物线y＝﹣x2+3，。

重庆市2019年中考22题专题训练
1．小邱同学根据学习函数的经验，研究函数y＝的图象与性质．通过分析，该函数y与自变量x的几组对应值如下表，并画出了部分函数图象如图所示．
x13456…
y﹣1﹣2﹣3.4﹣7.5 2.4 1.410.8…
（1）函数y＝的自变量x的取值范围是；
（2）在图中补全当1≤x＜2的函数图象；
（3）观察图象，写出该函数的一条性质：；
（4）若关于x的方程＝x+b有两个不相等的实数根，
结合图象，可知实数b的取值范围是．
2.根据我们学习函数的过程与方法，对函数的图象和性质进行探究。

已知该函数图
象经过与两点。

(1)求这个函数的表达式；
(2)在给出的平面直角坐标系中：①请用你喜欢的方法补全这个函数的图象并写出这个函数的一条性质；②
直线与函数图象有三个交点，则______.
(3)结合你所画得图象与函数的图象，直接写出不等式
的解集。

3.
4.。

人教版九年级上册第二十二章二次函数单元检测（含答案）(5)一．选择题（ 30 分）1．已知二次函数y x 2bx c的图象上有 （3， 8） （ 5， 8）和 两点，则此抛物线的对称轴 是（）y A ．直线 x 4B ．直线 x3C ． x 1D ． x52．已知二次函数yax 2bx c 的图象以下图，则abc ，2b ， a bc 这四个式子中，值为正数的有（-1 O1xb 4ac ， 2a）A ． 4 个B ． 3 个C ． 2 个D ． 1 个3．以知二次函数y ax 2c a 0 x ，（x x x ）x x，当 x 取 1212 时，函数值相等， 则当 x 取12时，函数值为（）A ． a cB ． a cC ． cD ． c4．函数 y2bxc ，的图象经过 （ 1，0）则a b c 的值是（ ） axbcc a abA ． 3B ． 3C ．1D ．1225．把二次函数 y1x 23x5 的图象向右平移 2 个单位后， 再向上平移 3 个单位， 所得的22函数图象极点是 ()A ． (－5， 1)B ． (1，－ 5)C ． (－ 1， 1)D ． (－ 1， 3)6．若点 (2，5)， (4， 5)在抛物线 y ＝ ax 2＋ bx ＋ c 上，则它的对称轴是直线 ()A ． xbB ． x ＝ 1C ． x ＝2D ． x ＝3a7．已知函数 y1 x2 x 4 ，当函数值 y 随 x 的增大而减小时， x 的取值范围是 ()2A ． x ＜ 1B ． x ＞ 1C ． x ＞－ 2D ．－ 2＜ x ＜ 48．二次函数 y ＝ a(x ＋ k)2＋ k ，当 k 取不一样的实数值时，图象极点所在的直线是()A ． y ＝ xB ． x 轴C ． y ＝－ xD ． y 轴9．已知二次函数 y ＝ ax 2＋bx ＋ c(a ≠0)的图象以下图，有以下结论：① abc ＞0； ② a ＋ b ＋1()c ＝ 2； ③ a； ④b＜ 1．此中正确的结论是2A ． ①②B ．②③C ． ②④D ． ③④10．以下命题中，正确的选项是 ()① 若 a ＋b ＋c ＝0，则 b 2－ 4ac ＜ 0；2＋bx ＋c ＝ 0 有两个不相等的实数根；② 若 b ＝2a ＋3c ，则一元二次方程 ax ③ 若 b 2－4ac ＞ 0，则二次函数 y ＝ ax 2＋bx ＋c 的图象与坐标轴的公共点的个数是 2 或 3；④ 若 b ＞a ＋c ，则一元二次方程ax 2＋bx ＋ c ＝0 有两个不相等的实数根．A ．②④B ． ①③C ． ②③D ． ③④二．填空题11．抛物线 y ＝－x 2＋ 15 有最 ______点，其坐标是 ______．12．若抛物线y＝x2－2x－2 的极点为A，与 y 轴的交点为B，则过 A，B 两点的直线的分析式为 ____________．13．若抛物线y＝ax2＋bx＋c(a ≠0)的图象与抛物线y＝x2－4x＋3 的图象对于y 轴对称，则函数 y＝ax2＋bx＋ c 的分析式为______．14．若抛物线y＝x2＋bx＋c 与 y 轴交于点A，与 x 轴正半轴交于B，C 两点，且 BC＝ 2，S△ABC ＝3，则 b＝______．15．二次函数 y＝x2－6x＋c 的图象的极点与原点的距离为5，则 c＝ ______．16．二次函数 y1x22x 2的图象在座标平面内绕极点旋转180 °，再向左平移 3 个单位，2向上平移 5 个单位后图象对应的二次函数分析式为___________．17．抛物线 y x22x m ，若其极点在x 轴上，则 m=___________ ．18．极点为（- 2，且过点的抛物线的分析式为___________．5）（1 ，-14）三．解答题19．把二次函数y1x2x4 配方成 y＝a(x+m)2＋k 的形式，并求出它的图象的极点坐23标．对称轴方程，y＜ 0 时 x 的取值范围，并画出图象．20．已知二次函数 y＝ax2＋bx＋c(a ≠0)的图象经过一次函数 y 3x 3 的图象与 x 轴． y 轴2的交点，并也经过 (1，1)点．求这个二次函数分析式，并求 x 为什么值时，有最大 (最小 )值，这个值是什么 ?2的图象与 x 轴交于点 A ，点 B ，与 y 轴交于点 C ，其顶21．已知二次函数 y ax 2ax 3点为 D ，直线 DC 的函数关系式为 y kx 3 ，又 CBO 45（ 1）求二次函数的分析式和直线DC 的函数关系式（ 2）求 △ ABC 的面积y DCAO B x22．已知抛物线 y ＝－ x 2＋bx ＋c 与 x 轴的两个交点分别为 A(m ，0)，B(n ，0)，且 m n4 ，m 1 n3人教版九年级上册第二十二章二次函数单元检测（含答案）(5)一．选择题（ 30 分）2（3， 8） （ 5， 8）1．已知二次函数y xbxc 的图象上有和 两点，则此抛物线的对称轴是（）yA ．直线 x4B ．直线 x 3C ． x 1D ． x52．已知二次函数y ax 2 bxc 的图象以下图，则 abc ，2b ， a bc 这四个式子中，值为正数的有（-1O 1 xb 4ac ， 2a）A ． 4 个B ． 3 个C ． 2 个D ． 1 个4．以知二次函数y ax 2c a0 ，当 x 取 x 1 ，（x 2 x 1 x 2）时，函数值相等， 则当 x 取 x 1x 2时，函数值为（）A ． a cB ． a cC ． cD ． c4．函数 yax 2 bx c ，的图象经过 （ 1，0）则 a bc 的值是（）b c c a a bA ． 3B ． 3C ．1D ． 1225．把二次函数 y1x 25 23x的图象向右平移 2 个单位后， 再向上平移 3 个单位， 所得的2函数图象极点是 ()A ． (－5， 1)B ． (1，－ 5)C ． (－ 1， 1)D ． (－ 1， 3)6．若点 (2，5)， (4， 5)在抛物线 y ＝ ax 2＋ bx ＋ c 上，则它的对称轴是直线 ()A ． xbB ． x ＝ 1C ． x ＝2D ． x ＝3a7．已知函数y 1 x2x 4 ，当函数值y随x的增大而减小时，x 的取值范围是 () 2A． x＜ 1B． x＞ 1C． x＞－ 2D．－ 2＜ x＜ 48．二次函数 y＝ a(x＋ k)2＋ k，当 k 取不一样的实数值时，图象极点所在的直线是() A． y＝ x B． x 轴C． y＝－ x D． y 轴9．已知二次函数y＝ ax2＋bx＋ c(a≠0)的图象以下图，有以下结论：① abc＞0；② a＋ b＋c＝ 2；③a 1()；④b＜ 1．此中正确的结论是2A．①②B．②③C．②④D．③④10．以下命题中，正确的选项是()①若 a＋b＋c＝0，则 b2－ 4ac＜ 0；②若 b＝2a＋3c，则一元二次方程 ax2＋bx＋c＝ 0 有两个不相等的实数根；③若 b2－4ac＞ 0，则二次函数y＝ ax2＋bx＋c 的图象与坐标轴的公共点的个数是 2 或 3；④若 b＞a＋c，则一元二次方程ax2＋bx＋ c＝0 有两个不相等的实数根．A．②④B．①③C．②③D．③④二．填空题11．抛物线 y＝－x2＋ 15有最 ______点，其坐标是 ______．12．若抛物线y＝x2－2x－2 的极点为A，与 y 轴的交点为B，则过 A，B 两点的直线的分析式为 ____________．13．若抛物线 y＝ax2＋bx＋c(a ≠0)的图象与抛物线y＝x2－4x＋3 的图象对于 y 轴对称，则函数 y ＝ax2＋＋bx c 的分析式为 ______．14．若抛物线y＝x2＋bx＋c 与 y 轴交于点A，与 x 轴正半轴交于B，C 两点，且 BC＝ 2，S△ABC ＝3，则 b＝______．15．二次函数 y＝x2－6x＋c 的图象的极点与原点的距离为5，则 c＝ ______．16．二次函数 y 1 x22x 2 的图象在座标平面内绕极点旋转180 °，再向左平移 3 个单位，2向上平移 5 个单位后图象对应的二次函数分析式为___________．17．抛物线 y x22x m ，若其极点在 x 轴上，则 m=___________ ．18．极点为（- 2 ，5）且过点（1 ，-14）的抛物线的分析式为___________．三．解答题19．把二次函数 y 1x2x2＋k 的形式，并求出它的图象的极点坐4配方成 y＝a(x+m)23标．对称轴方程，y＜ 0 时 x 的取值范围，并画出图象．20．已知二次函数2bx c(a ≠0)的图象经过一次函数y3x 3 的图象与 x 轴． y 轴y＝ax ＋＋2的交点，并也经过 (1，1)点．求这个二次函数分析式，并求 x 为什么值时，有最大 (最小 )值，这个值是什么 ?21．已知二次函数y ax22ax 3 的图象与x 轴交于点 A ，点 B ，与y 轴交于点 C ，其顶点为 D ，直线DC的函数关系式为y kx 3 ，又CBO45（ 1）求二次函数的分析式和直线DC 的函数关系式（ 2）求△ ABC 的面积y DCA OB x22．已知抛物线y＝－ x2＋bx＋c 与 x 轴的两个交点分别为 A(m，0)，B(n，0)，且m n 4 ，m 1n 3人教版九年级上册第二十二章二次函数单元检测（含答案）(5)一．选择题（30 分）1．已知二次函数 y x2bx c 的图象上有（3， 8）和（5， 8）两点，则此抛物线的对称轴是（）y A．直线 x4B．直线 x 3C． x1D． x 52．已知二次函数y ax 2c 的图象以下图，则abc ，bx-1O1xb 24ac ， 2a b ， a b c 这四个式子中，值为正数的有（）A ． 4 个B ． 3 个C ． 2 个D ． 1 个5．以知二次函数 y ax 2c a 0，当 x取x ，（x xx ）x 取x x1212 时，函数值相等， 则当 12时，函数值为（）A ． a cB ． a cC ． cD ． c2bx c ，的图象经过 （ 1，0）则a bc的值是（） 4．函数 y ax b cc a abA ． 3B ． 3C ．112D ．25．把二次函数 y1 x2 3x 5的图象向右平移 2 个单位后， 再向上平移3 个单位， 所得的22函数图象极点是 ()A ． (－5， 1)B ． (1，－ 5)C ． (－ 1， 1)D ． (－ 1， 3)6．若点 (2，5)， (4， 5)在抛物线 y ＝ ax 2＋ bx ＋ c 上，则它的对称轴是直线 ()bB ． x ＝ 1C ． x ＝2D ． x ＝3A ． xa7．已知函数 y1 x2 x 4 ，当函数值 y 随 x 的增大而减小时， x 的取值范围是 ()2A ． x ＜ 1B ． x ＞ 1C ． x ＞－ 2D ．－ 2＜ x ＜ 48．二次函数 y ＝ a(x ＋ k)2＋ k ，当 k 取不一样的实数值时，图象极点所在的直线是()A ． y ＝ xB ． x 轴C ． y ＝－ xD ． y 轴9．已知二次函数y ＝ ax 2＋bx ＋ c(a ≠0)的图象以下图，有以下结论：① abc ＞0； ② a ＋ b ＋1()c ＝ 2； ③ a； ④b＜ 1．此中正确的结论是2A ． ①②B ．②③C ． ②④D ． ③④10．以下命题中，正确的选项是 ()① 若 a ＋b ＋c ＝0，则 b 2－ 4ac ＜ 0；② 若 b ＝2a ＋3c ，则一元二次方程 ax 2＋bx ＋c ＝ 0 有两个不相等的实数根；③ 若 b 2－4ac ＞ 0，则二次函数 y ＝ ax 2＋bx ＋c 的图象与坐标轴的公共点的个数是 2 或 3；④ 若 b ＞a ＋c ，则一元二次方程 ax 2＋bx ＋ c ＝0 有两个不相等的实数根．A ．②④B ． ①③C ． ②③D ． ③④二．填空题11．抛物线 y ＝－x 2＋ 15 有最 ______点，其坐标是 ______．12．若抛物线 y ＝x 2－ 2x －2 的极点为 A ，与 y 轴的交点为 B ，则过 A ，B 两点的直线的分析式为 ____________．13．若抛物线 y ＝ax 2＋bx ＋c(a ≠0)的图象与抛物线y ＝x 2－4x ＋3 的图象对于 y 轴对称，则函数 y ＝ax 2＋bx ＋ c 的分析式为 ______．14．若抛物线 y ＝x 2 ＋bx ＋c 与 y 轴交于点A ，与 x 轴正半轴交于B ，C 两点，且 BC ＝ 2，S △ABC＝3，则 b＝______．15．二次函数 y＝x2－6x＋c 的图象的极点与原点的距离为5，则 c＝ ______．16．二次函数 y 1 x22x 2 的图象在座标平面内绕极点旋转180 °，再向左平移 3 个单位，2向上平移 5 个单位后图象对应的二次函数分析式为___________．17．抛物线 y x22x m ，若其极点在x 轴上，则 m=___________ ．18．极点为（- 2，且过点的抛物线的分析式为___________．5）（1，-14）三．解答题y1x2x＝2＋k 的形式，并求出它的图象的极点坐19．把二次函数 4 配方成 y a(x+m)23标．对称轴方程，y＜ 0 时 x 的取值范围，并画出图象．20．已知二次函数 y＝ax2＋bx＋c(a ≠0)的图象经过一次函数 y 3x 3 的图象与 x 轴． y 轴2的交点，并也经过 (1，1)点．求这个二次函数分析式，并求 x 为什么值时，有最大 (最小 )值，这个值是什么 ?2的图象与 x 轴交于点A，点B，与y轴交于点C，其顶21．已知二次函数 y ax 2ax 3点为 D ，直线DC的函数关系式为y kx 3 ，又CBO 45（ 1）求二次函数的分析式和直线DC 的函数关系式（ 2）求△ABC的面积y DCA OB x 22．已知抛物线 y＝－ x2＋bx＋c 与 x 轴的两个交点分别为 A(m，0)，B(n，0)，且m n 4 ，m 1n 3人教版九年级上册单元检测：第二十二章二次函数（含答案）(1)一．选择题1．以下函数表达式中，必定是二次函数的是（）A．y＝3x﹣ 1B．y＝ax2 +bx+c C．y＝ 3x2﹣ 2x+1D．y＝x2+2．抛物线y＝﹣ x2+2x+6的对称轴是（）A．直线x＝ 1B．直线x＝﹣ 1C．直线x＝﹣ 2D．直线x＝ 23．在平面直角坐标系中，对于二次函数y＝（ x﹣2）2+1，以下说法中错误的选项是（）A．y的最小值为1B．图象极点坐标为（2，1），对称轴为直线x＝2C．当x＜ 2 时，y的值随x值的增大而增大，当x≥ 2 时，y的值随x值的增大而减小D．它的图象能够由y＝x2的图象向右平移 2 个单位长度，再向上平移 1 个单位长度获取4．二次函数y＝﹣x2 +mx，对称轴为直线x＝3，若对于 x 的一元二次方程﹣ x2+mx﹣ t ＝0（ t 为实数）在2＜x＜ 7 的范围内有解，则t 的取值范围是（）A．t＞﹣ 7B．﹣ 7＜t＜ 8C． 8＜t≤ 9D．﹣ 7＜t≤ 95．若正比率函数y＝mx（m≠ 0），y随x的增大而减小，则它和二次函数2y＝ mx+m的图象大致是（）A．B．C．D．6．把抛物线y＝﹣2x 2向上平移 1 个单位，再向右平移 1 个单位，获取的抛物线是（）A．y＝﹣ 2（x+1）2+1B．y＝﹣ 2（x﹣ 1）2+1C．y＝﹣ 2（x﹣1）2﹣1D．y＝﹣ 2（x+1）2﹣ 17．如图，排球运动员站在点O处练习发球，将球从 O点正上方2m的 A 处发出，把球当作点，其运转的高度y（m）与运转的水平距离x（ m）知足关系式y＝ a（ x﹣ k）2+h．已知球与O点的水平距离为6m时，达到最高 2.6 m，球网与 O点的水平距离为9m．高度为 2.43 m，球场的界限距 O点的水平距离为18m，则以下判断正确的选项是（）A．球不会过网B．球会过球网但不会出界C．球会过球网并会出界D．没法确立8．若函数y＝（a﹣ 2）x2﹣ 2ax+a﹣与x轴有交点，且对于x的不等式组无解，则切合条件的整数 a 的值有（）个A． 3B． 4C． 5D．69．在平面直角坐标系中，二次函数y＝ ax2+bx+c（ a≠0）的图象以下图，现给予下结论：①abc＜0；② c+2a＜0；③ 9a﹣3b+c＝ 0；④a﹣ b≥ m（ am+b）（ m为实数）；⑤ 4ac﹣b2＜0．此中错误结论的个数有（）A． 1 个B． 2 个C． 3 个D．4 个10．如图，抛物线y＝ a（ x+1）（ x﹣3）的图象与 x 轴交于 A，B两点（点 A 在点 B 的左侧），与y 轴正半轴交于点 C，点 D为抛物线的极点．点 P 为线段 BC上的动点，以 AC，AP为邻边结构 ?APEC，连结BE．若△ACP的面积与△BEP的面积之比为 1： 2 时，ED⊥BD，则a 的值为（）A．﹣ 1B．﹣C．﹣D．﹣ 2二．填空题11．已知一个二次函数的图象张口向上，极点坐标为（2， 3），那么这个二次函数的分析式能够是．12．某斜拉索大桥主索塔呈抛物线，主索塔底部在水面部分的宽度AB＝50米，主索塔的最高点E距水面的垂直距离为100 米，桥面CD距水面的咨度为36 米，桥的宽度CD米．13．某二次函数的图象过点（﹣ 3，m）和（ 7，m），则此二次函数的图象的对称轴为．14．抛物线y＝﹣ x2+bx+c的部分图象以下图，已知对于x的一元二次方程﹣x2+bx+c＝0的一个解为x1＝1，则该方程的另一个解为x2＝．15．抛物线 y ＝ 3x 2﹣ 6x +a 与坐标轴只有一个公共点，则 a 取值范围为．16．已知二次函数 ＝2+4 +3 的极点为，与y 轴交于点 ，作它对于以（ 1， 0）为中心y x xABP的中心对称的图象极点为，交y 轴于点，则四边形面积为．CDABCD三．解答题17．如图，已知抛物线y ＝x 2 +bx +c 与 x 轴交于点 A ， B ， AB ＝ 2，与 y 轴交于点 C ，对称轴为直线 x ＝ 2．（ 1）求抛物线的函数表达式；（ 2）设 D 为抛物线的极点，连结 DA 、 DB ，试判断△ ABD 的形状，并说明原因；（ 3）设 P 为对称轴上一动点，要使 PC ﹣ PB 的值最大，求出 P 点的坐标．18．如图，已知抛物线y ＝﹣x 2+ + 的极点C 的坐标为（﹣ 3，2），此抛物线交 x 轴于点bx c， 两点，交 y 轴于点 ，点P 为直线上方抛物线上一点，过点P 作 ⊥轴垂足为A B D ADPE xE ，交直线 AD 于点 N ，连结 AP ， PD ．（ 1）求抛物线和直线 AD 的分析式；（ 2）求线段 PN 的最大值；（ 3）当△的面积是△ 的面积的 时，求点P 的坐标．APDABC19．已知抛物线y ＝ax 2 +bx +c （ a 、 b 、 c 是常数，a ≠0）的对称轴为直线x ＝﹣ 1．（ 1） b ＝；（用含 a 的代数式表示）（ 2）当a ＝﹣ 1 时，若对于x 的方程ax 2 +bx +c ＝ 0 在﹣ 4＜ x ＜1 的范围内有解，求c 的取值范围；（ 3）若抛物线过点（﹣ 1，﹣ 1），当 0≤x≤1 时，抛物线上的点到x轴距离的最大值为4，求 a 的值．20．如图，一地道的横截面是由一段抛物线及矩形的三边围成的，地道宽BC＝10米，矩形x 轴，部分高AB＝3米，抛物线型的最高点 E 离地面OE＝6米，按如图成立一个以BC为OEy 轴的直角坐标系．为（ 1）求抛物线的分析式；（ 2）假如该地道内设有双车道，现有一辆货运卡车高 4.5 米，宽 3 米，这辆货运卡车能顺利经过地道吗？21．某服饰商场购进单价为30 元的童装若干件，物价部门规定其销售单价不低于每件30元，不高于每件60 元．销售一段时间后发现：当销售单价为60 元时，均匀每个月销售量为 80 件，而当销售单价每降低10 元时，均匀每个月能多售出20 件．同时，在销售过程中，450 元．设销售单价为x 元，均匀月销售量为y 件．每个月还要支付其余花费（ 1）求出y 与x 的函数关系式，并写出自变量x 的取值范围．（ 2）当销售单价为多少元时，销售这类童装每个月可赢利1800 元？（ 3）当销售单价为多少元时，销售这类童装每个月获取收益最大？最大收益是多少？22．如图，抛物线y＝﹣x2﹣x+c 与 x 轴交于 A，B 两点，且点 B 的坐标为（3，0），与 y 轴交于点 C，连结 AC，BC，点 P 是抛物线上在第二象限内的一个动点，点P的横坐标为a，过点 P作 x 轴的垂线，交AC于点 Q．（1）求A，C两点的坐标．（2）请用含a的代数式表示线段PQ的长，并求出a为什么值时PQ获得最大值．（3）尝试究在点P运动的过程中，能否存在这样的点Q，使得以 B， C，Q为极点的三角形是等腰三角形？若存在，请写出此时点Q的坐标；若不存在，请说明原因．23．在平面直角坐标系中，假如某点的横坐标与纵坐标的和为10，则称此点为“适合点”比如，点（ 1， 9），（﹣ 2019， 2029）都是“适合点”．（1）求函数y＝2x+1 的图象上的“适合点”的坐标；（2）求二次函数y＝x2﹣ 5x﹣2 的图象上的两个“适合点”A，B之间线段的长；（3）若二次函数y＝ax2+4x+c的图象上有且只有一个适合点” ，其坐标为（ 4， 6），求二次函数 y＝ ax2+4x+c 的表达式；（ 4）我们将抛物线y＝2（ x﹣ n）2﹣3在 x 轴下方的图象记为G1，在 x 轴及 x 轴上方图象记为 G，现将 G 沿 x 轴向上翻折获取G，图象 G 和图象 G 两部分构成的记为G，当图21323象 G上恰有两个“适合点”时，直接写出n 的取值范围．参照答案一．选择题1．解：A、是一次函数，故此选项错误；B、当 a＝0时， y＝ ax2+bx+c 不是二次函数，故此选项错误；C、是二次函数，故此选项正确；D、含有分式，不是二次函数，故此选项错误；应选： C．2．解：∵抛物线y＝﹣ x2+2x+6＝﹣（ x﹣1）2+7，∴该抛物线的对称轴是直线x＝1，应选： A．3．解：二次函数y＝（ x﹣2）2+1， a＝1＞0，∴该函数的图象张口向上，对称轴为直线x＝2，极点为（2，1），当 x＝2时， y 有最小值1，当x＞ 2 时，y的值随x值的增大而增大，当x＜2 时，y的值随x值的增大而减小；应选项 A、 B 的说法正确， C的说法错误；依据平移的规律， y＝ x2的图象向右平移2个单位长度获取 y＝（ x﹣2）2，再向上平移1个单位长度获取 y＝（ x﹣2）2+1；应选项 D的说法正确，应选： C．4．解：∵抛物线y＝﹣ x2+mx的对称轴为直线x＝3，∴﹣＝ 3，解得 m＝6，∴抛物线分析式为y＝﹣ x2+6x＝﹣（ x﹣3）2+9，抛物线的极点坐标为（3，9），当 x＝2时， y＝﹣ x2+6x＝8；当 x＝7时， y＝﹣ x2+6x＝﹣7，∵对于 x 的一元二次方程﹣x2+mx﹣ t ＝0（t 为实数）在2＜x＜ 7 的范围内有解，∴抛物线 y＝﹣ x2+6x 与直线 y＝t 在2＜ x＜7的范围内有公共点，∴﹣ 7＜t＜ 8．应选： B．5．解：∵y＝mx（m≠ 0），y随x的增大而减小，∴ m＜0，2∴二次函数y＝ mx+m的图象的张口向下，与y 则交于负半轴上，应选： A．6．解：∵函数y＝﹣2x2的极点为（0，0），∴向上平移 1 个单位，再向右平移 1 个单位的极点为（1， 1），∴将函数y＝﹣2x2的图象向上平移 1 个单位，再向右平移 1 个单位，获取抛物线的分析式为y＝﹣2（ x﹣1）2+1，应选： B．7．解：∵球与O点的水平距离为6m时，达到最高 2.6 m，∴抛物线为y＝ a（ x﹣6）2+2.6过点，∵抛物线 y＝ a（x﹣6）2+2.6过点（0，2），∴2＝a（ 0﹣ 6）2+2.6 ，解得： a＝﹣，故 y 与 x 的关系式为：y＝﹣（ x﹣6）2+2.6，当 x＝9时， y＝﹣（ x﹣6）2+2.6＝2.45＞2.43，因此球能过球网；当 y＝0时，﹣（ x﹣6）2+2.6＝0，解得： x1＝6+2＞ 18，x2＝ 6﹣2（舍去）故会出界．应选： C．8．解：，解不等式①得：x≤ a，解不等式②得：x＞5，∵对于 x 的不等式组无解，∴ a≤5．①当二次函数y＝（ a﹣2） x2﹣2ax+a﹣与x轴有交点时，方程（ a﹣2） x2﹣2ax+a﹣＝0的△＝（﹣2a）2﹣4（a﹣2）（a﹣）≥ 0，解得： a≥，∴≤a≤5．又∵ a≠2，整数有 1， 3， 4， 5，共 4 个．②当函数 y＝（ a﹣2） x2﹣2ax+a﹣是一次函数时，a﹣2＝0，此时 a＝2．综上所述，整数有1， 2，3， 4， 5，共 5 个．应选： C．9．解：①由抛物线可知：a＞0， c＜0，对称轴 x＝﹣＜0，∴b＞0，∴abc＜0，故①正确；②由对称轴可知：﹣＝﹣ 1，∴b＝2a，∵x＝1时，y＝a+b+c＝0，∴ c+3a＝0，∴ c+2a＝﹣3a+2a＝﹣ a＜0，故②正确；③（ 1， 0）对于x＝﹣ 1 的对称点为（﹣3， 0），∴ x＝﹣3时， y＝9a﹣3b+c＝0，故③正确；④当 x＝﹣1时， y 的最小值为a﹣b+c，2∴ x＝m时， y＝ am+bm+c，2∴ am+bm+c≥ a﹣ b+c，即 a﹣b≤ m（ am+b），故④错误；⑤抛物线与x 轴有两个交点，∴△＞ 0，即b2﹣4ac＞0，∴4ac﹣b2＜0，故⑤正确；应选： A．10．解：在y＝ a（ x+1）（ x﹣3）中，令 x＝0，得 x＝﹣1或3∴A（﹣1，0），B（3，0）令 x＝0，得 y＝﹣3a∴C（0，﹣3a），∵ y＝ a（ x+1）（x﹣3）＝ a（ x﹣1）2﹣4a∴ D（1，﹣4a），∵四边形 APEC是平行四边形∴ AP∥CE， AP＝CE， S△＝S△ACP EPC∵△ ACP的面积与△ BEP的面积之比为1： 2∴＝∴＝∴P（1，﹣2a）∴E（2，﹣5a），如图，连结 BD，则∠ BDE＝90°222∴ BD+DE＝ BE∴（ 3﹣ 1）2+（ 4a）2+（ 1﹣2）2 +（﹣ 4a+5a）2＝（ 3﹣ 2）2+（ 5a）2，解得： a＝±，∵a＜0∴ a＝﹣．应选： B．二．填空题11．解：设抛物线的分析式为y＝ a（ x﹣2）2+3，且该抛物线的图象张口向上，∴a＞0，∴y＝（ x﹣2）2+3，故答案为： y＝（ x﹣2）2+3．12．解：如图，以所在直线为x 轴，过点E的直线为y轴成立平面直角坐标系，CD 依据图象知点极点E 的坐标为（0， 64），点B的坐标为（ 25，﹣ 36），B设分析式为 y＝ ax2+64，将点 B（25，﹣36）代入得：﹣36＝625a+64，解得： a＝﹣，∴分析式为 y＝﹣x2+64，令 y＝0，得： y＝﹣x2+64＝0，解得： x＝±20，∴CD＝20﹣（﹣20）＝40，故答案为： 40．13．解：∵二次函数的图象过点（﹣3，m）和（ 7，m），∴此二次函数的图象的对称轴为直线x＝＝2，故答案为：直线x＝2．14．解：函数的对称轴为：x＝﹣1，此中一个交点坐标为（1， 0），则此外一个交点坐标为（﹣3， 0），故答案为﹣ 3．15．解：∵y＝ 3x2﹣ 6x+a＝ 3（x﹣ 1）2﹣ 3+a，∴抛物线的张口向上，极点为（1，a﹣ 3），∵抛物线 y＝3x2﹣6x+a 与坐标轴只有一个公共点，∴极点在第一象限，∴a﹣3＞0，即a＞3，故答案为 a＞3．16．解：以下图：过点C作 CE⊥ y 轴于点 E，过点 A 作 CE⊥ y 轴于点 F，令 x＝0，则 y＝3，故 B（0，3）；由于 y＝ x2+4x+3＝ x2+4x+4﹣1＝（ x+2）2﹣1，故极点坐标为A（﹣2，﹣1）．∵作它对于以P（1，0）为中心的中心对称的图象极点为C，∴ C点坐标为：（4，1），B 点对应点 M为（2，﹣3），设二次函数分析式为：y＝a（ x﹣4）2+1，﹣3＝a（ 2﹣ 4）2+1，解得： a＝﹣1，故y＝﹣（ x﹣4）2+1，令 x＝0，则 y＝﹣15，故友 y 轴于点 D坐标为：（0，﹣15），则四边形 ABCD面积为： S△CBD+S△ABD＝EC× BD+× AF×BD＝BD（EC+AF）＝× 18× 6＝54．故答案为： 54．三．解答题17．解：（ 1）如图，∵AB＝ 2，对称轴为直线x＝2．∴点 A的坐标是（1，0），点 B 的坐标是（3，0）．∵抛物线 y＝ x2+bx+c 与 x 轴交于点 A， B，∴ 1、3 是对于x的一元二次方程x2+bx+c＝0的两根．由韦达定理，1+3＝﹣b， 1× 3＝c，∴b＝﹣4， c＝3，∴抛物线的函数表达式为 y＝ x2﹣4x+3；（2）∵y＝x2﹣ 4x+3＝（x﹣ 2）2﹣ 1，∴ D（2，﹣1），222222∴ AD+BD＝（2﹣1）+（﹣ 1） +（ 2﹣3） +（﹣ 1）＝ 4，22∵ AB＝2＝4，222∴ AD+BD＝ AB，∴△ ADB是直角三角形，由对称性有AD＝BD，∴△ ADB是等腰直角三角形；（ 3）连结CA，延伸CA与直线x＝2 交于点P，连结BP，如图 2，∵A、B两点对于直线 x＝2对称，∴ PB＝PA，∴ PC﹣PB＝ PC﹣PA＝ AC其值最大（∵另取一点P′，有 P′ C﹣P′ B＝ P′C﹣ P′ A＜ AC），A 令 x＝0，得 y＝ x2﹣4x+3＝3，∴C（0，3），∵ A（1，0），∴易求直线 AC的分析式为： y＝﹣3x+3，当x ＝2时， y＝﹣3x+3＝﹣3，∴P（2，﹣3）．18．解：（ 1）∵抛物线y＝﹣x2+bx+c 的极点 C的坐标为（﹣3，2），∴抛物线的分析式为y ＝﹣（+3）2 +2，即y＝﹣x2﹣ 3 ﹣；x x令 y＝0，则0＝﹣x2﹣3x﹣，解得 x＝﹣1或 x＝﹣5，∴A（﹣5，0），B（﹣1，0），令 x＝0，则 y＝﹣，∴D（0，﹣），设直线 AD的分析式为y＝kx+n，则，解得∴直线 AD的分析式为： y＝﹣x﹣；（ 2）设点P的坐标为（m，﹣2N的坐标为（ m，﹣m﹣）m﹣3m﹣），则点2m﹣2m＝﹣（ m+2+，∴ PN＝﹣ m﹣3m﹣﹣（﹣）＝﹣ m﹣）∴ 的最大值为；PN（3）∵极点C的坐标为（﹣ 3， 2），A（﹣ 5， 0），B（﹣ 1，0），∴ S△ABC＝（﹣1+5）×2＝4，∵△ APD的面积是△ ABC的面积的，∴ S△＝× 4＝5，APD2∴×5×（﹣m﹣m）＝5，解得： m＝﹣4或 m＝﹣1，则点 P的坐标为（﹣4，）或（﹣ 1， 0）．19．解：（ 1）＝﹣＝﹣ 1，故＝2a ，x b故答案为： 2a；（ 2）当a＝﹣ 1 时，函数表达式为：y＝﹣ x2﹣2x+c，方程为： x2+2x﹣ c＝0，该方程在在﹣4＜x＜ 1 的范围内有解，则△＝ 4+4c≥ 0，即c≥﹣ 1；同时要知足：当x＝﹣4时， y＜0或 x＝1时， y ＜0，即﹣ 16+8+c＜ 0 或﹣ 1﹣ 2+c＜ 0，故c＜8或 c＜3，故 c＜8，故﹣ 1≤c＜ 8；（ 3）抛物线过点（﹣ 1，﹣ 1），该点是抛物线的极点，则函数的表达式为：y ＝（+1）a x2﹣1，当 0≤x≤ 1 时，抛物线上的点到x轴距离的最大值为4，而极点到x轴的距离为1，则 x＝1时，该点的 y 坐标为4或﹣4，即该点坐标为（1， 4）或（ 1，﹣ 4），将点（ 1， 4）或（ 1，﹣ 4），代入函数表达式得：4＝a（1+1）2﹣ 1 或﹣ 4＝a（ 1+1）2﹣ 1，解得： a＝或﹣．220．解：（ 1）设抛物线的分析式为y＝ ax +c，∴，得，∴此抛物线的分析式为＝+6；y（ 2）当x＝± 3 时，y＝+6＝ 4.92 ＞ 4.5 ，即这辆货运卡车能顺利经过地道．21．解：（ 1）由题意得：y＝80+20×∴函数的关系式为：y＝﹣2x+200（ 30≤x≤ 60）（2）由题意得：（x﹣30）（﹣2x+200）﹣450＝1800解得 x1＝55， x2＝75（不切合题意，舍去）答：当销售单价为55 元时，销售这类童装每个月可赢利1800 元．（ 3）设每个月获取的收益为w元，由题意得：w＝（ x﹣30）（﹣2x+200）﹣450＝﹣ 2（x﹣ 65）2+2000∵﹣ 2＜ 0∴当 x≤65时， w随 x 的增大而增大∵30≤x≤ 60∴当 x＝60时， w最大＝﹣2（60﹣65）2+2000＝1950答：当销售单价为60 元时，销售这类童装每个月获取收益最大，最大收益是1950 元．22．解：（ 1）把点B的坐标（ 3， 0）代入抛物线分析式得，，解得： c＝4，令 y＝0，则，解得 x1＝3，x2＝﹣4，∴ A（﹣4，0），C（0，4）；（2）∵A（﹣ 4， 0），C（0， 4），设直线 AC的分析式为 y＝kx+b，∴，∴，∴直线 AC的分析式 y＝ x+4，点 P 的横坐标为 a， P（ a，），则点 Q（ a， a+4），∴ PQ＝＝，∵，∴a ＝﹣ 2 时，有最大值；PQ（ 3）存在，原因：点 A、B、 C的坐标分别为（﹣4， 0）、（ 3， 0）、（ 0， 4），则 BC＝5， AB＝7， AC＝4，∠ OAC＝∠ OCA＝45°，将点、的坐标代入一次函数表达式：y ＝+ 并解得：，B C mx n∴直线 BC的分析式为 y＝﹣ x+4，设的中点为，由中点坐标公式可得（），BC H H∴过 BC的中点 H且与直线 BC垂直直线的表达式为： y＝，①当＝时，如图 1，BC BQ∴BC＝BQ＝5，设： QM＝ AM＝ n，则 BM＝7﹣ n，由勾股定理得：（ 7﹣n）2+n2＝ 25，解得： n＝3或4（舍去4），故点 Q1（﹣1，3）；②当 BC＝ CQ时，如图1，∴CQ＝5，则 AQ＝AC﹣ CQ＝4，∴，∴，③当CQ＝ BQ时，y＝ x+4和y＝，联立直线AC分析式解得x＝﹣（不合题意，舍去），综合以上可得点Q的坐标为：Q（﹣1，3）或（）．23．解：（ 1）联立x+y＝ 10 和y＝ 2x+1 并解得：x＝ 3，y＝ 7，故“适合点”的坐标为（ 3， 7）；（2）联立x+y＝10 和y＝x2﹣5x﹣ 2 并解得：x＝﹣ 2 或 6，故点 A、 B 的坐标分别为：（﹣2，12）、（6，4），则 AB＝＝8；（ 3）将点（ 4，6）代入二次函数表达式得：16a+16+c＝ 6①，联立 y＝10﹣ x 和 y＝ ax2+4x+c 并整理得：ax2+5x+（ c﹣10）＝0，△＝ 25﹣ 4a（c﹣ 10）＝ 0②，联立①②并解得：a＝﹣，c＝0，故抛物线的表达式为：y＝﹣x2+4x；（ 4）图象G，以以下图所示：G 的极点坐标为（n，3），则 G 的函数表达式为：y＝﹣2（ x﹣ n）2+3，22x+y＝10，则 y＝10﹣ x，设直线 m为： y＝10﹣ x，①当直线 m与图象 G2只有一个交点时，直线 m与图象 G有3个交点，即有 3 个“适合点” ，联立直线 m与 G 的表达式得： y＝﹣2（ x﹣n）2+3＝10﹣ x，整理得：22x2﹣（ 4n+1）x+（ 2n2+7）＝ 0，△＝ b2﹣4ac＝8n﹣55＝0，解得： n＝，故当＜时，图象G 恰巧有 2 个“适合点” ；n②当直线 m经过点 A、 B时，直线 m与图象 G有3个交点，即有3个“适合点”，则在这两个点之间有 2 个“适合点” ，直线 m与 x 轴的交点为（10，0），将（ 10， 0）代入y＝ 2（x﹣n）2﹣ 3 并解得：n＝10，故 10﹣＜n＜10+；综上， n 的取值范围为：n＜或10﹣＜n＜10+．人教版九年级数学单元测试（含答案）——第22 章二次函数培优测试一．选择题1. 二次函数y＝ ax2＋ bx＋ c的图象以下图，那么一次函数y＝ ax＋ b 的图象大概()2．在以下 4 个不一样的情境中，两个变量所知足的函数关系属于二次函数关系的有（）①设正方形的边长为x 面积为 y，则 y 与 x 有函数关系；②x 个球队参加竞赛，每两个队之间竞赛一场，则竞赛的场次数y 与 x 之间有函数关系；③设正方体的棱长为x，表面积为y，则 y 与 x 有函数关系；④若一辆汽车以120km/h的速度匀速行驶，那么汽车行驶的里程y（ km）与行驶时间x（ h）有函数关系．A． 1 个B． 2 个C． 3 个D．4 个23．将函数y=kx 与 y=kx+k 的图象画在同一个直角坐标系中，可能的是（）A．B．C．D．4．抛物线y＝ (x ＋3) 2－ 4 向左平移 1 个单位，再向下平移 2 个单位后所得抛物线的表达式为( )A．y＝ ( x＋4) 2－ 6B ．y＝ ( x＋2) 2－ 6C．y＝ ( x＋6) 2－ 2D ．y＝ ( x＋2) 2－ 25．在美化校园的活动中，某兴趣小组想借助以下图的直角墙角（两边足够长），用28m长的篱笆围成一个矩形花园 ABCD（篱笆只围 AB，BC两边），设 AB=m．若在 P 处有一棵树与墙 CD，AD的距离分别是15m和 6m，要将这棵树围在花园内（含界限，不考虑树的粗细），则花园面积S 的最大值为（）A． 193B． 194C． 195D． 1966．若 a、 b、 c 是△ ABC中∠ A、∠ B、∠ C 的对边，抛物线y=x 2﹣ 2ax+b2交 x 轴于 M（ a+c，0），则△ ABC是（）A．等腰三角形B．等边三角形C．直角三角形D．不确立7.若1351A( － 4 ，y1) ，B( － 4，y2) ，C(4，y3) 为二次函数y＝ x2＋4x－ 5 的图象上的三点，则y1，y2，y3的大小关系为()A．y1＜y2＜y3B．y2＜y1＜y3 C．y3＜y1＜y2D．y1＜y3＜y22y 轴围成的图形的面积S（图中暗影部分）是（轴上，以下图，则两条抛物线、对称轴和）A． 1B． 2C． 3D． 49．如图，在二次函数y=ax 2+bx+c 的图象中，小林察看得出下边六条信息：①ab＞ 0；② c＜2此中正确信息的个数有（）A． 1 个C． 3 个B． 2 个D． 4 个10．如图是二次函数y＝ ax2＋ bx＋ c图象的一部分，图象过点A(－ 3， 0) ，对称轴为直线x ＝－ 1，给出四个结论：①c＞ 0；②若点 B(－35y ＜ y ；2， y) ， C(－2， y ) 为函数图象上的两点，则1212③2a－ b＝ 0；④4ac － b2) 4a＜ 0，此中，正确结论的个数是 (A． 1 个B． 2 个C．3个D．4个11．已知抛物线y=ax2+bx+c 的图象以下图，以下结论正确的选项是（）①b＜ 1；② 2a+b＞ 0；③ a+c+1＞ 0；④ a﹣ b+c＜0；⑤最大值为 3．A．②③④⑤B．②③④C．②③D．①②④二．填空题12．已知抛物线y=﹣ 3x2+6x+c 经过点（﹣ 2， 0），则与 x 轴的另一个交点坐标为．13．抛物线 y＝ 2(x － 2) 2－ 7 的极点为 C，若函数 y＝－ kx － 3 的图象经过点 C，则它与两坐标轴所围成的三角形的面积为 ___．14．教练对小明推铅球的录像进行技术剖析（如图），发现铅球前进高度y（ m）与水平距离x（ m）之间的关系为y= ﹣x2+ x+，由此可知小明铅球推出的距离是m．15．抛物线y=ax 2+bx+3 经过点（ 2， 4），则代数式4a+2b 的值为．16．已知二次函数y＝x2＋ 2mx＋ 2，当 x＞ 2 时， y 的值随 x 的增大而增大，则实数m的取值范围是．三．解答题17．已知二次函数的图象经过点（3， 0），对称轴是直线x=﹣ 2，与 y 轴的交点（ 0，﹣ 3）．（1）求抛物线与x 轴的另一个交点坐标；（2）求抛物线的分析式．18.二次函数y＝ax2＋bx＋c(a≠0)的图象以下图，依据图象解答以下问题：(1)写出方程 ax2＋ bx＋c＝ 0 的两个根；(2)写出知足不等式 ax2＋ bx＋ c＞0 时， x 的取值范围；(3)写出 y 随 x 的增大而减小的自变量 x 的取值范围；(4)若方程 ax2＋ bx ＋ c＝k 有两个不相等的实数根，求k 的取值范围．19．某商场销售一种成本为每台20 元的台灯，规定销售单价不低于成本价，又不高于每台32 元．销售中均匀每个月销售量 y（台）与销售单价 x（元）的关系能够近似地看做一次函数，以下表所示：x22242628y90807060（1）请直接写出 y 与 x 之间的函数关系式；（2）为了实现均匀每个月 375 元的台灯销售收益，这类台灯的售价应定为多少？这时每个月应购进台灯多少个？（3）设商场每个月台灯销售收益ω（元），求ω 与x 之间的函数关系式，当x 取何值时，为ω 的值最大？最大值是多少？20．已知二次函数y=x2﹣ 2x﹣ 32（1）请你把已知的二次函数化成y= （ x﹣h） +k 的形式，并在平面直角坐标系中画出它的图象；（2）假如A（ x1，y1）、 B（x2，y2）是（ 1）中像上的两点，且x1＜x2＜ 1，请直接写出y1、y2的大小关系为．（3）利用（ 1）中的图象表示出方程 x2﹣ 2x﹣ 1=0 的根，画在（ 1）的图象上即可，要求保存绘图印迹．21．如图，极点为 D 的抛物线y=x2+bx﹣ 3 与 x 轴订交于 A， B 两点，与y轴订交于点C，连接BC，已知△ BOC是等腰三角形．（1）求点 B 的坐标及抛物线 y=x 2+bx﹣ 3 的分析式；（2）求四边形 ACDB的面积；（3）若点 E（x，y）是 y 轴右边的抛物线上不一样于点 B 的随意一点，设以A，B，C， E为顶点的四边形的面积为S．①求 S 与 x 之间的函数关系式．②若以 A，B， C， E 为极点的四边形与四边形ACDB的面积相等，求点 E 的坐标．22．如图，在平面直角坐标系中，△ABC的一边 AB 在 x 轴上，∠ ABC=90°，点C（ 4，8）在第一象限内， AC与 y 轴交于点E，抛物线 y=+bx+c 经过 A、B 两点，与 y 轴交于点D （ 0，﹣ 6）．（1）请直接写出抛物线的表达式；（2）求 ED的长；（3）点 P 是 x 轴下方抛物线上一动点，设点P 的横坐标为 m，△ PAC的面积为 S，试求出 S 与m的函数关系式；N，使∠ CAN=∠ MAN．若（4）若点 M是 x 轴上一点（不与点 A 重合），抛物线上能否存在点存在，请直接写出点N 的坐标；若不存在，请说明原因．第 22 章二次函数培优测试1. A2． C ．3． C ．4． A5． C ．6． C ．7. B8． B ．9． C ．10． B11． B ．12．（ 4，0）．913． _ 414． 10 ．15． 1 ．16． m≥－ 217．（ 1）∵抛物线与x 轴的一个交点坐标为（3， 0），对称轴是直线x=﹣ 2，∴抛物线与x 轴的另一个交点坐标为（﹣7， 0）；（2）设抛物线分析式为y=a（x+7）（ x﹣ 3），把（ 0，﹣ 3）代入得a（ 0+7）（ 0﹣ 3）=﹣ 3，解得 a=，∴抛物线分析式为y=（x+7）（x﹣3），即y= x2+ x﹣ 3．18.(1)x 1＝1， x2＝ 3(2)1 ＜ x＜ 3(3)x＞ 2(4)k＜ 219．解：（1）设 y 与 x 之间的函数关系式是y=kx+b ，，得，即 y 与 x 之间的函数关系式是y=﹣ 5x+200；（2）由题意可得，（x﹣ 20）（﹣ 5x+200） =375，解得， x1=25，x2=35（舍去），y=﹣ 5× 25+200=75，答：这类台灯的售价应定25 元，这时每个月应购进台灯75 个；（3）由题意可得，ω=（ x﹣ 20）（﹣ 5x+200） =﹣5（ x﹣ 30）2+500，∵20≤ x≤ 32，∴当 x=30 时，ω 获得最大值，最大值是500．20．解：（1） y=x 2﹣ 2x﹣ 3=（ x﹣ 1）2﹣ 4，抛物线的极点坐标为（ 1，﹣ 4），当 x=0 时， y=x 2﹣ 2x﹣3=﹣ 3，则抛物线与y 轴的交点坐标为（0，﹣ 3），当 y=0 时， x2﹣ 2x﹣ 3= 0，解得 x1=﹣ 1，x2=3，抛物线与 x 轴的交点坐标为（﹣1， 0），（ 3，0），如图，。