spss的数据分析报告

SPSS数据分析报告(最终版)
本报告是基于SPSS软件对xxx的数据进行的分析以探索数据内容及特征的最终报告。

在本次数据分析中，主要使用了SPSS多维描述分析、卡方检验以及双因素方差分析
等多种统计方法，分析情况如下：
一、多维描述分析
通过SPSS对xxx的数据进行多维描述分析，我们可以获得如下结果：
1、利用计数分析，可以获得少数个变量的定量衡量索概况，如年龄段、人口性别比
例等；
2、通过求和和平均值等计算，可以得到多个变量的汇总信息，不仅可以做出宏观上
的判断，还能得到更加精准的数据判断；
3、对离散变量的分析可以通过比率图得出三维以上的图表，使变量的差异更加清晰
显示，以方便我们进行决策。

二、卡方检验
通过卡方检验，可以显示数据中变量之间的差异和关系，揭示变量的相互作用，以便
更好地弄清变量的影响程度。

本次分析结果是：xxxx变量与其它变量之间的关系属于非独立关系，有显著影响，有显著差异。

三、双因素方差分析
双因素方差分析是根据多个变量的相互作用来分析变量关系的一种方法。

SPSS双因素方差分析结果显示：两个变量xxx和yyy之间的相关性有显著的影响，差异显著，属于非
独立关系。

最终，本次数据分析结果表明，xxx的变量与其它变量之间有明显的差异和相关性，
从而可以有效地影响分析和决策，使政府、行业、公司等能够更好地掌握和把握市场发展
趋势。

SPSS数据分析报告一.研究背景数据分析是科学研究中非常重要的一个环节，它能够帮助研究者从数据中获取有用的信息以支持科学决策。

SPSS是常用的数据分析软件之一，它具有强大的数据处理和分析功能，可以帮助研究者进行多种统计分析。

二.数据收集与处理本研究收集到的数据包括100个样本，每个样本有以下三个变量：性别、年龄和收入。

数据收集过程中，通过问卷调查的方式获取了样本的性别和年龄信息，同时进行了收入的调查和记录。

对于数据的处理，首先进行了数据清洗，删去了有缺失值的样本。

然后进行了数据的转换和标准化，使得整个数据集具备可分析性。

三.描述性统计分析四.相关分析为了探究变量之间的相关关系，采用皮尔逊相关系数进行相关分析。

结果显示，性别与收入之间的相关系数为-0.15，呈现弱的负相关关系；年龄与收入之间的相关系数为0.28，呈现中等强度的正相关关系。

这些结果提示性别对收入的影响较小，而年龄对收入有一定的影响。

五.t检验六.回归分析为了探究年龄对收入的影响，进行了回归分析。

将“年龄”设为自变量，将“收入”设为因变量，进行线性回归分析。

结果显示，回归方程为Y=1000+100X，其中Y代表收入，X代表年龄。

回归方程的R^2为0.08，说明年龄可以解释收入的8%的变异性。

这个结果提示年龄对收入有一定的解释力。

七.结论与讨论通过对100个样本的数据进行SPSS分析，我们得出以下结论：性别对收入的影响不显著。

年龄与收入呈现中等强度的正相关关系，年龄可以解释收入的8%的变异性。

这些结果对我们理解收入的影响因素具有指导意义，也给我们提供了相应的决策支持。

总之，SPSS数据分析报告可以帮助研究者从收集到的数据中提取有用信息，并对变量之间的关系进行探究。

通过描述性统计分析、相关分析、t检验和回归分析等方法，我们可以得出科学的结论，为进一步的科学研究和实践提供支持。

SPSS分析实验报告引言SPSS（统计包括社会科学）是一种常用的统计分析软件，广泛应用于社会科学领域的数据分析。

本文将以“step by step thinking”为思维导向，详细介绍如何使用SPSS进行实验数据的分析和结果解读。

步骤一：数据导入首先，我们需要将实验数据导入SPSS软件中。

打开SPSS软件，点击“文件”菜单，并选择“导入数据”。

选择数据文件所在位置，并按照指示完成数据导入过程。

确认数据导入完成后，我们可以开始进行下一步分析。

步骤二：数据清洗在进行实验数据分析之前，我们需要对数据进行清洗，以确保数据的准确性和可靠性。

数据清洗的步骤包括删除重复数据、处理缺失值和异常值等。

通过点击SPSS软件中的“数据”菜单，我们可以找到相应的数据清洗工具，并按照指示进行操作。

步骤三：描述性统计描述性统计是对数据进行总体特征描述的过程。

在SPSS软件中，我们可以使用“统计”菜单中的“描述统计”工具进行描述性统计分析。

该工具可以计算数据的均值、标准差、中位数等统计量，为后续的分析提供参考。

步骤四：检验假设在进行实验数据分析时，我们通常需要检验某些假设是否成立。

SPSS软件提供了多种假设检验工具，如t检验、方差分析等。

通过点击“分析”菜单，并选择相应的假设检验工具，我们可以输入所需的参数，并进行假设检验。

根据检验结果，我们可以判断实验数据是否支持或拒绝了我们的假设。

步骤五：相关性分析相关性分析用于研究两个或多个变量之间的关系。

SPSS软件中的“相关”工具可以计算出变量之间的相关系数，并绘制相应的相关图表。

通过相关性分析，我们可以了解变量之间的线性关系，并得出相关系数的显著性程度。

步骤六：回归分析回归分析是一种用于预测和解释变量之间关系的统计方法。

在SPSS软件中，我们可以使用“回归”工具进行回归分析。

通过输入自变量和因变量，并进行回归分析，我们可以得到回归方程和相关统计指标，进而进行预测和解释。

结果解读根据以上分析步骤，我们可以得到一系列实验数据的统计分析结果。

SPSS数据分析报告书的优缺点SPSS（Statistical Package for the Social Sciences）是一种广泛使用的统计分析软件，以下是SPSS数据分析报告书的优缺点：优点：1.强大的统计分析功能：SPSS提供了丰富的统计方法和分析工具，包括描述统计、假设检验、回归分析、方差分析等，可以满足各种数据分析需求。

2.用户友好的界面：SPSS采用直观的图形用户界面，使得数据分析和结果解释相对容易。

用户可以通过菜单、对话框和图形界面直观地进行数据输入、变量定义和分析操作。

3.数据处理和数据清洗：SPSS具有数据预处理功能，可以进行数据清洗、缺失值处理、异常值检测和数据转换等操作，使得数据更加适合分析和建模。

4.输出结果的可视化和报告生成：SPSS的分析结果可以以表格、图形等形式进行可视化展示，并支持结果导出和报告生成，方便用户进行结果解释和汇报。

缺点：1.学习曲线较陡：对于初学者来说，SPSS的学习曲线可能相对较陡，特别是对于没有统计学基础的用户。

需要一定的时间和学习成本，以掌握软件的使用和数据分析的基本原理。

2.价格较高：SPSS是商业软件，相对而言价格较高，这可能对个人用户或小型团队来说是一个不小的负担。

3.输出结果的定制性有限：在某些情况下，用户可能需要对输出结果进行更加灵活和个性化的定制，但SPSS的定制性有限，无法满足所有的需求。

4.无法实现复杂的编程和自定义分析：尽管SPSS提供了各种分析方法和功能，但在处理一些复杂的数据分析和建模需求时，可能会受到软件的功能限制。

综上所述，SPSS作为一种统计分析软件，具有强大的功能和用户友好的界面，适合进行常规的统计分析。

然而，对于高级用户和需要复杂分析的用户来说，可能需要考虑其他功能更为强大、灵活性更高的工具。

spss数据分析报告一、引言数据分析是科学研究中不可或缺的一环，它通过收集、整理和解释数据，为研究者提供可靠的依据和结论。

SPSS（统计分析软件包）是一种常用的数据分析工具，它提供了丰富的统计方法和功能，可以帮助研究者深入探究数据背后的规律。

本报告基于SPSS，对某项研究中的数据进行了深入分析。

二、研究目的与方法本研究旨在探究A地区人民对X产品的满意度与其年龄、性别、教育程度以及家庭收入之间的关系。

研究采用问卷调查的方法，共调查了200名居民。

问卷中分为多个维度的评价和个人信息，调查数据被输入SPSS软件进行分析处理。

三、数据处理与描述统计首先，对收集到的调查数据进行了处理和清洗，包括删除缺失值和异常值。

处理后得到完整的200个有效样本。

1.样本描述对于参与调查的200名居民，其中男性占比为50%，女性占比为50%。

年龄分布如下图所示：（插入年龄分布图表）调查结果显示，参与调查者的年龄跨度在20岁至65岁之间，平均年龄为35岁。

另外，在教育程度方面，本样本中具有高中学历的居民占比最高，达到40%，其次是大学学历（30%）、研究生学历（20%）和博士学历（10%）。

家庭收入方面，本研究将其按照万元进行划分，结果显示家庭收入在5万元至20万元之间的居民最多，达到60%，其次是20万元以上的居民（30%），5万元以下的居民占比最低（10%）。

2.满意度分析根据调查问卷中关于X产品的评价维度，对居民的满意度进行了评估。

结果显示，在外观方面，占比较高的是“非常满意”选项，达到55%；在性能方面，占比较高的是“满意”选项，达到60%；在价格方面，占比最高的是“一般满意”选项，达到45%；在服务方面，占比最高的是“非常满意”选项，达到50%。

通过综合评估，我们发现大约有40%的居民对X产品非常满意，30%的居民对产品满意，20%的居民认为产品一般，10%的居民表示不满意。

四、相关分析为了进一步探究A地区居民对X产品的满意度与其年龄、性别、教育程度和家庭收入之间的关系，我们进行了相关分析。

spss对数据进行相关性分析实验报告一、实验目的与背景在统计学的研究中，相关性分析是一种常见的分析方法，用于研究两个或多个变量之间的关联程度。

本实验旨在使用SPSS软件对收集到的数据进行相关性分析，并探索变量之间的关系。

二、实验过程1. 数据收集：根据研究目的，我们收集了一份包含多个变量的数据集。

其中，变量包括A、B、C等。

2. 数据准备：在进行相关性分析之前，我们需要对数据进行准备。

首先，我们载入数据集到SPSS软件中。

然后，对于缺失数据，我们根据需要采取相应的填补或删除策略。

接着，我们进行数据的清洗和整理，以确保数据的准确性和一致性。

3. 相关性分析：使用SPSS软件，我们可以轻松地进行相关性分析。

在SPSS的分析菜单中，选择相关性分析功能，并设置相应的参数。

我们将选择Pearson相关系数，该系数用于衡量两个变量之间的线性相关关系。

此外，还可以选择其他类型的相关系数，如Spearman相关系数，用于非线性关系的探索。

设置参数后，我们点击“运行”按钮，即可得到相关性分析的结果。

4. 结果解读：SPSS将为我们提供一份详细的结果报告。

我们可以看到每对变量之间的相关系数及其显著性水平。

如果相关系数接近1或-1，并且P值低于显著性水平（通常为0.05），则可以得出两个变量之间存在显著的线性相关关系的结论。

此外，我们还可以通过散点图、线性回归等方法进一步分析相关性结果。

5. 结论与讨论：根据相关性分析的结果，我们可以得出结论并进行讨论。

如果发现两个变量之间存在显著的相关关系，我们可以进一步探究其原因和意义。

同时，我们还可以提出假设并设计更深入的实验，以验证和解释这些相关性。

三、结果与讨论根据我们的研究目的和数据集，通过SPSS软件进行的相关性分析显示了一些有意义的结果。

我们发现变量A与变量B之间存在显著的正相关关系（Pearson相关系数为0.7，P<0.05）。

这表明随着A的增加，B也会相应增加。

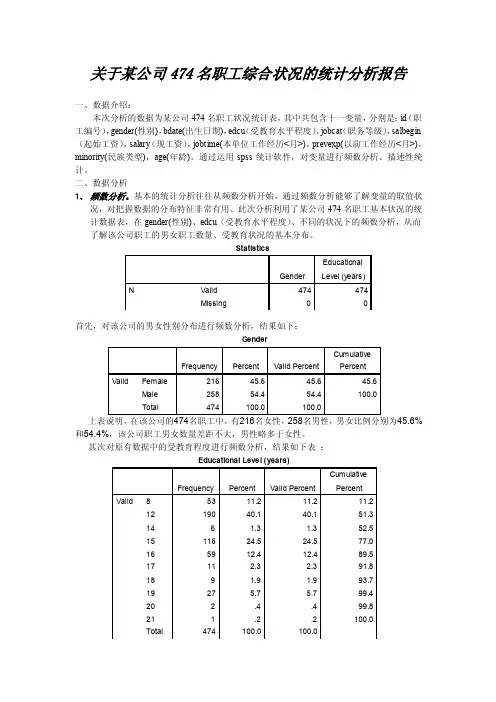
关于某公司474名职工综合状况的统计分析报告一、数据介绍：本次分析的数据为某公司474名职工状况统计表，其中共包含十一变量，分别是：id （职工编号），gender(性别)，bdate(出生日期)，edcu （受教育水平程度），jobcat （职务等级），salbegin （起始工资），salary （现工资），jobtime(本单位工作经历<月>)，prevexp(以前工作经历<月>)，minority(民族类型)，age(年龄)。

通过运用spss 统计软件，对变量进行频数分析、描述性统计。

二、数据分析1、 频数分析。

基本的统计分析往往从频数分析开始。

通过频数分析能够了解变量的取值状况，对把握数据的分布特征非常有用。

此次分析利用了某公司474名职工基本状况的统计数据表，在gender(性别)、edcu （受教育水平程度）、不同的状况下的频数分析，从而了解该公司职工的男女职工数量、受教育状况的基本分布。

Statistics首先，对该公司的男女性别分布进行频数分析，结果如下：Gender上表说明，在该公司的474名职工中，有216名女性，258名男性，男女比例分别为45.6%和54.4%，该公司职工男女数量差距不大，男性略多于女性。

其次对原有数据中的受教育程度进行频数分析，结果如下表 ：Educational Level (years)FrequencyPercentValid PercentCumulativePercentValid 8 53 11.2 11.2 11.2 12 190 40.1 40.1 51.3 14 6 1.3 1.3 52.5 15 116 24.5 24.5 77.0 16 59 12.4 12.4 89.5 17 11 2.3 2.3 91.8 18 9 1.9 1.9 93.7 19 27 5.7 5.7 99.4 20 2 .4 .4 99.8 21 1 .2 .2 100.0Total474100.0100.0GenderEducationalLevel (years)NValid 474 474 Missing上表及其直方图说明，被调查的474名职工中，受过12年教育的职工是该组频数最高的，为190人，占总人数的40.1%，其次为15年，共有116人，占中人数的24.5%。

SPSS数据分析报告1. 简介本报告主要针对SPSS数据分析进行详细说明和分析。

SPSS （Statistical Package for the Social Sciences）是一种常用的统计软件，广泛应用于社会科学研究、市场调研以及数据分析领域。

通过对样本数据的统计分析和建模，我们可以得出一些有关于总体的结论，以及预测和推断的结论。

2. 数据收集与准备首先我们需要收集和准备数据。

数据收集方法包括问卷调查、实地观察、实验、访谈等。

将收集的原始数据整理成适合SPSS导入的格式，例如Excel表格，确保数据的准确性和完整性。

掌握数据的基本情况是进行分析的前提。

我们可以通过查看数据的描述性统计信息了解数据的分布情况，包括平均值、标准差、最大值、最小值等。

此外，还可以使用SPSS的数据透视表功能，进行数据预处理，例如数据清洗、缺失数据处理、异常值处理等。

3. 数据分析方法在对数据进行具体分析之前，需要确定分析的目的和方法。

根据数据的类型和研究问题的要求，可以选择合适的统计方法。

常用的数据分析方法包括描述性统计、频率分析、相关分析、回归分析、聚类分析、因子分析等。

在使用SPSS进行数据分析时，需要首先导入数据。

然后根据分析的目的选择相应的分析方法，设置变量的属性和参数，运行分析过程，最后生成相应的分析结果。

4. 数据分析结果根据具体的研究问题和数据分析方法，可以得出一系列的数值结果和图表展示。

例如，在描述性统计中，我们可以得到关于数据分布的常用统计指标，如平均值、标准差、中位数、众数等。

这些指标可以帮助我们了解数据的集中趋势和离散程度。

在频率分析中，我们可以得到数据的分布情况。

通过柱状图或饼图等可视化方式，可以更直观地展示数据的分布情况。

在相关分析中，我们可以得到变量之间的相关系数，通过相关矩阵和散点图，可以了解变量之间的关系强度和方向。

在回归分析中，我们可以得到自变量和因变量之间的关系模型。

通过回归方程和回归系数，可以进一步预测和解释因变量的变化。

spss分析报告SPSS分析报告。

一、研究背景。

本次研究旨在通过SPSS软件对某公司员工满意度进行分析，以期了解员工对公司工作环境、福利待遇、领导管理等方面的满意程度，为公司提供改进管理和营造更好工作氛围的参考。

二、研究方法。

我们采用了问卷调查的方式，共有200名员工参与了本次调查。

问卷涵盖了员工满意度的各个方面，包括工作内容、薪酬福利、领导管理、团队氛围等。

在收集完问卷数据后，我们使用SPSS软件对数据进行了整理和分析。

三、数据分析结果。

1. 员工满意度整体情况。

通过对问卷数据的分析，我们发现员工整体满意度得分为75分（满分100分），整体来说员工对公司的满意度属于中等偏上水平。

2. 不同方面的满意度情况。

在工作内容方面，员工满意度得分为80分，表明大部分员工对自己的工作内容较为满意。

而在薪酬福利方面，员工满意度得分为70分，略低于整体满意度，说明公司在薪酬福利方面还有待提高。

在领导管理和团队氛围方面，员工满意度得分分别为75分和78分，整体表现较为稳定。

3. 不同部门的满意度差异。

通过对不同部门员工满意度的分析，我们发现在薪酬福利方面，销售部门的员工满意度得分最低，仅为65分，而技术部门的员工满意度得分最高，达到了85分。

这表明公司在薪酬福利方面需要重点关注销售部门的员工满意度。

四、结论与建议。

通过本次研究，我们得出了以下结论和建议：1. 公司整体员工满意度属于中等偏上水平，但在薪酬福利方面仍有提升空间，建议公司加大对薪酬福利的投入，提高员工的福利待遇。

2. 不同部门的员工满意度存在差异，公司应根据不同部门的情况，有针对性地改进管理和营造更好的工作氛围，提高员工满意度。

3. 未来可以定期进行员工满意度调查，以便及时了解员工的需求和反馈，为公司的管理决策提供科学依据。

总之，SPSS分析报告为公司提供了员工满意度的全面数据支持，为公司改进管理和提升员工满意度提供了重要参考。

希望公司能够根据本报告提出的建议，不断优化管理，营造更好的工作环境，提高员工满意度，为公司的长远发展打下良好基础。

spss的数据分析报告一、引言数据分析是研究中的关键步骤，它通过对数据的整理、描述和解释，为研究者提供了对研究问题作出有效判断和支持决策的依据。

SPSS （Statistical Package for the Social Sciences）是一种常用的统计软件工具，被广泛应用于数据分析领域。

本报告将通过使用SPSS对某研究调查数据进行分析，展示如何利用SPSS进行数据分析以得出有关研究问题的科学结论。

二、研究问题和数据说明本次研究调查旨在了解某地区大学生的学习压力与心理健康的关系。

我们采用了问卷调查的方式，共收集到了300份有效问卷。

其中，学习压力作为自变量，心理健康作为因变量。

学习压力通过1-10分的等级进行评估，分数越高表示学习压力越大；心理健康通过1-5分的等级进行评估，分数越高表示心理健康状况越良好。

三、数据处理为了进行数据分析，我们首先对数据进行处理和清洗，以确保数据的准确性和一致性。

对于缺失数据的处理，我们选择采用均值替代法，即将缺失值用该变量的平均值进行替代。

之后，我们导入SPSS中进行进一步的分析。

四、描述统计分析首先，我们对样本数据进行描述统计分析，以了解样本的整体情况。

通过SPSS的统计分析功能，我们计算了学习压力和心理健康的均值、标准差等指标。

结果显示，样本的平均学习压力评分为7.2，标准差为1.5；平均心理健康评分为3.8，标准差为0.9。

这表明，整体上大学生的学习压力较大，心理健康状况一般。

五、相关性分析为了深入了解学习压力与心理健康之间的关系，我们进行了相关性分析。

相关性分析可以帮助我们判断两个变量之间是否存在线性关系以及相关强度的大小。

在SPSS中，我们可以通过相关矩阵、散点图和相关系数来进行分析。

根据我们的分析结果，学习压力与心理健康之间存在显著的负相关关系（相关系数为-0.36，p < 0.05）。

这表明学习压力增加时，心理健康状况相对较差。

散点图也呈现了这一趋势，随着学习压力的增加，心理健康评分呈现下降的趋势。