第10讲答案

第10讲恒成立能成立3种常见题型【考点分析】考点一：恒成立问题若函数()f x 在区间D 上存在最小值()min f x 和最大值()max f x ，则不等式()f x a >在区间D 上恒成立()min f x a ⇔>；不等式()f x a ≥在区间D 上恒成立()min f x a ⇔≥；不等式()f x b <在区间D 上恒成立()max f x b ⇔<；不等式()f x b ≤在区间D 上恒成立()max f x b ⇔≤；考点二：存在性问题若函数()f x 在区间Ｄ上存在最小值()min f x 和最大值()max f x ，即()[],f x m n ∈，则对不等式有解问题有以下结论：不等式()a f x <在区间D 上有解()max a f x ⇔<；不等式()a f x ≤在区间D 上有解()max a f x ⇔≤；不等式()a f x >在区间D 上有解()min a f x ⇔>；不等式()a f x ≥在区间D 上有解()min a f x ⇔≥；考点三：双变量问题①对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≤⇔≤；②对于任意的[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≥⇔≥；③若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212min min f x g x f x g x ≤⇔≤；④若存在[]1,x a b ∈，对于任意的[]2m,x n ∈，使得()()()()1212max max f x g x f x g x ≥⇔≥；⑤对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212max min f x g x f x g x ≤⇔≤；⑥对于任意的[]1,x a b ∈，[]2m,x n ∈使得()()()()1212min max f x g x f x g x ≥⇔≥；⑦若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212min max f x g x f x g x ≤⇔≤⑧若存在[]1,x a b ∈，总存在[]2m,x n ∈，使得()()()()1212max min f x g x f x g x ≥⇔≥．【题型目录】题型一：利用导数研究恒成立问题题型二：利用导数研究存在性问题题型三：利用导数处理恒成立与有解问题【典型例题】题型一：利用导数研究恒成立问题【例1】（2022·福建省福安市第一中学高二阶段练习）对任意正实数x ，不等式ln 1x x a -+>恒成立，则a 的取值范围是（）A ．1a <B ．2a <C ．1a >D ．2a >【答案】B【详解】令()ln 1f x x x =-+，其中0x >，则()min a f x <，()111x f x x x-'=-=，当01x <<时，()0f x '<，此时函数()f x 单调递减，当1x >时，()0f x '>，此时函数()f x 单调递增，所以，()()min 12f x f ==，2a ∴<.故选：B.【例2】【2022年全国甲卷】已知函数()a x x xe xf x-+-=ln ．(1)若≥0，求a 的取值范围；【答案】(1)(−∞,+1]【解析】(1)op 的定义域为(0,+∞)，'(p =(1−12)e −1+1=1(1−1)e +(1−1)=K1(e+1)令op =0,得=1当∈(0,1),'(p <0,op 单调递减，当∈(1,+∞),'(p >0,op 单调递增o )≥o1)=e +1−，若op ≥0,则e +1−≥0,即≤e +1，所以的取值范围为(−∞,+1]【例3】已知函数211()(1)ln (,0)22f x x a x a a =-+-∈≠R ．（1）讨论函数的单调性；（2）若对任意的[1,)x ∈+∞，都有()0f x ≥成立，求a 的取值范围．【答案】（1）答案见解析；（2）0a ≤.【解析】【分析】（1）求()'f x ，分别讨论a 不同范围下()'f x 的正负，分别求单调性；（2）由（1）所求的单调性，结合()10f =，分别求出a 的范围再求并集即可.【详解】解：（1）由已知定义域为()0,∞+，()211'()x a a f x x x x-++=-=当10a +≤，即1a ≤-时，()'0f x >恒成立，则()f x 在()0,∞+上单调递增；当10a +>，即1a >-时，x =或x =，所以()f x 在(上单调递减，在)+∞上单调递增.所以1a ≤-时，()f x 在()0,∞+上单调递增；1a >-时，()f x 在(上单调递减，在)+∞上单调递增.（2）由（1）可知，当1a ≤-时，()f x 在()1,+∞上单调递增，若()0f x ≥对任意的[1,)x ∈+∞恒成立，只需(1)0f ≥，而(1)0f =恒成立，所以1a ≤-成立；当1a >-1≤，即10a -<≤，则()f x 在()1,+∞上单调递增，又(1)0f =，所以10a -<≤成立；若0a >，则()f x在(上单调递减，在)+∞上单调递增，又(1)0f =，所以(0x ∃∈，()0()10f x f <=，不满足()0f x ≥对任意的[1,)x ∈+∞恒成立.所以综上所述：0a ≤.【例4】已知函数()ln f x x ax =-（a 是正常数）.（1）当2a =时，求()f x 的单调区间与极值；（2）若0x ∀>，()0f x <，求a 的取值范围；【答案】（1）()f x 在10,2⎛⎫ ⎪⎝⎭上单调递增，在1,2⎛⎫+∞ ⎪⎝⎭上单调递减，()f x 的极大值是ln 21--，无极小值；（2）1,e ⎛⎫+∞ ⎪⎝⎭.【解析】【分析】（1）求出函数的导函数，解关于导函数的不等式即可求出函数的单调区间；（2）依题意可得maxln x a x ⎛⎫< ⎪⎝⎭，设()ln x g x x =，利用导数研究函数的单调性，求出函数的最大值，即可得解；【详解】解：（1）当2a =时，()ln 2f x x x =-，定义域为()0,∞+，()1122x f x x x-'=-=，令()0f x '>，解得102x <<，令()0f x '<，解得12x >，所以函数()f x 在10,2⎛⎫ ⎪⎝⎭上单调递增，在1,2⎛⎫+∞ ⎪⎝⎭上单调递减，所以()f x 的极大值是1ln 212f ⎛⎫=-- ⎪⎝⎭，无极小值.（2）因为0x ∀>，()0f x <，即ln 0x ax -<恒成立，即maxln x a x ⎛⎫< ⎪⎝⎭.设()ln x g x x =，可得()21ln xg x x -'=，当0x e <<时()0g x '>，当x e >时()0g x '<，所以()g x 在()0,e 上单调递增，在(),e +∞上单调递减，所以()()max 1e e g x g ==，所以1a e >，即1,a e ⎛⎫∈+∞ ⎪⎝⎭.【例5】已知函数()xf x xe=（1）求()f x 的极值点；（2）若()2f x ax ≥对任意0x >恒成立，求a 的取值范围．【答案】（1）1x =-是()f x 的极小值点，无极大值点；（2）a e ≤.【解析】【分析】（1）利用导数研究函数的极值点.（2）由题设知：xe a x≤在0x >上恒成立，构造()x e g x x =并应用导数研究单调性求最小值，即可求a 的范围．【详解】（1）由题设，()(1)xf x e x '=+，∴1x <-时，()0<'x f ，()f x 单调递减；1x >-时，()0>'x f ，()f x 单调递增减；∴1x =-是()f x 的极小值点，无极大值点.（2）由题设，()2xx f x xe a =≥对0x ∀>恒成立，即x ea x≤在0x >上恒成立，令()xe g x x =，则2(1)()xe x g x x'-=，∴01x <<时，()0g x '<，()g x 递减；1x >时，()0g x '>，()g x 递增；∴()(1)e g x g ≥=，故a e ≤.【题型专练】1.（2022·四川广安·模拟预测（文））不等式ln 0x kx -≤恒成立，则实数k 的取值范围是（）A ．[)0,eB ．(],e -∞C ．10,e ⎡⎤⎢⎥⎣⎦D ．1,e ∞⎡⎫+⎪⎢⎣⎭【答案】D 【解析】【分析】由题可得ln xk x ≥在区间(0,)+∞上恒成立，然后求函数()()ln 0x f x x x=>的最大值即得.【详解】由题可得ln xk x≥在区间(0,)+∞上恒成立，令()()ln 0x f x x x =>，则()()21ln 0xf x x x-'=>，当()0,e x ∈时，()0f x '>，当()e,x ∈+∞时，()0f x '<，所以()f x 的单调增区间为()0,e ，单调减区间为()e,+∞；所以()()max 1e ef x f ==，所以1ek ≥.故选：D.2.（2022·北京·景山学校模拟预测）已知函数()ln 2f x x x ax =++．(1)当0a =时，求()f x 的极值；(2)若对任意的21,e x ⎡⎤∈⎣⎦，()0f x ≤恒成立，求实数a 的取值范围．【答案】(1)极小值是11+2e e f ⎛⎫=- ⎪⎝⎭，无极大值.(2)222,e ⎡⎫--+∞⎪⎢⎣⎭【解析】【分析】（1）由题设可得()ln 1f x x '=+，根据()f x '的符号研究()f x 的单调性，进而确定极值.（2）()ln 20f x x x ax =++≤对任意的21,e x ⎡⎤∈⎣⎦恒成立，转化为：2ln 2ln x x a x x x+-≥=+对任意的21,e x ⎡⎤∈⎣⎦恒成立，令()2ln g x x x=+，通过求导求()g x 的单调性进而求得()g x 的最大值，即可求出实数a 的取值范围.(1)当0a =时，()ln 2f x x x =+，()f x 的定义域为()0+∞，，()ln 1=0f x x '=+，则1ex =.令()0f x '>，则1,e x ⎛⎫∈+∞ ⎪⎝⎭，令()0f x '<，则10,e ⎛⎫∈ ⎪⎝⎭x ，所以()f x 在10,e ⎛⎫ ⎪⎝⎭上单调递减，在1,e ⎛⎫+∞ ⎪⎝⎭上单调递增.当1e x =时，()f x 取得极小值且为1111ln 2+2e e ee f ⎛⎫=+=- ⎪⎝⎭，无极大值.(2)()ln 20f x x x ax =++≤对任意的21,e x ⎡⎤∈⎣⎦恒成立，则2ln 2ln x x a x x x+-≥=+对任意的21,e x ⎡⎤∈⎣⎦恒成立，令()2ln g x x x=+，()222120x g x x x x -+'=-+==，所以2x =，则()g x 在[)1,2上单调递减，在(22,e ⎤⎦上单调递增，所以()12g =，()222e 2e g =+，所以()()22max 2e 2e g x g ==+，则222e a -≥+，则222ea ≤--.实数a 的取值范围为：222,e ⎡⎫--+∞⎪⎢⎣⎭.3.（2022·新疆克拉玛依·三模（文））已知函数()ln f x x x =，()()23g x x ax a R =-+-∈.(1)求函数()f x 的单调递增区间；(2)若对任意()0,x ∞∈+，不等式()()12f xg x ≥恒成立，求a 的取值范围.【答案】(1)1,e ⎛⎫+∞ ⎪⎝⎭，(2)(],4-∞【解析】【分析】（1）求函数()f x 的单调递增区间，即解不等式()0f x '>；（2）参变分离得32ln a x x x≤++，即求()()()32ln 0,h x x x x x =++∈+∞的最小值.(1)()ln f x x x =定义域为(0,)+∞，()ln +1f x x '=()0f x '>即ln +10x >解得1e x >，所以()f x 在1,)e∞+（单调递增(2)对任意()0,x ∞∈+，不等式()()12f xg x ≥恒成立，即()21ln 32x x x ax ≥-+-恒成立，分离参数得32ln a x x x≤++.令()()()32ln 0,h x x x x x =++∈+∞，则()()()231x x h x x +-'=．。

第二单元股东权利P77 ）】分红权（★★★）（【考点 1分取红利；但是，全体股东可以事先约定不按、有限责任公司的股东按照1 实缴的出资比例照出资比例分取红利。

、股份有限公司按照股东持有的股份比例分配红利，但股份有限公司章程规定不按持股比例2分配的除外。

、司法解释四3为被告。

公司）股东请求公司分配利润案件，应当列（ 1）股东提交载明具体分配方案的股东会或者股东大会的有效决议，请求公司分配利润，公 2 （司拒绝分配利润且其关于无法执行决议的抗辩理由不成立的，人民法院应当判决公司按照决议载明的具体分配方案向股东分配利润。

年新增）、司法解释五（ 2020 4分配利润的股东会或者股东大会决议作出后，公司应当在决议载明的时间内完成利润分配。

决年超过1议没有载明时间的，以公司章程规定的为准。

决议、章程中均未规定时间或者时间完成利润分配。

决议中载明的利润分配完成时间超过公司1年内的，公司应当自决议作出之日起，请求人民法院撤销决议中关于该时间的规60日内章程规定时间的，股东可以自决议作出之日起定。

P47 ） 2 】知情权（★★★）（【考点（不包括复制）公司会计账簿。

股东要求查阅公司查阅有限责任公司1 、的股东可以要求，说明目的。

公司有合理根据认为股东查阅会计账簿有不会计账簿的，应当向公司提出书面请求 15 正当目的，可能损害公司合法利益的，可以拒绝提供查阅，并应当自股东提出书面请求之日起日内书面答复股东并说明理由。

公司拒绝提供查阅的，股东可以请求人民法院要求公司提供查阅。

、有限责任公司有证据证明股东存在下列情形之一的，人民法院应当认定股东有不正当目2的：（ 1 ）股东自营或者为他人经营与公司主营业务有实质性竞争关系业务的，但公司章程另有规定或者全体股东另有约定的除外；（ 2 ）股东为了向他人通报有关信息查阅公司会计账簿，可能损害公司合法利益的；（ 3 ）股东在向公司提出查阅请求之日前的3年内，曾通过查阅公司会计账簿，向他人通报有关信息损害公司合法利益的；（ 4 ）股东有不正当目的的其他情形。

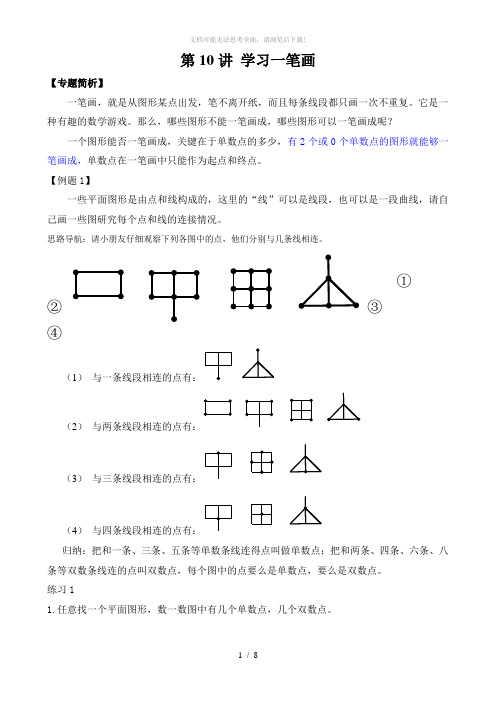
第10讲学习一笔画【专题简析】一笔画，就是从图形某点出发，笔不离开纸，而且每条线段都只画一次不重复。

它是一种有趣的数学游戏。

那么，哪些图形不能一笔画成，哪些图形可以一笔画成呢？一个图形能否一笔画成，关键在于单数点的多少，有2个或0个单数点的图形就能够一笔画成，单数点在一笔画中只能作为起点和终点。

【例题1】一些平面图形是由点和线构成的，这里的“线”可以是线段，也可以是一段曲线，请自己画一些图研究每个点和线的连接情况。

思路导航：请小朋友仔细观察下列各图中的点，他们分别与几条线相连。

①③ ④（1）与一条线段相连的点有：（2）与两条线段相连的点有：（3）与三条线段相连的点有：（4）与四条线段相连的点有：归纳：把和一条、三条、五条等单数条线连得点叫做单数点；把和两条、四条、六条、八条等双数条线连的点叫双数点，每个图中的点要么是单数点，要么是双数点。

练习11.任意找一个平面图形，数一数图中有几个单数点，几个双数点。

2.下面图形中有哪几个单数点？B答案：A D3.数一数下面图形中有几个双数点，分别是哪些点？B 答案：A BCDE F【例题2】下面的图形能不能一笔画成？如果能，应该怎样画？（1） O （2）B DD E F（3）【思路导航】图（1）中A 、B 、C 、D 、O 五个点都是双数点，所以这个图形可以一笔画成。

画时可以从任意一点出发。

图（2）中A 、C 、D 、F 四个点都是双数点，B 和E 两个点是单数点，所以这个图形也可以一笔画成。

画时要从单数点出发，最后回到另一个单数点。

图（3）中A 、D 是双数点，B 、C 、E 和F 四个点是单数点，单数点的个数超过了两个，这个图形不能一笔画成。

练习21.下面的图形能不能一笔画成，如果能，请说明画法，如果不能，请说明理由（1）（2）答案：图（1）可以一笔画成，因为单数点有两个图（2）不能一笔画成，因为单数点大于两个2.下列图形能一笔画成吗?为什么？答：图（1）可以一笔画成，因为单数点个数为零图（2）不可以画成，因为单数点只有一个图（3）不可以画成，单数点个数大于两个3.观察下列图形，哪个图形可以一笔画成？怎么画？图（1）单数点个数为0，可以一笔画出图（2）单数点个数为4个，不可以一笔画出图（3）单数点2个，可以画出【例题3】下图是某地区所有街道的平面图，甲、乙两人同时分别从A、B出发，以相同的速度走遍所有的街道，最后到达C.那么两人谁先到达？AC思路导航：题中要求两人必须走遍所有街道，最后到达C.仔细观察，可以发现图中有两个单数点：A 、C 。

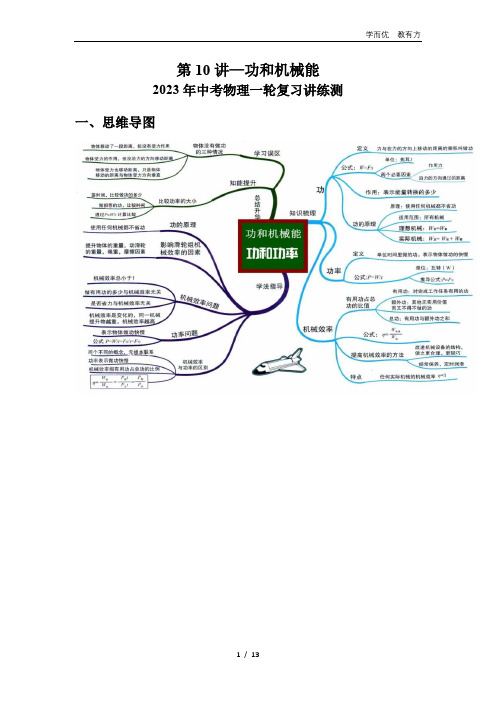
第10讲—功和机械能2023年中考物理一轮复习讲练测一、思维导图二、考点精讲考点1 功1. 功（1）定义：如果一个力作用在物体上，物体在这个力的方向移动了一段距离，这个力的作用就显示出成效，力学里就说这个力做了功。

（2）做功的两个必要因素：①作用在物体上的力，②物体在这个力的方向上移动的距离。

（3）不做功的三种情况：①有力无距离；②有距离无力；③有力有距离，但是力垂直距离。

【归纳总结】不做功的三种情况图示特点物体运动但在水平方向不受力，因惯性而动物体受力，但静止有力有距离，但力的方向与运动方向垂直举例 踢出去的足球会继续往前滚动，但是人已经没有对它做功 推而未动，搬而未起 人提水桶水平前进，提水桶的力水桶的重力均不做功(1)计算公式：物理学中，功等于力与力的方向上移动的距离的乘积。

即：W=Fs 。

(2)符号的意义及单位：W 表示功，单位是焦耳(J)，1J=1N ·m ；F 表示力，单位是牛顿(N)；s 表示距离，单位是米(m)。

注意事项：①分清是哪个力对物体做功，即明确公式中的F 。

②公式中的“s ”是在力F 的方向上通过的距离，必须与“F ”对应。

③F 、s 的单位分别是N 、m ，得出的功的单位才是J 。

(4)变形公式：求距离：s ＝F W ；求力：F ＝ SW ． (5)常考功的估算a ．将地面上的物理课本捡起放到课桌上，人对课本做的功约为2 J ；b.从地上拿起一个鸡蛋，缓缓举过头顶做的功约为1 J ；c.一名普通中学生从一楼走到三楼，克服自身重力做的功约为3 000 J.考点2 功率1. 定义：功与做功所用的时间的比值叫做功率，它在数值上等于单位时间内所做的功，用符号“P ”表示。

2. 物理意义：功率是表示物体做功快慢的物理量。

3. 公式：P ＝tW ．在国际制单位中，功的单位是焦耳，时间的单位是秒，则功率的单位是焦耳每秒，它有个专门的名称叫做瓦特，简称瓦，符号是W ．工程技术上常用千瓦(kW)作为功率的单位．4. 单位换算：1 kW ＝1000W.5. 变形公式：求物体所做的功：W ＝Pt ；求做功所用的时间：t ＝PW . 6. 做匀速直线运动的物体的功率公式推导：P ＝Fv.(1)要特别注意公式中速度v 的单位必须是m/s ，力F 的单位是N ，功率P 的单位是W.(2)由公式可知，当功率一定时，减小速度可以增大牵引力．(如汽车上坡时换挡减速)7. 功率的估测：中学生跳绳的功率约为60 W、中学生正常步行上楼的功率约为150 W、家用小轿车正常行驶的功率约为80 kW.考点3 动能和势能1. 能量（1）物体能够对外做功，表示这个物体具有能量，简称能。

第10讲 集合的基本运算一、 集合的运算 (一)交集文字语言对于两个给定的集合A ，B ，由属于A 又属于B 的所有元素构成的集合，叫做A ，B 的交集，记作A ∩B ，读作“A 交B ”符号语言A ∩B ＝{x |x ∈A 且x ∈B }图形语言阴影部分为A ∩B .例如(1){}{}1,2,3,4,5,3,4,5,6,8A B ==,{}3,4,5AB =(2)}31|{<<=x x A ,}42|{<<=x x B ,}32|{<<=x x B A性质A ∩B ＝B ∩A ，A ∩A ＝A ，A ∩∅＝∅∩A ＝∅，如果A ⊆B ，则A ∩B ＝A【例1】交集（1）已知集合A ＝{1,2,3}，B ＝{－1,2}，则A ∩B 等于( )A ．{1}B ．{2}C ．{－1,2}D ．{1,2,3} 【答案】B【解析】由题得A ∩B ＝{}2（2）已知A ＝{y |y ≤1}，B ＝{x|x ≥0}，则集合A ∩B 等于( )A ．∅B ．{x |x ≤1}C ．{x |0≤x ≤1}D ．{x |0<x <1} 【答案】C,利用数轴，容易得到答案。

这里注意，不少同学会认为是A 答案，为什么不对？ （3）已知集合A ＝{(0,1)，(1,1)，(－1,2)}，B ＝{(x ，y )|x ＋y －1＝0，x ，y ∈Z}，则A ∩B ＝________. 【答案】{(0,1)，(－1,2)}【解析】A ，B 都表示点集，A ∩B 即是由A 中在直线x ＋y －1＝0上的所有点组成的集合，代入验证即可．(4)集合A ＝{x |2k <x <2k ＋1，k ∈Z}，B ＝{x |1<x <6}，求A ∩B ； (4)A ∩B ＝{x |2<x <3或4<x <5}．【变式1】(1)设集合{1,2,3,4}A =，{2,4}B =，则集合A B = .答案：(1)AB ={2,4}(2)集合A ＝{x |－2<x <3}，B ＝{x |x ≤0或x >5}，求A ∩B ； 答案：(2)A ∩B ＝{x |－2<x ≤0}．(3)集合A ＝{(x ，y )|y ＝x ＋2}，B ＝{(x ，y )|y ＝x ＋3}，求A ∩B . 答案：(3)A ∩B ＝∅.(4)设集合{}{}290,30A x x B x x a =-≤=+≥，且{}13A B x x ⋂=≤≤，则a =（ ）A ．1-B ．3-C ．1D ．3【答案】B 【分析】求出集合A ，B ，然后结合交集的结果得到关于a 的方程，求解方程即可确定实数a 的值. 【详解】{}{}29033A x x x x =-≤=-≤≤，3a B x x ⎧⎫=≥-⎨⎬⎩⎭,由{}13A B x x ⋂=≤≤，所以13a-=，即3a =-. 故选：B.（二）并集，阴影部分为A ∈B例如(1){}{}{}1,3,52,3,4,62,3,4,5,6=(2)}31|{<<=x x A ,}42|{<<=x x B ,}41|{<<=x x B A性质A ∈B ＝B ∈A ，A ∈A ＝A ，A ∈∅＝∅∈A ＝A ，如果A ∈B ，则A ∈B ＝B .【例2(1) 设集合A ＝{1,2,3}，B ＝{2,3,4}，则A ∪B =( ) A ．{1,2,3,4} B ．{1,2,3} C ．{2,3,4} D ．{1,3,4} 【答案】A【解析】∈A ＝{1,2,3}，B ＝{2,3,4}，∈A ∈B ＝{1,2,3,4}．故选A. (2) A ＝{x |－1<x <2}，B ＝{x |x ≤1或x >3}，求A ∈B . 【解析】如图：由图知A ∈B ＝{x |x <2或x >3}．(3)已知集合2{|20}A x x x =-≥，{|}B x x a =<，且A B =R ，则实数a 的取值范围是 . 【答案】2a ≥ 【分析】先求出集合A ，然后由条件A B =R 结合数轴可得答案. 【详解】由220x x -≥解得0x ≤或2x ≥，则{|0,A x x =≤或}2x ≥，又{|}B x x a =<，若A B =R ， 则2a ≥.故选：D .(4)A ＝{(x ，y )|x ＝2}，B ＝{(x ，y )|y ＝2}．求A ∈B ，并说明其几何意义．【解析】A ∈B ＝{(x ，y )|x ＝2或y ＝2}，其几何意义是直线x ＝2和直线y ＝2上所有的点组成的集合．【变式2】(1)已知集合{}=23A x x -≤≤，{}240B x x x =-≤，则AB = .A ．[]2,4-B ．[]2,0-C ．[]0,3D ．[]4,3-【答案】A 【分析】先解出集合B ,再求A B .【详解】由{}240B x x x =-≤解得：{}04B x x =≤≤，所以A B =[]2,4-.故选：A(2)已知集合A ＝⎩⎨⎧x ⎪⎪⎪ ⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫3－x >0，3x ＋6>0，集合B ＝{m |3>2m －1}，求A ∩B ，A ∪B .解 解不等式组⎩⎪⎨⎪⎧3－x >0，3x ＋6>0，得－2<x <3，则A ＝{x |－2<x <3}，解不等式3>2m －1得m <2， 则B ＝{m |m <2}．用数轴表示集合A 和B ，如图所示，则A ∩B ＝{x |－2<x <2}，A ∪B ＝{x |x <3}．（三）补集 （1）全集定义：在研究集合与集合之间的关系时，如果所要研究的集合都是某一给定集合的子集，那么称这个给定的集合为全集．记法：全集通常记作U . （2）补集例如(1)}{1,2,3,4,5=U ，{3,4}=A ，{1,2,5}=A C U(2)}51|{<<=x x U ,}32|{<<=x x B ,,21|{≤<=x x A C U 或}53<≤x性质A ∈∈A ＝U ；A ∩∈A ＝∈；∈(∈A )＝A .【例3】(1)设集合U ＝{1,2,3,4,5}，集合A ＝{1,2}，则A C U ＝________. 【答案】{3,4,5}(2)若全集U ＝{x ∈R|－2≤x ≤2}，A ＝{x ∈R|－2≤x ≤0}，求A C U 【解析】∈U ＝{x ∈R|－2≤x ≤2}，A ＝{x ∈R|－2≤x ≤0}， ∈A C U ＝{x ∈R|0<x ≤2}.(3)设全集U ＝{x |x 是三角形}，A ＝{x |x 是锐角三角形}，B ＝{x |x 是钝角三角形}，求A ∩B ，)(B A C U ． 【解析】根据三角形的分类可知，A ∩B ＝∈，A ∈B ＝{x |x 是锐角三角形或钝角三角形}，)(B A C U ＝{x |x 是直角三角形}．【变式3】(1)设U ＝{x |x 是小于9的正整数}，A ＝{1,2,3}，B ＝{3，4,5,6}，求A C U ，B C U .【解析】根据题意可知，U ＝{1,2,3,4,5,6,7,8}，所以A C U ＝{4,5,6,7,8}，B C U ＝{1,2,7,8}． (2)已知集合U ＝R ，A ＝{x |x 2－x －2≥0}，则A C R ＝________. 【答案】{x |－1<x <2}（四）集合运算的综合【例4】（1）已知全集U ＝R ，A ＝{x |x ≤0}，B ＝{x |x ≥1}，则集合∁U (A ∪B )＝______，(∁U A )∩(∁U B )＝________. 答案 {x |0<x <1} {x |0<x <1}解析 A ∪B ＝{x |x ≤0或x ≥1}，∁U (A ∪B )＝{x |0<x <1}．∁U A ＝{x |x >0}，∁U B ＝{x |x <1}，∴(∁U A )∩(∁U B )＝{x |0<x <1}．（2）设集合A ＝{x |－1≤x <2}，B ＝{x |x <a }，若A ∩B ≠∅，则a 的取值范围是( )A ．－1<a ≤2B ．a >2C ．a ≥－1D ．a >－1 【答案】D【解析】因为A ∩B ≠∅，所以集合A ，B 有公共元素，在数轴上表示出两个集合，如图所示，易知a >－1.故选D 。

第10讲甲午中日战争与列强瓜分中国狂潮【学习目标】学习要点：黄海海战和辽东陆战；《马关条约》签订；瓜分高潮。

学习提示：分析甲午战争失败对中国人民觉醒的巨大刺激作用；了解爱国官兵反抗侵略的斗争精神。

【基础知识】1．甲午中日战争：（1）背景：明治维新后日本国力大增，开始对外侵略扩张，矛头直指中国。

（2）导火线：朝鲜东学党起义。

（3）时间：1894-1895年。

（4）主要战役事件：致远舰管带邓世昌在黄海大战中壮烈殉国。

（5）结果：李鸿章代表清政府签订了不平等条约《马关条约》。

2．《马关条约》：（1）签订：1895年，李鸿章同日本首相伊藤博文在马关签订了丧权辱国的《马关条约》。

（2）主要内容：①割地：清政府割辽东半岛、台湾全岛及所有附属各岛屿、澎湖列岛给日本。

②赔款：赔偿日本兵费白银2亿两。

③通商：开放沙市、重庆、苏州、杭州为通商口岸。

④设厂：允许日本在通商口岸开设工厂。

（3）影响：《马关条约》使外国侵略势力进一步深入中国腹地，大大加深了中国的半殖民地化程度。

3．瓜分中国狂潮（1）三国干涉还辽：《马关条约》签订后，沙俄联合法国、德国迫使日本放弃辽东半岛，日本则向中国索取了3000万两白银作为“赎辽费”。

（2）瓜分狂潮：列强以干涉还辽为契机，在中国掀起了抢夺利权、强租海港、划分“势力范围”的瓜分中国狂潮。

（3）“门户开放”：1899年，美国向英、俄、德、日、意、法六国提出“门户开放”的照会，承认各国在中国的“势力范围”和既得特权，同时要求在各国租借地和“势力范围”内享有均等贸易机会。

“门户开放”政策反映出美国与其他帝国主义国家在侵华政策上的矛盾。

【考点剖析】考点一：甲午中日战争背景例1．下图是张滨的漫画《甲午轶事》。

就甲午中日战争的结局而言，该漫画反映了（）A．中国战败的原因在于落后的经济结构B．甲午战后中国救亡图存运动日益高涨C．甲午战争是日本资本主义改革的结果D．战争的结局在于中国落后的思想观念【答案】A【详解】根据漫画中“倭寇不知我大清的GDP是他们五倍吗”，可以看出漫画从经济方面分析了甲午战争中国战败的原因在于落后的经济结构，故A项符合题意；B项反映的是甲午战争对中国的影响，不符合题意，所以排除B； C项从日本方面分析了日本发动这场侵略战争的背景，不符合题意，所以排除C；D项从思想观念方面分析了中国战败的原因，不符合题意，排除D。

第二节固定资产的后续计量◇固定资产折旧◇固定资产的后续支出一、固定资产折旧（一）固定资产折旧的定义折旧，是指在固定资产使用寿命内，按照确定的方法对应计折旧额进行的系统分摊。

应计折旧额，是指固定资产原价扣除其预计净残值后的金额，如果已对固定资产计提减值准备，还应当扣除已计提固定资产减值准备累计金额。

（二）影响固定资产折旧的因素1.固定资产原价2.预计净残值3.固定资产减值准备4.固定资产的使用寿命（三）固定资产折旧范围企业应当对所有的固定资产计提折旧，但是，已提足折旧仍继续使用的固定资产和单独计价入账的土地除外。

在确定计提折旧的范围时还应注意以下几点：1.固定资产应当按月计提折旧。

固定资产应自达到预定可使用状态时开始计提折旧，终止确认时或划分为持有待售非流动资产时停止计提折旧。

当月增加的固定资产，当月不计提折旧，从下月起计提折旧；当月减少的固定资产，当月仍计提折旧，从下月起不计提折旧。

2.固定资产提足折旧后，不论能否继续使用，均不再计提折旧，提前报废的固定资产也不再补提折旧。

所谓提足折旧是指已经提足该项固定资产的应计折旧额。

3.已达到预定可使用状态但尚未办理竣工决算的固定资产，应当按照估计价值确定其成本，并计提折旧；待办理竣工决算后再按实际成本调整原来的暂估价值，但不需要调整原已计提的折旧额。

4.处于更新改造过程停止使用的固定资产，应将其账面价值转入在建工程，不再计提折旧。

更新改造项目达到预定可使用状态转为固定资产后，再按重新确定的折旧方法和该项固定资产尚可使用寿命计提折旧。

【例题·多选题】下列关于固定资产折旧会计处理的表述中，正确的有（）。

（2015年）A.处于季节性修理过程中的固定资产在修理期间应当停止计提折旧B.已达到预定可使用状态但尚未办理竣工决算的固定资产应当按暂估价价值计提折旧C.自用固定资产转为成本模式后续计量的投资性房地产后仍应当计提折旧D.与固定资产有关的经济利益预期消耗方式发生重大改变的，应当调整折旧方法【答案】BCD【解析】选项A，应该继续计提折旧。

第10讲 三角形个数及判断三角形形状问题题型一：三角形解的个数问题已知a 、b 、A ，△ABC 解的情况如下图示． (ⅰ)A 为钝角或直角时解的情况如下：(ⅱ)A 为锐角时，解的情况如下：【例1】在ABC 中，30C =︒，b =c x =. 若满足条件的ABC 有且只有一个，则x 的可能取值是（ ）A ．12 B C ．1 D 因为ABC 只有一解，30︒>，则30B ︒<≤显然满足题意，10sin 2B或sin B 2x ≥或22x =；故选：D【例2】在ABC 中，若3b =，c =，45B =，则此三角形解的情况为（ ）A ．无解B ．两解C ．一解D ．解的个数不能确定为锐角，故满足条件的ABC 只有一个【例3】设ABC 的内角A 、B 、C 所对的边长分别为a 、b 、c ，S 和R 分别为ABC 的面积和外接圆半径．若2,3b c ==，则选项中能使ABC 有两解的是（ ）A ．30B =︒ B ．30C =︒ C ．3S =D ．2R =【例4】在ABC 中，根据下列条件解三角形，其中有一解的是（ ） A ．9,4,30=︒==b c C B ．5,4,45=︒==b c B C ．6,60==︒=a b B D ．20,30,30︒===a b A【答案】BC【分析】由正弦定理逐项判断.【题型专练】1．在ABC 中，内角,,A B C 所对的边分别为,,a b c ，则下列条件能确定三角形有两解的是（ ） A ．5,4,6a b A π=== B ．4,5,4a b A π===C ．55,4,6a b A π=== D ．4,5,3a b A π===，故三角形ABC 有一解；sin b B =⇒，故三角形ABC 有两解；sin b A B =⇒一定为锐角，故三角形ABC 有一解；sin sin b B A B =⇒=，故故三角形ABC 无解故选：B.2．在ABC 中，已知2,45a b A ===，则满足条件的三角形（ ） A ．有2个 B ．有1个 C ．不存在 D ．无法确定45 3．在ABC 中，已知2,3,30=︒==a b B ，则此三角形（ ） A ．有一解 B ．有两解 C ．无解 D ．无法判断有几解【详解】在ABC 中，3013=，，有30A B <=，即4．在ABC 中，内角A ，B ，C 的对边分别为a ，b ，c .已知6,6a b A π===，则此三角形（ ）A ．无解B ．一解C ．两解D ．解的个数不确定故此三角形有两解， 故选：C.5．在解三角形时，往往要判断三角形解的情况，现有∵ABC 满足条件：边20c =，角60B =︒，我想让它有两解，那么边b 的整数值我认为可取______（只填符合条件的一种即可） 2020sin60b ，320b，的整数值为18或19. 18或19.6.在ABC 中，a ，b ，c 分别为内角A ，B ，C 所对的边，若b =60B =︒，若ABC 仅有一个解，则a 的取值范围是（ ）A ．({}2⋃B ．30,2C ．{}30,22⎛⎤⋃ ⎥⎝⎦D ．2【答案】A【解析】：解法一：因为b =60B =︒，由正弦定理得sin sin a b A B=，所以sin 2sin sin b Aa A B ==， 因为()0,120∈︒A ，2sin =y A 的图象如图所示：因为ABC 仅有一个解，所以y a =与2sin =y A 的图象只有一个交点，所以0a <≤或2a =，故选：A解法二：可知当B a b b a sin 0=≤<或时，ABC 仅有一个解，所以0a <≤2a =，题型二：判断三角行形状 判断三角形形状的思路： 1.转化为三角形的边来判断：(1)∵ABC 为直角三角形⇔a 2=b 2+c 2或b 2=a 2+c 2或c 2=a 2+b 2； (2)∵ABC 为锐角三角形⇔a 2+b 2>c 2且b 2+c 2>a 2且c 2+a 2>b 2； (3)∵ABC 为钝角三角形⇔a 2+b 2<c 2或b 2+c 2<a 2或c 2+a 2<b 2； (4)按等腰或等边三角形的定义判断. 2.转化为角的三角函数(值)来判断：(1)若cosA =0，则A =90°，∵ABC 为直角三角形； (2)若cosA <0，则∵ABC 为钝角三角形；(3)若cosA >0且cosB >0且cosC >0，则∵ABC 为锐角三角形； (4)若sin 2A +sin 2B =sin 2C ，则C =90°，∵ABC 为直角角形； (5)若sinA =sinB 或sin (A -B )=0，则A =B ，∵ABC 为等腰三角形；(6)若sin 2A =sin 2B ，则A =B 或A +B =90°，∵ABC 为等腰三角形或直角三角形.在具体判断的过程中，应注意灵活地应用正、余弦定理进行边角的转化，究竟是角化边还是边化角应依具体情况决定.【例1】在ABC 中，2cos 0a c B -=则此三角形的形状为（ ）A ．等腰三角形B ．直角三角形C ．等腰直角三角形D ．等边三角形【答案】A【解析】由正弦定理sin 2sin cos 0A C B -=，又因为A B C π++=，所以sin sin()A B C =+．即sin()2sin cos B C C B +=，用两角和的正弦公式展开左边，得：sin cos cos sin 2sin cos B C B C C B +=，整理得sin cos sin cos 0B C C B -=，所以sin()0B C -=，又因为B ∠和C ∠是三角形的内角，所以0,B C B C -==，此三角形为等腰三角形．【例2】（多选）下列命题中，正确的是（ ） A ．在ABC ∆中，A B >，sin sin A B ∴> B ．在锐角ABC ∆中，不等式sin cos A B >恒成立C ．在ABC ∆中，若cos cos a A b B =，则ABC ∆必是等腰直角三角形D ．在ABC ∆中，若060B =，2b ac =，则ABC ∆必是等边三角形 【答案】ABD【解析】对于A ，由A B >，可得：a b >，利用正弦定理可得：sin sin A B >，正确； 对于B ，在锐角ABC ∆中，A ，(0,)2B π∈，2A B π+>，∴022A B ππ>>->，sin sin()cos 2A B B π∴>-=，因此不等式sin cos A B >恒成立，正确；对于C ，在ABC ∆中，由cos cos a A b B =，利用正弦定理可得：sin cos sin cos A A B B =，sin 2sin 2A B ∴=，A ，(0,)B π∈，22A B ∴=或222A B π=-，A B ∴=或2A B π+=，ABC ∆∴是等腰三角形或直角三角形，因此是假命题，C 错误.对于D ，由于060B =，2b ac =，由余弦定理可得：222b ac a c ac ==+-，可得2()0a c -=，解得a c =，可得60A C B ===︒，故正确.故选：ABD .【例3】（多选题）ABC 的内角,,A B C 的对边分别为,,a b c ，下列四个命题中正确．．的是（ ） A ．若2220a b c +->，则ABC 一定是锐角三角形 B ．若cos cos cos a b cA B C==，则ABC 一定是等边三角形 C ．若cos cos a A b B =，则ABC 一定是等腰三角形D ．若cos cos a B b A a +=，则ABC 一定是等腰三角形【答案】BD 【解析】A 选项：当423a b c ===，，时，2220a b c +->，ABC 为钝角.错误.B 选项：因为cos cos cos a b cA B C==， 所以tan tan tan A B C ==，且(0,)A B C π∈，，所以A B C ==，ABC 为等边三角形.正确.C 选项：cos cos sin 2sin 2a A b B A B A B =⇒=⇒=或2A B π+=.ABC 不一定是等腰三角形.错误.D 选项：cos cos sin cos sin cos sin a B b A a A B B A A +=⇒+=sin()sin A B A ⇒+=sin sin C A ⇒=又因为(0,)A C π∈，，所以A C =.即ABC 为等腰三角形.正确.【例4】已知在ABC 中，3332sin sin sin sin sin sin sin A B CC A B C+-=+-，且sin 2cos sin C A B =，则该ABC 的形状为（ ）[附：()()3322a b a b a b ab +=++-]A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形∵sin cos cos sin 0A B A B -=，即()sin 0A B -=， ∵A B =．∵ABC 为等边三角形， 故选：D ．【例5】在∵ABC 中，如果 lg lg lg sin a c B -==-，且B 为锐角，试判断此三角形的形状（ ）． A ．等腰三角形 B ．直角三角形 C ．等腰直角三角形 D ．等腰或直角三角形【例6】ABC 的三个内角A ，B ，C 的对边分别是a ，b ，c ，若sin :sin :sin 3:4:5A B C =，则ABC 的形状是（ ） A ．锐角三角形 B ．直角三角形 C ．钝角三角形 D ．等腰三角形【答案】B【分析】根据正弦定理的三边比值，然后能得到222+=a b c ，即可得到答案 【详解】由正弦定理可知::sin :sin :sin 3:4:5a b c A B C ==， 设3,4,5,(0)a t b t c t t ===>，所以222225a b t c +==，所以AC BC ⊥，所以ABC 的形状是直角三角形， 故选：B【例7】已知ABC 的三个内角,,A B C 所对应的边分别为,,a b c ，且满足222cos cos cos 1sin sin A B C A C -+=+，且sin sin sin 2A C π+=，且ABC 的形状是（ ）A ．等边三角形B ．等腰直角三角形C ．顶角为56π的等腰三角形 D ．顶角为23π的等腰三角形 又(0,B π∈sin sin A +整理得sin(A ABC ∆ 为顶角为【例8】在ABC 中，角A ，B ，C 对应边分别为a ，b ，c ，已知三个向量,cos 2A m a ⎛⎫= ⎪⎝⎭，,cos 2B n b ⎛⎫= ⎪⎝⎭，,cos 2p c C ⎛⎫= ⎪⎝⎭共线，则ABC 形状为（ ）A ．等边三角形B ．等腰三角形C ．直角三角形D ．等腰直角三角形【详解】解：向量(,cos m a =，(,cos 2B n b =cossin 22B A=． B 02A π<<所以cos 则sin2A =∴22A B=同理由,cos n b ⎛= ⎝，,cos p c ⎛= ⎝ABC ∴形状为等边三角形．故选：A ．【例9】已知三角形的三边长分别为3，4，x ，若该三角形是钝角三角形，则x 的取值范围是（ ） A ．()7,7B ．()7,5C ．()()+∞⋃,57,0D ．()()7,57,1⋃【答案】D【详解】由题意，ABC 为钝角三角形，三边长分别为3，4，x ， 可得当4是最大边时，4所对的角是钝角，即此角的余弦值小于零，则2224334x x <+⎧⎨+<⎩，解得1x <<x 是最大边时，x 所对的角是钝角，即此角的余弦值小于零， 则2224334x x<+⎧⎨+<⎩，解得57x <<，综上可得，x 的取值范围是()()7,57,1⋃ 故选：D . 【题型专练】1．在ABC 中，已知tan tan a ba b A B+=+，则ABC 的形状一定是（ ） A ．等腰三角形 B ．直角三角形 C ．等边三角形 D ．等腰直角三角形综上所述：ABC 的形状一定是直角三角形，2．在ABC 中，,,A B C 的对边分别是,,a b c ，若222a b c +<，则ABC 的形状是（ ） A ．锐角三角形 B ．直角三角形C ．钝角三角形D ．锐角或直角三角形【答案】C【分析】由余弦定理确定C 角是钝角．3．ABC 的三内角,,A B C 的对边分别为,,a b c 且满足cos cos 2cos a B b A c C +=，且sin sin A B =，则ABC 的形状是（ ） A ．等腰三角形 B ．等边三角形C ．等腰直角三角形D ．等腰三角形或直角三角形在ABC 中，由于A B C ==所以ABC 为等边三角形故选：B.4．已知ABC 内角A ､B ､C 所对的边分别为a ､b ､c 面积为S ，若sin sin 2A Ca b A +=，23S BA CA =⋅，则ABC 的形状是（ ） A ．钝角三角形 B ．直角三角形 C ．正三角形 D ．等腰直角三角形6333322BA CA AB AC bc ⋅=⋅=cos sin A A =，故tan 3A =综上，ABC 为正三角形. 故选：C5．已知在ABC 中，()33323a b c c a b c +-=+-，且sin 2cos sin CA B=，则该ABC 的形状为（ ）[附：()()3322a b a b a b ab +=++-]A ．直角三角形B ．等腰三角形C ．等腰直角三角形D ．等边三角形；由此可得ABC 形状，20A <<ABC ∴为等边三角形故选：D.6．ABC 中，a 、b 、c 分别是内角A 、B 、C 的对边，若222ABC a b c =+-，且()0||||AB ACBC AB AC +⋅=，则ABC 的形状是（ ） A ．等腰非直角三角形 B ．三边均不相等的直角三角形 C ．等边三角形 D ．等腰直角三角形)0||||AB ACBC AB AC +⋅=，可判断ABCS 可得2cos 2ab C =，由()0||||AB AC BC AB AC +⋅=可得7．在∵ABC 中，角A 、B 、C 所对的边分别为a 、b 、c ，且222b c a bc +=+，若2sin sin sin B C A =，则∵ABC 的形状是（ ） A ．等腰三角形 B ．直角三角形 C ．等边三角形 D ．等腰直角三角形8．已知角,,A B C 是ABC 的内角，向量()()sin ,sin ,cos ,cos m A B n A B ==且m 与n 共线，则可以判断ABC 的形状为（ ） A ．等腰三角形 B ．等腰直角三角形 C ．直角三角形D ．等边三角形【答案】A【分析】根据向量共线的坐标运算，可得sin cos sin cos A B B A =，根据角A 、B 的范围，即可得tan tan A B =，即可得答案.【详解】因为m 与n 共线， 所以sin cos sin cos A B B A =， 所以in 0()s A B -=因为,(0,)A B π∈，所以(,)A B ππ-∈-， 所以0A B -=，即A B =，所以 ABC 为等腰三角形， 故选：A9．在ABC ∆中，若222cos cos 2sin A B C +>-，则ABC ∆的形状是（ ） A ．钝角三角形 B ．直角三角形 C ．锐角三角形 D ．无法判断10．已知在ABC 中，22tan tan A a B b =，判断ABC 的形状为（ ）. A ．等腰三角形 B ．直角三角形 C ．等腰或直角三角形 D ．等腰直角三角形【详解】tan tan A a B b =sin sin A B=，∴sin 2B =B 或2+2A 或+=A B πABC 是等腰或直角三角形故选：C ．【点睛】判断三角形形状的常用技巧若已知条件中既有边又有角，则(1)化边：通过因式分解、配方等得出边的相应关系，从而判断三角形的形状．(2)化角：通过三角恒等变换，得出内角的关系，从而判断三角形的形状．此时要注意应用A B C +＝这个结论．11．在ABC ∆中，角A ，B ，C 所对的边分别为a ，b ，c ，且(cos cos )a b c A B +=⋅+，则ABC ∆的形状是 A ．等腰三角形 B ．直角三角形C ．锐角三角形D ．不能判断12．在ABC 中，a ，b 分别是角A ，B 的对边，若cos cos a bB A=成立，那么ABC 的形状是（ ） A ．直角三角形 B ．等腰三角形 C ．等腰或直角三角形 D ．无法判断【详解】ABC 中，sin 2A B =2B =或2A +所以ABC 是等腰三角形或者直角三角形故选：C.。

第10讲 函数的单调性【基础知识回顾】 1．函数的单调性 (1)单调函数的定义自左向右看图象是上升的自左向右看图象是下降的(2)单调区间的定义如果函数y ＝f (x )在区间D 上是增函数或减函数，那么就说函数y ＝f (x )在这一区间具有(严格的)单调性，区间D 叫做y ＝f (x )的单调区间． 2．函数的最值常用结论1．∀x 1，x 2∈D 且x 1≠x 2，有f (x 1)－f (x 2)x 1－x 2>0(<0)或(x 1－x 2)[f (x 1)－f (x 2)]>0(<0)⇔f (x )在区间D 上单调递增(减)．2．在公共定义域内，增函数＋增函数＝增函数，减函数＋减函数＝减函数． 3．函数y ＝f (x )(f (x )>0或f (x )<0)在公共定义域内与y ＝－f (x )，y ＝1f (x )的单调性相反．4．复合函数的单调性：函数y ＝f (u )，u ＝φ(x )在函数y ＝f (φ(x ))的定义域上，如果y ＝f (u )与u ＝φ(x )的单调性相同，那么y ＝f (φ(x ))单调递增；如果y ＝f (u )与u ＝φ(x )的单调性相反，那么y ＝f (φ(x ))单调递减．1、下列函数中，定义域是R 且为增函数的是A ．xy e -= B ．3y x = C ．ln y x = D ．y x =【答案】B【解析】四个函数的图象如下显然B 成立．2、列函数中，既是偶函数，又在区间(1，2)内是增函数的为A ．cos 2,y x x R =∈B ．2log ||,0y x x R x =∈≠且C ．,2x xe e y x R --=∈ D ．31y x =+ 【答案】B【解析】函数x y 2log =为偶函数，且当0>x 时，函数x x y 22log log ==为增函数，所以在)2,1(上也为增函数，选B ．3、已知函数f (x )是定义在区间[0，＋∞)上的函数，且在该区间上单调递增，则满足f (2x －1)<f ⎝⎛⎭⎫13的x 的取值范围是( )A.⎝⎛⎭⎫13，23 B.⎣⎡⎭⎫13，23 C.⎝⎛⎭⎫12，23 D.⎣⎡⎭⎫12，23【答案】D【解析】因为函数f (x )是定义在区间[0，＋∞)上的增函数，满足f (2x －1)<f ⎝⎛⎭⎫13.所以0≤2x －1<13， 解得12≤x <23.故选D.4、函数y ＝|－x 2＋2x ＋1|；单调递减区间是 ． 【答案】(1－2，1)，(1＋2，＋∞)；(，(1，1＋2)．【解析】作出函数y ＝|－x 2＋2x ＋1|的图像如图所示．由图像可知，函数y ＝|－x 2＋2x ＋1|的单调增区间为(1－2，1)，(1＋2，＋∞)；单调递减区间是(－∞，1－2)，(1，1＋2)．故应分别考向一 函数单调性的证明与判断例1、判断函数f(x)＝x1＋x2在区间[1，＋∞)上的单调性并证明你的结论．【解析】 函数f （x ）＝21xx+在区间[1，＋∞）上是单调减函数，证明如下： 设x 1、x 2∈[1，＋∞），且x 1<x 2，则f （x 1）－f （x 2）＝1211x x +－2221x x +＝2212212212(1)(1)1)(1)x x x x x x +-+++（＝11122212()(1)1)(1)x x x x x x -++（. ∵x 1、x 2∈[1，＋∞），且x 1<x 2，∴ x 1－x 2<0，1－x 1x 2<0.又（1＋x 21）（1＋x 22）>0，∴ f （x 1）－f （x 2）>0， 即f （x 1）>f （x 2）.∴ f （x ）＝21xx+在[1，＋∞）上为减函数. 变式1、试讨论函数f (x )＝axx －1(a ≠0)在(－1,1)上的单调性．【解析】 设－1<x 1<x 2<1， f (x )＝a ⎝⎛⎭⎪⎫x －1＋1x －1＝a ⎝⎛⎭⎫1＋1x －1，f (x 1)－f (x 2)＝a ⎝⎛⎭⎫1＋1x 1－1－a ⎝⎛⎭⎫1＋1x 2－1＝a (x 2－x 1)(x 1－1)(x 2－1)，由于－1<x 1<x 2<1，所以x 2－x 1>0，x 1－1<0，x 2－1<0，故当a >0时，f (x 1)－f (x 2)>0，即f (x 1)>f (x 2)，函数f (x )在(－1,1)上单调递减； 当a <0时，f (x 1)－f (x 2)<0，即f (x 1)<f (x 2)，函数f (x )在(－1,1)上单调递增．变式2、下列函数中，既是偶函数又在单调递增的函数是（ ） A ． B ． C ． D ．【答案】B【解析】3y x =为奇函数，21y x =-+在(0,)+∞上为减函数，在(0,)+∞上为减函数，故选B ．+∞（0，）3y x =1y x =+21y x =-+2xy -=2xy -=方法总结： 1. 判断函数的单调性，通常的方法有：（1）定义法；（2）图像法；（3）利用常见函数的单调性；（4）导数法.而要证明一个函数的单调性，基本方法是利用单调性定义或导数法.2. 应用函数单调性的定义证明函数的单调性，其基本步骤如下：取值→作差→变形→确定符号→得出结论其中，变形是十分重要的一步，其目的是使得变形后的式子易于判断符号，常用的方法是(1)分解因式；(2)配方；(3)通分约分等．考向二 函数的单调区间例1、求下列函数的单调区间 （1）y ＝－x 2＋2|x|＋1；（2）、函数y ＝|x |(1－x )的单调递增区间是________.【解析】（1）由2221,0-x 21,0x x x x x ⎧-++⎪⎨-+⎪⎩≥，＜，即22(1)2,0-1)2,0.x x y x x ⎧--+⎪=⎨++⎪⎩≥（＜画出函数图像如图所示，单调增区间为(－∞，－1]，[0，1]，单调减区间为[－1，0]， [1，＋∞)．（2）y ＝|x |(1－x )＝⎩⎨⎧x （1－x ），x ≥0，－x （1－x ），x <0＝⎩⎨⎧－x 2＋x ，x ≥0，x 2－x ，x <0，函数的大致图象如图所示.由图易知函数的单调递增区间是⎣⎢⎡⎦⎥⎤0，12. 变式1、函数f (x )＝|x －2|x 的单调递减区间是________． 【答案】 [1,2]【解析】 f (x )＝⎩⎪⎨⎪⎧x 2－2x ，x ≥2，－x 2＋2x ，x <2.画出f(x)的大致图象(如图所示)，由图知f(x)的单调递减区间是[1,2]．方法总结：求函数的单调区间的常用方法与判断函数的单调性的方法类似，有定义法、图像法、利用常见函数的单调性、导数法等．值得引起高度重视的是：(1)函数的单调区间是函数定义域的子区间，所以求单调区间，必须先求出定义域； (2)对于基本初等函数的单调区间，可以直接利用已知结论求解考向三 复合函数的单调区间例3、(2022·沭阳如东中学期初考试)函数y ＝log 5(x 2＋2x －3)的单调递增区间是______． 【答案】(1，＋∞)【解析】由题意，令x 2＋2x －3＞0，解得x ＜－3或x ＞1，因为t ＝x 2＋2x －3在(1，＋∞)上单调递增，所以函数y ＝log 5(x 2＋2x －3)的单调递增区间为(1，＋∞)．变式1、.函数y ＝log 12(－x 2＋x ＋6)的单调递增区间为( )A.⎝⎛⎭⎫12，3B.⎝⎛⎭⎫－2，12 C.(－2，3)D.⎝⎛⎭⎫12，＋∞【答案】 A【解析】由－x 2＋x ＋6>0，得－2<x <3，故函数的定义域为(－2，3)，令t ＝－x 2＋x ＋6，则y ＝log 12t ，易知其为减函数.由复合函数的单调性法则可知本题等价于求函数t ＝－x 2＋x ＋6在(－2，3)上的单调递减区间.利用二次函数的性质可得t ＝－x 2＋x ＋6在定义域(－2，3)上的单调递减区间为⎝⎛⎭⎫12，3.方法总结：求复合函数的单调性，首先要注意复合函数的定义域，其次要确定函数是有哪些基本函数复合而成，根据同增异减的性质确定复合函数的单调性。