山东省淄博市2008—2009学年第一学期期中考试高三数学试题(理工农医类)

2008—2009学年度第一学期阶段性检测高三基本能力试题本试卷分第I卷和第Ⅱ卷两部分，共14页，满分100分，考试时间90分钟。

第Ⅰ卷（共30分）注意事项：1．每小题选出答案后，用2B铅笔把答题卡上对应的答案标号涂黑。

如需改动，用橡皮擦干净以后，再选涂其它答案标号。

不涂答题卡，只答在试题卷上不得分。

2．第Ⅰ卷共30小题，全部为单项选择题，每小题1分，共30分。

一、人类文明像是一个争奇斗艳的百花园，各时代、各地区、各民族所创造的文明色彩缤纷，千姿百态。

1．右图为举世瞩目的北京奥运会开幕式点火瞬间。

与此盛会起源有关的国家，不仅为人类传下了奥林匹克精神，还为人类的政治文明留下了宝贵的管理经验，这种经验是指A．中央集权制度 B．民主运作方式C．比较完备的法律 D．福利国家制度2．某古代水利工程修成后，“水旱从人，不知饥馑”，推动当地成为“天府之国”，该工程现在已被确定为世界文化遗产。

据此判断，这项水利工程是A．都江堰 B．郑国渠 C．灵渠 D．芍陂3．中国人曾经生活在一大堆花花绿绿的票证里，买粮要粮票（右图所示），买布要布票；曾经新三年，旧三年，缝缝补补又三年。

如今，餐桌日益丰富、下馆子成为家常便饭；补丁衣服摇身一变成为时尚，各种款式的衣服让人眼花缭乱；很多年轻人都不知道粮票、布票为何物了。

这些变化的发生是因为我国①确立改革开放方针②以经济建设为中心③实行计划经济体制④建立社会主义市场经济体制A．①②③ B．①②④ C．②③④ D．①③④4．2008年12月20日，幸福村千余村民齐聚村篮球场，通过“自荐直选”的方式选出本村的“当家人”。

这描写的是我国的A．人民代表大会制度 B．多党合作和政治协商制度C．民族区域自治制度 D．基层群众自治制度5．某学校组织了一次主题为“世界文明成果”的图片展，展览内容按时间、地域分为若干板块，在近代欧洲国家文明成果板块中可能展出的图片包括①《权利法案》书影②《1787年宪法》书影③嫦娥一号月球探测卫星④史蒂芬孙发明的火车机车A．①② B．②③ C．①④ D．③④二、第61届联合国大会通过决议将2008年定为国际环境卫生年，以引起国际社会对环境卫生问题的关注，并呼吁世界各国和有关国际组织为改善全球环境卫生做出更多努力。

山东省淄博市重点中学2011届高三上学期期中考试数学试题(理)淄博高三第一学期期中模块考试（理科数学）第Ⅰ卷 60分一、选择题（把答案涂到答题卡上，每个小题5分，共12个小题60分）1．已知命题p:x R,sinx1,则p是（）A x R,sinx 1B x R,sinx 1C x R,sinx 1 Dx R,sinx 12．设集合A＝{1, 2}，则满足A∪B＝{1,2,3}的集合B的个数是( )A．1 B．3 C．4 D．813．函数f(x)lgx的零点所在的区间是（） xA．（0，1] B．(1,10] C．(10,100] D．（100，+∞）4．设函数f x g x x2,曲线y=g(x)在点(1,g(1))处的切线方程为y=2x+1,则曲线y=f(x)在点(1,f(1))处切线的斜率为 ( ) 11 A.4 B. C.2 D. 42115．由直线x＝2，x＝2，曲线y＝x及x轴所围成图形的面积为( )15171A.4 B.4 C.2ln2 D．2ln26．已知函数f x sin x(x∈R),下面结论错误的是（） 2A.函数f(x)的最小正周期为2；B.函数f(x)在区间0,是增函数；2C.函数f(x)的图象关于直线x=0对称；D.函数f(x)是奇函数7．已知{an}是等差数列，a1a24，a7a828，则该数列前10项和S10等于（）A．64 B．100 C．110 D．1208已知||1,||2,0,点C在∠AOB内，且∠AOC=45°，设OC mOA nOB(m,n R),则m等于（） nA．12 B． C．2 D．2 229．已知{an}是递增数列，且对任意n∈N*都有an＝n2＋λn恒成立，则实数λ的取值范围是( )7A．(－2) B．(0，＋∞) C．[－2，＋∞) D．(－3，＋∞)第 - 1 - 页共 8 页10．已知向量1,2,2,45,若5,则a与c的夹角为( ) 2A．30°或150° B．60°或120° C．120° D．150°11．设y f(t)是某港口水的深度y（米）关于时间t（时）的函数，其中0t24.经长期观察，函数y f(t)的图象可以近似地看成函数y k Asin(t)的图象.下面的函数中，最能近似表示表中数据间对应关系的函数是（）A．y123sint,t[0,24] B．y123sin(t),t[0,24] 66C．y123sint,t[0,24] D．y123sin(t),t[0,24] 1212212．符号[x]表示不超过x的最大整数,如 2.53,[-1.1]=-2，定义函数{x}=x-[x]，给出下列四个1 命题:①函数{x}的定义域是R，值域为[0,1];②方程x有无数解；③函数{x}2是周期函数;④函数{x}是增函数.其中正确的命题序号有（）A.②③B.①④C.③④D.②④第Ⅱ卷 90分二、填空题（把答案写到答题纸相应位置上，每个小题4分，共4个小题16分）12a,0a n n6213．数列{an}满足an1，若a1，则a2010的值为172an1,an12________.14．设向量a1,2,b2,3，若向量a b与向量c4,7共线，则．215. 点P在曲线y x3x上移动，设点P处切线的倾斜角为，角的取值3范围是_______16. 如图，当甲船位于A处时获悉，在其正东方向相距20海里的B处有一艘渔船遇险等待营救，甲船立即前往营救，同时把消息告知在甲船的南偏西30°，相距10海里C处的乙船，乙船立即朝北偏东θ角的方向沿直线前往B处救援，则sinθ的值等于__________第 - 2 - 页共 8 页三、解答题（每个小题应该写出必要的解题步骤，只有结果没有步骤的不得分，步骤要清晰规范。

2008年山东省淄博市高三第二次模拟训练题数学（理工农医类）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

满分150分。

考试用时120分钟。

第Ⅰ卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的．1．复数()221i z i+=-（i 是虚数单位）在复平面上对应的点位于 A ．第一象限B ．第二象限C ．第三象限D ．第四象限2. 设全集,U R =且{}|12A x x =->,{}2|680B x x x =-+<,则()U C A B 等于A ．[1,4)-B ． (2,3)C ． (2,3]D ．(1,4)- 3．由曲线x y =2和直线x=1围成图形的面积是A ． 3B ．23C ．34 D ．324. 若5)1(-ax 的展开式中3x 的系数是80，则实数a 的值 A ．2- B ． 22 C ．34 D ．25．已知三条不重合的直线m 、n 、l 两个不重合的平面α、β，有下列命题 ①若αα//,,//m n n m 则⊂； ②若βαβα//,//,则且m l m l ⊥⊥； ③若βαββαα//,//,//,,则n m n m ⊂⊂； ④若αββαβα⊥⊥⊂=⊥n m n n m 则,,,, ；其中正确的命题个数是A ．1B ． 2C ．3D ．46．数列{}n a 中，123,7a a ==，当1n ≥时，2n a +等于1n n a a +的个位数，则该数列的第2010 项是A ．1B ． 3C ．7D ．97．一个几何体的三视图如下图所示，其中正视图中△ABC 是边长为2的正三角形，俯视图为正六边形，那么该几何体的侧视图的面积为正视图 侧视图 俯视图 A ．23 B ．32 C ．12 D ．68．电视台连续播放5个广告，其中3个不同的商业广告和2个不同的奥运宣传广告，要求最后播放的必须是奥运宣传广告，且2个奥运宣传广告不能连续播放，则不同的播放方式有A ．120种B ． 48种C ．36种D ．18种9. 点P 到点1(,0),(,2)2A B a 及到直线12x =-的距离都相等，如果这样的点恰好只有一个，那么a 的值是A ．12 B ． 32 C ．1322或 D ．1122-或 10．设奇函数()f x 的定义域为Ｒ，最小正周期3T =，若23(1)1,(2)1a f f a -≥=+，则a 的取值范围是 A ． 213a a <-≥或 B ． 1a <- C ．213a -<≤ D ．23a ≤ 11．在平面直角坐标系xoy 中，已知△ABC 的顶点)0,6(-A 和)0,6(C ，顶点B 在双曲线1112522=-y x 的右支上，则sin sin sin A CB- 等于A ．56 B ． 65- C ．56± D ．111-12．设函数()f x 的定义域为R ，若存在常数0M >，使|()|||f x M x ≤对一切实数x 均成立，则称()f x 为β函数．现给出如下４个函数：①()0f x =；②2()f x x =；③()cos )f x x x =+；④2()1xf x x x =++，其中是β函数的序号是A ． ① ④B ． ① ③C ．② ④D ． ② ③第Ⅱ卷(非选择题 共90分)二、填空题：本大题共4小题，每小题4分，共16分.13．若直线与直线m y m x -=++2)1(01642=++y mx 平行，则m 的值为 . 14．如图所示，这是计算111124620++++的值的一个程序框图，其中判断框内应填入的条件是 .15．若平面向量22(,),(,),(2,2),(1,1)a x y b x y c d ====，则满足1=⋅=⋅的向量a 有 个.16．定义：若对定义域Ｄ上的任意实数x 都有()0f x =，则称函数()f x 为Ｄ上的零函数．根据以上定义，“()f x 是Ｄ上的零函数或()g x 是Ｄ上的零函数”为“()f x 与()g x 的积函数是Ｄ上的零函数”的 条件.三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤. 17．(本小题满分12分)已知函数()sin()(0 02 ||)f x A x B A πωϕωϕ=++><<<，，的一系列对应值如下表：（Ⅰ）根据表格提供的数据求函数()y f x =的解析式；（Ⅱ） 若对任意的实数a ，函数()y f k x =（0k >），2(]3x a a π∈+，的图像与直线1y =有且仅有两个不同的交点，求k 的值． 18． (本小题满分12分)一个盒子装有六张卡片，上面分别写着如下六个定义域为R 的函数：23123456()()()()sin ()cos ()2f x x f x x f x x f x x f x x f x ======，，，，，.（Ⅰ）现从盒子中任取两张卡片，将卡片上的函数相加得一个新函数，求所得函数是奇函数的概率；（Ⅱ）现从盒子中进行逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行，求抽取次数ξ的分布列和数学期望. 19．(本小题满分12分)已知梯形ABCD 中，AD ∥BC ，2π=∠=∠BAD ABC ，42===AD BC AB ，E 、F 分别是AB 、CD 上的点，EF ∥BC ，x AE =，G 是BC 的中点.沿EF 将梯形ABCD 翻折，使平面AEFD ⊥平面EBCF (如图) .(Ⅰ) 当2=x 时，求证：BD ⊥EG ；(Ⅱ) 若以F 、B 、C 、D 为顶点的三棱锥的体积记为 ()x f ，求()x f 的最大值； (Ⅲ)当()x f 取得最大值时，求二面角C BF D --的余弦值.20．(本小题满分12分)已知各项均为正数的数列{}n a 的前n 项和n S 满足11S >，且*6(1)(2)()n n n S a a n N =++∈.（Ⅰ）求{}n a 的通项公式； （Ⅱ）设数列{}n b 满足{,2,n n a n a n b n =为偶数为奇数，求n n b b b T 2212 ++=.21．(本小题满分12分)若1F 、2F 分别是椭圆2214x y +=的左、右焦点. （Ⅰ）若P 是该椭圆上的一个动点，求1PF 2PF ⋅的最大值和最小值； （Ⅱ）设过定点M (1，)2的直线l 与椭圆交于同的两点A 、B ，且AOB ∠为锐角（其中O 为坐标原点），求直线l 的斜率k 的取值范围. 22． (本小题满分14分)已知函数x a x x f ln )(2-=在]2,1(是增函数,x a x x g -=)(在(0,1)为减函数. （I ）求)(x f 、)(x g 的表达式；（II ）求证:当0>x 时,方程2)()(+=x g x f 有唯一解； (III ）当1->b 时,若212)(x bx x f -≥在x ∈]1,0(内恒成立,求b 的取值范围.。

山东省淄博市2008—2009学年第一学期期中考试高三数学试题（文史类）本试卷共4页，分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

共150分。

考试用时120分钟。

考试结束后，将本试卷答题纸和答题卡一并交回。

第Ⅰ卷（选择题 共60分）1． 2．1A ．2）A ．3A ．4A ．C ．5．函数)32sin(π-=x y 在区间[ππ,2-]上的简图是 ( )6 A7 A 8A 9 A 10 A 11 A 12．若函数32)(kx k x x h +-=在),1(+∞上是增函数，则实数k 的取值范围是 ( ) A ．[),2+∞- B ．[),2+∞ C ．2,(--∞] D ．2,(-∞]第Ⅱ卷 (非选择题 共90分)注意事项：1．第Ⅱ卷包括填空题和解答题共两个大题．2．第Ⅱ卷所有题目的答案考生需用0. 5毫米黑色签字笔答在答题纸指定的位置上二、填空题：本大题共4小题，每小题4分，共16分13．函数)0()(>=x xInx x f 的单调递增区间是__________________≤0,cos x x π17 P Q 18 已知函数)0,0)(cos()(πϕωϕω≤≤>+=x x f 是R 上的奇函数，且最小正周期为π (I)求ϕ和ω的值；(II)求)4(3)()(π++=x f x f x g 取最小值时的x 的集合．19．(12分)已知函数2()22,[5,5]f x x ax x =++∈-（I ）求实数a 的值，使)(x f y =在其定义域[一5，5]上是偶函数； (Ⅱ)求实数a 的取值范围，使)(x f y =在区间[一5，5]上是单调函数； (20 （I ( 21 ( （I (22点()(2)()(000x f x x f x x f =-++成立，则函数)(x f y =的图像关于点()(,00x f x )对称．已知函数223)(23++-=x x x x f ，请回答下列问题： (I)求函数f (x)的“拐点”A 的坐标；(Ⅱ)检验函数f (x)的图象是否关于“拐点”A 对称，对于任意的三次函数写出一个有关“拐点”的结论(不必证明)；(Ⅲ)写出一个三次函数G(x)，使得它的“拐点”是()1,3-(不要过程)．1A ．2A ．3A ．4A ．1≥x xB ．21<≤x xC ．{}10≤<x xD ．{}1≤x x5．（文）函数)32sin(π-=x y 在区间[ππ,2-]上的简图是 ( A )6．78A 9 A 1011 A ．222- B ．222+ C ．32- D ．32+ 12．若函数32)(kx k x x h +-=在),1(+∞上是增函数，则实数k 的取值范围是 ( ) A ．[),2+∞- B ．[),2+∞ C ．2,(--∞] D ．2,(-∞]第Ⅱ卷 (非选择题 共90分)注意事项：1．第Ⅱ卷包括填空题和解答题共两个大题．2．第Ⅱ卷所有题目的答案考生需用0. 5毫米黑色签字笔答在答题纸指定的位置上二、填空题：本大题共4小题，每小题4分，共16分17． P Q 如果P 和Q 有且仅有一个正确，求c 的取值范围．解：指数函数xc c y )75(2+-=在R 上单调递增1752>+-⇔c c解得c<2或c>3, 即P ：c<2或c>3……………………………………………………….3分 二次函数c cx x y ++=22在R 上无零点,0442<-⇔c c解得0<c<1, 即Q ：0<c<1…………………………………………………………………6分于是10:,32:≥≤≤≤⌝⌝c c Q c P 或…………………………………………………...8分 若P 正确且Q 不正确, 则;3210><≤≤c c c 或或………………………………..10分 若P 不正确且Q 正确, 则Φ∈c所以c 的取值范围是),3()2,1[]0,(+∞-∞ ………………………………………12分18．(文科12分)已知函数)0,0)(cos()(πϕωϕω≤≤>+=x x f 是R 上的奇函数，且最小正周期为π (I)求ϕ解：又∵所以当所以19． （I ( (解:即 a ≤-5或a ≥5于是, 实数a 的取值范围是a ≤-5或a ≥5…………………………………………….7分 (Ⅲ)当无解时即⎩⎨⎧=-=-==+==≥-≤-11027)5()(371027)5()(55min max a f x f a f x f a a ………………..8分当112)()(371027)5()(5a 0052min max =⎩⎨⎧=-=-==+==<≤≤-<-a a a f x f a f x f a 解得时即……..9分 当112)()(371027)5()(0a 5502min max -=⎩⎨⎧=-=-==-=-=<<-<-<a a a f x f a f x f a 解得时即…10分 当无解时即⎨⎧=-=-=-≤≥-371027)5()(5a 5max a f x f a ……………………….11分20 解∵∴∴=-(又CB sin sin ∴551010221sin sin =⨯=⋅=B C c b 即所求最短边的长为55…………………………………………………………………12分21．(12分)某公司计划投资A 、B 两种金融产品，根据市场调查与预测，A 产品的利润与投资量 成正比例，其关系如图l ，B 产品的利润与投资量的算术平方根成正比例，其关系如图2， (注：利润与投资量单位：万元)（I ）分别将A 、B 两产品的利润表示为投资量的函数关系式；(Ⅱ)该公司已有10万元资金，并全部投入A 、B 两种产品中，问：怎样分配这10万元22． 解0x ，则称点()(,00x f x )为函数)(x f y =的“拐点”；定义：(2)设0x 为常数，若定义在R 上的函数)(x f y =对于定义域内的一切实数x ，都有)(2)()(000x f x x f x x f =-++成立，则函数)(x f y =的图像关于点()(,00x f x )对称．已知函数223)(23++-=x x x x f ，请回答下列问题： (I)求函数f (x)的“拐点”A 的坐标；黄牛课件 (Ⅱ)检验函数f (x)的图象是否关于“拐点”A 对称，对于任意的三次函数写出一个有关“拐点”的结论(不必证明)；(Ⅲ)写出一个三次函数G(x)，使得它的“拐点”是(一l ，3)(不要过程)．解：(I)依题意，得：263)(2+-='x x x f∴66)(-=''x x f …………………………………………………………………….2分。

2009届高三年级第二次质量检测理科数学试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

全卷满分150分，考试用时120分钟。

第Ⅰ卷（选择题 共50分）一、选择题：本次题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的。

1．已知全集U={1，2，3，4，5}，集合A ，B ≠⊂U ，若A∩B={2}，（A C U ）∩B={4}，（A C U ）∩（B C U ）={1，5}，则下列结论中正确的是A ．B A ∈∈3,3 B ．B A ∉∉3,3C ．B A ∈∉3,3D ．B A ∉∈3,3 2．下列函数中既是奇函数，又在区间[－1，1]上单调递减的函数是 A ．x x f sin )(= B ．|1|)(--=x x fC ．)(21)(x x a a x f -+=D ．xxx f +-=22ln )( 3．条件p ：|1|2x +>，条件q ：113x>-，则p ⌝是q ⌝的 A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知)(x f =a －122+x是定义在R 上的奇函数，则f1-(－53)的值是 A ．53B ．－2C ．21 D ．35 5．函数)4lg(12-+++=x x x y 的最小值为A ．2lg -B ．2lg 2+C ．2lg 3+D ．不存在 6．已知函数()x 1f (x)a 0,a 1a-=>≠，在同一坐标系中，y=f -1(x)与y=x 1a-的图象可能是xx7．已知函数)(x f 的导函数为x x f cos 5)('+=，()1,1-∈x ，且0)0(=f ，如果0)1()1(2<-+-x f x f ，则实数x 的取值范围为A ．（10，）B ．()2,1 C ．)2,2(-- D．⋃）－，（－12 8．已知04)(21]1,(2>-++-∞∈x x a a ，x 不等式时恒成立，则a 的取值范围是A ．)41,1(-B ．)23,21(-C ．]41,(-∞D ．]6,(-∞9．已知y =f (x )是奇函数，且满足)1()1(-=+x f x f ，当0(∈x ,1)时，xx f -=11log )(2则y =f (x )在(1,2)内是 A ．单调减函数，且f (x )<0 B ．单调减函数，且f (x )>0 C ．单调增函数，且f (x )>0D ．单调增函数，且f (x )<010．已知函数(](),1,0(),0,1ax b x f x x b x x a ⎧+∈-⎪=⎨-∈⎪-⎩,其中,0,0>>b a 若)(lim 0x f x →存在,且)(x f 在()1,1-上有最大值,则b 的取值范围是A ． 10≤<bB ．1>bC ．1≥bD ．121≤<b 第Ⅱ卷（非选择题 共100分）二、填空题：本大题共5小题，每小题5分，共25分.把答案填在答题卡相应位置上.11．已知集合B A x y y B y x A xx 则},0,)21(|{},log |{)1(2≤====-等于12．函数()f x 对于任意实数x 满足条件()()12f x f x +=，若()15,f =-则()()5f f =_________13．已知函数1(),2()2(1),2xx f x f x x ⎧≥⎪=⎨⎪+<⎩，则函数2(log 3)f 的值为_________14．已知()f x 是以2为周期的偶函数，当[]0,1x ∈时，()f x x =，且在[]1,3-内，关于x 的方程()()1,1f x kx k k R k =++∈≠-有四个根，则k 得取值范围是 15．设()f x 是定义在R 上的偶函数，其图像关于直线1x =对称，对任意1x ，2x 10,2⎡⎤∈⎢⎥⎣⎦，有1212()()()f x x f x f x +=⋅，(1)0f a =>，则（1）11()()24f f ⋅= （2）若记1(2)2n a f n n=+，那么lim(ln )n n a →∞=三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤. 16．（本小题满分12分）设命题:p 函数3()()2xf x a=-是R 上的减函数，命题:q 函数2()43f x x x =-+，在[]0,a 的值域为[]1,3-．若“p 且q ”为假命题，“p 或q ”为真命题，求a 的取值范围17．（本小题满分12分）一个盒子中装有6张卡片，上面分别写着如下6个定义域均为R 的函数：6)(,5cos )(,4sin )(,)(,)(,)(65433221======x f x x f x x f x x f x x f x x f .（1）现从盒子中任取两张卡片，将卡片上的函数相加得到一个新函数，求所得函数为奇函数的概率；（2）现从盒子中逐一抽取卡片，且每次取出后均不放回，若取到一张记有偶函数的卡片则停止抽取，否则继续进行。

2008-2009学年度山东省淄博市第一学期高三阶段性检测地理试卷第I卷一、每小题1.5分，共51分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

读下图完成1—2题。

1．如图所示，交通与土地利用转化率的关系为①据交通干线越近，土地利用转化率越高②据交通干线越远，土地利用转化率越高③据交通干线越近，土地利用转化率越低④据交通干线越远，土地利用转化率越低A．①④B．②③C．①②D．③④2．图示现象可以解释为A．交通干线两侧的土地，适合开辟为第一产业用地B．交通干线两侧的土地，适合开辟为第三产业用地C．远离交通干线的土地，适合开辟为第二产业用地D．远离交通干线的土地，适合开辟为第三产业用地下图所示区域有“一山有四季，十里不同天”之说，读图完成3—5题。

3．图中公路线的选择，主要是考虑了A．气候因素B．居民点分布C．地形因素D．工业分布4．图示区域位于我国的A．东北地区B．东南地区C．西北地区D．西南地区5．图示区域多发性的自然灾害是A．台风B．寒潮C．泥石流D．洪涝读下列一组景观图，完成第6题。

6．关于景观图显示内容，描述正确的是A．左图：水田—种植水稻—现代农业右图：旱地—种植谷物—传统农业B．左图：旱地—种植谷物—现代农业右图：水田—种植水稻—传统农业C．左图：水田—我国南方—夏季高温多雨，冬季低温少雨右图：旱地—我国北方—夏季高温多雨，冬季寒冷干燥D．左图：旱地—我国南方—夏季高温多雨，冬季寒冷干燥右图：水田—我国北方—夏季高温多雨，冬季低温少雨合作是企业技术创新的主要方式之一，上图为企业对合作伙伴不满意度示意图，下图为企业合作伙伴空间分布图，读图完成7—9题。

7．企业最不满意的合作伙伴是A．科研机构B．市场方面C．中介服务D．合作公司8．企业的合作伙伴，主要来自于A．国际方面B．国内方面C．亚洲以内D．亚洲以外9．对于目前我国企业技术创新存在的问题，应采取的措施是A．努力拓展国际市场B．扩大企业的规模C．引导创新人才向企业流动D．开发新的原料供应基地读甲、乙两幅图，完成10—12题。

淄博市二○○八年中等学校招生考试数学试题（A 卷）参考答案及评分标准评卷说明：1．选择题和填空题中的每小题，只有满分和零分两个评分档，不给中间分． 2．解答题每小题的解答中所对应的分数，是指考生正确解答到该步骤所应得的累计分数．每小题只给出一种或两种解法，对考生的其他解法，请参照评分意见进行评分．3．如果考生在解答的中间过程出现计算错误，但并没有改变试题的实质和难度，其后续部分酌情给分，但最多不超过正确解答分数的一半；若出现严重的逻辑错误，后续部分就不再给分．一、选择题（本大题共12小题，每小题3分，共36分）：二、填空题 (本大题共5小题，每小题4分，共20分) ：13．7；14．①，③（或②，④）；15．60；16．13；17．32m -<≤-或23m <≤．三、解答题 (本大题共8小题，共64分) ： 18．(本题满分6分)解：224224xx x x ⋅-+-- ＝()()()()242222xx x x x -+-+- ……………………………………2分＝()()2422x x x -+- ……………………………………3分＝()()()2222x x x -+- ………………………………………5分＝22x + …………………………………………………6分19．(本题满分6分) 证明：（1）在A B C ∆和BAD ∆中， ∵A C B D =，C A BD B ∠=∠，A B B A =， ……………………………………………2分∴△ABC ≌△BAD ， ……………………………………3分∴C D∠=∠．……………………………………4分（2）∵∠AOC=∠BOD，C D∠=∠，A C B D=，∴△AOC≌△BOD．……………………………………6分20．(本题满分8分)解：（１）众数为５，……………………………………2分中位数为５；……………………………………4分（２）条形统计图；……………………………………6分（３）68.7510⨯个．………………………………………8分21．(本题满分8分)解：设矩形的一边长为x cm，则其另一边长为（18－x）cm．………………1分由题意，等腰三角形的周长为36cm，已知腰长为13cm，则其底边长为10cm，根据勾12=(cm)．……………………………3分由矩形面积与等腰三角形面积相等，得x（18－x）＝110122⨯⨯，…………6分解得x＝9±当x＝9+18-x=9-x＝9-18-x=9+．答：矩形的一边长为(9+，另一边长为(9-)cm．………………8分22．（本题满分8分）解：（1）因为AB是⊙O的直径，所以∠ACB＝90º．………………1分又因为∠ABC＝∠AQC＝30º，AC=6，则AB＝12．……………………3分（2）由（1）可知∠BAC=60º，AO=6，由于AQ是∠BAC的平分线，所以∠CAQ＝∠BAQ＝30º，则有∠BAQ＝∠ABC＝30º，所以△APB是等腰三角形．连接PO，则PO就是点P到AB的距离．………………………………………５分在Rt△AOP中，PO=AO·tan30º＝．故所求点P到AB的距离为……………………………………………６分（3）因为∠BCQ＝∠BAQ＝30º，所以∠AQC=∠ＢCQ，则PQ=CP．由于AP是∠BAC的平分线，∠ACP＝∠AOP＝90º所以CP=PO，那么PQ=……………………………………………8分23．（本题满分8分）解：（1）已知甲库运往A地x吨，则从甲库运往B地（80－x）吨，由乙库运往A地（50－x）吨，运往B地（x－10）吨．……………………………………1分所以y=10x+40(80－x)+20(50－x)+30(x－10)＝3900－20x. …………………………4分（2）根据已知可知10≤x≤50，…………………………………6分所以，当x=50时，总运费最省，为2900元；…………………………………7分当x=10时，总运费最多，为3700元．……………………………………………8分24．（本题满分10分）解：（1）已知原抛物线经过原点O (0,0)与A (4,0)点，因此可设原抛物线的表达式为(4)y ax x =-． …………………………………1分 配方得2(2)4y a x a =--，则其顶点B 的坐标为(2,4)a -． …………………2分 因为顶点B 在直线2(0)y kx k k =+≠上，将(2,4)a -代入可得k a =-． ……3分 由题意可知平移后得到的抛物线的顶点B '的坐标为(2,4)m a m +-+，即(2,4)m k m ++．因为B '点仍然在直线2y kx k =+上，则4(2)2k m k m k +=++，整理得m km =，因为0m >，所以1k =， ……………………………………4分 则1a =-，所以原抛物线的表达式为(4)y x x =--．（或24y x x =-+）……5分 （2）方法一：由（1）知，点B '的坐标为(2,4)m m ++，由题意，点A '的坐标为(4,)m m +， ……………………………………6分 作C B '垂直于y 轴于C ，作D A '垂直于y 轴于D ，………………………………7分 因为0m >，所以△B O A ''的面积＝△OC B '的面积＋梯形A CD B ''的面积－△OD A '的面积 ＝()()m m ++4221＋()()m m m m--+++24421－()m m +421＝83+m ， ………………8分 603283=+m ，解得2008m =． ……………………………………10分 方法二：由（1）知，点B '的坐标为(2,4)m m ++，由题意，点A '的坐标为(4,)m m +， ……………………………………6分设直线A B ''的表达式为y k x b '=+，则()()42,4.m m k b m m k b '+=++⎧⎪⎨'=++⎪⎩解得2,38.k b m '=-⎧⎨=+⎩ ……………………………………7分则直线A B ''的表达式为238y x m =-++． 设直线A B ''与x 轴的交点为C ，则点C 的坐标为38(,0)2m +． ………………8分因为0m >，所以382m O C +=＞０，A y m '=＞０，4B y m '=+＞０，所以111()222A OB B A B A S OC y O C y O C y y ''''''=⋅-⋅=-138(4)38603222m m m m +⋅⋅+-=+= 解得2008m =． ……………………………………10分 25．（本题满分10分） 解：（1）由于四边形ABCD 是平行四边形，所以OA ＝OC ． 又△AOB ，△BOC 的边OA ，OC 上的高相同，所以，S 1＝S 2．同理S 2＝S 3，S 3＝S 4，S 4＝S 1，所以S 1＝S 2＝S 3＝S 4． ……………………2分 （2）由于AC ⊥BD ，垂足为O ，所以S 1＝12OA ·OB ，S 2＝12OB ·OC ，S 3＝12OC ·OD ，S 4＝12OD ·OA ，则有S 1S 3＝S 2S 4． ………………………………4分（3）设点B 到线段AC 所在直线的距离为h 1，点D 到线段AC 所在直线的距离为h 2， 则S 1＝12OA ·h 1，S 2＝12OC ·h 1，S 3＝12OC ·h 2，S 4＝12OA ·h 2，所以有S 1S 3＝S 2S 4． …………………………………6分 （4）解法一：已知∠BAC =∠BDC ，又∠AOB =∠DOC ，那么∠DCA =∠ABD ． 当AB 与CD 不平行时，必相交于一点， 不妨设线段BA 与CD 的延长线交于点E ．已知AC =BD ，又∠AEC =∠DEB ，所以△AEC ≌△DEB ，则AE ＝DE ，CE ＝BE ，所以AB ＝DC ，所以△AOB ≌△DOC ，则S 1＝S 3． 由于有S 1S 3=S 2S 4，所以S 12=S 2S 4，那么S =S 1+S 2+S 3+S 4＝2S 1+S 2+S 4＝S 2+S 4（或＝2）；………8分 当AB 与CD 平行时，则△ABD 与△BAC 同底等高，有S 1+S 2=S 1+S 4，则S 2＝S 4，由于有S 1S 3=S 2S 4，所以S 22= S 1S 3，S ＝S 1+S 3+2S 2＝S 1+S 32）． ………10分解法二：在△AOB 和△DOC 中，已知∠BAC=∠BDC ，又∠AOB=∠DOC ，那么∠DCA=∠ABD ， 所以△AOB ∽△DOC ，则O A O D＝O B O C．设点A 到线段BD 所在直线的距离为h 3，点B 到线段AC 所在直线的距离为h 4， 点C 到线段BD 所在直线的距离为h 5，点D 到线段AC 所在直线的距离为h 6． 由于S 4＝12OA ·h 6＝12OD ·h 3，所以O A O D＝36h h ．同理O B O C＝45h h ，那么36h h ＝45h h ．已知AC ＝BD ，所以ABD D ACS S ∆∆＝BAC C D BS S ∆∆，即1434S S S S ++＝1223S S S S ++，整理得S 1S 2+S 3S 4＝S 2S 3+S 1S 4，所以有S 2（S 1－S 3）=S 4（S 1－S 3）， ………………8分 当S 1≠S 3时,有S 2＝S 4．由于有S 1S 3＝S 2S 4，所以S 22＝S 1S 3， 那么S ＝S 1+S 32）．当S 1＝S 3时，同理有S ＝S 2＋S 4（或＝(2）． ………………10分。

2008-2009学年度山东省淄博市高三模拟考试数学试卷（理）本试卷分第I 卷（选择题）和第II 卷（非选择题）两部分.共150分.考试用时120分钟.考试结束后，试卷答题卡交回.答卷前，考生务必将自己的姓名、考号、考试科目填涂在试卷答题卡规定的位置.第Ⅰ卷（选择题 共60分）注意事项：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再改涂其它答案标号，不能答在试题卷上.一、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．已知命题1cos ,:≤∈∀x x p R ，则（ ）A ．1cos ,:≥∈∃⌝x x p RB ．1cos ,:≥∈∀⌝R x pC ．1cos ,:>∈∃⌝x x p RD ．1cos ,:>∈∀⌝R x p2．若复数),(213为虚数单位i a iia R ∈-+是纯虚数，则实数a 的值为 （ ）A ．－6B ．6C ．－2D ．4 3．下列几何体各自的三视图中，至少．．有两个视图相同的是（ ）A ．①②③B ．①④C ．②④D ．①②④4．5位同学报名参加两个研究性学习小组，每位同学限报其中一个小组，则不同的报名方法共有 （ ）A ．10种B ．20种C ．25种D ．32种5．若不等式组⎪⎩⎪⎨⎧≤≤≥≥+-3005x a y y x 表示的平面区域是一个三角形，则a 的取值范围是 （ ）A ．a<5B ．a ≥8C ．5≤a ＜8D ．a ＜5或a ≥86．过点（0，1）的直线与圆422=+y x 相交于A 、B 两点，则|AB|的最小值为 （ ）A ．2B ．32C ．3D ．527．在三角形ABC 中，A=120°，AB=5，BC=7，则CBsin sin 的值为 （ ）A ．53B ．35 C ．58 D ．85 8．已知非零向量22||||,0||||(,==⋅+BC AC BC AC AB BC AC AB 满足和，则△ABC 为（ ） A ．等边三角形 B ．等腰非直角三角形C ．非等腰三角形D ．等腰直角三角形9．函数)(x f y =的图象如图所示，是函数)(log 5.0x f y =的图象大致是（ ）10．若点P （2，0）到双曲线12222=-by a x 的一条渐近线的距离为2，则该双曲线的离心率为 （ ）A ．2B ．3C ．22D ．2311．为了了解某校高三学生的视力情况，随机地抽查了该校1000名高三学生的视力情况，得到频率分布直方图，如下图，由于不慎将分布数据丢失，但知道前4组的频数成等比数列，后6组的频数成等数列，设最大频率为a ，视力在4.6到5.0之间的学生数为b ，则a 、b 的值分别为（ ）A ．2.7,780B ．2.7,830C ．0.27,780D ．0.27,83012．设)(x f 是定义在R 上的奇函数，且当,)(,02x x f x =≥时若对任意的]2,[+∈t t x ，不等式)()(2x f t x f ≤+恒成立，则实数t 的取值范围是 （ ）A ．(]⎪⎭⎫⎢⎣⎡+∞⋃-∞-,412, B ．[)+∞⋃⎥⎦⎤ ⎝⎛-∞-,241,C ．(][)+∞⋃∞-,20,D ． ]2,41[-第Ⅱ卷（非选择题 共90分）注意事项：1．第II 卷包括填空题和解答题共两个大题.2．第II 所有题目的答案考生需用0.5毫米黑色签字笔答在答题纸木指定的位置上. 二、填空题：本大题共4小题，每小题4分，共16分. 13．二项式6)12(xx -的展开式中含x 2项的系数是 .14．在如下程序框中，输入x x f sin )(0=，则输出的是 .15．已知m 、n 是不同的直线，α、β是不重合的平面，给出下列命题：①若内的无数条直线平行于平面则ααm m ,// ②若n m n m //,,,//则βαβα⊂⊂ ③若βαβα//,//,,则n m n m ⊥⊥④若βαβα//,,//m m 则⊂上面命题中，真命题的序号是 （写出所有真命题的序号）16．在技术工程中，常用到的双曲正弦函数22xx x x e e chx e e shx --+=-=和双曲余弦函数，而双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有类似的性质.比如关于正、余弦函数有y x y x y x sin cos cos sin )sin(+=+成立，而关于双曲正、余弦函数满足.)(chxshy shxchy y x sh +=+请你运用类比的思想，写出关于双曲正弦、双曲余弦函数的一个新关系式 .三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤. 17．（12分）已知)s i n 3,(c o s ),cos ,(cos 2x x b x x a ωωωω==（其中10<<ω），函数)(3,)(x f x x f 是函数若直线π=⋅=图象上的一条对称轴，（I ）试求ω的值；（II ）先列表再作出函数],[)(ππ-在区间x f 上的图象.18．（12分）某研究机构准备举办一次数学新课程研讨会，共邀请50名一线教师参加，使用不同版本教材的教师人数如下表所示（I ）从这50名教师中随机选出2名，问这2人使用相同版本教材的概率是多少？ （II ）现从这50名教师中随机选出3名教师做问卷调查，若选出的3名教师都使用人教版教材，求恰有1人使用人教A 版的概率是多少？（III ）若随机选出的2名教师都使用人教版教材，设其中使用人教A 版教材的教师人数为ξ，求随机变量ξ的分布列和数学期望.19．（12分）如图，已知四棱锥P —ABCD 的底面为直角梯形，AD//BC ，∠BCD=90°，PA=PB ，PC=PD.（I ）证明平面PAB ⊥平面ABCD ；（II ）如果AD=1，BC=3，CD=4，且二面角P —CD —A 等于60°，求二面角P —BC —A的大小.20．（12分）已知函数).(1)(R ∈-=a xanx x f （I ）讨论)(x f 在[1，e]上的单调性；（II ）若)(x f <x 在[1，+∞）上恒成立，试求a 的取值范围.. 21．（12分）已知数列{a n }满足2),2(22211=≥++=-a n a a nn n .（I ）求432,,a a a ；（II ）是否存在一个实数}2{,nn a λλ+使得数列成等差数列，若存在，求出λ的值；若不存在，请说明理由；（III ）设S n 为数列{a n }的前n 项和，证明：.23n n S n +≥22．（14分）已知中心在原点、焦点在x 轴上的椭圆，其离心率.4,222的焦点且经过抛物线y x e == （I ）求椭圆的标准方程；=，（II）若过点B（2，0）的直线l与椭圆交于不同的两点E、F（E在B、F之间），且λ试求实数λ的取值范围.。

2008-2009学年度山东省淄博市高三模拟考试数学试卷（理）本试卷分第I卷（选择题）和第II卷（非选择题）两部分•共150分•考试用时120分钟. 考试结束后，试卷答题卡交回•答卷前，考生务必将自己的姓名、考号、考试科目填涂在试卷答题卡规定的位置.第I卷（选择题共60分）注意事项：每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再改涂其它答案标号，不能答在试题卷上一项是符合题目要求的1.已知命题p : -x • R, cosx _ 1，贝U( )A . 一p : T x R ,cosx - 1B . — p : 一x R, cos _ 1C. 一p : T x R ,cosx 12亠3i2.若复数（a • R, i为虚数单位）是纯虚数，则实数a的值为3. 下列几何体各自的三视图中，至少..有两个视图相同的是A .①②③B .①④C .②④D .①②④4. 5位同学报名参加两个研究性学习小组，每位同学限报其中一个小组，则不同的报名方法共有（）A. 10 种 B . 20 种 C . 25 种 D . 32 种X - y 5 一05. 若不等式组y-a 表示的平面区域是一个三角形，则a的取值范围是（）0空x空3、选择题：本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有D . a v 5 或 a > 8oox y =4相交于A 、B 两点，贝y |AB|的最小值为AB c n2 210.若点P （2, 0）到双曲线二-爲 =1的一条渐近线的距离为、2，则该双曲线的离心a b率为 （）A . 2B . 、3C . 2 . 2D . 2.311.为了了解某校高三学生的视力情况，随机地抽查了该校1000名高三学生的视力情况，得到频率分布直方图， 如下图，由于不慎将分布数据丢失，但知道前4组的频数成等比数列，后6组的频数成等数列，设最大频率为 a ,视力在4.6到5.0之间的学生数为b , 则a 、b 的值分别为（A.2B . 2.3C . 3D . 2, 57.在三角形 ABC 中， A=120 ° , AB=5, BC=7, …sin B 砧” 则的值为( )si nC3585A .-B . —C . —D . —5358ABACAC BC .28 .已知非零向量 AB,AC 和BC 满足（+)BC -0,且，则| AB|| AC| | AC || BC |2ABC 为( )A .等边三角形B . 等腰非直角三角形C .非等腰三角形D .等腰直角三角形9.函数y 二f （x ）的图象如图所示，是函数B . a > 8 6.过点（0, 1）的直线与圆y = log 0.5 f (x)的图象大致是A . 2.7,780B . 2.7,830C . 0.27,780D . 0.27,830212•设f(x)是定义在 R 上的奇函数，且当x _0时，f(x)= x ,若对任意的[t,t 2],不等式f (x ・t)M f(x 2)恒成立，则实数t 的取值范围是()1[肓2]注意事项:1•第II 卷包括填空题和解答题共两个大题 2•第II 所有题目的答案考生需用0.5毫米黑色签字笔答在答题纸木指定的位置上二、填空题：本大题共 4小题，每小题4分，共16分. 13.二项式(2j{-土 )6的展开式中含 x 2项的系数是Vx① 若m 〃二则m 平行于平面：•内的无数条直线② 若：〃 ：，m 二很，n :,则 m // n ③ 若 m _ ：•, n _ :, m// n,则〉// :第n 卷(非选择题共 90 分）14.在如下程序框中，输入f °(x)二sinx ，则输出的是15.已知m 、n 是不同的直线，a 、B 是不重合的平面，给出下列命题:④ 若］// :, m 二卅,则m 〃 -上面命题中，真命题的序号是 ________ (写出所有真命题的序号)而双曲正弦函数和双曲余弦函数与我们学过的正弦函数和余弦函数有类似的性质 •比如关于正、余弦函数有 sin(x - y) =sinxcosy - cosxsin y 成立，而关于双曲正、余弦 函数满足sh(x • y) = shxchy • chxshy.请你运用类比的思想，写出关于双曲正弦、双 曲余弦函数的一个新关系式 _____________________________________ .三、解答题：本大题共 6小题，共74分，解答应写出文字说明、证明过程或演算步骤 17. (12 分)—* f —已知 a = 2(cos x, cos x), b = ( c o sx, 3 s i n x)(其中 0 ：：： 1 ),函数—1f (x) =a b,若直线x 是函数f (x)图象上的一条对称轴，3(I )试求3的值； (II )先列表再作出函数f(X)在区间［-二，二］上的图象.18. （12 分）某研究机构准备举办一次数学新课程研讨会， 共邀请50名一线教师参加，使用不同版本教材的教师人数如下表所示版本 人教A 版人教B 版苏教版 北师大版 人数2015510(I) 从这50名教师中随机选出2名，问这2人使用相同版本教材的概率是多少？ (II)现从这50名教师中随机选出 3名教师做问卷调查，若选出的3名教师都使用人教版教材，求恰有1人使用人教A 版的概率是多少？16•在技术工程中，常用到的双曲正弦函数g Xshx =X X, e +e _chx =和双曲余弦函数(III )若随机选出的2名教师都使用人教版教材，设其中使用人教A版教材的教师人数为E，求随机变量E的分布列和数学期望19. (12 分)如图，已知四棱锥P—ABCD的底面为直角梯形，AD//BC，/ BCD=90 °, PA=PB , PC=PD.(I)证明平面PAB丄平面ABCD ;(II)如果AD=1 , BC=3 , CD=4，且二面角P—CD —A 等于60°,求二面角P—BC —A 的大小.20. (12 分)a已知函数f(x)=1 nx .(a • R)x(I)讨论f (x)在［1 , e］上的单调性;(II)若f (x) <x在［1 , +：：)上恒成立，试求a的取值范围..21. (12 分)已知数列｛a n｝满足a n =2a nJ- 2n• 2(n —2), a^2.(I)求a2,a3, a4;一 a +九(II )是否存在一个实数',使得数列｛亀｝成等差数列，若存在，求出•的值；若不存在，请说明理由；(III )设S n为数列｛a n｝的前n项和，证明：S n- n3• n2.22. (14 分)42已知中心在原点、焦点在x轴上的椭圆，其离心率e ,且经过抛物线x2 =4y的焦点.2 (I)求椭圆的标准方程;(II)若过点B(2,0)的直线l与椭圆交于不同的两点E、F(E在B、F之间)，且BE — BF , 试求实数‘的取值范围。

山东省淄博市2008-2009学年度高三第一次模拟考试理科数学注意事项：每小题选出答案后，用2B 铅笔把答题卡对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再改涂其它答案标号，不能答在试卷上。

一、 选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1 已知命题:,cos 1p x R x ∀∈≤则A :,cos 1p x R x ⌝∃∈≥B :,cos 1p x R ⌝∀∈≥C :,cos 1p x R x ⌝∀∈>D :,cos 1p x R ⌝∀∈> 2若复数312a ii+-（,a R i ∈为虚数单位）是纯虚数，则实数a 的值为 A -6 B 6 C -2 D 4 3 下列几何体各自的三视图中，至少有两个试图相同的是A ①②③B ①④C ②④D ①②④4 5位同学报名参加两个研究性学习小组，每位同学限报其中的一个小组，则不同的报名方法共有 A 10种 B20种 C25种 D32种5若不等式组5003x y x y a x -+≥⎧⎪≥⎨⎪≤≤⎩表示的平面区域是一个三角形，则a 得取值范围是A 5a < Ba 8≥ C 58a ≤< D 58a a <≥或6 过点（0，1）的直线与224x y +=相交于A 、B 两点，则|AB|的最小值为 A 2B 2C 38已7 在三角形ABC 中，A=1200，AB=5，BC=7，则sin sin BC的值为 A35 B 53 C 85 D 58知非零向量AB BC 、 和BC 满足2()0=2||||||||AB AC AC BC BC AB AC AC BC +=且，则∆ABC 为 A 等边三角形 B 等腰非直角三角形 C 非等要三角形 D 等腰直角三角形 9函数()y f x =的图像如图所示，则函数0.5log ()y f x =的图像大致是10 若点p(2,0)到双曲线22221x y a b-=AB C D 11 为了解某校高三学生的视力情况，随机地抽查了该校1000名高三学生的视力情况，得到频率分布直 方图，如图，由于不慎将部分数据丢失，但知道前 4组的频数成等比数列，后6组的频数成等差数列， 设最大频率为a ，视力在4.6到5.0之间的学生数b ，则a b 、的值分别为A 2.7，780 B2.7，830 C 0.27，780 D 0.27，83012 设()f x 是定义在R 上的齐函数，且党0x ≥时2()f x x =，若对任意的[2x ∈-不等式()2()f x t f x +≤恒成立，则实数t 的取值范围是A )+∞B (-∞C [4)++∞D ([4)⋃++∞第II 卷（非选择题 共90分）注意事项：1 第II 卷包括填空题和解答题共两个大题2第II 卷所有题目的答案考生需要用0.5毫米黑色签字笔答在答题纸制定的位置上 二、填空题：本大题共4小题，每小题4分，共16分13 二项式6展开式中韩x 2项的系数是 。

2008-2009学年度山东省淄博市高三模拟考试地理试卷本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，满分100分。

考试时间90分钟。

考试结束后，将答题纸和答题卡一交回。

答卷前，考生务必将自己的姓名、考号、考试科目填涂在试卷、答题卡和答题纸规定的位置。

第Ⅰ卷（选择题共51分）注意事项：1．每小题选出的答案后，用铅笔把答题卡上对应的答案标号涂黑。

如需改动，用橡皮干净后，再选涂其它答案标号。

不能答在试题卷上。

2．本卷共34小题，每小题1.5分，共51分。

在每题给出的四个选项中，只有一项是最符合题目要求的。

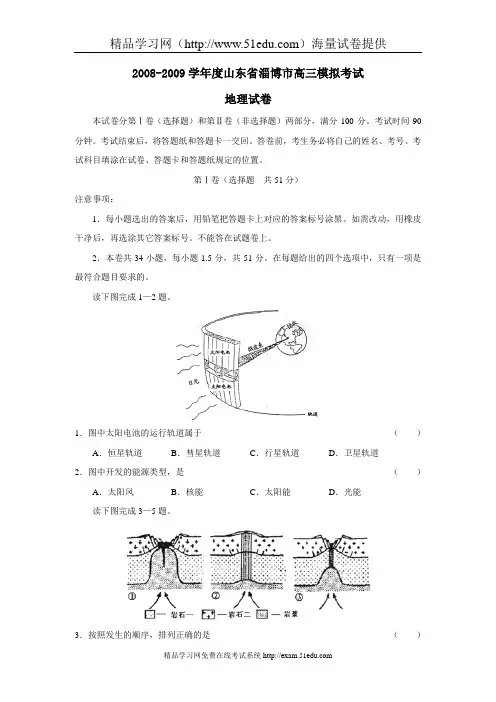
读下图完成1—2题。

1．图中太阳电池的运行轨道属于（）A．恒星轨道B．彗星轨道C．行星轨道D．卫星轨道2．图中开发的能源类型，是（）A．太阳风B．核能C．太阳能D．光能读下图完成3—5题。

3．按照发生的顺序，排列正确的是（）A．①②③B．②③①C．①③②D．②①③4．图中所示的地理现象，可能位于（）A．太平洋板块与大陆板块的张裂地带B．大陆板块与大陆板块的碰撞地带C．大洋板块与大洋板块的碰撞地带D．大洋板块与大洋板块的张裂地带5．图中所示的地理现象，可能是（）①裂谷②海岭③山系④海沟A．①②B．③④C．①③D．②④读下列两幅图完成6—7题。

6．两图所显示的含义是（）①零售商业面积与行人流量之间存在负相关关系②零售商业面积与行人流量之间既存在负相关、也存在正相关关系③道路交叉口对零售商业的吸引力小于公交站点④道路交叉口对零售商业的吸引力大于公交站点A．①②B．③④C．①③D．②④7．如图所示，影响零售商业布局的主导因素是（）A．交通、市场B．行人、营业面积C．营业面积、人口密度D．人口密度、交通左下图为某区域路网示意图，右下表为当地路况资料。

据此完成8—9题。

8．若你是救护人员，要在最短时间内由Z点赶到S点救助伤者，你该选择下列哪一条路线？（）A．Z→X→N→S B．Z→X→Q→W→SC．Z→Q→W→S D．Z→Q→X→N→S9．图中各点中，交通通达度最好的是（）A．Z B．Q C．W D．X下图为太阳辐射随纬度的变化坐标图，读图完成10—12题。

2008-2009学年度山东省淄博市高三模拟考试理科综合能力测试试卷生物部分本试卷分第I卷和第□卷两部分，满分为240分。

考试用时150分钟。

考试结束后.将答题纸交回。

答卷前，考生务必将自己的姓名、考号、考试科目填涂在试卷和答题纸规定的第I卷（必做共88 分）注意事项：1. 每小题选出答案后.用2B铅笔把答题卡上对应的答案标号涂黑。

如需改动，用橡皮擦干净后，再涂写其他答案标号。

不涂答题卡.只答在试卷上不得分。

2. 第I卷共22小题，每小题4分。

共88分。

一、选择题（本题包括15小题。

每小题只有一个选项符合题意）1. 下列有关生物学实验的叙述，正确的一项是（）A .糖类（如淀粉、葡萄糖等）与斐林试剂发生作用生成砖红色沉淀B. 用甲基绿对DNA染色来鉴定原核细胞和真核细胞C. 在丙氨酸溶液中加入双缩脲试剂可发生紫色反应D. 健那绿可以使活细胞中的线粒体染成蓝绿色，有利于在高倍镜下观察生活状态线粒体的分布及形态2. 下列与水有关的叙述中，正确的是（）A .细胞有氧呼吸过程的第三阶段，既有水的生成，又有水的分解B. 人体绝大部分细胞中的结合水与自由水之比大于IC. 夏天，苹果树的光合作用出现“午休”现象的主要限制因素是水D. 如果白天用含18O的水浇花草，周围空气中的出0、02和CO2中都可能检测到1803 .下图a、b是某种雄性哺乳动物体内细胞分裂示意图，下列叙述正确的是（）A. a细胞会发生基因重组和基因突变B. a细胞含有8条染色体，b细胞含有两个染色体组C. a细胞和b细胞不能同时存在于某一器官内D. a细胞处于有丝分裂后期，b细胞处于减数第一次分裂后期4. 科研人员测得一多肽链片段为"一甲硫氨酸一脯氨酸一苏氨酸一甘氩酸一缬氨酸一”，其密码分别为：甲硫氨酸（AUG ）、脯氨酸（CCU、CCC、CCA ）、苏氩酸（ACU、ACC、ACA ）、甘氨酸（GGU、GGA、GGG）、缬氨酸（GUU、GUC、GUA、GUG ）控制该多肽链合成的相应的DNA片段如下图：根据以上材料判断，下列叙述错误的是（）A •基因突变往往发生在细胞分裂间期，因为DNA解旋后形成的单链结构不稳定T _B. 若该DNA片段最右侧碱基对'被替换，不会引起性状的改变C. 解旋酶作用于②处，使氢键断裂形成核糖核苷酸单链D. —般来说，基因中插入一个碱基对要比改变一个碱基列更能影响蛋白质的结构5. 某农科所按照下图育种过程培育成了高品质的小麦，下列相关叙述哪一项能够正确解释该育种过程（）A .该育种过程中，所涉及到的育种原理有杂交育种、单倍体育种一和多倍体育种B. a过程能提高突变率，从而明显缩短了育种年限C. a、c过程都需要使用秋水仙素，都作用于萌发的种子D. 通过b过程获得yyRR，需要进行不断的自交来提高纯合率6•下列给出的四个选项中，后者随前者变化情况与图走势不相符的是（）A •饮水量与抗利尿激素的分泌量的关系B. 02浓度与酵母菌产生酒精量的关系C. 杂合子连续自交次数与后代中杂合子所占比例的关系D. 物种的丰富度与生态系统抵抗力稳定性的关系7.下列有关光合作用的叙述，正确的是A .酶的专一性决定了暗反应只能在叶绿体类囊体薄膜上进行B. 在暗反应过程中酶和C5化合物的数量不会因消耗而减少C. 在适宜光照下，光合作用强度随着C02浓度的提高而不断增强D. 水的光解和C02的固定速率基本不受温度的影响&下图是生态系统能量流动图解。