数学建模 历年试题及论文

中国大学生数学建模竞赛(CUMCM)历年赛题一览!CUMCM历年赛题一览!!CUMCM从1992年到2007年的16年中共出了45个题目,供大家浏览1992年Ａ)施肥效果分析问题(北京理工大学：叶其孝）(B)实验数据分解问题（复旦大学：谭永基）1993年Ａ)非线性交调的频率设计问题（北京大学：谢衷洁）(Ｂ)足球排名次问题（清华大学：蔡大用）1994年Ａ)逢山开路问题（西安电子科技大学：何大可）(Ｂ)锁具装箱问题（复旦大学:谭永基，华东理工大学:俞文此）1995年:(Ａ)飞行管理问题（复旦大学:谭永基，华东理工大学:俞文此）(Ｂ)天车与冶炼炉的作业调度问题（浙江大学：刘祥官,李吉鸾）1996年:(A)最优捕鱼策略问题（北京师范大学：刘来福）(B)节水洗衣机问题（重庆大学：付鹂）1997年:(A)零件参数设计问题（清华大学：姜启源）(B)截断切割问题（复旦大学:谭永基，华东理工大学:俞文此）1998年:(A)投资的收益和风险问题（浙江大学：陈淑平）(B)灾情巡视路线问题（上海海运学院：丁颂康）1999年:(A)自动化车床管理问题（北京大学：孙山泽）(B)钻井布局问题（郑州大学：林诒勋）(C)煤矸石堆积问题（太原理工大学：贾晓峰）(D)钻井布局问题（郑州大学：林诒勋）2000年:(A)DNA序列分类问题（北京工业大学：孟大志）(B)钢管订购和运输问题（武汉大学：费甫生）(C)飞越北极问题（复旦大学：谭永基）(D)空洞探测问题（东北电力学院：关信）2001年:(A)血管的三维重建问题（浙江大学：汪国昭）(B)公交车调度问题（清华大学：谭泽光）(C)基金使用计划问题（东南大学：陈恩水）(D)公交车调度问题（清华大学：谭泽光）2002年:(A)车灯线光源的优化设计问题（复旦大学:谭永基，华东理工大学:俞文此）(B)彩票中的数学问题（解放军信息工程大学：韩中庚）(C)车灯线光源的优化设计问题（复旦大学:谭永基，华东理工大学:俞文此））(D)赛程安排问题（清华大学：姜启源）2003年:(A)SARS的传播问题（组委会）(B)露天矿生产的车辆安排问题（吉林大学：方沛辰）(C)SARS的传播问题（组委会）(D)抢渡长江问题（华中农业大学：殷建肃）2004年:(A)奥运会临时超市网点设计问题(北京工业大学：孟大志)(B)电力市场的输电阻塞管理问题(浙江大学:刘康生)(C)酒后开车问题（清华大学：姜启源）(D)招聘公务员问题（解放军信息工程大学：韩中庚）2005年: (A) 长江水质的评价和预测问题（解放军信息工程大学：韩中庚）(B) DVD在线租赁问题(清华大学:谢金星等)(C) 雨量预报方法的评价问题(复旦大学:谭永基)(D) 同(B)2006年：（A）出版社的资源配置问题(北京工业大学：孟大志)（B）艾滋病疗法的评价及疗效的预测问题（天津大学：边馥萍）（C）易拉罐的优化设计问题（北京理工大学：叶其孝）（D）煤矿瓦斯和煤尘的监测与控制问题（解放军信息工程大学：韩中庚）2007年：（A）中国人口增长预测问题(清华大学：唐云)（B）乘公交，看奥运问题（吉林大学：方沛辰，国防科大：吴孟达）（C）手机“套餐”优惠几何问题（解放军信息工程大学：韩中庚）（D）体能测试时间安排问题（全国组委会）。

1、 血样的分组检验在一个很大的人群中通过血样检验普查某种疾病,假定血样为阳性的先验概率为p(通常p 很小).为减少检验次数,将人群分组,一组人的血样混合在一起化验.当某组的混合血样呈阴性时,即可不经检验就判定该组每个人的血样都为阴性;而当某组的混合血样呈阳性时,则可判定该组至少有一人血样为阳性,于是需要对这组的每个人再作检验.(1)、当p 固定时(如0.01%,…,0.1%,…,1%)如何分组,即多少人一组,可使平均总检验次数最少,与不分组的情况比较. (2)、当p 多大时不应分组检验.(3)、当p 固定时如何进行二次分组(即把混合血样呈阳性的组再分成小组检验,重复一次分组时的程序).模型假设与符号约定1 血样检查到为阳性的则患有某种疾病,血样呈阴性时的情况为正常2 血样检验时仅会出现阴性、阳性两种情况,除此之外无其它情况出现,检验血样的药剂灵敏度很高，不会因为血样组数的增大而受影响. 3 阳性血样与阳性血样混合也为阳性 4 阳性血样与阴性血样混合也为阳性 5 阴性血样与阴性血样混合为阴性 n 人群总数 p 先验概率血样阴性的概率q=1-p血样检验为阳性（患有某种疾病）的人数为:z=np 发生概率:x i P i ,,2,1, = 检查次数:x i R i ,,2,1, = 平均总检验次数:∑==xi i i R P N 1解1设分x 组,每组k 人（n 很大,x 能整除n,k=n/x ）,混合血样检验x 次.阳性组的概率为k q p -=11,分组时是随机的,而且每个组的血样为阳性的机率是均等的,阳性组数的平均值为1xp ,这些组的成员需逐一检验,平均次数为1kxp ,所以平均检验次数1kxp x N +=,一个人的平均检验次数为N/n,记作:k k p kq k k E )1(1111)(--+=-+=(1) 问题是给定p 求k 使E(k)最小. p 很小时利用kp p k -≈-1)1(可得kp kk E +=1)( (2) 显然2/1-=p k 时E(k)最小.因为K 需为整数,所以应取][2/1-=p k 和1][2/1+=-p k ,2当E （k ）>1时,不应分组,即:1)1(11>--+k p k,用数学软件求解得k k p /11-->检查k=2,3,可知当p>0.307不应分组.3将第1次检验的每个阳性组再分y 小组,每小组m 人（y 整除k,m=k/y ）.因为第1次阳性组的平均值为1xp ,所以第2次需分小组平均检验1yxp 次,而阳性小组的概率为m q p -=12（为计算2p 简单起见,将第1次所有阳性组合在一起分小组）,阳性小组总数的平均值为21yp xp ,这些小组需每人检验,平均检验次数为21yp mxp ,所以平均总检验次数211yp mxp yxp x N ++=,一个人的平均检验次数为N/n,记作(注意:n=kx=myx)p q q q mk p p m p k m k E m k -=-+-+=++=1),1()1(111),(211 (3) 问题是给定p 求k,m 使E （k,m ）最小.P 很小时（3）式可简化为21),(kmp mkpk m k E ++≈ (4)对（4）分别对k,m 求导并令其等于零,得方程组:⎪⎪⎩⎪⎪⎨⎧=+-=++-0012222kp m kp mp mp k 舍去负数解可得:2/14/3,21--==p m p k (5)且要求k,m,k/m 均为整数.经在（5）的结果附近计算,比较E(k,m),得到k,m 的最与表1比较可知,二次分组的效果E(k,m)比一次分组的效果E(k)更好.2、铅球掷远问题铅球掷远比赛要求运动员在直径2.135m 的圆内将重7.257kg 的铅球投掷在 45的扇形区域内，建立模型讨论以下问题1．以出手速度、出手角度、出手高度 为参数，建立铅球掷远的数学模型；2．考虑运动员推铅球时用力展臂的动 作，改进以上模型．3．在此基础上，给定出手高度，对于 不同的出手速度，确定最佳出手角度 问题1模型的假设与符号约定1 忽略空气阻力对铅球运动的影响．2 出手速度与出手角度是相互独立的．3 不考虑铅球脱手前的整个阶段的运动状态． v 铅球的出手速度 θ 铅球的出手角度 h 铅球的出手高度 t 铅球的运动时间 L 铅球投掷的距离g 地球的重力加速度(2/8.9s m g=)铅球出手后，由于是在一个竖直平面上运动．我们，以铅球出手点的铅垂方向为y 轴，以y 轴与地面的交点到铅球落地点方向为x 轴构造平面直角坐标系．这样，铅球脱手后的运动路径可用平面直角坐标系表示，如图．因为，铅球出手后，只受重力作用（假设中忽略空气阻力的影响），所以，在x 轴上的加速度0=，在y 轴上的加速度g a y -=．如此，从解析几何角度上，以时间 t 为参数，易求得铅球的运动方程：⎪⎩⎪⎨⎧+-==h gt t v y t v x 221sin cos θθ 对方程组消去参数t ，得h x x v gy ++-=)(tan cos 2222θθ……………………………………………(1) 当铅球落地时，即是0=y ，代入方程(1)解出x 的值v ggh gh v g v x θθθθθ2222sin 22cos sin cos sin 2-++=对以上式子化简后得到铅球的掷远模型θθθ22222cos 22sin 222sin g v h g v g v L +⎪⎪⎭⎫ ⎝⎛+=………………………………(2) 问题2我们观察以上两个阶段，铅球从A 点运动到B 点,其运动状态是匀加速直线运动的,加速距离是2L 段．且出手高度与手臂长及出手角度是有一定的联系，进而合理地细化各个因素对掷远成绩的约束，改进模型Ⅰ．在投掷角度为上进行受力分析，如图(3)由牛顿第二定 律可得，ma mg F =-θsin 再由上式可得，θsin g mFa -=………………………………………(3) 又，22022aL v v =-，即22022aL v v += (4)将(3)代入(4)可得，θsin 2222202g L m FL v v -⎪⎭⎫⎝⎛+= ………………………(5) (5)式进一步说明了，出手速度v 与出手角度θ有关，随着θ的增加而减小．模型Ⅰ假设出手速度与出手角度相互独立是不合理的． 又根据图(2),有θsin 1'L h h += (6)由模型Ⅰ,同理可以得到铅球脱手后运动的距离θθθ22222cos 22sin 222sin g v h g v g v L +⎪⎪⎭⎫ ⎝⎛+= 将 (4)、(5)、(6)式代入上式整理，得到铅球运动的距离()⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎦⎤⎢⎣⎡-⎪⎭⎫⎝⎛++++-⎪⎭⎫ ⎝⎛+=θθθθθ22220'2220sin sin 22sin 2112sin 2sin 22g L m FL v h g g g L m FL v L 对上式进行化简：将m=7.257kg,2/8.9s m g = 代入上式，再令m h 60.1'= (我国铅球运动员的平均肩高)，代入上式进一步化简得，()⎪⎪⎭⎫ ⎝⎛-++-++⨯θθθθθ2222232222sin sin 6.192756.06.19sin 6.19sin 2756.0sin 1L FL v L FL v ………………(7) 所以,运动员投掷的总成绩θcos 1L L S +=问题3给定出手高度，对于不同的出手速度，要确定最佳的出手角度．显然，是求极值的问题，根据微积分的知识，我们要先求出驻点，首先，模型一中L 对θ求导得，g hv g v g hv v g v d dL θθθθθθθθ22224242cos 82sin sin cos 42cos 2sin 2cos +-+=令0=θd dL,化简后为， 0sin cos 42cos 2sin cos 82sin 2cos 2422242=-++θθθθθθθhgv v hgv v v根据倍角与半角的三角关系，将以上方程转化成关于θ2cos 的方程，然后得，hv g g vgh gh222cos +=+=θ (3)()θθ2sin sin 6.192756.051.0222L FL v L -+=从(3)式可以看出，给定铅球的出手高度h ，出手速度v 变大，相应的最佳出手角度θ也随之变大．对(3)式进行分析，由于0,0>>θh ，所以02cos >θ，则40πθ≤<．所以，最佳出手角度为)arccos(212vgh gh +=θ θ是以π2为周期变化的，当且仅当N k k ∈⎪⎭⎫⎝⎛∈±,4,02ππθ时，πθk 2±为最佳出手角度．特别地，当h=0时（即出手点与落地点在同一高度），最佳出手角度︒=45α3、零件的参数设计粒子分离器某参数（记作y ）由7个零件的参数（记作x x 12，，…x 7）决定，经验公式为：y x x x x x x x x x x x =⎛⎝ ⎫⎭⎪-⎛⎝ ⎫⎭⎪⨯--⎛⎝ ⎫⎭⎪⎡⎣⎢⎢⎤⎦⎥⎥⎛⎝ ⎫⎭⎪-17442126210361532108542056324211667......y 的目标值（记作y 0）为1.50。

目录前言................................................................................................. 错误!未定义书签。

目录........................................................................................................................... - 0 - 一、什么是数学模型............................................................................................... - 3 -2001年B题……公交车调度......................................................................... - 4 - 2001年C题……基金使用计划..................................................................... - 9 - 2002年A题……车灯线光源的优化设计................................................... - 10 - 2002年B题……彩票中的数学................................................................... - 11 - 2003年A题……SARS的传播.................................................................... - 15 - 2003年B题……露天矿生产的车辆安排................................................... - 26 - 2003年D题……抢渡长江........................................................................... - 29 - 2004年C题……饮酒驾车........................................................................... - 32 - 2004年B题……电力市场的输电阻塞管理............................................... - 34 - 电力市场交易规则：............................................................................. - 35 -输电阻塞管理原则：............................................................................. - 36 -表1各机组出力方案（单位：兆瓦，记作MW） ............................ - 39 -表2各线路的潮流值（各方案与表1相对应，单位：MW） ......... - 41 -表3各机组的段容量（单位：MW） ................................................. - 42 -表4各机组的段价（单位：元/兆瓦小时，记作元/MWh）............. - 42 -表5各机组的爬坡速率（单位：MW/分钟） .................................... - 43 -表6各线路的潮流限值（单位：MW）和相对安全裕度 ................. - 43 -2008年B题……高等教育学费标准探讨................................................... - 43 - 2008年D题……NBA赛程的分析与评价 ................................................. - 45 - 2009年A题……制动器试验台的控制方法分析....................................... - 47 - 2009年B题……眼科病床的合理安排....................................................... - 50 - 【附录】2008-07-13到2008-09-11的病人信息 ................................ - 51 - 2009年D题……会议筹备........................................................................... - 77 - 附表1……10家备选宾馆的有关数据................................................. - 78 -附表2……本届会议的代表回执中有关住房要求的信息（单位：人）- 79 -附表3……以往几届会议代表回执和与会情况.................................. - 80 -附图（其中500等数字是两宾馆间距，单位为米）......................... - 81 -二、为什么要学习数学模型................................................................................. - 83 -1、数学模型无处不在，我们的生活、工作、学习都离不开它............... - 83 -例1买房贷款问题................................................................................. - 83 -例2物体冷却过程的数学模型............................................................. - 84 -2、是学好数学用好数学的必经之路........................................................... - 86 -3、是数学教学改革的重要手段和有效路径............................................... - 88 -4、数学建模竞赛所提唱的团队精神是现代大学生必须具备素质........... - 91 -5、数学建模竞赛鼓励学生用跳跃式的、发散式的形象思维方法，这有利于培养学生的创新意识。

全国研究生数学建模竞赛历年题目
以下是全国研究生数学建模竞赛历年题目的一些例子：
1. 2019年题目：小型机翼气动弹性特性分析及优化设计
2. 2018年题目：风险规避投资组合模型
3. 2017年题目：基于某高速磁悬浮列车系统动力学模型的优化设计
4. 2016年题目：区域旅游吸引力与经济发展耦合对策研究
5. 2015年题目：地铁线网方案设计
6. 2014年题目：基于对抗博弈的恶意代码入侵防御策略设计
7. 2013年题目：煤矿安全监控系统优化设计
8. 2012年题目：基于机器学习的电子商务推荐系统设计
以上只是一些例子，每年竞赛的题目都不同，但都涵盖了数学建模的基本内容，如模型构建、问题分析、数据处理、优化设计等。

具体的题目可以通过全国研究生数学建模竞赛的官方网站或相关渠道获取。

全国大学生数学建模竞赛历年赛题1992：A 施肥效果分析 B 实验数据分解1993：A 非线性交调的频率设计 B 足球队排名次1994：A 逢山开路 B 锁具装箱1995：A 一个飞行管理问题 B 天车与冶炼炉的作业调度1996：A 最优捕鱼策略 B 节水洗衣机1997：A 零件参数 B 截断切割1998：A 投资的收益和风险 B 灾情巡视路线1999：A 自动化车床管理 B 钻井布局 C 煤矸石堆积 D 钻井布局2000：A DNA序列分类 B 钢管购运 C 飞越北极 D 空洞探测2001：A 血管三维重建 B 公交车调度 C 基金使用2002：A 车灯线光源 B 彩票中数学 D 赛程安排2003：A SARS的传播 B 露天矿生产 D 抢渡长江2004：A 奥运会临时超市网点设计 B 电力市场的输电阻塞管理C 饮酒驾车D 公务员招聘2005：A 长江水质的评价和预测 B DVD在线租赁C 雨量预报方法的评价D DVD在线租赁2006：A出版社的资源配置 B 艾滋病疗法的评价及疗效的预测C易拉罐形状和尺寸的最优设计D 煤矿瓦斯和煤尘的监测与控制2007：A 中国人口增长预测 B 乘公交，看奥运C 手机“套餐”优惠几何D 体能测试时间安排2008：A 数码相机定位 B 高等教育学费标准探讨C 地面搜索D NBA赛程的分析与评价2009：A 制动器试验台的控制方法分析 B 眼科病床的合理安排C 卫星和飞船的跟踪测控 D会议筹备2010：A储油罐的变位识别与罐容表标定B 2010年上海世博会影响力的定量评估C输油管的布置D对学生宿舍设计方案的评价2011: A 城市表层土壤重金属污染分析B 交巡警服务平台的设置与调度C 企业退休职工养老金制度的改革D 天然肠衣搭配问题2012: A 葡萄酒的评价B 太阳能小屋的设计C 脑卒中发病环境因素分析及干预D 机器人避障问题2013: A 车道被占用对城市道路通行能力的影响B 碎纸片的拼接复原C 古塔的变形D 公共自行车服务系统2014: A 嫦娥三号软着陆轨道设计与控制策略B 创意平板折叠桌C 生猪养殖场的经营管理D 储药柜的设计2015: A 太阳影子定位B “互联网+”时代的出租车资源配置C 月上柳梢头D 众筹筑屋规划方案设计。

数学建模论文（精选4篇）数学建模论文模板篇一1数学建模竞赛培训过程中存在的问题1.1学生数学、计算机基础薄弱，参赛学生人数少以我校理学院为例，数学专业是本校开设最早的专业，面向全国２８个省、市、自治区招生，包括内地较发达地区的学生、贫困地区（包括民族地区）的学生，招收的学生数学基础水平参差不齐．内地较发达地区的学生由于所处地区的经济文化条件较好，教育水平较高，高考数学成绩普遍高于民族地区的学生．民族地区由于所处地区经济文化较落后，中小学师资力量严重不足，使得少数民族学生数学基础薄弱，对数学学习普遍抱有畏难情绪，从每年理学院新生入学申请转系的同学较多可以窥见一斑．虽然学校每年都组织学生参加全国大学生数学建模竞赛，但人数都不算多．从专业来看，参赛学生主要以数学系和计算机系的学生为主，间有化学、生科、医学等理工科学生，文科学生则相对更少．理工科类的学生基本功比较扎实，他们在参赛过程中起到了重要作用．文科学生数学和计算机功底大多薄弱，更多的只是一种参与．从年级来看，参赛学生以大二的学生居多；大一的学生已学的数学和计算机课程有限，基本功还有些欠缺；大三、大四的学生忙着考研和找工作，对数学建模竞赛兴趣不大．从参赛的目的来看，有２０％左右的学生是非常希望通过数学建模提高自己的综合能力，他们一般能坚持到最后；还有５０％的学生抱着试试看的态度参加培训，想锻炼但又怕学不懂，觉得可以坚持就坚持，不能则中途放弃；剩下的３０％的学生则抱着好奇好玩的态度，他们大多早早就出局了．学生的参赛积极性不高，是制约数学建模教学及竞赛有效开展的不利因素．1.2无专职数学建模培训教师，培训教师水平有限，培训方法落后数学建模的培训教师主要由理学院选派数学老师临时组成，没有专职从事数学建模的教师．由于学校扩招，学生人数多，教师人数少，数学教师所承担的专业课和公共课课程多，授课任务重；备课、授课、批改作业占用了教师的大部分工作时间，并且还要完成相应的科研任务．而参加数学建模教学及竞赛培训等工作需要花费很多时间和精力，很多老师都没有时间和精力去认真从事数学建模的教学工作．培训教师队伍整体素质不够强、能力欠缺，指导起学生来也不是那么得心应手，且从事数学建模教学的老师每年都在调整，不利于经验的积累．另外，学校对参与数学建模教学及竞赛培训的教师的鼓励措施还不是十分到位和吸引人，培训教师对数学建模相关的工作热情不够，缺乏奉献精神．在２０１１年以前，数学建模培训主要采用教师授课的方式进行，但各位老师授课的内容互不联系．比如说上概率论的老师就讲概率论的内容，上常微分方程的老师就讲常微分的内容．学生学习了这些知识，不知道有什么用，怎么用，不能将这些知识联系起来转化为数学建模的能力．这中间缺少了很重要的一个环节，就是没有进行真题实训．结果就是学生既没有运用这些知识构建数学模型的能力，也谈不上数学建模论文写作的技巧．虽然学校年年都组织学生参加全国大学生数学建模竞赛，但结果却不尽如人意，获奖等次不高，获奖数量不多．1.3学校重视程度不够，相关配套措施还有待完善任何一项工作离开了学校的支持，都是不可能开展得好的，数学建模也不例外．在前些年，数学建模并没有引起足够的重视，学校盼望出成绩但是结果并不理想，对老师和学生的信心不足．由于经费紧张，并未专门对数学建模安排实验室，图书资料很少，学生用电脑和查资料不方便，没有学习氛围．每年数学建模竞赛主要由分管教学的副院长兼任组长，没有相应专职的负责人，培训教师去参加数学建模相关交流会议和学习的机会很少．学校和二级学院对参加数学建模教学、培训的老师奖励很少，学生则几乎没有．在课程的开设上也未引起重视，虽然理学院早在１９９７年就将数学实验和数学建模课列为专业必修课，但非数学专业只是近几年才开始列为公选课开设，且选修率低．2针对存在问题所采取的相应措施2.1扩大宣传，重视数学和计算机公选课开设，举办数学建模学习讨论班最近两年，学院组建了数学建模协会，负责数学建模的宣传和参赛队员的海选，通过各种方式扩大了对数学建模的宣传和影响，安排数学任课教师鼓励数学基础不错的学生参赛．同时邀请重点大学具有丰富培训经验的老师来做数学建模专题讲座，交流经验．学院重视数学专业的基础课程、核心课程的教学，选派经验丰富的老教师、青年骨干教师担任主讲，随时抽查教学质量，教学效果．严抓考风学风，对考试作弊学生绝不姑息；学生上课迟到、早退、旷课一律严肃处理．通过这些举措，学生学习态度明显好转，数学能力慢慢得到提高．学校有意识在大一新生中开设数学实验、数学建模和相关计算机公选课，让对数学有兴趣的学生能多接触这方面的知识，减少距离感．选用的教材内容浅显而有趣味，主要目的是让同学们感受到数学建模并非高不可攀，数学是有用的，增加学生学习数学的热情和参加数学建模竞赛的可能性．为了解决学生学习数学建模过程中的遇到的困难，学院组织老师、学生参加数学建模周末讨论班，老师就学生学习过程中遇到的普遍问题进行讲解，学生分小组相互讨论，尽量不让问题堆积，影响后续学习积极性．通过这些措施，参赛学生的人数比以往有了大的改观，参赛过程中退赛的学生越来越少，参赛过程中的主动性也越来越明显．2.2成立数学建模指导教师组，分批培养培训教师，改进培训方法近年来，学院开始重视对数学建模培训教师的梯队建设，成立了数学建模指导教师组．把培训教师分批送出去进修，参加交流会议，学习其它高校的经验，并安排老教师带新教师，培训教师队伍越来越稳定、壮大．从去年开始，理学院组织学生进行了为期一个月的暑期数学建模真题实训，从８月初到８月底，培训共分为７轮．学生首先进行三天封闭式真题训练———其次答辩———最后交流讨论．效果明显，学生的数学建模能力普遍得到了提高，学习积极性普遍高涨．９月份顺利参加了全国大学生数学建模竞赛．从竞赛结果来看，比以前有了比较大的进步，不管是获奖的等次还是获奖的人数上都取得了历史性突破．有了这些可喜的变化，教师和学生的积极性都得到了提高，对以后的数学建模教学和培训工作将起着极大的促进作用．除了这种集训，今后，数学建模还需要加强平时的教学和培训工作．2.3学校逐渐重视，加大了相关投入，完善了激励措施最近几年，学校加大了对数学建模教学和培训工作的相关投入和鼓励措施．安排了专门的数学建模实验室，配备了学院最先进的电脑、打印机等设备，购买了数学建模相关的书籍．划拨了数学建模教学和培训专项经费．虽然数学建模教学还没有计入教学工作量，但已经考虑计入职称评定的相关工作量中，对参加数学建模教学和培训的老师减少了基本的教学工作量，使他们有更多的时间和精力投入到数学建模的相关工作中去．对参加全国大学生数学建模竞赛获奖的老师和学生的奖励额度也比以前有了很大的提高，老师和学生的积极性得到了极大的提高．3结束语对我们这类院校而言，最重要的数学建模赛事就是一年一度的全国大学生数学建模竞赛了．竞赛结果大体可以衡量老师和学生的付出与收获，但不是绝对的，教育部组织这项赛事的初衷主要是为了促进各个院校数学建模教学的有效开展．如果过分的看重获奖等次和数量，对学校的数学建模教学和组织工作都是一种伤害．参赛的过程对学生而言，肯定是有益的，绝大多数参加过数学建模竞赛的学生都认为这个过程很重要．这个过程可能是四年的大学学习过程中体会最深的，它用枯燥的理论知识解决了活生生的现实中存在的问题，虽然这种解决还有部分的理想化．由于我校地处偏远山区，教育经费相对紧张，投入不可能跟重点院校的水平比，只能按照自身实际来．只要学校、老师、学生三方都重视并积极参与这一赛事，数学建模活动就能开展的更好．数学建模论文模板篇二培养应用型人才是我国高等教育从精英教育向大众教育发展的必然产物，也是知识经济飞速发展和市场对人才多元化需求的必然要求。

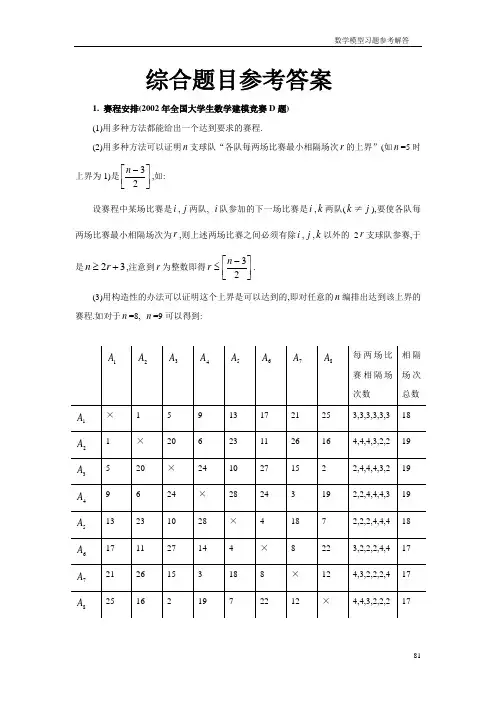
综合题目参考答案1. 赛程安排(2002年全国大学生数学建模竞赛D 题) (1)用多种方法都能给出一个达到要求的赛程.(2)用多种方法可以证明n 支球队“各队每两场比赛最小相隔场次r 的上界”(如n =5时上界为1)是⎥⎦⎤⎢⎣⎡-23n ,如: 设赛程中某场比赛是i ,j 两队, i 队参加的下一场比赛是i ,k 两队(k ≠j ),要使各队每两场比赛最小相隔场次为r ,则上述两场比赛之间必须有除i ,j ,k 以外的2r 支球队参赛,于是32+≥r n ,注意到r 为整数即得⎥⎦⎤⎢⎣⎡-≤23n r . (3)用构造性的办法可以证明这个上界是可以达到的,即对任意的n 编排出达到该上界的赛程.如对于n =8, n =9可以得到:可以看到, n =8时每两场比赛相隔场次数只有2,3,4, n =9时每两场比赛相隔场次数只有3,4,以上结果可以推广,即n 为偶数时每两场比赛相隔场次数只有22-n ,12-n ,2n,n 为奇数时只有23-n ,21-n . (4)衡量赛程优劣的其他指标如平均相隔场次 记第i 队第j 个间隔场次数为ij c ,2,2,1,,,2,1-==n j n i ,则平均相隔场次为∑∑=-=-=n i n j ij c n n r 121)2(1r 是赛程整体意义下的指标,它越大越好.可以计算n =8,n =9的r ,并讨论它是否达到上界.相隔场次的最大偏差 定义||,r c Max f ij j i -=∑-=--=21|)2(|n j ij r n c Max gf 为整个赛程相隔场次的最大偏差,g 为球队之间相隔场次的最大偏差,它们都是越小越好.可以计算n =8,n =9的f ,g ,并讨论它是否达到上界.参考文献工程数学学报第20卷第5期2003 2. 影院座位设计建立满意度函数),(βαf ,可以认为α和β无关, ()()βαβαh g f -=),(,g ,h 取尽量简单的形式,如αα=)(g ;0)(=βh (030≤β),0)(h h =β)30(0>β. (1)可030≤β将作为必要条件,以α最大为最佳座位的标准.在上图中以第1排座位为坐标原点建立坐标轴x ,可以得到⎪⎭⎫⎝⎛+----⎪⎭⎫ ⎝⎛+--=⎪⎭⎫⎝⎛+--=d x x h c H d x x c H d x x c H θθαθβtan arctan tan arctan ,tan arctan β是x 的减函数.可得x ≈1.7m,即第3(或4)排处030=β.又通过计算或分析可知α也是x 的减函数,所以第3(或4)排处是最佳座位.(2)设定一个座位间隔l (如0.5m), x 从0(或030≤β处)到d D -按l 离散,对于)20~0(00θ计算α的平均值,得020=θ时其值最大.(3)可设地板线是x 的二次曲线2bx ax +,寻求a ,b 使α的平均值最大. 实际上,还应考虑前排不应挡住后排的视线.3.节水洗衣机(1996年全国大学生数学建模竞赛B 题)该问题不要求对洗衣机的微观机制(物理、化学方面)深入研究,只需要从宏观层次去把握.宏观上洗衣的基本原理是用洗涤剂通过漂洗把吸附在衣物上的污物溶于水中,再脱去污水带走污物;洗衣的过程是通过“加水——漂洗——脱水”程序的反复运行,使残留在衣物的污物越来越少,直到满意的程度;洗涤剂也是不希望留在衣物上的东西,可将“污物”定义为衣物上原有污物与洗涤剂的总和.假设每轮漂洗后污物均匀地溶于水中;每轮脱水后衣物含水量为常数c .0x ~初始污水量,~k u 第k 轮加水量,k x ~第k 轮脱水量),,2,1( =k .设每轮脱水前后污物在水中的浓度不变.于是cx c u x c xc u x c x u x n n n =+=+=--11221110,,, , 得到)()(210c u c u u c x x n n n ++=. 在最终污物量与初始污物量之比0/x x n 小于给定的清洁度条件下,求各轮加水量k u ),,1(n k =,使总用水量最小,即∑=nk k u u Min k 1()ε<++)(..21c u c u u c t s n n等价于)()(21c u c u u Min n u k +++++ α=++)()(..21c u c u u t s na 为常数可得c u c u u n +==+= 21,即第n ~2轮加水量u u k =(常数),第1轮加水量c u u +=1.令cx u =,问题简化为nx Min u n , ε<⎪⎭⎫ ⎝⎛+nx t s 11.. 其解为0→x ,即0→u ,而∞→n .这与实际上是不合理的.应该加上对u 的限制:21v u v ≤≤.则得max min n n n ≤≤,其中 m a x m i n n n n ≤≤,1)/1ln(2min +⎥⎦⎤⎢⎣⎡+=c v n α这样,n为有限的几个数,可一一比较,具体数据计算从略.参考文献:《数学的实践与认识》第27卷第1期,19974.教师工资调整方案(1995年美国大学生数学建模竞赛B 题)题目对职称提升年限表述得不甚清楚(如未提及助理教授的提升),教龄也未区分是什么职称下工作的年限,所以应该作出一些相应的简化假设.按所给信息,工资仅取决于职称和教龄.建立新方案的一种办法是将职称折合成教龄,如定义x=教龄t+7×k (对于讲师、助理教授、副教授、教授,k 分别取值0,1,2,3),然后寻求工资函数I(x),使之满足题目的要求,如I(0)=27000,I(7)=32000等,以及x 较大时022<dxId .另一种办法是职称、教龄分别对待,工资函数J(k,t)从多种函数中选择,如最简单的线性函数J(k,t)=k k k k b a t b a ,,+(k=0,1,2,3)根据一定条件确定.按照第一种办法得到的新工资方案,以职称和教龄综合指标为x 的教师的工资都应为I(x),而人们的目前工资会低于或高于它.根据题目要求,高工资不应降低,低工资则应逐渐提高,尽快达到理想值I(x).需要做的只是根据每人(目前)工资与(理想值的)差额,制定学校提供的提薪资金的分配方案.它应该是简单、合理、容易被人接受的.按以上原则可以建立不同的模型,应通过检验比较其恶劣.检验可基于题目所给数据,按照提薪计划运行若干年,考察接近理想方案的情况,即用过渡时期的情况检验模型;也可进行随机模拟,按照一定规则随机产生数据(可以包括聘用、提职、解聘、退休的人数和时间等),再按照提薪计划运行,考察接近理想方案的情况.参考文献：叶其孝，《大学生数学建模竞赛辅导教材》（四），湖南教育出版社，2001 5. 一个飞行管理问题（1995年全国大学生数学建模竞赛A 题） 设ij a 为第i 架飞机与第j 架飞机的碰撞角（即)8arcsin(ijij r a =其中ij r 为这两架飞机连线的长度），ij β为第i 架飞机相对于第j 架飞机的相对速度（矢量）与这两架飞机连线（从i 指向j 的矢量）的夹角（以连线矢量为基准，逆时针方向为正，顺时针方向为负），i θ为第架飞机飞行方向角调整量.本问题中的优化目标函数可以有不同的形式：如使所有飞机的最大调整量最小；所有飞机的调整量绝对值之和最小等.以所有飞机的调整量绝对值之和最小，可以得到如下的数学规划模型：∑=61i i Min θs.t.,)(21ij j i ij a >++θθβ j i j i ≠=,6,,1,30≤i θ , 6,,1 =i为了利用LINGO 求解这个数学规划模型，可以首先采用其他数学软件计算出ij α和ij β.其实，ij α和ij β也是可以直接使用LINGO 来计算的，这相当于解关于ij α和ij β的方程，只是解方程并非LINDO 软件的特长，这里我们作为一个例子，看看如何利用LINGO 计算ij α，可输入如下模型到LINGO 求解ij α：MIDEL ： 1]SETS:2] PLANE/1..6/：x0,y0; 3] link(plane,plane):alpha,sin2: 4]ENDSETS5] @FOR(LINK(I,J)|I#NE#J:6] sin2(I,J)=64/((X0(I)-X0(J))*(X0(I)-X0(J))+ 7] (Y0(I)-Y0(J))*(Y0(I)-Y0(J))); 8] ）；9] @FOR(LINK(I,J)|I#NE#J:10] (@SIN(alpha*3.14159265/180.0))^2=SIN2; 11] ); 12]DATA:13] X0=150,85,150,145,130,0; 14] Y0=140,85,155,50,150,0; 15]endata END 计算结果如下：β也可类似地利用LINGO求得，计算结果如下：ij于是，该飞机管理的数学规划模型可如下输入LINGO求解：MODEL:1]SETS2] plane/1..6/:cita:3] link(plane,plane):alpha,beta;4]ENDSETS5] min=@sum(plane:@abs(cita));6] @for(plane(I):7] @bnd(-30,cita(I),30);8] );9] @fpr(link(I,j)|I#NE#J:10] @ABS(beta(I,J)+0.5*cit(I)+0.5*cita(J))11] >alpha(I,J);12] ）;13]DATA:14] A;[JA=0.000 0 5.391.2…..…2.309 8 0.000 020] ;21] BETA=0.000 010 9.263 6………1.914 4 0.000 027] ;28]enddataEND[注] alpha,beta中数据略去，见上面表格.求解结果如下：OPTIMUM FOUND AT STEP 197SOLUTION OBJECTIVE V ALUE= 3.630V ARIABLE V ALUE REDUCED COSTCITA(1) 0.2974033E-06 -1.000 000 CITA(2) -0.1424833E-05 -0.715 033 4CITA(3) 2.557 866 1.000 000 CITA(4) -0.3856641E-04 0.0000000E+00 CITA(5) 0.2098838E-05 -1.000 000 CITA(6) 1.071 594 0.0000000E+00 ………. (以下略)由此可知最优解为：︒︒≈≈07.1,56.263θθ （其它调整角度为0）.评注：如果将目标改为最大调整量最小，则可进一步化简得到线形规划模型，也可用LINDO 或LINGO 求解.参考文献：《数学的实践与认识》第26卷第1期，1996 6. 降落伞的选择这个优化问题的决策变量是降落伞数量n 和每一个伞的半径r ，可先将n 和r 看作连续变量，建立优化模型，求得最优解后，再按题目要求作适当调整.目标函数之降落伞的费用，可以根据表1数据拟合伞面费用1C 与伞的半径r 的关系。

数学建模期末考试试题# 数学建模期末考试试题## 第一部分：选择题### 题目1在数学建模中，以下哪个选项不是模型的组成部分？A) 假设B) 目标C) 约束条件D) 计算工具### 题目2以下哪个是线性规划问题的一个特征？A) 目标函数和约束条件都是非线性的B) 目标函数和约束条件都是线性的C) 目标函数是线性的，约束条件是非线性的D) 目标函数是非线性的，约束条件是线性的### 题目3在数学建模中，敏感性分析的主要目的是什么？A) 确定模型的最优解B) 评估模型参数变化对结果的影响C) 简化模型结构D) 确定模型的稳定性## 第二部分：简答题简述数学建模中模型的校验过程。

### 题目2解释什么是多目标优化问题，并给出一个实际应用的例子。

### 题目3在进行数学建模时，为什么需要对模型进行敏感性分析？请说明其重要性。

## 第三部分：应用题### 题目1假设你被要求为一家工厂设计一个生产调度模型。

工厂有三种产品A、B和C，每种产品都需要经过三个不同的生产阶段：加工、装配和包装。

每个阶段的机器数量有限，且每种产品在每个阶段所需的时间不同。

请建立一个线性规划模型来最大化工厂的日利润。

### 题目2考虑一个城市交通流量的优化问题。

城市有多个交叉路口，每个交叉路口在不同时间段的交通流量是不同的。

如何建立一个数学模型来预测交通流量，并提出减少交通拥堵的策略？### 题目3一个公司想要评估其产品在市场上的竞争力。

公司有多个产品，每个产品都有不同的成本和利润率。

同时，公司需要考虑市场需求和竞争对手的情况。

请为该公司设计一个多目标优化模型，以确定最优的产品组合和市场策略。

## 第四部分：论文题选择一个你感兴趣的实际问题，建立一个数学模型来解决这个问题。

请详细描述你的建模过程，包括问题的定义、模型的假设、模型的建立、求解方法以及模型的验证。

### 题目2在数学建模中，模型的可解释性是一个重要的考虑因素。

请讨论模型可解释性的重要性，并给出一个例子来说明你的观点。

2007高教社杯全国大学生数学建模竞赛题目（请先阅读“对论文格式的统一要求”）A题：中国人口增长预测中国是一个人口大国，人口问题始终是制约我国发展的关键因素之一。

根据已有数据，运用数学建模的方法，对中国人口做出分析和预测是一个重要问题。

近年来中国的人口发展出现了一些新的特点，例如，老龄化进程加速、出生人口性别比持续升高，以及乡村人口城镇化等因素，这些都影响着中国人口的增长。

2007年初发布的《国家人口发展战略研究报告》(附录1) 还做出了进一步的分析。

关于中国人口问题已有多方面的研究，并积累了大量数据资料。

附录2就是从《中国人口统计年鉴》上收集到的部分数据。

试从中国的实际情况和人口增长的上述特点出发，参考附录2中的相关数据（也可以搜索相关文献和补充新的数据），建立中国人口增长的数学模型，并由此对中国人口增长的中短期和长期趋势做出预测；特别要指出你们模型中的优点与不足之处。

附录1 《国家人口发展战略研究报告》附录2 人口数据（《中国人口统计年鉴》中的部分数据）及其说明2007高教社杯全国大学生数学建模竞赛题目（请先阅读“对论文格式的统一要求”）B题：乘公交，看奥运我国人民翘首企盼的第29届奥运会明年8月将在北京举行，届时有大量观众到现场观看奥运比赛，其中大部分人将会乘坐公共交通工具（简称公交，包括公汽、地铁等）出行。

这些年来，城市的公交系统有了很大发展，北京市的公交线路已达800条以上，使得公众的出行更加通畅、便利，但同时也面临多条线路的选择问题。

针对市场需求，某公司准备研制开发一个解决公交线路选择问题的自主查询计算机系统。

为了设计这样一个系统，其核心是线路选择的模型与算法，应该从实际情况出发考虑，满足查询者的各种不同需求。

请你们解决如下问题：1、仅考虑公汽线路，给出任意两公汽站点之间线路选择问题的一般数学模型与算法。

并根据附录数据，利用你们的模型与算法，求出以下6对起始站→终到站之间的最佳路线（要有清晰的评价说明）。

第31卷第1期2001年1月数学的实践与认识M A TH EM A T I CS I N PRA CT I CE AND TH EO R YV o l131　N o11　Jan.2001　D NA序列分类的数学模型吕金翅,　马小龙,　曹　芳指导老师:　陶大程(中国科学技术大学,合肥　230026)编者按:　本文能从生物学背景提出不同的三种判别模型.建模的分析和文字叙述条理清楚,模型一对21—40和182样本均进行了分类,分类正确率较高.摘要:　本文从三个不同的角度分别论述了如何对DNA序列进行分类的问题,依据这三个角度分别建立了三类模型.首先,从生物学背景和几何对称观点出发,建立了DNA序列的三维空间曲线的表达形式.建立了初步数学模型-积分模型,并且通过模型函数计算得到了1到20号DNA序列的分类结果,发现与题目所给分类结果相同,然后我们又对后20个DNA序列进行了分类.然后,从人工神经网络的角度出发,得到了第二类数学模型-人工神经网络模型.并且选择了三种适用于模式分类的基本网络,即感知机模型,多层感知机(BP网络)模型以及LVQ矢量量化学习器,同时就本问题提出了对BP网络的改进(改进型多层感知机),最后采用多种训练方案,均得到了较理想的分类结果.同时也发现了通过人工神经网络的方法得到的分类结果与积分模型得到的分类结果是相同的(前四十个).最后,我们对碱基赋予几何意义:A.C.G.T分别表示右.下.左.上.用DNA序列控制平面上点的移动,每个序列得到一个游动曲线,提取游动方向趋势作为特征,建立起了模型函数,同时也得到了后二十个DNA序列的分类结果,而且发现结果与上述两个模型所得到的分类结果几乎相同(其中有一个不同,在本模型中表示为不可分的).此模型保留的信息量更多,而且稳定性更强.1　问题的重述(略)2　基本假设及模型建立:第一类数学模型:积分模型DNA序列是一种用4种字母符号(A、T、G、C)表达的一维链.在这条链上不仅包含有制造人类全部蛋白质的信息(也就是基因),还有按照特定的时空模式把这些蛋白质装配成生物体的四维调控信息(三维空间和一维时间),找到这些信息的编码方式和调节规律是人类基因组研究的首要科学问题.下面我们首先将着手从几何学的角度来分析DNA序列.鉴于自然界对称这一朴素原理,我们的模型始于对4种碱基对称性的考察.图111(略)从纯化学的角度,我们可以将碱基进行两类划分:(1)按双环或单环结构,可分为:嘌呤碱基R(A 或G)与嘧啶碱基Y(C或T)(2)按环中对应位置上是否存在氨基或酮基,可分为:氨基碱基M(A或C)与酮基碱基K(G或T)从生物学的角度,在双螺旋结构中,按碱基对形成氢键的数目或强弱,碱基又可分:强氢键碱基S(G或C)与弱氢键碱基W(A或T),这一种划分既包含了化学的也包含了DNA双螺旋的结构信息在内.参照基本粒子理论中的做法,我们利用三维Euclid空间中的对称几何图形——立方体G来表示碱基的上述三种对称性.如图112所示,以G的中心为坐标原点建立三维直角坐标系,使G 的三组对面分别与三条坐标轴相垂直.分别与X ,Y ,Z 轴相交的G 的三组对面称为嘧啶 嘌呤面,酮基 氨基面,弱氢键 强氢键面.在G 的六个面中各引一条对角线,使相对面的对角线两两相互垂直,如图112所示.在嘌呤面对角线的两端分别标上A 和G ;在嘧啶面对角线的两端分别标上C 和T ,如图112所示.显然,此时上述碱基的三种对称关系全部自动成立.而且,六条对角线刚好是正四面体A CGT 的六条棱.图112　用立方体表示碱基的三种对称性现在考察一个长为L 的单链DNA 序列,阅读方向不限.从第一个碱基开始,依次考察此序列,每次只考察一个碱基.当考察到第n 个碱基时(n =1,2,…,L ),统计一下从1到n 这个子序列中四种碱基各自出现的次数,并以A n 、C n 、G n 、T n 分别表示4种碱基A 、C 、G 、T 出现的次数,如图113所示.显然它们都是非负整数.根据正四面体的对称性我们可以证明,正四面体内存在唯一的一个点P n 与这四个非负整数一一对应.在图113所示建立的坐标系之下,点P n 的坐标可用四个非负整数来表达. X n =2(A n +G n )-n ,Y n =2(A n +C n )-n ,Z n =2(A n +T n )-n ,X n ,Y n ,Z n ∈[-n ,n ],n =1,2,…,L ;其中X n ,Y n 和Z n 为点P n 的三个坐标分量.当n 从1到L 时,我们依次得到P 1,P 2,…,P L 共L 个点.将相邻两点用适当的曲线连接所得到的整条曲线,就成为表示此DNA 序列的P 2曲线.可以证明,P 2曲线与所表示的DNA 序列是一一对应的,也就是说,给定一定DNA 序列,存在唯一的一条P 2曲线与之对应;反之,给定一条P 2曲线,可以找到唯一的一个DNA 序列与之对应.换言之,P 2曲线很大程度上包含了DNA 序列的内蕴信息.P 2曲线741期吕金翅等:DNA 序列分类的数学模型84数　学　的　实　践　与　认　识31卷图1.3　DNA序列示意图是与符号DNA序列等价的另一种几何表现形式.我们的核心想法就是通过对P2曲线的研究来挖掘DNA序列的内蕴信息.P2曲线的三个分量都具有明确的生物学意义:X n表示嘌呤 嘧啶碱基沿序列的分布.当从1到n这个子序列中嘌呤碱基多于嘧啶碱基时,X n>0;否则X n<0;当两者相等时X n =0.同样,Y n表示氨基 酮基碱基沿序列的分布.当在子序列中氨基碱基多于酮基碱基时, Y n>0;否则,Y n<0;当两者相等时Y n=0.Z n表示强 弱氢键碱基沿序列的分布.当弱氢键碱基多于强氢键碱基时,Z n>0;否则,Z n<0;当两者相等时Z n=0.由概率论中的结论:如果任何一种分布均不能由其他两种分布的线性叠加表示出来,则这三种分布是相互独立的.给定的DNA序列唯一的决定了这三种分布;这三种分布唯一的描述了DNA序列.我们对P n的三个坐标分量分别积分,发现Y n、Z n两个方向上并没有什么区别,而在X n 方向上,A组均大于零,B组均小于零.f(t)=∫L0X n(t)d t这表明在整个序列上不同结构的碱基对所占的成分,即A组嘌呤的含量较大,B组嘧啶的含量较大.以“X方向分量大于 小于零”为标准对给出的序列21～40进行分类,得到如下结果: A类:2,3,5,7,9,14,15,17,19;B类:1,4,6,8,10,11,12,13,16,18,20第二类数学模型:神经网络模型由于神经网络具有运用已知认识新信息,解决新问题,学习新方法,预见新趋势,创造新思维的能力,所以我们将神经网络处理问题的方法介入进来,处理模式分类的问题.在本题中,采用如下几种方案:1.单层感知机;2.双层感知机;3.改进型双层感知机.4.LVQ矢量量化学习对于每种算法我们又采用了三种统计方案,即:1.统计a　c　g　t在DNA序列中出现的次数(共有4种)2.统计a　c　g　t的两两组合在DNA序列中出现的次数(共有42种不同的组合)3.统计a　c　g　t的三三组合在DNA序列中出现的次数(共有43种不同的组合)所以总共可以得到12种模式分类模型.下面给出详细讨论,但只列出12种方案中的四种,因为剩下八种只是在统计方案上有所不同,其训练实质和学习实质以及最后的模拟实质是相同的,所以不需要一一罗列.第一方案(单层感知机)1.综述:单层感知机是一个具有单层计算神经元的神经网络,并由线形域值单元组成.原始的Percep tron 算法只有一个输出节点,它相当于单个神经元.当它用于两类模式的分类时,相当于在高维样本空间中,用一个超平面将两类样本分开.F .Ro senb latt 也已证明,如果两类模式是线形可分的(指存在一个超平面将它们分开),则算法一定收敛.感知器特别适用于简单的模式分类问题,也可用于基于模式分类的学习控制和多模态控制中.2.修正方案:首先分析问题实质,即采用一个单一神经元解决简单分类问题:将n 个输入矢量分为两类,其中一部分为1,另一部分为0.最后确定网络结构(图114):图1143.训练算法:(采用单层感知机的经典算法,这里略去)判定网络收敛的标准有两种:一是平均平方误差,二是误差平方和.这里采用第二种.学习结束后的网络将学习样本模式以连接权的形式分布记忆下来.当给网络提供一输入模式时,网络将按上式计算出输出值y k ,并可根据yk 为1或0判断出这一输入模式属于记忆中的哪一种模式.4.训练和模拟结果:a )从20个已知结果的DNA 序列中随机选取不同的4个序列(向量)进行训练,再对20个序列(向量)进行重新模拟,其正确率为90%,发现出错的原因在于,第4个和第17个序列在这几种统计方式下具有相似性.b )每次从20个已知结果的DNA 序列中随机选取不同的4个序列(向量)进行训练,共进行两次,再对20个序列(向量)进行重新模拟,其正确率为95%,依然发现出错的原因在于,第4个和第17个序列在这几种统计方式下具有相似性.c )每次从20个已知结果的DNA 序列中随机选取不同的4个序列(向量)进行训练,共进行三次,再对20个序列(向量)进行重新模拟,其正确率为95%,依然发现出错的原因在于,第4个和第17个序列在这几种统计方式下具有相似性.51结论:数据为线性不可分的,所以单层网络不能实现完全识别.6.优缺点分析:以上采用的是单个神经元的网络进行分类,其优点是运算速度快,但模式分类正确率较低.第二方案(双层感知机,即B P 网络)1.综述:B P 神经网络,由于含有隐藏层,所以可实现非线性分类.B P 算法属于∆算法,941期吕金翅等:DNA 序列分类的数学模型是一种监督式的学习算法.2.算法推导:(略)3.网络结构(图115):图1154.训练算法:由于其训练过程与学习过程相似,所以这里不再赘述.5.训练和模拟结果:与第一方案相似,只是分类正确率有所提高.7.结论:本题所给数据是线性不可分的,而且通过简单的模式分类也很难行得通,所以即使用多(双)层网络也难以实现完全识别.8.优缺点分析:以上采用的是多个神经元的带有一个隐藏层的网络进行分类,其优点是运算速度较快,且模式分类正确率较高,但依然存在不可完全识别的问题.第三方案(改进型双层感知机)1.综述:为了改进上述算法的不可完全识别的缺点,现在对网络进行改进,其目的是使网络可以对所有向量进行正确的分类.2.改进的方案:以提取更多的1分类信息为原网络结构与B P 神经网络相似,但随机感知机层的响应函数采用sigm o id 函数.3.训练算法:采用与B P 网络相同的训练算法.4.训练和模拟结果:(分类正确率有所提高,这里略去)5.结论:数据是线性不可分的,而且通过简单的模式分类也很难行的通,所以只是简单改进网络结构,是很难实现完全识别的.所以下面将采用其它方法(LVQ 矢量量化学习)进行模式识别.6.优缺点分析:以上采用的是改进型多个神经元的带有一个隐藏层的网络(也就是改进型B P 神经网络)进行分类,其优点是运算速度较快,且模式分类正确率较高,但依然存在不可完全识别的问题.第四方案(LVQ 学习向量量化)1.综述:学习向量量化(LVQ )是在监督状态下对竞争层进行训练的一种学习算法.竞争层将自动学习对输入向量进行分类,这种分类的结果仅仅依赖于输入向量之间的距离.如果两个输入向量之间特别相近,竞争层就把他们分在同一类.05数　学　的　实　践　与　认　识31卷2.训练算法:(采用经典算法这里略去)3.训练和模拟结果:(分类正确率有所提高,这里略去)4.要想从网络角度和学习算法上调整,使得对已有的数据进行正确分类,必须进行大规模学习,但是如果对所有的样本进行训练再检策网络分类能力,其可信服程度就大大降低了.所以最后将采用改进网络输入的办法,即结合生物学结论.5.优缺点分析:可靠性较高,但算法复杂度较大.第五方案:仅从神经网络结构上的角度考虑,我们发现很难找到一个很好的网络,所以将结合生物学重建神经网络.引用生物学的结论,我们将输入模式变为10034,其中4表示从20个已知样本中随机抽取4个样本.100表示(A +G )含量的输入序列.采用B P 神经网络结构.训练方案采用方案二中的误差逆传播算法.训练和模拟结果:a )从20个已知结果的DNA 序列中随机选取不同的4个向量进行训练,再对20个向量进行重新模拟,其正确率为95%(较单层感知机有所改进,但与B P 网络和LVQ 向量量化学习是相同的),发现出错的原因是由于学习不充分造成的.其本质是第4组数据和第17组数据可分性不好,所以反应到网络上其可学习性又较大;但如果学习不足,则会导制误判,所以应加大学习力度.b )每次从20个已知结果的DNA 序列中随机选取不同的4个向量进行训练,共进行两次,在对20个向量进行重新模拟,其正确率为100%.这次的结果充分说明了上述问题.结论:目前的方法已很好的解决了分类的问题,所以如果加大训练力度可以对其它数据进行正确率更高的分类.我们对网络进行了100次随机抽取,每次抽取的结果均进行训练,最后对40个数据进行模拟,发现前20个数的输出完全正确,而且发现误差曲线也是十分好的,所以有理由认为这个结论的正确性.模拟结果序列21～40为:A 类:22,23,25,27,29,34,35,37,39;B 类:21,24,26,28,30,31,32,33,36,38,40第三类数学模型:二维随机游动模型以四种碱基分别代表复平面上四个不同的方向,顺序读取DNA 序列,得到一条由原点出发的每次向相应方向移动单位长度的轨迹.发现曲线明显地向两个相反的方向收敛(图116)(略).我们依此建立如下的数学模型:设DNA 序列长为L ,记A n ,G n ,C n ,T n 为1到n 这个子序列中碱基A ,G ,C ,T 所出现的次数,令P n 为复平面上的点,且P n =A n +G n i -T n -C n =(A n -T n )+i (G n -C n )=r n e i Ηn ,其中r n =(A n -T n )2+(G n -C n )2,Ηn =A rg P n ,Η=1L ∑L k =1ΗK假设n =0时,A n =G n =C n =T n =0,当n 从0到L 时,在复平面上便得到了L +1个点,并且得到了从原点出发的一条游动轨迹.鉴于幅角信息的突出重要地位,我们依此对DNA 序列进行分类,为了避免那种螺旋轨151期吕金翅等:DNA 序列分类的数学模型迹我们假设DNA序列可分类,当且仅当ϖp∈N,s.t.当n>p时∑ni=1Ηi保持定号.模型一:对20个参数已知的DNA序列,分别求出其相应的游动方程P n=(A n-T n)+ i(G n-C n),设Ηi j,k为第i类第j个DNA序列的A rg P KΗi j=1L ∑Lk=1Ηi j,k,j=1,2,…,10,i=1,2.在每一类中求出Ηi m in=m in1≤j≤10Ηi j,Ηi m ax=m ax1≤j≤10Ηi j,从而得到每个类的辐角特征区间[Ηi m in,Ηi m ax].如果[Η1m in,Η1m ax]∩[Η2m in,Η2m ax]= ,则对任意DNA序列,若可分类,则满足Η∈[Ηi m in,Ηi m ax]的属于第i类;否则,不可分类.显然,这时存在着不可分类的情形,这主要是由于我们从DNA序列样本中提取了两类游动在辐角上的趋势信息并将作为我们进行分类的标准.这一点,在模型二中得到了改进.而实际上L总有限,前面关于可分类的假设是基于对游动辐角变化总体趋势的一种控制,对于有限而言,对此也有刻画即ϖp∈N s.t.当n>p,辐角保持后续信息.模型二、上面模型一提取了DNA序列的最本质的辅角特征,这里我们假设各类的DNA序列的Η在如下变换后满足正态分布.首先辐角值可以与复平面中的圆周上的点建立自然的对应关系,并且圆周挖去一点之后同胚于实直线,为方便起见,投影后的点仍用原来的字母表示,从{Ηi j∶1≤j≤10}可得均值Λi和方差Ρi及在第i类的概率密度函数为p i(Η)=12ΠΡie-(Η-Λi)2.任给一个DNA序列,Η它属于第i类的概率:P i(Η)=li mΗ→0+∫Η+ΗΗ-Ηp i(Η)dΗ∫Η+ΗΗ-Η[p1(Η)+p2(Η)]dΗ=p i(Η)p1(Η)+p2(Η)以概率0.5为阀值,如p i(Η)〉0.5,则属于第i类.下面再用区间估计法给出结果在统计意义上的可信度,设n个相互独立的样本X i～N(a,Ρ2),i=1,2,…,n,令Z=(X1+X2+…+X n) n,则Y=(Z-a) (Ρ2 n)1 2～N(0,1),但Ρ2未知,必须先把它估计出来,用S n2=[(X1-Z)2+(X2-Z)2+…+(X n-Z)2] (n-1)代替Ρ2,(Z-a) (S n2 n)1 2=(Z-a)(Ρ2 n)-1 2 (S n2 Ρ2)1 2=Y (S n2 Ρ2)1 2,因Y～N(0, 1),(S n2 Ρ2)1 2={[(X1-Z) Ρ]2+[(X2-Z) Ρ]2+…+[(X n-Z) Ρ]2} (n-1)～ς2(n-1),因而t=(Z-a) (S n2 n)1 2～t(n-1),这里要求Y与(S n2 Ρ2)1 2相互独立.于是给定Α后,查表t(n-1)可得t3,使得P r( t ≤t3)=1-Α,即P r( Z-a (S n2 n)1 2≤t3)=1-Α,从而我们便得到了a的1-Α水平上的置信区间为[Z-t3S n n1 2,Z+t3S n n1 2].现在共有10个已知样本点X1,X2,…,X10,为了保证Y与(S n2 Ρ2)1 2相互独立,现将这10个样本点等分成两组这样便得到Z=(X1+X2+…+X5) 5,Z′=(X6+X7+…+X10) 5,Y=(Z-a) (Ρ2 5)1 2,S52=[(X6-Z′)2+(X7-Z′)2+…+(X10-Z′)2] (5-1),t=(Z-a) (S525)1 2,依前所述给定Α,我们可得a的1-Α水平上的置信区间为[Z-t3S5 51 2,Z+t3S5 51 2].由该模型可以看出曲线的趋向正代表着序列中所含对应元素的整体含量和分布.当基因序列中所含的非特征随机信息较多时,会导致游动曲线螺旋摇摆情形,从而导致前进距离25数　学　的　实　践　与　认　识31卷变短,但是由随机信号在各方向上的平均性,总体前进方向并未受到影响,故我们只提取方向而忽略距离作为特征信息.我们从不同角度,提取序列整体上和局部之间的特征,建立了以上三种数学模型.三种模型各有优劣,但他们在特征提取,模式识别和分类上的都具有一定的普适性和优越性.参考文献:[1]　郝柏林,刘寄星.理论物理与生命科学.上海科学技术出版社.[2]　金冬燕,金　奇,侯云德.核酸和蛋白质的化学合成与序列分析.科学出版社.The M athematical M odels on the Classif icationof The D NA SequencesLU J in 2ch i ,　M A X iao 2long ,　CAO Fang(T he U niversity of Science and T echno logy of Ch ina ,H efei 230026)Abstract :　T h is paper deals w ith the p roblem of how to classify the DNA sequences from th reedifferent angles and acco rdingly establishes th ree k inds of models.F irstly ,on the po int of bi o logical background and geom etrical symm etry ,w e established a descri p tive model of 32di m ensi onal space curve on the DNA sequence ,by w h ich w e go t arudi m entary m athem aticalmodel 2Calculus model.T h rough the integrati on of the model functi on ,w e have acquired the classificati on results of the DNA sequences from 1to 20,and found them identical to the classificati on results given by the p roblem .T hen w e classified the latter 20DNAsequences.T hen ,on the view of the artificial neural netw o rk s ,a second model -T he A rtificial neural netw o rk s model w as established .W e cho sen th ree k inds of basic netw o rk s ,w h ich w ell fit into the classificati on at last .A nd by the sam e ti m e ,w e p ropo sed the i m p rovem ent of the BP netw o rk ,and finally p rocured comparatively ideal classificati on results by vari ous training p rogramm es .also ,w e found the results identical to w hat w e have go t by Calculus model.By the end ,w e endow ed A ,C ,G ,T w ith geom etrical m eaning :A indicates righ t ,w h ile C as dow n ,G as up ,T as left .W e go t a mobile curve from each sequence w ith the po ints of the p lain moving acco rding to the contro lling of the DNA sequence .By fo llow ing the feature of the moving directi on ,the model functi on w as established .By the w ay w e acquired the classificati on results of the latter 20DNA sequences and found them p ractically identical to the results of the tw o above models (O ne of results differently show ed in th is model is regarded as indivisible ).T h is model contains mo re info r m ati on ,and is mo re stable .351期吕金翅等:DNA 序列分类的数学模型。

全国数学建模大赛题目
题目一：城市交通优化方案
某城市的交通状况日益拥堵，为了解决交通问题，需要制定一个交通优化方案。

假设该城市的道路网络呈现网状结构，拥有多个交叉口和道路，每个交叉口都有多个入口和出口道路。

现在需要你们设计一个算法，以找到最优的交通优化方案，使得城市的车辆数最小化，同时满足交通流量平衡和道路容量约束。

题目二：无人机配送路径规划
某公司使用无人机进行货物配送，无人机需要从指定的起点出发，依次经过多个目标点进行货物的投放，最后返回起点。

每个目标点有不同的货物量和不同的时间窗限制。

现在需要你们设计一个路径规划算法，以最小化无人机在配送过程中的总飞行距离，同时满足货物量和时间窗的要求。

题目三：自然灾害预测与应急响应
某地区常常受到洪水的威胁，为了及时应对洪水灾害，需要建立一个洪水预测和应急响应系统。

现有该地区多个监测站点，能够实时测量水位、降雨量等数据，并预测洪水的发生时间和范围。

现在需要你们设计一个预测模型，以准确预测洪水的发生时间和范围，并制定相应的应急响应措施，以最大程度地减少洪灾对人民生命和财产的威胁。

题目四：物流中心选址与配送路径规划
某公司计划在某区域新建一个物流中心，以提高货物配送的效率。

现在需要你们选取一个最佳的物流中心位置，并设计一个配送路径规划算法，以最小化货物配送的总距离和成本。

同时，
由于该区域存在不同的道路类型和限制条件，需要考虑不同道路类型的通行能力和限制，以确保货物配送的顺利进行。

历届数学建模优秀论文引言数学建模是一种将现实问题转化为数学模型，并通过数学方法进行求解和分析的方法。

在数学建模竞赛中，评选出的优秀论文不仅反映了参赛团队的实力，也对数学建模的发展起到了积极的推动作用。

本文将对历届数学建模优秀论文进行回顾和总结，以展示数学建模领域的发展趋势和研究方向。

第一届数学建模优秀论文第一届数学建模竞赛于1995年举办，该届共有来自全国50个高校的120支队伍参赛。

在该届中，以下论文脱颖而出，成为第一届数学建模的优秀论文：1.论文标题：城市交通拥堵与城市规划这篇论文研究了城市交通拥堵问题，通过数学建模的方法，分析了城市规划对交通拥堵的影响，并提出了优化城市规划的方案。

这篇论文不仅展示了数学建模在解决实际问题中的效果，也对城市交通规划提供了有益的参考意见。

2.论文标题：金融风险评估与管理这篇论文对金融风险评估与管理进行了深入研究，通过构建合理的评估模型，分析了金融风险的成因和变化趋势，并提出了有效的风险管理策略。

该论文在金融行业引起了广泛的关注，为金融机构的风险管理提供了有力的支持。

第二届数学建模优秀论文第二届数学建模竞赛于1996年举办，参赛高校增加到100所。

以下是第二届的优秀论文：1.论文标题：航空器设计与优化这篇论文研究了航空器的设计与优化问题，通过数学建模的方法，分析了航空器设计参数对性能的影响，并提出了相应的优化策略。

该论文对航空器设计的理论和实践具有重要意义。

2.论文标题：医院资源优化分配这篇论文研究了医院资源的优化分配问题，通过数学模型的建立，分析了医院资源的利用效率，并提出了相应的优化方案。

该论文在医疗卫生领域引起了广泛的关注，为医院资源的合理配置提供了重要的参考。

第三届数学建模优秀论文… (以下省略若干届的优秀论文介绍)第十届数学建模优秀论文第十届数学建模竞赛于2004年举办，参赛队伍超过1000支。

以下是第十届的优秀论文：1.论文标题：气象预测模型的研究与改进这篇论文对气象预测模型进行了深入研究，通过改进传统的气象预测模型，提高了气象预测的准确度。

路灯的更换策略摘要本文针对路灯的更换策略中最佳更换周期的确定做了深入的研究，根据路灯更换的周期对平均费用影响的分析可知该问题是一类基于概率模型的周期性更换策略问题。

对此，本文建立了微分方程模型进行讨论求解。

首先，我们采用数理统计的思想，利用题中给出了200个抽样灯泡的寿命，借助SPSS 应用统计软件和MATLAB软件工具箱对样本进行了假设检验以及参数估计，检验结果显示，样本中的灯泡的寿命均服从均值为4002.67，标准差为96.047的正态分布。

对于问题（1），先确定了以单位时间内路政部门所花费最小为判断指标，通过计算推导得到了单位时间所花费的平均费用关于周期的表达式，即单位时间内所花的平均费用为一个周期内所花的总费用除以一个周期的小时数，周期的总费用包括灯泡成本以及罚款费用。

然后对该函数进行微分求导，在导数为0的情况下求解最佳更换周期T的表达式，经化简，得到T为最佳周期时的等式。

对于问题（2），在问题（1）以及数据处理阶段的基础上，对模型进行了求解。

采用遍历的思想，用MATLAB对周期在某一范围内进行遍历代入问题（1）中求得的关系式进行计算，当（1）中关系式成立时，输出的周期T为最佳周期，即4314小时。

对于问题（3），在问题（1）的基础上，考虑更换下来的未损坏路灯的回收价值，对模型进行修改，在从费用中减去该部分的价格，按照问题（1）的推导的思路以及问题（2）中的算法对该问题进行分析求解，最佳更换周期为3926.5小时。

最后，本文对模型中涉及的罚款费用做了敏感性分析，并结合实际做了的优缺点进行了评价，提出了离散的时间模型的改进方案，对模型进行了简单的推广。

关键词：假设检验；周期性更换策略；微分方程模型；敏感性分析一、问题的提出和重述1.1问题的提出路灯的更换和维护是路政部门的一项重要的工作，在更换路灯时间的选择上，路政部门需要考虑到跟换的成本，灯泡的寿命等众多因素。

而在更换时，花费的精力和成本主要是要专用云梯车进行线路检测和更换灯泡，向相应的管理部门提出电力使用和道路管制申请，雇用的各类人员支付的报酬等，这些工作需要的费用往往比灯泡本身的费用更高，因此，灯泡坏一个换一个的办法是不可取的。