金属丝直径的测量.ppt

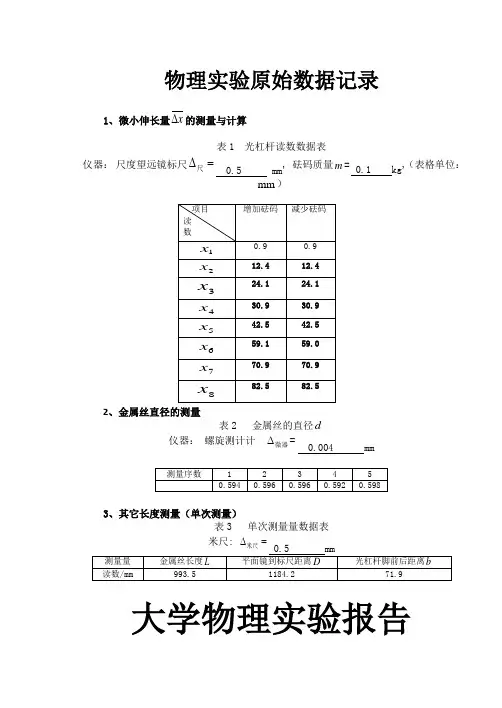
物理实验原始数据记录1、微小伸长量x ∆的测量与计算表1 光杠杆读数数据表仪器： 尺度望远镜标尺∆=尺 0.5 mm, 砝码质量m = 0.1 kg ,（表格单位：mm ）2、金属丝直径的测量表2 金属丝的直径d仪器： 螺旋测计计 ∆微器=0.004 mm3、其它长度测量（单次测量）表3 单次测量量数据表 米尺: ∆=米尺大学物理实验报告实验名称拉伸法测金属丝的杨氏模量实验名称： 拉伸法测金属丝的杨氏模量 实验时间：2020.06.08 小组成员：张振勇 实验地点：实验目的：1．学会用拉伸法测金属丝的杨氏模量。

2．掌握用光杠杆法测量微小长度的变化。

3．学会用逐差法处理数据。

仪器、设备和材料：杨氏模量测定仪、光杠杆、尺读望远镜、游标卡尺、螺旋测微计及米尺 实验原理：⑴固体材料的杨氏模量材料力学告诉我们，固体受外力作用时都会发生形变。

外力与形变之间的关系一般情况下是比较复杂的，这里考虑最简单的情况；一根细而长的均匀棒状固体，只受轴向外力的作用，可以认为该物体只产生轴向形变。

设棒状固体的长度为L ,横截面积为S ，轴向力F 作用时，长度伸长量为L ∆，在弹性限度内，应力/F S 和应变/L L ∆成正比（胡克定律），即F L YSL ∆= 式中，比例系数Y 就是固体的杨氏模量。

杨氏模量取决于固体材料本身性质，与所施外力、物体长度、材料截面积的大小无关。

杨氏模量的单位为牛顿每平方米(N/m 2)。

我们对上式整理可以得到//F SY L L =∆ (4-5-1)式(4-5-1)可见，只要测出F 、S 、L 、L ∆，就会得到杨氏模量Y 值。

F 、S 、L 各量可用一般的测量仪器测得，而L ∆通常很小，用一般仪器和方法测量较为困难，本实验采用光杠杆法测量L ∆。

⑵．利用光杠杆法测量微小长度变化量光杠杆由平面全反射镜、主杠支脚和刀口组成，如图4-5-1所示，镜面倾角及主杠尖脚到刀口间距离均可调。

测量微小长度变化量原理如图4-5-2所示。

吉林大学珠海学院课程设计报告设计题目测量金属丝的直径学生姓名学号********学生姓名学号********所属院系电子信息系专业电子信息科学与技术班级电子一班指导教师王天会设计地点实验楼4372016年12月12日一、 实验目的1、 学习读数显微镜的使用方法2、 观察劈尖干涉现象及其特点3、 用劈尖干涉法测量金属丝直径 二、劈尖测量金属丝直径的原理如图1-1所示，G 1、G 2为两片叠放在一起的平板玻璃，起一端的棱边相接触，另一端被一直径为D 的细丝隔开，故在G 1的下边卖女和G 2的上表面之间形成一层空气薄层，叫做空气劈尖。

图中M 为倾斜45°角放置的半透明半反射平面镜，L 为透镜，T 为显微镜。

单色光源S 发出的光经透镜L 后成为平行光，经M 反射后垂直射入劈尖（入射角i=0）。

自空气劈尖上、下两面反射的光相互干涉，从显微镜T 中可观察到明暗交替、均匀分布的干涉条纹，如图1-2所示。

图中相邻两暗纹（或明纹）的中心间距b 叫做劈尖干涉的条纹宽度。

在图1-3中，D 为细丝直径，L 为玻璃片长度，θ为两玻璃片间的夹角。

由于θ实际很小（为清晰期间被，图中θ被夸大），所以在劈尖的上表面处反射的光线都可看作垂直与劈尖表面，他们在劈尖表面处。

相遇并相干叠加。

由于劈尖层空气的折射率n 比比玻璃的折射率n 1小，所以光在劈尖下表面反射时因有相位跃变而产生附加光程差λ/2。

这样，由kλ, k=1,2,…（加强）Δr=2n2d+λ/2=(2k+1), λ/2, k=0,1,2,…（减弱）可得劈尖上下表面反射的两相干光的总光程差为Δ=2nd+λ/2式中d为劈尖上下表面间的距离。

劈尖反射光干涉条纹极大（明纹）的条件为2nd+λ/2=kλ,k=1,2,3,… (1-1)产生干涉条纹极小（暗纹）的条件为2nd+λ/2=（2k+1）λ/2, k=0,1,2,… (1-2)从师1-1和1-2可以看出，凡劈尖内厚度d相同的地方均满足相同的干涉条件。

不同方法测量金属细丝直径的精确度比较（实验者：秦佳蕾 同组实验者：杨莹 指导教师：竺江峰）（A09生科 0 652506， A09生科 0 652514）摘要：分别用螺旋测微器法，缠绕法，劈尖干涉法测漆包线的直径，然后比较三种方法所测得结果的准确性以及它们的优缺点。

结果表明：缠绕法所测结果误差最大，劈尖干涉法所测结果误差最小。

关键词：螺旋测微器法 缠绕法 劈尖干涉法 准确性 优缺点 1、 引言：目前，测细金属丝直径的方法有很多种，但是，并不是每一种都很精确，每一种都存在一定的误差。

所以在本实验中，我们将采用三种我们平时就熟悉的三种方法: 螺旋测微器法，缠绕法，劈尖干涉法来测细金属丝的直径，用三个结果分别与理论值来进行比较，从而来得出三种方法的准确性；同时得出它们的优缺点。

本次实验中所采用的细金属丝是漆包线。

2、 设计原理及方法： 2.1 原理2.1.1 用螺旋测微器法：用螺旋测微器直接测量出细金属丝的直径1d . 2.1.2 用缠绕法测：Ld N=(L 为N 圈细金属丝的宽度) 2.1.3 用劈尖干涉法测：干涉和衍射是光的波动性的具体表现。

等厚干涉又是光的干涉中的重要物理实验。

把直径为d 的细金属丝垫进两片光学玻璃之间的一端，在两玻璃片之间形成的空气薄膜称为劈尖，两玻璃的交线称为棱边。

平行于棱边的线上，劈尖空气薄膜厚度相等。

如图2（a ）所示，当平行单色光垂直入射到玻面上时，从空气薄膜上、下表面反射的光就在薄膜表面附近相遇而发生干涉。

因此观察介质表面就会看到明暗相间的直线干涉条纹，如图2（b ）所示。

图2（a ） 图2（b ）两束光的光程差：2e λδ=2+(1——1)当δ=Kλ（k=1，2，…）是为亮条纹；2λδ=(2K +1)（k=1，2，…）是为暗条纹。

两相邻暗纹（或亮纹）对应的劈尖厚度之差为：12k k e e +λ-=（1——2） 若两暗纹之间的距离为l ，则夹角为θ：tg lλ/2=（1——3） 设细金属丝至棱边的距离为L ，则细金属丝的直径为;2L d Ltg l θλ==⋅ （1——4） 2.2 实验方法（包括仪器、步骤）读数显微镜 螺旋测微器 游标卡尺 漆包线 笔杆 劈尖（1）、用螺旋测微器测：在漆包线上取4个不同的点，用螺旋测微器分别量出其直径，并记录到表格。

吉林大学珠海学院课程设计报告设计题目测量金属丝的直径学生姓名学号********学生姓名学号********所属院系电子信息系专业电子信息科学与技术班级电子一班指导教师王天会设计地点实验楼4372016年12月12日一、 实验目的1、 学习读数显微镜的使用方法2、 观察劈尖干涉现象及其特点3、 用劈尖干涉法测量金属丝直径 二、劈尖测量金属丝直径的原理如图1-1所示，G 1、G 2为两片叠放在一起的平板玻璃，起一端的棱边相接触，另一端被一直径为D 的细丝隔开，故在G 1的下边卖女和G 2的上表面之间形成一层空气薄层，叫做空气劈尖。

图中M 为倾斜45°角放置的半透明半反射平面镜，L 为透镜，T 为显微镜。

单色光源S 发出的光经透镜L 后成为平行光，经M 反射后垂直射入劈尖（入射角i=0）。

自空气劈尖上、下两面反射的光相互干涉，从显微镜T 中可观察到明暗交替、均匀分布的干涉条纹，如图1-2所示。

图中相邻两暗纹（或明纹）的中心间距b 叫做劈尖干涉的条纹宽度。

在图1-3中，D 为细丝直径，L 为玻璃片长度，θ为两玻璃片间的夹角。

由于θ实际很小（为清晰期间被，图中θ被夸大），所以在劈尖的上表面处反射的光线都可看作垂直与劈尖表面，他们在劈尖表面处。

相遇并相干叠加。

由于劈尖层空气的折射率n 比比玻璃的折射率n 1小，所以光在劈尖下表面反射时因有相位跃变而产生附加光程差λ/2。

这样，由kλ, k=1,2,…（加强）Δr=2n2d+λ/2=(2k+1), λ/2, k=0,1,2,…（减弱）可得劈尖上下表面反射的两相干光的总光程差为Δ=2nd+λ/2式中d为劈尖上下表面间的距离。

劈尖反射光干涉条纹极大（明纹）的条件为2nd+λ/2=kλ,k=1,2,3,… (1-1)产生干涉条纹极小（暗纹）的条件为2nd+λ/2=（2k+1）λ/2, k=0,1,2,… (1-2)从师1-1和1-2可以看出，凡劈尖内厚度d相同的地方均满足相同的干涉条件。