【知识点整理】第二讲：巧求面积word版本

《面积》知识点总结面积是几何学中的一个重要概念，它描述了一个平面图形所占据的区域大小。

在现实生活和学习中，我们经常需要计算图形的面积，以求解各种问题。

面积的概念和计算方法有很多重要的知识点，下面将对这些知识进行总结。

一、基本概念1.面积的定义：面积是指平面上其中一个面或者图形所占据的区域大小。

2. 面积的单位：常用的面积单位有平方米（m²）、平方厘米（cm²）、平方毫米（mm²）等。

3.面积的符号：表示面积通常使用大写字母A表示。

二、常见平面图形的面积计算1.矩形：矩形的面积计算公式是A=长×宽。

2.正方形：正方形的面积计算公式是A=边长×边长。

3.三角形：三角形的面积计算公式是A=底×高÷24.平行四边形：平行四边形的面积计算公式是A=底×高。

5.梯形：梯形的面积计算公式是A=（上底+下底）×高÷26.圆：圆的面积计算公式是A=π×半径²（π取近似值3.14或3.1415）。

7.扇形：扇形的面积计算公式是A=弧长×半径÷2或A=半径²×弧度÷2（其中，弧度等于圆心角的度数除以360度再乘以2π）。

三、复杂图形的面积计算1.复杂图形的分解法：将复杂的图形分解成多个简单的图形，计算出各个简单图形的面积，再将各个简单图形的面积相加，即可得到复杂图形的面积。

这种方法适用于不规则图形、多边形等复杂图形的面积计算。

2.高度法：对于有高度的梯形、三角形等图形，可以利用垂直高度计算面积。

通过画高线，将图形分成上下两个部分，分别计算上下两部分图形的面积，再将两部分面积相加，即可得到整个图形的面积。

3.面积差法：对于有相似图形或同心图形的给定面积的图形，可以通过面积差法计算图形的面积。

将给定面积的图形与另一规定图形进行重合，计算重合图形的面积，再用给定面积减去重合图形的面积，即可得到所求图形的面积。

巧算面积的七种方法
《巧算面积的七种方法》
１、古典梯形法
众所周知，梯形是以一条垂线为分界，两个直角边在一边，二个钝角边在另一边的四边形，面积的计算方法是将梯形分成两个三角形，用三角形的公式即可，即A = 1/2 (a + b) * h，其中a、b分别为梯形的底边长度，h为梯形的高。

2、测量法
测量法是最简单有效的面积计算方法，只要将物体边缘分别测量出来，然后将测量出来的尺寸记录下来，最后求和就可以得出物体的面积。

3、尺规法
尺规法也是一种常用的面积计算方法，其具体操作为：使用尺规将物体边界轮廓放大或缩小到尺规上，根据尺规刻度记录出轮廓的长度就可以计算出面积了。

4、数学方法
如果地面的图形符合一定的数学方程，例如椭圆、抛物线等，那么可以通过数学方法，借助积分的方式计算出面积。

例如，用积分计算椭圆面积的公式为A = 3/2 * pi * a * b，其中a、b分别为椭圆的短半轴和长半轴长度。

5、立体几何法
立体几何法是一种非常神奇、有效的面积计算方法。

它依据立体几何的几何关系建立模型，根据立体几何的有关定律解出问题的求解方法，这种方法十分的有效。

6、计算机技术法
随着科技的发展，计算机技术也发展得很快，许多计算机软件已经可以非常方便地计算出地面物体的面积了，主要是根据空间几何关系来计算，所以很精确，而且快速。

7、三点定标法
三点定标法是一种利用GPS技术测量工程地物面积的方法，其原理是将地物内部三点定向，并记下该三点之间的距离，最后将距离相乘即可得出地物的面积。

总结
以上就是常用的七种面积计算方法，不仅效率高，而且精确度也非常高，它们可以满足各种不同的地物测量需求，获得更准确更有效的结果。

面积知识点归纳面积是一个常见而重要的数学概念，在几何学和实际生活中经常用到。

本文将从几何图形的角度出发，对常见的面积知识点进行归纳总结，以帮助读者更好地理解和运用面积概念。

一、三角形的面积计算三角形是最基本的几何图形之一，计算三角形的面积方法主要有两种：通过底边和高的乘积，以及通过海伦公式。

1. 底边和高的乘积对于任意三角形，我们可以通过将底边与高相乘再除以2来计算其面积。

设三角形的底边为a，高为h，则该三角形的面积S等于S = (a *h) / 2。

2. 海伦公式对于已知三角形的三边长度分别为a、b、c的情况，可以使用海伦公式来计算其面积。

海伦公式的表达式为S = √[s(s-a)(s-b)(s-c)]，其中s 为半周长，s = (a + b + c) / 2。

二、矩形和正方形的面积计算矩形和正方形是常见的矩形类几何图形，其面积计算方法如下：1. 矩形的面积计算矩形的面积可以通过底边和高的乘积来计算。

设矩形的底边长度为a，高度为b，则矩形的面积S等于S = a * b。

2. 正方形的面积计算正方形的面积计算与矩形类似，由于正方形的四边长度相等，因此其面积可以通过边长的平方来计算。

设正方形的边长为a，则正方形的面积S等于S = a^2。

三、圆的面积计算圆是常见的圆形几何图形，其面积计算方法如下：圆的面积计算需要使用圆周率π，一般可取3.14或取更精确的值。

设圆的半径为r，则圆的面积S等于S = π * r^2。

四、其他常见几何图形的面积计算除了三角形、矩形和圆之外，还有一些常见的几何图形，其面积计算方法如下：1. 梯形的面积计算梯形的面积可以通过将上底和下底的和乘以高再除以2来计算。

设梯形的上底长度为a，下底长度为b，高度为h，则梯形的面积S等于S = (a + b) * h / 2。

2. 平行四边形的面积计算平行四边形的面积可以通过底边和高的乘积来计算。

设平行四边形的底边长度为a，高度为h，则平行四边形的面积S等于S = a * h。

上课日期： 上课时间： 教师姓名：知识点一：格点面积 一、正方形格点问题在一张纸上，先画出一些水平直线和一些竖直直线，并使任意两条相邻的平行线的距离都相等(通常规定是1个单位)，这样在纸上就形成了一个方格网，其中的每个交点就叫做一个格点．在方格网中，以格点为顶点画出的多边形叫做格点多边形，例如，右图中的乡村小屋图形就是一个格点多边形．那么，格点多边形的面积如何计算？它与格点数目有没有关系？如果有，这两者之间的关系能否用计算公式来表达？下面就让我们一起来探讨这些问题吧！用N 表示多边形内部格点，L 表示多边形周界上的格点，S 表示多边形面积，请同学们分析前几个例题的格点数．我们能发现如下规律：12LS N =+-．这个规律就是毕克定理．二、 三角形格点问题1、定义：所谓三角形格点多边形是指：每相邻三点成“∵”或“∴”，所形成的三角形都是等边三角形．规定它的面积为1，以这样的点为顶点画出的多边形为三角形格点多边形．2、公式：关于三角形格点多边形的面积同样有它的计算公式：如果用S 表示面积，N 表示图形内包含的格点数，L 表示图形周界上的格点数，那么有22S N L =⨯+-，就是格点多边形面积等于图形内部所包含格点数的2倍与周界上格点数的和减去2．知识点二：图形剪拼巧求面积知识框架毕克定理若一个格点多边形内部有N 个格点，它的边界上有L 个格点，则它的面积为12LS N =+-．本讲中很多类型的题目还要求同学们去动手尝试．通过本讲知识的学习，让同学们了解不同图形的分割、拼合、剪拼的方法，锻炼同学们的平面想象能力以及增强学生的动手操作能力．（1）把一个几何图形按某种要求分成几个图形，就叫做图形的分割．（2）反过来，按一定的要求也可以把几个图形拼成一个完美的图形，就叫做图形的拼合．（3）将一个或者多个图形先分割开，再拼成一种指定的图形，则叫做图形的剪拼．我们在图形的分割、拼合和剪拼的过程中，都要结合所提供的图形特点来思考．（1）如果把一个图形分割成若干个大小、形状相等的部分，那么就要想办法找图形的对称点，把图形先分少，再分多．（2）图形中，如果有数量方面的要求，可以先从数量入手，找出平分后每块上所含数量的多少，再结合数量来分割图形．（3）如果是要把几个图形拼合成一个大图形，要特别注意每条边的长度，把相等的边长拼合在一起，先拼少的，再拼多的．（4）如果是剪拼图形，要抓住“剪、拼前后图形的面积相等”这个关键，根据已知条件和图形的特点，通过分析推理和必要的计算，确定剪拼的方法．一、解题关键：分割其实就是运用特殊的三角形（等角直角三角形、等边三角形等）、正方形、等边图形的特殊性质进行分割而得，所以分割的关键是利用了特殊图形的关系解题。

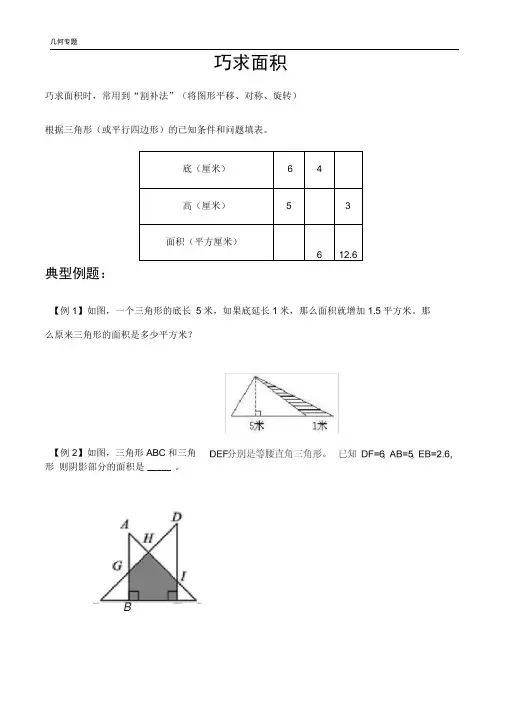
巧求面积巧求面积时，常用到“割补法”（将图形平移、对称、旋转）根据三角形（或平行四边形）的已知条件和问题填表。

底（厘米）64高（厘米）53面积（平方厘米）612.6典型例题：【例1】如图，一个三角形的底长5米，如果底延长1米，那么面积就增加1.5平方米。

那么原来三角形的面积是多少平方米？【例2】如图，三角形ABC和三角形则阴影部分的面积是_____ 。

B【例3】如图，在一块长24米，宽16米的绿地地上，有一条宽2米的小路。

请你列式计算出这条小路的面积。

（第八届“中环杯”小学生思维能力训练活动四年级决赛第二（1）题）（单位：米）【例4】如图是一个水上公园，中间有一条长廊，水中养着食人鱼，已知1平方米养4条鱼, 路的宽度为2米，公园的长和宽分别为18米、25米，求这里面共养了多少条鱼？（长廊下面不养鱼）。

【例5】如图，最外面的正方形的面积是60平方厘米，则最里面的正方形的面积是 ________ 平方厘米。

（第五届小学“希望杯”全国数学邀请赛四年级第1试第16题）【例6】如图，圆外切正三角形ABC，面积为100cm2，问圆内接正三角形的面积是多少? （新加坡亚太小学数学奥林匹克邀请赛选拔赛第8题）【例7】如图所示，大正方形的边长为10厘米，连接大正方形的各边中点得小正方形，将小正方形每边三等分，再将三等分点与大正方形的中心和一个顶点相连，那么图中阴影部分的面积总和等于多少平方厘米？【例8】图中两个四边形都是正方形，而且外边大正方形的边长为4厘米，求图中阴影部分的面积是_______（第七届“中环杯”小学生思维能力训练活动四年级复赛第一（9 ）题）【例9】有一大一小两块正方形试验田，他们的周长相差40米，面积相差220平方米，那么小正方形试验田的面积是多少平方米？【例10】⑴如左图所示，把一个正方形的相邻两边分别增加2厘米和4厘米，结果面积增加了50平方厘米（阴影部分）。

原正方形的面积为多少平方厘米？⑵如右图所示，把一个正方形的相邻两边分别减少3厘米和5厘米，结果面积减少了65 平方厘米（阴影部分）。

面积的计算知识点总结面积是几何学中的一个重要概念，用于描述平面图形所占据的空间大小。

在数学和物理学中，面积的计算是一个基本而必不可少的技能。

本文将对常见图形的面积计算方法进行总结和归纳，帮助读者掌握面积计算的知识点。

一、三角形的面积计算三角形是最简单的平面图形之一，其面积计算公式可以根据已知信息的不同而有所区别。

1. 根据底和高计算：若已知三角形的底长度为a，高为h，则三角形的面积S可通过公式S = 0.5 * a * h计算得出。

2. 根据两边和夹角计算：若已知三角形的两边长度分别为a、b，夹角为θ，则三角形的面积S可通过公式S = 0.5 * a * b * sin(θ)计算得出。

二、矩形和正方形的面积计算矩形和正方形是最常见的平面图形之一，面积的计算非常简单。

1. 矩形的面积计算：若已知矩形的长为a，宽为b，则矩形的面积S可通过公式S = a * b计算得出。

2. 正方形的面积计算：若已知正方形的边长为a，则正方形的面积S可通过公式S = a * a 或S = a^2计算得出。

三、圆的面积计算圆是几何学中的一个特殊图形，其面积计算需要用到圆周率π。

1. 圆的面积计算：若已知圆的半径为r，则圆的面积S可通过公式S = π * r^2计算得出。

四、梯形的面积计算梯形是一个具有两个平行底边的四边形，其面积的计算依赖于梯形的上底、下底和高。

1. 梯形的面积计算：若已知梯形的上底长为a，下底长为b，高为h，则梯形的面积S 可通过公式S = 0.5 * (a + b) * h计算得出。

五、其他图形的面积计算除了以上提到的几种常见图形外，其他图形的面积计算方法也有所不同。

1. 正多边形的面积计算：若已知正多边形的边长为a，则正多边形的面积S可通过公式S = (a^2 * n) / (4 * tan(π / n))计算得出，其中n为多边形的边数。

2. 楔形的面积计算：若已知楔形的圆心角为θ，半径为r，则楔形的面积S可通过公式S = 0.5 * r^2 * θ计算得出。

面积总结归纳在日常生活中，面积是一种用来描述物体表面大小的计量单位。

它在各个领域都有着广泛的应用，无论是在建筑设计、农业生产还是科学研究中，都需要准确地计算和比较不同物体的面积。

本文将对面积的概念进行简要介绍，并总结归纳面积的计算方法和应用场景。

一、什么是面积面积是平面几何中一种用来描述物体表面大小的量度。

它通常以平方单位（如平方米、平方厘米）表示。

在二维平面中，一个物体的面积等于其所占据的平面区域的大小。

二、常见物体的面积计算方法1. 矩形的面积计算：对于一个矩形，其面积可以通过将其宽度与长度相乘得到。

公式为：面积 = 宽度 ×长度。

2. 正方形的面积计算：对于一个正方形，其面积可以通过将其边长的平方得到。

公式为：面积 = 边长 ×边长。

3. 圆的面积计算：对于一个圆，其面积可以通过将其半径的平方乘以π（圆周率）得到。

公式为：面积 = 半径 ×半径× π。

4. 三角形的面积计算：对于一个三角形，其面积可以通过将其底边长度与高的乘积再除以2得到。

公式为：面积= （底边长度×高）/ 2。

三、面积的应用场景1. 建筑设计中的面积计算：在建筑设计过程中，需要计算各个房间、楼层、建筑物的面积，以便进行合理的空间规划和材料使用。

面积计算还有助于评估建筑的使用效率和设计质量。

2. 农业生产中的面积计算：在农业生产中，面积计算是农田规划、种植布局和农作物产量评估的重要依据。

通过计算田地面积，农民可以准确地安排种植区域，合理使用肥料和水资源，提高农作物的产量和质量。

3. 科学研究中的面积计算：在科学研究中，面积计算在各个学科领域都有广泛的应用。

例如，在地理学中，需要计算陆地和海洋的面积以研究地球表面的特征和分布；在生物学中，需要计算生物群落的面积以评估生态系统的健康状况。

4. 商业活动中的面积计算：在商业活动中，面积计算是商场、仓库和办公室管理的重要环节。

通过准确计算商业场所的面积，可以合理配置商品陈列、库存管理和工作空间，提高经营效率和顾客体验。

面积的基本概念与计算知识点总结面积，作为几何学中的重要概念之一，用于描述平面上图形所占的空间大小。

在日常生活以及各种工程领域中，我们经常会接触到对面积的计算和应用。

本文将对面积的基本概念及其计算方法进行总结和说明。

1. 面积的基本概念面积是描述平面图形大小的物理量，通常用单位面积所包含的单位个数来表示。

常见的单位面积有平方米（m²）、平方厘米（cm²）、平方千米（km²）等。

面积的概念适用于各种平面图形，如矩形、三角形、圆形等。

2. 矩形的面积计算矩形是最常见的平面图形之一，其面积计算公式为：面积 = 长 ×宽。

即将矩形的长与宽相乘即可得到矩形的面积。

单位面积为平方单位。

3. 三角形的面积计算三角形的面积计算公式为：面积 = 底边长 ×高 ÷ 2。

其中，底边指的是三角形的底边，高是从顶点到底边的垂直距离。

同样，计算出的面积单位为平方单位。

4. 圆形的面积计算圆形的面积计算公式为：面积= π × 半径²。

其中，半径是指圆形的半径长度，π是一个无理数，近似值为3.14。

根据圆形的定义，圆的面积也是平方单位。

5. 多边形的面积计算对于不规则形状的多边形，我们可以将其分割为若干个矩形或三角形，然后计算每个图形的面积并求和。

这是一种常见的方法来计算不规则多边形的面积。

6. 面积计算的注意事项在进行面积计算时，需要注意以下几点：- 单位的统一：在计算面积时，需要保持所使用的长度单位和面积单位一致，避免出现单位不统一的错误。

- 测量精度：测量图形边长或半径时，需要尽可能准确，以保证计算出的面积结果的准确性。

- 数学公式的正确应用：根据不同图形的特点，选择正确的计算公式，避免在计算过程中出现错误。

综上所述，面积是描述平面图形大小的物理量，可以通过对矩形、三角形、圆形等不同图形的特定公式进行计算得出。

在进行面积计算时，需要注意单位的统一、测量精度和数学公式的正确应用。

关于面积的知识点总结在几何学中，面积是一个重要的概念，描述了平面图形所占据的空间大小。

面积计算是数学和实际生活中的常见任务，它涉及到各种形状的图形。

本文将总结一些常见的面积计算方法和相关的知识点。

1.矩形和正方形的面积计算矩形和正方形是最简单的图形，它们的面积计算非常直观。

矩形的面积可以通过将长乘以宽来计算，公式为A = 长 × 宽。

正方形是一种特殊的矩形，它的边长相等，所以面积公式简化为A = 边长 × 边长。

2.三角形的面积计算三角形是另一个常见的图形，它的面积计算稍微复杂一些。

当我们知道三角形的底和高时，可以使用公式A = 1/2 × 底 × 高来计算面积。

这个公式的推导可以通过将三角形划分为两个矩形来理解。

3.圆的面积计算圆是一个没有直角边的图形，它的面积计算需要使用到圆周率π。

当我们知道圆的半径时，可以使用公式A = π × 半径的平方来计算面积。

圆周率π是一个无理数，约等于3.14159。

它是一个重要的数学常数，出现在许多面积计算中。

4.梯形的面积计算梯形是一个具有两个平行边的四边形，它的面积计算需要使用到梯形的上底、下底和高。

面积公式为A = 1/2 × (上底 + 下底) ×高。

这个公式可以通过将梯形划分为一个矩形和两个直角三角形来推导。

5.平行四边形的面积计算平行四边形是一个具有两组平行边的四边形，它的面积计算与矩形非常类似。

当我们知道平行四边形的底和高时，可以使用公式A = 底 × 高来计算面积。

平行四边形的面积计算也可以通过将其划分为两个直角三角形来推导。

6.正多边形的面积计算正多边形是一个具有相等边和相等角度的多边形，它的面积计算需要使用到边长和中心到顶点的距离。

正多边形的面积可以通过将其划分为一系列的三角形来计算，公式为A = 1/2 × 边长 × 中心到顶点的距离。

总结: 面积计算是一个广泛应用于数学和实际生活中的概念。

小学数学易考知识点面积的计算方法计算面积是小学数学中的一个常见知识点，学好这个知识点可以帮助孩子更好地应对数学考试。

本文将为您介绍小学数学中常见的面积计算方法，帮助孩子掌握这一知识点。

一、长方形面积的计算方法1. 长方形的面积公式：面积 = 长 ×宽。

2. 举例说明：如果一个长方形的长为5厘米，宽为3厘米，那么它的面积是15平方厘米。

二、正方形面积的计算方法1. 正方形的面积公式：面积 = 边长 ×边长。

2. 举例说明：如果一个正方形的边长为4厘米，那么它的面积是16平方厘米。

三、三角形面积的计算方法1. 三角形的面积计算方法有两种：底边法和高度法。

2. 底边法：面积 = 底边 ×高 ÷ 2。

其中，底边为三角形的一条边的长度，高为从底边到顶点的垂直距离。

3. 高度法：面积 = 底边 ×高度 ÷ 2。

其中，底边为三角形的一条边的长度，高度为从底边到顶点的垂直距离。

4. 举例说明：如果一个三角形的底边长度为6厘米，高度为4厘米，那么使用底边法计算得出的面积是12平方厘米，使用高度法计算得出的面积也是12平方厘米。

四、圆的面积的计算方法1. 圆的面积公式：面积= π ×半径×半径。

其中，π取近似值3.14。

2. 举例说明：如果一个圆的半径为2厘米，那么它的面积约为12.56平方厘米。

五、梯形面积的计算方法1. 梯形的面积计算方法：面积 = 上底 + 下底 ×高 ÷ 2。

其中，上底和下底为梯形的顶边和底边的长度，高为从顶边到底边的垂直距离。

2. 举例说明：如果一个梯形的上底长为3厘米，下底长为5厘米，高为2厘米，那么它的面积为8平方厘米。

六、总结1. 小学数学中常见的面积计算方法包括长方形面积的计算、正方形面积的计算、三角形面积的计算、圆的面积的计算以及梯形面积的计算。

2. 理解和熟练掌握这些面积计算方法，有助于孩子在数学考试中提高得分。

九年级面积问题知识点归纳总结面积是数学中一个重要的概念，它在日常生活中的应用广泛。

九年级学生需要掌握与面积有关的几何图形的计算方法，理解面积的性质和应用。

本文将对九年级面积问题的知识点进行归纳总结。

一、矩形的面积计算方法矩形是最基础的几何图形之一，其面积可以通过长度和宽度相乘得到。

设矩形的长度为l，宽度为w，则矩形的面积S为S = l * w。

二、平行四边形的面积计算方法平行四边形是另一个常见的几何图形，它的面积可以通过底边和高的乘积得到。

设平行四边形的底边为b，高为h，则平行四边形的面积S为S = b * h。

三、三角形的面积计算方法三角形也是常见的几何图形，它的面积计算稍微复杂一些。

九年级学生需要掌握两种计算三角形面积的方法：通过底边和高的乘积，以及通过三边的长度计算。

1. 通过底边和高的乘积：设三角形的底边为b，高为h，则三角形的面积S为S = 0.5 * b * h。

2. 通过三边的长度计算：设三角形的三边分别为a、b、c，则可以使用海伦公式计算三角形的面积。

海伦公式为S = √[s(s-a)(s-b)(s-c)]，其中s = (a + b + c) / 2。

利用海伦公式，可以根据三边的长度计算出三角形的面积。

四、圆的面积计算方法圆是一个特殊的几何图形，九年级学生需要掌握圆的面积计算方法。

圆的面积可以通过半径的平方乘以圆周率π来计算。

设圆的半径为r，则圆的面积S为S = π * r^2。

五、复合图形的面积计算方法复合图形是由两个或多个基本图形组成的图形。

计算复合图形的面积需要将其分解为基本图形的面积之和。

九年级学生需要学会计算常见的复合图形，如矩形与三角形的组合、矩形与圆的组合等。

六、面积性质和应用九年级学生还需要了解面积的性质和应用。

以下是一些常见的性质和应用：1. 对于相似的图形，其面积与边长的比例为平方关系。

即如果两个图形的边长之比为a：b，那么它们的面积之比为a^2：b^2。

2. 面积可以应用于解决实际问题，如计算土地面积、涂料要求以及物体的表面积等。

巧求表面积教课目的掌握长方体和正方体的特色、表面积和体积计算公式，并能运用公式解决一些实质问题。

教课过程一、例题解说我们已经学习了长方体和正方体，知道长方体或正方体六个面面积的总和叫做长方体或正方体的表面积。

假如长方体的长用 a 表示、宽用 b 表示、高用 h 表示，那么，长方体的表面积 =（ ab＋ ah＋ bh ）× 2。

假如正方体的棱长用 a 表示，则正方体的表面积=6a2。

关于由几个长方体或正方体组合而成的几何体，或许是一个长方体或正方体组合而成的几何形体，它们的表面积又怎样求呢？波及立体图形的问题，常常可考察同学们的看图能力和空间想象能力。

小学阶段碰到的立体图形主假如长方体和正方体，这些图形的特色都是能够从六个方向去看，特别是求表面积时，就是上下、左右和前后六个方向（有时只考虑上、左、前三个方向）的平面图形的面积的总和。

有了这个原则，在解决近似问题时就十分方便了。

例 1在一个棱长为 5 分米的正方体上放一个棱长为 4 分米的小正方体（下列图），求这个立体图形的表面积。

（例 1 图）（例2图）剖析我们把上边的小正方体想象成是能够向下“压缩” 的，“压缩” 后我们发现：小正方体的上边与大正方体上边中的暗影部分合在一同，正好是大正方体的上边。

这样这个立体图形有表面积就能够分红这样两部分：上下方向：大正方体的两个底面；侧面：小正方体的四个侧面大正方体的四个侧面。

解：上下方向：5× 5× 2=50（平方分米）侧面：5× 5×4=100（平方分米）4× 4× 4=64（平方分米）这个立体图形的表面积为：50＋ 100＋64=214（平方分米）答：这个立体图形的表面积为214 平方分米。

例 2下列图是一个棱长为 2 厘米的正方体，在正方体上表面的正中，向下挖一个棱长为 1 厘米的正方体小洞，接着在小洞的底面正中向下挖一个棱长为1厘米的正方体2小洞，第三个正方体小洞的挖法与前两个同样，棱长为1厘米。

面积求解技巧面积求解是一个非常常见且基础的数学问题。

在日常生活中，我们经常需要计算各种物体的面积，比如房屋的面积、地块的面积、图形的面积等等。

本文将介绍一些常用的面积求解技巧，帮助大家更加轻松高效地解决这类问题。

一、直角三角形的面积求解直角三角形是最简单的三角形之一，其面积可通过两条直角边的长度来求解，公式为：面积 = 0.5 ×直角边1 ×直角边2。

这个公式非常简单，只需要将直角边的长度代入即可。

二、普通三角形的面积求解普通三角形由三条边组成，通常使用海伦公式求解其面积。

设三边分别为a、b、c，则海伦公式为：面积= sqrt(s × (s - a) × (s - b) × (s - c))，其中s为三边之和的一半。

三、矩形的面积求解矩形是一个非常简单的几何形状，其面积可通过长和宽来求解，公式为：面积 = 长×宽。

四、正方形的面积求解正方形是特殊的矩形，其四条边长度相等，面积也可通过边长的平方来求解，公式为：面积 = 边长×边长。

五、圆的面积求解圆是一个非常常见的几何形状，其面积可通过半径的平方来求解，公式为：面积= π×半径的平方。

其中，π是一个无理数，近似值为3.14159。

六、椭圆的面积求解椭圆是一个非常特殊的几何形状，其面积公式为：面积 = π×长半轴×短半轴。

其中，长半轴和短半轴分别是椭圆两个轴的长度。

七、多边形的面积求解多边形的面积求解相对来说较为复杂，通常需要将多边形拆分成多个简单的几何形状，然后对每个简单形状求解面积，最后将所有面积相加。

常见的多边形拆分方法有三角形拆分、矩形拆分等。

八、曲线下的面积求解有时候，我们需要求解的不是几何形状的面积，而是曲线下的面积，这需要使用积分的方法求解。

根据积分的定义，可将曲线下的面积表示为一个定积分的形式，通过对定积分的计算求解曲线下的面积。

除了以上介绍的常用面积求解技巧外，还有一些特殊情况的面积求解需要通过一些特殊的方法来解决，比如多边形中一点到多边形边界的最短距离的面积求解、扇形的面积求解等等。

一、基本概念1.1 面积的概念面积是描述二维图形所占据的空间大小的物理量。

它是用来衡量图形大小的一个重要指标，通常用单位平方米（m²）来计量。

1.2 面积的计算对于常见的平面图形，可以根据其形状和给定的尺寸计算其面积。

常见的计算方法包括几何图形的面积公式、积分法、几何分割法等。

1.3 面积的单位面积的常用单位有平方米（m²）、平方厘米（cm²）、平方分米（dm²）、平方公里（km²）等。

在实际应用中，选择合适的单位可以方便计算和理解。

二、常见图形的面积计算方法2.1 矩形的面积设矩形的长为l，宽为w，则矩形的面积S=lw。

2.2 正方形的面积设正方形的边长为a，则正方形的面积S=a²。

2.3 三角形的面积设三角形的底边长为b，高为h，则三角形的面积S=1/2bh。

2.4 梯形的面积设梯形的上底长为a，下底长为b，高为h，则梯形的面积S=1/2h(a+b)。

2.5 圆的面积设圆的半径为r，则圆的面积S=πr²。

2.6 长方体的表面积设长方体的长、宽、高分别为l、w、h，则长方体的表面积S=2lw+2lh+2wh。

以上是常见图形的面积计算方法，通过掌握这些方法，可以快速准确地计算各种图形的面积。

3.1 矩形对于同一矩形，当其周长一定时，长增加、宽减少，使得面积增加；长减少、宽增加，使得面积减少。

3.2 三角形对于同一三角形，当其周长一定时，底增加、高减少，使得面积增加；底减少、高增加，使得面积减少。

3.3 圆对于同一圆，当其周长一定时，半径增加，使得面积增加；半径减少，使得面积减少。

通过研究面积与周长的关系，可以更好地理解图形的特性，为实际应用提供便利。

四、面积与体积的关系4.1 二维图形与三维图形在几何学中，二维图形和三维图形之间存在着一定的关系。

例如，一个长方体的底面积与其体积之间存在关系，可通过计算面积来推导出体积。

4.2 二维图形的堆叠我们可以将一些相同形状的二维图形进行堆叠，从而形成一个三维的物体。

面积知识点归纳在我们的日常生活和学习中，面积是一个经常会遇到的概念。

无论是计算房间的大小、土地的面积，还是制作物品所需材料的多少，都离不开对面积的理解和计算。

下面，让我们一起来归纳一下面积的相关知识点。

一、什么是面积面积，简单来说，就是一个平面图形所占空间的大小。

它用来衡量物体表面或平面图形的大小程度。

比如，我们说一张桌子的桌面有多大，一块地有多少面积，都是在谈论面积。

为了更直观地感受面积，我们可以想象一下：把一个图形用许多小正方形铺满，小正方形的数量越多，这个图形的面积就越大。

二、常见图形的面积计算公式1、长方形长方形的面积＝长 ×宽。

如果一个长方形的长是 5 厘米，宽是 3厘米，那么它的面积就是 5×3 ＝ 15 平方厘米。

2、正方形正方形的面积＝边长×边长。

例如，一个正方形的边长是4 厘米，它的面积就是 4×4 ＝ 16 平方厘米。

3、三角形三角形的面积＝底 ×高 ÷ 2。

假设一个三角形的底是 6 厘米，高是4 厘米，那它的面积就是 6×4÷2 ＝ 12 平方厘米。

4、平行四边形平行四边形的面积＝底 ×高。

比如，底为 8 厘米，高为 5 厘米的平行四边形，面积为 8×5 ＝ 40 平方厘米。

5、梯形梯形的面积＝（上底＋下底）×高 ÷ 2 。

若梯形的上底是 3 厘米，下底是 7 厘米，高是 6 厘米，面积就是（3 ＋ 7）× 6 ÷ 2 ＝ 30 平方厘米。

6、圆形圆形的面积＝π × 半径的平方。

π通常取 314，若圆的半径是 5 厘米，面积就是 314×5×5 ＝ 785 平方厘米。

三、面积单位在计算面积时，我们需要使用特定的单位来表示大小。

常见的面积单位有：1、平方厘米（cm²）这是一个很小的面积单位，通常用来衡量较小的物体的面积，比如邮票、指甲盖等。

面积单元知识梳理
面积是指平面图形所占据的空间大小。

常用的面积单位包括平方米（㎡）、平方厘米（㎠）、平方毫米（㎟）、平方千米（㎞²）等。

以下是一些常见的面积单元及其换算关系：
1 平方米（㎡）= 10,000 平方厘米（㎠）
1 平方米（㎡）= 1,000,000 平方毫米（㎟）
1 平方千米（㎞²）= 1,000,000 平方米（㎡）
1 平方千米（㎞²）= 100,000,000 平方厘米（㎠）
对于常见的平面图形，它们的面积计算公式如下：
1. 正方形：面积 = 边长²
2. 长方形：面积 = 长 ×宽
3. 圆形：面积= π × 半径²（其中，π ≈ 3.14 或π ≈ 22/7）
4. 三角形：面积 = 底 ×高 / 2 （其中，底为底边的长度，高为从底边到顶点的垂直距离）
上述是常见面积计算公式，对于其他特殊形状的图形，面积计算公式可能会有所不同。

除了常见的面积计算方法，还有一些面积的相关知识点需要注意：
1. 面积的分配：当一个平面图形被分割成若干个较简单的图形
时，可以对每个部分的面积进行求和以得到整个图形的面积。

2. 面积的比较：面积越大表示占据的空间越大，可以通过比较两个图形的面积来判断它们的大小关系。

3. 面积的应用：面积的概念在日常生活中有许多实际应用，比如房屋面积的计算、土地面积的测量等。

以上是面积单元的知识梳理，希望对你有所帮助。

如需进一步了解，请参考相关数学教材或网上资源。

面积知识点归纳范文面积是描述平面图形所占据的空间大小的量度，可以是一个二维平面图形的大小，也可以是一个三维物体的一些表面的大小。

在数学中，面积是一个重要的概念，应用广泛，如几何学、代数学、物理学等等。

下面将介绍与面积相关的一些重要的知识点。

1.正方形的面积：正方形是一种特殊的长方形，它的四条边相等且四个角都是直角。

正方形的面积计算公式为：面积=边长²。

2.长方形的面积：长方形是一种有两条平行且相等的边的四边形。

长方形的面积计算公式为：面积=长×宽。

3.三角形的面积：三角形是一个有三条边和三个角的多边形。

三角形的面积计算公式有多个，其中最常用的是海伦公式和底高公式。

海伦公式适用于已知三边长度的情况，其公式为：面积=√(s×(s-a)×(s-b)×(s-c))，其中s表示三边长度之和的一半，a、b、c表示三边的长度。

底高公式适用于已知底边和对应的高的情况，其公式为：面积=底边×高÷24.梯形的面积：梯形是一个有两条平行边和两个非平行边的四边形。

梯形的面积计算公式为：面积=(上底+下底)×高÷26.四边形的面积：四边形是一个有四条边和四个角的多边形。

不同类型的四边形有不同的面积计算公式，如矩形、正方形、梯形等。

7.多边形的面积：多边形是一个有多条边和多个角的封闭平面图形。

多边形的面积可以通过将其分割成一些已知形状的简单图形，计算每个简单图形的面积并相加得到。

8.平行四边形的面积：平行四边形是一个有两组平行且相等的边的四边形。

平行四边形的面积计算公式为：面积=底边×高。

9.扇形的面积：扇形是一个由圆心和两条半径围成的封闭平面图形。

扇形的面积计算公式为：面积=弧长×半径÷210.球的表面积：球是一个由所有到球心距离相等的点组成的封闭曲面。

球的表面积计算公式为：表面积=4π×半径²。