试卷B

保育员中级操作技能考核B试卷及答案注意事项：1.本试卷为保育员中级操作技能考核试卷B，考试时间为180分钟。

2.在试卷标封处填写姓名、准考证号和单位名称。

3.仔细阅读题目回答要求，填写答案区。

4.不要在试卷上乱写乱画，不要在标封区填写无关内容。

一、问答题（共7题，每题10-20分，总分85分）1.观看案例演示片3遍，指出保育员在组织进餐时出现的3个工作失误，以及正确做法。

并讲述婴幼儿撒饭后的清洁工作步骤和要点。

（10分）2.观看案例演示片3遍，指出保育员在幼儿洗手环节中出现的2个工作失误，以及正确做法。

并讲述指导婴幼儿正确洗手的动作要领。

（10分）3.观看案例演示片3遍，指出保育员在配合室内游戏活动中出现的3个工作失误，以及正确做法。

讲述保育员配合室内教育活动的工作内容。

（10分）4.分析案例：在操场上排团体操时，幼儿XXX感到不舒服，保育员XXX认为她中暑了，将她扶到树下椅子上，并搽驱风油在她的太阳穴上，让她喝了一杯暖开水。

请回答保育员的做法是否正确，以及保育员应如何处理幼儿中暑问题。

（10分）5.分析案例：保育员小王带几个孩子到保健室做体检，自己测量孩子的身高和体重并告诉医生记录。

请指出正确的幼儿测量身高和体重方法。

（10分）6.分析案例：保育员XXX通知缺席孩子XXX的家长明天将进行预防针接种，但XXX的妈妈回答说XXX发烧正在家里养病。

XXX建议XXX来幼儿园接种预防针，否则要等很久才有补打机会。

请分析XXX的做法是否正确，以及保育员在幼儿预防接种过程中需要做哪些工作。

（20分）7.列出幼儿园常用的消毒剂，并写出配制6L 1:100的84消毒液的工作程序和具体操作方法。

（15分）二、论述题（15分）设计一份胆怯儿的指导方案，内容包括婴幼儿胆怯的危害、保育员对胆怯儿正确的指导态度、正确的指导方法，以及与家长配合的内容。

婴幼儿的胆怯会对其成长产生不良影响，包括影响社交能力、自信心、以及心理健康等方面。

第1页，共3页二、填空题：（18）1、三角形螺纹的牙型为 ，因其具有较好的 性能，所以，通常用于 。

2、轮齿折断一般发生在 部位，为防止轮齿折断，应进行 强度计算。

3、曲柄摇杆机构中，当 与 处于两次共线位置之一时，出现小传动角。

4、在凸轮机构四种常用的推杆运动规律中， 运动规律有刚性冲击； 运动规律和 运动规律有柔性冲击； 运动规律无冲击。

5、普通螺栓的公称直径为螺纹 ，梯形螺纹的公称直径为螺纹 。

6、轴按所受载荷的性质分类，自行车前轴是7、铰链四杆机构的杆长为a=60mm ，b=200mm ,c=100mm ，d=90mm 。

若以c 为机架，则此四杆机构为 。

8、润滑剂有 、 和 三类。

三、判断题：（15分）1、选择带轮直径时，直径越小越好 （ ）2、局部自由度是与机构运动无关的自由度 （ ）3、压力角越大对传动越有利 （ ）4、受横向载荷的螺栓联接中的螺栓必受剪切力 （ ）5、偏心轮机构是由曲柄摇杆机构演化而来的 （ ）6、挤压就是压缩 （ ）7、圆柱销与销孔之间必须采用过盈配合 （ ）8、对载荷小，而工作平衡的轴可选用球轴承 （ ）9、作用在物体上的力，向一指定点平行移动必须同时在物体上附加一个力偶。

（ ）10、Y 型V 带所能传递功率最大 （ ）第2页，共3页班 级学 号 姓 名※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※※装订 线 四、简答题1、何谓标准件？它最重要的特点是什么？试列举出五种标准件。

（6分） 答：2、根据构件的强度条件可以解决工程和实际中的哪三方面的问题？（5分） 答：3、何谓带传动的弹性滑动和打滑？能否避免？（8分） 答：4、齿轮为什么会发生根切现象？（5分） 答：五、计算题：1、机械传动如图所示，根据图示参数和信息，求运动链末端构件的运动速度或行程并标明其运动员方向。

中央银行学试卷B一、填空（每空1分，共10分）1.中国人民银行在国务院领导下，制定和实施___ 货币政策_____，对金融业实施___监督管理______。

2.中央银行买卖证券的交易方式包括___数量招标__和___价格（利率）_ _____。

3.中央银行或金融监管当局对商业银行日常经营的监管主要包括__制定并发布审慎监管政策__和__实施稽核与检查监督__。

4. 中央银行可通过调整法定存款准备金率来增加或减少商业银行的超额准备，以收缩或扩张信用，实现货币政策所要达到的目标。

5.中央银行还可通过___道义劝告__和___窗口指导__ 的方式对信用变动方向和重点实施间接指导。

二、单项选择（每题1分，共10分）1.中央银行之所以成为中央银行，最基本、最重要的标志（ B ）A.集中存款准备金B.集中与垄断货币发行C.充当“最后贷款人”D.代理国库2. 按独立性程度不同分类，属于独立性较弱的中央银行是（ D ）。

A．美国联邦储备体系B．日本银行C．英格兰银行D．意大利银行3. 以下不属于中央银行管理性业务的是（ C ）。

A．金融统计业务B．对金融机构的检查业务C．支付清算业务D．对金融机构的审计业务4. 中国人民银行对各授权窗口的再贴现操作效果实行量化考核，其中总量比例：按发生额计算，再贴现与贴现、商业汇票三者之比不高于（C ）。

A.1：1：1B.1：2：3C.1：2：4D.1：3：65. 在外汇储备构成中，风险性较大的是（B ）。

A.黄金B.外汇资产C.特别提款权D.在IMF的头寸6. 支付系统对各金融机构的每笔转账业务进行一一对应结算是指何种结算方式（A）。

A．全额结算B．净额结算C．定时结算D．实时结算7. 目前，我国中央银行对商业银行的市场准人采取（D ）原则。

A.自由主义B.特许主义C.准则主义D.核准主义8. 以下不是可供选择的货币政策中介指标的是（C ）。

A. 货币供给量B.利率C.准备金D.汇率9. 证券市场信用控制，是指中央银行对有价证券的交易，规定应支付的（ B ），目的在于限制用借款购买有价证券的比重。

济宁市技师学院2011/2012学年第一学期期末考试 数车1121、1122、1123、车工1121（中）《公差》试卷（B ）一、填空题（每空 1 分，共 30 分）1．几何量公差就是零件几何参数 的 ，它包括 和 。

2．尺寸由 和 两部分组成，如30mm 、60m 等。

3．ES 表示 ，es 表示 。

4．代表过渡配合松紧程度的特征值是 和 。

5．用以确定公差带相对于零线位置的上极限偏差或下极限偏差叫 ， 此偏差一般为靠近 的那个偏差。

6．同一公差等级对所有公称尺寸的一组公差，被认为具有 的精确程度，但却有 的公差数值。

7．检验是指确定被测几何量是否在规定的 之内，从而判断被测对象是否合格，而无须得出 。

8．螺纹千分尺主要用于测量螺纹的 尺寸。

9．机械式量仪是借助 、齿轮、齿条或扭簧的传动，将测量杆的微小直线移动经传动放大机构转变为表盘上指针的角位移，从而指示出相应的数值。

10．偏摆仪是工厂中常用的一种计量器具，利用百分表、千分表可对回转体零件进行各种 的检测。

11．确定几何公差带的四要素分别是形状、 、方向和 。

12．轮廓参数包括R 轮廓、W 轮廓、P 轮廓。

其中R 轮廓参数（表面粗糙度参数）的高度评定参数包括 和 。

13．表面结构代号由表面结构 和表面结构 ，以及其他有关规定的项目组成。

14．螺纹按其牙型可分为 、 、 和 。

15．螺距误差包括两部分,即与旋合长度有关的累积误差和与旋合长度无关的局部误差。

从互换性的角度看，螺距的 是主要的。

二、判断题（每题 1 分，共 10 分）（ ）1．螺纹公差带代号与孔、轴公差带代号相同，同样由公差等级数字和基本偏差字母组成，它们的标记方法也一样。

（ ）2．具有互换性的零件应该是形状和尺寸完全相同的零件。

（ ）3．某一零件的实际（组成）要素正好等于其公称尺寸，则该尺寸必然合格。

（ ）4．不论公差数值是否相等，只要公差等级相同，则尺寸精度就相同。

（ ）5．用游标卡尺测量轴颈时，由于没有看准对齐的刻线而产生的误差，从误差产生原因上看属于方法误差。

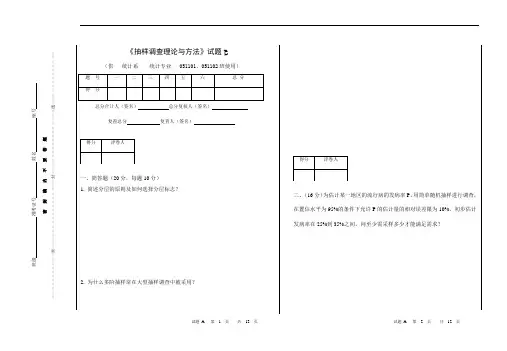
二、（16分）为估计某一地区的流行病的发病率P，用简单随机抽样进行调查，在置信水平为95%的条件下允许P的估计量的相对误差限为10%，初步估计发病率在25%到35%之间，问至少需采样多少才能满足需求？三、（16分）为调查某个高血压高发病地区青少年与成年人高血压的患病率，的绝对误差为1.25%，试确定neyman 分配下的总样本量及各层样本量。

四、（16分）某地区抽取由33个住户组成的简单随机样本，对每户调查两个指标：人口数x i 和每天用于食品的支出的费用y i ，经计算得：5.3595,28224,2.907533,123,3333133123313312331======∑∑∑∑∑=====i i i i i i ii i i i y x y yx x n试用比估计来估计该地区平均每人每天用于食品的支出，并求其置信水平95%的置信区间。

五、（16分）某地区有75308个农场，设y i 为第i 个农场养牛的头数， x i 为第i 个农场的面积。

已知农场平均面积为31.25英亩，选取一个样本容量为2055的简单随机样本。

经计算得：763.10073375525.35717915.27410065.30,53.12=====xx xy yy l l l x y试用回归估计给出该地区农场总的养牛头数的估计及其标准差的估计。

六、（16分）汽车运输公司抽样检查在使用的车辆中部安全轮胎的比例，在试卷B 参考答案及评分标准一、简答题（20分，每题10分）1. 简述分层的原则及如何选择分层标志？答：分层的原则是：一种是为了满足估计各层指标的需要或为了组织实施的便利。

此时，应以需估计的子总体为层或单位自然构成的系统或类为层；另一种是尽可能提高抽样精度，分层应做到“层内差异大，层间差异小”。

(6分)最好直接以调查指标的数值作为选择分层标志，若做不到通常选择一个与调查指标有较大线性相关的指标作为分层标志。

这个标志可以是调查指标的前期指标，也可以完全是另一个变量。

2024年重庆市中考数学试卷（B卷）一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A、B、C、D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.1．（4分）下列四个数中，最小的数是（）A．﹣1B．0C．1D．22．（4分）下列标点符号中，是轴对称图形的是（）A．B．C．D．3．（4分）反比例函数y＝﹣的图象一定经过的点是（）A．（1，10）B．（﹣2，5）C．（2，5）D．（2，8）4．（4分）如图，AB∥CD，若∠1＝125°，则∠2的度数为（）A．35°B．45°C．55°D．125°5．（4分）若两个相似三角形的相似比为1：4，则这两个三角形面积的比是（）A．1：2B．1：4C．1：8D．1：166．（4分）估计的值应在（）A．8和9之间B．9和10之间C．10和11之间D．11和12之间7．（4分）用菱形按如图所示的规律拼图案，其中第①个图案中有2个菱形，第②个图案中有5个菱形，第③个图案中有8个菱形，第④个图案中有11个菱形，…，按此规律，则第⑧个图案中，菱形的个数是（）A．20B．21C．23D．268．（4分）如图，AB是⊙O的弦，OC⊥AB交⊙O于点C，点D是⊙O上一点，连接BD，CD．若∠D＝28°，则∠OAB的度数为（）A．28°B．34°C．56°D．62°9．（4分）如图，在边长为4的正方形ABCD中，点E是BC上一点，点F是CD延长线上一点，连接AE，AF，AM平分∠EAF交CD于点M．若BE＝DF＝1，则DM的长度为（）A．2B．C．D．10．（4分）已知整式M：a n x n＋a n﹣1x n﹣1＋…＋a1x＋a0，其中n，a n﹣1，…，a0为自然数，a n为正整数，且n＋a n＋a n﹣1＋…＋a1＋a0＝5．下列说法：①满足条件的整式M中有5个单项式；②不存在任何一个n，使得满足条件的整式M有且只有3个；③满足条件的整式M共有16个．其中正确的个数是（）A．0B．1C．2D．3二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上。

安徽省高等学校教师资格认定《高等教育学》考试卷（B卷）参考答案一、解释下列概念（每小题4分，计16分）1．专业专业是高等学校根据社会专业分工需要和学科体系的内在逻辑而划分的学科门类。

（2分）按专业设置组织教学，进行专业训练，培养专门人才是现代高校的特点之一（2分）2．专才教育与通才教育不同，专才教育是指培养专门人才的教育（2分）。

专才教育的目的是通过系统地讲授某一门学科的专门知识，培养掌握一定专业知识，同时具备一定专门技能的人才（2分）。

3．课程体系课程体系是一个专业所设置课程相互间的分工和配合（2分）。

高等学校各专业课程体系主要反映在以下几个比例关系上，即普通课程、专业课程、职业课程及跨学科课程，理论性课程与实践性课程，必修课程与选修课程，大、中、小课程，显性课程与隐蔽课程等（2分）。

4．教育目的是指把受教育者培养成为一定社会所需要的人的基本要求，它规定了各级各类教育所要培养的人的基本规格和质量要求（2分）。

教育目的明确了教育对象未来发展的方向和预定的发展结果，支配着教育工作的各个方面和全过程（2分）。

二、辨析题（每小题8分，计16分）要求辨别正误，分析清楚，言之成理。

1．高校师生关系主要表现为师生之间的教育关系和心理关系。

此说不完整（4分）。

高校师生关系就其表现形式而言，既表现为教育关系、心理关系，也表现为道德关系（2分）。

其中教育关系是最基本的师生关系，是心理关系和道德关系建立的基础；反之良好的心理关系和道德关系能够维持师生间良好的教育关系（2分）。

2．大学教学的基本任务有两个方面，一是促进学生的知识积累和知识结构的优化，二是促进学生能力的发展。

此说不完整（4分）。

大学教学的基本任务，除了上述两个方面外，还要促进大学生辩证唯物主义世界观、社会主义道德和良好的个性品质的开展与发展。

（2分）知识的积累、能力的发展、世界观的形成以及良好的个性品质的形成等是相互制约的、相互促进的，忽视其中任何一方面都会影响到培养人才的质量（2分）。

2023年重庆市中考试卷（B卷）数学注意事项:1.本试卷共7页，满分为120分。

考试时间为120分钟。

2.答题前，考生务必先将自己的考生号、姓名、座位号等信息填写在试卷和答题卡的指定位置。

请认真核对条形码上的相关信息后，将条形码粘贴在答题卡的指定位置上。

3.答选择题时，必须使用2B铅笔将答题卡上对应题目的答案标号涂黑，修改时用橡皮擦干净，再选涂其他各案。

4.答非选择题时，必须使用0.5毫米的黑色字迹签字笔书写，作图题可先用铅笔绘出，确认后再用0.5毫米的黑色字迹签字笔描清楚。

要求字体工整，笔迹清晰。

严格按题号所示的答题区域作答，超出答题区域书写的答案无效：在试卷、草稿纸上答题无效。

5.保持答题卡清洁、完整，严禁折叠、损坏。

严禁在答题卡上做任何标记，严禁使用涂改液、胶带纸、修正带。

考试结束后，将本试卷和答题卡一并交回。

一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.1．（4分）4的相反数是（）A．B．C．﹣4D．42．（4分）四个大小相同的正方体搭成的几何体如图所示，从正面看到的视图是（）A．B．C．D．3．（4分）如图，直线a，b被直线c所截，若a∥b，∠1＝63°，则∠2的度数为（）A．27°B．53°C．63°D．117°4．（4分）如图，已知△ABC∽△EDC，AC：EC＝2：3，若AB的长度为6，则DE的长度为（）A．4B．9C．12D．13.55．（4分）反比例函数y＝的图象一定经过的点是（）A．（﹣3，2）B．（2，﹣3）C．（﹣2，﹣4）D．（2，3）6．（4分）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）A．14B．20C．23D．267．（4分）估计×（﹣）的值应在（）A．4和5之间B．5和6之间C．6和7之间D．7和8之间8．（4分）如图，AB为⊙O的直径，直线CD与⊙O相切于点C，连接AC，若∠ACD＝50°，则∠BAC的度数为（）A．30°B．40°C．50°D．60°9．（4分）如图，在正方形ABCD中，O为对角线AC的中点，E为正方形内一点，连接BE，BE＝BA，连接CE并延长，与∠ABE的平分线交于点F，连接OF，若AB＝2，则OF的长度为（）A．2B．C．1D．10．（4分）在多项式x﹣y﹣z﹣m﹣n（其中x＞y＞z＞m＞n）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如：x﹣y﹣|z﹣m|﹣n＝x﹣y﹣z+m﹣n，|x﹣y|﹣z﹣|m﹣n|＝x﹣y﹣z﹣m+n，…．下列说法：①存在“绝对操作”，使其运算结果与原多项式相等；②不存在“绝对操作”，使其运算结果与原多项式之和为0；③所有的“绝对操作”共有7种不同运算结果．其中正确的个数是（）A．0B．1C．2D．3二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上.11．（4分）计算：|﹣5|+（2﹣）0＝．12．（4分）有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片，将其背面朝上并洗匀，从中随机抽取一张，记下卡片正面上的汉字后放回，洗匀后再从中随机抽取一张，则抽取的两张卡片上的汉字相同的概率是．13．（4分）若七边形的内角中有一个角为100°，则其余六个内角之和为．14．（4分）如图，在△ABC 中，AB ＝AC ，AD 是BC 边的中线，若AB ＝5，BC ＝6，则AD 的长度为．15．（4分）为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为x ，根据题意，请列出方程．16．（4分）如图，在矩形ABCD 中，AB ＝2，BC ＝4，E 为BC 的中点，连接AE ．DE ．以E 为圆心，EB 长为半径画弧，分别与AE ，DE 交于点M ，N ．则图中阴影部分的面积为（结果保留π）．17．（4分）若关于x 的不等式组的解集为x ＜﹣2，且关于y 的分式方程+＝2的解为正数，则所有满足条件的整数a 的值之和为．18．（4分）对于一个四位自然数M ，若它的千位数字比个位数字多6，百位数字比十位数字多2，则称M 为“天真数”．如：四位数7311，∵7﹣1＝6，3﹣1＝2，∴7311是“天真数”；四位数8421，∵8﹣1≠6，∴8421不是“天真数”，则最小的“天真数”为；一个“天真数”M 的千位数字为a ，百位数字为b ，十位数字为c ，个位数字为d ，记P （M ）＝3（a +b ）+c +d ，Q （M ）＝a ﹣5，若能被10整除，则满足条件的M 的最大值为．三、解答题：（本大题8个小题，第19题8分，其余每题各10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.19．（8分）计算：（1）2)3()6(-++x x x x ；（2）mn m m n 229)3(-÷+．20．（10分）在学习了平行四边形的相关知识后，小虹进行了拓展性研究，她发现，如果作平行四边形一条对角线的垂直平分线，那么这条垂直平分线在该四边形内部的线段被这条对角线平分．其解决问题的思路为通过证明对应线段所在两个三角形全等即可得出结论．请根据她的思路完成以下作图和填空：用直尺和圆规作平行四边形ABCD对角线AC的垂直平分线，交DC于点E，交AB于点F，垂足为O．（只保留作图痕迹）如图，四边形ABCD是平行四边形，AC是对角线，EF垂直平分AC，垂足为O．求证：EO＝FO．证明：∵四边形ABCD是平行四边形∴DC∥AB．∴∠ECO＝．∵EF垂直平分AC，∴．又∠EOC＝，∴△COE≌△AOF（ASA）．∴EO＝FO．再进一步研究发现，过平行四边形对角线中点的所有与该四边形一组对边相交所得的线段均具备此特征，请你依照题目中的相关表述完成下面命题的填空：过平行四边形对角线中点的直线．21．（10分）某洗车公司安装了A，B两款自动洗车设备，工作人员从消费者对A、B两款设备的满意度评分中各随机抽取20份，并对数据进行整理、描述和分析（评分分数用x 表示，分为四个等级：不满意x＜70，比较满意70≤x＜80，满意80≤x＜90，非常满意x≥90），下面给出了部分信息：抽取的对A款设备的评分数据中“满意”包含的所有数据：83，85，85，87，87，89；抽取的对B款设备的评分数据：68，69，76，78，81，84，85，86，87，87，87，89，95，97，98，98，98，98，99，100．抽取的对A，B款设备的评分统计表设备平均数中位数众数“非常满意”所占百分比A88m9645%B8887n40%根据以上信息，解答下列问题：（1）填空：a＝，m＝，n＝；（2）5月份，有600名消费者对A款自动洗车设备进行评分，估计其中对A款自动洗车设备“比较满意”的人数；（3）根据以上数据，你认为哪一款自动洗车设备更受消费者欢迎？请说明理由（写出一条理由即可）．22．（10分）如图，△ABC是边长为4的等边三角形，动点E，F均以每秒1个单位长度的速度同时从点A出发，E沿折线A→B→C方向运动，F沿折线A→C→B方向运动，当两点相遇时停止运动．设运动的时间为t秒，点E，F的距离为y．（1）请直接写出y关于t的函数关系式并注明自变量t的取值范围；（2）在给定的平面直角坐标系中，画出这个函数图象，并写出该函数的一条性质；（3）结合函数图象，直接写出点E，F相距3个单位长度时t的值．23．（10分）某粮食生产基地为了落实在适宜地区开展双季稻中间季节再种一季油菜的号召，积极扩大粮食生产规模，计划用基地的甲、乙两区农田进行油菜试种，甲区的农田比乙区的农田多10000亩，甲区农田的80%和乙区全部农田均适宜试种，且两区适宜试种农田的面积刚好相同．（1）求甲、乙两区各有农田多少亩？（2）在甲、乙两区适宜试种的农田全部种上油菜后，为加强油菜的虫害治理，基地派出一批性能相同的无人机，对试种农田喷洒除虫药，由于两区地势差别，派往乙区的无人机架次是甲区的1.2倍（每架次无人机喷洒时间相同），喷洒任务完成后，发现派往甲区的每架次无人机比乙区的平均多喷洒亩，求派往甲区每架次无人机平均喷洒多少亩？24．（10分）人工海产养殖合作社安排甲、乙两组人员分别前往海面A，B养殖场捕捞海产品．经测量，A在灯塔C的南偏西60°方向，B在灯塔C的南偏东45°方向，且在A的正东方向，AC＝3600米．（1）求B养殖场与灯塔C的距离（结果精确到个位）；（2）甲组完成捕捞后，乙组还未完成捕捞，甲组决定前往B处协助捕捞，若甲组航行的平均速度为600米每分钟，请计算说明甲组能否在9分钟内到达B处？（参考数据：≈1.414，≈1.732）2）25．（10分）如图，在平面直角坐标系中，抛物线y＝x2+bx+c与x轴交于点A，B，与y 轴交于点C，其中B（3，0），C（0，﹣3）．（1）求该抛物线的表达式；（2）点P是直线AC下方抛物线上一动点，过点P作PD⊥AC于点D，求PD的最大值及此时点P的坐标；（3）在（2）的条件下，将该抛物线向右平移5个单位，点E为点P的对应点，平移后的抛物线与y轴交于点F，Q为平移后的抛物线的对称轴上任意一点．写出所有使得以QF为腰的△QEF是等腰三角形的点Q的坐标，并把求其中一个点Q的坐标的过程写出来．26．（10分）如图，在等边△ABC中，AD⊥BC于点D，E为线段AD上一动点（不与A，D 重合），连接BE，CE，将CE绕点C顺时针旋转60°得到线段CF，连接AF．（1）如图1，求证：∠CBE＝∠CAF；（2）如图2，连接BF交AC于点G，连接DG，EF，EF与DG所在直线交于点H，求证：EH＝FH；（3）如图3，连接BF交AC于点G，连接DG，EG，将△AEG沿AG所在直线翻折至△ABC所在平面内，得到△APG，将△DEG沿DG所在直线翻折至△ABC所在平面内，得到△DQG，连接PQ，QF．若AB＝4，直接写出PQ+QF的最小值．2023年重庆市中考数学试卷（B卷）参考答案与试题解析一、选择题：（本大题10个小题，每小题4分，共40分）在每个小题的下面，都给出了代号为A，B，C，D的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑.1．（4分）4的相反数是（）A．B．C．﹣4D．4【分析】只有符号不同的两个数叫做互为相反数，由此即可得到答案．【解答】解：4的相反数是﹣4．故选：C．【点评】本题考查相反数，关键是掌握相反数的定义．2．（4分）四个大小相同的正方体搭成的几何体如图所示，从正面看到的视图是（）A．B．C．D．【分析】根据从正面看得到的图形是主视图，可得答案．【解答】解：从正面看，可得选项A的图形．故选：A．【点评】本题考查了简单组合体的三视图．解题的关键是理解简单组合体的三视图的定义，明确从正面看得到的图形是主视图．3．（4分）如图，直线a，b被直线c所截，若a∥b，∠1＝63°，则∠2的度数为（）A．27°B．53°C．63°D．117°【分析】根据平行线的性质可以得到∠1＝∠2，然后根据∠1的度数，即可得到∠2的度数．【解答】解：∵a∥b，∴∠1＝∠2，∵∠1＝63°，∴∠2＝63°，故选：C．【点评】本题考查平行线的性质，解答本题的关键是明确题意，利用平行线的性质解答．4．（4分）如图，已知△ABC∽△EDC，AC：EC＝2：3，若AB的长度为6，则DE的长度为（）A．4B．9C．12D．13.5【分析】根据相似三角形的性质联立方程即可求解．【解答】解：∵△ABC∽△EDC，AC：EC＝2：3．∴，∴当AB＝6时，DE＝9．故选：B．【点评】本题主要考查了相似三角形的性质，找到对应的边成比例是解题的关键．5．（4分）反比例函数y＝的图象一定经过的点是（）A．（﹣3，2）B．（2，﹣3）C．（﹣2，﹣4）D．（2，3）【分析】根据k＝xy对各选项进行逐一判断即可．【解答】解：反比例函数y＝中k＝6，A、∵（﹣3）×2＝﹣6≠6，∴此点不在函数图象上，故本选项不合题意；B、∵2×（﹣3）＝﹣6≠6，∴此点不在函数图象上，故本选项不合题意；C、∵﹣2×（﹣4）＝8≠6，∴此点不在函数图象上，故本选项不合题意；D、∵2×3＝6，∴此点在函数图象上，故本选项符合题意．故选：D．【点评】本题考查的是反比例函数图象上点的坐标特点，熟知反比例函数中k＝xy为定值是解答此题的关键．6．（4分）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）A．14B．20C．23D．26【分析】根据前4个图中的个数找到规律，再求解．【解答】解：第①个图案中有2个圆圈，第②个图案中有2+3×1＝5个圆圈，第③个图案中有2+3×2＝8个圆圈，第④个图案中有2+3×3＝11个圆圈，...，则第⑦个图案中圆圈的个数为：2+3×6＝20，故选：B．【点评】本题考查了规律型﹣图形的变化类，找到变换规律是解题的关键．7．（4分）估计×（﹣）的值应在（）A．4和5之间B．5和6之间C．6和7之间D．7和8之间【分析】先化简题干中的式子得到﹣1，明确的范围，利用不等式的性质求出﹣1的范围得出答案．【解答】解：原式＝﹣1．∵5＜＜6．∴4＜﹣1＜5．故选：A．【点评】本题以计算选择为背景考查了无理数的估算，考核了学生对式子的化简和比较大小的能力，解题关键是将式子化简，确定无理数的范围最后利用不等式的性质．8．（4分）如图，AB为⊙O的直径，直线CD与⊙O相切于点C，连接AC，若∠ACD＝50°，则∠BAC的度数为（）A．30°B．40°C．50°D．60°【分析】连接OC，根据切线的性质得到∠OCD＝90°，求得∠ACO＝40°，根据等腰三角形的性质得到∠A＝∠ACO＝40°．【解答】解：连接OC，∵直线CD与⊙O相切于点C，∴∠OCD＝90°，∵∠ACD＝50°，∴∠ACO＝90°﹣50°＝40°，∵OC＝OA，∴∠BAC＝∠ACO＝40°，故选：B．【点评】本题考查了切线的性质，正确地作出辅助线是解题的关键．9．（4分）如图，在正方形ABCD中，O为对角线AC的中点，E为正方形内一点，连接BE，BE＝BA，连接CE并延长，与∠ABE的平分线交于点F，连接OF，若AB＝2，则OF的长度为（）A．2B．C．1D．【分析】连接AF，根据正方形ABCD得到AB＝BC＝BE，∠ABC＝90°，根据角平分线的性质和等腰三角形的性质，求得∠BFE＝45°，再证明△ABF≌△EBF，求得∠AFC＝90°，最后根据直角三角形斜边上的中线等于斜边的一半，即可求出OF的长度．【解答】解：如图，连接AF，∵四边形ABCD是正方形，∴AB＝BE＝BC，∠ABC＝90°，AC＝AB＝2，∴∠BEC＝∠BCE，∴∠EBC＝180°﹣2∠BEC，∴∠ABE＝∠ABC﹣∠EBC＝2∠BEC﹣90°，∵BF平分∠ABE，∴∠ABF＝∠EBF＝∠ABE＝∠BEC﹣45°，∴∠BFE＝∠BEC﹣∠EBF＝45°，在△BAF与△BEF中，，∴△BAF≌△BEF（SAS），∴∠BFE＝∠BFA＝45°，∴∠AFC＝∠BAF+∠BFE＝90°，∵O为对角线AC的中点，∴OF＝AC＝，故选：D．【点评】本题考查了等腰三角形的判定和性质，三角形内角和定理，正方形的性质，直角三角形特征，作出正确的辅助线，求得∠BFE＝45°是解题的关键．10．（4分）在多项式x﹣y﹣z﹣m﹣n（其中x＞y＞z＞m＞n）中，对相邻的两个字母间任意添加绝对值符号，添加绝对值符号后仍只有减法运算，然后进行去绝对值运算，称此为“绝对操作”．例如：x﹣y﹣|z﹣m|﹣n＝x﹣y﹣z+m﹣n，|x﹣y|﹣z﹣|m﹣n|＝x﹣y﹣z﹣m+n，…．下列说法：①存在“绝对操作”，使其运算结果与原多项式相等；②不存在“绝对操作”，使其运算结果与原多项式之和为0；③所有的“绝对操作”共有7种不同运算结果．其中正确的个数是（）A．0B．1C．2D．3【分析】根据给定的定义，举出符合条件的说法①和②．说法③需要对绝对操作分析添加一个和两个绝对值的情况，并将结果进行比较排除相等的结果，汇总得出答案．【解答】解：|x﹣y|﹣z﹣m﹣n＝x﹣y﹣z﹣m﹣n，故说法①正确．若使其运算结果与原多项式之和为0，需出现﹣x，显然无论怎么添加绝对值，都无法使x的符号为负号，故说法②正确．当添加一个绝对值时，共有4种情况，分别是|x﹣y|﹣z﹣m﹣n＝x﹣y﹣z﹣m﹣n；x﹣|y ﹣z|﹣m﹣n＝x﹣y+z﹣m﹣n；x﹣y﹣|z﹣m|﹣n＝x﹣y﹣z+m﹣n；x﹣y﹣z﹣|m﹣n|＝x﹣y ﹣z﹣m+n．当添加两个绝对值时，共有3种情况，分别是|x﹣y|﹣|z﹣m|﹣n＝x﹣y﹣z+m ﹣n；|x﹣y|﹣z﹣|m﹣n|＝x﹣y﹣z﹣m+n；x﹣|y﹣z|﹣|m﹣n|＝x﹣y+z﹣m+n．共有7种情况；有两对运算结果相同，故共有5种不同运算结果，故说法③不符合题意．故选：C．【点评】本题考查新定义题型，根据多给的定义，举出符合条件的代数式进行情况讨论；需要注意去绝对值时的符号，和所有结果可能的比较．主要考查绝对值计算和分类讨论思想的应用．二、填空题：（本大题8个小题，每小题4分，共32分）请将每小题的答案直接填在答题卡中对应的横线上.11．（4分）计算：|﹣5|+（2﹣）0＝6．【分析】由|﹣5|＝5，（2﹣）0＝1【解答】解：|﹣5|+（2﹣）0＝5+1＝6．故答案为：6．【点评】本题考查实数的运算．解题的关键是去绝对值注意符号；掌握任意非零实数的零次幂都等于1．12．（4分）有四张完全一样正面分别写有汉字“清”“风”“朗”“月”的卡片，将其背面朝上并洗匀，从中随机抽取一张，记下卡片正面上的汉字后放回，洗匀后再从中随机抽取一张，则抽取的两张卡片上的汉字相同的概率是．【分析】根据题意，可以画出相应的树状图，然后即可求出相应的概率．【解答】解：树状图如图所示，由上可得，一共有16种等可能性，其中抽取的两张卡片上的汉字相同的有4种可能性，∴抽取的两张卡片上的汉字相同的概率为＝，故答案为：．【点评】本题考查列表法与树状图法，解答本题的关键是明确题意，画出相应的树状图，求出相应的概率．13．（4分）若七边形的内角中有一个角为100°，则其余六个内角之和为800°．【分析】利用多边形内角和公式求得七边形的内角和后与100°作差即可．【解答】解：由题意可得七边形的内角和为：（7﹣2）×180°＝900°，∵该七边形的一个内角为100°，∴其余六个内角之和为900°﹣100°＝800°，故答案为：800°．【点评】本题主要考查多边形的内角和，此为基础且重要知识点，必须熟练掌握．14．（4分）如图，在△ABC中，AB＝AC，AD是BC边的中线，若AB＝5，BC＝6，则AD的长度为4．【分析】根据等腰三角形的性质可得AD⊥BC，在Rt△ABD中，根据勾股定理即可求出AD的长．【解答】解：∵AB＝AC，AD是BC边的中线，∴AD⊥BC，∴∠ADB＝90°，∵AB＝5，BC＝6，∴BD＝CD＝3，在Rt△ABD中，根据勾股定理，得AD＝＝＝4，故答案为：4．【点评】本题考查了等腰三角形的性质，涉及勾股定理，熟练掌握等腰三角形的性质是解题的关键．15．（4分）为了加快数字化城市建设，某市计划新建一批智能充电桩，第一个月新建了301个充电桩，第三个月新建了500个充电桩，设该市新建智能充电桩个数的月平均增长率为x，根据题意，请列出方程301（1+x）2＝500．【分析】设该市新建智能充电桩个数的月平均增长率为x，根据第一个月新建了301个充电桩，第三个月新建了500个充电桩，即可得出关于x的一元二次方程．【解答】解：设该市新建智能充电桩个数的月平均增长率为x，依题意得：301（1+x）2＝500．故答案为：301（1+x）2＝500．【点评】本题考查了由实际问题抽象出一元二次方程，找准等量关系，正确列出一元二次方程是解题的关键．15．（4分）如图，在矩形ABCD中，AB＝2，BC＝4，E为BC的中点，连接AE．DE．以E为圆心，EB长为半径画弧，分别与AE，DE交于点M，N．则图中阴影部分的面积为4﹣π（结果保留π）．【分析】用三角形ADE的面积减去2个扇形的面积即可．【解答】解：∵AD＝2AB＝4，E为BC的中点，∴AB＝2，BE＝CE＝2，∴∠BAE＝∠AEB＝∠CDE＝∠DEC＝45°，∴阴影部分的面积为﹣2×＝4﹣π．故答案为：4﹣π．【点评】此题主要考查了扇形面积求法以及等腰直角三角形的性质，应用扇形面积的计算方法进行求解是解决本题的关键．17．（4分）若关于x的不等式组的解集为x＜﹣2，且关于y的分式方程+＝2的解为正数，则所有满足条件的整数a的值之和为13．【分析】先通过不等式组的解确定a的范围，再根据分式方程的解求a值即可得出答案．【解答】解：解不等式组，得：，∵原不等式组的解集为：x＜﹣2，∴﹣≥﹣2，∴a≤5，解分式方程+＝2，得y＝，∵y＞0且y≠1，∴＞0且≠1，∴a＞﹣2且a≠1，∴﹣2＜a≤5，且a≠1，∴符合条件的整数a有：﹣1，0，2，3，4，5，∴﹣1+0+2+3+4+5＝13．故答案为：13．【点评】本题主要考查解一元一次不等式组、解分式方程，熟练掌握一元一次不等式组、分式方程的解法是解决本题的关键．18．（4分）对于一个四位自然数M，若它的千位数字比个位数字多6，百位数字比十位数字多2，则称M为“天真数”．如：四位数7311，∵7﹣1＝6，3﹣1＝2，∴7311是“天真数”；四位数8421，∵8﹣1≠6，∴8421不是“天真数”，则最小的“天真数”为6200；一个“天真数”M的千位数字为a，百位数字为b，十位数字为c，个位数字为d，记P（M）＝3（a+b）+c+d，Q（M）＝a﹣5，若能被10整除，则满足条件的M的最大值为9313．【分析】它的千位数字比个位数字多6，百位数字比十位数字多2，则称M为“天真数”．分为两部分：第一部分千位数和个位数之间的关系，第二部分百位数和十位数之前的关系．【解答】解：求最小的“天真数”，首先知道最小的自然数的0．先看它的千位数字比个位数字多6，个位数为最小的自然数0时，千位数为6；百位数字比十位数字多2，十位数为最小的的自然数0时，百位数是2；则最小的“天真数”为6200．故答案为：6200．一个“天真数”M的千位数字为a，百位数字为b，十位数字为c，个位数字为d．由“天真数”的定义得a＝d+6，所以6≤a≤9，b＝c+2，所以0≤c≤7，又P（M）＝3（a+b）+c+d＝3（a+c+2）+c+a﹣6＝4a+4c；Q（M）＝a﹣5.＝论能被10整除当a取最大值9时，即当a＝9时，满足能被10整除，则c＝1，“天真数”M为9313．故答案为：9313．【点评】新定义题型，各数字的取值范围，最值：最小自然数0．三、解答题：（本大题8个小题，第19题8分，其余每题各10分，共78分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上.19．（8分）计算：（1）x（x+6）+（x﹣3）2；（2）（3+）÷．【分析】（1）按照单项式乘以多项式的法则以及完全平方公式进行计算即可；（2）按照分式的混合运算法则进行计算即可．【解答】解：（1）x（x+6）+（x﹣3）2＝x2+6x+x2﹣6x+9＝2x2+9；（2）＝＝＝．【点评】本题考查了分式的混合运算和整式的混合运算，熟练掌握混合运算法则是解题的关键，计算时一定要细心．20．（10分）在学习了平行四边形的相关知识后，小虹进行了拓展性研究，她发现，如果作平行四边形一条对角线的垂直平分线，那么这条垂直平分线在该四边形内部的线段被这条对角线平分．其解决问题的思路为通过证明对应线段所在两个三角形全等即可得出结论．请根据她的思路完成以下作图和填空：用直尺和圆规作平行四边形ABCD对角线AC的垂直平分线，交DC于点E，交AB于点F，垂足为O．（只保留作图痕迹）如图，四边形ABCD是平行四边形，AC是对角线，EF垂直平分AC，垂足为O．求证：EO＝FO．证明：∵四边形ABCD是平行四边形∴DC∥AB．∴∠ECO＝∠FAO．∵EF垂直平分AC，∴OA＝OC．又∠EOC＝∠FOA，∴△COE≌△AOF（ASA）．∴EO＝FO．再进一步研究发现，过平行四边形对角线中点的所有与该四边形一组对边相交所得的线段均具备此特征，请你依照题目中的相关表述完成下面命题的填空：过平行四边形对角线中点的直线被平行四边形一组对边所截，截得的线段被对角线中点平分．【分析】根据要求画出图形，证明△COE≌△AOF（ASA），可得结论．【解答】解：图形如图所示：理由：∵四边形ABCD是平行四边形，∴DC∥AB．∴∠ECO＝∠FAO，∵EF垂直平分AC，∴AO＝OC．又∠EOC＝∠FOA，∴△COE≌△AOF（ASA）．∴EO＝FO．再进一步研究发现，过平行四边形对角线中点的所有与该四边形一组对边相交所得的线段均具备此特征，所以过平行四边形对角线中点的直线被平行四边形一组对边所截，截得的线段被对角线中点平分，故答案为：∠FAO，OA＝OC，∠FOA，过平行四边形对角线中点的直线被平行四边形一组对边所截，截得的线段被对角线中点平分．【点评】本题考查命题与定理，平行四边形的性质，全等三角形的判定和性质等知识，解题的关键是理解题意，正确寻找全等三角形解决问题．21．（10分）某洗车公司安装了A，B两款自动洗车设备，工作人员从消费者对A、B两款设备的满意度评分中各随机抽取20份，并对数据进行整理、描述和分析（评分分数用x 表示，分为四个等级：不满意x＜70，比较满意70≤x＜80，满意80≤x＜90，非常满意x≥90），下面给出了部分信息：抽取的对A款设备的评分数据中“满意”包含的所有数据：83，85，85，87，87，89；抽取的对B款设备的评分数据：68，69，76，78，81，84，85，86，87，87，87，89，95，97，98，98，98，98，99，100．抽取的对A，B款设备的评分统计表设备平均数中位数众数“非常满意”所占百分比A88m9645%B8887n40%根据以上信息，解答下列问题：（1）填空：a＝15，m＝88，n＝98；（2）5月份，有600名消费者对A款自动洗车设备进行评分，估计其中对A款自动洗车设备“比较满意”的人数；（3）根据以上数据，你认为哪一款自动洗车设备更受消费者欢迎？请说明理由（写出一条理由即可）．【分析】（1）用“1”分别减去其他三个等级所占百分比可得a的值，根据中位数的定义可得m的值，根据众数的定义可得n的值；（2）用600乘A款自动洗车设备“比较满意”所占百分比即可；（3）通过比较A，B款设备的评分统计表的数据解答即可．【解答】解：（1）由题意得，a%＝1﹣10%﹣45%﹣＝15%，即a＝15；把A款设备的评分数据从小到大排列，排在中间的两个数是87，89，故中位数m＝＝88；在B款设备的评分数据中，98出现的次数最多，故众数n＝98．故答案为：15；88；98；（2）600×15%＝90（名），答：估计其中对A款自动洗车设备“比较满意”的人数大约为90名；（3）A款自动洗车设备更受消费者欢迎，理由如下：因为两款自动洗车设备的评分数据的平均数相同，但A款自动洗车设备的评分数据的中位数比B款高，所以A款自动洗车设备更受消费者欢迎（答案不唯一）．【点评】本题考查扇形统计图，中位数、众数以及样本估计总体，理解中位数、众数的意义，掌握中位数、众数的计算方法是解决问题的前提．22．（10分）如图，△ABC是边长为4的等边三角形，动点E，F均以每秒1个单位长度的速度同时从点A出发，E沿折线A→B→C方向运动，F沿折线A→C→B方向运动，当两点相遇时停止运动．设运动的时间为t秒，点E，F的距离为y．（1）请直接写出y关于t的函数关系式并注明自变量t的取值范围；（2）在给定的平面直角坐标系中，画出这个函数图象，并写出该函数的一条性质；。

广西财经学院2０1３－201４学年第二学期 《经济法》课程期末试卷（B)卷 适用班级:会计1321-１32５ 时 间：1２0分钟 （闭卷) 考试课程 课程院部:法学院 题 号 一 二 三 四 五 总 分 核分人 应得分 ２0 20 10 10 4０ 实得分 得分 评卷教师 一、单项选择题 ( 每小题１分,共2０ 分) 1。

有限责任公司的执行机构是( ) A. 股东会 B. 监事会 C 。

职工代表大会 Ｄ. 董事会 ２。

下列有关有限合伙企业设立条件的表述中，不符合新颁布的《合伙企业法》规定的是（ )。

A.有限合伙企业至少应当有一个普通合伙人 B ．有限合伙企业名称中应当标明“特殊普通合伙”字样 C.有限合伙人可以用知识产权作价出资 D ．有限合伙企业登记事项中应载明有限合伙人的姓名或名称 3．下列可以以劳务出资的有:（ ) A ．有限责任公司 B.个人独资企业 C.合伙企业 D.股份公司 4．甲、乙、丙成立一合伙企业。

其合伙合同中约定:“合伙企业的事务由甲全权负责，乙、丙不得过问亦不承担企业亏损的民事责任”。

对该约定的效力应如何认定( ） Ａ．该约定有效，应由甲一人承担全部民事责任 B 。

该约定无效，应由甲、乙、丙共同承担民事责任 Ｃ。

该约定部分有效，应由甲一人承担全部民事责任 Ｄ.该约定部分无效,应由甲、乙、丙共同承担民事责任 5。

根据合伙企业法的有关规定,合伙企业存续期间，下列行为中,必须经姓名：学号：班级： ……………装…………………订……………………线………………………装……………………订………………………线…………………………全体合伙人一致同意的有:（ )A.合伙企业存续期间，合伙人向合伙人以外的人转让其在合伙企业中的全部或部分财产份额B.合伙人之间转让在合伙企业中的全部或者部分财产份额Ｃ．处分从合伙企业分取的财产D.合伙人以自己名义为他人提供担保6．有限责任公司与股份有限公司的分类标准是( ）Ａ.股东人数的多少 B．股东责任的不同C．公司注册资本的多少 D．公司是否可发行股份７．股东不按章程足额交纳出资的，除应向公司补交外,还应向谁承担违约责任？ ( )A．公司Ｂ．全体股东C.已按期足额交纳出资的股东D.工商行政管理局8。

重庆市中考化学试卷（B卷）参考答案与试题解析一、选择题（本大题包括16个小题，每小题2分，共32分）每小题只有一个选项符合题意。

1．（2分）“构建生命共同体”体现人与自然和谐共生。

下列说法与该理念不相符的是（）A．全民义务植树活动B．大肆开采矿物资源C．生活废水处理排放D．长江流域十年禁渔【解析】解：A、义务植树能保护环境，故不合题意；B、大肆开采矿物资源会造成资源的浪费，且破坏环境，故符合题意；C、生活废水处理排放可以防止水体污染，故不合题意；D、长江流域十年禁渔有利于保护生态平衡，故不合题意。

故选：B。

2．（2分）成语蕴含丰富的中华文化。

下列成语的本义一定体现化学变化的是（）A．盲人摸象B．南辕北辙C．火中取栗D．绳锯木断【解析】解：A.盲人摸象，没有新物质生成，属于物理变化，故A错误；B.南辕北辙，没有新物质生成，属于物理变化，故B错误；C.火中取栗，发生了燃烧，有新物质生成，属于化学变化，故C正确；D.绳锯木断，没有新物质生成，属于物理变化，故D错误。

故选：C。

3．（2分）安全是化学实验成功的保障。

下列操作安全的是（）A．B．C．D．【解析】解：A、稀释浓硫酸时，要把浓硫酸缓缓地沿器壁注入水中，同时用玻璃棒不断搅拌，以使热量及时的扩散；一定不能把水注入浓硫酸中，以防止酸液飞溅；图中所示操作错误。

B、闻气体的气味时，应用手在瓶口轻轻的扇动，使极少量的气体飘进鼻子中，不能将鼻子凑到集气瓶口去闻气体的气味，图中所示操作正确。

C、给试管中的液体加热时，用酒精灯的外焰加热试管里的液体，且液体体积不能超过试管容积的三分之一，图中液体超过试管容积的三分之一、大拇指不能放在短柄上，图中所示操作错误。

D、使用酒精灯时要注意“两查、两禁、一不可”，禁止用酒精灯去引燃另一只酒精灯，图中所示操作错误。

故选：B。

4．（2分）食品包装袋内常放有内装铁粉和生石灰的小包。

下列空气成分一定不能与它们反应的是（）A．N2B．O2C．H2O D．CO2【解析】解：A、铁粉和生石灰均不与氮气反应，故A符合题意；B、铁在与氧气、水同时共存时会发生锈蚀，因此氧气能与铁粉反应，故B不合题意；C、铁在与氧气、水同时共存时会发生锈蚀；生石灰能与水反应生成熟石灰，故C不合题意；D、生石灰与水反应生成熟石灰，熟石灰与二氧化碳反应生成碳酸钙和水，故D不合题意。

作业治疗学试卷（B卷）诚信考试，考试作弊者将不授予学⼠学位！（详见学校学⼠学位授予细则⽂件）《作业治疗学》考试试卷（B卷）专业班级学号姓名考试⽇期：年⽉⽇考试时间：100分钟⼀、名词解释（每个2.5分，共10分）1、辅助技术：2、失⽤症：3、滑动转移：4、⽣产性作业活动：⼆、填空题（每空1分，共15分）1、穿⾐训练中，如果患者不能⾃⼰系纽扣，可⽤替代。

2、职业康复的内容可概括为、、职业培训、职业指导和⼯作安置等⽅⾯。

3、作业内容包括、和。

4、患者转移活动⼀般包括床上翻⾝、床椅转移、、坐站转移。

5、⾃我照顾性⽇常⽣活活动中，修饰活动⼀般包括、和。

6、环境控制系统包括两⼤部分，分别是和。

7、Tinel’s征检查⽅法是沿神经⾛⾏敲击，直到出现神经⽀配区放射状针刺感。

8、主要是通过反复、系统的训练，提⾼患者感觉阈值，从⽽达到降低异常感觉敏感程度的⽬的的⼀门技术，叫。

三、单选题（每题1分，共45分）1、脑出⾎患者在恢复过程中，肌痉挛开始出现的时间，发⽣于Brunnstrom 分期的（）A.Ⅳ期B.Ⅲ期C.Ⅱ期D.Ⅰ期2、压⼒治疗每天应持续的时间（）A.⼤于2⼩时B.⼤于12⼩时3、下列说法正确的是（）A.⽇常⽣活活动包括基本的⽇常⽣活活动及⼯具性⽇常⽣活活动两个⽅⾯B.基本的⽇常⽣活活动包括饮⾷、穿裤、洗澡、个⼈卫⽣等C.⼯具性⽇常⽣活活动包括操作轮椅、洗⾐、购物、使⽤家电等D.转移活动训练只包括床椅转移、进出厕所、进出浴室4、下列符合办公室⼈体功效学设计的是（）A.⼯作台上摆上所有的⽤具，⽅便取⽤B.座椅靠背要倾斜，更为舒适C.座椅要有五点⽀撑，即腰部、背部、臀部、前臂、⾜部均应有⽀撑D.坐姿时，保持头部直⽴，不可向上或向下倾斜5、慢性阻塞性肺病患者呼吸训练的⽅法是（）A.张⼝呼吸B.缩唇呼吸C.胸式呼吸D.腹式呼吸6、蹦床适应证不包括（）A.多动症B.孤独症C.触觉防御D.触觉迟钝7、⽬前国际标准和国家标准中辅助器具的分类⽅法是如何分类的（）A.按制作材料分类B.按使⽤环境分类C.按使⽤功能分类D.按使⽤阶段分类8、视觉障碍者可⽤的辅助器具不包括（）A.语⾳⼿机B.盲⽂C.传呼机D.有声电⼦书9、以下主要⽤于改善上肢ROM的作业活动是（）A.⾳乐欣赏B.太极拳操10、⼊厕训练适合（）岁以上的孩⼦A.1.5岁B.2岁C.2.5岁D.3岁11、压⼒治疗的理想压⼒为（）A.14～15mmHgB.24～25mmHgC.34～35mmHgD.20～30mmHg12、疾病恢复早期，应选⽤的腋杖步⾏⽅法是（）A.三点步⾏B.四点步⾏C.摆⾄步D.摆过步13、为保护⼿⼸，进⾏压⼒治疗时应（）A.⼿部⽤低压⼒B.加压⼒垫C.使⽤⽀架保护D.应⽤绷带加压法14、职业技术训练包括（）A.⽊⼯作业B.居室清洁装饰C.纺织作业D.办公室作业15、整个轮椅旋转360°，需要的直径为（）A.160cmB.150cmC.140cmD.130cm16、为防⽌脑⾎管意外的患者的异常模式发展，在急性期应注意（）A.进⾏按摩治疗B.进⾏关节被动运动D.促进分离运动的出现17、下列失认症除了哪⼀项以外均是视觉失认的表现（）A.形状失认B.物品失认C.相貌失认D.⼿指失认18、深感觉障碍主要表现为（）A.肌⼒的下降B.ROM的下降C.痛温觉的丧失D.运动失调19、轮椅椅座离地⾯约（）A.45.5cmB.46.5cmC.47.5cmD.48.5cm20、下列哪⼀个是体外⼒源性假肢（）A.钩状⼿B.索控式假⼿C.装饰性假肢D.肌电⼿21、⼤⼉⼦叫⼀⽑、⼆⼉⼦叫⼆⽑、三⼉⼦叫⼩⽑是下列哪种思维⽅式（）A.求同思维B.求异思维C.抽象思维D.形象思维22、⾜下垂的患者可以使⽤下列哪种矫形器（）A.HKAEOB.KAEOC.AFOD.TLO23、作业疗法功能评定初次评定的⽬标是（）A.确定治疗⽬标B.调整治疗⽅案D.判断患者的康复结局24、⽼年性痴呆的认知评估主要包括（）A.MMSEB.FIMC.MMTD.EPQ25、发现⽼年⼈跌倒，意识不清，下列做法正确的是（）A.⽴即将⽼⼈搬运⾄安全地带B.有呕吐，将头偏向⼀侧，并清理⼝、⿐腔呕吐物，保证呼吸通畅C.有抽搐，牵拉抽搐肢体，防⽌肢体过屈或过伸D.赶紧⾛开，以免惹事上⾝26、下列适合BrunnstromⅠ期患者改善⼿指功能的作业治疗活动是（）A.佩戴⼿指夹板，防⽌屈肌痉挛B.练习抓握各种形状、⼤⼩、重量的物体C.练习使⽤筷⼦D.在治疗师的帮助下进⾏患⼿抓握活动27、左前臂截肢者最可能需要的辅助器具是（）A.改装的筷⼦B.书写辅助器具C.剪指甲辅助器具D.改装的梳⼦28、⼤腿截肢后仰卧位时髋关节应保持在下列哪种位置（）A.伸展内收位B.伸展外展位C.屈曲内收位D.屈曲外展位29、关于作业治疗评估的步骤描述错误的是（）A.⾸先确定活动障碍的性质、部位和损害的程度B.其次判明疾病的状态，疾病的原因、程度C.根据评估结果得出作业治疗“诊断”，推断治疗潜⼒D.有的放⽮地制定出合适的治疗⽅案，选择正确的治疗⼿段30、使⽤筷⼦夹持跳棋进⾏训练不可达到哪项⽬的（）A.提⾼⼿的灵活性B.提⾼ADL能⼒31、蚓状肌的作⽤是（）A.伸指间关节、屈掌指关节B.屈指间关节、屈掌指关节C.伸指间关节、伸掌指关节D.屈指间关节、伸掌指关节32、正确穿戴压⼒⾐的⽅法是（）A.每天2hB.每天6hC.每天12hD.除洗澡外24h33、作业疗法的禁忌症不包括（）A.意识不清规B.严重认识障碍不能合作者C.危重症D.低热34、游戏疗法常不⽤于（）A.智能低下B.脑性瘫痪C.⾃闭症D.肘关节功能障碍35、格斯特曼综合征包括哪些症状（）A.失写B.失算C.双侧⼿指失认D.左右分辨障碍36、⽤于减轻疼痛的作业活动不包括（）A.挂线作业B.加热粘⼟作业C.温室内下棋D.书法37、供轮椅出⼊的门⾄少应有（）以上的有效宽度：A.85cmB.86cm38、以下哪种⽅法可以⽤来评定半侧空间失认症（）A.平分直线法B.写出⼝述的短句C.辨认图形D.物品分类检查39、KAFO全称为（）A.膝踝⾜矫形器B.髋膝踝⾜矫形器C.踝⾜矫形器D.⾜部矫形器40、近年来提出的⼀种能更为全⾯、客观地反映残疾者⽇常⽣活活动能⼒的评定⽅法是（）A.PULSES评定B.功能活动问卷（FAQ)C.功能独⽴性评定D.Barthel指数41、为改善患者⼿指精细协调活动能⼒，下列哪项作业活动选择是错误的（）A.系扣⼦B.编织⼿套C.拉锯D.⽤勺进⾷42、职业康复的任务不包括（）A.掌握残疾⼈的⾝体、⼼理和职业能⼒情况B.就残疾⼈职业训练和就业的可能性进⾏指导C.引导从事适当的职业D.给残疾⼈发放物资补助43、下列哪项不是⽇常⽣活活动训练的⽬的（）A.建⽴患者的⾃我康复意识，充分发挥主观能动性，提⾼信⼼，重新建⽴独⽴⽣活的⾃信B.重新学习或维持患者基本的⽇常⽣活活动，调动并挖掘其⾃⾝潜⼒，使其达到⽣活⾃理，降低对他⼈的⽣活依赖程度C.进⼀步改善患者躯体功能，达到通过⽇常⽣活活动训练的⽬的，以适应⽇后回归家庭、重返社会的需要D.帮助维持患者的关节活动度、肌⼒和平衡能⼒44、认知障碍常见类型不包括（）A.注意⼒障碍B.记忆⼒障碍45、删字试验主要⽤来评定下列哪种失认症（）A.单侧空间忽略B.记忆⼒障碍C.推理功能障碍D.定向⼒障碍四、简答题（每题5分，共15分）1、抑制脑损伤患者⼿指屈曲痉挛的⽅法有哪些？2、简述给患者进⾏穿脱上⾐训练的注意事项。

2022年陕西省中考数学试卷（B卷）一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．（3分）﹣37的相反数是（）A．﹣37B．﹣C．37D．2．（3分）如图，AB∥CD，BC∥EF．若∠1＝58°，则∠2的大小为（）A．120°B．122°C．132°D．148°3．（3分）计算：2x•（﹣3x2y3）＝（）A．﹣6x3y3B．6x3y3C．﹣6x2y3D．18x3y34．（3分）在下列条件中，能够判定▱ABCD为矩形的是（）A．AB＝AD B．AC⊥BD C．AB＝AC D．AC＝BD5．（3分）如图，AD是△ABC的高．若BD＝2CD＝6，tan C＝2，则边AB的长为（）A．3B．3C．6D．36．（3分）在同一平面直角坐标系中，直线y＝﹣x+4与y＝2x+m相交于点P（3，n），则关于x，y 的方程组的解为（）A．B．C．D．7．（3分）如图，△ABC内接于⊙O，∠C＝46°，连接OA，则∠OAB＝（）A．44°B．45°C．54°D．67°8．（3分）已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3．当﹣1＜x 1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（）A．y1＜y2＜y3B．y2＜y3＜y1C．y3＜y1＜y2D．y2＜y1＜y3二、填空题（共5小题，每小题3分，计15分）9．（3分）计算：3﹣＝．10．（3分）实数a，b在数轴上对应点的位置如图所示，则a﹣b．（填“＞”“＝”或“＜”）11．（3分）在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法，所作EF将矩形窗框ABCD分为上下两部分，其中E为边AB的黄金分割点，即BE2＝AE•AB．已知AB为2米，则线段BE的长为米．12．（3分）已知点A（﹣2，m）在一个反比例函数的图象上，点A'与点A关于y轴对称．若点A'在正比例函数y＝x的图象上，则这个反比例函数的表达式为．13．（3分）如图，在菱形ABCD中，AB＝4，BD＝7．若M、N分别是边AD、BC上的动点，且AM＝BN，作ME⊥BD，NF⊥BD，垂足分别为E、F，则ME+NF的值为．三、解答题（共13小题，计81分．解答应写出过程）14．（5分）计算：5×（﹣3）+|﹣|﹣（）0．15．（5分）解不等式组：．16．（5分）化简：（+1）÷．17．（5分）如图，已知△ABC，CA＝CB，∠ACD是△ABC的一个外角．请用尺规作图法，求作射线CP，使CP∥AB．（保留作图痕迹，不写作法）18．（5分）如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．19．（5分）如图，△ABC的顶点坐标分别为A（﹣2，3），B（﹣3，0），C（﹣1，﹣1）．将△ABC平移后得到△A'B'C'，且点A的对应点是A'（2，3），点B、C的对应点分别是B'、C'．（1）点A、A'之间的距离是；（2）请在图中画出△A'B'C'．20．（5分）有五个封装后外观完全相同的纸箱，且每个纸箱内各装有一个西瓜，其中，所装西瓜的重量分别为6kg，6kg，7kg，7kg，8kg．现将这五个纸箱随机摆放．（1）若从这五个纸箱中随机选1个，则所选纸箱里西瓜的重量为6kg的概率是；（2）若从这五个纸箱中随机选2个，请利用列表或画树状图的方法，求所选两个纸箱里西瓜的重量之和为15kg的概率．21．（6分）小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高．如图所示，在某一时刻，他们在阳光下，分别测得该建筑物OB的影长OC为16米，OA的影长OD为20米，小明的影长FG 为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且AO⊥OD，EF ⊥FG．已知小明的身高EF为1.8米，求旗杆的高AB．22．（7分）如图，是一个“函数求值机”的示意图，其中y是x的函数．下面表格中，是通过该“函数求值机”得到的几组x与y的对应值．输入x…﹣6﹣4﹣202…输出y…﹣6﹣22616…根据以上信息，解答下列问题：（1）当输入的x值为1时，输出的y值为；（2）求k，b的值；（3）当输出的y值为0时，求输入的x值．23．（7分）某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在本校随机调查了100名学生的“劳动时间”，并进行统计，绘制了如下统计表：组别“劳动时间”t/分钟频数组内学生的平均“劳动时间”/分钟A t＜60850B60≤t＜901675C90≤t＜12040105D t≥12036150根据上述信息，解答下列问题：（1）这100名学生的“劳动时间”的中位数落在组；（2）求这100名学生的平均“劳动时间”；（3）若该校有1200名学生，请估计在该校学生中，“劳动时间”不少于90分钟的人数．24．（8分）如图，AB是⊙O的直径，AM是⊙O的切线，AC、CD是⊙O的弦，且CD⊥AB，垂足为E，连接BD并延长，交AM于点P．（1）求证：∠CAB＝∠APB；（2）若⊙O的半径r＝5，AC＝8，求线段PD的长．25．（8分）现要修建一条隧道，其截面为抛物线型，如图所示，线段OE表示水平的路面，以O为坐标原点，以OE所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系．根据设计要求：OE＝10m，该抛物线的顶点P到OE的距离为9m．（1）求满足设计要求的抛物线的函数表达式；（2）现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯．已知点A、B到OE的距离均为6m，求点A、B的坐标．26．（10分）问题提出（1）如图1，AD是等边△ABC的中线，点P在AD的延长线上，且AP＝AC，则∠APC的度数为．问题探究（2）如图2，在△ABC中，CA＝CB＝6，∠C＝120°．过点A作AP∥BC，且AP＝BC，过点P作直线l⊥BC，分别交AB、BC于点O、E，求四边形OECA的面积．问题解决（3）如图3，现有一块△ABC型板材，∠ACB为钝角，∠BAC＝45°．工人师傅想用这块板材裁出一个△ABP型部件，并要求∠BAP＝15°，AP＝AC．工人师傅在这块板材上的作法如下：①以点C为圆心，以CA长为半径画弧，交AB于点D，连接CD；②作CD的垂直平分线l，与CD交于点E；③以点A为圆心，以AC长为半径画弧，交直线l于点P，连接AP、BP，得△ABP．请问，若按上述作法，裁得的△ABP型部件是否符合要求？请证明你的结论．2022年陕西省中考数学试卷（B卷）参考答案与试题解析一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．（3分）﹣37的相反数是（）A．﹣37B．﹣C．37D．【解答】解：﹣37的相反数是37．故选：C．2．（3分）如图，AB∥CD，BC∥EF．若∠1＝58°，则∠2的大小为（）A．120°B．122°C．132°D．148°【解答】解：∵AB∥CD，∠1＝58°，∴∠C＝∠1＝58°，∵BC∥EF，∴∠CGF＝∠C＝58°，∴∠2＝180°﹣∠CGF＝180°﹣58°＝122°，故选：B．3．（3分）计算：2x•（﹣3x2y3）＝（）A．﹣6x3y3B．6x3y3C．﹣6x2y3D．18x3y3【解答】解：2x•（﹣3x2y3）＝﹣6x3y3．故选：A．4．（3分）在下列条件中，能够判定▱ABCD为矩形的是（）A．AB＝AD B．AC⊥BD C．AB＝AC D．AC＝BD【解答】解：A．∵▱ABCD中，AB＝AD，∴▱ABCD是菱形，故选项A不符合题意；B．∵▱ABCD中，AC⊥BD，∴▱ABCD是菱形，故选项B不符合题意；C．▱ABCD中，AB＝AC，不能判定▱ABCD是矩形，故选项C不符合题意；D．∵▱ABCD中，AC＝BD，∴▱ABCD是矩形，故选项D符合题意；故选：D．5．（3分）如图，AD是△ABC的高．若BD＝2CD＝6，tan C＝2，则边AB的长为（）A．3B．3C．6D．3【解答】解：∵BD＝2CD＝6，∴CD＝3，BD＝6，∵tan C＝＝2，∴AD＝6，∴AB＝AD＝6故选：C．6．（3分）在同一平面直角坐标系中，直线y＝﹣x+4与y＝2x+m相交于点P（3，n），则关于x，y 的方程组的解为（）A．B．C．D．【解答】解：将点P（3，n）代入y＝﹣x+4，得n＝﹣3+4＝1，∴P（3，1），∴原方程组的解为，故选：B．7．（3分）如图，△ABC内接于⊙O，∠C＝46°，连接OA，则∠OAB＝（）A．44°B．45°C．54°D．67°【解答】解：如图，连接OB，∵∠C＝46°，∴∠AOB＝2∠C＝92°，∵OA＝OB，∴∠OAB＝＝44°．故选：A．8．（3分）已知二次函数y＝x2﹣2x﹣3的自变量x1，x2，x3对应的函数值分别为y1，y2，y3．当﹣1＜x 1＜0，1＜x2＜2，x3＞3时，y1，y2，y3三者之间的大小关系是（）A．y1＜y2＜y3B．y2＜y3＜y1C．y3＜y1＜y2D．y2＜y1＜y3【解答】解：∵抛物线y＝x2﹣2x﹣3＝（x﹣1）2﹣4，∴对称轴x＝1，顶点坐标为（1，﹣4），当y＝0时，（x﹣1）2﹣4＝0，解得x＝﹣1或x＝3，∴抛物线与x轴的两个交点坐标为：（﹣1，0），（3，0），∴当﹣1＜x1＜0，1＜x2＜2，x3＞3时，y2＜y1＜y3，故选：D．二、填空题（共5小题，每小题3分，计15分）9．（3分）计算：3﹣＝﹣2．【解答】解：原式＝3﹣5＝﹣2．故答案为：﹣2．10．（3分）实数a，b在数轴上对应点的位置如图所示，则a＜﹣b．（填“＞”“＝”或“＜”）【解答】解：∵b 与﹣b 互为相反数∴b 与﹣b 关于原点对称，即﹣b 位于3和4之间∵a 位于﹣b 左侧，∴a ＜﹣b ，故答案为：＜．11．（3分）在20世纪70年代，我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”，在全国大规模推广，取得了很大成果．如图，利用黄金分割法，所作EF 将矩形窗框ABCD 分为上下两部分，其中E 为边AB 的黄金分割点，即BE 2＝AE •AB ．已知AB 为2米，则线段BE 的长为（﹣1+）米．【解答】解：∵BE 2＝AE •AB ，设BE ＝x ，则AE ＝（2﹣x ），∵AB ＝2，∴x 2＝2（2﹣x ），即x 2+2x ﹣4＝0，解得：x 1＝﹣1，x 2＝﹣1﹣（舍去），∴线段BE 的长为（﹣1+）米．故答案为：（﹣1+）．12．（3分）已知点A （﹣2，m ）在一个反比例函数的图象上，点A '与点A 关于y 轴对称．若点A '在正比例函数y ＝x 的图象上，则这个反比例函数的表达式为y ＝﹣．【解答】解：∵点A '与点A 关于y 轴对称，点A （﹣2，m ），∴点A '（2，m ），∵点A '在正比例函数y ＝x 的图象上，∴m ＝＝1，∴A （﹣2，1），∵点A （﹣2，1）在一个反比例函数的图象上，∴反比例函数的表达式为y＝﹣，故答案为：y＝﹣．13．（3分）如图，在菱形ABCD中，AB＝4，BD＝7．若M、N分别是边AD、BC上的动点，且AM＝BN，作ME⊥BD，NF⊥BD，垂足分别为E、F，则ME+NF的值为．【解答】解：连接AC交BD于O，∵四边形ABCD为菱形，∴BD⊥AC，OB＝OD＝，OA＝OC，由勾股定理得：OA＝＝＝，∵ME⊥BD，AO⊥BD，∴ME∥AO，∴△DEM∽△DOA，∴＝，即＝，解得：ME＝，同理可得：NF＝，∴ME+NF＝，故答案为：．三、解答题（共13小题，计81分．解答应写出过程）14．（5分）计算：5×（﹣3）+|﹣|﹣（）0．【解答】解：5×（﹣3）+|﹣|﹣（）0＝﹣15+﹣1＝﹣16+．15．（5分）解不等式组：．【解答】解：由x+2＞﹣1，得：x＞﹣3，由x﹣5≤3（x﹣1），得：x≥﹣1，则不等式组的解集为x≥﹣1．16．（5分）化简：（+1）÷．【解答】解：（+1）÷＝•＝＝a+1．17．（5分）如图，已知△ABC，CA＝CB，∠ACD是△ABC的一个外角．请用尺规作图法，求作射线CP，使CP∥AB．（保留作图痕迹，不写作法）【解答】解：如图，射线CP即为所求．18．（5分）如图，在△ABC中，点D在边BC上，CD＝AB，DE∥AB，∠DCE＝∠A．求证：DE＝BC．【解答】证明：∵DE∥AB，∴∠EDC＝∠B，在△CDE和△ABC中，，∴△CDE≌△ABC（ASA），∴DE＝BC．19．（5分）如图，△ABC的顶点坐标分别为A（﹣2，3），B（﹣3，0），C（﹣1，﹣1）．将△ABC平移后得到△A'B'C'，且点A的对应点是A'（2，3），点B、C的对应点分别是B'、C'．（1）点A、A'之间的距离是4；（2）请在图中画出△A'B'C'．【解答】解：（1）∵A（﹣2，3），A'（2，3），∴点A、A'之间的距离是2﹣（﹣2）＝4，故答案为：4；（2）如图所示，△A'B'C'即为所求．20．（5分）有五个封装后外观完全相同的纸箱，且每个纸箱内各装有一个西瓜，其中，所装西瓜的重量分别为6kg，6kg，7kg，7kg，8kg．现将这五个纸箱随机摆放．（1）若从这五个纸箱中随机选1个，则所选纸箱里西瓜的重量为6kg的概率是；（2）若从这五个纸箱中随机选2个，请利用列表或画树状图的方法，求所选两个纸箱里西瓜的重量之和为15kg的概率．【解答】解：（1）若从这五个纸箱中随机选1个，则所选纸箱里西瓜的重量为6kg的概率是，故答案为：；（2）画树状图如下：共有20种等可能的结果，其中所选两个纸箱里西瓜的重量之和为15kg的结果有4种，∴所选两个纸箱里西瓜的重量之和为15kg的概率为＝．21．（6分）小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高．如图所示，在某一时刻，他们在阳光下，分别测得该建筑物OB的影长OC为16米，OA的影长OD为20米，小明的影长FG 为2.4米，其中O、C、D、F、G五点在同一直线上，A、B、O三点在同一直线上，且AO⊥OD，EF ⊥FG．已知小明的身高EF为1.8米，求旗杆的高AB．【解答】解：解法一：∵AD∥EG，∴∠ADO＝∠EGF，∵∠AOD＝∠EFG＝90°，∴△AOD∽△EFG，∴＝，即＝，∴AO＝15，∵AD∥BC，∴△BOC∽△AOD，∴＝，即＝，∴BO＝12，∴AB＝AO﹣BO＝15﹣12＝3（米）；解法二：如图，过点C作CM⊥OD于C，交AD于M，∵△EGF∽△MDC，∴＝，即＝，∴CM＝3，即AB＝CM＝3（米），答：旗杆的高AB是3米．22．（7分）如图，是一个“函数求值机”的示意图，其中y是x的函数．下面表格中，是通过该“函数求值机”得到的几组x与y的对应值．输入x…﹣6﹣4﹣202…输出y…﹣6﹣22616…根据以上信息，解答下列问题：（1）当输入的x值为1时，输出的y值为8；（2）求k，b的值；（3）当输出的y值为0时，求输入的x值．【解答】解：（1）当输入的x值为1时，输出的y值为y＝8x＝8×1＝8，故答案为：8；（2）将（﹣2，2）（0，6）代入y＝kx+b得，解得；（3）令y＝0，由y＝8x得0＝8x，∴x＝0＜1（舍去），由y＝2x+6，得0＝2x+6，∴x＝﹣3＜1，∴输出的y值为0时，输入的x值为﹣3．23．（7分）某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在本校随机调查了100名学生的“劳动时间”，并进行统计，绘制了如下统计表：组别“劳动时间”t/分钟频数组内学生的平均“劳动时间”/分钟A t＜60850B60≤t＜901675C90≤t＜12040105D t≥12036150根据上述信息，解答下列问题：（1）这100名学生的“劳动时间”的中位数落在C组；（2）求这100名学生的平均“劳动时间”；（3）若该校有1200名学生，请估计在该校学生中，“劳动时间”不少于90分钟的人数．【解答】解：（1）把100名学生的“劳动时间”从小到大排列，排在中间的两个数均在C组，故这100名学生的“劳动时间”的中位数落在C组，故答案为：C；（2）＝×（50×8+75×16+105×40+150×36）＝112（分钟），答：这100名学生的平均“劳动时间”为112分钟；（3）1200×＝912（人），答：估计在该校学生中，“劳动时间”不少于90分钟的人数为912人．24．（8分）如图，AB是⊙O的直径，AM是⊙O的切线，AC、CD是⊙O的弦，且CD⊥AB，垂足为E，连接BD并延长，交AM于点P．（1）求证：∠CAB＝∠APB；（2）若⊙O的半径r＝5，AC＝8，求线段PD的长．【解答】（1）证明：∵AM是⊙O的切线，∴∠BAM＝90°，∵∠CEA＝90°，∴AM∥CD，∴∠CDB＝∠APB，∵∠CAB＝∠CDB，∴∠CAB＝∠APB．（2）解：如图，连接AD，∵AB是直径，∴∠CDB+∠ADC＝90°，∵∠CAB+∠C＝90°，∠CDB＝∠CAB，∴∠ADC＝∠C，∴AD＝AC＝8，∵AB＝10，∴BD＝6，∵∠BAD+∠DAP＝90°，∠PAD+∠APD＝90°，∴∠APB＝∠DAB，∵∠BDA＝∠BAP∴△ADB∽△PAB，∴＝，∴PB＝＝＝，∴DP＝﹣6＝．故答案为：．25．（8分）现要修建一条隧道，其截面为抛物线型，如图所示，线段OE表示水平的路面，以O为坐标原点，以OE所在直线为x轴，以过点O垂直于x轴的直线为y轴，建立平面直角坐标系．根据设计要求：OE＝10m，该抛物线的顶点P到OE的距离为9m．（1）求满足设计要求的抛物线的函数表达式；（2）现需在这一隧道内壁上安装照明灯，如图所示，即在该抛物线上的点A、B处分别安装照明灯．已知点A、B到OE的距离均为6m，求点A、B的坐标．【解答】解：（1）由题意抛物线的顶点P（5，9），∴可以假设抛物线的解析式为y＝a（x﹣5）2+9，把（0，0）代入，可得a＝﹣，∴抛物线的解析式为y＝﹣（x﹣5）2+9；（2）令y＝6，得﹣（x﹣5）2+9＝6，解得x1＝+5，x2＝﹣+5，∴A（5﹣，6），B（5+，6）．26．（10分）问题提出（1）如图1，AD是等边△ABC的中线，点P在AD的延长线上，且AP＝AC，则∠APC的度数为75°．问题探究（2）如图2，在△ABC中，CA＝CB＝6，∠C＝120°．过点A作AP∥BC，且AP＝BC，过点P作直线l⊥BC，分别交AB、BC于点O、E，求四边形OECA的面积．问题解决（3）如图3，现有一块△ABC型板材，∠ACB为钝角，∠BAC＝45°．工人师傅想用这块板材裁出一个△ABP型部件，并要求∠BAP＝15°，AP＝AC．工人师傅在这块板材上的作法如下：①以点C为圆心，以CA长为半径画弧，交AB于点D，连接CD；②作CD的垂直平分线l，与CD交于点E；③以点A为圆心，以AC长为半径画弧，交直线l于点P，连接AP、BP，得△ABP．请问，若按上述作法，裁得的△ABP型部件是否符合要求？请证明你的结论．【解答】解：（1）∵△ABC为等边三角形，∴AB＝AC，∠BAC＝60°，∵AD是等边△ABC的中线，∴∠PAC＝∠BAC＝30°，∵AP＝AC，∴∠APC＝×（180°﹣30°）＝75°，故答案为：75°；（2）如图2，连接PB，∵AP∥BC，AP＝BC，∴四边形PBCA为平行四边形，∵CA＝CB，∴平行四边形PBCA为菱形，∴PB＝AC＝6，∠PBC＝180°﹣∠C＝60°，∴BE＝PB•cos∠PBC＝3，PE＝PB•sin∠PBC＝3，∵CA＝CB，∠C＝120°，∴∠ABC＝30°，∴OE＝BE•tan∠ABC＝，∴S四边形OECA ＝S△ABC﹣S△OBE＝×6×3﹣×3×＝；（3）符合要求，理由如下：如图3，过点A作CD的平行线，过点D作AC的平行线，两条平行线交于点F，∵CA＝CD，∠DAC＝45°，∴∠ACD＝90°，∴四边形FDCA为正方形，∵PE是CD的垂直平分线，∴PE是AF的垂直平分线，∴PF＝PA，∵AP＝AC，∴PF＝PA＝AF，∴△PAF为等边三角形，∴∠PAF＝60°，∴∠BAP＝60°﹣45°＝15°，∴裁得的△ABP型部件符合要求．第21页（共21页）。

中学英语试卷 B姓名：准考证号：说明：1．答题前，请将你的姓名和准考证号认真填涂在试卷和答题卡上。

2．全卷分为“听力”、“阅读”和“写作”三部分，共10页。

3．选择题的答案用铅笔涂在答题卡上，非选择题的答案写在答题卡上。

4．考试时间为90分钟，请合理安排答题时间。

5．考试结束后，请将试卷和答题卡一并交回。

PART ONE LISTENINGTask 1 Listen and chooseExampleYou will hear: “Hello, I’m Liu Hua. I like sports and I often wear a T-shirt.”You will read:0 Which boy is Liu Hua?[A] [B] [C]The boy in Picture [B] is wearing a T-shirt. The answer is [8].Listen and answer Question 1.1 .What did Ellen make?[A] [B] [C]Listen and answer Question 2.2. Where are Bob and Mike?Listen and answer Question 3.3. How many brothers does the girl have?[A] [B] [C]Listen and answer Question 4,5and 6.4 .What will Tom do this summer vacation?[A]Visit his grandmother. [B]Visit a city. [C]Stay at home.5. Why does Tom decide to take a ship this year?[A]It is fast. [B]It is cheap. [C]It is enjoyable.6. How long will it take to get there by ship?[A] It is fast. [B] About 4 hours. [C] About 5 hours.Listen and answer Questions 7,8and 9.7. Where is the boy going?[A] To the theatre. [B] To his school. [C] To the bank.8. When will the next train leave?[A] In 20 minutes. [B] In 30 minutes. [C] In 40 minutes.9. Which line should the boy follow to catch his train?[A] The red line. [B] The yellow line. [C] The orange line.Listen and answer Questions 10,11and 12.10. What is the woman doing this evening?[A] Having a meeting. [B] Writing a report. [C] Buying the tickets.11. What is the man planning to do tomorrow evening?[A] Go to a party. [B] See a doctor. [C] Have dinner with parents.12. When will they see the movie?[A] On Friday. [B] On Saturday. [C] On Sunday.Task2 Look, listen and matchExampleYou will hear: “In the wall opposite the door is a big bright window.”You know “O” is the window. The answer is [E][A] [B] [C] [D] [E] Example O [E]13.14.15.16.Task 3 Listen and writeExampleYou will hear: “Good morning. I’d like to see Doctor Lee and have a check-up for my teeth.”You will read: “O Purpose: ”.You should write “Check-up” on the line.PART TWO READINGTask1 Read and match[A] [B] [C] [D] [E] Example0 [E] It is a building where you can buy stamps, mail letters and parcels.22. It is a place where you can keep your money in an account.23. It is a place where you can buy and cat a meal.24. It is a building where people can do physical exercise to keep fit.25. It is a public building where interesting and valuable things are kept and shown. Task2 Read and chooseALewis Carroll, who was named Charles Lutwidge Dodgson at birth, hada terrible problem. He 26 speak as well as other children. Because of thisproblem, even as an adult, Charles felt 27 around children than adults.Charles loved to 28 and write stories, and he found that children loved tohear his stories.On July 4,1862,Charles went on a picnic with 29 friends up the IsisRiver. One of the children on the picnic 30 a ten-year-old girl named Alice. She begged Charles to tell 31 one of his stories. So he began telling her 32 a young girl named Alice and her adventures underground.At the end of 33 day, Alice told Charles that she hoped he would write Alice’s stories down for her. Charles promised her that he would try. Three years later to that very day, Alice 34 her very own copy of Alice’s Adventures in Wonderland. It wasn’t the first book that Charles wrote, 35 it was the first book that he wrote under the name Lewis Carroll.26. [A] couldn’t[B] shouldn’t[C] wouldn’t27. [A] comfortable [B] more comfortable [C] the most comfortable28. [A] tell [B] tells [C] telling29 .[A] some [B] any [C] one30. [A] is [B] was [C] were31. [A] she [B] her [C] hers32. [A] about [B] of [C] in33. [A] a [B] an [C] the34 .[A] receive [B] receives [C] received35. [A] and [B] but [C] soB“Ring…”the bell rang loudly. Everybody took their bags and got rea dy to go home. Then, they lined up in two rows and walked out of the classroom. Usually David’s mother would take him home from school, but today she was not there. David waited for 15 minutes be walked home.When he reached home, he knocked on the door as he did not bring his keys. Surprisingly,no one answered the door. David thought his mother was asleep so he waited patiently for his mother. After a few minutes there was still on response.David knocked again but still no one answered the door. Just as he was about to go to the nearby coffee shop where his father worked to get the keys, he heard the friendly voice of his neighbor, John, David told him that no one was home and John’s mother suggested that David stay in their house till his mother came back. David and John played happily till evening when David’s mother came back.David thanked John and his family before he went back into his house. David’s mother explained to David that she a bad pain in her back and she had to see a doctor. From this experience, David learnt an important lesson, “Neighbors are people who help each other.”36. With whom did David usually go home?[A]With his mother. [B]With his father.[C]By himself. [D]With his classmates.37 .How did David go home when his mother d idn’t come?[A]By bide. [B]By school bus. [C]On foot. [D]By car.38. What did David go home when his mother didn’t come?[A]His mother was in the bedroom. [B]John was waiting in his house.[C]Nobody was at home. [D]He lost his keys.39. Why did David want to go to the coffee shop?[A]To drink coffee. [B]To fetch the key.[C]To meet his friends. [D]To see his mother.40. Where did David’s mother go?[A]To a hospital. [B]TO an important lesson.[C]To a neighbour’s horse. [D]To a nearby shop.CVisiting PetsKim Thomas had a very bad car accident. She was in hospital and felt lonely. Life became difficult for her. Then one day, Bonnie came to her room. She sat quietly on Kim’s bed. She stayed with Kim when she slept, too. Kim felt better when Bonnie came to see her.People take good care of their pers. But some pets, like Bonnie, can take care of people now. this is called pet therapy. The pets visit sick people in hospitals. Some doctors believe it is very helpful. At Edward Hospital in the U.S., doctors think that the pets help patients, or the sick people, feel better. They bring animals to the patients for visits. The patients feel calm when the pets visit them. They smile more, too. Some pets also go to nursing homes to visit elderly people. The pets are happy to see the people. The elderly people are happy to see the pets, too.Kim Thomas got better fast. She left the hospital a few weeks after. The doctors believe that Bonnie helped Kim. Kim agrees and she doesn’t want to leave the dog. Today, only a few doctors use pet therapy. In the future, more doctors will use pets to help their patients. And they will use many different animals such as cats, dogs, and birds.41.Why was Kim in hospital?[A]She felt sick of being alone. [B]She was hit by a car.[C]She was bitten by a dog. [D]She had very bad cold.42 .What does “pet therapy” in the second paragraph mean?[A]people care for animals to home. [B]People visit animals in the zoo.[C]Animals help people feel better. [D]Animals live together with people.43 .What do doctors at Edward Hospital do?[A]They ring pets to sick people.[B]They want their patients to keep pets.[C]They help the old in nursing homes.[D]They make the elderly people happy.44 .who was Bonnie?[A]A nurse. [B]A doctor. [C]A cat. [D]A dog.45 .What’s the writer’s main purpose of writing this passage?[A]To help Kim Thomas. [B]To introduce Bonnie.[C]To introduce “pet therapy”.[D]To help Edward Hospital.Task3 Read and writeAnswer each of the following questions in No More Than 4 Words.46. When will the opening concert be held?47. why didn’t Mrs. Butl er get a ticket?48. What is the advice from the ticket office?49. Until when will the office keep the tickets for Mrs. Butler?50 .Who wrote the letter?PART THREE WRITINGTask 1 Make up sentencesExampleO gets up he early in the morningHe gets up early in the morning.51. or traveling are you by train by air52. have seven o’clock about breakfast usually at I53 .are many in the supermarket there people at the weekends54. science museum to and my parents last Sunday I the went55. at the door they watching were when knocked someone TVTask2 Write a diary56. Write a diary about your visit to your friend in the hospital with the help of the pictures (in at least 50 words).。

2020年重庆市中考数学试卷（B 卷）一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A ，B ，C ，D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．1．（4分）5的倒数是（ ）A ．5B ．C ．﹣5D ．15-152．（4分）围成下列立体图形的各个面中，每个面都是平的是（ ）A ．长方体B ．圆柱体C ．球体D ．圆锥体3．（4分）计算a •a 2结果正确的是（ ）A ．aB ．a 2C ．a 3D ．a 44．（4分）如图，AB 是⊙O 的切线，A 为切点，连接OA ，OB ．若∠B ＝35°，则∠AOB 的度数为（ ）A ．65°B ．55°C ．45°D ．35°5．（4分）已知a +b ＝4，则代数式1的值为（ ）+a 2+b 2A ．3B ．1C ．0D ．﹣16．（4分）如图，△ABC 与△DEF 位似，点O 为位似中心．已知OA ：OD ＝1：2，则△ABC 与△DEF 的面积比为（ ）A．1：2B．1：3C．1：4D．1：57．（4分）小明准备用40元钱购买作业本和签字笔．已知每个作业本6元，每支签字笔2.2元，小明买了7支签字笔，他最多还可以买的作业本个数为（ ）A．5B．4C．3D．28．（4分）下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规律排列下去，第⑥个图形中实心圆点的个数为（ ）A．18B．19C．20D．219．（4分）如图，垂直于水平面的5G信号塔AB建在垂直于水平面的悬崖边B点处，某测量员从山脚C点出发沿水平方向前行78米到D点（点A，B，C在同一直线上），再沿斜坡DE方向前行78米到E点（点A，B，C，D，E在同一平面内），在点E处测得5G信号塔顶端A的仰角为43°，悬崖BC的高为144.5米，斜坡DE的坡度（或坡比）i＝1：2.4，则信号塔AB的高度约为（ ）（参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）A．23米B．24米C．24.5米D．25米10．（4分）若关于x 的一元一次不等式组的解集为x ≥5，且关于{2x -1≤3(x -2)，x ‒a 2＞1y 的分式方程1有非负整数解，则符合条件的所有整数a 的和为（ ）y y ‒2+a 2‒y =‒A ．﹣1B ．﹣2C ．﹣3D ．011．（4分）如图，在△ABC 中，AC ＝2，∠ABC ＝45°，∠BAC ＝15°，将△ACB 沿直2线AC 翻折至△ABC 所在的平面内，得△ACD ．过点A 作AE ，使∠DAE ＝∠DAC ，与CD 的延长线交于点E ，连接BE ，则线段BE 的长为（ ）A ．B ．3C ．2D ．46312．（4分）如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （﹣2，3），AD ＝5，若反比例函数y （k ＞0，x ＞0）的图象经过点B ，=k x则k 的值为（ ）A ．B ．8C ．10D ．163323二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上．13．（4分）计算：（）﹣1 ．15-4=14．（4分）经过多年的精准扶贫，截至2019年底，我国的农村贫困人口减少了约94000000人．请把数94000000用科学记数法表示为 ．15．（4分）盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字1，2，3，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为奇数的概率是 ．16．（4分）如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，∠ABC ＝120°，AB ＝2，以点O 为圆心，OB 长为半径画弧，分别与菱形的边相交，则图中阴影部分的面积3为 ．（结果保留π）17．（4分）周末，自行车骑行爱好者甲、乙两人相约沿同一路线从A 地出发前往B 地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发5分钟．乙骑行25分钟后，甲以原速的继续骑行，经过一段时间，甲先到达B 地，乙一直保持原速前往B 85地．在此过程中，甲、乙两人相距的路程y （单位：米）与乙骑行的时间x （单位：分钟）之间的关系如图所示，则乙比甲晚 分钟到达B 地．18．（4分）为刺激顾客到实体店消费，某商场决定在星期六开展促销活动．活动方案如下：在商场收银台旁放置一个不透明的箱子，箱子里有红、黄、绿三种颜色的球各一个（除颜色外大小、形状、质地等完全相同），顾客购买的商品达到一定金额可获得一次摸球机会，摸中红、黄、绿三种颜色的球可分别返还现金50元、30元、10元．商场分三个时段统计摸球次数和返现金额，汇总统计结果为：第二时段摸到红球次数为第一时段的3倍，摸到黄球次数为第一时段的2倍，摸到绿球次数为第一时段的4倍；第三时段摸到红球次数与第一时段相同，摸到黄球次数为第一时段的4倍，摸到绿球次数为第一时段的2倍，三个时段返现总金额为2510元，第三时段返现金额比第一时段多420元，则第二时段返现金额为 元．三、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程写在答题卡中对应的位置上．19．（10分）计算：（1）（x +y ）2+y （3x ﹣y ）；（2）（a ）．4‒a 2a ‒1+÷a 2‒16a ‒120．（10分）如图，在平行四边形ABCD 中，AE ，CF 分别平分∠BAD 和∠DCB ，交对角线BD 于点E ，F ．（1）若∠BCF ＝60°，求∠ABC 的度数；（2）求证：BE ＝DF ．21．（10分）每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：八年级抽取的学生的竞赛成绩：4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．七、八年级抽取的学生的竞赛成绩统计表 年级七年级八年级平均数7.47.4中位数a b 众数7c 合格率85%90%根据以上信息，解答下列问题：（1）填空：a ＝ ，b ＝ ，c ＝ ；（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．22．（10分）在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数﹣﹣“好数”．定义：对于三位自然数n ，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数n 为“好数”．例如：426是“好数”，因为4，2，6都不为0，且4+2＝6，6能被6整除；643不是“好数”，因为6+4＝10，10不能被3整除．（1）判断312，675是否是“好数”？并说明理由；（2）求出百位数字比十位数字大5的所有“好数”的个数，并说明理由．23．（10分）探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，请画出函数y 的图象=-12x 2+2并探究该函数的性质． x…﹣4﹣3﹣2﹣101234…y … -23a ﹣2﹣4b ﹣4﹣2 -1211 -23…（1）列表，写出表中a ，b 的值：a ＝ ，b ＝ ；描点、连线，在所给的平面直角坐标系中画出该函数的图象．（2）观察函数图象，判断下列关于函数性质的结论是否正确（在答题卡相应位置正确的用“√”作答，错误的用“×”作答）：①函数y 的图象关于y 轴对称；=-12x 2+2②当x ＝0时，函数y 有最小值，最小值为﹣6；=-12x 2+2③在自变量的取值范围内函数y 的值随自变量x 的增大而减小．（3）已知函数y x 的图象如图所示，结合你所画的函数图象，直接写出不=-23-103等式x 的解集．-12x 2+2＜‒23-10324．（10分）为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对A ，B 两个玉米品种进行实验种植对比研究．去年A 、B 两个品种各种植了10亩．收获后A 、B 两个品种的售价均为2.4元/kg ，且B 品种的平均亩产量比A 品种高100千克，A 、B 两个品种全部售出后总收入为21600元．（1）求A 、B 两个品种去年平均亩产量分别是多少千克？（2）今年，科技小组优化了玉米的种植方法，在保持去年种植面积不变的情况下，预计A 、B 两个品种平均亩产量将在去年的基础上分别增加a %和2a %．由于B 品种深受市场欢迎，预计每千克售价将在去年的基础上上涨a %，而A 品种的售价保持不变，A 、B 两个品种全部售出后总收入将增加a %．求a 的值．20925．（10分）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +2（a ≠0）与y 轴交于点C ，与x 轴交于A ，B 两点（点A 在点B 的左侧），且A 点坐标为（，0），直线BC 的-2解析式为y x +2．=-23（1）求抛物线的解析式；（2）过点A 作AD ∥BC ，交抛物线于点D ，点E 为直线BC 上方抛物线上一动点，连接CE ，EB ，BD ，DC ．求四边形BECD 面积的最大值及相应点E 的坐标；（3）将抛物线y ＝ax 2+bx +2（a ≠0）向左平移个单位，已知点M 为抛物线y ＝2ax 2+bx +2（a ≠0）的对称轴上一动点，点N 为平移后的抛物线上一动点．在（2）中，当四边形BECD 的面积最大时，是否存在以A ，E ，M ，N 为顶点的四边形为平行四边形？若存在，直接写出点N 的坐标；若不存在，请说明理由．四、解答题：（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．26．（8分）△ABC为等边三角形，AB＝8，AD⊥BC于点D，E为线段AD上一点，AE＝2 3．以AE为边在直线AD右侧构造等边三角形AEF，连接CE，N为CE的中点．（1）如图1，EF与AC交于点G，连接NG，求线段NG的长；（2）如图2，将△AEF绕点A逆时针旋转，旋转角为α，M为线段EF的中点，连接DN，MN．当30°＜α＜120°时，猜想∠DNM的大小是否为定值，并证明你的结论；（3）连接BN，在△AEF绕点A逆时针旋转过程中，当线段BN最大时，请直接写出△ADN的面积．2020年重庆市中考数学试卷（B 卷）参考答案与试题解析一、选择题：（本大题12个小题，每小题4分，共48分）在每个小题的下面，都给出了代号为A ，B ，C ，D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑．1．（4分）5的倒数是（ ）A ．5B ．C ．﹣5D ．15-15【解答】解：5得倒数是，15故选：B ．2．（4分）围成下列立体图形的各个面中，每个面都是平的是（ ）A ．长方体B ．圆柱体C ．球体D ．圆锥体【解答】解：A 、六个面都是平面，故本选项正确；B 、侧面不是平面，故本选项错误；C 、球面不是平面，故本选项错误；D 、侧面不是平面，故本选项错误；故选：A ．3．（4分）计算a •a 2结果正确的是（ ）A ．aB ．a 2C ．a 3D ．a 4【解答】解：a •a 2＝a 1+2＝a 3．故选：C ．4．（4分）如图，AB 是⊙O 的切线，A 为切点，连接OA ，OB ．若∠B ＝35°，则∠AOB 的度数为（ ）A ．65°B ．55°C ．45°D ．35°【解答】解：∵AB 是⊙O 的切线，∴OA ⊥AB ，∴∠OAB ＝90°，∴∠AOB ＝90°﹣∠B ＝55°，故选：B ．5．（4分）已知a +b ＝4，则代数式1的值为（ ）+a 2+b 2A ．3B ．1C ．0D ．﹣1【解答】解：当a +b ＝4时，原式＝1（a +b ）+12＝14+12×＝1+2＝3，故选：A ．6．（4分）如图，△ABC 与△DEF 位似，点O 为位似中心．已知OA ：OD ＝1：2，则△ABC 与△DEF 的面积比为（ ）A ．1：2B ．1：3C ．1：4D ．1：5【解答】解：∵△ABC 与△DEF 是位似图形，OA ：OD ＝1：2，∴△ABC 与△DEF 的位似比是1：2．∴△ABC 与△DEF 的相似比为1：2，∴△ABC 与△DEF 的面积比为1：4，故选：C ．7．（4分）小明准备用40元钱购买作业本和签字笔．已知每个作业本6元，每支签字笔2.2元，小明买了7支签字笔，他最多还可以买的作业本个数为（ ）A ．5B ．4C ．3D ．2【解答】解：设还可以买x 个作业本，依题意，得：2.2×7+6x ≤40，解得：x ≤4．110又∵x 为正整数，∴x 的最大值为4．故选：B ．8．（4分）下列图形都是由同样大小的实心圆点按一定规律组成的，其中第①个图形一共有5个实心圆点，第②个图形一共有8个实心圆点，第③个图形一共有11个实心圆点，…，按此规律排列下去，第⑥个图形中实心圆点的个数为（ ）A ．18B ．19C ．20D ．21【解答】解：∵第①个图形中实心圆点的个数5＝2×1+3，第②个图形中实心圆点的个数8＝2×2+4，第③个图形中实心圆点的个数11＝2×3+5，……∴第⑥个图形中实心圆点的个数为2×6+8＝20，故选：C ．9．（4分）如图，垂直于水平面的5G 信号塔AB 建在垂直于水平面的悬崖边B 点处，某测量员从山脚C 点出发沿水平方向前行78米到D 点（点A ，B ，C 在同一直线上），再沿斜坡DE 方向前行78米到E 点（点A ，B ，C ，D ，E 在同一平面内），在点E 处测得5G 信号塔顶端A 的仰角为43°，悬崖BC 的高为144.5米，斜坡DE 的坡度（或坡比）i＝1：2.4，则信号塔AB的高度约为（ ）（参考数据：sin43°≈0.68，cos43°≈0.73，tan43°≈0.93）A．23米B．24米C．24.5米D．25米【解答】解：过点E作EF⊥DC交DC的延长线于点F，过点E作EM⊥AC于点M，∵斜坡DE的坡度（或坡比）i＝1：2.4，BE＝CD＝78米，∴设EF＝x，则DF＝2.4x．在Rt△DEF中，∵EF2+DF2＝DE2，即x2+（2.4x）2＝782，解得x＝30，∴EF＝30米，DF＝72米，∴CF＝DF+DC＝72+78＝150米．∵EM⊥AC，AC⊥CD，EF⊥CD，∴四边形EFCM是矩形，∴EM＝CF＝150米，CM＝EF＝30米．在Rt△AEM中，∵∠AEM＝43°，∴AM＝EM•tan43°≈150×0.93＝139.5米，∴AC＝AM+CM＝139.5+30＝169.5米．∴AB＝AC﹣BC＝169.5﹣144.5＝25米．故选：D．10．（4分）若关于x 的一元一次不等式组的解集为x ≥5，且关于{2x -1≤3(x -2)，x ‒a 2＞1y 的分式方程1有非负整数解，则符合条件的所有整数a 的和为（ ）y y ‒2+a2‒y=‒A ．﹣1B ．﹣2C ．﹣3D ．0【解答】解：不等式组整理得：，{x ≥5x ＞2+a 由解集为x ≥5，得到2+a ≤5，即a ≤3，分式方程去分母得：y ﹣a ＝﹣y +2，即2y ﹣2＝a ，解得：y 1，=a2+由y 为非负整数，且y ≠2，得到a ＝0，﹣2，之和为﹣2，故选：B ．11．（4分）如图，在△ABC 中，AC ＝2，∠ABC ＝45°，∠BAC ＝15°，将△ACB 沿直2线AC 翻折至△ABC 所在的平面内，得△ACD ．过点A 作AE ，使∠DAE ＝∠DAC ，与CD 的延长线交于点E ，连接BE ，则线段BE 的长为（ ）A ．B ．3C ．2D ．463【解答】解：如图，延长BC 交AE 于H ，∵∠ABC ＝45°，∠BAC ＝15°，∴∠ACB ＝120°，∵将△ACB 沿直线AC 翻折，∴∠DAC ＝∠BAC ＝15°，∠ADC ＝∠ABC ＝45°，∠ACB ＝∠ACD ＝120°，∴∠DAE ＝∠DAC ＝15°，∴∠CAE ＝30°，∵∠ADC ＝∠DAE +∠AED ，∴∠AED ＝45°﹣15°＝30°，∴∠AED ＝∠EAC ，∴AC ＝EC ，又∵∠BCE ＝360°﹣∠ACB ﹣∠ACE ＝120°＝∠ACB ，BC ＝BC ，∴△ABC ≌△EBC （SAS ），∴AB ＝BE ，∠ABC ＝∠EBC ＝45°，∴∠ABE ＝90°，∵AB ＝BE ，∠ABC ＝∠EBC ，∴AH ＝EH ，BH ⊥AE ，∵∠CAE ＝30°，∴CH AC ，AH CH ，=12=2=3=6∴AE ＝2，6∵AB ＝BE ，∠ABE ＝90°，∴BE 2，=AE 2=3故选：C ．12．（4分）如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （﹣2，3），AD ＝5，若反比例函数y （k ＞0，x ＞0）的图象经过点B ，=kx则k 的值为（ ）A ．B ．8C ．10D ．163323【解答】解：过D 作DE ⊥x 轴于E ，过B 作BF ⊥x 轴，BH ⊥y 轴，∵点D （﹣2，3），AD ＝5，∴DE ＝3，∴AE 4，=AD 2‒DE 2=∵四边形ABCD 是矩形，∴AD ＝BC ，∴∠BCD ＝∠ADC ＝90°，∴∠DCP +∠BCH ＝∠BCH +∠CBH ＝90°，∴∠CBH ＝∠DCH ，∵∠DCG +∠CPD ＝∠APO +∠DAE ＝90°，∠CPD ＝∠APO ，∴∠DCP ＝∠DAE ，∴∠CBH ＝∠DAE ，∵∠AED ＝∠BHC ＝90°，∴△ADE ≌△BCH （AAS ），∴BH ＝AE ＝4，∵OE ＝2，∴OA ＝2，∴AF ＝2，∵∠APO +∠PAO ＝∠BAF +∠PAO ＝90°，∴∠APO ＝∠BAF ，∴△APO ∽△BAF ，∴，OP AF =OABF∴，12×32=2BF∴BF ，=83∴B （4，），83∴k ，=323故选：D ．二、填空题：（本大题6个小题，每小题4分，共24分）请将每小题的答案直接填在答题卡中对应的横线上．13．（4分）计算：（）﹣1　3　．15-4=【解答】解：原式＝5﹣2＝3，故答案为：3．14．（4分）经过多年的精准扶贫，截至2019年底，我国的农村贫困人口减少了约94000000人．请把数94000000用科学记数法表示为　9.4×107　．【解答】解：94000000＝9.4×107，故答案为：9.4×107．15．（4分）盒子里有3张形状、大小、质地完全相同的卡片，上面分别标着数字1，2，3，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为奇数的概率是 ．23【解答】解：列表如下123134235345由表可知，共有6种等可能结果，其中两次抽出的卡片上的数字之和为奇数的有4种结果，所以两次抽出的卡片上的数字之和为奇数的概率为，46=23故答案为：．2316．（4分）如图，在菱形ABCD 中，对角线AC ，BD 交于点O ，∠ABC ＝120°，AB ＝2，以点O 为圆心，OB 长为半径画弧，分别与菱形的边相交，则图中阴影部分的面积3为　3π　．（结果保留π）3‒【解答】解：如图，设连接以点O 为圆心，OB 长为半径画弧，分别与AB ，AD 相交于E ，F ，连接EO ，FO ，∵四边形ABCD 是菱形，∠ABC ＝120°，∴AC ⊥BD ，BO ＝DO ，OA ＝OC ，AB ＝AD ，∠DAB ＝60°，∴△ABD 是等边三角形，∴AB ＝BD ＝2，∠ABD ＝∠ADB ＝60°，3∴BO ＝DO ，=3∵以点O 为圆心，OB 长为半径画弧，∴BO ＝OE ＝OD ＝OF ，∴△BEO ，△DFO 是等边三角形，∴∠DOF ＝∠BOE ＝60°，∴∠EOF ＝60°，∴阴影部分的面积＝2×（S △ABD ﹣S △DFO ﹣S △BEO ﹣S 扇形OEF ）＝2×（1234×-34×33）＝3π，-34×-60°×π×3360°3‒故答案为：3π．3‒17．（4分）周末，自行车骑行爱好者甲、乙两人相约沿同一路线从A 地出发前往B 地进行骑行训练，甲、乙分别以不同的速度匀速骑行，乙比甲早出发5分钟．乙骑行25分钟后，甲以原速的继续骑行，经过一段时间，甲先到达B 地，乙一直保持原速前往B85地．在此过程中，甲、乙两人相距的路程y （单位：米）与乙骑行的时间x （单位：分钟）之间的关系如图所示，则乙比甲晚　12　分钟到达B 地．【解答】解：由题意乙的速度为1500÷5＝300（米/分），设甲的速度为x 米/分．则有：7500﹣20x ＝2500，解得x ＝250，25分钟后甲的速度为250400（米/分）．×85=由题意总里程＝250×20+61×400＝29400（米），86分钟乙的路程为86×300＝25800（米），∴12（分钟）．29400‒25800300=故答案为12．18．（4分）为刺激顾客到实体店消费，某商场决定在星期六开展促销活动．活动方案如下：在商场收银台旁放置一个不透明的箱子，箱子里有红、黄、绿三种颜色的球各一个（除颜色外大小、形状、质地等完全相同），顾客购买的商品达到一定金额可获得一次摸球机会，摸中红、黄、绿三种颜色的球可分别返还现金50元、30元、10元．商场分三个时段统计摸球次数和返现金额，汇总统计结果为：第二时段摸到红球次数为第一时段的3倍，摸到黄球次数为第一时段的2倍，摸到绿球次数为第一时段的4倍；第三时段摸到红球次数与第一时段相同，摸到黄球次数为第一时段的4倍，摸到绿球次数为第一时段的2倍，三个时段返现总金额为2510元，第三时段返现金额比第一时段多420元，则第二时段返现金额为　1230　元．【解答】解：设第一时段摸到红球x 次，摸到黄球y 次，摸到绿球z 次，（x ，y ，z 均为非负整数），则第一时段返现金额为（50x +30y +10z ），第二时段摸到红球3x 次，摸到黄球2y 次，摸到绿球4z 次，则第二时段返现金额为（50×3x +30×2y +10×4z ），第三时段摸到红球x 次，摸到黄球4y 次，摸到绿球2z 次，则第三时段返现金额为（50x +30×4y +10×2z ），∵第三时段返现金额比第一时段多420元，∴（50x +30×4y +10×2z ）﹣（50x +30y +10z ）＝420，∴z ＝42﹣9y ①，∵z 为非负整数，∴42﹣9y ≥0，∴y ，≤429∵三个时段返现总金额为2510元，∴（50x +30y +10z ）+（50x +30×4y +10×2z ）+（50x +30×4y +10×2z ）＝2510，∴25x +21y +7z ＝251②，将①代入②中，化简整理得，25x ＝42y ﹣43，∴x ④，=42y ‒4325∵x 为非负整数，∴0，42y ‒4325≥∴y ，≥4342∴y ，4342≤≤429∵y 为非负整数，∴y ＝2，34，当y ＝2时，x ，不符合题意，=4125当y ＝3时，x ，不符合题意，=8325当y ＝4时，x ＝5，则z ＝6，∴第二时段返现金额为50×3x +30×2y +10×4z ＝10（15×5+6×4+4×6）＝1230（元），故答案为：1230．三、解答题：（本大题7个小题，每小题10分，共70分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程写在答题卡中对应的位置上．19．（10分）计算：（1）（x +y ）2+y （3x ﹣y ）；（2）（a ）．4‒a 2a ‒1+÷a 2‒16a ‒1【解答】解：（1）（x +y ）2+y （3x ﹣y ），＝x 2+2xy +y 2+3xy ﹣y 2，＝x 2+5xy ；（2）（a ），4‒a 2a ‒1+÷a 2‒16a ‒1＝（），4‒a 2a ‒1+a 2‒a a ‒1×a ‒1(a +4)(a ‒4)，=4‒a a ‒1×a ‒1(a +4)(a ‒4)．=-1a +420．（10分）如图，在平行四边形ABCD 中，AE ，CF 分别平分∠BAD 和∠DCB ，交对角线BD 于点E ，F ．（1）若∠BCF ＝60°，求∠ABC 的度数；（2）求证：BE ＝DF ．【解答】解：（1）∵四边形ABCD 是平行四边形，∴AB ∥CD ，∴∠ABC +∠BCD ＝180°，∵CF 平分∠DCB ，∴∠BCD ＝2∠BCF ，∵∠BCF ＝60°，∴∠BCD ＝120°，∴∠ABC ＝180°﹣120°＝60°；（2）∵四边形ABCD 是平行四边形，∴AB ∥CD ，AB ＝CD ，∠BAD ＝∠DCB ，∴∠ABE ＝∠CDF ，∵AE ，CF 分别平分∠BAD 和∠DCB ，∴∠BAE ，∠DCF ，=12∠BAD =12∠BCD ∴∠BAE ＝∠DCE ，∴△ABE ≌△CDF （ASA ），∴BE ＝CF ．21．（10分）每年的4月15日是我国全民国家安全教育日．某中学在全校七、八年级共800名学生中开展“国家安全法”知识竞赛，并从七、八年级学生中各抽取20名学生，统计这部分学生的竞赛成绩（竞赛成绩均为整数，满分10分，6分及以上为合格）．相关数据统计、整理如下：八年级抽取的学生的竞赛成绩：4，4，6，6，6，6，7，7，7，8，8，8，8，8，8，9，9，9，10，10．七、八年级抽取的学生的竞赛成绩统计表年级七年级八年级平均数7.47.4中位数a b 众数7c 合格率85%90%根据以上信息，解答下列问题：（1）填空：a ＝　7.5　，b ＝　8　，c ＝　8　；（2）估计该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数；（3）根据以上数据分析，从一个方面评价两个年级“国家安全法”知识竞赛的学生成绩谁更优异．【解答】解：（1）由图表可得：a 7.5，b 8，c ＝8，=7+82==8+82=故答案为：7.5，8，8；（2）该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数＝800×5+540200（人），=答：该校七、八年级共800名学生中竞赛成绩达到9分及以上的人数为200人；（3）∵八年级的合格率高于七年级的合格率，∴八年级“国家安全法”知识竞赛的学生成绩更优异．22．（10分）在数的学习过程中，我们总会对其中一些具有某种特性的数充满好奇，如学习自然数时，我们发现一种特殊的自然数﹣﹣“好数”．定义：对于三位自然数n ，各位数字都不为0，且百位数字与十位数字之和恰好能被个位数字整除，则称这个自然数n 为“好数”．例如：426是“好数”，因为4，2，6都不为0，且4+2＝6，6能被6整除；643不是“好数”，因为6+4＝10，10不能被3整除．（1）判断312，675是否是“好数”？并说明理由；（2）求出百位数字比十位数字大5的所有“好数”的个数，并说明理由．【解答】解：（1）312是“好数”，因为3，1，2都不为0，且3+1＝4，6能被2整除，675不是“好数”，因为6+7＝13，13不能被5整除；（2）611，617，721，723，729，831，941共7个，理由：设十位数数字为a ，则百位数字为a +5（0＜a ≤4的整数），∴a +a +5＝2a +5，当a ＝1时，2a +5＝7，∴7能被1，7整除，∴满足条件的三位数有611，617，当a ＝2时，2a +5＝9，∴9能被1，3，9整除，∴满足条件的三位数有721，723，729，当a ＝3时，2a +5＝11，∴11能被1整除，∴满足条件的三位数有831，当a ＝4时，2a +5＝13，∴13能被1整除，∴满足条件的三位数有941，即满足条件的三位自然数为611，617，721，723，729，831，941共7个．23．（10分）探究函数性质时，我们经历了列表、描点、连线画出函数图象，观察分析图象特征，概括函数性质的过程．结合已有的学习经验，请画出函数y 的图象=-12x 2+2并探究该函数的性质． x …﹣4﹣3﹣2﹣101234…y…-23a﹣2﹣4b﹣4﹣2-1211-23…（1）列表，写出表中a ，b 的值：a ＝ ，b ＝　﹣6　；-1211描点、连线，在所给的平面直角坐标系中画出该函数的图象．（2）观察函数图象，判断下列关于函数性质的结论是否正确（在答题卡相应位置正确的用“√”作答，错误的用“×”作答）：①函数y 的图象关于y 轴对称；=-12x 2+2②当x ＝0时，函数y 有最小值，最小值为﹣6；=-12x 2+2③在自变量的取值范围内函数y 的值随自变量x 的增大而减小．（3）已知函数y x 的图象如图所示，结合你所画的函数图象，直接写出不=-23-103等式x 的解集．-12x 2+2＜‒23-103【解答】解：（1）x ＝﹣3、0分别代入y ，得a ，b =-12x 2+2=-129+2=‒1211=6，-120+2=‒故答案为，﹣6；-1211画出函数的图象如图：，故答案为，﹣6；-1211（2）根据函数图象：①函数y 的图象关于y 轴对称，说法正确；=-12x 2+2②当x ＝0时，函数y 有最小值，最小值为﹣6，说法正确；=-12x 2+2③在自变量的取值范围内函数y 的值随自变量x 的增大而减小，说法错误．（3）由图象可知：不等式x 的解集为x ＜﹣4或﹣2＜x ＜1．-12x 2+2＜‒23-10324．（10分）为响应“把中国人的饭碗牢牢端在自己手中”的号召，确保粮食安全，优选品种，提高产量，某农业科技小组对A ，B 两个玉米品种进行实验种植对比研究．去年A 、B 两个品种各种植了10亩．收获后A 、B 两个品种的售价均为2.4元/kg ，且B 品种的平均亩产量比A 品种高100千克，A 、B 两个品种全部售出后总收入为21600元．（1）求A 、B 两个品种去年平均亩产量分别是多少千克？（2）今年，科技小组优化了玉米的种植方法，在保持去年种植面积不变的情况下，预计A 、B 两个品种平均亩产量将在去年的基础上分别增加a %和2a %．由于B 品种深受市场欢迎，预计每千克售价将在去年的基础上上涨a %，而A 品种的售价保持不变，A 、B两个品种全部售出后总收入将增加a %．求a 的值．209【解答】解：（1）设A 、B 两个品种去年平均亩产量分别是x 千克和y 千克；根据题意得，，{y -x =10010×2.4(x +y )=21600解得：，{x =400y =500答：A 、B 两个品种去年平均亩产量分别是400千克和500千克；（2）2.4×400×10（1+a %）+2.4（1+a %）×500×10（1+2a %）＝21600（1a %），+209解得：a ＝0.1，答：a 的值为0.1．25．（10分）如图，在平面直角坐标系中，抛物线y ＝ax 2+bx +2（a ≠0）与y 轴交于点C ，与x 轴交于A ，B 两点（点A 在点B 的左侧），且A 点坐标为（，0），直线BC 的-2解析式为y x +2．=-23（1）求抛物线的解析式；（2）过点A 作AD ∥BC ，交抛物线于点D ，点E 为直线BC 上方抛物线上一动点，连接CE ，EB ，BD ，DC ．求四边形BECD 面积的最大值及相应点E 的坐标；（3）将抛物线y ＝ax 2+bx +2（a ≠0）向左平移个单位，已知点M 为抛物线y ＝2ax 2+bx +2（a ≠0）的对称轴上一动点，点N 为平移后的抛物线上一动点．在（2）中，当四边形BECD 的面积最大时，是否存在以A ，E ，M ，N 为顶点的四边形为平行四边形？若存在，直接写出点N 的坐标；若不存在，请说明理由．【解答】解：（1）直线BC 的解析式为y x +2，令y ＝0，则x ＝3，令x ＝0，=-232则y ＝2，故点B 、C 的坐标分别为（3，0）、（0，2）；2则y ＝ax 2+bx +2＝a （x ）（x ﹣3）＝a （x 2﹣2x ﹣6）＝ax 2﹣2a ﹣6a ，+2222即﹣6a ＝2，解得：a ，=13故抛物线的表达式为：y x 2x +2①；=-13+223（2）如图，过点B 、E 分别作y 轴的平行线分别交CD 于点H ，交BC 于点F ，∵AD ∥BC ，则设直线AD 的表达式为：y （x ）②，=-23+2联立①②并解得：x ＝4，故点D （4，），22-103由点C 、D 的坐标得，直线CD 的表达式为：y x +2，=-223当x ＝3时，y BC x +2＝﹣2，即点H （3，﹣2），故BH ＝2，2=-232设点E （x ，x 2x +2），则点F （x ，x +2），-13+223-23则四边形BECD 的面积S ＝S △BCE +S △BCD EF ×OB （x D ﹣x C ）×BH =12×+12×=12（x 2x +2x ﹣2）×342x 2+3x +4，×-13+223+232+12×2×=-222∵0，故S 有最大值，当x 时，S 的最大值为，此时点E （，）；-22＜=322252432252（3）存在，理由：y x 2x +2（x ）2，抛物线y ＝ax 2+bx +2（a ≠0）向左平移=-13+223=-13-2+83个单位，2则新抛物线的表达式为：y x 2，=-13+83点A 、E 的坐标分别为（，0）、（，）；设点M （，m ），点N （n ，s ），s -2322522=n 2；-13+83①当AE 是平行四边形的边时，点A 向右平移个单位向上平移个单位得到E ，同样点M （N ）向右平移个单位向52252522上平移个单位得到N （M ），52即±n ，2522=则s n 2或，=-13+83=‒11256故点N 的坐标为（，）或（，）；722-112-32256②当AE 是平行四边形的对角线时，由中点公式得：n ，解得：n ，-2+322=+2=-22s n 2，=-13+83=156故点N 的坐标（，）；-22156综上点N 的坐标为：（，）或（，）或（，）．722-112-32256-22156四、解答题：（本大题1个小题，共8分）解答时必须给出必要的演算过程或推理步骤，画出必要的图形（包括辅助线），请将解答过程书写在答题卡中对应的位置上．26．（8分）△ABC 为等边三角形，AB ＝8，AD ⊥BC 于点D ，E 为线段AD 上一点，AE ＝2．以AE 为边在直线AD 右侧构造等边三角形AEF ，连接CE ，N 为CE 的中点．3（1）如图1，EF 与AC 交于点G ，连接NG ，求线段NG 的长；（2）如图2，将△AEF 绕点A 逆时针旋转，旋转角为α，M 为线段EF 的中点，连接DN ，MN ．当30°＜α＜120°时，猜想∠DNM 的大小是否为定值，并证明你的结论；（3）连接BN ，在△AEF 绕点A 逆时针旋转过程中，当线段BN 最大时，请直接写出△ADN 的面积．【解答】解：（1）如图1中，连接BE ，CF ．∵△ABC 是等边三角形，AD ⊥BC ，∴AB ＝BC ＝AC ＝8，BD ＝CD ＝4，∴AD BD ＝4，=33∵AE ＝2，3∴DE ＝AE ＝2，3∴BE 2，=BD 2+DE 2=42+(23)2=7∵△ABC ，△AEF 答等边三角形，∴AB ＝AC ，AE ＝AF ，∠BAC ＝∠EAF ＝60°，∴∠BAE ＝∠CAF ，∴△BAE ≌△CAF （SAS ），∴CF ＝BE ＝2，7∵EN ＝CN ，EG ＝FG ，∴GN CF ．=12=7（2）结论：∠DNM ＝120°是定值．理由：连接BE，CF．同法可证△BAE≌△CAF（SAS），∴∠ABE＝∠ACF，∵∠ABC+∠ACB＝60°+60°＝120°，∴∠EBC+∠BCF＝∠ABC﹣∠ABE+∠ACB+∠ACF＝120°，∵EN＝NC，EM＝MF，∴MN∥CF，∴∠ENM＝∠ECM，∵BD＝DC，EN＝NC，∴DN∥BE，∴∠CDN＝∠EBC，∵∠END＝∠NDC+∠ACB，∴∠DNM＝∠DNE+∠ENM＝∠NDC+∠ACN+∠ECM＝∠EBC+∠ACB+∠ACF＝∠EBC+∠BCF＝120°．（3）如图3﹣1中，取AC的中点，连接BJ，BN．∵AJ＝CJ，EN＝NC，∴JN AE ，=12=3∵BJ ＝AD ＝4，3∴BN ≤BJ +JN ，∴BN ≤5，3∴当点N 在BJ 的延长线上时，BN 的值最大，如图3﹣2中，过点N 作NH ⊥AD 于H ，设BJ 交AD 于K ，连接AN ．∵KJ ＝AJ •tan30°，JN ，=433=3∴KN ，=733在Rt △HKN 中，∵∠NHK ＝90°，∠NKH ＝60°，∴HN ＝NK •sin60°，=733×32=72∴S △ADN •AD •NH 47．=12=12×3×72=3。

重庆市2021年中考数学试卷（B 卷）一、单选题（共12题；共24分）1.−3 相反数是（ ） A. 13 B. −3 C. −13 D. 3【答案】 D【考点】相反数及有理数的相反数【解析】【解答】解： −3 的相反数是3.故答案为：D.【分析】利用求一个数的相反数就是在这个数的前面添上“-”号，可得答案.2.不等式 x >5 的解集在数轴上表示正确的是（ ）A.B.C.D.【答案】 A【考点】在数轴上表示不等式的解集【解析】【解答】解： x >5 在数轴上表示时，其点应是空心，方向为向右，因此，综合各选项，只有A 选项符合；故答案为：A.【分析】大于向右边画，不含等号用空心，由此可得答案.3.计算 x 4÷x 结果正确的是（ ）A. x 4B. x 3C. x 2D. x【答案】 B【考点】同底数幂的除法【解析】【解答】解： x 4÷x =x 4−1=x 3 ，故答案为：B.【分析】利用同底数幂相除，底数不变，指数相减，可得答案.4.如图，在平面直角坐标系中，将 △OAB 以原点O 为位似中心放大后得到 △OCD ，若 B(0,1) ， D(0,3) ，则 △OAB 与 △OCD 的相似比是（ ）A. 2：1B. 1：2C. 3：1D. 1：3 【答案】 D【考点】相似三角形的性质，位似变换【解析】【解答】解：由B、D两点坐标可知：OB=1，OD=3；△OAB 与△OCD的相似比等于OBOD =13；故答案为：D.【分析】利用点B，D的坐标可求出OB，OD的长，利用相似三角形的性质可求出两三角形的相似比. 5.如图，AB是⊙O的直径，AC，BC是⊙O的弦，若∠A=20°，则∠B的度数为（）A. 70°B. 90°C. 40°D. 60°【答案】A【考点】三角形内角和定理，圆周角定理【解析】【解答】解：∵AB是⊙O的直径，∴∠ACB=90°，∴在Rt△ABC中，∠B=90°-∠A=70°，故答案为：A.【分析】利用直径所对的圆周角是直角，可得到∠ACB=90°，再利用三角形的内角和定理求出∠B的度数.6.下列计算中，正确的是（）A. 5√7−2√7=21B. 2+√2=2√2C. √3×√6=3√2D. √15÷√5=3【答案】C【考点】二次根式的乘除法，二次根式的加减法【解析】【解答】解：A. 5√7−2√7=3√7，原选项错误，不符合题意；B. 2和√2不是同类二次根式，不能合并，原选项错误，不符合题意；C. √3×√6=3√2，原选项正确，符合题意；D. √15÷√5=√3 ，原选项错误，不符合题意；故答案为：C.【分析】只有同类二次根式才能合并，可对A ，B 作出判断；利用二次根式的除法和乘法运算，可对C ，D 作出判断.7.小明从家出发沿笔直的公路去图书馆，在图书馆阅读书报后按原路回到家.如图，反映了小明离家的距离y （单位：km ）与时间t （单位：h ）之间的对应关系.下列描述错误．．的是（ ）A. 小明家距图书馆3kmB. 小明在图书馆阅读时间为2hC. 小明在图书馆阅读书报和往返总时间不足4hD. 小明去图书馆的速度比回家时的速度快【答案】 D【考点】通过函数图象获取信息并解决问题【解析】【解答】解：根据题意可知，函数图象中，0-1h 对应的实际意义是小明从家到图书馆的过程，走过的路程为3km ，故A 正确；1-3h 对应的实际意义是小明在图书馆阅读，即阅读时间为3-1=2h ，故B 正确；3h 后直到纵坐标为0，对应的实际意义为小明从图书馆回到家中，显然，这段时间不足1h ，从而小明在图书馆阅读书报和往返总时间不足4h ，故C 正确；显然，从图中可知小明去图书馆的速度为 3km /h ，回来时，路程同样是3km ，但用时不足1h ，则回来时的速度大于 3km /h ，即大于去时的速度，故D 错误；故答案为：D.【分析】利用函数图象及小明从家出发沿笔直的公路去图书馆，在图书馆阅读书报后按原路回到家，再对各选项逐一判断.8.如图，在 △ABC 和 △DCB 中， ∠ACB =∠DBC ，添加一个条件，不能．．证明 △ABC 和 △DCB 全等的是（ ）A. ∠ABC =∠DCBB. AB = DCC. AC =DBD. ∠A =∠D【答案】 B【考点】三角形全等的判定【解析】【解答】解：选项A ，添加 ∠ABC =∠DCB ，在 △ABC 和 △DCB 中，{∠ABC =∠DCBBC =CB∠ACB =∠DBC， ∴ △ABC ≌ △DCB （ASA ），选项B ，添加 AB = DC ，在 △ABC 和 △DCB 中， AB = DC ， BC =CB ， ∠ACB =∠DBC ，无法证明 △ABC ≌ △DCB ；选项C ，添加 AC =DB ，在 △ABC 和 △DCB 中，{BC =CB∠ACB =∠DBC AC =DB，∴ △ABC ≌ △DCB （SAS ）；选项D ，添加 ∠A =∠D ，在 △ABC 和 △DCB 中，{∠A =∠D∠ACB =∠DBC BC =CB，∴ △ABC ≌ △DCB （AAS ）；综上，只有选项B 符合题意.故答案为：B.【分析】由图形可知：隐含条件为BC=CB ，已知了∠ACB=∠DBC ，可以添加另一组对应角相等或添加边AC=DB ，再对各选项逐一判断.9.如图，把含30°的直角三角板PMN 放置在正方形ABCD 中， ∠PMN =30° ，直角顶点P 在正方形ABCD 的对角线BD 上，点M ，N 分别在AB 和CD 边上，MN 与BD 交于点O ，且点O 为MN 的中点，则 ∠AMP 的度数为（ ）A. 60°B. 65°C. 75°D. 80°【答案】 C【考点】三角形的外角性质，等腰三角形的性质，正方形的性质【解析】【解答】解：∵四边形ABCD 是正方形中，∴∠MBO=∠NDO=45°，∵点O为MN的中点∴OM=ON，∵∠MPN=90°，∴OM=OP，∴∠PMN=∠MPO=30°，∴∠MOB=∠MPO+∠PMN =60°，∴∠BMO=180°-60°-45°=75°，∠AMP=180°−75°−30°=75°，故答案为：C.【分析】利用正方形的性质可证得∠MBO=∠NDO=45°，利用直角三角形斜边上的中线等于斜边的一半，可证得OM=ON=OP，利用等边对等角可求出∠MPO的度数；再利用三角形的外角的性质求出∠MOB的度数，利用正方形的性质求出∠DBM的度数，利用三角形的内角和定理可求出∠BMO的度数，从而可求出∠AMP的度数.10.如图，在建筑物AB左侧距楼底B点水平距离150米的C处有一山坡，斜坡CD的坡度（或坡比）为i= 1:2.4，坡顶D到BC的垂直距离DE=50米（点A，B，C，D，E在同一平面内），在点D处测得建筑物顶A点的仰角为50°，则建筑物AB的高度约为（参考数据：sin50°≈0.77；cos50°≈0.64；tan50°≈1.19）A. 69.2米B. 73.1米C. 80.0米D. 85.7米【答案】 D【考点】解直角三角形的应用﹣坡度坡角问题，解直角三角形的应用﹣仰角俯角问题【解析】【解答】解：如图所示，作DF⊥AB于F点，则四边形DEBF为矩形，∴DE=BF=50,∵斜坡CD的坡度（或坡比）为i=1:2.4，∴在Rt△CED中，tan∠C=12.4=DECE=512，∵DE=50，∴CE=120，∴BE=BC−CE=150−120=30，∴ DF =30 ，在Rt △ADF 中，∠ADF=50°，∴ tan ∠ADF =tan50°=AF DF =1.19 ，将 DF =30 代入解得： AF =35.7 ，∴AB=AF+BF=35.7+50=85.7米，故答案为：D.【分析】作DF ⊥AB 于F 点，则四边形DEBF 为矩形，可求出BF 的长，利用坡度的定义，可求出CE 的长，根据BE=BC-CE ，可求出BE ，DF 的长；在Rt △ADF 中，利用解直角三角形求出AF 的长，然后根据AB=AF+BF 求出AB 的长.11.关于x 的分式方程 ax−3x−2+1=3x−12−x 的解为正数，且使关于y 的一元一次不等式组 {3y−22≤y −1y +2>a有解，则所有满足条件的整数a 的值之和是（ ）A. −5B. −4C. −3D. −2【答案】 B【考点】解分式方程，解一元一次不等式组【解析】【解答】解： ax−3x−2+1=3x−12−x ,两边同时乘以（ x −2 )，ax −3+x −2=1−3x ,(a +4)x =6 ,由于该分式方程的解为正数，∴ x =6a+4 ，其中 a +4>0，a +4≠3 ;∴ a >−4 ，且 a ≠−1 ；∵关于y 的元一次不等式组 {3y−22≤y −1①y +2>a ② 有解，由①得： y ≤0 ;由②得： y >a −2 ;∴ a −2<0 ，∴ a <2 综上可得： −4<a <2 ,且 a ≠−1 ;∴满足条件的所有整数a 为： −3，−2,0,1 ；∴它们的和为 −4 ；故答案为：B.【分析】先求出分式方程的解，根据其解为正数，可得到关于a 的不等式，可求出a 的取值范围；再求出不等式组的解集，根据不等式组有解，可得到a 的取值范围，然后求出整数a 的值.12.如图，在平面直角坐标系中，矩形ABCD 的顶点A ，B 在x 轴的正半轴上，反比例函数 y =k x(k >0,x >0) 的图象经过顶点D ，分别与对角线AC ，边BC 交于点E ，F ，连接EF ，AF.若点E 为AC 的中点， △AEF 的面积为1，则k 的值为（ ）A. 125B. 32C. 2D. 3【答案】 D【考点】反比例函数系数k 的几何意义，三角形的面积，矩形的性质【解析】【解答】解：设D 点坐标为 (a ，k a ) ，∵四边形ABCD 是矩形，则A 点坐标为 (a ，0) ，C 点纵坐标为 k a， ∵点E 为AC 的中点，则E 点纵坐标为 0+k a 2=k 2a， ∵点E 在反比例函数图象上，代入解析式得 k 2a =k x ，解得， x =2a ，∴E 点坐标为 (2a ，k 2a ) ，同理可得C 点坐标为 (3a ，k a ) ，∵点F 在反比例函数图象上，同理可得F 点坐标为 (3a ，k 3a ) ，∵点E 为AC 的中点， △AEF 的面积为1，∴ S △ACF =2 ，即 12CF ⋅AB =2 ，可得， 12(k a −k 3a )(3a −a)=2 ，解得 k =3 ，故答案为：D.【分析】利用函数解析式，设D 点坐标为 (a ，k a ) ，四边形ABCD 是矩形，则A 点坐标为 (a ，0) ，C 点纵坐标为 k a ，利用中点坐标可得到点E 的纵坐标，利用函数解析式求出点E 的坐标，同理可求出点C 和点F 的坐标；利用点E 为AC 的中点，可求出△ACF 的面积；然后求出k 的值. 二、填空题（共6题；共6分）13.计算： √9−(π−1)0= ________.【答案】2【考点】实数的运算，0指数幂的运算性质【解析】【解答】解：√9−(π−1)0=3-1=2；故答案为：2【分析】先算乘方和开方运算，再利用有理数的加法法则进行计算.14.不透明袋子中装有黑球1个、白球2个，这些球除了颜色外无其他差别.从袋子中随机摸出一个球，记下颜色后放回，将袋子中的球摇匀，再随机摸出一个球，记下颜色，前后两次摸出的球都是白球的概率是________.【答案】49【考点】列表法与树状图法【解析】【解答】解：列表如图所示：由上表可知，所有等可能的情况共有9种，其中两次摸出的球都是白球的情况共有4种，∴两次摸出的球都是白球的概率P=4，9.故答案为：49【分析】利用已知条件，列表，可求出所有的可能的结果数及两次摸出的球都是白球的情况数；然后利用概率公式进行计算.15.方程2(x−3)=6的解是________.【答案】x=6【考点】解含括号的一元一次方程【解析】【解答】解：2(x−3)=6，去括号得，2x−6=6，移项得，2x=12，系数化为1得，x=6，故答案为：x=6.【分析】先去括号，再移项合并，然后将x的系数化为1.AB的长为16.如图，在菱形ABCD中，对角线AC=12，BD=16，分别以点A，B，C，D为圆心，12半径画弧，与该菱形的边相交，则图中阴影部分的面积为________.（结果保留π）【答案】96-25π【考点】菱形的性质，扇形面积的计算【解析】【解答】解：如图，∵四边形ABCD是菱形，AC=12，BD=16，∴AC⊥BD，AO=6，BO=8；∴AB=√OB2+OA2=10；∴菱形ABCD的面积= 12AC×BD=12×12×16=96∵四个扇形的半径相等，都为12AB=5，且四边形的内角和为360°，∴四个扇形的面积= 360π×52360=25π，∴阴影部分的面积= 96-25π；故答案为：96-25π.【分析】利用菱形的性质可求出AO，BO的长；再利用勾股定理求出AB的长，利用菱形的面积公式求出此菱形的面积；四个扇形的半径相等，且四边形的内角和为360°，然后利用扇形的面积公式可求求解. 17.如图，△ABC中，点D为边BC的中点，连接AD，将△ADC沿直线AD翻折至△ABC所在平面内，得△ADC′，连接CC′，分别与边AB交于点E，与AD交于点O.若AE=BE，BC′=2，则AD 的长为________.【答案】3【考点】翻折变换（折叠问题），平行线分线段成比例【解析】【解答】解：由翻折可知OC′=OC,∴O是CC′的中点，∵点D为边BC的中点，O是CC′的中点，∴OD是△CC′B的中位线，∴OD=12BC′=1,OD∥BC′，∴AOBC′=AEBE，∵AE=BE，∴AEBE=1，∴AOBC′=1，∴AO=BC′=2，∴AD=AO+OD=2+1=3.故答案为：3.【分析】利用折叠的性质可证得OC′=OC,再证明OD是△C＇CB的中位线，利用三角形的中位线定理可求出OD的长，同时可证得OD∥BC＇，利用平行线分线段成比例定理，可求出AO的长；然后根据AD=AO+OD，可求出AD的长.18.盲盒为消费市场注入了活力，既能够营造消费者购物过程中的趣味体验，也为商家实现销售额提升拓展了途径.某商家将蓝牙耳机、多接口优盘、迷你音箱共22个，搭配为A，B，C三种盲盒各一个，其中A 盒中有2个蓝牙耳机，3个多接口优盘，1个迷你音箱；B盒中蓝牙耳机与迷你音箱的数量之和等于多接口优盘的数量，蓝牙耳机与迷你音箱的数量之比为3：2；C盒中有1个蓝牙耳机，3个多接口优盘，2个迷你音箱.经核算，A盒的成本为145元，B盒的成本为245元（每种盲盒的成本为该盒中蓝牙耳机、多接口优盘、迷你音箱的成本之和），则C盒的成本为________元.【答案】155【考点】三元一次方程组解法及应用【解析】【解答】解：根据题意，设B盒中蓝牙耳机3a个，迷你音箱2a个，优盘的数量为3a+2a=5 a个，则2+3+1+3a+2a+5a+1+3+2=22，解得，a=1；设蓝牙耳机、多接口优盘、迷你音箱的成本分别为x、y、z元，根据题意列方程组得，{2x+3y+z=145①3x+5y+2z=245②②-①得，x+2y+z=100③，③×3-①得，x+3y+2z=155，故答案为：155.【分析】设B盒中蓝牙耳机3a个，迷你音箱2a个，优盘的数量为5a个，利用某商家将蓝牙耳机、多接口优盘、迷你音箱共22个，建立关于a的方程，解方程求出a的值；设蓝牙耳机、多接口优盘、迷你音箱的成本分别为x、y、z元，再根据A盒的成本为145元，B盒的成本为245元，据此列出x，y，z的方程组，解方程组求出C盒的成本.三、解答题（共8题；共81分）19.计算：（1）a(2a+3b)+(a−b)2；（2）x2−9x2+2x+1÷(x+3−x2x+1).【答案】（1）解：a(2a+3b)+(a−b)2=2a2+3ab+a2−2ab+b2=3a2+ab+b2（2）解：x2−9x2+2x+1÷(x+3−x2x+1)=(x+3)(x-3)(x+1)2÷(x2+x+3−x2x+1)=(x+3)(x-3)(x+1)2·x+1x+3=x-3x+1【考点】整式的混合运算，分式的混合运算【解析】【分析】（1）先去括号（括号前的数要与括号里的每一项相乘，不能漏乘；括号前是负号，去掉括号和负号，括号里的每一项都要变号），再合并同类项（同类项才能合并）.（2）先将括号里的分式通分计算，再将分式除法转化为乘法运算，然后约分化简.20. 2021年是中国共产党建党100周年，某校开展了全校教师学习党史活动并进行了党史知识竞赛，从七、八年级中各随机抽取了20名教师，统计这部分教师的竞赛成绩（竞赛成绩均为整数，满分为10分，9分及以上为优秀）.相关数据统计、整理如下：抽取七年级教师的竞赛成绩（单位：分）6，7，7，8，8，8，8，8，8，8，8，9，9，9，9，10，10，10，10，10.八年级教师竞赛成绩扇形统计图七，八年级教师竞赛成绩统计表根据以上信息，解答下列问题：（1）填空：a=________，b=________；（2）估计该校七年级120名教师中竞赛成绩达到8分及以上的人数；（3）根据以上数据分析，从一个方面评价两个年级教师学习党史的竞赛成绩谁更优异.【答案】（1）8；9（2）解：由题可知，七年被抽查的20名教师成绩中，8分及以上的人数为17人，∴120×17=102（人），20∴该校七年级120名教师中竞赛成绩达到8分及以上的人数为102人；（3）解：八年级教师更优异，因为八年级教师成绩的中位数高于七年级教师成绩的中位数.（不唯一，符合题意即可）【考点】用样本估计总体，统计表，扇形统计图，分析数据的集中趋势【解析】【解答】解：（1）题干中七年级的成绩已经从小到达排列，∴七年级的中位数为a=8；扇形统计图中，D的占比更多，D代表得分为9分的人数，∴八年级的众数为b=9；故答案为：8；9；【分析】（1）求中位数的方法是：把数据先按从小到大的顺序排列，位于最中间的一个数（或两个数的平均数）为中位数；众数是一组数据中出现次数最多的数据；就可得出答案.（2）用120×8分及以上的人数所占的百分比，列式计算.（3）利用表中数据进行分析，可得答案.21.如图，四边形ABCD为平行四边形，连接AC，且AC=2AB.请用尺规完成基本作图：作出∠BAC的角平分线与BC交于点E.连接BD交AE于点F，交AC于点O，猜想线段BF和线段DF的数量关系，并证明你的猜想.（尺规作图保留作图痕迹，不写作法）【答案】解：如图，AE即为∠BAC的角平分线，猜想：DF=3BF证明：∵四边形ABCD是平行四边形∴AO=CO，BO=DO∴AC=2AO∵AC=2AB∴AO=AB∵AE是∠BAC的角平分线∴BF=OF=1BO2∴BF=OF=1DO2∴DF=BO+OF=2BF+BF=3BF.【考点】等腰三角形的性质，平行四边形的性质，角平分线的定义，作图-角的平分线【解析】【分析】利用尺规作图作出∠BAC的角平分线AE，利用平行四边形的性质，可证得AO=CO，BO=DO，由此可推出AO=AB；利用等腰三角形的性质可证得BF=FO，根据DO=OB，可得到BF与DF之间的数量关系.22.探究函数性质时，我们经历了列表、描点、连线画函数图象，观察分析图象特征，概括函数性质的过程.以下是我们研究函数y=x+|−2x+6|+m性质及其应用的部分过程，请按要求完成下列各小题.（1）写出函数关系式中m及表格中a，b的值：m=________，a=________，b=________；（2）根据表格中的数据在所给的平面直角坐标系中画出该函数的图象，并根据图象写出该函数的一条性质：；的图象如图所示，结合你所画的函数图象，直接写出不等式x+|−2x+6|+m>（3）已知函数y=16x16的解集.x【答案】（1）−2；3；4（2）解：通过列表-描点-连线的方法作图，如图所示，根据图像可知：当x<3时，y随x的增大而减小，当x>3时，y随x的增大而增大；故答案为：当x<3时，y随x的增大而减小，当x>3时，y随x的增大而增大.的解集，（3）解：要求不等式x+|−2x+6|+m>16x图象上方的自变量的范围，实际上求出函数y=x+|−2x+6|+m的图象位于函数y=16x∴由图象可知，当x<0或x>4时，满图条件，故答案为：x<0或x>4.【考点】反比例函数的性质，反比例函数与一次函数的交点问题【解析】【解答】解：（1）由表格可知，点(3,1)在该函数图象上，∴将点(3,1)代入函数解析式可得：1=3+|−2×3+6|+m，解得：m=−2，∴原函数的解析式为：y=x+|−2x+6|−2；当x=1时，y=3；当x=4时，y=4；故答案为：−2；3；4；【分析】（1）利用表中点的坐标，可求出m的值，即可得到函数解析式；再求出当x=1和x=4时的函数值，可求出a，b的值.（2）利用描点法画出该函数的图象，利用函数图象写出该函数的一条性质即可.（3）观察函数y=x+|−2x+6|+m的图象位于函数y=16图象上方，利用交点坐标，可得到x的x取值范围.23.重庆小面是重庆美食的名片之一，深受外地游客和本地民众欢迎.某面馆向食客推出经典特色重庆小面，顾客可到店食用（简称“堂食”小面），也可购买搭配佐料的袋装生面（简称“生食”小面）.已知3份“堂食”小面和2份“生食”小面的总售价为31元，4份“堂食”小面和1份“生食”小面的总售价为33元.（1）求每份“堂食”小面和“生食”小面的价格分别是多少元？（2）该面馆在4月共卖出“堂食”小面4500份，“生食”小面2500份，为回馈广大食客，该面馆从5月1日起每份“堂食”小面的价格保持不变，每份“生食”小面的价格降低 34a% .统计5月的销量和销售额发现：“堂食”小面的销量与4月相同，“生食”小面的销量在4月的基础上增加 52a% ，这两种小面的总销售额在4月的基础上增加511a% .求a 的值.【答案】 （1）解：设每份“堂食”小面和“生食”小面的价格分别是x 、y 元，根据题意列方程组得 {3x +2y =314x +y =33 ， 解得， {x =7y =5， 答：每份“堂食”小面价格是7元，“生食”小面的价格是5元.（2）解：根据题意得， 4500×7+2500(1+52a%)×5(1−34a%)=(4500×7+2500×5)(1+511a%) ，解得， a 1=0 （舍去）， a 2=8 ， 答：a 的值为8.【考点】一元二次方程的实际应用-销售问题，二元一次方程组的应用-和差倍分问题【解析】【分析】（1）抓住关键已知条件：3份“堂食”小面和2份“生食”小面的总售价为31元，4份“堂食”小面和1份“生食”小面的总售价为33元，据此设未知数，列方程组，然后求出方程组的解. （2）抓住已知条件：两种小面的总销售额在4月的基础上增加 511a% ，列出关于a 的方程，解方程求出符合题意的a 的值.24.对于任意一个四位数m ，若千位上的数字与个位上的数字之和是百位上的数字与十位上的数字之和的2倍，则称这个四位数m 为“共生数”例如： m =3507 ，因为 3+7=2×(5+0) ，所以3507是“共生数”： m =4135 ，因为 4+5≠2×(1+3) ，所以4135不是“共生数”； （1）判断5313，6437是否为“共生数”？并说明理由；（2）对于“共生数”n ，当十位上的数字是千位上的数字的2倍，百位上的数字与个位上的数字之和能被9整除时，记 F(n)=n3 .求满足 F(n) 各数位上的数字之和是偶数的所有n. 【答案】 （1）解： ∵5+3=2×(1+3)=8, ∴5313 是“共生数”， ∵6+7=13≠2×(4+3)=14, ∴6437 不是“共生数”.（2）解：设“共生数” n 的千位上的数字为 a, 则十位上的数字为 2a, 设百位上的数字为 b, 个位上的数字为 c,∴1≤a＜5,0≤b≤9,0≤c≤9,且a,b,c为整数，所以：n=1000a+100b+20a+c=1020a+100b+c,由“共生数”的定义可得：a+c=2(2a+b),∴c=3a+2b,∴n=1023a+102b,∴F(n)=n=341a+34b,3∵百位上的数字与个位上的数字之和能被9整除，∴b+c=0或b+c=9或b+c=18,当b+c=0,则b=c=0,则a=0,不合题意，舍去，当b+c=9时，则3a+3b=9,∴a+b=3,当a=1时，b=2,c=7,=409，而4+0+9=13不为偶数，舍去，此时：n=1227,F(n)=12273当a=2时，b=1,c=8,=716,，而7+1+6=14为偶数，此时：n=2148,F(n)=21483当a=3时，b=0,c=9,=1023,，而1+0+2+3=6为偶数，此时：n=3069,F(n)=30693当b+c=18时，则b=c=9,而3a+3b=18,则a=−3不合题意，舍去，综上：满足F(n)各数位上的数字之和是偶数的n=2148或n=3069,【考点】二元一次方程组的应用-数字问题，整除（奥数类），奇数和偶数的应用（奥数类）【解析】【分析】（1）利用四位数m为“共生数”的定义，可作出判断.（2）设“共生数”n的千位上的数字为a，则十位上的数字为2a，设百位上的数字为b，个位上的数字为c，可得到a，b，c的取值范围；同时可表示出n的值；由“共生数”的定义可得c=3a+2b，可证得=341a+34b，再根据百位上的数字与个位上的数字之和能被9整除，分情况讨论，分别求F(n)=n3出a，b，c的值，即可得到满足F(n)各数位上的数字之和是偶数的所有n的值.25.如图，在平面直角坐标系中，抛物线y=ax2+bx−4(a≠0)与x轴交于点A(−1,0)，B(4,0)，与y轴交于点C.（1）求该抛物线的解析式；（2）直线l为该抛物线的对称轴，点D与点C关于直线l对称，点P为直线AD下方抛物线上一动点，连接PA，PD，求△PAD面积的最大值；（3）在（2）的条件下，将抛物线y=ax2+bx−4(a≠0)沿射线AD平移4√2个单位，得到新的抛物线y1，点E为点P的对应点，点F为y1的对称轴上任意一点，在y1上确定一点G，使得以点D，E，F，G为顶点的四边形是平行四边形，写出所有符合条件的点G的坐标，并任选其中一个点的坐标，写出求解过程.【答案】（1）解：将A（-1，0），B（4，0）代入y=ax2+bx-4得{a−b−4=016a+4b−4=0，解得：{a=1b=−3，∴该抛物线的解析式为y=x2-3x-4，（2）解：把x=0代入y=x2-3x-4中得：y=-4，∴C（0，-4），抛物线y=x2-3x-4的对称轴l为x=32∵点D与点C关于直线l对称，∴D（3，-4），∵A（-1，0），设直线AD的解析式为y=kx+b；∴{3k+b=-4-k+b=0，解得：{k=−1b=−1，∴直线AD的函数关系式为：y=-x-1，设P（m，m2-3m-4），作PE∥y轴交直线AD于E，∴E （m ，-m-1），∴PE=-m-1-（m 2-3m-4）=-m 2+2m+3，∴ S ΔAPD =12×PE ×|x D −x A |=2(−m 2+2m +3)=−2m 2+4m +6 ， ∴ S ΔAPD =−2m 2+4m +6=−2(m −1)2+8 ， ∴当m=1时， △PAD 的面积最大，最大值为：8（3）解：∵直线AD 的函数关系式为：y=-x-1， ∴直线AD 与x 轴正方向夹角为45°，∴抛物线沿射线AD 方向平移平移 4√2 个单位，相当于将抛物线向右平移4个单位，再向下平移4个单位，∵ A(−1,0) ， B(4,0) ，平移后的坐标分别为（3，-4），（8，-4）， 设平移后的抛物线的解析式为 y 1=x 2+dx +e 则 {9+3d +e =-464+8d +e =-4 ，解得： {d =−11e =20， ∴平移后y 1=x 2-11x+20， ∴抛物线y 1的对称轴为： x =112，∵P （1，-6）， ∴E （5，-10），∵以点D ，E ，F ，G 为顶点的四边形是平行四边形，分三种情况： 设G （n ，n 2-11n+20），F （112 ，y ），①当DE 为对角线时，平行四边形的对角线互相平分 ∴ 3+52=n+1122，∴ n=52∴G(52,−54)②当EF为对角线时，平行四边形的对角线互相平分∴3+n2=5+1122，∴n=152∴G(152,−254)③当EG为对角线时，平行四边形的对角线互相平分∴5+n2=3+1122，∴n=72∴G(72,−254)∴G(52,−54)或G(152,−254)或G(72,−254)【考点】待定系数法求二次函数解析式，二次函数与一次函数的综合应用，二次函数-动态几何问题【解析】【分析】（1）利用待定系数法，由点A，B的坐标求出函数解析式.（2）由x=0求出对应的y的值，可得到点C的坐标，利用函数解析式求出抛物线的对称轴，利用轴对称的性质可求出点D的坐标；再利用待定系数法求出直线AD的解析式，设P（m，m2-3m-4），作PE∥y 轴交直线AD于E，同时可表示出点E的坐标及PE的长，然后利用三角形的面积公式可得到△APD的面积与m之间的函数解析式，将其函数解析式转化为顶点式，利用二次函数的性质，可求出结果.（3）直线AD与x轴正方向夹角为45°，抛物线沿射线AD方向平移平移4√2个单位，相当于将抛物线向右平移4个单位，再向下平移4个单位，利用待定系数法求出平移后的函数解析式，同时可求出抛物线y1的对称轴及点E的坐标；以点D，E，F，G为顶点的四边形是平行四边形，分三种情况：设G（n，n2-11n+20），F（112，y），①当DE为对角线时，平行四边形的对角线互相平分；②当EF为对角线时，平行四边形的对角线互相平分；③当EG为对角线时，平行四边形的对角线互相平分；分别利用线段的中点坐标建立关于n的方程，解方程求出n的值，即可得到点G的坐标.26.在等边△ABC中，AB=6，BD⊥AC，垂足为D，点E为AB边上一点，点F为直线BD上一点，连接EF.（1）将线段EF绕点E逆时针旋转60°得到线段EG，连接FG.①如图1，当点E与点B重合，且GF的延长线过点C时，连接DG，求线段DG的长；②如图2，点E不与点A，B重合，GF的延长线交BC边于点H，连接EH，求证：BE+BH=√3BF；（2）如图3，当点E为AB中点时，点M为BE中点，点N在边AC上，且DN=2NC，点F从BD中点MP最小时，直接Q沿射线QD运动，将线段EF绕点E顺时针旋转60°得到线段EP，连接FP，当NP+12写出△DPN的面积.【答案】（1）解：①如图所示，连接AG，由题意可知，△ABC和△GEF均为等边三角形，∴∠GFB=60°，∵BD⊥AC，∴∠FBC=30°，∴∠FCB=30°，∠ACG=30°，∵AC=BC，GC=GC，∴△GBC≌△GAC（SAS），∴∠GAC=∠GBC=90°，AG=BG，∵AB=6，∴AD=3，AG=BG= 2√3，∴在Rt△ADG中，DG=√AD2+AG2=√(2√3)2+32=√21，∴DG=√21；②证明：以点F为圆心，FB的长为半径画弧，与BH的延长线交于点K，连接KF，如图，∵△ABC和△GEF均为等边三角形，∴∠ABC=60°，∠EFH=120°，∴∠BEF+∠BHF=180°，∵∠BHF+∠KHF=180°，∴∠BEF=∠KHF ，由辅助线作法可知，FB=FK ，则∠K=∠FBE ，∵BD 是等边△ABC 的高，∴∠K=∠DBC=∠DBA=30°，∴∠BFK=120°，在△FEB 与△FHK 中，{∠FEB =∠FHK∠FBE =∠K FB =FK∴△FEB ≌△FHK （AAS ），∴BE=KH ，∴BE+BH=KH+BH=BK ，∵FB=FK ，∠BFK=120°，∴BK= √3 BF ，即： BE +BH =√3BF ；（2）4√33【考点】三角形的综合，三角形-动点问题【解析】【解答】解：（2）如图1所示，以MP 为边构造∠PMJ=30°，∠PJM=90°，则PJ= 12 MP ，∴求 NP +12MP 的最小值，即为求 NP +PJ 的最小值，如图2所示，当运动至N 、P 、J 三点共线时，满足 NP +PJ 最小，此时，连接EQ，则根据题意可得EQ∥AD，且EQ= 12AD，∴∠MEQ=∠A=60°，∠EQF=90°，∵∠PEF=60°，∴∠MEP=∠QEF，由题意，EF=EP，∴△MEP≌△QEF（SAS），∴∠EMP=∠EQF=90°，又∵∠PMJ=30°，∴∠BMJ=60°，∴MJ∥AC，∴∠PMJ=∠DNP=90°，∵∠BDC=90°，∴四边形ODNJ为矩形，NJ=OD，再由题，AD=3，BD= 3√3，∵MJ∥AC，∴△BMO∽△BAD，∴BMBA =BOBD=MOAD=14，∴OD= 34BD= 9√34，OM= 34AD= 94，设PJ=x，则MJ= √3x，OJ= √3x- 94，由题意可知，DN= 23CD=2，∴√3x−94=2，解得：x=11√312，即：PJ= 11√312，∴PN=9√34−11√312=4√33，∴S△DPN =12DN·PN=12×2×4√33=4√33.【分析】（1）①连接AG，易证△ABC和△GEF均为等边三角形，∠GFB=60°，∠FCB=∠ACG，利用SAS 证明△GBC≌△GAC，利用全等三角形的性质，可证得∠GAC=∠GBC，AG=BG，可求出AD，AG的长；利用勾股定理求出DG的长；②以点F为圆心，FB的长为半径画弧，与BH的延长线交于点K，连接KF，利用等边三角形的性质可得∠ABC=60°，∠EFH=120°，利用补角的性质可得∠BEF=∠KHF，FB=FK，利用等边对等角，可证得∠K=∠FBE，同时可证得∠K=∠DBC=∠DBA=30°，即可求出∠BFK的度数；再利用AAS证明△FEB≌△FHK，利用全等三角形的性质可证得BE=KH，由此可推出BE+BH=BK；然后可证得BK= √3BF，由此可证得结论.（2）以MP为边构造∠PMJ=30°，∠PJM=90°，则PJ= 12MP，要求NP+12MP的最小值，就是求NP+PJ的最小值；当运动至N、P、J三点共线时，满足NP+PJ最小，连接EQ，则根据题意可得EQ∥AD，且EQ= 12AD；再利用SAS证明△MEP≌△QEF，利用全等三角形的性质可证得∠EMP=∠EQF=90°，证明四边形ODNJ为矩形，NJ=OD，由MJ∥AC可证得△BMO∽△BAD，利用相似三角形的对应边成比例可求出OD，OM，设PJ=x，利用解直角三角形可表示出MJ，OJ；然后根据DN= 23CD=2，建立关于x的方程，解方程求出x的值，可得到PJ的长，同时可求出PN的长，再利用三角形的面积公式可求出△DPN的面积.。

重庆市2020年初中学业水平暨高中招生考试语文试题(B卷)(全卷共四个大题，满分150分，考试时间120分钟)注意事项：1.试题的答案书写在答题卡上，不得在试卷上直接作答。

2.作答前认真阅读答题卡上的注意事项。

3.考试结束，由监考人员将试题和答题卡一并收回。

一、语文知识及运用(30分)1.下列句子中加点字注音有误的一项是( )(3分)A.缕缕晨光穿云透雾而来，照亮清澈．(chè) 的湖水，唤起声声鸟鸣，美好的一天开始了!B.谚．(yàn)语是古代劳动人民在长期生产实践中总结出来的活泼风趣的艺术性语句。

C.哀愁，从来不是颓废的代名词，相反，真正的哀愁是一种悲天悯．(mǐn)人的情怀。

D.她的散文既表现了仁爱、善良、宽厚等品德，同时也不乏百折不挠．(ráo) 的阳刚之气。

2.下列词语书写全部正确的一项是( )(3分)A.绅士渺小鄙视咄咄逼人B.帐蓬酝酿昔日不理不彩C.愕然伴铝囚犯长途拔涉D.强悍取蒂遂道自吹自擂3.下列句子中“附和”一词运用不当的一项是( )(3分)A.他话音一落，窗外的小鸟就叽叽喳喳叫起来，仿佛在附和他的观点。

B.当大家笑起来时，他也附和着笑，虽然他并不觉得那些话题有趣。

C.老师在凝神细听了那位同学的回答之后，立即附和道：“说得不错!”D.妈妈刚提出举行家庭晚会的主意，弟弟就急忙附和，“好!好!”4.将下列句子组成一段连贯的话，排序合理的一项是( )(3分)①入夜，华灯齐放，礼花飞舞，广场上空一片辉煌②每当国庆节到来，天安门广场花团锦簇，姥紫嫣红。

③鲜花、彩灯、礼花，映衬着人们的歌舞，天安门广场沸腾起来了。

④无数盆鲜花组成一个个大花坛，把广场装点得五彩缤纷。

A.①④②③B.②④①③C.①③④②D.②①④③5.仿照画线部分，补写两个句子，使之构成语意连贯的排比句。

(4分)握手，是心灵的交流。

大千世界，常常因握手而孕育出美好的境界。

微风与湖水握手，漾出轻柔的涟漪；_____________，_____________；_____________，_____________。