大学物理化学热力学
- 格式:pdf
- 大小:436.60 KB
- 文档页数:23


热力学第一定律课后习题一、是非题下列各题中的叙述是否正确?正确的在题后括号内画“√”,错误的画“⨯”。
1.在定温定压下,CO2由饱和液体转变为饱和蒸气,因温度不变,CO2的热力学能和焓也不变。
( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。
( )3. 一个系统从始态到终态,只有进行可逆过程才有熵变。
( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。
( )5. 稳定态单质的∆f H(800 K) = 0。
( )二、选择题选择正确答案的编号,填在各题后的括号内:1. 理想气体定温自由膨胀过程为:()。
(A)Q > 0;(B)∆U < 0;(C)W <0;(D)∆H = 0。
2. 对封闭系统来说,当过程的始态和终态确定后,下列各项中没有确定的值的是:( )。
( A ) Q;( B ) Q+W;(C ) W( Q = 0 );( D ) Q( W = 0 )。
3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是:( )(A)绝热过程;( B)理想气体绝热过程;( C )理想气体绝热可逆过程;(D)绝热可逆过程。
4. 在隔离系统内:( )。
( A ) 热力学能守恒,焓守恒;( B ) 热力学能不一定守恒,焓守恒;(C ) 热力学能守恒,焓不一定守恒;( D) 热力学能、焓均不一定守恒。
5. 从同一始态出发,理想气体经可逆与不可逆两种绝热过程:( )。
( A )可以到达同一终态;( B )不可能到达同一终态;( C )可以到达同一终态,但给环境留下不同影响。
6. 当理想气体反抗一定的压力作绝热膨胀时,则:( )。
( A )焓总是不变;(B )热力学能总是增加;( C )焓总是增加;(D )热力学能总是减少。
7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T),下列说法中不正确的是:()。

大学物理化学公式总结大学物理化学是自然科学中的重要分支,主要研究物质的结构、性质和变化规律。
在物理化学的学习中,公式是不可或缺的工具,能够帮助我们更好地理解和计算各种物理和化学现象。
下面我将总结一些常见的物理化学公式。
一、热力学1. 熵变公式:ΔS = S_final - S_initial2. 焓变公式:ΔH = H_final - H_initial3. 内能变化公式:ΔU = Q + W4. 等温过程熵变:ΔS = nRln(V_final/V_initial)5. 等温过程内能变化:ΔU = 0二、量子力学1. 德布罗意波长:λ = h/(mv)2. 薛定谔方程:Ĥψ = Eψ3. 单电子波函数:ψ = ψ(r,t)4. 束缚能级:E = -13.6eV/n^25. 能态数:N = 2n^2三、热力学平衡1. 平衡常数表达式:K = ([C]^c[D]^d) / ([A]^a[B]^b)2. 平衡常数和自由能变化的关系:ΔG = -RTlnK3. 反应速率表达式:v = k[A]^a[B]^b4. 阿累尼乌斯方程:ln(k2/k1) = (Ea/R)(1/T1 - 1/T2)四、电化学1. 法拉第定律:i = nFv2. 电解质浓度与导电率的关系:κ = λC3. 电解质浓度与摩尔导电率的关系:κ = λC4. 电解质摩尔导电率与离子浓度的关系:λ = κ/C五、化学动力学1. 反应速率表达式:v = k[A]^a[B]^b2. 速率常数和反应物浓度的关系:k = Ae^(-Ea/RT)3. 反应活化能:Ea = RT(ln(k/T) - ln(A))4. 反应级数:n = d(log[A])/dt = d(log[B])/dt = ...六、光化学1. 光电效应能量关系:E = hf = h(c/λ)2. 跃迁能级差:ΔE = E_final - E_initial3. 确定量子数:nλ = 2πr4. 单色光弹性散射能量变化:ΔE = 2(E_final - E_initial)以上只是其中一部分常见的物理化学公式,这些公式在研究和解决物理化学问题时起到了重要的作用,帮助我们理解和预测各种现象。


热力学第一定律课后习题一、是非题下列各题中的叙述是否正确?正确的在题后括号内画“√”,错误的画“⨯”。
1.在定温定压下,CO2由饱和液体转变为饱和蒸气,因温度不变,CO2的热力学能和焓也不变。
( )2. d U = nC V,m d T这个公式对一定量的理想气体的任何pVT过程均适用。
( )3. 一个系统从始态到终态,只有进行可逆过程才有熵变。
( )4. 25℃时H2(g)的标准摩尔燃烧焓等于25℃时H2O(g)的标准摩尔生成焓。
( )5. 稳定态单质的∆f H(800 K) = 0。
( )二、选择题选择正确答案的编号,填在各题后的括号内:1. 理想气体定温自由膨胀过程为:()。
(A)Q > 0;(B)∆U < 0;(C)W <0;(D)∆H = 0。
2. 对封闭系统来说,当过程的始态和终态确定后,下列各项中没有确定的值的是:( )。
( A ) Q;( B ) Q+W;(C ) W( Q = 0 );( D ) Q( W = 0 )。
3. pVγ = 常数(γ = C p,m/C V,m)适用的条件是:( )(A)绝热过程;( B)理想气体绝热过程;( C )理想气体绝热可逆过程;(D)绝热可逆过程。
4. 在隔离系统内:( )。
( A ) 热力学能守恒,焓守恒;( B ) 热力学能不一定守恒,焓守恒;(C ) 热力学能守恒,焓不一定守恒;( D) 热力学能、焓均不一定守恒。
5. 从同一始态出发,理想气体经可逆与不可逆两种绝热过程:( )。
( A )可以到达同一终态;( B )不可能到达同一终态;( C )可以到达同一终态,但给环境留下不同影响。
6. 当理想气体反抗一定的压力作绝热膨胀时,则:( )。
( A )焓总是不变;(B )热力学能总是增加;( C )焓总是增加;(D )热力学能总是减少。
7. 已知反应H2(g) +12O2(g) ==== H2O(g)的标准摩尔反应焓为∆r H(T),下列说法中不正确的是:()。





热力学第二定律课后习题答案习题1在300 K ,100 kPa 压力下,2 mol A 和2 mol B 的理想气体定温、定压混合后,再定容加热到600 K 。
求整个过程的S 为若干已知C V m A = 15 R ,C V m B = 2 5 R[题解] ⎪⎩⎪⎨⎧B(g)2mol A(g)2mol ,,纯态 3001001K kPa,()−→−−−− 混合态,,2mol A 2mol B 100kPa 300K1+==⎧⎨⎪⎪⎩⎪⎪p T 定容()−→−−2 混合态,,2mol A 2mol B 600K 2+=⎧⎨⎪⎩⎪T S = S 1 + S 2,n = 2 molS 1 = 2nR ln ( 2V / V ) = 2nR ln2 S 2 = ( 15nR + 25nR ) ln (T 2 / T 1)= 4nR ln2所以S = 6nR ln2= ( 6 2 mol 8314 J ·K 1·mol 1 ) ln2 = 6915 J ·K 1[导引]本题第一步为理想气体定温定压下的混合熵,相当于发生混合的气体分别在定温条件下的降压过程,第二步可视为两种理想气体分别进行定容降温过程,计算本题的关键是掌握理想气体各种变化过程熵变的计算公式。
习题22 mol 某理想气体,其定容摩尔热容C v ,m = ,由500 K ,405 2 kPa 的始态,依次经历下列过程:(1)恒外压202 6 kPa 下,绝热膨胀至平衡态; (2)再可逆绝热膨胀至101 3 kPa ; (3)最后定容加热至500 K 的终态。
试求整个过程的Q ,W ,U ,H 及S 。
[题解] (1)Q 1 = 0,U 1 = W 1,nC V m (T 2-T 1))(1122su p nRT p nRT p --=, K400546.2022.405)(5.11221211212====-=-T T kPa p kPa p T p T p T T ,得,代入,(2)Q 2 = 0,T T p p 3223111535325=-=-=--()γγγγ,, T T 320.42303==-()K(3)V = 0,W 3 = 0,Q U nC T T V 3343232831450030314491==-=⨯⨯⨯-=∆,()[.(.)].m J kJp p T T 434350030310131671==⨯=(.).kPa kPa 整个过程:Q = Q 1 + Q 2+ Q 3 =491kJ ,U = 0,H = 0,Q + W = U ,故W =-Q =-491 kJ∆S nR p p ==⨯=--ln (.ln ..).141128314405616711475J K J K ··[导引]本题的变化过程为单纯pVT 变化,其中U 、H 和S 是状态函数,而理想气体的U 和H 都只是温度的函数,始终态温度未变,故U = 0,H = 0。
大学物理化学知识点归纳一、物理化学的基本概念物理化学是研究物质的性质和变化规律的学科,它融合了物理学和化学的理论与方法,对于理解和探索物质世界具有重要意义。
二、物理化学的热力学1. 热力学基本概念:热力学研究物质在不同温度、压力和组成条件下的能量转化和热效应。
2. 热力学第一定律:能量守恒定律,描述了物质的内能和热交换之间的关系。
3. 热力学第二定律:能量的不可逆性原理,描述了自然界中能量转化的方向和过程的规律。
4. 熵的概念:熵是衡量系统混乱程度的物理量,与物质的排列和有序程度相关。
5. 自由能与平衡:自由能是描述系统稳定性和反应方向的指标,平衡状态下自由能取最小值。
三、物理化学的动力学1. 动力学基本概念:动力学研究物质内部结构与变化之间的关系,以及反应速率和反应机理等问题。
2. 反应速率与速率常数:反应速率描述了反应速度的快慢,速率常数与反应机理密切相关。
3. 反应平衡与化学平衡常数:反应平衡是指在一定条件下反应物与生成物浓度保持不变的状态,化学平衡常数决定了反应的平衡位置。
4. 反应机理与活化能:反应机理描述了反应的详细步骤和中间产物,活化能是指反应过程中所需的最小能量。
四、物理化学的量子化学1. 量子化学基本概念:量子化学研究微观粒子(如电子)在原子和分子尺度下的性质和行为。
2. 波粒二象性:微观粒子既具有波动性又具有粒子性,具体表现为波粒二象性。
3. 波函数与薛定谔方程:波函数是描述微观粒子状态的数学函数,薛定谔方程描述了波函数的演化和微观粒子的运动规律。
4. 量子力学的应用:量子力学提供了解释原子和分子结构、光谱学和化学键性质等的理论基础。
五、物理化学的电化学1. 电化学基本概念:电化学研究物质在电解质溶液中的电荷转移和电极反应等现象。
2. 电解与电解质:电解是指将化学物质转化为离子的过程,电解质是能够在溶液中导电的化合物。
3. 电流与电解质溶液:电流是指电荷流动的物理现象,电解质溶液中的电流与离子在电场中的迁移相关。
第二章热力学第一定律2.1 热力学的理论基础与方法1.热力学的理论基础热力学涉及由热所产生的力学作用的领域,是研究热、功及其相互转换关系的一门自然科学。
热力学的根据是三件事实:①不能制成永动机。
②不能使一个自然发生的过程完全复原。
③不能达到绝对零度。
热力学的理论基础是热力学第一、第二、第三定律。
这两个定律是人们生活实践、生产实践和科学实验的经验总结。
它们既不涉及物质的微观结构,也不能用数学加以推导和证明。
但它的正确性已被无数次的实验结果所证实。
而且从热力学严格地导出的结论都是非常精确和可靠的。
不过这都是指的在统计意义上的精确性和可靠性。
热力学第一定律是有关能量守恒的规律,即能量既不能创造,亦不能消灭,仅能由一种形式转化为另一种形式,它是定量研究各种形式能量(热、功—机械功、电功、表面功等)相互转化的理论基础。
热力学第二定律是有关热和功等能量形式相互转化的方向与限度的规律,进而推广到有关物质变化过程的方向与限度的普遍规律。
利用热力学第三定律来确定规定熵的数值,再结合其他热力学数据从而解决有关化学平衡的计算问题。
2.热力学的研究方法热力学方法是:从热力学第一和第二定律出发,通过总结、提高、归纳,引出或定义出热力学能U,焓H,熵S,亥姆霍茨函数A,吉布斯函数G;再加上可由实验直接测定的p,V,T等共八个最基本的热力学函数。
再应用演绎法,经过逻辑推理,导出一系列的热力学公式或结论。
进而用以解决物质的p,V,T变化、相变化和化学变化等过程的能量效应(功与热)及过程的方向与限度,即平衡问题。
这一方法也叫状态函数法。
热力学方法的特点是:(i)只研究物质变化过程中各宏观性质的关系,不考虑物质的微观结构;(ii)只研究物质变化过程的始态和终态,而不追究变化过程中的中间细节,也不研究变化过程的速率和完成过程所需要的时间。
因此,热力学方法属于宏观方法。
2.2 热力学的基本概念1.系统与环境系统:作为某热力学问题研究对象的部分;环境:与系统相关的周围部分;按系统与环境交换内容分为:(1)敞开系统(open system) :体系与环境间既有物质交换又有能量交换的体系。
大学物理化学公式总结物理化学作为一门综合性的学科,涉及到丰富而复杂的理论和实验内容。
公式作为物理化学研究的重要工具,既能简化问题的处理过程,又能揭示事物背后的规律和原理。
在这篇文章中,我们将总结一些大学物理化学中常见的公式,并探索它们背后的意义和应用。
1. 经典力学公式经典力学是物理学的基础,它研究物体在力的作用下的运动规律。
在这个领域中,公式起到了关键的作用,其中最基本的公式就是牛顿第二定律:F = ma该公式表示物体的加速度(a)与作用在物体上的力(F)的关系。
通过这个公式,我们可以推导出许多与运动相关的公式,如位移-时间关系、速度-时间关系等。
2. 热力学公式热力学研究物质的热现象和能量转化规律,是理解自然界中热现象的重要工具。
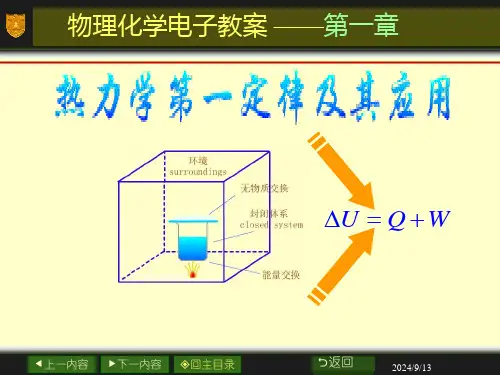
其中最基本的公式是热力学第一定律,也被称为能量守恒定律:ΔU = q + W该公式表示系统的内能(U)的变化等于系统所吸收的热量(q)与对外做功(W)的和。
这个公式揭示了能量在系统中的转化关系,并为热力学研究提供了基础。
3. 电磁学公式电磁学是物理学中的重要分支,研究电、磁场的相互作用及其规律。
其中,麦克斯韦方程组是电磁学研究的核心公式,它由四个方程组成:∇·E = ρ/ε₀∇·B = 0∇×E = -∂B/∂t∇×B = μ₀J + μ₀ε₀∂E/∂t这四个方程描述了电场(E)和磁场(B)的产生和相互作用,是现代电磁学研究的基础。
它们揭示了电磁波传播的规律,为电磁学中很多应用提供了理论依据。
4. 量子力学公式量子力学作为最前沿的物理学分支,研究微观世界的行为。
其中最著名的公式是薛定谔方程:Ĥψ =Eψ这个方程描述了量子系统的波函数(ψ)和能量(E)之间的关系。
它是揭示原子、分子结构和行为的关键公式,让我们能够理解原子和分子的性质,同时也为应用于量子计算和量子通信等领域提供了基础。
总结:在这篇文章中,我们总结了大学物理化学中的一些重要公式,并探讨了它们背后的意义和应用。
一、课程简介大学物理化学是一门研究物质的物理性质和化学性质之间关系的学科。
它涉及了热力学、动力学、量子化学、电化学等多个领域,是化学、材料科学、环境科学等学科的基础课程。
二、教学目标1. 理解物理化学的基本概念、原理和方法。
2. 掌握热力学、动力学、量子化学、电化学等基本理论。
3. 能够运用物理化学原理解决实际问题。
4. 培养学生的创新思维和科研能力。
三、教学内容1. 热力学基础- 状态函数与过程函数- 热力学第一定律- 热力学第二定律- 熵与自由能2. 动力学基础- 反应速率与活化能- 反应机理与速率方程- 链反应与自由基反应- 催化作用3. 量子化学基础- 原子结构与分子结构- 分子轨道理论- 分子轨道对称性原理- 配位场理论4. 电化学基础- 电化学基本原理- 电解质溶液- 电极过程- 电化学测量方法四、教学方法1. 讲授法:系统讲解物理化学的基本概念、原理和方法。
2. 案例分析法:通过分析实际问题,使学生掌握物理化学原理的应用。
3. 讨论法:组织学生进行课堂讨论,激发学生的思维,提高学生的表达能力。
4. 实验教学法:引导学生进行实验操作,培养学生的动手能力和实验技能。
五、教学过程1. 导入新课:通过生活中的实例,引入物理化学的基本概念,激发学生的学习兴趣。
2. 讲解原理:详细讲解物理化学的基本原理,使学生掌握相关知识点。
3. 案例分析:选取实际案例,引导学生运用物理化学原理解决实际问题。
4. 课堂讨论:组织学生进行课堂讨论,提高学生的思维能力和表达能力。
5. 实验教学:指导学生进行实验操作,培养学生的动手能力和实验技能。
6. 总结回顾:对本节课的知识点进行总结,帮助学生巩固所学内容。
六、作业布置1. 完成课后习题,巩固所学知识。
2. 查阅相关资料,了解物理化学在各个领域的应用。
3. 准备下一节课的讨论主题,提高学生的自主学习能力。
七、教学评价1. 课堂表现:关注学生在课堂上的发言、提问和参与度。
大学物理化学知识点物理化学是化学学科的一个重要分支,它综合运用物理学的原理和方法来研究化学现象和过程的本质。
对于大学化学相关专业的学生来说,掌握物理化学的知识点至关重要。
以下将为您详细介绍一些关键的大学物理化学知识点。
一、热力学第一定律热力学第一定律,也称为能量守恒定律,其核心表述为:能量可以在不同形式之间转换,但总量保持不变。
在物理化学中,常用热力学第一定律来分析各种热力学过程中的能量变化。
例如,对于一个封闭系统的绝热过程,系统与环境之间没有热量交换,此时系统内能的变化等于外界对系统所做的功。
而在等容过程中,系统体积不变,外界对系统做功为零,系统内能的变化就等于系统吸收或放出的热量。
二、热力学第二定律热力学第二定律主要描述了热现象的方向性。
克劳修斯表述指出:热量不能自发地从低温物体传向高温物体。
开尔文表述则为:不可能从单一热源吸取热量使之完全变为有用功而不产生其他影响。
熵是热力学第二定律中的一个重要概念。
熵增原理表明,在任何自发过程中,系统的熵总是增加的。
通过熵的变化,可以判断一个过程是否自发进行。
三、热力学第三定律热力学第三定律指出:绝对零度时,完美晶体的熵为零。
这一定律为计算物质在不同温度下的熵值提供了基础。
四、化学热力学化学热力学主要研究化学反应过程中的能量变化、方向和限度。
通过计算反应的焓变、熵变和自由能变,可以判断一个化学反应在给定条件下能否自发进行以及反应进行的程度。
例如,吉布斯自由能变(ΔG)小于零的反应在该条件下能够自发进行;ΔG 等于零时,反应达到平衡状态;ΔG 大于零时,反应不能自发进行。
五、多组分系统热力学在多组分系统中,需要引入偏摩尔量的概念来描述各组分的性质。
拉乌尔定律和亨利定律分别用于描述理想溶液和稀溶液中溶剂和溶质的蒸气压与组成的关系。
六、化学平衡化学平衡是指在一定条件下,化学反应达到动态平衡的状态。
平衡常数(K)是衡量化学平衡的重要参数,其大小与温度有关。
通过改变反应条件,如温度、压力、浓度等,可以影响化学平衡的移动。
第三章热力学第二定律§3.1 自发过程的共同特征一、自发过程“自发过程”⎯在一定条件下能自动进行的过程。
•推论:•一切自发过程都是有方向性的,人类经验没有发现哪一个自发过程可以自动地回复原状。
二、决定自发过程的方向和限度的因素•从表面上看,各种不同的过程有着不同的决定因素,例如:–i)决定热量流动方向的因素是温度T;–ii)决定气体流动方向的是压力P;–iii)决定电流方向的是电位V;–iv)而决定化学过程和限度的因素是什么呢?三、自发过程的共同特征分析:•根据人类经验,自发过程都是有方向性的(共同特点),即自发过程不能自动回复原状。
1、理想气体向真空膨胀•即:当系统回复到原状时,环境中有W的功变成了Q(=-W)的热。
•因此,环境最终能否回复原状(即理气向真空膨胀是否能成为可逆过程),就取决于(环境得到的)热能否全部变为功而没有任何其他变化。
2、热量由高温物体流向低温物体•因此,系统回复了原状的同时,环境最终能否回复原状( 即热由高温向低温流动能否成为一可逆过程),取决于(环境得到的) 热能否全部变为功而没有任何其他变化。
3、Cd放入PbCl2溶液转变成CdCl2 溶液和Pb•已知此过程是自发的,在反应进行时有∣Q∣的热量放出(放热反应,Q<0)•欲使系统回复原状,可进行电解反应。
•若电解时做的电功为W,同时还有∣Q′∣的热量放出,当反应系统回复原状时,环境中损失的功(电功)为W,得到的热为∣Q∣+∣Q′∣•根据能量守恒原理:∣W∣=∣Q∣+∣Q′∣•所以环境能否回复原状(即此反应能否成为可逆过程),取决于•(环境得到的)热(∣Q∣+∣Q′∣) 能否全部转化为功W (=∣Q∣+∣Q′∣)而没有任何其他变化。
•自发过程能否成为热力学可逆过程,最终均可归结为:•“热能否全部转变为功而没有任何其他变化”•然而经验证明:热功转化是有方向性的,即•“功可自发地全部变为热;但热不可能全部转变为功而不引起任何其他变化”。
•“一切自发过程都是不可逆过程。
”•这就是自发过程的共同特征。
§3.2 热力学第二定律的经典表述•一切自发过程的方向,最终都可归结为热功转化的方向问题:•“功可全部变为热,而热不能全部变为功而不引起任何其他变化”。
一、克劳修斯和开尔文对热力学第二定律的经典表述1.克劳修斯(Clausius) 表述:•“不可能把热从低温物体传到高温物体,而不引起任何其他变化。
”2. 开尔文(Kelvin) 表述•不可能从单一热源取出热使之完全变为功,而不发生其他变化。
•也可表达为:•“第二类永动机是不可能造成的。
”*热力学第二定律的克劳修斯表述与开尔文表述等价。
二、关于热力学第二定律表述的几点说明1. 第二类永动机并不违反热力学第一定律。
•它究竟能否实现,只有热力学第二定律才能回答。
但回答是:•“第二类永动机是不可能存在的。
”其所以不可能存在,也是人类经验的总结。
2. 对“不能仅从单一热源取出热量变为功而没有任何其他变化”这一表述的理解,应防止混淆:不是说热不能变成功,而是说不能全部变成功而没有任何其他变化。
3. 一切自发过程的方向性(不可逆性)最终均可归结为“热能否全部变为功而没有任何其他变化”的问题,亦即可归结为“第二类永动机能否成立”的问题。
•因此可根据“第二类永动机不能成立”这一原理来判断一个过程的(自发)方向。
解决的方向:•在热力学第二定律中是否也能找出类似的热力学函数,只要计算函数变化值,就可以判断过程的(自发)方向和限度呢?§3.3Carnot 定理'1Q W =I η1Q W =R η>'1Q W h T 高温热源cT 低温热源1Q W1Q 'W 1Q W−1Q 'W −R I(a)W W =假设I Rηη>11'Q Q >1Q W h T 高温热源cT 低温热源1Q W 1Q 'W 1Q W−1Q 'W−R I(b)'11()()Q W Q W −−−'11()0Q Q =−>从低温热源吸热I Rηη≤高温热源得到热'11()Q Q −这违反了Clausius 说法,只有一、Carnot 定理1、表述:2、推论:卡诺热机是在两个已定热源之间工作的热机效率最大的热机。
所有工作于同温热源与同温冷源之间的可逆热机,其热机效率都相等,即与热机的工作物质无关。
4、讨论(1)卡诺热机的效率(即热能转化为功的比例)只与两个热源的温度比有关。
两个热源的温差越大,则效率η愈高;反之就愈小。
•当T 2 −T 1 =0时,η=0,即热就完全不能变为功了。
3、意义:(1)引入了一个不等号,原则上解决了化学反应的方向问题;I R ηη≤(2)原则上解决了热机效率的极限值问题。
(2)卡诺热机中:-W = Q 1+ Q 2代入:η= -W /Q 2 = 1−(T 1/T 2 )⇒(Q 1+ Q 2 )/Q 2 = (T 2−T 1) /T 2⇒Q 1 /Q 2 = −T 1/T 2⇒(可逆卡诺循环)T Q T Q 2211=+结论:卡诺机在两个热源之间工作时,其“热温商”之和等于零。
§3.4 熵的概念•任意可逆循环过程可以由一系列可逆卡诺循环过程组成。
如图圆环ABA 表示任意一可逆循环过程。
•在每一个微循环中:δQ i /T i + δQ j /T j = 0•δQ i 表示微小的热量传递;将所有循环的热温商相加,即为曲折线循环过程的热温商之和:Σ(δQ i /T i )曲折线= 0∫=ABArTQ 0δ0=⎟⎟⎠⎞⎜⎜⎝⎛∑曲折线i iT Q δ⇒结论:任意可逆循环过程的热温商的闭合曲线积分为零。
•将任意可逆循环看作是由两个可逆过程α和β组成:)()(=+=∫∫∫TQ TQ TQ rABrBArδδδβα•结论:•积分值:0)()(=+=∫∫∫TQ TQ TQ rABrBArδδδβα可改写为:TQ TQ TQ r BAr ABr BAδδδββα∫∫∫=−=)()()(仅仅取决于始态A 和终态B ,而与可逆变化的途径无关。
∫BArT Q δ可表示从状态A →状态B ,系统某个状态函数的变化值。
•因此,积分值∫BAr TQ δ 将这个状态函数取名为“熵”,用符号“S ”表示。
熵:既有热(转递)的含义⎯“火”,又有热、温(相除)的含义⎯“商”,组合成汉字“熵”“Entropy”[′entr əpi]。
•于是,当系统的状态由A 变到B 时,状态函数熵(S )的变化为:ΔS A →B = S B −S A =∫A B (δQ r /T )•如果变化无限小,则(状态函数S 的变化)可写成微分形式:dS = δQ r /T注意:1)两式只能在可逆过程中才能应用;2)熵的单位为:J /K (与热容量相同)。
ΔS A →B = S B −S A =∫A B (δQ r /T )dS = δQ r /T §3.5 Clausius 不等式与熵增加原理一、Clausius 不等式设温度相同的两个高、低温热源间有一个可逆热机和一个不可逆热机。
hch c h R 1T TT T T −=−=ηI Rηη<根据Carnot 定理:0hhc c <+T Q T Q 则h c cI h h1Q Q QQ Q η+==+则推广为与n 个热源接触的任意不可逆过程:0<⎟⎟⎠⎞⎜⎜⎝⎛∑I n i i i T Q δR, A Bi B AQ S S T →δ⎛⎞=−⎜⎟⎝⎠∑A B IB A Q S T →δ⎛⎞Δ−>⎜⎟⎝⎠∑或B A I,i A BQ S S T →δ⎛⎞−>⎜⎟⎝⎠∑设有一个循环,为不可逆过程,为可逆过程,整个循环为不可逆循环。
A B →B A →I, R, 0i i A BB A Q Q T T →→δδ⎛⎞⎛⎞+⎜⎟⎜⎟⎝⎠⎝⎠∑∑<则有如A →B 为可逆过程A B R,A B0i Q S T →→δ⎛⎞Δ−=⎜⎟⎝⎠∑A B A B ()0iQS T→→δΔ−≥∑将两式合并得Clausius 不等式:是实际过程的热效应,T 是环境温度。
若是不可逆过程,用“>”号,可逆过程用“=”号,这时环境与系统温度相同。
Qδ都称为Clausius 不等式,也可作为热力学第二定律的数学表达式。
d Q S Tδ≥或d 0QS Tδ−≥对于微小变化:•注意:Q 表示系统的热效应;T 指热源温度,即恒温环境的温度,而非系统温度。
对于可逆过程,T 可以用系统的温度代替;对于不可逆过程,T 只能是热源(即环境)的温度。
二、熵增加原理对于绝热系统Q δ=d 0S ≥如果是一个隔离系统,则熵增加原理可表述为:所以Clausius 不等式为熵增加原理可表述为:在绝热条件下,趋向于平衡的过程使系统的熵增加。
一个隔离系统的熵永不减少。
(1)对于隔离系统iso d 0S ≥(2)若把与系统密切相关的环境部分包括在一起,作为一个隔离系统,则有:可以用来判断自发变化的方向和限度。
三、Clausius 不等式的意义“>”号为自发过程,“=”号为可逆过程。
≥Δ+Δ=Δsur sys iso S S S 注意:• 1. 当系统得到(或失去)热时,环境就失去(或得到)等量的热(Q sur = −Q sys )。
• 2. 通常将环境看作一热容量无限大的热源,传热过程中其温度不变;对于环境ΔS sur =ΣδQ sur / T sur = −ΣδQ sys / T sur适合于可逆或不可逆过程(1)熵是系统的状态函数,是容量性质。
四、熵的特点•无论过程A →B 可逆与否,系统熵变量ΔS A →B 均为定值(只取决于始、终态),数值上等于A →B 可逆过程的热温商,即:∫=Δ→BArB A TQ S δ 而Σ(δQ i ′/T i )A →B 仅表示不可逆过程的“热温商”,并不是系统A →B 的熵变量。
(2)可以用Clausius 不等式来判别过程的可逆性。
(3)在任何一个隔离系统中,若进行了不可逆过程,系统的熵就要增大,一切能自动进行的过程都引起熵的增大。
§3.6 热力学基本方程与T-S 图一、热力学基本方程熵是热力学能和体积的函数,即(,)S S U V =d d d V US S S U V U V ⎛⎞⎛⎞⎜⎟⎜⎟⎝⎠⎝⎠∂∂=+∂∂pdVdU TdS pdV TdS W Q dU r +=−=+=δδ热力学基本方程可表示为1d d d p S U V T T=+所以有1V S U T∂⎛⎞=⎜⎟∂⎝⎠VU T S ∂⎛⎞=⎜⎟∂⎝⎠或=U S p V T∂⎛⎞⎜⎟∂⎝⎠US p T V ∂⎛⎞=⎜⎟∂⎝⎠或二、T -S 图1、T -S 图R d Q S T=根据热力学第二定律T-S 图上曲线下的面积就等于系统在相应过程中的热效应。