数字高程模型实验教程(李发源[等]编著)思维导图

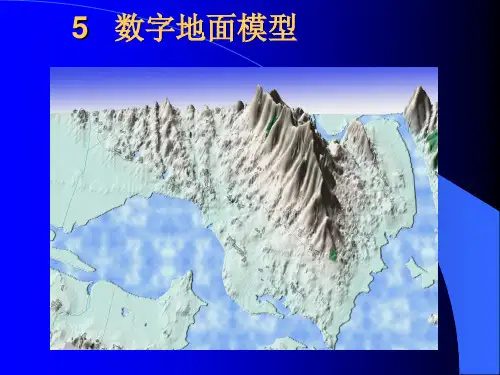
数字高程模型（ＤＥＭ）　在黄土高原研究中的应用与展望＊ 李发源　中国科学院成都山地灾害与环境研究所 成都 ６１００４１　南京师范大学地理科学学院 南京 ２１００９７　摘要：作为地理信息系统（ＧＩＳ）空间数据库中最重要的组成部分之一，ＤＥＭ已在地学空间三维模型构建与地学空间分析中得到广泛的应用。

但是，　ＤＥＭ不仅仅是单纯的地形数据库，更应作为一种地学分析的新方法。

ＤＥＭ分析方法的引入，给黄土高原研究带来了新的理念和思路。

如基于ＤＥＭ的黄土高原流域特征地貌的提取及分析、土壤侵蚀模型的校正等都取得了很好的效果，同时，产生了一些新的概念，如黄土高原地面坡谱等。

初步研究表明，坡谱是利用微观地形指标来反映宏观地形特征的有效方法，对它的研究旨在探索黄土高原地貌研究的新方法，也是为解决地理学界长期争论不休的基本自然地理单元的尺度问题的一次尝试。

　关键词：数字高程模型 黄土高原 应用 地面坡谱　Ａｂｓｔｒａｃｔ：　Ａｓ　ｏｎｅ　ｏｆ　ｔｈｅ　ｍｏｓｔ　ｉｍｐｏｒｔａｎｔ　ｃｏｍｐｏｎｅｎｔ　ｏｆ　ＧＩＳ　ｓｐａｔｉａｌ　ｄａｔａｂａｓｅ，　ＤＥＭ　ｈａｓ　ｂｅｅｎ　ｗｉｌｄｌｙ　ｕｓｅｄ　ｉｎ　ｃｏｎｓｔｒｕｃｔｉｎｇ　ｔｈｅ　ｇｅｏ－ｓｐａｔｉａｌ　ｔｈｒｅｅ－ｄｉｍｅｎｓｉｏｎ　ｍｏｄｅｌ　ａｎｄ　ｇｅｏ－ｓｐａｔｉａｌ　ａｎａｌｙｓｉｓ．　Ｎｏｗ　ｉｔ　ｉｓ　ｒｅｇａｒｄｅｄ　ｔｈａｔ　ＤＥＭ　ｉｓ　ｎｏｔ　ｏｎｌｙ　ａ　ｇｅｎｅｒａｌ　ｓｐａｔｉａｌ　ｄａｔａｂａｓｅ，　ｂｕｔ　ａ　ｎｅｗ　ｋｉｎｄ　ｏｆ　ｇｅｏ－ｓｃｉｅｎｃｅ　ａｎａｌｙｓｉｓ　ｍｅｔｈｏｄ．　ＤＥＭ　ａｎａｌｙｓｉｓ　ｍｅｔｈｏｄ　ｔａｋｅｓ　ｎｅｗ　ｉｄｅａｓ　ａｎｄ　ｔｈｉｎｋｉｎｇ　ｏｆ　Ｌｏｅｓｓ　Ｐｌａｔｅａｕ　ｒｅｓｅａｒｃｈ．　Ｆｏｒ　ｅｘａｍｐｌｅ，　ｉｔ　ｉｓ　ｅｆｆｅｃｔｉｖｅ　ｔｈａｔ　ＤＥＭ　ｂａｓｅｄ　ｅｘｔｒａｃｔｉｎｇ　ａｎｄ　ａｎａｌｙｓｉｓ　ｏｆ　ｗａｔｅｒｓｈｅｄ　ｇｅｏｍｏｒｐｈｏｌｏｇｙ　ｏｆ　Ｌｏｅｓｓ　Ｐｌａｔｅａｕ，　ａｎｄ　ｒｅｖｉｓｉｎｇ　ｏｆ　ｓｏｉｌ　ｅｒｏｓｉｏｎ　ｍｏｄｅｌ，　ｗｈｉｌｓｔ，　ｔｈｅ　ｎｅｗ　ｃｏｎｃｅｐｔ　ｓｌｏｐｅ　ｓｐｅｃｔｒｕｍ　ｉｓ　ｐｕｔ　ｆｏｒｗａｒｄ．　Ｐｒｉｍａｒｙ　ｒｅｓｅａｒｃｈ　ｓｈｏｗｓ　ｔｈａｔ　ｓｌｏｐｅ　ｓｐｅｃｔｒｕｍ　ｉｓ　ａｎ　ｅｆｆｅｃｔｉｖｅ　ｗａｙ　ｏｆ　ｕｓｉｎｇ　ｍｉｃｒｏｃｏｓｍｉｃ　ｔｅｒｒａｉｎ　ｉｎｄｅｘ　ｔｏ　ｒｅｆｌｅｃｔ　ｇｒａｎｔ　ｔｅｒｒａｉｎ　ｃｈａｒａｃｔｅｒ．　Ｉｔ　ｉｓ　ｐｒｏｐｏｓｅｄ　ｔｈａｔ　ｔｈｉｓ　ｒｅｓｅａｒｃｈ　ｉｓ　ａ　ｎｅｗ　ａｐｐｌｙｉｎｇ　ｉｎ　ｇｅｏｍｏｒｐｈｏｌｏｇｙ　ａｎｄ　ａｎ　ｅｘｐｅｒｉｍｅｎｔ　ｔｏ　ｒｅｓｏｌｖｅ　ｔｈｅ　ｓｃａｌｅ　ｏｆ　ｂａｓｉｃ　ｐｈｙｓｉｃａｌ　ｇｅｏｇｒａｐｈｙ　ｕｎｉｔ　ｔｈａｔ　ｂｅｅｎ　ｄｉｓｃｕｓｓｅｄ　ｆｏｒ　ａ　ｌｏｎｇ　ｔｉｍｅ．　Ｋｅｙ　ｗｏｒｄｓ：　ＤＥＭ；ＤＥＭ Ｌｏｅｓｓ　Ｐｌａｔｅａｕ ａｐｐｌｙｉｎｇ Ｓｌｏｐｅ　ｓｐｅｃｔｒｕｍ　１．　前言　数字高程模型（Ｄｉｇｉｔａｌ　Ｅｌｅｖａｔｉｏｎ　Ｍｏｄｅｌｓ，ＤＥＭ）是地球自然表面的数字表示，是地理信息系统地理数据库中最为重要的空间信息资料和赖以进行地形分析的核心数据系统。

+第一章绪论数字地形图：在测绘领域，地形图是一个专有名词。

国内的地形图（国外的不了解）一般特指那些特定比例尺系列、有着固定分幅范围的、全面表达地表面的地形、地物特征的地图。

其内容特点是全面、均衡、不突出表达某种要素。

一般包括：测量控制点、居民地、水系、交通、管线、地貌、植被等内容。

数字地形图的历史形态是模拟地形图，一般是纸质的。

数字高程模型(DEM)：地形图上的地貌是用等高线、高程点、陡坎、陡崖等表达的。

等高线和高程点，外加陡坎、陡崖及其比高构成了一种“高程模型”。

通过对他们的判读，可以得到对地表高程的总体印象，是对实际地貌的一种模拟。

数字地形图上的等高线和高程点是数字高程模型的一种。

不规则三角网、规则格网都可以是数字高程模型，其核心特点是都可以对地表高程信息进行完整的模拟。

数字地面(地形)模型(DTM)：地形是“地表形态”或“地貌形态”的简称。

地形可以用高程来描述，也可以用坡度、坡向等信息来描述。

数字地形模型包括数字高程模型、数字坡度模型、数字坡向模型等。

数字表面模型(DSM)：DEM必须是高程信息，是对地形和地貌的模拟，DSM可以是地物表面的模拟，包括植被表面、房屋的表面，对DSM进行加工，去掉房屋、植被等信息，可以形成DEM。

模型（Model）:用来表现其它事物的一个对象或概念，是按比例缩减并转变为能够理解的事物本体。

模型可用来表示系统或现象的最初状态，或表现某些假定或预测的情形。

三个层次：概念模型----基于个人的经验与知识在大脑中形成的关于状况或对象的模型。

物质模型----模拟的模型。

如沙盘，塑料地形模型。

数学模型----基于数字系统的定量模型。

用数学的语言、方法去近似地刻划实际，是由数字、字母或其它数学符号组成的，描述现实对象数量规律的数学公式、图形或算法。

•（1）按照模型的应用领域（或所属学科）如人口模型，生物模型，生态模型，交通模型，作战模型等。

•（2）按照建立模型的数学方法（或所属数学分支）如初等模型，微分方程模型、网络模型、运筹模型、随机模型等。