研究生《最优化方法》课程实验-最优化编程作业答案-东北大学
- 格式:doc
- 大小:33.50 KB
- 文档页数:6



练习题一1、建立优化模型应考虑哪些要素? 答:决策变量、目标函数和约束条件。
2、讨论优化模型最优解的存在性、迭代算法的收敛性及停止准则。
答:针对一般优化模型()()min ()..0,1,2, 0,1,,i j f x s t g x i m h x j p≥===,讨论解的可行域D ,若存在一点*X D ∈,对于X D ∀∈ 均有*()()f X f X ≤则称*X 为优化模型最优解,最优解存在;迭代算法的收敛性是指迭代所得到的序列(1)(2)(),,,K X X X ,满足(1)()()()K K f X f X +≤,则迭代法收敛;收敛的停止准则有(1)()k k x x ε+-<,(1)()()k k k x x x ε+-<,()()(1)()k k f x f x ε+-<,()()()(1)()()k k k f x f x f x ε+-<,()()k f x ε∇<等等。
练习题二1、某公司看中了例2.1中厂家所拥有的3种资源R 1、R2、和R 3,欲出价收购(可能用于生产附加值更高的产品)。
如果你是该公司的决策者,对这3种资源的收购报价是多少?(该问题称为例2.1的对偶问题)。
解:确定决策变量 对3种资源报价123,,y y y 作为本问题的决策变量。
确定目标函数 问题的目标很清楚——“收购价最小”。
确定约束条件 资源的报价至少应该高于原生产产品的利润,这样原厂家才可能卖。
因此有如下线性规划问题:123min 170100150w y y y =++1231231235210..23518,,0y y y s t y y y y y y ++≥⎧⎪++≥⎨⎪≥⎩ *2、研究线性规划的对偶理论和方法(包括对偶规划模型形式、对偶理论和对偶单纯形法)。
答:略。
3、用单纯形法求解下列线性规划问题:(1)⎪⎪⎩⎪⎪⎨⎧≥≤+-≤++≤-++-=0,,43222..min32131321321321x x x x x x x x x x x t s x x x z ; (2)⎪⎪⎩⎪⎪⎨⎧=≥=++=+-=+-+-=)5,,2,1(052222..4min53243232132 i x x x x x x x x x x t s x x z i解:(1)引入松弛变量x 4,x 5,x 6123456min 0*0*0*z x x x x x x =-++++12341232 =22 5 =3..13 6=41,2,3,4,5,60x x x x x x x x s t x x x x x x x x x +-+⎧⎪+++⎪⎨-++⎪⎪≥⎩因检验数σ2<0,故确定x 2为换入非基变量,以x 2的系数列的正分量对应去除常数列,最小比值所在行对应的基变量x 4作为换出的基变量。
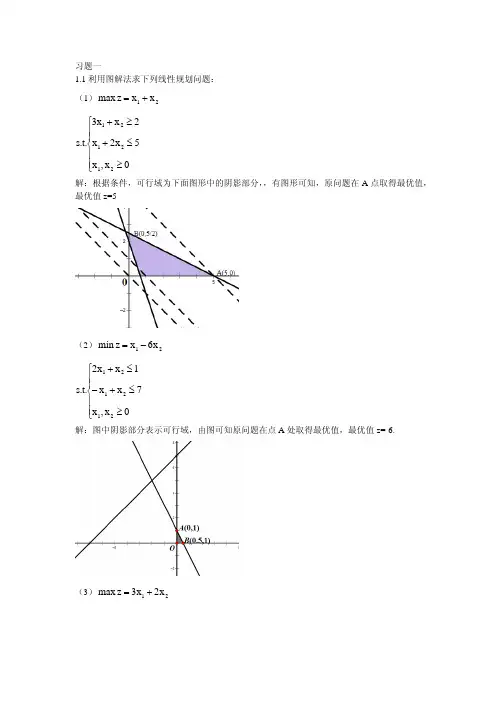
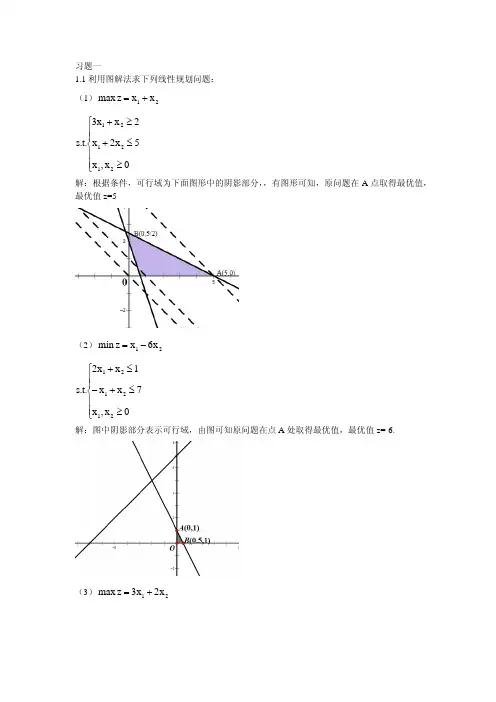
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。

习题二包括题目: P36页 5〔1〕〔4〕 5〔4〕习题三包括题目:P61页 1(1)(2); 3; 5; 6; 14;15(1) 1(1)(2)的解如下 3题的解如下 5,6题14题解如下14. 设22121212()(6)(233)f x x x x x x x =+++---, 求点在(4,6)T-处的牛顿方向。
解: (1)(4,6)T x=-,由题意得∴(1)1344()56g f x -⎛⎫=∇=⎪⎝⎭21212122211212122(3)22(3)(3)2(233)()22(3)(3)2(233)22(3)x x x x x x x f x x x x x x x x +--+--------⎛⎫∇= ⎪+--------+--⎝⎭∴(1)2(1)1656()()564G x f x --⎛⎫=∇=⎪-⎝⎭∴(1)(1)11141/100()574/100d G x g -⎛⎫=-=⎪-⎝⎭15〔1〕解如下15. 用DFP 方法求以下问题的极小点〔1〕22121212min 353x x x x x x ++++解:取 (0)(1,1)T x=,0H I =时,DFP 法的第一步与最速下降法一样2112352()156x x f x x x ++⎛⎫∇= ⎪++⎝⎭, (0)(1,1)T x =,(0)10()12f x ⎛⎫∇= ⎪⎝⎭(1)0.07800.2936x -⎛⎫= ⎪-⎝⎭, (1)1.3760() 1.1516f x ⎛⎫∇= ⎪-⎝⎭以下作第二次迭代(1)(0)1 1.07801.2936x x δ-⎛⎫=-= ⎪-⎝⎭, (1)(0)18.6240()()13.1516f x f x γ-⎛⎫=∇-∇= ⎪-⎝⎭其中,111011126.3096,247.3380T T TH δγγγγγ===11 1.1621 1.39451.3945 1.6734T δδ⎛⎫= ⎪⎝⎭ , 01101174.3734113.4194113.4194172.9646T TH H γγγγ⎛⎫== ⎪⎝⎭所以 令 (2)(1)(1)1xx d α=+ , 利用 (1)(1)()0df x d d αα+=,求得 10.5727α=-所以 (2)(1)(1)0.77540.57270.8535x x d ⎛⎫=-= ⎪-⎝⎭ , (2)0.2833()0.244f x ⎛⎫∇= ⎪-⎝⎭以下作第三次迭代(2)(1)20.85340.5599x x δ⎛⎫=-= ⎪-⎝⎭ , (2)(1)2 1.0927()()0.9076f x f x γ-⎛⎫=∇-∇= ⎪⎝⎭22 1.4407T δγ=- , 212 1.9922T H γγ=所以 令 (3)(2)(2)2xxdα=+ , 利用(2)(2)()0df x d d αα+=,求得 21α= 所以 (3)(2)(2)11x x d ⎛⎫=+=⎪-⎝⎭, 因为 (3)()0f x ∇=,于是停顿 (3)(1,1)T x =-即为最优解。


最优化方法-习题解答张彦斌计算机学院2014年10月20日Contents1第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、412第二章线搜索算法-P27习题2、4、643第三章最速下降法和牛顿法P41习题1,2,374第四章共轭梯度法P51习题1,3,6(1)105第五章拟牛顿法P73-2126第六章信赖域方法P86-8147第七章非线性最小二乘问题P98-1,2,6188第八章最优性条件P112-1,2,5,6239第九章罚函数法P132,1-(1)、2-(1)、3-(3),62610第十一章二次规划习题11P178-1(1),5291第一章最优化理论基础-P13习题1(1)、2(3)(4)、3、4 1.验证下列各集合是凸集:(1)S={(x1,x2)|2x1+x2≥1,x1−2x2≥1};需要验证:根据凸集的定义,对任意的x(x1,x2),y(y1,y2)∈S及任意的实数λ∈[0,1],都有λx+(1−λ)y∈S.即,(λx1+(1−λ)y1,λx2+(1−λ)y2)∈S证:由x(x1,x2),y(y1,y2)∈S得到,{2x1+x2≥1,x1−2x2≥12y1+y2≥1,y1−2y2≥1(1)1把(1)中的两个式子对应的左右两部分分别乘以λ和1−λ,然后再相加,即得λ(2x1+x2)+(1−λ)(2y1+y2)≥1,λ(x1−2x2)+(1−λ)(y1−2y2)≥1(2)合并同类项,2(λx1+(1−λ)y1)+(λx2+(1−λ)y2)≥1,(λx1+(1−λ)y1)−2(λx2+(1−λ)y2)≥1(3)证毕.2.判断下列函数为凸(凹)函数或严格凸(凹)函数:(3)f(x)=x21−2x1x2+x22+2x1+3x2首先二阶导数连续可微,根据定理1.5,f在凸集上是(I)凸函数的充分必要条件是∇2f(x)对一切x为半正定;(II)严格凸函数的充分条件是∇2f(x)对一切x为正定。


最优化方法大作业---------用优化算法求解函数最值问题摘要最优化(optimization) 是应用数学的重要研究领域.它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。
最优化问题一般包括最小化问题和最大化问题,而最大化问题可以通过简单的转化使之成最最小化问题。
最小化问题分为两类,即约束最小化和无约束最小化问题。
在此报告中,前两个问题属于无约束最小化问题的求解,报告中分别使用了“牛顿法”和“共轭梯度法”。
后两个问题属于有约束最小化问题的求解,报告中分别用“外点法”和“内点法”求解。
虽然命名不一样,其实质都是构造“惩罚函数”或者“障碍函数”,通过拉格朗日乘子法将有约束问题转化为无约束问题进行求解。
再此报告中,“外点法”和“内点法”分别用了直接求导和调用“牛顿法”来求解无约束优化问题。
在此实验中,用“共轭梯度法”对“牛顿法”所解函数进行求解时出现错误,报告中另取一函数用“共轭梯度法”求解得到正确的结果。
此实验中所有的函数其理论值都是显见的,分析计算结果可知程序正确,所求结果误差处于可接受范围内。
报告中对所用到的四种方法在其使用以前都有理论说明,对“外点法”中惩罚函数和“内点法”中障碍函数的选择也有相应的说明,另外,对此次试验中的收获也在报告的三部分给出。
本报告中所用程序代码一律用MATLAB编写。
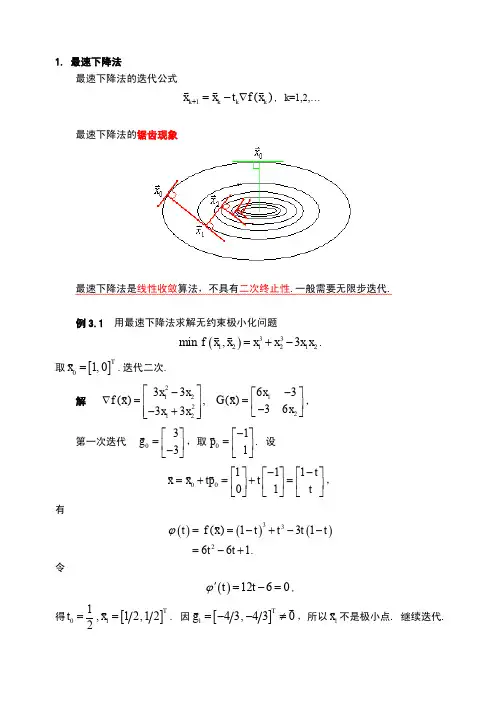
【关键字】函数最优化牛顿法共轭梯度法内点法外点法 MATLAB一,问题描述1,分别用共轭梯度发法和牛顿法来求解一下优化问题()()()()()441432243221102510min x x x x x x x x x f -+-+-++=2, 分别用外点法和内点发求解一下优化问题⎩⎨⎧≥-++01.min 212231x x t s x x二、问题求解1.1 用牛顿法求解()()()()()441432243221102510min x x x x x x x x x f -+-+-++=1.1.1问题分析:取步长为1而沿着牛顿方向迭代的方法称为牛顿法,在牛顿法中,初始点的取值随意,在以后的每次迭代中,()[]()k k k k x f x f x x ∇∇-=-+121,直到终止条件成立时停止。
最优化方法大作业---------用优化算法求解函数最值问题摘要最优化(optimization) 是应用数学的重要研究领域.它是研究在给定约束之下如何寻求某些因素(的量),以使某一(或某些)指标达到最优的一些学科的总称。
最优化问题一般包括最小化问题和最大化问题,而最大化问题可以通过简单的转化使之成最最小化问题。
最小化问题分为两类,即约束最小化和无约束最小化问题。
在此报告中,前两个问题属于无约束最小化问题的求解,报告中分别使用了“牛顿法”和“共轭梯度法”。
后两个问题属于有约束最小化问题的求解,报告中分别用“外点法”和“内点法”求解。
虽然命名不一样,其实质都是构造“惩罚函数”或者“障碍函数”,通过拉格朗日乘子法将有约束问题转化为无约束问题进行求解。
再此报告中,“外点法”和“内点法”分别用了直接求导和调用“牛顿法”来求解无约束优化问题。
在此实验中,用“共轭梯度法”对“牛顿法”所解函数进行求解时出现错误,报告中另取一函数用“共轭梯度法”求解得到正确的结果。
此实验中所有的函数其理论值都是显见的,分析计算结果可知程序正确,所求结果误差处于可接受范围内。
报告中对所用到的四种方法在其使用以前都有理论说明,对“外点法”中惩罚函数和“内点法”中障碍函数的选择也有相应的说明,另外,对此次试验中的收获也在报告的三部分给出。
本报告中所用程序代码一律用MATLAB编写。
【关键字】函数最优化牛顿法共轭梯度法内点法外点法 MATLAB一,问题描述1,分别用共轭梯度发法和牛顿法来求解一下优化问题()()()()()441432243221102510min x x x x x x x x x f -+-+-++=2, 分别用外点法和内点发求解一下优化问题⎩⎨⎧≥-++01.min 212231x x t s x x二、问题求解1.1 用牛顿法求解()()()()()441432243221102510min x x x x x x x x x f -+-+-++=1.1.1问题分析:取步长为1而沿着牛顿方向迭代的方法称为牛顿法,在牛顿法中,初始点的取值随意,在以后的每次迭代中,()[]()k k k k x f x f x x ∇∇-=-+121,直到终止条件成立时停止。
研究生《最优化方法》课程实验(第一部分)function a=li_H(x1,x2,f1,f2)t1=0.00001;t2=0.00001;t3=0.0001;a=0;if norm(grad(x2))>=t3a=1;endif (norm(x2-x1))/(norm(x1)+1)>=t1a=1;endif (abs(f2-f1))/(abs(f1)+1)>=t2a=1;endend---------------------------------------------------------------------------------------------------------------------- function t= line(f,a,b,e)B=0.618;t2=a+B *(b-a);hanshu2=subs(f,t2);t1=a+b-t2;f1=subs(f,t1);while abs(t1-t2)>=eif f1<=f2b=t2;t2=t1;f2=f1;t1=a+b-t2;f1=subs(f,t1);elsea=t1;t1=t2;f1=f2;t2=a+B *(b-a);f2=subs(f,t2);endendtb=0.5*(t1+t2);fb=subs(f,tb);f2=tb;---------------------------------------------------------------------------------------------------------------------- function y=qujian(x,p)t0=0.000001;h=0.5;y0=fv(x+t0*p);t2=t0+h;y2=fv(x+t2*p);if y2>=y0t1=t2;y1=y2;h=-h;t2=t0+h;y2=fv(x+t2*p);while(y2<=y0)t1=t0;y1=y0;t0=t2;y0=y2;h=2*h;t2=t0+h;y2=fv(x+t2*p);enda=min(t1,t2);b=max(t1,t2);elset1=t0;y1=y0;t0=t2;y0=y2;h=2*h;t2=t0+h;y2=fv(x+t2*p);while(y2<=y0)t1=t0;y1=y0;t0=t2;y0=y2;h=2*h;t2=t0+h;y2=fv(x+t2*p);enda=min(t1,t2);b=max(t1,t2);endsq=[a,b];end----------------------------------------------------------------------------------------------------------------------syms tq=1;f=input(' 请输入目标函数: ','s');M=sym(input(' 请输入目标函数的变量: ','s'));x0=input(' 请输入计算的初值: ');f0=subs(f,M,x0);g=jacobian(f,M);g0=subs(g,M,x0);p0=-g0;H0=eye(length(M));x1=x0-t*p0;yt=subs(f,M,x1);v=qujian (yt,0.001,0);t0=line(yt,v(1),v(3),0.001);x1=x0-t0*p0;f1=subs(f,M,x1);g1=subs(g,M,x1);xk=x0;xk1=x1;Hk=H0;gk=g0;gk1=g1;disp('中间运行结果')disp('n=1')disp('x=')fprintf(1,'%7.5f\n',xk')fprintf(1,'f(x)=%7.5f\n',f1)n=1;fk=f0;fk1=f1;flag= li_H(xk,xk1,fk,fk1);while flag==0n=n+1;sk=xk1-xk;yk=gk1-gk;Hk1=Hk+(sk'*sk)/(sk*yk')-(Hk*yk'*yk*Hk)/(yk*Hk*yk');pk1=Hk1*gk1';xk=xk1;xk1=xk-t*pk1';yt=subs(f,M,xk1);v=qujian(yt,0.001,0);tk=line(yt,v(1),v(3),0.001);xk1=xk-tk*pk1' ;fk=subs(f,M,xk);gk=subs(g,M,xk);fk1=subs(f,M,xk1);gk1=subs(g,M,xk1);fprintf(1,'n=%7.5f\n',n)disp('x=')fprintf(1,'%7.5f\n',xk1)fprintf(1,'f(x)=%7.5f\n',fk1)flag= li_H(xk,xk1,fk,fk1);if flag==0disp('不是极小点需要继续迭代')endendif q==1disp(' 目标函数的最优解是:');fprintf(1,' %7.5f\n',xk);disp(' 迭代次数为n=')fprintf(1,'%7.5f\n',n)disp('最优解是:')fprintf(1,'%7.5f\n',fk1)end----------------------------------------------------------------------------------------------------------------------请输入目标函数: x1^2+x2^2+x3^2+x4^2请输入目标函数的变量: [x1 x2 x3 x4] 请输入计算的初值: [1 0 1 0]中间运行结果n=1x=1.000000.000001.000000.00000f(x)=0.00023n=2.00000x=0.005210.000000.005210.00000f(x)=0.00005不是极小点需要继续迭代n=3.00000x=0.002540.000000.002540.00000f(x)=0.00001不是极小点需要继续迭代n=4.00000x=0.001240.000000.001240.00000f(x)=0.00000不是极小点需要继续迭代n=5.00000x=0.000600.000000.000600.00000f(x)=0.00000目标函数的最优解是:0.0001240.000000.0001240.00000迭代次数为n=5.00000最有解是:0.00000>>请输入目标函数: x1^4+2*x2^4+x3^4+x4^4+2*x5^4 请输入目标函数的变量: [x1 x2 x3 x4 x5] 请输入计算的初值: [1 0 1 0 0]中间运行结果n=1x=1.000000.000001.000000.000000.00000f(x)=0.02908n=2.00000x=-0.080260.000000.162550.000000.00000f(x)=0.00060不是极小点需要继续迭代n=3.00000x=0.001860.00000-0.006110.000000.00000f(x)=0.00000不是极小点需要继续迭代n=4.00000x=-0.000700.00000-0.000430.000000.00000f(x)=0.00000目标函数的最优解是:0.001860.00000-0.006110.000000.00000迭代次数为n=4.00000最有解是:0.00000>>。
第一章最优化问题与数学预备知识最优化分支:线性规划,整数规划,几何规划,非线性规划,动态规划。
又称规划论。
应用最优化方法解决问题时一般有以下几个特点:1. 实用性强2. 采用定量分析的科学手段3. 计算量大,必须借助于计算机4. 理论涉及面广应用领域:工业,农业,交通运输,能源开发,经济计划,企业管理,军事作战……。
§1.1 最优化问题实例最优化问题:追求最优目标的数学问题。
经典最优化理论:(1) 无约束极值问题:),,,(opt 21n x x x f(),,,(min 21n x x x f 或),,,(max 21n x x x f )其中,),,,(21n x x x f 是定义在n 维空间上的可微函数。
解法(求极值点):求驻点,即满足⎪⎪⎩⎪⎪⎨⎧='='='0),,(0),,(0),,(11121n x n x n x x x f x x f x x f n并验证这些驻点是否极值点。
(2) 约束极值问题:),,,(opt 21n x x x fs.t. )(,,2,1,0),,,(21n l l j x x x h n j <==解法:采用Lagrange 乘子法,即将问题转化为求Lagrange 函数),,(),,,(),,;,,,(1121121n j j lj n l n x x h x x x f x x x L λλλ∑=+=的无约束极值问题。
近代最优化理论的实例:例1 (生产计划问题) 设某工厂有3种资源B 1,B 2,B 3,数量各为b 1,b 2,b 3,要生产10种产品A 1,…,A 10 。
每生产一个单位的A j 需要消耗B i 的量为a ij ,根据合同规定,产品A j 的量不少于d j ,再设A j 的单价为c j 。
问如何安排生产计划,才能既完成合同,又使总收入最多?(线性规划问题)数学模型:设A j 的计划产量为 j x ,z 为总收入。
项目一 一维搜索算法(一)[实验目的]编写加步探索法、对分法、Newton 法的程序。
[实验准备]1.掌握一维收搜索中搜索区间的加步探索法的思想及迭代步骤; 2.掌握对分法的思想及迭代步骤;3.掌握Newton 法的思想及迭代步骤。
[实验内容及步骤]编程解决以下问题:1.用加步探索法确定一维最优化问题的搜索区间,要求选取.加步探索法算法的计算步骤: (1)选取初始点,计算.给出初始步长,加步系数,令。
(2) 比较目标函数值.令k k k h t t +=+1,计算 )(11++=k k t ϕϕ,若k k ϕϕ<+1,转(3),否则转(4)。
(3) 加大探索步长.令,同时,令,转(2)。
(4) 反向探索.若,转换探索方向,令,转(2)。
否则,停止迭代,令。
加步探索法算法的计算框图12)(min 30+-=≥t t t t ϕ2,1,000===αh t ])0[)(0[max 00t t t ,或,∈⊂∞+∈)(00t ϕϕ=00>h 1α>0=k k k h h α=+1,k t t =,1+=k k t t 1k k =+0=k ,k k h h -=1+=k t t 11min{}max{}k k a t t b t t ++==,,,程序清单加步探索法算法程序见附录1实验结果运行结果为:2.用对分法求解,已知初始单谷区间,要求按精度,分别计算.对分法迭代的计算步骤:(1)确定初始搜索区间],[b a ,要求。
(2) 计算],[b a 的中点)(21b ac +=. (3) 若0)(<'c ϕ,则c a = ,转(4);若0)(='c ϕ,则c t =*,转(5);若0)(>'c ϕ,则c b = ,转(4).(4) 若ε<-||b a ,则)(21*b a t +=,转(5);否则转(2).(5) 打印*t ,结束对分法的计算框图)2()(min +=t t t ϕ]5,3[],[-=b a 3.0=ε001.0=ε'()0'()0a b ϕϕ<>,程序清单对分法程序见附录2实验结果运行结果为:3.用Newton 法求解,已知初始单谷区间,要求精度.Newton 法的计算步骤(1) 确定初始搜索区间],[b a ,要求 (2) 选定0t(3) 计算(4) 若 ε≥-||0t t ,则t t =0,转(3);否则转(5).(5) 打印 ,结束.Newton 法的计算框图12)(min 3+-=t t t ϕ]1,0[],[=b a 01.0=ε'()0'()0a b ϕϕ<>,000'()/"()t t t t ϕϕ=-()t t ϕ,程序清单Newton 法程序见附录3实验结果运行结果为:项目二 一维搜索算法(二)[实验目的]编写黄金分割法、抛物线插值法的程序。
研究生《最优化方法》课程实验(第一部分)
function a=li_H(x1,x2,f1,f2)
t1=0.00001;t2=0.00001;t3=0.0001;
a=0;
if norm(grad(x2))>=t3
a=1;
end
if (norm(x2-x1))/(norm(x1)+1)>=t1
a=1;
end
if (abs(f2-f1))/(abs(f1)+1)>=t2
a=1;
end
end
---------------------------------------------------------------------------------------------------------------------- function t= line(f,a,b,e)
B=0.618;
t2=a+B *(b-a);
hanshu2=subs(f,t2);
t1=a+b-t2;
f1=subs(f,t1);
while abs(t1-t2)>=e
if f1<=f2
b=t2;
t2=t1;
f2=f1;
t1=a+b-t2;
f1=subs(f,t1);
else
a=t1;
t1=t2;
f1=f2;
t2=a+B *(b-a);
f2=subs(f,t2);
end
end
tb=0.5*(t1+t2);
fb=subs(f,tb);
f2=tb;
---------------------------------------------------------------------------------------------------------------------- function y=qujian(x,p)
t0=0.000001;h=0.5;
y0=fv(x+t0*p);t2=t0+h;y2=fv(x+t2*p);
if y2>=y0
t1=t2;y1=y2;h=-h;
t2=t0+h;y2=fv(x+t2*p);
while(y2<=y0)
t1=t0;y1=y0;t0=t2;y0=y2;h=2*h;
t2=t0+h;y2=fv(x+t2*p);
end
a=min(t1,t2);b=max(t1,t2);
else
t1=t0;y1=y0;t0=t2;y0=y2;h=2*h;t2=t0+h;y2=fv(x+t2*p);
while(y2<=y0)
t1=t0;y1=y0;t0=t2;y0=y2;h=2*h;
t2=t0+h;y2=fv(x+t2*p);
end
a=min(t1,t2);b=max(t1,t2);
end
sq=[a,b];
end
----------------------------------------------------------------------------------------------------------------------syms t
q=1;
f=input(' 请输入目标函数: ','s');
M=sym(input(' 请输入目标函数的变量: ','s'));
x0=input(' 请输入计算的初值: ');
f0=subs(f,M,x0);
g=jacobian(f,M);
g0=subs(g,M,x0);
p0=-g0;
H0=eye(length(M));
x1=x0-t*p0;
yt=subs(f,M,x1);
v=qujian (yt,0.001,0);
t0=line(yt,v(1),v(3),0.001);
x1=x0-t0*p0;
f1=subs(f,M,x1);
g1=subs(g,M,x1);
xk=x0;
xk1=x1;
Hk=H0;
gk=g0;
gk1=g1;
disp('中间运行结果')
disp('n=1')
disp('x=')
fprintf(1,'%7.5f\n',xk')
fprintf(1,'f(x)=%7.5f\n',f1)
n=1;
fk=f0;
fk1=f1;
flag= li_H(xk,xk1,fk,fk1);
while flag==0
n=n+1;
sk=xk1-xk;
yk=gk1-gk;
Hk1=Hk+(sk'*sk)/(sk*yk')-(Hk*yk'*yk*Hk)/(yk*Hk*yk');
pk1=Hk1*gk1';
xk=xk1;
xk1=xk-t*pk1';
yt=subs(f,M,xk1);
v=qujian(yt,0.001,0);
tk=line(yt,v(1),v(3),0.001);
xk1=xk-tk*pk1' ;
fk=subs(f,M,xk);
gk=subs(g,M,xk);
fk1=subs(f,M,xk1);
gk1=subs(g,M,xk1);
fprintf(1,'n=%7.5f\n',n)
disp('x=')
fprintf(1,'%7.5f\n',xk1)
fprintf(1,'f(x)=%7.5f\n',fk1)
flag= li_H(xk,xk1,fk,fk1);
if flag==0
disp('不是极小点需要继续迭代')
end
end
if q==1
disp(' 目标函数的最优解是:');
fprintf(1,' %7.5f\n',xk);
disp(' 迭代次数为n=')
fprintf(1,'%7.5f\n',n)
disp('最优解是:')
fprintf(1,'%7.5f\n',fk1)
end
----------------------------------------------------------------------------------------------------------------------
请输入目标函数: x1^2+x2^2+x3^2+x4^2
请输入目标函数的变量: [x1 x2 x3 x4] 请输入计算的初值: [1 0 1 0]
中间运行结果
n=1
x=
1.00000
0.00000
1.00000
0.00000
f(x)=0.00023
n=2.00000
x=
0.00521
0.00000
0.00521
0.00000
f(x)=0.00005
不是极小点需要继续迭代
n=3.00000
x=
0.00254
0.00000
0.00254
0.00000
f(x)=0.00001
不是极小点需要继续迭代
n=4.00000
x=
0.00124
0.00000
0.00124
0.00000
f(x)=0.00000
不是极小点需要继续迭代
n=5.00000
x=
0.00060
0.00000
0.00060
0.00000
f(x)=0.00000
目标函数的最优解是:
0.000124
0.00000
0.000124
0.00000
迭代次数为n=
5.00000
最有解是:
0.00000
>>
请输入目标函数: x1^4+2*x2^4+x3^4+x4^4+2*x5^4 请输入目标函数的变量: [x1 x2 x3 x4 x5] 请输入计算的初值: [1 0 1 0 0]
中间运行结果
n=1
x=
1.00000
0.00000
1.00000
0.00000
0.00000
f(x)=0.02908
n=2.00000
x=
-0.08026
0.00000
0.16255
0.00000
0.00000
f(x)=0.00060
不是极小点需要继续迭代
n=3.00000
x=
0.00186
0.00000
-0.00611
0.00000
0.00000
f(x)=0.00000
不是极小点需要继续迭代
n=4.00000
x=-0.00070
0.00000
-0.00043
0.00000
0.00000
f(x)=0.00000
目标函数的最优解是:
0.00186
0.00000
-0.00611
0.00000
0.00000
迭代次数为n=
4.00000
最有解是:
0.00000
>>。