2021春人教版数学七年级下册5.4《平移》课件 (共34张PPT)

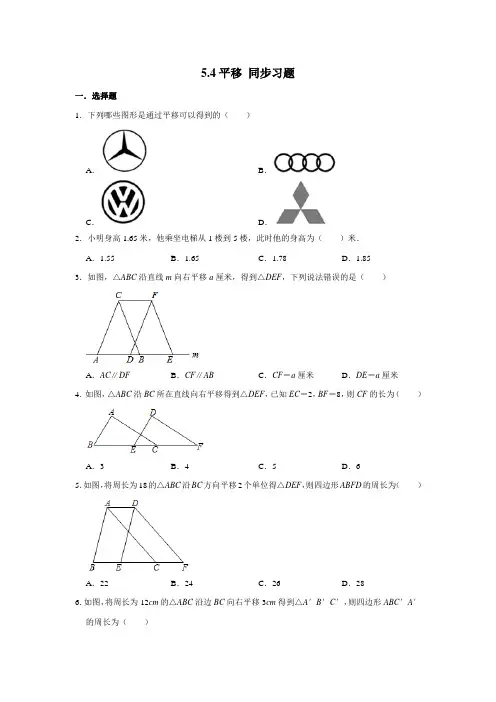
5.4平移同步习题一．选择题1．下列哪些图形是通过平移可以得到的（）A．B．C．D．2．小明身高1.65米，他乘坐电梯从1楼到5楼，此时他的身高为（）米．A．1.55 B．1.65 C．1.78 D．1.853．如图，△ABC沿直线m向右平移a厘米，得到△DEF，下列说法错误的是（）A．AC∥DF B．CF∥AB C．CF＝a厘米D．DE＝a厘米4．如图，△ABC沿BC所在直线向右平移得到△DEF，已知EC＝2，BF＝8，则CF的长为（）A．3 B．4 C．5 D．65．如图，将周长为18的△ABC沿BC方向平移2个单位得△DEF，则四边形ABFD的周长为（）A．22 B．24 C．26 D．286．如图，将周长为12cm的△ABC沿边BC向右平移3cm得到△A′B′C′，则四边形ABC′A′的周长为（）A．17cm B．18cm C．19cm D．20cm7．如图，在长为5，宽为3的公园图纸上准备设计两条款均为1的小路，求两条小路面积和为（）A．12 B．10 C．8 D．78．如图，直线L1是由直线L2平移得到的，若∠1＝56°，则∠2的度数为（）A．∠2＝56°B．∠2＝124°C．∠2＝134°D．∠2＝114°9．如图，∠1＝50°，直线a平移后得到直线b，则∠2﹣∠3＝（）A．130°B．120°C．100°D．80°10．如图，将边长为12cm的正方形纸片ABCD沿其对角线AC剪开，再把△ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分（见图中阴影）的面积为32cm2，则它移动的距离AA′等于（）A．6cm B．8cm C．6cm或8cm D．4cm或8cm二．填空题11．如图，将△ABC沿着射线BC的方向平移，得到△DEF，若EF＝13，EC＝7，则平移的距离为．12．如图，有一个长为20m，宽为10m的长方形草地，在草地中间有两条小路，两条小路的任何地方宽度都是1m，那么这片草地的面积是平方米．13．如图，已知线段DE是由线段AB平移而得，AB＝DC＝5cm，EC＝6cm，则△DCE的周长是cm．14．如图，将长为5cm，宽为3cm的长方形ABCD先向右平移2cm，再向下平移1cm，得到长方形A'B'C'D'，则阴影部分的面积为cm2．15．如图，直线m与∠AOB的一边射线OB相交，∠1＝30°，向上平移直线m得到直线n，与∠AOB的另一边射线OA相交，则∠2+∠3＝．三．解答题16．三角形ABC在正方形网格中的位置如图所示，网格中每个小方格的边长为1个单位长度，请根据下列提示作图．（1）将三角形ABC向上平移3个单位长度，再向右平移2个单位长度得到三角形A'B'C'，画出三角形A'B'C'．（2）连接AC'，BC'，则三角形ABC'的面积为．17．如图，网格中每个小正方形的边长为1个单位长度，三角形ABC中，点A、点B、点C均在格点上．（1）在图1中，过点C画出线段AB的垂线；（2）在图1中，过点B画出直线BM，使BM∥AC；（3）在图2中，先将三角形ABC向右平移5个单位长度，再向上平移4个单位长度，得到三角形A1B1C1，画出三角形A1B1C1．18．如图，在长方形地块内修筑同样宽的两条“之”字路，余下部分作为耕地，道路宽为2米时耕地面积为多少平方米？参考答案一．选择题1．解：A、通过旋转得到，故本选项错误；B、通过平移得到，故本选项正确；C、通过轴对称得到，故本选项错误；D、通过旋转得到，故本选项错误．故选：B．2．解：身高1.65米的小明乘电梯从1楼上升到5楼，则此时小明的身高为1.65米，故选：B．3．解：∵△ABC沿直线m向右平移a厘米，得到△DEF，∴AC∥DF，CF∥AB，CF＝AD＝BE＝a厘米．故选：D．4．解：由平移的性质可知，BC＝EF，∴BE＝CF，∵BF＝8，EC＝2，∴BE+CF＝8﹣2＝6，∴CF＝BE＝3，故选：A．5．解：∵△ABC沿BC方向平移2个单位得到△DEF，∴AD＝CF＝2，AC＝DF，∴四边形ABFD的周长＝AB+（BC+CF）+DF+AD＝AB+BC+AC+AD+CF，∵△ABC的周长＝18，∴AB+BC+AC＝18，∴四边形ABFD的周长＝18+2+2＝22．故选：A．6．解：由题意知，BB'＝CC'＝AA'＝3cm，则四边形ABC'A'的周长＝12+3+3＝18cm．故选：B．7．解：由图可知，两条小路的面积＝（3﹣1）×（5﹣1）＝8．8．解：∵直线L1是由直线L2平移得到的，∴L1∥L2，∴∠3＝∠1＝56°，∵∠3+∠2＝180°，∴∠2＝180°﹣56°＝124°．故选：B．9．解：如图．∵直线a平移后得到直线b，∴a∥b，∴∠1+∠ABO＝180°，∵∠1＝50°，∴∠ABO＝130°，∵∠3＝∠BOC，∠2＝∠BOC+∠ABO，∴∠2﹣∠3＝∠2﹣∠BOC＝∠ABO＝130°．故选：A．10．解：设AC交A′B′于H，∵∠A＝45°，∠D＝90°∴△A′HA是等腰直角三角形设AA′＝x，则阴影部分的底长为x，高A′D＝12﹣x ∴x•（12﹣x）＝32，解得x1＝4，x2＝8，即AA′＝4cm或AA′＝8cm二．填空题11．解：∵△ABC沿着射线BC的方向平移，得到△DEF，∴BE＝CF，∵EF＝13，EC＝7，∴CF＝EF﹣CE＝13﹣7＝6，即平移的距离为6．故答案为6．12．解：（20﹣1×2）×10＝18×10＝180（平方米）．故这片草地的面积是180平方米．故答案为：180．13．解：∵线段DE是由线段AB平移而得，∴DE＝AB＝5cm，∴△DCE的周长＝DE+CE+CD＝5+5+6＝16（cm）．答：△DCE的周长是16cm．故答案为：16．14．解：由题意，阴影部分是矩形，长为5﹣2＝3（cm），宽为3﹣1＝2（cm），∴阴影部分的面积＝2×3＝6（cm2），故答案为6．15．解：作OC∥m，如图，∵直线m向上平移直线m得到直线n，∴m∥n，∴OC∥n，∴∠1＝∠OBC＝30°，∠2+∠AOC＝180°，∴∠2+∠3＝180°+30°＝210°．故答案为210°．三．解答题16．解：（1）如图，△A'B'C'即为所求．（2）S△ABC′＝×5×3＝7.5，故答案为：7.5．17．解：（1）如图，CD为所作；（2）如图，BM为所作；（3）如图，△A1B1C1为所作．18．解：平移后可得道路的长和宽，再利用矩形的面积公式进行计算即可．解：平移后得耕地长为()202-米，宽为()322-米，面积为()()2023221830540-⨯-=⨯=（平方米）．。

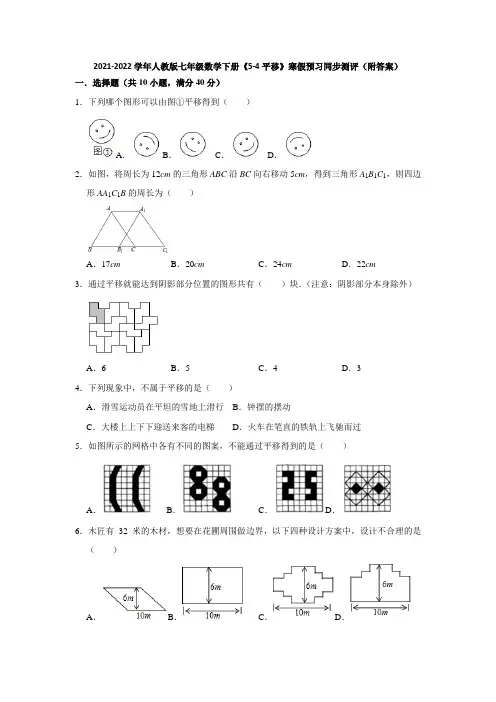
2021-2022学年人教版七年级数学下册《5-4平移》寒假预习同步测评（附答案）一．选择题（共10小题，满分40分）1．下列哪个图形可以由图①平移得到（）A．B．C．D．2．如图，将周长为12cm的三角形ABC沿BC向右移动5cm，得到三角形A1B1C1，则四边形AA1C1B的周长为（）A．17cm B．20cm C．24cm D．22cm3．通过平移就能达到阴影部分位置的图形共有（）块．（注意：阴影部分本身除外）A．6B．5C．4D．34．下列现象中，不属于平移的是（）A．滑雪运动员在平坦的雪地上滑行B．钟摆的摆动C．大楼上上下下迎送来客的电梯D．火车在笔直的铁轨上飞驰而过5．如图所示的网格中各有不同的图案，不能通过平移得到的是（）A．B．C．D．6．木匠有32米的木材，想要在花圃周围做边界，以下四种设计方案中，设计不合理的是（）A．B．C．D．7．如图，将△ABE向右平移2cm得到△DCF．如果△ABE的周长是16cm，那么四边形ABFD 的周长是（）A．16 cm B．18 cm C．20 cm D．21 cm8．如图，直角△ABC沿射线BC的方向平移3个单位长度，得到△DEF，线段DE交AC于点H，已知AB＝5，DH＝2，则图中阴影部分的面积为（）A．12B．24C．48D．不能确定9．下列现象属于平移的是（）①打气筒活塞的轮复运动，②电梯的上下运动，③钟摆的摆动，④转动的门，⑤汽车在一条笔直的马路上行走．A．③B．②③C．①②④D．①②⑤10．如图，两个相同的四边形重叠在一起，将其中一个四边形沿DA方向平移AE长，则下列关于阴影部分面积的说法正确的是（）A．S阴影＝S四边形EHGF B．S阴影＝S四边形DHGKC．S阴影＝S四边形EDKF D．S阴影＝S四边形EDKF﹣S四边形DHGK二．填空题（共6小题，满分30分）11．如图：矩形ABCD的对角线AC＝10，BC＝8，则图中五个小矩形的周长之和为．12．某酒店准备进行装修，把楼梯铺上地毯．已知楼梯的宽度是2米，楼梯的总长度为8米，总高度为6米，其侧面如图所示．已知这种地毯每平方米的售价是50元．请你帮老板算下，购买地毯至少需要花费元．13．如图所示，将△ABC沿BC边平移得到△A1B1C1，若BC1＝8，B1C＝2，则平移距离为．14．如图，要设计一幅长为3xcm，宽为2ycm的长方形图案，其中有两横两竖的彩条，横彩条的宽度为acm，竖彩条的宽度为bcm，问空白区域的面积是．15．如图，面积为12cm2的△ABC沿BC方向平移至△DEF位置，平移的距离是边BC长的两倍，则图中的四边形ACED的面积是cm2．16．已知△ABC面积为24，将△ABC沿BC的方向平移到△A′B′C′的位置，使B′和C 重合，连接AC′交A′C于D，则△C′DC的面积为．三．解答题（共5小题，满分50分）17．如图：在边长为1个单位长度的小正方形组成的网格中，△ABC的顶点A、B、C在小正方形的顶点上，将△ABC向右平移3单位，再向上平移2个单位得到三角形A1B1C1．（1）在网格中画出三角形A1B1C1．（2）求三角形A1B1C1的面积．18．如图，AN∥DM，点B在AN上（点B与点A不重合），点C在DM上（点C与点D 不重合），∠DAB＝∠BCD．（1）那么AD∥BC吗？试说明理由；（2）若平行移动BC，保持∠ABC＝100°；点E、F在DC上，且满足∠F AC＝∠BAC，AE平分∠DAF．①小红发现可求出∠EAC的度数，请你帮助小红写出求∠EAC的度数的过程；②在平行移动BC的过程中，是否存在某种情况，使∠BCA＝∠DEA？若存在，请直接写出∠BCA的度数；若不存在，请说明理由．19．小明同学在完成七年级下册数学第1章的线上学习后，遇到了一些问题，请你帮他解决（1）如图1，已知AB∥CD，则∠AEC＝∠BAE+∠DCE成立吗？请说明理由．（2）如图2，已知AB∥CD，BE平分∠ABC，DE平分∠ADC．BE、DE所在直线交于点E，若∠F AD＝50°，∠ABC＝40°，求∠BED的度数．（3）将图2中的线段BC沿DC所在的直线平移，使得点B在点A的右侧，若∠F AD＝m°，∠ABC＝n°，其他条件不变，得到图3，请你求出∠BED的度数（用含m，n的式子表示）．20．宾馆重新装修后，准备在大厅的主楼梯上铺设一种红地毯，已知这种地毯每平方米售价40元，主楼梯道宽2米，其侧面如图所示，求买地毯至少需要多少元？21．在一次数学课上，李老师让同学们独立完成课本第23页7．选择题（2）如图1，如果AB∥CD∥EF，那么∠BAC+∠ACE+∠CEF＝（）（A）180°（B）270°（C）360°（D）540°（1）请写出这道题的正确选项；（2）在同学们都正确解答这道题后，李老师对这道题进行了改编：如图2，AB∥EF，请直接写出∠BAD，∠ADE，∠DEF之间的数量关系．（3）善于思考的龙洋同学想：将图1平移至与图2重合（如图3所示）当AD，ED分别平分∠BAC，∠CEF时，∠ACE与∠ADE之间有怎样的数量关系？请你直接写出结果，不需要证明．（4）彭敏同学又提出来了，如果像图4这样，AB∥EF，当∠ACD＝90°时，∠BAC、∠CDE和∠DEF之间又有怎样的数量关系？请你直接写出结果，不需要证明．参考答案一．选择题（共10小题，满分40分）1．解：故选：C．2．解：∵三角形ABC沿BC向右移动5cm，得到三角形A1B1C1，∴AC＝A1C1，AA1＝CC1＝5cm，∵AB+BC+AC＝12cm，∴AB+BC+A1C1＝12cm，∴AB+BC+CC1+A1C1+AA1＝12+5+5＝22（cm），即四边形AA1C1B的周长为22cm．故选：D．3．解：通过平移就能达到阴影部分位置的图形共有3块，故选：D．4．解：A、滑雪运动员在平坦的雪地上滑雪，属于平移得到，故本选项不合题意；B、钟摆的摆动，不属于平移得到，故本选项符合题意；C、大楼上上下下迎送来客的电梯，属于平移得到，故本选项不合题意；D、火车在笔直的铁轨上飞驰而过，属于平移得到，故本选项不合题意．故选：B．5．解：A、可以通过平移得到，不符合题意；B、可以通过平移得到，不符合题意；C、不可以通过平移得到，符合题意；D、可以通过平移得到，不符合题意．故选：C．6．解：A、∵垂线段最短，∴平行四边形的另一边一定大于6m，∵2（10+6）＝32m，∴周长一定大于32m；B、周长＝2（10+6）＝32m；C、周长＝2（10+6）＝32m；D、周长＝2（10+6）＝32m；故选：A．7．解：∵△ABE向右平移2cm得到△DCF，∴DF＝AE，∴四边形ABFD的周长＝AB+BE+DF+AD+EF，＝AB+BE+AE+AD+EF，＝△ABE的周长+AD+EF，∵平移距离为2cm，∴AD＝EF＝2cm，∵△ABE的周长是16cm，∴四边形ABFD的周长＝16+2+2＝20cm．故选：C．8．解：∵将Rt△ABC沿射线BC方向平移得到△DEF，∴DE＝AB＝5，∵DH＝2，∴HE＝DE﹣DH＝3，∵∠B＝90°，∴四边形ABEH是梯形，S阴影＝S△DEF﹣S△CEH＝S△ABC﹣S△CEH＝S梯形ABEH＝（AB+HE）•BE＝×（5+3）×3＝12．故选：A．9．解：①②⑤都是平移现象；③④是旋转．故选：D．10．解：∵两个相同的四边形重叠在一起，将其中一个四边形沿DA方向平移AE长，∴阴影的面积+梯形EIKD的面积＝梯形EIKD的面积+梯形DKGH的面积，∴S阴影＝S四边形DHGK，故选：B．二．填空题（共6小题，满分30分）11．解：由勾股定理，得AB＝＝6，将五个小矩形的所有上边平移至AD，所有下边平移至BC，所有左边平移至AB，所有右边平移至CD，∴五个小矩形的周长之和＝2（AB+BC）＝2×（6+8）＝28．故答案为：28．12．解：如图，利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为8米，6米，即可得地毯的长度为6+8＝14（米），地毯的面积为14×2＝28（平方米），故买地毯至少需要28×50＝1400（元）．购买地毯至少需要1400元．故答案为：1400．13．解：∵△ABC沿BC边平移得到△A1B1C1，∴BC＝B1C1，BB1＝CC1，∵BC1＝8，B1C＝2，∴BB1＝CC1＝，即平移距离为3，故答案为：3．14．解：可设想将彩条平移到如图所示的长方形的靠边处，将9个小矩形组合成“整体”，一个大的空白长方形，则该长方形的面积就是空白区域的面积．而这个大长方形长（3x﹣2b）cm，宽为（2y﹣2a）cm．所以空白区域的面积为（3x﹣2b）（2y﹣2a）cm2．即（6xy﹣6xa﹣4by+4ab）cm2．故答案为：（6xy﹣6xa﹣4by+4ab）cm2．15．解：∵平移的距离是边BC长的两倍，∴BC＝CE＝EF，∴四边形ACED的面积是三个△ABC的面积；∴四边形ACED的面积＝12×3＝36cm2．16．解：∵AB∥A′B′，且BC＝CC′∴D为A′B′的中点，又∵BC＝CC′，∴S△C′DC＝S△ABC＝×24＝12．三．解答题（共4小题，满分50分）17．解：（1）如图所示；（2）S△A1B1C1＝×3×3＝．故答案为：．18．（1）解：结论：AD∥BC．理由：∵AB∥CD，∴∠D+∠DAB＝180°，∵∠DAB＝∠BCD，∴∠D+∠BCD＝180°，∴AD∥BC．（2）①∵AD∥BC，∴∠DAB+∠ABC＝180°，∵∠ABC＝100°，∴∠DAB＝80°，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠EAC＝∠DAF+∠F AB＝（∠DAF+∠F AB）＝40°．②存在．理由：∵AD∥BC，∴∠DAC＝∠ACB，∵CD∥AB，∴∠DEA＝∠EAB，∵∠ACB＝∠DEA，∴∠DAC＝∠EAB，∴∠DAE＝∠CAB，∵∠F AC＝∠BAC，AE平分∠DAF，∴∠DAE＝∠EAF＝∠F AC＝∠CAB＝20°，∴∠ACB＝∠DAC＝60°．19．解：（1）如图1中，作EF∥AB，则有EF∥CD，∴∠1＝∠BAE，∠2＝∠DCE，∴∠AEC＝∠1+∠2＝∠BAE+∠DCE．（2）如图2，过点E作EH∥AB，∵AB∥CD，∠F AD＝50°，∴∠F AD＝∠ADC＝50°，∵DE平分∠ADC，∠ADC＝50°，∴∠EDC＝∠ADC＝25°，∵BE平分∠ABC，∠ABC＝40°，∴∠ABE＝∠ABC＝20°，∵AB∥CD，∴AB∥CD∥EH，∴∠ABE＝∠BEH＝20°，∠CDE＝∠DEH＝25°，∴∠BED＝∠BEH+∠DEH＝45°．（3）∠BED的度数改变．过点E作EG∥AB，∵BE平分∠ABC，DE平分∠ADC，∠ABC＝n°，∠ADC＝∠F AD＝m°∴∠ABE＝∠ABC＝n°，∠CDE＝∠ADC＝m°∵AB∥CD，∴AB∥CD∥EG，∴∠BEG＝180°﹣∠ABE＝180°﹣n°，∠CDE＝∠DEG＝m°，∴∠BED＝∠BEG+∠DEG＝180°﹣n°+m°．20．解：如图，利用平移线段，把楼梯的横竖向上向左平移，构成一个矩形，长宽分别为6米，4米，∴地毯的长度为6+4＝10米，地毯的面积为10×2＝20平方米，∴买地毯至少需要20×40＝800元．21．解：（1）∵AB∥CD∥EF，∴∠A+∠ACD＝180°，∠E+∠ECD＝180°，∴∠A+∠ACD+∠E+∠ECD＝360°，即∠BAC+∠ACE+∠CEF＝360°，故选：C．（2）∠BAD+∠DEF＝∠ADE，如图，过D作DG∥AB，∵AB∥EF，∴DG∥AB∥EF，∴∠A＝∠ADG，∠E＝∠EDG，∴∠A+∠E＝∠ADG+∠EDG＝∠ADE；（3）∠C+2∠ADE＝360°，理由：由（1）可得，∠BAC+∠C+∠CEF＝360°，由（2）可得，∠D＝∠BAD+∠DEF，又∵AD，ED分别平分∠BAC，∠CEF，∴∠BAC＝2∠BAD，∠CEF＝2∠DEF，∴2∠BAD+∠C+2∠DEF＝360°，即2（∠BAD+∠DEF）+∠C＝360°，∴∠C+2∠ADE＝360°；（4）过点C作CG∥AB，过点D作DH∥EF，如图，∵AB∥EF，∴CG∥AB∥EF∥DH，∴∠BAC+∠ACG＝180°，∠GCD＝∠HDC，∠DEF＝∠HDE，∴∠ACG＝180°﹣∠BAC，∵∠ACD＝90°，∴∠CDH＝∠DCG＝90°﹣∠ACG＝90°﹣（180°﹣∠BAC）＝∠BAC﹣90°，∴∠CDE＝∠BAC﹣90°+∠DEF，∴∠BAC+∠DEF﹣∠CDE＝90°．。