初中数学《分式》单元教学设计以及思维导图
- 格式:doc
- 大小:612.50 KB
- 文档页数:20

分式的基本性质思维导图分式是代数中一种带有变量的表达式,它由分子和分母组成。
分式的基本性质包括:1.分式的加减法:在加减分式时,必须先约分分式,然后对分子分别进行加减运算,分母不变。
2.分式的乘除法:在乘除分式时,可以先将分子和分母分别进行乘除运算,然后约分分式。
3.分式的约分:约分是指将分式化简为最简分式,这通常通过求最大公约数来实现。
4.分式的倒数:倒数是指将分子和分母互换位置,即分子变为分母,分母变为分子。
5.分式的含义:分式表示一个量与另一个量的比值,分子表示被除数,分母表示除数。
1.分式的加减法:在加减分式时,必须先约分分式,然后对分子分别进行加减运算,分母不变。
例如:(2/3) + (4/6) = (2/3) + (2/3) = (2+2)/3 = 4/3(x/2) - (2x/4) = (x/2) - (x/2) = 02.分式的乘除法:在乘除分式时,可以先将分子和分母分别进行乘除运算,然后约分分式。
例如:(2/3) * (4/5) = (24)/(35) = 8/15(x/2) / (2x/4) = (x/2) * (4/2x) = x/4x = 1/43.分式的约分:约分是指将分式化简为最简分式,这通常通过求最大公约数来实现。
例如:8/15 约分为8/15 = 8/5 * 3/3 = 8/5 * 1 = 8/54.分式的倒数:倒数是指将分子和分母互换位置,即分子变为分母,分母变为分子。
例如:1/x 的倒数为x/1 = x5.分式的含义:分式表示一个量与另一个量的比值,分子表示被除数,分母表示除数。
例如:2/3 表示2个物品与3个物品的比值,即2/3。
x/y 表示x个量与y个量的比值,即x/y6.分式的零值:分母不能为零,因为除数不能为零。
如果分母为零,则分式的值为无穷大或不存在。
7.分式的混合运算:分式的混合运算就是分式的加减乘除混合运算,例如:(2x + 3)/(4x - 5) + (6x - 7)/(8x + 9) = (2x + 3)(8x + 9) + (6x - 7)(4x - 5) / (4x - 5)(8x + 9)8.分式的次数: 分式中变量的次数称为分式的次数。



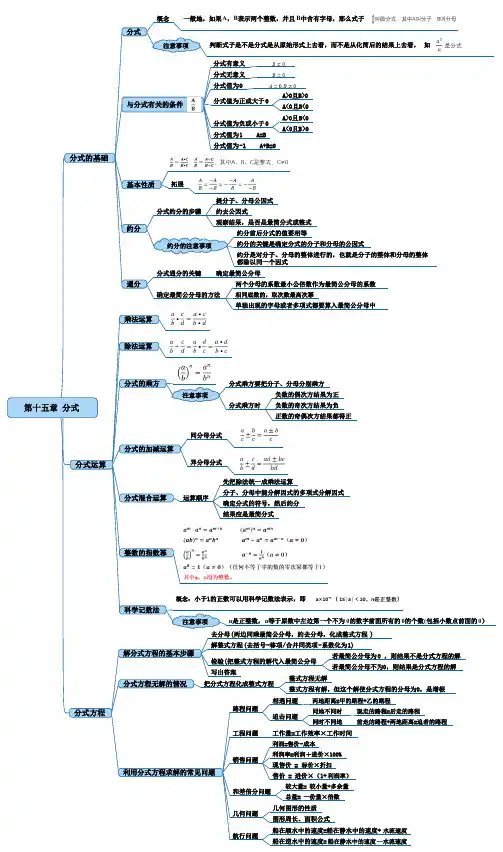
现走的路程=后走的路程前走的路程+两地距离=追者的路程负数的偶次方结果为正负数的奇次方结果为负正数的奇偶次方结果都得正两地距离=甲的路程+乙的路程同地不同时同时不同地一般地,如果A ,B 表示两个整数,并且B 中含有字母,那么式子判断式子是不是分式是从原始形式上去看,而不是从化简后的结果上去看,如A>0且B>0A<0且B<0A>0且B<0A<0且B>0A=B A+B=0提分子、分母公因式约去公因式观察结果,是否是最简分式或整式约分前后分式的值要相等约分的关键是确定分式的分子和分母的公因式约分是对分子、分母的整体进行的,也就是分子的整体和分母的整体都除以同一个因式确定最简公分母两个分母的系数最小公倍数作为最简公分母的系数相同底数的,取次数最高次幂单独出现的字母或者多项式都要算入最简公分母中分式乘方要把分子、分母分别乘方分式乘方时先把除法统一成乘法运算分子、分母中能分解因式的多项式分解因式确定分式的符号,然后约分结果应是最简分式n 是正整数,n 等于原数中左边第一个不为0的数字前面所有的0的个数(包括小数点前面的0)若最简公分母为0 ,则结果不是分式方程的解若最简公分母不为0,则结果是分式方程的解整式方程无解整式方程有解,但这个解使分式方程的分母为0,是增根相遇问题追击问题工作量=工作效率×工作时间利润=售价-成本利润率=利润÷进价×100%现售价 = 标价×折扣售价 = 进价×(1+利润率)较大量= 较小量+多余量总量= 一份量×倍数几何图形的性质图形周长、面积公式船在顺水中的速度=船在静水中的速度+水流速度船在逆水中的速度=船在静水中的速度—水流速度概念注意事项分式有意义分式无意义分式值为0分式值为正或大于0分式值为负或小于0分式值为1分式值为-1拓展分式约分的步骤约分的注意事项分式通分的关键确定最简公分母的方法注意事项同分母分式异分母分式运算顺序概念:小于1的正数可以用科学记数法表示,即注意事项去分母(两边同乘最简公分母,约去分母,化成整式方程)解整式方程(去括号-移项/合并同类项-系数化为1)检验(把整式方程的解代入最简公分母写出答案把分式方程化成整式方程路程问题工程问题销售问题和差倍分问题几何问题航行问题分式与分式有关的条件基本性质约分通分乘法运算除法运算分式的乘方分式的加减运算分式混合运算整数的指数幂科学记数法解分式方程的基本步骤分式方程无解的情况利用分式方程求解的常见问题分式的基础分式运算分式方程第十五章 分式。

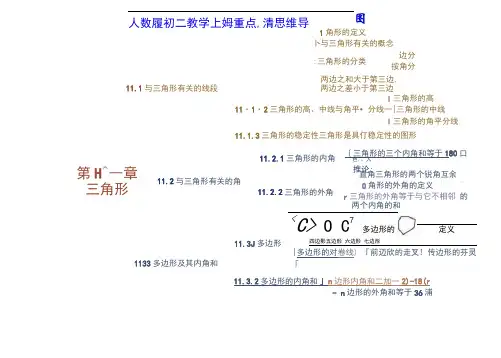
1角形的定义卜与三角形有关的概念I 三角形的高11・1・2三角形的高、中线与角平•分线一|三角形的中线I 三角形的角平分线 11.1.3三角形的稳定性三角形是具仃稳定性的图形<C> O C 7多边形的定义四边影五边形 六边形 七边形|多边形的对卷线) 『前迈欣的走叉! 传边形的芬灵「11.3.2多边形的内角和j n 边形内角和二加一2)-18(r- n 边形的外角和等于36浦人数履初二教学上姆重点,清思维导第H ^一章三角形11.2与三角形有关的角11.2.1三角形的内角色,、人推论;11.2.2三角形的外角{三角形的三个内角和等于180口直角三角形的两个锐角互余< __________________ u L ____________________________ __ 2_2 ________JO 角形的外角的定义r 三角形的外角等于与它不相邻 的两个内角的和:三角形的分类边分 按角分两边之和大于第三边, 11.1与三角形有关的线段两边之差小于第三边11.3J 多边形1133多边形及其内角和fl、11 J.1三角形的边不等边一:角形(三边都不相等)顶点用个大写字母来表示.如A、B、C等腰三角形(底边和腰不相等c的等腹三角形)按边分与三角形有关概念边AB.边BC、边AC角<rtA) /A, ZB,^2C三角形记作5等边三角形«(三边都相等)三角形分类△ ABC对角BC边的对角是/A百箱三角形锐角三角形L及詹金钝角三角形•对边NC的对边是BA.通常简记为c; 从三角形的一个顶点向它的对边所在直线 /X 做垂线,顶点和垂足之间的线段叫做三角 ,学一"形的高线,筒称三角形的高锐角三角形的高 锐角三角形的三条高交于同一点, ------ ---------- 「且在三角形的内部 Pi 在三角形中,一个内角的角平分线与它的Ax 对边相交,这个角的顶点与交点之间的线•7 3段,叫做三角形的角平分线/K !三角形的三条角平分线相交于一点,交点 八”、在三角形的内部,三角形三条角平分线的 LW 交点叫做三角形的内心三角形的高 三角形的高直角三角形的三条高直角顶点钝角三角形的高六;落钝角三角形的三条高不相交于一点, 厂钝角三角形的三条高所在直线相交 于一点11 J.2三角形的高、 中线与角平分线三角形 的中线连结三角形ABC 的顶点A 和它所 对的边BC 的中点D,线段AD 叫 做二角形ABC 的边BC 上的中线 三角形的三条中线相交于一 点,交点在三角形的内部, 三角形三条中线的交点叫做 三角形的重心[ 一.角形的先平分线二角形的稳定性三角形木架的形状不会改变,而四边形木架的形状会改变. [这就是说,三角形是具有稳定的图形,而四边形没有稳定性. &11J.3三角形的稳定性I,三角形的稳定性实例三角形的三个内角的和等于180。
初中数学《分式》单元教学设计以及思维导图 分式 适用年级 八年级 所需时间 课内八课时 主题单元学习概述 1.本章是继整式之后对代数式的进一步的研究。 2.分式是对分数的进一步抽象------字母的意义 3.分数的讨论框架的继承------小学时分数都研究哪些性质? 4.从实际意义或者问题解决上,分式也是分数的实际意义的抽象------列方程解应用题 5.需要了解学生对于小学分数的了解情况,特别是是否还记得分数的性质框架 6.分式的基础是分数、整式的四则运算、多项式的因式分解、一元一次方程等知识。同时它是今后进一步学习函数、一元二次方程的基础。
主题单元规划思维导图 主题单元学习目标 知识与技能: 1.了解分式的概念,明确分式和整式的区别; 2.掌握分式的基本性质和分式的约分; 3.分式的乘除运算法则; 4.经历探索分式加减运算法则,理解其算理; 5.异分母分式加减法的法则及分式的通分; 6.通过对实际问题的分析,感受分式方程是刻画现实世界的有效模型,归纳分式方程的概念; 7.经历探索分式方程解法的过程,会解可化为一元一次方程的分式方程,会检验根的合理性; 8.用分式方程的数学模型反映现实情境中的实际问题. 过程与方法: 1.体会分式的意义,进一步发展符号感,掌握分式的符号法则; 2.会进行简单的分式的乘除法运算; 3.会进行简单分式的加减运算,具有一定的代数化归能力; 4.经历异分母分式的加减运算和通分的过程,训练学生的分式运算能力,培养学习学习中转化未知问题为已知问题的能力; 5.经历“求解-解释解的合理性”的过程,发展学生分析问题、解决问题的能力,培养学生的应用意识; 6.用分式方程来解决现实情境中的问题. 情感态度与价值观: 1.经历分式探索,体会并掌握有效的数学转化思想; 2.能解决一些简单的实际问题,进一步体会分式的模型思想; 3.在学生已有数学经验的基础上,探求新知,从而获得成功的快乐,提高学生“用数学”意识; 4.在活动中培养学生乐于探究合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值; 5.在活动中培养学生乐于探究、合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值; 6.经历建立分式方程模型解决实际问题的过程,体会数学模型的应用价值,从而提高学习数学的兴趣.
对应课标 1.抽象出分式概念; 2.类比分数的基本性质,了解分式的基本性质;掌握分式的约分和通分法则; 3.类比分数的四则运算法则,探究分式的四则运算,归纳并掌握这些运算法则; 4.结合分式的运算,将指数的讨论范围从正整数扩大到全体整数,构建和发展相联系的知识体系; 5.结合分析和解决实际问题,讨论可化为一元一次方程的分式方程,掌握这种方程的解法,体会解方程中的化归思想;利用分式方程解决 实际问题,体会建模思想. 主题单元问题设计 1.什么叫分式?及其分式的意义. 2.如何进行分式的乘除,加减运算? 3.解分式方程的步骤是什么? 4.解分式方程需要注意什么?
专题划分 专题一:相关概念 ( 三课时) 专题二: 探究性质,运算法则 (四课时) 专题三: 实际应用 (一课时)
专题一 相关概念
所需课时 课内三课时
专题学习目标 知识技能: 1.了解分式的概念,明确分式和整式的区别; 2.经历分式的约分及其通分; 3.认识和了解分式方程的概念及增根; 过程与方法: 1.体会分式的意义,进一步发展符号感,掌握分式的符号法则; 2.会进行简单的分式的乘除法运算; 3.会进行简单分式的加减运算,具有一定的代数化归能力; 4.经历异分母分式的加减运算和通分的过程,训练学生的分式运算能力,培养学习学习中转化未知问题为已知问题的能力; 情感态度与价值观: 1.经历分式探索,体会并掌握有效的数学转化思想; 2.能解决一些简单的实际问题,进一步体会分式的模型思想.
专题问题设计 1.怎样给分式,分式方程及增根下定义? 2.分式的意义是什么? 3.分式如何来约分?
所需教学环境和教学资源
分式、分式方程课件,纸笔等 学习活动设计 第一课时:分式 活动一:预习作业 1. 分式的概念: . 2. 分式有意义的条件: . 活动二:引例 问题情景:面对目前严重的土地沙化问题,某县决定分期分批固沙造林,一期工程计划在一定期限内固沙造林2400公顷,实际 每月固沙造林的面积比原计划多30公顷,结果提前4个月完成原计划任务,原计划每月固沙造林多少公顷? (1)这一问题中有哪些等量关系? (2)如果设原计划每月固沙造林x公顷,那么原计划完成一期工程需要 个月,实际完成一期工程用了 个月。根据 题意, 可得方程: . 问题情景(2):正n边形的每个内角为 度。 问题情景(3):新华书店库存一批图书,其中一种图书的原价是每册a元,]现降价x元销售,当这种图书的库存全部售出时,其 销售额为b元.降价销售开始时,新华书店这种图书的库存量是多少? 小结: 分式的概念: 分式有意义的条件: 分式无意义的条件: 活动三:典型例题 例1:下列各式中,哪些是整式?哪些是分式?
例2:根据要求,解答下列各题 (1)当x为何值时,分式
无意义? (2)当x为何值时,分式
有意义? (3)x为何值时,分式
的值为0? 第二课时:分式(二) 活动一:预习作业 请同学们预习作业教材P68~P70的内容,在学习过程中请弄清以下几个问题: 1.分式的基本性质: . 2.什么叫分式的约分?根据是什么? 3.什么是最简分式? [来源:Z#xx#k.C om]4.分式的符号法则? 活动二:引例 问题:
的依据是什么?你认为分式 与 相等吗? 与 呢? 引出分式的基本性质并用式子表示: 活动三:典型例题 例1.下列等式的右边是怎样从左边得到的?[来源 (1)
(2) 例2、化简下列分式: (1)
(2)
小结:1.分式的约分 2.注意事项:在应用分式的基本性质时,分式的分子与分母应同时乘以或除以同一个公因式 。 3.不改变分式的值,使下列分式的分子与分母的最高次项的系数是整数: 4.不改变分式的值,把分式分子和分母的系数化为整数:
第三课时:分式方程(一) 活动一:认识分式方程 问题1:某市从今年1月1日起调整居民用水价格,每立方米水费 上涨0.4元.小丽家去年12月的水费是15元,而今年7月份的水费 是25元.如果设去年每立方米水费为x元.那么今年每立方米水费为 元。 小丽家去年12月的用水量是 立方米. 今年7月份的用水量是 立方米. 问题2:有两快面积相同的小麦实验田,第一块使用原品种,第二块使用新品种,分别收获小麦9000 ㎏和15000 ㎏,已知 第一块的小麦实验田每公顷的产量比第二块少3000㎏,如何设未知数列方程? 问:(1)如果设第一块小麦实验田的每公顷的产量为 x ㎏,那么第二块实验田每公顷的产量为 ㎏. (2)第一块试验田有 公顷?第二块试验田有 公顷? X|k|b|1.c|o|m (3)你能发现这个问题中的等量关系吗? K] (4)你能根据面积相等列出方程吗? 题问3:从甲地到乙地有两条路可以走:一条全长600 km普通公路,另一条是全长 480km 的高速公路,某客车在高速公路上行 驶的平均速度比普通公路上快45km/h,由高速公路从甲地到乙地的所需的时间是由普通公路从甲地到乙地所需时间的一半,求该客 车由高速公路从甲地到乙地所需要的时间? (1).你能发现这个问题中的等量关系吗? (2).你能根据等量关系列出分式方程吗? 比较左右两边的方程, 有什么不同? 活动二:总结 分母中含有 的方程叫做分式方程
评价要点 1.分式及分式方程概念的探索过程 2.分式通分的的探索过程
专题二 探究性质,运算法则
所需课时 课内四课时
专题学习目标 知识技能: 1.分式的乘除运算法则; 2.经历探索分式加减运算法则,理解其算理; 3.异分母分式加减法的法则及分式的通分; 4.经历探索分式方程解法的过程,会解可化为一元一次方程的分式方程,会检验根的合理性; 过程与方法: 1.会进行简单的分式的乘除法运算; 2.经历异分母分式的加减运算和通分的过程,训练学生的分式运算能力,培养学习学习中转化未知问题为已知问题的能力; 3.会进行简单分式的加减运算,具有一定的代数化归能力; 情感态度与价值观: 1.在学生已有数学经验的基础上,探求新知,从而获得成功的快乐,提高学生“用数学”意识; 2.在活动中培养学生乐于探究合作学习的习惯,培养学生努力寻找解决问题的进取心,体会数学的应用价值
专题问题设计
1.分式的基本性质内容是什么? 2.分式乘除,加减运算的依据是什么? 3.如何进行分式通分? 4.解分式方程需要注意什么?
所需教学环境和教学资源
分式、分式方程课件,纸笔等 学习活动设计 第一课时:分式的乘除法 活动一:自主探究 阅读课本74-76页,回答下列问题: