第一章解直角三角形复习最新版

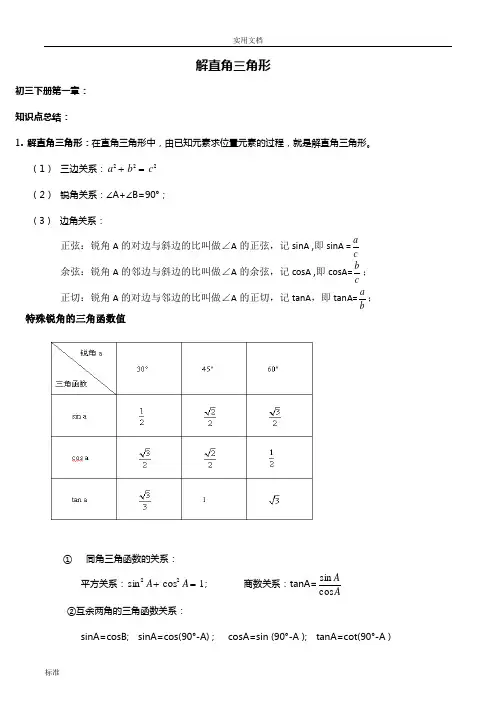
解直角三角形初三下册第一章： 知识点总结：1. 解直角三角形：在直角三角形中，由已知元素求位置元素的过程，就是解直角三角形。

（1） 三边关系：222c b a （2） 锐角关系：∠A+∠B=90°； ( 3 ) 边角关系：正弦：锐角A 的对边与斜边的比叫做∠A 的正弦，记sinA ,即sinA =c a余弦：锐角A 的邻边与斜边的比叫做∠A 的余弦，记cosA ,即cosA=c b；正切：锐角A 的对边与邻边的比叫做∠A 的正切，记tanA ，即tanA=ba；特殊锐角的三角函数值① 同角三角函数的关系：平方关系：1cos sin 22 A A ; 商数关系：tanA=AAcos sin ②互余两角的三角函数关系：sinA=cosB; sinA=cos(90°-A) ; cosA=sin (90°-A ); tanA=cot(90°-A )2.实际问题仰角：进行高度测量时，在视线与水平线所成的角中，当视线在水平线上方时叫做仰角。

俯角：进行高度测量时，在视线与水平线所成的角中，当视线在水平线下方时叫做俯角。

坡度（坡比）：坡面的铅垂高度和水平宽度的比叫做坡面的坡度，记作i=h:l。

坡角：坡面与水平面的夹角叫做坡角，记作a,即i=h:l=tana.方位角：从某点的正北方向沿顺时针方向旋转到目标方向所形成的角叫做方位角。

方向角：从正北方向或正南方向到目标方向形成的小雨90°的角叫做方向角。

典型例题：题型一：特殊三角函数值1、计算2sin30°-sin245°+cot60°的结果是（）A、B、C、D、2、已知a=3，且（4tan 45°-b）2+=0，以a，b，c为边组成的三角形面积等于（）A、6B、7C、8D、93、已知a为锐角，且sin（a-10°）=，则a等于（）A、50°B、60°C、70°D、80°4、在△ABC中，∠C=90°，∠B=2∠A，则cosA等于（）A、B、C、D、5、如图，如果∠A是等边三角形的一个内角，那么cosA的值等于（）A、B、C、D、16、△ABC中，∠A、∠B都是锐角，且sinA=，cosB=，则△ABC的形状是（）A、直角三角形B、钝角三角形C、锐角三角形D、不能确定7、计算：sin213°+cos213°+sin60°-tan30°．8、求下列各式的值：（1）a、b、c是△ABC的三边，且满足a2=（c+b）（c-b）和4c-5b=0，求cosA+cosB的值；（2）已知A为锐角，且tanA=，求sin2A+2sinAcosA+cos2A的值．题型二：解直角三角形1、如图，在△ABC中，∠C=90°，∠B=60°，D是AC上一点，DE⊥AB于E，且CD=2，DE=1，则BC的长为（）A、2B、C、2D、42、等腰三角形的顶角为120°，腰长为2cm，则它的底边长为（）A、cmB、cmC、2cmD、cm3、如图，梯形ABCD中，AD∥BC，∠B=45°，∠D=120°，AB=8cm，则DC的长为（）A、cmB、cmC、cmD、8cm4、如图，在Rt△ABC中，∠ACB为90°，CD⊥AB，cos∠BCD=，BD=1，则边AB的长是（）A、B、C、2 D、5、如图，将等腰直角三角形ABC绕点A逆时针旋转15°后得到△AB′C′，若AC=1，则图中阴影部分的面积为（）A、B、C、D、6、在△ABC中，∠A=120°，AB=4，AC=2，则sinB的值是（）A、B、C、D、7、如图，矩形ABCD中，对角线AC、BD相交于点0，∠AOB=60°，AB=5，则AD的长是（）A、5B、5C、5D、108、如图，在菱形ABCD中，DE⊥AB，，BE=2，则tan∠DBE的值（）A、B、2 C、D、9、如图，四边形ABCD和四边形BEFD都是矩形，且点C恰好在EF上．若AB=1，AD=2，则S△BCE为（）A、1B、C、D、10、如图，在Rt△ABC中，∠A=90°，AB=AC=8，点E为AC的中点，点F在底边BC上，且FE⊥BE，则△CEF的面积是（）A、16B、18C、6D、711、如图，在梯形ABCD中，∠A=∠B=90°，AB=，点E在AB上，∠AED=45°，DE=6，CE=7．求：AE的长及sin∠BCE的值．12、如图，直角梯形ABCD中，AD∥BC，∠A=90°，AB=AD=6，DE⊥DC交AB于E，DF平分∠EDC交BC 于F，连接EF．（1）证明：EF=CF；（2）当tan∠ADE=时，求EF的长．题型三：解直角三角形的应用1、如图，某市在“旧城改造”中计划在一块如图所示的三角形空地上种植某种草皮以美化环境，已知这种草皮每平方米a元，则购买这种草皮至少要（）A、450a元B、225a元C、150a元D、300a元2、如图，AB是斜靠在墙上的长梯，D是梯上一点，梯脚B与墙脚的距离为1.6m（即BC的长），点D与墙的距离为1.4m（即DE的长），BD长为0.55m，则梯子的长为（）A、4.50mB、4.40mC、4.00mD、3.85m3、如图，太阳光线与地面成60°角，一棵倾斜的大树AB与地面成30°角，这时测得大树在地面的影长BC为10m，则大树的长为（）m．A、5B、10C、15D、204、如图，小明同学在东西走向的文一路A处，测得一处公共自行车租用服务点P在北偏东60°方向上，在A 处往东90米的B处，又测得该服务点P在北偏东30°方向上，则该服务点P到文一路的距离PC为（）A、60米B、45米C、30米D、45米5、如图是某货站传送货物的平面示意图．为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°．已知原传送带AB长为4米．（1）求新传送带AC的长度；（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．（说明：（1）（2）的计算结果精确到0.1米，参考数据：≈1.41，≈1.73，≈2.24，≈2.45）6、如图，河流的两岸PQ、MN互相平行，河岸PQ上有一排小树，已知相邻两树之间的距离CD=50米，某人在河岸MN的A处测得∠DAN=35°，然后沿河岸走了120米到达B处，测得∠CBN=70°．求河流的宽度CE（结果保留两个有效数字）．（参考数据：sin35°≈0.57，cos35°≈0.82，tan35°≈0.70，sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）7、某市为缓解城市交通压力，决定修建人行天桥，原设计天桥的楼梯长AB=6m，∠ABC=45°，后考虑到安全因素，将楼梯脚B移到CB延长线上点D处，使∠ADC=30°（如图所示）．（1）求调整后楼梯AD的长；（2）求BD的长．（结果保留根号）8、某河道上有一个半圆形的拱桥，河两岸筑有拦水堤坝．其半圆形桥洞的横截面如图所示．已知上、下桥的坡面线ME、NF与半圆相切，上、下桥斜面的坡度i=1：3.7，桥下水深=5米．水面宽度CD=24米．设半圆的圆心为O，直径AB在坡角顶点M、N的连线上．求从M点上坡、过桥、下坡到N点的最短路径长．（参考数据：π≈3，≈1.7，tan15°=）题型四：坡度坡角问题及仰角俯角问题1、如图，是一水库大坝横断面的一部分，坝高h=6m，迎水斜坡AB=10m，斜坡的坡角为α，则tanα的值为（）A、B、C、D、2、如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）为4m．如果在坡度为0.75的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（）A、5mB、6mC、7mD、8m3、周末，身高都为1.6米的小芳、小丽来到溪江公园，准备用她们所学的知识测算南塔的高度．如图，小芳站在A处测得她看塔顶的仰角α为45°，小丽站在B处（A、B与塔的轴心共线）测得她看塔顶的仰角β为30°．她们又测出A、B两点的距离为30米．假设她们的眼睛离头顶都为10cm，则可计算出塔高约为（结果精确到0.01，参考数据：≈1.414，≈1.732）（）A、36.21米B、37.71米C、40.98米D、42.48米4、一次数学活动中，小迪利用自己制作的测角器测量小山的高度CD．已知她的眼睛与地面的距离为1.6米，小迪在B处测量时，测角器中的∠AOP=60°（量角器零度线AC和铅垂线OP的夹角，如图）；然后她向小山走50米到达点F处（点B，F，D在同一直线上），这时测角器中的∠EO′P′=45°，那么小山的高度CD约为（）（注：数据≈1.732，≈1.414供计算时选用）A、68米B、70米C、121米D、123米5、如图，已知楼高AB为50m，铁塔基与楼房房基间的水平距离BD为50m，塔高DC为m，下列结论中，正确的是（）A、由楼顶望塔顶仰角为60°；B、由楼顶望塔基俯角为60°；C、由楼顶望塔顶仰角为30°；D、由楼顶望塔基俯角为30°6、已知小芳站在层高为2.5米的六层楼的屋顶上来估计旁边一支烟囱的高度，当小芳以俯角∠COB=45°向下看时，刚好可以看到烟囱的底部，当小芳以仰角∠AOB=30°向上看时，刚好可以看到烟囱的顶部，若小芳的身高为1.5米，请你估计烟囱的高度（=1.414，=1.732结果保留三个有效数字）（）A、22.1米B、26.0米C、27.9米D、32.8米7、如图，小明在大楼30米高（即PH=30米）的窗口P处进行观测，测得山坡上A处的俯角为15°，山脚B 处的俯角为60°，巳知该山坡的坡度i（即tan∠ABC）为1：，点P，H，B，C，A在同一个平面上，点H、B、C在同一条直线上，且PH丄HC．（1）山坡坡角（即∠ABC）的度数等于多少度；（2）求A、B两点间的距离（结果精确到0.1米，参考数据：≈1.732）．8、如图，某校综合实践活动小组的同学欲测量公园内一棵树DE的高度．他们在这棵树正前方一座楼亭前的台阶上A点处测得树顶端D的仰角为30°，朝着这棵树的方向走到台阶下的点C处，测得树顶端D的仰角为60°．已知A点的高度AB为2米，台阶AC的坡度为（即AB：BC=），且B、C、E三点在同一条直线上．请根据以上条件求出树DE的高度（测倾器的高度忽略不计）．题型五：方向角问题1、如图，已知一渔船上的渔民在A处看见灯塔M在北偏东60°方向，这艘渔船以28海里/时的速度向正东方向航行，半小时后到达B处，在B处看见灯塔M在北偏东15°方向，此时灯塔M与渔船的距离是（）A、7海里B、14海里C、7海里D、14海里2、在一次夏令营活动中，小霞同学从营地A点出发，要到距离A点10千米的C地去，先沿北偏东70°方向走了8千米到达B地，然后再从B地走了6千米到达目的地C，此时小霞在B地的（）A、北偏东20°方向上B、北偏西20°方向上C、北偏西30°方向上D、北偏西40°方向上3、如图，小亮家到学校有两条路，一条沿北偏东45°方向可直达学校前门，另一条从小明家一直往东，到商店处向正北走100米，到学校后门；若两条路程相等，学校南北走向，学校后门在小明家北偏东67.5°处，学校前门到后门的距离是（）A、100米B、米C、米D、米4、综合实践课上，小明所在小组要测量护城河的宽度．如图所示是护城河的一段，两岸ABCD，河岸AB上有一排大树，相邻两棵大树之间的距离均为10米．小明先用测角仪在河岸CD的M处测得∠α=36°，然后沿河岸走50米到达N点，测得∠β=72°．请你根据这些数据帮小明他们算出河宽FR（结果保留两位有效数字）（参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73，sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）5、如图，自来水厂A和村庄B在小河l的两侧，现要在A，B间铺设一知输水管道．为了搞好工程预算，需测算出A，B间的距离．一小船在点P处测得A在正北方向，B位于南偏东24.5°方向，前行1200m，到达点Q处，测得A位于北偏东49°方向，B位于南偏西41°方向．（1）线段BQ与PQ是否相等？请说明理由；（2）求A，B间的距离．（参考数据cos41°=0.75）．6、如图所示，一艘轮船以30海里/小时的速度向正北方向航行，在A处得灯塔C在北偏西30°方向，轮船航行2小时后到达B处，在B处时测得灯塔C在北偏西45°方向．当轮船到达灯塔C的正东方向的D处时，求此时轮船与灯塔C的距离．（结果精确到0.1海里，参考数据≈1.41，≈1.73）．7如图，港口B在港口A的西北方向，上午8时，一艘轮船从港口A出发，以15海里∕时的速度向正北方向航行，同时一艘快艇从港口B出发也向正北方向航行，上午10时轮船到达D处，同时快艇到达C处，测得C 处在D处得北偏西30°的方向上，且C、D两地相距100海里，求快艇每小时航行多少海里？（结果精确到0.1海里∕时，参考数据≈1.41，≈1.73）8、（2010•陕西）在一次测量活动中，同学们要测量某公园的码头A与他正东方向的亭子B之间的距离，如图他们选择了与码头A、亭子B在同一水平面上的点P在点P处测得码头A位于点P北偏西方向30°方向，亭子B位于点P北偏东43°方向；又测得P与码头A之间的距离为200米，请你运用以上数据求出A与B的距离．练习作业：1、在Rt△ABC中，∠C=90°，∠B=35°，AB=7，则BC的长为（）A、7sin35°B、C、7cos35°D、7tan35°2、Rt△ABC中，∠C=90°，a、b、c分别是∠A、∠B、∠C的对边．那么c等于（）A、acos A+bsin BB、asin A+bsin BC、D、3、如图AD⊥CD，AB=13，BC=12，CD=3，AD=4，则sinB=（）A、B、C、D、4、如图，已知一坡面的坡度i=1：，则坡角α为（）A、15°B、20°C、30°D、45°5、如图所示，CD是平面镜，光线从A点出发经CD上的E点反射后到达B点，若入射角为α，AC⊥CD，BD⊥CD，垂足分别为C，D，且AC=3，BD=6，CD=11，则tanα的值是（）A、B、C、D、6、如图，沿AC方向开山修路，为了加快施工进度，要在小山的另一边同时施工，从AC上的一点B，取∠ABD=145°，BD=500米，∠D=55度．要使A，C，E成一直线．那么开挖点E离点D的距离是（）A、500sin55°米B、500cos55°米C、500tan55°米D、500cot55°米7、如图，在矩形ABCD中，DE⊥AC于E，设∠ADE=α，且cosα=，AB=4，则AD的长为（）A、3 B、C、D、8、如图，在梯形ABCD中，AD∥BC，AB=CD=AD，BD⊥CD．（1）求sin∠DBC的值；（2）若BC长度为4cm，求梯形ABCD的面积．9、路边路灯的灯柱BC垂直于地面，灯杆BA的长为2米，灯杆与灯柱BC成120°角，锥形灯罩的轴线AD 与灯杆AB垂直，且灯罩轴线AD正好通过道路路面的中心线（D在中心线上）．已知点C与点D之间的距离为12米，求灯柱BC的高．（结果保留根号）10、如图，为了测量某建筑物CD的高度，先在地面上用测角仪自A处测得建筑物顶部的仰角是30°，然后在水平地面上向建筑物前进了100m，此时自B处测得建筑物顶部的仰角是45°．已知测角仪的高度是1.5m，请你计算出该建筑物的高度．（取=1.732，结果精确到1m）．11、如图，某船由西向东航行，在点A测得小岛O在北偏东60°，船航行了10海里后到达点B，这时测得小岛O在北偏东45°，船继续航行到点C时，测得小岛O恰好在船的正北方，求此时船到小岛的距离．。

解直角三角形 一教学目标1.掌握锐角三角函数的有关性质；2.掌握特殊角的三角函数值，并会利用进行简单的计算；3.会解直角三角形.教学过程师：（画出图形）图中有几个直角三角形？（生答）AC BC 与AEDE的值有何关系？为什么？（一生答）师：由此可见，在直角三角形中，当某个锐角的度数相等时，它的对边与相邻直角边的比值是一个定值，我们把这个定值叫做这个角的正切值.由上图你还发现了什么？（学生说出正弦、余弦的概念）（注意说明：三角函数值只与角的度数有关，与所在的三角形无关）考点一、锐角三角函数【处理办法】1.由图让学生分别表示出A ∠、B ∠的三个三角函数值； 2.得出锐角三角函数的有关性质.【教师说明】1.如何记住三角函数的概念？（正弦值是正对的边与弦的比值，余弦值是余下的直角边与弦的比值，正切值是正对的直角边与相邻直角边的比值）2.三角函数的增减性.如：sinA=ca，当a 不变时，随着点A 向点C 逐渐靠近，A ∠逐渐变大，斜边逐渐变短（让学生从图中直接观察发现），在0°----90°之间，正弦值随着角度的增大而增大；由于a<c, 故 sinA<1.其它类似得出.为便于学生记忆可告知：正弦、正切中有“正”，故成正比，即正弦、正切值随着角度的增大而增大.3.互为余角的三角函数关系：sinA=cosB ，cosA=sinB ；同角的三角函数关系：平方关系sin 2A+cos 2A=1,商数关系：tanA=AAcos sin .(可由直角三角形图形去记） 例（2015•淄博）若锐角α满足cosα＜22且tanα＜3，则α的范围是（ ） A ．30°＜α＜45° B ．45°＜α＜60° C ．60°＜α＜90° D ．30°＜α＜60° 【说明】教师说明思路即可.答案：B.考点二、特殊角的三角函数值【教师说明】可采用两种方法记住：（1）直观法，由左图及三角函数概念记住.(2)规律法，由右图表格中规律记住.（记30°、60°角正切值时，由增减性知角度大时为3）训练：（展示）1.（2013孝感）式子2)60tan 1(45tan 30cos 2︒--︒-︒的值是（ ） A. 23 －2 B. 0 C. 23 D.22.（2014四川凉山）在△ABC 中，若0)tan 1(21cos 2=-+-B A ，则∠C 的度数是（ ） A. 45° B. 60° C. 75° D. 105° 3.（2015•甘肃武威）已知α、β均为锐角，且满足|sinα﹣|+ =0，则α+β= ．4.（2011兰州）已知α是锐角，且sin(α+15°)=3计算1184cos ( 3.14)tan 3απα-⎛⎫---++ ⎪⎝⎭的值.【处理办法】前三道题一生回答并说明理由即可，第4题找两生黑板上做，其他学生在练习本上给出解题过程.【参考答案】1.B 2.C 3.75° 4.由sin(α+15°)=32得α=45°后代入求出原式=3. 考点三、解直角三角形【教师说明】解直角三角形就是根据已知条件（除直角外另两个条件其中至少有一个是边）利用锐角三角函数的概念、锐角三角函数间的关系、直角三角形中的边角关系求出未知边、角的过程.若图形中没有直角三角形，可通过作垂线构造出直角三角形.（一）直接求例（2011宜昌）如图是教学用直角三角板，边AC=30cm ，∠C=90°，tan ∠BAC=33,则边BC 的长为( )α 30°45°60°sin α 2122 23cos α 23 2221 tan α33 13A. 303cmB. 203cmC.103cmD. 53cm 【答案】C.（二）构造直角三角形例1（2015•山东日照）如图，在直角△BAD 中，延长斜边BD 到点C ，使DC=BD ，连接AC ，若tanB=，则tan ∠CAD 的值（ ）A ．B ．C ．D ．【说明】引导学生思考∠CAD 在直角三角形中吗？要构造出直角三角形有哪些方法？哪种方法能与已知条件联系起来？【答案】过点C 作AD 的垂线求出.选D.另：本题也可采用度量估算的方法.例2(展示）（2010咸宁市）如图，已知直线1l ∥2l ∥3l ∥4l ，相邻两条平行直线间的距离 都是1，如果正方形ABCD 的四个顶点分别在四条直线上，则sin α= ．【处理办法】学生思考、讨论、回答. 必要时教师引导.（引导语：1.要求sin α=?,必须放到直角三角形中，如何构造直角三角形？2.题中有“距离”如何应用上距离是1？）【提示】教师讲解时可与基本图形联系起来. 【参考答案】（1）过点D 作平行线的垂线，利用三角形全等、勾股定理求出.（2）利用平行线分线段成比例定理知AB 被平分，在小直角三角形中直接求出.答案：5训练：（展示）1.在△ABC 中，∠A ＝120°，AB ＝4，AC ＝2，则B sin 的值是( ) A ．1475 B ．53 C ．721 D ．14212.（2014山东威海）如图，在下列网格中，小正方形的边长均为1，点A 、B 、O 都在格点上，则∠AOB 的正弦值是（ ）A ．10103 B ．21C ．31D ．10103.（2015•浙江湖州）如图，以点O为圆心的两个圆中，大圆的弦AB切小圆于点C，OA交小圆于点D，若OD=2， tan∠OAB=21，则AB的长是( )A. 4B. 23C. 8D. 43【处理办法】学生充分思考、交流后，教师再给以强调说明.【参考答案】1. D（说明：出现120°角时想到60°角，要求Bsin的值必须出现直角三角形）2.D(提示：过点B作AO的垂线，求出垂线段的长即可，注意垂线段的长用面积来求简单.也可延长OB交到第一个格点，连接点A和这个格点，得到直角三角形）（三）等角的转移例（2015•山东聊城改）如图，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BC垂直于PD，交PD的延长线于点C，若PA=2，cosB=53，求⊙O半径的长．【说明】连接OD，把∠B转到∠POD后求出.【答案】3.训练：1.（2011兰州）如图，A、B、C三点在正方形网格线的交点处，若将△ACB绕着点A逆时针旋转得到△AC＇B＇，则tanB＇的值为 ( )A．12B．13C．14D．24第1题图第2题图2.（2011芜湖）如图，直径为10的⊙A经过点C(0，5)和点O (0，0)，B是y轴右侧⊙A优弧上一点,则∠OBC 的余弦值为( ).A．12B．34C．32D．453.（2014苏州）如图，在△ABC中，AB=AC=5，BC=8.若∠BPC=21∠BAC，则tan∠BPC= . 【答案】1.B 2.C(提示：把B∠转化到直角三角形中） 3.34（提示：①以点A为圆心，AB为半径作圆，然后把∠BPC转移到直角三角形中；②过点A作BC的垂线AD，求∠CAD的正切值即可.）回顾本节内容（学生回顾后教师展示）⎪⎩⎪⎨⎧解简单的直角三角形特殊角的三角函数值性质锐角三角函数的概念与解直角三角形。

期末复习：浙教版九年级数学学下册第一章解直角三角形一、单选题（共10题；共30分）1.在△ABC中，∠C=90°，如果AB=6，BC=3，那么cosB的值是（）A. √32B. √55C. √33D. 122.已知tanA=1，则锐角A的度数是A. 30°B . 45° C.60° D.75°3.在Rt△ABC中，∠C＝90°，若BC＝1，AC＝2，则cosA的值为( )A. √55B. 2√55C. 12D. 24.如图，其中A，B，C三地在同一直线上，D地在A地北偏东30°方向、在C地北偏西45°方向．C 地在A地北偏东75°方向．且BD=BC=30cm．从A地到D地的距离是（）A. 30 √3 mB. 20 √5m C. 30 √2m D. 15 √6 m5.如图，在Rt△ABC中，∠ACB=90°，CD⊥AB，垂足为D．若AC=2，BC=1，则sin∠ACD=（）A. √53B. 2√55C. √52D. 236.如图，一渔船由西往东航行，在A点测得海岛C位于北偏东60°的方向，前进40海里到达B点，此时，测得海岛C位于北偏东30°的方向，则海里C到航线AB的距离CD是（）A. 20海里B. 40海里 C. 20√3海里 D. 40√3海里7.如图，在Rt△ABC中，斜边AB的长为m，∠A=35°，则直角边BC的长是（）A. msin35°B. mcos35°C. msin35°D. mcos35°8.若直角三角形中的两个锐角之差为22°，则较小的一个锐角的度数是（）A. 24°B . 34° C.44° D.46°，AB=6cm．动点P从点A开始沿边AB向点B以1cm/s的9.如图，在△ABC中，∠B=90°，tan∠C= 34速度移动，动点Q从点B开始沿边BC向点C以2cm/s的速度移动．若P，Q两点分别从A，B两点同时出发，在运动过程中，△PBQ的最大面积是（）A. 18cm2B. 12cm2C. 9cm2D. 3cm210.如图，已知mm是△mmm的角平分线，mm是mm的垂直平分线，∠mmm=90°，mm=3，则mm的长为（）A. 6B. 5C. 4D. 3√3二、填空题（共8题；共24分）11.计算：3tan30°+sin45°=________．）﹣2﹣|1﹣√3 |﹣（π﹣2015）0﹣2sin60°+ √12 =________．12.计算：（12，那么∠A=________゜．13.如果∠A是锐角，且sinA= 1214.B在A北偏东30°方向（距A）2千米处，C在B的正东方向（距B）2千米处，则C和A之间的距离为________ 千米．15.如图，在平面直角坐标系xOy内有一点Q（3，4），那么射线OQ与x轴正半轴的夹角α的余弦值是________，则BC的长是________16.如图，在△ABC中，∠C=90°，AB=8，sinA=3417.如图，在△ABC中，∠C=90°，AB=5，BC=3，则cosA的值是________．x于点B1， B2，18.如图，点A1（1，1）在直线y=x上，过点A1分别作y轴、x轴的平行线交直线y= √32x于点B3，…，按过点B2作y轴的平行线交直线y=x于点A2，过点A2作x轴的平行线交直线y= √32照此规律进行下去，则点A n的横坐标为________．三、解答题（共9题；共66分）19.计算：√12−|−2|+(1−√3)0−9tan30°20.甲、乙两船同时从港口A出发，甲船以12海里/时的速度向北偏东35°航行，乙船向南偏东55°航行，2小时后，甲船到达C岛，乙船到达B岛，若C、B两船相距30海里，问乙船的速度是每小时多少海里？21.某游乐场一转角滑梯如图所示，滑梯立柱mm,mm均垂直于地面，点m在线段mm上.在m点测得点m的仰角为300，点m的俯角也为300，测得m,m间的距离为10米，立柱mm高30米.求立柱mm 的高（结果保留根号）.22.小敏同学测量一建筑物CD的高度，她站在B处仰望楼顶C，测得仰角为30°，再往建筑物方向走30m，到达点F处测得楼顶C的仰角为45°（B,F,D在同一条直线上）。

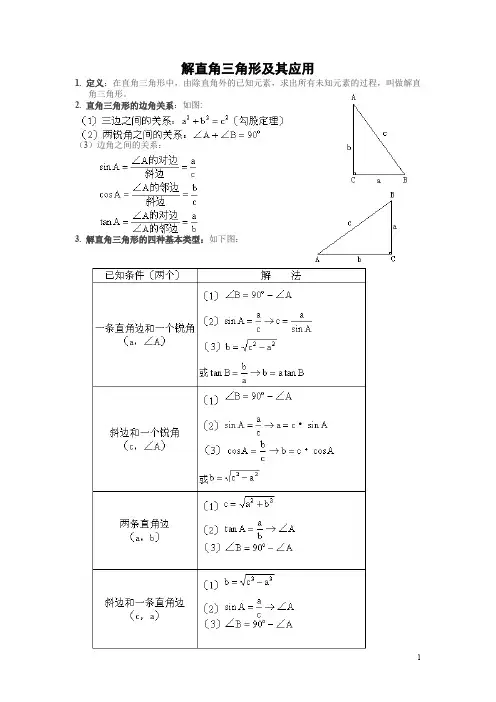
解直角三角形及其应用1. 定义：在直角三角形中，由除直角外的已知元素，求出所有未知元素的过程，叫做解直角三角形。

2. 直角三角形的边角关系：如图:（3）边角之间的关系：3. 解直角三角形的四种基本类型：如下图：已知直角三角形的两个基本元素（至少有一个是边），利用以上关系就可以求出其余的未知元素，其中恰当地选用边角关系是关键。

应注意以下原则：（1）有“斜”选“弦”，无“斜”选“切”。

（2）尽量使未知元素在分子的位置上，以便利用乘法运算求未知元素。

（3）尽量使用原始数据：以减少误差的积累，也可避免由于中间数据有错而产生新的误差。

4. 几个常用概念：（1）仰角：在测量时，从下向上看，视线与水平线的夹角叫仰角。

（2）俯角：在测量时，从上向下看，视线与水平线的夹角叫俯角。

（3）坡度：（坡比）如图:坡面的铅直高度（h）和水平长度（l）的比，叫做坡面的坡度。

（4）坡角：坡面与水平面的夹角叫做坡角，记作α。

坡度越大，坡角越大，坡面越陡。

（5）方向角（如图）OA：北偏东30°OB：东南方（南偏东45°）OC：南偏西70°OD：北偏西60°东西与南北方向线互相垂直。

5. 运用解直角三角形的方法解决实际问题：基本思路：要善于将某些实际问题中的数量关系归结为直角三角形中的边角关系。

（即构建数学模型：直角三角形），才能运用解直角三角形的方法求解。

一般有以下几个步骤：（1）审题：根据题意画出正确的平面图或截面示意图，在图形中弄清已知和未知。

（2）将已知条件转化为示意图中的边、角关系，把实际问题转化为解直角三角形的问题。

（3）选择适当关系式解直角三角形。

典型例题例1.在Rt△ABC中，∠C＝90°，解直角三角形：（1）a＝8，b＝6（2）c＝16，∠A＝32°分析：略解：例2. 如图某公园入口处原有三级台阶，每级台阶高为20cm，深为30cm，为方便残疾人士，可以将台阶改为斜坡，设台阶的起点为A，斜坡的起点为C，现将斜坡的坡角∠BCA设计为12°，求AC的长度（精确到1cm）。

第1章 解直角三角形 专项练习一．填空题（每题4分;计40分)1．已知是等腰直角三角形的一个锐角;则sin α的值为（ ）A ．12 B ．22 C ．32D ．1 2．在Rt ABC △中;90C ∠=;5BC =;15AC =;则A ∠=（ ） A ．90 B ．60 C ．45 D ．303．在△ABC 中;∠C ＝90°;tan A ＝31;则sin B ＝ （ ）A ．1010B ．32C ．43D ．101034．如图;在Rt ABC △中;CD 是斜边AB 上的中线;已知2CD =; 3AC =;则sin B 的值是（ ） A ．23 B ．32 C ．34 D ．435．在正方形网格中;ABC △的位置如右图所示; 则cos B ∠的值为（ ） A ．12B ．22C ．32D ．336、若0°＜α＜90°;则的值等于（ ）。

（A ）0 （B ）1 （C ）2 （D ）37、下列各式正确的是（ ）（A ）sin20°＋sin20°＝sin40° （B ）ctg31°＝tg （90°－59°）（C ）sin 2A ＋cos 2（90°－A ）＝1 （D ）sin 2B A +＝cos 2C（其中A+B+C ＝180°） 8 如图2所示;Rt △ABC ∽Rt △DEF ;则cosE 的值等于（ ）A.122339．如图;AC 是电杆AB 的一根拉线;测得BC =6米;∠ACB =52°;则拉线AC 的长为( ) A. ︒526sin 米 B. ︒526tan 米 C. 6·cos 52°米 D. ︒526cos 米 10．在△ABC 中;∠A=60°3;那么∠B 为（ ）A ．60°B ．60°或120°C ．30°或150°D ．30° 二．填空题（每题5分;计20分）11．如图所示;某河堤的横断面是梯形ABCD ;BC AD ∥;迎水坡AB 长13米;且12tan 5BAE ∠=;则河堤的高BE 为 米． 12．如图;小明同学在东西方向的环海路A 处;测得海中灯塔P 在北偏东60°方向上;在A 处东500米的BC ABD（第4题图） ABC┐第9题处;测得海中灯塔P 在北偏东30°方向上;则灯塔P 到环海路的距离PC ＝ 米（用根号表示）．13． 一棵树因雪灾于A 处折断;如图所示;测得树梢触地点B 到树根C 处的距离为4米;∠ABC 约45°;树干AC 垂直于地面;那么此树在未折断之前的高度约为 米（答案可保留根号）．14.如图;小明在楼顶处测得对面大楼楼顶点C 处的仰角为52°;楼底点处的俯角为13°．若两座楼AB 与CD 相距60米;则楼CD 的高度约为 米．（结果保留三个有效数字）（sin130.2250︒≈;cos130.9744≈;tan130.2309≈;sin 520.7880≈;cos520.6157≈;tan52 1.2799≈） 三．解答题(计90分）15.计算（每题6分;计12分）(1)cos 245°+sin60°·tan30°－)30tan 1(-(2)230sin 430cos 45tan 60sin -+16.（每小题7分;共14分）在Rt △ABC 中;∠C ＝90° (1)、已知∠A ＝60°;b ＝310;求a 、c;(2)c ＝32;b ＝3;求a 、A17（10分）18、如图;三角形△ABC 中;∠B ＝45°;∠C ＝60°;AB ＝23;AD ⊥BC 于D;求CDPA BC30°60°北（第12题）BC DEA 第11题图 DBC1352A60米AB CD第13题图第14题图18..(10分）如图9;山顶建有一座铁塔;塔高CD=30m;某人在点A 处测得塔底C 的仰角为200塔顶D 的仰角为23°;求此人距CD 的水平距离AB 。

2021-2022学年浙教版九年级数学下册《第1章解直角三角形》期末综合复习训练（附答案）1．某商场准备改善原有楼梯的安全性能，把坡角由37°减至30°，已知原楼梯长为5米，调整后的楼梯会加长（）（参考数据：sin37°≈，cos37°≈，tan37°≈）．A．6米B．3米C．2米D．1米2．如图，在一次数学实践活动中，小明同学要测量一座与地面垂直的古塔AB的高度，他从古塔底部点B处前行30m到达斜坡CE的底部点C处，然后沿斜坡CE前行20m到达最佳测量点D处，在点D处测得塔顶A的仰角为30°，已知斜坡的斜面坡度i＝1：，且点A，B，C，D，E在同一平面内，小明同学测得古塔AB的高度是（）A．（10+20）m B．（10+10）m C．20m D．40m3．如图，在△ABC中，∠ACB＝90°，点D在AB的延长线上，连接CD，若AB＝2BD，tan∠BCD＝，则的值为（）A．1B．2C．D．4．如图，△ABC底边BC上的高为h1，△PQR底边QR上的高为h2，则有（）A．h1＝h2 B．h1＜h2 C．h1＞h2 D．以上都有可能5．如图，在△ABC中，点O是角平分线AD、BE的交点，若AB＝AC＝10，BC＝12，则tan ∠OBD的值是（）A．B．2C．D．6．如图，为了测量某建筑物BC的高度，小颖采用了如下的方法：先从与建筑物底端B在同一水平线上的A点出发，沿斜坡AD行走130米至坡顶D处，再从D处沿水平方向继续前行若干米后至点E处，在E点测得该建筑物顶端C的仰角为60°，建筑物底端B 的俯角为45°，点A、B、C、D、E在同一平面内，斜坡AD的坡度i＝1：2.4．根据小颖的测量数据，计算出建筑物BC的高度约为（参考数据：≈1.732）（）A．136.6米B．86.7米C．186.7米D．86.6米7．构建几何图形解决代数问题是“数形结合”思想的重要应用，在计算tan15°时，如图．在Rt△ACB中，∠C＝90°，∠ABC＝30°，延长CB使BD＝AB，连接AD，得∠D＝15°，所以tan15°＝＝＝＝2﹣．类比这种方法，计算tan22.5°的值为（）A．+1B．﹣1C．D．8．已知，在△ABC中，∠A＝45°，AB＝4，BC＝5，则△ABC的面积为．9．数学活动小组为测量山顶电视塔的高度，在塔的椭圆平台遥控无人机．当无人机飞到点P处时，与平台中心O点的水平距离为15米，测得塔顶A点的仰角为30°，塔底B点的俯角为60°，则电视塔的高度为米．10．如图，一艘轮船位于灯塔P的南偏东60°方向，距离灯塔50海里的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东45°方向上的B处，此时B处与灯塔P 的距离为海里（结果保留根号）．11．如图，某活动小组利用无人机航拍校园，已知无人机的飞行速度为3m/s，从A处沿水平方向飞行至B处需10s．同时在地面C处分别测得A处的仰角为75°，B处的仰角为30°，则这架无人机的飞行高度大约是m（≈1.732，结果保留整数）．12．如图1是一台手机支架，图2是其侧面示意图，AB，BC可分别绕点A，B转动，测量知BC＝8cm，AB＝16cm．当AB，BC转动到∠BAE＝60°，∠ABC＝50°时，点C到AE的距离为cm．（结果保留小数点后一位，参考数据：sin70°≈0.94，≈1.73）13．如图，我国某海域有A，B两个港口，相距80海里，港口B在港口A的东北方向，点C处有一艘货船，该货船在港口A的北偏西30°方向，在港口B的北偏西75°方向，求货船与港口A之间的距离．（结果保留根号）14．2020年7月23日，我国首次火星探测“天问一号”探测器，由长征五号遥四运载火箭在中国文昌航天发射场发射成功，正式开启了中国的火星探测之旅．运载火箭从地面O 处发射，当火箭到达点A时，地面D处的雷达站测得AD＝4000米，仰角为30°.3秒后，火箭直线上升到达点B处，此时地面C处的雷达站测得B处的仰角为45°．O，C，D 在同一直线上，已知C，D两处相距460米，求火箭从A到B处的平均速度．（结果保留整数，参考数据：≈1.732，≈1.414）15．小宸想利用测量知识测算湖中小山的高度．他站在湖边看台上，清晰地看到小山倒映在平静的湖水中，如图所示，他在点O处测得小山顶端的仰角为45°，小山顶端A在水中倒影A′的俯角为60°．已知：点O到湖面的距离OD＝3m，OD⊥DB，AB⊥DB，A、B、A′三点共线，A'B＝AB，求小山的高度AB．（光线的折射忽略不计；结果保留根号）16．某海域有一小岛P，在以P为圆心，半径r为10（3+）海里的圆形海域内有暗礁．一海监船自西向东航行，它在A处测得小岛P位于北偏东60°的方向上，当海监船行驶20海里后到达B处，此时观测小岛P位于B处北偏东45°方向上．（1）求A，P之间的距离AP；（2）若海监船由B处继续向东航行是否有触礁危险？请说明理由．如果有触礁危险，那么海监船由B处开始沿南偏东至多多少度的方向航行能安全通过这一海域？17．如图，莽山五指峰景区新建了一座垂直观光电梯．某测绘兴趣小组为测算电梯AC的高度，测得斜坡AB＝105米，坡度i＝1：2，在B处测得电梯顶端C的仰角α＝45°，求观光电梯AC的高度．（参考数据：≈1.41，≈1.73，≈2.24．结果精确到0.1米）18．如图，在某小区内拐角处的一段道路上，有一儿童在C处玩耍，一辆汽车从被楼房遮挡的拐角另一侧的A处驶来，已知CM＝3m，CO＝5m，DO＝3m，∠AOD＝70°，汽车从A处前行多少米才能发现C处的儿童（结果保留整数）？（参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75；sin70°≈0.94，cos70°≈0.34，tan70°≈2.75）19．王刚同学在学习了解直角三角形及其应用的知识后，尝试利用所学知识测量河对岸大树AB的高度，他在点C处测得大树顶端A的仰角为45°，再从C点出发沿斜坡走2米到达斜坡上D点，在点D处测得树顶端A的仰角为30°，若斜坡CF的坡比为i＝1：3（点E、C、B在同一水平线上）．（1）求王刚同学从点C到点D的过程中上升的高度；（2）求大树AB的高度（结果保留根号）．20．一架无人机沿水平直线飞行进行测绘工作，在点P处测得正前方水平地面上某建筑物AB的顶端A的俯角为30°，面向AB方向继续飞行5米，测得该建筑物底端B的俯角为45°，已知建筑物AB的高为3米，求无人机飞行的高度（结果精确到1米，参考数据：≈1.414，≈1.732）．21．小明和小华约定一同去公园游玩，公园有南北两个门，北门A在南门B的正北方向，小明自公园北门A处出发，沿南偏东30°方向前往游乐场D处；小华自南门B处出发，沿正东方向行走150m到达C处，再沿北偏东22.6°方向前往游乐场D处与小明汇合（如图所示），两人所走的路程相同．求公园北门A与南门B之间的距离．（结果取整数．参考数据：sin22.6°≈，cos22.6°≈，tan22.6°≈，≈1.732）22．小张早起在一条东西走向的笔直马路上晨跑，他在A处时，D处学校和E处图书馆都在他的东北方向，当小张沿正东方向跑了600m到达B处时，E处图书馆在他的北偏东15°方向，然后他由B处继续向正东方向跑600m到达C处，此时D处学校在他的北偏西63.4°方向，求D处学校和E处图书馆之间的距离．（结果保留整数）（参考数据：sin63.4°≈0.9，cos63.4°≈0.4，tan63.4°≈2.0，≈1.4，≈1.7，≈2.4）23．如图，已知△ABD中，AC⊥BD，BC＝8，CD＝4，cos∠ABC＝，BF为AD边上的中线．（1）求AC的长；（2）求tan∠FBD的值．24．在全民健身运动中，骑行运动颇受市民青睐．一市民骑自行车由A地出发，途经B地去往C地，如图．当他由A地出发时，发现他的北偏东45°方向有一信号发射塔P．他由A地沿正东方向骑行4km到达B地，此时发现信号塔P在他的北偏东15°方向，然后他由B地沿北偏东75°方向骑行12km到达C地．（1）求A地与信号发射塔P之间的距离；（2）求C地与信号发射塔P之间的距离．（计算结果保留根号）25．某天，北海舰队在中国南海例行训练，位于A处的济南舰突然发现北偏西30°方向上的C处有一可疑舰艇，济南舰马上通知位于正东方向200海里B处的西安舰，西安舰测得C处位于其北偏西60°方向上，请问此时两舰距C处的距离分别是多少？26．如图，A，B是海面上位于东西方向的两个观测点，有一艘海轮在C点处遇险发出求救信号，此时测得C点位于观测点A的北偏东45°方向上，同时位于观测点B的北偏西60°方向上，且测得C点与观测点A的距离为25海里．（1）求观测点B与C点之间的距离；（2）有一艘救援船位于观测点B的正南方向且与观测点B相距30海里的D点处，在接到海轮的求救信号后立即前往营救，其航行速度为42海里/小时，求救援船到达C点需要的最少时间．参考答案1．解：在Rt△BAD中，AB＝5米，∠BAD＝37°，则BD＝AB•sin∠BAD≈5×＝3（米），在Rt△BCD中，∠C＝30°，∴BC＝2BD＝6（米），则调整后的楼梯会加长：6﹣5＝1（米），故选：D．2．解：过D作DF⊥BC于F，DH⊥AB于H，∴DH＝BF，BH＝DF，∵斜坡的斜面坡度i＝1：，∴＝1：，设DF＝xm，CF＝xm，∴CD＝＝2x＝20m，∴x＝10，∴BH＝DF＝10m，CF＝10m，∴DH＝BF＝（10+30）m，∵∠ADH＝30°，∴AH＝DH＝×（10+30）＝（10+10）m，∴AB＝AH+BH＝（20+10）m，故选：A．3．解：过点D作DM⊥BC，交CB的延长线于点M，∵∠ACB＝∠DMB＝90°，∠ABC＝∠DBM，∴△ABC∽△DBM，∴＝＝，∵AB＝2BD，∴＝＝＝，在Rt△CDM中，由于tan∠MCD＝＝，设DM＝2k，则CM＝3k，又∵＝＝，∴BC＝2k，AC＝4k，∴＝＝2，故选：B．4．解：如图，分别作出△ABC底边BC上的高为AD即h1，△PQR底边QR上的高为PE 即h2，在Rt△ADC中，h1＝AD＝5×sin55°，在Rt△PER中，h2＝PE＝5×sin55°，∴h1＝h2，故选：A．5．解：如图：作OF⊥AB于F，∵AB＝AC，AD平分∠BAC．∴∠ODB＝90°．BD＝CD＝6．∴根据勾股定理得：AD＝＝8．∵BE平分∠ABC．∴OF＝OD，BF＝BD＝6，AF＝10﹣6＝4．设OD＝OF＝x，则AO＝8﹣x，在Rt△AOF中，根据勾股定理得：（8﹣x）2＝x2+42．∴x＝3．∴OD＝3．在Rt△OBD中，tan∠OBD＝＝＝．故选：A．6．解：如图作DH⊥AB于H，延长DE交BC于F．在Rt△ADH中，AD＝130米，DH：AH＝1：2.4，∴DH＝50（米），∵四边形DHBF是矩形，∴BF＝DH＝50（米），在Rt△EFB中，∠BEF＝45°，∴EF＝BF＝50（米），在Rt△EFC中，FC＝EF•tan60°，∴CF＝50×≈86.6（米），∴BC＝BF+CF＝136.6（米）．故选：A．7．解：在Rt△ACB中，∠C＝90°，∠ABC＝45°，延长CB使BD＝AB，连接AD，得∠D＝22.5°，设AC＝BC＝1，则AB＝BD＝，∴tan22.5°＝＝＝﹣1，故选：B．8．解：过点B作AC边的高BD，Rt△ABD中，∠A＝45°，AB＝4，∴BD＝AD＝4，在Rt△BDC中，BC＝4，∴CD＝＝5，①△ABC是钝角三角形时，AC＝AD﹣CD＝1，∴S△ABC＝AC•BD＝＝2；②△ABC是锐角三角形时，AC＝AD+CD＝7，∴S△ABC＝AC•BD＝×7×4＝14，故答案为：2或14．9．解：在Rt△APO中，OP＝15米，∠APO＝30°，∴OA＝OP•tan30°＝（米），在Rt△POB中，OP＝15米，∠OPB＝60°，∴OB＝（米），∴AB＝OA+OB＝20（米），故答案为：20．10．解：过P作PC⊥AB于C，如图所示：由题意得：∠APC＝30°，∠BPC＝45°，P A＝50海里，在Rt△APC中，cos∠APC＝，∴PC＝P A•cos∠APC＝50×＝25（海里），在Rt△PCB中，cos∠BPC＝，∴PB＝＝＝25（海里），故答案为：25．11．解：过A点作AH⊥BC于H，过B点作BD垂直于过C点的水平线，垂足为D，如图，根据题意得∠ACD＝75°，∠BCD＝30°，AB＝3×10＝30m，∵AB∥CD，∴∠ABH＝∠BCD＝30°，在Rt△ABH中，AH＝AB＝15m，∵tan∠ABH＝，∴BH＝＝＝15，∵∠ACH＝∠ACD﹣∠BCD＝75°﹣30°＝45°，∴CH＝AH＝15m，∴BC＝BH+CH＝（15+15）m，在Rt△BCD中，∵∠BCD＝30°，∴BD＝BC＝≈20（m）．答：这架无人机的飞行高度大约是20m．故答案为20．12．解：如图，过点B、C分别作AE的垂线，垂足分别为M、N，过点C作CD⊥BM，垂足为D，在Rt△ABM中，∵∠BAE＝60°，AB＝16，∴BM＝sin60°•AB＝×16＝8（cm），∠ABM＝90°﹣60°＝30°，在Rt△BCD中，∵∠DBC＝∠ABC﹣∠ABM＝50°﹣30°＝20°，∴∠BCD＝90°﹣20°＝70°，又∵BC＝8，∴BD＝sin70°×8≈0.94×8＝7.52（cm），∴CN＝DM＝BM﹣BD＝8﹣7.52≈6.3（cm），即点C到AE的距离约为6.3cm，故答案为：6.3．13．解：过点A作AD⊥BC于D，如图所示：由题意得：∠ABC＝180°﹣75°﹣45°＝60°，∵AD⊥BC，∴∠ADB＝∠ADC＝90°，在Rt△ABD中，∠DAB＝90°﹣60°＝30°，AD＝AB•sin∠ABD＝80×sin60°＝80×＝40（海里），∵∠CAB＝30°+45°＝75°，∴∠DAC＝∠CAB﹣∠DAB＝75°﹣30°＝45°，∴△ADC是等腰直角三角形，∴AC＝AD＝×40＝40（海里）．答：货船与港口A之间的距离是40海里．14．解：由题意得，AD＝4000米，∠ADO＝30°，CD＝460米，∠BCO＝45°，在Rt△AOD中，∵AD＝4000米，∠ADO＝30°，∴OA＝AD＝2000（米），OD＝AD＝2000（米），在Rt△BOC中，∠BCO＝45°，∴OB＝OC＝OD﹣CD＝（2000﹣460）米，∴AB＝OB﹣OA＝2000﹣460﹣2000≈1004（米），∴火箭的速度为1004÷3≈335（米/秒），答：火箭的速度约为335米/秒．15．解：过点O作OE⊥AB于点E，则BE＝OD＝3m，设AE＝xm，则AB＝（x+3）m，A′E＝（x+6）m，∵∠AOE＝45°，∴OE＝AE＝xm，∵∠A′OE＝60°，∴tan60°＝＝，即＝，解得x＝3+3，∴AB＝3+3+3＝（6+3）m．16．解：（1）过点P作PC⊥AB，交AB的延长线于点C，由题意得，∠P AC＝30°，∠PBC＝45°，AB＝20，设PC＝x，则BC＝x，在Rt△P AC中，∵tan30°＝＝＝，∴x＝10+10，∴P A＝2x＝20+20，答：A，P之间的距离AP为（20+20）海里；（2）因为PC﹣10（3+）＝10+10﹣30﹣10＝10（+1）（﹣）＜0，所以有触礁的危险；设海监船无触礁危险的新航线为射线BD，作PE⊥BD，垂足为E，当P到BD的距离PE＝10（3+）海里时，有sin∠PBE＝＝＝，∴∠PBD＝60°，∴∠CBD＝60°﹣45°＝15°，90°﹣15°＝75°即海监船由B处开始沿南偏东至多75°的方向航行能安全通过这一海域．17．解：过B作BM⊥水平地面于M，BN⊥AC于N，如图所示：则四边形AMBN是矩形，∴AN＝BM，BN＝MA，∵斜坡AB＝105米，坡度i＝1：2＝，∴设BM＝x米，则AM＝2x米，∴AB＝＝＝x＝105，∴x＝21，∴AN＝BM＝21（米），BN＝AM＝42（米），在Rt△BCN中，∠CBN＝α＝45°，∴△BCN是等腰直角三角形，∴CN＝BN＝42（米），∴AC＝AN+CN＝21+42＝63≈141.1（米），答：观光电梯AC的高度约为141.1米．18．解：∵CM＝3m，OC＝5m，∴OM＝＝4（m），∵∠CMO＝∠BDO＝90°，∠COM＝∠BOD，∴△COM∽△BOD，∴，即，∴BD＝＝2.25（m），∴tan∠AOD＝tan70°＝，即≈2.75，解得：AB＝6m，∴汽车从A处前行约6米才能发现C处的儿童．19．解：（1）过点D作DH⊥CE于点H，由题意知CD＝2米，∵斜坡CF的坡比为i＝1：3，∴，设DH＝x米，CH＝3x米，∵DH2+CH2＝DC2，∴，∴x＝2，∴DH＝2（米），CH＝6（米），答：王刚同学从点C到点D的过程中上升的高度为2米；（2）过点D作DG⊥AB于点G，设BC＝a米，∵∠DHB＝∠DGB＝∠ABC＝90°，∴四边形DHBG为矩形，∴DH＝BG＝2米，DG＝BH＝（a+6）米，∵∠ACB＝45°，∴BC＝AB＝a（米），∴AG＝（a﹣2）米，∵∠ADG＝30°，∴，∴，∴a＝6+4，∴AB＝（6+4）（米）．答：大树AB的高度是（6+4）米．20．解：过A作AC⊥PQ，交PQ的延长线于C，如图所示：设AC＝x米，由题意得：PQ＝5米，∠APC＝30°，∠BQC＝45°，在Rt△APC中，tan∠APC＝＝tan30°＝，∴PC＝AC＝x（米），在Rt△BCQ中，tan∠BQC＝＝tan45°＝1，∴QC＝BC＝AC+AB＝（x+3）米，∵PC﹣QC＝PQ＝5米，∴x﹣（x+3）＝5，解得：x＝4（+1），∴BC＝4（+1）+3＝4+7≈14（米），答：无人机飞行的高度约为14米．21．解：作DE⊥AB于E，CF⊥DE于F，∵BC⊥AB，∴四边形BCFE是矩形，∴BE＝CF，EF＝BC＝150 m，设DF＝xm，则DE＝（x+150）m，在Rt△ADE中，∠BAD＝30°，∴AD＝2DE＝2（x+150）m，在Rt△DCF中，∠FCD＝22.6°，∴CD＝≈＝xm，∵AD＝CD+BC，∴2（x+150）＝+150，解得x＝250（m），∴DF＝250 m，∴DE＝250+150＝400 m，∴AD＝2DE＝800 m，∴CD＝800﹣150＝650 m，由勾股定理得AE＝＝＝400m，BE＝CF＝＝＝600 m，∴AB＝AE+BE＝400+600≈1293（m），答：公园北门A与南门B之间的距离约为1293 m．22．解：过D作DM⊥AC于M，设MD＝x，在Rt△MAD中，∠MAD＝45°，∴△ADM是等腰直角三角形，∴AM＝MD＝x，∴AD＝x，在Rt△MCD中，∠MDC＝63.4°，∴MC≈2MD＝2x，∵AC＝600+600＝1200，∴x+2x＝1200，解得：x＝400，∴MD＝400m，∴AD＝MD＝400，过B作BN⊥AE于N，∵∠EAB＝45°，∠EBC＝75°，∴∠E＝30°，在Rt△ABN中，∠NAB＝45°，AB＝600，∴BN＝AN＝AB＝300，∴DN＝AD﹣AN＝400﹣300＝100，在Rt△NBE中，∠E＝30°，∴NE＝BN＝×300＝300，∴DE＝NE﹣DN＝300﹣100≈580（m），即D处学校和E处图书馆之间的距离约是580m．23．解：（1）∵AC⊥BD，cos∠ABC＝＝，BC＝8，∴AB＝10，在Rt△ACB中，由勾股定理得，AC＝＝＝6，即AC的长为6；（2）如图，连接CF，过F点作BD的垂线，垂足E，∵BF为AD边上的中线，即F为AD的中点，∴CF＝AD＝FD，在Rt△ACD中，由勾股定理得，AD＝＝＝2，∵三角形CFD为等腰三角形，FE⊥CD，∴CE＝CD＝2，在Rt△EFC中，EF＝＝＝3，∴tan∠FBD＝＝＝．解法二：∵BF为AD边上的中线，∴F是AD中点，∵FE⊥BD，AC⊥BD，∴FE∥AC，∴FE是△ACD的中位线，∴FE＝AC＝3，CE＝CD＝2，∴在Rt△BFE中，tan∠FBD＝＝＝．24．解：（1）依题意知：∠P AB＝45°，∠PBG＝15°，∠GBC＝75°，过点B作BD⊥AP于D点，∵∠DAB＝45°，，∴AD＝BD＝4，∵∠ABD＝∠GBD＝45°，∠GBP＝15°，∴∠PBD＝60°，∵BD＝4，∴，∴P A＝（4+4）（km）；（2）∵∠PBD＝60°，BD＝4，∴PB＝8，过点P作PE⊥BC于E，∵∠PBG＝15°，∠GBC＝75°，∴∠PBE＝60°，∵PB＝8，∴BE＝4，，∵BC＝12，∴CE＝8，∴PC＝＝4（km）．25．解：过点C作CD⊥BA的延长线于点D，如图．由题意可得：∠CAD＝60°，∠CBD＝30°＝∠DCA，∴∠BCA＝∠CAD﹣∠CBD＝60°﹣30°＝30°．即∠BCA＝∠CBD，∴AC＝AB＝200（海里）．在Rt△CDA中，CD＝sin∠CAD×AC＝＝100（海里）．在Rt△CDB中，CB＝2CD＝200（海里）．故位于A处的济南舰距C处的距离200海里，位于B处的西安舰距C处的距离200海里．26．解：（1）如图，过点C作CE⊥AB于点E，根据题意可知：∠ACE＝∠CAE＝45°，AC＝25海里，∴AE＝CE＝25（海里），∵∠CBE＝30°，∴BE＝25（海里），∴BC＝2CE＝50（海里）．答：观测点B与C点之间的距离为50海里；（2）如图，作CF⊥DB于点F，∵CF⊥DB，FB⊥EB，CE⊥AB，∴四边形CEBF是矩形，∴FB＝CE＝25（海里），CF＝BE＝25（海里），∴DF＝BD+BF＝30+25＝55（海里），在Rt△DCF中，根据勾股定理，得CD＝＝＝70（海里），∴70÷42＝（小时）．答：救援船到达C点需要的最少时间是小时．。

第1章解直角三角形类型之一锐角三角函数的概念图1－X－11．如图1－X－1，在平面直角坐标系中，点A的坐标为(4，3)，那么cosα的值是( )A.34B.43C.35D.452．直角三角形纸片的两直角边长分别为6，8，现将△ABC如图1－X－2那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是( )1－X－2A.247B.73C.724D.133．如图1－X－3，在△ABC中，∠A＝120°，AB＝4，AC＝2，则sin B的值是( )A.5 514B.35C.217D.21141－X－31－X－44．如图1－X－4，点P在等边三角形ABC的内部，且PC＝6，PA＝8，PB＝10，将线段PC绕点C顺时针旋转60°得到P′C，连结AP′，则sin∠PAP′的值为________．类型之二 特殊角的三角函数值的计算 5．若α的余角是30°，则cos α的值是( ) A.12 B.32 C.22 D.336．点M (－sin60°，cos60°)关于x 轴对称的点的坐标是( ) A.⎝⎛⎭⎪⎫32，12 B.⎝ ⎛⎭⎪⎫－32，－12C.⎝ ⎛⎭⎪⎫－32，12 D.⎝ ⎛⎭⎪⎫－12，－32 7．计算：(1)12＋2－1－4cos30°＋⎪⎪⎪⎪⎪⎪－12；(2)||2－3＋2sin60°＋(12)－1－()2018＋10；(3)2cos45°－()n ＋10＋14＋(12)－1(n 是自然数)．类型之三解直角三角形及其应用8．2017·南宁如图1－X－5，一艘海轮位于灯塔P的南偏东45°方向，距离灯塔60 n mile的A处，它沿正北方向航行一段时间后，到达位于灯塔P的北偏东30°方向上的B处，这时，B处与灯塔P之间的距离为( )A．60 3 n mile B．60 2 n mileC．30 3 n mile D．30 2 n mile1－X－51－X－69．如图1－X－6，将45°的∠AOB按下面的方式放置在一把刻度尺上：顶点O与尺下沿的端点重合，OA与尺下沿重合，OB与尺上沿的交点B在尺上的读数恰为2 cm.若按相同的方式将37°的∠AOC放置在该刻度尺上，则OC与尺上的交点C在尺上的读数约为________cm.(结果精确到0.1 cm，参考数据：sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)图1－X－710．如图1－X－7，∠AOB的边OB与x轴正半轴重合，P是OA上的一动点，N(3，0)是OB上的一定点，M是ON的中点，∠AOB＝30°，要使PM＋PN最小，则点P的坐标为________．11．2016·舟山太阳能光伏建筑是现代绿色环保建筑之一，老张准备把自家屋顶改建成光伏瓦面，改建前屋顶截面△ABC如图1－X－8所示，BC＝10米，∠ABC＝∠ACB＝36°，改建后顶点D在BA的延长线上，且∠BDC＝90°，求改建后屋顶面边沿增加部分AD的长．(结果精确到0.1米)(参考数据：sin18°≈0.31，cos18°≈0.95，tan18°≈0.32，sin36°≈0.59，cos36°≈0.81，tan36°≈0.73)图1－X－812．2017·岳阳某太阳能热水器的横截面示意图如图1－X－9所示，已知真空热水管AB与支架CD所在直线相交于点O，且OB＝OD.支架CD与水平线AE垂直，∠BAC＝∠CDE＝30°，DE＝80 cm，AC＝165 cm.(1)求支架CD的长；(2)求真空热水管AB的长．(结果均保留根号)图1－X－913．2017·株洲如图1－X－10，从一架水平飞行的无人机AB的尾端点A测得正前方的桥的左端点P的俯角为α，其中tanα＝2 3，无人机的飞行高度AH＝500 3米，桥的长度为1255米．(1)求点H到桥的左端点P的距离；(2)若从无人机前端点B测得正前方的桥的右端点Q的俯角为30°，求这架无人机的长度．图1－X－1014．2016·杭州如图1－X－11，已知四边形ABCD和四边形DEFG均为正方形，点E在线段DC上，点A，D，G在同一直线上，且AD＝3，DE＝1，连结AC，CG，AE，并延长AE交CG于点H.(1)求sin∠EAC的值；(2)求线段AH的长．图1－X－11详解详析1．D2．C [解析] 根据题意，BE ＝AE . 设CE ＝x ，则BE ＝AE ＝8－x ， 在Rt △BCE 中，根据勾股定理，得BE 2＝BC 2＋CE 2，即(8－x )2＝62＋x 2，解得x ＝74，∴tan ∠CBE ＝CE CB ＝746＝724.故选C.3．D [解析] 过点C 作CD ⊥BA 交BA 的延长线于点D . ∵∠BAC ＝120°，AB ＝4，AC ＝2, ∴∠DAC ＝60°，∠ACD ＝30°， ∴2AD ＝AC ＝2， ∴AD ＝1，CD ＝3， ∴BD ＝5，∴BC ＝2 7， ∴sin B ＝32 7＝2114.4.35[解析] 连结PP ′，∵线段PC 绕点C 顺时针旋转60°得到P ′C ，∴CP ＝CP ′＝6， ∠PCP ′＝60°， ∴△CPP ′为等边三角形， ∴PP ′＝PC ＝6. ∵△ABC 为等边三角形， ∴CB ＝CA ，∠ACB ＝60°， ∴∠PCB ＝∠P ′CA ， ∴△PCB ≌△P ′CA (SAS )， ∴PB ＝P ′A ＝10.∵62＋82＝102，∴PP ′2＋AP 2＝P ′A 2， ∴△APP ′为直角三角形，且∠APP ′＝90°， ∴sin ∠PAP ′＝PP ′P ′A ＝610＝35. 5．A [解析] α＝90°－30°＝60°，cos α＝cos60°＝12.故选A.6．B [解析] ∵sin60°＝32，cos60°＝ 12， ∴点M 的坐标为⎝ ⎛⎭⎪⎫－32，12. ∵点P (m ，n )关于x 轴对称的点为P ′(m ，－n )， ∴点M 关于x 轴的对称点的坐标是⎝ ⎛⎭⎪⎫－32，－12.故选B. 7．解：(1)原式＝2 3＋12－4×32＋12＝2 3＋12－2 3＋12＝1.(2)原式＝2－3＋2×32＋2－1＝3.(3)原式＝2×22－1＋12＋2＝2＋32. 8．B [解析] 如图，作PE ⊥AB 于点E .在Rt △PAE 中，∵∠PAE ＝45°，PA ＝60 n mile ，∴PE ＝AE ＝22×60＝30 2(n mile)． 在Rt △PBE 中，∵∠B ＝30°， ∴PB ＝2PE ＝60 2 n mile.9．2.710．(32，32) [解析] 作点N 关于OA 的对称点N ′，连结MN ′交OA 于点P ，则点P为所求．显然ON ＝ON ′，∠NON ′＝2∠AOB ＝2×30°＝60°，∴△ONN ′为等边三角形，MN ′⊥ON .∵OM ＝32，∴PM ＝OM ·tan30°＝32×33＝32，∴点P 的坐标为⎝ ⎛⎭⎪⎫32，32.11．解：∵∠BDC ＝90°，BC ＝10米，sin B ＝CDBC， ∴CD ＝BC ·sin B ≈10×0.59＝5.9(米)．∵在Rt △BCD 中，∠BCD ＝90°－∠B ＝90°－36°＝54°， ∴∠ACD ＝∠BCD －∠ACB ＝54°－36°＝18°， ∴在Rt △ACD 中，tan ∠ACD ＝AD CD，∴AD ＝CD ·tan ∠ACD ≈5.9×0.32＝1.888≈1.9(米)， 则改建后屋顶面边沿增加部分AD 的长约为1.9米．12．解：(1)在Rt △CDE 中，∠CDE ＝30°，DE ＝80 cm ，∴cos30°＝CD 80＝32，解得CD＝40 3(cm)．故支架CD 的长为40 3 cm.(2)在Rt △OAC 中，∠BAC ＝30°，AC ＝165 cm ，∴tan30°＝OC 165＝33，解得OC ＝55 3(cm)，∴OA ＝2OC ＝110 3 cm ，OB ＝OD ＝OC －CD ＝55 3－40 3＝15 3(cm)， ∴AB ＝OA －OB ＝110 3－15 3＝95 3(cm)． 故真空热水管AB 的长为95 3 cm. 13．解：(1)在Rt △AHP 中， ∵∠APH ＝α，AH ＝500 3米， ∴tan ∠APH ＝AH HP＝tan α， ∴500 3HP＝2 3，解得HP ＝250(米)．故点H 到桥的左端点P 的距离为250米． (2)过点Q 作QM ⊥AB 交其延长线于点M ，则可得AM ＝HQ ＝HP ＋PQ ＝250＋1255＝1505(米)，QM ＝AH ＝500 3米． ∵在Rt △QMB 中，∠QMB ＝90°，∠QBM ＝30°，QM ＝500 3米， ∴BM ＝1500米，∴AB ＝AM －BM ＝1505－1500＝5(米)． 故这架无人机的长度为5米．14．解：(1)由题意知EC ＝2，AE ＝10. 过点E 作EM ⊥AC 于点M ，所以∠EMC ＝90°，易知∠ACD ＝45°， 所以△EMC 是等腰直角三角形，所以EM ＝2，所以sin ∠EAC ＝EM AE ＝55. (2)在△GDC 与△EDA 中，因为⎩⎪⎨⎪⎧DG ＝DE ，∠GDC ＝∠EDA ，DC ＝DA ，所以△GDC ≌△EDA ，所以∠GCD ＝∠EAD . 又因为∠HEC ＝∠DEA ，所以∠EHC ＝∠EDA ＝90°，所以AH ⊥GC . 由△GDC ≌△EDA ，得GC ＝EA ＝10. 因为S △AGC ＝12AG ·DC ＝12GC ·AH ，所以12×4×3＝12×10×AH ，所以AH ＝6510.。

第一章解直角三角形复习一、锐角三角函数：1、根据三角函数定义下列函数：正弦： 余弦：α 正切：2、各三角函数之间的关系：⑴sin α＝cos ⑵sin 2α＋cos 2α＝ ⑶tan α＝ 31、在Rt △ABC 中，∠C ＝900，AC ＝12，BC ＝15。

（1）求AB 的长； （2）求sinA 、cosA 的值；（3）求A A 22cos sin +的值； （4）比较sinA 、cosB 的大小。

2、（1）在Rt △ABC 中，∠C ＝900，5=a ，2=b ，则sinA ＝ 。

（2）在Rt △ABC 中，∠A ＝900，如果BC ＝10，sinB ＝0.6，那么AC ＝ 。

（3）在ABC Rt ∆中，C ∠＝90︒，c = 8 , sinA =41，则b = . 3、选择：（1）在Rt △ABC 中，∠C ＝900，31tan =A ，AC ＝6，则BC 的长为（ ） A 、6B 、5C 、4D 、2 （2）Rt ABC ∆中，C ∠＝90︒，43AC BC ==，,cos B 的值为 （ ）15A 、35B、 43C、 34D、 （3）ABC ∆中，C ∠＝90︒，tan 1A =，则sin B 的值是 （ ）A 、B、1C、 2D、4、计算：（1)sin 30º+cos 45º; (2) sin ²60º+cos ²60º-tan 45º.（3）︒∙︒-︒∙+︒60tan 60sin 45cos 230sin5、用计算器求下列余弦值，并用“<”连接：cos27.5°, cos85°, cos63°36’15”, cos54°23’, cos38°39’52” 你从这些能找到什么规律。

二、解直角三角形：1、三边之间的关系:2、锐角之间的关系:3、边角之间的关系: 如图，在Rt △ABC 中，∠ C ＝Rt ∠ 各边分别为a ，b ，c 。