大学物理学下册第15章
- 格式:doc
- 大小:514.00 KB
- 文档页数:7

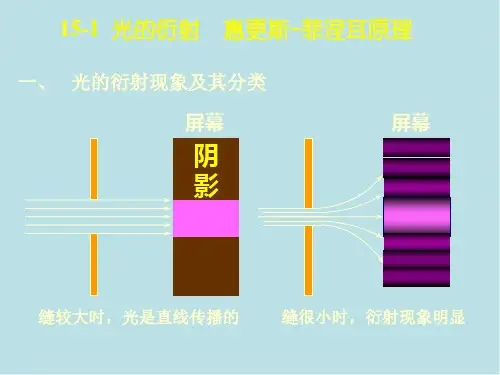
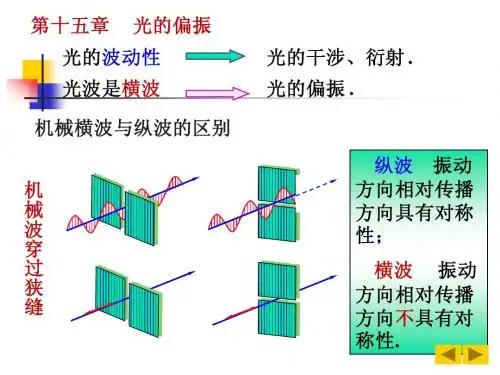
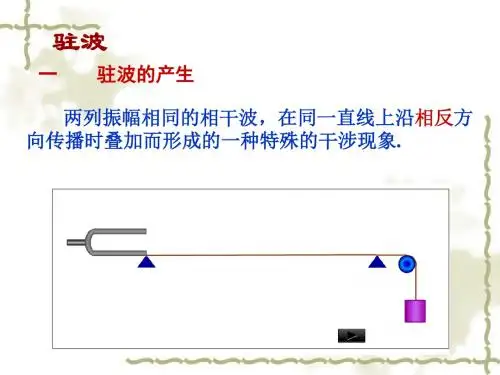





1习 题1515.1选择题(1)用一定频率的单色光照射在某种金属上,测出其光电流I 与电势差U 的关系曲线如题16.1图中实线所示.然后在光强度I 不变的条件下增大照射光的频率,测出其光电流的曲线用虚线表示.符合题意的图是: [ ][答案:D 。
光强度I φ不变,光的频率v 增大,光子数(光子密度)N φ减少,则逸出光电子数 N e 减少,饱和光电流I e 减少;光的频率v 增大,由爱因斯坦光电效应方程21A 2m m hv υ=-知初动能增大,则遏止电压增加。
](2) 康普顿散射的主要特点是: [ ](A) 散射光的波长均与入射光的波长相同,与散射角、散射体性质无关.(B) 散射光中既有与入射光波长相同的,也有比入射光波长长的和比入射光波长短的.这与散射体性质有关.(C) 散射光的波长均比入射光的波长短,且随散射角增大而减小,但与散射体的性质无关.(D) 散射光中有些波长比入射光的波长长,且随散射角增大而增大,有些散射光波长与入射光波长相同.这都与散射体的性质无关.[答案:D 。
](3)假定氢原子原是静止的,质量为1.67×10-27 kg ,则氢原子从n = 3 的激发状态直接通过辐射跃迁到基态时的反冲速度大约是 [ ](A) 4 m/s . (B) 10 m/s . (C) 100 m/s . (D) 400 m/s .[答案:A 。
动量守恒 -m υ+h/λ34722711 6.62610 1.096108()13 1.67109H h R m υ--⨯⨯⨯=-=⨯⨯≈4m/s](4) 关于不确定关系2x p x ∆∆≥,有以下几种理解: (a ) 粒子的动量不可能确定.(b ) 粒子的坐标不可能确定.(c ) 粒子的动量和坐标不可能同时准确地确定.(d ) 不确定关系不仅适用于电子和光子,也适用于其它粒子.其中正确的是: [ ]O(A ) (B ) (C ) (D )题15.1图。


第15章 磁介质的磁化15.1 一均匀磁化的磁介质棒,直径为25mm ,长为75mm ,其总磁矩为12000A·m 2.求棒的磁化强度M 为多少?[解答]介质棒的面积为S = πr 2,体积为 V = Sl = πr 2l ,磁矩为p m = 12000A·m 2,磁化强度为m m p p M V V ∑==∆32312000(2510/2)7510π--=⨯⨯⨯=3.26×108(A·m -1).15.2一铁环中心线的周长为30cm ,横截面积为1.0cm 2,在环上密绕线圈共300匝,当通有电流32mA 时,通过环的磁通量为2.0×10-6Wb ,求:(1)环内磁感应强度B 的值和磁场强度H 的值;(2)铁的磁导率μ、磁化率χm 和磁化强度M .[解答](1)根据公式B = Φ/S 得磁感应强度为642.0101.010B --⨯=⨯= 0.02(T).根据磁场的安培环路定理∑⎰=⋅,d I L l H由于B 与d l 的方向相同,得磁场强度为3230032103010NI H l --⨯⨯==⨯= 32(A·m -1).(2)根据公式B = μH ,得铁的磁导率为0.0232B H μ=== 6.25×10-4(Wb·A -1·m -1).由于μ = μr μ0,其中μ0 = 4π×10-7为真空磁导率,而相对磁导率为μr = 1 + χm ,所以磁化率为470 6.251011496.4410m μχμπ--⨯=-=-=⨯.磁化强度为M = χm H = 496.4×32 = 1.59×104(A·m -1).15.3一螺绕环中心周长l = 10cm ,线圈匝数N = 200匝,线圈中通有电流I = 100mA .求:(1)管内磁感应强度B 0和磁场强度H 0为多少?(2)设管内充满相对磁导率μr = 4200的铁磁质,管内的B 和H 是多少?(3)磁介质内部由传导电流产生的B 0和由磁化电流产生的B`各是多少?[解答](1)管内的磁场强度为302200100101010NI H l --⨯⨯==⨯= 200(A·m -1).磁感应强度为B = μ0H 0 = 4π×10-7×200 = 2.5×10-4(T).(2)当管内充满铁磁质之后,磁场强度不变H = H 0 =200(A·m -1).磁感应强度为B = μH = μr μ0H= 4200×4π×10-7×200 = 1.056(T).(3)由传导电流产生的B 0为2.5×10-4T .由于B = B 0 + B`,所以磁化电流产生的磁感应强度为B` = B - B 0 ≈1.056(T).15.4一根无限长的直圆柱形铜导线,外包一层相对磁导率为μr 的圆筒形磁介质,导线半径为R 1,磁介质外半径为R 2,导线内有电流I 通过(I 均匀分布),求:(1)磁介质内、外的磁场强度H 和磁感应强度B 的分布,画H-r ,B-r 曲线说明之(r 是磁场中某点到圆柱轴线的距离);(2)磁能密度分布.[解答](1)导线的横截面积为S 0 = πR 12,导线内的电流密度为 δ = I/S 0 = I/πR 12.在导线内以轴线的点为圆心作一半径为r 的圆,其面积为 S =πr 2,通过的电流为 ΣI = δS = Ir 2/R 12.根据磁场中的安培环路定理∑⎰=⋅,d I L l H环路的周长为l = 2πr ,由于B 与d l 的方向相同,得磁场强度为 212I Ir H l R π∑==,(0≦r ≦R 1).在介质之中和介质之外同样作一半径为r 的环路,其周长为l = 2πr ,包围的电流为I ,可得磁场强度为2I I H l r π∑==,(r ≧R 1).导线之内的磁感应强度为00121,(0)2Ir B H r R R μμπ==≤≤;介质之内的磁感应强度为0012,()2r r I B H H R r R r μμμμμπ===≤≤;介质之外的磁感应强度为002,()2I B H r R r μμπ==≥. (2)导线之内的磁能密度为200001122m w H μ=⋅=B H 2201241,(0)8I r r R R μπ=≤≤;介质之中的磁能密度为220111222m r w H H μμμ=⋅==B H201222,()8r I R r R r μμπ=≤≤;介质之外的磁感应强度为220022211,()228m I w H r R r μμπ=⋅==≥B H .15.5一根磁棒的矫顽力为H c = 4.0×103A·m -1,把它放在每厘米上绕5匝的线圈的长螺线管中退磁,求导线中至少需通入多大的电流?[解答]螺线管能过电流I 时,产生的磁感应强度为 B = μ0nI . 根据题意,螺线管产生的磁场强度至少要与磁棒的矫顽力大小相等,但方向相反,因此 B = μ0H c ,所以电流强度为I = H c /n = 4.0×103/500 = 8(A).15.6 同轴电缆由两个同轴导体组成.内层是半径为R 1的圆柱,外层是半径分别为R 2和R 3的圆筒,如图所示.两导体间充满相对磁导率为μr 2的均匀不导电的磁介质.设电流强度由内筒流入由外筒流出,均匀分布是横截面上,导体的相对磁导率为μr 1.求H 和B 的分布以及i m 为多少?[解答](1)导体圆柱的横截面积为S 0 = πR 12,圆柱体内的电流密度为δ = I/S 0 = I/πR 12.在圆柱体内以轴线的点为圆心作一半径为r 的圆,其面积为 S = πr 2,通过的电流为 ΣI = δS = Ir 2/R 12.根据磁场中的安培环路定理∑⎰=⋅,d I L l H环路的周长为l = 2πr ,由于B 与d l 的方向相同,得磁场强度为图15.6212I Ir H l R π∑==,(0≦r ≦R 1).磁感应强度为1010212r r IrB H R μμμμπ==,(0≦r ≦R 1).(2)在介质之中同样作一半径为r 的环路,其周长为l = 2πr ,包围的电流为I ,可得磁场强度为2I I H l r π∑==,(R 1≦r ≦R 2).磁感应强度为20202r r IB H r μμμμπ==,(R 1≦r ≦R 2).磁化强度为220(1)(1)2r r I BM H H r μμμπ-=-=-=.磁化面电流的线密度为 i m = M ×n 0,n 0是介质表面的法向单位矢量.在介质的两个圆形表面,由于M 与n 0垂直,i m = |M ×n 0| = M .在介质的内表面,由于r = R 1,所以磁化电流为21(1)2r m Ii R μπ-=.在介质的外表面,由于r = R 2,所以22(1)2r m Ii R μπ-=.(3)导体圆筒的横截面积为S` = π(R 32 - R 22),圆筒内的电流密度为δ` = I/S`.在圆筒内以作一半径为r 的圆,其面积为 S = π(r 2 - R 22), 圆所包围的电流为``SI I S I I S δ=-=-∑22223222223232(1)R r r R I I R R R R --=-=--, 根据安培环路定理∑⎰=⋅,d I L l H 得磁场强度为 2232232()22()I R r I H r R R r ππ-∑==-,(R 2≦r ≦R 3).磁感应强度为22103102232()2()r r I R r B H R R r μμμμπ-==-,(R 2≦r ≦R 3).(4)在圆筒之外作一圆,由于包围的电流为零,所以磁场强度和磁感应强度都为零.15.7在平均半径r = 0.1m ,横截面积S = 6×10-4m 2铸钢环上,均匀密绕N = 200匝线圈,当线圈内通有I 1 = 0.63安的电流时,钢环中的磁通量Φ1 = 3.24×10-4Wb .当电流增大到I 2 = 4.7安时,磁通量Φ2 =6.18×10-4Wb ,求两种情况下钢环的绝对磁导率.[解答]钢环中的磁感应强度为 B = Φ/S ;根据安培环路定理∑⎰=⋅,d I L l H 得磁场强度为H = NI /2πr .根据公式B = μH ,得绝对磁导率为2B r H NIS πΦμ==.(1)在第一种情况下4420.1 3.24102000.63610πμ--⨯⨯⨯=⨯⨯⨯= 2.69×10-3(H·m -1) .(2)在第二种情况下4420.1 6.1810200 4.7610πμ--⨯⨯⨯=⨯⨯⨯= 6.88×10-4(H·m -1) .15.8 一矩磁材料,如图所示.反向磁场一超过矫顽力H c ,磁化方向立即翻转.用矩磁材料制造的电子计算机中存储元件的环形磁芯,其外径为0.8mm ,内径为0.5mm ,高为0.3mm .若磁芯原来已被磁化,方向如图所示,现在需使磁芯从内到外的磁化方向全部翻转,导线中脉冲电流I 的峰值至少需要多大?设磁性材料的矫顽力H c 12π=⨯103(A·m -1).[解答]直线电流I 产生磁感应强度为B = μ0I /2πr ,产生的磁场为 H = B/μ0 = I /2πr .为了磁芯从内到外的磁化方向全部翻转,电流在磁芯外侧r = 0.4mm 处产生的磁场应该为 H = H c ,即 H c =I /2πr ,图15.8所以,脉冲电流为I = 2πrH c33120.410100.4(A)2ππ-=⨯⨯⨯=。
第15章 量子物理一 选择题15-1 下列物体中属于绝对黑体的是[ ](A) 不辐射可见光的物体 (B) 不辐射任何光线的物体 (C) 不能反射可见光的物体 (D) 不能反射任何光线的物体 解:选(D)。
绝对黑体能够100%吸收任何入射光线,因而不能反射任何光线。
15-2 用频率为υ的单色光照射某种金属时,逸出光电子的最大动能为k E ;若改用频率为2υ的单色光照射此金属,则逸出光电子的最大初动能为[ ](A) k 2E (B) k 2h E υ- (C) k h E υ- (D) k h E υ+ 解:选(D)。
由k E h W υ=-,'2k E h W υ=-,得逸出光电子的最大初动能'k ()k E hv hv W hv E =+-=+。
15-3 某金属产生光电效应的红限波长为0λ,今以波长为λ(0λλ<)的单色光照射该金属,金属释放出的电子(质量为e m )的动量大小为[ ](A) /h λ (B) 0/h λ (C)(D)解:选(C)。
由2e m 012hv m v hv =+,2e m 012hc hc m v λλ=+,得m v =,因此e m p m v ==。
15-4 根据玻尔氢原子理论,氢原子中的电子在第一和第三轨道上运动速率之比13/v v 是[ ](A) 1/3 (B) 1/9 (C) 3 (D) 9解:选(C)。
由213.6n E n =-,n 分别代入1和3,得221122331329112mvE E mv ===,因此133v v =。
15-5 将处于第一激发态的氢原子电离,需要的最小能量为[ ] (A) 13.6eV (B) 3.4eV (C) 1.5eV (D) 0eV 解:选(B)。
由213.6n E n =-,第一激发态2n =,得2 3.4eV E =-,设氢原子电离需要的能量为2'E ,当2'20E E +>时,氢原子发生电离,得2' 3.4eV E >,因此最小能量为3.4eV 。
15-6 关于不确定关系x x p h ∆∆≥有以下几种理解,其中正确的是[ ] (1) 粒子的动量不可能确定 (2) 粒子的坐标不可能确定(3) 粒子的动量和坐标不可能同时确定(4) 不确定关系不仅适用于电子和光子,也适用于其他粒子 (A) (1), (2) (B) (2), (4) (C) (3), (4) (D) (4), (1) 解:选(C)。
根据h p x x ≥∆⋅∆可知,(1)、(2)错误,(3)正确;不确定关系适用于微观粒子,包括电子、光子和其他粒子,(4)正确。
二 填空题15-7 已知某金属的逸出功为W ,用频率为1υ的光照射该金属能产生光电效应,则该金属的红限频率0υ=________,截止电势差c U =________。
解:由0W hv =,得hW v =0;由21e m12hv m v W =+,而2e m c 12m v eU =,所以 1c hv eU W =+,得1c h WU eυ-=。
15-8 在康普顿效应中,波长为0λ的入射光子与静止的自由电子碰撞后反向弹回,而散射光子的波长变为λ,则反冲电子获得的动能为________。
解:由2200+=+hv m c hv mc ,得2200ν-=-mc m c h hv ,其中220-mc m c 为反冲电子获得的动能k E ,因此k 0011()E h hv hc νλλ=-=-。
15-9 根据玻尔氢原子理论,若大量氢原子处于主量子数n = 5的激发态,则跃迁辐射的谱线可以有________条,其中属于巴耳末系的谱线有________条。
解:n 从5到4、3、2、1,从4到3、2、1,从3到2、1,从2到1,一共有10条;巴尔末系2=k ,从5到2,从4到2,从3到2,一共有3条。
15-10 氢原子由定态l 跃迁到定态k 可发射一个光子。
已知定态l 的电离能为0.85eV ,又知使氢原子从基态激发到定态k 所需能量为10.2eV ,则在上述跃迁中氢原子所发射的光子的能量为________。
解:基态的能量113.6eV E =-,则定态k 的能量13.610.2 3.4eV k E =-+=-,已知定态l 的电离能为0.85eV ,则定态l 的能量0.85eV l E =-,因此由定态l 跃迁到定态k ,所发射的光子的能量为 2.55eV l k E E -=。
15-11 运动速率等于在300K 时方均根速率的氢原子的德布罗意波长是________;质量为1g m =,以速度1cm/s v =运动的小球的德布罗意波长是________。
(氢原子质量27H 1.6710kg m -=⨯)解:方均根速率为rms v =,代入数据,得3rms 2.7310 m/s v =⨯,因为rms v c =,所以氢原子的德布罗意波长H rmsh h p m v λ==,代入数据,得0.145nm λ=;同样,小球速度v c =,德布罗意波长h hp mvλ==,代入数据,得206.6310nm λ-=⨯15-12 在电子单缝衍射实验中,若缝宽为0.1nm a =(91nm=10m -),电子束垂直射在单缝上,则衍射的电子横向动量的最小不确定量p ∆=________。
解:由a p h ⋅∆≥,得hp a∆≥,代入数据,得246.6310kg.m/s p -∆≥⨯。
15-13 已知粒子在一维矩形无限深势阱中运动,其波函数为3() (0)x x x a aπψ=≤≤ 那么粒子在/6x a =处出现的概率密度为________。
解:概率密度为2223()sin x x a a πψ=,/6x a =代入,得22()x aψ=。
三 计算题15-14 已知从铝金属逸出一个电子需要4.2eV 的能量,若用可见光投射到铝的表面,能否产生光电效应?解:由2e m 12hv m v W =+可知,只有当hv W >时,才能产生光电效应;可见光的波长范围为400760nm :,当波长为400nm 时,能量最大, 3.1eV hchv λ==,而4.2eV W =,因此hv W <,即不能产生光电效应。
15-15 如图所示为在一次光电效应实验中得出的曲线,(1)证明对不同材料的金属,AB 线的斜率相同;(2)由图上数据求出普朗克常量h 。
解:(1)证明:纵坐标为c U ,横坐标为υ,列出两者关系式即可得斜率。
由2e m 12hv m v W =+,而2e m c 12m v eU =,得 c hv eU W =+,因此c h W U e e υ=-,斜率h e为常数,即对不同材料的金属,AB 线的斜率相同;习题15-15图(2)由图可知斜率为15142410510-=⨯⨯,由15410h e-=⨯,得346.410J.S h -=⨯。
15-16 在康普顿效应中,入射光子的波长为33.010nm -⨯,反冲电子的速度为光速的60%,求散射光子的波长及散射角。
解:由2200+=+hv m c hv mc ,得2200ν-=-mc m c h hv ,由于反冲电子的速度为光速的60%,2200hchcm c λλ-=-,代入数据,得34.3510nm λ-=⨯;由()001cos hm cλλλθ∆=-=-,代入数据,得arccos0.44463.66336'θ==︒=︒。
15-17 波长为0.1nm 的辐射,射在碳上,从而产生康普顿效应。
从实验中,测量到散射辐射的方向与入射辐射的方向相垂直。
求:(1)散射辐射的波长;(2)反冲电子的动能和运动方向。
解:(1)由()001cos hm cλλλθ∆=-=-,90θ=︒,代入数据,得0.1024nm λ=; (2)由2200+=+hv m c hv mc ,得2200ν-=-mc m c h hv ,其中220-mc m c 为反冲电子获得的动能k E ,因此k 0011()E h hv hc νλλ=-=-,代入数据,得17k 4.6610J E -=⨯;设反冲电子的方向与入射辐射的方向夹角为ϕ,而散射辐射的方向与入射辐射的方向相垂直,即90θ=︒,通过矢量作图可知,0tan pp ϕ=,因此000/arctan()arctan()arctan()/p h p h λλϕλλ===,代入数据,得4418'ϕ=︒。
15-18 处于基态的氢原子被外来单色光激发后发出的谱线仅有三条,问此外来光的频率为多少?解:由于谱线仅有三条,得3n =,n 从3到2、1,从2到1;因此1931213.6[()(13.6)] 1.6103E E h ν--=---⨯⨯=,得15=2.9210Hz ν⨯15-19 处于基态的氢原子吸收了一个能量为15eV hv =的光子后,其电子成为自由电子,求该电子的速率。
解:由基态能量113.6eV E =-,吸收光子后,电子动能为k 1 1.4eV E E h ν=+=,对于电子,其静能200c m E ==0.51 MeV ,由于1 .4eV 的电子动能远远小于电子的静能,因此可以用非相对论公式计算,2k e 11.4eV =2E m v =,代入数据,得5=7.0110m/s v ⨯15-20 同时确定能量为1 keV 的电子的位置与动量时,若位置的不确定值在0.01nm 以内,则动量不确定值的相对比值/p p ∆至少为多少?解:对于电子,其静能200c m E ==0.51 MeV ,由于1keV E =远远小于电子的静能,因此可以用非相对论公式计算,2e2p E m =,代入数据,得23=1.70710kg.m/s p -⨯,根据不确定度关系x p h ∆⋅∆≥可知,236.6310kg.m/s p -∆≥⨯,所以/p p ∆至少为23236.6310/1.70710 3.88--⨯⨯=。
15-21 设有一电子在宽为0.20nm 的一维无限深的方势阱中。
(1)计算电子在最低能级的能量;(2)当电子处于第一激发态时,在势阱何处出现的概率最小,其值为多少?解:(1)能量E 只能取一系列分立的值22222man E n ηπ=,最低能级1n =,代入数据,得19.43eV E =;(2)一维无限深的方势阱中波函数为x an a x n πψsin 2)(=,)0;,3,2,1(a x n ≤≤=Λ,电子处于第一激发态2n =时,波函数为22()x x aπψ=,概率密度为22222()sin x x a a πψ=。
出现的概率最小,即22d ()0d x xψ=,且2222d ()0d x x ψ>,由22d ()0d x xψ=,得2822sin cos 0x x a a aπππ=,244sin 0x a a ππ=,考虑到0x a ≤≤,因此,30,,,,424a a ax a =,又由2222d ()0d x x ψ>,得23164cos0x a a ππ>,仅当0,,2a x a =时,23164cos 0x a a ππ>,所以0,,2ax a =,代入数据,得0,0.10nm,0.20nm x =。