《向量的加法运算及其几何意义》

《向量的加法运算及其几何意义》教案完美版第一章：向量的概念回顾1.1 向量的定义向量是从数学和物理学中引入的概念，具有大小和方向。

向量通常用字母表示，如\(\vec{a}\)、\(\vec{b}\) 等，也可以用箭头表示。

1.2 向量的表示方法向量可以用坐标形式表示，如\(\vec{a} = (a_x, a_y)\)。

向量还可以用图形表示，在坐标系中表示向量的起点和终点。

第二章：向量的加法运算2.1 向量加法的定义向量加法是将两个向量相加得到一个新的向量。

如果\(\vec{a} = (a_x, a_y)\) 和\(\vec{b} = (b_x, b_y)\)，它们的和\(\vec{c}\) 可以表示为\(\vec{c} = \vec{a} + \vec{b} = (a_x + b_x, a_y + b_y)\)。

2.2 向量加法的几何意义向量加法可以直观地理解为在坐标系中将两个向量的终点相连，得到一个新的向量。

几何上，向量加法表示的是两个向量的位移合成。

第三章：平行向量的加法3.1 平行向量的定义平行向量是指方向相同或相反的向量。

如果两个向量平行，它们的坐标成比例。

3.2 平行向量的加法规则平行向量相加时，可以直接将它们的大小相加，方向不变。

如果\(\vec{a}\) 和\(\vec{b}\) 是平行向量，\(\vec{a} + \vec{b} = (a + b, c)\)，其中\(a\) 和\(b\) 是向量的大小，\(c\) 是它们的方向。

第四章：向量的减法运算4.1 向量减法的定义向量减法是将一个向量从另一个向量中减去。

如果\(\vec{a} = (a_x, a_y)\) 和\(\vec{b} = (b_x, b_y)\)，它们的差\(\vec{d}\) 可以表示为\(\vec{d} = \vec{a} \vec{b} = (a_x b_x, a_y b_y)\)。

4.2 向量减法的几何意义向量减法可以理解为从起点到终点的位移减去从起点到另一个终点的位移。

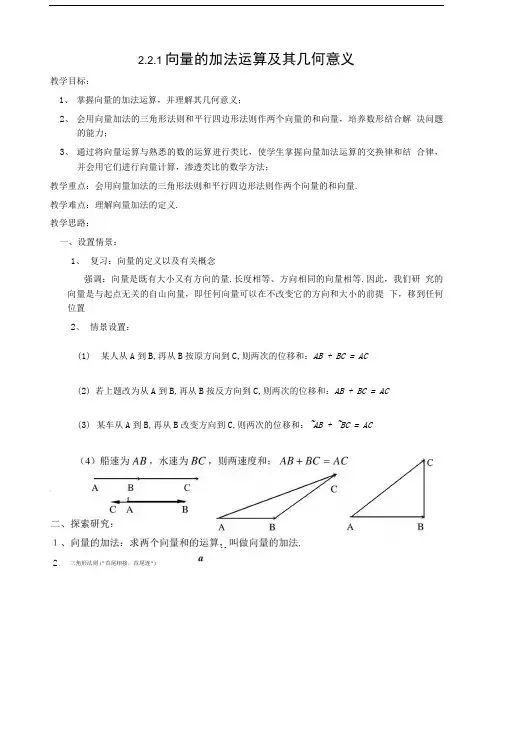
如图，己知向量a 、b.在平面内任取一点A,作AB=a, BC=b,则向量AC 叫做a 与b 的和，记作 a+ b ,艮P a+ b = AB + BC = AC , 规定： a + O-=O + ab a+b 2.2.1向量的加法运算及其几何意义教学目标：1、 掌握向量的加法运算，并理解其几何意义；2、 会用向量加法的三角形法则和平行四边形法则作两个向量的和向量，培养数形结合解 决问题的能力；3、 通过将向量运算与熟悉的数的运算进行类比，使学生掌握向量加法运算的交换律和结 合律，并会用它们进行向量计算，渗透类比的数学方法；教学重点：会用向量加法的三角形法则和平行四边形法则作两个向量的和向量.教学难点：理解向量加法的定义.教学思路：一、设置情景：1、 复习：向量的定义以及有关概念强调：向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此，我们研 究的向量是与起点无关的自山向量，即任何向量可以在不改变它的方向和大小的前提 下，移到任何位置2、 情景设置：(1) 某人从A 到B,再从B 按原方向到C,则两次的位移和：AB + BC = AC(2) 若上题改为从A 到B,再从B 按反方向到C,则两次的位移和：AB + BC = AC(3) 某车从A 到B,再从B 改变方向到C,则两次的位移和：~AB + ~BC = AC三角形法则(“首尾相接，首尾连”)2、探究：（1）两向量的和与两个数的和有什么关系？两向量的和仍是一个向量;（2）当向量。

与人不共线时，I。

+5 Ivl。

1+1人I；什么时候\a + b \=\ a \+\b \ ,什么时候\a+b \=\a\—\b\,当向量〃与5不共线时，a + b的方向不同向，且\ a+ b \<\ a \+\b当。

与同向时，则a + b、a > /?同向，且1。

+ &1=1。

1+1/?1,当口与/?反向时，若\a\>\h\,则a + h的方向与白相同，且\ a+h \=\ a \-\h \；若\a\<\h I,则ci + b的方向与/?相同，且\a+b\=\b \-\a\.OB（3）“向量平移”（自由向量）：使前一个向量的终点为后一个向量的起点，可以推广到n个向量连加3 .例一、已知向量q、b ,求作向量。

向量加法运算及其几何意义向量加法是指将两个或多个向量相加的运算。

在数学中，向量加法遵循以下规则：1.向量加法是可交换的。

即，对于任意向量a和b，a+b=b+a。

2.向量加法是可结合的。

即，对于任意向量a、b和c，(a+b)+c=a+(b+c)。

3.零向量是向量加法的单位元素。

即，对于任意向量a，a+0=0+a=a。

几何意义方面，向量加法可以用于描述物体的位移、力的合成以及速度的合成等。

下面以位移和力的合成为例进行解释：1.位移的合成：假设有一辆汽车沿东西方向行驶了100米，然后又沿南北方向行驶了50米。

我们可以将汽车的东西方向的位移表示为向量a=100i，南北方向的位移表示为向量b=50j。

那么，汽车的总位移可以表示为向量c=a+b，即c=100i+50j。

这个向量c表示汽车最终的位置相对于起始位置的位移。

2.力的合成：假设有两个力F1和F2作用在一个物体上，F1的大小为10牛顿，方向为东，F2的大小为5牛顿，方向为北。

我们可以将力F1表示为向量a=10i，力F2表示为向量b=5j。

那么，两个力的合力可以表示为向量c=a+b，即c=10i+5j。

这个向量c表示两个力的合力的大小和方向。

在几何上，向量加法的结果可以通过平行四边形法则进行图示。

以位移为例，我们可以将向量a和向量b的起点放在同一位置，然后将向量a按照其方向和大小绘制出来，再将向量b按照其方向和大小绘制出来。

通过平行四边形法则，我们可以找到一个平行四边形，其两条对角线的交点即为向量a和向量b的和向量c的终点。

总结起来，向量加法是一种将多个向量相加的运算，它遵循可交换和可结合的规则，并且零向量是其单位元素。

在几何上，向量加法可以用于描述位移和力的合成等。

通过平行四边形法则，我们可以找到向量加法的结果的几何意义。

《向量的加法运算及其几何意义》教案完美版第一章：向量的概念回顾1.1 向量的定义1.2 向量的表示方法1.3 向量的长度和方向第二章：向量的加法运算2.1 向量加法的定义2.2 向量加法的几何意义2.3 向量加法的三角形法则2.4 向量加法的平行四边形法则第三章：向量加法的性质3.1 交换律3.2 结合律3.3 存在零向量3.4 存在相反向量第四章：向量的减法运算4.1 向量减法的定义4.2 向量减法的几何意义4.3 向量减法的三角形法则4.4 向量减法的平行四边形法则第五章：向量减法的性质5.1 减去一个向量等于加上它的相反向量5.2 减去两个向量等于减去它们的和5.3 减法运算与加法运算的关系第六章：向量的数乘运算6.1 向量的数乘定义6.2 向量的数乘几何意义6.3 向量的数乘与向量长度的关系6.4 向量的数乘与向量方向的关系第七章：向量的数乘运算性质7.1 数乘运算的分配律7.2 数乘运算的结合律7.3 数乘运算的单位元7.4 数乘运算的逆元第八章：向量的点积运算8.1 向量点积的定义8.2 向量点积的几何意义8.3 向量点积的计算公式8.4 向量点积的性质第九章：向量的叉积运算9.1 向量叉积的定义9.2 向量叉积的几何意义9.3 向量叉积的计算公式9.4 向量叉积的性质第十章：向量的应用10.1 向量在几何中的应用10.2 向量在物理中的应用10.3 向量在其他领域中的应用10.4 向量的进一步研究第六章：向量的线性组合与基底6.1 向量的线性组合定义6.2 向量的线性组合的几何意义6.3 基底的概念6.4 基底的选取方法第七章：向量空间与线性相关性7.1 向量空间的概念7.2 线性相关的定义7.3 线性无关的定义7.4 线性相关性与线性无关性的判断方法第八章：向量的坐标表示8.1 坐标系的概念8.2 向量的坐标表示方法8.3 坐标变换与向量的关系8.4 坐标表示在几何中的应用第九章：向量组的线性表示9.1 向量组的线性表示概念9.2 矩阵与向量组的关系9.3 矩阵的基本运算9.4 矩阵的逆与向量组的线性表示第十章：向量的进一步研究10.1 向量范数的概念10.2 向量范数的性质10.3 向量内积的概念10.4 向量内积的性质10.5 向量组的内积空间重点和难点解析一、向量的概念回顾：重点关注向量的定义、表示方法、长度和方向，为学生奠定扎实的向量基础。

向量的加法运算及其几何意义引言向量是数学中一个重要的概念，广泛应用于物理学、工程学、计算机科学等领域。

向量的加法运算是向量计算中的基本操作之一，具有重要的几何意义。

本文将介绍向量的加法运算的定义、性质以及其在几何上的意义。

向量的加法定义向量是具有大小和方向的量，可以用有序数对表示。

向量的加法定义如下：设有两个向量a和a，表示为a = (a₁, a₂, …, aa)和a = (a₁, a₂, …, aa)，则两个向量的和记为a + a，它的每个分量等于对应分量之和，即(a₁ + a₁, a₂ + a₂, …, aa + aa)。

向量的加法性质向量的加法满足以下性质：1.交换律：a + a = a + a，即向量的加法是可交换的。

2.结合律：(a + a) + a = a + (a + a)，即向量的加法满足结合律。

3.零向量：对于任意向量a，存在一个称为零向量的特殊向量a，满足a + a = a。

4.相反向量：对于任意向量a，存在一个称为相反向量的特殊向量−a，满足a + (−a) = a。

这些性质使得向量的加法成为一个群运算，为后续的研究提供了基础。

向量加法与向量几何意义向量的加法在几何上有很重要的意义。

几何向量可以通过箭头表示，箭头的长度表示向量的大小，箭头的方向表示向量的方向。

向量的加法运算可以通过将两个向量的箭头连接起来得到。

当两个向量的方向相同且大小相等时，它们的加法运算结果是一个与它们方向相同且大小等于它们之和的向量。

这可以用以下图形表示：--------- --------------- --------- ----------------------------------当两个向量的方向相反且大小相等时，它们的加法运算结果是一个大小为零的向量。

这可以用以下图形表示：---------------------------------- --------- --------------- ---------当两个向量的方向不同且大小不等时，它们的加法运算结果是一个向量。

向量加法运算及其几何意义向量加法是指将两个或多个向量相加的运算。

在向量加法中，将两个向量的对应分量相加，得到的结果向量被称为它们的和向量。

下面将从数学和几何的角度分别探讨向量加法的运算及其几何意义。

一、数学角度：1.向量的表示：向量通常用一个有向线段或箭头表示，箭头所指的方向表示向量的方向，箭头的长度表示向量的大小或模。

一个向量通常用字母加上一个箭头上的向量符号表示，例如向量a可以表示为→a。

2.向量的分量表示：向量在坐标系中的表示通常采用分量表示法。

例如，向量a的表示可以表示为(a₁,a₂,a₃)。

这表示向量a在x、y、z轴上的分量分别为a₁、a₂、a₃。

3.向量的加法：给定两个向量a和b，其分量表示分别为(a₁,a₂,a₃)和(b₁,b₂,b₃)，那么它们的和向量c可以表示为(c₁,c₂,c₃)，其中c₁=a₁+b₁，c₂=a₂+b₂，c₃=a₃+b₃。

4.向量加法的性质：向量加法满足交换律和结合律，即a+b=b+a和(a+b)+c=a+(b+c)。

这意味着可以按照任意顺序加法运算，并且可以同时对多个向量进行加法运算。

二、几何角度：1.平行向量：如果两个向量的方向相同或相反，它们被称为平行向量。

对于平行向量a和b，它们的和向量c的方向与它们相同，并且大小是它们的大小之和。

2.共线向量：如果两个向量的方向相同或者它们的起点和终点相同，那么它们是共线向量。

对于共线向量a和b，它们的和向量c的起点和终点分别是a和b的起点和终点。

3.零向量：零向量是一个大小为0的向量，在坐标系中表示为(0,0,0)。

任何向量与零向量相加的结果都等于该向量本身。

4.平行四边形法则：根据平行四边形法则，可以通过将两个向量的起点放在一起，然后将它们的终点连接起来得到一个平行四边形。

两个向量的和向量等于对角线的向量。

5.三角形法则：根据三角形法则，如果两个向量的起点相同，那么可以通过将它们的终点连接起来得到一个三角形。

两个向量的和向量等于这个三角形的第三条边的向量。