信息的编码 二进制与十进制转换

课堂教学设计表
课程名称《二进制与十进制》设计者单位（学校）授课班级高一
人……
方法二：同时点两堆火→两个敌人如果出现两百个敌人呢？如何用烽火表示？同学们想想要怎么表示？
反馈评价同学的回答，公布教师的方法：用8堆火就可以表示200名敌人，十进制的200转换成二级制的11001000 进制和十进制
知识讲解1、二进制→十进制：权值法
举例125=1×100+2×10+5×1
=1×10²＋2×10¹＋5×10º
每个数在不同的数位上对应不同的权值
模仿学习二进制
1×2³＋0×2²＋1×2¹＋1×2º
=8＋0＋2＋1
=11
记录、听讲
2、十进制→二进制：除二取余法（85）10=（？）2
（85）10=（1010101）2
除二取余法温馨tips：
①除二：除到商为0，即停止
②取余：从下往上读数
课堂小结课堂小结，书写板书：
二级制与十进制
①二进制→十进制：权值法
②十进制→二进制：除二取余法
总结方法
小试牛刀小试牛刀：
➢十进制转换成二进制
①78
课堂练习
课堂巩固，
反馈教学效
果
教学反思。

二进制与十进制转换在计算机科学和数学中，二进制和十进制是两种常用的数制系统。

二进制是一种由0和1组成的基数为2的数制，而十进制是一种由0到9组成的基数为10的数制。

在计算机中，二进制是最基本的数据表示方式，而十进制则是人们日常生活中最常见的数制。

因此，了解二进制和十进制之间的转换方法非常重要。

一、二进制转换为十进制要将二进制数转换为十进制数，可以使用权重法。

二进制数的每一位上的数字与对应位置的权重相乘，然后将各位的结果相加即可得到对应的十进制数。

举个例子，假设我们有一个二进制数1011，需要将其转换为十进制数。

首先，将二进制数的每一位与对应位置的权重相乘：1 * 2^3 = 80 * 2^2 = 01 * 2^1 = 21 * 2^0 = 1然后，将各位的结果相加：8 + 0 + 2 + 1 = 11所以，二进制数1011转换为十进制数为11。

二、十进制转换为二进制要将十进制数转换为二进制数，可以使用除2取余法。

将十进制数反复除以2，将每次的余数从下往上排列，直到商为0为止，得到的余数序列即为对应的二进制数。

举个例子，假设我们有一个十进制数19，需要将其转换为二进制数。

首先，将19除以2，得到商9和余数1。

将余数1记为二进制数的最低位。

然后，将商9除以2，得到商4和余数1。

将余数1记为二进制数的次低位。

继续将商4除以2，得到商2和余数0。

将余数0记为二进制数的次高位。

最后，将商2除以2，得到商1和余数0。

将余数0记为二进制数的最高位。

得到的二进制数为10011，即为19的二进制表示。

三、扩展二进制和负数表示除了标准的二进制和十进制表示外，计算机中还使用了一种扩展二进制表示法，以及负数的表示。

在扩展二进制表示法中，最高位位数为符号位，0表示正数，1表示负数。

符号位后面的位数则为正常的二进制位数。

例如，如果使用8位扩展二进制，可以表示的范围是-128至127。

其中，最高位为0表示正数，为1表示负数。

二进制数信息编码
二进制数信息编码是指将二进制数转换成相应的信息或符号，以便在计算机系统或其他电子设备中传输、存储和处理。

常见的二进制数信息编码方式有：
1. 十进制数编码：将二进制数转换成十进制数，以方便人们阅读和理解。

二进制数与十进制数之间的转换可以通过查表或者计算得出。

2. ASCII码：将二进制数转换成字符，以便在计算机中显示和传输。

ASCII
码是计算机中最常用的字符编码标准，它规定了128个字符的二进制编码。

3. Unicode码：将二进制数转换成统一的字符编码标准，以支持各种语言
和符号。

Unicode码采用16位二进制数表示一个字符，可以支持超过一百万个字符。

4. 二进制码：将二进制数直接转换成相应的信息或命令，以便在计算机或其他电子设备中执行。

例如，在计算机中，0表示逻辑“假”，1表示逻辑“真”。

总之，不同的二进制数信息编码方式有不同的应用场景和优缺点，选择合适的编码方式可以提高信息传输和处理的效率。

数字的二进制与十进制在日常生活和计算机科学领域中，我们经常会遇到数字的二进制和十进制表示。

二进制是一种基于2的计数系统，而十进制则是我们最为熟悉的基于10的计数系统。

本文将详细介绍二进制和十进制之间的转换方法以及它们在计算机科学中的应用。

一、二进制表示法二进制是一种使用0和1来表示数值的计数系统。

它是一种适用于计算机内部电子元件的表示方法，因为计算机内部的电子元件只能识别高电压（用1表示）和低电压（用0表示）。

二进制中的每一位被称为一个比特（bit），八个比特为一个字节（byte）。

在二进制表示法中，每一位上的数字都是2的幂的倍数。

最右边的位称为最低位，它表示2^0；向左依次递增，每一位的权重都是前一位权重的2倍。

例如，十进制数21用二进制表示为10101。

我们可以将其解读为：1个16，0个8，1个4，0个2，1个1，总和为21。

二、十进制表示法十进制是我们最为熟悉的计数系统。

它使用十个数字0-9来表示所有的数值。

每一位的权重都是前一位权重的10倍。

例如，数字431的十进制表示法可以解读为：4个百，3个十，1个个，总和为431。

三、二进制与十进制的转换在计算机科学中，我们经常需要将二进制和十进制之间进行转换。

以下是两者相互转换的方法：1. 二进制转换为十进制要将二进制数转换为十进制数，我们需要按权相加的方法。

例如，对于二进制数10110，我们可以将其转换为十进制数的步骤如下：1 * 2^4 + 0 * 2^3 + 1 * 2^2 + 1 * 2^1 + 0 * 2^0 = 16 + 0 + 4 + 2 + 0 = 22因此，二进制数10110等于十进制数22。

2. 十进制转换为二进制要将十进制数转换为二进制数，我们可以使用除2取余（mod 2）的方法。

下面是一个将十进制数43转换为二进制数的示例：43 / 2 = 21 余 121 / 2 = 10 余 110 / 2 = 5 余 05 / 2 = 2 余 12 / 2 = 1 余 01 /2 = 0 余 1二进制数为101011，即十进制数43转换为二进制为101011。

二进制与十进制的转化方法一、二进制转十进制：二进制是一种由0和1组成的数字系统，而十进制是我们平常使用的数字系统，由0到9的数字构成。

在计算机科学和信息技术领域，我们经常需要将二进制数转换为十进制数，以便更好地理解和处理数据。

二进制数的每一位称为一个二进制位（bit），其权值按照2的幂次递增。

例如，二进制数1011可以表示为：1 * 2^3 + 0 * 2^2 + 1 * 2^1 + 1 * 2^0 = 8 + 0 + 2 + 1 = 11要将二进制数转换为十进制数，我们只需要按照上述方法计算出每位的权值，并将它们相加即可。

下面以一个实例进行说明：例子：将二进制数1101转换为十进制数。

根据上述方法，我们可以得到：1 * 2^3 + 1 * 2^2 + 0 * 2^1 + 1 * 2^0 = 8 + 4 + 0 + 1 = 13所以，二进制数1101转换为十进制数为13。

二、十进制转二进制：十进制数是我们常用的数字系统，由0到9的数字组成。

而在计算机科学和信息技术领域，我们经常需要将十进制数转换为二进制数，以便更好地进行数据存储和处理。

将十进制数转换为二进制数的方法是通过除2取余，从最低位开始逐位计算。

具体步骤如下：1. 将十进制数除以2，得到的商和余数分别表示当前位的二进制数字和下一位的十进制数。

2. 将上一步得到的商继续除以2，重复上述步骤，直到商为0为止。

3. 将每一步得到的余数按照求得的顺序排列起来，即可得到转换后的二进制数。

下面以一个实例进行说明：例子：将十进制数26转换为二进制数。

根据上述方法，我们可以得到：26 ÷ 2 = 商13 余数013 ÷ 2 = 商6 余数16 ÷ 2 = 商3 余数03 ÷ 2 = 商1 余数11 ÷2 = 商0 余数1将每一步得到的余数按照求得的顺序排列起来，即得到二进制数11010。

所以，十进制数26转换为二进制数为11010。

十进制与二进制的转换在计算机科学中，十进制与二进制的转换是一个基础而重要的概念。

十进制是我们平时所使用的数字系统，它使用了数字0-9来表示不同的数值。

而二进制是计算机内部使用的数字系统，它仅使用了0和1两个数字来表示数值。

在这篇文章中，我们将讨论十进制与二进制之间的转换方法及其应用。

一、十进制转换为二进制十进制转换为二进制的方法主要是通过除以2取余数的方式来实现。

具体步骤如下：1. 将给定的十进制数除以2，并记录商和余数。

2. 将得到的商再次除以2，并记录商和余数。

3. 重复上述步骤，直到商为0为止。

4. 将记录的余数按从下往上的顺序排列即得到对应的二进制数。

例如，我们要将十进制数28转换为二进制数：28 ÷ 2 = 14 014 ÷ 2 = 7 07 ÷ 2 = 3 (1)3 ÷ 2 = 1 (1)1 ÷ 2 = 0 (1)将上述余数从下往上排列，得到二进制数11100。

因此，十进制数28的二进制表示为11100。

二、二进制转换为十进制二进制转换为十进制的方法主要是通过权重相加的方式实现。

具体步骤如下：1. 将给定的二进制数从右往左分别记为bn、bn-1、bn-2...b1、b0。

2. 根据位置确定每一位的权重，第n位的权重为2的n次方，第n-1位的权重为2的n-1次方，依此类推。

3. 将每一位的权重与对应的二进制位相乘，并将结果相加得到最终的十进制数。

例如，我们要将二进制数10110转换为十进制数：1 × 2^4 + 0 × 2^3 + 1 × 2^2 + 1 × 2^1 + 0 × 2^0 = 16 + 0 + 4 + 2 + 0 = 22因此，二进制数10110的十进制表示为22。

三、应用与实践十进制与二进制的转换在计算机科学中有着广泛的应用。

在计算机内部，数据的存储和传输通常以二进制的形式进行。

计算机基础二进制与十进制转换计算机科学是一门与数字和计算有关的科学，而二进制与十进制是计算机中最基本的数字系统。

在计算机中，所有的数据和指令最终都会被转换为二进制形式，然后才能够被计算机理解和处理。

因此，对于计算机基础知识的学习者来说，掌握二进制与十进制之间的转换是至关重要的。

1. 二进制和十进制的定义二进制（Binary）是一种采用了“0”和“1”这两个数字来表示数值的计数系统。

相比于人类常用的十进制（Decimal）系统，二进制系统只有两个数码，因此被广泛应用于计算机科学中。

2. 十进制转换为二进制在十进制转换为二进制时，我们需要用到除以2这个操作，将十进制数不断地除以2并记录余数，直到商为0为止。

最后，将记录的余数倒序排列起来，就得到了对应的二进制数。

举个例子，将十进制数42转换为二进制：42 ÷ 2 = 21 余 021 ÷ 2 = 10 余 110 ÷ 2 = 5 余 05 ÷ 2 = 2 余 12 ÷ 2 = 1 余 01 ÷2 = 0 余 1将余数倒序排列起来，就得到了42的二进制表示为101010。

3. 二进制转换为十进制在二进制转换为十进制时，我们需要用到乘以2这个操作。

将二进制数从右向左分别对应到2的不同次方，然后将对应的结果进行求和，即可得到对应的十进制数。

举个例子，将二进制数101010转换为十进制：1 × 2^5 + 0 × 2^4 + 1 × 2^3 + 0 × 2^2 + 1 × 2^1 + 0 × 2^0 = 42因此，101010的二进制数在十进制中表示为42。

4. 应用实例二进制与十进制转换在计算机科学中有着广泛的应用。

比如，在计算机网络中，IP地址通常以二进制形式存储，但是为了方便人们的阅读和理解，会将其转换为十进制形式，以便更好地进行网络管理和配置。

二进制数与十进制数的相互转换文章标题：深度探讨二进制数与十进制数的相互转换一、引言在日常生活和工作中，我们经常会接触到二进制数和十进制数。

二进制数是计算机中使用的一种数制，而十进制数则是我们常见的数学表示方法。

本文将深入探讨二进制数与十进制数的相互转换，帮助读者更深入地了解这两种数制的关系。

二、二进制数与十进制数的基本概念1. 二进制数的表示方法二进制数是由0和1组成的数字系统，每一位上的数称为一个二进制位。

1011表示十进制的11。

2. 十进制数的表示方法十进制数是由0到9组成的数字系统，每一位上的数表示对应的数量级。

123表示1*100 + 2*10 + 3*1。

三、二进制数转换为十进制数1. 从右向左的求和方法以二进制数1011为例，按照2的幂次方从右向左求和，即1*2^3 + 0*2^2 + 1*2^1 + 1*2^0，得到十进制数11。

2. 通用公式转换对于任意长度的二进制数，可以使用通用公式进行转换，即将每一位上的二进制数乘以2的对应次方再求和。

四、十进制数转换为二进制数1. 除2取余法以十进制数11为例，通过反复除2取余的方法可以得到二进制数1011。

即11÷2=5余1，5÷2=2余1，2÷2=1余0，1÷2=0余1。

2. 通用公式转换对于任意十进制数，同样可以使用通用公式进行转换，即反复除2取余直至商为0，再将余数倒序排列得到二进制数。

五、总结与回顾通过本文的深度探讨，我们了解了二进制数与十进制数之间的转换方法。

无论是从二进制数转换为十进制数，还是相反，都可以通过简单的算法和公式来实现。

这种转换方法在计算机领域具有重要意义，同时也有助于我们对数制间的转换有更深刻的理解。

六、个人观点与理解在我看来，二进制数与十进制数的转换虽然在表面上涉及了不同的数制与算法，但本质上都是在不同的进位制下表示和计算数值。

通过学习和掌握转换方法，我们可以更好地理解计算机运行原理，以及更灵活地处理数字计算和逻辑运算。

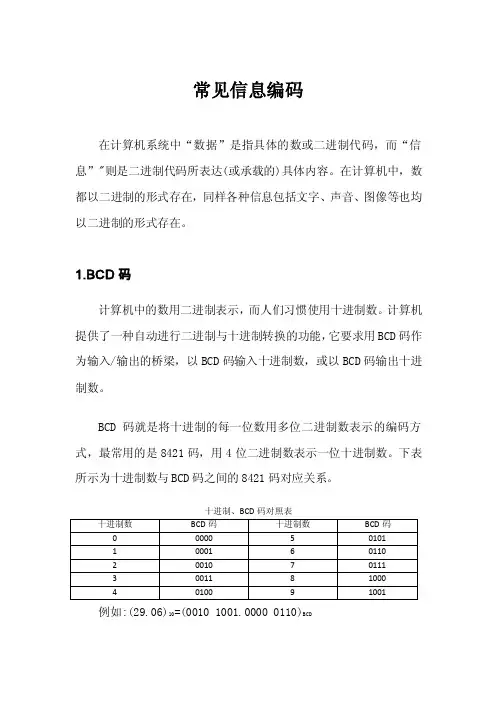
常见信息编码在计算机系统中“数据”是指具体的数或二进制代码，而“信息”"则是二进制代码所表达(或承载的)具体内容。

在计算机中，数都以二进制的形式存在，同样各种信息包括文字、声音、图像等也均以二进制的形式存在。

1.BCD码计算机中的数用二进制表示，而人们习惯使用十进制数。

计算机提供了一种自动进行二进制与十进制转换的功能，它要求用BCD码作为输入/输出的桥梁，以BCD码输入十进制数，或以BCD码输出十进制数。

BCD码就是将十进制的每一位数用多位二进制数表示的编码方式，最常用的是8421码，用4位二进制数表示一位十进制数。

下表所示为十进制数与BCD码之间的8421码对应关系。

十进制、BCD码对照表例如:(29.06)10=(0010 1001.0000 0110)BCD.字符的ASCII计算机中常用的基本字符包括十进制数字符号0~9，大小写英文字母A~Z，a~z，各种运算符号、标点符号以及一些控制符、总数不超过128个，在计算机中它们都被转换成能被计算机识别的二进制编码形式。

目前，在计算机中普遍采用的一种字符编码方式，就是已被国际标准化组织(ISO)采纳的美国标准信息交换码(ASCII),如下表所示。

其中:NUL 空； FF 走纸控制； CAN 作废；SOH 标题开始； CR 回车； EM 纸尽；STX 正文开始； SO 移位输出； SUB 换置；EIX 正文结束； SI 移位输入； ESC 换码；EOT 结束传输； DLE 数据链换码； FS 文字分隔符；ENQ 询问； DC1 设备控制1； GS 组分隔符；ACK 承认； DC2 设备控制2； RS 记录分隔符；BEL 报警; DC3 设备控制3; US 单元分隔符；BS 退格； DC4 设备控制4; SP 空格；HT 横向列表； NAK 否定; DEL 删除;LF 换行； SYN 空转同步;VT 纵向列表； ETB 信息组传送结束；在ASCII中，每个字符用位二进制代码表示。

试讲教案课程名称信息技术基础假定教学对象新平一中高一课型理论课授课人尹绍美课题 1.2信息的编码学时 2教学目标1、知识技能目标：(1)了解为什么要对信息进行编码.(2)重新认识是进制.(3)了解ASCII字符编码和汉字编码.2、过程与方法目标：(1)掌握二进制与十进制的转换方法.(2)通过观察字符内码,让学生直观地了解字符和汉字编码的形式.3、情感与价值观目标：(1)通过信息编码与二进制的学习讲解,激励学生进一步学习计算机原理,鼓励学生不断探究新知,为以后学习计算机技术打下基础.(2)培养学生对已有知识的应用能力及知识的转换能力.(3)激发学生的探索科学的热情,增强学生的求知欲.学生分析高一学生身心渐趋成熟，逻辑思维趋于严密，并且已经具备一定的信息技术使用经验，只是对所学的内容欠缺系统的提炼、重组和内化。

本节主要介绍的是二进制、字符编码和汉字编码,内容比较抽象、学起来较乏味、知识概念偏深、可操作内容少,教师需要有层次、有选择地设计实例分析、讨论归纳、合作探究等活动，引导学生从不同层面分析和归纳问题，鼓励学生将自己形成的理解结合老师的讲解与课本上的知识相比较，加深理解.信息编码的原理很抽象,对于学生来说是难以理解的。

如何化抽象为形象,使学生更容易理解是一个关键。

对于二进制，虽然在初中学生可能有一点初步的了解，但可能已经忘记或者都是似懂非懂，所以总的来说学生在这方面的基础是比较薄弱的，这些都是教学设计过程中必须考虑到的。

教学应从学生熟悉的内容着手，先从十进制着手,对于十进制,有必要进行再次讲解,引导同学们一起重新认识十进制,归纳出十进制的规律,为讲解二进制做铺垫.重点难点分析重点：(1)十进制进制的规律.(2)二进制与十进制的转换.(3)字符编码.(4)汉字编码.难点：(1)灵活应用所学知识解决实际问题.(2)二进制与十进制的转换.教学地点、教具教学地点:多媒体教室教具：计算机,黑板,粉笔,ppt.教学内容及过程教师活动学生活动设计说明1、导入部分（所用方法）上节课我们已经学了信息及其信息的基本特征,通过上节课的学习我们已经知道信息本身是看不见摸不着的,那么现在请同学们回顾一下信息的表现形式有哪些?（声音、视频、文字、数字、字符）.在生活中我们看到一些数字就会知道它所表示的信息,比如当我们看到110(报警电话)、120(急救电话)、119(火警)、12315(消费者权益保护)等这些数字时,他们所代表的就不仅仅是数字了,这是为什么呢?(因为这些信息已经被编码了).同学们还知道那些信息是被编码了的?(身份证、学生证、电话号码、邮政编码、条形码、WC标志、交通标志、车牌号、信号灯).从这些信息被编码的例子中我们可以看出信息编码就是采用某种原则或方法编制代码来表示信息.在信息科技中,特别是计算机领域,”代码”两个字具有特指性,是指有”0”和”1”两个数字组成的数字代码,因为数字计算机只能识别和处理有”0”和”1”符号串组成的代码.所以,其他信息代码都要转换成这种有”0”和“1”符号串构成的代码,才能被计算机识别和处理,所以这就需要对各种信息进行编码.2、讲授新课一.进制的规则1、我们接触的是十进制,规则是：（结合十进制的认数过程,教师和学生一起总结）回忆十进制数的认数过程.教师用幻灯片动态展示十进制的认数过程,以56789为例,引导学生去发现数制的原理或规律.56789=5*104+6*103+7*102+8*101+9*100学生回忆生活经历，体验生活中的信息编码的常用方法。

二进制与十进制的转化方法二进制和十进制是计算机科学中最常用的两种数制。

在计算机科学中，二进制被广泛用于表示和处理数字和数据，而十进制则是人类日常生活中最常用的数制。

在进行二进制与十进制的转化时，我们需要了解二者的基本原理和转化方法。

一、二进制与十进制的基本原理1. 二进制：二进制使用两个数字0和1来表示数值。

它采用了权值的概念，每一位的权值是2的幂次方。

例如，二进制数1101表示1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 13。

2. 十进制：十进制是我们日常生活中最常用的数制，使用十个数字0-9来表示数值。

每一位的权值是10的幂次方。

例如，十进制数256表示2*10^2 + 5*10^1 + 6*10^0 = 256。

二、十进制转二进制的方法将十进制数转化为二进制数的方法是通过不断除以2，并将余数逆序排列的方式进行的。

具体步骤如下：1. 将给定的十进制数除以2，得到商和余数。

2. 将余数记录下来，并将商作为新的被除数。

3. 重复步骤1和步骤2，直到商为0为止。

4. 将记录的余数按照从下到上的顺序排列，即为转换后的二进制数。

例如，将十进制数13转换为二进制数的过程如下：6 ÷ 2 = 3 余 03 ÷ 2 = 1 余 11 ÷2 = 0 余 1将记录的余数逆序排列，得到二进制数1101，即十进制数13转换为二进制数为1101。

三、二进制转十进制的方法将二进制数转化为十进制数的方法是通过按照权值相加的方式进行的。

具体步骤如下：1. 从二进制数的最右边（个位）开始，每一位的权值依次为2的0次方、2的1次方、2的2次方，依此类推。

2. 将每一位的二进制数与对应的权值相乘，并将结果相加。

例如，将二进制数1101转换为十进制数的过程如下：1*2^3 + 1*2^2 + 0*2^1 + 1*2^0 = 8 + 4 + 0 + 1 = 13因此，二进制数1101转换为十进制数为13。

二进制与十进制的转换在计算机科学中，二进制和十进制是两种常见的数字表示方式。

二进制使用数字0和1来表示，而十进制使用数字0到9。

在计算机中，我们经常需要进行二进制和十进制之间的转换，以便在不同的情境中使用正确的数字表示方式。

本文将介绍二进制与十进制之间的相互转换方法。

一、二进制转换为十进制要将一个二进制数转换为十进制，我们需要按照以下步骤进行：1. 从二进制数的最右边开始，将每位上的数字与2的幂相乘。

2. 将每个乘积相加得到十进制数的结果。

例如，我们有一个二进制数1101。

按照上述步骤，我们将进行如下计算：(1 * 2^3) + (1 * 2^2) + (0 * 2^1) + (1 * 2^0) = 8 + 4 + 0 + 1 = 13因此，二进制数1101转换为十进制数为13。

二、十进制转换为二进制要将一个十进制数转换为二进制，我们需要按照以下步骤进行：1. 将十进制数除以2，得到的商和余数。

2. 将余数从下往上排列，直到除法的商为0为止。

例如，我们有一个十进制数27。

按照上述步骤，我们将进行如下计算：27 / 2 = 13 余 113 / 2 = 6 余 16 / 2 = 3 余 03 / 2 = 1 余 11 /2 = 0 余 1将余数从下往上排列，得到二进制数11011。

因此，十进制数27转换为二进制数为11011。

三、实际应用二进制和十进制的转换在计算机科学中有着广泛的应用。

计算机内部使用二进制表示数据和指令，而人们习惯于使用十进制进行计算和交流。

因此，在计算机与人之间的数据交互中，经常需要进行二进制与十进制的相互转换。

例如，在计算机网络中，IP地址是用二进制表示的。

但是在实际的网络配置中，我们更习惯使用十进制点分十进制表示法（Dotted Decimal Notation）来表示IP地址。

这就需要进行二进制与十进制的转换。

另一个实际应用是文件大小的表示。

在计算机中，文件大小以字节（Byte）为单位进行表示。

二到十进制码的编码方式二进制码是一种只使用0和1两个数字来表示数值的编码方式。

每一位二进制码称为一个位（bit），是计算机中最基本的数据存储和传输单位。

而十进制码则是我们平常生活中最常用的数字表示方式。

本文将详细介绍从二进制码到十进制码的编码过程，帮助读者更好地理解编码方式的转换。

一、什么是二进制码二进制码是由0和1两个数字组成的编码方式。

它是计算机理解和处理信息的基础，因为计算机中的数据和指令都是以二进制码的形式存储和传输的。

每一位二进制码都代表一个权重，权重从右向左依次为1、2、4、8、16、32……。

二、二进制码转换为十进制码二进制码转换为十进制码的方法很简单，只需将每一位二进制位数与对应的权重相乘，然后将结果相加即可。

步骤一：准备待转换的二进制码。

例如，我们有一个八位的二进制码10101100。

步骤二：确定二进制位数的权重。

根据权重规律，我们可以得到如下权重值：1 0 4 8 0 32 64 128步骤三：将二进制码的每一位与对应权重相乘。

根据二进制码的每一位与权重的对应关系，可以得到如下结果：1*128 + 0*64 + 1*32 + 0*16 + 1*8 + 1*4 + 0*2 + 0*1步骤四：将结果相加得到十进制码。

计算得到的结果为：128 + 0 + 32 + 0 + 8 + 4 + 0 + 0 = 172因此，二进制码10101100转换为十进制码为172。

三、十进制码转换为二进制码十进制码转换为二进制码的方法需要用到除法和取余的运算。

步骤一：准备待转换的十进制码。

例如，我们有一个十进制码248。

步骤二：确定二进制位数的权重。

由于二进制码每一位的权重依次为1、2、4、8、16、32……，我们需要找到最大的权重，使得它小于或等于待转换的十进制码。

在本例中，最大的权重小于248的二进制位数为128。

步骤三：进行除法运算，直到商为0为止。

以本例为例，我们用248除以128，商为1，余数为120。

数字的编码之道二进制与十进制的转换数字的编码之道：二进制与十进制的转换数字编码是在计算机科学和信息技术领域中应用广泛的重要概念。

其中，二进制和十进制编码是最为常见和基础的两种编码方式。

本文将介绍二进制和十进制之间的转换方法，帮助读者更好地理解数字编码的原理和应用。

一、十进制与二进制的转换在介绍具体的转换方法之前，我们先来了解一下十进制和二进制的基本概念。

十进制是我们日常生活中使用的数字系统，其中包含0到9这10个数字。

而二进制则是计算机中广泛使用的数字系统，仅包含0和1这两个数字。

现在我们来看看如何将十进制数转换为二进制数以及如何将二进制数转换为十进制数。

1. 将十进制转换为二进制将十进制数转换为二进制数的方法是通过除以2的余数来获取二进制数的各位数字，然后逆序排列。

具体操作如下：举例说明：将十进制数29转换为二进制数。

步骤1：将29除以2，得到商14和余数1。

步骤2：将14再除以2，得到商7和余数0。

步骤3：将7再除以2，得到商3和余数1。

步骤4：将3再除以2，得到商1和余数1。

步骤5：将1再除以2，得到商0和余数1。

按照步骤的顺序，将每一步得到的余数从下往上排列，得到二进制数1101。

因此，十进制数29对应的二进制数为1101。

2. 将二进制转换为十进制将二进制数转换为十进制数的方法是根据二进制数的权重，将每一位的值与权重相乘，并求和。

具体操作如下：举例说明：将二进制数1101转换为十进制数。

步骤1：从右向左，依次为二进制数的各位确定权重，即第一位为2^0，第二位为2^1，第三位为2^2，第四位为2^3。

步骤2：依次将二进制数的每一位的值与权重相乘，并求和。

1 * 2^0 + 0 * 2^1 + 1 * 2^2 + 1 * 2^3 = 1 + 0 +4 + 8 = 13因此，二进制数1101对应的十进制数为13。

二、应用举例理解了二进制和十进制的转换方法后，我们可以通过一些实际的应用举例来加深对数字编码的理解。

bcd码十进制转换BCD码（二进制编码十进制）是一种用于表示十进制数的二进制编码方式。

在计算机领域中，BCD码常用于将十进制数转换为二进制数，便于计算机进行处理和存储。

本文将从BCD码的定义、原理、转换方法和应用等方面进行介绍，以帮助读者更好地理解和应用BCD码。

我们来了解一下BCD码的定义。

BCD码是一种二进制编码方式，其中每个十进制数位用4位二进制数表示。

例如，十进制数0用BCD码表示为0000，十进制数1用BCD码表示为0001，以此类推，十进制数9用BCD码表示为1001。

BCD码的优点在于能够直接表示十进制数，无需进行二进制转换，方便计算机进行处理。

接下来，我们来了解一下BCD码的原理。

BCD码的原理是将十进制数的每个数位分别用4位二进制数表示。

例如，将十进制数23转换为BCD码，首先分别将十位和个位数转换为4位二进制数，即2和3，分别表示为0010和0011，然后将它们组合起来，得到BCD码0010 0011。

这样，我们就可以用BCD码表示十进制数，并进行计算和存储。

接下来，我们来了解一下BCD码的转换方法。

将十进制数转换为BCD码的方法非常简单，只需要将十进制数的每个数位分别转换为4位二进制数即可。

例如，将十进制数67转换为BCD码，首先将十位数6转换为4位二进制数0110，然后将个位数7转换为4位二进制数0111，最后将它们组合起来，得到BCD码0110 0111。

同样，我们也可以将BCD码转换为十进制数，只需要将每4位二进制数转换为十进制数位即可。

BCD码在计算机领域中有着广泛的应用。

首先，BCD码常用于计算机的时钟芯片中，用于表示时间和日期等信息。

其次，BCD码还常用于计算机的存储系统中，可以将十进制数以BCD码的形式存储，减少存储空间的占用。

此外，BCD码还常用于计算机的显示系统中，可以将十进制数以BCD码的形式显示在屏幕上。

总结起来，BCD码是一种用于表示十进制数的二进制编码方式，其优点在于能够直接表示十进制数，方便计算机进行处理和存储。

二进制和十进制转换方法在二进制中，每一位数字为2的幂。

最右边的位数为2^0，往左边依次增大，每一位数字的权值都是上一位的2倍。

例如，二进制数1011表示1*2^3+0*2^2+1*2^1+1*2^0=8+0+2+1=11十进制数表示了每一位数字的权重。

最右边的位数为10^0，往左边依次增大，每一位数字的权值都是上一位的10倍。

例如，十进制数359表示3*10^2+5*10^1+9*10^0=300+50+9=359现在，让我们来看一些二进制和十进制互相转换的方法。

1.二进制转十进制的方法：(a)从二进制的最右边开始，每一位数字与2的幂相乘。

(b)将结果相加得到十进制数。

例如，将二进制数1011转换为十进制数：1*2^3+0*2^2+1*2^1+1*2^0=8+0+2+1=112.十进制转二进制的方法：(a)将十进制数除以2，将余数记录下来。

(b)将结果再次除以2，将新的余数记录下来。

(c)重复上述步骤，直到除以2的结果为0为止，将所有余数颠倒顺序排列。

例如，将十进制数11转换为二进制数：11/2=5余15/2=2余12/2=1余01/2=0余1将余数倒序排列得到二进制数1011除了上述方法外，还有其他的转换方法。

3.二进制转十进制的快速方法：(a)从二进制的最右边开始，每一位数字与2的幂相乘。

(b)从右边第二位开始，每一位数字与2的幂相乘，并将结果加到上一步的结果上。

例如，将二进制数1011转换为十进制数：1*2^3=80*2^2=01*2^1=21*2^0=18+0+2+1=114.十进制转二进制的快速方法：(a)从十进制数中找到最大的2的幂，使得这个幂小于或等于给定的十进制数。

(b)将这个幂作为二进制数的最高位，然后用该幂减去给定的十进制数。

(c)重复上述步骤，直到剩余的十进制数为0为止。

例如，将十进制数11转换为二进制数：找到最大的2的幂，2^3=8、此时最高位为111-8=3、剩余的十进制数为3找到最大的2的幂，2^1=2、此时次高位为13-2=1、剩余的十进制数为1找到最大的2的幂，2^0=1、此时最低位为11-1=0。