奥数训练题库：相对位置与空间想象

空间想象不仅是认识现实世界空间形式不可缺少的能力因素，而且是形成和发展创造力的源泉，因此，空间想象能力是数学教学必须培养的基本数学能力之一。

空间想象能力的培养与几何教学有关。

直观几何教学的主要任务是通过学生制作模型、搭积木、画图、识图，对图形进行描述、分类、整理等学习活动，认识、理解我们所处的现实世界的几何空间，以形成空间观念。

综合几何教学的主要任务是运用逻辑推理的方法研究图形的性质，帮助学生从逻辑的角度进一步弄清几何空间的意义，学会几何思考的方法，培养空间想象能力和逻辑推理能力。

模块一、对称图形【例 1】将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆洞，再展开正方形纸片，得到图1中的。

（填序号）①②③④【考点】几何中的空间想象【难度】1星【题型】填空【解析】逆推法③【答案】③【例 2】(希望杯五年级一试第8题，6分)下面四幅图形中不是轴对称图形的是。

（填序号）（注：如果一个图形沿一条直线折叠后，直线两旁的部分能够互相重合，那么这个图形叫做对称图形。

）【考点】几何中的空间想象【难度】1星【题型】填空【解析】③④【答案】③④模块二、平面图形【例 3】(希望杯四年级二试第5题，6分)将一张长方形纸对折再对折（如图），然后沿着图中的虚线剪下，得到①、②两部分，将①展开后得到的平面图形一定是。

（填“三角形”、“长方形”、“梯形”或“菱形”）展开②①例题精讲知识点拨4-1-4.几何中的空间想象【考点】几何中的空间想象【难度】2星【题型】填空【解析】菱形【答案】菱形【例 4】(希望杯六年级一试第18题，6分)如图，房间里有一只老鼠，门外有一只小猫，如果每块正方形地砖的连长为50厘米，那么老鼠在地面上能避开小猫视线的活动范围为_________平方厘米.(将小猫和老鼠分别看作两个点,墙的厚度忽略不计)【考点】几何中的空间想象【难度】4星【题型】填空【解析】猫看不到的地方如图所示阴影部分，其中梯形面积为（1+3.5）×2.5÷2=5.625平方米.三角形的面积为2×1÷2=1平方米.老鼠的活动范围共6.625平方米，即66250平方厘米.【答案】66250平方厘米模块三、立体图形【例 5】用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上，每一个面只涂一种颜色．如图所示，现有涂色方式完全一样的四块小正方体拼成了一个长方体．试回答：每个小正方体中，红色面的对面涂的是什么色？黄色面的对面涂的是什么色？黑色面的对面是什么色？【考点】几何中的空间想象【难度】3星【题型】解答【解析】在能看见的9个面中红色出现的次数最多．观察图8—4中最上面的一个正方体，由于红色和黑色、黄色相邻，所以它的对面不可能是黑黄两色．同理，由第二个正方体可知，红色的对面不能是白色；由第三个正方体知，红色的对面不能是蓝色．所以红色的面的对面只可能是绿色．同理，黄色面的对面不可能是红色、黑色或白色，又已推知不可能是绿色，所以黄色面的对面只可能是蓝色．这样黑色面的对面就只可能是涂白色的了．【答案】红色的对面是绿色黄色的对面是蓝色黑色的对面是白色【例 6】 将“猫”“狗”“兔”“鸡”“猴”“虎”六个动物名称分别写在六个正方体的六个面上，从下面三种不同摆法中，判断这个正方体上哪些动物名名称分别写在相对面上.兔狗猫鸡狗兔猫猴兔【考点】几何中的空间想象 【难度】3星 【题型】解答 【解析】 本题给的是一组立方图形，在这三幅图中，“兔”所在的一面始终不改变位置，因此，这三个图的转化只能是前后转动.把第一幅图向后反转一次得到第二幅图，由此可知，“猫”的对面是“鸡”；把第一幅图向前翻转一次得到第三幅图，所以“狗”的对面是“猴”，那么剩下的只有“兔”和“虎”相对.【答案】猫的对面是鸡；狗的对面是猴； 兔的对面是虎。

五年级奥数：展开图与空间想象知识框架重难点例题精讲1.数一数下图中有多少个正方体木块？<><?从下到上各层分别有書个、3个.1个，因此共有3+3十1=7个方块.【巩固】右图中共有多少个面？多少条棱?I觅右图所示；可叹分前、后、左、右、上、下六个方向看这个立体图彩*前，后看各有1入面，左面看有1个面，右<&看有2个面，上面看有2个面，下面看有1牛面”所礙共有1m+2+LlX（个）面.前后方向的棱有6条，左右方向的棱有6秦，上下方向的棱也有6所以共有棱柠十（S+柠-1$（条）.2立方厘米.如图从长为13厘米，宽为9厘米的长方形硬纸板的四角去掉边长2厘米的正方形，然 后，沿虚线折叠成长方体容器．这个容器的体积是多少立方厘米？客器的底曲积是〔1勺一斗）xf9-4）=45（平方厘米）：高为2厘来，所以容•器的体积是,45x2=90（立方厘米）.巩固】沿图4的虚线折叠，可以围成一个长方体，它的体积是宽十高=7,,长=5,长+高立，所以长高=入宽=4,体积为3x4x5=60立方厘，3. 下列图形经过折叠不能围成正方体的是【巩固】左下图是一个正方体，四边形APQC 表示用平面截正方体的截面.请在右下方的展开图中画出四边形APQC的四条边．附4DCABF\ E A4把空间图形弦面的践条画在平面展开图上，只要抓住四边形APQC 四个顶点所在的位置这个托键，再进一步貓定四边形的四条边所在的平面就可容场地画出.⑴瀋虑到展开图上疽犬个顶点没肴标出，可想家瘠展开图折成立侬形、并在顶点上标出对应的符号，忆左下图. ⑵根据四边形所在立体图形上的往置，确定其顶点所在的点和棱，以及四条边所在的平面：顶点：A-A 7C -C 7尸在EF 边上，©在GF 边上+边/I 匸在卫BCJQ 面上’AF 在力用FE 面上’QC 在BCGF 面上1尸么在CFGH 面上. ⑶将上面菇足的位置标在展界图上，并在对应平面上连线.需婪注意的是，立休圈上的月‘£点在展开图上有三个，B 7D 点在展开图上有二个，所以在标点连线吋必须注意连簸所在的平面”连好线的图形如右上图”4. 图1是下面的表面展开图 ① 甲正方体； ② 乙正方体；③丙正方体；④甲正方体或丙正方体．AG从展开图可以看曲，毎个面上至少有一块阴影，从而排除丙；又毎个面上没有相邻的两块阴影从而排除乙，故选甲答案为①.巩固】选项中有4个立方体，其中是用左边图形折成的是()．D图中齐，C・D项展开盾的图形均为下圏，只有©项展开后前图形与题中左边图形相捋，所叹答集为B・5.将A、B、C、D、E、F六个字母分别写在正方体的六个面上，从下面三种不同摆法中判断这个正方体中，哪些字母分别写在相对的面上．C ABDB都不相对，故(：和尸相对，A^BE不相对故盘和D相对，最后剩下的班相对A-D,B-E,C-F【巩固】用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上，每一个面只涂一种颜色．如图所示，现有涂色方式完全一样的四块小正方体拼成了一个长方体．试回答：每个小正方体中，哪些颜色分别涂在相对的面上？IBR—d滋和黑黄白蓝部不柏对’故红和錄1相対，黃和黒白不相对故黄和蓝相对，最后剩下的黑白相对红-緑，黄-蓝，黑-白6.把2、4、6、8、10、12这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图1，最左边的正方形上的数字是12，则最右边的正方形上的数字是.最右边的正方形是在2的对面，也就是背面，为4【巩固】如下图，一个正方体木块放在桌面上，每个面内都画有若干个点，相对的两个面内的点数和都是13，京京看见上、左、前三个面内的点数的和诗16，庆庆看见上、右、后三个面内的点数和是24.那么贴着桌面的那个面的点数是___.7. 【解析】上十左.■*■前=16上+右十后=24因此：上十上十（左+右〕十（前十后）=40又因为左■右=前+后=13,因上二40_13—[3=7,则T=L3_?=6i用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体ABCD-A I B I C I D I （如图），大正方体内的对角线AC i ，BD i ，C A I ，DB 1所穿的小正方体都是红色玻璃小正方体，其它部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明小正方体用了多少个？叫CA.,叫四条时角线部穿过在正由央的那个小正方体.除此而外+每条对角线穿过相同的小正方体*所以毎条対角线穿过鋼二Im 们个小正才体達就表明尢亚方体的每条边由101个卜正方徉组成.因此火正方■体由101"个小正方体组成；其中无色透明的小正方体有IO13-401=1030301-401^1029900. 即用了l （J29M0个无色透明的小正方体.【巩固】如图，用若干个体积相同的小正方体堆积成一个大正方体，要使大正方体的对角线（正方体八个顶点中距离最远的两个顶点的连线）穿过的小正方体都是黑色的，其余小正方体都是白色的，并保证大正方体每条边上有偶数个小正方体.当堆积完成后，白色正方体的体积占总体积的93.75%，那么一共用了多少个黑色的小正方体？C 1CI白色.it方体的体积占总体积的9化7$罷即占整个的12,白色止方体与黑色正方体之比为；1：15,16观察可知，厝一层黑邑正方体有4伞，则白色正方体有“个I所以每一层共有54个正方体，则正方体的边畏为1,则蔗有呂层，所以一拱用了4*432仆卜的黑邑的正方体*8.有许多相同的立方体，每个立方体的六个面上都写着同一个数字（不同的立方体可以写相同的数字）先将写着2的立方体与写着1的立方体的三个面相邻，再将写着3的立方体写着2的立方体相邻（见左下图）．依这样构成右下图所示的立方体，它的六个面上的所有数字之和是多少?1/第一层如节图：第二层、第三层依兔比上面一层每格都多1（见下图）*上向的9个数之和足27,由对称性知，上面、前面、右面的所有数之利輔逻匕.同理，下海的9个数之和是45,下面、左面、后面的所有数之和都是45”所以天个面上所有数之和是（27+45）x3=216.【巩固】如图，原来的大正方体是由125个小正方体所构成的．其中有些小正方体已经被挖除图中涂黑色的部分就是贯穿整个大正方体的挖除部分．请问剩下的部分共有多少个小正方体？第8题I对于it一类从立体图形中间挖掉一部曲后再求体禅（就小止君体数目）的趣目一般可以農用“切片法刃来做，所谓“切片法役就是把整个虫体图形切嵐一片--片的（或--层--层的），然后分别计算每一片或毎一层的体相或小正方体数目,最后再把它们相加.采用切片法，俯视第一层到第五层的图母依次如下.其屮黑色部分蔻示挖除掉的部分.从图申可以看出，第'_、2.3、4,5层剩下的小正方体势别有22牛.11牛、11个，◎个、11所以总共还剩下22^J1+11+5+22=72（介）小正方体*審易看出这个展开图可以拼成一个封闭的立体图步，展开图外围一共有12条边；这个封囲的立体图像要展开成图由的展开图，每剪开一条嵐就会产生外围的2条迦所叹需要剪开幔：2=占条檯【巩固】如图，剪一块硬纸片可以做成一个多面体的纸模型（沿虚线折，沿实线粘）.这个多面体的面数、顶点数和棱数的总和是多少？多面体的向毀,可以直接从侧面展开圈中数岀来，12个正方形加8个三角形，共20曲.右上图是多面体上部的示意图共有9个顶盘；同样，下部也是9个顶蛊：共”个顶点•橈数要孑成三层来载，上层.从示盍图数，有巧条；下层也是15条；中间部分为6条.一共15*2+6=36总和为；20+18+36-74（个〕.10.图中是一个直三棱柱的表面展开图，其中，黄色和绿色的部分都是边长等于1的正方形．问这个直三棱柱的体积是多少？这个展开图折辰直三按柱母状，如右图所示，可见这个三技柱是单Z方体的--半，其体歆为【巩固】如图是一个四棱锥的展开图，该展开图由正三角形和正方形构成，其中正方形的对角2线长4厘米，那么该四棱锥的体积为多少？AI睿易知道四按锥的底面面积，只要知道四猿锥的高就能求得四植锥的体积.將四技锥沼对角践和顶点枸说的平面剖开，剖面是--个三角形.该三角形的斜边等于正方形的对角线，直角边等于正方形和聲边三甬形的边长，所汰三角形是一个尊腰直角三角形.它的高等于时角线的一半，根据对称脛，这条商也等于四植锥的高.即四梭锥昭高度为2.四棱锥肘体祺为「4m2-3=—豆方厘来.31|吵课堂检测it1.右图中共有多少个面？多少条棱?9个面亍21条梭.2.____________________________________________________________ 右边正方体是用左边图形折成的，则小正方形在正方体的面.3.将1,2,3,4,5,6分别写在正方体六面上，使正方体中对面数字的和相等•正方体如图放置在A格上，沿格子滚动到B点时，在正方体右面的数字是滚到右下角时如下图:35再滾动到右上角时:456所以到J3点叶在右面的为34.如图所示，一个5X5X5的立方体，在一个方向上开有l x l x5的孔，在另一个方向上开有2x l x5的孔，在第三个方向上开有3x l x5的孔，剩余部分的体积是多少？表面积为多少?r*2”21i12I 2222 1121 1121、i2111\211z111211222221求体积：开了"25的礼，穗去3x25=1—fl-T1x^5的乳,挖去Ix]x5-I=4；开了"25的乳,挖去2S|x5-t2+2）=6?劇余部芬的体和是：5x5x5-（154-4+0=100（另解）特螯个图形切片，如果切飾平行于纸面，那么五夺切片分别如團:求■表而积：表面积可以看成卉部和內部两部分.外部的表面恋为亍d以-12=皿"内部的囲积可以分为前后*左右、上下三丰方询，面积分别为如*■'-'>1x5-1.1-21=14^所帜总昭表面积为1H我302='*（另解）运用类似于三视團的方法；记录毎一方向上砖不同位査上的操露正方形年数:前■后方向：覚上下方向：加左右方向：4ft总表面积为2x(32+3(}+40)-30\家庭作业作业检测【例1】右图是由22个小正方体组成的立体图形，其中共有多少个大大小小的正方体？由两个小正方体组成的长方体有多少个？Z77正方体只可能有西种：由1芋小正方体构成的止方体，有22个；由妆芋小正方体构成的2x2x2的止方体，有4个.所以共有正方体224-J=2b(心.由两牛小正方体组戚的长方体，祖据摆菽的方向可分为下国所示的上下位、左右住，前后＜1三种,其中上下位有13个，左右位有13仆前后住有14牛，共有134134-14=10W.【例2】将一个长28cm，宽18cm的长方形铁片的四个角各截去一个边长为4cm的正方形.再将此铁片折成一个无盖的长方形容器•容器的容积为cm3.四个角各栽击--个边悅为心的止方形，再折成--个无蓋硒悅方形容器，则悅方形容器的底面的长和宽分别比铁片的说和宽掘仙即2。

小学奥数竞赛试题小学奥数竞赛是一项旨在培养小学生数学思维和解决问题能力的竞赛活动。

它不仅考察学生的数学基础知识，还考验他们的逻辑推理、空间想象和创新能力。

以下是一些精选的小学奥数竞赛试题，供学生练习和挑战。

试题一：数字填空题在下面的数字序列中，每个数字代表一个特定的数，数字之间的运算符号是加号或乘号。

请找出正确的运算符号，使得等式成立。

```1 □2 □3 □4 = 24```提示：考虑使用乘法来达到较大的结果。

试题二：几何问题一个圆的直径为10厘米，求这个圆的面积。

试题三：逻辑推理题一个班级有45名学生，其中会游泳的有30人，会骑自行车的有25人，两者都不会的有5人。

问：既会游泳又会骑自行车的学生有多少人？试题四：数列问题给定数列：2, 4, 8, 16, ...，求第10项的值。

试题五：组合问题一个盒子里有5个红球和3个蓝球，如果随机取出3个球，求取出的球中至少有2个红球的概率。

答案解析：试题一答案：1 *2 +3 *4 = 24试题二答案：圆的面积公式为A = πr²，其中 r 为半径。

由于直径为10厘米，半径为5厘米。

所以面积 A = π * 5² = 25π ≈ 78.54 平方厘米。

试题三答案：会游泳的有30人，会骑自行车的有25人，两者都不会的有5人。

所以两者都会的人数为：30 + 25 - (45 - 5) = 55 - 40 = 15人。

试题四答案：这是一个等比数列，公比为2。

第10项的值为：2 * 2^(10-1) = 2^9 = 512。

试题五答案：首先计算没有红球的概率，即全部取出蓝球的概率：(3/8) * (2/7) * (1/6) = 1/56。

然后用1减去这个概率，得到至少有2个红球的概率：1 - 1/56 ≈ 55/56。

奥数竞赛不仅能够激发学生对数学的兴趣，还能帮助他们在解决实际问题时更加灵活和创新。

希望这些题目能够为参加小学奥数竞赛的学生们提供一些帮助。

四年级奥数题正方体复习资料
有两个相同的正方体，每个正方体的六个面上分别标有数字1、2、3、4、5、6.将两个正方体放到桌面上，向上的一面数字之和为偶数的有多少种情形?
答案与解析：
要使两个数字之和为偶数，只要这两个数字的奇偶性相同，即这两个数字要么同为奇数，要么同为偶数，所以，要分两大类来考虑.
第一类，两个数字同为奇数.由于放两个正方体可认为是一个一个地放.放第一个正方体时，出现奇数有三种可能，即1，3，5;放第二个正方体，出现奇数也有三种可能，由乘法原理，这时共有3×3=9种不同的情形.
第二类，两个数字同为偶数，类似第一类的.讨论方法，也有3×3=9种不同情形.
最后再由加法原理即可求解.
【答案】两个正方体向上的一面同为奇数共有3×3=9(种)不同的情形;
两个正方体向上的一面同为偶数共有
3×3=9(种)不同的情形.
所以，两个正方体向上的一面数字之和为偶数的共有
3×3+3×3=18(种)不同的情形.。

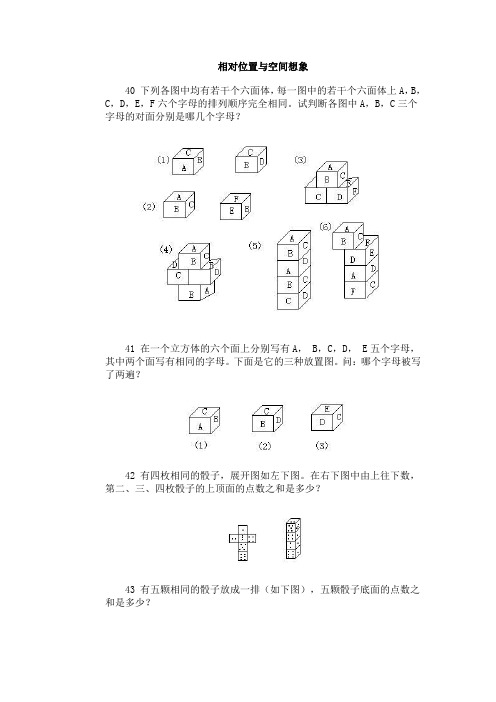
相对位置与空间想象40 下列各图中均有若干个六面体，每一图中的若干个六面体上A，B，C，D，E，F六个字母的排列顺序完全相同。

试判断各图中A，B，C三个字母的对面分别是哪几个字母？41 在一个立方体的六个面上分别写有A， B，C，D， E五个字母，其中两个面写有相同的字母。

下面是它的三种放置图。

问：哪个字母被写了两遍？42 有四枚相同的骰子，展开图如左下图。

在右下图中由上往下数，第二、三、四枚骰子的上顶面的点数之和是多少？43 有五颗相同的骰子放成一排（如下图），五颗骰子底面的点数之和是多少？44 有三块相同的数字积木，摆放如下图，相对两个面上的数字之积最大是几？45 有三块相同的数字积木，摆放如下图，相对两个面上的数字的乘积最小是几？46 一个正四棱锥和一个正方体，其中正方体的面与正四棱锥的底面是全等的图形（见下图），将这两个面对齐粘合后，这个多面体有几个面？47 有一个正方体，它的六个面分别被涂上互不相同的颜色。

如果从不同的角度给这个正方体拍照，那么有时只能拍照到一个面，有时能拍照到两个面，最多能同时拍照到三个面。

洗出照片后，照片中正方体的面的颜色搭配种类最多有多少种？48 左下图中共有多少个面？多少条棱？49 右上图中共有多少个面？多少条棱？50 一个正方体的8个顶点被截去后，得到一个新的几何体（如右图），这个新的几何体有几个面？几个顶点？几条棱？51 一个正方体的12条棱分别被染成白色或红色，如果要求每个面上至少要有一条边是白色的，那么，至少有几条棱要被染成白色？52 有一个正方体，红、黄、蓝色的面各有两面。

在这个正方体中，有一些顶点是三种颜色都不同的面的交点，这种顶点最多有几个？最少有几个？53 给一个正方体的每个面分别涂上红、黄、蓝三种颜色中的一种，每种颜色涂两个面，共有多少种不同的涂法？（注：两种涂法，如果经过翻动能使各种颜色的位置相同，就认为是相同的涂法。

）54 一个正方体，锯掉一个角后，剩下的部分有几个角？（画图表示各种情况）55 用125个同样的小正方体组成一个5×5×5的大正方体，一个人最多能同时看到多少个小正方体？56 在上题中，如果是11×11×11的大正方体呢？57 右图是一个三棱柱，如果将不相交的两条棱称为一对，那么图中不相交的棱共有多少对？58 桌面上摆着一些相同的正方体木块，从正南方向看如左下图，从正西方向看如右下图。

知识框架重难点例题精讲【例1】数一数下图中有多少个正方体木块？【巩固】右图中共有多少个面？多少条棱？展开图与空间想象线折叠成长方体容器．这个容器的体积是多少立方厘米？欢迎关注：奥数轻松学余老师薇芯：69039270【巩固】沿图4的虚线折叠，可以围成一个长方体，它的体积是立方厘米。

【例3】下列图形经过折叠不能围成正方体的是________.【巩固】左下图是一个正方体，四边形APQC 表示用平面截正方体的截面．请在右下方的展开图中画出四边形APQC 的四条边．H F QGB CD EA FEH G D C B A【例4】图1是下面的表面展开图①甲正方体；②乙正方体；③丙正方体；④甲正方体或丙正方体．甲乙丙【巩固】选项中有4个立方体，其中是用左边图形折成的是()．欢迎关注：奥数轻松学余老师薇芯：69039270【例5】将A、B、C、D、E、F六个字母分别写在正方体的六个面上，从下面三种不同摆法中判断这个正方体中，哪些字母分别写在相对的面上．【巩固】用红、黄、蓝、白、黑、绿六种颜色分别涂在正方体的各个面上，每一个面只涂一种颜色．如图所示，现有涂色方式完全一样的四块小正方体拼成了一个长方体．试回答：每个小正方体中，哪些颜色分别涂在相对的面上？【例6】把2、4、6、8、10、12这六个数字依次写在一个立方体的正面、背面、两个侧面以及两个底面上，然后把立方体展开，如图1，最左边的正方形上的数字是12，则最右边的正方形上的数字是。

【巩固】如下图，一个正方体木块放在桌面上，每个面内都画有若干个点，相对的两个面内的点数和都是13，京京看见上、左、前三个面内的点数的和诗16，庆庆看见上、右、后三个面内的点数和是24。

那么贴着桌面的那个面的点数是___.【例7】用大小相等的无色透明玻璃小正方体和红色玻璃小正方体拼成一个大正方体1111ABCD A B C D (如图)，大正方体内的对角线1AC ，1BD ，1CA ，1DB 所穿的小正方体都是红色玻璃小正方体，其它部分都是无色透明玻璃小正方体，小红正方体共用了401个，问：无色透明小正方体用了多少个?D 1C 1B 1A 1D C B A欢迎关注：奥数轻松学余老师薇芯：69039270【巩固】如图，用若干个体积相同的小正方体堆积成一个大正方体，要使大正方体的对角线（正方体八个顶点中距离最远的两个顶点的连线）穿过的小正方体都是黑色的，其余小正方体都是白色的，并保证大正方体每条边上有偶数个小正方体。

以下为你提供40道考察不同思维方式的三年级上册奥数题：1. 标题：逆向思维题目**题目：**有一个数字，如果倒过来写，例如56变成65，但是它比原来的数大7。

那么这个数字是多少？解析：这道题考察逆向思维，我们需要从题目的反面去思考，找出符合条件的数字。

2. 标题：观察与推理思维题目**题目：**观察下面的图形序列，找出其中的规律，并预测下一个图形是什么。

解析：这道题考察观察和推理能力，需要找出图形的变化规律，从而预测下一个图形。

3. 标题：创造性思维题目**题目：**如果所有动物都没有尾巴，那么哪种动物最有可能长出尾巴？解析：这道题考察创造性思维，需要从无到有地想象动物长出尾巴的情况。

4. 标题：逻辑思维题目**题目：**有五个人分别戴着帽子、围巾、手表、手套、鞋子，他们分别来自北方和南方，其中鞋子和手套是北方人买的，帽子和围巾是南方人买的。

某个人买了两样东西，请问这个人是谁？解析：这道题考察逻辑推理能力，需要分析条件并找出符合所有条件的人。

5. 标题：分类与归纳思维题目**题目：**将以下词语分类并归纳它们的共同点：狗、猫、鱼、鸟、兔子。

解析：这道题考察分类和归纳能力，需要找出给定词语的共同特点或属性，并进行分类。

6. 标题：批判性思维题目**题目：**评价以下观点的合理性和缺陷：所有人都应该遵守交通规则，以保持道路安全。

解析：这道题考察批判性思维能力，需要分析交通规则的作用和可能的缺陷，并提出自己的看法。

7. 标题：空间思维题目**题目：**一个立方体的六个面上分别标有数字1、2、3、4、5、6。

根据下面的三种摆放方式，推测数字“1”的对面数字是什么？解析：这道题考察空间思维能力，需要理解立方体的空间关系，找出数字“1”的对面数字。

8. 标题：假设思维题目**题目：**一个袋子里有黑白两种颜色的球，其中黑球10个，白球9个。

如果闭上眼睛随机从袋子里摸出一个球，那么摸到白球的可能性是多少？解析：这道题考察假设思维能力，需要在给定条件的基础上进行合理的假设和推断。

4-1-4.幾何中的空間想像知識點撥空間想像不僅是認識現實世界空間形式不可缺少的能力因素，而且是形成和發展創造力的源泉，因此，空間想像能力是數學教學必須培養的基本數學能力之一。

空間想像能力的培養與幾何教學有關。

直觀幾何教學的主要任務是通過學生製作模型、搭積木、畫圖、識圖，對圖形進行描述、分類、整理等學習活動，認識、理解我們所處的現實世界的幾何空間，以形成空間觀念。

綜合幾何教學的主要任務是運用邏輯推理的方法研究圖形的性質，幫助學生從邏輯的角度進一步弄清幾何空間的意義，學會幾何思考的方法，培養空間想像能力和邏輯推理能力。

例題精講模組一、對稱圖形【例 1】將一塊正方形紙片沿對角線折疊一次，然後在得到的三角形的三個角上各挖去一個圓洞，再展開正方形紙片，得到圖1中的。

（填序號）①②③④【考點】幾何中的空間想像【難度】1星【題型】填空【解析】逆推法③【答案】③【例 2】(希望杯五年級一試第8題，6分)下麵四幅圖形中不是軸對稱圖形的是。

（填序號）（注：如果一個圖形沿一條直線折疊後，直線兩旁的部分能夠互相重合，那麼這個圖形叫做對稱圖形。

）【考點】幾何中的空間想像【難度】1星【題型】填空【解析】③④【答案】③④模組二、平面圖形【例 3】(希望杯四年級二試第5題，6分)將一張長方形紙對折再對折（如圖），然後沿著圖中的虛線剪下，得到①、②兩部分，將①展開後得到的平面圖形一定是。

（填“三角形”、“長方形”、“梯形”或“菱形”）②展开①【考點】幾何中的空間想像【難度】2星【題型】填空【解析】菱形【答案】菱形【例 4】(希望杯六年級一試第18題，6分)如圖，房間裏有一只老鼠，門外有一只小貓，如果每塊正方形地磚的連長為50釐米，那麼老鼠在地面上能避開小貓視線的活動範圍為_________平方釐米.(將小貓和老鼠分別看作兩個點,牆的厚度忽略不計)【考點】幾何中的空間想像【難度】4星【題型】填空【解析】貓看不到的地方如圖所示陰影部分，其中梯形面積為（1+3.5）×2.5÷2=5.625平方米.三角形的面積為2×1÷2=1平方米.老鼠的活動範圍共6.625平方米，即66250平方釐米.【答案】66250平方釐米模組三、立體圖形【例 5】用紅、黃、藍、白、黑、綠六種顏色分別塗在正方體的各個面上，每一個面只塗一種顏色．如圖所示，現有塗色方式完全一樣的四塊小正方體拼成了一個長方體．試回答：每個小正方體中，紅色面的對面塗的是什麼色？黃色面的對面塗的是什麼色？黑色面的對面是什麼色？【考點】幾何中的空間想像【難度】3星【題型】解答【解析】在能看見的9個面中紅色出現的次數最多．觀察圖8—4中最上面的一個正方體，由於紅色和黑色、黃色相鄰，所以它的對面不可能是黑黃兩色．同理，由第二個正方體可知，紅色的對面不能是白色；由第三個正方體知，紅色的對面不能是藍色．所以紅色的面的對面只可能是綠色．同理，黃色面的對面不可能是紅色、黑色或白色，又已推知不可能是綠色，所以黃色面的對面只可能是藍色．這樣黑色面的對面就只可能是塗白色的了．【答案】紅色的對面是綠色黃色的對面是藍色黑色的對面是白色【例 6】將“貓”“狗”“兔”“雞”“猴”“虎”六個動物名稱分別寫在六個正方體的六個面上，從下麵三種不同擺法中，判斷這個正方體上哪些動物名名稱分別寫在相對面上.兔狗猫鸡狗兔猫猴兔【考點】幾何中的空間想像 【難度】3星 【題型】解答 【解析】 本題給的是一組立方圖形，在這三幅圖中，“兔”所在的一面始終不改變位置，因此，這三個圖的轉化只能是前後轉動.把第一幅圖向後反轉一次得到第二幅圖，由此可知，“貓”的對面是“雞”；把第一幅圖向前翻轉一次得到第三幅圖，所以“狗”的對面是“猴”，那麼剩下的只有“兔”和“虎”相對.【答案】貓的對面是雞；狗的對面是猴； 兔的對面是虎。

拓展小学生数学空间想象能力的习题练习数学空间想象力是指人们在脑海中构建和操作空间概念的能力。

它是数学学习的基础，也是培养孩子创造力、逻辑思维和几何思维的关键。

然而，对于一些小学生来说，数学空间想象力的发展可能会遇到困难。

因此，为了拓展小学生的数学空间想象能力，我们设计了以下习题练习，希望能够提供帮助和指导。

1. 用积木搭建立体模型要求学生使用积木搭建各种不同形状的立体模型。

可以从简单的正方体、长方体开始，逐渐过渡到更复杂的立体模型，如金字塔、立方体等。

通过这种方式，学生可以直观地感受到不同形状之间的关系，并培养对于空间结构的认知能力。

2. 计算表面积和体积给定一个简单的立体模型，要求学生计算其表面积和体积。

通过这样的练习，学生能够更好地理解表面积和体积的概念，并能够将抽象的数学概念与具体的实际问题联系起来。

3. 推理图形的变换关系给出一个图形，并要求学生通过观察，找出其中的变换规律，进而推理出下一个图形。

可以包括平移、旋转、翻转等不同形式的变换。

这样的练习可以培养学生的空间观察能力，并锻炼他们的逻辑思维和推理能力。

4. 绘制简单的几何图形要求学生根据给定的条件，绘制出一个符合要求的几何图形。

这样的练习可以提高学生对于几何图形的认知能力，并激发他们的创造力和想象力。

例如，给定一个正方形，要求学生在其中绘制一个等边三角形，从而让他们通过操作图形来掌握几何知识。

5. 构建平面图形的立体模型给定一个平面图形，要求学生使用纸板或者折纸等材料，构建出其对应的立体模型。

通过这样的练习，学生可以将平面图形与空间模型进行转化，并进一步加深对于图形的理解和认知。

通过以上的习题练习，我们可以有效地拓展小学生的数学空间想象能力。

当然，教师在引导学生进行练习的过程中，也要注重激发学生的兴趣和培养他们的思维能力。

同时，教师还可以根据学生的具体情况，适当调整习题的难度和数量，以保证学生的学习效果和兴趣。

通过持续的训练和练习，相信小学生的数学空间想象能力将得到有效地提升，为他们未来的数学学习和发展打下坚实的基础。