高中数学知识点易错点梳理一集合与简易逻辑 (1)

怀安县高中数学集合与常用逻辑用语易错知识点总结单选题1、命题“∀x<0,x2+ax−1≥0”的否定是（）A．∃x≥0,x2+ax−1<0B．∃x≥0,x2+ax−1≥0C．∃x<0,x2+ax−1<0D．∃x<0,x2+ax−1≥0答案：C分析：根据全称命题的否定是特称命题判断即可.根据全称命题的否定是特称命题，所以“∀x<0,x2+ax−1≥0”的否定是“∃x<0,x2+ax−1<0”.故选：C2、集合A={0,−1,a2},B={−2,a4}.若A∪B={−2,−1,0,4,16}，则a=（）A．±1B．±2C．±3D．±4答案：B分析：根据并集运算，结合集合的元素种类数，求得a的值.由A∪B={−2,−1,0,4,16}知，{a2=4a4=16，解得a=±2故选：B3、已知全集U={x|−3<x<3}，集合A={x|−2<x≤1}，则∁U A=（）A．(−2,1]B．(−3,−2)∪[1,3)C．[−2,1)D．(−3,−2]∪(1,3)答案：D分析：利用补集的定义可得正确的选项．由补集定义可知：∁U A={x|−3<x≤−2或1<x<3}，即∁U A=(−3,−2]∪(1,3)，故选：D．4、已知集合A={(x,y)||x|+|y|≤2,x∈Z,y∈Z}，则A中元素的个数为（）A．9B．10C．12D．13答案：D分析：利用列举法列举出集合A中所有的元素，即可得解.由题意可知，集合A中的元素有：(−2,0)、(−1,−1)、(−1,0)、(−1,1)、(0,−2)、(0,−1)、(0,0)、(0,1)、(0,2)、(1,−1)、(1,0)、(1,1)、(2,0)，共13个.故选：D.5、设集合A={−1,0,1,2}，B={1,2}，C={x|x=ab,a∈A,b∈B}，则集合C中元素的个数为（）A．5B．6C．7D．8答案：B分析：分别在集合A,B中取a,b，由此可求得x所有可能的取值，进而得到结果.当a=−1，b=1时，ab=−1；当a=−1，b=2时，ab=−2；当a=0，b=1或2时，ab=0；当a=1，b=1时，ab=1；当a=1，b=2或a=2，b=1时，ab=2；当a=2，b=2时，；∴C={−2,−1,0,1,2,4}，故C中元素的个数为6个.故选：B.6、已知U=R，M={x|x≤2}，N={x|−1≤x≤1}，则M∩∁U N=（）A．{x|x<−1或1<x≤2}B．{x|1<x≤2}C．{x|x≤−1或1≤x≤2}D．{x|1≤x≤2}答案：A分析：先求∁U N，再求M∩∁U N的值.因为∁U N={x|x<−1或x>1}，所以M∩C U N={x|x<−1或1<x≤2}.故选：A.7、已知集合A={(x,y)|x,y∈N∗,y≥x}，B={(x,y)|x+y=8}，则A∩B中元素的个数为（）A．2B．3C．4D．6答案：C分析：采用列举法列举出A∩B中元素的即可.由题意，A∩B中的元素满足{y≥xx+y=8，且x,y∈N∗，由x+y=8≥2x，得x≤4，所以满足x+y=8的有(1,7),(2,6),(3,5),(4,4)，故A∩B中元素的个数为4.故选：C.4 ab【点晴】本题主要考查集合的交集运算，考查学生对交集定义的理解，是一道容易题.8、已知集合M={−3,−2,−1,0,1,2,3}，非空集合P满足：（1）P⊆M；（2）若x∈P，则−x∈P，则集合P的个数是（）A．7B．8C．15D．16答案：C分析：根据题意把M中元素按相反数分成4组，这4组元素中一定是一组元素全属于P或全不属于P，由此结合集合的子集的性质可得P的个数．满足条件的集合P应同时含有−3,3或−2,2或−1,1或0，又因为集合P非空，所以集合P的个数为24−1=15个，故选：C.9、已知a∈R，则“a>6”是“a2>36”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案：A分析：由充分条件、必要条件的定义判断即可得解.由题意，若a>6，则a2>36，故充分性成立；若a2>36，则a>6或a<−6，推不出a>6，故必要性不成立；所以“a>6”是“a2>36”的充分不必要条件.故选：A.10、设集合A ={x |x 2=1},B ={x |ax =1}．若A ∩B =B ，则实数a 的值为（ ）A ．1B ．−1C ．1或−1D ．0或1或−1答案：D分析：对a 进行分类讨论，结合B ⊆A 求得a 的值.由题可得A ={x|x 2=1}={1,−1}，B ⊆A ，当a =0时，B =∅，满足B ⊆A ；当a ≠0时， B ={1a }，则1a =1或1a =−1，即a =±1.综上所述，a =0或a =±1.故选：D.11、已知集合A ={x |1x >1}，则∁R A =（ ）A ．{x |x <1}B ．{x |x ≤0或x ≥1}C ．{x|x <0}∪{x|x >1}D ．{x |1≤x }答案：B分析：先解不等式，求出集合A ，再求出集合A 的补集由1x >1，得1−x x >0，x(1−x)>0，解得0<x <1，所以A ={x |0<x <1}，所以∁R A ={x |x ≤0或x ≥1}故选：B12、某班45名学生参加“3·12”植树节活动，每位学生都参加除草､植树两项劳动.依据劳动表现，评定为“优秀”､“合格”2个等级，结果如下表：若在两个项目中都“合格”的学生最多有10人，则在两个项目中都“优秀”的人数最多为（）A．5B．10C．15D．20答案：C分析：用集合A表示除草优秀的学生，B表示植树优秀的学生，全班学生用全集U表示，则∁U A表示除草合格的学生，则∁U B表示植树合格的学生，作出Venn图，易得它们的关系，从而得出结论．用集合A表示除草优秀的学生，B表示植树优秀的学生，全班学生用全集U表示，则∁U A表示除草合格的学生，则∁U B表示植树合格的学生，作出Venn图，如图，设两个项目都优秀的人数为x，两个项目都是合格的人数为y，由图可得20−x+x+30−x+y= 45，x=y+5，因为y=10，所以x max=10+5=15．max故选：C．小提示：关键点点睛：本题考查集合的应用，解题关键是用集合A,B表示优秀学生，全体学生用全集表示，用Venn图表示集合的关系后，易知全部优秀的人数与全部合格的人数之间的关系，从而得出最大值．13、已知集合A={x|x+2<0}，B={0,1,2,3,4,5}，则(∁R A)∩B=（）x−4A．{5}B．{4,5}C．{2,3,4}D．{0,1,2,3}答案：B分析：首先化简集合A，再根据补集的运算得到∁R A，再根据交集的运算即可得出答案.因为A={x|x+2<0}=(−2,4)，x−4所以∁R A={x|x≤−2或x≥4}.所以(∁R A)∩B={4,5}故选：B.14、设集合A={1,2},B={2,4,6}，则A∪B=（）A．{2}B．{1,2}C．{2,4,6}D．{1,2,4,6}答案：D分析：利用并集的定义可得正确的选项.A∪B={1,2,4,6}，故选：D.15、设集合M={1,3,5,7,9},N={x|2x>7}，则M∩N=（）A．{7,9}B．{5,7,9}C．{3,5,7,9}D．{1,3,5,7,9}答案：B分析：求出集合N后可求M∩N.N=(7,+∞)，故M∩N={5,7,9}，2故选：B.16、已知集合M={x|x=m−56,m∈Z}，N={x|x=n2−13,n∈Z}，P={x|x=p2+16,p∈Z}，则集合M，N，P的关系为（）A．M=N=P B．M⊆N=PC．M⊆N P D．M⊆N，N∩P=∅答案：B分析：对集合M,N,P中的元素通项进行通分，注意3n−2与3p+1都是表示同一类数，6m−5表示的数的集合是前者表示的数的集合的子集，即可得到结果.对于集合M={x|x=m−56,m∈Z}，x=m−56=6m−56=6(m−1)+16，对于集合N={x|x=n2−13,n∈Z}，x=n2−13=3n−26=3(n−1)+16，对于集合P={x|x=p2+16,p∈Z}，x=p2+16=3p+16，由于集合M,N,P中元素的分母一样，只需要比较其分子即可，且m,n,p∈Z，注意到3(n−1)+1与3p+1表示的数都是3的倍数加1，6(m−1)+1表示的数是6的倍数加1，所以6(m−1)+1表示的数的集合是前者表示的数的集合的子集，所以M⊆N=P.故选：B.17、已知集合A={x∈N|x≤1},B={−1,0,1,2}，则A∩B的子集的个数为（）A．1B．2C．3D．4答案：D分析：根据集合交集的定义，结合子集个数公式进行求解即可．由题意A∩B={0,1}，因此它的子集个数为4．故选：D．18、设集合A={2,a2−a+2,1−a}，若4∈A，则a的值为（）．A．−1，2B．−3C．−1，−3，2D．−3，2答案：D分析：由集合中元素确定性得到：a=−1，a=2或a=−3，通过检验，排除掉a=−1.由集合中元素的确定性知a2−a+2=4或1−a=4．当a2−a+2=4时，a=−1或a=2；当1−a=4时，a=−3．当a=−1时，A={2,4,2}不满足集合中元素的互异性，故a=−1舍去；当a=2时，A={2,4,−1}满足集合中元素的互异性，故a=2满足要求；当a=−3时，A={2,14,4}满足集合中元素的互异性，故a=−3满足要求．综上，a=2或a=−3．故选：D．19、已知全集U=R，集合M={x∣(x−1)(x+2)≥0}，N={x∣−1≤x≤3}，则(∁U M)∩N=（）A．[−1,1)B．[−1,2]C．[−2,−1]D．[1,2]答案：A分析：先由一元二次不等式的解法求得集合M，再由集合的补集、交集运算求得答案.解：由题意可得：由(x−1)(x+2)≥0得x≥1或x≤−2，所以M=(−∞，−2]∪[1，+∞)，则：C U M =(−2,1)，又N ={x ∣−1≤x ≤3}，所以(∁U M )∩N = [−1,1).故选：A ．20、设条件甲：“事件A 与事件B 是对立事件”，结论乙：“概率满足P （A ）＋P （B ）＝1”，则甲是乙的（ ）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件答案：A解析：将两个条件相互推导，根据能否推导的情况选出正确答案.①若事件A 与事件B 是对立事件，则A ∪B 为必然事件，再由概率的加法公式得P （A ）＋P （B ）＝1；②投掷一枚硬币3次，满足P （A ）＋P （B ）＝1，但A ，B 不一定是对立事件，如：事件A ：“至少出现一次正面”，事件B ：“出现3次正面”，则P （A ）＝78，P （B ）＝18，满足P （A ）＋P （B ）＝1，但A ，B 不是对立事件.所以甲是乙的充分不必要条件.故选：A小提示：本小题主要考查充分、必要条件的判断，考查对立事件的理解，属于基础题.填空题21、若∀x ∈R,2x 2−mx +3≥0恒成立，则实数m 的取值范围为________.答案：[−2√6,2√6].分析：根据命题∀x∈R,2x2−mx+3≥0恒成立，结合二次函数的图象与性质，即可求解.由题意，命题∀x∈R,2x2−mx+3≥0恒成立，可得Δ=m2−24≤0，解得−2√6≤m≤2√6，即实数m的取值范围为[−2√6,2√6].所以答案是：[−2√6,2√6].22、命题“任意x∈[−1,2]，x2−2x−a≤0”为真命题，则实数a的取值范围是______.答案：[3,+∞)分析：分离常数，将问题转化为求函数最值问题.任意x∈[−1,2]，x2−2x−a≤0恒成立⇔x2−2x≤a恒成立，故只需(x2−2x)max≤a，记f(x)==f(−1)=3，所以3≤a.x2−2x=(x−1)2−1，x∈[−1,2]，易知f(x)max所以答案是：[3,+∞)23、用∈或∉填空：0________N答案：∈解析：可知0是自然数，即可得出.∵0是自然数，∴0∈N.所以答案是：∈.24、命题p:∀x∈R，x2+ax+a≥0，若命题p为真命题，则实数a的取值范围为___________.答案：[0,4]分析：根据二次函数的性质判别式解题即可.∀x∈R，要使得x2+ax+a≥0，则Δ=a2−4a≤0，解得0≤a≤4.若命题p为真命题，则实数a的取值范围为[0,4].所以答案是：[0,4].25、集合A={x∈N|8∈N∗}，用列举法可以表示为A=_________．3−x答案：{1,2}##{2,1}分析：根据集合元素属性特征进行求解即可.因为8∈N∗，所以3−x=1,2,4,8，可得x=2,1,−1,−5，因为x∈N，所以x=1,2，集合A= 3−x{1,2}．所以答案是：{1,2}26、命题“所有无理数的平方都是有理数”的否定是__________．答案：存在一个无理数，它的平方不是有理数分析：根据全称命题的否定形式，即可求解结论.存在一个无理数，它的平方不是有理数，全称性命题的否定是先改变量词，然后否定结论，故所求的否定是“存在一个无理数，它的平方不是有理数”．所以答案是：存在一个无理数，它的平方不是有理数小提示：本题考查命题的否定形式，要注意量词之间的转化，属于基础题.27、若命题“∀x∈(3,+∞),x>a”是真命题，则a的取值范围是__________.答案：(−∞,3]分析：根据不等式恒成立求解即可.对于任意x >3,x >a 恒成立，即大于3的数恒大于a,∴a ⩽3.所以答案是：(−∞,3].28、若“x >3”是“x >m ”的必要不充分条件，则m 的取值范围是________．答案：m >3分析：由题，“x >3”是“x >m ”的必要不充分条件，则是(3,+∞)的真子集，可得答案. 因为“x >3”是“x >m ”的必要不充分条件，所以是(3,+∞)的真子集，所以m >3，故答案为m >3.小提示：本题考查了不要不充分条件，属于基础题.29、已知命题“∃x ∈R,m x 2−x +1<0”是假命题，则实数m 的取值范围是_________.答案：m ≥14解析：求得原命题的否定，根据其为真命题，即可结合二次不等式恒成求得参数范围若命题“∃x ∈R,m x 2−x +1<0”是假命题，则“∀x ∈R,m x 2−x +1≥0”为真命题，显然m =0时，不满足题意，故只需满足{m >0Δ=1−4m ≤0，解得m ≥14. 所以答案是：m ≥14.(),m +∞(),m +∞小提示：本题考查根据含量词命题的真假求参数范围的问题，涉及二次不等式在R上恒成立求参数的问题，属综合基础题.30、设全集U={x|x3−x=0}，集合A={0,1}，则∁U A=___________.答案：{−1}分析：先化简集合U，再求∁U A由x3−x=0解得：x1=1,x2=−1,x3=0，所以U={1,−1,0}，故∁U A={−1}所以答案是：{−1}解答题31、已知集合A={x|−2<x<5},B={x|m+1≤x≤2m−1}（1）当m=3时，求(∁R A)∩B；（2）若A∪B=A，求实数m的取值范围.答案：（1）(∁R A)∩B={5}；（2）m<3.分析：（1）根据集合的运算法则计算；（2）由A∪B=A得B⊆A，然后分类B=∅和B≠∅求解．（1）当m=3时，B中不等式为4≤x≤5，即B={x|4≤x≤5}，∴∁A={x|x≤−2或x≥5}，则(∁R A)∩B={5}R（2）∵A∪B=A，∴B⊆A，①当B=∅时，m+1>2m−1，即m<2，此时B⊆A；②当B≠∅时，{m+1≤2m+1m+1>−22m−1<5，即2≤m<3，此时B⊆A.综上m的取值范围为m<3.32、设A＝{x|x2＋ax＋12＝0}，B＝{x|x2＋3x＋2b＝0}，A∩B＝{2}，C＝{2，－3}.（1）求a，b的值及A，B；（2）求(A∪B)∩C．答案：（1）a＝－8，b＝－5，A＝{2，6}，B＝{2，－5}.（2）{2}解析：（1）根据已知2是方程x2＋ax＋12＝0,x2＋3x＋2b＝0的解，2代入方程即可求出a,b；进而求出A,B；（2）按并集、交集定义，即可求解.（1）∵A∩B＝{2}，∴4＋2a＋12＝0，即a＝－8，4＋6＋2b＝0，即b＝－5，∴A＝{x|x2－8x＋12＝0}＝{2，6}，B＝{x|x2＋3x－10＝0}＝{2，－5}.（2）∵A∪B＝{－5，2，6}，C＝{2，－3}，∴(A∪B)∩C＝{2}.小提示：本题考查由交集结果求参数、集合间的运算，属于基础题.33、已知集合A={x|−3≤x≤2}，B={x|2m−1≤x≤m+3}．(1)当m=0时，求∁R(A∩B)；(2)若A∪B=A，求实数m的取值范围．答案：(1){x|x<−1或x>2}(2)m>4或m=−1分析：（1）先求交集，再求补集，即可得到答案；（2）由集合间的基本关系可得：B ⊆A ，对集合B 进行讨论，即可得到答案；（1）当m =0时，B ={x ∣−1≤x ≤3}，∴A ∩B ={x ∣−1⩽x ⩽2}，∴∁R (A ∩B)={x|x <−1或x >2}（2）∵A ∪B =A ⇒B ⊆A ，当B =∅时，2m −1>m +3⇒m >4；当B ≠∅时，m ⩽4且{2m −1⩾−3m +3⩽2，解得：m =−1， 综上所述：m >4或m =−134、已知p:∃x ∈R ，x 2+ax +2=0.q:∀x ∈(0,1)，x 2−a <0.(1)若p 为真命题，求a 的取值范围；(2)若p ，q 一个是真命题，一个是假命题，求a 的取值范围．答案：(1)[2√2,+∞)∪(−∞,−2√2](2)(−∞,−2√2]∪[1,2√2)分析：（1）根据p 为真命题，则Δ≥0，解之即可；（2）分别求出p ，q 是真命题时，a 的范围，再分p 是真命题，q 是假命题时和p 是假命题，q 是真命题时，两种情况讨论，即可得出答案.（1）解：由p:∃x ∈R ，x 2+ax +2=0，若p 为真命题，则Δ=a 2−8≥0，解得a ≥2√2或a ≤−2√2，所以a 的取值范围为[2√2,+∞)∪(−∞,−2√2]；（2）解：若q 为真命题时，则a >x 2对∀x ∈(0,1)恒成立，所以a ≥1，若p ，q 一个是真命题，一个是假命题，当p 是真命题，q 是假命题时，则{a ≥2√2a <1或{a ≤−2√2a <1，解得a ≤−2√2，当p 是假命题，q 是真命题时，则{−2√2<a <2√2a ≥1，解得1≤a <2√2，综上所述a ∈(−∞,−2√2]∪[1,2√2).35、已知集合A ＝{a ﹣2，2a 2+5a }，且﹣3∈A ．(1)求a ；(2)写出集合A 的所有真子集．答案：(1)a =−32 ；(2)∅，{−72}，{﹣3} ．分析：（1）由题意知a ﹣2＝﹣3或2a 2+5a ＝﹣3，分类讨论并检验即可求得a =−32；（2）由真子集的定义直接写出即可．（1）∵A ＝{a ﹣2，2a 2+5a }，且﹣3∈A ，∴a ﹣2＝﹣3或2a 2+5a ＝﹣3，①若a ﹣2＝﹣3，a ＝﹣1，2a 2+5a ＝﹣3，故不成立，②若2a 2+5a ＝﹣3，a ＝﹣1或a =−32，由①知a ＝﹣1不成立，若a =−32，a ﹣2=−72，2a 2+5a ＝﹣3，成立，故a =−32；（2）∵A ={−72，−3}，∴A 的真子集有∅，{−72} ，{﹣3}．。

高一数学一知识点：集合、不等式和简易逻辑重点知识归纳、总结（1）集合的分类（2）集合的运算①子集，真子集，非空子集；②A∩B={x|x∈A且x∈B}③A∪B={x|x∈A或x∈B}④A={x|x∈S且xA}，其中AS.2、不等式的解法（1）含有绝对值的不等式的解法①|x|0）-a|x|；a（a；0）x；a，或x；-a.②|f（x）||f（x）|；g（x）f（x）；g（x）或f（x）；-g（x）。

③|f（x）|；|g（x）|[f（x）]2；[g（x）]2[f（x）+g（x）]·[f（x）-g （x）]；0.④关于含有两个或两个以上的绝对值符号的绝对值不等式，利用“零点分段讨论法”去绝对值。

如解不等式：|x+3|-|2x-1|；3x+2.3、简易逻辑知识逻辑联结词"或”、“且”、“非”是判定简单合题与复合命题的依据；真值表是由简单命题和真假判定复合命题真假的依据，明白得好四种命题的关系，对判定命题的真假有专门大关心；把握好反证法证明问题的步骤。

（2）复合命题的真值表非p形式复合命题的真假能够用下表表示。

p非p真假假真p且q形式复合命题的真假能够用下表表示。

p或q形式复合命题的真假能够用下表表示。

（3）四种命题及其相互之间的关系一个命题与它的逆否命题是等价的。

（4）充分、必要条件的判定①若pq且qp，则p是q的充分不必要条件；②若pq且qp，则p是q的必要不充分条件；③若pq且qp，则p是q的充要条件；死记硬背是一种传统的教学方式,在我国有悠久的历史。

但随着素养教育的开展,死记硬背被作为一种僵化的、阻碍学生能力进展的教学方式,慢慢为人们所摒弃;而另一方面,老师们又为提高学生的语文素养煞费苦心。

事实上,只要应用得当,“死记硬背”与提高学生素养并不矛盾。

相反,它恰是提高学生语文水平的重要前提和基础。

④若pq且qp，则p是q的既不充分也不必要条件。

观看内容的选择，我本着先静后动，由近及远的原则，有目的、有打算的先安排与幼儿生活接近的，能明白得的观看内容。

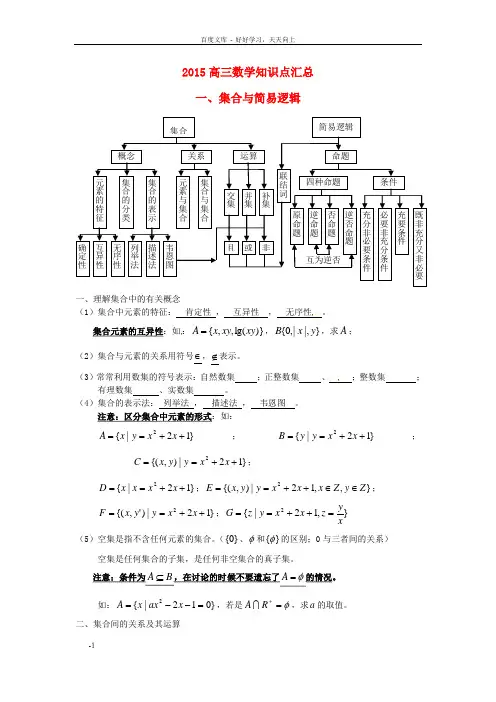
2015高三数学知识点汇总 一、集合与简易逻辑一、理解集合中的有关概念（1）集合中元素的特征： 肯定性 ， 互异性 ， 无序性 。

集合元素的互异性：如：)}lg(,,{xy xy x A =，}|,|,0{y x B ，求A ； （2）集合与元素的关系用符号∈，∉表示。

（3）常常利用数集的符号表示：自然数集 ；正整数集 、 ；整数集 ；有理数集 、实数集 。

（4）集合的表示法： 列举法 ， 描述法 ， 韦恩图 。

注意：区分集合中元素的形式：如：}12|{2++==x x y x A ；}12|{2++==x x y y B ；}12|),{(2++==x x y y x C ；}12|{2++==x x x x D ；},,12|),{(2Z y Z x x x y y x E ∈∈++==；}12|)',{(2++==x x y y x F ；},12|{2xyz x x y z G =++==（5）空集是指不含任何元素的集合。

（}0{、φ和}{φ的区别；0与三者间的关系） 空集是任何集合的子集，是任何非空集合的真子集。

注意：条件为B A ⊆，在讨论的时候不要遗忘了φ=A 的情况。

如：}012|{2=--=x ax x A ，若是φ=+R A ，求a 的取值。

二、集合间的关系及其运算集合概念元素的特征 集合的表示集合的分类无序性互异性确定性韦恩图描述法列举法关系元素与集合集合与集合运算补集并集交集非或且简易逻辑命题 联结词四种命题条件否命题逆命题原命题逆否命题充要条件必要非充分条件充分非必要条件既非充分又非必要互为逆否（1）符号“∉∈,”是表示元素与集合之间关系的，立体几何中的表现 点与直线（面）的关系 ；符号“⊄⊂,”是表示集合与集合之间关系的，立体几何中的表现 面与直线(面)的关系 。

（2）_}__________{_________=B A ；____}__________{_________=B A ； _}__________{_________=A C U （3）对于任意集合B A ,，则：①A B B A ___；A B B A ___；B A B A ___； ②⇔=A B A ；⇔=A B A ；⇔=U B A C U ；⇔=φB A C U ；③=B C A C U U ； )(B A C U =；（4）①若n 为偶数，则=n ；若n 为奇数，则=n ；②若n 被3除余0，则=n ；若n 被3除余1，则=n ；若n 被3除余2，则=n ；三、集合中元素的个数的计算：（1）若集合A 中有n 个元素，则集合A 的所有不同的子集个数为_________，所有真子集的个数是__________，所有非空真子集的个数是 。

高考数学频道为大家提供高考数学易错知识点：集合与简单逻辑，由于思维定式的原因，考生往往会在解题中遗忘空集，导致解题错误或是解题不全面。

更多高考资讯请关注我们网站的更新!高考数学易错知识点：集合与简单逻辑1.易错点遗忘空集致误错因分析：由于空集是任何非空集合的真子集，因此，对于集合B，就有B=A，φ≠B，B≠φ，三种情况，在解题中如果思维不够缜密就有可能忽视了B≠φ这种情况，导致解题结果错误。

尤其是在解含有参数的集合问题时，更要充分注意当参数在某个范围内取值时所给的集合可能是空集这种情况。

空集是一个特殊的集合，由于思维定式的原因，考生往往会在解题中遗忘了这个集合，导致解题错误或是解题不全面。

2.易错点忽视集合元素的三性致误错因分析：集合中的元素具有确定性、无序性、互异性，集合元素的三性中互异性对解题的影响最大，特别是带有字母参数的集合，实际上就隐含着对字母参数的一些要求。

在解题时也可以先确定字母参数的范围后，再具体解决问题。

3.易错点四种命题的结构不明致误错因分析：如果原命题是“若A则B”，则这个命题的逆命题是“若B则A”，否命题是“若┐A则┐B”，逆否命题是“若┐B则┐A”。

这里面有两组等价的命题，即“原命题和它的逆否命题等价，否命题与逆命题等价”。

在解答由一个命题写出该命题的其他形式的命题时，一定要明确四种命题的结构以及它们之间的等价关系。

另外，在否定一个命题时，要注意全称命题的否定是特称命题，特称命题的否定是全称命题。

如对“a，b都是偶数”的否定应该是“a，b不都是偶数”，而不应该是“a，b都是奇数”。

4.易错点充分必要条件颠倒致误错因分析：对于两个条件A，B，如果A=>B成立，则A是B的充分条件，B是A的必要条件;如果B=>A成立，则A是B的必要条件，B是A的充分条件;如果A<=>B，则A，B互为充分必要条件。

解题时最容易出错的就是颠倒了充分性与必要性，所以在解决这类问题时一定要根据充要条件的概念作出准确的判断。

高考数学函数、不等式、三角函数等68条知识点汇总,易错点帮你整理啦！一、集合和简易逻辑【易错提醒】01.遗忘空集致误由于空集是任何非空集合的真子集，因此B＝∅时也满足B⊆A。

解含有参数的集合问题时，要特别注意当参数在某个范围内取值时所给的集合可能是空集这种情况。

02.忽视集合元素的三性致误集合中的元素具有确定性、无序性、互异性，集合元素的三性中互异性对解题的影响最大，特别是带有字母参数的集合，实际上就隐含着对字母参数的一些要求。

03.混淆命题的否定与否命题命题的“否定”与命题的“否命题”是两个不同的概念，命题p 的否定是否定命题所作的判断，而“否命题”是对“若p，则q”形式的命题而言，既要否定条件也要否定结论。

04.充分条件、必要条件颠倒致误对于两个条件A，B，如果A⇒B成立，则A是B的充分条件，B 是A的必要条件；如果B⇒A成立，则A是B的必要条件，B是A的充分条件；如果A⇔B，则A，B互为充分必要条件．解题时*容易出错的就是颠倒了充分性与必要性，所以在解决这类问题时一定要根据充分条件和必要条件的概念作出准确的判断。

05.“或”“且”“非”理解不准致误命题p∨q真⇔p真或q真，命题p∨q假⇔p假且q假(概括为一真即真)；命题p∧q真⇔p真且q真，命题p∧q假⇔p假或q假(概括为一假即假)；綈p真⇔p假，綈p假⇔p真(概括为一真一假)．求参数取值范围的题目，也可以把“或”“且”“非”与集合的“并”“交”“补”对应起来进行理解，通过集合的运算求解。

二、不等式的解法三、函数底数与图像位置关系：在第一象限指数函数是“底大图高”对数函数是“底大图低”【易错提醒】01.函数的单调区间理解不准致误在研究函数问题时要时时刻刻想到“函数的图像”，学会从函数图像上去分析问题、寻找解决问题的方法．对于函数的几个不同的单调递增(减)区间，切忌使用并集，只要指明这几个区间是该函数的单调递增(减)区间即可。

02.判断函数奇偶性忽略定义域致误判断函数的奇偶性，首先要考虑函数的定义域，一个函数具备奇偶性的必要条件是这个函数的定义域关于原点对称，如果不具备这个条件，函数一定是非奇非偶函数。

集合与简易逻辑高中数学知识点有哪些集合与简易逻辑高中数学知识点1.集合的元素具有确定性、无序性和互异性.2.对集合，时，必须注意到“极端”情况：或;求集合的子集时是否注意到是任何集合的子集、是任何非空集合的真子集.3.判断命题的真假关键是“抓住关联字词”;注意：“不‘或’即‘且’，不‘且’即‘或’”.4.“或命题”的真假特点是“一真即真，要假全假”;“且命题”的真假特点是“一假即假，要真全真”;“非命题”的真假特点是“一真一假”.5.四种命题中“‘逆’者‘交换’也”、“‘否’者‘否定’也”.原命题等价于逆否命题，但原命题与逆命题、否命题都不等价.反证法分为三步：假设、推矛、得果.8.充要条件高中数学考试技巧掌握时间由于，基础中考能力，所以要注重解题的快法和巧法，能在30分钟左右，完成全部的选择填空题，这是夺取高分的关键。

在平时当中一定要求自己选择填空一分钟一道题。

用数学思想方法高速解答选择填空题。

先易后难所以，只做选择，填空和前三道大题是不够全面的。

因为，后“三难”题中的容易部分比前面的基础部分还要容易，所以我们应该志在必得。

在复习的时候，根据自己的情况，如果基础较好那首先争取选择，填空前三道大题得满分。

然后，再提高解答“三难”题的能力，争取“三难”题得分20分到30分。

这样，你的总分就可以超过130分，向145分冲刺。

后三题尽量多得分第二段是解答题的前三题，分值不到40分。

这样前两个阶段的总分在110分左右。

第三段是最后“三难”题，分值不到40分。

“三难”题并不全难，难点的分值只有12分到18分，平均每道题只有4分到6分。

首先，应在“三难”题中夺得12分到20分，剩下最难的步骤分在努力争取。

后3题不是只做第一问的问题，而应该猜想评分标准，按步骤由前向后争取高分。

高中数学怎么快速提分1、加强学法指导，培养良好的学习习惯，良好的学习习惯包括制定计划、课前自学、专心上课、及时复习、独立作业、解决疑难、系统小结和课外学习的几个方面。

高中数学易错知识点梳理高中数学易错知识点梳理数学是人们生活中不可缺少的一部分。

以下是店铺为大家整理的高中数学易错知识点，希望可以解决您所遇到的相关问题，加油，店铺直陪伴您。

集合与简单逻辑第一、遗忘空集是任何非空集合的真子集，因此对于集合B，就有B=A、φ≠B、B≠φ三种情况出现。

在实际解题中，如果考生思维不够缜密，就有可能忽视第三种情况，导致结果出错。

尤其是在解含有参数的集合问题时，要充分注意当参数在某个范围内取值时所给的集合可能是空集这种情况。

空集是一个特殊集合，考生因思维定式遗忘集合导致结果出错或不全面是常见的错误，一定要倍加当心。

第二、忽视集合元素的三性集合元素具有确定性、无序性、互异性的特点，在三性中，数互异性对答题的影响最大，尤其是带有字母参数的集合，实际上就隐含着对考生字母参数掌握程度的要求。

在考场答题时，考生可先确定字母参数的范围，再一一具体解决。

第三、四种命题结构不明若原命题为“若A则B”，则逆命题是“若B则A”，否命题是“若┐A则┐B”，逆否命题是“若┐B则┐A”。

这里将会出现两组等价的命题：“原命题和它的逆否命题等价”，“否命题与逆命题等价”。

考生在遇到“由某一个命题写出其他形式命题”的题型时，要首先明确四种命题的结构以及它们之间的等价关系。

在否定一个命题时，要记住“全称命题的否定是特称命题，特称命题的否定是全称命题”的规律。

如对“a，b都是偶数”的否定应该是“a，b不都是偶数”，不是“a ，b都是奇数”。

第四、充分必要条件颠倒两个条件A与B，若A=>B成立，则A 是B的充分条件，B是A的必要条件;若B=>A成立，则A是B的必要条件，B是A的充分条件;若A<=>B，则AB互为充分必要条件。

考生在解这类题时最容易出错的点就是颠倒了充分性与必要性，一定要根据充要条件的概念作出准确的判断。

函数与导数第一、求函数定义域题忽视细节函数的定义域是使函数有意义的自变量的取值范围，考生想要在考场上准确求出定义域，就要根据函数解析式把各种情况下的自变量的限制条件找出来，列成不等式组，不等式组的解集就是该函数的定义域。

(名师选题)（精选试题附答案）高中数学第一章集合与常用逻辑用语易错知识点总结单选题1、已知x∈R，则“(x−2)(x−3)≤0成立”是“|x−2|+|x−3|=1成立”的（）条件．A．充分不必要B．必要不充分C．充分必要D．既不充分也不必要答案：C分析：先证充分性，由（x−2）(x−3）≤0求出x的取值范围，再根据x的取值范围化简|x−2|+|x−3|即可，再证必要性，若|x−2|+|x−3|=1，即|x−2|+|x−3|=|（x−2）−（x−3）|，再根据绝对值的性质可知（x−2）(x−3）≤0．充分性：若（x−2）(x−3）≤0，则2≤x≤3，∴|x−2|+|x−3|=x−2+3−x=1，必要性：若|x−2|+|x−3|=1，又∵|（x−2）−（x−3）|=1，∴|x−2|+|x−3|=|（x−2）−（x−3）|，由绝对值的性质：若ab≤0，则|a|+|b|=|a−b|，∴（x−2）(x−3）≤0，所以“（x−2）(x−3）≤0成立”是“|x−2|+|x−3|=1成立”的充要条件，故选：C．2、已知集合M={x|x=m−56,m∈Z}，N={x|x=n2−13,n∈Z}，P={x|x=p2+16,p∈Z}，则集合M，N，P的关系为（）A．M=N=P B．M⊆N=PC．M⊆N⊈P D．M⊆N，N∩P=∅答案：B分析：对集合M,N,P中的元素通项进行通分，注意3n-2与3p+1都是表示同一类数，6m-5表示的数的集合是前者表示的数的集合的子集，即可得到结果.对于集合M={x|x=m-56,m∈Z}，x=m-56=6m-56=6(m-1)+16，对于集合N={x|x=n2-13,n∈Z}，x=n2-13=3n-26=3(n-1)+16，对于集合P={x|x=p2+16,p∈Z}，x=p2+16=3p+16，由于集合M,N,P中元素的分母一样，只需要比较其分子即可，且m,n,p∈Z，注意到3(n-1)+1与3p+1表示的数都是3的倍数加1，6(m-1)+1表示的数是6的倍数加1，所以6(m-1)+1表示的数的集合是前者表示的数的集合的子集，所以M∈N=P.故选：B.3、已知集合A={x|ax2+2x+1=0,a∈R}只有一个元素，则a的取值集合为（）A．{1}B．{0}C．{0,−1,1}D．{0,1}答案：D分析：对参数分类讨论，结合判别式法得到结果.解：①当a=0时，A={−12}，此时满足条件；②当a≠0时，A中只有一个元素的话，∆=4−4a=0，解得a=1，综上，a的取值集合为{0，1}．故选：D．4、设集合A={−1,0,1,2}，B={1,2}，C={x|x=ab,a∈A,b∈B}，则集合C中元素的个数为（）A．5B．6C．7D．8答案：B分析：分别在集合A,B中取a,b，由此可求得x所有可能的取值，进而得到结果.当a=−1，b=1时，ab=−1；当a=−1，b=2时，ab=−2；当a=0，b=1或2时，ab=0；当a=1，b=1时，ab=1；当a=1，b=2或a=2，b=1时，ab=2；当a=2，b=2时，ab=4；∴C={−2,−1,0,1,2,4}，故C中元素的个数为6个.故选：B.5、已知a∈R，则“a>6”是“a2>36”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件答案：A分析：由充分条件、必要条件的定义判断即可得解.由题意，若a>6，则a2>36，故充分性成立；若a2>36，则a>6或a<−6，推不出a>6，故必要性不成立；所以“a>6”是“a2>36”的充分不必要条件.故选：A.6、已知集合A={−1,0,1,2}，B={x|x2≤1}，则A∩B=（）A．{−1,0,1}B．{0,1}C．{−1,1}D．{0,1,2}答案：A分析：先计算集合B里的不等式，将B所代表的区间计算出来，再根据交集的定义计算即可. 不等式x2≤1，即−1≤x≤1，B=[−1,1]，A={−1,0,1,2}，B={x|−1≤x≤1}，所以A∩B={−1,0,1}；7、设集合A={2,a2−a+2,1−a}，若4∈A，则a的值为（）．A．−1，2B．−3C．−1，−3，2D．−3，2答案：D分析：由集合中元素确定性得到：a=−1，a=2或a=−3，通过检验，排除掉a=−1. 由集合中元素的确定性知a2−a+2=4或1−a=4．当a2−a+2=4时，a=−1或a=2；当1−a=4时，a=−3．当a=−1时，A={2,4,2}不满足集合中元素的互异性，故a=−1舍去；当a=2时，A={2,4,−1}满足集合中元素的互异性，故a=2满足要求；当a=−3时，A={2,14,4}满足集合中元素的互异性，故a=−3满足要求．综上，a=2或a=−3．故选：D．8、已知非空集合A、B、C满足：A∩B⊆C，A∩C⊆B．则（）．A．B=C B．A⊆(B∪C)C．(B∩C)⊆A D．A∩B=A∩C答案：C分析：作出符合题意的三个集合之间关系的venn图即可判断.解：因为非空集合A、B、C满足：A∩B⊆C，A∩C⊆B，作出符合题意的三个集合之间关系的venn图，如图所示，所以A∩B=A∩C．9、“a=0”是关于x的不等式ax−b≥1的解集为R的（）A．充分非必要条件B．必要非充分条件C．充要条件D．非充分非必要条件答案：B分析：取a=0，b=1时可判断充分性；当不等式ax−b≥1的解集为R时，分a>0，a<0，a=0讨论可判断必要性.若a=0，取b=1时，不等式ax−b≥1⇔−1≥1，此时不等式解集为∅；}，当a>0时，不等式ax−b≥1的解集为{x|x≥b+1a}，当a<0时，不等式ax−b≥1的解集为{x|x≤b+1a当a=0，且b≤−1时，不等式ax−b≥1⇔−b≥1⇔b≤−1，所以，若关于x的不等式ax−b≥1的解集为R，则a=0.综上，“a=0”是关于x的不等式ax−b≥1的解集为R的必要非充分条件.故选：B10、命题∃x∈R,x2+1≤0的否定是（）A．∀x∈R，x2+1>0B．∃x∈R，x2+1>0C．∀x∈R，x2+1≥0D．∃x∈R，x2+1≥0答案：A分析：根据特称命题的否定形式直接求解.特称命题的否定是全称命题，即命题“∃x∈R,x2+1≤0”的否定是“∀x∈R,x2+1>0”.故选：A填空题11、已知[x]表示不超过x的最大整数.例如[2.1]=2，[−1.3]=−2，[0]=0，若A={y∣y=x−[x]}，B={y∣0≤y≤m}，y∈A是y∈B的充分不必要条件，则m的取值范围是______.答案：[1,+∞)分析：由题可得A={y∣y=x−[x]}=[0,1)，然后利用充分不必要条件的定义及集合的包含关系即求.∵[x]表示不超过x的最大整数，∴[x]≤x，0≤x−[x]<1，即A={y∣y=x−[x]}=[0,1)，又y∈A是y∈B的充分不必要条件，B={y∣0≤y≤m}，∴A⊊B，故m≥1，即m的取值范围是[1,+∞).所以答案是：[1,+∞).12、设集合A={−1,1,3}，B={a+2,a2+4}，A∩B={3}.则实数a=_______.答案：1分析：由A∩B={3}可得3∈A,3∈B，从而得到a+2=3，即可得到答案.因为A∩B={3}，所以3∈A,3∈B，显然a2+4≠3，所以a+2=3，解得：a=1.所以答案是：1.小提示：本题考查利用集合的基本运算求参数值，考查逻辑推理能力和运算求解能力，属于基础题.13、满足{1}⊆A{1，2，3}的所有集合A是___________．答案：{1}或{1，2}或{1，3}分析：由题意可得集合A中至少有一个元素1，且为集合{1，2，3}的真子集，从而可求出集合A因为{1}⊆A{1，2，3}，所以集合A中至少有一个元素1，且为集合{1，2，3}的真子集，所以集合A是{1}或{1，2}或{1，3}，所以答案是：{1}或{1，2}或{1，3}14、已知命题“存在x∈R，使ax2−x+2≤0”是假命题，则实数a的取值范围是___________.答案：a>18分析：转化为命题“∀x∈R，使得ax2−x+2>0”是真命题，根据二次函数知识列式可解得结果. 因为命题“存在x∈R，使ax2−x+2≤0”是假命题，所以命题“∀x∈R，使得ax2−x+2>0”是真命题，当a=0时，得x<2，故命题“∀x∈R，使得ax2−x+2>0”是假命题，不合题意；当a≠0时，得{a>0Δ=1−8a<0，解得a>1 8 .所以答案是：a>18小提示：关键点点睛：转化为命题“∀x∈R，使得ax2−x+2>0”是真命题求解是解题关键.15、已知集合A={x|x≥4或x<−5}，B={x|a+1≤x≤a+3}，若B⊆A，则实数a的取值范围_________．答案：{a|a<−8或a≥3}分析：根据B⊆A，利用数轴，列出不等式组，即可求出实数a的取值范围.用数轴表示两集合的位置关系，如上图所示，或要使B⊆A，只需a+3<−5或a+1≥4，解得a<−8或a≥3．所以实数a的取值范围{a|a<−8或a≥3}.所以答案是：{a|a<−8或a≥3}解答题16、在①x ∈A 是x ∈B 的充分不必要条件；②A ∪B =B ；③A ∩B =∅这三个条件中任选一个，补充到本题第（2）问的横线处，求解下列问题：已知集合A ={x |a −1≤x ≤a +1 }，B ={x |−1≤x ≤3 }．(1)当a =2时，求A ∪B ；(2)若选______，求实数a 的取值范围．答案：(1)A ∪B ={x |−1≤x ≤3 }(2)条件选择见解析，答案见解析分析：（1）利用并集的定义可求得集合A ∪B ；（2）选①，可得出AB ，根据题意可得出关于实数a 的不等式组，由此可求得实数a 的取值范围；选②，可得出A ⊆B ，根据题意可得出关于实数a 的不等式组，由此可求得实数a 的取值范围；选③，由题意可得出关于实数a 的不等式，解之即可.（1）解：当a =2时，A ={x |1≤x ≤3 }，则A ∪B ={x |−1≤x ≤3 }.（2）解：选①，由题意可知AB ，则{a −1≥−1a +1≤3，解得0≤a ≤2， 当a =0时，A ={x |−1≤x ≤1 }B ，合乎题意，当a =2时，A ={x |1≤x ≤3 }B ，合乎题意.综上所述，0≤a ≤2；选②，由题意可知A ⊆B ，则{a −1≥−1a +1≤3，解得0≤a ≤2， 所以，0≤a ≤2；选③，A ∩B =∅，则a +1<−1或a −1>3，解得a <−2或a >4.所以，a <−2或a >4.17、已知p:A ={x|x <−2或x >10},q:B ={x|x <1−m 或x >1+m,m >0}，若p 是q 的必要不充分条件，求实数m 的取值范围.答案：{m|m≥9}.分析：由题设p、q间的关系可得B⊂≠A，根据集合A、B的描述列方程组求m的参数即可. 由p是q的必要不充分条件，所以B⊂≠A，则{m>01−m⩽−21+m>10或{m>01−m<−21+m⩾10，解得：m⩾9.∴m的取值范围是{m|m≥9}.18、集合A={x|−1≤x≤2}，B={x|x<a}．（1）若A∩B=A，求实数a的取值范围；（2）若A∩B=∅，求实数a的取值范围．答案：（1）a>2；（2）a≤−1解析：（1）由A∩B=A，可得A⊆B，即可列出不等关系，求出a的取值范围；（2）由A∩B=∅，且B≠∅，可列出不等关系，求出a的取值范围.（1）由集合A={x|−1≤x≤2}，B={x|x<a}，因为A∩B=A，所以A⊆B，则a>2，即实数a的取值范围为a>2.（2）因为A∩B=∅，且B≠∅，所以a≤−1，故实数a的取值范围为a≤−1.19、已知集合{a，ba，1}与集合{a2，a+b，0}是两个相等的集合，求a2020+b2020的值. 答案：a2020+b2020=1分析：先由集合相等及集合中元素的互异性求出a、b，代入求值即可.由a，ba ，1组成一个集合，可知a≠0，a≠1，由题意可得ba＝0，即b＝0，此时两集合中的元素分别为a，0，1和a2，a，0，因此a2＝1，解得a＝－1(a＝1不满足集合中元素的互异性，舍去)，因此a＝－1，且b＝0，所以a2020＋b2020＝(－1)2020＋0＝1.。

高中数学的易错知识点归纳关于高中数学的易错知识点归纳集合与简单逻辑1易错点遗忘空集致误错因分析：由于空集是任何非空集合的真子集，因此，对于集合B,就有B=A,φ≠B,B≠φ，三种情况，在解题中如果思维不够缜密就有可能忽视了B≠φ这种情况，导致解题结果错误。

尤其是在解含有参数的集合问题时，更要充分注意当参数在某个范围内取值时所给的集合可能是空集这种情况。

空集是一个特殊的集合，由于思维定式的原因，考生往往会在解题中遗忘了这个集合，导致解题错误或是解题不全面。

2易错点忽视集合元素的三性致误错因分析：集合中的元素具有确定性、无序性、互异性，集合元素的三性中互异性对解题的影响最大，特别是带有字母参数的集合，实际上就隐含着对字母参数的一些要求。

在解题时也可以先确定字母参数的范围后，再具体解决问题。

3易错点四种命题的结构不明致误错因分析：如果原命题是“若A则B”，则这个命题的逆命题是“若B则A”，否命题是“若┐A则┐B”，逆否命题是“若┐B则┐A”。

另外，在否定一个命题时，要注意全称命题的否定是特称命题，特称命题的否定是全称命题。

如对“a,b都是偶数”的否定应该是“a,b不都是偶数”，而不应该是“a,b都是奇数”。

4易错点充分必要条件颠倒致误错因分析：对于两个条件A,B,如果A=>B成立，则A是B的充分条件，B是A的必要条件；如果B=>A成立，则A是B的必要条件，B是A的充分条件；如果A<=>B,则A,B互为充分必要条件。

解题时最容易出错的就是颠倒了充分性与必要性，所以在解决这类问题时一定要根据充要条件的概念作出准确的判断。

5易错点逻辑联结词理解不准致误错因分析：在判断含逻辑联结词的命题时很容易因为理解不准确而出现错误，在这里我们给出一些常用的判断方法，希望对大家有所帮助：p∨q真<=>p真或q真，p∨q假<=>p假且q假(概括为一真即真)；p∧q真<=>p真且q真，p∧q假<=>p假或q假(概括为一假即假)；┐p真<=>p假，┐p假<=>p真(概括为一真一假)。

例谈高考数学常考、易错、失分点--集合简易逻辑篇【易错点1】有关集合的常见错误例1、已知21|23A x y x x ⎧⎫==⎨⎬-++⎩⎭，{}|B x x P =<，若B A ，则实数P 的取值范围是（）A 、(]0,1B 、(],1-∞C 、(]1,3-D 、(),1-∞【易错点诊断】解类此题最常见的错误就是一方面易忽略空集这种特殊情况，而直接将集合B 化简为{}|x p x P -<<进行解答，另一方面解答集合问题特别是利用数轴进行集合运算时易忽视端点值等号是否取到，在解答时要注意这一细节，须知细节决定成败。

解析：据题意可知集合A 表示函数2123y x x =-++的定义域，易化简得{}|13A x x =-<<，由于B A ，故当B φ=时，即0P ≤时易知符合题意；当0p >时，{}|B p x p -<<，要使B A ，结合数轴知需13p p -<-⎧⎨<⎩或1p -=-（经验证符合题意）或3p =（经验证不合题意舍去），解得01P <≤，故综上所述可知满足条件的P 的取值范围是(],1-∞，答案：B【迷津指点】在解答集合一类问题时，特别注意象空集这种特殊集合的讨论、集合中元素的互异性的要求以及利用数轴进行运算时端点值等号是否取得这些易出现错误的方面。

高考中对集合的考查主要集中在对概念及运算的考查上，同时还体现在集合的语言表达（集合语言与自然语言的转化）、符号表示、直观图形（韦恩图）这三方面，要在先“代表元素”后“元素属性”的原则下加以理解与解题；此外还应注意集合与不等式、集事与方程、集合与函数的关系，以体现集合的工具性和它在解决其它数学问题中的作用。

【适用性练习】①设函数()1x a f x x -=-,集合M={|()0}x f x <,P='{|()0}x f x >,若M P,则实数a 的取值范围是 ( )A 、(-∞,1) B 、(0,1) C 、(1,+∞) D 、 [1,+∞)答案:C.②设函数()321x f x x +=-+A,()()()()lg 121g x x a a x a =---<⎡⎤⎣⎦的定义域为B,若B A ⊆,求实数a 的取值范围.答案:2a ≤-或112a ≤<. ③已知集合},2|{},1|{R y y y R x x x M ∈≠⋃∈≠=，集合}2211|{><<<=x x x x P 或或， 则P M 与之间的关系是（ ）A 、P M ⊂B 、M P ⊂C 、M P =D 、φ=⋂P M答案：B 解析：结合数轴解答。

高一数学知识点：集合、不等式和简易逻辑重点知识归纳、总结(1)集合的分类(2)集合的运算①子集，真子集，非空子集;②A∩B={x|x∈A且x∈B}③A∪B={x|x∈A或x∈B}④A={x|x∈S且x A}，其中A S.2、不等式的解法(1)含有绝对值的不等式的解法①|x|0) -a|x|0) xa，或x-a.②|f(x)||f(x)|g(x) f(x)g(x)或f(x)-g(x).③|f(x)||g(x)| [f(x)]2[g(x)]2 [f(x)+g(x)]·[f(x)-g(x)]0.④关于含有两个或两个以上的绝对值符号的绝对值不等式，利用“零点分段讨论法”去绝对值. 如解不等式：|x+3|-|2x-1|3x+2.3、简易逻辑知识逻辑联结词“或”、“且”、“非”是判定简单合题与复合命题的依据;真值表是由简单命题和真假判定复合命题真假的依据，明白得好四种命题的关系，对判定命题的真假有专门大关心;把握好反证法证明问题的步骤。

(2)复合命题的真值表非p形式复合命题的真假能够用下表表示.p 非p真假假真p且q形式复合命题的真假能够用下表表示.p或q形式复合命题的真假能够用下表表示.(3)四种命题及其相互之间的关系一个命题与它的逆否命题是等价的.(4)充分、必要条件的判定①若p q且q p，则p是q的充分不必要条件;②若p q且q p，则p是q的必要不充分条件;与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

金代元好问《示侄孙伯安》诗云：“伯安入小学，颖悟专门貌，属句有夙性，说字惊老师。

”因此看，宋元时期小学教师被称为“老师”有案可稽。

清代称主考官也为“老师”，而一样学堂里的先生则称为“教师”或“教习”。

可见，“教师”一说是比较晚的事了。

现在体会，“教师”的含义比之“老师”一说，具有资历和学识程度上较低一些的差别。

辛亥革命后，教师与其他官员一样依法令任命，故又称“教师”为“教员”。

高中数学易错点梳理一、集合与简易逻辑易错点1 对集合表示方法理解存在偏差【问题】1: 已知A = {x | x > 0}, B = {y y > 1}，求A B 。

错解：A B =Φ剖析：概念模糊，未能真正理解集合的本质。

正确结果：A B =B【问题】2: 已知A = {y | y =x + 2}, B = {(x, y) | x 2 +y 2 = 4} ，求A B 。

错解： A B = {(0, 2), (-2, 0)}正确答案：A B =Φ剖析：审题不慎，忽视代表元素，误认为A 为点集。

反思：对集合表示法部分学生只从形式上“掌握”，对其本质的理解存在误区，常见的错误是不理解集合的表示法，忽视集合的代表元素。

易错点2 在解含参数集合问题时忽视空集【问题】: 已知A = {x | 2a <x <a 2}, B = {x | -2 <x < 1} ，且A ⊆B ，求a 的取值范围。

错解：[-1，0）剖析：忽视A =∅的情况。

正确答案：[-1，2]反思：由于空集是一个特殊的集合，它是任何集合的子集，因此对于集合A ⊆B 就有可能忽视了A =∅，导致解题结果错误。

尤其是在解含参数的集合问题时，更应注意到当参数在某个范围内取值时，所给的集合可能是空集的情况。

考生由于思维定式的原因，往往会在解题中遗忘了这个集合，导致答案错误或答案不全面。

易错点3 在解含参数问题时忽视元素的互异性【问题】: 已知1∈{ a + 2 , (a +1)2 , a2 + 3a +3 }，求实数a 的值。

错解：a =-2, -1, 0剖析：忽视元素的互异性，其实当a =-2 时，(a +1)2 = a2 + 3a + 3 =1；当a =-1时，a + 2 = a2 + 3a + 3 =1；均不符合题意。

正确答案：a = 0反思：集合中的元素具有确定性、互异性、无序性，集合元素的三性中的互异性对解题的影响最大，特别是含参数的集合，实际上就隐含着对字母参数的一些要求。

一、集合概念概念指定的某些对象的全体称为集合元素与集合元素与集合的关系有且仅有两种：属于（∈）或不属于（∉）.元素特性确定性、互异性、无序性常用数集实数集R；有理数集Q；整数集Z；自然数集N；正整数集N*(或N＋)表示方法列举法、描述法基本关系子集A⊆B①空集是任何集合的子集.②空集是任何非空集合的真子集.③若A⊆B，B⊆C，则A⊆C.④A＝B⇔A⊆B且B⊆A.⑤有限集合的子集个数：n个元素的集合有2n个子集；其中有2n－1个真子集；有2n－1个非空子集；有2n－2个非空真子集.真子集A⊂B相等集合A＝B基本运算交集A∩B A∩B＝{x|x∈A且x∈B}A∩B⊆AA∩B⊆BA∩Ø＝Ø并集A∪B A∪B＝{x|x∈A或x∈B}B⊆A∪BA⊆A∪BA∪Ø＝A补集∁U A∁U A＝{x|x∈U且x∉A}A∪(∁U A)＝UA∩(∁U A)＝Ø∁U(∁U A)＝A二、简易逻辑命题概念能够判断真假的语句四种命题原命题：若p，则q逆命题：若q，则p否命题：若¬p，则¬q逆否命题：若¬q，则¬p充要条件充分条件p⇒q，p是q的充分条件若命题p对应集合A，命题q对应集合B，则：p⇒q等价于A⊆B；p⇒q且q⇒p等价于A＝B.必要条件p⇒q，q是p的必要条件充要条件p⇒q且q⇒p，p、q互为充要条件逻辑联结词且命题“p∧q”：一假则假，同真为真.类比集合的“交”或命题“p∨q”：一真则真，同假为假.类比集合的“并”非命题“¬p”：真假相反类比集合的“补”量词全称量词∀，含全称量词的命题叫全称命题，其否定为特称命题.存在量词∃，含存在量词的命题叫特称命题，其否定为全称命题.。

热门题型题型1 集合的基本概念题型2 集合间的基本关系 题型3 集合的运算题型1 集合的基本概念例1 设,a b R ∈，集合{}1,,0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭，则b a -=（ ） A ．1 B ．1- C ．2 D ．2-【解题技巧】利用集合元素的特征：确定性、无序性、互异性．变式 1. 已知集合{}{}1,2,3,4,5,(,)|,A B x y x A y A ==∈∈，则B 中所含元素的个数为（ ）A ．3B ．6C ．8D ．10题型2 集合间的基本关系例2 若{}{}{}|41,,|43,,|81,A x x n n Z B x x n n Z C x x n n Z ==+∈==-∈==+∈，则A ，B ，C 之间的关系为（ ）． A ．CB A B ．A BC ⊆ C ．C A B =D ．A B C ==解析：解法一：集合B 中元素434(1)1,x n n n Z =-=-+∈，故集合A B =，而集合C 中元素421,x n n Z =⨯+∈，故C A ．解法二：列举{}{},7,3,1,5,9,,,7,3,1,5,9,A B =--=--，{},7,1,9,C =-．因此C A B =，故选C ．【解题技巧】判断两集合的关系常用两种方法：一是逻辑分析法，即先化简集合，再从表达式中寻找两集合的关系，即“求同比异”；二是用列举法表示各集合，从元素中寻找关系，即“合情推理”.变式1.（重庆理1）已知集合{}1,2,3A =，{}2,3B =，则（ ）. A.A B = B. A B =∅ C. A B D. B A解析 集合B 的元素2,3A A ∈∈，但是集合A 的元素B ∉1，所以B 是A 的真子集. 故选D.变式2.（湖南理2）设A ，B 是两个集合，则“A B A =”是“A B ⊆”的（ ）.A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件题型3 集合的运算例3 已知集合{}{}22|1,,|9M y y x x R N x y x ==+∈==-，则M N ⋂=（ ） A ．{}|13x x <≤ B ．{}|13x x ≤< C ．{}|13x x ≤≤ D ．{}|14x x << 解析：{}{}2|1,|1M y y x x R y y ==+∈=≥，{}{}22|9|90N x y x x x ==-=-≥，即{}|33N x x =-≤≤，所以{}|13M N x x ⋂=≤≤，故选C.【解题技巧】遇到集合的运算（交、并、补）问题，应注意对集合元素属性的识别，如集合{}|(),y y f x x A =∈是函数的值域，是数集，求出值域可以使之简化；集合{}(,)|(),x y y f x x A =∈是点集，表示函数()y f x =图像上所有点的集合.变式1.（山东理1）设函数24y x =-的定义域A ，函数()ln 1y x =-的定义域为B ，则A B =（ ）A.()1,2B.(]1,2C.()2,1-D.[)2,1- 解析：由240x -，解得22x -，所以[]22A =-，.由10x ->，解得1x <，所以(),1B =-∞.从而{}{}{}=|22|1|21A B x x x x x x -<=-<.故选D.变式2.（全国3理1）已知集合A ={}22(,)1x y x y +=，{}(,)B x y y x ==，则A B 中元素的个数为（ ）.A ．3B ．2C ．1D ．0解析 集合A 表示圆221x y +=上所有点的集合，B 表示直线y x =上所有点的集合，如图所示，所以A B 表示两直线与圆的交点，由图可知交点的个数为2，即A B 元素的个数为2.故选B.y=xx 2+y 2=1yxO【高考真题链接】1.（广东理1）若集合()(){}410M x x x =++=，()(){}410N x x x =--=， 则MN =（ ）.A ．{}1,4B ．{}1,4--C ．{}0D ．∅2.（全国II 理1）已知集合{}2,1,0,2A =--，()(){}120B x x x =-+<，则A B =（ ）． A.{}1,0-B. {}0,1C.{}1,0,1-D. {}0,1,22.解析 对于B 集合，由已知得，{}21B x x =-<<，用数轴可得{}1,0AB =-.故选A.3.(山东理1)已知集合{}2|430A x x x =-+<，{}|24B x x =<<，则A B =（ ）． A.()13，B. ()14，C.()23，D.()24，3.解析 由题意{}13A x x =<<，而{}24B x x =<<，所以{}23A B x x =<<．故选C ． 4.（陕西理1）设集合2{|}M x x x ==，{|lg 0}N x x =，则MN =（ ）． A ．[0,1] B.(0,1] C.[0,1) D.(,1]-∞4.解析 依题意{0,1}M =，{|01}N x x =<，所以{|01}MN x x =.故选A ．5. (四川理1)设集合()(){}120A x x x =+-<，集合{}13B x x =<<，则A B =（ ）.A. {}13x x -<<B. {}11x x -<<C. {}12x x <<D. {}23x x << 5.解析 由题意可得，{}12A x x =-<<，则{}13AB x x =-<<.故选A.6.（天津理1）已知全集{}1,2,3,4,5,6,7,8U = ，集合{}2,3,5,6A = ， 集合{}1,3,4,6,7B = ，则集合UAB =（ ）.A.{}2,5B.{}3,6C. {}2,5,6D.{}2,3,5,6,87.（浙江理1）已知集合2{20},{12}P x x xQ x x=-=<，则()P Q =R （ ）． A.[0,1) B.(0,2] C.(1,2) D.[1,2] 7.解析 依题意{02}P x x x =或，()0,2RP =，所以()R P Q =(1,2)．故选C ．8.(北京理1) 已知集合{}2A x x =<，{}1,0,1,2,3B =-，则A B =（ ）.A.{}0,1B.{}0,1,2C.{}1,0,1-D.{}1,0,1,2-8. C 解析 由已知集合(2,2)A =-，{}1,0,1,2,3B =-，所以A B ={}1,0,1-.故选C.9.（全国丙理1）设集合{}(2)(3)0S x x x =--，{}0T x x =>，则S T =（ ）.A.[]2,3B.(][),23,-∞+∞C.[)3,+∞D.(][)0,23,+∞9. D 解析 由{}{}32,0S x x xT x x ==>或，得S T ={}0<23.x xx或故选D.10.（全国甲理2）已知集合{123}A =，,，{|(1)(2)0}B x x x x =+-<∈Z ，，则A B =（ ）. A.{}1B.{12}，C.{}0123，，，D.{10123}-，，，， 10. C 解析 因为()(){}120B x x x x =+-<∈Z ，{}12x x x =-<<∈Z，，所以{}01B =，，所以{}0123A B =，，，.故选C.11.（山东理2）设集合{|2,}xA y y x ==∈R ，2{|10}B x x =-<，则A B =（ ）.A.(1,1)-B.(0,1)C.(1,)-+∞D.(0,)+∞11. C 解析 由题意，0,11A B =+∞=-（，）（，），所以AB =1+-∞（，）.故选C. 12.（四川理1）设集合{|22}A x x =-，Z 为整数集，则A Z 中元素的个数是（ ）.A.3B.4C.5D.6 12.解析 由题意，{2,1,0,1,2}A=--Z .故其中的元素个数为5.故选C.13.（天津理1）已知集合{1,2,3,4}A =，{|32}B y y x x A ==-∈，，则A B =（ ）.A.{1}B.{4}C.{1,3}D.{1,4}14.（全国乙理1）设集合2{|430}A x x x =-+<，{|230}B x x =->，则A B =（ ）.A.33,2⎛⎫-- ⎪⎝⎭B.33,2⎛⎫- ⎪⎝⎭C.31,2⎛⎫ ⎪⎝⎭D.3,32⎛⎫⎪⎝⎭14.D 解析 由题意可得()1,3A =，3,2B ⎛⎫=+∞⎪⎝⎭，所以3,32A B ⎛⎫= ⎪⎝⎭.故选D. 15.（浙江理1）已知集合{}13P x x =∈R ≤≤，{}24Q x x =∈R ≥，则()P Q =R（ ）.A.[]2,3B.(]2,3-C.[)1,2D.(,2][1,)-∞-+∞ 15.B 解析 因为{}24Q x x=∈R ，所以{}24(2,2)Q x x =<=-R，所以[](]()(2,2)1,32,3Q P =-=-R .故选B.16.（江苏1）已知集合{}1,2,3,6A =-，{}23B x x =-<<，则A B = .16.{}1,2- 解析 由交集的运算法则可得{}1,2A B =-.17.（上海理1）设x ∈R ，则不等式31x -<的解集为 .17.()2,4 解析 由题意131x -<-<，即24x <<，则解集为()2,4.18.（江苏01）已知集合{}1,2A =，{}2,3B a a =+，若{}1A B =，则实数a 的值为 ．18.解析 由题意233a +，故由{}1AB =，得1a =．故填1．19.（天津理1）设集合{}1,2,6A =，{}2,4B =，{}|15C x x =∈-R ，则()A B C =（ ）.A.{}2B.{}1,2,4C.{}1,2,4,6D.{}|15x x ∈-R 19.解析 因为{1,2,6},{2,4}A B ==，所以{1,2,6}{2,4}{1,2,4,6}A B ==，从而(){1,2,4,6}[1,5]{1,2,4}AB C =-=.故选B ．20.(北京理1)若集合{}–2<1A x x =<，{}–13B x x x =<>或，则A B =（ ）.A.{}–2<1x x <- B.{}–2<3x x < C.{}–1<1x x <D.{}1<3x x <20.解析 画出数轴图如图所示，则{}21AB x x =-<<-.故选A.31-1-221.（全国1理1）已知集合{}1A x x =<，{}31xB x =<，则（ ）. A. {}0AB x x =< B. A B =R C. {}1A B x x => D. A B =∅21.解析 {}1A x x =<，{}{}310x B x x x =<=<，所以{}0AB x x =<，{}1AB x x =<.故选A.22.（全国2理2）设集合{}1,2,4A =，{}240B x x x m =-+=.若1AB =，则B =（ ）. A ．{}1,3- B ．{}1,0 C ．{}1,3 D ．{}1,523.(浙江理1)已知集合{}11P x x =-<<，{}02Q x x =<<，那么P Q =（ ）.A.()1,2-B.()01，C.()1,0-D.()1,223.解析P Q是取,P Q集合的所有元素，即12x-<<.故选A．。