Fractional Quantum Hall States in Graphene

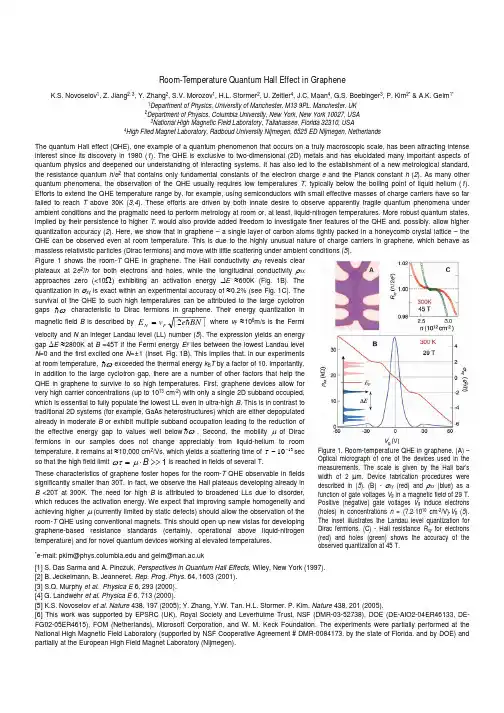
Room -Temperature Quantum Hall Effect in GrapheneK.S. Novoselov 1, Z. Jiang 2, 3, Y. Zhang 2, S.V. Morozov 1, H.L. Stormer 2, U. Zeitler 4, J.C. Maan 4, G.S. Boebinger 3, P. Kim 2* & A.K. Geim 1*1Department of Physics, University of Manchester, M13 9PL, Manchester, UK2Department of Physics, Columbia University, New York, New York 10027, USA3National High Magnetic Field Laboratory, Tallahassee, Florida 32310, USA4High Filed Magnet Laboratory, Radboud University Nijmegen, 6525 ED Nijmegen, NetherlandsThe quantum Hall effect (QHE), one example of a quantum phenomenon that occurs on a truly macroscopic scale, has been attracting intense interest since its discovery in 1980 (1). The QHE is exclusive to two-dimensional (2D) metals and has elucidated many important aspects of quantum physics and deepened our understanding of interacting systems. It has also led to the establishment of a new metrological standard, the resistance quantum h /e 2 that contains only fundamental constants of the electron charge e and the Planck constant h (2). As many other quantum phenomena, the observation of the QHE usually requires low temperatures T , typically below the boiling point of liquid helium (1). Efforts to extend the QHE temperature range by, for example, using semiconductors with small effective masses of charge carriers have so far failed to reach T above 30K (3,4). These efforts are driven by both innate desire to observe apparently fragile quantum phenomena under ambient conditions and the pragmatic need to perform metrology at room or, at least, liquid-nitrogen temperatures. More robust quantum states, implied by their persistence to higher T , would also provide added freedom to investigate finer features of the QHE and, possibly, allow higher quantization accuracy (2). Here, we show that in graphene – a single layer of carbon atoms tightly packed in a honeycomb crystal lattice – the QHE can be observed even at room temperature. This is due to the highly unusual nature of charge carriers in graphene, which behave as massless relativistic particles (Dirac fermions) and move with little scattering under ambient conditions (5).Figure 1 shows the room-T QHE in graphene. The Hall conductivity σxy reveals clearplateaux at 2e 2/h for both electrons and holes, while the longitudinal conductivity ρxxapproaches zero (<10Ω) exhibiting an activation energy ∆E ≈600K (Fig. 1B). Thequantization in σxy is exact within an experimental accuracy of ≈0.2% (see Fig. 1C). Thesurvival of the QHE to such high temperatures can be attributed to the large cyclotrongaps ωh characteristic to Dirac fermions in graphene. Their energy quantization inmagnetic field B is described by |2|BN e v E F N h = where v F ≈106m/s is the Fermivelocity and N an integer Landau level (LL) number (5). The expression yields an energygap ∆E ≈2800K at B =45T if the Fermi energy E F lies between the lowest Landau levelN =0 and the first excited one N =±1 (inset, Fig. 1B). This implies that, in our experimentsat room temperature, ωh exceeded the thermal energy k B T by a factor of 10. Importantly,in addition to the large cyclotron gap, there are a number of other factors that help theQHE in graphene to survive to so high temperatures. First, graphene devices allow forvery high carrier concentrations (up to 1013 cm -2) with only a single 2D subband occupied,which is essential to fully populate the lowest LL even in ultra-high B . This is in contrast totraditional 2D systems (for example, GaAs heterostructures) which are either depopulatedalready in moderate B or exhibit multiple subband occupation leading to the reduction ofthe effective energy gap to values well below ωh . Second, the mobility µ of Diracfermions in our samples does not change appreciably from liquid-helium to roomtemperature. It remains at ≈10,000 cm 2/Vs, which yields a scattering time of 1310~−τsecso that the high field limit 1>>⋅=B µωτ is reached in fields of several T.These characteristics of graphene foster hopes for the room-T QHE observable in fieldssignificantly smaller than 30T. In fact, we observe the Hall plateaus developing already inB <20T at 300K. The need for high B is attributed to broadened LLs due to disorder,which reduces the activation energy. We expect that improving sample homogeneity andachieving higher µ (currently limited by static defects) should allow the observation of theroom-T QHE using conventional magnets. This should open up new vistas for developing graphene-based resistance standards (certainly, operational above liquid-nitrogen temperature) and for novel quantum devices working at elevated temperatures. *e-mail: pkim@ and geim@[1] S. Das Sarma and A. Pinczuk, Perspectives in Quantum Hall Effects , Wiley, New York (1997).[2] B. Jeckelmann, B. Jeanneret. Rep. Prog. Phys. 64, 1603 (2001).[3] S.Q. Murphy et al . Physica E 6, 293 (2000).[4] G. Landwehr et al. Physica E 6, 713 (2000).[5] K.S. Novoselov et al . Nature 438, 197 (2005); Y. Zhang, Y.W. Tan, H.L. Stormer, P. Kim. Nature 438, 201 (2005).[6] This work was supported by EPSRC (UK), Royal Society and Leverhulme Trust, NSF (DMR-03-52738), DOE (DE-AIO2-04ER46133, DE-FG02-05ER4615), FOM (Netherlands), Microsoft Corporation, and W. M. Keck Foundation. The experiments were partially performed at the National High Magnetic Field Laboratory (supported by NSF Cooperative Agreement # DMR-0084173, by the state of Florida, and by DOE) and partially at the European High Field Magnet Laboratory (Nijmegen).Figure 1. Room-temperature QHE in graphene. (A ) – Optical micrograph of one of the devices used in the measurements. The scale is given by the Hall bar’s width of 2 µm. Device fabrication procedures were described in (5). (B ) - σxy (red) and ρxx (blue) as a function of gate voltages V g in a magnetic field of 29 T. Positive (negative) gate voltages V g induce electrons (holes) in concentrations n = (7.2⋅1010 cm -2/V)⋅V g (5). The inset illustrates the Landau level quantization for Dirac fermions. (C ) - Hall resistance R xy for electrons (red) and holes (green) shows the accuracy of the observed quantization at 45 T.。

Quantum Hall effectFrom Wikipedia, the free encyclopediaThe quantum Hall effect (or integer quantum Hall effect) is a quantum-mechanical version of the Hall effect, observed in two-dimensional electron systems subjected to low temperatures and strong magnetic fields, in which the Hall conductance G undergoes certain quantum Hall transitions to take on the quantized valueswhere is the channel current, is the Hall voltage, e is the elementary charge and h is Planck's constant. The prefactor ν is known as the "filling factor", and can take on either integer (ν = 1, 2, 3, .. ) or fractional (ν = 1/3, 2/5, 3/7, 2/3, 3/5, 1/5, 2/9, 3/13, 5/2, 12/5 ...) values. The quantum Hall effect is referred to as the integer or fractional quantum Hall effect depending on whether ν is an integer or fraction respectively. The integer quantum Hall effect is very well understood, and can be simply explained in terms of single-particle orbitals of an electron in a magnetic field (see Landau quantization). The fractional quantum Hall effect is more complicated, as its existence relies fundamentally on electron–electron interactions. It is also very well understood as an integer quantum Hall effect, not of electrons but of charge-flux composites known as composite fermions. In 1988, it was proposed that there was quantum Hall effect without Landau levels. This quantum Hall effect is referred to as the quantum anomalous Hall (QAH) effect. There is also a new concept of the quantum spin Hall effect which is an analogue of the quantum Hall effect, where spin currents flow instead of charge currents.[1]Contents◾1 Applications◾2 History◾3 Integer quantum Hall effect – Landau levels◾4 Mathematics◾5 See also◾6 References◾7 Further readingApplicationsThe quantization of the Hall conductance has the important property of being incredibly precise. Actual measurements of the Hall conductance have been found to be integer or fractional multiples of e2/h to nearly one part in a billion. This phenomenon, referred to as "exact quantization", has been shown to be a subtle manifestation of the principle of gauge invariance.[2] It has allowed for the definition of a new practical standard for electrical resistance, based on the resistance quantum givenby the von Klitzing constant R K = h/e2 = 25812.807557(18) Ω.[3] This is named after Klaus von Klitzing, the discoverer of exact quantization. Since 1990, a fixed conventional value R K-90 is used in resistance calibrations worldwide.[4] The quantum Hall effect also provides an extremely precise independent determination of the fine structure constant, a quantity of fundamental importance in quantum electrodynamics.HistoryThe integer quantization of the Hall conductance was originally predicted by Ando, Matsumoto, and Uemura in 1975, on the basis of an approximate calculation which they themselves did not believe to be true. Several workers subsequently observed the effect in experiments carried out on the inversion layer of MOSFETs. It was only in 1980 that Klaus von Klitzing, working at the high magnetic field laboratory in Grenoble with silicon-based samples developed by Michael Pepper and Gerhard Dorda, made the unexpected discovery that the Hall conductivity was exactly quantized. For this finding, von Klitzing was awarded the 1985 Nobel Prize in Physics. The link between exact quantization and gauge invariance was subsequently found by Robert Laughlin. Most integer quantum Hall experiments are now performed on gallium arsenide heterostructures, although many other semiconductor materials can be used. In 2007, the integer quantum Hall effect was reported in graphene at temperatures as high as room temperature,[5] and in the oxide ZnO-Mg x Zn1-x O.[6] Integer quantum Hall effect – Landau levelsIn two dimensions, when classical electrons are subjected to a magnetic field they follow circular cyclotron orbits. When the system is treated quantum mechanically, these orbits are quantized. The energy levels of these quantized orbitals take on discrete values: , where ωc = eB/m is the cyclotron frequency. These orbitals are known as Landau levels, and at weak magnetic fields, their existence gives rise to many interesting "quantum oscillations" such as the Shubnikov–de Haas oscillations and the de Haas–van Alphen effect (which is often used to map the Fermi surface of metals). For strong magnetic fields, each Landau level is highly degenerate (i.e. there are many single particle states which have the same energy E n). Specifically, for a sample of area A, inmagnetic field B, the degeneracy of each Landau level is (where g s represents a factor of 2 for spin degeneracy, and is the magnetic flux quantum). ForHofstadter's butterfly sufficiently strong B-fields, each Landau level may have so many states that all of the free electrons in the system sit in only a few Landau levels; it is in this regime where one observes the quantum Hall effect.MathematicsThe integers that appear in the Hall effect are examples oftopological quantum numbers. They are known inmathematics as the first Chern numbers and are closelyrelated to Berry's phase. A striking model of much interest inthis context is the Azbel-Harper-Hofstadter model whosequantum phase diagram is the Hofstadter butterfly shown inthe figure. The vertical axis is the strength of the magneticfield and the horizontal axis is the chemical potential, whichfixes the electron density. The colors represent the integer Hall conductances. Warm colors represent positive integersand cold colors negative integers. The phase diagram isfractal and has structure on all scales. In the figure there is an obvious self-similarity.Concerning physical mechanisms, impurities and/or particular states (e.g., edge currents) are important for both the 'integer' and 'fractional' effects. In addition, Coulomb interaction is also essential in the fractional quantum Hall effect. The observed strong similarity between integer and fractional quantum Hall effects is explained by the tendency of electrons to form bound states with an even number of magnetic flux quanta, called composite fermions .See also◾quantum Hall transitions◾Fractional quantum Hall effect◾Composite fermions◾Hall effect◾Hall probe◾Graphene◾Quantum spin Hall effect◾Coulomb potential between two current loops embedded in a magnetic fieldReferences1.^ Ezawa, Zyun F. (2013). Quantum Hall Effects: Recent Theoretical and Experimental Developments (3rd ed.). World Scientific. ISBN 978-981-4360-75-3.2.^ Laughlin, R. (1981). "Quantized Hall conductivity in twodimensions" (/abstract/PRB/v23/i10/p5632_1). Physical Review B 23 (10): 5632–5633. Bibcode:1981PhRvB..23.5632L (/abs/1981PhRvB..23.5632L).doi:10.1103/PhysRevB.23.5632 (/10.1103%2FPhysRevB.23.5632). Retrieved 8 May 2012.3.^ Tzalenchuk, Alexander; Lara-Avila, Samuel; Kalaboukhov, Alexei; Paolillo, Sara; Syväjärvi, Mikael;Yakimova, Rositza; Kazakova, Olga; Janssen, T. J. B. M.; Fal'ko, Vladimir; Kubatkin, Sergey (2010)."Towards a quantum resistance standard based on epitaxialgraphene" (/nnano/journal/v5/n3/abs/nnano.2009.474.html). NatureNanotechnology5 (3): 186–189. arXiv:0909.1220 (https:///abs/0909.1220).Bibcode:2010NatNa...5..186T (/abs/2010NatNa...5..186T).doi:10.1038/nnano.2009.474 (/10.1038%2Fnnano.2009.474). PMID 20081845(https:///pubmed/20081845).4.^ "conventional value of von Klitzing constant" (/cgi-bin/cuu/Value?rk90). NIST.5.^ Novoselov, K. S.; Jiang, Z.; Zhang, Y.; Morozov, S. V.; Stormer, H. L.; Zeitler, U.; Maan, J. C.;Boebinger, G. S.; Kim, P.; Geim, A. K. (2007). "Room-Temperature Quantum Hall Effect in Graphene".Science315 (5817): 1379. arXiv:cond-mat/0702408 (https:///abs/cond-mat/0702408).Bibcode:2007Sci...315.1379N (/abs/2007Sci...315.1379N).doi:10.1126/science.1137201 (/10.1126%2Fscience.1137201). PMID 17303717(https:///pubmed/17303717).6.^ Tsukazaki, A.; Ohtomo, A.; Kita, T.; Ohno, Y.; Ohno, H.; Kawasaki, M. (2007). "Quantum Hall Effectin Polar Oxide Heterostructures". Science315 (5817): 1388–91. Bibcode:2007Sci...315.1388T(/abs/2007Sci...315.1388T). doi:10.1126/science.1137430(/10.1126%2Fscience.1137430). PMID 17255474(https:///pubmed/17255474).Further reading◾Ando, Tsuneya; Matsumoto, Yukio; Uemura, Yasutada (1975). "Theory of Hall Effect in a Two-Dimensional Electron System". J. Phys. Soc. Jpn.39 (2): 279–288.Bibcode:1975JPSJ...39..279A (/abs/1975JPSJ...39..279A).doi:10.1143/JPSJ.39.279 (/10.1143%2FJPSJ.39.279).◾Klitzing, K.; Dorda, G.; Pepper, M. (1980). "New Method for High-Accuracy Determination of the Fine-Structure Constant Based on Quantized Hall Resistance". Phys. Rev. Lett.45 (6): 494–497. Bibcode:1980PhRvL..45..494K(/abs/1980PhRvL..45..494K). doi:10.1103/PhysRevLett.45.494(/10.1103%2FPhysRevLett.45.494).◾Laughlin, R. B. (1981). "Quantized Hall conductivity in two dimensions". Phys. Rev. B.23(10): 5632–5633. Bibcode:1981PhRvB..23.5632L(/abs/1981PhRvB..23.5632L). doi:10.1103/PhysRevB.23.5632(/10.1103%2FPhysRevB.23.5632).◾Yennie, D. R. (1987). "Integral quantum Hall effect for nonspecialists". Rev. Mod. Phys.59(3): 781–824. Bibcode:1987RvMP...59..781Y(/abs/1987RvMP...59..781Y). doi:10.1103/RevModPhys.59.781(/10.1103%2FRevModPhys.59.781).◾Hsieh, D.; Qian, D.; Wray, L.; Xia, Y.; Hor, Y. S.; Cava, R. J.; Hasan, M. Z. (2008). "A topological Dirac insulator in a quantum spin Hall phase". Nature452 (7190): 970–974.arXiv:0902.1356 (https:///abs/0902.1356). Bibcode:2008Natur.452..970H(/abs/2008Natur.452..970H). doi:10.1038/nature06843(/10.1038%2Fnature06843). PMID 18432240(https:///pubmed/18432240).◾25 years of Quantum Hall Effect, K. von Klitzing, Poincaré Seminar (Paris-2004). Postscript (http://parthe.lpthe.jussieu.fr/poincare/textes/novembre2004.html). Pdf(/PhysicsHorizon/25yearsQHE-lecture.pdf).◾Magnet Lab Press Release Quantum Hall Effect Observed at Room Temperature (/mediacenter/news/pressreleases/2007february15.html)◾Avron, Joseph E.; Osadchy, Daniel, Seiler, Ruedi (2003). "A Topological Look at the Quantum Hall Effect" (/resource/1/phtoad/v56/i8/p38_s1).Physics Today56 (8): 38. Bibcode:2003PhT....56h..38A(/abs/2003PhT....56h..38A). doi:10.1063/1.1611351(/10.1063%2F1.1611351). Retrieved 8 May 2012.◾Zyun F. Ezawa: Quantum Hall Effects - Field Theoretical Approach and Related Topics.World Scientific, Singapore 2008, ISBN 978-981-270-032-2◾Sankar D. Sarma, Aron Pinczuk: Perspectives in Quantum Hall Effects. Wiley-VCH, Weinheim 2004, ISBN 978-0-471-11216-7◾Baumgartner, A.; Ihn, T.; Ensslin, K.; Maranowski, K.; Gossard, A. (2007). "Quantum Hall effect transition in scanning gate experiments". Physical Review B76 (8).Bibcode:2007PhRvB..76h5316B (/abs/2007PhRvB..76h5316B).doi:10.1103/PhysRevB.76.085316 (/10.1103%2FPhysRevB.76.085316).◾E. I. Rashba and V. B. Timofeev, Quantum Hall Effect, Sov. Phys. - Semiconductors v. 20, pp.617-647 (1986).Retrieved from "/w/index.php?title=Quantum_Hall_effect&oldid=605304404"Categories: Hall effect Condensed matter physics Quantum electronics SpintronicsQuantum phases Mesoscopic physics◾This page was last modified on 22 April 2014 at 14:51.◾Text is available under the Creative Commons Attribution-ShareAlike License; additional terms may apply. By using this site, you agree to the Terms of Use and Privacy Policy.Wikipedia® is a registered trademark of the Wikimedia Foundation, Inc., a non-profitorganization.。

量子分数霍尔效应量子分数霍尔效应（Quantum Fractional Hall Effect，简称QFHE）是指电子系统中，当在外加的磁场达到一个特定的值时，由于量子效应而产生的一种具有特殊性质的新型介质状态。

这种介质状态对外加的磁场的变化和电子的物理特性有着独特的响应，并表现出一种特殊的“分数”霍尔效应，因此得名。

QFHE是在1980年由K. von Klitzing首次发现的，根据国际单位系统（SI）提出的“霍尔定律”，当一个2D 电子系统受到外加的磁场时，在该系统中会出现一种特殊的“霍尔导电状态”，其电阻R的值为h/ne2（e为电子的电荷，n为电子的浓度，h为普朗克常数）。

但是，在1986年，Eisenstein等人发现，在低温时，在超低磁场强度下，2D电子系统会出现一种新的电阻状态，其电阻值不再是上述h/ne2，而是为h/me2，m为一个分数，因此，这种状态又被称为“分数霍尔效应” 。

QFHE也可以看作是一种模拟量子计算机系统，它能够模拟一个真正的量子计算机，有着相似的效应，而且它所考虑的是物理上的问题，因此，它可以很好地模拟出量子力学的运动。

在实验上，我们可以通过改变外加的磁场来控制QFHE，以调节QFHE的特性，从而模拟出一个真正的量子计算机系统。

QFHE还具有许多有趣的物理性质，例如它具有超流性和超导性，在低温下，它可以显示出一种有趣的“抗磁性”，这与普通霍尔效应的行为是完全不同的。

此外，QFHE的电阻也会呈非线性变化，这表明电子在外加磁场的作用下会受到一种强烈的量子效应。

QFHE的研究可以推动量子计算技术的发展，这不仅可以深入研究和理解量子力学的行为，而且还可以为量子计算技术提供一个可行的应用。

此外，QFHE也可以用于研究低温物理中的许多问题，这些问题一直是物理学家和工程师们努力去解决的，例如量子液体、量子气体等等。

综上所述，量子分数霍尔效应（QFHE）是一种由量子效应引起的特殊介质状态，它可以帮助我们更好地理解量子力学，也可以为量子计算技术提供可行的应用，是一种重要的物理现象。

The Physics of Quantum Hall Effect量子霍尔效应的物理学原理量子霍尔效应（Quantum Hall Effect）是量子力学中一个非常重要的现象。

它的发现和研究不仅对纳米科技、信息技术等领域具有重要的应用价值，而且对理解固态物理学的本质也有着重要的意义。

一、莫尔（Klaus von Klitzing）发现的量子霍尔效应1980年，德国物理学家莫尔通过研究二维电子气体，发现了量子霍尔效应。

因为他的发现，莫尔获得了1985年的诺贝尔奖。

莫尔通过实验观察到，在低温下，二维电子气体在强磁场中呈现出应变与电荷的非经典的关联，电阻率出现了奇特的分数倍量子化现象。

这个现象表明，在一个固定大小的电场中，电子所携带的负电荷在移动时产生的电荷分布与物质的特性相应地变化了。

这种现象被称为量子霍尔效应。

二、量子霍尔效应的物理学原理量子霍尔效应源自于量子化的电磁波动态。

它发生的表面是由电子在二维材料中受到两个垂直电场的影响，一个是外磁场，一个是表面势场。

背后的基本机理涉及到一个参数，即电子的荷质比，在二维材料中会产生一种平均的自由电场，被称为Lorentz力。

随着磁场的增强，这种力将越发强大。

这个力将会导致一种称为 Hall 电场的场的形成，它代表了在电子在磁场中的移动，因为在电子磁矩和磁场之间的相互作用会产生一个横向的电场。

电子在普通的材料中会受到散射。

在一个均匀的磁场下，这对电子的运动根本没有影响，但是在超出一定范围或者在密度较高的系统中，电子将会遇到一些携带着相反荷电的电子，因此会产生库伦相互作用。

当电子的速度增加时，不仅需要克服磁场导致的阻力，还需要克服由于原子核以及组成材料的其他电子的排斥所产生的力。

量子霍尔效应发生的原因是，当电子在固定的磁场下运动时，磁场的影响会将它们绑定在材料内部、数量有限的位置上。

当电子密度十分低时，电子将会分别占据这些位置，并将它们所携带的电荷向内部传递，导致出现整数量子霍尔效应。

量子自旋霍尔效应的实验观测量子自旋霍尔效应（Quantum Spin Hall Effect，简称QSHE）是量子力学中的一种现象，它引起了物理学界的广泛关注。

QSHE是指当材料处于二维平面时，电子在其表面上的自旋分裂成上、下自旋分量，同时，这两种自旋分量的电子会在材料内部形成两个相互独立的电流环路。

这种自旋分裂和电流环路相互作用的行为被称为QSHE，被认为是一种潜在的拓扑绝缘体状态。

在过去的几十年中，科学家们对QSHE进行了大量的理论研究，并提出了一些模型来解释这一现象。

其中最著名的是狄拉克费米子模型，该模型认为在二维零能隙材料中，存在两个相互悬殊的自旋极化的反常量子霍尔边缘态。

这些反常量子霍尔边缘态可通过QSHE的电导测量来观察和量化。

为了验证QSHE，科学家们进行了一系列的实验观测。

最早的实验观测是在2005年由Konig等人在汞镉碲（HgTe）量子阱中实现的，他们发现在一定的温度下，HgTe量子阱的二维电子气体的电导发生了突变，出现了QSHE的电导特征。

这一突变被称为QSHE的拓扑相变，成为QSHE研究的里程碑。

随后的实验观测表明，在更多的材料体系中，如砷化铟（InAs）和铋锗（Bi2Se3）等，也可以观察到QSHE的现象。

这些实验结果证实了QSHE的普遍性，使得科学家们对该现象更加感兴趣。

然而，虽然QSHE已经在实验中得到观察，但其机理和应用仍然是一个广泛的研究领域。

首先，科学家们正在努力理解QSHE的微观机制，例如自旋-轨道相互作用、拓扑绝缘体的表面态等等。

这些研究有助于揭示QSHE的本质，并为进一步的应用提供理论基础。

其次，QSHE还有许多重要的实际应用。

例如，QSHE在量子计算和量子通信中具有重要意义。

由于QSHE可以使电子在材料中传输时具有低能量损耗和高速度，因此可以用来构建高效的量子比特传输通道。

此外，QSHE还可以用于制备低功耗的拓扑自旋电子学器件。

为了进一步探索QSHE的应用前景，科学家们将不断寻找新的QSHE材料和量子器件。

1998年诺贝尔物理学奖——分数量子霍耳效应的发现1998年诺贝尔物理学奖授予美国加州斯坦福大学的劳克林（Robert ughlin，195O—），美国纽约哥伦比亚大学与新泽西州贝尔实验室的施特默（Horst L.St rmer，1949—）和美国新泽西州普林斯顿大学电气工程系的崔琦（Daniel C.Tsui，1939—），以表彰他们发现了一种具有分数电荷激发状态的新型量子流体，这种状态起因于所谓的分数量子霍耳效应。

量子流体早在研究极低温状态下的液氦和超导体时就已有所了解。

在这些领域里，已经有好几位物理学家获得过诺贝尔物理学奖。

例如，卡末林－昂内斯由于液氦的研究和超导电性的发现获1913年诺贝尔物理学奖；朗道由于液氦和超流理论获1962年诺贝尔物理学奖；巴丁、库珀和施里弗由于提出超导电性的BCS 理论获1972年诺贝尔物理学奖；卡皮查由于发现氦的超流动性获1978年诺贝尔物理学奖；柏诺兹和缪勒由于发现高温超导获1987年诺贝尔物理学奖；戴维·李、奥谢罗夫和R.C.里查森则因发现氦－3的超流动性获1996年诺贝尔物理学奖。

这么多的物理学家受到如此殊荣，说明凝聚态物理学在20世纪有极大的发展，而低温和超导在这一领域内又具有特殊重要的地位。

分数量子霍耳效应正是继高温超导之后凝聚态物理学又一项崭新课题。

分数量子霍耳效应是继霍耳效应和量子霍耳效应①的发现之后发现的又一项有重要意义的凝聚态物质中的宏观量子效应。

冯·克利青由于在1980年发现了量子霍耳效应而于1985年获得诺贝尔物理学奖。

图98－1表示冯·克利青所得霍耳电阻随磁场变化的台阶形曲线。

台阶高度等于物理常数h/e2除以整数i。

e与h是自然的基本常数——e是电子的基本电荷，h是普朗克常数。

h/e2值大约为25kΩ。

图中给出了i＝2，3，4，5，6，8，10的各层平台。

下面带峰的曲线表示欧姆电阻，在每个平台处趋于消失。

量子数i也可用填充因子f 代替，填充因子f由电子密度和磁通密度确定，可以定义为电子数N与磁通量子数Nφ（＝φ/φ0）之比，即f＝N/Nφ，其中φ为通过某一截面的磁通，φ0为磁通量子，φ0＝h/e＝4.1×10-15Vs.当f是整数时，电子完全填充相应数量的简并能级（朗道能级），这种情况的量子霍耳效应叫做整数量子霍耳效应，以与分数量子霍耳效应相区别。

a r X i v :0806.2429v 1 [c o n d -m a t .m e s -h a l l ] 15 J u n 2008Edge states for the n =0Laudau level in grapheneMitsuhiro Arikawa 1,Yasuhiro Hatsugai 1,Hideo Aoki 21Institute of Physics,University of Tsukuba,Tsukuba,305-8571,Japan2Department of Physics,University of Tokyo,Hongo,Tokyo 113-0033,JapanE-mail:arikawa@.tsukuba.ac.jpAbstract.In the anomalous quantum Hall effect (QHE),a hallmark of graphene,nature of the edge states in magnetic fields poses an important question,since the edge and bulk should be intimately related in QHE.Here we have theoretically studied the edge states,focusing on the E =0edge mode,which is unusual in that the mode is embedded right within the n =0bulk Landau level,while usual QHE edge modes reside across adjacent Landau levels.Here we show that the n =0Landau level,including the edge mode,has a wave function amplitude accumulated along zigzag edges whose width scales with the magnetic length,l B .This contrasts with the usual QHE where the charge is depleted from the edge.The implications are:(i)The E =0edge states in strong magnetic fields have a topological origin in the honeycomb lattice,so that they are outside the continuum (“massless Dirac”)model.(ii)The edge-mode contribution decays only algebraically into the bulk,but this is “topologically”compensated by the bulk contribution,resulting in the accumulation over l B .(iii)The real space behavior obtained here should be observable in STM experiments.Ever since the anomalous quantum Hall effect (QHE)was experimentally observed,[1,2]fascination with graphene is mounting.The interests have been focused on the “massless Dirac”dispersions around Brillouin zone corners in graphene,where the Dirac cone is topologically protected due to the chiral symmetry[3].The peculiar dispersion is responsible for the appearance of the n =0Landau level (n :Landau index)precisely around energy E =0in magnetic fields[4].For the ordinary integer QHE an important question is how the bulk and edge QHE conductions are related for finite samples.Many authors have addressed this question[5,6],and the bulk QHE conductivity,a topological quantity,is shown to coincide with the edge QHE conductivity,itself another topological quantity.This is an example of the phenomena that,when a bulk system has a topological order[7,8,9,10]that reflects the geometrical phase of the system[11],this should be reflected and become visible in the edge states in a bounded system.[12,13]This “bulk-edge correspondence”persists in graphene,as shown both from an analytic treatment of the topological numbers and numerical results for the honeycomb lattice[14,15].In this paper,we reveal the features in the real-space profile of the edges states in graphene in magnetic fields B in the one-body problem.A pecurier point on the graphene edge states is that the E =0edge mode,despite being embedded right within the n =0bulk Landau level in the energy spectrum,has a wave function whose charge is accumulated along zigzag edges.This is drastically different from the ordinary QHE,where edge modes reside,in energy,between adjacent Landau levels,and their charge is depleted toward an edge.The physics here indicates a topological origin in a honeycomb lattice,which is in fact totally outside continuum models.In B =0,a zigzag edge in graphene has been known to have a flat dispersion at E =0,[16]Figure 1.Honeycomb lattice with armchair(a)or zigzag(b)edges with e 1,e 2being respective unit translation vectors.Local charge density (∝area of each circle)in a magnetic field φ=1/41for the energy window −0.05<E <0.05around n =0Landau level is displayed.(c)Energy spectrum for a zigzag edge against k 2(momentum along the edge)in a magnetic field of φ=1/41for zigzag edges.(d)Blowup around the n =0Landau level for a zigzag edge,in a magnetic field of φ=1/5here for clarity,with shaded regions represent the bulk energy spectra,while red curves the modes localized on the zigzag edge.which is protected by the bipartite symmetry of the honeycomb lattice.Here we focus on the edge states in strong magnetic fields,which has a flat dispersion at E =0.We consider the tight-binding model on the honeycomb lattice with nearest-neighbor hopping t (which is taken to the the unit of energy hereafter).The magnetic field is introduced as a Peierls phase.The flux in units of the magnetic flux quantum is φ≡BS 6/(2π)=1/q in each hexagon with an area S 6=(3√2πE 2E 1dEdk 2|ψα(E,j 1,k 2)|2.(1)Here x is the distance from the edge (as related to j 1via e 1which is not normal to the edge),and E 1<E <E 2is the energy window to be included in the charge density (which is normalized to unitywhen the window covers the whole spectrum).Figure 1(c)shows the energy spectrum for a zigzag edge in a magnetic field φ=1/41.For this magnetic field the n =0Landau level around E =0,with a narrow energy width,almost looks like a line spectrum on this plot.We calculate the local charge density defined in eq.(1)for the armchair and zigzag edges.Figure 2(a)depicts the charge density I (x )normalized by thebulk value I0(=φ)against the distance from the edge x measured by the magnetic length l B for φ=1/41,with the energy window|E|<0.05set to cover the n=0Landau level(along with the embedded E=0edge mode).The charge density for an armchair edge decreases monotonically toward the edge,where the depletion occurs on the magnetic length scale(l B=33/4a/√π 1dtt2(n−1)(1−t2)1−t2/4.(2)Asymptotically p n has an algebraic decay as p n≃n−2/(π√(a) n=0 Landau level (near E=0)(b) Landau levels (near band botom)I (x )/I 0I (x )/I 0BFigure 2.(a)Scaled plot of the charge density I (x )for magntic flux φ=1/41against x/l B ,thedistance from the edge normalized by the magnetic length,for the n =0Landau level (marked with A in Fig.1(c)).(b)The same plot for the outermost Landau levels (marked with B and C in Fig.1(c)),for which I 0=φ/2.0 I (x )/I 0x/l B(a) E=0 contribution(b) n=0 Landau level and E=0 contributionFigure 3.Scaled plot of I (x )at E =0edge mode for φ(=1/q )=1/21and 1/41(a)and comparison with n =0Landau Level contribution for φ=1/41.[2]Zhang Y,Tan Y W,Stormer H L,and Kim P 2005Nature (London)438201[3]Ryu S and Hatsugai Y 2002Phys.Rev.Lett.89077002[4]Brey L and Fertig H A 2006Phys.Rev.B 73195408[5]Laughlin R B 1981Phys.Rev.B 235632[6]Halperin B I 1982Phys.Rev.B 252185[7]Wen X G 1989Phys.Rev.B 407387[8]Shapere A and Wilczek F ed.1989Geometric Phases in Physics (Singapore:World Scientific)[9]Hatsugai Y 2004J.Phys.Soc.Jpn.732604[10]Hatsugai Y 2004J.Phys.Soc.Jpn.741374[11]Berry M V 1984Proc.R.Soc.London,Ser.A 39245[12]Hatsugai Y 1993Phys.Rev.B 4811851[13]Hatsugai Y 1993Phys.Rev.Lett.713697[14]Hatsugai Y,Fukui T and Aoki H 2006Phys.Rev.B 74205414[15]Hatsugai Y,Fukui T and Aoki H 2007Eur.Phys.J.Special Topics 148133[16]Fujita M,Wakabayashi K,Nakada K and Kusakabe K 1996J.Phys.Soc.Jpn.651920;Wakabayashi K,Fujita M,Ajiki H and Sigrist M 1999Phys.Rev.B 598271[17]Arikawa M,Hatsugai Y and Aoki H 2008Preprint arXiv:0805.3240[18]Niimi Y et al 2006Phys.Rev.Lett.97236804has obtained STM and STS results for graphite.。

美法两国物理学家获2012年诺贝尔物理学家2012-10-09 18:28:30 来源：新浪科技查看评论进入光明网BBS手机看新闻北京时间10月9日消息，据诺贝尔奖委员会官方网站报道，2012年度诺贝尔物理学奖已经于北京时间10月9日17:45公布，由于“使用突破性的方法实现单个量子系统的测量和操控”，今年的物理学奖项授予法国量子物理学家塞吉·哈罗什(Serge Haroche)和美国物理学家大卫·维恩兰德(David Wineland)。

今年的物理学奖项授予法国量子物理学家塞吉·哈罗什(左)和美国物理学家大卫·维恩兰德(右)科学背景粒子操控与量子世界塞吉·哈罗什和大卫·维恩兰德各自独立地创立并发展了在不影响粒子量子力学特征的情况下对于单个粒子的测量与操控方法，这种方式在此之前曾经被人们认为是不可能做到的。

这两位科学家开启了量子物理学实验领域的崭新大门，因为他们向我们展示了对于单个量子粒子进行直接测量而不破坏其量子状态是可能做到的。

对于单个的光火物质粒子而言，经典物理学已经不适用，量子力学取而代之。

但是单个粒子很难从其周围的环境中被分离出来，并且一旦它和周围环境发生相互作用便会立即丧失其神秘的量子特性。

这样一来很多在量子力学中预言的怪异现象就将不再能被直接观察到，因此科学家们只能借助那些可能会影响其量子特性的实验方法来进行观察研究。

量子物理学家塞吉·哈罗什和大卫·维恩兰德各自带领着自己的研究小组发展出一种方法，可以用于测量并操控非常脆弱的量子态，而这在之前是被认为是不可能进行直接观察的。

有了他们开发的新方法，物理学家们得以研究，操控粒子或对粒子进行计数。

具体而言，他们两人所采用的方法具有很多共通之处。

大卫·维恩兰德捕获带电的原子，即离子，随后使用光，即光子对其进行操控和测量。

而塞吉·哈罗什采用了相反的手段：他将光子捕获并使用原子对其进行操控和测量。

andre k. geim英文介绍Andre K. Geim is a renowned physicist and materials scientist who was born on October 21, 1958, in Sochi, Russia. He is best known for his groundbreaking work on graphene, a two-dimensional material with extraordinary properties.Geim obtained his bachelor's degree in physics from the Moscow Institute of Physics and Technology in 1982. He then pursued his Ph.D. in physics at the Institute of Solid State Physics in Chernogolovka, Russia, which he completed in 1987. Following his doctoral studies, Geim worked as a research scientist at the Institute for Microelectronics Technology in Chernogolovka.In 1994, Geim moved to the Netherlands to work at the University of Nijmegen as a postdoctoral researcher. During his time there, he made significant contributions to the field of mesoscopic physics, particularly in the area of quantum Hall effect. His innovative experiments led to the discovery of the fractional quantum Hall effect in graphene, which earned him theprestigious Oliver E. Buckley Condensed Matter Prize in 2002.In 2001, Geim joined the University of Manchesterin the United Kingdom as a professor of physics. It was at Manchester that he and his colleague, Konstantin Novoselov, made their groundbreaking discovery of graphene in 2004. They successfully isolated graphene, a single layer of carbon atoms arranged in a hexagonal lattice, using a simple method of peeling graphite with adhesive tape. This discovery revolutionized the field of materials science and opened up numerous possibilities for technological advancements.For their groundbreaking work on graphene, Geim and Novoselov were awarded the Nobel Prize in Physicsin 2010. Geim became the first person to have received both the Nobel Prize and the Ig Nobel Prize, which he had won in 2000 for his experiment involving levitating a frog using magnets.In addition to his work on graphene, Geim has made significant contributions to other areas of physics, including magnetism, superconductivity, and low-temperature physics. He has published numerous scientific papers and has received numerous awards and honors for his contributions to the field.Andre K. Geim's research has not only advanced our understanding of fundamental physics but has also paved the way for the development of newtechnologies and materials. His innovative thinkingand unconventional approach to scientific research have made him one of the most influential scientists of our time.。

量子霍尔效应实验量子霍尔效应（Quantum Hall Effect，QHE）是量子力学效应在固体物理中的一种重要体现。

它在1980年由德国物理学家Klaus von Klitzing首次发现，并因此获得了1985年度诺贝尔物理学奖。

量子霍尔效应是一种特殊的电导现象，只出现在低温（通常在几个开尔文度以下）且高磁场下，并且在宏观尺度下呈现出量子行为。

要进行量子霍尔效应的实验，我们需要准备一些基本的器材和实验装置。

首先，我们需要一个高强度磁场，以及一个低温实验室，因为量子霍尔效应只发生在低温和高磁场条件下。

为了产生高磁场，可以使用超导磁体或者霍尔效应样品上方通过电磁铁来产生。

对于低温实验室，我们通常使用液氦或者冷却剂来降低温度。

实验中，我们选择一个具有高度二维结构的样品，例如硅、石墨烯或者半导体材料。

这些材料具有良好的载流子导电性，且可以在高磁场下表现出量子特性。

通过光刻技术，我们可以制备出微米尺寸的霍尔效应器件，通常为一个狭窄的长条形导体，具有两个平行的侧边和一个中间导电区域。

在实验准备阶段，我们首先将样品安装在低温实验室中，并将磁场调整到所需的强度。

然后，我们将用导线连接样品的两个侧边并施加电压，以产生电流。

同时，我们还需要将样品的纵向电压测量引线连接到样品的中间导电区域。

在实验过程中，我们可以通过改变磁场强度或者样品温度来观察量子霍尔效应。

通常实验中使用的磁场强度可以达到数特斯拉（T），而样品温度可以冷却到几开尔文的低温。

通过在一定范围内调节磁场强度，我们可以观察到电阻率的一系列突跃现象，这些突跃点对应着电子在不同的能级上运动。

量子霍尔效应的基本特征是霍尔电导和纵向电导具有精确的整数和分数倍数关系，这是量子行为的重要标志。

量子霍尔效应的应用非常广泛。

首先，它在电学计量学中具有重要意义，因为可以利用整数量子霍尔效应提供精确的电阻标准。

其次，量子霍尔效应可以用于研究材料的电子结构以及量子态的特性。

量子hall效应量子Hall效应量子Hall效应是一种在强磁场下出现的电学现象，其具有高度的稳定性和精度。

该效应在许多领域中都有重要的应用，如材料科学、半导体技术、纳米电子学等。

本文将对量子Hall效应进行详细的介绍。

一、量子Hall效应的基本概念1.1 什么是量子Hall效应量子Hall效应是指在低温和强磁场下，二维电子气体中出现的一种电阻率为零而且霍尔电导σxy只有在一个精确值上非零的现象。

这个精确值就是普朗克常数h/e²的整数倍，即σxy=n(e²/h)。

1.2 量子Hall效应的发现历程1980年代初期，德国物理学家Klitzing等人在实验中发现了这个奇特的现象，并于1985年获得了诺贝尔物理学奖。

他们使用了一种被称为“分式量子霍尔效应”的方法来观察这个现象。

这种方法使用了一个特殊的二维电子气体结构，在低温和强磁场下可以产生非常稳定和精确的量子霍尔电导。

1.3 量子Hall效应的分类根据量子Hall效应的电导类型，可以将其分为整数量子霍尔效应和分数量子霍尔效应两种。

整数量子霍尔效应只在σxy=n(e²/h)时出现，而分数量子霍尔效应则在σxy=p/q(e²/h)时出现，其中p和q是互质的整数。

二、量子Hall效应的物理机制2.1 电荷输运理论在强磁场下，二维电子气体中的电荷输运受到约束。

由于磁场的作用，电子被限制在能级上移动，并且只能沿着轨道运动。

这些轨道被称为朗道能级。

当磁场足够强时，只有朗道能级最低的几个能级才会被占据。

因此，在低温下，只有这些占据态才对输运产生影响。

2.2 拓扑物理学理论拓扑物理学是一种新兴的物理学领域，它研究了材料中自旋、电荷等性质如何受到拓扑结构影响。

近年来，拓扑物理学已经成为了研究量子Hall效应的主要理论框架之一。

根据拓扑物理学的理论，量子Hall效应是由于电子在二维材料中运动时受到了拓扑结构的限制，从而导致霍尔电导只能在特定的值上出现。

物理专业英语词汇(F)物理专业英语词汇(F)物理专业英语词汇(F)f bandf 带f centerf 心f center laserf 心激光器f center maserf 心微波激射器f layerf 层f value振子强度f/d ratiof/d 比face centered crystal面心晶体face centered cubic lattice面心立方晶格face centered cubic structure面心立方结构face centered lattice面心点阵factor因子factor group剩余群facula光斑faddeev equation法捷耶夫方程faddeev popov ghost法捷耶夫波波夫鬼态fading衰退;褪色fahrenheit scale华氏温标fahrenheit temperature scale华氏温标fahrenheit thermometer华氏温度计fall降低fall of potential电压降fall time下降时间falling sphere viscometer落球粘度计fallout放射性沉降物false image鬼象family族family of asteroids小行星族family of comets彗星族fano factor法诺因子far field pattern远场图样far infrared远红外区far infrared laser远红外激光器far infrared radiation远红外辐射far infrared rays远红外线far point远点far ultraviolet远紫外区far ultraviolet laser远紫外激光器far ultraviolet radiation紫外线辐射far ultraviolet rays远紫外线farad法faraday法拉第faraday cage法拉第笼faraday cell法拉第盒faraday constant法拉第常数faraday cup法拉第笼faraday dark space法拉第暗区faraday effect磁致旋光faraday rotation磁致旋光faraday tube法拉第管faraday's law法拉第定律farvitron线振质谱仪fast迅速的fast breeder reactor快增殖堆fast fission快中子裂变fast fission effect快中子裂变效应fast fourier transform快速傅里叶变换fast neutron快中子fast neutron reactor快中子堆fast nova快新星fast reactor快中子堆fatigue疲劳fatigue limit疲劳极限fatigue strength疲劳强度fcc structure面心立方结构feedback反馈feedback amplifier反馈放大器feedback circuit反馈电路feedback control反馈控制feedback factor反馈系数feedback ratio反馈比feeder馈电线femto飞femtometer费密femtosecond飞秒femtosecond region飞秒区域fermat's principle费马原理fermi费密fermi acceleration费密加速fermi age费密年龄fermi dirac statistics费密统计法fermi distribution费密分布fermi energy费密能fermi gas费密气体fermi glass费密玻璃fermi hole费密空穴fermi interaction费密相互酌fermi level费密能级fermi liquid费密液体fermi particle费密子fermi pasta ulam problem费密巴斯德乌拉姆问题fermi resonance费密共振fermi selection rule费密选择定则fermi statistics费密统计法fermi surface费密面fermi temperature费密温度fermi transition费密跃迁fermi's golden rule费密黄金定律fermiology费密面学fermion费密子fermionic dark matter费密子暗物质fermium镄ferrielectricity亚电性ferrimagnetic resonance亚铁磁共振ferrimagnetism铁氧体磁性ferrite铁氧体ferrite magnetostrictive vibrator铁氧体磁致伸缩振子ferro resonance铁磁共振ferroelastic phase transition铁弹性相变ferroelasticity铁弹性ferroelectric铁电的ferroelectric domain铁电畴ferroelectric mode铁电模ferroelectric phase transition铁电相变ferroelectric semiconductor铁电半导体ferroelectric substance铁电性材料ferroelectricity铁电性ferrofluid铁磁铃ferromagnet铁磁体ferromagnetic铁磁的ferromagnetic dielectrics铁磁电介质ferromagnetic fluid铁磁铃ferromagnetic material铁磁性材料ferromagnetic resonance铁磁共振ferromagnetic substance铁磁性材料ferromagnetic superconductor铁磁超导体ferromagnetic thin film铁磁薄膜ferromagnetism铁磁性feynman diagram费因曼图feynman path integral费因曼的路径积分feynman spectrum费因曼谱ffag synchrotron固定场交变梯度回旋加速器fiber纤维fiber bundle纤维丛fiber electrometer悬丝静电计fiber laser纤维激光器fiber optics纤维光学fiber structure纤维结构fibonacci semiconductor superlattice菲博纳奇半导体超晶格fibril小纤维fibril structure纤维结构fick's law斐克定律fictitious spin quantum number假想自旋量子数fictitious year假年field场;体field adsorption场吸附field current励磁电流field density场密度field desorption场致退吸field distortion场畸变field distribution场的分布field effect transistor场效应晶体管field electron emission场致电子发射field emission场致发射field emission microscope场致发射显微镜;自动电子显微镜field emitted electron场致发射电子field equation场方程field intensity场强field ion microscope场致离子显微镜field lens场镜field magnet场磁铁field of forces力场field of gravity重力场field of view视场field of vision视场field operator场算符field particle场粒子field quantum场量子field stop场栏field strength场强field structure场结构field theory场论fifth force第五种力fifth fundamental force第五种基本力figure图形figure of merit优值figure of noise噪声指数file文件filled band满带filled level满带能级filled shell满壳层film软片film badge胶片剂量计film boiling膜态沸腾film dosimeter胶片剂量计film type condensation膜状凝结filter滤器滤光器滤波器filtration过滤final product最终产物final state interaction终态相互酌final vacuum极限真空finder取景器finding telescope寻星镜fine particle微粒子fine structure精细结构fine structure constant精细结构常数fine structure splitting精细结构劈裂finesse锐度finite difference method差分法finite element method有限元法finite group有限群finite universe有限宇宙fireball火球fireball model火球模型first harmonics基波first integral初积分first law of thermodynamics热力学第一定律first order phase transition一级相转变first point of aries春分点first quarter上弦first resonance一次共振first sound第一次声波fish finder鱼群探测器fissible可裂变的fissile可裂变的fissile nucleus可分裂的核fissility可分变性fission分裂fission chain reaction裂变链式反应fission chamber裂变室fission counter裂变计数器fission energy裂变能量fission event裂变事件fission fragment裂变碎片fission neutron裂变中子fission yield裂变产额fissionable可裂变的fissionable nucleus可裂变核fissioning isomer裂变同质异能素fit适合five minute oscillations五分钟振动fixation定影fixed capacitor固定电容器fixed point定点fixed resistor固定电阻器fixed star恒星fixing定影fixing solution定影液fizeau fringe菲佐条纹fizeau interferometer菲佐干涉仪flame火焰flame photometer火焰光度计flame photometry火焰光度法flame spectrum火焰光谱flare太阳耀斑flare star耀星flash闪光flash of light闪光flash photolysis闪烁光解flash spectrum闪光光谱flat surface平面flatness problem平坦性问题flattening扁率flavor味flexibility挠性flexible polymer挠性聚合体flexural rigidity弯曲刚度flexural strength抗挠强度flexure挠曲flexure vibration弯曲振动flicker闪烁flicker effect闪烁效应flicker noise闪变噪声flicker photometer闪烁光度计flight path飞越距离flight time飞越时间flint glass火石玻璃flip flop触发器flip flop circuit双稳态触发电路floating body浮体floating point representation浮点表示floating zone melting method浮区熔炼法flocculation凝聚flood and ebb潮汐flooding溢流floppy disk软磁盘flow流flow birefringence怜双折射flow counter柳式计数管flow dichroism怜二色性flow equation怜方程flow parameter怜参数flow pattern镣flow proportional counter怜正比计数器flow rate量flow visualization辽视化flowmeter量计fluctuating force涨落力fluctuation起伏fluctuation dissipation theorem涨落耗散定理fluctuon起伏量子fluent变数fluid铃fluid dynamics铃动力学fluid elasticity水弹性fluid model铃模型fluidal铃的fluidic铃的fluidity怜性fluorescence荧光fluorescence center荧光中心fluorescence dosimeter荧光剂量计fluorescence spectrophotometer荧光分光光度计fluorescence spectrum荧光光谱fluorescence yield荧光产额fluorescent萤光的fluorescent indicator tube荧光指示管fluorescent lamp荧光灯fluorescent material萤光材料fluorescent radiation特狰射fluorescent scattering荧光散射fluorescent screen荧光屏fluorescent x rays荧光x 射线fluorimeter荧光计fluorine氟fluorite structure萤石型结构fluorography荧光照相法fluorometer荧光计fluorometric analysis荧光分析fluoroscope荧光镜fluoroscopy荧光检查法fluorspar structure萤石型结构flux通量flux creep磁通量蠕变flux density通量密度flux flow磁通量流flux jump磁通量跃变flux method熔剂法flux motion磁通量运动flux of energy能通量flux of light光通量flux of radiation辐射通量flux pinning通量锁住flux pump通量泵flux quantization磁通量量子化flux quantum磁通量子fluxmeter磁通计fluxoid磁通量子fluxon磁通量子fly苍蝇座flying spot electron microscope扫描电子显微镜fm receiver档接受器focal distance焦距focal length焦距focal line焦线focal plane焦面focal point焦点focal power光焦度focal surface焦曲面fock representation福克表示fock space福克空间focometer焦距计focon聚焦锥focus焦点focused ion beam聚焦离子束focusing倒focusing camera倒照相机focusing coil聚焦线圈focusing cone聚焦锥focusing lens聚焦透镜focusing quadrupole magnet聚焦四极磁铁focuson聚焦子foil箔fokker planck equation福克普朗克方程follow up control随动控制foot pound second system英尺磅秒单位制forbidden禁戒的forbidden band禁带forbidden decay禁戒衰变forbidden line禁线forbidden lines in astrophysics天体物理学中的禁线forbidden reflection禁戒反射forbidden transition禁戒跃迁forbiddenness禁戒force力force function力函数force of attraction引力force of gravity重力force of inertia惯性力force of repulsion斥力force of rolling friction滚动摩擦力force of sliding friction滑动摩擦力force polygon力的多边形force triangle力的三角形forced circulation强制循环forced convection强制对流forced emission强迫发射forced oscillations受迫振荡forced vibration受迫振荡forced vortex强迫涡流fore vacuum前级真空forecast预报forecast of solar activity太阳活动预告foreign atom杂质原子forepump预备真空泵fork mounting叉式装置form drag型阻form factor形状因子formant共振峰formation of order秩序形成formula公式formulation公式化fornax天炉座fortran程序语言forward scattering前方散射foucault currents涡电流foucault knife edge test傅科刀口检验foucault's pendulum傅科摆fountain effect喷水效应four current四维电流four dimensional space四维空间four dimensional structure of the universe宇宙四维结构four dimensionality四维性four factor formula四因子公式four force四维力four momentum四维动量four potential四维势four terminal network四端网络four vector四维矢four velocity四维速度four wave mixing四波混合fourier component谐波分量fourier integral傅里叶积分fourier number傅里叶数fourier series傅里叶级数fourier spectroscopy傅里叶光谱学fourier transform hologram傅里叶变换全息图fourier transform spectrometer傅里叶光谱仪fourier transformation傅里叶变换fourth sound第四次声波fractal分形fractal dimension分形维数fractional charge分数电荷fractional crystallization分级结晶fractional quantum hall effect分数量子霍尔效应fracton分形子fracture破裂fracture mechanics断裂力学fragility脆性frame antenna环形天线frame of reference参考系francium钫franck condon principle富兰克康登原理franck hertz's experiment富兰克赫兹实验frank read source弗朗克里德源franklin富兰克林fraunhofer diffraction夫琅和费衍射fraunhofer hologram夫琅和费全息图fraunhofer line夫琅和费谱线fre量子free自由的free charge自由电荷free convection自由对流自然对流free electron自由电子free electron laser自由电子激光器free energy自由能free energy of activation激活的自由能free field自由场free free transition自由自由跃迁free group自由群free gyroscope自由陀螺仪free motion自由运动free neutron自由中子free oscillation自由振动free path自由程free pendulum自由摆free rotation自由旋转free space自由空间free state自由态free surface自由面free system自由系free vibration自由振动free volume自由体积free volume theory自由体积理论freedom自由freezing凝固freezing mixture冷冻剂freezing point凝固点frenkel defect夫伦克尔缺陷frenkel exciton夫伦克尔激子frequency频率frequency analysis频率分析frequency band频带frequency characteristic频率特性frequency converter变频器frequency converter tube变频管frequency counter频率计数器frequency divider分频器frequency domain频域frequency factor频率因子frequency meter频率计frequency modulation档frequency multiplier倍频器频率倍增器frequency range频率范围frequency response频率响应frequency response method频率特性法frequency shift移频frequency spectrum频谱frequency stability频率稳定度frequency stabilized laser稳频激光器frequency transfer function频率传递函数fresnel diffraction菲涅耳衍射fresnel half period zones菲涅耳半周期带fresnel hologram菲涅耳全息图fresnel lens菲涅耳透镜fresnel prism菲涅耳棱镜fresnel rhomb菲涅耳斜方系fresnel zone菲涅耳带fresnel's biprism菲涅耳双棱镜fresnel's dragging coefficient菲涅耳曳引系数fresnel's zone plate菲涅耳波带片friction摩擦friction coefficient摩擦系数friction cone摩擦锥friction layer摩擦层friction loss摩擦损失friction of fluid lubrication液体润滑摩擦frictional drag摩擦阻力frictional electricity摩擦电frictional force摩擦力frictional oscillation摩擦振动frictional resistance摩擦阻力friedel sum rule弗里德尔的求和定则friedmann equation弗里德曼方程friedmann universe弗里德曼宇宙frigorimeter深冷温度计fringes with white light白光干涉条纹froude number弗劳德数frozen in magnetic field冻结磁场frustrated total internal reflection衰减全内反射frustration抑止ft valueft 值fuel assembly燃料组件fuel cell燃料电池fuel cycle燃料循环fuel regeneration燃料再生fuel reprocessing燃料再生fuel rod燃料元件棒fugacity挥发性fulcrum支点full load满载full moon望月full wave rectification全波整流full width at half maximum半宽度fullerene球壳状碳分子function函数functional泛函functional analysis泛函分析functional ceramics机能陶瓷functional derivative泛函微分fundamental absorption基本吸收fundamental catalog基本星表fundamental constants基本常数fundamental doublet基本双重线fundamental frequency基频率fundamental interaction基本相互酌fundamental law基本定律fundamental magnitude基本量fundamental mode郑fundamental particle基础粒子fundamental research基础研究fundamental series伯格曼系fundamental star基本星fundamental theorem基本定理fundamental tone基音fundamental unit基本单位furnace炉furry's theorem弗里定理fuse熔断器保险丝fused quartz熔融石英fusible alloy易熔合金fusing point熔点fusion熔化fusion fission hybrid reactor核聚变裂变混合反应堆fusion point熔点fusion reaction聚变反应fusion reactor热核堆fusion temperature聚变温度物理专业英语词汇(F) 相关内容:。