线面垂直习题精选

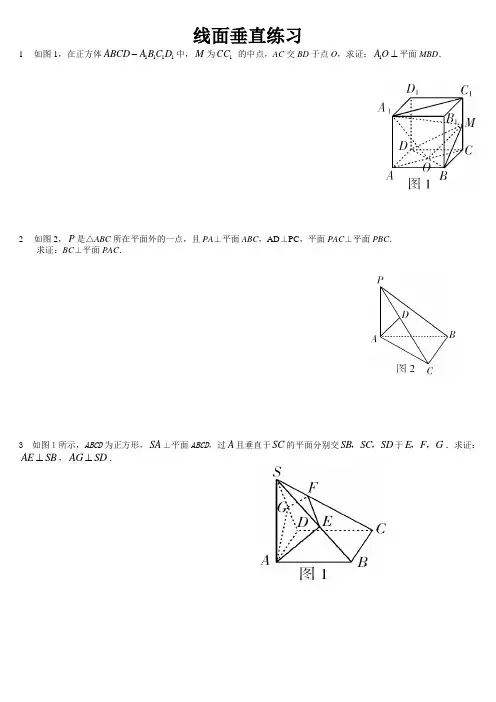
线面垂直练习1 如图1，在正方体1111ABCD A BC D -中，M 为1CC 的中点，AC 交BD 于点O ，求证：1AO ⊥平面MBD ．2 如图2，P 是△ABC 所在平面外的一点，且PA ⊥平面ABC ，AD ⊥PC ，平面PAC ⊥平面PBC ．求证：BC ⊥平面PAC ．3 如图１所示，ABCD 为正方形，SA ⊥平面ABCD ，过A 且垂直于SC 的平面分别交SB SC SD ，，于E F G ，，．求证：AE SB ⊥，AG SD ⊥．4 如图２，在三棱锥Ａ－BCD 中，BC ＝AC ，AD ＝BD ，F 是AB 中点， 作BE ⊥CD ，Ｅ为垂足，作AH ⊥BE 于Ｈ．求证：AH ⊥平面BCD ．5 如图３，AB 是圆Ｏ的直径，Ｃ是圆周上一点，PA 平面ABC ．若AE ⊥PC ，Ｅ为垂足，Ｆ是PB 上任意一点，求证：平面AEF ⊥平面PBC ．6. 空间四边形ABCD 中，若AB ⊥CD ，BC ⊥AD ，求证：AC ⊥BDD7. 证明：在正方体ABCD －A 1B 1C 1D 1中，A 1C ⊥平面BC 1DAC证明：连结ACBD AC ⊥AC 为A 1C 在平面AC 上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面8. 如图，PA ⊥平面ABCD ，ABCD 是矩形，M 、N 分别是AB 、PC 的中点，求证：MN AB ⊥C. 证：取PD 中点E ，则EN DC //12C⇒ENAM// ∴AE MN//又平面平面平面 CD AD PA AC CD PAD AE PAD ⊥⊥⎫⎬⎭⇒⊥⊂⎫⎬⎭ ⇒⊥⎫⎬⎪⎭⎪⇒⊥CD AE CD AB AE MN MN AB////9如图在ΔABC 中， AD ⊥BC ， ED=2AE ， 过E 作FG ∥BC ， 且将ΔAFG 沿FG 折起，使∠A 'ED=60°，求证:A 'E ⊥平面A 'BC分析：弄清折叠前后，图形中各元素之间的数量关系和位置关系。

立体几何线面垂直-题型全归纳题型一利用等腰三角形“三线合一”例题1、如图，在正三棱锥P-ABC中，E，F，G分别为线段PA，PB，BC的中点，证明：BC⊥平面PAG。

证明：在正三棱锥P-ABC中，ＡＢ＝ＡＣ，Ｇ是ＢＣ的中点，∴ＡＧ⊥ＢＣ，又 ＰＢ＝ＰＣ，Ｇ是ＢＣ的中点，∴ＰＧ⊥ＢＣ，ＰＧ⋂ＡＧ＝Ｇ，ＰＧ，ＡＧ⊂平面ＰＡＧ，∴ＢＣ⊥平面ＰＡＧ，解题步骤（1）根据线段的中点，找出相应的等腰三角形；（2）格式“因为D是BC的中点，且AB=AC，所以AD⊥BC”；（3）依据“三线合一”得到线线垂直。

变式训练1、已知四面体ABCD中，AB=AC，BD=CD，E为棱BC的中点，求证：AD⊥BC证明：连接ＤＥ，ＡＢ＝ＡＣ，Ｅ是ＢＣ的中点，∴ＡＥ⊥ＢＣ，又 ＢＤ＝ＣＤ，Ｅ是ＢＣ的中点，∴ＤＥ⊥ＢＣ，ＡＥ⋂ＤＥ＝Ｅ，ＡＥ，ＤＥ⊂平面ＡＤＥ，∴ＢＣ⊥平面ＡＤＥ，ＡＤ⊂平面ＡＤＥ，∴ＡＤ⊥ＢＣ变式训练2、在三棱锥P ABC -中，2AC BC ==，90ACB ∠=，AP BP AB ==，PC AC ⊥．求证：PC AB ⊥证明：取ＡＢ的中点Ｏ，连接ＯＰ，ＯＣ， ＡＰ＝ＢＰ，Ｏ是ＡＢ的中点，∴ＰＥ⊥ＡＢ，又 ＡＣ＝ＢＣ，Ｏ是ＡＢ的中点，∴ＯＣ⊥ＡＢ，ＰＯ⋂ＣＯ＝Ｏ，ＰＯ，ＣＯ⊂平面ＰＯＣ，∴ＡＢ⊥平面ＰＯＣ，ＰＣ⊂平面ＰＯＣ，∴ＡＢ⊥ＰＣ。

变式训练3、如图，在四棱锥Ｐ－ＡＢＣＤ中，ＰＡ⊥平面ＡＢＣＤ，底面ＡＢＣＤ是菱形，Ｅ为ＣＤ的中点，060=∠ABC ，求证：ＡＢ⊥平面ＰＡＥ。

证明： 底面ＡＢＣＤ是菱形，060=∠ABC ，∴ＡＥ⊥ＣＤ，又 ＡＢ//ＣＤ，∴ＡＢ⊥ＡＥ，又ＰＡ⊥平面ＡＢＣＤ，ＡＢ⊂平面ＡＢＣＤ，∴ＡＢ⊥ＰＡ，ＡＰ⋂ＡＥ＝Ａ，ＡＰ，ＡＥ⊂平面ＰＡＥ，∴ＡＢ⊥平面ＰＡＥ。

A CB P题型二利用勾股定理逆定理例题2、如图，在正方体1111D C B A ABCD -中，M 为棱1CC 的中点，AC 交BD 于点O ，求证：BDM1平面⊥O A 证明：连接ＯＭ，M A 1，11C A ，设正方体的棱长为2，则6222222121=+=+=AO A A O A 32122222=+=+=OC CM OM 91)22(222121121=+=+=M C C A M A 21221M A OM O A =+∴即：ＯＭ⊥OA 1又 在正方体1111D CB A ABCD -中，∴ＢＤ⊥OA 1 ＯＭ，ＢＤ⊂平面ＢＤＭ，∴BDM1平面⊥O A 解题步骤（1）根据题干给出的线段长度（没有长度的可以假设），标示在图形上，找出相应的三角形；（2）把线段的长度分别求平方，判断能否构成“222c b a =+”；（3）根据平方关系得到线线垂直。

线面垂直题型20道
1. 两条直线的夹角为90度，则它们一定垂直。

2. 如果一条直线垂直于另一条直线，那么任意一条过这两条直线的线段，这条线段上的点就分别与这两条直线的交点连成的线段垂直。

3. 两条直线分别垂直于第三条直线，则这两条直线平行。

4. 一条线段的中垂线与线段垂直。

5. 任意一个点到平面上一直线的垂足所在的直线与这条直线垂直。

6. 如果一个三角形的两条边互相垂直，则这个三角形是直角三角形。

7. 如果一条直线与一个平面垂直，则这条直线称为这个平面的法线。

8. 一个正方体的某个面与它所在的平面垂直。

9. 一个矩形的对角线互相垂直。

10. 一个正方形的对角线互相垂直。

11. 如果两个面互相垂直，则它们的法线互相平行。

12. 如果平面P垂直于直线L1，且L1垂直于直线L2，则平面P和直线L2互相平行。

13. 如果两条直线互相垂直，则它们的斜率的乘积为-1。

14. 如果一条直线过一个圆的圆心，则这条直线与圆的切线垂直。

15. 如果一条直线垂直于直径所在的直线，则它和圆的切线互相平行。

16. 直角梯形的两条腰互相垂直。

17. 如果两个向量垂直，则它们的点积为0。

18. 如果直线L1垂直于平面P，那么L1上任意一点到P的距离均相等。

19. 一个正六面体的某个面与它所在的平面垂直。

20. 如果两个三维空间中的直线垂直，则它们的方向向量的点积为0。

线面垂直练习题一、选择题1. 若直线a与平面α内的直线b垂直，且b⊂α，那么直线a与平面α的关系是（）。

A. 平行B. 垂直B. 相交D. 无法确定2. 在空间几何中，若直线m与平面α垂直，直线n在平面α内，且m与n相交，那么直线m与直线n的关系是（）。

A. 垂直B. 平行C. 异面D. 相交3. 已知直线l垂直于平面α，点P在平面α外，若要确定过点P且垂直于平面α的直线，需要（）。

A. 一条直线B. 两条直线C. 至少两条直线D. 无数条直线4. 若直线a与直线b相交，且a垂直于平面α，b在平面α内，则直线b与平面α的关系是（）。

A. 垂直B. 平行C. 相交D. 无法确定5. 已知直线m垂直于直线n，直线m在平面β内，直线n在平面α内，若平面α与平面β垂直，则直线m与平面α的关系是（）。

A. 垂直B. 平行C. 相交D. 异面二、填空题6. 若直线a与平面α垂直，直线a上的点A到平面α的距离为d，则直线a上任意一点到平面α的距离都是________。

7. 在空间几何中，若直线l1与直线l2垂直，且l1在平面α内，l2在平面β内，若平面α与平面β垂直，则直线l1与直线l2的位置关系是________。

8. 已知直线m垂直于平面α，若平面β与平面α垂直，且直线m在平面β内，则直线m与平面α的位置关系是________。

9. 若直线a与直线b垂直，直线a在平面α内，直线b在平面β内，且平面α与平面β垂直，则直线a与平面β的位置关系是________。

10. 若直线l垂直于平面α，点P在平面α上，直线l'过点P且与直线l垂直，则直线l'与平面α的位置关系是________。

三、解答题11. 已知直线a与平面α垂直，直线b在平面α内，直线a与直线b 相交于点A。

求证：点A是直线b在平面α上的垂足。

12. 已知平面α与平面β垂直，直线m垂直于平面α且在平面β内，直线n在平面α内。

求证：直线m与直线n垂直。

线面垂直判定经典证明题1.已知：在三角形ABC中，PA垂直于AB和AC。

证明PA垂直于平面ABC。

2.已知：在三角形ABC中，PA垂直于AB，BC垂直于平面PAC。

证明PA垂直于BC。

3.已知：在三棱锥V-ABC中，VA=VC，AB=BC。

证明VB垂直于AC。

4.已知：在正方体ABCD-EFGH中，O为底面ABCD的中心。

证明BD垂直于平面AEGC。

5.已知：在圆O中，AB是直径，PA垂直于AC和AB。

证明BC垂直于平面PAC。

6.已知：在三角形ABC中，AD垂直于BD和DC，AD=BD=CD，∠BAC=60°。

证明BD垂直于平面ADC。

7.已知：在矩形ABCD中，PA垂直于平面ABCD，M和N分别是AB和PC的中点。

1) 证明MN平行于平面PAD。

2) 证明XXX垂直于CD。

3) 若∠PDA=45°，证明MN垂直于平面PCD。

8.已知：在棱形ABCD所在平面外，P满足PA=PC。

证明AC垂直于平面PBD。

9.已知四面体ABCD中，AB=AC，BD=CD，平面ABC垂直于平面BCD，E是棱BC的中点。

1) 证明AE垂直于平面BCD。

2) 证明AD垂直于BC。

10.在三棱锥ABCD中，AB=1，BC=2，BD=AC=3，AD=2.证明AB垂直于平面BCD。

11.在四棱锥S-ABCD中，SD垂直于平面ABCD，底面ABCD是正方形。

证明AC垂直于平面SBD。

12.已知：正方形ABCD所在平面与三角形CDE所在平面相交于CD，AE垂直于平面CDE。

证明AB垂直于平面ADE。

13.在三棱锥P-ABC中，PA、PB、PC两两垂直，H是△XXX的垂心。

证明PH垂直于底面ABC。

14.在正方体ABCD-A1B1C1D1中，证明A1C垂直于平面BC1D1.15.在△ABC所在平面外一点S，SA垂直于平面ABC，平面SAB垂直于平面SBC。

证明AB垂直于BC。

16.在直三棱柱ABC-A1B1C1中，AC=BC=1，∠ACB=90°，AA1=2，D是A1B1的中点。

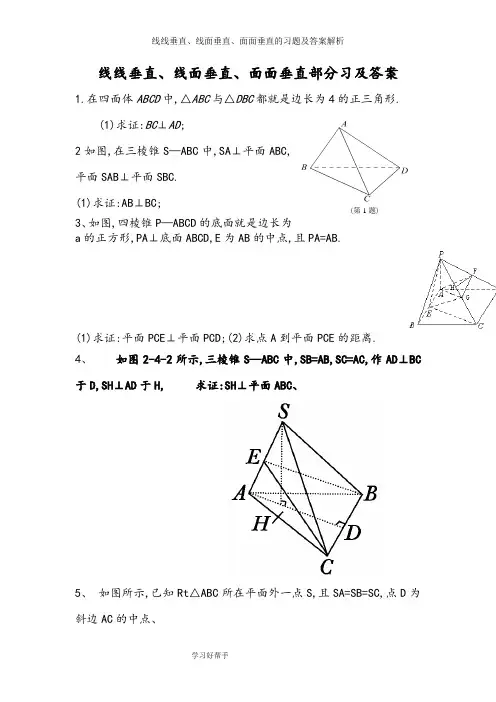
线线垂直、线面垂直、面面垂直部分习及答案1.在四面体ABCD中,△ABC与△DBC都就是边长为4的正三角形.(1)求证:BC⊥AD;2如图,在三棱锥S—ABC中,SA⊥平面ABC,平面SAB⊥平面SBC.(1)求证:AB⊥BC;(第1题)3、如图,四棱锥P—ABCD的底面就是边长为PA=AB.a的正方形,PA⊥底面ABCD,E为AB的中点,且Array(1)求证:平面PCE⊥平面PCD;(2)求点A到平面PCE的距离.4、如图2-4-2所示,三棱锥S—ABC中,SB=AB,SC=AC,作AD⊥BC于D,SH⊥AD于H, 求证:SH⊥平面ABC、5、如图所示,已知Rt△ABC所在平面外一点S,且SA=SB=SC,点D为斜边AC的中点、(1)求证:SD⊥平面ABC;(2)若AB=BC,求证:BD⊥平面SAC、6、证明:在正方体ABCD－A1B1C1D1中,A1C⊥平面BC1DD1C1A1B1D CA B7、如图所示,直三棱柱中,∠ACB=90°,AC=1,,侧棱,侧面的两条对角线交点为D,的中点为M、求证:CD⊥平面BDM、8、在三棱锥Ａ－BCD中,BC＝AC,AD＝BD,作BE⊥CD,Ｅ为垂足,作AH⊥BE于Ｈ.求证:AH⊥平面BCD.9、如图,过S引三条长度相等但不共面的线段SA、SB、SC,且∠ASB=∠ASC=60°,∠BSC=90°,求证:平面ABC⊥平面BSC.10、如图,在长方体ABCD—A1B1C1D1中,AB＝2,BB1＝BC＝1,E为D1C1的中点,连结ED,EC,EB与DB.(1)求证:平面EDB⊥平面EBC;(2)求二面角E－DB－C的正切值、11:已知直线PA垂直于圆O所在的平面,A为垂足,AB为圆O的直径,C就是圆周上异于A、B的一点。

求证:平面PAC 平面PBC。

12、、如图1-10-3所示,过点S引三条不共面的直线,使∠BSC=90°,∠ASB=∠ASC=60°,若截取SA=SB=SC、求证:平面ABC⊥平面BSC2AB=AD=BC=CD=AC=a、求证:平面ABD⊥平面BCD、14、如图所示,△ABC 为正三角形,CE ⊥平面ABC,BD ∥CE,且CE=AC=2BD,M就是AE的中点,求证:(1)DE=DA;(2)平面BDM ⊥平面ECA;(3)平面DEA ⊥平面ECA.15、如图所示,已知PA ⊥矩形ABCD 所在平面,M 、N 分别就是AB 、PC 的中点.(1)求证:MN ∥平面PAD;(2)求证:MN ⊥CD;(3)若∠PDA=45°,求证:MN ⊥平面PCD.16、 如图1,在正方体1111ABCD A B C D -中,M 为1CC 的中点,AC 交BD 于点O ,求证:1A O ⊥平面MBD答案与提示:1、 证明:(1)取BC 中点O ,连结AO ,DO .∵△ABC ,△BCD 都就是边长为4的正三角形, ∴AO ⊥BC ,DO ⊥BC ,且AO ∩DO ＝O, ∴BC ⊥平面AOD .又AD ⊂平面AOD , ∴BC ⊥AD .2、 【证明】作AH ⊥SB 于H,∵平面SAB ⊥平面SBC.平面SAB ∩平面SBC=SB,∴AH ⊥平面SBC,又SA ⊥平面ABC,∴SA ⊥BC,而SA 在平面SBC 上的射影为SB,∴BC ⊥SB,又SA ∩SB=S,∴BC ⊥平面SAB.∴BC ⊥AB.3、 【证明】PA ⊥平面ABCD,AD 就是PD 在底面上的射影,又∵四边形ABCD 为矩形,∴CD ⊥AD,∴CD ⊥PD,∵AD ∩PD=D ∴CD ⊥面PAD,∴∠PDA 为二面角P —CD —B 的平面角,∵PA=PB=AD,PA ⊥AD ∴∠PDA=45°,取Rt △PAD 斜边PD 的中点F,则AF ⊥PD,∵AF ⊂面PAD ∴CD ⊥AF,又PD ∩CD=D ∴AF ⊥平面PCD,取PC 的中点G,连GF 、AG 、EG,则GF21CD 又AE21CD,∴GF AE ∴四边形AGEF 为平行四边形∴AF ∥EG,∴EG ⊥平面PDC 又EG ⊂平面PEC,∴平面PEC ⊥平面PCD.(2)【解】由(1)知AF ∥平面PEC,平面PCD ⊥平面PEC,过F 作FH ⊥PC 于H,则FH ⊥平面PEC∴FH 为F 到平面PEC 的距离,即为A 到平面PEC 的距离.在△PFH 与 △PCD 中,∠P 为公共角,而∠FHP=∠CDP=90°,∴△PFH ∽△PCD.∴PC PFCD FH =,设AD=2,∴PF=2,PC=324822=+=+CD PD ,∴FH=362322=⋅∴A 到平面PEC 的距离为36. 4、 【证明】取SA 的中点E,连接EC,EB 、 ∵SB=AB,SC=AC, ∴SA ⊥BE,SA ⊥CE 、 又∵CE ∩BE=E, ∴SA ⊥平面BCE 、∵BC平面BCE5、 证明:(1)因为SA=SC,D 为AC 的中点, 所以SD ⊥AC 、连接BD 、 在Rt △ABC 中,有AD=DC=DB,所以△SDB ≌△SDA, 所以∠SDB=∠SDA, 所以SD ⊥BD 、又AC ∩BD=D, 所以SD ⊥平面ABC 、 (2)因为AB=BC,D 就是AC 的中点, 所以BD ⊥AC 、 又由(1)知SD ⊥BD, 所以BD 垂直于平面SAC 内的两条相交直线,所以BD ⊥平面SAC 、 6、证明:连结AC ΘBD AC ⊥AC为A1C在平面AC上的射影∴⊥⊥⎫⎬⎭⇒⊥BD A CA C BC A C BC D11111同理可证平面7、证明:如右图,连接、、,则、∵,∴为等腰三角形、又知D 为其底边的中点, ∴、∵,, ∴、又,∴、∵为直角三角形,D 为的中点, ∴,、又,, ∴、、即CD⊥DM、∵、为平面BDM内两条相交直线, ∴ CD⊥平面BDM、8、证明:取AB的中点Ｆ,连结CF,DF.∵AC BC=,∴CF AB⊥.∵AD BD=,∴DF AB⊥.又CF DF F=I,∴AB⊥平面CDF.∵CD⊂平面CDF,∴CD AB⊥.又CD BE ⊥,BE AB B =I , ∴CD ⊥平面ABE ,CD AH ⊥. ∵AH CD ⊥,AH BE ⊥,CD BE E =I ,∴ AH ⊥平面BCD . 9、证明:如图,已知PA=PB=PC=a,由∠APB=∠APC=60°,△PAC,△PAB 为正三角形, 则有:PA=PB=PC=AB=AC=a, 取BC 中点为E直角△BPC中,, ,由AB=AC,AE ⊥BC, 直角△ABE 中,,,,在△PEA 中,,,∴ ,平面ABC ⊥平面BPC、10、 证明:(1)在长方体ABCD －A 1B 1C 1D 1中,AB ＝2,BB 1＝BC ＝1,E 为D 1C 1的中点.∴△DD 1E 为等腰直角三角形,∠D 1ED ＝45°.同理∠C 1EC ＝45°.∴︒=∠90DEC ,即DE ⊥EC .在长方体ABCD －1111D C B A 中,BC ⊥平面11DCC D ,又DE ⊂平面11DCC D , ∴BC ⊥DE .又C BC EC =I ,∴DE ⊥平面EBC .∵平面DEB 过DE ,∴平面DEB ⊥平面EBC .(2)解:如图,过E 在平面11DCC D 中作EO ⊥DC 于O .在长方体ABCD －1111D C B A 中,∵面ABCD⊥面11DCC D ,∴EO ⊥面ABCD .过O 在平面DBC 中作OF ⊥DB 于F ,连结EF ,∴EF ⊥BD .∠EFO 为二面角E －DB －C 的平面角.利用平面几何知识可得OF ＝51, (第10题)又OE ＝1,所以,tan ∠EFO ＝5.11、(1)【证明】∵C 就是AB 为直径的圆O 的圆周上一点,AB 就是圆O 的直径∴BC ⊥AC;又PA ⊥平面ABC,BC ⊂平面ABC, ∴BC ⊥PA,从而BC ⊥平面PAC. ∵BC ⊂平面PBC,∴平面PAC ⊥平面PBC.、12、证明:如图1-10-4所示,取BC的中点D,连接AD,SD、由题意知△ASB与△ASC就是等边三角形,则AB=AC,∴AD⊥BC,SD⊥BC、令SA=a,在△SBC中,SD= a,又AD= = a,∴AD2+SD2=SA2,即AD⊥SD、又∵AD⊥BC,∴AD⊥平面SBC、∵AD平面ABC,∴平面ABC⊥平面SBC、13、证明:取BD的中点E,连接AE,CE、则AE⊥BD,BD⊥CE、在△ABD中,AB=a,BE= BD= ,∴AE= ,同理,CE= 、在△AEC中,AE=EC= ,AC=a,∴AC2=AE2+EC2,即AE⊥EC、∵BD∩EC=E,∴AE⊥平面BCD、又∵AE平面ABD,∴平面ABD⊥平面BCD14、证明: ((1)取EC的中点F,连接DF.∵ CE⊥平面ABC,∴ CE⊥BC.易知DF∥BC,CE⊥DF.∵ BD∥CE,∴ BD⊥平面ABC.在Rt△EFD与Rt△DBA中,∵,,∴ Rt△EFD≌Rt△DBA.故DE=AD.(2)取AC的中点N,连接MN、BN,MN CF.∵ BD CF,∴ MN BD.N平面BDM.∵ EC⊥平面ABC,∴ EC⊥BN.又∵ AC⊥BN,∴ BN⊥平面ECA.又∵ BN平面MNBD,∴平面BDM⊥平面ECA.(3)∵ DM∥BN,BN⊥平面ECA,∴ DM⊥平面ECA.又∵ DM平面DEA,∴平面DEA⊥平面ECA.15、证明:(1)取PD的中点E,连接AE、EN,则,故AMNE为平行四边形,∴ MN∥AE.∵ AE平面PAD,MN平面PAD,∴ MN∥平面PAD.(2)要证MN⊥CD,可证MN⊥AB.由(1)知,需证AE⊥AB.∵ PA⊥平面ABCD,∴ PA⊥AB.又AD⊥AB,∴ AB⊥平面PAD.∴ AB⊥AE.即AB⊥MN.又CD∥AB,∴ MN⊥CD.(3)由(2)知,MN⊥CD,即AE⊥CD,再证AE⊥PD即可.∵ PA⊥平面ABCD,∴ PA⊥AD.又∠PDA=45°,E为PD的中点.∴ AE⊥PD,即MN⊥PD.又MN⊥CD,∴ MN⊥平面PCD.16、证明:连结MO ,1A M ,∵DB ⊥1A A ,DB ⊥AC ,1A A AC A =I , ∴DB ⊥平面11A ACC ,而1AO ⊂平面11A ACC ∴DB ⊥1A O .设正方体棱长为a ,则22132A O a =,2234MO a =.在Rt △11A C M 中,22194A M a =.∵22211A O MO A M +=,∴1AO OM ⊥. ∵OM ∩DB =O ,∴ 1A O ⊥平面MBD .。

线面垂直习题精选证明：取 AB 的中点F ,连结CF , DFT AC BC ，二 CF ABTADBD ，二 DF AB .又CF I DF F ，二 AB平面CDFTCD 平面CDF - CDAB • 又CD BE , BE I AB B , •- CD 平面 ABE CD AH •T AH CD , AH BE ,CD I E 二 AH平面BCD之间的关系非常密切，可以互相转化，从前面推出后面是判定定理，而从后面推出前面是性质定理•同学们应当学会灵活应用这些定理证明 问题•下面举例说明.3如图1所示，ABCC 为正方形，SA 丄平面ABCD 过A 且垂直于SC 的平面分别交SB SC, SD 于E ，F ，G •求证：AE SB ， AG SD .证明：T SA 平面ABCD I"1二 SA BC . T AB BC ，二 BC 平面 SAB 又AE 平面 SAB 二 BC AE . T SC 平面 AEFG 二 SC AE •二 AE 平面SBC /. AE SB •同理可证 AG SD .评注：本题欲证线线垂直，可转化为证线面垂直，在线线垂直与线面垂直的转化中，平面起到了关键作用，同学们应多注意考虑线和线所 在平面的特征，从而顺利实现证明所需要的转化.4 如图2,在三棱锥 A — BCD 中, BC= AC ，AD= BD作BE 丄CD E 为垂足，作 AH^ BE 于H .求证：AH1平面 BCD习题精选精讲 线面垂直的证明中的找线技巧通过计算，运用勾股定理寻求线线垂直1如图1,在正方体ABCD A 1B 1C 1D 1中，M 为CC 1的中点，AC 交BD 于点O,求证:证明：连结 MO , A f M , T DB 丄 AfA , DB 丄AC , AAI ••• DB 丄平面 A 1ACC 1，而 AO 平面 A1ACC 1 二 DB 丄32a .4 设正方体棱长为a , 则 A 1O 2AO平面MBD .AC A ，AO .在 Rt △ A 1C 1M 中, A 1M 23 2 2 a 2，MO 22 9a 2. T AO 24MO 2 2 A 1M ，二 AO OM . •/ OM n DB=o,「. A 1O 丄平面 评注：在证明垂直关系时，有时可以利用棱长、角度大小等数据， 利用面面垂直寻求线面垂直 2 如图2, P 是厶ABC 所在平面外的一点，且 PA 丄平面ABC , 丄平面PAC . 证明：在平面 PAC 内作AD 丄PC 交PC 于D . 因为平面PAC 丄平面PBC ，且两平面交于 PC , AD 平面PAC ，且AD 丄PC, PBC,「. AD 丄 BC . T PA 丄平面 ABC , BC 平面ABC , T AD n PA=A,「. BC 丄平面 PAC . (另外还可证BC 分别与相交直线 AD , MBD . 通过计算来证明. 平面PAC 丄平面 PBC .求证: BC 由面面垂直的性质，得 AD 丄平面PBC . /• PA 丄 BC . AC 垂直，从而得到BC 丄平面PAC).评注：已知条件是线面垂直和面面垂直，要证明两条直线垂直，应将两条直线中的一条纳入一个平面 中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直•在空间图形中，高一级的垂直关系中蕴含 着低一级的垂直关系，通过本题可以看到，面面垂直 线面垂直 线线垂直. 一般来说，线线垂直或面面垂直都可转化为线面垂直来分析解决，其关系为：线线垂直判定 性质(:# "'A平面线面垂直性质B平面ABC BC 平面ABC BC • . BC 平面 APC 平面PBC已知条件岀发寻找线线垂直的关系.6.空间四边形 ABCD 中，若 AB 丄CD , BC 丄AD ，求证：AC 丄BDA 作AO 丄平面BCD 于0 CD， CD B0同理BC 丄DO . 0 ABC 的垂心7.证明：在正方体 ABCD - A i B i C i D i 中，A i C 丄平面BC i D证明：过AB于是BD CO BD ACA i C 平面 BC i D同理可证A 1C BC 1评注：本题在运用判定定理证明线面垂直时，将问题转化为证明线线垂直；而证明线线垂直时，又转化为证明线面垂直•如此反复，直 到证得结论. 5如图3，AB 是圆O 的直径，C 是圆周上一点， PA 平面ABC 若AE 丄PC ，E 为垂足，F 是PB 上任意一点，求证：平面 AEH 平面 PBC证明：丁 AB 是圆o 的直径，二AC BC ••- PA•- PA •- BC二平面 APCL 平面PBC丁 AE 丄PC 平面APC P 平面PBC= PCAE 丄平面PBCTAE 平面AEF 二平面 AEH 平面PBC评注：证明两个平面垂直时，一般可先从现有的直线中寻找平面的垂线，证明：连结ACBD ACAC 为A i C 在平面AC 上的射影BD A i C8.如图，PA 平面ABCD ，ABCD 是矩形，M 、N 分别是AB 、PC 的中点，求证： MN ABpH即证线面垂直，而证线面垂直则需从EN 仏1DC .证：取PD中点E ,_则2EN 仏 AM AE//MN又 CD ADPA 平面ACCD 平面PAD AE 平面PAD.△ PAB 为正三角形 在 RT A BPC 中，PB=PC=aCD AECD / /AB MN ABAE // MN分析：弄清折叠前后，图形中各元素之间的数量关系和位置关系。

线面垂直练习题及答案一、选择题（每题2分，共10分）1. 在空间几何中，如果一条直线与一个平面内的两条相交直线都垂直，那么这条直线与这个平面的关系是什么？A. 平行B. 垂直C. 相交D. 无法确定2. 若直线l与平面α垂直，直线m在平面α内，且直线l与直线m相交于点P，那么直线l与直线m的关系是什么？A. 平行B. 垂直C. 异面D. 相交但非垂直3. 在一个正方体中，如果一条直线垂直于正方体的一个面，那么这条直线与正方体的对角线的关系是什么？A. 垂直B. 平行C. 相交D. 异面4. 已知直线AB与直线CD相交于点P，且直线AB垂直于平面α，直线CD在平面α内，那么点P到平面α的距离是多少？A. 0B. 长度APC. 长度CPD. 无法确定5. 如果直线a与平面β垂直，直线b在平面β内，且直线a与直线b不共面，那么直线a与直线b的关系是什么？A. 平行B. 垂直C. 相交D. 异面二、填空题（每空1分，共5分）6. 已知直线l垂直于平面α，若直线m在平面α内，且直线l与直线m的距离为d，则直线l与直线m的夹角为________。

7. 在三棱锥P-ABC中，若PA垂直于平面ABC，且AB垂直于AC，则PA 与AB的夹角为________。

8. 已知直线a垂直于直线b，直线c垂直于直线b，且直线a与直线c 相交，那么直线a与直线c的夹角为________。

三、计算题（每题5分，共10分）9. 在空间直角坐标系中，设直线l的方程为 \( x - 2y + z = 0 \)，平面α的方程为 \( 3x + y - 2z + 5 = 0 \)。

求证直线l与平面α垂直。

10. 已知直线AB通过点A(1,2,3)和点B(4,5,6)，求证直线AB垂直于平面xOy。

13. 如 图 1-10-5 所 示 ， 在 四 面 体 ABCD 中 ， BD= 2 a, AB=AD=BC=CD=AC=a. 求 证 ： 平 面 ABD ⊥ 平 面 BCD.
14.如图所示，△ABC 为正三角形，CE⊥平面 ABC，BD∥CE，且 CE=AC=2BD ， M 是 AE 的 中 点 ， 求 证 ： (1)DE=DA；(2)平面 BDM⊥平面 ECA；(3)平面 DEA⊥平面 ECA．
直 角 △ BPC 中 ，
，
，
由 AB=AC，AE⊥BC，
直角△ABE 中，
，
，
，
在△PEA 中，
，
，
∴
，
平面 ABC⊥平面 BPC
.
10. 证明：(1)在长方体 ABCD－A1B1C1D1 中，AB＝2，BB1＝BC＝1， E 为 D1C1 的中点．∴△DD1E 为等腰直角三角形，∠D1ED＝45°．同 理∠C1EC＝45°．∴ DEC 90 ，即 DE⊥EC．
15.如图所示，已知 PA⊥矩形 ABCD 所在平面，M、N 分别是 AB、 PC 的中点．
(1)求证：MN∥平面 PAD；(2)求证：MN⊥CD；(3)若∠PDA=45°， 求证：MCD A1B1C1D1 中，M 为 CC1 的中点，AC 交 BD 于点 O，求证： A1O 平面 MBD
O 的直径
∴BC⊥AC； 又 PA⊥平面 ABC，BC 平面 ABC， ∴BC⊥PA，从而 BC⊥平面 PAC． ∵BC 平面 PBC， ∴平面 PAC⊥平面 PBC．
.
12. 证明：如图 1-10-4 所示,取 BC 的中点 D，连接 AD，SD.
由题意知△ASB 与△ASC 是等边三角形，则 AB=AC，

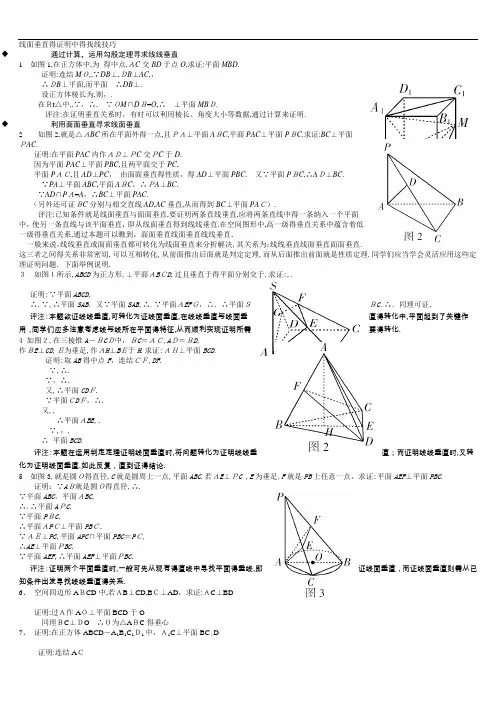
线面垂直得证明中得找线技巧◆通过计算，运用勾股定理寻求线线垂直1 如图1,在正方体中,为得中点,ＡC交BD于点O,求证:平面MBD.证明:连结MＯ,,∵DB⊥,ＤB⊥AC,，∴ＤB⊥平面,而平面∴DB⊥.设正方体棱长为,则，.在Ｒt△中,.∵，∴.∵ＯM∩DＢ=O,∴⊥平面MBＤ.评注:在证明垂直关系时，有时可以利用棱长、角度大小等数据,通过计算来证明.◆利用面面垂直寻求线面垂直2 如图2,就是△ＡBC所在平面外得一点,且ＰＡ⊥平面AＢC,平面PAC⊥平面PＢC.求证:BC⊥平面ＰAC.证明:在平面PAC内作ＡＤ⊥ＰC交ＰC于D.因为平面PAC⊥平面PBC,且两平面交于PC,平面PＡＣ,且AD⊥PC，由面面垂直得性质，得AD⊥平面PBC. 又∵平面PＢC,∴AＤ⊥BC.∵PA⊥平面ABC,平面AＢC，∴ＰA⊥BC.∵AD∩PＡ=A，∴BC⊥平面PAC.（另外还可证ＢC分别与相交直线AD,AC垂直,从而得到BC⊥平面PAＣ）.评注:已知条件就是线面垂直与面面垂直,要证明两条直线垂直,应将两条直线中得一条纳入一个平面中，使另一条直线与该平面垂直，即从线面垂直得到线线垂直.在空间图形中,高一级得垂直关系中蕴含着低一级得垂直关系,通过本题可以瞧到，面面垂直线面垂直线线垂直．一般来说，线线垂直或面面垂直都可转化为线面垂直来分析解决,其关系为：线线垂直线面垂直面面垂直.这三者之间得关系非常密切,可以互相转化,从前面推出后面就是判定定理,而从后面推出前面就是性质定理.同学们应当学会灵活应用这些定理证明问题．下面举例说明.３如图１所示,ABCD为正方形,⊥平面ＡBＣD,过且垂直于得平面分别交于.求证:,.证明:∵平面ABCD,∴.∵,∴平面SAB．又∵平面SAB,∴.∵平面ＡEFＧ，∴．∴平面ＳＢC.∴．同理可证．评注:本题欲证线线垂直,可转化为证线面垂直,在线线垂直与线面垂直得转化中,平面起到了关键作用，同学们应多注意考虑线与线所在平面得特征,从而顺利实现证明所需要得转化.4 如图２,在三棱锥A－ＢCＤ中，ＢC＝ＡＣ,AＤ＝ＢD,作ＢE⊥CD,Ｅ为垂足,作ＡH⊥BＥ于H.求证:ＡＨ⊥平面BCD.证明:取AB得中点F，连结ＣＦ,DF.∵,∴.∵，∴．又,∴平面CDＦ.∵平面ＣDＦ，∴.又,,∴平面ＡBE,．∵,，,∴平面BCD.评注:本题在运用判定定理证明线面垂直时,将问题转化为证明线线垂直；而证明线线垂直时,又转化为证明线面垂直.如此反复，直到证得结论.5 如图3,就是圆Ｏ得直径,C就是圆周上一点,平面ABC.若ＡE⊥ＰC ,E为垂足,F就是PB上任意一点，求证:平面AEF⊥平面PBC.证明：∵AＢ就是圆Ｏ得直径,∴.∵平面ABC，平面ＡBC,∴.∴平面AＰC.∵平面PＢC,∴平面ＡPＣ⊥平面PBＣ．∵ＡＥ⊥PC,平面APC∩平面PBC＝PＣ,∴AE⊥平面ＰBC.∵平面AEF,∴平面AEF⊥平面ＰBC.评注:证明两个平面垂直时,一般可先从现有得直线中寻找平面得垂线,即证线面垂直，而证线面垂直则需从已知条件出发寻找线线垂直得关系.6、空间四边形AＢCD中,若ＡB⊥CD,BＣ⊥AD，求证:ＡC⊥BD证明:过Ａ作AＯ⊥平面BCD于O同理ＢC⊥ＤO ∴Ｏ为△AＢC得垂心7、证明:在正方体ABCD－A1B1C1Ｄ1中，Ａ1C⊥平面BC１D证明:连结AＣAC 为A 1C 在平面A Ｃ上得射影8、 如图，平面A ＢCD,ＡBCD 就是矩形,M 、N 分别就是ＡB 、PC 得中点,求证:、 证：取PD 中点E,则9如图在ΔＡＢC 中, AD ⊥ＢC, ED=2AE, 过E 作FG ∥BC, 且将ΔＡFG 沿F Ｇ折起,使∠A 'ＥD ＝6０°,求证:A ＇E ⊥平面A 'BC 分析： 弄清折叠前后,图形中各元素之间得数量关系与位置关系。

线面垂直判定经典证明题第一篇：线面垂直判定经典证明题线面垂直判定1、已知：如图，PA⊥AB，PA⊥AC。

求证：PA⊥平面ABC。

2、已知：如图，PA⊥AB，BC⊥平面PAC。

求证：PA⊥BC。

3、如图，在三棱锥V-ABC中，VA=VC，AB=BC。

求证：VB⊥AC4、在正方体ABCD-EFGH中，O为底面ABCD中心。

求证：BD⊥平面AEGC5、如图，AB是圆O的直径，PA⊥AC, PA⊥AB,求证：BC⊥平面PAC6、如图，AD⊥BD, AD⊥DC,AD=BD=CD,∠BAC=60°求证：BD⊥平面ADC7、.如图所示，PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点.(1)求证：MN∥平面PAD.(2)求证：MN⊥CD.(3)若∠PDA＝45°，求证：MN⊥平面PCD.8、已知：如图，P是棱形ABCD所在平面外一点，且PA=PC 求证：AC⊥平面PBD __C9、已知四面体ABCD中，AB=AC,BD=CD,平面ABC⊥平面BCD,E为棱BC的中点。

（1）求证：AE⊥平面BCD;（2）求证：AD⊥BC;BECD10、三棱锥A-BCD中，AB=1，AD=2，求证：AB⊥平面BCD11、在四棱锥S-ABCD中，SD⊥平面ABCD，底面ABCD是正方形求证：AC⊥平面SBD12、如图，正方形ABCD所在平面与三角形CDE所在平面相交于CD，AE⊥平面CDE，求证：AB⊥平面ADE；AED13、三棱锥P-ABC中，三条侧棱PA，PB，PC两两垂直，H是△ABC的垂心求证:PH 底面ABC14、正方体ABCD-A1B1C1D1中，求证：A1C⊥平面BC1D._A_115、S是△ABC所在平面外一点，SA⊥平面ABC,平面SAB⊥平面SBC,求证AB⊥BCSCAB16、如图，直三棱柱ABC—A1B1C1 中，AC ＝BC ＝1，∠ACB ＝90°，AA1 ＝2，D 是A1B1 中点．求证C1D ⊥平面A1B ；第二篇：线面垂直的判定漯河高中2013—2014高一数学必修二导学案2.3.3直线与平面垂直的性质2.3.4平面与平面垂直的性质编制人：魏艳丽方玉辉审核人：高一数学组时间：2013.12.03【课前预习】一、预习导学1、直线与平面垂直的性质定理：_________________________________________.2、垂直于同一条直线的两个平面____________.3、平面与平面垂直的性质定理：_________________________________________.4、如果两个平面互相垂直，那么经过第一个平面内的一点垂直于第二个平面的直线在___________.二、预习检测教材P71、P73【课内探究】［例1］如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面.［例2］如图，已知矩形ABCD，过A作SA⊥平面AC，再过A作AE⊥SB交SB于E，过E作EF⊥SC交SC于F.（1）求证：AF⊥SC；（2）若平面AEF交SD于G，求证：AG⊥SD.我主动，我参与，我体验，我成功第1页（共4页）［例3］10、在三棱锥P—ABC中，△PAB是等边三角形，∠PAC=∠PBC=90º.（1）证明：AB⊥PC；（2）若PC=4，且平面PAC⊥平面PBC，求三棱锥P—ABC的体积.［例4］如图所示，在斜三棱柱A1B1C1—ABC中，底面是等腰三角形，AB=AC，侧面BB1C1C⊥底面ABC.（1）若D是BC的中点，求证：AD⊥CC1；（2）过侧面BB1C1C的对角线BC1的平面交侧棱于M，若AM=MA1，求证：截面MBC1⊥侧面BB1C1C；（3）若截面MBC1⊥平面BB1C1C，则AM=MA1吗？请叙述你的判断理由.我主动，我参与，我体验，我成功第2页（共4页）【巩固训练】1．已知两个平面互相垂直，那么下列说法中正确的个数是()①一个平面内的直线必垂直于另一个平面内的无数条直线；②一个平面内垂直于这两个平面交线的直线必垂直于另一个平面内的任意一条直线；③过一个平面内一点垂直于另一个平面的直线，垂足必落在交线上；④过一个平面内的任意一点作交线的垂线，则此直线必垂直于另一个平面． A．4B．3C．2D．1()()2．在圆柱的一个底面上任取一点(该点不在底面圆周上)，过该点作另一底面的垂线，则这条垂线与圆柱的母线所在直线的位置关系是A．相交B．平行C．异面D．相交或平行3．若m、n表示直线，α表示平面，则下列命题中，正确命题的个数为m∥n⎫m⊥α⎫⎪⎪⎬⎬⇒m∥n；①⇒n⊥α；②⎪⎪m⊥α⎭n⊥α⎭m⊥α⎫m∥α⎫⎪⎪⎬⎬⇒n⊥α.③⇒m⊥n;④⎪⎪n∥α⎭m⊥n⎭A．4B．3C．2D．1D．重心oo4．在△ABC所在的平面α外有一点P，且PA＝PB＝PC，则P在α内的射影是△ABC的()A．垂心B．外心C．内心5.如图所示，平面α⊥平面β，A∈α，B∈β，AB与两平面α、β所成的角分别为45和30.过A、B分别作两平面交线的垂线，垂足分别为A′、B′，则AB∶A′B′等于()A．3∶1B．2∶1C．3∶2D．4∶36．设α－l－β是直二面角，直线a⊂α，直线b⊂β，a，b与l都不垂直，那么()A．a与b可能垂直，但不可能平行B．a与b不可能垂直，但可能平行 C．a与b可能垂直，也可能平行 D．a与b不可能垂直，也不可能平行7．若α⊥β，α∩β＝AB，a∥α，a⊥AB，则a与β的关系为________．8．直线a和b在正方体ABCD－A1B1C1D1的两个不同平面内，使a∥b成立的条件是________．①a和b垂直于正方体的同一个面；②a和b在正方体两个相对的面内，且共面；③a和b平行于同一条棱；④a和b在正方体的两个面内，且与正方体的同一条棱垂直．9.如图，在三棱锥P－ABC中，PA⊥平面ABC，平面PAB⊥平面PBC.我主动，我参与，我体验，我成功第3页（共4页）求证：BC⊥AB.10.如图所示，在正方体ABCD—A1B1C1D1中，M是AB上一点，N是A1C的中点，MN⊥平面A1DC.求证：(1)MN∥AD1；(2)M是AB的中点．11．如图所示，在多面体P—ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知BD＝2AD＝8，AB＝2DC＝4(1)设M是PC上的一点，求证：平面M BD⊥平面PAD；(2)求四棱锥P—ABCD的体积．※12．如图，直三棱柱ABC－A1B1C1中，AC＝BC＝1，D是棱AA12的中点，DC1⊥BD.(1)证明：DC1⊥BC；(2)求二面角A1－BD－C1的大小．我主动，我参与，我体验，我成功第4页（共4页）第三篇：线面垂直的判定1（模版）深圳市第二课堂文化教育徐老师***直线与平面垂直的判定1．一条直线和三角形的两边同时垂直，则这条直线和三角形的第三边的位置关系是（）A．平行B．垂直C．相交不垂直D．不确定2．直线a与b垂直，b⊥平面α，则a与平面α的位置关系是()A．a∥αB．a⊥αC．a⊂αD．a⊂α或a∥α3．已知m，n为两条不同的直线，α，β为两个不同的平面，则下列命题中正确的是（）A ．m⊂α,n⊂α,m//β,n//β⇒α//βB．α//β,m⊂α,n⊂β⇒m//nC．m⊥α,m⊥n⇒n//αD． m//n,n⊥α⇒m⊥α4．已知两条直线m,n，两个平面α,β，给出下面四个命题：①m//n,m⊥α⇒n⊥α②α//β,m⊂α,n⊂β⇒m//n③m//n,m//α⇒n//α④α//β,m//n,m⊥α⇒n⊥β其中正确命题的序号是（）A．①③B．②④C．①④D．②③5．已知正三棱柱ABC－A1B1C1的侧棱长与底面边长相等，则AB1与侧面ACC1A1所成角的正弦等于（）A．BC．D26．如图，已知正三棱柱ABC-A1B1C1的所有棱长都相等，D是A1C1的中点，则直线AD 与平面B1DC所成角的正弦值为.7．如图，在正三棱柱ABC-A1B1C1中，侧棱长为2，底面三角形的边长为1，则BC1与侧面ACC1A1所成的角是．（第6题图）（第7题图）8．已知∆ABC所在平面外一点P到∆ABC三顶点的距离都相等，则点P在平面ABC内的射影是∆ABC的。

线面垂直判定定理测试题1.如图，在三棱锥P-ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA＝AB＝BC＝2，D为线上一点．段AC的中点，E为线段PC（2）求证：平面BDE⊥平面PAC；（3）当PA//平面BDE时，求三棱锥E-BCD的体积．2.如图，在四棱锥P-ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：AB∥EF；（2）若PA=AD，且平面PAD⊥平面ABCD，求证：AF⊥平面PCD．第1页，共11页3.如图，已知AF⊥面ABCD，四边形ABEF为矩形，四边形ABCD为直角梯形，∠DAB=90°，AB∥CD，AD=AF=CD=1，AB=2 （1）求证：AF∥面BCE；（2）求证：AC⊥面BCE；的体积．（3）求三棱锥E-BCF的体积．4.如图，四面体ABCD中，△ABC是正三角形，AD＝CD． （1）证明：AC⊥BD；（2）已知△ACD是直角三角形，AB＝BD，若E为棱BD上与D不重合的点，的体积比．且AE⊥EC，求四面体ABCE与四面体ACDE的体积比．5.如图，多面体ABCDS中，面ABCD为矩形，SD⊥AD，且SD⊥AB，AD=1，AB=2，SD=．（1）求证：CD⊥平面ADS；（2）求AD与SB所成角的余弦值；所成角的余弦值；的余弦值．（3）求二面角A-SB-D的余弦值．6.如图，在四棱锥P-ABCD中，底面ABCD是矩形，平面PAD⊥平面ABCD，AP=AD，M，N分别为棱PD，PC的中点．求证：的中点．求证：（1）MN∥平面PAB；（2）AM⊥平面PCD．7.如图所示四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，BC∥AD，PA=AB=BC=2，AD=4，E为PD的中点，F为PC中点．中点．（Ⅰ）求证：CD⊥平面PAC；（Ⅱ）求证：BF∥平面ACE；所成的角的正弦值．（Ⅲ）求直线PD与平面PAC所成的角的正弦值．答案和解析1.【答案】（1）证明：由PA⊥AB，PA⊥BC，AB⊂平面ABC，BC⊂平面ABC，且AB∩BC=B，A B可得PA⊥平面ABC，由BD⊂平面ABC，可得PA⊥BD；的中点，（2）证明：由AB=BC，D为线段AC的中点，可得BD⊥AC，由PA⊥平面ABC，PA⊂平面PAC，可得平面PAC⊥平面ABC，又平面PAC∩平面ABC=AC，BD⊂平面ABC，且BD⊥AC，即有BD⊥平面PAC，BD⊂平面BDE，可得平面BDE⊥平面PAC；（3）解:PA//平面BDE，PA⊂平面PAC，且平面PAC∩平面BDE=DE，可得PA//DE，又D为AC的中点，的中点，可得E为PC的中点，且DE=PA=1，由PA⊥平面ABC，可得DE⊥平面ABC，2=1，可得S△BDC=S△ABC=××2×2×2=1则三棱锥E-BCD的体积为DE•S△BDC=×1×1×1=1=．【解析】本题考查空间的线线、线面和面面的位置关系的判断，主要是平行和垂直的关系，注意运用线面平行的性质定理以及线面垂直的判定定理和性质定理，面面垂直的判定定理和性质定理，同时考查三棱锥的体积的求法，考查空间想象能力和推理能力，属于中档题．（1）运用线面垂直的判定定理可得PA⊥平面ABC，再由性质定理即可得证；（2）要证平面BDE⊥平面PAC，可证BD⊥平面PAC，由（1）运用面面垂直的判定定理可得平面PAC⊥平面ABC，再由等腰三角形的性质可得BD⊥AC，运用面面垂直的性质定理，即可得证；（3）由线面平行的性质定理可得PA//DE，运用中位线定理，可得DE的长，以及DE⊥平面ABC，求得三角形BCD的面积，运用三棱锥的体积公式计算即可得到所求值．2.【答案】解：（1）证明：是正方形，）证明： 底面ABCD是正方形，AB∥CD , 又AB⊄平面PCD，CD⊂平面PCD，AB∥平面PCD , 又A，B，E，F四点共面，且平面ABEF∩平面PCD=EF，AB∥EF ; （2）证明：在正方形ABCD中，CD⊥AD , 又平面PAD⊥平面ABCD，且平面PAD∩平面ABCD=AD，CD⊂平面ABCD,CD⊄平面PADCD⊥平面PAD , 又AF⊂平面PAD , CD⊥AF , 由（1）可知，AB∥EF，在同一平面内，又AB∥CD，C,D,E,F在同一平面内，CD∥EF , 中点，点E是棱PC中点，点F是棱PD中点, 中， PA=AD，在△PAD中，AF⊥PD , 又PD∩CD=D，PD、CD⊂平面PCD, AF⊥平面PCD．【解析】（1）证明AB∥平面PCD，即可得AB∥EF；（2）利用平面PAD⊥平面ABCD，证明CD⊥AF，PA=AD，所以AF⊥PD，即可证明AF⊥平面PCD；本题考查线面平行的性质，平面与平面垂直的性质，考查线面垂直，考查学生分析解决问题的能力，属于中档题．3.【答案】（1）证明：）证明：四边形ABEF 为矩形，AF ∥BE ，AF ⊄平面BCE ，BE ⊄平面BCE ，AF ∥面BCE ．（2）证明：）证明： AF ⊥面ABCD ，四边形ABEF 为矩形，为矩形，BE ⊥平面ABCD ，AC ⊂平面ABCD ， AC ⊥BE ，四边形ABCD 为直角梯形，∠DAB =90°，AB ∥CD ，AD =AF =CD =1，AB =2 AC =BC = = ，AC 2+BC 2=AB 2， AC ⊥BC ， BC ∩BE =B ， AC ⊥面BCE ．（3）解：三棱锥E -BCF 的体积：V E -BCF =V C -BEF =△ = == ．【解析】本题考查线面平行、线面垂直的证明，考查三棱锥的体积的求法，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、转化化归思想，考查数据处理能力和运用意识，是中档题．（1）推导出AF ∥BE ，由此能证明AF ∥面BCE ．（2）推导出AC ⊥BE ，AC ⊥BC ，由此能证明AC ⊥面BCE ．（3）三棱锥E-BCF 的体积V E-BCF =V C-BEF ，由此能求出结果．4.【答案】证明：（1）取AC 中点O ，连结DO 、BO ， △ABC 是正三角形，AD =CD ，DO ⊥AC ，BO ⊥AC ，DO ∩BO =O ， AC ⊥平面BDO ，BD ⊂平面BDO ， AC ⊥BD ．（2）解：连结OE ，由（1）知AC ⊥平面OBD ，OE ⊂平面OBD ， OE ⊥AC ，设AD =CD = ，则OC =OA =1，EC =EA ，AE ⊥CE ，AC =2， EC 2+EA 2=AC 2，EC =EA = =CD ，E 是线段AC 垂直平分线上的点，垂直平分线上的点， EC =EA =CD = ，由余弦定理得：由余弦定理得：cos ∠CBD = = ， 即 ，解得BE =1或BE =2，BE ＜BD =2， BE =1， BE =ED ，四面体ABCE 与四面体ACDE 的高都是点A 到平面BCD 的高h ，BE =ED ， S △DCE =S △BCE ，四面体ABCE 与四面体ACDE 的体积比为1．【解析】本题考查线线垂直的证明，考查两个四面体的体积之比的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力、空间想象能力，考查数形结合思想、化归与转化思想，是中档题．（1）取AC 中点O ，连结DO 、BO ，推导出DO ⊥AC ，BO ⊥AC ，从而AC ⊥平面BDO ，由此能证明AC ⊥BD ．（2）连结OE ，设AD=CD=，则OC=OA=1，由余弦定理求出BE=1，由BE=ED ，四面体ABCE 与四面体ACDE 的高都是点A 到平面BCD 的高h ，S △DCE =S △BCE ，由此能求出四面体ABCE 与四面体ACDE 的体积比．5.【答案】解：（I ）证明：）证明：ABCD 是矩形，是矩形， CD ⊥AD 又SD ⊥AB ，AB ∥CD ，则CD ⊥SD （2分）分）AD ⊥SDCD ⊥平面ADS（II ）矩形ABCD ， AD ∥BC ，即BC =1，要求AD 与SB 所成的角，即求BC 与SB 所成的角所成的角在△SBC 中，由（1）知，SD ⊥面ABCD ．Rt △SDC 中， CD 是CS 在面ABCD 内的射影，且BC ⊥CD ，SC ⊥BCtan ∠SBC = cos ∠SBC =从而SB 与AD 的成的角的余弦为 ．（III ） △SAD 中SD ⊥AD ，且SD ⊥ABSD ⊥面ABCD ．平面SDB ⊥平面ABCD ，BD 为面SDB 与面ABCD 的交线．的交线．过A 作AE ⊥DB 于E AE ⊥平面SDB又过A 作AF ⊥SB 于F ，连接EF ，从而得：EF ⊥SB ∠AFB 为二面角A -SB -D 的平面角的平面角在矩形ABCD 中，对角线中，对角线 BD = 在△ABD 中，AE = 由（2）知在Rt △SBC ， ． 而Rt △SAD 中，SA =2，且AB =2， SB 2=SA 2+AB 2， △SAB 为等腰直角三角形且∠SAB 为直角，为直角，所以所求的二面角的余弦为【解析】 （1）要证CD ⊥平面ADS ，只需证明直线CD 垂直平面ADS 内的两条相交直线AD 、SD 即可；（2）要求AD 与SB 所成的角，即求BC 与SB 所成的角，解三角形可求AD 与SB 所成角的余弦值；（3）过A 作AE ⊥DB 于E 又过A 作AF ⊥SB 于F ，连接EF ，说明∠AFB 为二面角A-SB-D 的平面角，解三角形可求二面角A-SB-D 的余弦值．本题考查直线与平面垂直的判定，二面角的求法，异面直线所成的角，考查学生逻辑思维能力，计算能力，是中档题．6.【答案】证明：（1）因为M 、N 分别为PD 、PC的中点，的中点，所以MN ∥DC ，又因为底面ABCD 是矩形，是矩形，所以AB ∥DC ．所以MN ∥AB ，又AB ⊂平面PAB ，MN ⊄平面PAB ，所以MN ∥平面PAB ．（2）因为AP =AD ，P 为PD 的中点，所以AM ⊥PD ． 因为平面PAD ⊥平面ABCD ，又平面PAD ∩平面ABCD =AD ，CD ⊥AD ，CD ⊂平面ABCD ，所以CD ⊥平面PAD ， 又AM ⊂平面PAD ，所以CD ⊥AM ．因为CD 、PD ⊂平面PCD ，CD ∩PD =D ，AM ⊥平面PCD ．【解析】（1）推导出MN ∥DC ，AB ∥DC ．从而MN ∥AB ，由此能证明MN ∥平面PAB ．（2）推导出AM ⊥PD ，CD ⊥AD ，从而CD ⊥平面PAD ，进而CD ⊥AM ，由此能证明AM ⊥平面PCD ．本题考查线面平行、线面垂直的证明，考查空间中线线、线面、面面间的位置关系等基础知识，考查推理论证能力、运算求解能力，考查化归与转化思想、数形结合思想，是中档题．7.【答案】（Ⅰ）证明：因为PA ⊥底面ABCD ，CD ⊂面ABCD ，所以PA ⊥CD ，又因为直角梯形ABCD 中， ， ，所以AC 2+CD 2=AD 2，即AC ⊥CD ，又PA ∩AC =A ，所以CD ⊥平面PAC ；（Ⅱ）解法一：如图，连接BD ，交AC 于O ，取PE 中点G ，连接BG ，FG ，EO ，则在△PCE 中，FG ∥CE ，又EC ⊂平面ACE ，FG ⊄平面ACE ，所以FG ∥平面ACE ，因为BC ∥AD ，所以 ，则OE ∥BG ，又OE ⊂平面ACE ，BG ⊄平面ACE ，所以BG ∥平面ACE ，又BG ∩FG =G ，所以平面BFG ∥平面ACE ，因为BF ⊂平面BFG ，所以BF ∥平面ACE ．解法二：如图，连接BD ，交AC 于O ，取PE 中点G ， 连接FD 交CE 于H ，连接OH ，则FG ∥CE ，在△DFG 中，HE ∥FG ，则 ，在底面ABCD 中，BC ∥AD ，所以 ， 所以 ，故BF ∥OH ，又OH ⊂平面ACE ，BF ⊄平面ACE ，所以BF ∥平面ACE ．（Ⅲ）由（Ⅰ）可知，CD ⊥平面PAC ，所以∠DPC 为直线PD 与平面PAC 所成的角，所成的角，在Rt △PCD 中， ， ，所以 ，所以直线PD 与平面PAC 所成的角的正弦值为． 【解析】本题考查线面垂直、线面平行，考查线面角，解题的关键是掌握线面垂直、线面平行的判定方法，正确找出线面角．（Ⅰ）证明CD⊥平面PAC，证明PA⊥CD，AC⊥CD即可；（Ⅱ）解法一：连接BD，交AC于O，取PE中点G，连接BG，FG，EO，证明平面BFG∥平面ACE，即可证得BF∥平面ACE；解法二：如图，连接BD，交AC于O，取PE中点G，连接FD交CE于H，连接OH，则证明BF∥OH，即可证得BF∥平面ACE；（Ⅲ）确定∠DPC为直线PD与平面PAC所成的角，在Rt△PCD中，即可求得直线PD与平面PAC所成的角的正弦值．第11页，共11页。

线面、面面垂直练习卷1．如图，在四棱锥P−ABCD中，底面ABCD为平行四形,AB=2AD=2,∠DAB=600,PD=BD,，且PD⊥底面ABCD.(Ⅰ)证明：BC⊥平面PBD；（Ⅱ）若Q为PC的中点，求三棱锥A−PBQ的体积.-中，底面ABCD是菱形，PA⊥平面ABCD，2．如图，在四棱锥P ABCDM N分别为,PB PD的中点．,MN平面ABCD；（1）求证：//（2）求证：平面PAC⊥平面AMN．3．如图，在四棱锥P−ABCD中，底面ABCD是正方形．点E是棱PC的中点，平面ABE与棱PD交于点F．（1）求证：AB//EF；（2）若PA=AD，且平面PAD⊥平面ABCD，试证明AF⊥平面PCD.4．如图，在三棱锥P–ABC中，PA⊥AB，PA⊥BC，AB⊥BC，PA=AB=BC=2，D为线段AC的中点，E为线段PC上一点．（1）求证：PA⊥BD；（2）求证：平面BDE⊥平面PAC；（3）当PA∥平面BDE时，求三棱锥E–BCD的体积．5．在三棱锥P ABC -中，PB ⊥底面,90,ABC BCA M ∠= 为AB 的中点，E 为PC 的中点，点F 在PA 上，且2AF FP =.（1）求证：AC ⊥平面PBC ；（2）求证：//CM 平面BEF ；（3）若2PB BC CA ===，求三棱锥E ABC -的体积.6．如图，四棱锥P −ABCD 中，底面ABCD 是平行四边形，且平面PAC ⊥平面ABCD ，E 为PD 的中点，PA =PC ，AB =2BC =2，∠ABC =60°．（Ⅰ）求证：PB//平面ACE ；（Ⅱ）求证：平面PBC ⊥平面PAC ．7．如图，正方体1111D C B A ABCD -中，E 是1DD 的中点．（1）求证：1BD ∥平面AEC ；（2）求1BC 与平面11A ACC 所成的角.8，如图，DC ⊥平面ABC ，//EB DC ，22AC BC EB DC ====，120ACB ∠= ，,P Q 分别为,AE AB 的中点．（I ）证明：//PQ 平面ACD ；（II ）求AD 与平面ABE 所成角的正弦值．。

立体几何1．P 点在则ABC ∆所在的平面外，O 点是P 点在平面ABC 内的射影 ,PA 、PB 、PC 两两垂直，则D 点是则ABC ∆ （ B )（A)重心 (B) 垂心 (C)内心 (D ）外心2．与两个相交平面的交线平行的直线和这两个平面的位置关系是 （ A ）（A)都平行 (B) 都相交（C) 在两个平面内 （D)至少与其中一个平行3．若两个平面内分别有一条直线，这两条直线互相平行，那么这两平面的位置关系是（ A ）(A)平行 （B ） 相交 (C ）平行或相交 (D ）垂直4．在空间,下述命题正确的是 （ B )（A)若直线//a 平面M ,直线b a ⊥,则直线⊥b 平面M(B ）若平面M //平面N ,则平面M 内任意直线a //平面N(C ）若平面M 与N 的交线为a ，平面M 内的直线a b ⊥,则N b ⊥(D ）若平面N 的两条直线都平行平面M ，则平面N //平面M5．a 、b 表示两条直线，α、β、γ表示三个平面，下列命题中错误的是 （A)(A ）,,αα⊂⊂b a 且ββ//,//b a ,则βα// （B ）a 、b 是异面直线，则存在唯一的平面与a 、b 等距 （C) ,,,b a b a ⊥⊂⊥βα则βα// （D),,,//,βαβγγα⊥⊥⊥b a 则b a ⊥6.直线l //平面α,αβ⊥，则l 与平面β的位置关系是 ( D )（A ） l β⊂ （B ） //l β （C) l β与相交 (D ） 以上三种情况均有可能7．已知直线l ⊥平面α，直线m ⊂平面β，有以下四个命题：①//l m αβ⇒⊥②//l m αβ⊥⇒③//l m αβ⇒⊥④//l m αβ⊥⇒,其中正确的是（D ）（A) ①② (B) ②④ (C) ③④ （D ） ①③8．αβγδ，，，是四个不同的平面，且αγβγαδβδ⊥⊥⊥⊥，，，，则（ B )（A) ////αβγδ或 （B ） ////αβγδ且(C) 四个平面中可能任意两个都不平行 (D ） 四个平面中至多有一对平面平行9．已知平面α和平面β相交,a 是α内的一条直线,则（ D ）（A) 在β内一定存在与a 平行的直线 (B) 在β内一定存在与a 垂直的直线(C) 在β内一定不存在与a 平行的直线 （D ） 在β内一定不存在与a 垂直的直线10．已知PA ⊥正方形ABCD 所在平面,垂足为A ,连PB PC PD AC BD ，，、，,则互相垂直的平面有（ C ）（A) 5对 (B) 6对 （C) 7对 （D ） 8对12。

2.3 线面垂直和面面垂直线面垂直专题练习一、定理填空：1.直线和平面垂直假如一条直线和，就说这条直线和这个平面垂直 .2.线面垂直判断定理和性质定理 线面垂直判断定理：假如一条直线和一个平面内的两条订交直线都垂直，那么这条直线垂直于这个平面 .判断定理 1：假如两条平行线中的一条垂直于一个平面，那么判断定理 2：假如一条直线垂直于两个平行平面中的一个平面，那么 .线面垂直性质定理：垂直于同一个平面的两条直线相互平行.性质定理 1：垂直于同一条直线的两个平面相互平行。

二、优选习题：1.设 M 表示平面， a 、 b 表示直线，给出以下四个命题：a //b a M a M a // M b ⊥ M.①b M②ba //b ③bb ∥ M ④aMMaa b此中正确的命题是 ()A. ①②B.①②③C.②③④D.①②④2.如下图，在正方形 ABCD 中，E 、F 分别是 AB 、BC 的中点 .此刻沿 DE 、DF 及 EF 把△ ADE 、 △ CDF 和 △ BEF 折起，使 A 、B 、 C 三点重合，重合后的点记为P.那么，在四周体P — DEF中，必有 ()第 3 题图A. DP ⊥平面 PEFB.DM ⊥平面⊥平面 DEFD.PF ⊥平面 DEF 3.设 a 、 b 是异面直线，以下命题正确的选项是()A. 过不在 a 、 b 上的一点 P 必定能够作一条直线和 a 、b 都订交B.过不在 a 、 b 上的一点 P 必定能够作一个平面和 a 、 b 都垂直C.过 a 必定能够作一个平面与 b 垂直D.过 a 必定能够作一个平面与b 平行4.假如直线 l,m 与平面 α , β满,足γ :l=β∩γ,l ∥α,m α和 m ⊥ γ,那么必有( )A. α⊥ γ且 l ⊥ m B . α⊥ γ且 m ∥ β∥ β且 l ⊥ mD. α∥β且 α⊥ γ5.有三个命题：②过平面α的一条斜线 l 有且仅有一个平面与α垂直；③异面直线a、 b 不垂直，那么过 a 的任一个平面与 b 都不垂直此中正确命题的个数为6.设 l 、 m 为直线，α为平面，且l ⊥ α，给出以下命题①若m⊥ α，则m∥ l；②若m⊥ l，则m∥ α；③若m∥ α，则m⊥l；④若m∥ l，则m⊥ α，此中真命题的序号是()．．．A. ①②③B. ①②④C.②③④D.①③④7.如下图 ,三棱锥 V-ABC 中,AH ⊥侧面 VBC,且 H 是△ VBC 的垂心， BE 是 VC 边上的高 . 求证 :VC⊥ AB;8.如下图， PA⊥矩形 ABCD 所在平面， M、 N 分别是 AB、PC 的中点 .(1)求证： MN ∥平面 PAD .(2)求证： MN ⊥ CD .(3)若∠ PDA＝ 45°，求证： MN ⊥平面 PCD.9.已知直三棱柱ABC-A1B1C1中，∠ ACB =90°,∠ BAC=30°,BC=1 ，AA1=6 ，M是CC1的中点，求证： AB 1⊥ A1 M．10.如下图，正方体 ABCD — A′B′C′D′的棱长为 a， M 是 AD 的中点， N 是 BD ′上一点，且D ′N∶ NB＝ 1∶ 2，MC 与 BD 交于 P.(1)求证： NP⊥平面 ABCD .(2)求平面 PNC 与平面 CC′D′D 所成的角 .⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯11. 假如两条平行直线中的一条垂直于一个平面，那么另一条也垂直于同一个平面.解：已知a∥b，a⊥ α . 求证： b⊥ α .12.已知点 P 为平面 ABC外一点， PA⊥BC，PC⊥ AB，求证： PB⊥AC.13.在正方体 ABCD— A1B1C1D1中，求直线 A1B 和平面 A1B1CD所成的角 .14.如图，四周体 A— BCD的棱长都相等， Q 是 AD的中点，求 CQ与平面 DBC所成的角的正弦值 .15.如图11(1) ，在直四棱柱ABCD—A1B1C1D1中，已知 DC=DD1=2AD=2AB，AD⊥DC，AB∥DC.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯(1)求证： D1C⊥AC1；（2）设 E 是 DC上一点，试确立 E 的地点，使 D1E∥平面 A1BD，并说明原因 .16.如图 12，在正方体 ABCD— A1B1C1D1， G为 CC1的中点，O为底面 ABCD的中心 .求证： A1O⊥平面 GBD.17. 如图，已知a、 b 是两条相互垂直的异面直线，线段AB与两异面直线a、 b 垂直且订交，线段 AB的长为定值 m，定长为 n（ n＞ m）的线段 PQ的两个端点分别在 a、b 上挪动， M、N 分别是 AB、 PQ的中点 .求证：（ 1）AB⊥MN；（2）MN的长是定值.18.如图，已知在侧棱垂直于底面三棱柱ABC— A1B1C1中 ,AC=3 ， AB=5， BC=4,AA1=4, 点 D 是 AB 的中点 .（1）求证： AC⊥BC1;（2）求证： AC1∥平面 CDB1.面面垂直专题练习一、定理填空⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯最新料介绍⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯面面垂直的判断定理：面面垂直的性质定理：二、优选习题1、正方形 ABCD沿对角线 AC折成直二面角后，AB与 CD所成的角等于____________2、三棱锥P ABC 的三条侧棱相等，则点P 在平面 ABC上的射影是△ ABC的 ____心 .3、一条直线与两个平面所成角相等，那么这两个平面的地点关系为______________4、在正三棱锥中，相邻两面所成二面角的取值范围为___________________5、已知l是直二面角， A, B, A、 B l ，设直线AB与成 30 角，AB=2，B到 A 在l上的射影 N 的距离为 2 ，则AB与所成角为 ______________.6、在直二面角AB棱AB上取一点P，过P分别在,平面内作与棱成45°角的斜线 PC、 PD，则∠ CPD的大小是 _____________7、正四周体中相邻双侧面所成的二面角的余弦值为___________________.8. 如图，在正方体ABCD-A1B1C1D1中. 求证：平面 ACD1⊥平面 BB1D1DD1C1A1B1DCA B10、如图，三棱锥P ABC 中，PA⊥平面ABC，AC⊥BC，求证：平面PAC⊥平面 PBC．PA BC11、如图，三棱锥P ABC中， PA⊥平面 ABC，平面 PAC⊥平面 PBC．问△ ABC能否为直角三角形，假如，请给出证明；若不是，请举出反例．PA BC。