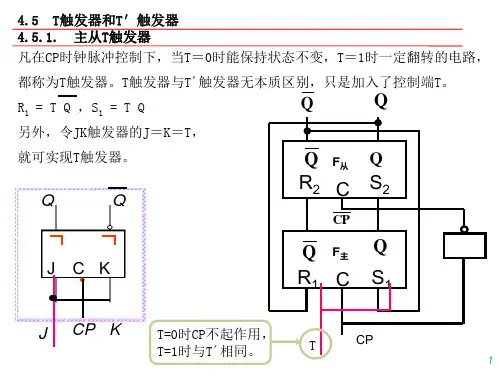
触发器的特性方程及时序图
- 格式:doc
- 大小:19.50 KB
- 文档页数:8







各触发器的特点触发器是数字电路中重要的组成部分,它们用于存储和传输数据。
触发器的特点包括稳态、传输、存储和时序等方面。
本文将对各种常见的触发器进行详细介绍。
一、SR触发器SR触发器是最简单的触发器之一,由两个交叉连通的输入端S和R组成,它们分别代表“设置”和“复位”,可以通过这些输入来控制输出Q和Q'。
当S=1、R=0时,输出Q为1;当S=0、R=1时,输出Q为0;当S=R=0时,输出保持原状态。
SR触发器的特点:1. 稳态:SR触发器有两个稳态:SET(S=1,R=0)和RESET(S=0,R=1)。
在这些状态下,输出保持不变。
2. 传输:当输入为(S,R)=(1,1)时,SR触发器处于不稳定状态,并且无法确定输出。
此外,在SET或RESET状态下输入(S,R)=(0,0),也会导致不确定性。
3. 存储:在SET或RESET状态下输入(S,R)=(0,1)或(1,0),SR触发器会从当前状态转换到相反的状态。
4. 时序:在SET或RESET状态下输入(S,R)=(1,0)或(0,1)时,SR 触发器会在下一个时钟沿发生状态转换。
二、D触发器D触发器是一种单稳态触发器,由一个输入端D和一个时钟输入端CLK组成。
当CLK的上升沿到来时,D触发器将输入信号D复制到输出Q上。
D触发器的特点:1. 稳态:D触发器只有一个稳态。
在没有输入信号时,输出保持不变。
2. 传输:当输入信号改变时,需要等待下一个时钟沿才能反映在输出上。
3. 存储:当输入信号改变后,在下一个时钟沿之前,输出保持原样。
4. 时序:在每个时钟周期内,D触发器都会从输入端读取数据,并将其复制到输出端。
三、JK触发器JK触发器是一种双稳态触发器,由两个交叉连通的输入端J和K组成。
与SR触发器类似,JK触发器可以通过这些输入来控制输出Q和Q'。
但与SR不同的是,在JK中不存在无法确定状态的情况。
JK触发器的特点:1. 稳态:JK触发器有两个稳态:SET(J=1,K=0)和RESET(J=0,K=1)。



触发器的特性方程及时序图注意:1) CP 脉冲的画法(高低电平脉宽一致);2) 状态不定时高低电平都画上,中间斜线填充;3) 触发器的输出端为Q 。
4) 触发器的初态题意未明确时,要用文字说明设为0。
1、基本RS 触发器(锁存器)(1)特性方程 ⎪⎩⎪⎨⎧=++=+)(11约束条件R S RQ S Q n n (2)时序图例1用与非门组成的基本RS 触发器,设初始状态为0,已知输入R 、S 的波形图如图,画出输出Q 、Q 的波形图。
解:将每个时段对应的R 、S 的波形高电平设为1低电平设为0,代入特性方程⎪⎩⎪⎨⎧=++=+)(11约束条件R S RQ S Q n n计算出Q n+1的值并还原成波形。
如在t1时刻R =1,S =0,Q n =0,通过特性方程计算可知Q n+1=1,因此在t1时刻是高电平,同理画出结果如图所示。
注意,如果输入的波形信号使基本RS 触发器处于不定态时,Q n+1的波形可以是高电平也可以是低电平。
RSQ Qt12、RS 触发器 (1)特性方程 ⎪⎩⎪⎨⎧=+=+)(01约束条件SR Q R S Q n n 例2 同步RS 触发器,设初始状态为0,已知输入R 、S 的波形图如图,画出输出Q 的波形图。
解:将每个时段对应的R 、S 的波形高电平设为1低电平设为0,代入特性方程⎪⎩⎪⎨⎧=+=+)(01约束条件SR Q R S Q n n (当CP =1时有效) 计算出Q n+1的值并还原成波形。
对于同步RS 触发器要注意在CP 信号时有效时输入端的波形会影响输出端得输出状态,在CP 信号时无效时输入端的波形就不会影响输出端得输出状态此时触发器的状态不变。
如:在t1~t2时刻CP =1,此时触发器处于工作状态此时R =0,S =1,Q n =0,通过特性方程计算可知Q n+1=1高电平。
同理t2~t3时刻,触发器仍处于工作状态将输入信息和电路的原来状态带入公式计算得到Q n+1=0低电平。
触发器的特性方程及时序图
注意:
1) CP脉冲的画法(高低电平脉宽一致);
2) 状态不定时高低电平都画上,中间斜线填
充;
3) 触发器的输出端为Q。
4) 触发器的初态题意未明确时,要用文字说明
设为0。
1、基本RS触发器(锁存器)
(1)特性方程
n,1n,Q,S,RQ,
, ,S,R,1(约束条件),
(2)时序图
例1用与非门组成的基本RS 触发器,设初始状态为0,已知输入R、S的波形图如图,画出输出Q、的波形图。
Q解:将每个时段对应的R、S的波形高电平设为1低电
n,1n,Q,S,RQ,
,平设为0,代入特性方程 ,S,R,1(约束条件),
n+1计算出Q的值并还原成波形。
如在t1时刻R=1,
nn+1S=0,Q=0,通过特性方程计算可知Q=1,因此在t1时刻是高电平,同理画出结果如图所示。
注意,如果输入的波形信号使基本RS触发器处于
n+1不定态时,Q的波形可以是高电平也可以是低电平。
R
S
Q
Q
t1
2、RS触发器
(1)特性方程
n,1n,Q,S,RQ,
,
,SR,0(约束条件),
例2 同步RS触发器,设初始状态为0,已知输入R、S的波形图如图,画出输出Q的波形图。
解:将每个时段对应的R、S的波形高电平设为1低电平设为0,代入特性方程n,1n,Q,S,RQ,
,
(当CP=1时有效) ,SR0(约束条件),,
n+1计算出Q的值并还原成波形。
对于同步RS触发器要注意在CP信号时有效时输入端的波形会影响输出端得输出状态,在CP信号时无效时输入端的波形就不会影响输出端得输出状态此时触发器的状态不变。
如:
在t1,t2时刻CP=1,此时触发器处于工作状态此
nn+1时R=0,S=1,Q=0,通过特性方程计算可知Q=1高电平。
同理t2,t3时刻,触发器仍处于工作状态将输入
n+1信息和电路的原来状态带入公式计算得到Q=0低电平。
在t3,t4时刻CP=0,电路处于非工作状态,因此触发器的状态不会随输入信号变化而变化,所以输出信号保持不变。
同理画出结果如图所示。
注意,如果在CP=1期间输入的波形信号使基本RS
n+1触发器处于不定态时,Q的波形可以是高电平也可以是低电平。
CP
R
S
Q
t1t2t3t4 例3 主从RS触发器,设初始状态为0,已知输入R、S的波形图如图,画出输出Q的波形图。
解:
将每个有效时刻对应的R、S的波形高电平设为1低电平设为0,代入特性方程n,1n,Q,S,RQ,
, (CP下降沿到来时有效) ,SR,0(约束条件),
n+1计算出Q的值并还原成波形。
但在主从结构的触发器中电路发生变化的时间是某一个特定的时刻。
如:
在t1时刻主从RS触发器处于工作状态,R=1,S=0,nn+1Q=0,代入特性方程得Q=1高电平。
在此时刻之后触发器不工作,触发器得状态保持不变,因此波形不变化。
同理触发器下一次工作是在t2时刻,将信号量和
n+1原状态代如公式得Q=1。
依此类推画出结果如图所
示。
CP
S
R
Q
t1t2
3、JK触发器
(1)特性方程
n,1nn
Q,JQ,KQ
(2)时序图
例4 同步JK触发器,设初始状态为0,已知J、 K两个输入端,J、 K的波形图如图所示,画出输出Q的波形图。
解:
将每个时段对应的J、 K的波形高电平设为1低电平设为0,代入特性方程n,1nn (CP=1时有效) Q,JQ,KQ
n+1计算出Q的值并还原成波形。
如:
在t1,t2时刻CP=1,此时触发器处于工作状态此
nn+1时J=1,K=0,Q=0,通过特性方程计算可知Q=1高电平。
同理t2,t3时刻,触发器仍处于工作状态将输入
n信息和电路的原来状态J=0,K=0,Q=1带入公式计算
n+1=1得到Q高电平。
在t3,t4时刻CP=0,电路处于非工作状态,因此触发器的状态不会随输入信号变化而变化,所以输出信号保持不变。
依此类推,画出结果如图所示。
CP
J
K
Q
t1t2t3t4 例5 主从JK触发器,设初始状态为0,已知J、 K两个输入端,J、 K的波形图如图所示,画出输出Q的波形图。
解:
将每个有效时刻对应的J、 K的波形高电平设为1低电平设为0,代入特性方程
n,1nn (CP下降沿到来时有效) Q,JQ,KQ
n+1计算出Q的值并还原成波形。
如:
在t1时此时触发器处于工作状态此时J=1,K=0,nn+1Q=0,通过特性方程计算可知Q=1高电平。
在此时刻之后触发器不工作,触发器得状态保持不变,因此波形不变化。
同理触发器下一次工作是在t2时刻,将信号量和
n+1原状态代如公式得Q=0。
依此类推,画出结果如图所示。
CP
J
K
Qt4,t1,t2t3, 例6 边沿JK触发器,设初始状态为0,已知J、 K两个输入端,J、 K的波形图如图,画出输出Q的波形图。
解:
将每个有效时刻对应的J、 K的波形高电平设为1低电平设为0,代入特性方程
n,1nn (CP下降沿有效) Q,JQ,KQ
n+1计算出Q的值并还原成波形。
如:
在t1时此时触发器处于工作状态此时J=0,K=0,nn+1=1,通过特性方程计算可知=1高电平。
在此时刻QQ
之后触发器不工作,触发器得状态保持不变,因此波形不变化。
同理触发器下一次工作是在t2时刻,将信号量和
n+1原状态代如公式得Q=0低电平。
依此类推,画出结果如图所示。
CP
J
K
Q
t4,t1,t2t3, 4、D触发器
(1)特性方程:
n,1
Q,D
(2)时序图
例7 同步D触发器,设初始状态为0,已知输入端D的波形图如图,画出输出Q的波形图。
解:
将每个时段对应的D的波形高电平设为1低电平设为0,代入特性方程
n,1 (当CP=1时有效) Q,D
n+1计算出Q的值并还原成波形。
如:
在t1,t2时刻CP=1,此时触发器处于工作状态此
n+1时D=0,通过特性方程计算可知Q=0低电平。
同理t2,t3时刻,触发器仍处于工作状态将输入
n+1信息和电路的原来状态带入公式计算得到Q=1高电平。
在t3,t4时刻CP=0,电路处于非工作状态,因此触发器的状态不会随输入信号变化而变化,所以输出信号保持不变。
同理画出结果如图所示。
CP
D
Q
t1t2t3t4
例8 现设维持—阻塞D触发器的初始状态为0,已知输入端D信号的波形图如图所示,画出输出Q的波形图。
解:
由于是边沿触发器,因此触发器的触发翻转发生在时钟脉冲的触发沿(这里是上升沿)。
而且判断触发器次态的依据是时钟脉冲触发沿前一瞬间(这里是上升沿前一瞬间)输入端的状态。
根据D触发器的特性方程
n,1 (CP上升沿有效) Q,D
在t1时此时触发器处于工作状态此时D=1,通过
n+1特性方程计算可知Q=1高电平。
在此时刻之后触发器不工作,触发器得状态保持不变,因此波形不变化。
同理触发器下一次工作是在t2时刻,将信号量和
n+1原状态代如公式得Q=0低电平。
依此类推,画出结果如图所示。
CP
D
Q
,t4t5t1t2t3。