(精心整理)反比例函数中的模型

反比例函数的常见模型解决反比例函数的问题，除了掌握反比例函数的图像及性质以及反比例函数常见的面积模型之外，还要熟练掌握以下几个经典模型：【模型1】正比例函数图像被反比例函数图像所截得的线段相等【模型2】一次函数图像被坐标系和反比例函数图像所截得的相等线段【模型3】同一象限内反比例函数图像上两点连线的平行线【模型4】反比例函数与矩形（1）【模型5】反比例函数与矩形（2）【模型6】反比例函数与最值【模型7】反比例函数与黄金分割让我们一起领略反比例函数的神奇一、个人对反比例函数的几点困惑与感悟 1.为何正比例函数的比例系数是比xyk =，而反比例函数的比例系数却不是比xy k =？ 2.为何我市中考的反比例函数问题总不像其它函数那么深入？只探究一些皮毛问题！至 多探究一下k 的几何意义（面积），例如2016年台州市中考考查的也是“函数的研究 通法”，并非专门深入研究反比例函数.3.过去我们遇到稍难一点的反比例函数问题，就只有“暴力设元”这一途径，总无法避开 多元方程、分式方程、高次方程.4.个人认为作为老师，不应该只应付中考，而应该研究更纯粹的数学，站在更高的位置来 了解数学本质！做到居高临下、解有依据！5.实际上，反比例函数中也存在很多的“比”，斜比、直比（纵比、横比、纵横比）、面积 比，可以说“比比皆是”！现在就让我们一起来比出精彩、比出神奇. 二、一道曾经困惑我多时的中考题某年宁波市中考的填空压轴题: 如图，AOB Rt Δ的顶点B (2，4)，双曲线xky =经过 点C 、D ，当以B 、C 、D 为顶点的三角形与AOB Δ的相似时，则=k .1.常规性解法：通过设元，例如设C (m ，m 2)，则D (2，2m )，再根据条件列方程： (1)利用CD BC 2=、224=CD BC 、CD BD 5=或225=CD BD 列方程；(2)利用)(D C C D y y x x -2=-列方程；(3)利用“一线三等角”模型、和D D C C y x y x ⋅=⋅列方程.实际上，在上述常规处理方法中，已经透着一点智慧、一点灵性了，具体操作方法中也具 备了一定的技巧性. 但我本人对此，却一直难言满意，耿耿于怀！2.挖掘隐含性质，巧解此题(1)实际上，此图中含有一些很重要的性质：过点C 作y CP ⊥轴于P ，连接PA ，直线CD 分别交坐标轴于点M 、N . 则有①PA ∥CD ；②AN PC =，AD PM =； ③DN MC =，CN MD =. 基于以上这些性质，有如下解法. (2)我的第一种解法（整体思想）：由OM ON 2=，PM AD AN 2=2=可得，)(PM OM AN ON -2=-，即OP OA 2=，于是1=21=OA OP ，21=21=OP PC ，…… (3)我一个同事的解法（斜边转直比）：由421=::::CN OC MC ，DN MC =可得，131=::::DN CD MC ，转为横比，131=--::)(:)(:D N C D C x x x x x ，因此21=41=OA x C ，…… (4)我一个学生的解法（斜等转直等）： 由CN MD =得2==-OA x x C N ，则1=-21=)(C N C x x y ，…… (5)我的第二种解法（平行导角度）：由PA ∥CD 得，B MNO PAO ∠=∠=∠，于是1=21=OA OP ，…… (6)下面我们要着重解决两件事： ①上述性质是否永远成立？如何证明？②解题技巧除上述方法：整体思想、斜边转直比、斜等转直等、平行导角度外，还有斜长转直长、面积比与边比互转、纯面积转化等等，后面将一、一介绍.三、探究性质 1.如图，双曲线xky =与矩形OABC 边交于点M 、N ，直线MN 交坐标轴于点D 、E . ①如图1，若21=::AB AM ，则=CB CN : ； ②如图2，若41=::AB AM ，则=CB CN : ； ③如图3，若n AB AM ::1=，则=CB CN : ，直线MN 与AC 的位置关系是 ，EN 与MD 的大小关系 .图1 图2 图3 2.①如图1，双曲线xky =与直线DE 交于点M 、N ，y MA ⊥轴于点A ，x NC ⊥轴于 点C ，请探究直线MN 与AC 的位置关系，线段EN 与MD 的大小关系. ②如图2，双曲线xky =与直线EF 交于点M 、N ，y MA ⊥轴于A ，x MC ⊥轴于C ， y ND ⊥轴于D ，x NB ⊥轴于B ，请探究直线MN 与AB 、CD 的位置关系，以及线段ME 与FN 的大小关系.图1 图2四、最常见思想方法（斜转直）：斜边转直比、斜等转直等、斜长转直长 1.如图，直线4+-=x y 反比例函数xky =(0>x )图象交直线AB 于点C 、D ，且CD AB 2=， 则k 的值为 . (1)常规方法（斜长转直长）：22=21=AB CD ，则2=22=-CD x x C D ， 可设C (m ，m -4)，则D (2+m ，m -2)，列方程解决； (2)口算巧解（斜边转直比）：由DB AC =，CD AB 2=得，121=::::DB CD AC ，转为横比得，121=--::)(:)(:D B C D C x x x x x ，则1=C x ，3=1-4=C y ，……2.同类变式题：如图，直线2+-=x y 交坐标轴于点A 、B ， 双曲线xky =交直线AB 于点C 、D . 若AB CD 2=，则k 的值为 ；3.难题展示（中国数学教育名师讲堂481230254，每日一题第8题，2017/3/29）如图，点A (2，2)，B ，C 在双曲线上，o BAC 45=∠，AB 分别交x ，y 轴于D ，F ， AC 分别交x ，y 轴于D ，E . (1)求DOE Δ的面积； (2)求证：DBCE ADE S S 四边形=Δ.4.原创清新小题和近年的中考题：(1)如图1，BC AB =，AOB Δ的面积为3，则k 的值为 . (2)如图2，点A ，B 在双曲线xky =上运动，x AB ⊥轴，BC AC =. ①在运动过程中，ABC Δ的面积是不是定值？答： ； ②若32=k ，且ABC Δ是正三角形，则点A 的坐标为 .(3)如图3，□OABC 中，o B 60=∠，3=OA ，双曲线经过点C 和AB 中点D ，则该双曲线的解析式为 . (4)如图4，直线x y 21=与3+21=x y 分别与双曲线xky =交于点A 、B ，BC OA 2=，则k 的值为 .图1 图2 图3 图4(5)(十堰)如图5，正AOB Δ的边长为5，双曲线xky =经过点C 、D ，且OB CD ⊥， 则k 的值为 . (6)如图6，双曲线xky =与直线b mx y +=交于点C 、D . ①(原创、铺垫②)若3-=m 、6=b ，且CD AB 3=，则=k ；②(常州模拟·改编)若6=b ，且CD AB 3=，则=⋅m k ；③(杭州模拟·改编)若3-=m ，且8=⋅AD AC ，则=k . (7)(据上题改编)如图7，P 为双曲线xy 2-=上的动点，过点P 作矩形PAOB ，直线 CD 的解析式为b x y +2=，交矩形边于M ，N ，则=⋅DN CM .图5 图6 图7五、面积比、边比互转1.①(原创、铺垫)如图1①，直线x y 23=与双曲线xy 6=交于点A ，C 为双曲线上一点， 射线CA 交y 轴于点D ，若COD Δ的面积为9，则点C 坐标为 ； ②(成都)如图1②，直线x y 23=与双曲线xy 6=交于点A 、B ，C 为双曲线上一点， 射线CA 交y 轴于点D ，若BCD Δ的面积为20，则点C 坐标为 . 2.(无锡)如图2，x AB ⊥轴，BC ∥x 轴，双曲线过点C 、D ，且21=::DB OD ， 已知OBC Δ的面积为3，则k 的值为 .图1① 图1② 图33.(宁波)如图3，正AOB Δ的顶点A 在双曲线xy 9=上，双曲线x y 1=与边OA 交于点C ，连接BC ，则ABC Δ的面积为 . 4.(丽水)如图4，双曲线xy 4=与直线b x y +-=交于点A 、B ，⊥AE x 轴，设点A 的 横坐标为m .①用含m 的式子表示=b ；②若AOF Δ与四边形BCEF 的面积和为4，则=m . 5.如图5，双曲线xky =与直线b mx y +=交于点C 、D . ①(常州模拟)若6=b ，且COD AOB S S ΔΔ3=，则=⋅m k ；②(改编自①)若6=k 、3-=m ，且CD AB 2=，则=COD S Δ .图3 图4 图56.如图6，⊥AB x 轴，C 为AB 中点，延长OC 到E ，延长OA 到D ，若双曲线xk y =恰 好经过点D ，E ，且CE OC =，则=OD OA : . 7.如图7，双曲线x k y 1=过点A ，B ，xky 2=过点C ，D ，若AC ，BD 均与x 轴平行， 6=AC ，4=BD ，且它们之间的距离EF 长为5，则=-21k k . 8.如图8，直线AB 交双曲线xy 5=于点C ，D ，若8=AOB S Δ，则=BOC S Δ .图6 图7 图89.如图，点A 在双曲线xky =上，x AB ⊥轴，CD AD 2=，DB 延长线交y 轴于E ，若 BCE Δ的面积为4，则k 的值为 . 10.如图，点A 、B 在双曲线xky =上，x AC ⊥轴，x BD ⊥轴，垂足C 、D 分别在x 轴的 正半轴和负半轴上，k CD =，AC AB 25=，E 是AB 的中点，若BCE Δ面积是ADE Δ的2倍，则k 的值为 .六、反比例函数图象中的“一线三等角”构造，初探黄金比例 1.如图1，ABC Δ中，BA OB =，o OBA 90=∠，双曲线xky =经过点A 、B ，且点B 的 纵坐标为2，则k 的值为 .(1)剖析：对于坐标系中的一个直角，若两条边均“倾斜”，我们经常构造“K ”形全等或相似，即“一线三等角”模型，或叫“矩形大法”，见图2，得1-5=m .(2)后感：我们可以发现，矩形ODCE 恰好是一个“黄金矩形”，这到底是一种偶然的巧 合，还是一种必然的存在呢？这有待于我们进一步探究… (3)探究(2016临沭模拟)：如图3，双曲线xky =与矩形ODCE 的边交于点A ，B ，若 设点B 的坐标为(a ，b )，且有AB OB =，AB OB ⊥，则=b a : .图1 图2 图32.类似题：①(2015临海模拟·填空压轴题)如图， AB OA =，oOAB 90=∠，双曲线xky =经过 点A ，双曲线xk y -=经过点B ，已知点A 的纵坐标为2-，则=k ，点B 的坐标为 . ②(个人原创)如图2，ABC Δ中，BA OB =，o OBA 90=∠，双曲线x k y =经过点B ，双曲线xk y 1+=经过点A ，且 点B 的纵坐标为2，则k 的值为 .3.难题展示（常州·于新华老师原创题） (1)如图1，点A (3，4)，B 均在双曲线xky =上，过点A 作y 轴垂线，过点B 作x 轴 垂线，两垂线交于点P ，垂足分别为E ，F ，将PAB Δ沿AB 翻折，点P 恰好落在x 轴上的点Q 处. 求点B 的坐标.(2)如图2，点A (3，4)，B 均在双曲线xky =上，过点A 作y 轴垂线，过点B 作x 轴 垂线，两垂线交于点P ，垂足分别为E ，F ，将PAB Δ沿AB 翻折，点P 恰好落在x 轴上的点Q 处. 求点B 的坐标.图1 图24.如图，矩形ABCD 的边AB 的解析式为2+=kx y ，顶点C ，D 在双曲线xmy =上. ①若2=∠ADB tan ，则点D 的坐标为 ； ②连接OC ，OD ，若COD Δ是等边三角形，则=∠ADB tan .后感：若能发现OB OA =，本题将更简单！拓展：如图，正方形ABCD 的顶点A 、B 在双曲线x y 3=上，C 、D 在双曲线xy 7=上， 则正方形ABCD 的面积为 .5.(2013湖州模拟) 如图1，矩形OABC 的顶点A 、B 在 双曲线xky =上，若点A (1，2)，则点B 的坐标为 . 6.如图2，矩形ABCD 中，AD AB 2=，点A (0，1)，点C ，D 在双曲线xky =上，若E 为 AB 中点，则k 的值为 .图1 图27.①如图1，点A ，B 在双曲线xy 2=上运动，以AB 为底边作等腰直角ABC Δ，则点 C 也在一条双曲线上运动，则该双曲线的解析式为 ；②如图2，点A ，B 在双曲线xy 2=上运动，以AB 为底边作等腰ABC Δ，则点C 也 在一条双曲线上运动，若2=∠CAB tan ，则该双曲线解析式为 ； ③如图3，点A ，B 在双曲线xky =上运动，以AB 为底作等腰ABC Δ，点C 在另一 双曲线xk y '=上运动，若m CAB =∠tan ，请用m ，k 表示='k .图1 图2 图3七、平行导角度，角度导比例 1.如图，点A ，B 在双曲线xky =上，AB 经过原点O ，过点A 作AC ∥x 轴，连接BC 并延长，交双曲线于点D . ①求证：CD AD =； ②求BD AD :的值.根据本题的发现，改编了一个清新小题： 如图，点A ，B 在双曲线xky =上，AB 经过原点O ，过点A 的直线b x y +3=交该 双曲线于点C ，分别交x 轴，y 轴于点D ，E ，若4=BC ，8=AC . 求k 的值.2.如图，直线x y 3=交在双曲线xky =于点A 、B ，AB 经过原点O ，过A 作AB AC ⊥ 交y 轴于点C ，连接BC 并延长，交双曲线于点D .求BD AD :的值.3.如图，双曲线xky =与过原点的直线l 交于点A 、B ，点M 在双曲线上，直线AM 、 BM 分别交y 轴于点P 、Q .若设PM m AM ⋅=，QM n BM ⋅=，则=-n m .4.如图，AB OA =，双曲线经过点C 、D 、E ，求证：AE AC AD ⋅=2.八、纯面积推导1. 如图，点A (2，2)，B ，C 在双曲线上，o BAC 45=∠，AB 分别交x ，y 轴于D ，F ， AC 分别交x ，y 轴于D ，E . 求证：DBCE ADE S S 四边形=Δ.(此方法感谢江苏·于新华老师的指导！)2.(2016菏泽)如图，AOC Δ，ABD Δ均是等腰直角三角形，双曲线xy 6=经过点B ，交线 段OA 与点E ，求AOC Δ与ABD Δ的面积之差.后感：①题中条件“AOC Δ，ABD Δ均是等腰直角三角形”可如何改变？ ②写出2OA ，2OE ，2AB 的关系： . 3.(十堰)如图5，正AOB Δ的边长为5，双曲线xky =经过点C 、D ，且OB CD ⊥， 则k 的值为 .4.(常州)如图1，AB OA =，双曲线经过点C 、D ，且a b OC BD =，求ADAC的值； 5.如图2，AB OA =，双曲线经过点C 、D 、E ，求证：AE AC AD ⋅=2.图1 图2。

反比例函数常见模型一、知识点回顾1。

反比例函数的图像是双曲线,故也称双曲线y=k x （k≠0）．其解析式有三种表示方法：①xky = （0≠k ）；②1-=kx y (0≠k ）；③k xy = 2．反比例函数y=kx（k≠0)的性质 （1）当k>0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内，y 随x 的增大而减小． （2）当k 〈0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y 随x 的增大而增大．(3）在反比例函数y=kx中,其解析式变形为xy=k,故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).（4）若双曲线y=k x图像上一点(a,b ）满足a ，b 是方程Z 2－4Z －2=0的两根,求双曲线的解析式．由根与系数关系得ab=－2，又ab=k,∴k=－2，故双曲线的解析式是y=2x-．（5）由于反比例函数中自变量x 和函数y 的值都不能为零,所以图像和x 轴，y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势．二、新知讲解与例题训练 模型一：如图,点A为反比例函数xky =图象上的任意一点，且AB 垂直于x 轴，则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线xm在第一象限的交点，且3=∆AOB S ，（1)求m 的值 （2）求ABC ∆的面积变式题1、如图所示，点1A ,2A ,3A 在x 轴上，且O 1A =21A A =32A A ,分别过1A ，2A ,3A 作y 轴平行线，与反比例函数y=x8(x 〉0)的图像交于点1B ，2B ,3B ，分别过点1B ,2B ,3B 作x 轴的平行线，分别与y 轴交于点1C ,2C ，3C ，连结321,,OB OB OB ，那么图中阴影部分的面积之和为__________2、 如图,点A 在双曲线1y x =上，点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上,若四边形ABCD 为矩形,则它的面积为 .模型二：如图:点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点，直线AB 交x 轴于M 点，交y 轴于N 点，再过A 、B 两点分别作y AD ⊥轴于D 点，x BF ⊥轴于F 点，再连结DF 两点，则有：AB DF ||且BM ＝AN例2:如图，一次函数y a x b =+的图象与x 轴,y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ,D 两点，分别过C ,D 两点作y 轴，x 轴的垂线,垂足为E ,F ，连接CF ,DE ．有下列四个结论：①DEF CEF S S ∆∆=；②AOB ∆相似于FOE ∆；③△DCE ≌△CDF ；④A C B D=其中正确的结论是 ．（把你认为正确结论的序号都填上）y DA B ODFAB DF MN xy O例3:一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴,AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴,BD y ⊥轴，垂足分别为F D ，，AC 与BD 交于点K ,连接CD ． （1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1,试证明: ①AEDK CFBK S S =四边形四边形；②AN BM =． （2）若点A B ，分别在反比例函数ky x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．模型三:如图，已知反比例函数ky x=(k ≠0,x>0)上任意两点P 、C ，过P 做PA ⊥x 轴，交x 轴于点A ，过C 做CD ⊥x 轴,交x 轴于点D ，则OPC PADC S S ∆=梯形.图1图2例4:如图，在直角坐标系中，一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A （1，4)、B (4,1）两点，则△AOB 的面积是______.反比例函数例5：如图，在直角坐标系中，一次函数1y k x b =+的图象与是______.2k y x=的图象交于A (1，4）、B （3，m ）两点,则△AOB 的面积两点，且点例6：如图1,已知直线12y x =与双曲线(0)k y k x=>交于A 、BA 的横坐标为4．（1）求k的值；（2）如图2，过原点O 的另一条直线l 交双曲线(0)k y k x=>于C 、D 两点（点C 在第一象限且在点A 的左边），当四边形ACBD 的面积为24时，求点C 的坐标．模型四：在矩形AOBC 中，OB =a ，OA =b ,分别以OB ,OA 所在直线为x 轴和y 轴，建立如图所示的平面直角坐标系．F 是BC 上的一个动点（不与B 、C 重合），过F 点的反比例函数(0)ky x x=>的图象与AC边交于点E ，则CE aCF b=.例7：两个反比例函数k y x =和1y x =在第一象限内的图象如图所示,点P 在k y x=的图象上，PC ⊥x轴于点C ，交1y x=的图象于点A ，PD ⊥y 轴于点D ,交1y x=的图象于点B ，当点P 在k y x=的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等；④当点A 是PC 的中点时,点B 一定是PD 的中点．其中一定正确的是 _________（把你认为正确结论的序号都填上）．课堂练习： 一、选择题1、已知m<0，则函数mx y =1与xmy -=2的图像如图，大致是（ ）A. B 。

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线，故也称双曲线y=kx（k≠0）．其解析式有三种表示方法：①xk y =（0≠k ）；②1-=kx y （0≠k ）；③k xy = 2．反比例函数y=kx（k≠0）的性质（1）当k>0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内，y 随x 的增大而减小．（2）当k<0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y 随x 的增大而增大．（3）在反比例函数y=kx中，其解析式变形为xy=k ，故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).（4）若双曲线y=kx图像上一点（a ，b ）满足a ，b 是方程Z 2－4Z －2=0的两根，求双曲线的解析式．由根与系数关系得ab=－2，又ab=k ，∴k=－2，故双曲线的解析式是y=2x-．（5）由于反比例函数中自变量x 和函数y 的值都不能为零，所以图像和x 轴，y 轴都没有交点，但画图时要体现出图像和坐标轴无限贴近的趋势．二、新知讲解与例题训练 模型一：||=||,2k S k S ∆=矩形xyO已知 点P 是反比例函数 在第一象限内图象上的一动点.如图，若 轴于点B ， 轴于点N ，连接PM ，PN ，则矩形MONP 的面积为|K|yxMO PNyxMO PNyxMO PNyxMOPN已知 点P 是反比例函数 在第一象限内图象上的一动点.如图，若点B 为y 轴（不同于O ）的任意一点，连接 ，则△PAB 的面积为|K|/2.y x AO PByxA O PByxA O P ByxA O P（B ）已知 点P 是反比例函数 在第一象限内图象上的一动点.如图，若 轴于点M ，N 为 轴上任意一点，连接MN ，PN ，则△PMN 的面积为_________yx MO P（N ）yx MOPNyx MOPNyxMOPN例1：如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点，且3=∆AOB S ,（1）求m 的值 （2）求ABC ∆的面积变式题1、如图所示，点1A ,2A ,3A 在x 轴上，且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线，与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ，分别过点1B ,2B ,3B 作x 轴的平行线，分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________模型二：如图：点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点，直线AB 交x 轴于M点，交y 轴于N 点，再过A 、B 两点分别作y AD ⊥轴于D 点，x BF ⊥轴于F 点，再连结DF 两点，则有：AB DF ||且BM ＝AN如图，直线 与反比例函数 相交于A 、B 两点，分别过点A 、B 作AE ⊥y 轴、BF ⊥x 轴，求证： ①AC=BD ，AE=BF ②AB ∥EF③△ACE ≌△BDFy x EC D FOBAy x EC D F O BAyxP EC D FOB ADFAB DF MN xy O例2：如图，一次函数y a x b =+的图象与x 轴，y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ．有下列四个结论：①DEF CEF S S ∆∆=；②AOB ∆相似于FOE ∆；③△DCE ≌△CDF ；④A C B D =其中正确的结论是 ．（把你认为正确结论的序号都填上）例3：一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴，BD y ⊥轴，垂足分别为F D ，，AC 与BD 交于点K ，连接CD ．（1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1，试证明： ①AEDK CFBK S S =四边形四边形；②AN BM =． （2）若点A B ，分别在反比例函数ky x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．y x DC A B O F E图1图2模型三：如图，A 、B 是反比例函数 在第一象限内图象上的一两个不重合的动点，AC ⊥x 轴于点C ， BD ⊥x 轴于点D ，求证：S △OAB=S 梯ACDB .yx DC OAByxS 2S 1DC OAB例4：如图，在直角坐标系中，一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4，1)两点，则△AOB 的面积是______.例5：如图，在直角坐标系中，一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A （1,4）、B （3，m ）两点，则△AOB 的面积是______.例6：如图1，已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点，且点A 的横坐标为4． （1）求k 的值；（2）如图2，过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点（点C 在第一象限且在点A 的左边），当四边形ACBD 的面积为24时，求点C 的坐标．模型四：在矩形AOBC 中，OB =a ，OA =b ，分别以OB ，OA 所在直线为x 轴和y 轴，建立如图所示的平面直角坐标系．F 是BC 上的一个动点（不与B 、C 重合），过F 点的反比例函数(0)ky x x =>的图象与AC 边交于点E ，则CE a CF b=.A 、B 是反比例函数 在第一象限内图象上的一两个不重合的动点， AC ⊥y 轴于点C ， BD ⊥x 轴于点D ，AC 与BD 相交于点E ，求证：A EB EA CB D=y xCE DO AByxS 1S 2CE DOABxB FC E A O y例7：两个反比例函数k y x =和1y x =在第一象限内的图象如图所示，点P 在ky x=的图象上，PC ⊥x 轴于点C ，交1y x =的图象于点A ，PD ⊥y 轴于点D ，交1y x =的图象于点B ，当点P 在ky x=的图象上运动时，以下结论：①△ODB 与△OCA 的面积相等；②四边形P AOB 的面积不会发生变化；③P A 与PB 始终相等；④当点A 是PC 的中点时，点B 一定是PD 的中点．其中一定正确的是 _________（把你认为正确结论的序号都填上）．【结论1】一次函数y= - x+b(b ＞0)与反比例函数xy=k(k ＞0)的图像交于点A ，B ，一次函数图像与y 轴和x 轴分别交于点C 、D 。

反比例函数常见几何模型反比例函数是一种特殊的函数类型，它描述了一种比例关系，其中一个变量的变化与另一个变量的变化成反比。

它在数学上的一般形式为y=k/x，其中k是一个常数，x和y是变量。

在几何学中，反比例函数常见于许多不同的模型中。

以下是一些常见的几何模型，这些模型可以用反比例函数来描述。

1.电阻和电流：欧姆定律描述了电阻和电流之间的关系，即电流与电阻成反比。

根据欧姆定律，电流I在电阻R中的关系为I=V/R，其中V是电压。

这个关系可以使用反比例函数来描述。

2.凸透镜的放大力：凸透镜的放大力与物体离透镜的距离成反比。

放大力是指通过透镜放大影像的能力。

根据物理学的知识，放大力F与物体离透镜的距离s的关系为F=k/s，其中k是一个常数。

这个关系可以使用反比例函数来表示。

3.时间和速度：根据物理学中的速度定义，速度v等于物体所走的距离d除以所花费的时间t。

因此，速度与时间成反比。

速度v和时间t之间的关系可以表示为v=k/t，其中k是一个常数。

这个关系可以使用反比例函数来描述。

4.管道流量和管道直径：在液体或气体流体力学中，管道的直径和流量之间成反比。

根据伯努利原理，如果管道的截面积减小，则液体或气体的速度增加，从而使流量增加。

因此，管道的直径和流量之间的关系可以用反比例函数表示。

5.球体的表面积和半径：球体的表面积与其半径成反比。

根据数学知识，球体的表面积S与其半径r之间的关系为S=4πr^2、从这个方程可以看出，当半径增加时，表面积会减小。

因此，球体的表面积和半径之间可以用反比例函数描述。

6.声波的衰减：声波在传播过程中会经历衰减，衰减的程度与传播距离成反比。

声波的衰减率与传播距离之间的关系可以用反比例函数来描述。

以上是反比例函数在几何模型中的一些常见应用。

这些模型在科学研究和实际应用中都具有重要的意义。

通过理解和运用反比例函数，我们可以更好地了解和解释这些几何模型。

反比例函数的常见模型解决反比例函数的问题，除了掌握反比例函数的图像及性质以及反比例函数常见的面积模型之外，还要熟练掌握以下几个经典模型：【模型1】正比例函数图像被反比例函数图像所截得的线段相等【模型2】一次函数图像被坐标系和反比例函数图像所截得的相等线段【模型3】同一象限内反比例函数图像上两点连线的平行线【模型4】反比例函数与矩形（1）【模型5】反比例函数与矩形（2）【模型6】反比例函数与最值【模型7】反比例函数与黄金分割让我们一起领略反比例函数的神奇一、个人对反比例函数的几点困惑与感悟1.为何正比例函数的比例系数是比，而反比例函数的比例系数却不是比？2.为何我市中考的反比例函数问题总不像其它函数那么深入？只探究一些皮毛问题！至多探究一下的几何意义（面积），例如2016年台州市中考考查的也是“函数的研究通法”，并非专门深入研究反比例函数.3.过去我们遇到稍难一点的反比例函数问题，就只有“暴力设元”这一途径，总无法避开多元方程、分式方程、高次方程.4.个人认为作为老师，不应该只应付中考，而应该研究更纯粹的数学，站在更高的位置来了解数学本质！做到居高临下、解有依据！5.实际上，反比例函数中也存在很多的“比”，斜比、直比（纵比、横比、纵横比）、面积比，可以说“比比皆是”！现在就让我们一起来比出精彩、比出神奇.二、一道曾经困惑我多时的中考题某年宁波市中考的填空压轴题:如图，的顶点(，)，双曲线经过点、，当以、、为顶点的三角形与的相似时，则.1.常规性解法：通过设元，例如设(，)，则(，)，再根据条件列方程：(1)利用、、或列方程；(2)利用列方程；(3)利用“一线三等角”模型、和列方程.实际上，在上述常规处理方法中，已经透着一点智慧、一点灵性了，具体操作方法中也具备了一定的技巧性.但我本人对此，却一直难言满意，耿耿于怀！2.挖掘隐含性质，巧解此题(1)实际上，此图中含有一些很重要的性质：过点作轴于，连接，直线分别交坐标轴于点、.则有①∥；②，；③，.基于以上这些性质，有如下解法.(2)我的第一种解法（整体思想）：由，可得，，即，于是，，……(3)我一个同事的解法（斜边转直比）：由，可得，，转为横比，，因此，……(4)我一个学生的解法（斜等转直等）：由得，则，……(5)我的第二种解法（平行导角度）：由∥得，，于是，……(6)下面我们要着重解决两件事：①上述性质是否永远成立？如何证明？②解题技巧除上述方法：整体思想、斜边转直比、斜等转直等、平行导角度外，还有斜长转直长、面积比与边比互转、纯面积转化等等，后面将一、一介绍.三、探究性质1.如图，双曲线与矩形边交于点、，直线交坐标轴于点、.①如图1，若，则；②如图2，若，则；③如图3，若，则，直线与的位置关系是，与的大小关系.图1图2图32.①如图1，双曲线与直线交于点、，轴于点，轴于点，请探究直线与的位置关系，线段与的大小关系.②如图2，双曲线与直线交于点、，轴于，轴于，轴于，轴于，请探究直线与、的位置关系，以及线段与的大小关系.图1图2四、最常见思想方法（斜转直）：斜边转直比、斜等转直等、斜长转直长1.如图，直线反比例函数()图象交直线于点、，且，则的值为.(1)常规方法（斜长转直长）：，则，可设(，)，则(，)，列方程解决；(2)口算巧解（斜边转直比）：由，得，，转为横比得，，则，，……2.同类变式题：如图，直线交坐标轴于点、，双曲线交直线于点、.若，则的值为；3.难题展示（中国数学教育名师讲堂481230254，每日一题第8题，2017/3/29）如图，点(，)，，在双曲线上，，分别交，轴于，，分别交，轴于，.(1)求的面积；(2)求证：.4.原创清新小题和近年的中考题：(1)如图1，，的面积为，则的值为.(2)如图2，点，在双曲线上运动，轴，.①在运动过程中，的面积是不是定值？答：；②若，且是正三角形，则点的坐标为.(3)如图3，□中，，，双曲线经过点和中点，则该双曲线的解析式为.(4)如图4，直线与分别与双曲线交于点、，，则的值为.图1图2图3图4(5)(十堰)如图5，正的边长为，双曲线经过点、，且，则的值为.(6)如图6，双曲线与直线交于点、.①(原创、铺垫②)若、，且，则；②(常州模拟·改编)若，且，则；③(杭州模拟·改编)若，且，则.(7)(据上题改编)如图7，为双曲线上的动点，过点作矩形，直线的解析式为，交矩形边于，，则.图5图6图7五、面积比、边比互转1.①(原创、铺垫)如图1①，直线与双曲线交于点，为双曲线上一点，射线交轴于点，若的面积为，则点坐标为；②(成都)如图1②，直线与双曲线交于点、，为双曲线上一点，射线交轴于点，若的面积为，则点坐标为.2.(无锡)如图2，轴，∥轴，双曲线过点、，且，已知的面积为，则的值为.图1①图1②图33.(宁波)如图3，正的顶点在双曲线上，双曲线与边交于点，连接，则的面积为.4.(丽水)如图4，双曲线与直线交于点、，轴，设点的横坐标为.①用含的式子表示；②若与四边形的面积和为，则.5.如图5，双曲线与直线交于点、.①(常州模拟)若，且，则；②(改编自①)若、，且，则.图3图4图56.如图6，轴，为中点，延长到，延长到，若双曲线恰好经过点，，且，则.7.如图7，双曲线过点，，过点，，若，均与轴平行，，，且它们之间的距离长为，则.8.如图8，直线交双曲线于点，，若，则.图6图7图89.如图，点在双曲线上，轴，，延长线交轴于，若的面积为，则的值为.10.如图，点、在双曲线上，轴，轴，垂足、分别在轴的正半轴和负半轴上，，，是的中点，若面积是的倍，则的值为.六、反比例函数图象中的“一线三等角”构造，初探黄金比例1.如图1，中，，，双曲线经过点、，且点的纵坐标为，则的值为.(1)剖析：对于坐标系中的一个直角，若两条边均“倾斜”，我们经常构造“”形全等或相似，即“一线三等角”模型，或叫“矩形大法”，见图2，得. (2)后感：我们可以发现，矩形恰好是一个“黄金矩形”，这到底是一种偶然的巧合，还是一种必然的存在呢？这有待于我们进一步探究…(3)探究(2016临沭模拟)：如图3，双曲线与矩形的边交于点，，若设点的坐标为(，)，且有，，则.图1图2图32.类似题：①(2015临海模拟·填空压轴题)如图，，，双曲线经过点，双曲线经过点，已知点的纵坐标为，则，点的坐标为.②(个人原创)如图2，中，，，双曲线经过点，双曲线经过点，且点的纵坐标为，则的值为.3.难题展示（常州·于新华老师原创题）(1)如图1，点(，)，均在双曲线上，过点作轴垂线，过点作轴垂线，两垂线交于点，垂足分别为，，将沿翻折，点恰好落在轴上的点处.求点的坐标.(2)如图2，点(，)，均在双曲线上，过点作轴垂线，过点作轴垂线，两垂线交于点，垂足分别为，，将沿翻折，点恰好落在轴上的点处.求点的坐标.图1图24.如图，矩形的边的解析式为，顶点，在双曲线上.①若，则点的坐标为；②连接，，若是等边三角形，则.后感：若能发现，本题将更简单！拓展：如图，正方形的顶点、在双曲线上，、在双曲线上，则正方形的面积为.5.(2013湖州模拟)如图1，矩形的顶点、在双曲线上，若点(，)，则点的坐标为.6.如图2，矩形中，，点(，)，点，在双曲线上，若为中点，则的值为.图1图27.①如图1，点，在双曲线上运动，以为底边作等腰直角，则点也在一条双曲线上运动，则该双曲线的解析式为；②如图2，点，在双曲线上运动，以为底边作等腰，则点也在一条双曲线上运动，若，则该双曲线解析式为；③如图3，点，在双曲线上运动，以为底作等腰，点在另一双曲线上运动，若，请用，表示.图1图2图3七、平行导角度，角度导比例1.如图，点，在双曲线上，经过原点，过点作∥轴，连接并延长，交双曲线于点.①求证：；②求的值.根据本题的发现，改编了一个清新小题：如图，点，在双曲线上，经过原点，过点的直线交该双曲线于点，分别交轴，轴于点，，若，.求的值.2.如图，直线交在双曲线于点、，经过原点，过作交轴于点，连接并延长，交双曲线于点.求的值.3.如图，双曲线与过原点的直线交于点、，点在双曲线上，直线、分别交轴于点、.若设，，则.4.如图，，双曲线经过点、、，求证：.八、纯面积推导1.如图，点(，)，，在双曲线上，，分别交，轴于，，分别交，轴于，.求证：.(此方法感谢江苏·于新华老师的指导！)2.(2016菏泽)如图，，均是等腰直角三角形，双曲线经过点，交线段与点，求与的面积之差.后感：①题中条件“，均是等腰直角三角形”可如何改变？②写出，，的关系：.3.(十堰)如图5，正的边长为，双曲线经过点、，且，则的值为.4.(常州)如图1，，双曲线经过点、，且，求的值；5.如图2，，双曲线经过点、、，求证：.图1图2。

反比例函数常见社会模型
概述
反比例函数是一种常见的函数模型，它描述了两个变量之间的相反比例关系。

在社会科学中，反比例函数常被用来分析和预测一些社会模型。

本文将介绍一些常见的反比例函数社会模型。

1. 人口增长模型
人口增长模型是社会科学中应用反比例函数的典型例子之一。

反比例函数可以描述人口增长与人口稠密度之间的关系。

随着人口稠密度增加，资源利用率变高，导致人口增长率下降。

这种模型在城市规划、环境保护等领域中具有重要的应用价值。

2. 教育资源配置模型
教育资源配置模型是另一个应用反比例函数的社会模型。

该模型用于分配有限的教育资源，以实现公平和效率。

根据反比例函数的特性，资源将更倾向于投入到资源匮乏的地区，以提高整体的教育水平。

3. 税收与经济发展模型
税收与经济发展模型也可以使用反比例函数进行建模。

这种模
型可以描述税收与经济发展之间的关系。

随着经济的发展，税收往
往会增加，但增长速度会相对减缓。

这是因为随着经济规模的扩大，税收增长所带来的负担也会逐渐增加。

4. 社会服务分配模型
反比例函数在社会服务分配模型中也有应用。

例如，医疗资源
可以根据人口密度进行合理的分配。

使用反比例函数，可以根据需
求和资源的匹配程度来确定资源分配的合理性，以确保社会公平。

结论
反比例函数在社会科学中具有广泛的应用。

通过理解和应用这
些反比例函数社会模型，我们可以更好地分析和解决一些社会问题。

这些模型可以帮助我们做出更明智的决策，实现社会的可持续发展。

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线，故也称双曲线y=kx（k≠0）．其解析式有三种表示方法：①x k y =（0≠k ）；②1-=kx y (0≠k )；③k xy = 2．反比例函数y=kx（k≠0）的性质 （1)当k 〉0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内,y 随x 的增大而减小． （2）当k 〈0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y 随x 的增大而增大．（3)在反比例函数y=kx中，其解析式变形为xy=k ，故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积）.（4）若双曲线y=k x图像上一点(a,b ）满足a ，b 是方程Z 2－4Z －2=0的两根，求双曲线的解析式．由根与系数关系得ab=－2，又ab=k ，∴k=－2，故双曲线的解析式是y=2x-．（5）由于反比例函数中自变量x 和函数y 的值都不能为零，所以图像和x 轴，y 轴都没有交点,但画图时要体现出图像和坐标轴无限贴近的趋势．二、新知讲解与例题训练 模型一：如图，点A为反比例函数xky =图象上的任意一点，且AB 垂直于x 轴，则有2||k S OAB =∆例1:如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线xm在第一象限的交点，且3=∆AOB S ，(1）求m 的值 （2）求ABC ∆的面积变式题1、如图所示，点1A ，2A ,3A 在x 轴上，且O 1A =21A A =32A A ,分别过1A ，2A ,3A 作y 轴平行线，与反比例函数y=x 8（x>0)的图像交于点1B ,2B ，3B ，分别过点1B ，2B ，3B 作x 轴的平行线，分别与y 轴交于点1C ，2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图，点A 在双曲线1y x =上,点B 在双曲线3y x=上,且AB ∥x 轴,C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为 .模型二:如图：点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点，直线AB 交x 轴于M 点，交y 轴于N 点，再过A 、B 两点分别作y AD ⊥轴于D 点，x BF ⊥轴于F 点，再连结DF 两点，则有：AB DF ||且BM ＝AN例2:如图，一次函数y a x b =+的图象与x 轴，y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ，D 两点,分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ．有下列四个结论：①DEF CEF S S ∆∆=;②AOB ∆相似于FOE ∆；③△DCE ≌△CDF ；④A C B D =其中正确的结论是 ．（把你认为正确结论的序号都填上）y DA B ODFAB DF MN xy O例3：一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴,BD y⊥轴,垂足分别为F D ，，AC 与BD 交于点K ，连接CD ． （1）若点A B ，在反比例函数k y x=的图象的同一分支上，如图1，试证明：①AEDK CFBK S S =四边形四边形;②AN BM =．(2）若点A B ，分别在反比例函数k y x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．模型三：如图，已知反比例函数k y x=(k ≠0，x>0）上任意两点P 、C ，过P 做PA ⊥x 轴,交x 轴于点A ，过C 做CD ⊥x 轴,交x 轴于点D ，则OPC PADC S S ∆=梯形.图1图2例4：如图，在直角坐标系中，一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1，4）、B （4，1)两点，则△AOB 的面积是______.比例函数例5：如图,在直角坐标系中,一次函数1y k x b =+的图象与反是______.2k y x=的图象交于A (1,4）、B （3，m ）两点，则△AOB 的面积两点，且点例6：如图1，已知直线12y x =与双曲线(0)k y k x =>交于A 、BA 的横坐标为4．（1）求k的值；（2)如图2，过原点O 的另一条直线l 交双曲线(0)k y k x=>于C 、D 两点（点C 在第一象限且在点A 的左边），当四边形ACBD 的面积为24时，求点C 的坐标．模型四：在矩形AOBC 中,OB =a ，OA =b ,分别以OB ，OA 所在直线为x 轴和y 轴,建立如图所示的平面直角坐标系．F 是BC 上的一个动点（不与B 、C 重合），过F 点的反比例函数(0)ky x x=>的图象与AC 边交于点E ,则CE aCF b=。

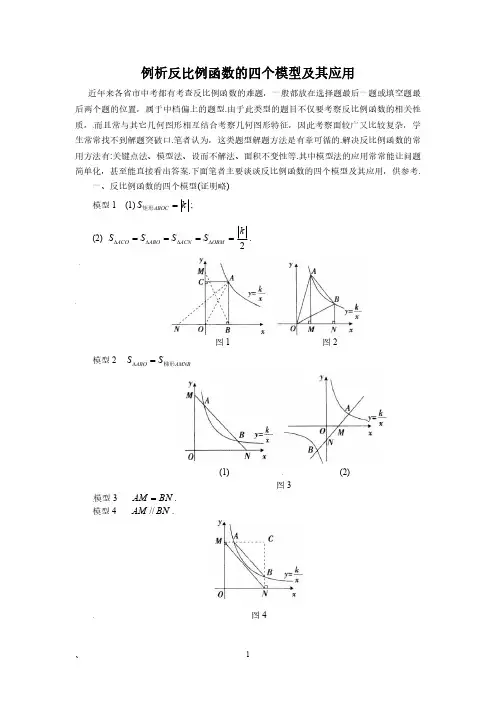
例析反比例函数的四个模型及其应用近年来各省市中考都有考查反比例函数的难题，一般都放在选择题最后一题或填空题最后两个题的位置，属于中档偏上的题型.由于此类型的题目不仅要考察反比例函数的相关性质，而且常与其它几何图形相互结合考察几何图形特征，因此考察面较广又比较复杂，学生常常找不到解题突破口.笔者认为，这类题型解题方法是有章可循的.解决反比例函数的常用方法有:关键点法、模型法、设而不解法、面积不变性等.其中模型法的应用常常能让问题简单化，甚至能直接看出答案.下面笔者主要谈谈反比例函数的四个模型及其应用，供参考.一、反比例函数的四个模型(证明略)模型1(1)ABOC S k =矩形;(2)2ACO ABO ACN OBM kS S S S ∆∆∆∆====.图1图2模型2ABO AMNBS S ∆=梯形(1)(2)图3模型3AM BN =.模型4AM //BN .图4注以上四个模型中点A 、B 都是反比例函数上的任一点.二、模型的应用例1如图5，一次函数y ax b =+的图象与x 轴、y 轴交于A 、B 两点，与反比例函数k y x=的图象交于C 、D 两点，过C 、D 两点分别作y 轴，x 轴的垂线，垂足为E 、F ，连接,CF DE .有下列四个结论:①DEF ∆与CEF ∆的面积相等;②AOB ∆∽FOE ∆;③DCE ∆≌CDF ∆;④AC BD =.其中正确的结论是(填写序号).图5解析此题主要考察模型1,3.对结论①，,,,22DEF CEF DEF CEF kkS S S S ∆∆∆∆==∴=∴ ①正确;对结论②， DEF CEF S S ∆∆=，且两三角形同底，∴两三角形EF 边上的高相等，AB ∴∥,EF AOB ∴∆∽,FOE ∆∴②正确;结论③中， 找不到全等条件，∴③错误;对于结论④，直接运用模型3可得AC DB =,∴④正确.例2已知反比例函数(0)k y k x=>的图象与一次函数6y x =-+相交与第一象限的A 、B 两点，如图6所示，过A 、B 两点分别作x 、y 轴的垂线，线段AC 、BD 相交与P .给出以下结论:①OA OB =;②OAM ∆∽OBN ∆;③若ABP ∆的面积是8，则5k =;④P 点一定在直线y x =上.其中正确的结论是(填写序号).图6解析对于结论①，先求出直线6y x =-+与两坐标轴的交点坐标，可得出OEF ∆是等腰直角三角形，由模型3可得AE BF =，即OAE ∆≌OBF ∆，所以OA OB =，故①正确;对于结论②，AM OE ⊥,BN OF ⊥，且由①AOM BON ∠=∠，知OAM ∆∽OBN ∆，故②正确;对于③，设A (x ,6一x )，则B (6一x ,x )，P (x ,6一2x ).再由三角形的面积公式求出x 的值，故可得出A 点坐标.再根据点A 在反比例函数的图象上即可求出反比例函数的解析式.故③正确;对于④，由②得AM BN =，所以PD PC =.又因为,AC OF BD OE ⊥⊥，所以点P 在线段AB 的垂直平分线上，所以点P 在直线y x =上，故④正确.例3如图7，反比例函数(0)k y k x =>的图象与矩形ABCO 的两边相交于E 、F 两点，若E 是AB 的中点，2BEF S ∆=，则k 的值为.图7解析由模型4，可得EF //AC ，所以BEF ∆∽BAC ∆.又因为E 是AB 的中点，2BEF S ∆=,即:1:4,16BEF BAC AOCB S S S ∆∆==矩形,所以182AOME AOCB S k S ===矩形矩形,即8k =.例4(2013年重庆中考题)如图8，在直角坐标系中，正方形OABC 的顶点O 与原点重合，顶点A 、C 分别在x 轴、y 轴上，反比例函数(0)k y k x=>的图象与正方形的两边AB 、BC 分别交于点M 、N ,ND x ⊥轴，垂足为D ，连结OM 、ON 、MN .下列结论:①OAM ∆≌OCN ∆;②四边形DAMN 与MON ∆面积相等;③若45,2MON MN ∠=︒=，则点C 的坐标为2+1).其中正确的结论是(填写序号)图8解析对于①，由模型1可得2ONC OMA kS S ∆∆==,而OC OA =，则NC AM =;再根据“SAS ”可判断OCN ∆≌OAM ∆,故①正确;对于②，由模型2可得OMN DAMN S S ∆=四边形,故②正确;对于③，作NE OM ⊥于E 点，则ONE ∆为等腰直角三角形.设NE x =，则2OM ON x ==,221)EM x x x =-=.在Rt NEM ∆中，利用勾股定理，可求出222x =+,所以222)42ON x ==+易得BMN ∆为等腰直角三角形，得到222BN MN ==.设正方形ABCO 的边长为a ，在Rt OCN ∆中，利用勾股定理，可求出a 的值为21+,从而得到C 点坐标为2+1).故③正确.总之，利用反比例函数的以上4个模型，是处理反比例函数问题的重要方法之一，我们在教学中应该重视这些几何模型的掌握和应用.。

反比例函数的常见模型
解决反比例函数的问题，除了掌握反比例函数的图像及性质以及反比例函数常见的面积模型之外，还要熟练掌握以下几个经典模型：【模型 1】正比例函数图像被反比例函数图像所截得的线段相等【模型2】一次函数图像被坐标系和反比例函数图像所截得的相等线段
【模型 3】同一象限内反比例函数图像上两点连线的平行线
【模型 4】反比例函数与矩形（1）
【模型 5】反比例函数与矩形（2）
【模型 6】反比例函数与最值
【模型 7】反比例函数与黄金分割。

第15节 反比例函数解题四大模型近几年全国各地中考，与反比例函数相关的综合题、压轴题频频出现在试卷中，特别是反比例函数与一次函数的综合题以及反比例函数与几何的综合题，以较为突出的综合性、信息的隐蔽性以及难于找到合适的转化关系而成为许多同学的“解题难点”，问题的根源往往是不能关注有效信息，对反比例函数的性质理解深度不够，不了解相关解题模型。

本文对近几年的反比例函数综合题进行梳理，通过典型习题体验信息的提取，解题模型的应用，提高解反比例函数“综合题”的能力。

模型一：坐标特点。

关注反比例函数图象上点的坐标特点，利用xy=k 构造方程或直接求解。

例1．（2014•济宁）如图1，四边形OABC 是矩形，ADEF 是正方形，点A 、D 在x 轴的正半轴上，点C 在y 轴的正半轴上，点F 在AB 上，点B 、E 在反比例函数xky 的图象上，OA=1，OC=6，则正方形ADEF 的边长为 .解析： 函数图象信息问题要注意数形结合，据图形分析可得点B 坐标（1，6），设正方形边长为m ，则AD=DE=m ，则OD=1+m ，所以E 点坐标为（1+m ，m ）， 再利用反比例函数图象上点的坐标特征得（1+m ）•m=6×1，解得m 1=﹣3（舍去），m 2=2， ∴正方形ADEF 的边长为2． 故答案为2．点评：本题考查了反比例函数图象上点的坐标特征：反比例函数y=（k 为常数，k≠0）的图象是双曲线，图象上的点（x ，y ）的横纵坐标的积是定值k ，即xy=k ．求出（或构造）反比例函数图象上点的坐标，利用横纵坐标的积相等（定值k ）列方程，是解反比例函数题的一个重要模型。

yxFEBCO A D图1例2 (2011•武汉) 如图2，□ABCD 的顶点A ，B 的坐标分别是A （-1，0），B （0，-2），顶点C ，D 都在双曲线ky x=上，边AD 交y 轴于点E ，且四边形BCDE 的面积是△ABE 面积的5倍，则k = .解析：由面积关系和A 、B 两点坐标入手，分析C 、D 两点坐标特点， 借助xy=k 求解。

……………………………………………………………最新资料推荐………………………………………………… - 1 - 反比例函数常见模型 一、知识点回顾 1..反比例函数的图像是双曲线，故也称双曲线y=kx（k≠0）．其解析式有三种表示方法：①xky （0k）；②1kxy （0k）；③kxy 2．反比例函数y=kx（k≠0）的性质 （1）当k>0时函数图像的两个分支分别在第一，三象限内在每一象限内，y随x的增大而减小． （2）当k<0时函数图像的两个分支分别在第二，四象限内在每一象限内，y随x的增大而增大． （3）在反比例函数y=kx中，其解析式变形为xy=k，故要求k的值(也就是求其图像上一点横坐标与纵坐标之积). （4）若双曲线y=kx图像上一点（a，b）满足a，b是方程Z2－4Z－2=0的两根，求双曲线的解析式．由根与系数关系得ab=－2，又ab=k，∴k=－2，故双曲线的解析式是y=2x． （5）由于反比例函数中自变量x和函数y的值都不能为零，所以图像和x轴，y轴都没有交点，但画图时要体现出图像和坐标轴无限贴近的趋势．

二、新知讲解与例题训练 模型一： 如图，点A为反比例函数xky图象上的任意一点，且AB垂直于x轴，

则有2||kSOAB ……………………………………………………………最新资料推荐…………………………………………………

- 2 - 例1：如图ABCRt的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点，且3AOBS,（1）求m的值 （2）求ABC的面积

变式题 1、如图所示，点1A,2A,3A在x轴上，且O1A=21AA=32AA,分别过1A,2A,3A作y轴平行

线，与反比例函数y=x8(x>0)的图像交于点1B,2B,3B，分别过点1B,2B,3B作x轴的平行线，分别与y轴交于点1C,2C,3C,连结321,,OBOBOB,那么图中阴影部分的面积之和为__________

反比例函数是高中数学中的重要内容，也是考试中经常出现的题型之一。

掌握反比例函数的基本概念和解题方法对于提高数学成绩至关重要。

本文将通过七个模型和十三类题型，帮助读者全面了解并掌握反比例函数的相关知识。

一、反比例函数的基本概念1. 反比例函数的定义反比例函数是一种特殊的二元一次函数，其函数关系可以表示为y=k/x，其中k为比例系数。

当x增大时，y减小；当x减小时，y增大。

反比例函数的图像呈现出一条经过原点的曲线，并且不过原点，是一对对称的点。

2. 反比例函数的特点反比例函数的图像呈现出一种特殊的“反比例”关系，即x与y成反比。

在实际问题中，反比例函数常常用来描述一种随着某个变量的增大而导致另一个变量的减小，或者随着某个变量的减小而导致另一个变量的增大的情况。

二、反比例函数的模型分析1. 比例系数为正数的反比例函数模型当比例系数k大于0时，反比例函数的图像为一条经过第一象限和第三象限的曲线，随着x的增大，y的值减小；随着x的减小，y的值增大。

2. 比例系数为负数的反比例函数模型当比例系数k小于0时，反比例函数的图像为一条经过第二象限和第四象限的曲线，随着x的增大，y的值增大；随着x的减小，y的值减小。

3. 比例系数为零的反比例函数模型当比例系数k等于0时，函数变为y=0，即y始终为0，这时反比例函数的图像为一条水平直线。

4. 比例系数为整数的反比例函数模型当比例系数k为整数时，反比例函数的图像呈现出一种更为规律的变化规律，可以通过整数的变化来探究x和y之间的反比关系。

5. 比例系数为分数的反比例函数模型当比例系数k为分数时，反比例函数的图像表现出更为复杂的变化规律，需要通过分数的变化来揭示x和y之间的反比关系。

6. 反比例函数的图像变换反比例函数的图像可以通过平移、缩放、翻转等变换来形成新的图像，这些变换对于理解反比例函数的性质和特点非常重要。

7. 反比例函数的应用举例反比例函数在日常生活中有很多应用，比如收费问题、速度与时间问题、密度与体积问题等等。

反比例函数常见模型一、知识点回顾1..反比例函数的图像是双曲线，故也称双曲线y=kxk≠0）．其解析式有三种表示方法：①xk y =（0≠k ）；②1-=kx y （0≠k ）；③k xy = 2．反比例函数y=kx（k≠0）的性质（1）当k>0时⇔函数图像的两个分支分别在第一，三象限内⇔在每一象限内，y 随x 的增大而减小．（2）当k<0时⇔函数图像的两个分支分别在第二，四象限内⇔在每一象限内，y 随x 的增大而增大．（3）在反比例函数y=kx中，其解析式变形为xy=k ，故要求k 的值(也就是求其图像上一点横坐标与纵坐标之积).（4）若双曲线y=kx图像上一点（a ，b ）满足a ，b 是方程Z 2－4Z －2=0的两根，求双曲线的解析式．由根与系数关系得ab=－2，又ab=k ，∴k=－2，故双曲线的解析式是y=2x-．（5）由于反比例函数中自变量x 和函数y 的值都不能为零，所以图像和x 轴，y 轴都没有交点，但画图时要体现出图像和坐标轴无限贴近的趋势．二、新知讲解与例题训练 模型一：如图，点A 为反比例函数xk y =图象上的任意一点，且AB 垂直于x 轴，则有2||k S OAB =∆例1：如图ABC Rt ∆的锐角顶点是直线y=x+m 与双曲线y=xm在第一象限的交点，且3=∆AOB S ,（1）求m 的值 （2）求ABC ∆的面积变式题1、如图所示，点1A ,2A ,3A 在x 轴上，且O 1A =21A A =32A A ,分别过1A ,2A ,3A 作y 轴平行线，与反比例函数y=x8(x>0)的图像交于点1B ,2B ,3B ，分别过点1B ,2B ,3B 作x 轴的平行线，分别与y 轴交于点1C ,2C ,3C ,连结321,,OB OB OB ,那么图中阴影部分的面积之和为__________2、 如图，点A 在双曲线1y x =上，点B 在双曲线3y x=上，且AB ∥x 轴，C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为 .模型二：如图：点A 、B 是双曲线)0(≠=k xk y 任意不重合的两点，直线AB 交x 轴于M点，交y 轴于N 点，再过A 、B 两点分别作y AD ⊥轴于D 点，x BF ⊥轴于F 点，再连结DF 两点，则有：AB DF ||且BM ＝ANDFABDF MNxy O例2：如图，一次函数y a x b =+的图象与x 轴，y 轴交于A ，B 两点，与反比例函数ky x=的图象相交于C ，D 两点，分别过C ，D 两点作y 轴，x 轴的垂线，垂足为E ，F ，连接CF ，DE ．有下列四个结论：①DEF CEF S S ∆∆=；②AOB ∆相似于FOE ∆；③△DCE ≌△CDF ；④A C B D =其中正确的结论是 ．（把你认为正确结论的序号都填上）例3：一次函数y ax b =+的图象分别与x 轴、y 轴交于点,M N ，与反比例函数ky x=的图象相交于点,A B ．过点A 分别作AC x ⊥轴，AE y ⊥轴，垂足分别为,C E ；过点B 分别作BF x ⊥轴，BD y ⊥轴，垂足分别为F D ，，AC 与BD 交于点K ，连接CD ．（1）若点A B ，在反比例函数ky x=的图象的同一分支上，如图1，试证明： ①AEDK CFBK S S =四边形四边形；②AN BM =． （2）若点A B ，分别在反比例函数ky x=的图象的不同分支上，如图2，则AN 与BM 还相等吗？试证明你的结论．y x DC A B O F E图1图2模型三：如图，已知反比例函数ky x=（k ≠0，x>0）上任意两点P 、C ，过P 做PA ⊥x 轴，交x 轴于点A ，过C 做CD ⊥x 轴，交x 轴于点D ，则OPC PADC S S ∆=梯形.例4：如图，在直角坐标系中，一次函数y =k 1x+b 的图象与反比例函数2k y x=的图象交于A (1,4)、B (4，1)两点，则△AOB 的面积是______.例5：如图，在直角坐标系中，一次函数1y k x b =+的图象与反比例函数2k y x=的图象交于A （1,4）、B （3，m ）两点，则△AOB 的面积是______.例6：如图1，已知直线12y x =与双曲线(0)ky k x=>交于A 、B 两点，且点A 的横坐标为4． （1）求k 的值；（2）如图2，过原点O 的另一条直线l 交双曲线(0)ky k x=>于C 、D 两点（点C 在第一象限且在点A 的左边），当四边形ACBD 的面积为24时，求点C 的坐标．模型四：在矩形AOBC中，OB=a，OA=b，分别以OB，OA所在直线为x轴和y轴，建立如图所示的平面直角坐标系．F是BC上的一个动点（不与B、C重合），过F点的反比例函数(0)ky xx=>的图象与AC边交于点E，则CE aCF b=.例7：两个反比例函数kyx=和1yx=在第一象限内的图象如图所示，点P在kyx=的图象上，PC⊥x轴于点C，交1yx=的图象于点A，PD⊥y轴于点D，交1yx=的图象于点B，当点P在kyx=的图象上运动时，以下结论：①△ODB与△OCA的面积相等；②四边形P AOB的面积不会发生变化；③P A与PB始终相等；④当点A是PC的中点时，点B一定是PD的中点．其中一定正确的是_________（把你认为正确结论的序号都填上）．课堂练习：一、选择题1、已知m<0，则函数mxy=1与xmy-=2的图像如图，大致是（）xBFCEAOyA. B. C. D 2、如图，点A 在双曲线xy 6=上，且OA=4,过点 A 作AC ⊥x 轴，垂足为c ，OA 的垂直平分线交OC 于B,则ABC ∆的周长为（ ）A.72B.5C.74D.22 3、如图，双曲线xky =（k>0）经过矩形OABC 的边BC 的中点E ，交AB 于点D ，若梯形ODBC 的面积为3，则双曲线的解析式为（ ） A.x y 1=B. x y 2=C. x y 3=D. xy 6=题 3 题 4 题54、如图，A,B 是函数xy 2=的图像上关于原点对称的任意两点，BC//x 轴，AC//y 轴，ABC ∆的面积记为S ，则S （ ）A.S=2B.S=4C.2<S<4D.S>45、如图所示，等腰直角三角形ABC 位于第一象限，AB=AC=2，直角顶点A 在直线y=x 上，其中A 点的横坐标为1，且两条直角边AB ，AC 分别平行于x 轴，y 轴，若双曲线y=k x（k≠0）与△ABC 有交点，则k 的取值范围是（ ）A ．1<k<2B ．1≤k≤3C ．1≤k≤4D ．1≤k<4二、填空题DB AyxO C1、如图，点A 在双曲线1y x =上，点B 在双曲线3y x=上，且AB ∥x 轴，C 、D 在x 轴上，若四边形ABCD 为矩形，则它的面积为 .2、如图，双曲线)0(2φx xy =经过四边形OABC 的顶点A 、C ，∠ABC ＝90°，OC 平分OA 与x 轴正半轴的夹角，AB ∥x 轴，将△ABC 沿AC 翻折后得到△AB ＇C ，B ＇点落在OA 上，则四边形OABC 的面积是 .3、如图，将一块直角三角板OAB 放在平面直角坐标系中，B （2，0），∠AOB ＝60°，点A 在第一象限，过点A 的双曲线为y = k x，在x 轴上取一点P ，过点P 作直线OA 的垂线l ，以直线l 为对称轴，线段OB 经轴对称变换后的像是O ′B ′. （1）当点O ′与点A 重合时，点P 的坐标是 .（2）设P （t ，0）,当O ′B ′与双曲线有交点时，t 的取值范围是 .4、如图，已知双曲线(0)ky k x=<经过直角三角形OAB 斜边OA 的中点D ，且与直角边AB 相交于点C ．若点A 的坐标为（6-，4），则△AOC 的面积为 .5、双曲线1y 、2y 在第一象限的图像如图，14y x=， 过1y 上的任意一点A ，作x 轴的平行线交2y 于B ，交y轴于C，若1AOBS∆=，则2y的解析式是．课后习练一、填空题1、如图，直线y=kx（k>0）与双曲线y=4x交于A（x1，y1），B（x2，y2）两点，则2x1y2－7x2y1的值等于_______．2、反比例函数y=kx的图像上有一点P（a，b），且a，b是方程t2－4t－2=0的两个根，则k=_______；点P到原点的距离OP=_______．3、已知双曲线xy=1与直线y=－x+b无交点，则b的取值范围是______．4、反比例函数y=kx的图像经过点P（a，b），其中a，b是一元二次方程x2+kx+4=0的两个根，那么点P的坐标是_______．5、如图，已知双曲线)0k(xky＞=经过直角三角形OAB斜边OB的中点D，与直角边AB相交于点C．若△OBC的面积为3，则k＝___．第5题图第6题图像与反比例函数y=2x的图6、如图，已知点A是一次函数y=x的图像在第一象限内的交点，点B在x轴的负半轴上，且OA=OB，那么△AOB的面积为（）A．2 B．22C．2D．227、已知P为函数y=2x的图像上一点，且P到原点的距离为3，则符合条件的P点数为（）ABCDEyxOA．0个B．2个C．4个D．无数个。