数据结构迷宫问题实验报告

实验报告课程名：数据结构（C语言版）实验名：迷宫问题I姓名：班级：学号：撰写时间：2014/10/05一实验目的与要求1. 了解栈的应用2. 利用栈在迷宫中找到一条路二实验内容•一个迷宫如图1所示, 是由若干个方格构成的一个矩形, 其中有唯一的一个入口(用标示), 有唯一的一个出口(用△标示). 图中深色的方格无法到达, 浅色的方格都是可以到达的. 每一次只能从当前方格前进到与当前方格有公共边的方格中(因此前进方向最多有四个).•本次实验的迷宫问题要求求解一条从入口到出口的路.图1：迷宫三实验结果与分析程序：#include <stdio.h>#include <stdlib.h>/* run this program using the console pauser or add your own getch, system("pause") or input loop */int Maze(int ox,int oy,int ex,int ey,int rnum,int cnum,int a[rnum][cnum]){int b[rnum][cnum];int i,j,Znum=0;for(i=0;i<rnum;++i){for(j=0;j<cnum;++j){b[i][j]=a[i][j];if(a[i][j]==0){Znum=Znum+1;}}}int Sx[Znum+1], Sy[Znum+1], p=0;for(i=0;i<Znum+1;++i){Sx[i]=-1;Sy[i]=-1;}int dx[4] = {0,1,0,-1};int dy[4] = {-1,0,1,0};Sx[p]=ox;Sy[p]=oy;b[ox][oy]=2;p=1;int brand = -1;//------------------------------------- while(p>0){if(Sx[p-1]==ex && Sy[p-1]==ey){brand = 1;break;}else{int tb = -1;for(i=1;i<4;++i){int tx = Sx[p-1]+dx[i];int ty = Sy[p-1]+dy[i];if(b[tx][ty]==0){tb = 1;Sx[p]=tx;Sy[p]=ty;b[tx][ty]=2;p=p+1;}}if(tb<0){b[Sx[p-1]][Sy[p-1]]=-1;p=p-1;}}}if(brand>0){while(p>0){printf("(%d,%d), ",Sx[p-1],Sy[p-1]);p=p-1;}}return(brand);}int main(int argc, char *argv[]) {int rnum = 10; //rnum和cnum分别对应行和列int cnum = 10;int a[10][10]={{1,1,1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,1,0,0,0,1,0,1},{1,0,0,0,0,1,1,0,0,1},{1,0,1,1,1,0,0,0,0,1},{1,0,0,0,1,0,0,0,0,1},{1,0,1,0,0,0,1,0,0,1},{1,0,1,1,1,0,1,1,0,1},{1,1,0,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1,1,1}};//假设迷宫外围有一层不可到达的方块，则方块变成了10X10 int ox=1,oy=1,ex=rnum-2,ey=cnum-2;int brand = Maze(ox,oy,ex,ey,rnum,cnum,a);if(brand<0){printf("There is no way\n");}return 0;}图1：实验结果截图。

v1.0 可编辑可修改云南大学软件学院数据结构实验报告（本实验项目方案受“教育部人才培养模式创新实验区（X3108005）”项目资助）实验难度： A □ B □ C □实验难度 A □ B □ C □承担任务（难度为C时填写）指导教师评分（签名）【实验题目】实验4.数组的表示极其应用【问题描述】以一个m×n的长方阵表示迷宫，0和1分别表示迷宫中的通路和障碍。

设计一个程序，对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

【基本要求】首先实现一个以链表作存储结构的栈类型，然后编写一个求解迷宫的非递归程序。

求得的通路以三元组(i，j，d)的形式输出，其中:(i，j)指示迷宫中的一个坐标，d 表示走到下一坐标的方向。

如；对于下列数据的迷宫，输出的一条通路为：(l，1，1)，(1，2，2)，(2，2，2)，(3，2，3)，(3，1，2)，…。

•（下面的内容由学生填写，格式统一为，字体: 楷体, 行距: 固定行距18，字号: 小四，个人报告按下面每一项的百分比打分。

难度A满分70分，难度B满分90分）一、【实验构思（Conceive）】(10%)（本部分应包括：描述实验实现的基本思路，包括所用到的离散数学、工程数学、程序设计、算法等相关知识）本实验的目的是设计一个程序，实现手动或者自动生成一个n×m矩阵的迷宫，寻找一条从入口点到出口点的通路。

我们将其简化成具体实验内容如下：选择手动或者自动生成一个n×m的迷宫，将迷宫的左上角作入口，右下角作出口，设“0”为通路，“1”为墙，即无法穿越。

假设从起点出发，目的为右下角终点，可向“上、下、左、右、左上、左下、右上、右下”8个方向行走。

如果迷宫可以走通，则用“■”代表“1”，用“□”代表“0”，用“→”代表行走迷宫的路径。

输出迷宫原型图、迷宫路线图以及迷宫行走路径。

如果迷宫为死迷宫，输出信息。

可以二维数组存储迷宫数据，用户指定入口下标和出口下标。

迷宫问题实验报告武汉纺织大学数学与计算机学院数据结构课程设计报告迷宫问题求解学生姓名：学号：班级：指导老师：报告日期：一、问题描述以一个m x n的长方矩阵表示迷宫，1和0分别表示迷宫中的通路和障碍。

设计一个程序，对任意设定的迷宫，求出从入口到出口的通路，或者没有通路的结论。

二、需求分析1、以二维数组maze[10][10]表示迷宫，数组中以元素1表示通路，0表示障碍，迷宫的大小理论上可以不限制，但现在只提供10*10大小迷宫。

2、迷宫的入口和出口需由用户自行设置。

3、以长方形矩阵的形式将迷宫及其通路输出，输出中“#”表示迷宫通路，“1”表示障碍。

4、本程序只求出一条成功的通路。

但是只要对函数进行小量的修改，就可以求出其他全部的路径。

5、程序执行命令为：（1）输入迷宫；（2）、求解迷宫；（3）、输出迷宫。

三、概要设计1、设定栈的抽象数据类型定义：ADT zhan{基本操作：InitStack(SqStack &S)操作结果：构造一个空栈push（*s，*e）初始条件：栈已经存在操作结果：将e所指向的数据加入到栈s中pop（*s,*e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元素，并删除栈顶元素getpop（*s，*e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元素stackempty(*s)初始条件：栈已经存在操作结果：判断栈是否为空。

若栈为空，返回1，否则返回0 }ADT zhan2、设定迷宫的抽象数据类型定义ADT migong{基本操作：Status print(MazeType maze)； //显示迷宫Status Pass(MazeType maze,PosType curpos); //判断当前位置是否可通Status FootPrint(MazeType &maze,PosType curpos);//标记当前位置已经走过Status MarkPrint(MazeType &maze,PosType curpos); //标记当前位置不可通PosType NextPos(PosType curpos,DirectiveTypedi);// 进入下一位置}ADT yanshu3、本程序包括三个模块a、主程序模块void main(){初始化；迷宫求解；迷宫输出；}b、栈模块——实现栈的抽象数据类型c、迷宫模块——实现迷宫的抽象数据类型四、流程图五、数据结构t ypedef struct //位置结构{int row; //行位置int col; //列位置}PosType;typedef struct //迷宫类型{int arr[10][10];}MazeType;typedef struct{int step; //当前位置在路径上的"序号"PosType seat; //当前的坐标位置DirectiveType di; //往下一个坐标位置的方向 }SElemType;typedef struct //栈类型{SElemType *base; //栈的尾指针 SElemType *top; //栈的头指针int stacksize; //栈的大小 }SqStack;六、调试结果和分析a)测试结果实际程序执行过程如下图所示：参考文献[1] 严蔚敏、吴伟民：《数据结构（C语言版）》[M]，清华大学出版社 2007年版[2] 谭浩强：《C语言设计（第三版）》[M]，清华大学出版社2005年版心得体会通过这段时间的课程设计，本人对计算机的应用，数据结构的作用以及C 语言的使用都有了更深的了解。

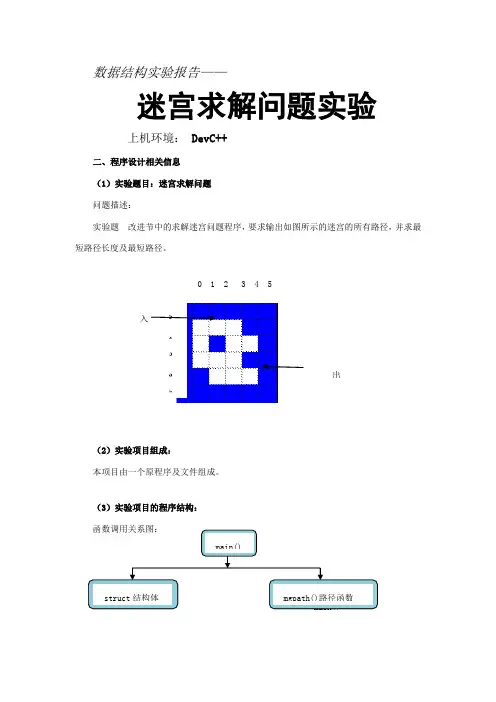
数据结构实验报告——迷宫求解问题实验上机环境： DevC++二、程序设计相关信息（1）实验题目：迷宫求解问题问题描述：实验题 改进节中的求解迷宫问题程序，要求输出如图所示的迷宫的所有路径，并求最短路径长度及最短路径。

（2）实验项目组成：本项目由一个原程序及文件组成。

（3）实验项目的程序结构： 函数调用关系图：0 1 2 3 4 5 01234 出入main() main()struct 结构体 mgpath()路径函数（4）实验项目包含的函数的功能描述： mg[M+1][N+1] =1;Stack[top].j=1;Stack[top].di=-1;mg[1][1]=-1;printf("迷宫所有路径如下:\n");while(top>-1){i=Stack[top].i;j=Stack[top].j;di=Stack[top].di; if(i==M-2&&j==N-2){printf("%4d:",count++);for(k=0;k<=top;k++){printf("(%d,%d)",Stack[k].i,Stack[k].j); if((k+1)%5==0) mg=0回mg=1进循环for下一下一个方块前一个方块值下一个方块值输出方位坐标入口结束printf("\n ");}printf("\n");if(top+1<min){for(k=0;k<=top;k++)Path[k]=Stack[k];min=top+1;}mg[Stack[top].i][Stack[top].j]=0;top--;i=Stack[top].i;j=Stack[top].j;di=Stack[top].di; }find=0;while(di<4&&find==0){di++;switch(di){case 0:i=Stack[top].i-1;j=Stack[top].j;break; case 1:i=Stack[top].i;j=Stack[top].j+1;break; case 2:i=Stack[top].i+1;j=Stack[top].j;break; case 3:i=Stack[top].i;j=Stack[top].j-1;break; }if(mg[i][j]==0)find=1;}if(find==1){Stack[top].di=di;top++;Stack[top].i=i;Stack[top].j=j;Stack[top].di=-1;mg[i][j]=-1;}else{mg[Stack[top].i][Stack[top].j]=0; top--;}}printf("\n");printf("最短路径如下：\n");printf("路径最短长度：%d\n",min);printf("最短路径路径：\n");for(k=0;k<min;k++){printf("(%d,%d)",Path[k].i,Path[k].j); }printf("\n\n");}int main(){mgpath();system("PAUSE"); return 0;}。

实验报告入口（没有通路）。

在探索前进路径时，需要将搜索的踪迹记录下来，以便走不通时，可沿原路返回到前一个点换一个方向再进行新的探索。

后退的尝试路径与前进路径正好相反，因此可以借用一个栈来记录前进路径。

方向：每一个可通点有4个可尝试的方向，向不同的方向前进时，目的地的坐标不同。

预先把4个方向上的位移存在一个数组中。

如把上、右、下、左（即顺时针方向）依次编号为0、1、2、3.其增量数组move[4]如图3所示。

move[4] x y0 -1 01 0 12 1 03 0 -1图2数组move[4]方位示意图如下：从前一个方块找到相邻可走方块之后，再从当前方块找在、相邻可走方块，若没有这样的方快，说明当前方块不可能是从入口路径到出口路径的一个方块，则从当前方块回溯到前一个方块，继续从前一个方块找可走的方块。

为了保证试探的可走的相邻方块不是已走路径上的方块，如（i,j）已经进栈，在试探（i+1，j）的下一方块时，又试探道（i，j），这样会很悲剧的引起死循环，为此，在一个方块进栈后，将对应的mg数组元素的值改为-1（变为不可走的相邻方块），当退栈时（表示该方块没有相邻的可走方块），将其值恢复0，其算法代码和相应的解释如下：find=0;while (di<4 && find==0) //找下一个可走方块{di++;switch(di){case 0:i=st[top].i-1;j=st[top].j;break;case 1:i=st[top].i;j=st[top].j+1;break;case 2:i=st[top].i+1;j=st[top].j;break;case 3:i=st[top].i,j=st[top].j-1;break;}if (mg[i][j]==0) find=1;//找到下一个可走相邻方块}if (find==1) //找到了下一个可走方块{st[top].di=di; //修改原栈顶元素的di值top++; //下一个可走方块进栈st[top].i=i;st[top].j=j;st[top].di=-1;mg[i][j]=-1; //避免重复走到该方块}else //没有路径可走,则退栈{mg[st[top].i][st[top].j]=0;//让该位置变为其他路径可走方块top--; //将该方块退栈}}return(0); //表示没有可走路径,返回0（2）求解主程序建立主函数调用上面的算法，将mg和st栈指针定义为全局变量void main(){mgpath(1,1,M,N);四、界面设计设计很简单的界面，输出路径。

迷宫问题实验报告篇一：迷宫问题实验报告武汉纺织大学数学与计算机学院数据结构课程设计报告迷宫问题求解学生姓名：学号：班级：指导老师：报告日期：一、问题描述以一个m x n的长方矩阵表示迷宫，1和0分别表示迷宫中的通路和障碍。

设计一个程序，对任意设定的迷宫，求出从入口到出口的通路，或者没有通路的结论。

二、需求分析1、以二维数组maze[10][10]表示迷宫，数组中以元素1表示通路，0表示障碍，迷宫的大小理论上可以不限制，但现在只提供10*10大小迷宫。

2、迷宫的入口和出口需由用户自行设置。

3、以长方形矩阵的形式将迷宫及其通路输出，输出中“#”表示迷宫通路，“1”表示障碍。

4、本程序只求出一条成功的通路。

但是只要对函数进行小量的修改，就可以求出其他全部的路径。

5、程序执行命令为：（1）输入迷宫；（2）、求解迷宫；（3）、输出迷宫。

三、概要设计1、设定栈的抽象数据类型定义：ADT zhan{ 基本操作：InitStack操作结果：构造一个空栈push（*s，*e）初始条件：栈已经存在操作结果：将e所指向的数据加入到栈s中pop（*s,*e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元素，并删除栈顶元素getpop（*s，*e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元素stackempty初始条件：栈已经存在操作结果：判断栈是否为空。

若栈为空，返回1，否则返回0 }ADT zhan 2、设定迷宫的抽象数据类型定义ADT migong{基本操作：Status print；//显示迷宫Status Pass; //判断当前位置是否可通Status FootPrint;//标记当前位置已经走过Status MarkPrint; //标记当前位置不可通PosType NextPos; // 进入下一位置}ADT yanshu3、本程序包括三个模块a、主程序模块void main {初始化；迷宫求解；迷宫输出；}b、栈模块——实现栈的抽象数据类型c、迷宫模块——实现迷宫的抽象数据类型四、流程图五、数据结构typedef struct //位置结构{ int row; //行位置int col; //列位置}PosType;typedef struct//迷宫类型{ int arr[10][10]; }MazeType;typedef struct {int step; //当前位置在路径上的”序号”PosType seat; //当前的坐标位置DirectiveType di; //往下一个坐标位置的方向}SElemType;typedef struct // 栈类型{SElemType *base; //栈的尾指针SElemType *top;//栈的头指针int stacksize;//栈的大小}SqStack;六、调试结果和分析a) 测试结果实际程序执行过程如下图所示：篇二：迷宫求解实验报告数据结构（迷宫求解实验报告）一、实验构思（Conceive）（本部分应包括：描述实验实现的基本思路，包括所用到的离散数学、工程数学、程序设计、算法等相关知识）实验实现基本思路：若当前位置可通，则纳入当前路径，并继续朝下一个位置探索，即切换下一位置为当前位置，如此重复直至到达出口；若当前位置不可通，则应顺着来向退回到前一通道块，然后朝着除来向之外的其他方向继续探索；若该通道块的四周4个方块均不可通，则应从当前路径上删除该通道块。

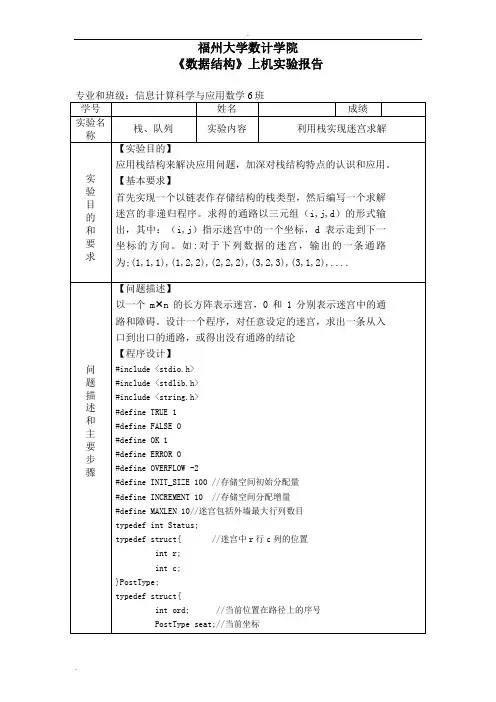
数据结构实验报告——迷宫求解问题实验上机环境： DevC++二、程序设计相关信息（1）实验题目：迷宫求解问题问题描述：实验题3.5 改进3.1.4节中的求解迷宫问题程序，要求输出如图3.14所示的迷宫的所有路径，并求最短路径长度及最短路径。

（2）实验项目组成：本项目由一个原程序mg.cpp 及mg.exe 文件组成。

（3）实验项目的程序结构：（4）实验项目包含的函数的功能描述：mg[M+1][N+1] //构造迷宫二维数组，1表示墙不可走方块，0表示通道mgpath(int xi,int yi,int xe,int ye)//求解路径为：（xi,yi ）->（xe,ye ）//采用顺序栈存储，进栈，回溯，退栈等（5）算法描述：求解迷宫从入口到出口的所有路径，从入口出发，顺某一个方向向前试探，对于可走的方块都进栈，并将这个可走发方位保存，且top+1，然后试探下一个方块，若下一个方块能走通则继续，0 1 2 3 4 512345 出口入口 main() main() struct 结构体 mgpath()路径函数否则则回溯到前一个方块，且top-1。

为记录所有的路径调用Path[k]=Stack[k]记录，从次方块向不同方向去试探，已经走过的方块则为不可走方块。

最后比较top 值找到一条最短路径并输出。

试探路径过程的算法利用了“广度优先搜索遍历”算法。

流程图：（6）实验数据：迷宫数组如下：int mg[M+1][N+1]={{1,1,1,1,1,1},{1,0,0,0,1,1},{1,0,1,0,0,1},{1,0,0,0,1,1},{1,1,0,0,0,1},{1,1,1,1,1,1}};实验结果：mg=0回溯mg=1进栈 循环for下一个方块变成前一个方块下一个方块值 mg[i][j] 前一个方块值mg[][]=0下一个方块值mg[][]=0输出方位坐标( , )入口 结束三、程序代码：#include <stdio.h>#include <stdlib.h>#define M 6#define N 6#define Maxsize 100int mg[M+1][N+1]={{1,1,1,1,1,1},{1,0,0,0,1,1},{1,0,1,0,0,1},{1,0,0,0,1,1},{1,1,0,0,0,1},{1,1,1,1,1,1}};struct{int i;int j;int di;}Stack[Maxsize],Path[Maxsize];int top=-1;int count=1;int min=Maxsize;int mgpath(){int i,j,di,find,k;top++;Stack[top].i=1;Stack[top].j=1;Stack[top].di=-1;mg[1][1]=-1;printf("迷宫所有路径如下:\n");while(top>-1){i=Stack[top].i;j=Stack[top].j;di=Stack[top].di;if(i==M-2&&j==N-2){printf("%4d:",count++);for(k=0;k<=top;k++){printf("(%d,%d)",Stack[k].i,Stack[k].j);if((k+1)%5==0)printf("\n ");}printf("\n");if(top+1<min){for(k=0;k<=top;k++)Path[k]=Stack[k];min=top+1;}mg[Stack[top].i][Stack[top].j]=0;top--;i=Stack[top].i;j=Stack[top].j;di=Stack[top].di; }find=0;while(di<4&&find==0){di++;switch(di){case 0:i=Stack[top].i-1;j=Stack[top].j;break;case 1:i=Stack[top].i;j=Stack[top].j+1;break;case 2:i=Stack[top].i+1;j=Stack[top].j;break;case 3:i=Stack[top].i;j=Stack[top].j-1;break;}if(mg[i][j]==0)find=1;}if(find==1){Stack[top].di=di;top++;Stack[top].i=i;Stack[top].j=j;Stack[top].di=-1;mg[i][j]=-1;}else{mg[Stack[top].i][Stack[top].j]=0;top--;}}printf("\n");printf("最短路径如下：\n");printf("路径最短长度：%d\n",min);printf("最短路径路径：\n");for(k=0;k<min;k++){printf("(%d,%d)",Path[k].i,Path[k].j);}printf("\n\n");} int main(){mgpath();system("PAUSE"); return 0;}。

数据结构实验-迷宫问题数据结构实验迷宫问题在计算机科学领域，数据结构实验是我们深入理解和应用各种数据结构和算法的重要途径。

而迷宫问题，作为一个经典且富有挑战性的课题，不仅能够检验我们对数据结构的掌握程度，还能锻炼我们的逻辑思维和问题解决能力。

迷宫，通常是一个由墙壁和通道组成的复杂网络。

想象一下，在一个封闭的空间里，有无数的岔路和死胡同，我们的目标是从起点找到通往终点的正确路径。

这听起来似乎简单，但当面对实际的迷宫结构时，情况就变得复杂起来。

为了解决迷宫问题，我们首先需要一种合适的数据结构来表示迷宫。

常见的选择是使用二维数组。

我们可以将迷宫中的每个位置表示为数组中的一个元素，用特定的值来表示通道、墙壁或者已经访问过的位置。

接下来，就是选择合适的算法来探索迷宫。

深度优先搜索（DepthFirst Search，简称DFS）和广度优先搜索（BreadthFirst Search，简称 BFS）是两种常用的方法。

深度优先搜索就像是一个勇往直前的探险家，一旦选择了一个方向，就会一直走下去，直到走不通或者到达终点。

它的特点是深入探索，可能会在一条路径上走得很远，但也容易陷入死胡同。

不过，正是这种勇往直前的精神，使得它在一些复杂的迷宫中有可能快速找到一条路径。

广度优先搜索则更加稳健和全面。

它会先逐层地探索迷宫，就像一层一层地剥开洋葱。

从起点开始，先访问距离起点最近的所有节点，然后再逐步向外扩展。

这种方法能够保证找到的路径是最短的，但在计算资源和时间上的消耗可能会相对较大。

在实际的编程实现中，我们需要定义一些辅助的数据结构来记录已经访问过的节点、待访问的节点以及当前的路径等信息。

比如，使用一个栈来实现深度优先搜索，使用一个队列来实现广度优先搜索。

当我们运行算法来解决迷宫问题时，程序会不断地探索各个位置，判断是否是墙壁、是否已经访问过，然后根据搜索策略决定下一步的走向。

这个过程中，会不断地更新迷宫的状态和相关的记录信息。

数据结构上机报告（迷宫）迷宫求解小组成员问题提出:利用栈结构实现迷宫求解问题。

迷宫求解问题如下:心理学家把一只老鼠从一个无顶盖的大盒子的入口赶进迷宫, 迷宫中设置很多隔壁, 对前进方向形成了多处障碍, 心理学家在迷宫的唯一出口放置了一块奶酪, 吸引老鼠在迷宫中寻找通路以到达出口, 测试算法的迷宫如下图所示：问题分析及算法设计:1.迷宫中有障碍物的地方设置为1, 没有障碍物的地方设置为0；2.设起点下标为(1,1), 终点下标为(10,8)；3.从起点出发(起点入栈), 栈中存放走过的路径(坐标)；4.每次取栈顶元素, 在其上下左右中选一个能走通的且没有走过的点入栈；5.若该点为终点；则结束, 输出路径；6.若上下左右都不通或已走过, 则出栈, 栈空, 则走不通。

一．程序设计:1.用户手册:2.运行程序；3.根据提示, 在“请输入迷宫矩阵, <10*10>: ”后输入迷宫矩阵；4.按enter键, 根据提示, 在“请输入起始点<0~9>: ”后输入起始点；5.按enter键, 根据提示, 在“请输入结束点<0~9>: ”后输入结束点；6.按enter键, 即可得出最短路径的长度和最短路径的坐标表示；关闭操作窗口, 结束运行。

附图例:二．调试报告:附录: 程序代码:#include<iostream>using namespace std;struct Point{int x;int y;int pre;};void Copy(Point &a, Point &b){a.x =b.x;a.y =b.y;a.pre =b.pre;}struct Queue{Point p[100];int head=0;int tail=0;};void Append(Queue &d, Point p){d.p[d.tail].x = p.x;d.p[d.tail].y = p.y;d.p[d.tail].pre = p.pre;d.tail++;}void Delete(Queue &d,Point &a){Copy(a, d.p[d.head]);d.head++;}struct Stack{Point q[100];int head=0;};void push(Stack &s, Point p){s.q[s.head].x = p.x;s.q[s.head].y = p.y;s.head++;}void pop(Stack &s){s.head--;cout << "(" << s.q[s.head].x << "," << s.q[s.head].y << ")" << endl; }class Maze{public:Point p0;Point pn;int m[10][10];int i=0;int l;public:void Initp0();void Initpn();void pdp0pn();void InitM();void kz(Queue &Q,Point a);};void main(){int u=0;Queue Q;Stack S;Maze M;M.InitM();M.Initp0();Point a = M.p0;M.Initpn();Append(Q, a);while (1){if (u == 1)break;M.l = Q.tail;while (Q.head < M.l){Delete(Q,a);if (a.x == M.pn.x&&a.y == M.pn.y){u = 1;break;}else{M.kz(Q, a);M.m[a.x][a.y] = 1;}}M.i++;}cout <<"最短路径的长度为: "<< M.i-1 << endl;cout << "最短路径为: " << endl;while (a.pre>=0){push(S, a);a = Q.p[a.pre];}push(S,M.p0);while (S.head>0){pop(S);}}void Maze::Initp0(){cout << "请输入起始点(0~9):" << endl;cin >> p0.x >> p0.y;}void Maze::Initpn(){cout << "请输入结束点(0~9):" << endl;cin >> pn.x >> pn.y;}void Maze::InitM(){cout << "请输入迷宫矩阵(10*10):" << endl;for (int i = 0; i < 10; i++){for (int j = 0; j < 10; j++)cin >> m[i][j];}}void Maze::pdp0pn(){if (m[p0.x][p0.y] == 1 || m[pn.x][pn.y] == 1)cout << "输入的点不符合条件。

南昌航空大学实验报告课程名称：数据结构实验名称：实验三、四：栈和队列应用—迷宫问题班级：学生姓名：学号：指导教师评定：签名:题目：假设迷宫由m行n列构成，有一个入口和一个出口，入口坐标为(1，1)，出口坐标为(m，n)，试找出一条从入口通往出口的最短路径。

设计算法并编程输出一条通过迷宫的最短路径或报告一个“无法通过”的信息。

要求：用栈和队列实现，不允许使用递归算法。

一、需求分析1.用户可以根据自己的需求进行输入所需的迷宫，其中1表示迷宫的墙壁，0表示迷宫的通路，从而建立自己的迷宫；或则使用程序中提供的迷宫。

其中用栈和队列的基本操作完成迷宫问题的求解；2.用户还可以自己设计迷宫的入口坐标，当然也可以设计出口了，但是应该在合法范围内；3.用户进入菜单页面选择输入迷宫的状态（0：表示用户根据自己的需求创建迷宫： 1：表示用户使用程序提供的迷宫； 2：表示退出程序状态）4.程序执行的命令包括：（1）构造栈sqmaze （2）构造抽象迷宫数组maze （3）选择自己要的迷宫（4）输出迷宫（5）在迷宫中寻找一条最短的通路（6）打印出所找到的最短通路（输出搜索结果）二、概要设计⒈为实现上述算法，需要线性表的抽象数据类型：ADT Stack {数据对象：D={a i:|a i∈ElemSet,i=1…n,n≥0}数据关系：R1={<a i-1,a i>|a i-1,a i∈D,i=2,…n≥0}基本操作:initstack(& S)操作结果：构造一个空的栈S。

StackLength(S)初始条件：栈S已经存在操作结果：返回S中数据元素的个数。

Stackempty(S)初始条件：栈S已经存在操作结果：判断S中是否为空，若为空，则返回TURE，否则FALSE。

GetTop(S,&e)初始条件：栈S已存在且不为空操作结果：用e返回S的栈顶的元素。

Push(&S ,e)初始条件：栈S已存在操作结果：插入元素e为新的栈顶元素。

迷宫问题实验报告迷宫求解实验报告数据结构（迷宫求解实验报告）一、【实验构思（Conceive）】(10%)（本部分应包括：描述实验实现的基本思路，包括所用到的离散数学、工程数学、程序设计、算法等相关知识）实验实现基本思路：若当前位置可通，则纳入当前路径，并继续朝下一个位置探索，即切换下一位置为当前位置，如此重复直至到达出口；若当前位置不可通，则应顺着来向退回到前一通道块，然后朝着除来向之外的其他方向继续探索；若该通道块的四周4个方块均不可通，则应从当前路径上删除该通道块。

设以栈记录当前路径，则栈顶中存放的是当前路径上最后一个通道块。

由此，纳入路径的操作即为当前位置入栈；从当前路径上删除前一通道块的才操作即为出栈。

二、【实验设计(Design)】(20%)（本部分应包括：抽象数据类型的功能规格说明、主程序模块、各子程序模块的伪码说明，主程序模块与各子程序模块间的调用关系）抽象数据类型：typedef struct{int x; //当前位置的横坐标int y; //当前位置的纵坐标char type; //当前位置的属性：墙壁或通道(0/1)bool isfoot; //判断当位置是否已走过, true代表已走过}Position; //当前位置信息typedef struct{int order; //脚步在地图上的序号Position seat; //行走的当前位置int aspect; //下一步的方向}Block; //脚步typedef struct{int width; //地图的长度int height; //地图的宽度Position* site; //地图内的各个位置}Maze; //地图typedef struct{Block* base;Block* top;int length;int stacksize;}Stack;主程序模块：int main(int argc, _TCHAR* argv[]){Position start,end;Block blk;Stack S;int width,height;printf(输入迷宫比例X*Y\n);printf(输入X:);scanf(%d,&amp;width);printf(输入Y:);scanf(%d,&amp;height);Maze* maze=GreatMaze(width,height); PrintMaze(maze);printf(\n);printf(请输入入口坐标X:);scanf( %d,&amp;start.x);printf(请输入入口坐标Y:);scanf( %d,&amp;start.y);printf(请输入出后坐标X:);scanf( %d,&amp;end.x);printf(请输入出口坐标Y:);scanf( %d,&amp;end.y);MazePath(maze,start,end,S);printf(走完所需路径长度为:%d,S.length);printf(\n);Stack Sa;InitStack(Sa);while(S.length!=0){Pop(S,blk); Push(Sa,blk); } while(Sa.length!=0) {Pop(Sa,blk); if(Sa.length!=0) printf([%d,%d]-,blk.seat.x,blk.seat.y); //打印足迹else printf([%d,%d],blk.seat.x,blk.seat.y); //打印最后一步 }}各子程序函数：Maze* GreatMaze(int width,int height) //创建地图void PrintMaze(Maze* maze) //打印地图int PositionComparison(Position maze,Position pos) //判断当前位置是否合法int Pass(Maze* maze,Position curpos) //判断当前位置是否可以前进或者是否走过void FootSet(Maze* maze,Position site) //留下足迹Position NextPos(Position &amp;cur,int aspect)//判断方向Int MazePath(Maze* maze,Position start,Position end,Stack&amp;S)//搜索从入口到出口的路径三、【实现描述（Implement）】(30%)（本部分应包括：抽象数据类型具体实现的函数原型说明、关键操作实现的伪码算法、函数设计、函数间的调用关系，关键的程序流程图等，给出关键算法的时间复杂度分析。

实验报告实验课名称：数据结构实验实验名称：迷宫问题班级：20130613 学号：16 姓名：施洋时间：2015-5-18一、问题描述这是心理学中的一个经典问题。

心理学家把一只老鼠从一个无顶盖的大盒子的入口处放入，让老鼠自行找到出口出来。

迷宫中设置很多障碍阻止老鼠前行，迷宫唯一的出口处放有一块奶酪，吸引老鼠找到出口。

简而言之，迷宫问题是解决从布置了许多障碍的通道中寻找出路的问题。

本题设置的迷宫如图1所示。

入口出口图1 迷宫示意图迷宫四周设为墙；无填充处，为可通处。

设每个点有四个可通方向，分别为东、南、西、北。

左上角为入口。

右下角为出口。

迷宫有一个入口，一个出口。

设计程序求解迷宫的一条通路。

二、数据结构设计以一个m×n的数组mg表示迷宫，每个元素表示一个方块状态，数组元素0和1分别表示迷宫中的通路和障碍。

迷宫四周为墙，对应的迷宫数组的边界元素均为1。

根据题目中的数据，设置一个数组mg如下int mg[M+2][N+2]={{1,1,1,1,1,1,1,1},{1,0,0,1,0,0,0,1},{1,1,0,0,0,1,1,1},{1,0,0,1,0,0,0,1},{1,0,0,0,0,0,0,1},{1,1,1,1,1,1,1,1}};在算法中用到的栈采用顺序存储结构，将栈定义为Struct{ int i; //当前方块的行号int j; //当前方块的列号int di; //di是下一个相邻的可走的方位号}st[MaxSize];// 定义栈int top=-1 //初始化栈三、算法设计要寻找一条通过迷宫的路径，就必须进行试探性搜索，只要有路可走就前进一步，无路可进，换一个方向进行尝试；当所有方向均不可走时，则沿原路退回一步（称为回溯），重新选择未走过可走的路，如此继续，直至到达出口或返回入口（没有通路）。

在探索前进路径时，需要将搜索的踪迹记录下来，以便走不通时，可沿原路返回到前一个点换一个方向再进行新的探索。

数据结构实验报告云南大学软件学院 项目资助）”（本实验项目方案受“教育部人才培养模式创新实验区）X3108005

（

C □□ B □A 实验难度：

实验难度 手动输入生成迷宫查找路径迷宫有解迷宫无解输出路径打印通路 □ C B □ A □2

承担任务 （难度为C时填写）m,n

m,n结束

指导教师评分 （签名） 自动

生成

【实验题目】 4.实验数组的表示极其应用 【问题描述】和1分别表示迷宫中的通路和障碍。设计一×n的长方阵表示迷宫，0m以一个个程序，对任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

【基本要求】 首先实现一个以链表作存储结构的栈类型，然后编写一个求解迷宫的非递归程序。求得的通路以三元组(i，j，d)的形式输出，其中:(i，j)指示迷宫中的一个坐标，d表示走到下一坐标的方向。如；对于下列数据的迷宫，输出的一条通路为：(l，1，1)，(1， ?，…。2)，1，(3，3)，2，(3，2)，2，(2，2)，2．

（下面的内容由学生填写，格式统一为，字体: 楷体, 行距: 固定行距18，字号: 小四，个人报告按下面每一项的百分比打分。难度A满分70分，难度B满分90分） 一、【实验构思（Conceive）】(10%) （本部分应包括：描述实验实现的基本思路，包括所用到的离散数学、工程数学、程序设计、算法等相关知识）

本实验的目的是设计一个程序，实现手动或者自动生成一个n×m矩阵的迷宫，寻找一条从入口点到出口点的通路。我们将其简化成具体实验内容如下： 选择手动或者自动生成一个n×m的迷宫，将迷宫的左上角作入口，右下角作出

口，设“0”为通路，“1”为墙，即无法穿越。假设从起点出发，目的为右下角终点，可向“上、下、左、右、左上、左下、右上、右下”8个方向行走。如果迷宫可以走通，则用“■”代表“1”，用“□”代表“0”，用“→”代表行走迷宫的路径。输出迷宫原型图、迷宫路线图以及迷宫行走路径。如果迷宫为死迷宫，输出信息。 可以二维数组存储迷宫数据，用户指定入口下标和出口下标。为处理方便起见，可在迷宫的四周加一圈障碍。对于迷宫中任一位置，均可约定有东、南、西、北四个方向可通。?

目录一、实验要求（需求分析） (1)a. 实验目的 (1)b. 实验内容 (2)c．程序功能 (2)二、程序分析 (2)2.1 存储结构 (2)2.2 关键算法分析 (3)三、程序运行分析 (7)1.程序运行流程图： (7)2.程序运行结果截图： (8)四．总结 (10)五、附录 (11)一、实验要求（需求分析）a. 实验目的通过实验，掌握如下内容：➢进一步掌握指针、模板类、异常处理的使用➢掌握队列的操作的实现方法➢学习使用队列解决实际问题的能力➢学习使用图的广度优先搜索解决实际问题的能力b. 实验内容利用队的结构实现迷宫求解问题。

迷宫求解问题如下：心理学家把一只老鼠从一个无顶盖的大盒子的入口赶进迷宫，迷宫中设置很多隔壁，对前进方向形成了多处障碍，心理学家在迷宫的唯一出口放置了一块奶酪，吸引老鼠在迷宫中寻找通路以到达出口，测试算法的迷宫如下图所示。

c．程序功能输入起始点的坐标，输出走出迷宫最短路径的长度。

二、程序分析2.1 存储结构存储结构: 队列顺序存储结构示意图如下:2.2 关键算法分析核心算法思想：1.如果采用直接递归的方式，用栈很容易实现路径的输出，但是这条路径不一定是最短路径。

为了改进算法，达到输出最短路径的目标，采用队列的实现方式。

2.为查找最短路径，使用了“图”中的算法：广度优先搜索。

关键算法思想描述和实现：关键算法1：为寻求最短路径，采用广度优先搜索算法，使用队列实现路径存储，队列中每个元素用结构体存储系，包含迷宫坐标、队列中的序号、父节点的序号，实现了对路径的记录。

C++实现：struct Node{int parent_id; //保存父节点的位置int node_id; //当前节点的序号，以便传递给孩子节点int x,y; //当前结点对应的坐标}Q[10*10]; //每个节点包含迷宫坐标、队列中的序号、父节点的序号，多个节点形成队列关键算法2：遍历每个位置四周的位置，将没有走过的位置入队，形成树形的队列，通过出队操作就能找到最短路径。