山西省太原市师范学院附属中学2017-2018学年高二上学期第一次月考理数试题 含答案 精品

太原师院附中师苑中学2017-2018学年度第一次月考数学试题一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列说法中正确的个数为( )①三角形一定是平面图形；②若四边形的两对角线相交于一点，则该四边形是平面图形；③圆心和圆上两点可确定一个平面；④三条平行线最多可确定三个平面.A. 1B. 2C. 3D. 4【答案】C【解析】∵不共线的三点确定一个平面，∴三角形一定是平面图形，故①正确；∵两条相交线确定一个平面，∴若四边形的两条对角线相交于一点，则该四边形是平面图形，故②正确；当圆心和圆上两点共线时，圆心和圆上两点确定无数个平面，故③不正确；三条平行线最多可确定3个平面，故④正确，故选C.2.设直线与平面相交但不垂直，则下列说法中正确的是A. 在平面内有且只有一条直线与直线垂直B. 过直线有且只有一个平面与平面垂直C. 与直线垂直的直线不可能与平面平行D. 与直线平行的平面不可能与平面垂直【答案】C【解析】由题意知，m与α斜交，令其在α内的射影为m′，则在α内可作无数条与m′垂直的直线，它们都与m垂直，A错；如图(1)，在α外，可作与α内直线l平行的直线，C错；如图(2)，m⊂β，α⊥β，可作β的平行平面γ，则m∥γ且γ⊥α，D错．考点：平面与平面垂直的判定.【此处有视频，请去附件查看】3.如图所示，正方形的边长为1，它是水平放置的一个平面图形的直观图，则原图形的周长是A. 6B. 8C.D.【答案】B【解析】【分析】根据题目给出的直观图的形状，画出对应的原平面图形的形状，求出相应的边长，则问题可求．【详解】作出该直观图的原图形，如图所示，因为直观图中的线段轴，所以在原图形中对应的线段平行于x轴且长度不变，点和在原图形中对应的点C和B的纵坐标是的2倍，则，所以，则四边形OABC的长度为8．故选：B．【点睛】本题考查了平面图形的直观图及其应用，着重考查了数形结合思想，解答此题的关键是掌握平面图形的直观图的画法，能正确的画出直观图的原图形．4.如图，已知为斜边的中点，平面，则（）A. B. C. D. 【答案】C【解析】∵为斜边的中点，∴，∵平面，∴由勾股定理得，故选.5.已知在三棱锥中，分别是的中点，则下列结论正确的是（）A. B.C. D.【答案】D【解析】如图所示，.取的中点，连接、，在中，∵，，∴，同理可得，在中，∵三角形两边之和大于第三边即，∴，即，故选D.6.三棱柱侧棱与底面垂直，体积为，高为，底面是正三角形，若是中心，则与平面所成的角大小是（）A B. C. D.【答案】B【解析】试题分析：利用三棱柱的侧棱与底面垂直和线面角的定义可知，∠APA1为PA与平面A1B1C1所成角，即∠APA1为PA与平面ABC所成角．利用三棱锥的体积计算公式可得AA1，再利用正三角形的性质可得A1P，在Rt△AA1P中，利用tan∠APA1=即可求出．如图所示，∵AA1⊥底面A1B1C1，∴∠APA1为PA与平面A1B1C1所成角，又∵平面ABC∥平面A1B1C1，∴∠APA1为PA与平面ABC所成角．，解得：AA1=．又P为底面正三角形的中心，在Rt△AA1P中，tan∠APA1=，故选B．考点：直线与平面所成的角．7.如图，在四面体中，若，，是的中点，则下列正确的是（）A. 平面平面B. 平面平面C. 平面平面，且平面平面D. 平面平面，且平面平面【答案】C【解析】因为，，是的中点，⇒平面，由面面垂直判定定理可得平面平面，平面平面，故选C.点睛：破解线面垂直关系的技巧：(1)解答此类问题的关键在于熟练把握空间垂直关系的判定与性质，注意平面图形中的一些线线垂直关系的灵活利用，这是证明空间垂直关系的基础．(2)由于“线线垂直”“线面垂直”“面面垂直”之间可以相互转化，因此整个证明过程围绕着线面垂直这个核心而展开，这是化解空间垂直关系难点的技巧所在．.8.在梯形中，，，.将梯形绕所在直线旋转一周而形成的曲面所围成的几何体的体积为（）A. B. C. D.【答案】C【解析】直角梯形ABCD绕AD所在的直线旋转一周而形成的曲面所围成的几何体是一个底面半径为1，母线长为2的圆柱挖去一个底面半径同样是1、高为1的圆锥后得到的组合体，所以该组合体的体积为：故选C考点：1、空间几何体的结构特征；2、空间几何体的体积.【此处有视频，请去附件查看】9.半径为的半圆卷成一个圆锥，则它的体积为（）.A. B. C. D.【答案】A【解析】设此圆锥的底面半径为r,高为h,则.10. 某三棱锥的三视图如图所示，该三棱锥的表面积是（）A. B. C. D.【答案】B【解析】从所给的三视图可以得到该几何体为三棱锥，如右图所示。

2017-2018学年山西大学附中高二（上）第一次月考数学试卷一、选择题（本大题共12小题，每小题3分，共36分）1．设a 、b 是正实数，以下不等式：①＞；②a ＞|a ﹣b |﹣b ；③a 2+b 2＞4ab ﹣3b 2；④ab +＞2恒成立的序号为（ ）A ．①③B ．①④C ．②③D ．②④2．在数列{a n }中，a n =2n +3，前n 项和S n =an 2+bn +c ，n ∈N *，其中a ，b ，c 为常数，则a ﹣b +c=（ ）A ．﹣3B ．﹣4C ．﹣5D ．﹣63．若不等式ax 2+2ax ﹣4＜2x 2+4x 对任意实数x 均成立，则实数a 的取值范围是（ ） A ．（﹣2，2） B ．（﹣2，2] C ．（﹣∞，﹣2）∪[2，∞） D ．（∞，2]4．已知点A （﹣1，1），B （1，2），C （﹣2，﹣1），D （3，4），则向量在方向上的投影为（ ）A ．B ．C ．D ．5．已知数列{a n }满足3a n +1+a n =0，a 2=﹣，则{a n }的前10项和等于（ ）A ．﹣6（1﹣3﹣10）B ．C ．3（1﹣3﹣10）D ．3（1+3﹣10）6．已知，则tan2α=（ ）A ．B ．C ．D ．7．在△ABC 中，若，则△ABC 是（ ）A ．等腰三角形B ．直角三角形C ．等腰或直角三角形D ．等腰直角三角形8．将函数y=cosx +sinx （x ∈R ）的图象向左平移m （m ＞0）个单位长度后，所得到的图象关于y 轴对称，则m 的最小值是（ ）A ．B ．C ．D ．9．在△ABC 中，角A 、B 、C 的对边分别为a 、b 、c ，如果cos （2B +C ）+2sinAsinB ＜0，那么三边长a 、b 、c 之间满足的关系是（ ）A ．2ab ＞c 2B ．a 2+b 2＜c 2C ．2bc ＞a 2D ．b 2+c 2＜a 210．已知函数f （x ）=sin （2x +φ），其中φ为实数，若f （x ）≤|f （）|对x ∈R 恒成立，且f （）＜f （π）．则下列结论正确的是（ ）A．f（π）=﹣1B．f（）C．f（x）是奇函数D．f（x）的单调递增区间是[kπ﹣，kπ+]（k∈Z）11．已知△ABC的外接圆半径为1，圆心为O，且3+4+5=，则•的值为（）A．﹣B．C．﹣D．12．已知点G是△ABC的重心，且AG⊥BG， +=，则实数λ的值为（）A．B．C．3 D．2二．填空题（每小题3分，共12分）13．数列{a n}为等比数列，其前n项的乘积为T n，若T2=T8，则T10=．14．在△ABC中，角A，B，C所对的边分别是a，b，c，若b2+c2=a2+bc，且=4，则△ABC的面积等于．15．已知数列{a n}为正项等差数列，满足+≤1（其中k∈N*，且k≥2），则a k的最小值为．16．如图，在正方形ABCD中，E为AB的中点，P为以A为圆心、AB为半径的圆弧上的任意一点，设向量，则λ+μ的最小值为．三．解答题：（本大题共5小题，共52分．解答应写出文字说明，证明过程或演算步骤．）17．已知数列{a n}满足a1=3，a n﹣3a n=3n（n∈N*），数列{b n}满足b n=．+1（Ⅰ）求证：数列{b n}是等差数列，并求数列{a n}的通项公式；（Ⅱ）求数列{a n}的前n项和S n．18．设△ABC的三边为a，b，c满足．（Ⅰ）求A的值；（Ⅱ）求的取值范围．19．某隧道长2150m，通过隧道的车速不能超过20m/s．一列有55辆车身长都为10m的同一车型的车队（这种型号的车能行驶的最高速为40m/s）匀速通过该隧道，设车队的速度为xm/s，根据安全和车流的需要，当0＜x≤10时，相邻两车之间保持20m的距离；当10＜x≤20时，相邻两车之间保持m的距离．自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为y（s）．（1）将y表示为x的函数；（2）求车队通过隧道时间y的最小值及此时车队的速度．20．在△ABC中，∠A，B，C所对应的边分别为a，b，c，面积为S．（1）若≤2S，求A的取值范围；（2）若tanA：tanB：tanC=1：2：3，且c=1，求b．21．已知数列{a n}的前n项和为S n，且满足S，数列{b n}满足，T n为数列{b n}的前n项和．（I）求数列{a n}的通项公式a n和T n；（II）若对任意的n∈N*不等式恒成立，求实数λ的取值范围．2016-2017学年山西大学附中高二（上）第一次月考数学试卷参考答案与试题解析一、选择题（本大题共12小题，每小题3分，共36分）1．设a、b是正实数，以下不等式：①＞；②a＞|a﹣b|﹣b；③a2+b2＞4ab﹣3b2；④ab+＞2恒成立的序号为（）A．①③B．①④C．②③D．②④【考点】不等关系与不等式．【分析】由a，b为正实数，对于①①利用基本不等式变形分析取值特点即可；对于②利用含绝对值不等式的性质即可加以判断；对于③取出反例数值即可；对于④利用均值不等式进行条件下的等价变形即可．【解答】解：∵a、b是正实数，∴①a+b≥2⇒1≥⇒≥．当且仅当a=b时取等号，∴①不恒成立；②a+b＞|a﹣b|⇒a＞|a﹣b|﹣b恒成立；③a2+b2﹣4ab+3b2=（a﹣2b）2≥0，当a=2b时，取等号，例如：a=2，b=1时，左边=5，右边=4×1×2﹣3×22=﹣4∴③不恒成立；④ab+≥2=2＞2恒成立．答案：D2．在数列{a n}中，a n=2n+3，前n项和S n=an2+bn+c，n∈N*，其中a，b，c为常数，则a﹣b+c=（）A．﹣3 B．﹣4 C．﹣5 D．﹣6【考点】等差数列的前n项和．【分析】把n等于1代入a n=2n+3求出数列的首项，然后利用等差数列的前n项和的公式根据首项和第n项表示出前n项的和，得到前n项的和为一个关于n的多项式，根据多项式相等时，各对应的系数相等即可求出a，b，c的值，即可求出a﹣b+c的值．【解答】解：令n=1，得到a1=2+3=5，所以，而S n=an2+bn+c，则an2+bn+c=n2+4n，所以a=1，b=4，c=0，则a﹣b+c=1﹣4+0=﹣3．故选A3．若不等式ax2+2ax﹣4＜2x2+4x对任意实数x均成立，则实数a的取值范围是（）A．（﹣2，2）B．（﹣2，2] C．（﹣∞，﹣2）∪[2，∞）D．（∞，2]【考点】函数恒成立问题．【分析】将原不等式整理成关于x的二次不等式，结合二次函数的图象与性质解决即可，注意对二次项系数分类讨论【解答】解：不等式ax2+2ax﹣4＜2x2+4x，可化为（a﹣2）x2+2（a﹣2）x﹣4＜0，当a﹣2=0，即a=2时，恒成立，合题意．当a﹣2≠0时，要使不等式恒成立，需，解得﹣2＜a＜2．所以a的取值范围为（﹣2，2]．故选B．4．已知点A（﹣1，1），B（1，2），C（﹣2，﹣1），D（3，4），则向量在方向上的投影为（）A．B．C．D．【考点】平面向量数量积的含义与物理意义．【分析】先求出向量、，根据投影定义即可求得答案．【解答】解：，，则向量方向上的投影为：•cos＜＞=•===，故选A．5．已知数列{a n}满足3a n+a n=0，a2=﹣，则{a n}的前10项和等于（）+1A．﹣6（1﹣3﹣10）B．C．3（1﹣3﹣10）D．3（1+3﹣10）【考点】等比数列的前n项和．【分析】由已知可知，数列{a n}是以﹣为公比的等比数列，结合已知可求a1，然后代入等比数列的求和公式可求+a n=0【解答】解：∵3a n+1∴∴数列{a n}是以﹣为公比的等比数列∵∴a1=4由等比数列的求和公式可得，S10==3（1﹣3﹣10）故选C6．已知，则tan2α=（）A．B．C． D．【考点】二倍角的正切；同角三角函数间的基本关系．【分析】由题意结合sin2α+cos2α=1可解得sinα，和cosα，进而可得tanα，再代入二倍角的正切公式可得答案．【解答】解：∵，又sin2α+cos2α=1，联立解得，或故tanα==，或tanα=3，代入可得tan2α===﹣，或tan2α===故选C7．在△ABC中，若，则△ABC是（）A．等腰三角形B．直角三角形C．等腰或直角三角形 D．等腰直角三角形【考点】三角形的形状判断．【分析】利用二倍角公式将已知条件转化为acosA=bcosB，再利用正弦定理与二倍角的正弦化简后判断即可．【解答】解：∵2﹣1=cosA，=cosB，∴已知关系是变形为：acosA=bcosB，在△ABC中，由正弦定理得：sinAcosA=sinBcosB，∴sin2A=sin2B，∴2A=2B或2A=π﹣2B，∴A=B或A+B=．∴△ABC是等腰或直角三角形．故选C．8．将函数y=cosx+sinx（x∈R）的图象向左平移m（m＞0）个单位长度后，所得到的图象关于y轴对称，则m的最小值是（）A．B．C．D．【考点】两角和与差的正弦函数；函数y=Asin（ωx+φ）的图象变换．【分析】函数解析式提取2变形后，利用两角和与差的正弦函数公式化为一个角的正弦函数，利用平移规律得到平移后的解析式，根据所得的图象关于y轴对称，即可求出m的最小值．【解答】解：y=cosx+sinx=2（cosx+sinx）=2sin（x+），∴图象向左平移m（m＞0）个单位长度得到y=2sin[（x+m）+]=2sin（x+m+），∵所得的图象关于y轴对称，∴m+=kπ+（k∈Z），则m的最小值为．故选B9．在△ABC中，角A、B、C的对边分别为a、b、c，如果cos（2B+C）+2sinAsinB＜0，那么三边长a、b、c之间满足的关系是（）A．2ab＞c2B．a2+b2＜c2 C．2bc＞a2D．b2+c2＜a2【考点】余弦定理的应用．【分析】由条件利用诱导公式以及两角和与差的余弦函数公式求得cos（A+B）＞0，可得A+B＜，C＞，故△ABC形状一定是钝角三角形，从而得到a2+b2＜c2 ，由此得出结论．【解答】解：在△ABC中，由cos（2B+C）+2sinAsinB＜0可得，cos（B+B+C）+2sinAsinB ＜0．∴cosBcos（B+C）﹣sinBsin（B+C）+2sinAsinB＜0，即cosBcos（π﹣A）﹣sinBsin（π﹣A）+2sinAsinB＜0．∴﹣cosBcosA﹣sinBsinA+2sinAsinB＜0，﹣cosBcosA+sinBsinA＜0．即﹣cos（A+B）＜0，cos（A+B）＞0．∴A+B＜，∴C＞，故△ABC形状一定是钝角三角形，故有a2+b2＜c2 ．故选B．10．已知函数f（x）=sin（2x+φ），其中φ为实数，若f（x）≤|f（）|对x∈R恒成立，且f（）＜f（π）．则下列结论正确的是（）A．f（π）=﹣1B．f（）C．f（x）是奇函数D．f（x）的单调递增区间是[kπ﹣，kπ+]（k∈Z）【考点】命题的真假判断与应用；正弦函数的单调性．【分析】根据题意首先判断φ的取值，然后逐条验证．对A，代入求值即可；对B，代入比较大小即可；对C，根据奇函数定义，验证是否适合；对D，通过解不等式求单调区间的方法求解．【解答】解：∵f（x）≤|f（）|对x∈R恒成立，∴2×+φ=kπ+⇒φ=kπ+，k∈Z．∵f（）＜f（π）⇒sin（π+φ）=﹣sinφ＜sin（2π+φ）=sinφ⇒sinφ＞0．∴φ=2kπ+，k∈Z．不妨取φ=f（）=sin2π=0，∴A×；∵f（）=sin（+）=sin=﹣sin＜0，f（）=sin（+）=sin＞0，∴B×；∵f（﹣x）≠﹣f（x），∴C×；∵2kπ﹣≤2x+≤2kπ+⇒kπ﹣≤x≤kπ+，k∈Z．∴D√；故选D11．已知△ABC的外接圆半径为1，圆心为O，且3+4+5=，则•的值为（）A．﹣B．C．﹣D．【考点】向量在几何中的应用．【分析】先将一个向量用其余两个向量表示出来，然后借助于平方使其出现向量模的平方，则才好用上外接圆半径，然后进一步分析结论，容易化简出要求的结果．【解答】解：因为3+4+5=，所以，所以，因为A ，B ，C 在圆上，所以．代入原式得，所以==．故选：A ．12．已知点G 是△ABC 的重心，且AG ⊥BG ， +=，则实数λ的值为（ ）A ．B ．C ．3D ．2【考点】正弦定理；同角三角函数基本关系的运用．【分析】首先根据三角形的重心性质及直角三角形的斜边的中线等于斜边的一半，得到CD=AB ，再应用余弦定理推出AC 2+BC 2=5AB 2，将+=应用三角恒等变换公式化简得λ=，然后运用正弦定理和余弦定理，结合前面的结论，即可求出实数λ的值．【解答】解：如图，连接CG ，延长交AB 于D ， 由于G 为重心，故D 为中点，∵AG ⊥BG ，∴DG=AB ，由重心的性质得，CD=3DG ，即CD=AB ，由余弦定理得，AC 2=AD 2+CD 2﹣2AD •CD •cos ∠ADC ， BC 2=BD 2+CD 2﹣2BD •CD •cos ∠BDC ， ∵∠ADC +∠BDC=π，AD=BD ， ∴AC 2+BC 2=2AD 2+2CD 2，∴AC 2+BC 2=AB 2+AB 2=5AB 2，又∵+=，∴，即λ=，∴λ======．即．故选B．二．填空题（每小题3分，共12分）13．数列{a n}为等比数列，其前n项的乘积为T n，若T2=T8，则T10=1．【考点】等比数列的前n项和．【分析】由已知利用等比数列的性质得a3×a8=1．从而T10=（a3×a8）5=1．【解答】解：∵数列{a n}为等比数列，其前n项的乘积为T n，T2=T8，∴a3×a4×…×a8=1，∴（a3×a8）3=1，a3×a8=1．从而T10=a1×a2×…×a10=（a1×a10）5=（a3×a8）5=1．故答案为：1．14．在△ABC中，角A，B，C所对的边分别是a，b，c，若b2+c2=a2+bc，且=4，则△ABC的面积等于2．【考点】余弦定理；平面向量数量积的运算；正弦定理．【分析】利用已知表达式，通过余弦定理求出cosA，求出sinA，通过向量的数量积求出bc 的值，然后求出三角形的面积．【解答】解：因为b2+c2=a2+bc，所以cosA==，∴sinA=．因为，所以，bccosA=4，∴bc=8，△ABC的面积：S===2．故答案为：2．15．已知数列{a n}为正项等差数列，满足+≤1（其中k∈N*，且k≥2），则a k的最小值为．【考点】数列递推式．【分析】由等差数列的性质得，结合+≤1利用基本不等式求得a k 的最小值．【解答】解：∵数列{a n }为正项等差数列，且+≤1，∴≥•（+）=≥=．当且仅当+=1，且，即a 1=3，a 2k ﹣1=6时上式等号成立．∴a k 的最小值为．故答案为：．16．如图，在正方形ABCD 中，E 为AB 的中点，P 为以A 为圆心、AB 为半径的圆弧上的任意一点，设向量，则λ+μ的最小值为．【考点】平面向量的基本定理及其意义．【分析】建立坐标系，设正方形ABCD 的边长为1，求出向量=（，﹣λ+μsin θ ）=（1，1），用cos θ，sin θ表示 λ和μ，根据cos θ，sin θ 的取值范围，再结合λ+μ的单调性，求出λ+μ=的最小值．【解答】解：以A 为原点，以AB 所在的为x 轴，建立坐标系，设正方形ABCD 的边长为1，则E （，0），C （1，1），D （0，1），A （0，0）．设 P （cos θ，sin θ），∴=（1，1）．再由向量=λ（，﹣1）+μ（cos θ，sin θ）=（，﹣λ+μsin θ ），∴，∴，∴λ+μ===﹣1+．由题意得0≤θ≤，∴0≤cosθ≤1，0≤sinθ≤1．求得（λ+μ）′==＞0，故λ+μ在[0，]上是增函数，故当θ=0时，即cosθ=1，这时λ+μ取最小值为=，故答案为：．三．解答题：（本大题共5小题，共52分．解答应写出文字说明，证明过程或演算步骤．）17．已知数列{a n}满足a1=3，a n﹣3a n=3n（n∈N*），数列{b n}满足b n=．+1（Ⅰ）求证：数列{b n}是等差数列，并求数列{a n}的通项公式；（Ⅱ）求数列{a n}的前n项和S n．【考点】数列递推式．【分析】（Ⅰ）利用条件，结合等差数列的定义，即可证明数列{b n}是等差数列，从而求数列{a n}的通项公式；（Ⅱ）利用错位相减法求数列{a n}的前n项和S n．【解答】（I）证明：∵，，，∴b n﹣b n=，…+1∴数列{b n}是等差数列，…∵，∴，∴数列{a n}的通项公式；…（II）解：∵，∴，当n≥2时，相减得：∴，…整理得，当n=1时，，…综上，数列{a n}的前n项和．…18．设△ABC的三边为a，b，c满足．（Ⅰ）求A的值；（Ⅱ）求的取值范围．【考点】正弦定理．【分析】（Ⅰ）已知等式左边利用正弦定理化简，再利用和差化积公式及二倍角的正弦函数公式化简，整理后求出B+C的度数，即可确定出A的值；（Ⅱ）原式利用二倍角的余弦函数公式化简，再利用诱导公式变形，用B表示出C，代入后利用两角和与差的正弦函数公式化为一个角的正弦函数，根据正弦函数的值域即可确定出范围．【解答】解：（Ⅰ）∵===2R，∴==cosB+cosC，整理得：=2cos cos，即cos2=，∴cos=，即=，∴B+C=，即A=；（Ⅱ）∵B+C=，∴C=﹣B，即cosC=sinB，∴2cos2+2cos2=1+cosB+（1+cosC）=cosB+cosC++1=cosB+sinB++1=2sin（B+）++1，∵0＜B＜，即＜B+＜，∴＜sin（B+）≤1，即+2＜2sin（B+）++1≤+3，则2cos2+2cos2的取值范围为（+2， +3]．19．某隧道长2150m，通过隧道的车速不能超过20m/s．一列有55辆车身长都为10m的同一车型的车队（这种型号的车能行驶的最高速为40m/s）匀速通过该隧道，设车队的速度为xm/s，根据安全和车流的需要，当0＜x≤10时，相邻两车之间保持20m的距离；当10＜x≤20时，相邻两车之间保持m的距离．自第1辆车车头进入隧道至第55辆车尾离开隧道所用的时间为y（s）．（1）将y表示为x的函数；（2）求车队通过隧道时间y的最小值及此时车队的速度．【考点】函数模型的选择与应用．【分析】（1）由题目条件，利用对x进行分类讨论，求出离开隧道所用的时间为y；（2）分别求分段函数中上下两个函数式子的最小值，综合它们中的较小者，即可得原函数的最小值，从而车队通过隧道时间y有最小值．【解答】解：（1）当0＜x≤10时，，当10＜x≤20时，=，所以，，（2）当x∈（0，10]时，在x=10时，，当x∈（10，20]时，≈329.4（s），当且仅当，即：x≈17.3（m/s）时取等号．因为17.3∈（10，20]，所以当x=17.3（m/s）时，y min=329.4（s），而378＞329.4，所以，当车队的速度为17.3（m/s）时，车队通过隧道时间y有最小值329.4（s）．20．在△ABC中，∠A，B，C所对应的边分别为a，b，c，面积为S．（1）若≤2S，求A的取值范围；（2）若tanA：tanB：tanC=1：2：3，且c=1，求b．【考点】余弦定理；向量在几何中的应用；同角三角函数间的基本关系．【分析】（1）已知不等式左边利用平面向量的数量积运算法则变形，右边利用三角形面积公式化简，整理求出tanA的范围，即可确定出A的范围；（2）由已知的比例式，设一份为x，表示出tanA，tanB，tanC，由A=π﹣（B+C），利用诱导公式得到tanA=﹣tan（B+C），再利用两角和与差的正切函数公式将等式右边进行变形，将表示出tanA，tanB，tanC代入，列出关于x的方程，求出方程的解得到x的值，即为tanA 的值，确定出tanB与tanC的值，进而求出sinB与sinC的值，由c的值，利用正弦定理即可求出b的值．【解答】解：（1）∵•=cbcosA，S=bcsinA，∴cbcosA≤×2bcsinA，若A为钝角或直角，显然成立；若A为锐角，即tanA≥，∵A为三角形内角，∴≤A＜π；（2）由tanA：tanB：tanC=1：2：3，设tanA=x，tanB=2x，tanC=3x，∴tanA=tan[π﹣（B+C）]=﹣tan（B+C）=﹣=﹣=x，整理得：x2=1，解得：x=1或x=﹣1，∴tanA=1或tanA=﹣1（不合题意，舍去），∴tanA=1，tanB=2，tanC=3，三个角为锐角，∴cosB==，cosC==，∴sinB=，sinC=，∵c=1，∴由正弦定理=得：b===．21．已知数列{a n}的前n项和为S n，且满足S，数列{b n}满足，T n为数列{b n}的前n项和．（I）求数列{a n}的通项公式a n和T n；（II）若对任意的n∈N*不等式恒成立，求实数λ的取值范围．【考点】数列与函数的综合；数列与不等式的综合．【分析】（I）当n=1时，a1=S1=1，当n≥2时，a n==2n﹣1，由此推导出a n=2n﹣1，从而得到b n==（），由此能求出数列{a n}的通项公式a n和T n．（II）由（I）得：λ＜，由此进行分类讨论，能推导出对于任意的正整数n，原不等式恒成立，λ的取值范围．【解答】解：（I）当n=1时，a1=S1=1，当n≥2时，a n==2n﹣1，验证当n=1时，也成立；所以，a n=2n﹣1，b n===（）所以，T n==．（II）由（I）得：λ＜，当n为奇数时，λ＜=2n﹣恒成立，因为当n为奇数时，2n﹣单调递增，所以当n=1时，2n﹣﹣1取得最小值为0，此时，λ＜0．当n为偶数时，=2n++3恒成立，因为当n为偶数时，2n++3单调递增，所以当n=2时，2n++3取得最小值为，此时，λ＜．综上所述，对于任意的正整数n，原不等式恒成立，λ的取值范围是（﹣∞，0）．2016年12月24日。

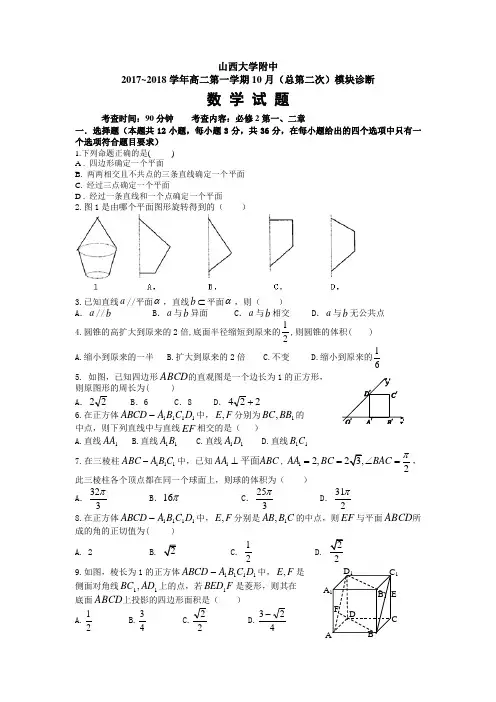
ABC DA 1B 1C 1D 1 FE山西大学附中2017~2018学年高二第一学期10月（总第二次）模块诊断数 学 试 题考查时间：90分钟 考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1.下列命题正确的是( ) A . 四边形确定一个平面B. 两两相交且不共点的三条直线确定一个平面C. 经过三点确定一个平面D . 经过一条直线和一个点确定一个平面2.图1是由哪个平面图形旋转得到的（）3.已知直线a //平面α，直线b ⊂平面α，则（ ）A ．a //bB ．a 与b 异面C ．a 与b 相交D ．a 与b 无公共点4.圆锥的高扩大到原来的2倍,底面半径缩短到原来的21,则圆锥的体积( ) A .缩小到原来的一半 B .扩大到原来的2倍 C .不变 D .缩小到原来的615. 如图，已知四边形ABCD 的直观图是一个边长为1的正方形，则原图形的周长为( )A ．22B ．6C ．8D ．224+6.在正方体1111D C B A ABCD -中，F E ,分别为1,BB BC 的 中点，则下列直线中与直线EF 相交的是（ ） A.直线1AA B.直线11B A C.直线11D A D.直线11C B7.在三棱柱111ABC A B C -中，已知1AA ABC ⊥平面,12,2AA BC BAC π==∠=，此三棱柱各个顶点都在同一个球面上，则球的体积为（ ）A ．323πB ．16πC ．253π D ．312π8.在正方体1111D C B A ABCD -中，F E ,分别是C B AB 1,的中点，则EF 与平面ABCD 所成的角的正切值为( )129.如图，棱长为1的正方体1111D C B A ABCD -中，F E ,是侧面对角线11,AD BC 上的点，若F BED 1是菱形，则其在 底面ABCD 上投影的四边形面积是（ ）A.21B.43C.22 D.423-10.如图，已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面 直线AB 与1CC 所成的角的余弦值为（ ）A.D.3411.如图，四面体ABCD 中，截面PQMN 是正方形， 则在下列结论中，下列说法错误的是（ ） A ．AC BD ⊥ B ．AC BD = C.//AC 截面PQMN D ．异面直线PM 与BD 所成的角为4512．如图，矩形ABCD 中，AD AB 2=，E 为边AB 的中点， 将ADE ∆沿直线DE 翻转成DE A 1∆（∉1A 平面ABCD ）．若O M ,分别为线段C A 1,DE 的中点，则在ADE ∆翻转过程中，下列说法错误的是（ ）A. 与平面DE A 1垂直的直线必与直线BM 垂直B. 异面直线BM 与E A 1所成角是定值C. 一定存在某个位置，使MO DE ⊥D. 三棱锥ADE A -1外接球半径与棱AD 的长之比为定值 二．填空题（本大题共4小题，每小题4分，共16分） 13.若一个正四面体的棱长为a ，则它的表面积为_________. 14.如图,是一个无盖器皿的三视图，正视图、侧视图和俯视图 中的正方形边长为2，正视图、侧视图中的虚线都是半圆， 则该器皿的表面积是___________.15.设甲、乙两个圆柱的底面积分别为21S S ，，体积分别为21V V ，，若它们的侧面积相等，且4921=S S ，则21V V的值是________．16. 如图，PA ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上的一点，E 、F 分别是点A 在PB 、PC 上的射影．给出下列结论：①AF ⊥PB ；②EF ⊥PB ； ③AF ⊥BC ； ④AE ⊥平面PBC ． 其中正确命题的序号是 （把正确的序号都填上）三．解答题（本题共5大题，共48分）（解答题不能用空间向量）17．如图，在四边形ABCD 中，AD DC ⊥，//AD BC ，3AD =，2CD =，AB =45DAB ∠=，四边形绕着直线AD 旋转一周.(1)求所形成的封闭几何体的表面积； (2)求所形成的封闭几何体的体积.18.如图，在三棱锥P ABC -中，H G,F,,E 分别是BC PC,AC,AB,的中点，且BC AC PB,PA ==(1)证明：PC AB ⊥；(2)证明：平面PAB //平面FGH19. 如图，四边形ABEF 是等腰梯形，2,//==BE AF EF AB ，24=EF ,22=AB ，四边形ABCD 是矩形．AD ⊥平面ABEF ，其中M Q ,分别是EF AC ,的中点，P 是BM 中点．（1）求证：//PQ 平面BCE ； （2）求证：AM ⊥平面BCM .20.如图，在四棱锥O ABCD -中，底面ABCD 是边长为1的菱形，4ABC π∠=, OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点（1）证明：直线MN OCD平面‖；（2）求异面直线AB 与MD 所成角的大小；21.如图，在四棱锥P A B C D -中，底面A B C D 是平行四边形，45ADC ∠=︒，1AD AC ==，O 为AC 的中点，PO ⊥平面ABCD ，2PO =，M 为PD 的中点．（1）证明：AD ⊥平面PAC ；（2）求直线AM 与平面ABCD 所成角的正切值．山西大学附中2016~2017学年高二第一学期10月（总第二次）模块诊断数 学 试 题考查时间：90分钟 考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1-6 BADACD 7-12 ADBDBC二．填空题（本大题共4小题，每小题4分，共16分）13. 23a 14. π+24 15.2316. ①②③ 三．解答题（本题共5大题，共48分） 17．解：过点B 作BE AD ⊥于点E ，因为AB =45DAB ∠=，所以2BE =，所以1DE = 所以四边形ABCD 绕着直线AD 旋转一周所形成的封闭几何体为一个底面半径为2，母线为1的圆柱及一个底面半径为2，高为2的圆锥的组合体. 2分（1）所以几何体的表面积为(2222128S ππππ=⨯+⨯⨯+⨯⨯+, 5分（2）体积为22120212233V πππ=⨯⨯+⨯⨯⨯=. 8分 18. 试题解析：（Ⅰ）证明：连接EC ，AB EC ⊥有 2分又,PB PA =PE AB ⊥∴ 2分PEC PC PEC AB 面面⊂⊥∴,PC AB ⊥∴ 5分（Ⅱ）连结FH ，交于EC 于O ，连接GO ，则FH//AB 7分 在,//.PEC GO PE ∆中 9分 PE ∩AB E =， GO ∩FH O =所以平面PAB//平面FGH 10分 19. 解：（1）因为AB ∥EM ，且AB ＝EM ，所以四边形ABEM 为平行四边形． 连接AE ，则AE 过点P ，且P 为AE 中点，又Q 为AC 中点， 所以PQ 是△ACE 的中位线，于是PQ ∥CE ． 4分 ∵CE ⊂平面BCE ，PQ ⊄平面BCE ，∴PQ ∥平面BCE ． 5分（2）AD ⊥平面ABEF ⇒BC ⊥平面ABEF ⇒BC ⊥AM ． 7分 在等腰梯形ABEF 中，由AF ＝BE ＝2，EF ＝24，AB ＝22， 可得∠BEF ＝45°，BM ＝AM ＝2，∴AB 2＝AM 2＋BM 2，∴AM ⊥BM ． 9分 又BC∩BM＝B ，∴AM ⊥平面BCM ． 10分20．方法一（1）取OB 中点E ，连接ME ，NEME CD ME CD ∴，‖AB,AB ‖‖，又,NE OC MNE OCD ∴平面平面‖‖，MN OCD ∴平面‖,方法二取OD的中点F ，因为MF //AD ,AD NF 21=,NC //AD ,AD NC 21=,MFCN 为平行四边形，MN //FC ,MN OCD ∴平面‖（2）CD ‖AB, M D C ∠∴为异面直线AB 与MD 所成的角（或其补角）作,AP CD P ⊥于连接MP ⊥⊥平面A BC D ，∵OA ∴CD MP,4ADP π∠=∵∴DP =MD ，所以 AB 与MD 所成角的大小为3π 21. （1）证明：∵45ADC ∠=︒，且1AD AC ==，∴90DAC ∠=︒，即AD AC ⊥。

山西大学附中2017-2018高二数学10月月考试卷（有答案）山西大学附中2017～2018学年高一第一学期10月（总第一次）模块诊断数学试题考试时间:80分钟总分100分考查范围:集合函数不等式一．填空题（每小题4分，共40分）1．设集合，集合，则集合＝()A．{1,3,1,2,4,5}B．{1}C．{1,2,3,4,5}D．{2,3,4,5}2．若且，则（)A．2B．2或-2C．0或2D．0或2或-23．下列集合A到B的对应中，不能构成映射的是（）A.①②③B.①②④C.①③④D.②③④4.设全集是实数集，，，则如图所示阴影部分所表示的集合是（）A．B．C．D．5.已知，则=（）.A．5B.4C．3D.26．已知，则的表达式是（）A.B.C.D.7．若函数在区间上是减函数，则实数的取值范围是（）A.B.C.D.8.下列四个函数：①；②；③；④，其中定义域与值域相同的是()A．①②③B．①②④C．②③D．②③④9．设集合，，则（）A．B．C．D．10.已知函数的定义域为，则函数的定义域是() A．B．C．D．二．填空题（每小题4分，共16分）11．函数的值域是.12．设是非空集合，定义．已知集合，，则＝.13.函数的单调增区间是.14.有下列四个命题：①已知，则集合中有0个元素；②函数的值域为；③不等式对任意实数恒成立，则；④不等式的解集是.其中正确命题的序号是．三．解答题：（共44分）15．（本题10分）设，，求：（1）；（2）.16.（本题10分）求下列函数的定义域：（1）（2）17．（本题12分）已知集合，集合.（1）若，求的取值范围；（2）若，求实数的取值范围.18．（本题12分）已知二次函数满足，且.（1）求函数的解析式；（2）令，求函数在上的最小值.山西大学附中2017～2018学年高一第一学期10月（总第一次）模块诊断数学试题评分细则一、选择题（4×10=40分）12345678910CDACDABBBD二、填空题（4×4=16分）11.12.13.14.③三、解答题（共44分）15.解析：…………1分（1）又…………3分…………5分（2）又…………7分得…………10分16.解析：（1）要使函数有意义，只需…………2分…………4分所以定义域为…………5分（2）要使函数有意义，只需…………7分…………9分所以定义域为…………10分17.解析：（1）.…………5分（2）,①当时，满足要求，此时，得;②当时，要，则，解得，由①②得，，实数的取值范围.…………12分18.解析：（1）设二次函数（），…………1分则…………2分∴，，∴，…………4分又，∴.…………5分∴…………6分（2）∵∴.，，对称轴，…………8分当时，；…………9分当时，；…………10分当时，…………11分综上所述，…………12分。

（Ⅱ）由（Ⅰ）知：AM=BE=2， 同理可得：BM=AF=2， 又 AB=2 2 ， ∴AB2=AM2+BM2， ∴AM⊥BM， ∵四边形 ABCD 为矩形， ∴BC∥AD， 又 AD⊥平面 ABEF， ∴BC⊥平面 ABEF， ∴BC⊥AM， 又 BC∩BM=B， ∴AM⊥平面 BCM．
-2-
20. 解：（1）取 OB 中点 E，连接 ME，NE
（2）体积为V 22 1 1 22 2 20 ．
3
3
18. 解：（Ⅰ）证明：连接 EC，则 EC⊥AB 又∵PA=PB，∴AB⊥PE， ∴AB⊥面 PEC， ∵BC⊂面 PEC， ∴AB⊥PC
（Ⅱ）连结 FH，交于 EC 于 O，连接 GO，则 FH∥AB 在△PEC 中，GO∥PE， ∵PE∩AB=E，GO∩FH=O ∴平面 PAB∥平面 FGH
AN= 1 DO= 5 ，
2
4
在 Rt△ANM 中，tan∠MAN= MN 1 4 5 ， AN 5 5
4
即直线 AM 与平面 ABCD 所成角的正切值为 4 5 ． 5
-3-
∵AC⊂平面 PAC，PO⊂平面 PAC，且 AC∩PO=O，
∴由直线和平面垂直的判定定理知 AD⊥平面 PAC．
（2）解：取 DO 中点 N，连接 MN，AN，
由 PO⊥平面 ABCD，得 MN⊥平面 ABCD，
∴∠MAN 是直线 AM 与平面 ABCD 所成的角，
∵M 为 PD 的中点，
∴MN∥PO，且 MN= 1 PO=1， 2
4
2
∴ cos∠MDP DP 1 ,∠MDC ∠MDP
MD 2
3
所以 AB 与 MD 所成角的大小为 ． 3
21. 解：（1）证明：∵PO⊥平Байду номын сангаас ABCD，且 AD⊂平面 ABCD，

-1 -
（2）三棱锥 A′﹣BC′D 的体积为 a3 4 1 1 a3 1 a3 ． 32 3
20. 解：(1)证明：∵PA⊥平面 ABCD，CD⊂平面 ABCD
∴CD⊥PA 又∵CD⊥PC 而 PC∩PA=P 所以，CD⊥面 PAC （2）∵AB⊥BC，AB=BC=1 ∴∠BAC=45°∴∠CAD=45° 又由（1）CD⊥面 PAC ∴CD⊥AC ∴△ACD 为等腰直角三角形 又 E 为 AD 中点∴CE⊥AD 又∵BC∥AD∴CE⊥BC 所以，∴CE∥AB 而 AB⊂面 PAB，CE⊄面 PAB 所以 CE∥面 PAB 21. 解：（1）证明：由题设知，直三棱柱的侧面为矩形， 由 D 为 AA1 的中点，则 DC=DC1， 又 AA1=2AC，可得 DC12+DC2=CC12， 则 CD⊥DC1， 而 CD⊥B1D，B1D∩DC1=D， 则 CD⊥平面 B1C1D， 由于 B1C1⊂平面 B1C1D， 故 CD⊥B1C1； （2）解：由（1）知，CD⊥B1C1， 且 B1C1⊥C1C，则 B1C1⊥平面 ACC1A1， 设 V1 是平面 CDB1 上方部分的体积， V2 是平面 CDB1 下方部分的体积，
太原师院附中 师苑中学 2017-2018 学年度第一次月考数学（答案）
一、 选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 C B B C D B C C A B B B
二、 填空题
题号
13
14
15
16
答案
60
1 a2b
①②③
23
6
三、 解答题 17. 解：当 Q 为 CC1 的中点时，平面 D1BQ∥平面 PAO．
由△POM 也为直角三角形得： PM2=PO2+OM2=a2+ 3 ，

2017-2018学年下学期山西大学附属中学高二第一次月考试卷理科数学注意事项：1．答题前，先将自己的姓名．准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷．草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷．草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1．若直线1x =的倾斜角为α，则α（ ） A ．等于0B ．等于4πC ．等于2π D ．不存在2．函数x x y ln =的导数为（ ） A ．xB ．x ln 1+C ．x x ln 1+D ．13．已知空间向量()1,3,x =m ，()2,1,2x =-n ，则“1x =”是“⊥m n ”的（ ） A ．充分不必要条件 B ．必要不充分条件 C ．充要条件D ．既不充分也不必要条件4．设n m 、是不同的直线，βα、是不同的平面，有以下四个命题： ①若βα⊥，α//m ，则β⊥m ；② 若α⊥m ，α⊥n ，则n m //； ③若α⊥m ，n m ⊥，则α//n ；④若α⊥n ，β⊥n ，则αβ//； 其中真命题的序号为（ ） A ．①③B ．②③C ．①④D ．②④5．若直线4:=+ny mx l 和圆4:22=+y x O 没有交点，则过点),(n m 的直线与椭圆14922=+y x 的交点个数为（ ） A ．0个 B ．至多一个 C ．1个 D ．2个6．焦点为()6,0±且与双曲线1222=-y x 有相同渐近线的双曲线方程是（ ）A ．1241222=-y xB ．1241222=-x yC ．1122422=-x yD ．1122422=-y x7．如图，已知三棱柱111ABC A B C -的侧棱与底面边长都相等，1A 在底面ABC 上的射影为BC 的中点，则异面直线AB 与1CC 所成的角的余弦值为（ ）AB．CD ．348．椭圆2212516x y +=的左、右焦点分别为12,F F ，弦AB 过1F ，若2ABF △的内切圆的周长为2π，,A B 两点的坐标分别为()11,x y ，()22,x y ，则21y y -=（ ）A ．35B ．310 C ．320 D ．35 9．已知平面区域()430,352501x y D x y x y x ⎧⎫-+≤⎧⎪⎪⎪=+-≤⎨⎨⎬⎪⎪⎪≥⎩⎩⎭，2yZ x =+．若命题“(),x y D ∀∈，Z m ≥”为真命题，则实数m 的最大值为（ ） A ．2215B ．27 C ．13D ．1410．一个几何的三视图如图所示，则表面积为（ ）此卷只装订不密封班级 姓名 准考证号 考场号 座位号A．18+B．18+12+C．18+12+D．9+11．如图，P 是正四面体V ABC -的面VBC 上一点，点P 到平面ABC 距离与到点V 的距离相等，则动点P 的轨迹是（ ）A ．直线B ．抛物线CD ．离心率为3的双曲线12．如图，在三棱锥B ACD -中，3ABC ABD DBC ∠∠=∠=π=，3,2AB BC BD ===， 则三棱锥B ACD -的外接球的表面积为（ ）A ．192πB ．19π CD第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．命题“若20x x -≥，则2x >”的否命题是__________．14．已知ABC △在斜二测画法下的平面直观图A B C '''△，A B C '''△是边长为a 的正三角形，那么在原ABC △的面积为__________．15．已知抛物线24y x =的准线与双曲线22214x y a -=交于,A B 两点，点F 为抛物线的交点，若FAB ∆为正三角形，则双曲线的离心率是_______．16．已知直线()():21440l m x m y m ++-+-=上总存在点M ，使得过M 点作的圆C ：222430x y x y ++-+=的两条切线互相垂直，则实数m 的取值范围是_______．三．解答题（本题共6个大题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．（10分）命题:p 方程()2221mx m y +-=表示双曲线；命题:q 不等式()()21120m x m x -+-+>的解集是R ．p q ∧为假，p q ∨为真，求m 的取值范围．18．（12分）三棱柱111C B A ABC -中，N M 、分别是B A 1、11C B 上的点，且12BM A M =，112C N B N =．设AB =a ，AC =b ，1AA =c ． （1）试用a ，b ，c 表示向量MN ；（2）若90BAC ∠=︒，1160BAA CAA ∠=∠=︒，11AB AC AA ===，求MN 的长．19．（12分）已知点P(2,2)，圆C：x2＋y2－8y＝0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点．（1）求M的轨迹方程；（2）当|OP|＝|OM|时，求l的方程．20．（12分）已知曲线3:()C f x x x=-．（1）求曲线C在点(1,(1))f处的切线方程；（2）求与直线53y x=+平行的曲线C的切线方程．21．（12分）如图，在等腰梯形ABCD 中，//AB CD ，1AD DC CB ===，60ABC ∠=︒，四边形ACFE 为矩形，平面ACFE ⊥平面ABCD ，1CF =． （1）求证：BC ⊥EF ；（2）点M 在线段EF 上运动，设平面MAB 与平面FCB 二面角的平面角为(90)θθ≤︒，试求cos θ的取值范围．22．（12（1）求椭圆的方程；（2）若过点()1,0C -且斜率为k 的直线l 与椭圆相交于不同的两点B A ,，试问在x 轴上是否存在点M ，使5MA MB ⋅+k 无关的常数？若存在，求出点M 的坐标；若不存在，请说明理由．2017-2018学年下学期山西大学附属中学高二第一次月考试卷理 科 数 学 答 案第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．）第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．若20x x -<，则2x ≤ 1421516．210m -≤≤三．解答题（本题共6个小题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．【答案】{}0129m m m <<≤<或． 【解析】p 真()20m m -<，02m <<，q 真，1m =或1m >∆<⎧⎨⎩，19m <<，∴19m ≤<， p 真q 假，01m <<；p 假q 真，29m ≤<，∴m 范围为{}0129m m m <<≤<或．18．【答案】（1）111333MN =++a b c ；（2）53MN =．【解析】（1）1111MN MA A B B N =++1111133BA AB B C =++11111()()33333=-++-=++c a a b a a b c ． （2）2()222++=+++⋅+⋅+⋅222a b c a b c a b b c c a111110211211522=++++⨯⨯⨯+⨯⨯⨯=，||++=a b c 1||||3MN =++=a b c ． 19．【答案】（1）M 的轨迹方程：()()22132x y -+=-；（2）l 的方程：380x y +-=． 【解析】（1）圆C 的方程可化为x 2＋(y －4)2＝16，所以圆心为C(0，4)，半径为4． 设M(x ，y)，则CM→＝(x ，y －4)，MP →＝(2－x ，2－y)．由题设知CM →·MP →＝0，故x(2－x)＋(y －4)(2－y)＝0，即(x －1)2＋(y －3)2＝2．由于点P 在圆C 的内部，所以M 的轨迹方程是()()22132x y -+=-．（2）由（1）可知M 的轨迹是以点N(1，3)为圆心，2为半径的圆．由于|OP|＝|OM|，故O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM ． 因为ON 的斜率为3，所以l 的斜率为－13，故l 的方程为380x y +-=． 20．【答案】（1）；（2）或．【解析】（1）∵，∴，求导数得，∴切线的斜率为， ∴所求切线方程为，即．（2）设与直线平行的切线的切点为，则切线的斜率为． 又∵所求切线与直线平行，∴， 解得，代入曲线方程得切点为或，∴所求切线方程为或，即或． 21．【答案】（1）见解析；（2）1cos 2θ⎤∈⎥⎣⎦． 【解析】（1）证明：在梯形ABCD 中，∵//AB CD ，1AD DC CB ===，60ABC ∠=︒，∴2AB =， ∴2222cos603AC AB BC AB BC =+-⋅⋅︒=， ∴222AB AC BC =+，∴BC AC ⊥，∵平面ACFE ⊥平面ABCD ，平面ACFE 平面ABCD AC =，BC ⊂平面ABCD ， ∴BC ⊥平面ACFE ，∴BC ⊥EF ．（2）由（1）可建立分别以直线CA ，CB ，CF 为x 轴，y 轴，z 轴的如图所示空间直角坐标系，令(0FM λλ=≤≤，则(0,0,0)C，A ，(0,1,0)B ，(,0,1)M λ，∴(,0)AB =，(,1,1)BM λ=-． 设1(,,)x y z =n 为平面MAB 的一个法向量，由1100AB BM ⎧⋅=⎪⎨⋅=⎪⎩n n，得00y x y z λ⎧+=⎪⎨-+=⎪⎩，取1x =，则1(1)λ=n ，∵2(1,0,0)=n 是平面FCB 的一个法向量，∴1212||cos ||||θ⋅===n n n n ．∵0λ≤≤0λ=时，cos θ当λ=cos θ有最大值12，∴1cos 2θ⎤∈⎥⎣⎦． 22．【答案】（1）椭圆方程：22x 3y 5+=；（2）存在，M．【解析】（1c a =，∴2213b a =．又椭圆过点（1）221553x y +=，即22x 3y 5+=．（2）在x 轴上存在点，使5MA MB ⋅+K 无关的常数．证明：假设在x 轴上存在点M （m ，0），使5MA MB ⋅+k 无关的常数，∵直线L 过点C （-1，0）且斜率为K ，∴L 方程为y k(x 1)=+，由⎩⎨⎧+==+),1(,5322x k y y x ，得0536)13(2222=-+++k x k x k ． 设),(),,(2211y x B y x A ，则∵1122MA (x m,y ),MB (x m,y ),=-=- ∴5MA MB ⋅+=()()()()21212251131x m x m k x x k --+++++=()()()2222121225131k x x k m x x m k k ++-+++++ =()()22222222235651313131k k k k m m k k kk --++-++++++ =2222226331k mk m k m k -++++． 设常数为t 整理得222(3m 6m 13t)k m t 0+--+-=对任意的k 恒成立，223m 6m 13t 0,m t 0.⎧+--=⎪∴⎨-=⎪⎩解得即在x 轴上存在点M ，使5MA MB ⋅+K 无关的常数．。

a 0，b 0
3a b 2 ba
3
当且仅当
3a b
b a
，即
b
3a 时等号成立
\
3a a
+b ib
的最小值为
2
34
答案： 2 3 4
三．解答题（本大题共 5 小题，共 52 分，解答需要写出文字说明、证明过程或演算步骤）
17、已知 ABC 的三个顶点坐标分别是 A(2, 1), B(2,1),C(1,3) . （I）求边 AB 高所在直线的点斜式方程； （II）求边 AB 上的中线所在直线的一般式方程. 考点：直线方程
B. 2 3 5 2 10 2
C. 11 3 5 2
D. 11 2
考点：三视图
解析：由三视图还原直观图可知，该几何体为底面是直角三角形的直三棱锥，解得该几何体表面积
为 5 3 5 2 10 2
答案：A
11.若关于 x 的方程 x m 1 x2 有两个不同实数根，则实数 m 的取值范围是（ ）
带入可得 3 2 4
答案：A
7. 如图， OAB 是 OAB 用斜二测画法画出来的直观图，其中 OB 4，AC 6，AC // y ，则 OAB
的面积（ ）
A.6
B.12
C.24
D.48
考点：斜二测画法
解析：根据直观图的画法可以得到 OAB 的底为 4，高为 12，所以面积为 24
答案： C
ìx - y + 3³ 0 8.已知实数 x, y 满足条件 íïx + y ³ 0 ，则 z x 2y 的最大值为（ ）
16.如图，三棱锥 P ABC 中， PA，PB，PC 两两垂直， PA PB PC 2 ，设点 K 是 ABC 内一点，现定义 f K x, y, z ，其中

2017～2018学年高二第一学期期中模块诊断数 学 试 题考试时间：90分钟 考试内容：必修二一．选择题：(每小题3分)1.下列几何体中为棱柱的是（ ）A. B. C. D.220y --=的倾斜角为（ ）A. 30︒B. 60︒C. 120︒D. 150︒3. 若直线1:(x 4)l y k =-与直线2l 关于点(2,1)对称，则直线2l 恒过定点（ ） A.(2，0) B.(0，2) C.(1，0) D.(0，1)4．直线()2140x m y +++=与直线360mx y +-=平行，那么m 的值是（ ） A. 2 B. 3- C. 2或3- D. 2-或35．某几何体的正视图和侧视图如图（1）所示，它的俯视图的直观图是A B C '''，如图（2）所示，其中2O A O B ''''==， O C ''=）A. 24+36+6．两直线12,l l 的方程分别为0x b +=和sin 0x a θ+= （,a b 为实常数），θ为第三象限角，则两直线12,l l 的位置关系是（ ） A. 相交且垂直 B. 相交但不垂直 C. 平行 D. 不确定7．若,,,a b c d R ∈， M N ==则（ ）A. M N ≥B. M N =C. M N ≤D. 不能确定，与,,,a b c d 有关 8. 若直线m l ,与平面α、β、γ满足l =⋂γβ,α//l ，,m m αγ⊂⊥，则有( ) A ．m ∥β且l m ⊥ B ．α⊥γ且l m ⊥ C ．α⊥β且m ∥γ D ．α∥β且α⊥γ9.已知正四棱柱1111ABCD A B C D -中，12,AB CC ==，E 为1CC 的中点，则直线1AC 与平面BED 的距离为( )A ．2 B．110．已知直三棱柱111ABC A B C -中，︒=∠120ABC ，1,21===CC BC AB 则异面直线1AB 与1BC 所成角的余弦值为（ ）A.B. C. 515D. 51011．如图，在正三棱锥BCD A -中，F E 、分别是BC AB 、的中点，DE EF ⊥，且2=BC ，则正三棱锥BCD A -的体积是( ) A.22 B. 243 C.242 D. 3212.如图，三棱柱111ABC A B C -中，侧棱1AA ⊥底面ABC ， 12AA =， 1AB BC ==，90ABC ∠=︒，外接球的球心为O ，点E 是侧棱1BB 上的一个动点．有下列判断：①直线CO 与直线E A 1是异面直线；②1A E 一定不垂直于1AC ；③三棱锥1E AAO -的体积为定值；④1AE EC +的最小值为．其中错误的个数是（ ） A. 1 B. 2 C. 3 D. 4二．填空题：(每小题4分)13．圆22643x y x y +-+=的圆心坐标14.已知实数,x y 满足1,{3, 10,x y x y +≥≤-≥若2z x y =+的最大值为1A15. Rt ABC ∆中CA CB ==, M 为AB 的中点，将ABC ∆沿CM 折叠，使A B 、之间的距离为1，则三棱锥M ABC -外接球的体积为__________ 16. 如图，在正方体1111ABCD A B C D -中， E 是AB 的中点， F 在1CC 上，且12CF FC =，点P 是侧面11AA D D （包括边界）上一动点，且1//PB 平面DEF ，则t a n ABP ∠的取值范围是三．解答题：（共48分）(立体几何解答题不能用空间向量) 17．（8分）已知直线02:,052:21=-=-+y x l y x l （1）求直线1l 和直线2l 交点P 的坐标；（2）若直线l 经过点P 且在两坐标轴上的截距互为相反数，求直线l 的一般式方程18.（10分）过点()2,2-A 作直线l 交y 轴于点B ，交直线x y l 21:1-=于点C ，且AB BC =2，求直线l 的一般式方程19．（10分）三棱柱111C B A A B C-，侧棱与底面垂直，︒=∠90ABC ，21===BB BC AB ，M ，N 分别是11B A ，1AC 的中点．（1）求证：MN ∥平面11B BCC ． （2）求证：平面⊥1MAC 平面1ABC ．20. （10分）如图，在四棱锥P ABCD -中， PD ⊥平面ABCD ， AD CD ⊥， DB平分ADC ∠，E 是PC 的中点，1AD CD ==， DB =，BE =（1）证明： AC ⊥平面PBD .（2）求直线BE 与平面PBD 所成的角的正弦值.21. （10分）（理）如图,在矩形ABCD 中, 3,AB BC ==点H E ,分别是所在边靠近D B ,的三等分点, O 是的EH 中点,现沿着EH 将矩形折成直二面角,分别连接CB AC AD ,,形成如图所示的多面体.（1）证明:AC EH ⊥（2）求二面角O AC B --的平面角的余弦值.21. （10分）（文）如图，四边形ABCD 为矩形， PA ⊥平面ABCD ， //DE PA . （1）若直线m ⊂平面PAB ，试判断直线m 与平面CDE 的位置关系，并说明理由；（2）若22AB PA DE ===， 3AD =，求三棱锥E PCD -的体积.山西大学附中2017～2018学年高二第一学期11月（总第三次）模块诊断数学答案二、填空题：(每小题4分)13． 14．1015． 16．三．解答题：17．（8分）解（1）由，所以点P的坐标为(2)或18. （10分）解析：或19. (10分)（）连接，．在中，∵，是，的中点，∴，又∵平面，∴平面．（）∵三棱柱中，侧棱与底面垂直∴四边形是正方形，∴，∴，连接，，则≌，∴，∵是的中点，∴，∵，∴平面，∵平面，∴平面平面．20. (10分)（1）证明：因为平面，平面，所以，由（1）可得，，又，故平面.（2）于F,连接PF, 取PF中点H,连接BH,则EH平行CA,由平面可知，平面PBD,所以为直线BE与平面所成的角，由，，，可得，.21.（10分）理(1)证明:在多面体中,过点A作EH的垂线交EH于点O,连接OC.∵二面角A-EH-C为直二面角,∴AO⊥平面EHC.由对称性可知CO⊥EH,又AO∩CO=O.∴EH⊥平面AOC,而平面AOC,∴EH⊥AC.(2)解:过点B在平面ABEH内作BP⊥AO垂足为P,过点P在平面AOC内作PQ⊥AC垂足为Q,连接BQ.∵△ABO是边长为3的等边三角形,∴点P为中点, .∵△AOC是直角边长为3的等腰直角三角形,∴.又∵CO⊥平面ABEH,∴CO⊥BP,BP⊥AO,AO∩CO=O,∴BP⊥平面AOC.∴BQP为二面角B-AC-O的平面角,在直角三角形BPQ中,∴.21.（10分）（1）若直线平面，则直线平面，证明如下：因为，且平面，平面，所以平面.在矩形中，，且平面，平面，所以平面.又因为，所以平面平面.又因为直线平面，所以直线平面.（2）易知，三棱锥的体积等于三棱锥的体积.因为底面，，所以底面，所以，又因为底面为矩形，所以，又因为，所以平面，又因为，所以平面易知，平面，所以点到平面的距离等于的长.因为，，所以所以三棱锥的体积.。

2017-2018学年下学期山西大学附属中学高二第一次月考试卷文科数学注意事项：1．答题前，先将自己的姓名．准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷．草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷．草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1．若直线1x =的倾斜角为α，则α（ ） A ．等于0B ．等于4πC ．等于2π D ．不存在2．函数x x y ln =的导数为（ ） A ．xB ．x ln 1+C ．x x ln 1+D ．13．已知a R ∈，那么“直线1y ax =-与42y ax =-+垂直”是“12a =”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．设n m 、是不同的直线，βα、是不同的平面，有以下四个命题： ①若βα⊥，α//m ，则β⊥m ；②若α⊥m ，α⊥n ，则n m //；③若α⊥m ，n m ⊥，则α//n ；④若α⊥n ，β⊥n ，则αβ//． 其中真命题的序号为（ ） A ．①③B ．②③C ．①④D ．②④5．若直线4:=+ny mx l 和圆4:22=+y x O 没有交点，则过点),(n m 的直线与椭圆14922=+y x 的交点个数为（ ） A ．0个 B ．至多一个 C ．1个 D ．2个6．焦点为()6,0±且与双曲线1222=-y x 有相同渐近线的双曲线方程是（ ）A ．1241222=-y xB ．1241222=-x yC ．1122422=-x yD ．1122422=-y x7．已知正四棱柱1111ABCD A B C D -中，12AA AB =，E 为1AA 中点，则异面直线BE 与1CD 所成的角的余弦值为（ ） AB ．15CD ．358．椭圆2212516x y +=的左、右焦点分别为12,F F ，弦AB 过1F ，若2ABF ∆的内切圆的周长为2π，,A B 两点的坐标分别为()11,x y ，()22,x y ，则21y y -=（ ）A ．35B ．310 C ．320 D ．35 9．已知平面区域()430,|352501x y D x y x y x ⎧-+≤⎫⎧⎪⎪⎪=+-≤⎨⎨⎬⎪⎪⎪≥⎩⎩⎭，2yZ x =+．若命题“(),,x y D Z m ∀∈≥”为真命题，则实数m 的最大值为（ ） A ．2215B ．27 C ．13D ．1410．一个几何的三视图如图所示，则表面积为（ ）A．18+ B．18+12+C．18+12+D．9+此卷只装订不密封班级 姓名 准考证号 考场号 座位号11．如图所示正方体1111ABCD A B C D -设Ｍ是底面正方形ABCD 内的一个动点，且满足直线1C D 与直线1C Ｍ所成的角等于30︒，则以下说法正确的是（ ）A ．点Ｍ的轨迹是圆的一部分B ．点Ｍ的轨迹是双曲线的一部分C ．点Ｍ的轨迹是椭圆的一部分D ．点Ｍ的轨迹是抛物线的一部分12．如图，在三棱锥B ACD -中，3ABC ABD DBC ∠∠=∠=π=，3,2AB BC BD ===， 则三棱锥B ACD -的外接球的表面积为（ ）A ．192πB ．19π CD第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．命题“若20x x -≥，则2x >”的否命题是__________．14．已知ABC ∆在斜二测画法下的平面直观图,A B C A B C ∆∆''''''是边长为a 的正三角形，那么在原ABC ∆的面积为__________．15．已知抛物线24y x =的准线与双曲线22214x y a -=交于,A B 两点，点F 为抛物线的交点，若FAB ∆为正三角形，则双曲线的离心率是_______．16．已知直线()():21440l m x m y m ++-+-=上总存在点M ，使得过M 点作的圆C ：222430x y x y ++-+=的两条切线互相垂直，则实数m 的取值范围是_______．三．解答题（本题共6个大题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．（10分）命题:p 方程()2221mx m y +-=表示双曲线；命题:q 不等式()()21120m x m x -+-+>的解集是R ．p q ∧为假，p q ∨为真，求m 的取值范围．18．（12分）已知点P(2，2)，圆C ：x 2＋y 2－8y ＝0，过点P 的动直线l 与圆C 交于A ，B 两点，线段AB 的中点为M ，O 为坐标原点． （1）求M 的轨迹方程；（2）当|OP|＝|OM|时，求l 的方程．19．（12分）已知曲线3:()C f x x x =-． （1）求曲线C 在点(1,(1))f 处的切线方程； （2）求与直线53y x =+平行的曲线C 的切线方程．20．（12分）在三棱柱111ABC A B C -中，12AB BC CA AA ====，侧棱1AA ⊥平面ABC ，且D ，E 分别是棱11A B ，1AA 的中点，点F 在棱AB 上，且14AF AB =． （1）求证：//EF 平面1BDC ； （2）求三棱锥1D BEC -的体积．21．（12（1）求椭圆的方程；（2）若过点(1,0C -）且斜率为k 的直线l 与椭圆相交于不同的两点B A ,，试问在x 轴上是否存在点M ，使5MA MB ⋅+k 无关的常数？若存在，求出点M 的坐标；若不存在，请说明理由．22．（12分）已知函数()(1)ln af x a x x x=++-，其中a R ∈．（1）求()f x 的单调区间；（2）若在[]1,e 上存在0x ，使得0()0f x <成立，求a 的取值范围．2017-2018学年下学期山西大学附属中学高二第一次月考试卷文 科 数 学 答 案第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．）第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．若20x x -<，则2x ≤ 1421516．210m -≤≤三．解答题（本题共6个小题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．【答案】{}0129m m m <<≤<或． 【解析】p 真，()20m m -<，02m <<；q 真，1m =或1m >∆<⎧⎨⎩，19m <<，∴19m ≤<， p 真q 假，01m <<；p 假q 真，29m ≤<，∴m 范围为{}0129m m m <<≤<或．18．【答案】（1）M 的轨迹方程：()()22132x y -+=-；（2）l 的方程：380x +-=． 【解析】（1）圆C 的方程可化为x 2＋(y －4)2＝16，所以圆心为C(0，4)，半径为4． 设M(x ，y)，则CM→＝(x ，y －4)，MP →＝(2－x ，2－y)．由题设知CM →·MP →＝0，故x(2－x)＋(y －4)(2－y)＝0，即(x －1)2＋(y －3)2＝2．由于点P 在圆C 的内部，所以M 的轨迹方程是()()22132x y -+=-． （2）由（1）可知M 的轨迹是以点N(1，3)为圆心，2为半径的圆．由于|OP|＝|OM|，故O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM ． 因为ON 的斜率为3，所以l 的斜率为－13，故l 的方程为380x +-=． 19．【答案】（1）；（2）或．【解析】（1），，求导数得，∴切线的斜率为， ∴所求切线方程为，即．（2）设与直线平行的切线的切点为，则切线的斜率为． 又∵所求切线与直线平行，∴， 解得，代入曲线方程得切点为或，∴所求切线方程为或，即或．20．【答案】（1）见解析；（2）1D BEC V -=． 【解析】（1）设O 为AB 的中点，连结1A O ， ∵14AF AB =，O 为AB 的中点，∴F 为AO 的中点， 又∵E 为1AA 的中点，∴1EF AO ∥，又∵D 为11A B 的中点，O 为AB 的中点，∴1A D OB =， 又∵1//A D OB ，∴四边形1A DBO 为平行四边形，∴1//AO BD ， 又∵1//EF AO ，∴//EF BD ， 又∵EF ⊄平面1DBC ，BD ⊂平面1DBC ，∴//EF 平面1DBC ． （2）∵12AB BC CA AA ====，D ，E 分别为11A B ，1AA 的中点，14AF AB =，∴1C D ⊥面11ABB A ， 而11D BEC C BDE V V --=，1111BDE ABA B BDB ABE A DE S S S S S ∆∆∆∆=---1113222121112222=⨯-⨯⨯-⨯⨯-⨯⨯=，∵1C D =，∴111113332D BEC C BDE BDE V V S C D --∆==⋅=⨯=．21．【答案】（1）椭圆方程：22x 3y 5+=；（2）存在，M．【解析】（1c a =，∴2213b a =．又椭圆过点（1）221553x y +=，即22x 3y 5+=．（2）在x轴上存在点，使5MA MB ⋅+K 无关的常数．证明：假设在x 轴上存在点M （m ，0），使5MA MB ⋅+k 无关的常数，∵直线L 过点C （-1，0）且斜率为K ，∴L 方程为y k(x 1)=+，由⎩⎨⎧+==+),1(,5322x k y y x ，得0536)13(2222=-+++k x k x k ． 设),(),,(2211y x B y x A ，则∵1122MA (x m,y ),MB (x m,y ),=-=- ∴5MA MB ⋅+=()()()()21212251131x m x m k x x k --+++++=()()()2222121225131k x x k m x x m k k ++-+++++=()()22222222235651313131k k k k m m k k kk --++-++++++ =2222226331k mk m k mk -++++．设常数为t整理得222(3m 6m 13t)k m t 0+--+-=对任意的k 恒成立，223m 6m 13t 0,m t 0.⎧+--=⎪∴⎨-=⎪⎩解得即在x 轴上存在点M ，使5MA MB ⋅+K 无关的常数．22．【答案】（1）见解析；（2）()()e e 1,1,e 1⎛+⎫-∞-+∞ ⎪-⎝⎭．【解析】（1）．22221(1)(1)()()1a a x a x ax x a f x x x xx++++++'=++==，0x >，当0a ≥时，在(0,)x ∈+∞上()0,f x '>()f x 在(0,)+∞上单调递增； 当0a <时，在(0,-)x a ∈上()0f x '<；在(,)x a ∈-+∞上()0f x '>； 所以()f x 在(0,-)a 上单调递减，在(,)a -+∞上单调递增．综上所述，当0a ≥时，()f x 的单调递增区间为(0,)+∞；当0a <时，()f x 的单调递减区间为(0,-)a ，单调递增区间为(,)a -+∞．（2）若在[]1,e 上存在0x ，使得0()0f x <成立，则()f x 在[]1,e 上的最小值小于0． ①当1a -≤，即1a ≥-时，由（1）可知()f x 在[]1,e 上单调递增，()f x 在[]1,e 上的最小值为(1)f ，由(1)10f a =-<，可得1a >；②当a e -≥，即a e ≤-时，由（1）可知()f x 在[]1,e 上单调递减，()f x 在[]1,e 上的最小值为()f e ，由()(1)0a f e a e e =++-<，可得(1)1e e a e +<--； ③当1a e <-<，即1e a -<<-时，由（1）可知()f x 在(1,)a -上单调递减，在(,)a e -上单调递增，()f x 在[]1,e 上的最小值为()(1)ln()1f a a a a -=+--+，因为0ln()1a <-<，所以(1)(1)ln()0a a a +<+-<，即()(1)ln()1112a a a a a +--+>+-+>， 即()2f a ->，不满足题意，舍去． 综上所述，实数a 的取值范围为()()e e 1,1,e 1⎛+⎫-∞-+∞ ⎪-⎝⎭．。

高二年级第一学期第一次调研考试数学试题第Ⅰ卷（选择题，共60分）一、选择题（本大题包括12小题，每小题5分，共60分，每小题给出的四个选项中，只有．．一项．．是符合题目要求的，请将正确选项填涂在答题卡上） 1.给出下列四个命题：①若平面α∥平面β，直线a ⊂α，直线b ⊂β，则a ∥b ；②若直线a ∥直线b ，直线a 、c ∥平面α，b 、c ∥平面β，则α∥β； ③若平面α∥平面β，直线a ⊂α，则a ∥β； ④若直线a ∥平面α，直线a ∥平面β，则α∥β. 其中正确命题的个数为( )A ．1B ．2C ．3D ．42.在棱长为1的正方体上，分别用过共顶点的三条棱中点的平面截该正方形，则截去8个三棱锥后 ，剩下的几何体的体积是 （ ） A ．23 B ．76 C ．45D ．563.有三个球,一球切于正方体的各面,一球切于正方体的各侧棱,一球过正方体的各顶点,求这三个球的体积之比( )A 3:2:1B 3:2:1C 33:22:1D 9:4:1 4.如图，1111ABCD A BC D -为正方体，下面结论错误．．的是( )(填序号)A.BD ∥平面11D CBB.BD AC ⊥1C.⊥1AC 平面11D CBD.异面直线AD 与1CB 所成的角为60°.5.将正三棱柱截去三个角如图一所示，A,B,C 分别是GHI ∆三边的中点，得到几何体如图2，则该几何体按图2所示方向的侧视图为（ ）6.直角三角形ABC 的斜边AB 在平面α内，直角顶点C 在平面α外，C 在平面α内的射影为1C ,且AB C ∉1,则AB C 1∆为（ ）A 锐角三角形B 直角三角形C 钝角三角形D 以上都不对4题图7．如图，矩形''''C B A O 是水平放置的一个平面图形的直观图，其中,6''cm A O = cm C O 2''=，则原图形是( )A.正方形B. 菱形C. 矩形D.一般的平行四边形8.某工件的三视图如图所示，现将该工件通过切割，加工成一个体积尽可能大的正方体新工件，并使新工件的一个面落在原工件的一个面内，则原工件材料的利用率为（材料利用率=原工件的体积新工件的体积）（ ）Aπ278 B π98Cπ3)128-（ Dπ3)1224-（9.正方体1111ABCD A BC D -中，点M 是棱CD 的中点，点O 是侧面D D AA 11的中点，若点P 在侧面C C BB 11及其边界上运动，并且总是保持AM OP ⊥,则动点P 的轨迹是（ ） A. 线段C B 1 B. 线段B B 1 C. 线段C C 1 D. 线段1BC 10.梯形ABCD 中， 90=∠ABC ,以A 为圆心，AD 为半径作圆，如图所示（单位：cm ），则图中阴影部分绕AD 旋转一周所形成的几何体的表面积为（ )A π80B 84πC 60πD 68π 11．已知,,A B C 三点的坐标分别是(3,0)A ，(0,3)B ，(cos ,sin )C αα，3(,)22ππα∈，若1AC BC ⋅=-，则21tan 2sin sin 2ααα++的值为 （ ）A ．59-B ．95-C ．2D ．312.已知0,0>>b a ，若不等式0133≤--+ba b a m 恒成立，则m 的最大值为（ ） A.4 B.3 C.9 D.16第Ⅱ卷（非选择题 共90分）二、填空题(本大题包括4小题，每小题5分，共20分，把正确答案填在答题卡中的横线上). 13．我国古代数学名著 《数书九章》中有云：“今有木长二丈四尺，围之五尺，葛生其下，缠木两周，上与木齐，问葛长几何？”其意思为“圆木长2丈4尺，圆周为5尺，葛藤从圆木的底部开始向上生长，绕圆木两周，刚好顶部与圆木平齐，问葛藤最少长 尺。

ABC DA 1B 1C 1D 1 F E山西大学附中2017~2018学年高二第一学期10月（总第二次）模块诊断数 学 试 题考查时间：90分钟 考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1.下列命题正确的是( ) A . 四边形确定一个平面B. 两两相交且不共点的三条直线确定一个平面C. 经过三点确定一个平面D . 经过一条直线和一个点确定一个平面2.图1是由哪个平面图形旋转得到的（ ）3.已知直线a αb ⊂αa b a b a b a b 锥的高扩大到原来的2倍,底面半径缩短到原来的21,则圆锥的体积( ) A .缩小到原来的一半 B .扩大到原来的2倍 C .不变 D .缩小到原来的61 5. 如图，已知四边形ABCD 的直观图是一个边长为1的正方形， 则原图形的周长为( )A ．22B ．6C ．8D ．224+6.在正方体1111D C B A ABCD -中，F E ,分别为1,BB BC 的 中点，则下列直线中与直线EF 相交的是（ ）A.直线1AAB.直线11B AC.直线11D AD.直线11C B7.在三棱柱111ABC A B C -中，已知1AA ABC ⊥平面,12,23,2AA BC BAC π==∠=，此三棱柱各个顶点都在同一个球面上，则球的体积为（ ）A ．323πB ．16πC ．253π D ．312π8.在正方体1111D C B A ABCD -中，F E ,分别是C B AB 1,的中点，则EF 与平面ABCD 所成的角的正切值为( )2 C. 1229.如图，棱长为1的正方体1111D C B A ABCD -中，F E ,是侧面对角线11,AD BC 上的点，若F BED 1是菱形，则其在 底面ABCD 上投影的四边形面积是（ ）A.21B.43C.22D.423-10.如图，已知三棱柱111ABC A B C -的侧棱与底面边长都 相等，1A 在底面ABC 上的射影为BC 的中点，则异面 直线AB 与1CC 所成的角的余弦值为（ ）A.3 B.5 C.7 D.3411.如图，四面体ABCD 中，截面PQMN 是正方形， 则在下列结论中，下列说法错误的是（ ） A ．AC BD ⊥ B ．AC BD = C.//AC 截面PQMN D ．异面直线PM 与BD 所成的角为45 12．如图，矩形ABCD 中，AD AB 2=，E 为边AB 的中点， 将ADE ∆沿直线DE 翻转成DE A 1∆（∉1A 平面ABCD ）．若O M ,分别为线段C A 1,DE 的中点，则在ADE ∆ 翻转过程中，下列说法错误的是（ ）A. 与平面DE A 1垂直的直线必与直线BM 垂直B. 异面直线BM 与E A 1所成角是定值C. 一定存在某个位置，使MO DE ⊥D. 三棱锥ADE A -1外接球半径与棱AD 的长之比为定值 二．填空题（本大题共4小题，每小题4分，共16分） 13.若一个正四面体的棱长为a ，则它的表面积为_________. 14.如图,是一个无盖器皿的三视图，正视图、侧视图和俯视图 中的正方形边长为2，正视图、侧视图中的虚线都是半圆， 则该器皿的表面积是___________.15.设甲、乙两个圆柱的底面积分别为21S S ，，体积分别为21V V ，，若它们的侧面积相等，且4921=S S ，则21V V的值是________． 16. 如图，PA ⊥⊙O 所在的平面，AB 是⊙O 的直径，C 是⊙O 上的一点，E 、F 分别是点A 在PB 、PC 上的射影．给出下列结论：①AF⊥PB ；②EF ⊥PB ； ③AF ⊥BC ； ④AE ⊥平面PBC ．其中正确命题的序号是 （把正确的序号都填上）三．解答题（本题共5大题，共48分）（解答题不能用空间向量）17．如图，在四边形ABCD 中，AD DC ⊥，//AD BC ，3AD =，2CD =，22AB =45DAB ∠=，四边形绕着直线AD 旋转一周.(1)求所形成的封闭几何体的表面积； (2)求所形成的封闭几何体的体积.NMA BDCO18.如图，在三棱锥P ABC -中，H G,F,,E 分别是BC PC,AC,AB,的中点，且BC AC PB,PA ==(1)证明：PC AB ⊥； (2)证明：平面PA B FGH ABEF 2,//==BE AF EF AB 24=EF 22=AB ABCD AD ABEFM Q ,EF AC ,P BM //PQ BCE AM BCM20.如图，在四棱锥O ABCD -中，底面ABCD 是边长为1的菱形，4ABC π∠=, OA ABCD ⊥底面, 2OA =,M 为OA 的中点，N 为BC 的中点（1）证明：直线MN OCD平面‖；（2）求异面直线AB 与MD 所成角的大小；21.如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，45ADC ∠=︒，1AD AC ==，O 为AC 的中点，PO ⊥平面ABCD ，2PO =，M 为PD 的中点． （1）证明：AD ⊥平面PAC ；（2）求直线AM 与平面ABCD 所成角的正切值．山西大学附中2016~2017学年高二第一学期10月（总第二次）模块诊断数 学 试 题考查时间：90分钟 考查内容：必修2第一、二章一．选择题（本题共12小题，每小题3分，共36分，在每小题给出的四个选项中只有一个选项符合题目要求）1-6 BADACD 7-12 ADBDBC二．填空题（本大题共4小题，每小题4分，共16分） 13. 23a 14. π+24 15.2316. ①②③ 三．解答题（本题共5大题，共48分） 17．解：过点B 作BE AD ⊥于点E ，因为22AB =45DAB ∠=，所以2BE =，所以1DE = 所以四边形ABCD 绕着直线AD 旋转一周所形成的封闭几何体为一个底面半径为2，母线为1的圆柱及一个底面半径为2，高为2的圆锥的组合体. 2分（1）所以几何体的表面积为(22221222842S ππππ=⨯+⨯⨯+⨯⨯=+, 5分 （2）体积为22120212233V πππ=⨯⨯+⨯⨯⨯=. 8分 18. 试题解析：（Ⅰ）证明：连接EC ，AB EC ⊥有 2分又,PB PA =PE AB ⊥∴ 2分PEC PC PEC AB 面面⊂⊥∴,PC AB ⊥∴ 5分（Ⅱ）连结FH ，交于EC 于O ，连接GO ，则FH ,//.PEC GO PE ∆中AB E =FH O =解：（1）因为AB ∥EM ，且AB ＝EM ，所以四边形ABEM 为平行四边形． 连接AE ，则AE 过点P ，且P 为AE 中点，又Q 为AC 中点， 所以PQ 是△ACE 的中位线，于是PQ ∥CE ． 4分 ∵CE ⊂平面BCE ，PQ ⊄平面BCE ，∴PQ ∥平面BCE ． 5分（2）AD ⊥平面ABEF ⇒BC ⊥平面ABEF ⇒BC ⊥AM ． 7分 在等腰梯形ABEF 中，由AF ＝BE ＝2，EF ＝24，AB ＝22， 可得∠BEF ＝45°，BM ＝AM ＝2，∴AB 2＝AM 2＋BM 2，∴AM ⊥BM ． 9分 又BC∩BM＝B ，∴AM ⊥平面BCM ． 10分20．方法一（1）取OB 中点E ，连接ME ，NEME CD ME CD ∴，‖AB,AB ‖‖，又,NE OC MNE OCD ∴平面平面‖‖，MN OCD ∴平面‖,方法二取OD的中点F ，因为MF AD AD NF 21=NC AD AD NC 21=MFCN MN FC MN OCD ∴平面‖CD ‖AB,MDC ∠∴AB MD ,AP CD P ⊥于MP ⊥⊥平面A BC D ，∵OA ∴CD MP 2,42ADP π∠=∵∴DP =222MD MA AD =+=AB MD 3π（1）证明：∵45ADC ∠=︒，且1AD AC ==，∴90DAC ∠=︒，即AD AC ⊥。

2017-2018学年下学期山西大学附属中学高二第一次月考试卷文科数学注意事项：1．答题前，先将自己的姓名．准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷．草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷．草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．） 1．若直线1x =的倾斜角为α，则α（ ） A ．等于0B ．等于4πC ．等于2π D ．不存在2．函数x x y ln =的导数为（ ） A ．xB ．x ln 1+C ．x x ln 1+D ．13．已知a R ∈，那么“直线1y ax =-与42y ax =-+垂直”是“12a =”的（ ） A ．充分不必要条件 B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件4．设n m 、是不同的直线，βα、是不同的平面，有以下四个命题： ①若βα⊥，α//m ，则β⊥m ；②若α⊥m ，α⊥n ，则n m //；③若α⊥m ，n m ⊥，则α//n ；④若α⊥n ，β⊥n ，则αβ//． 其中真命题的序号为（ ） A ．①③B ．②③C ．①④D ．②④5．若直线4:=+ny mx l 和圆4:22=+y x O 没有交点，则过点),(n m 的直线与椭圆14922=+y x 的交点个数为（ ） A ．0个 B ．至多一个 C ．1个 D ．2个6．焦点为()6,0±且与双曲线1222=-y x 有相同渐近线的双曲线方程是（ ）A ．1241222=-y xB ．1241222=-x yC ．1122422=-x yD ．1122422=-y x7．已知正四棱柱1111ABCD A B C D -中，12AA AB =，E 为1AA 中点，则异面直线BE 与1CD 所成的角的余弦值为（ ） AB ．15CD ．358．椭圆2212516x y +=的左、右焦点分别为12,F F ，弦AB 过1F ，若2ABF ∆的内切圆的周长为2π，,A B 两点的坐标分别为()11,x y ，()22,x y ，则21y y -=（ ）A ．35B ．310 C ．320 D ．35 9．已知平面区域()430,|352501x y D x y x y x ⎧-+≤⎫⎧⎪⎪⎪=+-≤⎨⎨⎬⎪⎪⎪≥⎩⎩⎭，2yZ x =+．若命题“(),,x y D Z m ∀∈≥”为真命题，则实数m 的最大值为（ ） A ．2215B ．27 C ．13D ．1410．一个几何的三视图如图所示，则表面积为（ ）A．18+ B．18+12+C．18+12+D．9+此卷只装订不密封班级 姓名 准考证号 考场号 座位号11．如图所示正方体1111ABCD A B C D -设Ｍ是底面正方形ABCD 内的一个动点，且满足直线1C D 与直线1C Ｍ所成的角等于30︒，则以下说法正确的是（ ）A ．点Ｍ的轨迹是圆的一部分B ．点Ｍ的轨迹是双曲线的一部分C ．点Ｍ的轨迹是椭圆的一部分D ．点Ｍ的轨迹是抛物线的一部分12．如图，在三棱锥B ACD -中，3ABC ABD DBC ∠∠=∠=π=，3,2AB BC BD ===， 则三棱锥B ACD -的外接球的表面积为（ ）A ．192πB ．19π CD第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．命题“若20x x -≥，则2x >”的否命题是__________．14．已知ABC ∆在斜二测画法下的平面直观图,A B C A B C ∆∆''''''是边长为a 的正三角形，那么在原ABC ∆的面积为__________．15．已知抛物线24y x =的准线与双曲线22214x y a -=交于,A B 两点，点F 为抛物线的交点，若FAB ∆为正三角形，则双曲线的离心率是_______．16．已知直线()():21440l m x m y m ++-+-=上总存在点M ，使得过M 点作的圆C ：222430x y x y ++-+=的两条切线互相垂直，则实数m 的取值范围是_______．三．解答题（本题共6个大题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．（10分）命题:p 方程()2221mx m y +-=表示双曲线；命题:q 不等式()()21120m x m x -+-+>的解集是R ．p q ∧为假，p q ∨为真，求m 的取值范围．18．（12分）已知点P(2，2)，圆C ：x 2＋y 2－8y ＝0，过点P 的动直线l 与圆C 交于A ，B 两点，线段AB 的中点为M ，O 为坐标原点． （1）求M 的轨迹方程；（2）当|OP|＝|OM|时，求l 的方程．19．（12分）已知曲线3:()C f x x x =-． （1）求曲线C 在点(1,(1))f 处的切线方程； （2）求与直线53y x =+平行的曲线C 的切线方程．20．（12分）在三棱柱111ABC A B C -中，12AB BC CA AA ====，侧棱1AA ⊥平面ABC ，且D ，E 分别是棱11A B ，1AA 的中点，点F 在棱AB 上，且14AF AB =． （1）求证：//EF 平面1BDC ； （2）求三棱锥1D BEC -的体积．21．（12（1）求椭圆的方程；（2）若过点(1,0C -）且斜率为k 的直线l 与椭圆相交于不同的两点B A ,，试问在x 轴上是否存在点M ，使5MA MB ⋅+k 无关的常数？若存在，求出点M 的坐标；若不存在，请说明理由．22．（12分）已知函数()(1)ln af x a x x x=++-，其中a R ∈．（1）求()f x 的单调区间；（2）若在[]1,e 上存在0x ，使得0()0f x <成立，求a 的取值范围．2017-2018学年下学期山西大学附属中学高二第一次月考试卷文 科 数 学 答 案第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写．．．．．在答题卷上．．．．．）第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．若20x x -<，则2x ≤ 1421516．210m -≤≤三．解答题（本题共6个小题，共70分．解答应写出必要的文字说明．证明过程或演．．．．．．．．．．．．．．．．．．．算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．） 17．【答案】{}0129m m m <<≤<或． 【解析】p 真，()20m m -<，02m <<；q 真，1m =或1m >∆<⎧⎨⎩，19m <<，∴19m ≤<， p 真q 假，01m <<；p 假q 真，29m ≤<，∴m 范围为{}0129m m m <<≤<或．18．【答案】（1）M 的轨迹方程：()()22132x y -+=-；（2）l 的方程：380x +-=． 【解析】（1）圆C 的方程可化为x 2＋(y －4)2＝16，所以圆心为C(0，4)，半径为4． 设M(x ，y)，则CM→＝(x ，y －4)，MP →＝(2－x ，2－y)．由题设知CM →·MP →＝0，故x(2－x)＋(y －4)(2－y)＝0，即(x －1)2＋(y －3)2＝2．由于点P 在圆C 的内部，所以M 的轨迹方程是()()22132x y -+=-． （2）由（1）可知M 的轨迹是以点N(1，3)为圆心，2为半径的圆．由于|OP|＝|OM|，故O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM ． 因为ON 的斜率为3，所以l 的斜率为－13，故l 的方程为380x +-=． 19．【答案】（1）；（2）或．【解析】（1），，求导数得，∴切线的斜率为， ∴所求切线方程为，即．（2）设与直线平行的切线的切点为，则切线的斜率为． 又∵所求切线与直线平行，∴， 解得，代入曲线方程得切点为或，∴所求切线方程为或，即或．20．【答案】（1）见解析；（2）1D BEC V -=． 【解析】（1）设O 为AB 的中点，连结1A O ， ∵14AF AB =，O 为AB 的中点，∴F 为AO 的中点， 又∵E 为1AA 的中点，∴1EF AO ∥，又∵D 为11A B 的中点，O 为AB 的中点，∴1A D OB =， 又∵1//A D OB ，∴四边形1A DBO 为平行四边形，∴1//AO BD ， 又∵1//EF AO ，∴//EF BD ， 又∵EF ⊄平面1DBC ，BD ⊂平面1DBC ，∴//EF 平面1DBC ． （2）∵12AB BC CA AA ====，D ，E 分别为11A B ，1AA 的中点，14AF AB =，∴1C D ⊥面11ABB A ， 而11D BEC C BDE V V --=，1111BDE ABA B BDB ABE A DE S S S S S ∆∆∆∆=---1113222121112222=⨯-⨯⨯-⨯⨯-⨯⨯=，∵1C D =，∴111113332D BEC C BDE BDE V V S C D --∆==⋅=⨯=．21．【答案】（1）椭圆方程：22x 3y 5+=；（2）存在，M．【解析】（1c a =，∴2213b a =．又椭圆过点（1）221553x y +=，即22x 3y 5+=．（2）在x轴上存在点，使5MA MB ⋅+K 无关的常数．证明：假设在x 轴上存在点M （m ，0），使5MA MB ⋅+k 无关的常数，∵直线L 过点C （-1，0）且斜率为K ，∴L 方程为y k(x 1)=+，由⎩⎨⎧+==+),1(,5322x k y y x ，得0536)13(2222=-+++k x k x k ． 设),(),,(2211y x B y x A ，则∵1122MA (x m,y ),MB (x m,y ),=-=- ∴5MA MB ⋅+=()()()()21212251131x m x m k x x k --+++++=()()()2222121225131k x x k m x x m k k ++-+++++=()()22222222235651313131k k k k m m k k kk --++-++++++ =2222226331k mk m k mk -++++．设常数为t整理得222(3m 6m 13t)k m t 0+--+-=对任意的k 恒成立，223m 6m 13t 0,m t 0.⎧+--=⎪∴⎨-=⎪⎩解得即在x 轴上存在点M ，使5MA MB ⋅+K 无关的常数．22．【答案】（1）见解析；（2）()()e e 1,1,e 1⎛+⎫-∞-+∞ ⎪-⎝⎭．【解析】（1）．22221(1)(1)()()1a a x a x ax x a f x x x xx++++++'=++==，0x >，当0a ≥时，在(0,)x ∈+∞上()0,f x '>()f x 在(0,)+∞上单调递增； 当0a <时，在(0,-)x a ∈上()0f x '<；在(,)x a ∈-+∞上()0f x '>； 所以()f x 在(0,-)a 上单调递减，在(,)a -+∞上单调递增．综上所述，当0a ≥时，()f x 的单调递增区间为(0,)+∞；当0a <时，()f x 的单调递减区间为(0,-)a ，单调递增区间为(,)a -+∞．（2）若在[]1,e 上存在0x ，使得0()0f x <成立，则()f x 在[]1,e 上的最小值小于0． ①当1a -≤，即1a ≥-时，由（1）可知()f x 在[]1,e 上单调递增，()f x 在[]1,e 上的最小值为(1)f ，由(1)10f a =-<，可得1a >；②当a e -≥，即a e ≤-时，由（1）可知()f x 在[]1,e 上单调递减，()f x 在[]1,e 上的最小值为()f e ，由()(1)0a f e a e e =++-<，可得(1)1e e a e +<--； ③当1a e <-<，即1e a -<<-时，由（1）可知()f x 在(1,)a -上单调递减，在(,)a e -上单调递增，()f x 在[]1,e 上的最小值为()(1)ln()1f a a a a -=+--+，因为0ln()1a <-<，所以(1)(1)ln()0a a a +<+-<，即()(1)ln()1112a a a a a +--+>+-+>， 即()2f a ->，不满足题意，舍去． 综上所述，实数a 的取值范围为()()e e 1,1,e 1⎛+⎫-∞-+∞ ⎪-⎝⎭．。

山西大学附属中学2017-2018学年高二3月月考（理）数学一、选择题：共12题1.若直线的倾斜角为，则A. 等于B. 等于C. 等于D. 不存在2.函数的导数为（）A. B. C. D. 13.已知空间向量，，则“”是“”的A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.设是不同的直线，是不同的平面，有以下四个命题：①若，，则②若，，则③若，，则④若，，则.其中真命题的序号为A. ①③B. ②③C. ①④D. ②④5.若直线和圆没有交点，则过点的直线与椭圆的交点个数为（）A. 0个B. 至多一个C. 1个D. 2个6.焦点为且与双曲线有相同渐近线的双曲线方程是A. B. C. D.7.如图,已知三棱柱的侧棱与底面边长都相等,在底面上的射影为的中点D,则异面直线与所成的角的余弦值为...A. B. C. D.8.椭圆+=1的左、右焦点分别为F1,F2,弦AB过点F1,若△ABF2的内切圆周长为π,A,B两点的坐标分别为(x1,y1)和(x2,y2),则|y2-y1|的值为A. B. C. D.9.已知平面区域，.若命题“”为真命题，则实数m的最大值为A. B. C. D.10.一个几何的三视图如图所示，则表面积为A. B. 或C. 或D.11.如图，P是正四面体V-ABC的面VBC上一点，点P到平面ABC距离与到点V的距离相等，则动点P的轨迹是( )A. 直线B. 抛物线C. 离心率为的椭圆D. 离心率为3的双曲线12.如图，在三棱锥中，，，则三棱锥的外接球的表面积为A. B. C. D.二、填空题：共4题13.命题“若，则”的否命题是__________.14.已知在斜二测画法下的平面直观图是边长为的正三角形，那么原的面积为__________.15.已知抛物线的准线与双曲线交于两点，点F为抛物线的焦点，若为正三角形，则双曲线的离心率是_______________.16.已知直线上总存在点，使得过点作的圆：的两条切线互相垂直，则实数的取值范围是________________．三、解答题：共6题17.命题方程表示双曲线；命题不等式的解集是. 为假，为真，求的取值范围.18.三棱柱中，分别是、上的点，且，.设，，.(1)试用表示向量；(2)若，，，求MN的长.19.已知点P(2,2)，圆C：x2＋y2－8y＝0，过点P的动直线l与圆C交于A，B两点，线段AB的中点为M，O为坐标原点.(1)求M的轨迹方程；(2)当|OP|＝|OM|时，求l的方程.20.已知曲线.(1)求曲线在点处的切线方程；(2)求与直线平行的曲线的切线方程.21.如图,在等腰梯形ABCD中,AB∥CD,AD=DC=CB=1,∠ABC=60°,四边形ACFE为矩形,平面ACFE⊥平面ABCD,CF=1.(1)求证:BC⊥平面ACFE;(2)点M在线段EF上运动,设平面MAB与平面FCB所成二面角的平面角为θ(θ≤90°),试求cosθ的取值范围.22.已知椭圆的离心率为，且过点.(1)求椭圆的方程；(2)若过点且斜率为k的直线l与椭圆相交于不同的两点A,B，试问在x轴上是否存在点，使是与无关的常数？若存在，求出点的坐标；若不存在，请说明理由.。

2018学年下学期山西大学附属中学高二第一次月考试卷理科数学注意事项：1．答题前，先将自己的姓名．准考证号填写在试题卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2．选择题的作答：每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑，写在试题卷．草稿纸和答题卡上的非答题区域均无效。

3．非选择题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷．草稿纸和答题卡上的非答题区域均无效。

4．考试结束后，请将本试题卷和答题卡一并上交。

第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写在答题卷上．．．．．．．．．．） 1．若直线的倾斜角为，则（ ） A ．等于B ．等于C ．等于D ．不存在2．函数的导数为（ ） A ．B ．C ．D ．3．已知空间向量，，则“”是“”的（ ）1x =αα04π2πx x y ln =x x ln 1+x x ln 1+1()1,3,x =m ()2,1,2x =-n 1x =⊥m n 此卷只装订不密封班 姓名 准考证号 考场号 座位号A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．设是不同的直线，是不同的平面，有以下四个命题： ①若，，则；② 若，，则； ③若，，则；④若，，则； 其中真命题的序号为（ ） A ．①③B ．②③C ．①④D ．②④5．若直线和圆没有交点，则过点的直线与椭圆的交点个数为（ ） A ．0个 B ．至多一个 C ．1个 D ．2个6．焦点为且与双曲线有相同渐近线的双曲线方程是（ ）A ．B ．C ．D ．7．如图，已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为（ ）n m 、βα、βα⊥α//m β⊥m α⊥m α⊥n n m //α⊥m n m ⊥α//n α⊥n β⊥n αβ//4:=+ny mxl 4:22=+y x O ),(n m 14922=+y x ()6,0±1222=-y x 1241222=-y x 1241222=-x y 1122422=-x y 1122422=-y x 111ABC A B C -1A ABC BC AB 1CCA ．B ．C ．D ．8．椭圆的左、右焦点分别为，弦过，若的内切圆的周长为，两点的坐标分别为，，则（ ）A ．B ．C ．D ．9．已知平面区域，．若命题“，”为真命题，则实数的最大值为（ ） A ．B ．C ．D ．10．一个几何的三视图如图所示，则表面积为（ ）A ．B ．C ．D ．11．如图，P 是正四面体的面上一点，点P 到平面ABC 距离与到点V 的距离相等，则动点P 的轨迹是（ ）444342212516x y +=12,F F AB 1F 2ABF △2π,A B ()11,x y ()22,x y 21y y -=3531032035()430,352501x y D x y x y x ⎧⎫-+≤⎧⎪⎪⎪=+-≤⎨⎨⎬⎪⎪⎪≥⎩⎩⎭2yZ x =+(),x y D ∀∈Z m ≥m 221527131418+18+12+18+12+9+V ABC -VBCA ．直线B ．抛物线C的椭圆 D ．离心率为3的双曲线12．如图，在三棱锥中，，，则三棱锥的外接球的表面积为（ ）A ．B ． CD第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．命题“若，则”的否命题是__________．14．已知在斜二测画法下的平面直观图，是边长为的正三角形，那么在原的面积为__________．B ACD -3ABC ABD DBC ∠∠=∠=π=3,2AB BC BD ===B ACD -192π19π20x x -≥2x >ABC △A B C '''△A B C '''△a ABC △15．已知抛物线的准线与双曲线交于两点，点为抛物线的交点，若为正三角形，则双曲线的离心率是_______．16．已知直线上总存在点，使得过点作的圆：的两条切线互相垂直，则实数的取值范围是_______．三．解答题（本题共6个大题，共70分．解答应写出必要的文字说明．证明．．．．．．．．．．．．．．．过程或演算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．．．．．） 17．（10分）命题方程表示双曲线；命题不等式的解集是．为假，为真，求的取值范围．24y x =22214x y a -=,A B F FAB ∆()():21440l m x m y m ++-+-=M M C 222430x y x y ++-+=m :p ()2221mx m y +-=:q ()()21120m x m x -+-+>R p q ∧p q ∨m18．（12分）三棱柱中，分别是、上的点，且，．设，，． （1）试用，，表示向量；（2）若，，，求MN 的长．111C B A ABC -N M 、B A 111C B 12BM A M =112C N B N =AB =a AC =b 1AA =c a b c MN 90BAC ∠=︒1160BAA CAA ∠=∠=︒11AB AC AA ===19．（12分）已知点P(2,2)，圆C ：x 2＋y 2－8y ＝0，过点P 的动直线与圆C 交于A ，B 两点，线段AB 的中点为M ，O 为坐标原点． （1）求M 的轨迹方程；（2）当|OP|＝|OM|时，求的方程．l l20．（12分）已知曲线． （1）求曲线在点处的切线方程； （2）求与直线平行的曲线的切线方程．3:()C f x x x =-C (1,(1))f 53y x =+C21．（12分）如图，在等腰梯形中，，，，四边形为矩形，平面平面，．（1）求证：；（2）点在线段上运动，设平面与平面二面角的平面角为，试求的取值范围．ABCD //AB CD 1AD DC CB ===60ABC ∠=︒ACFE ACFE ⊥ABCD 1CF =BC ⊥EF M EF MAB FCB (90)θθ≤︒cosθ22．（12（1）求椭圆的方程；（2）若过点且斜率为的直线与椭圆相交于不同的两点，试问在轴上是否存在点无关的常数？若存在，求出点的坐标； 若不存在，请说明理由．()1,0C -k l B A ,x M 5MA MB ⋅+k M2018学年下学期山西大学附属中学高二第一次月考试卷理 科 数 学 答 案第Ⅰ卷一．选择题（本题共12小题，每小题5分，共60分，只有一个选项正确，请把答案写在答题卷上．．．．．．．．．．）第Ⅱ卷二．填空题（本题共4小题，每小题5分，共20分，请把答案写在答题卷上．．．．．．．．．．） 13．若20x x -<，则2x ≤142a 1516．210m -≤≤三．解答题（本题共6个小题，共70分．解答应写出必要的文字说明．证明．．．．．．．．．．．．．．．过程或演算步骤，请把答案写在答题卷上．．．．．．．．．．．．．．．．．．） 17．【答案】． 【解析】真，，真，或，，∴， 真假，；假真，，∴范围为．18．【答案】（1）；（2）．【解析】（1）． （2），． 19．【答案】（1）的轨迹方程：；（2）的方程：．【解析】（1）圆C 的方程可化为x 2＋(y －4)2＝16，所以圆心为C(0，4)，半{}0129m m m <<≤<或p ()20m m -<02m <<q 1m =1m >∆<⎧⎨⎩19m <<19m ≤<p q 01m <<p q 29m ≤<m {}0129m m m <<≤<或111333MN =++a b c 5MN =1111MN MA A B B N =++1111133BA AB B C =++11111()()33333=-++-=++c a a b a a b c 2()222++=+++⋅+⋅+⋅222a b c a b c a b b c c a 111110211211522=++++⨯⨯⨯+⨯⨯⨯=||++=a b c 1||||33MN =++=a b c M ()()22132x y -+=-l 380x y +-=径为4．设M(x ，y)，则＝(x ，y －4)，＝(2－x ，2－y)．由题设知·＝0，故x(2－x)＋(y －4)(2－y)＝0，即(x －1)2＋(y －3)2＝2． 由于点P 在圆C 的内部，所以的轨迹方程是． （2）由（1）可知M 的轨迹是以点N(1，3)为圆心，2为半径的圆． 由于|OP|＝|OM|，故O 在线段PM 的垂直平分线上，又P 在圆N 上，从而ON ⊥PM ．因为ON 的斜率为3，所以l 的斜率为－13，故的方程为．20．【答案】（1）；（2）或．【解析】（1）∵，∴，求导数得，∴切线的斜率为， ∴所求切线方程为，即．（2）设与直线平行的切线的切点为，则切线的斜率为． 又∵所求切线与直线平行，∴， 解得，代入曲线方程得切点为或，∴所求切线方程为或，M ()()22132x y -+=-l 380x y +-=即或．21．【答案】（1）见解析；（2）． 【解析】（1）证明：在梯形中，∵，，，∴， ∴， ∴，∴，∵平面平面，平面平面，平面，∴平面，∴．（2）由（1）可建立分别以直线，，为轴，轴，轴的如图所示空间直角坐标系，令，则，，，， ∴，． 设为平面的一个法向量，1cos 2θ⎤∈⎥⎣⎦ABCD //AB CD 1AD DC CB ===60ABC ∠=︒2AB =2222cos603AC AB BC AB BC =+-⋅⋅︒=222AB AC BC =+BC AC ⊥ACFE ⊥ABCD ACFE ABCD AC =BC ⊂ABCD BC ⊥ACFE BC ⊥EF CA CB CF x yz (0FM λλ=≤≤(0,0,0)C A (0,1,0)B (,0,1)Mλ(,0)AB =(,1,1)BM λ=-1(,,)x y z =n MAB由，得，取，则，∵是平面的一个法向量， ∴． ∵时，， 当有最大值，∴． 22．【答案】（1）椭圆方程：；（2）存在，M．【解析】（1，∴．又椭圆过点（1），即．（2）在x 轴上存在点K 无关的常数．证明：假设在x 轴上存在点M （m ，0）k 无关的常数，∵直线L 过点C （-1，0）且斜率为K ，∴L 方程为，由，得． 1100AB BM ⎧⋅=⎪⎨⋅=⎪⎩n n 00y x y z λ⎧+=⎪⎨-+=⎪⎩1x =1(1)λ=n 2(1,0,0)=n FCB 1212||cos ||||θ⋅===n n n n 0λ≤≤0λ=cos θλ=cos θ121cos 2θ⎤∈⎥⎣⎦22x 3y 5+=3c a =2213b a =221553x y +=22x 3y 5+=5MA MB ⋅+5MA MB ⋅+y k(x 1)=+⎩⎨⎧+==+),1(,5322x k y y x 0536)13(2222=-+++k x k x k设∵ ∴== = =． 设常数为t整理得对任意的k 恒成立，解得 即在x 轴上存在点M K 无关的常数．),(),,(2211y x B y x A 1122MA (x m,y ),MB (x m,y ),=-=-5MA MB ⋅+()()()()21212251131x m x m k x x k --+++++()()()2222121225131k x x k m x x m k k ++-+++++()()22222222235651313131k k k k m m k k k k --++-++++++2222226331k mk m k m k -++++222(3m 6m 13t)k m t 0+--+-=223m 6m 13t 0,m t 0.⎧+--=⎪∴⎨-=⎪⎩5MA MB ⋅+。

山西省太原市2017-2018学年高二数学10月月考试题 理一、选择题（每小题4分,共40分,每小题只有一个正确答案）1. 若一个圆锥的轴截面是等边三角形，其面积为3，则这个圆锥的全面积为 A . 3π B. 33π C . 6π D. 9π2.已知,m n 是两条不同直线，,,αβγ是三个不同平面，下列命题中正确的是 A. 若αα⊥⊥n m ,，则n m // B. 若γβγα⊥⊥,，则βα//C. 若βα//,//m m ，则βα//D. 若αα//,//n m ，则n m //3. 如图，网格纸上小正方形的边长为1，用粗实线画出某几何体的三视图，则该几何体的体积为A．12π+．124π+ C ．48π+ D ．843π+4. 设,,,A B C D 是空间四个不同的点，在下列命题中，不正确．．．的是 A ．若AC 与BD 共面,则AD 与BC 共面B ．若AC 与BD 是异面直线,则AD 与BC 是异面直线 C ．若AB AC =,DB DC =,则AD BC ⊥ D ．若AB AC =,DB DC =,则AD BC =5. 正四棱锥的体积为12，底面对角线的长为则侧面与底面所成的二面角的正切值等于 A6. 《九章算术》是我国古代数学名著，它在几何学中的研究比西方早一千多年.例如堑堵指底面为直角三角形，且侧棱垂直于底面的三棱柱；阳马指底面为矩形，一侧棱垂直于底面的四棱锥.如图，在堑堵ABC-A 1B 1C 1中，AC ⊥BC ，若A 1A=AB=2 ，当阳马B-A 1ACC 1体积最大时，则堑堵ABC-A 1B 1C 1的体积为A.23D. 7. 已知某几何体的三视图如右图所示，则该几何体的外接球表面积为 A.8πB. 32πC. 8πD. 9. “牟合方盖”是我国古代数学家刘徽在研究球的体积的过程中构造的一个和谐优美的几何体．它由完全相同的四个曲面构成，相对的两个曲面在同一个圆柱的侧面上，好似两个扣合（牟合）在一起的方形伞（方盖）．其直观图如下左图，图中四边形是为体现其直观性所作的辅助线．其实际直观图中四边形不存在．当其正视图和侧视图完全相同时，它的正视图和俯视图分别可能是A ．,a bB ．,a cC ．,c bD ．,b d10．已知正方体ABCD ­A 1B 1C 1D 1的棱长为1，E ，F 分别为棱AA 1与CC 1的中点，过直线EF的平面分别与BB 1，DD 1相交于点M ，N.设BM ＝x ，x ∈[0，1]，有以下四个结论，其中不．正确．．的结论是 A. 平面MENF⊥平面BDD 1B 1B. 当x ＝12时，四边形MENF 的面积最小C. 四边形MENF 的周长L ＝f (x )，x ∈[0，1]是单调函数D. 四棱锥C 1­MENF 的体积V ＝g (x )为常函数 二、填空题（每小题4分，共16分）11. 已知一个圆台的下底面半径为r ，高为h ，当圆台的上底半径r′变化时，圆台体积的变化范围是________．12. 设甲，乙两个圆柱的底面面积分别为12,S S ，体积为12,V V ，若它们的侧面积相等,且1294S S =，则12V V 的值是 . 13. 如图，四棱台ABCD A'B'C'D'-的底面为菱形，P 、Q 分 别为B'C'，C'D '的中点.若AA '∥平面BPQD ，则此棱台上下 底面边长的比值为 .14. 如图，在直三棱柱ABC A'B'C'-中，底面为直角三角形，∠ACB＝90︒，AC ＝6，BC ＝CC'P 是BC'上一动点，则CP ＋PA '的最小值是___________. 三、解答题（共44分）15. （本小题满分10分）如图所示，已知四棱锥P ­ABCD 的侧棱PD ⊥底面ABCD ，且底面ABCD 是直角梯形，AD⊥CD，AB∥CD，AB ＝AD ＝12CD ＝2，点M 在侧棱PC 上． （1）求证：BC⊥平面BDP ；（2）若侧棱PC 与底面ABCD 所成角的正切值为12，点M为侧棱PC 的中点，求异面直线BM 与PA 所成角的余弦值．16. （本小题满分10分）如图，C 、D 是以AB 为直径的圆上两点，==AD AB 232，BC AC =，F 是AB 上一点，且AB AF 31=，将圆沿直径AB 折起，使点C 在平面ABD 的射影E 在BD 上，已知2=CE .（1）求证：AD⊥BC；（2）求三棱锥CFD A -的体积．17.（本小题满分12分）如图所示，在多面体111A B D DCBA 中，四边形11AA B B ，11,ADD A ABCD 均为正方形，E 为11B D 的中点，过1,,A D E 的平面交1CD 于F（1）证明：1//EF B C ；（2）求二面角11E A D B --余弦值.18. （本小题满分12分）如图所示,长方体1111D C B A ABCD -中，2111==B A AA ，2=BC ,E 为线段1CC 中点.（1）求证：平面BE A 1⊥平面CD B 1；（2）若点P 为侧面11ABB A （包含边界）内的一个动点，且//1P C平面BEA 1,求线段P C 1长度的最小值.太原五中2017-2018学年度第一学期月考A高 二 数 学(理科)答案一、选择题（每小题4分,共40分,每小题只有一个正确答案）二、填空题（每小题4分，共16分）11.⎝ ⎛⎭⎪⎫13πr 2h ，πr 2h ；12.32；13.23；14. 三、解答题（共44分）15．解：(1)证明：由已知可得BD ＝BC ＝2 2，∴BD 2＋BC 2＝16＝DC 2，故BD⊥BC. 又PD⊥平面ABCD ，BC ⊂平面ABCD ，故PD⊥BC， 又BD∩PD＝D ，∴BC⊥平面BDP.(2)如图，取PD 的中点N ，并连接AN ，MN ， BM∥AN，则∠PAN 即为异面直线BM 与PA 所成的角． 又PD⊥底面ABCD ，∴∠PCD 即为PC 与底面ABCD 所成的角， 即tan ∠PCD＝12，∴PD＝12CD ＝2，即PN ＝12PD ＝1，AN ＝5，PA ＝2 2，则在△PAN 中，cos ∠PAN＝AP 2＋AN 2－PN 22AP·AN ＝3 1010，即异面直线BM 与PA 所成角的余弦值为3 1010.16. （1）证明：依题⊥AD BD ， ⊥CE 平面ABD ∴⊥CE ADBD E CE = ∴⊥AD 平面BCE ∴AD⊥BC ……5分（2）解： F 到AD 的距离等于13BD ∴231321=⋅⋅=∆FAD S ．⊥CE 平面ABD∴662233131=⋅⋅=⋅⋅==∆--CE S V V FAD AFD C CFD A ． 17.解：（1）因为111//,AD BC A D ⊂平面1A DE ,1B C ⊄平面1ADE ，所以1//B C 平面1A D E ,又1B C ⊂平面11B CD ，平面1A DE ⋂平面11B CD =EF ，所以EF//1B C .(2)将几何体补成正方体知，BD 1⊥平面1A DE ，所以BD 1⊥A 1DAD 1⊥平面11A B CD ，所以AD 1⊥A 1D ，所以交线A 1D⊥平面ABD 1.二面角11E A D B --的平面角与∠AD 1B =18. 解：（Ⅰ）在长方体1111D C B A ABCD -中，CD ⊥平面11B BCC ∴BE CD ⊥又∵E 为线段1CC 的中点，由已知易得BC B Rt 1∆∽BCE Rt ∆∴C BB EBC 1∠=∠，∴01190=∠+∠C BB EBB ,故C B BE 1⊥，且C CD C B = 1，∴BE ⊥平面CD B 1 又⊂BE 平面BE A 1，∴平面BE A 1⊥平面CD B 1（2）取线段A 1B 1的中点M ，线段BB 1的中点N ，连接C 1M ，C 1N ，MN ，则 C 1N ∥BE ，MN ∥A 1B.又∵MN ∩C 1N=N ，BA 1∩BE=B ， ∴平面C 1MN ∥平面A 1BE.要使得线段C 1P 长度最小，则C 1P⊥MN,在⊿C 1MN 中，C 1M=C 1N=3MN=2，则C 1P=210。

山西大学附中2017-2018高二数学10月月考试卷（含答案）山西大学附中2017－2018学年高二第一学期10月（总第二次）模块诊断数学试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.下列命题正确的是()A．四边形确定一个平面B．两两相交且不共点的三条直线确定一个平面C．经过三点确定一个平面D．经过一条直线和一个点确定一个平面2.如图的直观图是由哪个平面图形旋转得到的()3.已知直线平面，直线平面，则()A．B．异面C．相交D．无公共点4.圆锥的高扩大到原来的2倍，底面半径缩短到原来的，则圆锥的体积()A．缩小到原来的一半B．扩大到原来的2倍C.不变D．缩小到原来的5.如图，已知四边形的直观图是一个边长为1的正方形，则原图形的周长为（）A．B．6C.8D．6.在正方体中，分别为、的中点，则下列直线中与直线相交的是（）A．直线B．直线C.直线D．直线7.在三棱柱已知中，平面，，此三棱柱各个顶点都在同一球面上，则球的体积为（）A．B．C.D．8.在正方体中，分别为、的中点，则与平面所成的角的正切值为（）A．2B．C.D．9.如图，棱长为1的正方体中，是侧面对角线上一点，若是菱形，则其在底面上投影的四边形面积（）A．B．C.D．10.如图，已知三棱柱已知的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为（）A．B．C.D．11.如图，在四面体中，截面是正方形，则下列命题中，错误的为（）A．B．C.截面D．异面直线所成的角为45&ordm;12.如图，矩形中，为边的中点，将沿直线翻转成，若分别为的中点，则在翻转过程中，下列说法错误的是（）A．与平面垂直的直线必与直线垂直B．异面直线与所成角是定值C.一定存在某个位置，使D．三棱锥外接球半径与棱的长之比为定值第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若一个正面体的棱长为，则它的表面积为．14.如图是一个无盖器皿的三视图，正视图，侧视图，和俯视图中的正方形边长为2，正视图，侧视图中的虚线都是半圆，则该器皿的表面积是．15.设甲、乙两个圆柱的底面积分别为，体积分别为，若它们的侧面积相等且，则的值是．16.如图，所在的平面，是的直径，是上的一点，分别是点在上的射影，给出下列结论：①；②；③；④平面.其中正确命题的序号是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.如图，在四边形中，，四边形绕着直线旋转一周，（1）求所形成的封闭几何体的表面积；(2)求所形成的封闭几何体的体积.18.如图，在三棱锥中，分别是的中点，且（1）证明：；（2）证明：平面平面.19.如图四边形是等腰梯形，是矩形，平面，其中分别是的中点，是中点.（1）求证平面；（2）求证平面.20.如图，在四棱锥中，底面是边长为1的菱形，底面为的中点，为的中点（1）证明：直线平面；（2）求异面直线所成角的大小.21.如图，在四棱锥中，底面是平行四边形，的中点，的中点.(1)证明：；(2)求直线与平面所成角的正切值.试卷答案一、选择题1-5:BADAC6-10:DADBD11、12：BC二、填空题13.14.15.16.①②③三、解答题17.解：过点作交于点∵∴由四边形绕着直线旋转一周所形成的封闭几何体为一个底面半径为2，母线为1的圆柱及一个底面半径为2，高为2的圆锥的组合体.（1）几何体的表面积为；（2）体积为.18.（1）证明：连接，则又∵，∴面，∴；（2）连接，交于，连接，则在∵∴平面平面.19.（1）∵中点，，∴，∴，∴四边形为平行四边形，连接，∵是的中点，∴是的中点，∵中点，∴在中，，∵（2）由（1）知：，同理可得：，又，∴∵四边形为矩形，∴,又平面，∴平面，，又∴平面.20.解：（1）取中点，连接∵又∵,∴平面平面平面（2）∵,∴为异面直线所成的角（或其补角）作于，连接∵平面，∴∵∴所以所成角的大小为.21.解：(1)证明：∵，∴∵∴∴∴∵平面平面∴由直线和平面垂直的判定定理知.(2)取中点，连接，由，得∴是直线与平面所成的角，∵的中点，∴，在中，，即直线与平面所成角的正切值为.。