自考信号与线性系统分析内部题库含答案

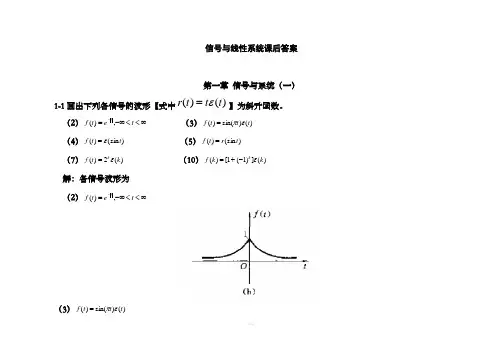
信号与线性系统课后答案第一章 信号与系统（一）1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。

（2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 解：各信号波形为 （2）∞<<-∞=-t e t f t ,)(（3）)()sin()(t t t f επ=（4）)t fε=(sin)(t（5）)t f=r)(t(sin（7）)(t f kε2)(k=（10）)(])1k(kf kε()1[=-+1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。

（1）)2()1(3)1(2)(-+--+=t t t t f εεε （2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε （8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ （12）)]()3([2)(k k k f k---=εε 解：各信号波形为 （1）)2()1(3)1(2)(-+--+=t t t t f εεε（2）)2()1(2)()(-+--=t r t r t r t f（5）)2()2()(t t r t f -=ε（8）)]5()([)(--=k k k k f εε（11）)]7()()[6sin()(--=k k k k f εεπ（12）)]()3([2)(k k k f k ---=εε1-3 写出图1-3所示各波形的表达式。

1-4 写出图1-4所示各序列的闭合形式表达式。

1-5 判别下列各序列是否为周期性的。

信号与线性系统分析答案信号与线性系统分析答案第一部分考试说明一、考试性质全国硕士研究生入学考试是为高等学校招收硕士研究生而设置的。

其中，《信号与线性系统》实行按一级学科统考。

它的评价标准是高等学校优良本科毕业生能达到的及格或及格以上水平，以保证被录取者具有基本的专业水平，并有利于各高等学校的择优选拔。

考试对象为参加2018年全国硕士研究生入学考试的本科应届毕业生，或具有同等学历的在职人员。

科学学位硕士研究生和专业学位硕士研究生招生考试中的《信号与线性系统》均采用本考试大纲。

二、考试形式与试卷结构（一）答卷方式：闭卷，笔试。

（二）答题时间：180分钟。

（三）各部分内容的考试比例（满分150分）基本概念及技能：25分傅里叶级数及傅里叶变换：40分拉普拉斯变换：35分Z变换：35分状态模型分析：15分（四）题型比例填空题：30分选择题：20分画图题：10分计算题：90分第二部分考查要点一、信号与系统1．单位冲激信号和单位阶跃信号的概念及性质2．信号的波形图、基本运算与奇、偶分解3．离散正弦、指数的周期性4．计算信号的能量与功率5．确定信号的基波周期6．判断系统的线性、时不变、因果、稳定、可逆等性质二、线性时不变系统1. 线性时不变系统的卷积积分（卷积和）特性2．线性时不变系统的零输入响应、零状态响应3. 卷积积分（卷积和）的性质及计算4．单位冲激响应和单位阶跃响应5. 根据单位冲激响应判断系统的因果性和稳定性6．线性常系数微分方程的时域解法7．线性常系数差分方程的时域解法三、周期信号的傅里叶级数表示1. 线性时不变（LTI）系统的特征函数2. 连续时间周期信号的傅里叶级数表示3. 连续时间傅里叶级数的性质4. 离散时间周期信号的傅里叶级数表示5. 离散时间傅里叶级数的性质6. 周期信号的频谱7. 周期信号激励下线性时不变系统的响应8. 理想低通、高通、全通、带通、带阻滤波器的概念及频率特性四、连续时间傅里叶变换1. 连续时间傅里叶变换及非周期连续信号的频谱2. 连续周期信号的傅里叶变换3. 连续时间傅里叶变换的性质4.连续时间LTI系统的频率响应函数、幅频响应和相频响应5. 连续时间LTI系统的频域分析6．信号经过系统无失真传输的条件7．线性相位的概念五、离散时间傅里叶变换1. 离散时间傅里叶变换及非周期离散信号的频谱2. 离散周期信号的傅里叶变换3. 离散时间傅里叶变换的性质4. 离散时间LTI系统的频率响应、幅频响应和相频响应5. 离散时间LTI系统的频域分析六、连续时间信号抽样1．冲激抽样原理2．抽样定理3．由取样值重建原始连续时间信号的方法七、拉普拉斯变换1. 拉普拉斯变换及其收敛域2. 拉普拉斯逆变换3. 拉普拉斯变换的性质4．连续时间LTI系统的系统函数H(s)5．系统函数与系统因果性和稳定性的关系6. 利用系统函数的极-零图获得一阶或二阶系统的幅频特性曲线7．利用拉氏变换求零状态响应8．连续系统的框图表示9．信号流图表示与梅森公式10. 反馈系统的稳定性分析11．单边拉普拉斯变换及其性质12．利用单边拉普拉斯变换求解线性常系数微分方程八、Z变换1. Z变换及其收敛域2. 逆Z变换3. Z变换的性质4．离散时间系统的系统函数H(z)5．系统函数与系统因果性和稳定性的关系6. 利用系统函数的极-零图获得一阶或二阶系统的幅频特性曲线7. 利用Z变换求零状态响应8．离散时间系统的框图表示9. 单边Z变换及其性质10．利用单边Z变换求解线性常系数差分方程九、状态模型分析1. 连续时间和离散时间LTI系统的状态模型表示2. 状态模型（状态方程、输出方程）的建立3. 状态方程的求解（包括时域及变换域解法）如有出入，请以华科研究生逛网公布为准。

单项选择题。

1. 已知序列3()cos()5f k k π=为周期序列，其周期为 （） A ． 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 （ ）图题2A ．()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+- 3.已知sin()()()t f t t dt tπδ∞-∞=⎰，其值是 （）A ．π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 （ ） A ． 1 B. 2 C. 3 D. 45.为了使信号无失真传输，系统的频率响应函数应为 （ ） A ． ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 （）A ．13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 （ A ） A ．0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ，那么(3)f t +的傅里叶变换为 （ ） A ．()jwF jw e B. 2()j wF jw eC. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f k εα=，)2()(-=k k h δ，那么()()f k h k *的值为（ ） A ．)1(1--k k εα B.)2(2--k k εα C. )3(3--k k εα D. )4(4--k k εα10.持续系统的零输入响应的“零”是指（ A ） A. 鼓励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列k j ek f 3)(π=为周期序列，其周期为 （ ）A ． 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为 （ ）A ．)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ，那么 12()()f t f t *的值是 （ ） A ．)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(，那么其对应的原函数为 （ ） A ．)(t δ B.)('t δ C. )(''t δ D. )('''t δ15.持续因果系统的充分必要条件是 （ ） A ． 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为 （ ）A ．1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=，那么其单位冲激响应()h t 为 （ ）A ．)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ，那么)5(t f 的拉普拉斯变换为 （ ） A ．)5(s F B.)5(31s F C. )5(51s F D. )5(71s Ft19.已知)2()(2-=-k k f k εα，)2()(-=k k h δ，那么()()f k h k *的值为（ ） A ．)1(1--k k εα B. )2(2--k k εαC.)3(3--k k εα D. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ，那么)(jt F 的傅里叶变换为（ ） A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 以下微分或差分方程所描述的系统是时变系统的是 （ ） A ． )(2)()(2)(''t f t f t y t y -=+ B. )()(sin )('t f t ty t y =+ C. )()]([)(2't f t y t y =+ D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==，那么)()(21t f t f *的值是 （ ） A ．)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 （ ）A ．ωj 1 B. ωj 2 C. ωj 3 D. ωj 4 24.持续系统是稳固系统的充分必要条件是 （ ） A ． M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ，那么原函数)(t f 的初值为 （ ）A ． 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ，那么该系统的单位冲激响应为 （ ） A ．)(t etε- B.)(2t e t ε- C.)(3t e t ε- D. )(4t e t ε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα，那么)()(k h k f *的值为 （ ）A ．)(k kεαB.)1(1--k k εαC.)2(2--k k εαD. )3(3--k k εα28. 系统的零输入响应是指（ ） A.系统无鼓励信号 B. 系统的初始状态为零C. 系统的鼓励为零，仅由系统的初始状态引发的响应D. 系统的初始状态为零，仅由系统的鼓励引发的响应 29.偶函数的傅里叶级数展开式中 （ ）A ．只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形，那么)2(t f 的波形为 （ ） A ．将()f t 以原点为基准，沿横轴紧缩到原先的12B. 将()f t 以原点为基准，沿横轴展宽到原先的2倍C. 将()f t 以原点为基准，沿横轴紧缩到原先的14D. 将()f t 以原点为基准，沿横轴展宽到原先的4倍 填空题1. 已知象函数223()(1)s F s s +=+，其原函数的初值(0)f +为___________________。

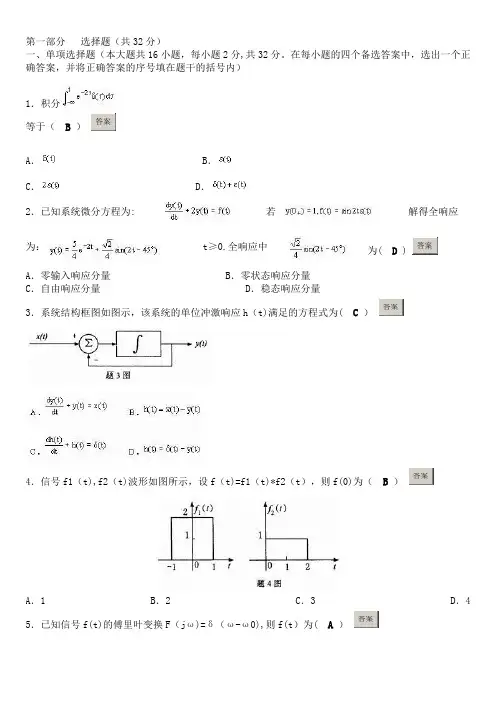
第一部分选择题（共32分）一、单项选择题（本大题共16小题，每小题2分,共32分。

在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内）1．积分等于（B）答案A． B．C． D．2．已知系统微分方程为: 若解得全响应为：t≥0.全响应中为( D ) 答案A．零输入响应分量 B．零状态响应分量C．自由响应分量 D．稳态响应分量3．系统结构框图如图示，该系统的单位冲激响应h（t)满足的方程式为( C）答案4．信号f1（t),f2（t)波形如图所示，设f（t)=f1（t)*f2（t），则f(0)为（B）答案A．1 B．2 C．3 D．4 5．已知信号f(t)的傅里叶变换F（jω)=δ（ω-ω0),则f(t）为( A）答案6．已知信号f（t）如图所示，则其傅里叶变换为（C）答案7．f（t）=ε(t）-ε(t—1)的拉氏变换为（A）答案8. 的拉氏反变换为（D）答案9．图（a）中ab段电路是某复杂电路的一部分，其中电感L和电容C都含有初始状态，请在图(b）中选出该电路的复频域模型。

（B ) 答案10．离散信号f(n)是指（B）答案A．n的取值是连续的，而f（n)的取值是任意的信号B．n的取值是离散的，而f(n)的取值是任意的信号C．n的取值是连续的，而f(n)的取值是连续的信号D．n的取值是连续的,而f（n）的取值是离散的信号11．若序列f（n）的图形如图(a)所示,那么f（—n+1）的图形为图(b)中的( D）答案12．差分方程的齐次解为，特解为，那么系统的稳态响应为( B ) 答案13．已知离散系统的单位序列响应和系统输入如图所示，f（n)作用于系统引起的零状态响应为,那么序列不为零的点数为（C）答案A．3个 B．4个C．5个 D．6个第二部分非选题（共68分）二、填空题(本大题共9小题，每小题2分，共18分）14．=（)。

答案15．GLC并联电路发生谐振时，电容上电流的幅值是电流源幅值的（Q）倍。

信号与系统全国自考试题真题及答案1.城市轨道交通(包括地下铁道和轻轨铁路)是指以运输方式为主要技术特征，以城市客运公共交通为服务形式的交通运输方式，是现代化都市的重要基础设施。

（）[单选题] *A.轨道(正确答案)B.公路C.水路D.航空2.专用电话包括电话、站内电话、站间电话和轨旁电话。

（） [单选题] *A.客服B.调度(正确答案)C.固定D.移动3.监视器用于显示由各监控点摄像机送来的信号。

（） [单选题] *A.音频B.数字C.视频(正确答案)D.模拟4.在非运营时间内所有固定信号必须保持为信号，除正在进行信号调试和工程车或特别列车需要通过进路区段外，不可开放信号机。

（） [单选题] *A.进行B.停车(正确答案)C.减速D.允许5.录音系统应能提供 24 小时、365 天不间断录音服务，应能保存个月记录数据，并可外置储存。

（） [单选题] *A.12B.6C.3(正确答案)D.16.地下铁道列车速度通常不超过。

（） [单选题] *A.120km/hB.8Okm/h(正确答案)C.4Okm/hD.25km/h7.任何人高举双手或任何物件用力摇动都是信号。

（） [单选题] *A.停车(正确答案)B.进行C.减速D.允许8.ATO 系统是 ATC 系统的一个子系统，主要实现。

（） [单选题] *A.车对车控制B.车对地控制C.地对车控制(正确答案)D.地对地控制9.按调制方式分类可分为调幅轨道电路和轨道电路。

（） [单选题] *A.音频B.工频C.调频(正确答案)D.脉冲10.控制中心配备在线式 UPS 及可提供后备电源的蓄电池。

（） [单选题] *A.15minB. 30min(正确答案)C.60minD.120min11.轻轨交通单向每小时运送能力在人次之间。

（） [单选题] *A.1000B.8000C.10000〜30000(正确答案)D.30000〜7000012.轨道电路按信息处理技术可分为模拟轨道电路和轨道电路。

1、 若系统的输入f (t)、输出y (t) 满足()3()4t y t e ft -=，则系统为 线性的 （线性的、非线性的）、 时变的 （时变的、时不变）、 稳定的 （稳定的、非稳定的）。

2、 非周期、连续时间信号具有 连续 、非周期频谱；周期、连续时间信号具有离散、非周期 频谱；非周期、离散时间信号具有 连续 、周期频谱；周期、离散时间信号具有离散、 周期 频谱。

3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10-5 s . 4、 )100()(2t Sa t f =是 能量信号 （功率信号、能量信号、既非功率亦非能量信号）。

5、 ()2cos()f t t =+是 功率信号 （功率信号、能量信号、既非功率亦非能量信号）。

6、 连续信号f(t)=sint 的周期T 0=,若对f(t)以fs=1Hz 进行取样，所得离散序列f(k)=sin(k) ,该离散序列是周期序列？ 否 。

7、 周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑，此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。

8、 f (t) 的周期为0.1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。

试写出此信号的时域表达式f (t) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) 。

9、 f (k) 为周期N=5的实数序列，若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、 则F 5 (3 )= ()54512πjeF +=- 、F 5 (4 )= ()52511πj eF +=- 、F 5 (5 )= 2 ；f(k) =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。

信号与系统考试方式：闭卷 考试题型：1、简答题（5个小题），占30分；计算题（7个大题），占70分。

一、简答题：1．dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态，为全响应，为激励，)()(t y t f 试回答该系统是否是线性的？[答案：非线性]2．)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的，是时变的还是非时变的？[答案：线性时变的]3．已知有限频带信号)(t f 的最高频率为100Hz ，若对)3(*)2(t f t f 进行时域取样，求最小取样频率s f =？[答案：400s f Hz =]4．简述无失真传输的理想条件。

[答案：系统的幅频特性为一常数，而相频特性为通过原点的直线]5．求[]⎰∞∞--+dt t t e t )()('2δδ的值。

[答案：3]6．已知)()(ωj F t f ↔，求信号)52(-t f 的傅立叶变换。

[答案：521(25)()22j f t e F j ωω--↔]7．已知)(t f 的波形图如图所示，画出)2()2(t t f --ε的波形。

[答案： ]8．已知线性时不变系统，当输入)()()(3t e e t x t t ε--+=时，其零状态响应为)()22()(4t e e t y t t ε--+=，求系统的频率响应。

[答案：())4)(2(52)3(++++ωωωωj j j j ]9．求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。

[答案：)0(+f =2，0)(=∞f ]10．若LTI 离散系统的阶跃响应为)(k g ，求其单位序列响应。

其中：)()21()(k k g k ε=。

[答案：1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11．已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ，()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*，求()3?f =。

标准答案(一)一、填空题（每空1分，共30分）1、无线电通信中，信号是以电磁波形式发射出去的。

它的调制方式有调幅、调频、调相。

2、针对不同的调制方式有三种解调方式，分别是检波、鉴频、和鉴相。

3、在单调谐放大器中，矩形系数越接近于1、其选择性越好；在单调谐的多级放大器中，级数越多，通频带越窄、（宽或窄），其矩形系数越（大或小）小。

4、调幅波的表达式为：uAM（t）= 20（1 +0.2COS100πt）COS107πt（V）；调幅波的振幅最大值为24V，调幅度Ma为20℅，带宽fBW为100Hz，载波fc为5*106Hz。

5、在无线电技术中，一个信号的表示方法有三种，分别是数学表达式、波形、频谱。

6、调频电路有直接调频、间接调频两种方式。

7、检波有同步、和非同步检波两种形式。

8、反馈式正弦波振荡器按照选频网络的不同，可分为LC、RC、石英晶振等三种。

9、变频器可由混频器、和带通滤波器两部分组成。

10、列出三个常见的频谱搬移电路调幅、检波、变频。

11、用模拟乘法器非线性器件实现调幅最为理想。

二、选择题（每小题2分、共20分）将一个正确选项前的字母填在括号内1、下列哪种信号携带有调制信号的信息（C ）A、载波信号B、本振信号C、已调波信号2、小信号谐振放大器的主要技术指标不包含（B ）A、谐振电压增益B、失真系数C、通频带D、选择性3、丙类谐振功放其谐振回路调谐于（ A ）分量A、基波B、二次谐波C、其它高次谐波D、直流分量4、并联型石英晶振中，石英谐振器相当于（C ）元件A、电容B、电阻C、电感D、短路线5、反馈式正弦波振荡器的起振条件为（ B ）A、|AF|=1，φA+φF= 2nπB、|AF| >1，φA+φF = 2nπC、|AF|>1，φA+φF ≠2nπD、|AF| =1，φA+φF ≠2nπ6、要实现集电极调制特性应使功放工作在（B ）状态A、欠压状态B、过压状态C、临界状态D、任意状态7、自动增益控制可简称为（ B ）A、MGCB、AGCC、AFCD、PLL8、利用非线性器件相乘作用来实现频率变换其有用项为（ B ）A、一次方项B、二次方项C、高次方项D、全部项9、如右图所示的电路是（D ）A、普通调幅电路B、双边带调幅电路C、混频器D、同步检波器10、在大信号包络检波器中，由于检波电容放电时间过长而引起的失真是（B）A、频率失真B、惰性失真C、负峰切割失真D、截止失真三、判断题，对的打“√”,错的打“×”（每空1分，共10分）1、谐振放大器是采用谐振回路作负载的放大器。

信号与系统考试方式：闭卷 考试题型：1、简答题（5个小题），占30分；计算题（7个大题），占70分。

一、简答题：1．dtt df t f x e t y t )()()0()(+=-其中x(0)是初始状态，为全响应，为激励，)()(t y t f 试回答该系统是否是线性的？[答案：非线性]2．)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的，是时变的还是非时变的？[答案：线性时变的]3．已知有限频带信号)(t f 的最高频率为100Hz ，若对)3(*)2(t f t f 进行时域取样，求最小取样频率s f =？[答案：400s f Hz =]4．简述无失真传输的理想条件。

[答案：系统的幅频特性为一常数，而相频特性为通过原点的直线]5．求[]⎰∞∞--+dt t t e t )()('2δδ的值。

[答案：3]6．已知)()(ωj F t f ↔，求信号)52(-t f 的傅立叶变换。

[答案：521(25)()22j f t e F j ωω--↔]7．已知)(t f 的波形图如图所示，画出)2()2(t t f --ε的波形。

[答案： ]8．已知线性时不变系统，当输入)()()(3t e e t x t t ε--+=时，其零状态响应为)()22()(4t e e t y t t ε--+=，求系统的频率响应。

[答案：())4)(2(52)3(++++ωωωωj j j j ]9．求象函数2)1(32)(++=s s s F ,的初值)0(+f 和终值)(∞f 。

[答案：)0(+f =2，0)(=∞f ]10．若LTI 离散系统的阶跃响应为)(k g ，求其单位序列响应。

其中：)()21()(k k g k ε=。

[答案：1111()()(1)()()()(1)()()(1)222k k k h k g k g k k k k k εεδε-=--=--=--]11．已知()1 1 , 0,1,20 , k f k else ==⎧⎨⎩ ，()2 1 , 0,1,2,30 , k k f k else -==⎧⎨⎩设()()()12f k f k f k =*，求()3?f =。

单项选择题。

1. 已知序列3()cos()5f k k π=为周期序列，其周期为 （） A ． 2 B. 5 C. 10 D. 122. 题2图所示()f t 的数学表达式为 （ ）图题2A ．()10sin()[()(1)]f t t t t πεε=+- B. ()10sin()[()(1)]f t t t t πεε=-- C. ()10sin()[()(2)]f t t t t πεε=-- D. ()10sin()[()(2)]f t t t t πεε=+-3.已知sin()()()t f t t dt t πδ∞-∞=⎰，其值是 （）A ．π B. 2π C. 3π D. 4π4.冲激函数()t δ的拉普拉斯变换为 （ ）A ． 1 B. 2 C. 3 D. 45.为了使信号无失真传输，系统的频率响应函数应为 （ ） A ． ()djwt H jw e= B. ()djwt H jw e-= C. ()djwt H jw Ke= D. ()djwt H jw Ke-=6.已知序列1()()()3kf k k ε=,其z 变换为 （）A ．13z z + B.13z z - C.14z z + D.14z z -7.离散因果系统的充分必要条件是 （ A ） A ．0,0)(<=k k h B. 0,0)(>=k k h C. 0,0)(<<k k h D. 0,0)(>>k k h8.已知()f t 的傅里叶变换为()F jw ，则(3)f t +的傅里叶变换为 （ ） A ．()jwF jw e B. 2()j wF jw e C. 3()j wF jw eD. 4()j wF jw e9.已知)()(k k f k εα=，)2()(-=k k h δ，则()()f k h k *的值为（ ）A ．)1(1--k k εα B. )2(2--k k εα C. )3(3--k k εα D. )4(4--k k εα10.连续时间系统的零输入响应的“零”是指（ A ） A. 激励为零 B. 系统的初始状态为零 C. 系统的冲激响应为零 D. 系统的阶跃响应为零 11. 已知序列k j ek f 3)(π=为周期序列，其周期为 （ ）A ． 2 B. 4 C. 6 D. 812. 题2图所示()f t 的数学表达式为 （ ）A ．)1()1()(--+=t t t f εε B.)1()1()(-++=t t t f εε C. )1()()(--=t t t f εε D. )1()()(-+=t t t f εε13.已知)2()(),1()(21-=-=t t f t t f εδ，则 12()()f t f t *的值是 （ ） A ．)(t ε B. )1(-t ε C. )2(-t ε D. )3(-t ε14.已知ωωj j F =)(，则其对应的原函数为 （ ） A ．)(t δ B.)('t δ C. )(''t δ D. )('''t δ15.连续因果系统的充分必要条件是 （ ） A ． 0,0)(==t t h B. 0,0)(<=t t h C. 0,0)(>=t t h D. 0,0)(≠=t t h16.单位阶跃序列)(k ε的z 变换为 （ ）A ．1,1<+z z z B. 1,1>+z z z C. 1,1<-z z z D. 1,1>-z z z 17.已知系统函数ss H 1)(=，则其单位冲激响应()h t 为 （ ）A ．)(t ε B. )(t t ε C. )(2t t ε D. )(3t t ε18.已知()f t 的拉普拉斯变换为()F s ，则)5(t f 的拉普拉斯变换为 （ ） A ．)5(s F B. )5(31s F C. )5(51s F D. )5(71s F 19.已知)2()(2-=-k k f k εα，)2()(-=k k h δ，则()()f k h k *的值为（ ）tA ．)1(1--k k εα B. )2(2--k k εαC.)3(3--k k εα D. )4(4--k k εα20.已知)(t f 的傅里叶变换为)(ωj F ，则)(jt F 的傅里叶变换为（ ） A. )(ωπ-fB. )(ωπfC. )(2ωπ-fD. )(2ωπf21. 下列微分或差分方程所描述的系统是时变系统的是 （ ） A ． )(2)()(2)(''t f t f t y t y -=+ B. )()(sin )('t f t ty t y =+ C. )()]([)(2't f t y t y =+ D. )()2()1()(k f k y k y k y =--+22. 已知)()(),()(21t t f t t t f εε==，则)()(21t f t f *的值是 （ ） A ．)(1.02t t ε B. )(3.02t t ε C. )(5.02t t ε D. )(7.02t t ε23.符号函数)sgn(t 的频谱函数为 （ ）A ．ωj 1 B. ωj 2 C. ωj 3 D. ωj 4 24.连续系统是稳定系统的充分必要条件是 （ ） A ． M dt t h ≤⎰∞∞-)( B. M dt t h ≥⎰∞∞-)(C.M dt t h ≤⎰∞∞-)( D.M dt t h ≥⎰∞∞-)(25.已知函数)(t f 的象函数)5)(2()6()(+++=s s s s F ，则原函数)(t f 的初值为 （ ）A ． 0 B. 1 C. 2 D. 3 26.已知系统函数13)(+=s s H ，则该系统的单位冲激响应为 （ ） A ．)(t etε- B.)(2t e t ε- C.)(3t e t ε- D. )(4t e t ε-27.已知)2()(),1()(1-=-=-k k h k k f k δεα，则)()(k h k f *的值为 （ ）A ．)(k kεαB.)1(1--k k εαC.)2(2--k k εαD. )3(3--k k εα28. 系统的零输入响应是指（ ） A.系统无激励信号 B. 系统的初始状态为零C. 系统的激励为零，仅由系统的初始状态引起的响应D. 系统的初始状态为零，仅由系统的激励引起的响应 29.偶函数的傅里叶级数展开式中 （ ）A ．只有正弦项 B.只有余弦项 C. 只有偶次谐波 D. 只有奇次谐波 10. 已知信号()f t 的波形，则)2(t f 的波形为 （ ） A ．将()f t 以原点为基准，沿横轴压缩到原来的12B. 将()f t 以原点为基准，沿横轴展宽到原来的2倍C. 将()f t 以原点为基准，沿横轴压缩到原来的14D. 将()f t 以原点为基准，沿横轴展宽到原来的4倍 填空题1. 已知象函数223()(1)s F s s +=+，其原函数的初值(0)f +为___________________。

1全国2018年7月自学考试信号与系统试题课程代码：02354一、单项选择题（本大题共12小题，每小题2分，共24分）在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.下列参数的量纲仅为导纳的是( ) A.Z 参数 B.Y 参数 C.A 参数D.H 参数2.双口网络可以用四种不同的方程和参数来描述，这些参数仅决定于( ) A.信号源的方向或极性 B.信号源的幅度 C.负载的大小D.信号源的频率3.若连续LTI 系统的初始状态不为零，当激励信号增大一倍时，其零状态响应( ) A.增大一倍B.保持不变C.增大，但不能确定增大倍数D.增大两倍4.设f (t )为系统输入，y (t )为系统输出，则下列关系式中为线性时不变系统的是( ) A.y (t )=x (t )f (t ) B.y (t )=tf (t ) C.)()()()(22t f t f dt d t y t y dtd +=+D.y (t )=f (2t )5.式⎰∞∞-⎪⎭⎫⎝⎛-+6)sin (πδt t t dt 的值是( )A.6πB.6π-1 C.6π-21 D.6π+21 6.已知f （t ）的傅里叶变换为F （j ω），y (t )=f ⎪⎭⎫⎝⎛+b a t ，其中a 、b 为常数，则Y （j ω）为( )A.|a |F (j ω)ωjab eB.|a |F (ja ω)ωjab e -C.||1a F (j aω)ωa b j e D.||1a F ⎪⎭⎫ ⎝⎛a j ωωa bj e -27.已知信号f (t )如题7图所示，其傅里叶变换为F （j ω），则F (0)为( ) A.2 B.π C.π21 D.48.信号t n ε(t )的拉普拉斯变换为( )A.1!+n Sn B.n S n !C.1!-n Sn D.1)!1(+-n S n9.已知拉普拉斯变换F (s )=)4(822+s s ，则原函数f (t )为( )A.[])()2sin(2t t t ε+B.[])()2sin(2t t t ε-C.[])()2cos(2t t t ε+D.[])()2cos(2t t t ε-10.已知某系统的系统函数H (s )=122++s s s,则该系统一定是( ) A.稳定系统 B.不稳定系统 C.临界稳定系统 D.不确定11.离散系统y （n ）=∑=ni if 03（n -i ）的单位序列响应h （n ）是( )A.3δ(n )B.3n ε(n )C.3D.3ε(n )12.已知若f （n ）的z 变换为F (z )，其收敛域为|z |>ρ0，则a -n f (n )的z 变换为( ) A.F （az ），|z |>||0a ρ B.F ,⎪⎭⎫⎝⎛a z |z |>|a |0ρC.F （-az ），|z |>||0a ρD. F ,⎪⎭⎫⎝⎛-a z |z |>|a |0ρ二、填空题（本大题共12小题，每小题2分，共24分）请在每小题的空格中填上正确答案，错填、不填均无分。

全国自考2018年7月信号与系统试卷课程代码：02354一、单项选择题(本大题共12小题，每小题2分，共24分)在每小题列出的四个备选项中只有一个是符合题目要求的，请将其代码填写在题后的括号内。

错选、多选或未选均无分。

1.题1图所示二端口网络A参数中，a12为( )A.1B.ZC.0D.不存在2.RLC串联谐振电路，若串联谐振频率为f0，当输入信号频率f < f0时，此时电路性质为( )A.容性B.感性C.阻性D.无法测定3.原已充电到3V电压的电容，现通过强度为8δ(t)的冲激电流，则在冲激电流作用时刻，电容电压的跃变量为( )A.7VB.4VC.3VD.-4V4.信号f (6-3t)表示( )A.f (3t)左移6B.f (3t)左移2C.f (3t)右移6D.f (-3t)右移25.周期信号满足f (t)=-f (-t)时，其傅里叶级数展开式的结构特点是( )A.只有正弦项B.只有余弦项C.有直流分量D.正弦余弦项都有12 6.已知f (t)的傅里叶变换为F(j ω)，则（t-a ）f(t)的傅里叶变换为( ) A.)()(ω-ωωj aF d j dF B.)()(ω-ωω-j aF d j dFC.)()(ω-ωωj aF d j dF j D.)()(ω-ωω-j aF d j dF j7.信号ej2t δ′(t)的傅里叶变换为( )A.j(ω+2)B.2+j ωC.j(ω-2)D.j ω-28.已知系统的冲激响应h(t)=8e-3t ε(t)，则系统函数H （s ）为() A.S 8 B.38-SC.38+SD.S 39.因果系统的系统函数为H(s)=2322++S S ，则该系统是() A.稳定的 B.不稳定的C.临界稳定的D.不确定10.函数f (t)=δ(t-t0)的拉氏变换为( )A.1B.0st eC.)(e 0-st 0t t -εD.0-st e11.信号f (n-i)，（i>0）表示为( )A.信号f (n)左移序iB.信号f (n)右移序iC.信号f (n)的翻转D.信号f (n)翻转再移序i12.序列an ε(n)的Z 变换为( )A.a Z -1B.a Z +1C.a Z Z -D.a Z Z+二、填空题(本大题共12小题，每小题2分，共24分)3 13.如题13图所示，二端口网络A 参数a11为__________。

参考答案一、画出函数的波形图1. 2.3. 4.5. 6.7.二、波形的变换1. 2.3. 4.5. 6.7. 8.三、冲激函数()t δ的性质 1.()()t t δδ+' 2. 33. 34. eπ-1 5. 3 6. 1 7. 10 8.()()t U t +δ9. 4 10. ()t U 2-11. ()()t U e t t 33--δ 12. 013.()t '21δ 14. 715. 6 16. 2 17. –A 18. eπ-1 19. 0 20. 0 四、 求卷积（和）1. ()ωωj F2. ()()212+-z z z3. ()k kU4. te -5. -16. 37. 28. ()()k U k 1+9.()()2412t te e U t --- 五、求拉氏变换 1.()2221+-+s e s 2. ()4222+-s s3. C4.()22411⎪⎭⎫⎝⎛+++πs s5. ()sses e --+-112 6. 332+++-s s s e s 7. sSee --+1 8. ()1+as aF 9. ()()⎥⎥⎦⎤⎢⎢⎣⎡+-++-2222229273818141s s s s 10. ⎪⎭⎫⎝⎛+s a 1ln 六、求拉氏反变换1. ()()t U et t t⎥⎦⎤⎢⎣⎡+--5/42c o s 42s i n 3512. B3. D4. ()()()()t U e t t t -++-1'δδ5.()()()111-----t U e t t δ 6. ()()()32332-----t U e t t δ7. ()()()[]()t U e e t t t 12132----+- 8. ()[]()t U e e t t t t 221---+- 9.()119--te t七、求付里叶变换1. ωωωa bj ea j F a j -⋅⎪⎭⎫ ⎝⎛ 2. ωωj e j -23. ()()ωδn n j4.()()ωδπωωω02221F e j F j j +⎪⎭⎫⎝⎛- 5. E 6.ωωj e j -+217. ω/2j 8. ()ωπω24j e G - 9. ωπa e-2 10. ωω25221j e j F -⎪⎭⎫ ⎝⎛11.()()()ωωωπδωωωd j dF j d j dF +1 八、求付里叶反变换１．()()11-++t t δδ 2.()jt a +π213.()()[]118144++-t G t G 4. ()[]124+t Sa π5.()tj t πδ1-6. ()422+t Sa7. ()t t t 21sgn 21--或 8. ()ωπsgn j - ； ()t δπ2- 9. ()()[]222+--t t j δδ 九、求Z 变换 1.()21+-z z2. az bz --ln3.()2211-+-z z z ， 1>z 4. 122-z z5.()2211-z z 6.()31-z z7.()311-+z z十、求Z 反变换1. ()k U k ⎪⎭⎫⎝⎛-3c o 12π 2.()()11-+-k U k δ3. ()()23525-+--k k U k δ4. ()k U k ⎪⎭⎫⎝⎛2cos π 5.()()k U k k ωωωs i n s i n 1s i n ++十一、求系统函数及响应()()()()()()z Y z F z H s Y s F s H ,,;,, 1.()()t U t 2+δ 2. ()()[]()k U k k 3223--3. ()()8.04.0242+-+z z zz ； A 4. ()()()()1121--=-+k f k f k y k y 5. ()()k kU k4sin22π- 6.2212++s s7. 233222+++z z z z ， ()()[]()k U kk 21-+-8. ()()t U e t2121-- 9. 32322zz z z +++ 十二、根据信号流图求系统函数()()z H s H ,1. 252162232+--+-s s s s s 2. 22123+++z z z 3. ()()()()k f k y k y k y =++++3122 ； 3212++z z十三、求系统响应()t Y x ，()t Y f ，()t h ,()t g 1.()()t U e t t 2--δ ；()()t U e t 2121-+ 2. E 3.32542+++s s s ； ()t U t t e t ⎪⎭⎫ ⎝⎛+-2sin 212cos 4 4. ()()[]()k U k k212-+-δ 5. ()()[]()k U kk142/16---6. ()()()()()2112-------t U e t U e t t7. ()()t U e t t --32δ 8. ()()k U k 21+ 9. ()[]()k U k2/12- 10. ()()t U e e t t 22---十四、根据初值定理、终值定理计算初值和终值1. 1 ， 02. 1 ， 23. 0 ， 14. 0 ， 55. 1 ， 3/2 ， 26. 1 ， 不存在 十五、Routh 、Jury 判据的应用1. 20<<k2. 5<k3. 05.1<<-k4. 10<<k 十六、香农定理的应用 1.s 4π2. Hz 80≥3. Hz 200≥4. Hz 400≥5. 510- s ； 4105⨯Hz十七、综合应用题 1. τπ2 2. ()()ωωπω2324G e Sa j - 3.()222/cos πωωπ--4. ()t Sa π ，5. ()t U e t2- 6. ()()πωπω44-++Sa Sa7. ()()t U e t--18.()()()()()()()332211--+------t U t t U t t U t t tU ，9. ()t U e t 2- 10. ()k U - 十八、S 域计算题1. 2.()()()()[]()t U e t t y t e t t y t f t x 223630,68--+-=≥+=()(),22,2,32≥-==-=-=--t e e t y c b a t t x3.()()t tu t h =24.()()()()()t u e u t u t i t u e u t u t t R 3100310913231--+==δ5.()()()[]()()()0,2562330,23222≥+-=+-=≥-=------t e t e t y t u e t et y t e e t y t t t tf t t x6. 7.()()()t u e t t t u t c -⎥⎦⎤⎢⎣⎡++=110412 ()0,3sin 343cos 5≥⎥⎦⎤⎢⎣⎡-=-t V t t e t y t8.(1) ()()()()0,21213132≥+=++=--t e e t y s s s s H t t x (2) ()()()t u t t f 21+-= 9.(1) ()()()A t u e e t i t t4320---= (2) 4,321-=-=p p10.()()()()()525251050,680,2522222强迫，自由，稳态，瞬态，t t t t t t f t t x t t e e e e t u e e t u t e e t u t e e t u --------------+-=≥-=≥--=十九、ω域计算题1. ()()t t Sa t y 2cos =2. ()()t t Sa t y 1000cos 21π= 3. ()()()t u e e et y t t tf 42243---+-= 4. ()()t t Sa t y 4sin 22=5. (1) ()47222++=s s s s H(2)(3) ()⎪⎪⎭⎫⎝⎛=3_23cos 35πt t y s6. ()1=t y7. 证明：()()()()()()()()()()()()⎰⎰⎰⎰⎰⎰∞∞-∞∞-∞∞-∞∞--∞∞--∞∞--⋅==⋅=*=→*=dtt f dt t f dt t y dt e t f dt et f dt et y j F j F j Y t f t f t y t j tj t j 21212121,0ωωωωωωω令 证毕8. ()()()()t U e et U e t y t tt322/1392/1----+-=9. ()()t f t y -= 10. ()ttt t y π3sin 999cos 2⋅= 11. ()tt t t ttt h ππππ23sin 2sin22sin ⋅+=二十、Z 域、差分方程计算题1.()()()()()()()()()()0,23/212/1616123/412/1;2,221≥---+=⎥⎦⎤⎢⎣⎡+-+--=-≥---=k t y k u t y k k y kk kk f kkx2.()()()()()()()()()()()()(1)3/411/82(2)21/21/4(3)8/321/21/31/4k kk ky k y k y k f k h k U k y k U k --+-=⎡⎤=-⎣⎦⎡⎤=-+⎣⎦3.()()()()()()[]系统稳定收敛域：,6.04.04.04.16.0,6.04.02kkk h z z z z z z H --=>+-+= 4.()()()()()()()()()()21211.0)4()3(11.08110)2(1.012)1(1-+-=-+----=++=-k f k f k y k y k U k k h z z z z H k 稳定δ5.()()()()()()()()14sin22)3(22222/1)2(122/11)1(442-⋅=-+--=+-=-=-+---⎪⎭⎫ ⎝⎛-k U k k h e z z je z z j z z zz H k f k y k y k y kj jπππ6.()()()()()()k U k k h z z z z H k k⎥⎦⎤⎢⎣⎡-+-=+--=2213221)2(653)1(22δ7. a=1/28.()()121211-⎪⎭⎫⎝⎛=-k U k f k9.()()()[]()()()()()k U k y k U k y kk f kk x ⎥⎦⎤⎢⎣⎡--+=--=++2/31212121110.)(])1()2.0([)( )(])2.0([)( 0 )1()2.0()( )5()()2.0()( )4()1()()2(2.0)1(8.0)( (3) 1 2.0 )2(2.08.0)1()( )1(3212174541453235212k u k y k u k y k k y k u k h k f k f k y k y k y p p z z z z z H k k k f k k x k--+=-=≥--==-+=---+-==-++=临界稳定。