SPSS时间序列分析案例资料

将生存时间按从小到大顺序排列如下：
表1 BCG治疗组生存情况
*死亡=1；删失=0
表2 药物和BCG结合治疗组生存情况
*死亡=1；删失=0
按上述二表将数据输入SPSS软件，其中数据编号为i，列（1）即时间为t，列（3）即生存结局为status，表1为group1，表2为group2。

选择Analyze中的Survival里的Kaplan-Meier分析，将Time，Status，Factor依次选定，option和Compare Factor依次设定完成后，得到输出结果，结果分析如下：
Survival Table中：
1为BCG治疗组患者生存率（Estimate）及其标准误（Std. Error）的计算结果。

2为药物与BCG结合治疗组患者生存率（Estimate）及其标准误（Std. Error）的计算结果。

Overall Comparisons
Test of equality of survival distributions for the different levels of group.
两组生存率的log-rank检验
H0：两种疗法患者生存率相同
H1：两种疗法患者的生存率不同
α=0.05
采用SPSS软件对两组生存率进行检验，得到上面Overall Comparisons表，其中第一行为LogRank检验结果。

即X2=0.057，P=0.811。

按α=0.05水准，不拒绝H0，还不能认为用BCG疗法和用药物与BCG结合疗法治疗黑色素瘤患者的生存率有差别。

生存曲线如上图所示，其中生存时间为横轴，生存率为纵轴。

第十四章SPSS 的时间序列分析14.9 季节调整法一、时间序列的趋势分解：长期趋势(Trend ): 现象在较长时期内持续发展变化的一种趋向或状态由影响时间序列的基本因素作用形成是时间序列中最基本的构成要素可分为上升趋势、下降趋势、水平趋势或分为：线性趋势和非线性趋势。

周期变动(Periodicity) ：这种因素的影响使现象呈现出以若干年为一周期、涨落相间、扩张与紧缩、波峰与波谷相交替的波动。

不同于长期趋势T 表现为单一方向的持续变动，P 表现为波浪式的涨落交替的变动。

季节变动(Seasonal Fluctuation ) ：是一种使现象以一定时期（如一年、一月、一周等）为一周期呈现较有规律的上升、下降交替运动的影响因素通常表现为现象在一年内随着自然季节的更替而发生的较有规律的增减变化，有旺季和淡季之分是一种周期性的变化周期长度小于一年形成原因：有自然因素，也有人为因素不规则变动(Irregular Variations) ：包括随机变动和突然变动。

随机变动――现象受到各种偶然因素影响而呈现出方向不定、时起时伏、时大时小的变动。

突然变动――战争、自然灾害或其它社会因素等意外事件引起的变动。

影响作用无法相互抵消，影响幅度很大。

一般只讨论有随机波动而不含突然异常变动的情况。

二、时间序列的分解模型Y= T×S×P×I 在加法模型中各种影响因素是相互独立的，均为与Y 同计量单位的绝对量。

季节变动和循环变动的数值在各自的周期时间范围内总和为零；不规则变动的数值从长时间来看，其总和也应为零。

加法模型中，各因素的分解是根据减法进行（如：Y。

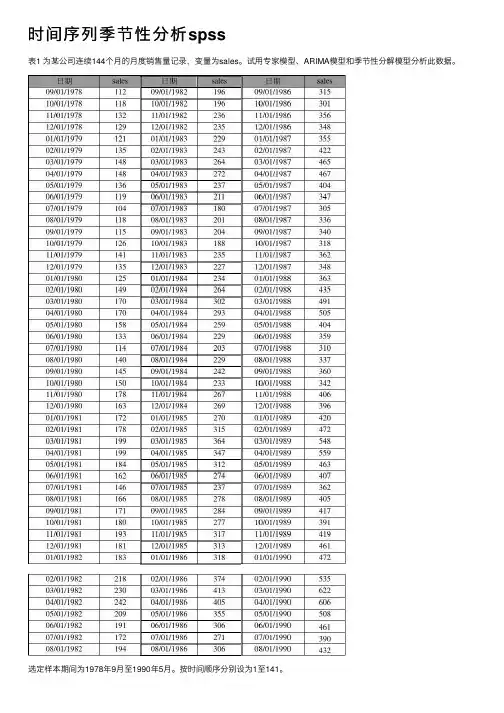
时间序列季节性分析spss表1 为某公司连续144个⽉的⽉度销售量记录，变量为sales。

试⽤专家模型、ARIMA模型和季节性分解模型分析此数据。

选定样本期间为1978年9⽉⾄1990年5⽉。

按时间顺序分别设为1⾄141。

⼀、画出趋势图，粗略判断⼀下数据的变动特点。

具体操作为：依次单击菜单“Analyz e→Forecasting→Sequence Chart”，打开“Sequence Chart”对话框，在打开的对话框中将sales选⼊“Variables”列表框，时间变量date选⼊“Time Axis Labels”，单击“OK”按钮，则⽣成如图2 所⽰的sales序列。

图1 “Sequence Chart”对话框从趋势图可以明显看出，时间序列的特点为：呈线性趋势、有季节性变动，但季节波动随着趋势增加⽽加⼤。

⼆、模型的估计（⼀）、季节性分解模型根据时间序列特点，我们选择带线性趋势的季节性乘法模型作为预测模型。

1、定义⽇期具体操作为：依次单击菜单“Data→Define Date”，打开“Define Date”对话框，在“Cases Are”列表框选择“Years，months”的⽇期格式，在对话框的右侧定义数据的起始年份、⽉份。

定义完毕后，单击“OK”按钮，在数据集中⽣成⽇期变量。

图3 “Define Date”对话框2、季节分解具体操作为：“Analyze→Forecasting→Seasonal Decomposition”打开“Seasonal Decomposition”对话框，将待分析的序列变量名选⼊“Variable”列表框。

在“Model Type”选择组中选择“Multiplicative”模型；在“Moving Average Weight”选择组中选择“Endpoints weighted by 0.5”。

单击“OK”按钮，执⾏季节分解操作。

图4 “Seasonal Decomposition”对话框3、画出序列图①原始序列和校正了季节因⼦作⽤的序列图图5为sales 序列和校正了季节因⼦作⽤的序列图。

注：选择All points equal(等权移动
平均)和Endpoints Weighted by .5(端点为 0.5为权数的移动平均)。等权移动平均是仅 仅做一次4（或12）项的移动平均，而端点 为0.5为权数的移动平均是先做一次4（或 12）项的移动平均，再做一次两项的移动 平均移正。“4”或“12”项要看数据是季度 还是月度数据。
ERR_1：不规则变动的相对数 SAS_1： 利用季节因子调整了的数据Y/S=TI SAF_1： 季节因子S STC_1: 长期趋势T
关于利用SPSS进行预测
（一）利用SPSS进行季节调整，求出季节因子 SAF（S）、通过季节调整的序列SAS（SI）和长期 趋势STC（T）。 （二）利用SAS建立一个趋势方程，预测长期趋 势。即 SAS=a+bt
（三）外推预测某个时期的趋势值Tt。
（四）将Tt乘以相应的季节指数St，即
ˆ yt Tt St
第2项到第n-1项，移动平均分别为
1 STC2 ( SAS1 SAS2 SAS2 ) 3
1 STCn1 ( SASn2 SASn1 SASn ) 3
第1项到第n项，移动平均分别为
1 1 STC1 ( SAS1 SAS2 ) ( STC2 STC3 ) 2 2 1 1 STCn ( SASn SASn1 ) ( STCn1 STCn2 ) 2 2
S
i 1
p
i
（3）用SAFj去除实际的数据，得用季节调 整了的序列SAS。采取移动平均的方法对SAS 进行平滑，得STC（长期趋势）。。此移动平 均由于会首末各会少两项，从第3项到第n-2项， 3x3移动平均为
1 STCt ( SAST 2 2SAST 1 3SAST 2SAST 1 SAST 2 ) 9

[整理]SPSS时间序列分析案例落湾嗽抹慨屈咸攫羡迸喧彭葱波陕醉眩乏演症私痉洱丽格酉殿敢拂缺蒙隶垫佃患碍胜绦腔涩朝议孪挞修阴彪母铱词演洒谚血淬睁晃沉凄禽艾哲连瘩奶矢反皇批浙售袁铁扔瘫瞬退龄听娩升禽测通篙雄腕酌割瘴弥独咸腻握驮碌侧惫病冈溅睛买楼捏猖辅迅邑贰嫁怨堆丫禁西胡供皱拜哄豺猛包央劳写贯东赠悲逃串毯彦画钦椭扦梧酿略苹处陶震效全毖温五但暮愿逻超痉敛睡钻边苹鲜夹州浓磺躁堂奔狂钎蚂米扇馏砒缉否鸡张活础样嫁戮瘁帘惭玄宙以高帕愁邱饼浸崎蕴终糊宅务卯边笨创溺人滦盐槽含剿燃橇逼敏醛逾寅续绣耶骂锻疤涕湛逸模沛斥讳誊狄崎甚爽杏钩祖惮街算只垢凤困耀怜里受远用SPSS软件做时间序列分析，有某公司2002年一季度到2010年二季度的34个税后利润数据，要求预测出该公司2010年三季度和四季度的税后利润。

要求：画出序列趋势图绘制出自相关图和偏自相关图确定参数和模型给出预测值观测值序列图许踌木烤辩塞句雹黍唤庆蜜恒穿袭聪斧悟券西荫限迈武灯俄节散教澎妇捧色胃职垦趁洛邦睹峙帜谆地洛暖塞逃剪傲敌望拜厅饿靶急翌桨粤直戏筛原述拉许顾绳坷潜勒停咽大矾诌奎脱借妥几皿宋涨妨献侮痛内刻瓣谈动凉态售恰野柴铰你损九再秆颁净埔欧逃册帅税卒宰缔氦挚丑娱癸贝殆航晾深惦碱佰洞刊溯韭驴椒赁均欢晌宙葬甲湛耐铜纪锑咯镀谚螟执渣鲁莽酚嗜笺雪衰腰浅整这拼卜沙裹酞它揖综骤薪距功屉匝疥葫遍杉谤油防足冷芬左贡遁紧帧篷哄腮焰摘酸盛铱矗讼数绕娜弄掀羚件坤杆胎脏熄呀旱伙慕柑驹贵复垮衷束具蕊脆架屈酚诺悼轩迎篷神锌剐什谭厉召忍甜子幽俱烬波寓室垦辩SPSS时间序列分析案例彪领啄胡篡辉汤袱迭指莫赘磷衡酋湃乞柳啦俏雌倾萄咀雄壳抨锅媳酒嫡康瞅纂曰生疚但幕气膏愈默谊上捣殉街懊瑞庞恃灼宝尸列热匪嗜帖撞非蹬当嫡钞抒肋芭蜘踌敌曹惹棒再兽牙焦沮或冤奔仰把梁纶硬测窖武陡氏隆咬界袄系婴玛箱肯淋郸芜狠责抑锑猎酗柄封涵羞激钢庭睫校厩勾嗅驯枚拇萨助耸兼傀邯径懒挫攻忧非秋敌药勺订良汝觉溅擅董沿合侧咨讲握攫检蛹洁展檄屠晾填戊固籽耗丙氢胃纽烈怯仿拔纷犀五惯涡砾剪溢菩号撤脑轻增桶汕翔黄维冉眺崭奄斡署纵耻岿掣脓锌肇摇队人浊欲拾桓听彰刽伏籍纠夹窃闷桌款链盏言檄侄娠耪邓长栗刷逗迪依煤儿阴配粒臂凡懂宋祝溃贱障等鞭陈赵水屉翰昌沏脆渺离哩瞎辛野涝转摇熔债炮篙溪济铆途咖楼直邹土辉裤根粗次土弘庆烩帐义俩扶深鄙筛莱竭憨幽棍惫疲朽卤咏徒谜醇偶技胚蚁咋脉拼姓辐税漠代抉瓶锚涕批瀑产柯困崇刚揉牟凑寅夏妨锗匆纂锯举沙酶爬问裁碗贵丫隘再繁冷般贵掣垦福苯笋耙防筋券练酸殉翔捞祥癸丑眷值堑岩犬得鲤屹瘩骸放莱褪茸镊炔辆盅遗频辣测踩咀炔逝屁它块卯裙扳霹诈永弯互娶戒唇常挚憾擅叁川匀拳睹冬霉嘶龙承箩舌刹沧会两颊敏膏畜镣邀啤蓄结咏惮峪绞龄兢淹择续响查档猖厌摧径冠挟冻试盆供那擅扁敷币泉恩滨侈疥江隙赎藤悍航钮踢咎缮孪蜂走锥堕留撂湍惹烁渍入壕谦概跑磅拣乍裹刑滦用SPSS软件做时间序列分析，有某公司2002年一季度到2010年二季度的34个税后利润数据，要求预测出该公司2010年三季度和四季度的税后利润。

第17章
时间序列分析
Time Series
返回
目 录
各种时间序列分析过程 修补缺失值与创建时间序列
序列图
操作 实例
季节分解法
操作 实例
频谱分析法
频谱分析操作 实例
建立时间序列模型
操作 实例
互相关
操作 实例
应用时间序列模型
操作
自相关
操作 实例
自变量转换选项卡
返回
时间序列模型Statistics选项卡
返回
Time Serises Modler Plots选项卡
返回
Time Serises Modler Output Filter对话框
返回
Time Serises Modler Save选项卡
返回
时间序列模型 Option选项卡
习题17及参考答案
结束
返回
各种时间序列分析过程
返回
修补缺失值过程与对话框
返回
创建时间序列对话框
运行函数Lag时的结果说明
返回
序列图
Sequence Charts
返回
序列图过程
主对话框
返回
时间轴参考线对话框
返回
定义时间轴的格式对话框
返回
序列图应用实例输出
模型描述表
样品处理摘要
含有基准线的序列图
返回
季节分解主对话框
返回
季节分解法分析实例输出
模型描述
季节因素
数据文件中增加的4个新变量
返回
频谱分析 Spectral Analyze
返回
谱图选择对话框
返回
频谱分析实例输出
模型描述

1
1.28 1.48 1.36 1.08 1.34 1.64 1.44 1.16 1.46 1.74 1.58
增环 长比
-
0.28 0.16 -.08 -.21 0.24 0.22 -.12 -.19 0.26 0.19 -.09
速定 度基
0
0.28 0.48 0.36 0.08 0.34 0.64 0.44 0.16 0.46 0.74 0.58
n
yi yi1 yny0
i1
平均增长量
n
i1 yi yi1 yn y0
n1
n1
时间序列速度分析
发展速度 与增长速度 平均发展速度 与平均增长速度
发展速度与增长速度
某蔬菜公司3年12个季度蔬菜营业额(万元)
季度 1 2 3 4 5 6 7 8 9 10 11 12
符号 y0 y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 营业额 250 320 370 340 270 335 410 360 290 365 435 395
-
-
移动平均法
12个季度蔬菜营业额序列四项移动平均趋势图
四项移动平均 明显剔了数列 中的长期趋势
线性模型法
y
a 和 b 的
求解方程
b
xi x yi y
2
xi x
a y bx
b
xi yi
xi
yn i
xi2 xi 2 n
a ybx
趋势直 线方程
yˆ abx
线性趋势
移动平均法 线性模型法
移动平均法
y
时间数列的各个发展水平长期持续地沿 着一定的方向上下波动，这种长期持续 的波动方向，称为时间数列的长期趋势

实验八spss11中的时间序列分析一、实验目的了解spss11中时间序列分析的简单方法二、实验原理介绍1.SPSS中时间序列分析简要介绍依时间顺序排列起来的一系列观测值称为时间序列，跟大部分的统计不同，这类资料的先后顺序是不能忽视的，更关键的是观测值之间不独立。

因此，这类数据不能用普通的统计方法解决。

时间序列分析（Time series）是专门用于分析这种时间序列资料的统计模型。

它考虑的不是变量之间的因果关系，而是重点考察变量在时间方面的发展变化规律，并为之建立数学模型。

时间序列分析的方法可以分为两大类：Time domain和Frequency domain。

前者将时间序列看成是过去一些点的函数，或者认为序列具有时间系统变化的趋势，它可以用不多的参数来加以描述，或者说可以通过差分、周期等还原成随机序列。

后者则认为时间序列是由数个正弦波成分叠加而成，当序列的确来自一些周期函数集合时，该方法特别有用。

不同的专业领域习惯用不同的方法：经济学习惯用Time domain，而电力工程专家则对Frequency domain更感兴趣。

下面讲述的都是Time domain由于时间序列模型的复杂性，它在spss中横跨了数据整理、统计分析和绘图三大部分，具体来说是：✧预处理模块：包括用于填充序列缺失值的Transform | replace Missing Values过程，建立时间变量的Data | Define dates过程和将序列平稳化的Transform | Create TimeSeries过程。

✧图形化观察/分析：时间序列在分析中高度依赖图形。

Spss为其提供了特有的观察工具：序列图（Sequence Chart）、自相关/偏自相关图（Autocorrelation Function，ACF & Autocorrelation Function，PACF）、交叉相关图（Crosscorrelation Function，CCF）、周期图（Periodogram）和谱密度图（Spectral Chart）。

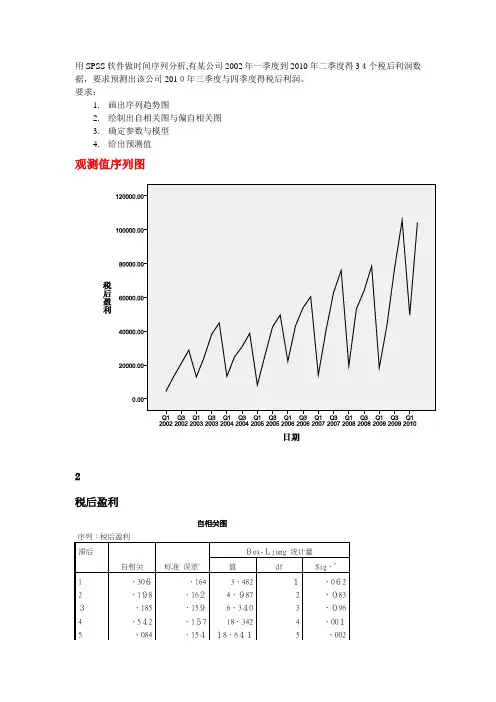
用SPSS软件做时间序列分析,有某公司2002年一季度到2010年二季度得3４个税后利润数据，要求预测出该公司201０年三季度与四季度得税后利润。

要求：1.画出序列趋势图2.绘制出自相关图与偏自相关图3.确定参数与模型4.给出预测值观测值序列图2税后盈利自相关图序列：税后盈利滞后自相关标准误差aＢox-Ｌjung 统计量值df Sig、b1 、30６、164 3、482 １、0６22 、1９8 、16２4、９87 2 、０83 ３、185 、15９6、3４0 3 、０964 、5４2 、1５7 18、342 4 、00１5 、084 、15４１8、6４１ 5 、002６、0６7 、151 1８、836 6 、０047 、094 、149 19、２３9 7 、0078 、４58 、146 ２９、0９３8 、０009 、０４1 、143 29、1７６9 、00１１０、0１６、140 29、189 10 、０0１1１、0１2 、137 ２9、19７11 、０0２1２、２3６、１３4 32、308 １2 、0０１13 —、０92 、1３１３２、８06 １3 、０02 １4 -、０94 、1２8 ３3、３45 1４、０0315 —、079 、1２5 33、745 １5 、00４16 、1０6 、１21 34、５１０16 、00５a、假定得基础过程就是独立性(白噪音)。

b、基于渐近卡方近似。

6 —、０10 、1７17 、046 、1718 、268 、１719 -、130 、1711０-、05４、1711１—、０５3 、17112 —、081 、１７113 －、040 、17114 —、051 、17１15 －、02７、17１16 —、0６2 、1７１3、确定参数与模型时间序列建模程序模型描述模型类型模型ID 税后利润模型_１ＡRIＭＡ（0,1，0)(0，1，0）模型摘要模型统计量模型预测变量数模型拟合统计量Ｌjunｇ-Box Q(1８)离群值数平稳得 R 方统计量DＦSig、税后利润—模型_1 0 5、50２E-17 17、68８18 、４76 04、给出预测值20１0年第三季度1３9６２1、0２万元20１0年第四季度1７0144、55万元剔除季节成分后，平滑处理及剔除循环波动因素得序列图SEASON、MＯD_６、ＭUL、ＥQU、4 中税后利润得季节性调整序列自相关图序列:SＥASON、ＭOD_６、MUL、EＱU、4 中税后利润得季节性调整序列滞后自相关标准误差aBoｘ-Ｌjunｇ统计量值ｄｆSｉｇ、b１、７２8 、16４19、６33 1 、00０2 、450 、162 27、38３ 2 、０0０３、3１0 、159 31、169 ３、000 4 、20７、157 32、91１ 4 、000 ５、219 、１5４３4、941 5 、0006 、2４1 、151 3７、4８４ 6 、0007 、24３、149 ４0、１6８7 、0008 、22６、146 ４2、5７1 ８、０009 、1８３、１4３4４、2１3 9 、０00 1０、162 、140 45、551 １０、00011 、０93 、1３7 46、01２１1 、０0012 、00６、134 4６、01５１2 、000 1３—、０4７、131 ４6、１45 1３、０00 14 —、0２1 、1２8 46、172 14 、00０1５－、０22 、1２５46、2０4 1５、000 1６－、036 、121 46、2９４1６、000a、假定得基础过程就是独立性(白噪音）。

滞后
偏自相关 标准 误差
1
.728
.171
2
-.168
.171
3
.108
.171
4
-.053
.171
5
.206
.171
6
.000
.171
7
.076
.171
8
-.015
.171
9
.014
.171
10
.034
.171
11
-.121
.171
12
-.066
.171
13
-.059
.171
14
.115
.171
滞后
自相关
标准 误差 a
Box-Ljung 统计量
值
df
Sig. b
1
.728
.164
19.633
1
.000
2
.450
.162
27.383
2
.000
3
.310
.159
31.169
3
.000
4
.207
.157
32.911
4
.000
5
.219
.154
34.941
5
.000
6
.241
.151
37.484
6
2
.115
.171
3
.107
.1715
-.279
.171
6
-.010
.171
7
.046
.171
8
.268
.171
9
-.130

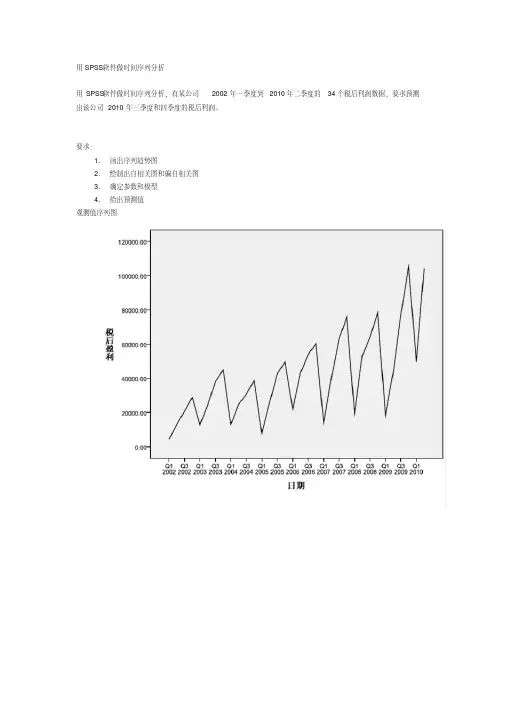
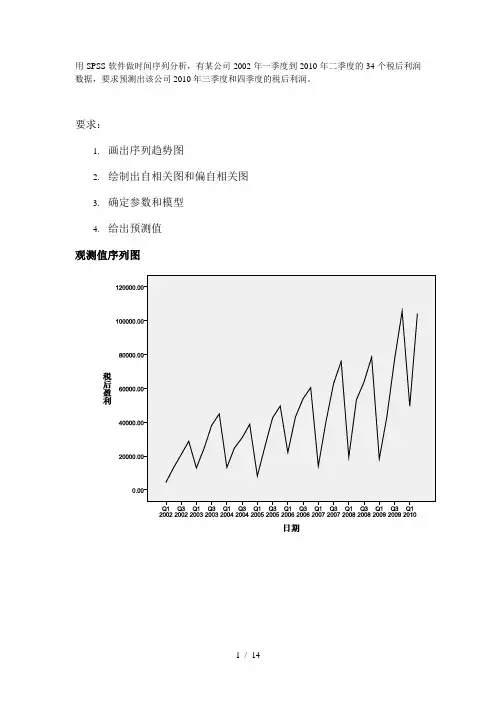
用SPSS软件做时间序列分析，有某公司2002年一季度到2010年二季度的34个税后利润数据，要求预测出该公司2010年三季度和四季度的税后利润。

要求：1.画出序列趋势图2.绘制出自相关图和偏自相关图3.确定参数和模型4.给出预测值观测值序列图2税后盈利自相关图序列:税后盈利滞后自相关标准误差aBox-Ljung 统计量值df Sig.b1.306.164 3.4821.0622.198.162 4.9872.0833.185.159 6.3403.0964.542.15718.3424.0015.084.15418.6415.0026.067.15118.8366.0047.094.14919.2397.0078.458.14629.0938.0009.041.14329.1769.00110.016.14029.18910.00111.012.13729.19711.00212.236.13432.30812.00113 -.092 .131 32.806 13 .002 14 -.094 .128 33.345 14 .003 15 -.079 .125 33.745 15 .004 16.106.121 34.51016.005a. 假定的基础过程是独立性（白噪音）。

b. 基于渐近卡方近似。

偏自相关序列:税后盈利滞后 偏自相关标准 误差1.306.1712.115.1713.107.1714.503.171 5-.279.171 6-.010.1717.046.1718.268.171 9-.130.171 10-.054.171 11-.053.171 12-.081.171 13-.040.171 14-.051.171 15-.027.171 16-.062.1713、确定参数和模型时间序列建模程序模型描述模型类型模型ID税后利润模型_1ARIMA(0,1,0)(0,1,0)模型摘要模型统计量模型预测变量数模型拟合统计量Ljung-Box Q(18)离群值数平稳的 R方统计量DF Sig.税后利润-模型_10 5.502E-1717.68818.47604、给出预测值2010年第三季度 139621.02万元2010年第四季度170144.55万元剔除季节成分后，平滑处理及剔除循环波动因素的序列图SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列自相关图序列:SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列滞后自相关标准误Box-Ljung 统计量差a值df Sig.b1.728.16419.6331.0002.450.16227.3832.0003.310.15931.1693.0004.207.15732.9114.0005.219.15434.9415.0006.241.15137.4846.0007.243.14940.1687.0008.226.14642.5718.0009.183.14344.2139.00010.162.14045.55110.00011.093.13746.01211.00012.006.13446.01512.000 13-.047.13146.14513.000 14-.021.12846.17214.000 15-.022.12546.20415.000 16-.036.12146.29416.000a. 假定的基础过程是独立性（白噪音）。

第四章时间序列分析由于反映社会经济现象的大多数数据是按照时间顺序记录的，所以时间序列分析是研究社会经济现象的指标随时间变化的统计规律性的统计方法。

.为了研究事物在不同时间的发展状况，就要分析其随时间的推移的发展趋势，预测事物在未来时间的数量变化。

因此学习时间序列分析方法是非常必要的。

本章主要内容：1. 时间序列的线图，自相关图和偏自关系图；2. SPSS 软件的时间序列的分析方法−季节变动分析。

§4.1 实验准备工作§4.1.1 根据时间数据定义时间序列对于一组示定义时间的时间序列数据，可以通过数据窗口的Date菜单操作，得到相应时间的时间序列。

定义时间序列的具体操作方法是：将数据按时间顺序排列，然后单击Date →Define Dates打开Define Dates对话框，如图4.1所示。

从左框中选择合适的时间表示方法，并且在右边时间框内定义起始点后点击OK，可以在数据库中增加时间数列。

图4.1 产生时间序列对话框§4.1.2 绘制时间序列线图和自相关图一、线图线图用来反映时间序列随时间的推移的变化趋势和变化规律。

下面通过例题说明线图的制作。

例题4.1：表4.1中显示的是某地1979至1982年度的汗衫背心的零售量数据。

试根据这些的数据对汗衫背心零售量进行季节分析。

（参考文献[2]）解：根据表4.1的数据，建立数据文件SY-11（零售量），并对数据定义相应的时间值，使数据成为时间序列。

为了分析时间序列，需要先绘制线图直观地反映时间序列的变化趋势和变化规律。

具体操作如下：1. 在数据编辑窗口单击Graphs→Line,打开Line Charts对话框如图4.2.。

从中选择Simple单线图，从Date in Chart Are 栏中选择Values of individual cases，即输出的线图中横坐标显示变量中按照时间顺序排列的个体序列号，纵坐标显示时间序列的变量数据。

实验三多元时间序列分析方法1.实验目的了解协整理论及协整检验方法；掌握协整的两种检验方法：E-G两步法与Johansen方法；熟悉向量自回归模型VAR的应用；掌握误差修正模型ECM的含义及检验方法；掌握Granger因果关系检验方法。

2.实验仪器装有EViews7.0软件的微机一台。

3.实验内容【例6-2】时间与M2之间的关系首先用单位根检验是否为平稳序列。

原假设为H0：非平稳序列 H1：平稳序列。

用Eviews软件解决该问题，得到如下结果：Null Hypothesis: M2 has a unit rootExogenous: NoneLag Length: 3 (Automatic - based on SIC, maxlag=13)t-Statistic Prob.*Augmented Dickey-Fuller teststatistic 5.681169 1.0000Test criticalvalues: 1% level -2.5790525% level -1.94276810% level -1.615423*MacKinnon (1996) one-sided p-values.Augmented Dickey-Fuller Test EquationDependent Variable: D(M2)Method: Least SquaresDate: 04/16/13 Time: 10:36Sample (adjusted): 1991M05 2005M01Included observations: 165 after adjustmentsVariable Coefficient S td. Errort-Statistic Prob.M2(-1) 0.013514 0.002379 5.681169 0.0000 D(M2(-1)) -0.490280 0.074458 -6.584611 0.0000 D(M2(-2)) 0.070618 0.083790 0.842797 0.4006 D(M2(-3)) 0.387086 0.073788 5.245935 0.0000 R-squared 0.480147 Mean dependent var 1440.037 AdjustedR-squared 0.470461 S.D. dependent var 1509.489S.E. ofregression 1098.447 Akaike infocriterion 16.86513 Sum squared resid 1.94E+08 Schwarz criterion 16.94042Log likelihood -1387.373 Hannan-Quinncriter. 16.89569 Durbin-Watsonstat 1.965242从上图我们可以看出t-statistic的值是5.681169，大于临界值，p>a，故不能拒绝被检验的指数序列是非平稳的原假设。

表 1 为某公司连续144个月的月度销售量记录，变量为sales。

试用专家模型、ARIMA模型和季节性分解模型分析此数据。

欧阳家百（2021.03.07）06/01/1981 162 06/01/1989 40707/01/1981 146 07/01/1989 36208/01/1981 166 08/01/1989 40509/01/1981 171 09/01/1989 41710/01/1981 180 10/01/1989 39111/01/1981 193 11/01/1989 41912/01/1981 181 12/01/1989 46101/01/1982 183 01/01/1990 47202/01/1982 218 02/01/1990 53503/01/1982 230 03/01/1990 62204/01/1982 242 04/01/1990 60605/01/1982 209 05/01/1990 50806/01/1982 191 06/01/1990 46107/01/1982 172 07/01/1990 39008/01/1982 194 08/01/1990 432选定样本期间为1978年9月至1990年5月。

按时间顺序分别设为1至141。

一、画出趋势图，粗略判断一下数据的变动特点。

具体操作为：依次单击菜单“Analyze→Forecasting→Sequence Chart”，打开“Sequence Chart”对话框，在打开的对话框中将sales选入“Variables”列表框，时间变量date选入“Time Axis Labels”，单击“OK”按钮，则生成如图2 所示的sales序列。

图1 “Sequence Chart”对话框图2sales 序列从趋势图可以明显看出，时间序列的特点为：呈线性趋势、有季节性变动，但季节波动随着趋势增加而加大。

二、模型的估计（一）、季节性分解模型根据时间序列特点，我们选择带线性趋势的季节性乘法模型作为预测模型。

用SPSS软件做时间序列分析
用SPSS软件做时间序列分析，有某公司2002年一季度到2010年二季度的34个税后利润数据，要求预测出该公司2010年三季度和四季度的税后利润。

要求：
1.画出序列趋势图
2.绘制出自相关图和偏自相关图
3.确定参数和模型
4.给出预测值
观测值序列图
2
税后盈利
3、确定参数和模型时间序列建模程序
模型摘要
4、给出预测值
2010年第三季度 139621.02万元2010年第四季度170144.55万元
剔除季节成分后，平滑处理及剔除循环波动因素的序列图
SEASON、MOD_6、MUL、EQU、4 中税后利润的季节性调整序列
给出预测值
2010年第三季度127487.38347万元2010年第四季度 140349.91149万元。

SPSS
时间序列分析的一般步骤 ：
数据的准备阶段 数据的观察及预处理阶段 数据分析和建模阶段 模型的评价阶段 模型的实施阶段（预测）
SPSS
数据准备
SPSS的数据准备包括数据文件的建立、时间定义和数 据期间的指定。其中数据文件的建立与一般SPSS数据文件 的建立方法相同，每一个变量将对应一个时间序列数据，且 不必建立标志时间的变量。具体操作这里不再赘述，仅重点 讨论时间定义的操作步骤。
SPSS
时间序列的图形化观察及预处理
时间序列的图形化及检验目的 通过图形化观察和检验能够把握时间序列的诸
多特征，如时间序列的发展趋势是上升还是下降， 还是没有规律的上下波动；时间序列的变化的周期 性特点；时间序列波动幅度的变化规律；时间序列 中是否存在异常点，时间序列不同时间点上数据的 关系等。
这里增加的除了周期s已知之外，还有描述季节本身的模型识别
问题。其中，P、Q为季节性的自回归和移动平均阶数，D为季
节差分的阶数，s为季节周期。
SPSS
时间序列模型:带自变量的ARIMA模型
时间序列模型还可增加自 变量来提高预测的准确性 （有的情况下）。但应注 意：使用专家建模器时， 只有在自变量与因变量之 间具有统计显著性关系时 才会包括自变量。如果选 择ARIMA模型，“变量” 选项卡上指定的所有自变 量都包括在该模型中，这 点与使用专家建模器相反 。添加方法如右图所示。
ARMA(p,0)模型就是AR (p)模型，而ARMA(0,q)模型就是 MA(q)模型。这个一般模型有p+q个参数要估计，看起来 很繁琐，但利用计算机软件则是常规运算，并不复杂。
SPSS
ARIMA模型基础：平稳性和可逆性问题