(遵义专版)2018年中考数学总复习 第一篇 知识篇 第1章 数与式 第5节 二次根式(精练)试题含答案

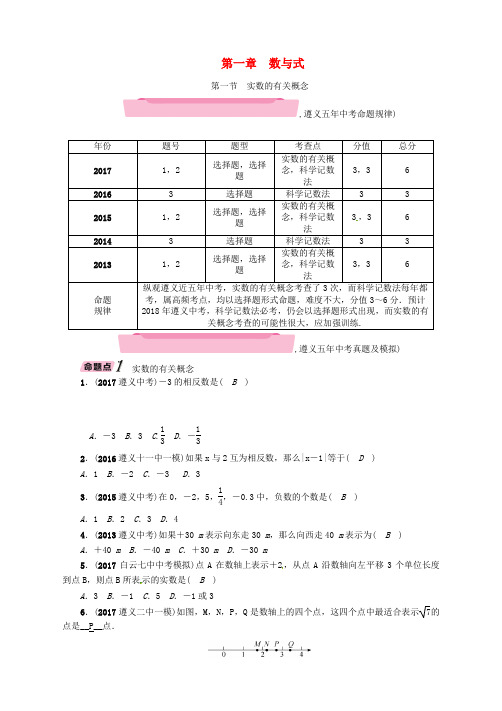
第一章 数与式第一节 实数的有关概念,遵义五年中考命题规律)年份 题号题型考查点 分值 总分 2017 1，2 选择题，选择题实数的有关概念，科学记数法3，3 62016 3 选择题 科学记数法 3 32015 1，2 选择题，选择题实数的有关概念，科学记数法3，3 62014 3 选择题 科学记数法 3 320131，2 选择题，选择题实数的有关概念，科学记数法3，3 6命题规律纵观遵义近五年中考，实数的有关概念考查了3次，而科学记数法每年都考，属高频考点，均以选择题形式命题，难度不大，分值3～6分．预计2018年遵义中考，科学记数法必考，仍会以选择题形式出现，而实数的有关概念考查的可能性很大，应加强训练.,遵义五年中考真题及模拟)实数的有关概念1．(2017遵义中考)－3的相反数是( B )A ．－3B ．3C .13D ．－132．(2016遵义十一中一模)如果x 与2互为相反数，那么|x －1|等于( D )A ．1B ．－2C ．－3D ．33．(2015遵义中考)在0，－2，5，14，－0.3中，负数的个数是( B )A ．1B ．2C ．3D ．44．(2013遵义中考)如果＋30 m 表示向东走30 m ，那么向西走40 m 表示为( B )A ．＋40 mB ．－40 mC ．＋30 mD ．－30 m5．(2017白云七中中考模拟)点A 在数轴上表示＋2，从点A 沿数轴向左平移3个单位长度到点B ，则点B 所表示的实数是( B )A ．3B ．－1C ．5D ．－1或36．(2017遵义二中一模)如图，M ，N ，P ，Q 是数轴上的四个点，这四个点中最适合表示7的点是__P__点．科学记数法7．(2017遵义中考)2017年遵义市固定资产总投资计划为2 580亿元，将2 580亿用科学记数法可表示为( A )A ．2.58×1011B ．2.58×1012C ．2.58×1013D ．2.58×1014,中考考点清单)实数的有关概念及分类1．整数和__分数__统称为有理数；__无限不循环小数__叫无理数；有理数和无理数统称为__实数__．2．分类 (1)按定义分类实,数)⎩⎪⎨⎪⎧有理数⎩⎪⎨⎪⎧整数：正整数、0、负整数分数⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫正分数负分数有限小数和 无限循环 小数无理数⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫正无理数负无理数无限不循环 小数 (2)按正负分类实,数)⎩⎪⎨⎪⎧正实数： 正有理数 （正整数、正分数）、正无理数 零 负实数 ：负有理数（负整数、负分数）、 负无理数3．数轴的三要素是：__原点__、__正方向__、__单位长度__；数轴上的点和__实数__是一一对应的．4．相反数(1)实数a 的相反数是__－a__(a 与b 互为相反数⇔a ＋b ＝__0__)；(2)相反数的几何意义：在数轴上，表示相反数的两个点位于原点的__两侧__，且到原点的距离__相等__．5．绝对值(1)在数轴上表示一个数的点离原点的__距离__叫做这个数的绝对值；(2)|a|＝⎩⎪⎨⎪⎧ a （a≥0）， －a （a ＜0），即正数的绝对值是__它本身__，0的绝对值是__0__，负数的绝对值是它的__相反数__；(3)一个数的绝对值是__非负__数，即|a|__≥__0. 6．倒数(1)若两个非零数a ，b 的积为1，即__a·b＝1__，则a 与b 互为倒数，反之亦然； (2)非零数a 的倒数为__1a__ ；__0__没有倒数．近似数和科学记数法7．科学记数法：把一个数写成__a×10n__的形式(其中__1__≤|a|<__10__，n 为整数)，这种记数法称为科学记数法．例如574 000记作__5.74×105__，－0.000 737记作__－7.37×10－4__．8．精确度与近似数：近似数与准确数的接近程度通常用__精确度__表示：近似数一般由__四舍五入__取得，__四舍五入__到哪一位，就说这个近似数精确到哪一位，如 5.374 6精确到0.001或精确到千分位是__5.375__，4.46万是精确到__百__位．【方法点拨】用科学记数法表示一个数时，需要从两个方面入手，关键是确定a和n的值．(1)a值的确定：1≤|a|<10；(2)n值的确定：①当原数大于或等于10时，n等于原数的整数位数减1；②当原数大于0且小于1时，n是负整数，它的绝对值等于原数左起第一位非零数字前所有零的个数(含小数点前的零)；③有计数(量)单位的数，先把数字单位转化为纯数字表示，再用科学记数法表示．常用的计数单位有：1亿＝108，1万＝104，计量单位有：1 mm＝10－3 m，1 nm＝10－9m等．,中考重难点突破)无理数的判断【例1】(2017荆门中考)在实数－722，9，π，38中，是无理数的是( )A．－722B.9 C．πD.38【解析】要把能化简的化简后再判断，－722，9，38是有理数，π是无理数．【答案】C1．(2017沭阳一模)在下列实数：π2，3，4，227，－1.010 010 001…中，无理数有( C)A．1个B．2个C．3个D．4个2．(2017福建中考)下列实数2，－34，0.32··，227，π3，(2－1)0，－9，0.101 001000 1…中，其中非无理数共有( C)A．2个B．3个C．4个D．5个3．(北京中考)写出一个比3大且比4小的无理数：__π(答案不唯一)__．实数的相关概念【例2】(2017遵义航中一模)－12的绝对值的相反数是( )A .12B ．－12C ．2D ．－2【解析】紧扣绝对值及相反数的意义分两层来思考：①－12的绝对值是多少；②其绝对值的相反数是多少．【答案】B4．(2017贺州中考)－12的倒数是( A )A ．－2B ．2C .12D ．－125．(2017黔东南中考)|－2|的值是( B )A ．－2B ．2C ．－12D .12科学记数法【例3】(2017天水中考)我国平均每平方千米的土地一年从太阳得到的能量，相当于燃烧130 000 000 kg 的煤所产生的能量．把130 000 000 kg 用科学记数法可表示为( )A ．13×107 kgB ．0.13×108 kgC ．1.3×107 kgD ．1.3×108 kg【解析】将一个较大数表示成a×10n的形式，其中1≤|a|<10，n 的值为原数的整数位数减一．【答案】D6．(2017白银中考)据报道，2016年10月17日7时30分28秒，神舟十一号载人飞船在甘肃酒泉发射升空，与天宫二号在距离地面393 000 m 的太空轨道进行交会对接，而这也是未来我国空间站运行的轨道高度.393 000用科学记数法表示为( B )A ．39.3×104B ．3.93×105C ．3.93×106D ．0.393×1067．(2017泰安中考)“2014年至2016年，中国同‘一带一路’沿线国家贸易总额超过3万亿美元”，将数据3万亿美元用科学记数法表示为( C )A ．3×1014美元B ．3×1013美元C ．3×1012美元D ．0.393×1068．(2017菏泽中考)生物学家发现了一种病毒，其长度约为0.000 000 32 mm ，数据0.000 000 32用科学记数法表示正确的是( C )A ．3.2×107B ．3.2×108C ．3.2×10－7D ．3.2×10－8。

中档题型专训(五)圆的有关计算、证明与探究圆的有关计算与证明是遵义中考的必考内容之一，占有较大的比重，通常结合三角形、四边形等知识综合考查，以计算题、证明题的形式出现，解答此类问题要熟练掌握圆的基本性质，特别是切线的性质和判定，同时要注意已知条件之间的相互联系．与圆的有关性质【例1】如图，已知OA ，OB 是⊙O 的两条半径，C ，D 为OA ，OB 上的两点，且AC ＝BD.求证：AD ＝BC.【解析】首先证明OC ＝OD ，再证明△OCB≌△ODA，进而得到AD ＝BC. 【答案】证明：∵OA，OB 是⊙O 的两条半径， ∴AO ＝BO.∵AC ＝BD ，∴OC ＝OD ，在△ODA 和△OCB 中，⎩⎪⎨⎪⎧AO ＝BO ，∠O ＝∠O，OD ＝OC ，∴△ODA ≌△OCB(SAS )， ∴AD ＝BC.1．(2017玉林一模)如图，AB 是半圆O 上的直径，E 是BC ︵的中点，OE 交弦BC 于点D ，过点C 作⊙O 的切线交OE 的延长线于点F ，已知BC ＝8，DE ＝2.(1)求⊙O 的半径； (2)求CF 的长．解：(1)设⊙O 的半径为x ， ∵E 点是BC ︵的中点，O 点是圆心， ∴OD ⊥BC ，DC ＝12BC ＝4，在Rt △ODC 中，OD ＝x －2，∴OD 2＋DC 2＝OC 2， ∴(x －2)2＋42＝x 2， ∴x ＝5，即⊙O 的半径为5； (2)∵FC 是⊙O 的切线， ∴OC ⊥CF.又∵E 是BC ︵的中点．∴OD ⊥BC ，∴OC 2＝OD·OF，即52＝3·OF， ∴OF ＝253.在Rt △OCF 中，OC 2＋CF 2＝OF 2，∴CF ＝203.圆的切线的性质与判定【例2】(2017遵义二中一模)如图，AB 是⊙O 的直径，BC 为⊙O 的切线，D 为⊙O 上的一点，CD ＝CB ，延长CD 交BA 的延长线于点E.(1)求证：CD 为⊙O 的切线；(2)若BD 的弦心距OF ＝1，∠ABD ＝30°，求图中阴影部分的面积．(结果保留π)【解析】(1)证∠ODC＝∠ABC＝90°；(2)在Rt △OBF 中，∠ABD ＝30°，OF ＝1，可求得BD 的长，∠BOD 的度数，又由S 阴影＝S 扇形OBD －S △BOD ，即可求解．【答案】解：(1)连接OD ，∵BC 是⊙O 的切线，∴∠ABC ＝90°. ∵CD ＝CB ，∴∠CBD ＝∠CDB. ∵OB ＝OD ，∴∠OBD ＝∠ODB， ∴∠ODC ＝∠ABC＝90°，即OD ⊥CD. ∵点D 在⊙O 上，∴CD 为⊙O 的切线； (2)在Rt △OBF 中， ∵∠ABD ＝30°，OF ＝1， ∴∠BOF ＝60°，OB ＝2，BF ＝ 3. ∵OF ⊥BD ，∴BD ＝2BF ＝23，∠BOD ＝2∠BOF＝120°. ∴S 阴影＝S 扇形OBD －S △BOD＝120π×22360－12×23×1＝43π－ 3.2．(2017南宁中考)如图，AB 是⊙O 的直径，弦CD⊥AB，垂足为H ，连接AC ，过BD ︵上一点E 作EG∥AC 交CD的延长线于点G ，连接AE 交CD 于点F ，且EG ＝FG ，连接CE.(1)求证：△ECF∽△GCE； (2)求证：EG 是⊙O 的切线；(3)延长AB 交GE 的延长线于点M ，若tan G ＝34，AH ＝33，求EM 的值．解：(1)∵AC∥EG， ∴∠G ＝∠ACG. ∵AB ⊥CD ， ∴AD ︵＝AC ︵， ∴∠CEF ＝∠ACD， ∴∠G ＝∠CEF. ∵∠ECF ＝∠ECG， ∴△ECF ∽△GCE ； (2)连接OE. ∵GF ＝GE ，∴∠GFE ＝∠GEF＝∠AFH. ∵OA ＝OE ， ∴∠OAE ＝∠OEA. ∵∠AFH ＋∠FAH＝90°， ∴∠GEF ＋∠AEO＝90°， ∴∠GEO ＝90°， ∴GE ⊥OE.又∵OE 为⊙O 半径， ∴EG 是⊙O 的切线，(3)连接OC.设⊙O 的半径为r.在Rt △AHC 中，tan ∠ACH ＝tan G ＝AH HC ＝34，∵AH ＝33， ∴HC ＝43， 在Rt △HOC 中，∵OC ＝r ，OH ＝r －33，HC ＝43， ∴(r －33)2＋(43)2＝r 2， ∴r ＝2536.∵GM ∥AC ，∴∠CAH ＝∠M. ∵∠OEM ＝∠AHC， ∴△AHC ∽△MEO ， ∴AH EM ＝HC OE ， ∴33EM ＝432536，∴EM ＝2538.圆与相似及三角函数综合【例3】(2017无锡中考)如图，以原点O 为圆心，3为半径的圆与x 轴分别交于A ，B 两点(点B 在点A 的右边)，P 是半径OB 上一点，过P 且垂直于AB 的直线与⊙O 分别交于C ，D 两点(点C 在点D 的上方)，直线AC ，DB 交于点E.若AC∶CE＝1∶2.(1)求点P 的坐标；(2)求过点A 和点E ，且顶点在直线CD 上的抛物线的函数解析式．【解析】(1)如图，作EF⊥y 轴于F ，DC 的延长线交EF 于H.设C(m ，n)，则P(m ，0)，PA ＝m ＋3，PB ＝3－m.首先证明△ACP∽△ECH，推出AC CE ＝PC CH ＝AP HE ＝12，推出CH ＝2n ，EH ＝2m ＋6，再证明△DPB∽△DHE，推出PB EH ＝DP DH ＝n4n ＝14，可得3－m 2m ＋6＝14，求出m 即可解决问题；(2)由题意设抛物线的解析式为y ＝a(x ＋3)(x －5)，求出E 点坐标代入即可解决问题．【答案】解：(1)如图，作EF⊥y 轴于F ，DC 的延长线交EF 于H.设C(m ，n)，则P(m ，0)，PA ＝m ＋3，PB ＝3－m.∵EH ∥AP ，∴△ACP ∽△ECH ， ∴AC CE ＝PC CH ＝AP HE ＝12， ∴CH ＝2n ，EH ＝2m ＋6， ∵CD ⊥AB ，∴PC ＝PD ＝n ， ∵PB ∥HE ，∴△DPB ∽△DHE ， ∴PB EH ＝DP DH ＝n 4n ＝14， ∴3－m 2m ＋6＝14，∴m ＝1，∴P(1，0)； (2)由(1)可知，PA ＝4，HE ＝8，EF ＝9，连接OC ，在Rt △OCP 中， PC ＝OC 2－OP 2＝22， ∴CH ＝2PC ＝42，PH ＝62，∴E(9，62)，∵抛物线的对称轴为直线CD ，∴(－3，0)和(5，0)在抛物线上，设抛物线的解析式为y ＝a(x ＋3)(x －5)， 把E(9，62)代入得到a ＝28， ∴抛物线的解析式为y ＝28(x ＋3)(x －5)， 即y ＝28x 2－24x －1528.3．(2017呼和浩特中考)如图，点A ，B ，C ，D 是直径为AB 的⊙O 上的四个点，C 是劣弧BD ︵的中点，AC 与BD 交于点E.(1)求证：DC 2＝CE·AC；(2)若AE ＝2，EC ＝1，求证：△AOD 是正三角形；(3)在(2)的条件下，过点C 作⊙O 的切线，交AB 的延长线于点H ，求△ACH 的面积． 解：(1)∵C 是劣弧BD ︵的中点， ∴∠DAC ＝∠CDB， ∵∠ACD ＝∠DCE， ∴△ACD ∽△DCE ， ∴AC DC ＝CD CE， ∴DC 2＝CE·AC； (2)连接OC ，OD ， ∵AE ＝2，EC ＝1， ∴AC ＝3，∴DC 2＝CE·AC＝1×3＝3， ∴DC ＝ 3.∵C 是劣弧BD ︵的中点， ∴OC 平分∠DOB，BC ＝DC ＝ 3. ∵AB 是⊙O 的直径， ∴∠AC B ＝90°， ∴AB ＝AC 2＋BC 2＝23，∴OB ＝OC ＝OD ＝DC ＝BC ＝3， ∴△OCD ，△OBC 是正三角形， ∴∠COD ＝∠BOC＝∠OBC＝60°， ∴∠AOD ＝180°－2×60°＝60°. 又∵OA＝OD ， ∴△AOD 是正三角形； (3)∵CH 是⊙O 的切线， ∴OC ⊥CH. ∵∠COH ＝60°， ∴∠H ＝30°，∵∠BAC ＝90°－60°＝30°， ∴∠H ＝∠BAC， ∴AC ＝CH ＝3，∴OH ＝CH 2＋OC 2＝23， ∴AH ＝33，∴AH 上的高为BC·sin 60°＝32，∴△ACH 的面积＝12×33×32＝934.4．(2017云南中考)已知AB 是⊙O 的直径，PB 是⊙O 的切线，C 是⊙O 上的点，AC ∥OP ，M 是直径AB 上的动点，A 与直线CM 上的点连线距离的最小值为d ，B 与直线CM 上的点连线距离的最小值为f.(1)求证：PC 是⊙O 的切线； (2)设OP ＝32AC ，求∠CPO 的正弦值；(3)设AC ＝9，AB ＝15，求d ＋f 的取值范围．解：(1)连接OC ， ∵OA ＝OC ， ∴∠A ＝∠OCA， ∵AC ∥OP ，∴∠A ＝∠BOP，∠ACO ＝∠COP， ∴∠COP ＝∠BOP.∵PB 是⊙O 的切线，AB 是⊙O 的直径， ∴∠OBP ＝90°.在△POC 与△P OB 中，⎩⎪⎨⎪⎧OC ＝OB ，∠COP ＝∠BOP，OP ＝OP ，∴△COP ≌△BOP ， ∴∠OCP ＝∠OBP＝90°. 又∵OC 为⊙O 的半径， ∴PC 是⊙O 的切线； (2)过O 作OD⊥AC 于D ，∴∠ODC ＝∠OCP＝90°，CD ＝12AC ，∵∠DCO ＝∠COP， ∴△ODC ∽△PCO ， ∴CD OC ＝OC PO， ∴CD ·OP ＝OC 2. ∵OP ＝32AC ，∴AC ＝23OP ，∴CD ＝13OP ，∴13OP ·OP ＝OC 2， ∴OC OP ＝33， ∴sin ∠CPO ＝OC OP ＝33；(3)连接BC ， ∵AB 是⊙O 的直径， ∴AC ⊥BC ， ∵AC ＝9，AB ＝15， ∴BC ＝AB 2－AC 2＝12，当M 与A 重合时，d ＝0，f ＝BC ＝12， ∴d ＋f ＝12，当M 与B 重合时，d ＝9，f ＝0， ∴d ＋f ＝9，∴d ＋f 的取值范围是：9≤d＋f≤12.。

中考数学复习资料第一章实数考点一、数的观点及分1、数的分（3 分）数有理数正有理数零有理数正无理数有限小数和无穷循小数无理数无穷不循小数无理数2、无理数在理解无理数，要抓住“无穷不循” 一之，起来有四：（ 1）开方开不尽的数，如7,32 等；（ 2）有特定意的数，如周率π，或化后含有π的数，如π+8等；3（3）有特定构的数，如 0.1010010001 ⋯等；（4）某些三角函数，如 sin60o等考点二、数的倒数、相反数和1、相反数（3分）数与它的相反数一数（只有符号不一样的两个数叫做互相反数，零的相反数是零），从数上看，互相反数的两个数所的点对于原点称，假如 a 与 b 互相反数，有a+b=0， a=—b，反之亦成立。

2、一个数的就是表示个数的点与原点的距离，|a|≥0。

零的它自己，也可当作它的相反数，若 |a|=a， a≥0；若 |a|=-a， a≤0。

正数大于零，数小于零，正数大于全部数，两个数，大的反而小。

3、倒数假如 a 与 b 互倒数，有ab=1，反之亦成立。

倒数等于自己的数是考点三、平方根、算数平方根和立方根（3—10 分）1 和-1。

零没有倒数。

1、平方根假如一个数的平方等于a，那么个数就叫做 a 的平方根（或二次方跟）一个数有两个平方根，他互相反数；零的平方根是零；数没有平方根。

正数 a 的平方根做“ a ”。

2、算平方根正数 a 的正的平方根叫做 a 的算平方根，作“ a ”。

正数和零的算平方根都只有一个，零的算平方根是零。

a （ a）a0a 2a；注意 a 的两重非性：- a（a <0）a03、立方根假如一个数的立方等于a，那么个数就叫做 a 的立方根（或 a 的三次方根）。

一个正数有一个正的立方根；一个数有一个的立方根；零的立方根是零。

注意： 3a3a ，这说明三次根号内的负号能够移到根号外面。

考点四、科学记数法和近似数（3—6 分）1、有效数字一个近似数四舍五入到哪一位，就说它精准到哪一位，这时，从左边第一个不是零的数字起到右边精准的数位止的全部数字，都叫做这个数的有效数字。

第一节 一次方程(组)及应用,遵义五年中考命题规律)填空题，解答的解法，还牵涉到列,遵义五年中考真题及模拟)一元一次方程及其解法1．(2017遵义中考)明代数学家程大位的《算法统宗》中有这样一个问题(如图)，其大意为：有一群人分银子，如果每人分七两，则剩余四两；如果每人分九两，则还差八两，请问：所分的银子共有__46__两．(注：明代时1斤＝16两，故有“半斤八两”这个成语)2．(2016遵义中考)六一期间，小明、小亮等同学随家长一同到某公园游玩，如图是购买门票时，小明与他爸爸的对话，设去了x 个成人，则根据图中的信息，下面所列方程中正确的是( A )A ．40x ＋20(12－x)＝400B ．40(12－x)＋20x ＝400C ．24(12－x)＋20x ＝400D ．24x ＋12(12－x)＝4003．(2016遵义十一中一模)希望中学九年级(1)班共有学生49人，当该班少一名男生时，男生的人数恰好为女生人数的一半．设该班有男生x 人，则下列方程中，正确的是( A )A ．2(x －1)＋x ＝49B ．2(x ＋1)＋x ＝49C ．x －1＋2x ＝49D ．x ＋1＋2x ＝49二元一次方程组及其解法4．(2016遵义二中二模)小明在解关于x ，y 的二元一次方程组⎩⎪⎨⎪⎧x ＋y ＝△， 2x －3y ＝5时，解得⎩⎪⎨⎪⎧x ＝4， y ＝⊗，则△和⊗代表的数分别是( B )A ．△＝1，⊗＝5B ．△＝5，⊗＝1C ．△＝－1，⊗＝3D ．△＝3，⊗＝－15．(2013遵义中考)解方程组：⎩⎪⎨⎪⎧x －2y ＝4，① 2x ＋y －3＝0.②解：由①得x ＝2y ＋4.将x ＝2y ＋4代入②，得2(2y ＋4)＋y －3＝0.解得y ＝－1.∴x＝2y ＋4＝2×(－1)＋4＝2.∴方程组的解是⎩⎪⎨⎪⎧x ＝2，y ＝－1.6．(2016遵义二中三模)某地为了打造风光带，将一段长为360 m 的河道整治任务交由甲、乙两个工程队先后接力完成，共用时20天，已知甲工程队每天整治24 m ，乙工程队每天整治16 m ．求甲、乙两个工程队分别整治了多长的河道．解：设甲工程队整治河道x m ，则乙工程队整治河道(360－x)m .由题意，得x 24＋360－x16＝20，解得x ＝120.当x ＝120时，360－x ＝240.答：甲工程队整治河道 120 m ，乙工程队整治河道240 m .7．(2017改编)已知关于x ，y 的二元一次方程ax ＋by ＝10(ab≠0)的两个解分别为⎩⎪⎨⎪⎧x ＝－1， y ＝2和⎩⎪⎨⎪⎧x ＝－2，y ＝－4，求1－a 2＋4b 2的值．解：把⎩⎪⎨⎪⎧x ＝－1， y ＝2代入方程ax ＋by ＝10中，得－a ＋2b ＝10，把⎩⎪⎨⎪⎧x ＝－2，y ＝－4代入方程ax ＋by ＝10中，得－a －2b ＝5，∴(－a ＋2b)(－a －2b)＝a 2－4b 2＝50，∴1－a 2＋4b 2＝1－50＝－49.一元一次方程组的应用8．(2017遵义中考)为厉行节能减排，倡导绿色出行，今年3月以来．“共享单车”(俗称“小黄车”)公益活动登陆我市中心城区，某公司拟在甲、乙两个街道社区投放一批“小黄车”，这批自行车包括A ，B 两种不同款型，请回答下列问题：问题1：单价该公司早期在甲街区进行了试点投放，共投放A ，B 两型自行车各50辆，投放成本共计7 500元，其中B 型车的成本单价比A 型车高10元，A ，B 两型自行车的单价各是多少？问题2：投放方式该公司决定采取如下投放方式：甲街区每1 000人投放a 辆“小黄车”，乙街区每1 000人投放8a ＋240a 辆“小黄车”，按照这种投放方式，甲街区共投放1 500辆，乙街区共投放1 200辆，如果两个街区共有15万人，试求a 的值．解：问题1：设A 型车的成本单价为x 元，则B 型车的成本单价为(x ＋10)元．依题意，得 50x ＋50(x ＋10)＝7 500， 解得x ＝70，∴x ＋10＝80，答：A 、B 两型自行车的单价分别是70元和80元； 问题2：由题意可得1 500a ×1 000＋1 2008a ＋24a×1 000＝150 000，解得a ＝15.经检验，a ＝15是所列方程的解．故a 的值为15.9．(2016遵义中考)上网流量、语音通话是手机通信消费的两大主体．日前，某通信公司推出消费优惠新招——“定制套餐”．消费者可根据实际情况自由定制每月上网流量与语音通话时间，并按照二者的阶梯资费标准缴纳通信费．下表是流量与语音的阶梯定价标准．0.[小提示：阶梯定价收费计算方法，如600 min 语音通话费＝0.15×500＋0.12×(600－500)＝87元] (1)甲定制了600 MB 的月流量，花费48元；乙定制了2 GB 的月流量，花费120.4元．求a ，b 的值；(注：1GB ＝1 024 MB )(2)甲的套餐费用为199元，其中含600 MB 的月流量；丙的套餐费用为244.2元，其中包含 1 GB 的月流量．二人均定制了超过1 000 min 的每月通话时间，并且丙的语音通话时间比甲多300 min ，求m 的值．解：(1)由题意，得⎩⎪⎨⎪⎧100a ＋（500－100）×0.07＋（600－500）b ＝48，100a ＋（500－100）×0.07＋（1 024×2－500）b ＝120.4， 解得⎩⎪⎨⎪⎧a ＝0.15， b ＝0.05；(2)设甲每月定制x(x ＞100)min 通话时间，则丙定制(x ＋300)min 通话时间，丙定制了1 GB 月流量套餐需花费100×0.15＋(500－100)×0.07＋(1 024－500)×0.05＝69.2(元)，由题意得⎩⎪⎨⎪⎧48＋500×0.15＋（1 000－500）×0.12＋（x －1 000）m ＝199，69.2＋500×0.15＋（1 000－500）×0.12＋（x ＋300－1 000）m ＝244.2. ∴m ＝0.08.,中考考点清单)方程、方程的解与解方程1．含有未知数的__等式__叫方程．2．使方程左右两边相等的__未知数__的值叫方程的解． 3．求方程__解__的过程叫解方程．等式的基本性质4．性质1：等式两边同时加上(或减去)同一个数或同一个式子，所得的结果仍__相等__．如果a ＝b ，那么a±c __＝__b±c.性质2：等式两边同时乘以(或除以)同一个数(除数不为0)，所得结果仍__相等__，如果a ＝b ，那么ac ＝bc(c≠0)，a c ＝bc(c≠0)．一次方程(组)5．概念与解法 (1)一元一次方程概念：含有__一个__未知数且未知数的次数是__1__，这样的方程叫做一元一次方程．解法：解一元一次方程的一般步骤：①去分母；②去括号；③移项；④合并同类项；⑤系数化为1. (2)二元一次方程概念：含有两个__未知数__，并且含有未知数的项的__次数__都是1的方程叫做二元一次方程． 解法：一般需找出满足方程的整数解即可． (3)二元一次方程组概念：两个__二元一次方程__所组成的一组方程，叫做二元一次方程组．解法：解二元一次方程组的基本思路是__消元__．基本解法有：__代入__消元法和__加减__消元法． (4)三元一次方程组概念：三个一次方程组成的含有三个未知数的一组方程叫三元一次方程组． 解法：解三元一次方程组的基本思想是：三元――→转化二元――→转化一元一次方程． 【温馨提示】(1)解一元一次方程去分母时，常数项不要漏乘，移项一定要变号；(2)二元一次方程组的解应写成⎩⎪⎨⎪⎧x ＝a ，y ＝b 的形式.列方程(组)解应用题的一般步骤6．(1)审：审清题意，分清题中的已知量、未知量；(2)设：设__未知数__，设其中某个量为未知数，并注意单位，对含有两个未知数的问题，需设两个未知数； (3)列：弄清题意，找出__相等关系__；根据__相等关系__，列方程(组)； (4)解：解方程(组)；(5)验：检验结果是否符合题意； (6)答：答题(包括单位)．【方法点拨】一次方程(组)用到的思想方法：(1)消元思想：将二元一次方程组通过消元使其变成一元一次方程；(2)整体思想：在解方程时结合方程的结构特点，灵活采取整体思想，使整个过程简捷；(3)转化思想：解一元一次方程最终要转化成ax ＝b ；解二元一次方程组先转化成一元一次方程； (4)数形结合思想：利用图形的性质建立方程模型解决几何图形中的问题； (5)方程思想：利用其他知识构造方程解决问题．,中考重难点突破)一元一次方程及解法【例1】(1)(2017瑞安中考模拟)关于x 的方程2x －m3＝1的解为2，则m 的值是( )A ．2.5B ．1C ．－1D ．3 (2)(河池中考)解方程：2x ＋13－5x －16＝1.【解析】(1)把x ＝2代入方程，得4－m3＝1，解得m ＝1.(2)按去分母→去括号→移项→合并同类项→系数化为1来解．【答案】(1)B ；(2)x ＝－3.1．(2017滨州中考)解方程：2－2x ＋13＝1＋x2.解：去分母，得12－2(2x ＋1)＝3(1＋x)， 去括号，得12－4x －2＝3＋3x ， 移项、合并同类项，得7x ＝7， 系数化为1，得x ＝1.二元一次方程组及解法【例2】(2017宝安中考)若方程mx ＋ny ＝6的两个解是⎩⎪⎨⎪⎧x ＝1， y ＝1和⎩⎪⎨⎪⎧x ＝2，y ＝－1，则m ，n 的值为( )A .⎩⎪⎨⎪⎧m ＝4， n ＝2B .⎩⎪⎨⎪⎧m ＝2， n ＝4C .⎩⎪⎨⎪⎧m ＝－2， n ＝－4D .⎩⎪⎨⎪⎧m ＝－4，n ＝－2 【解析】此题考查二元一次方程的解，方程的解即为能使方程左右两边相等的未知数的值． 【答案】A2．(2017天门中考)已知⎩⎪⎨⎪⎧x ＝2， y ＝1是二元一次方程组⎩⎪⎨⎪⎧mx ＋ny ＝8， nx －my ＝1的解，则2m －n 的算术平方根是( B ) A ．4 B ．2 C . 2 D ．±23．(2017乐山中考)二元一次方程组x ＋y 2＝2x －y3＝x ＋2的解是__⎩⎪⎨⎪⎧x ＝－5， y ＝－1__．一次方程(组)的应用【例3】(2017宁阳中考)某服装店用6 000元购进A ，B 两种新式服装，按标价售出后可获得毛利润3 800元(毛利润＝售价－进价)，这两种服装的进价，标价如表所示．(1)求这两种服装各购进的件数；(2)如果A 种服装按标价的八折出售，B 种服装按标价的七折出售，那么这批服装全部售完后，服装店比按标价出售少收入多少元？【解析】(1)设A 种服装购进x 件，B 种服装购进y 件，由总价＝单价×数量，利润＝售价－进价建立方程组求出其解即可；(2)分别求出打折后的价格，再根据少收入的利润＝总利润－打折后A 种服装的利润－打折后B 种服装的利润，求出其解即可．【答案】解：(1)设A 种服装购进x 件，B 种服装购进y 件．由题意，得⎩⎪⎨⎪⎧60x ＋100y ＝6 000， （100－60）x ＋（160－100）y ＝3 800， 解得⎩⎪⎨⎪⎧x ＝50，y ＝30.答：A 种服装购进50件，B 种服装购进30件； (2)由题意，得3 800－50(100×0.8－60)－30(160×0.7－100) ＝3 800－1 000－360 ＝2 440(元)．答：服装店比按标价售出少收入2 440元．4．(2017新泰中考模拟)某商场经销一种商品，由于进货时价格比原进价降低了 6.4%，使得利润率增加了8个百分点，那么经销这种商品原来的利润率是__17__%.(注：利润率＝销售价－进价进价×100%)5．(安顺中考)某校住校生宿舍有大小两种寝室若干间，据统计该校高一年级男生740人，使用了55间大寝室和50间小寝室，正好住满；女生730人，使用了大寝室50间和小寝室55间，也正好住满，求该校的大小寝室每间各住多少人．解：设该校大寝室每间住x 人，小寝室每间住y 人．由题意，得⎩⎪⎨⎪⎧55x ＋50y ＝740， 50x ＋55y ＝730，解得⎩⎪⎨⎪⎧x ＝8， y ＝6. 答：该校大寝室每间住8人，小寝室每间住6人．。

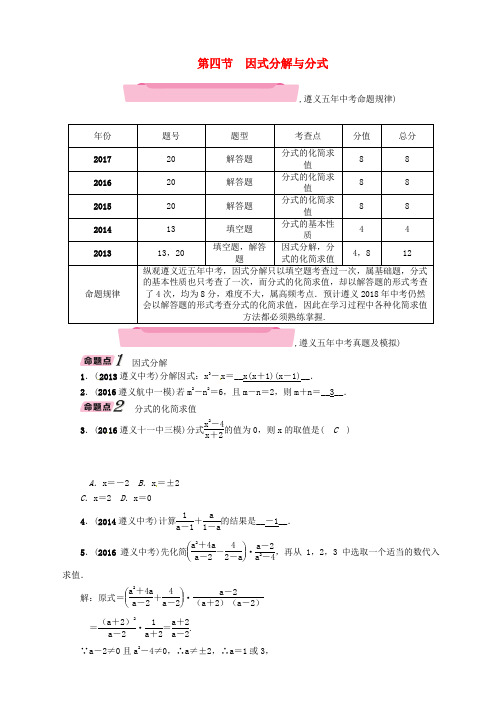
第四节因式分解与分式,遵义五年中考命题规律),遵义五年中考真题及模拟)因式分解1．(2013遵义中考)分解因式：x3－x＝__x(x＋1)(x－1)__．2．(2016遵义航中一模)若m2－n2＝6，且m－n＝2，则m＋n＝__3__．分式的化简求值3．(2016遵义十一中三模)分式x2－4x＋2的值为0，则x的取值是( C)A．x＝－2 B．x＝±2C．x＝2 D．x＝04．(2014遵义中考)计算1a－1＋a1－a的结果是__－1__．5．(2016遵义中考)先化简⎝⎛⎭⎪⎫a2＋4aa－2－42－a·a－2a2－4，再从1，2，3中选取一个适当的数代入求值．解：原式＝⎝⎛⎭⎪⎫a2＋4aa－2＋4a－2·a－2（a＋2）（a－2）＝（a＋2）2a－2·1a＋2＝a＋2a－2.∵a－2≠0且a2－4≠0，∴a≠±2，∴a＝1或3，当a ＝1时，原式＝－3；当a ＝3时，原式＝5. 6．(2015遵义中考)先化简，再求值： 3a －3a ÷a 2－2a ＋1a 2－aa －1，其中a ＝2. 解：化简得2a a －1，当a ＝2时，原式＝2×22－1＝4.7．(2013遵义中考)已知实数a 满足a 2＋2a －15＝0，求1a ＋1－a ＋2a 2－1÷（a ＋1）（a ＋2）a 2－2a ＋1的值．解：原式＝1a ＋1－a ＋2（a ＋1）（a －1）·（a －1）2（a ＋1）（a ＋2）＝1a ＋1－a －1（a ＋1）2＝2（a ＋1）2，∵a 2＋2a －15＝0，∴(a ＋1)2＝16，∴原式＝216＝18.8．(2016汇川升学模拟)先化简，再求值：⎝ ⎛⎭⎪⎫1x －1－1x ＋1÷x ＋2x 2－1，其中x 是不等式2(3－x)＋1≥3的正整数解．解：原式＝2（x －1）（x ＋1）×（x ＋1）（x －1）x ＋2＝2x ＋2，解不等式2(3－x)＋1≥3，得x≤2. ∵x 为正整数，∴x ＝1或2. 又∵(x－1)(x ＋1)≠0且x ＋2≠0， ∴x ≠±1且x≠－2， ∴x ＝2.∴当x ＝2时，原式＝22＋2＝12.9．(2017遵义中考)化简分式：⎝ ⎛⎭⎪⎫x 2－2x x 2－4x ＋4－3x －2÷x －3x 2－4，并从1，2，3，4这四个数中取一个合适的数作为x 的值代入求值．解：原式＝⎣⎢⎡⎦⎥⎤x （x －2）（x －2）2－3x －2÷x －3x 2－4＝⎝⎛⎭⎪⎫x x －2－3x －2÷x －3x 2－4＝x －3x －2×（x ＋2）（x －2）x －3＝x ＋2，∵x 2－4≠0且x －3≠0， ∴x ≠2且x≠－2且x≠3，∴x 可取1或4，当x ＝1时，原式＝3；当x ＝4时，原式＝6.,中考考点清单)因式分解的概念1．把一个多项式化成几个__整式__的__积__的形式，这种变形叫做把这个多项式因式分解．2．分解因式与整式乘法的关系：多项式__因式分解整式乘法__整式的积．因式分解的基本方法3．提公因式法：ma ＋mb ＋mc ＝__m(a ＋b ＋c)__． 4．公式法：(1)平方差公式：a 2－b 2＝__(a ＋b)(a －b)__； (2)完全平方公式：a 2±2ab ＋b 2＝__(a±b)2__． 【方法点拨】因式分解的一般步骤：(1)如果多项式各项有公因式，应先提取公因式；(2)如果各项没有公因式，可以尝试使用公式法来分解因式； (3)检查因式分解是否彻底，必须分解到每一个因式不能再分解为止．整式的运算5．分式：形如__AB __(A ，B 是整式，且B 中含有__字母__，B ≠0)的式子叫分式，其中A 叫分子，B 叫分母．6．与分式有关的“五个条件”的字母表示： (1)分式AB 无意义时，B__＝0__；(2)分式AB有意义时，B__≠0__；(3)分式AB的值为零时，A__＝0__且B__≠0__；(4)分式AB 的值为正时，A ，B__同号__，即⎩⎪⎨⎪⎧A ＞0， B ＞ 0或⎩⎪⎨⎪⎧A ＜0，B ＜ 0；(5)分式AB 的值为负时，A ，B__异号__，即⎩⎪⎨⎪⎧A ＞0， B ＜ 0或⎩⎪⎨⎪⎧A ＜0， B ＞ 0.7．最简分式：分子与分母没有__公因式__的分式． 8．有理式：__整式__和__分式__统称为有理式．分式的基本性质9.a×m b×m ＝__a b __，a÷m b÷m ＝__ab__．(m≠0) 10．通分的关键是确定几个分式的__最简公分母__，约分的关键是确定分式的分子、分母的__最大公因式__．分式运算11.b a ±c a ＝b±c a ；异分母分式加减通过通分转化为__同分母分式__加减，即b a ±d c ＝bc±ad ac. 12.b a ×d c ＝__bd ac __，b a ÷d c ＝__bc ad __，⎝ ⎛⎭⎪⎫a b n ＝__a nb n __．13．分式的混合运算：在分式的混合运算中，应先算__乘方__，再算__乘除__，最后进行__加减运算__，遇到括号，先算__括号里面的__．分式运算的结果要化成整式或最简分式．【方法点拨】分式化简求值题的一般步骤：(1)若有括号的，先计算括号内的分式运算，括号内如果是异分母加减运算时，需将异分母分式通分化为同分母分式运算，然后将分子合并同类项，把括号去掉．简称：去括号；(2)若有除法运算的，将分式中除号(÷)后面的式子分子分母颠倒，并把这个式子前的“÷”变为“×”，保证几个分式之间除了“＋”“－”就只有“×”或“·”，简称：除法变乘法；(3)利用因式分解、约分来计算分式乘法运算；(4)最后按照式子顺序，从左到右计算分式加减运算，直到化为最简形式；(5)将所给数值代入求值，代入数值时要注意使原分式有意义(即使原分式分母不为0)．,中考重难点突破)因式分解【例1】(1)(2016遵义中考模拟)下面因式分解正确的是( )A ．x 2＋2x ＋1＝x(x ＋2)＋1B ．(x 2＋4)x ＝x 3－4xC ．ax ＋bx ＝(a ＋b)xD ．m 2－2mn ＋n 2＝(m ＋n)2(2)(2017常德中考)下列各式由左到右的变形中，属于分解因式的是( )A ．a(m ＋n)＝am ＋anB ．a 2－b 2－c 2＝(a －b)(a ＋b)－c 2C ．10x 2－5x ＝5x(2x －1)D ．x 2－16＋6x ＝(x ＋4)(x －4)＋6x【解析】(1)紧扣因式分解的概念来判断；(2)因式分解的步骤是：“一提二套三彻底”，即分解到不能再分解为止．【答案】(1)C ；(2)C1．(1)(2017安顺中考)分解因式：x 3－9x ＝__x(x ＋3)(x －3)__；(2)分解因式：a 2b ＋2ab 2＋b 3＝__b(a ＋b)2__．分式的概念及其基本性质【例2】(1)(2016遵义升学样卷)当分式|x|－2（x ＋2）2的值为0时，x 的值是( )A ．0B ．2C ．－2D ．2或－2(2)(2017重庆中考)若分式1x －3有意义，则x 的取值范围是( ) A ．x ＞3 B ．x ＜3 C ．x ≠3 D ．x ＝3【解析】熟练掌握分式有意义的条件以及分式的值为0的条件． 【答案】(1)B ；(2)C2．(2017原创)式子x －1x ＋3÷xx ＋2有意义的条件为__x≠－3且x≠0且x≠－2__．分式的化简求值【例3】(2017达州中考)设A ＝a －21＋2a ＋a 2÷⎝ ⎛⎭⎪⎫a －3a a ＋1. (1)化简A ；(2)当a ＝3时，记此时A 的值为f(3)；当a ＝4时，记此时A 的值为f(4)；…解关于x 的不等式：x －22－7－x4≤f(3)＋f(4)＋…＋f(11)，并将解集在数轴上表示出来．【解析】(1)根据分式的除法和减法可以解答本题；(2)根据(1)中的结果可以解答题目中的不等式并在数轴上表示出不等式的解集．【答案】解：(1)A ＝a －2（a ＋1）2÷a （a ＋1）－3a a ＋1 ＝a －2（a ＋1）2·a ＋1a （a －2） ＝1a （a ＋1）＝1a 2＋a；(2)∵a＝3时，f(3)＝132＋3＝112＝13×14，a ＝4时，f(4)＝142＋4＝120＝14×15，a ＝5时，f(5)＝152＋5＝130＝15×16，……∴x －22－7－x 4≤f(3)＋f(4)＋…＋f(11)，即x －22－7－x 4≤13×4＋14×5＋…＋111×12，∴x －22－7－x 4≤13－14＋14－15…＋111－112，∴x －22－7－x 4≤13－112，∴x －22－7－x 4≤14，解得x≤4，∴原不等式的解集是x≤4，在数轴上表示如图所示．3．(2017绥化中考)计算：⎝⎛⎭⎪⎫a a ＋b ＋2b a ＋b ·a a ＋2b＝__a a ＋b __.4．(2016遵义十一中二模)若1a ＋a ＝3，则⎝ ⎛⎭⎪⎫1a －a 2的值是__5____．5．(2016遵义升学三模)先化简，再求值：⎝ ⎛⎭⎪⎫2x －1x －1÷1x 2－x ，其中(x －2)2＋2(x －2)＋1＝0.解：原式＝2x －2－x x （x －1）·x(x－1)＝x －2，由(x －2)2＋2(x －2)＋1＝0得，x －2＝－1， ∴原式＝－1.。

第五节二次根式,遵义五年中考命题规律),遵义五年中考真题及模拟)二次根式的概念1．(2015遵义中考)使二次根式5x－2有意义的x的取值范围是__x≥25__．二次根式的运算2．(2017遵义中考)8＋2＝__．3．(2016遵义中考)计算2－18的结果是．4．(2014遵义中考)计算：27＋3＝．5．(2016遵义一中一模)函数y＝x＋3x－1中自变量x的取值范围是( D)A．x≥－3 B．x≥3C．x≥0且x≠1 D．x≥－3且x≠16．(2016遵义十一中二模)与1＋5最接近的整数是( B)A．4 B．3 C．2 D．1,中考考点清单)1平方根、算术平方根1．若x 2＝a ，则x 叫a 的__平方根__．当a≥0时，a 是a 的__算术平方根__．正数b 的平方根记作__.a 是一个__非负__数．只有__非负__数才有平方根．立方根及性质2．若x 3＝a ，则x 叫a 的__立方根__，求一个数的立方根的运算叫__开立方__；任一实数a 的立方根记作；3a 3＝__a__，(3a)3＝__a__，3－a ＝．二次根式的概念3．(1)形如a(__a≥0__)的式子叫二次根式，而a 为二次根式的条件是__a≥0__； (2)满足下列两个条件的二次根式叫最简二次根式： ①被开方数的因数是__整数__，因式是__整式__； ②被开方数中不含有__开得尽方的因数或因式__．二次根式的性质4．(1)ab ＝b ≥0)；a b ＝b ＞0)； (2)(a)2＝__a__(a__≥__0)；(3)a 2＝|a|＝⎩⎪⎨⎪⎧ a （a≥0），－a （a ＜0）.二次根式的性质5．(1)二次根式的加减：二次根式相加减，先把各个二次根式化成__最简二次根式__，再把__同类二次根式__分别合并． (2)二次根式的乘法：a ·b ＝b ≥0)． (3)二次根式的除法：a b ＝b>0)． (4)二次根式的估值：二次根式的估算，一般采用“夹逼法”确定其值所在范围．具体地说，先对二次根式平方，找出与平方后所得的数__相邻__的两个能开得尽方的整数，对其进行__开方__，即可确定这个二次根式在哪两个整数之间．(5)在二次根式的运算中，实数的运算性质和法则同样适用．二次根式的混合运算顺序是：先算__乘除__，后算__加减__，有括号时，先算括号内的(或先去括号)．【温馨提示】(1)若a 是二次根式，则a ≥0(a≥0)，这个性质称为二次根式的双重非负性；(2)二次根式运算的结果可以是数或整式，也可以是最简二次根式，如果二次根式的运算结果不是最简二次根式，必须化为最简二次根式．,中考重难点突破)平方根、算术平方根与立方根【例1】(2017南京中考)若方程(x －5)2＝19的两根为a 和b ，且a ＞b ，则下列结论中正确的是( )A ．a 是19的算术平方根B ．b 是19的平方根C ．a －5是19的算术平方根D ．b ＋5是19的平方根【解析】本题考查平方根的基本定义． 【答案】C1．若单项式2x 2y a ＋b与－xa －2b y 5的和仍然是一个单项式，则a －5b 的立方根为( A )A ．－1B ．1C ．0D ．22．(2017蚌埠中考)已知2a －1的平方根是±3，3a ＋2b ＋4的立方根是3，求a ＋b 的平方根．解：由题意，得⎩⎪⎨⎪⎧2a －1＝9， 3a ＋2b ＋4＝27，解得⎩⎪⎨⎪⎧a ＝5，b ＝4.∴±a ＋b ＝ ±5＋4＝±3. 故a ＋b 的平方根为±3.3．(2017北流中考)已知a －1与5－2a 是m 的平方根，求a 和m 的值． 解：①当a －1与5－2a 是同一个平方根时， a －1＝5－2a ， 解得a ＝2， 此时，m ＝12＝1；②当a －1与5－2a 是两个平方根时， a －1＋5－2a ＝0， 解得a ＝4， 此时m ＝(4－1)2＝9.二次根式的概念与性质【例2】(1)(2017新区一模)若3x －6在实数范围内有意义，则x 的取值范围是________．(2)(2017张家界中考)实数a ，b 在数轴上的位置如图所示，且|a|＞|b|，则化简a 2－|a ＋b|的结果为( )A ．2a ＋bB ．－2a ＋bC ．bD ．ab【解析】(1)根据式子a 有意义的条件为a≥0得到3x －6≥0，然后解不等式即可；(2)化简a 2时，要先判断a 的取值范围，当a≥0时，a 2＝a ，当a<0时，a 2＝－a.【答案】(1)x≥2；(2)C4．(2017静安中考)下列二次根式里，被开方数中各因式的指数都为1的是( B )A .x 2y 2B .x 2＋y 2C .（x ＋y ）2D .xy 25．(2017围场中考)下列式子一定是二次根式的是( C )A .x －1B .xC .x 2＋2D .x 2－26．(2017枣庄中考)实数a ，b 在数轴上对应点的位置如图所示，化简|a|＋（a －b ）2的结果是( A )A ．－2a ＋bB ．2a －bC ．－bD ．b二次根式的运算【例3】(1)(2017澧县中考)下列运算正确的是( )A .10·10＝210B ．(a 2)3＝a 5C ．5a 4－4a 3＝aD ．3a 2＋4a 2＝7a 2(2)(2017农安中考)下列计算，正确的是( )A ．(2a 2b 3)2＝2a 4b 5B ．(a －b)2＝a 2－b 2C .x 2＋y 2x ＋y＝x ＋y D ．(x ＋y)(x －y)＝x －y 【解析】(1)A .10×10＝10，原式计算错误，故本选项错误；B .(a 2)3＝a 6，原式计算错误，故本选项错误；C .5a 4与4a 3不是同类项，不能直接合并，故本选项错误；D .3a 2＋4a 2＝7a 2，计算正确，故本选项正确．(2)A .(2a 2b 3)2＝4a 4b 6，错误；B .(a －b)2＝－2ab ＋a 2＋b 2，错误；C .x 2＋y2x ＋y为最简分式，错误；D .符合平方差公式，正确．【答案】(1)D ；(2)D7．(2017滨海中考)计算27－8·23的结果是( C ) A . 3 B .43 3 C .533 D ．2 3 8．(2017沂源中考)下列计算正确的是( C )A ．23＋33＝5 6B ．(2＋1)(1－2)＝1C ．(xy)－1⎝ ⎛⎭⎪⎫12xy 2＝14xyD ．－(－a)4÷a 2＝a 29．(2017陕西中考)计算：(－2)×6＋|3－2|－⎝ ⎛⎭⎪⎫12－1.解：原式＝－23＋2－3－2＝－3 3.10．(2017临沂中考)计算： 8÷2＋(2－ 2 014)0－(－1)2 014＋|2－2|＋⎝ ⎛⎭⎪⎫－12－2.解：原式＝2＋1－1＋2－2＋4 ＝8－ 2.11．(2017中山中考)计算： (1)3223÷1225×⎝ ⎛⎭⎪⎫－1415； 解：原式＝－15； (2)⎝ ⎛⎭⎪⎫18＋32÷6×12. 解：原式＝6＋62. 12．解方程：x ＋2x －1＋x －2x －1＝x －1.解：方程两边同时平方，得2x ＋2x 2－（2x －1）2＝x 2－2x ＋1， 变形，得2x ＋2x 2－4x ＋4＝x 2－2x ＋1， 2x ＋2（x －2）2＝x 2－2x ＋1， 2x ＋2|x －2|＝x 2－2x ＋1， ∵x －1≥0，即x≥1.∴①当1≤x＜2时，原方程化简为： 2x ＋2(2－x)＝x 2－2x ＋1， 即x 2－2x －3＝0，解得x 1＝－1，x 2＝3(都不符合题意，舍去)， ②当x≥2时，原方程化简为： 2x ＋2(x －2)＝x 2－2x ＋1， 即x 2－6x ＋5＝0，解得x 1＝1，x 2＝5(x ＝1不符合题意，舍去)， 综上，原方程的解为x ＝5.教后反思：____________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ______________________________________________________________________ ________________________________________________________________________。