单元滚动检测卷(九)

单元滚动检测卷(十)[测试范围：第十四单元时间：120分钟分值：150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题，每小题4分，共40分．请选出各小题中唯一的正确选项，不选、多选、错选，均不得分)1．下列调查适合作普查的是(D) A．了解在校大学生的主要娱乐方式B．了解宁波市居民对废电池的处理情况C．日光灯管厂要检测一批灯管的使用寿命D．对甲型H1N1流感患者的同一车厢乘客进行医学检查【解析】A、B项因为数目太大，而不适合进行普查，只能用抽查，C、因具有破坏性，也只能采用抽查的方式．D、了解某甲型H1N1流感患者同一车厢乘客的健康状况，精确度要求高、事关重大，必须选用普查．2．小明调查了本班同学最喜欢的课外活动项目，并作出如图10－1所示的扇形统计图，则从图中可以直接看出的信息是(D)图10－1A．全班总人数B．喜欢篮球活动的人数最多C．喜欢各种课外活动的具体人数D．喜欢各种课外活动的人数占本班总人数的百分比【解析】A、不能直接表示出总人数，故本选项错误；B、喜欢电脑的人数最多，故本选项错误；C、喜欢各种课外活动的比例可以直接得到，但具体人数不能确定，故本选项错误；D、正确．3．某次考试中，某班级的数学成绩统计图如图10－2所示，下列说法错误的是(D)图10－2A．得分在70～80分之间的人数最多B．该班的总人数为40C．得分在90～100分之间的人数最少D．及格(≥60分)人数是26【解析】A、得分在70～80分之间的人数最多，故正确；B、2＋4＋8＋12＋14＝40(人)，故该班的总人数为40人，所以正确；C、得分在90～100分之间的人数最少，有2人，故正确；D、40－4＝36(人)，及格(≥60分)人数是36人，故D错误，故选D.4．下列数据是2013年3月7日6点公布的中国六大城市的空气污染指数情况：) A．164和163B．105和163C．105和164 D．163和1645．下列说法正确的是(B) A．“打开电视机，正在播足球赛”是必然事件B．甲组数据的方差S甲2＝0.24，乙组数据的方差S乙2＝0.03，则乙组数据比甲组数据稳定C．一组数据2，4，5，5，3，6的众数和中位数都是5D．“掷一枚硬币正面朝上的概率是12”，表示每抛掷硬币2次就有1次正面朝上6．小伟5次引体向上的测试成绩(单位：个)分别为16，18，20，18，18，对此成绩描述错误的是( C )A ．平均数为18B ．众数为18C ．方差为0D ．极差为47．学生甲与学生乙玩一种转盘游戏．如图10－3是两个完全相同的转盘，每个转盘被分成面积相等的四个区域，分别用数字“1”、“2”、“3”、“4”表示．固定指针，同时转动两个转盘，任其自由停止，若两指针所指数字的积为奇数，则甲获胜；若两指针所指数字的积为偶数，则乙获胜；若指针指向扇形的分界线，则都重转一次．在该游戏中乙获胜的概率是( C )图10－3A.14B.12C.34D.56【解析】 所有出现的情况如下，共有16种情况，积为偶数的有12种情况，所以在该游戏中乙获胜的概率为1216＝34，故选C.8．在一个不透明的袋中装有编号为0，1，2，3的四个质地均匀、大小相同的小球，从中随机取出一个小球，取出编号为1的小球的概率为 ( C )A.12B.13C.14D ．1【解析】 由题意可知，4个小球中1个编号为1，所以取出编号为1的小球的概率为14.9．“服务他人，提升自我”，七一学校积极开展志愿者服务活动，来自初三的5名同学(三男两女)成立了“交通秩序维护”小分队，若从该小分队中任选两名同学进行交通秩序维护，则恰好是一男一女的概率是( D )A.16B.15C.25D.3510．如图10－4，在平面直角坐标系中，点A 1，A 2在x 轴上，点B 1，B 2在y 轴上，其坐标分别为A 1(1，0)，A 2(2，0)，B 1(0，1)，B 2(0，2)，分别以A 1，A 2，B 1，B 2其中的任意两点和点O 为顶点作三角形，所作三角形是等腰三角形的概率是( D )图10－4A.34B.13C.23D.12第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题，每小题5分，共30分) 11．若数据2，3，－1，7，x 的平均数为2，则x ＝__－1__；12．某市号召居民节约用水，为了解居民用水情况，随机抽查了20户家庭某月的用水量，结果如下表，则这20户家庭这个月的平均用水量是__5.8__吨.13.数据2，3，4，__3____3__，极差是__2__．【解析】2，3，4，4，3，2的平均数是(2＋3＋4＋4＋3＋2)÷6＝3，把这组数据从小到大排列为2，2，3，3，4，4，最中间两个数的平均数是(3＋3)÷2＝3，则这组数据的中位数是3；这组数据的最大数是4，最小数是2，则极差是4－2＝2.14．一副扑克牌52张(不含鬼牌)，分为黑桃、红心、方块及梅花4种花色，每种花色各有13张，分别标有字母A，K，Q，J和数字10，9，8，7，6，5，4，3，2.从这副牌中任意抽出一张，则这张牌是标有字母的牌的概率是__413__．15．某校决定从两名男生和两名女生中选出两名同学作为兰州国际马拉松赛的志愿者，则选出一男一女的概率是__23__．16．从3，0，－1，－2，－3这五个数中，随机抽取一个数，作为函数y＝(5－m2)x和关于x的方程(m＋1)x2＋mx＋1＝0中m的值，恰好使所得函数的图象经过第一、三象限，且方程有实数根的概率为__25__；三、解答题(本大题有6小题，第17～19题每题12分，第20题14分，第21题15分，第22题15分，共80分)17．已知一组数据：6，3，4，7，6，3，5，6.(1)求这组数据的平均数、众数、中位数；(2)求这组数据的方差和标准差．解：(1)将这组数据按从小到大的顺序排列为3，3，4，5，6，6，6，7，所以这组数据的平均数为18×(3＋3＋4＋5＋6＋6＋6＋7)＝5，众数为6，中位数为(5＋6)÷2＝5.5.(2)这组数据的方差S2＝18×[(5－3)2×2＋(5－4)2＋(5－5)2＋(5－6)2×3＋(5－7)2]＝2，标准差为 2.18．第16号台风“罗莎”在浙闽交界处登陆时，造成浙江178.7万人受灾，直接经济损失75亿．某学校举行“救灾区、献爱心”活动，自愿捐款资助．甲图的条形统计图表示学生人均捐款的情况，乙图是该校学生人数的比例分布扇形统计图(已知该校学生共1 400人)． (1)该校九年级学生有多少人？(2)在扇形统计图中，表示七年级学生部分的扇形的圆心角是多少度？ (3)该校学生平均每人捐款多少元？图10－5解：(1)九年级学生有：1 400×(1－35%－40%)＝1 400×25%＝350(人)； (2)圆心角度数＝360°×35%＝126°；(3)由扇形统计图知，七年级学生有1 400×35%＝490人，八年级学生有1 400×40%＝560人，九年级学生有350人， ∴x －＝7.6×490＋6.2×560＋5.4×3501 400＝6.49(元)，即该校学生平均每人捐款6.49元．19．某单位招聘员工，采取笔试与面试相结合的方式进行，两项成绩的原始分满分均为100分．前六名选手的得分如下：(综合成绩的满分仍为100分)(1)这6名选手笔试成绩的中位数是__84.5__分，众数是__84__分；(2)现得知1号选手的综合成绩为88分，求笔试成绩和面试成绩各占的百分比； (3)求出其余5名选手的综合成绩，并以综合成绩排序确定前两名人选． 解：(2)设笔试成绩和面试成绩所占的百分比分别为x ，y ，由题意，得⎩⎨⎧x ＋y ＝1，85x ＋90y ＝88， 解这个方程组，得⎩⎨⎧x ＝0.4，y ＝0.6.∴笔试成绩和面试成绩所占的百分比分别为40%和60%. (3)2号选手的综合成绩为 92×0.4＋88×0.6＝89.6(分)； 3号选手的综合成绩为 84×0.4＋86×0.6＝85.2(分)； 4号选手的综合成绩为 90×0.4＋90×0.6＝90(分)； 5号选手的综合成绩为 84×0.4＋80×0.6＝81.6(分)； 6号选手的综合成绩为 80×0.4＋85×0.6＝83(分)；∴综合成绩最高的两名选手是4号和2号．20．如图10－6，有四张背面相同的纸牌A ，B ，C ，D ，其正面分别是红桃，方块，黑桃，梅花，其中红桃，方块为红色，黑桃，梅花为黑色，小明将这4张纸牌背面朝上洗匀后，摸出一张，将剩余3张洗匀后再摸出一张． (1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌用A ，B ，C ，D 表示)；(2)求摸出的两张纸牌同为红色的概率．图10－6解：(1)树状图如图所示：第20题答图列表法：(2)P ＝212＝16.21．一个不透明的袋子里装有编号分别为1，2，3的球(除编号以外，其余都相同)，其中1号球1个，3号球3个，从中随机摸出一个球是2号球的概率为13. (1)求袋子里2号球的个数．(2)甲、乙两人分别从袋中摸出一个球(不放回)，甲摸出球的编号记为x ，乙摸出球的编号记为y ，用列表法求点A (x ，y )在直线y ＝x 下方的概率． 解：(1)设袋子里2号球的个数为x ，则 x 1＋x ＋3＝13，解得x ＝2.经检验，x ＝2为所列方程的解． ∴袋子里2号球的个数为2. (2)用列表法表示为：(3，1)、(3，1)、(3，1)、(3，2)、(3，2)、(3，2)、(3，2)、(3，2)、(3，2)，共11种．把事件“点A(x，y)在直线y＝x下方”记作事件A，∴P(A)＝11 30.22．某学校为了增强学生体质，决定开设以下体育课外活动项目：A：篮球，B：乒乓球，C：羽毛球，D：足球．为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：(1)这次被调查的学生共有________人；(2)请你将条形统计图补充完整；(3)在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率(用树状图或列表法解答)．图10－7解：(1)200(2)C：60人图略．(3)所有情况如下表所示：∴P(恰好选中甲，乙)＝212＝16.。

学习过程中，不可避免地伴随着遗忘。

“艾宾浩斯遗忘曲线”告诉我们，知识的遗忘是有规律的，遵循“先快后慢”的原则。

在一轮复习过程中，“滚动复习”模式能加深对知识前后、左右的联系，对于夯实基础、防止遗忘，效果是十分明显的。

针对以上思路，我们经过探索，编写了这套深具“滚动复习”特点的备考试卷。

本试卷立足教材基础知识，科学划分单元、合理编排试题，并有侧重地进行滚动复习。

特点如下：一、全面系统，立足一轮复习。

一轮复习，主要是对教材基础知识的梳理，强调复习的全面性、系统性。

本书以单元（章）为单位命制试卷，注重知识点的合理搭配，关注大纲和考试说明的要求，关注学习中的薄弱环节，关注重点、难点以及高考热点。

二、精心命题，拓展前沿视野。

题目来源：百强名校、重点中学2010届高三最新模拟、联考、质检、月考等试题；教育专家、一线名师的原创题和改编题；近年高考卷中典型性强的试题等。

充分保证了试题的前瞻性、新颖性，使学生练有所得，备考事半功倍。

三、滚动测试，减少知识遗忘。

所谓“滚动测试”，就是后面的习题中，兼顾考查前面的知识点。

这种考查不是简单的重复，而是对与本单元知识结合最为紧密、高考中常综合命题的知识的滚动考查。

每一部分结束，还适当安排综合检测卷，进行“小综合”训练。

四、温馨栏目，有助轻松备考。

本书设有“动感地带”栏目，包括学习方法、趣味知识、答疑解惑等内容，关注考生的学习、生活和心理。

这个栏目只是个桥梁，通过在线答疑、书信往来、电话沟通等，编辑老师与考生进行互动，扫除诸多备考路上的障碍。

这套试卷共10科，包括语文、文科数学、理科数学、英语、物理、化学、生物、政治、历史、地理。

单册定价：15.00元。

一轮备考最佳方法——滚动复习，知识积累就像“滚雪球”！。

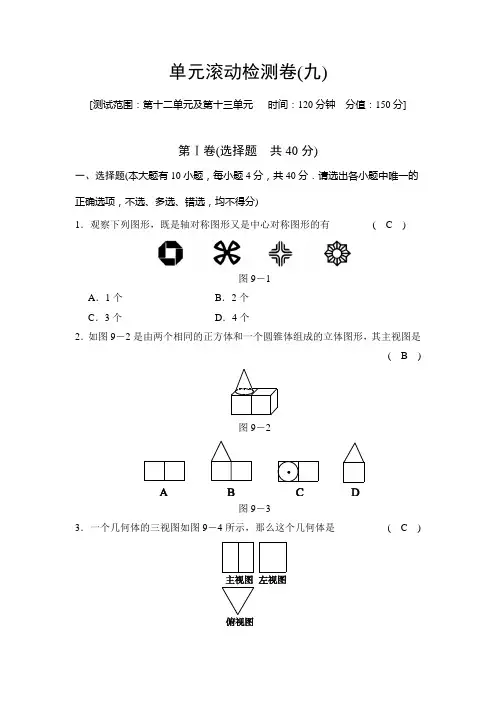
单元滚动检测卷(九)[测试范围：第十二单元及第十三单元时间：120分钟分值：150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题，每小题4分，共40分．请选出各小题中唯一的正确选项，不选、多选、错选，均不得分)1．观察下列图形，既是轴对称图形又是中心对称图形的有(C)图9－1A．1个B．2个C．3个D．4个2．如图9－2是由两个相同的正方体和一个圆锥体组成的立体图形，其主视图是(B)图9－2图9－33．一个几何体的三视图如图9－4所示，那么这个几何体是(C)图9－4图9－54．长方体的主视图，俯视图如图9－6所示，则其左视图面积为(A)图9－6A．3 B．4C．12 D．165．下列图形中，能通过折叠围成一个三棱柱的是(C)图9－76．如图9－8，正方形地砖的图案是轴对称图形，该图形的对称轴有(C) A．1条B．2条C．4条D．8条图9－87．图9－9是由6个同样大小的正方体摆成的几何体．将正方体①移走后，所得几何体(D)图9－9A ．主视图改变，左视图改变B ．俯视图不变，左视图不变C ．俯视图改变，左视图改变D ．主视图改变，左视图不变8．如图9－10是一个几何体的三视图，根据图中标注的数据可求得这个几何体的体积为( A )图9－10A ．24πB ．32πC ．36πD ．48π【解析】 该几何体为圆柱，其体积V ＝π⎝ ⎛⎭⎪⎫422×6＝24π，选A.9．如图9－11是某几何体的三视图及相关数据，则下面判断正确的是( D )图9－11A ．a ＞cB ．b ＞cC ．a 2＋4b 2＝c 2D ．a 2＋b 2＝c 2【解析】 此几何体为圆锥，其高为a ，母线长为c ，底面半径为b ，有如下关系：c 2＝a 2＋b 2，选D.10．由一些相同的小立方块搭成的几何体的三视图如图9－12所示，则搭成该几何体的小立方块有( B )图9－12A．3块B．4块C．6块D．9块【解析】共有4个小立方块，选B.第Ⅱ卷(非选择题共110分)二、填空题(本大题有6小题，每小题5分，共30分)11．如图9－13，在平面直角坐标系中，若△ABC与△A′B′C′关于E点成中心对称，则对称中心E的坐标是__(3，－1)__．图9－13【解析】只要连结各对应点，不难发现它们均交于点(3，－1)，∴对称中心为(3，－1)．12．如图9－14，将△ABC沿直线AB向右平移到达△BDE的位置，若∠CAB＝55°，∠ABC＝100°，则∠CBE的度数为__25°__．图9－14【解析】∵将△ABC沿直线AB向右平移到达△BDE的位置，∴△ACB≌△BED.∵∠CAB＝55°，∴∠EBD＝55°，则∠CBE的度数为180°－∠ABC－∠EBD＝180°－100°－55°＝25°. 13．如图9－15，将△OAB绕点O按逆时针方向旋转至△OA′B′，使点B恰好落在边A′B′上．已知AB＝4 cm，BB′＝1 cm，则A′B的长是__3__cm.图9－15【解析】根据旋转的性质，得A′B′＝AB＝4 cm，∴A′B＝A′B′－BB′＝4－1＝3(cm)．14．图9－16所示的4张扑克牌中，属于中心对称图形的有__1__个．图9－1615．如图9－17，在等腰Rt△ABC中，∠A＝90°，AC＝9，点O在AC上，且AO＝2，点P是AB上一动点，连结OP，将线段OP绕点O逆时针旋转90°得到线段OD，要使点D恰好落在BC上，则AP的长度等于__5__．图9－17【解析】如图，过点D作DE⊥AC于E，则∠DOE＋∠AOP＝90°，∠DOE＋∠ODE＝90°，∴∠ODE＝∠AOP，又∵OD＝OP，∠DEO＝∠OAP＝90°，∴△DEO≌△OAP，∴DE＝OA＝CE＝2，∴AP＝OE＝9－4＝5.第15题答图16．如图9－18所示，沿DE折叠长方形ABCD的一边，使点C落在AB边上的点F处，若AD＝8，且△AFD的面积为60，则△DEC的面积为__2898__．图9－18 【解析】∵四边形ABCD是矩形，∴∠A＝∠B＝90°，BC＝AD＝8，CD＝AB.∵△AFD的面积为60，即12AD·AF＝60，解得AF＝15，∴DF＝AD2＋AF2＝17.由折叠的性质，得CD＝DF＝17，∴AB＝17，∴BF＝AB－AF＝17－15＝2.设CE＝x，则EF＝CE＝x，BE＝BC－CE＝8－x，在Rt△BEF中，EF2＝BF2＋BE2，即x2＝22＋(8－x)2，解得x＝174，即CE＝174，∴△DEC的面积为12CD·CE＝12×17×174＝2898.三、解答题(本大题有7小题，第17～20题每题10分，第21题12分，第22、23题每题14分，共80分)17．已知：如图9－19，AB和DE是直立在地面上的两根立柱，AB＝5 m，某一时刻AB在阳光下的投影BC＝3 m.(1)请你在图中画出此时DE在阳光下的投影；(2)在测量AB的投影时，同时测量出DE在阳光下的投影长为6 m，请你计算DE的长．图9－19解：(1)如图，连结AC，过点D作DF∥AC，交直线BC于点F，线段EF即为DE的投影．第17题答图(2)∵AC∥DF，∴∠ACB＝∠DFE.∵∠ABC＝∠DEF＝90°，∴△ABC∽△DEF，∴ABDE＝BCEF，∴5DE＝36，∴DE＝10(m)．18．一位美术老师在课堂上进行立体模型素描教学时，把由圆锥与圆柱组成的几何体(如图9－20所示，圆锥在圆柱上底面正中间放置)摆在讲桌上，请你在指定的位置内分别画出这个几何体的三视图(从正面，左面，上面看到的视图)．图9－20【解析】从三个方向把看到的轮廓画成实线，看不到的轮廓画成虚线．解：如图所示．第18题答图19．如图9－21，点P是∠AOB内的一点，且点P关于射线OA，OB的对称点为P1，P2，连结P1P2，交OA于点M，交OB于点N.(1)根据题意，把图形补充完整；(2)若P1P2＝5 cm，求△PMN的周长．图9－21解：(1)如图所示：第19题答图(2)∵P与P1关于OA对称，∴OA为线段PP1的垂直平分线．∴MP＝MP1.同理可得NP＝NP2.∵P1P2＝5 cm，∴△PMN的周长＝MP＋MN＋NP＝P1M＋MN＋NP2＝P1P2＝5 cm.20．如图9－22，在10×10的正方形网格中，每个小正方形的边长均为1个单位．(1)作△ABC关于点P的对称图形△A′B′C′；(2)再把△A′B′C′，绕着C′逆时针旋转90°，得到△A″B″C′，请你画出△A′B′C′和△A″B″C′.(不要求写画法)图9－22解：(1)△A′B′C′如图所示．第20题答图(2)△A″B″C′如图所示．21．如图9－23是一个上下底密封纸盒的三视图，请回答下列问题：(1)说出该几何体的形状．(2)请你根据图中数据，计算这个密封纸盒的侧面积为多少？图9－23解：(1)由该几何体的三视图知道其是一个正六棱柱；(2)∵该几何体的高为12 cm，底面多边形边长为5 cm，∴该几何体的侧面积为6×5×12＝360(cm2)．故这个密封纸盒的侧面积为360 cm2.22．△ABC在平面直角坐标系xOy中的位置如图9－24所示．图9－24(1)作△ABC关于点C成中心对称的△A1B1C1.(2)将△A1B1C1向右平移4个单位，作出平移后的△A2B2C2.(3)在x轴上求作一点P，使P A1＋PC2的值最小，并写出点P的坐标(不写解答过程，直接写出结果)．解；(1)如图所示．(2)如图所示．第22题答图(3)如图所示，作出点A 1关于x 轴的对称点A ′，连结A ′C 2交x 轴于点P ，此时P A 1＋PC 2的值最小，可得P 点坐标为⎝ ⎛⎭⎪⎫83，0. 23．如图9－25，△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC ＝∠EDF ＝90°，△DEF 的顶点E 与△ABC 的斜边BC 的中点重合．将△DEF 绕点E 旋转，旋转过程中，线段DE 与线段AB 相交于点P ，线段EF 与射线CA 相交于点Q .(1)如图9－25①，当点Q 在线段AC 上，且AP ＝AQ 时，求证：△BPE ≌△CQE ；(2)如图9－25②，当点Q 在线段CA 的延长线上时，求证：△BPE ∽△CEQ ；并求当BP ＝a ，CQ ＝92a 时，P ，Q 两点间的距离(用含a 的代数式表示)．图9－25解：(1)∵E 为BC 的中点，∴BE ＝CE .∵△ABC 是等腰直角三角形，∴AB ＝AC ，∠B ＝∠C .∵AP ＝AQ ，∴AB －AP ＝AC －AQ ，即BP ＝CQ .在△BPE 和△CQE 中，⎩⎨⎧BP ＝CQ ，∠B ＝∠C ，BE ＝CE ，∴△BPE ≌△CQE .(2)∵△ABC 和△DEF 是等腰直角三角形， ∴∠B ＝∠C ＝∠DEF ＝45°.∵∠BEQ 是△QEC 的一个外角， ∴∠BEQ ＝∠C ＋∠CQE .又∵∠BEQ ＝∠BEP ＋∠DEF ，∴∠BEP ＝∠CQE ，∴△BPE ∽△CEQ ， ∴BP CE ＝BE CQ .又∵BE ＝CE ，∴BE 2＝BP ·CQ ＝9a 22， ∴BE ＝32a 2，∴BC ＝32a ，∴在Rt △ABC 中，AB ＝AC ＝3a ，∴AQ ＝CQ －AC ＝92a －3a ＝32a ，AP ＝AB －BP ＝3a －a ＝2a .连结PQ ，在Rt △APQ 中，PQ ＝AP 2＋AQ 2 ＝（2a ）2＋⎝ ⎛⎭⎪⎫32a 2＝52a .。

单元滚动检测卷(六)[测试范围：第九单元时间：120分钟分值：150分]第Ⅰ卷(选择题共40分)一、选择题(本大题有10小题，每小题4分，共40分．请选出各小题中唯一的正确选项，不选、多选、错选，均不得分)1．下列结论正确的是(B) A．长度相等的两条弧是等弧B．半圆是弧C．相等的圆心角所对的弧相等D．弧是半圆【解析】A、根据圆的某些概念的相关定义，能够完全重合的弧是等弧，故本选项错误，B、弧分为优弧、劣弧、半圆，故本选项正确；C、根据在同圆或等圆内，相等的圆心角所对的弧相等，故本选项错误；D、弧分为优弧、劣弧、半圆，故本选项错误．2．如图6－1，已知⊙O的半径OA＝10 cm，弦AB＝16 cm，P为弦AB上的一个动点，则OP的最短距离为(B)图6－1A．5 cm B．6 cmC．8 cm D．10 cm【解析】当OP为垂线段，即OP⊥AB时，OP为最短，∴AP＝BP＝12AB＝12×16＝8(cm)，而OA＝10 cm，在Rt△OAP中，OP＝OA2－AP2＝102－82＝6(cm)．故选B.3．如图6－2是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB 宽为8 cm，水的最大深度为2 cm，则该输水管的半径为(C)图6－2A．3 cm B．4 cmC．5 cm D．6 cm【解析】如图所示，过点O作OD⊥AB于点D，连结OA.∵OD⊥AB，∴AD＝12AB＝12×8＝4 (cm)．设OA＝r，则OD＝r－2，第3题答图在Rt△AOD中，OA2＝OD2＋AD2，即r2＝(r－2)2＋42，解得r＝5 cm.故选C.4．如图6－3，AB是⊙O的直径，∠AOC＝110°，则∠D＝(B)图6－3A．25°B．35°C ．55°D ．70°5．已知⊙O 1与⊙O 2外切，⊙O 1的半径R ＝5 cm ，⊙O 2的半径r ＝1 cm ，则⊙O 1与⊙O 2的圆心距是( D )A ．1 cmB ．4 cmC ．5 cmD ．6 cm【解析】 外切两圆的圆心距等于两圆半径的和，所以O 1O 2＝R ＋r ＝5 cm ＋ 1 cm ＝6 cm.6．用半径为3 cm ，圆心角是120°的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为( D )A ．2π cmB ．1.5 cmC ．π cmD ．1 cm7．如图6－4，半圆O 的直径AB ＝10，弦AC ＝6 cm ，AD 平分∠BAC ，则AD 的长为( A )图6－4A ．4 5 cmB ．3 5 cmC ．5 5 cmD ．4 cm【解析】 如图，连结OD ，OC ，作DE ⊥AB 于E ，OF ⊥AC 于F .第7题答图∵∠CAD ＝∠BAD (角平分线的定义)， ∴CD ︵＝BD ︵，∴∠DOB ＝∠OAC ＝2∠BAD . 又∵OA ＝OD ，∠AFO ＝∠DEO ＝90°， ∴△AOF ≌△ODE ，∴OE ＝AF ＝12AC ＝3 cm.在Rt △DOE 中，DE ＝OD 2－OE 2＝4 cm ， 在Rt △ADE 中，AD ＝DE 2＋AE 2＝4 5 cm.故选A.8．如图6－5，P A ，PB 是⊙O 的切线，AC 是⊙O 的直径，∠P ＝40°，则∠BAC 的度数是( B )图6－5A ．10°B ．20°C ．30°D ．40°【解析】 ∵P A ，PB 是⊙O 的切线，∴P A ＝PB ，∠OAP ＝90°，∴∠P AB ＝∠ABP ，又∠P ＝40°，∴∠P AB ＝70°，∴∠BAC ＝90°－70°＝20°. 9．如图6－6，AB 与⊙O 相切于点B ，AO 的延长线交⊙O 于点C ，连结BC ，若∠ABC ＝120°，OC ＝3，则BC ︵的长为( B )图6－6A ．πB ．2πC ．3πD ．5π【解析】 连结OB ，第9题答图∵AB 与⊙O 相切于点B ，∴∠ABO ＝90°. ∵∠ABC ＝120°， ∴∠OBC ＝30°.∵OB ＝OC ，∴∠OCB ＝30°， ∴∠BOC ＝120°，∴BC ︵的长为120π×3180＝2π，故选B.10．如图6－7，MN 是半径为1的⊙O 的直径，点A 在⊙O 上，∠AMN ＝30°，B 为AN ︵的中点，点P 是直径MN 上一个动点，则P A ＋PB 的最小值为( B )图6－7A ．2 2 B. 2 C ．1D ．2第Ⅱ卷(非选择题 共110分)二、填空题(本大题有6小题，每小题5分，共30分)11．图6－8中圆心角∠AOB ＝30°，弦CA ∥OB ，延长CO 与圆交于点D ，则∠BOD ＝__30°__．图6－812．平面上有⊙O 及一点P ，P 到⊙O 上的点的距离最长为6 cm ，最短为2 cm ，则⊙O 的半径为__4或2__cm.【解析】 当点P 在圆内时，则直径＝6＋2＝8(cm)，因而半径是4 cm ；当点P在圆外时，直径＝6－2＝4(cm)，因而半径是2 cm.所以⊙O的半径为4 cm或2 cm.13．当宽为3 cm的刻度尺的一边与圆相切时，另一边与圆的两个交点处的读数如图6－9所示(单位：cm)，那么该圆的半径为__256__cm.图6－9【解析】连结OA，过点O作OD⊥AB于点D，∵OD⊥AB，∴AD＝12AB＝12×(9－1)＝4，设OA＝r，则OD＝r－3，在Rt△OAD中，OA2－OD2＝AD2，即r2－(r－3)2＝42，解得r＝256cm.第13题答图14．如图6－10，“凸轮”的外围由以正三角形的顶点为圆心，以正三角形的边长为半径的三段等弧组成．已知正三角形的边长为1，则“凸轮”的周长等于__π__．图6－10【解析】 ∵△ABC 为正三角形，∴∠A ＝∠B ＝∠C ＝60°，AB ＝AC ＝BC ＝1， ∴AB ︵＝BC ︵＝AC ︵＝60π×1180＝π3，根据题意可知凸轮的周长为三个弧长的和， 即凸轮的周长＝AB ︵＋BC ︵＋AC ︵＝3×π3＝π.15．底面半径为1，高为3的圆锥的侧面积等于__2π__． 【解析】 ∵高线长为3，底面半径是1， ∴由勾股定理知：母线长＝（3）2＋1＝2， ∴圆锥侧面积＝π×1×2＝2π.16．如图6－11所示，AB 是⊙O 的直径，点D 在⊙O 上，∠AOD ＝130°，BC ∥OD 交⊙O 于点C ，则∠A ＝__40°__．图6－11【解析】 ∵∠AOD ＝130°， ∴∠BOD ＝50°， 又∵OD ∥BC ，∴∠ABC ＝∠BOD ＝50°， 又∵AB 为直径， ∴∠C ＝90°， ∴∠A ＝40°.三、解答题(本大题有8小题，第17～20题每题8分，第21题10分，第22、23 题每题12分，第24题14分，共80分)17．中华民族的科学文化历史悠久、灿烂辉煌，我们的祖先几千年前就能在生产实践中运用数学.1 300多年前，我国隋代建筑的赵州石拱桥的桥拱是圆弧形(如图6－12)．经测量，桥拱下的水面距拱顶6 m时，水面宽34.64 m，已知桥拱跨度是37.04 m，运用你所学的知识计算出赵州桥的大致拱高．(运算时取37.04≈147，34.64≈203)图6－12解：如图，设圆弧所在圆的圆心为O，第17题答图AB＝37.04≈147 m，CD＝34.64≈20 3 m，GE＝6 m.在Rt△OCE中，OE＝OG－6，CE＝103，∵OC2＝CE2＋OE2，∴OC2＝(103)2＋(OC－6)2，∴OC＝28(m)，∴OA＝28.在Rt△OAF中，AF＝77，∴OF＝OA2－AF2＝282－（77）2＝21(m)．∴拱高GF＝28－21＝7(m)．18．如图6－13，⊙O的半径为4 cm，点P是⊙O外一点，OP＝6 cm，求：图6－13(1)以P为圆心作⊙P与⊙O外切，小圆⊙P的半径是多少？(2)以P为圆心作⊙P与⊙O内切，大圆⊙P的半径是多少？(分别作出图形，并解答)解：(1)若两圆外切，则小圆⊙P的半径为6－4＝2 (cm)．第18题答图(2)若两圆内切，则大圆⊙P的半径为6＋4＝10 (cm)．19．如图6－14，实线部分是半径为15 m的两条等弧组成的游泳池，若每条弧所在的圆都经过另一个圆的圆心，求游泳池的周长．图6－14解：设两个圆的交点分别为C，D，连结O1C.O1D2，O2C，O2D，则易证四边形O，CO2D是菱形，所以∠CO1D＝∠CO2D＝120°，所以两条等弧所对的圆心角均为360°－120°＝240°.则游泳池的周长为2×nπr180＝2×240π×15180＝40π(m)．20．如图6－15，⊙O经过菱形ABCD的三个顶点A，D，C，且与AB相切于点A.(1)求证：BC为⊙O的切线；(2)求∠B的度数．图6－15解：(1)证明：如图，连结AO，CO.∵AB是⊙O的切线，∴OA⊥AB.∴∠BAO＝90°.∵四边形ABCD是菱形，∴AB＝BC.∵AO＝CO，BO＝BO，∴△BAO≌△BCO(SSS)．∴∠BCO＝∠BAO＝90°，即OC⊥BC.∴BC为⊙O的切线．第20题答图(2)如图，连结OD，则∠AOC＝2∠ADC.由(1)知∠BAO＝∠BCO＝90°，且四边形ABCO的内角和为360°，∴∠B＋∠AOC＝360°－∠BAO－∠BCO＝180°，即∠B＋2∠ADC＝180°.∵四边形ABCD是菱形，∴∠B＝∠ADC.∴∠B＋2∠B＝180°.∴∠B＝60°.21．如图6－16，已知AB是⊙O的直径，P为⊙O外一点，且OP∥BC，∠P＝∠BAC.(1)求证：P A为⊙O的切线；(2)若OB＝5，OP＝253，求AC的长．图6－16解：(1)设AC与OP相交于点H，∵AB是⊙O的直径，∴∠ACB＝90°.∵OP∥BC，∴∠AHO＝∠ACB＝90°，∴∠AOH＋∠OAH＝90°.∵∠P＝∠OAH，∴∠AOH＋∠P＝90°，∴∠OAP＝90°，即OA⊥AP，∴P A为⊙O的切线．(2)在Rt△OAP中，OA＝OB＝5，OP＝25 3，∴AP＝OP2－OA2＝20 3.∵S△OAP ＝12OA·AP＝12OP·AH.∴AH ＝OA ·AP OP ＝5×203253＝4.∵OH ⊥AC ，∴AC ＝2AH ＝8.22．如图6－17，将一块三角板和半圆形量角器按图中方式叠放，三角板一边与量角器的零刻度线所在直线重合，重叠部分的量角器弧(AB ︵)对应的圆心角(∠AOB )为120°，OC 的长为2 cm ，求三角板和量角器重叠部分的面积．图6－17解：∵∠AOB ＝120°，∴∠BOC ＝60°.在Rt △OBC 中，OC ＝2 cm ，∠BOC ＝60°，∴∠OBC ＝30°，∴OB ＝4 cm ，BC ＝2 3 cm ，则S 扇形OAB ＝120π×42360＝16π3，S △OBC ＝12OC ·BC ＝23，故S 重叠＝S 扇形OAB ＋S △OBC ＝16π3＋2 3.23．已知：如图6－18，在梯形ABCD 中，AD ∥BC ，DA ＝DC ，以点D 为圆心，DA 长为半径的⊙D 与AB 相切于点A ，与BC 交于点F ，过点D 作DE ⊥BC ，垂足为E .(1)求证：四边形ABED 为矩形；(2)若AB ＝4，AD BC ＝34，求CF 的长．图6－18解：(1)∵⊙D 与AB 相切于点A ，∴AB ⊥AD .∵AD ∥BC ，DE ⊥BC ，∴DE ⊥AD ，∴∠DAB ＝∠ADE ＝∠DEB ＝90°，∴四边形ABED 为矩形．(2)∵四边形ABED 为矩形，∴DE ＝AB ＝4.∵DA ＝DC ，∴点C 在⊙D 上．∵点D 为圆心，DE ⊥BC ，∴CF ＝2EC .∵AD BC ＝34，设AD ＝3k (k ＞0)，则BC ＝4k ，∴BE ＝3k ，EC ＝BC －BE ＝4k －3k ＝k ，DC ＝AD ＝3k .在Rt △DEC 中，由勾股定理得DE 2＋EC 2＝DC 2，∴42＋k 2＝(3k )2，∴k 2＝2.∵k ＞0，∴k ＝2，∴CF ＝2EC ＝2 2.24．如图6－19，AB 是⊙O 的直径，C 是半圆O 上的一点，AC 平分∠DAB ，AD ⊥CD ，垂足为D ，AD 交⊙O 于E ，连结CE .(1)判断CD 与⊙O 的位置关系，并证明你的结论；(2)若E 是AC ︵的中点，⊙O 的半径为1，求图中阴影部分的面积．图6－19解：(1)CD 与⊙O 相切，理由如下：∵AC 为∠DAB 的平分线，∴∠DAC ＝∠BAC .∵OA ＝OC ，∴∠OAC ＝∠OCA ，∴∠DAC ＝∠OCA ，∴OC ∥AD .∵AD ⊥CD ，∴OC ⊥CD ，∴CD 与⊙O 相切；(2)连结OE ，∵E 是AC ︵的中点，∴AE ︵＝EC ︵，∴S 弧形AE ︵＝S 弧形EC ︵，∴S 阴影＝S △DEC .∵∠DAC ＝∠BAC ，∴EC ︵＝BC ︵，即AE ︵＝EC ︵＝BC ︵.∴∠AOE ＝∠EOC ＝∠BOC ＝60°.又∵OE ＝OC ，∴△EOC 是等边三角形， ∴EC ＝OC ＝1，∠ECO ＝∠EOC ＝60°， ∴∠ECD ＝90°－∠ECO ＝30°.在Rt △EDC 中，∠ECD ＝30°，EC ＝1，∴ED ＝12EC ＝12，CD ＝EC 2－ED 2＝32， ∴S 阴影＝S △DEC ＝12ED ·CD ＝12×12×32 ＝38.。

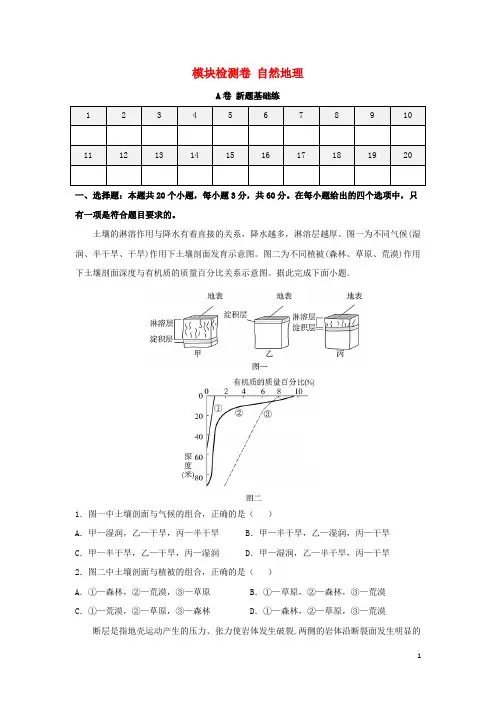
模块检测卷自然地理A卷新题基础练一、选择题：本题共20个小题，每小题3分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

土壤的淋溶作用与降水有着直接的关系，降水越多，淋溶层越厚。

图一为不同气候(湿润、半干旱、干旱)作用下土壤剖面发育示意图。

图二为不同植被(森林、草原、荒漠)作用下土壤剖面深度与有机质的质量百分比关系示意图。

据此完成下面小题。

1．图一中土壤剖面与气候的组合，正确的是（）A．甲—湿润，乙—干旱，丙—半干旱 B．甲—半干旱，乙—湿润，丙—干旱C．甲—半干旱，乙—干旱，丙—湿润 D．甲—湿润，乙—半干旱，丙—干旱2．图二中土壤剖面与植被的组合，正确的是（）A．①—森林，②—荒漠，③—草原 B．①—草原，②—森林，③—荒漠C．①—荒漠，②—草原，③—森林 D．①—森林，②—草原，③—荒漠断层是指地壳运动产生的压力、张力使岩体发生破裂,两侧的岩体沿断裂面发生明显的位移。

三叶虫、恐龙、大型哺乳动物分别为古生代、中生代、新生代的代表性动物。

下图是某地地层剖面图。

据此完成下面小题。

3．图中断层最可能发生在（）A．古生代前期B．古生代后期—中生代前期C．中生代后期—新生代前期D．新生代后期4．图中甲、乙、丙、丁四处地层形成的先后顺序是（）A．甲、乙、丙、丁B．乙、甲、丙、丁C．丙、乙、丁、甲D．乙、丙、丁、甲读某区域示意图，完成下面小题。

5．甲线路主要影响的水循环环节是（）A．地下径流B．地表径流C．水汽输送D．下渗6．关于乙工程对水循环和河流的影响，叙述正确的是（）A．河流水量增加B．上游含沙量变小C．地下径流增加D．蒸发减弱城市热岛效应是指城市中的气温明显高于外围郊区的现象，热岛强度用城市和郊区两个代表性观测点的气温差值来表示。

读我国某城市热岛强度日平均变化示意图，完成下面小题。

7．热岛效应最强的时间出现在（）A．夏季的白昼B．夏季的夜晚C．冬季的白昼D．冬季的夜晚8．影响城区与郊区温度存在差异的主要因素是（）A．地面状况B．气压分布C．降水量D．地下径流9．下列措施有利于减轻该市热岛效应的是（）①建筑物淡色化②实行机动车限行③增加楼房高度④适当增加水体面积A．①②③ B．②③④ C．①②④ D．①③④洗车指数是根据过去12h和未来48h有无雨雪天气，路面是否有积雪和泥水，是否容易使汽车溅上泥水，是否有沙尘等天气条件，给爱车族提供的是否适宜洗车的建议。

一、选择题（每题3分，共30分）1. 下列各数中，既是质数又是合数的是（）A. 2B. 9C. 15D. 292. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 平行四边形3. 一个数的3倍加上4等于12，这个数是（）A. 2B. 3C. 4D. 54. 一个正方形的周长是24厘米，它的面积是（）A. 36平方厘米B. 48平方厘米C. 54平方厘米D. 60平方厘米5. 下列运算中，正确的是（）A. 3.5 + 2.1 = 5.6B. 5.5 - 2.3 = 3.2C. 4.2 × 2.5 = 10.5D. 8 ÷2.4 =3.36. 一个数的十分之四是3.6，这个数是（）A. 36B. 36.3C. 36.4D. 3607. 下列各式中，完全平方数是（）A. 4 × 4B. 5 × 5C. 6 × 6D. 7 × 78. 一个长方体的长、宽、高分别是5厘米、3厘米、2厘米，它的体积是（）A. 30立方厘米B. 35立方厘米C. 40立方厘米D. 45立方厘米9. 下列各数中，能被3整除的是（）A. 25B. 28C. 30D. 3310. 下列各式中，能表示梯形面积的是（）A. （上底+下底）×高÷2B. 上底×高÷2C. （上底+下底）×高D. （上底-下底）×高二、填空题（每题3分，共30分）11. 0.5的十分之二是______，0.6的百分之二十是______。

12. 1.2千米等于______米，0.4吨等于______千克。

13. 一个圆的半径是3厘米，它的直径是______厘米，周长是______厘米。

14. 2.5乘以4.8等于______，1.2除以0.6等于______。

15. 下列各数中，最小的整数是______，最大的小数是______。

一、选择题（每题2分，共20分）1. 下列数中，最小的数是（）A. 3.14B. 3.11C. 3.15D. 3.13答案：B2. 一个长方形的长是6厘米，宽是3厘米，这个长方形的面积是（）A. 18平方厘米B. 9平方厘米C. 12平方厘米D. 15平方厘米答案：A3. 一个梯形的上底是4厘米，下底是6厘米，高是5厘米，这个梯形的面积是（）A. 20平方厘米B. 30平方厘米C. 25平方厘米D. 35平方厘米答案：C4. 下列数中，最大的数是（）A. 1/2B. 1/3C. 1/4D. 1/5答案：A5. 一个圆的半径是5厘米，这个圆的周长是（）A. 10π厘米B. 15π厘米C. 20π厘米D. 25π厘米答案：C6. 下列数中，最小的数是（）A. 2.5B. 2.4C. 2.6D. 2.3答案：D7. 一个长方体的长是8厘米，宽是4厘米，高是6厘米，这个长方体的体积是（）A. 192立方厘米B. 128立方厘米C. 96立方厘米D. 64立方厘米答案：A8. 一个正方形的边长是4厘米，这个正方形的面积是（）A. 16平方厘米B. 15平方厘米C. 14平方厘米D. 13平方厘米答案：A9. 下列数中，最大的数是（）A. 0.5B. 0.3C. 0.7D. 0.4答案：C10. 一个圆柱的高是10厘米，底面半径是5厘米，这个圆柱的体积是（）A. 250π立方厘米B. 500π立方厘米C. 750π立方厘米D. 1000π立方厘米答案：B二、填空题（每题2分，共20分）11. 一个数的十分位上是5，百分位上是2，这个数写作：（）答案：5.2512. 0.25与0.125的和是（）答案：0.37513. 0.375与0.625的差是（）答案：0.2514. 0.5乘以0.2等于（）答案：0.115. 一个长方形的长是12厘米，宽是8厘米，这个长方形的周长是（）答案：40厘米16. 一个圆的半径是7厘米，这个圆的面积是（）答案：153.86平方厘米17. 一个长方体的长是5厘米，宽是3厘米，高是4厘米，这个长方体的体积是（）答案：60立方厘米18. 一个正方形的边长是6厘米，这个正方形的面积是（）答案：36平方厘米19. 一个圆柱的高是8厘米，底面半径是3厘米，这个圆柱的体积是（）答案：226.08立方厘米20. 一个梯形的上底是5厘米，下底是10厘米，高是6厘米，这个梯形的面积是（）答案：30平方厘米三、解答题（每题10分，共20分）21. 一辆汽车从甲地开往乙地，每小时行驶60千米，2小时后到达乙地。

鲁教版（五四制）九年级数学上册《第四章实数》单元检测卷及答案一、单选题1．在实数1、0、﹣1、﹣2中，最小的实数是（ ）A ．-2B ．-1C ．1D ．02．实数16的平方根是（ ）．A ．4±B ．4C ．256D ．2± 3．如果＋（－13）＝0，则“”内应填实数是（ ） A ．0 B ．13 C ．－13 D ．34．若实数m n ，满足350m n --=，且m n ，恰好是Rt ABC △的两条边长，则第三条边长为（ ） A ．3或4 B ．434C ．5 D 345．下列实数中，是有理数的是（ ）A 2B 5C ．πD ．06．一个数值转换器的原理如图所示，当输入的x 为256时，输出的y 是( )A ．16B 2C 3D 87．如图所示的方格中，每个小正方形的边长为1，若把阴影部分剪拼成一个正方形，那么新正方形的边长是（ ）A 5B 6C 7D 88．设点 ()P x y ，，且320x y -+，则点P 的坐标是（ ）A ．()3-2，B ． ()32-，C ．()32-，D ．()23-，9．为了求2310012222+++++的值，可令23100S 12222=+++++，则23422222S =++++1012+，因此101221S S -=-，所以10121S =-，即231001*********+++++=-，仿照以上推理计算23202315555+++++的值是（ ） A ．2023512- B ．2024512- C ．2023514- D ．2024514- 10．已知123112113114,,,...,1232323438345415a a a =+==+==+=⨯⨯⨯⨯⨯⨯依据上述规律，则99a =（ ） A ．10099101⨯ B ．9998100⨯ C ．989799⨯ D ．101100102⨯二、填空题11．已知a 是25b 的立方根为﹣2，则a +b 的倒数为 ．12．有一种把整数分类的方法，指定一个整数n ，把所有除以n 后得到的余数相等的整数分为一类． 例：当3n =时，0，3，6，…除以3，余数为0，这是一类：1，4，7，…余数为1，这也是一类；2，5，8，…是最后一类． 定义：一个整数对称位置上的数字为同一类整数（按除以n 的余数分类），则称其为“n 的对称同余数”． 例：整数54340，是“5的对称同余数”，但不是“3的对称同余数”． 已知一个四位整数，既是“4的对称同余数”，又是完全平方数（即是某个整数的平方），则满足条件的最小的一个整数与最大的一个整数的和为 ．13．实数32227,,2,,0.2,0.10100100017π--⋯⋯中无理数有 个（填个数）． 14101- 12． 15．如图，有一个半径为12个单位长度的圆，将圆上的点A 放在原点，并把原片沿数轴逆时针滚动一周，点A 到达点A '的位置，则点A '表示的数是 ；若点B 表示的数是-3.14，则点B 在点A '的 （填“左边”、“右边”或“重合”）．1623(3)8- ．17．设n 为正整数，且n 3+2n 2是一个奇数的平方，则满足条件的n 中，最小的两个数之和为 ． 18．我们知道，同底数幂的乘法法则为m n m n a a a +⋅=（其中0a ≠，m ，n 为正整数），类似地，我们规定关于任意正整数m ，n 的一种新运算：()()()h m n h m h n +=⋅，请根据这种新运算填空：（1）若()213h =，则()2h = ； （2）若()()10h k k =≠，那么()()2023h n h ⋅= ．（用含n 和k 的代数式表示，其中n 为正整数）．三、解答题19．已知24a +的平方根是4±，41a b +-的立方根是3，c 70的整数部分．(1)求a ，b ，c 的值．(2)求24a b c +-的平方根．20．如图，O 是数轴的原点，过点O 作数轴的垂线OM 13A （保留作图痕迹），写出作法，并说明理由．21．已知：实数a ，b 满足230a b +-．(1)可得a =___________，b =___________；(2)若一个正实数m 的两个平方根分别是2x a +和b x -，求x 和m 的值．22．全球气候变暖导致一些冰川融化并消失.在冰川消失12年后，一种低等植物苔藓就开始在岩石上生长.每一个苔藓都会长成近似圆形，苔藓的直径和冰川消失后经过的时间近似地满足如下的关系式：)71212d t t =-≥.其中d 代表苔藓的直径（单位：厘米）；t 代表冰川消失后经过的时间（单位：年）.(1)计算冰川消失16年后苔藓的直径；(2)如果测得一些苔藓的直径是28厘米，问冰川约是在多少年前消失的？232我们知道面积是222121＋x，画出如下示意图．由图中面积计算，S正方形＝x2＋2×1·x＋1另一方面由题意知S正方形＝2所以x2＋2×1·x＋1＝2略去x2，得方程2x＋1＝2．解得x＝0.52．（1130.001）；(画出示意图，标明数据，并写出求解过程)（2）结合上述具体实例，已知非负整数a、b、m，若a m a＋1．且m＝a2＋b m≈ ．(用a、b的代数式表示)24．定义：如果一个数的平方等于﹣1，记为i2＝﹣1，这个数i叫做虚数单位，我们把形如a+bi（a，b为实数，i是虚数单位）的数叫做复数，其中a叫这个复数的实部，b叫做这个复数的虚部．复数的加、减、乘法运算与整式的加、减、乘法运算类似．例如:计算：（2+）+（3﹣5i）＝（2+3）+（1﹣5）i＝5﹣4i；（1+i）×（2﹣i）＝1×2﹣1×i+2×i﹣i2＝2+（﹣1+2）i﹣（﹣1）＝3+i．根据以上信息，解答下列问题：（1）下列等式或命题中，错误的是 A ．i 4＝1B ．复数（1+i ）2的实部为0C ．（1+i ）×（3﹣4i ）＝﹣1﹣iD ．i +i 2+i 3+i 4+…+i 2019＝﹣1（2）计算：①（1+2i ）（2﹣i ）+（2﹣i ）2； ①（1+2）3（1﹣2i ）3．参考答案 1．A2．A3．B4．B5．D6．B7．C8．C9．D10．A11．13-12．1089013．314．>15． π- 右边16．517．30．18． 49 2023n k +/2023nk +19．(1)6a = 4b = 8c =；(2)24a b c +-的平方根为5± 20．略21．(1)-2，3(2)1x =- 16m =22．(1)冰川消失16年后苔藓的直径为14厘米(2)冰川约是在28年前消失的23．（113 3.667≈；（2）2b a a + 24．（1）C ；（2）①7﹣i ；①﹣297+54i。

一、选择题（每题2分，共20分）1. 下列各数中，哪个数是质数？A. 21B. 25C. 29D. 332. 下列各数中，哪个数是合数？A. 17B. 19C. 28D. 293. 下列各数中，哪个数既是奇数又是偶数？A. 1B. 2C. 3D. 44. 下列各数中，哪个数是正数？A. -5B. 0C. 3D. -35. 下列各数中，哪个数是负数？A. 5B. 0C. -5D. 106. 下列各数中，哪个数是整数？A. 1.5B. 2.3C. 2.5D. 37. 下列各数中，哪个数是分数？A. 3B. 4C. 5/2D. 68. 下列各数中，哪个数是无理数？A. √4B. √9C. √16D. √259. 下列各数中，哪个数是有限小数？A. 0.5B. 0.125C. 0.25D. 0.62510. 下列各数中，哪个数是无限循环小数？A. 0.333…B. 0.666…C. 0.833…D. 0.999…二、填空题（每题2分，共20分）11. 一个数加上它的相反数等于0，这个数是______。

12. 一个数乘以它的倒数等于1，这个数是______。

13. 一个数的绝对值是它本身，这个数是______。

14. 一个数的绝对值是它的相反数，这个数是______。

15. 一个数的平方根是它本身，这个数是______。

16. 一个数的立方根是它本身，这个数是______。

17. 2的平方根是______。

18. 3的立方根是______。

19. 5的立方根是______。

20. 10的平方根是______。

三、解答题（每题5分，共25分）21. 计算：-5 + 3 - 2 + 422. 计算：3/4 × 2/323. 计算：-2 × (-5) × (-3)24. 计算下列各式的值：（1）√(16 + 9)（2）√(25 - 4)（3）√(36 ÷ 4)25. 小明有5个苹果，小红有3个苹果，他们两个人一共有多少个苹果？四、应用题（每题10分，共20分）26. 小华骑自行车从家出发，向东行驶了5千米，然后向北行驶了3千米，最后又向东行驶了2千米。

小学四年级滚动测试卷子一、选择题（每题2分，共20分）1. 下列哪个选项是正确的成语？A. 一鸣惊人B. 一鸣惊人（错误）C. 一鸣惊人（错误）D. 一鸣惊人（错误）2. 以下哪个数字是最小的正整数？A. 0B. 1C. 2D. 33. 下列哪个选项是正确的四字词语？A. 风和日丽B. 风和日丽（错误）C. 风和日丽（错误）D. 风和日丽（错误）4. 下列哪个选项是正确的成语？A. 画龙点睛B. 画龙点睛（错误）C. 画龙点睛（错误）D. 画龙点睛（错误）5. 下列哪个选项是正确的四字词语？A. 春暖花开C. 春暖花开（错误）D. 春暖花开（错误）6. 下列哪个选项是正确的成语？A. 一箭双雕B. 一箭双雕（错误）C. 一箭双雕（错误）D. 一箭双雕（错误）7. 下列哪个选项是正确的四字词语？A. 金榜题名B. 金榜提名（错误）C. 金榜题名（错误）D. 金榜题名（错误）8. 下列哪个选项是正确的成语？A. 掩耳盗铃B. 掩耳盗铃（错误）C. 掩耳盗铃（错误）D. 掩耳盗铃（错误）9. 下列哪个选项是正确的四字词语？A. 一帆风顺B. 一帆风顺（错误）C. 一帆风顺（错误）D. 一帆风顺（错误）10. 下列哪个选项是正确的成语？A. 画蛇添足B. 画蛇添足（错误）D. 画蛇添足（错误）二、填空题（每题2分，共20分）11. 春天到了，万物复苏，______。

12. 他学习非常努力，成绩一直______。

13. 我们要学会______，不浪费每一滴水。

14. 老师告诉我们，要______，做一个诚实的孩子。

15. 他在比赛中表现出色，获得了______。

16. 我们要保护环境，让地球更加______。

17. 他勇敢地面对困难，最终______。

18. 我们要尊重他人，学会______。

19. 他通过自己的努力，实现了自己的______。

20. 我们要珍惜时间，因为时间就是______。

三、阅读理解（每题5分，共30分）阅读下面的短文，回答问题。

综合检测卷(一)考生注意：1．本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页。

2．答卷前，考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上。

3．本次考试时间90分钟，满分100分。

4．请在密封线内作答，保持试卷清洁完整。

第Ⅰ卷一、选择题(本题包括20题，每小题2.5分，共50分)1．里约奥运会的跳水变为“绿池”与绿藻有关。

下列关于绿藻和蓝藻的说法错误的是( )A．都含有叶绿素B．都有以核膜为界限的细胞核C．都含有核糖体D．都属于自养生物2．寨卡病毒是单股正链RNA病毒，它主要通过蚊虫叮咬传播疾病。

下列关于该病毒的说法正确的是( )A．在人工配制的富含有机物的培养基上可以大量繁殖B．该病毒没有细胞结构，不属于生命系统，但可以以二分裂方式增殖C．其生活方式是寄生，但能进行无氧呼吸D．其能发生的可遗传变异类型有基因突变3．科研人员对某细胞器进行研究时，发现其膜上能产生气体，下列相关分析正确的是( )A．该过程可发生在所有细胞中B．产生气体过程消耗ATPC．该细胞器一定具有双层膜D．该过程不受外界因素影响4．下列有关结构与功能相统一的观点不正确的是( )A．细胞内的生物膜把各种细胞器分隔开，保证了细胞生命活动高效、有序地进行B．神经细胞轴突末梢有大量突起，有利于接受更多神经递质进行信息传递C．某些低等植物细胞中心体的存在，有利于其有丝分裂的正常进行D．线粒体内膜向内腔折叠形成嵴，有利于有氧呼吸快速进行5．如图是科学家利用酵母菌的不同类型研究分泌蛋白的分泌示意图，它揭示了囊泡的运输过程。

下列叙述错误的是( )A．A型表示内质网膜结构异常导致分泌过程出现障碍B．D型可能是高尔基体功能异常导致分泌过程出现障碍C．没有囊泡运输的精确组织，细胞代谢将陷入混乱状态D．囊泡和靶膜的识别并融合表明生物膜具有选择透过性6．由原癌基因编码的PDGF过量表达和持续释放会导致癌症，血小板分泌的PDGF能促进伤口愈合且不引发癌症，下列分析正确的是( )A．细胞癌变是由PDGF突变引起的B．伤口处PDGF能促进血小板分裂C．PDGF可能会促进伤口周围细胞的增殖D．血小板的原癌基因与其他体细胞不同7．家兔的皮毛灰色对白色为显性，由位于常染色体上的一对等位基因控制。

单元滚动检测卷（四）单元滚动检测卷(四)第Ⅰ卷选择题(共50分) 1．(2019·杭州市余杭区高三上学期期末)《青花瓷》中所描绘的“瓶身描绘的牡丹一如你初妆”、“色白花青的锦鲤跃然于碗底”等图案让人赏心悦目，但古瓷中所用颜料成分一直是个谜，近年来科学家才得知大多为硅酸盐，如蓝紫色的硅酸铜钡(BaCuSi2O6)。

下列关于硅酸铜钡的说法不正确的是()A．是一种硅酸盐B．性质稳定，不易脱色C．易溶于强酸和强碱D．可用氧化物形式表示为BaO·CuO·2SiO2答案 C解析根据题干知，蓝紫色的硅酸铜钡(BaCuSi2O6)为硅酸盐，A项正确；古瓷年代久远，CO2气体，碳酸钠会与二氧化碳、水反应生成碳酸氢钠，由于①碳酸氢钠溶解度小于碳酸钠、②反应消耗溶剂水、③碳酸钠转化成碳酸氢钠质量大，故溶液会有碳酸氢钠晶体析出，故A项错误；向硅酸钠溶液中通入氯化氢气体，硅酸钠与盐酸反应生成难溶物硅酸，故有沉淀产生，故B项错误；向氯化钙和盐酸的混合溶液中通入SO2气体，三者该条件下不反应，故无沉淀产生，故C项正确；向硝酸银溶液中通入氯气，氯气溶于水反应产生Cl－，则Ag＋与Cl－反应产生氯化银沉淀，有固体析出，故D项错误。

3．(2019·杭州市余杭区高三联考)下列叙述正确的是()A．光导纤维中所用材料为晶体硅B．SiO2是酸性氧化物，所以不与任何酸反应C．可用Na2SiO3溶液和CO2反应来制备H2SiO3 D．NaOH溶液可以盛装在带玻璃塞的磨口试剂瓶中答案 C解析光导纤维的所用材料为二氧化硅，故A项错误；SiO2是酸性氧化物，但可与氢氟酸反应，故B项错误；硅酸酸性弱于碳酸，故可用碳酸与硅酸钠反应制备硅酸，故C项正确；玻璃中含有二氧化硅，二氧化硅为酸性氧化物，可与氢氧化钠反应生成硅酸钠和水，故NaOH溶液不可以盛装在带玻璃塞的磨口试剂瓶中，应用带橡胶塞的试剂瓶，故D项错误。

4．(2019·浙江省温州中学高三上学期期末)下列反应或现象与浓硫酸的强氧化性有关的是() A．浓硫酸可以干燥SO2、H2等气体B．常温下浓硫酸可以使Al、Fe发生钝化C．浓硫酸溶于水放热D．用浓硫酸和NaCl固体加热制备HCl气体答案 B解析浓硫酸具有吸水性，可以干燥SO2、H2等气体，与氧化性无关，A错误；常温下浓硫酸可以使Al、Fe发生钝化，与其强氧化性有关系，B 正确；用浓硫酸和NaCl固体加热制备HCl气体利用的是浓硫酸的高沸点、难挥发性，与氧化性无关系，D错误。

一、选择题（每题5分，共50分）1. 下列各数中，不是有理数的是（）A. 0.1010010001…B. -3/4C. 2/5D. 32. 已知a、b是实数，且a + b = 0，那么下列各式中，正确的是（）A. a² = b²B. a² = -b²C. ab = 0D. a = -b3. 若x² - 3x + 2 = 0，则x的值为（）A. 1或2B. -1或2C. 1或-2D. -1或-24. 已知等差数列{an}的公差为d，且a1 = 3，a3 = 9，那么d的值为（）A. 3B. 6C. 9D. 125. 在平面直角坐标系中，点P（2，3）关于原点对称的点的坐标是（）A.（2，-3）B.（-2，3）C.（-2，-3）D.（2，-3）6. 下列函数中，是反比例函数的是（）A. y = 2x + 1B. y = 1/xC. y = x²D. y = √x7. 若直角三角形的两条直角边分别为3和4，那么斜边的长度是（）A. 5B. 6C. 7D. 88. 下列图形中，不是轴对称图形的是（）A. 正方形B. 等边三角形C. 长方形D. 梯形9. 下列各式中，正确的是（）A. 2x + 3 = 5x - 1B. 2x - 3 = 5x + 1C. 2x + 3 = 5x + 1D. 2x - 3 = 5x - 110. 若a、b是方程x² - 2ax + b = 0的两个实数根，那么下列各式中，正确的是（）A. a + b = 2aB. a + b = -2aC. ab = a²D. ab = b²二、填空题（每题5分，共50分）1. 已知x² - 3x + 2 = 0，则x的值为______。

2. 等差数列{an}的公差为d，且a1 = 3，a5 = 15，那么d的值为______。

3. 在平面直角坐标系中，点P（-2，3）关于y轴对称的点的坐标是______。

一、选择题（每题2分，共20分）1. 下列哪个数是奇数？A. 7B. 8C. 9D. 102. 下列哪个数是质数？A. 4B. 6C. 7D. 83. 一个长方形的长是10厘米，宽是5厘米，它的周长是多少厘米？A. 20B. 25C. 30D. 354. 下列哪个分数大于1/2？A. 1/4B. 1/3C. 2/3D. 3/45. 一个班级有36人，其中女生人数是男生人数的2倍，这个班级男生有多少人？A. 12B. 18C. 24D. 306. 下列哪个图形是正方形？A. 正三角形B. 正方形C. 长方形D. 梯形7. 一个篮子里有5个苹果，小明拿走了2个，篮子里还剩几个苹果？A. 3B. 4C. 5D. 68. 下列哪个数是两位数？A. 99B. 100C. 101D. 1029. 下列哪个算式是正确的？A. 3 + 4 = 7B. 3 + 4 = 8C. 3 + 4 = 9D. 3 + 4 = 1010. 一个圆形的半径是3厘米，它的周长是多少厘米？A. 6πB. 9πC. 12πD. 15π二、填空题（每题2分，共20分）11. 5个2相加的和是______。

12. 8减去3的差是______。

13. 12除以4的商是______。

14. 4乘以6等于______。

15. 100分等于______角。

16. 一个长方形的面积是24平方厘米，长是8厘米，宽是______厘米。

17. 一个班级有48人，男生人数是女生人数的3倍，女生有多少人？18. 下列哪个数是两位数：______、______、______。

19. 下列哪个图形是平行四边形：______、______、______。

20. 一个三角形的高是6厘米，底是4厘米，它的面积是______平方厘米。

三、解答题（每题10分，共30分）21. 一个苹果重150克，小明买了3个苹果，他一共买了多少克苹果？22. 一个长方形的长是12厘米，宽是4厘米，求它的周长和面积。

一、选择题（每题2分，共20分）1. 下列各数中，是质数的是（）。

A. 25B. 49C. 37D. 812. 一个长方形的长是8厘米，宽是5厘米，它的周长是（）厘米。

A. 26B. 27C. 28D. 293. 下列各图中，是平行四边形的是（）。

A. 图1B. 图2C. 图3D. 图44. 一个三位数，百位和十位上的数字之和是14，个位上的数字是3，这个数最大是（）。

A. 643B. 653C. 673D. 6835. 一个圆形的半径扩大到原来的2倍，它的面积将扩大到原来的（）倍。

A. 2B. 4C. 8D. 166. 小明从家出发，向北走了5千米，再向东走了10千米，此时他离家的距离是（）千米。

A. 5B. 10C. 15D. 207. 下列各数中，能同时被2和3整除的是（）。

A. 15B. 18C. 20D. 248. 一个数的十分位上是7，百分位上是3，这个数写作（）。

A. 0.73B. 0.37C. 7.03D. 37.09. 一箱苹果共有48个，平均分给4个同学，每人分得（）个苹果。

A. 12B. 11C. 10D. 910. 下列各数中，是最简分数的是（）。

A. 3/6B. 2/5C. 4/8D. 5/10二、填空题（每题2分，共20分）11. 0.5乘以2等于（）。

12. 100除以4等于（）。

13. 一个长方体的长、宽、高分别是4厘米、3厘米、2厘米，它的体积是（）立方厘米。

14. 一个圆的半径是5厘米，它的周长是（）厘米。

15. 一个三角形的三边长分别是3厘米、4厘米、5厘米，它是一个（）三角形。

16. 一个数的十分位上是4，百分位上是5，这个数写作（）。

17. 一个长方形的长是6厘米，宽是4厘米，它的周长是（）厘米。

18. 下列各数中，是合数的是（）。

19. 一个正方形的边长是6厘米，它的面积是（）平方厘米。

20. 一个数的千位上是3，百位上是5，十位上是8，个位上是2，这个数写作（）。