4.北京2016初三中考二模数学word版试题-顺义

DCBAADCB 北京市各城区中考二模数学——四边形的证明与计算题19题汇总1、（门头沟二模）19. 如图，在平行四边形ABCD 中，点E ，F 分别是AB ，CD 的中点.(1)求证：四边形AEFD 是平行四边形； (2)若∠A =60°，AB =6，AD =4，求BD 的长.2、（丰台二模）19．如图，在四边形ABCD 中，AD∥BC ，CA 是∠BCD 的平分线，且AB ⊥AC ，AB=4，AD=6，求AC 的长.3、（平谷二模）19．如图，在四边形ABCD 中，对角线BD 平分∠ABC ，∠A =120°， ∠C =60°，AB =5，AD =3． （1）求证：AD =DC ；（2）求四边形ABCD 的周长．4、(顺义二模) 19．如图，在ABC △中，D 、E 分别是AB 、AC 的中点，BE =2DE ，过点C 作CF ∥BE 交DE 的延长线于F ． （1）求证：四边形BCFE 是菱形；（2）若4CE =，120BCF ∠=°，求菱形BCFE 的面积．5、（石景山二模）19．如图1，在△OAB 中，∠OAB =90°，∠AOB =30°，BA =2．以OB 为边，向外作等边△OBC ，D 是OB 的中点，连接AD 并延长交OC 于E ． （1）求证：四边形ABCE 是平行四边形；（2）如图2，将图1中的四边形ABCO 折叠，使点C 与点A 重合，折痕为FG ，求OG 的长．6、（海淀二模）19．如图，在△ABC 中，点D 、E 分别是边BC 、AC 的中点，过点A 作AF∥BC 交DE 的延长线于F 点，连接CF . （1）求证：四边形ABDF 是平行四边形；（2）若∠CAF =45°，BC=4，CF=10，求△CAF 的面积.7、（西城二模）19．如图，在四边形ABCD 中，AB ∥DC ， DB 平分∠ADC ， E 是CD 的延长线上一点，且12AEC ADC ∠=∠．（1）求证：四边形ABDE 是平行四边形．（2）若DB ⊥CB ，∠BCD ＝60°，CD ＝12，作AH ⊥BD 于H ，求四边形AEDH 的周长．FEDCBAEADCBOG A BCFD E C B A O 图1 F GCBO A图2GDC BAEF8、（通州二模）20．如图，在平行四边形ABCD 中，E 为BC 边上的一点，连接AE 、BD 交于点F ，AE ＝AB .（1）若∠AEB ＝2∠ADB ，求证：四边形ABCD 是菱形. （2）若AB ＝10，BE ＝2EC ，求EF 的长.9、（东城二模）19．在平行四边形ABCD 中，AB =6，AD =9，∠BAD 的平分线交BC 于点E ，交DC 的延长线于点F ，BG ⊥AE 于点G ，42BG ，求EFC 的周长.10、（朝阳二模）19．如图，在四边形ABCD 中，AB =34，∠DAB =90°，∠B =60°，AC ⊥BC ．（1）求AC的长．（2）若AD=2，求CD 的长．11、（密云二模）19．如图，在平行四边形ABCD 中，AB=4，∠BAD 的平分线与BC 的延长线交于点E ，与DC 交于点F,且点F 为边DC 的中点，DG ⊥AE ，垂足为G ，若DG=1，求AE 的长.12、（延庆二模）13、(房山二模) 19. 已知：如图，梯形ABCD 中，AD=BC ，F 为BC 的中点，AB=2，∠A =120°，过点F 作EF⊥BC 交DC 于点E ，且EF = 3 ，求DC 的长.14、（昌平二模）18．如图，已知□ABCD ，E ，F 是对角线BD 上的两点，且BE =DF .（1）求证：四边形AECF 是平行四边形；（2）当AE 垂直平分BC 且四边形AECF 为菱形时，直接写出AE ∶AB 的值.15、（怀柔二模）19.如图，已知△ABC 是等边三角形，点D 、F 分别在线段BC 、AB 上，∠EFB=60°，DC=EF ． （1）求证：四边形EFCD 是平行四边形； （2）若BF=EF ，求证：AE=AD ．16、（大兴二模）19．已知： 如图，在平行四边形ABCD 中，点E 、F 分别是AB 、CD 的中点 .(1)求证：四边形AEFD 是平行四边形； (2)若∠A =60°，AB=8，AD=4，求BD 的长 .FDCEABFE DCBA17、（燕山二模）19. 如图，在四边形ABCD中，BC AD //，25=AB ，4=BC ，连接BD ，BAD ∠的平分线交BD 于点E ，且CD AE //． （1）求AD 的长；（2）若︒=∠30C ，求四边形ABCD 的周长．ED CBA。

2023年北京顺义中考二模数学试卷一、选择题1.已知直线上两点A(2, 4)和B(6, 8)，则这两个点的中点坐标为（）。

A. (4, 6)B. (5, 6)C. (6, 6)D. (8, 12)2.下面哪一个数是无理数？ A. 0.25B. 1.5C. -3D. √23.一辆客车自上午8:00开始，每40分钟从始发站发车一次，从终点站返回时速为每小时60千米，若该车每次停车10分钟，则某乘客在上午11:30时正好在回家的半路上，求该乘客的家距离始发站的路程。

A. 128 千米B. 136 千米C. 144 千米D. 152 千米4.若正方形的边长为a，则其对角线的长度为（）。

A. aB. a√2C. a/√2D. 2a5.已知一根棍子长度为4m，两个人同时从棍子两端相对走向中心点，速度分别为每秒1m和每秒2m，则他们相遇的位置距离哪一边端点较近？A. 1mB. 1.5mC. 2mD. 2.5m二、填空题1.一辆车从A地到B地经过4个小时，速度为每小时60千米。

返回时速度加快30%，共耗时多少小时？2.某个数加上65等于其平方根的3倍，求该数。

3.在一个平行四边形中，两个内角的大小分别是120°和30°，则其邻角的度数分别是_________和_________。

4.若a:b = 3:4，b:c = 5:6，则a+c:b的值为_________。

5.已知三角形ABC中，∠B = 65°，AB = 5，AC = 8，则BC的长度等于_________。

1.（20分）某公司今年的销售额是200万元，预计下一年销售额将比今年增加25%，请计算下一年预计的销售额。

显示详细的计算过程。

2.（25分）已知某个数加上3的四次方等于112，请求这个数。

3.（25分）一块菱形的顶角是72°，边长是5，求这个菱形的面积。

4.（30分）某个长方体的长、宽、高分别是3，4，5，求其表面积和体积。

2022北京顺义初三二模化 学学校______________ 班级_____________ 姓名_____________ 准考证号______________第一部分本部分共25题，每题1分，共25分。

在每题列出的四个选项中，选出最符合题目要求的一项。

1．右图为空气成分示意图（按体积计算），其中“c”代表的是 A ．氧气 B ．氮气 C ．二氧化碳 D ．稀有气体 2．地壳中含量最多的金属元素是 A ．OB ．SiC ．AlD ．Fe3. 为防止骨质疏松，应补充的元素是 A. 铁B. 钙C. 锌D. 碘4．下列物质在氧气中燃烧，火星四射、生成黑色固体的是 A ．铁丝B ．木炭C ．红磷D ．氢气5．下列实验操作中，不正确．．．的是A ．蒸发食盐水B ．检查装置气密性C ．取固体粉末D ．倾倒液体6．草木灰是一种农家肥料，其有效成分是K 2CO 3，它属于 A ．氮肥B ．磷肥C ．钾肥D ．复合肥7. 下列属于二氧化碳用途的是A ．火箭燃料B ．作气体肥料C ．供给呼吸D ．制霓虹灯8. 右图是某方便面的营养成分表，其中没有．．列出的营养素为 A.糖类 B.油脂 C.蛋白质 D.维生素9. 氢氧化钠的俗称是A．纯碱 B．烧碱 C．熟石灰 D．小苏打10. 下列物质含有氢分子的是A．H2 B．H2O C．H2CO3 D．HCl11. 右图所示的图标表示A. 严禁烟火B. 禁止带火种C. 禁止燃放鞭炮D. 禁止堆放易燃物12. 下图是生活中常见洗涤用品的p H，其中显酸性的是A.洁厕灵B.消毒液C.肥皂水D.油污净13．下列清洗方法中，利用乳化原理的是A．用汽油洗去衣服上的油污 B．用自来水洗手C．用洗洁精洗去餐具上的油渍 D．用醋清洗水壶中的水垢14．6000L氧气在加压下可装入容积为40L的钢瓶中，主要原因是A. 氧分子体积小B. 氧分子在不断运动C. 氧分子质量小D. 氧分子间有空隙15．高山滑雪是冬奥会项目之一。

实数的有关计算问题（北京真题10道+模拟30道）【方法归纳】题型概述，方法小结，有的放矢1.实数的运算（1）实数的运算和在有理数范围内一样，值得一提的是，实数既可以进行加、减、乘、除、乘方运算，又可以进行开方运算，其中正实数可以开平方．（2）在进行实数运算时，和有理数运算一样，要从高级到低级，即先算乘方、开方，再算乘除，最后算加减，有括号的要先算括号里面的，同级运算要按照从左到右的顺序进行．另外，有理数的运算律在实数范围内仍然适用．2.实数运算的“三个关键”（1）．运算法则：乘方和开方运算、幂的运算、指数（特别是负整数指数，0指数）运算、根式运算、特殊三角函数值的计算以及绝对值的化简等．（2）．运算顺序：先乘方，再乘除，后加减，有括号的先算括号里面的，在同一级运算中要从左到右依次运算，无论何种运算，都要注意先定符号后运算．（3）．运算律的使用：使用运算律可以简化运算，提高运算速度和准确度．【典例剖析】典例精讲，方法提炼，精准提分【例1】（2021·北京·中考真题）计算：2sin60°+√12+|−5|−(π+√2)0．【答案】3√3+4【解析】【分析】根据特殊三角函数值、零次幂及二次根式的运算可直接进行求解．【详解】+2√3+5−1=3√3+4．解：原式=2×√32【点睛】本题主要考查特殊三角函数值、零次幂及二次根式的运算，熟练掌握特殊三角函数值、零次幂及二次根式的运算是解题的关键．【例2】（2022·北京·中考真题）计算：(π−1)0+4sin45∘−√8+|−3|.【答案】4【解析】【分析】根据零次幂、特殊角的正弦值、二次根式和去绝对值即可求解．【详解】解：(π−1)0+4sin45∘−√8+|−3|.=1+4×√22−2√2+3=4．【点睛】本题考查了实数的混合运算，掌握零次幂、特殊角的正弦值、二次根式的化简及去绝对值是解题的关键．【真题再现】必刷真题，关注素养，把握核心1．（2013·北京·中考真题）计算：．【答案】5【解析】【分析】针对零指数幂，绝对值，特殊角的三角函数值，负整数指数幂4个考点分别进行计算，然后根据实数的运算法则求得计算结果．【详解】解：原式＝1+√2−2×√22+4=5．2．（2014·北京·中考真题）计算：(6−π)0+(−15)−1−3tan30°+|−√3|.【答案】-4【解析】【详解】特殊角的三角函数值，按顺序计算即可试题解析：原式=1+(−5)−√3+√3=-4考点：1、零指数幂；2特殊角的三角函数值；3、绝对值；4、负指数幂3．（2015·北京·中考真题）计算：(12)−2−(π−√7)0+|√3−2|+4sin60°．【答案】5+√3【解析】【分析】先根据一个数的负指数幂等于正指数幂的倒数，一个不等于零的数的零指数幂为１，一个数的绝对值是非负数，特殊角三角函数值sin60°=√32，求出各项的值即可． 【详解】解：原式=4−1+2−√3+4×√32=5−√3+2√3 =5+√3 【点睛】本题考查实数的混合运算；特殊角三角函数值．4．（2016·北京·中考真题）计算：(3−π)0+4sin45∘−√8+|1−√3|． 【答案】√3．【解析】【分析】根据实数的运算顺序，首先计算乘方、开方和乘法，然后从左向右依次计算即可．【详解】解：原式=1+4×√22−2√2+√3−1=√3． 5．（2017·北京·中考真题）计算：4cos30°+(1−√2)°−√12+|−2|．【答案】3．【解析】【详解】试题分析：利用特殊三角函数值，零指数幂，算术平方根，绝对值计算即可.试题解析：原式=4×√32 +1-2√3+2=2√3+1-2√3+2=3 . 6．（2018·北京·中考真题）计算：4sin45°+(π−2)0−√18+|−1|．【答案】2−√2【解析】【分析】按照实数的运算顺序进行运算即可.【详解】原式=4×√22+1−3√2+1=2−√2．【点睛】本题考查实数的运算，主要考查零次幂，绝对值，特殊角的三角函数值以及二次根式，熟练掌握各个知识点是解题的关键.7．（2019·北京·中考真题）计算：|−√3|−(4−π)0−2sin60∘+（14）−1.【答案】3【解析】【分析】根据绝对值、零指数幂、特殊角的三角函数值、负指数幂法则计算即可【详解】原式=√3−1+2×√32+4=√3−1−√3+4=3【点睛】本题考查零指数幂、特殊角的三角函数值，负指数幂，熟练掌握相关的知识是解题的关键．8．（2020·北京·中考真题）计算：(13)−1+√18+|−2|−6sin45°【答案】5【解析】【分析】分别计算负整数指数幂，算术平方根，绝对值，锐角三角函数，再合并即可得到答案．【详解】解：原式=3+3√2+2−6×√22=3+3√2+2−3√2=5.【点睛】本题考查的是负整数指数幂，算术平方根，绝对值，锐角三角函数，以及合并同类二次根式，掌握以上的知识是解题的关键．【模拟精练】押题必刷，巅峰冲刺，提分培优1．（2022·北京房山·二模）计算：tan60°+(3−π)0+|1−√3|+√27．【答案】5√3【解析】【分析】分别计算三角函数值、零指数幂，化简绝对值和二次根式，再进行加减即可．【详解】解：原式=√3+1+√3−1+3√3=5√3．【点睛】本题考查特殊角三角函数、零指数幂以及绝对值和二次根式的化简，属于基础题，熟练掌握上述基本知识是解题的关键．2．（2022·北京朝阳·二模）计算√18+2sin45∘−(12)−1+|√2−2|．【答案】3√2【解析】【分析】分别根据二次根式的性质，45°角的三角函数值，负整数指数幂及绝对值的性质进行化简，最后再由二次根式的运算法则合并即可．【详解】解：原式=3√2+2×√22−2+2−√2 =3√2．故答案为：3√2．【点睛】 此题考查了实数的混合运算，正确掌握二次根式的性质，45°角的三角函数值，负整数指数幂定义及绝对值的性质是解题的关键．3．（2022·北京平谷·二模）计算：√83+(13)−1−2cos30°+|1−√3|．【答案】4【解析】【分析】先利用负整数指数幂，特殊角锐角三角函数值，绝对值的性质，立方根的性质化简，再合并，即可求解．【详解】 解：√83+(13)−1−2cos30°+|1−√3|=2+3−2×√32+√3−1=2+3−√3+√3−1 =4．【点睛】本题主要考查了负整数指数幂，特殊角锐角三角函数值，绝对值的性质，立方根的性质，熟练掌握相关运算法则是解题的关键是解题的关键．4．（2022·北京北京·二模）计算：(12)−1−4cos30∘+√12+|−2|．【答案】4【解析】【分析】先计算乘方和化简二次根式，并把特殊角的三角函数值代入，去值符号，再计算乘法，最后计算加减即可．【详解】解：原式=2−4×√32+2√3+2 =2-2√3+2√3+2=4．【点睛】本题考查实数的混合运算，熟练掌握实数的运算法则，负整指数幂的运算，熟记特殊角的三角函数值是解题的关键．5．（2022·北京丰台·二模）计算：|−3|−2sin45∘+√8+(π+√3)0【答案】4+√2【解析】【分析】原式第一项利用绝对值的意义化简，第二项利用特殊角的三角函数值计算，第三项化为最简二次根式，第四项利用零指数幂法则计算即可得到结果．【详解】解：原式 = 3−2×√22+2√2+1 =3−√2+2√2+1=4+√2．【点睛】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．6．（2022·北京西城·二模）计算：|−√2|+2cos45°−√8+(13)−2． 【答案】9【解析】【分析】先去绝对符号，把特殊角三角函数值代入，化简二次根式并计算乘方，再进行乘法运算，最后计算加减即可．【详解】解：原式=√2+2×√22-2√2+9 =√2+√2-2√2+9=9．【点睛】本题考查实数的混合运算，熟练掌握特殊角的三角函数值、二次根式化简、负整指数幂的运算是解题的关键．7．（2022·北京顺义·二模）计算：√18−4cos45°+|−2|−(1−√2)0． 【答案】√2+1【解析】【分析】根据二次根式的性质化简，代入特殊角的三角函数值，化简绝对值，求零次幂，进行实数的计算即可求解．【详解】解：原式＝3√2−4×√22+2−1 =3√2−2√2+2−1 =√2+1．【点睛】本题考查了实数的混合运算，掌握二次根式的性质化简，代入特殊角的三角函数值，化简绝对值，求零次幂是解题的关键．8．（2022·北京市十一学校二模）计算：√3tan30°+|√2−2|−√83+(π−3)0【答案】2−√2【解析】【分析】先根据特殊角锐角三角函数值，绝对值的性质，立方根，零指数幂化简，再合并，即可求解．【详解】 解：√3tan30°+|√2−2|−√83+(π−3)0 =√3×√33+2−√2−2+1=1+2−√2−2+1=2−√2【点睛】本题主要考查了特殊角锐角三角函数值，绝对值的性质，立方根，零指数幂，熟练掌握相关运算法则是解题的关键．9．（2022·北京大兴·一模）计算：2sin30°+√8+|−5|−(−12)−1． 【答案】8+2√2【解析】【分析】先计算锐角三角函数、算术平方根、绝对值和负整数指数幂，再利用实数的加减法法则计算即可．【详解】解：原式=2×12+2√2+5−(−2)=1+2√2+5+2=8+2√2．【点睛】本题考查特殊三角函数值、负整数指数幂、算术平方根等内容，掌握运算法则是解题的关键．10．（2022·北京东城·二模）计算：(−1)2022+√83−(13)−1+√2sin45°．【答案】1【解析】【分析】先计算乘方和开方运算，并把特殊角的三角函数值代入，再计算乘法，最后计算加减即可求解．【详解】解：原式=1+2-3+√2×√22=1+2-3+1=1【点睛】本题考查实数的混合运算，熟练掌握负整指数幂的运算法则和熟记特殊角的三角函数值是解题的关键． 11．（2022·北京丰台·一模）计算：（12）﹣1﹣2cos30°+|﹣√12|﹣（3.14﹣π）0． 【答案】√3+1【解析】【分析】分别根据负整数指数幂、特殊角的三角函数值、绝对值的性质、零指数幂计算出各数，再根据混合运算的法则进行计算；【详解】解：（12）﹣1﹣2cos30°+|﹣√12|﹣（3.14﹣π）0＝2﹣2×√32+2√3﹣1 ＝2﹣√3+2√3﹣1 ＝√3+1【点睛】此题考查了负整数指数幂、特殊角的三角函数值、绝对值的性质、零指数幂，掌握相关运算法则是解题的关键．12．（2022·北京一七一中一模）计算：3tan30°+(13)−1+20220+|√3−2|.【答案】6【解析】【分析】根据特殊角三角函数值，负整数指数幂，零指数幂，绝对值的计算法则求解即可．【详解】解：3tan30°+(13)−1+20220+|√3−2|=3×√33+3+1+2−√3 =√3+3+1+2−√3=6．【点睛】本题主要考查了特殊角三角函数值，负整数指数幂，零指数幂，绝对值，实数的混合计算，熟知相关计算法则是解题的关键．13．（2022·北京平谷·一模）计算：√12+(15)−1−3tan30°−|−2|．【答案】3+√3【解析】【分析】根据特殊角三角函数值，负整数指数幂，绝对值，以及二次根式的性质进行求解即可．【详解】 解：√12+(15)−1−3tan30°−|−2|=2√3+5−3×√33−2 =2√3+5−√3−2=3+√3．【点睛】本题主要考查了特殊角三角函数值，负整数指数幂，绝对值，以及二次根式的性质，实数的运算，熟知相关计算法则是解题的关键．14．（2022·北京·东直门中学模拟预测）计算：2cos30°+√12−|−√3|−(π+√2)°．【答案】2√3−1【解析】【分析】根据0指数幂运算法则、绝对值的性质及特殊角的三角函数值计算出各数，再根据实数混合运算的法则进行计算即可．【详解】解：原式=2×√32+2√3−√3−1=√3+2√3−√3−1=2√3−1．【点睛】本题考查的是实数的运算，熟知0指数幂的运算法则、绝对值的性质及特殊角的三角函数值是解答此题的关键．15．（2022·北京市第一六一中学分校一模）计算：2sin45°+|√2−3|−(π−2022)0+(13)−2．【答案】11【解析】【分析】原式第一项利用特殊角的三角函数值计算，第二项利用绝对值的代数意义化简，第三项利用零指数幂法则计算，最后一项利用负整数指数幂法则计算即可得到结果．【详解】解：2sin45°+|√2−3|−(π−2022)0+(13)−2=2×√22+3−√2−1+32=√2+3−√2−1+9=11．【点睛】此题考查了实数的运算、特殊角的三角函数值、零指数幂和负整数指数幂，熟练掌握运算法则是解本题的关键．16．（2022·北京朝阳·一模）计算：2cos30°+|−√3|−(π−√3)0−√12．【答案】-1【解析】【分析】根据实数的计算，把各个部分的值求出来进行计算即可．【详解】解：原式=2×√32+√3−1−2√3 =√3+√3−1−2√3=-1．【点睛】本题考查了实数的混合运算，准确记忆特殊角的锐角三角函数值、绝对值化简、零指数幂、二次根式的化简是解题的关键．17．（2022·北京顺义·一模）计算：2tan60°−√27+(12)−2+|1−√3|．【答案】3【解析】【分析】直接利用二次根式的性质、绝对值的性质、特殊角的三角函数值、负整数指数幂的性质分别化简得出答案．【详解】解：原式=2×√3−3√3+4+√3−1=3【点睛】此题主要考查了特殊角的三角函数值、实数运算，正确化简各数是解题关键．18．（2022·北京·中国人民大学附属中学朝阳学校一模）计算：4cos45°+(√3−1)0−√8+2−1． 【答案】32【解析】【分析】先分别根据特殊角的三角函数值、零指数幂、二次根式的化简、负指数幂计算，然后根据实数混合运算法则计算即可求得结果．【详解】解：原式=4×√22+1−2√2+12 =2√2+32−2√2 =32． 【点睛】本题考查了特殊角的三角函数值、零指数幂、二次根式的化简、负指数幂，熟练掌握相关运算法则和熟记特殊角的三角函数值是解题的关键．19．（2022·北京·模拟预测）计算：cos 230°+|1﹣√2|﹣2sin45°+（π﹣3.14）0 【答案】34【解析】【分析】根据cos30°=√32，|1−√2|=√2−1，sin45°=√22，(π−3.14)0=1，再计算即可． 【详解】解：原式＝(√32)2+√2−1−2×√22+1 ＝34+√2−√2 ＝34【点睛】本题主要考查了实数的运算，掌握特殊角三角函数值，零指数次幂，绝对值的性质是解题的关键． 20．（2022·北京市师达中学模拟预测）计算：(15)−1−(π−2022)0+|√3−1|−3tan30°【答案】3【解析】【分析】先根据负指数幂、零指数幂、绝对值的意义和特殊角的三角函数值分别计算，然后再根据实数的混合运算法则计算即可求得结果．【详解】解：原式=5−1+√3−1−3×√33=3+√3−√3=3【点睛】本题主要考查负指数幂、零指数幂、绝对值的意义和特殊角的三角函数值，熟练掌握相关运算法则和熟记特殊角的三角函数值是解题的关键．21．（2022·北京朝阳·模拟预测）计算：（﹣1）2020﹣√9﹣（3﹣π）0+|3﹣√3|+（tan30°）﹣1．【答案】0【解析】【分析】计算乘方、算术平方根、零指数幂、去绝对值符号、代入三角函数值并计算负整数指数幂，再计算加减可得；【详解】解：原式=1﹣3﹣1+3﹣√3+（√33）-1=1﹣3﹣1+3﹣√3+√3=0．【点睛】本题考查了实数的运算，解决此类题目的关键是熟练掌握零指数幂、负整数指数幂、特殊角的三角函数值、绝对值等考点的运算．22．（2022·北京·一模）计算√2cos45°+(1−π)0+√14+|1−√2|．【答案】32+√2【解析】【分析】根据特殊角的三角函数值，零指数幂，二次根式的性质，化简绝对值进行计算即可．【详解】原式=√2×√22+1+12+(√2−1)=1+1+12+√2−1=32+√2【点睛】本题考查了实数的混合运算，掌握特殊角的三角函数值，零指数幂，二次根式的性质，化简绝对值是解题的关键．23．（2022·北京·北理工附中模拟预测）计算：−√274−(1−π)0+2tan 30°−|√32−（√32）−1| 【答案】−√3−1【解析】【分析】根据二次根式的性质化简，零指数幂，特殊角的三角函数值，负整数指数幂，化简绝对值，进行计算即可【详解】解：−√274−(1−π)0+2tan 30°−|√32−（√32）−1| =−3√32−1+2×√33−|√32−2√33| =−3√32+2√33−(2√33−√32)−1 =−√3−1 【点睛】本题考查了实数的混合运算，掌握二次根式的性质化简，零指数幂，特殊角的三角函数值，负整数指数幂，化简绝对值是解题的关键．24．（2022·北京师大附中模拟预测）计算：√8+(−12)−1−4cos45°+|−2|【答案】0【解析】【分析】根据二次根式的性质、负整数指数幂、特殊角的三角函数值分别计算各项，即可求解．【详解】解：原式=2√2−2−4×√22+2 =0．【点睛】本题考查实数的混合运算，掌握二次根式的性质、负整数指数幂、特殊角的三角函数值是解题的关键． 25．（2022·北京四中模拟预测）计算：(13)−1−√12+3tan30°+|√3−2|．【答案】5−2√3【解析】【分析】直接利用特殊角的三角函数值以及负指数幂的性质和绝对值的性质化简得出答案．【详解】解：原式＝3−2√3+3×√33+2−√3 =5−2√3．【点睛】本题主要考查了实数的运算，正确化简各数是解题的关键．26．（2021·北京平谷·二模）计算：|−√2|−2cos45°+(π−1)0+(12)−1【答案】3【解析】【分析】根据绝对值的性质、特殊角的三角函数值、零指数幂以及负整指数幂进行运算即可【详解】解：|−√2|−2cos45°+(π−1)0+(12)−1 ＝√2−2×√22+1+2 ＝3【点睛】本题考查了实数的混合运算，涉及到绝对值的性质、特殊角的三角函数值、零指数幂以及负整指数幂，熟练掌握法则是解题的关键27．（2021·北京朝阳·二模）计算：√12+(√5−2)0−(13)−1+tan60°． 【答案】3√3−2【解析】【分析】直接根据无理数的运算，零指数幂，负整数指数幂和特殊角的三角函数值计算即可．【详解】解：原式=2√3+1−3+√3=3√3−2．【点睛】本题主要考查实数的运算，掌握无理数的运算，零指数幂，负整数指数幂的运算法则和特殊角的三角函数值是关键．28．（2021·北京顺义·二模）计算：(2−π)0+3−1+|√2|−2sin45°．【答案】43【解析】【分析】根据混合运算公式运算即可【详解】解：原式＝1+13+√2−2×√22＝43【点睛】本题主要考查实数混合运算内容，注意运算中的易错点，避免犯错，属于常考题．29．（2021·北京房山·二模）计算：(13)−1−2sin60°+|−√3|−(π−2021)0【答案】2【解析】【分析】根据负整数指数幂，绝对值的化简，零指数幂定义依次化简及特殊角的三角函数值代入计算即可．【详解】解：原式=(13)−1−2sin60°+|−√3|−(π−2021)0=3−√3+√3−1=2．【点睛】此题考查实数的计算，正确掌握负整数指数幂，绝对值的化简，零指数幂定义依次化简及特殊角的三角函数值是解题的关键．30．（2021·北京海淀·二模）计算：(12)−1+√8+|√3−1|−2sin60°．【答案】1+2√2【解析】【分析】原式利用负整数指数幂法则、二次根式的性质、绝对值的性质以及特殊角的三角函数值计算即可求出值．【详解】原式=2+2√2+√3−1−2×√32=1+2√2．【点睛】此题考查了实数的运算，负整数指数幂，绝对值的性质以及特殊角的三角函数值，熟练掌握运算法则是解本题的关键．。

顺义区2024年高三第二次质量监测数学试卷本试卷共9页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题：共10小题，每小题4分，共40分。

在每小题列出的四个选项中，选出符合 题目要求的一项。

1. 设集合{}24U x x =∈≤Z ，{}1,2A =，则U C A = A.[2,0]−B.{}0C.{}2,1−−D.{}2,1,0−−2. 已知复数z 的共轭复数z 满足(1i)2i z +⋅=，则z z ⋅=B.1C.2D.43. 在5(21)x −的展开式中，4x 的系数为 A.80− B.40− C.40 D.804. 已知4log 2a =，e1()2b =，12πc =，则A.a b c >>B.b a c >>C.c b a >>D.c a b >>5. 已知各项均为正数的数列{}n a 的前n 项和为n S ，11a =，1lg lg lg 2n n n a a ++=，*n ∈N ， 则9S = A.511 B.61 C.41 D.96. 已知抛物线2:4C y x =的焦点为F ，准线为l ，P 为C 上一点，直线PF 与l 相交于点Q ，与y 轴交于点M . 若F 为PQ 的中点，则||PM =A.4B.6C. D.87. 若函数1,0()0, 01,0x x f x x x x −<⎧⎪==⎨⎪+>⎩，则“120x x +>”是“12()()0f x f x +>”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件8. 如图，正方体1111ABCD A B C D −中，P 是线段1BC 上的动点，有下列四个说法： ①存在点P ，使得1//D P 平面1A DB ；②对于任意点P ，四棱锥11P A ADD −体积为定值； ③存在点P ，使得1A P ⊥平面1C DB ； ④对于任意点P ，1A DP △都是锐角三角形， 其中，不正确．．．的是 A.①B.②C.③D.④9. 已知在平面内，圆22:1O x y +=，点P 为圆外一点，满足||2PO =，过点P 作圆O 的两条切线，切点分别为,A B . 若圆O 上存在异于,A B 的点M ，使得2(1)PM PA PB λλ=+−，则λ的值是A.23B.12C.14 D.12−10. 设1237,,,a a a a 是1,2,3,,7的一个排列. 且满足122367||||||a a a a a a −≥−≥≥−，则122367||||||a a a a a a −+−++−的最大值是A.23B.21C.20D.18第二部分（非选择题 共110分）二、填空题共5小题，每小题5分，共25分。

顺义区2024年初中学业水平考试综合练习（二）化学试卷可能用到的相对原子质量：H1C12N14O16第一部分本部分共25题，每题1分，共25分。

在每题列出的四个选项中，选出最符合题目要求的一项。

1.富硒大米中的“硒”是指（）A.元素B.原子C.分子D.离子2.下列金属活动性最强的是（）A.FeB.AlC.MgD.Cu 3.将密封良好的饼干从平原带到高原时，包装袋鼓起，是因为袋内的气体分子（）A.质量增大 B.间隔增大C.体积增大D.个数增多4.一些物质的pH 范围如下，其中呈碱性的是（）A.酱油（4～5）B.西瓜汁（5～6）C.胡萝卜（6～7）D.牙膏（8～9）5.决定元素种类的是（）A.质子数 B.中子数C.电子数D.最外层电子数6.下列物质属于有机化合物的是（）A.23H CO B.NaCl C.NaOHD.3CH COOH7.下列物质放入水中能形成溶液的是（）A.面粉B.蔗糖C.泥沙D.植物油8.2024年世界地球日的主题为“全球战塑”。

废弃塑料瓶属于（）A.可回收物B.其他垃圾C.厨余垃圾D.有害垃圾9.下列行为符合“低碳”理念的是（）A.废旧金属回收利用B.复印纸单面使用C.农作物秸秆就地焚烧D.使用一次性餐具10.下列关于水的说法正确的是（）A.电器着火，用水浇灭B.提倡“一水多用”C.水由氢气和氧气组成D.活性炭可以除去水中所有杂质铁是人体内的必需微量元素。

回答11～15题。

11.下列符号表示两个铁离子的是（）A.2FeB.3+2FeC.2+FeD.3Fe 12.铁在元素周期表中的信息如图所示，下列有关铁元素的说法不正确．．．的是（）A.原子序数是26B.属于金属元素C.原子中核外电子数为30D.相对原子质量为55.8513.下列属于铁化学性质的是（）A.银白色固体B.有金属光泽C.硬度小D.能与氧气反应14.用铁锅炒菜，主要利用铁的性质是（）A.延展性B.导热性C.导电性D.抗腐蚀性15.下列物质能除铁锈的是（）A.NaOH溶液B.植物油C.食盐水D.盐酸16.配制500g溶质的质量分数为16%的氯化钠溶液，不需要．．．的仪器是（）A.烧杯B.玻璃棒C.酒精灯D.量筒17.下列实验操作中，正确的是（）A.倾倒液体B.滴加液体C.点燃酒精灯D.加热液体18.下列方法不能．．区分氧气和二氧化碳两瓶气体的是（）A.伸入带火星的木条B.闻气味C.倒入紫色石蕊溶液D.将集气瓶倒扣在水中人类的生存和发展离不开空气。

2024北京初三二模数学汇编选择压轴（第8题）一、单选题1．（2024北京朝阳初三二模）如图1，在菱形中，，P 是菱形内部一点，动点M 从顶点B 出发，沿线段运动到点P ，再沿线段运动到顶点A ，停止运动．设点M 运动的路程为x ，，表示y 与x 的函数关系的图象如图2所示，则菱形的边长是（ ）A ．B ．4C ．D ．22．（2024北京燕山初三二模）如图，是半圆O 的直径，C 是半圆周上的动点(与A ，B 不重合），于点D ，连接．设，给出下面三个结论：①；②；③．上述结论中，所有正确结论的序号是（ ）A ．①②B ．②③C ．①③D ．①②③3．（2024北京东城初三二模）如图，在中，于点，点是的中点．设，，，，，，且，有以下三个结论：①；②点，，在以点为圆心，为半径的圆上；ABCD =60B ∠︒BP PA MA y MC=ABCD AB CD AB ⊥OC AD a BD b CD h ===，，2a b h +≤||2a b h -≤2a b +≥ABC AD BC ⊥D E BC AB c =AC b =AD h =BD m =CD n =m n <2h mn =22c m mn =+A B C E ()12m n +③．上述结论中，所有正确结论的序号是（ ）A ．①②B ．①③C ．②③D ．①②③4．（2024北京海淀初三二模）某种型号的纸杯如图所示，若将个这种型号的杯子按图中的方式叠放在一起，叠在一起的杯子的总高度为．则与满足的函数关系可能是（ ）A ．B ．C ．D ．5．（2024北京房山初三二模）如图，，，分别是直径为的的内接正六边形、正方形、等边三角形的一边．若，给出下而四个结论：①的直径为4；②③；④连接，则．上述结论中，所有正确结论的序号是（ ）A ．①③B ．②④C ．①②③D ．①②③④6．（2024北京顺义初三二模）如图，在中，是边上一动点（不与B ，C 重合），于点E ．设给出下面三个结论：①③上述结论中，所有正确结论的序号是（ ）2223b m h +>1n 2H H n 0.3H n =100.3H n =100.3H n =-100.3H n=+AB AC AD AE O 2AB =O AC = BCCD =CD ACD ABC 90,,C A C B C D ︒∠==BC DE AB ⊥,,.CD a BD b AE c ===;a b c +>);a b c +>2.a b +=A ．①③B ．②③C ．②D ．①②③7．（2024北京昌平初三二模）如图，为半圆O 的直径，C ，D 是直径上两点，且，过点D 作的垂线交半圆于点E ，．设，，，给出下面三个结论：①；②；③．所有正确结论的序号是（ ）A ．①②B．①③C ．②③D ．①②③8．（2024北京门头沟初三二模）如图所示，两个体积不等的圆柱形水杯，大小水杯口均朝上，现往大水杯中均匀注水，注水过程中小水杯始终在原来位置，设水面上升高度为h ，注水时间为t ，下列图象能正确反应注水高度随时间变化关系的是（ ）A ．B ．C ．D ．9．（2024北京北师大附属实验中学初三二模）如图，在平面直角坐标系中，矩形ABCD 的顶点A ，C 分别在x 轴，y 轴的正半轴上，点D （-2，3），AD =5，若反比例函数 （k ＞0，x ＞0）的图象经过点B ，则k 的值为（ ）AB AB AC BD =AB 2CD DE =AD a =AC b =DE c =2a b c -=c b a c=a b +=k y x=A．B ．8C ．10D ．10．（2024北京人大附中朝阳学校初三二模）如图，在平行四边形中，，，，是对角线上的动点，且，，分别是边，边上的动点．下列四种说法：①存在无数个平行四边形；②存在无数个矩形；③存在无数个菱形；④存在无数个正方形．其中正确的个数是（ ）A ．1B ．2C ．3D ．411．（2024北京广渠门中学初三二模）如图，在正方形中，是延长线上一点，在上取一点，使点关于直线的对称点落在上，连接交于点，连接交于点，连接．现有下列结论：①；②；③；④若，，则 ）A ．②③④B ．①②③C ．①③④D ．①②④12．（2024北京十一中学初三二模）筒车是我国古代发明的一种水利灌溉工具，如图1，筒车盛水桶的运行轨道是以轴心为圆心的圆，已知圆心在水面上方，且被水面截得弦长为4米，半径为163323ABCD 22AD AB ==60ABC ∠=︒E F BD BE DF =M N AD BC MENF MENF MENF MENF ABCD E BC AB F B EF G AD EG CD H BH EF M CM BHG BHC ∠=∠GBH BCM ∠=∠GD =1AG =2GD =BM =O O O AB O 3米，则点到弦所在直线的距离是（ ）A ．1米B ．2米C ．米D ．米13．（2024北京一零一中学初三二模）如图，正方形边长为a ，点E 是正方形内一点，满足，连接．给出下面四个结论：①；②；③的度数最大值为；④当时，．上述结论中，所有正确结论的序号为（ ）A ．①②B ．①③C ．①④D ．①③④14．（2024北京丰台初三二模）如图，在平面直角坐标系xOy 中 ，已知y 关于x 的函数图象与x 轴有且只有三个公共点，坐标分别为（-3，0），（-1，0），（3，0）．关于该函数的四个结论如下：①当y >0时，-3<x <-1；②当x >-3时，y 有最小值；③将该函数图象向右平移1个或3个单位长度后得到的函数图象经过原点；④点P （m ，-m -1）是该函数图象上一点，则符合要求的点P 只有两个．其中正确的结论有A ．1个B ．2个C ．3个D ．4个C AB (3(3+ABCD 90AEB ∠=︒CE AE CE +CE BCE ∠60︒CE a =1tan 2ABE ∠=15．（2024北京大兴初三二模）下面的三个问题中都有两个变量：①扇形的圆心角一定，面积S 与半径r ；②用长度为20的线绳围成一个矩形，矩形的面积S 与一边长；③汽车在高速公路上匀速行驶，行驶路程s 与行驶时间t ．其中，两个变量之间的函数关系可以利用二次函数表示的是（ ）A ．①②B ．①③C ．②③D ．①②③16．（2024北京石景山初三二模）在平面直角坐标系xOy 中，y 与x 的函数关系如图所示，图象与x 轴有三个交点，分别为，，．给出下面四个结论：①当时，；②当时，y 随x 的增大而增大；③点在此函数图象上，则符合要求的点只有一个；④将函数图象向右平移2个或4个单位长度，经过原点．上述结论中，所有正确结论的序号是（ ）A ．①②B ．②③C ．②④D ．③④x ()4,0-(2,0)-(3,0)0y >23x -<<502x -<<(,2)M m m +参考答案1．C【分析】首先根据题意作图，然后由图象判断出点P 在对角线上，，，设，则，利用勾股定理求解即可．【详解】如图所示，由图象可得，当x 从0到4时，∴∵四边形是菱形∴点P 在对角线上∴由图象可得，，∴∵在菱形中，，∴，∴设，则∴∴∴在中，∴解得∴∴菱形的边长是故选：C ．【点睛】此题考查了动点函数图象问题，菱形的性质，勾股定理，含角直角三角形的性质等知识，解题的关键是根据图象正确分析出点P 在对角线上．2．C【分析】本题考查了相似三角形的判定与性质：在判定两个三角形相似时，应注意利用图形中已有的公共角、公共边等隐含条件，以充分发挥基本图形的作用；灵活运用相似三角形的性质计算相应线段的长或表BD 4BP =6BP AP +=AO x =22AB AO x ==1MA y MC ==MA MC=ABCD BD 4BP =6BP AP +=2AP =ABCD =60B ∠︒30ABD ∠=︒AC BD⊥AO x =22AB AO x==4PO BP BO =-=BO ==Rt APO 222AP AO PO =+()22224x =+x =2AB x ==ABCD 30︒BD示线段之间的关系是解决问题的关键，也考查了圆周角定理，直角三角形的性质．根据是半圆O 的直径，得出，根据直角三角形的性质得出，根据C 是半圆周上的动点(与A ，B 不重合），即可判断①；根据点C 的运动轨迹确定，即可判定②；证明，根据相似三角形的性质得出①中结论即可判断③．【详解】解：∵是半圆O 的直径，∴，∵点O 是中点，∴，∵，，∴，，即，故①正确；∵C 是半圆周上的动点(与A ，B 不重合），∴，，∴，∴，故②错误；，，，，，，，∴，∴，∴∵，，故③正确；故选：C ．3．DAB 90ACB ∠=︒122a b CO AB +==2a b DO BD BO -=-=Rt ADC Rt CDB ∽h =AB 90ACB ∠=︒AB 12CO AB =CD AB ⊥AD a BD b CD h ===，，CD CO ≤()11222a b CO AO BO AB AD BD +====+=2a b h +≤OD AO <CD DO <222a b b a a b DO BD BO b +--=-=-==||2a b h -<DC AB ⊥ 90ACB ∠=︒90ADC BDC ∴∠=∠=︒90DAC ACD ∠+∠=︒ 90DCA DCB ∠+∠=︒DAC DCB∴∠=∠Rt ADC Rt CDB ∴ ∽AD CD CD DB∴=a h h b=2h ab =h =2a b h +≤2a b +≤【分析】本题考查了勾股定理，直角三角形的特征，完全平方公式的应用，相似三角形的判定与性质，利用勾股定理可判断①结论；利用线段中点以及直角三角形斜边中线等于斜边一半可判断②结论；利用勾股定理以及完全平方公式可判断③结论．【详解】解：，，，，，，且，，①结论正确；，，，即，，，，，，点是的中点，，则，此时点，，在以点为圆心，为半径的圆上，②结论正确；在中，，即，，，，，即，③结论正确，故选：D ．4．D【分析】本题考查了用字母表示数或数量关系，理解题目中的数量关系，掌握代数式的表示方法是解题的关键．根据一个杯子的高度和杯沿的高度，可得，由此即可求解．【详解】解：根据题意，1个杯子的高，1个杯子沿高为，∴个杯子叠在一起的总高度为，故选：D ．5．C【分析】根据正多边形的性质以及圆心角定理即可判断③；再利用即可判断①；借助AD BC ⊥ 90ADB ADC ∴∠=∠=︒222AB BD AD ∴=+AB c = BD m =AD h =2h mn =2222c m h m mn ∴=+=+BD m = CD n =2h mn =h m n h ∴=AD BD CD AD=90BDA ADC ∠=∠=︒ BDA ADC ∴ ∽BAD ACD ∴∠=∠90BAD BAC ACD DAC ∴∠+∠=∠+∠=︒90BAC ∴∠=︒ E BC AE BE EC ∴==()1122AE BC m n ==+A B C E ()12m n +Rt ADC 222AC AD CD =+222b h n =+()2222222222323h n m h n m mn n m b m h -=++-=+-=-∴+m n < ()20n m ∴->22203b m h -+>∴2223b m h +>0.3H h n =+10h =0.3n 100.3H n =+OA OB OC OD ===勾股定理可求出，即可判断②；过点A作交延长线于点F，过点D作交于点E，根据等腰三角形的性质先求出，再利用特殊三角函数值，可求得即可求解．【详解】解：连接，，∵，，分别是直径为的的内接正六边形、正方形、等边三角形的一边∴，，∴，∴，即故③正确；∵∴是等边三角形，是等腰直角三角形∴故①正确；由勾股定理可得，故②正确；过点A作交延长线于点F，过点D作交于点E∵，∴∵，∴，AC AF DC⊥DC DG AE⊥AE60DOG∠=︒AD=DF AF==CF=CDOB OC ODAB AC AD AE O60AOB∠=︒=90AOC︒∠120AOD∠=︒30BOC AOC AOB∠=∠-∠=︒30COD AOD AOC∠=∠-∠=︒BOC COD∠=∠BC CD=OA OB OC OD===AOBAOC224AE OA AB===AC==AF DC⊥DC DG AE⊥AE30COD∠=︒OC OD=()118030752OCD ODC∠=∠=⨯︒-︒=︒120AOD∠=︒OA OD=()1180120302OAD ODA∠=∠=⨯︒-︒=︒60DOG∠=︒∴∴即为等腰直角三角形∴∴在中，由勾股定理得∴∴故④错误；故选：C ．【点睛】本题考查正多边形和圆，圆心角定理，等腰三角形的性质和判定，勾股定理，解直角三角形，含角的直角三角形的性质，熟练掌握圆心角定理以及作辅助线构造直角三角形是解题的关键．6．B【分析】连接，当平分，即时，即证明，可得出，当不平分，若时，，若时，，可判定①错误；根据，又由，可判定②正确；证明，得出，又根据，则，可判定③正确．【详解】解：连接，当平分，即时，∵，，，∴，∴，∵，∴即；若时，，即，若时，，即，故①错误；∵，，sin 602DG OD =︒⋅=AD =45FDA CDO ODA ∠=∠-∠=︒AFD △cos 45DF AD =︒⋅==DF AF ==Rt AFC △CF =CD DF CF =-11322ACD S CD AF =⋅⋅=⨯= 30︒AD AD BAC ∠CAD EAD ∠=∠()AAS ACD AED ≌c a b =+AD BAC ∠CAD EAD ∠>∠c a b >+CAD EAD ∠<∠c a b <+)AB a b =+AB AE >)a b c +>BE DE =BE )AB a b =+)c a b =+2a b =+AD AD BAC ∠CAD EAD ∠=∠CAD EAD ∠=∠90C AED ∠=∠=︒AD AD =()AAS ACD AED ≌AE AB =AC BC =AE BC =c a b =+CAD EAD ∠>∠AE AC >c a b >+CAD EAD ∠<∠AE AC <c a b <+AC BC =90C ∠=︒∴，即，∵，，故正确；∵，，∴，，∵，∴，∴，∴，∵，∴，，故③正确；故选：B ．【点睛】本题考查等腰直三角形的性质，勾股定理，全等三角形的判定与性质，熟练掌握等腰直三角形的性质和勾股定理是解题的关键．7．D【分析】本题考查了直径所对的圆周角为直角，相似三角形的判定与性质，完全平方公式的变形．熟练掌握直径所对的圆周角为直角，相似三角形的判定与性质，完全平方公式的变形是解题的关键．由题意知，，，由，可得，可判断①的正误；如图，连接，则，证明，则，即，可判断②的正误；由，可得，可判断③的正误．【详解】解：由题意知，，，∵，∴，①正确，故符合要求；如图，连接，AB =)AB a b=+AB AE >)a b c +>AC BC =90C ∠=︒)AB a b ==+45A B ∠=∠=︒DE AB ⊥45BDE B ∠=∠=︒BE DE =BE )AB a b =+)c a b =+2a b =+BD AC b ==CD AD AC a b =-=-2CD DE =2a b c -=AE BE ，90AEB ∠=︒BED EAD ∽DE BD AD DE=c b a c =()()()222224248a b a b ab c c c +=-+=+=a b +=BD AC b ==CD AD AC a b =-=-2CD DE =2a b c -=AE BE ，∵为半圆O 的直径，∴，∵，∴，又∵，∴，∴，即，②正确，故符合要求；∴，∴，∴，③正确，故不符合要求；故选：D ．8．C【分析】本题主要考查函数的定义以及函数图象的识别．探究大水杯中水面上升高度h 与注水时间t 之间的函数关系，从而确定图象．【详解】解：开始往大水杯中均匀注水，h 的值由0逐渐增大，当水漫过小水杯向小水杯注水，此时h 的值保持不变，小烧杯注满后，水再次进入大水杯中直至到大水杯顶部时，h 的再次增大，但变化比开始时变慢．观察四个图象，选项C 符合题意．故选：C ．9．D【分析】先由D （-2，3），AD =5，求得A （2，0），即得AO =2；设AD 与y 轴交于E ，求得E （0，1.5），即得EO =1.5；作BF 垂直于x 轴于F ，求证△AOE ∽△CDE ，可得，求证△AOE ∽△BFA ，可得AF =2，BF =，进而可求得B （4，）；将B （4，）代入反比例函数，即可求得k 的值．【详解】解：如图，过D 作DH 垂直x 轴于H ，设AD 与y 轴交于E ，过B 作BF 垂直于x 轴于F ，∵点D （-2，3），AD =5，∴DH =3，AB 90AEB ∠=︒90AED BED AED EAD ∠+∠=︒=∠+∠BED EAD ∠=∠90BDE EDA ∠=︒=∠BED EAD ∽DE BD AD DE=c b a c =2ab c =()()()222224248a b a b ab c c c +=-+=+=a b +=103BA CD ==838383k y x=∴，∴A （2，0），即AO =2，∵D （-2，3），A （2，0），∴AD 所在直线方程为：，∴E （0，1.5），即EO =1.5，∴,∴ED=AD - AE=5-=，∵∠AOE=∠CDE ，∠AEO=∠CED ，∴△AOE ∽△CDE ，∴,∴,∴在矩形ABCD 中，，∵∠EAO+∠BAF=90°，又∠EAO+∠AEO=90°，∴∠AEO=∠BAF ，又∵∠AOE=∠BFA ，∴△BFA ∽△AOE ，∴,∴代入数值，可得AF =2，BF =，∴OF =AF+AO=4，∴B （4，），∴将B （4，）代入反比例函数，得，故选：D ．【点睛】本题主要考查了待定系数法求反比例函数的系数、相似三角形的判定与性质、勾股定理、矩形的性质等知识．解题关键是通过求证△AOE ∽△CDE ，△AOE ∽△BFA ，得到B 点坐标，将B 点坐标代入反比例函数，即可得解．10．C【分析】根据题意作出合适的辅助线，然后逐一分析即可．AH =3342y x =-+52AE ===5252EO AO ED CD=103ED CD AO EO =´=103BA CD ==BA AF BF AE EO AO==838383k y x=323k =【详解】如图，连接AC 、与BD 交于点O ，连接ME ，MF ，NF ，EN ，MN ，∵四边形ABCD 是平行四边形∴OA =OC ，OB =OD∵BE =DF∴OE =OF∵点E 、F 时BD 上的点，∴只要M ，N 过点O ，那么四边形MENF 就是平行四边形∴存在无数个平行四边形MENF ，故①正确；只要MN =EF ，MN 过点O ，则四边形MENF 是矩形，∵点E 、F 是BD 上的动点，∴存在无数个矩形MENF ，故②正确；只要MN ⊥EF ，MN 过点O ，则四边形MENF 是菱形；∵点E 、F 是BD 上的动点，∴存在无数个菱形MENF ，故③正确；只要MN =EF ，MN ⊥EF ，MN 过点O ，则四边形MENF 是正方形，而符合要求的正方形只有一个，故④错误；故选：C【点睛】本题考查正方形的判定、菱形的判定、矩形的判定、平行四边形的判定、解答本题的关键时明确题意，作出合适的辅助线．11．D【分析】本题考查了正方形的性质，全等三角形的判定和性质，等腰三角形的判定和性质等，熟练掌握知识点并添加适当的辅助线是解题的关键．如图1中，过点作于，证明即可判断①；过点作于，于，于．证明即可判断②；如图2中，过点作于，交于．先证明，再证明即可判断③；利用勾股定理计算，即可判断④．【详解】解：如图1中，过点作于．B BK GH ⊥K ()Rt Rt HL BHK BHC ≌M MQ GH ⊥Q MP CD ⊥P MR BC ⊥R 45GBH ∠=︒M MW AD ⊥W BC T MG MD =()AAS BTM MWG ≌B BK GH ⊥K，关于对称，，，四边形是正方形，，，，，，，，，，，，，，，，故①正确，，过点作于，于，于．，，，，，，，故②正确，如图2中，过点作于，交于．，关于对称，，B G EF EB EG ∴=EBG EGB ∴∠=∠ ABCD AB BC ∴=90A ABC BCD ∠=∠=∠=︒//AD BC AGB EBG ∴∠=∠AGB BGK ∴∠=∠90A BKG ∠=∠=︒ BG BG =()AAS BAG BKG ∴ ≌BK BA BC ∴==ABG KBG ∠=∠90BKH BCH ∠=∠=︒ BH BH =()Rt Rt HL BHK BHC ∴ ≌BHG BHC ∴∠=∠HBK HBC ∠=∠1452GBH GBK HBK ABC ∴∠=∠+∠=∠=︒M MQ GH ⊥Q MP CD ⊥P MR BC ⊥R BHG BHC ∠=∠ MQ MP \=MEQ MER ∠=∠ MQ MR ∴=MP MR ∴=1452BCM MCP BCD ∴∠=∠=∠=︒GBH BCM ∴∠=∠M MW AD ⊥W BC T B G EF BM MG ∴=，，，，，，，，，，，，，，，，，，故③错误，，，，，，④正确，故选：D ．12．C【分析】本题考查了垂径定理的应用和勾股定理的应用．连结，交于，由垂径定理得（米），再由勾股定理得，然后求出的长即可．【详解】解：连接交于，由题意得：米，，∴（米），，由勾股定理得，（米），∴米，CB CD = BCM MCD ∠=∠CM CM =()SAS MCB MCD ∴≌BM DM∴=MG MD ∴=MW DG ⊥ WG WD ∴=90BTM MWG BMG ∠=∠=∠=︒ 90BMT GMW ∴∠+∠=︒90GMW MGW ∠+∠=︒ BMT MGW ∴∠=∠MB MG = ()AAS BTM MWG ∴ ≌MT WG ∴=MC = 2DG WG =DG ∴=1AG = 2DG =3AD AB TW ∴===1TC WD TM ===2BT AW ==BM ∴===OC OC AB D 122AD BD AB ===OD CD OC AB D 3OA OC ==OC AB ⊥122AD BD AB ===90ADO ∠=︒OD ===(3CD OC OD =-=即点到弦所在直线的距离是米，故选：C ．13．C【分析】如图所示，连接交于H ，取中点O ，连接，先证明点E 在以点O 为圆心，为直径的圆上运动，当三点共线，即点E 运动到点H 时， 当三点共线时，有最小值，据此可判断①②；如下图所示，当与相切时有最大值，证明，得到，，则，再证明，得到，即可判断③④．【详解】解：如图所示，连接交于H ，取中点O ，连接，∵四边形是正方形，∴；∵，∴点E 在以点O 为圆心，为直径的圆上运动，∵，∴点H 在圆O 上，∵，∴当三点共线，即点E 运动到点H 时，，故①正确；∵点E 在以点O 为圆心，为直径的圆上运动，∴当三点共线时，有最小值，在中，由勾股定理得，∴，故②错误；如下图所示，当与相切时有最大值，∵，∴，C AB (3AC BD AB OC AB AE C 、、AE CE AC +=C O E 、、CE CE O BCE ∠Rt Rt OBC OEC △≌△CE BC a ==OCE OCB ∠=∠1tan 2OE OCE CE ==∠ABE BCO OCE ==∠∠∠1tan tan 2ABE OCE ==∠∠AC BD AB OC ABCD 90AHB ∠=︒90AEB ∠=︒AB 90AHB ∠=︒AE CE AC +≥==A E C 、、AE CE AC +=AB C O E 、、CE Rt OBC △OC ==CE 12a -=CE O BCE ∠OB OE OC OC ==，()Rt Rt HL OBC OEC ≌∴，，∴，∴，∴，∴的度数最大值不是，故③错误；∵，∴垂直平分，∴，∴，∴，故④正确；故选：C ．【点睛】本题主要考查了圆与正方形综合，解直角三角形，勾股定理等等，根据题意得到点E 的运动轨迹是解题的关键．14B 解析略15．A【分析】本题主要考查了二次函数的定义，根据二次函数的定义求解即可．【详解】解：①扇形的面积，扇形的圆心角n 一定， 面积S 与半径r 两个变量之间的函数关系可以利用二次函数表示，符合题意，②矩形的面积，矩形的面积S 与一边长两个变量之间的函数关系可以利用二次函数表示，符合题意，③行驶路程，行驶路程s 与行驶时间t 两个变量之间的函数关系可以利用一次函数表示，不符合题意，则①②符合题意，故选：A ．CE BC a ==OCE OCB ∠=∠1tan 2OE OCE CE ==∠30OCE ≠︒∠60BCE ≠︒∠BCE ∠60︒BC EC OB OE ==，OC BE ABE BOC BOC BCO +=+∠∠∠∠ABE BCO OCE ==∠∠∠1tan tan 2ABE OCE ==∠∠2360n S r π=()21010S x x x x =-=-+x s vt =x16．C【分析】本题考查了函数的图象与性质，一次函数图象，解题的关键是数形结合．结合函数图象逐个分析即可．【详解】由图象可得，当时，或，故①错误；当时，y 随x 的增大而增大；故②正确；∵∴点M 在一次函数的图象上，如图所示，由图象可得，有3个交点∴点在此函数图象上，则符合要求的点有3个，故③错误；∵函数经过点∴将函数图象向右平移2个或4个单位长度，经过原点，故④正确．综上所述，上述结论中，所有正确结论的序号是②④．故选：C．0y >23x -<<<4x -502x -<<(,2)M m m +2y x =+(,2)M m m +(2,0)-()0,0。

顺义区2016届初三第二次统一练习数学答案及评分参考一、选择题（本题共30分，每小题3分）二、填空题（本题共18分，每小题3分）11．3；12．>；13．21；14．70︒； 15．4y x =-+（不唯一）； 16.BCE ∠和线段BC ；思路：①在Rt BCE ∆中，由tan BEBCE BC∠=，求出tan BE BC BCE =⋅∠， ②由13AE AB =，可求23BE AB =，求得33tan 22AB BE BC BCE ==⋅∠．三、解答题（本题共72分，第17-26题，每小题5分，第27题7分，第28题7分，第29题8分）17．解：1112cos453-⎛⎫++-︒ ⎪⎝⎭312=+…………………………..…………………...………4分2=+.…………………………………………………….……….….…5分18．解：解不等式532x x -<，得1x <. …….…………….…….……….…1分 解不等式7332x x +>，得3x >- ..……………….…….……….…2分 ∴原不等式组的解集为31x -<< . ………….…………….…4分 ∴原不等式组的所有整数解为2-、1-、0 . ……….………….….…5分 19．解：原式=2(1)(1)11(1)12x x x x x x +-+⋅+-++……………….…….……….…1分=1112x x x ++-+……………………………………….………2分 =2(1)(1)(1)(2)(1)(2)x x x x x x x +-++-+-+………………….……….….…3分=2212x x x x +++-……………………………………….……….…4分∵230x x +-= ∴ 23x x +=∴原式=221314232x x x x +++==+--………………….………….….…5分 20． 证明：∵AB AC =，AD 是BC 边上的中线，∴90ADC ∠=︒．………………………………………………………………………….….1分 又∵E 是AC 的中点，∴AE DE =，………………………..…………………………………………………….….2分 ∴=90ADE EAD C ∠=∠-∠．………………………………………………………..…..3分 ∵BF CA ⊥延长线于点F ，∴=90CBF C ∠-∠．……………………………………………………………………….4分 ∴CBF ADE ∠=∠．……………………………………………………………………..….5分21．解：设甲工程队整治了x 米的河道，则乙工程队整治了(360)x -米的河道. …….………………………………1分 根据题意得：360202416x x -+=……………………………………….…...…3分 解得：120x =………………………………………….….….…4分 ∴360240x -=答：甲工程队整治了120米的河道，乙工程队整治了240米的河道 ….………..5分 22．（1）证明：∵AC BD ⊥，AE AC ⊥，∴AE ∥BD ，……………………………………………………………………..………….1分 ∵AB ∥DC ， ∴AB ∥DE ．∴四边形ABDE 为平行四边形．……………………………………………..…………..….2分 （2）解：∵四边形ABDE 为平行四边形，∴BD AE =，E ABD ∠=∠．………………………………………………………...….3分 ∵4sin 5ABD ∠=， ∴4sin 5E ∠=．……………………………………………………………….………....….4分 在RT △EAC 中，8AC =， ∴10CE =，6AE =，∴6BD =．………………………………………………………………………..…...….5分23．解：（1）把A （－4，n ）代入4y x=-中，得1n =，…………………....….1分把A （－4，1）代入y x k =-+中，得3k =-……………….….…….2分解方程组3,4.y x y x =--⎧⎪⎨=-⎪⎩得4,1.x y =-⎧⎨=⎩ , 1,4.x y =⎧⎨=-⎩∴点B 的坐标是(1,4)-……………………………………….…...…3分 （2）点P 的是坐标(3,0)或(11,0)-……………………………….…...…5分24． （1）证明：∵AB 为⊙O 的直径，∴90ADB ∠=︒.………………………………………………………………………..……1分又∵AD DC =，∴AB BC =.…………………………………………………………………………………2分 （2）解：∵BF 切⊙O 于点B ，∴90ABF ∠=︒.…………………………………………………………………………………………………..…………3分 ∴90BAF F ∠+∠=︒.又∵90BAF ABD ∠+∠=︒， ∴ABD F ∠=∠， ∴△ABD ∽△BFD ， ∴AD BDBD DF=， ∴2BD AD DF =⋅.又∵CF DC =， ∴CF DC AD ==，设=CF DC AD k ==，则2222BD AD DF k k k =⋅=⋅=，∴BD .在RT △BCD中，BC，sin 3CBD ∠==, 又∵CBD CAE ∠=∠，……………………..………………………………………………………………….……4分∴sin 3CAE ∠=.…………………………………………………………..…………5分 25． 解：（1）18，0.18；…………………………………..…………………………….……2分 （2）…………………………..………3分（3）80-90；…………………………………..…………………………………………4分（4）3500.30105⨯=（人）…………………………………..………………..……5分答：约有105人． 26． 解：（1） 结论：点是四边形在边上的相似点.……….…1分证明：∵50A B DEC ∠=∠=∠=︒， ∴1+2=130∠∠︒，1+3=130∠∠︒，∴2=3∠∠，………………………………………………..……2分 ∴△AED ∽△BCE ，∴点是四边形在边上的相似点.…………….…3分 （2）E ABCD AB E ABCD AB 321ABCDE 成绩/分9080706050010084频数或BA D CEE CD AB……………………………………………………………………5分27．解：（1）[]22224(21)42441(21)b ac m m m m m ∆=-=-+-⨯=-+=- -----1分∵不论m 为任何实数时 ，总有2(21)0m ∆=-≥，∴该方程总有两个实数根 . --------------------------------------------------2分（2）(21)(21)2m m x +±-==∴12x m =，21x =………………………………………………….… 4分 不妨设点(1,0)B ，依题意则点(3,0)A -∴32m =-∴抛物线的表达式为223y x x =+-…………….…………………5分 （3）134b >……………………………………………...………………….…7分 28.（1）①……………………….…………………1分②证明：∵90ACD ∠=︒， 又∵CE CB ⊥， ∴90=ECB ACD ∠=︒∠, ∴1=2∠∠.∵DB MN ⊥于点B ， ∴90ABD ∠=︒， ∴180BAC D ∠+∠=︒．E12NMABCD又∵180BAC EAC ∠+∠=︒，∴D EAC ∠=∠．……………………………………………….…..……2分 ∴△CAE ≌△CDB ，∴CE CB =．………………………………………………………..……3分BD AB =+．……………………………………………....….4分（2AB BD =-BD AB =-.……………….…………6分（31.…………………………………………………..……7分 29．解：（1）① 在点M ，N ，E ，F 中，⊙O 的关联点是M ，N ；….………..2分② ∵过点F 作直线l 交y 于点G ，使30GFO ∠=︒，点F∴OF =2OG =∴点G 的坐标是（0 ，2） ----------------------------------------------------3分设直线l 的表达式为y kx b =+，又直线l 过点点F 和点(0,2)G∴直线l 的表达式为23y x =-+ ----------------------------------------4分 ∵直线l 上的点(,)P m n 是⊙O 的关联点∴直线l 上的点(,)P m n 满足2OP ≤的所有点都是⊙O 的关联点∴当2OP =时，224m n +=，即22(2)4m ++= --------5分∴10m =，2m =∴m 的取值范围是0m ≤≤ ------------------------------------------------6分 （2）2r ≥ --------------------------------------------------------------------------------8分。

顺义区2023年初中学业水平考试第二次统一练习参考答案一、选择题（共16分，每题2分）9． 2； 10．540； 11．-1； 12． 3；13．10； 14．43； 15．21； 16．2，4，6， 3，8，10．三、解答题（共68分，第17-20题，每题5分，第21题6分，第22题5分，第23-24题，每题6分，第25题5分，第26题6分，第27-28题，每题7分）17．解：原式=2321221−⨯−+ …………………………………… 4分 =22− ………………………………………………………… 5分18. 解：解不等式①，得 x < 1． ……………………………………………… 2分 解不等式②，得 x > -2． …………………………………………… 4分 ∴原不等式组的解集为 -2 < x < 1． ………………………………… 5分19．解：由作法一可知： CB =AB ， ………………………………………… 1分∴ △ABC 是等腰三角形．由作法二可知：∠ ABG =∠BAM ， ……………………………………… 2分∴ CA =CB （ 等角对等边 ）（填推理依据）． ………………… 3分∴ △ABC 是等腰三角形．由作法三可知：PQ 是线段AB 的 垂直平分线 ，……………… 4分∴ CA =CB （ 线段垂直平分线上的点到线段两个端点的距离相等 ）（填推理依据）．……………………………………………………………… 5分∴ △ABC 是等腰三角形．20．（1）证明：∵△=222)4(168)42(4)(−=+−=−−−b b b b b ≥0，………… 1分 ∴方程总有两个实数根． ………………………………………… 2分 （2）解：∵2)4(2)4(2−±=−±=b b b b x ， ∴22)4(1−=−+==b b b x ，22)4(2=−−==b b x ． ……………… 3分 ∵方程有一个根为负数，∴02<−b ． ∴2<b ． …………………………………………… 4分 ∵ b 为正整数，∴ b=1． …………………………………………………………………… 5分121．（1）证明：∵A 关于BC 的对称点为D ，∴AB =BD ，AC =CD ． ………………………………………… 1分∵AB =AC ，∴AB =BD =AC =CD ， ………………………………………… 2分∴四边形ABDC 是菱形． ………………………………………… 3分（2）解一：∵AE ⊥BD ，AB =6，BE =4，∴∠AEB =90°．∴AE …………………… 4分 ∵四边形ABDC 是菱形，∴BD ∥AC ，AC=AB =6．∴△BEF ∽△CAF ． ………………………………………………… 5分∴AFEF AC BE =． ∴3264==AF EF ． 设EF =2x ，AF =3x ，有2x+3x =52．∴552=x ． ∴5563==x AF ． ……………………… 6分解二：连接AD ，交BC 于点O .∵AB =6，BE =4，∴DE =2.∵AE ⊥BD ，∴∠AEB =∠AED =90°，∴AE = ……………………… 4分AD ∵四边形ABDC 是菱形，∴∠BOA =90°，AO =21AD ∴∠BOA =∠AED =90°.∵∠OAF =∠EAD ，∴△AFO ∽△ADE ． ………………………………………………… 5分 ∴AF AO AD AE=．∴AF ………………………………………………………… 6分 222．解：（1）∵一次函数)0(≠+=k b kx y 的图象由y =-2x 的图象平移得到，∴ k =-2． …………………………………………………… 1分 ∵一次函数b x y +−=2的图象过点（2，-1），∴ -2×2+b =-1．∴ b =3． ……………………………………………………… 2分∴ 这个一次函数的解析式为：y =- 2x +3． …………………… 3分（2）m ≥-12 且m ≠0． …………………………………………… 5分23．解：（1）845.3)888(=⨯++=m ． …………………………………… 1分 806480675.9225.63849.966.685.74==+++++=n ．……… 3分 （2）选手 甲 发挥的稳定性更好． …………………………… 5分（3）最终得分最高的是 甲 ． …………………………………… 6分24．（1）证明一：如图，连接PO ，交AB 于点E ．∵P A 、PB 为⊙O 的切线，∴P A =PB ，∠1=∠2=12∠APB ，∠P AO = 90°． ∴PE ⊥AB ，∠3+∠BAC = 90°，∴∠PEA=90°．∴∠1+∠3=90°．∴∠BAC =∠1 ．∴∠BAC =12∠APB ． ……………………………………………… 3分 证明二：如图，连接OB ．∵P A 、PB 为⊙O 的切线，∴∠P AO=∠PBO=90°．∵∠P AO+∠PBO+∠P+∠1=360°，∴∠P+∠1=180°．∵∠2+∠1=180°，∴∠P=∠2．∵OA=OB ，∴∠BAC=∠3．∵∠2=∠BAC+∠3，∴∠2=2∠BAC ．∴∠P=2∠BAC ．即∠BAC =12∠APB ． ……………………………………………… 3分 3（2）解：∵cos ∠BAC =45， ∴sin ∠BAC =35， ∴sin ∠1=35， ∵AC =6，∴AO =3，∴OP =5，∴PD =OP -OD =2． ………………………………………………… 6分25．解：（1）根据表格可以得出函数图象过点（2，114），（4，216），代入函数关系式2y ax bx =+,可得 42114164216a b a b +=⎧⎨+=⎩ 解之得3260a b ⎧=−⎪⎨⎪=⎩, ∴函数关系式为23602y x x =−+． …………………………… 3分（2）当6020322()2b x a =−=−=⨯−时，232060206002y =−⨯+⨯=． ∴飞机着陆后滑行600m 能够停下来，此时滑行的时间是20s ．…… 5分26．解：（1）对称轴x = -222a a−= a ．……………………………………………… 1分 （2）∵a =1，∴抛物线解析式为y =x 2 -2 x -3，对称轴为x =1，开口向上．∵-2＜x ＜3，包含对称轴x =1，且x =-2比x =3距离对称轴远，∴当x =1时，y 最小=-4；当x =-2时，y =5．∴-4≤y ＜5． ………………………………………………………… 3分（3）∵y 1＜y 3＜y 2，B (a , y 2) ，对称轴为x =a ，∴B (a , y 2)为抛物线的顶点，a ＜0，C (a +2, y 3)在对称轴右侧，当A (2a -1, y 1)在对称轴左侧时：a -(2 a -1）＞（a +2）- a ，∴ a ＜-1．当A (2a -1, y 1)在对称轴右侧时：2a -1＞a +2，∴a ＞3，不符合题意，舍去． ∴a ＜-1．……………………………………………………………… 6分427．（1）证明：∵DE 绕着点D 逆时针旋转60°得到DF ，∴DE =DF ，∠EDF =60°．∴△DEF 是等边三角形． ………………………………………… 1分∴FE =FD ，∠DFE =60°．∵BD =BE ，∠ABC =120°，BF =BF ，∴∠BDE =30°，△BDF ≌△BEF ．∴∠BDF =90°，∠BFD =∠BFE =30°．∴BF =2BD ． …………………………………………………… 3分（2）依题意补全图2，如图．数量关系为：BF =BD + BE ． ………………………………………………… 4分 证明：在DA 上截取DG ，使DG =BE ，连接FG ．∵DE 绕着点D 逆时针旋转60°得到DF ，∴DE =DF ，∠EDF =60°．∴△DEF 是等边三角形．∴FE =FD ，∠DFE =60°．∵∠ABC =120°，∴∠BDF +∠BEF =180°．∵∠BDF +∠GDF =180°，∴∠GDF =∠BEF ．在△GDF 和△BEF 中DG BE GDF BEF DF EF =⎧⎪∠=∠⎨⎪=⎩∴△GDF ≌△BEF （SAS ）． ………………………………………… 5分∴GF =BF ，∠GFD =∠BFE ．∴∠GFB =∠DFE =60°．∴△GFB 是等边三角形．∴BG =BF ． ………………………………………………… 6分∵BG = BD +DG ，∴BF = BD +BE ． …………………………………………………… 7分528．解：（1）如图，直线24y x =−−与两坐标轴的交点分别是E （-2，0），F （0，-4），则点A 与直线24y x =−−上的任意一点所成的线段的中点，构成了直线E ’F ’．其中E ’ （1，0），F ’ （2，-2）．∴ 直线E ’F ’：22y x =−+．设直线E ’F ’：22y x =−+关于直线l ：x =a的对称直线与x 轴的交点为点H ，若要使直线24y x =−−关于点A 及直线l ：x =a 的“对应图形”与直线24y x =−−的交点在x 轴的上方，则只需要点H 在点E 左侧， 因此H E x x <，所以2H x <−． 又'2H E x x a +=，所以212a −+<，即 12a <− ． ………………………………… 3分 （2）2214−−≤t ≤2214+−或226−−≤t ≤226+−．………………… 7分6。

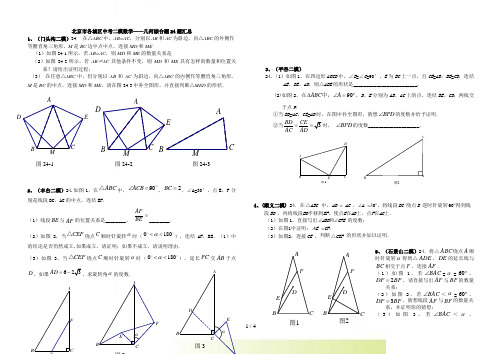
图2图1ED C B AA C EDBC EDBC MBC北京市各城区中考二模数学——几何综合题24题汇总1、（门头沟二模）24. 在△ABC 中，AB=AC ，分别以AB 和AC 为斜边，向△ABC 的外侧作等腰直角三角形，M 是BC 边中点中点，连接MD 和ME（1）如图24-1所示，若AB=AC ，则MD 和ME 的数量关系是（2）如图24-2所示，若AB ≠AC 其他条件不变，则MD 和ME 具有怎样的数量和位置关系？请给出证明过程；（3） 在任意△ABC 中，仍分别以AB 和AC 为斜边，向△ABC 的内侧．．作等腰直角三角形，M 是BC 的中点，连接MD 和ME ，请在图24-3中补全图形，并直接判断△MED 的形状．2、（丰台二模）24.如图1，在ABC △中，90ACB ∠=°，2BC =，∠A=30°，点E ，F 分别是线段BC ，AC 的中点，连结EF ．（1）线段BE 与AF 的位置关系是________， AFBE =________．（2）如图2，当CEF △绕点C 顺时针旋转α时（0180α<<），连结AF ，BE ，（1）中的结论是否仍然成立.如果成立，请证明；如果不成立，请说明理由．（3）如图3，当CEF △绕点C 顺时针旋转α时（0180α<<），延长FC 交AB 于点D ，如果63AD =-α的度数．3、（平谷二模）24.（1）如图1，在四边形ABCD 中，∠B =∠C =90°，E 为BC 上一点，且CE =AB ，BE =CD ，连结AE 、DE 、AD ，则△ADE 的形状是_________________________.(2)如图2，在90ABC A ∆∠=︒中，，D 、E 分别为AB 、AC 上的点，连结BE 、CD ，两线交于点P ．①当BD=AC ，CE=AD 时，在图中补全图形，猜想BPD ∠的度数并给予证明． ②当3BD CEAC AD==时， BPD ∠的度数____________________．4、(顺义二模) 24．在△ABC 中， AB = AC ，∠A =30︒，将线段 BC 绕点 B 逆时针旋转 60︒得到线段 BD ，再将线段BD 平移到EF ，使点E 在AB 上，点F 在AC 上． （1）如图 1，直接写出 ∠ABD 和∠CFE 的度数； （2）在图1中证明： A E =CF ； （3）如图2，连接 CE ，判断△CEF 的形状并加以证明．5、（石景山二模）24．将△ABC 绕点A 顺时针旋转α得到△ADE ，DE 的延长线与BC 相交于点F ，连接AF ．（1）如图1，若BAC ∠=α=︒60，BF DF 2=，请直接写出AF 与BF 的数量 关系；（2）如图2，若BAC ∠＜α=︒60，BF DF 3=，猜想线段AF 与BF 的数量关 系，并证明你的猜想；（3）如图3，若BAC ∠＜α，图2A BCDEF F EDBA DEAAFA图24-1图24-2图24-3EQPDCB AmBF DF =（m 为常数），请直接写出BFAF的值 （用含α、m 的式子表示）． 解：6、（海淀二模）24．在ABC △中，90ABC ∠=，D 为平面内一动点，AD a =，AC b =，其中a ， b 为常数，且 a b <. 将ABD △沿射线BC 方向平移，得到FCE △，点A 、B 、D 的对应点分别为点F 、C 、E .连接BE .（1）如图1，若D 在ABC △内部，请在图1中画出FCE △；（2）在（1）的条件下，若AD BE ⊥，求BE 的长（用含, a b 的式子表示）；（3）若=BAC α∠，当线段BE 的长度最大时，则BAD ∠的大小为__________；当线段BE 的长度最小时，则BAD ∠的大小为_______________（用含α的式子表示）.图1 备用图7、（西城二模）24．在△ABC ，∠BAC 为锐角，AB >AC ， AD 平分∠BAC 交BC 于点D ．（1）如图1，若△ABC 是等腰直角三角形，直接写出线段AC ，CD ，AB 之间的数量关系；（2）BC 的垂直平分线交AD 延长线于点E ，交BC 于点F ．①如图2，若∠ABE =60°，判断AC ，CE ，AB 之间有怎样的数量关系并加以证明；②如图3，若3AC AB +，求∠BAC 的度数．8、（通州二模）23．已知：△ABD 和△CBD 关于直线BD 对称（点A 的对称点是点C ），点E 、F 分别是线段BC 和线段BD 上的点，且点F 在线段EC 的垂直平分线上，连接AF 、AE ，AE 交BD 于点G ．（1）如图l ，求证：∠EAF ＝∠ABD ；（2）如图2，当AB ＝AD 时，M 是线段AG 上一点，连接BM 、ED 、MF ，MF 的延长线交ED 于点N ，∠MBF ＝12∠BAF ，AF ＝23AD ，请你判断线段FM 和FN 之间的数量关系，并证明你的判断是正确的．9、（东城二模）24．如图，等腰Rt △ABC 中，∠ACB =90°，AC =BC =4，P 是AC 边上一动点，由A 向C 运动（与A 、C 不重合），Q 是CB 延长线上一点，与点P 同时以相同的速度由B 向CB 延长线方向运动（Q 不与B 重合），过P 作PE ⊥AB 于E ，连接PQ 交AB 于D ．（1）当∠BQD =30°时，求AP 的长；（2）当运动过程中线段ED 的长是否发生变化？如果不变，求出AB CDAB D图1 图2图3ABCDE F FEDCBAFEDCBAGFBD ENG FDBA EM图2线段ED 的长；如果变化请说明理由；（3）在整个运动过程中，设AP 为x ，BD 为y ，求y 关于x 的函数关系式，并求出当△BDQ为等腰三角形时BD 的值．10、（朝阳二模）24. 已知∠ABC =90°，D 是直线AB 上的点，AD =BC ．（1）如图1，过点A 作AF ⊥AB ，并截取AF =BD ，连接DC 、DF 、CF ，判断△CDF 的形状并证明；（2）如图2，E 是直线BC 上的一点，直线AE 、CD 相交于点P ，且∠APD =45°，求证BD =CE ．11、（密云二模）24．已知等腰Rt ABC ∆和等腰Rt AED ∆中，∠ACB=∠AED=90°，且AD=AC （1）发现：如(图1)，当点E 在AB 上且点C 和点D 重合时，若点M 、N 分别是DB 、EC 的中点，则MN 与EC 的位置关系是 ，MN 与EC 的数量关系是（2）探究：若把（1）小题中的△AED 绕点A 旋转一定角度，如(图2)所示，连接BD 和EC,并连接DB 、EC 的中点M 、N,则MN 与EC 的位置关系和数量关系仍然能成立吗？若成立，以顺时针旋转45°得到的图形（图3）为例给予证明数量关系成立，若不成立，请说明理由;请以逆时针旋转45°得到的图形（图4）为例给予证明位置关系成立，12、（延庆二模）13、(房山二模) 24. 边长为2的正方形ABCD 的两顶点A 、C 分别在正方形EFGH 的两边DE 、DG 上(如图1)，现将正方形ABCD 绕D 点顺时针旋转，当A 点第一次落在DF 上时停止旋转，旋转过程中，AB 边交DF 于点M ，BC 边交DG 于点N . （1）求边DA 在旋转过程中所扫过的面积；（2）旋转过程中，当MN 和AC 平行时(如图2)，求正方形ABCD 旋转的度数；（3）如图3，设MBN ∆的周长为p ，在旋转正方形ABCD 的过程中，p 值是否有变化？请证明你的结论.14、（昌平二模）24．【探究】如图1，在△ABC 中， D 是AB 边的中点，AE ⊥BC 于点E ，BF⊥AC 于点F ，AE ，BF 相交于点M ，连接DE ，DF . 则DE ，DF 的数量关系为 .【拓展】如图2，在△ A B C 中 ，C B = C A ，点 D 是AB 边的 中点 ，点M 在 △ A B C 的内部 ，且 ∠MBC =∠MAC . 过点M 作ME ⊥BC 于点E ，MF ⊥AC 于点F ，连接DE ，DF . 求证：DE =DF ；【推广】如图3，若将上面【拓展】中的条件“CB =CA ”变为“CB ≠CA ”，其他条件不变，试探究DE 与DF 之间的数量关系，并证明你的结论.ADB EC M FADBE CMF MABCDF E图3图2图1P EC 图2 C B 图115、（怀柔二模）24．已知△ABC是等边三角形，E是AC边上一点，F是BC边延长线上一点，且CF=AE，连接BE、EF．（1）如图1，若E是AC边的中点，猜想BE与EF的数量关系为 .（2）如图2，若E是线段AC上的任意一点，其它条件不变，上述线段BE、EF的数量关系是否发生变化，写出你的猜想并加以证明．（3）如图3，若E是线段AC延长线上的任意一点，其它条件不变，上述线段BE、EF的数量关系是否发生变化，写出你的猜想并加以证明．16、（大兴二模）25. 已知：E是线段AC上一点，AE=AB，过点E作直线EF，在EF上取一点D，使得∠EDB=∠EAB，联结AD.（1）若直线EF与线段AB相交于点P，当∠EAB=60°时，如图1，求证：ED =AD+BD；（2）若直线EF与线段AB相交于点P，当∠EAB= α（0º﹤α﹤90º）时，如图2，请你直接写出线段ED、AD、BD之间的数量关系（用含α的式子表示）；（3）若直线EF与线段AB不相交，当∠EAB=90°时，如图3，请你补全图形，写出线段ED、AD、BD之间的数量关系，并证明你的结论. 17、（燕山二模）24.如图1，已知ABC∆是等腰直角三角形，︒=∠90BAC,点D是BC 的中点．作正方形DEFG，使点A、C分别在DG和DE上，连接AE，BG．（1）试猜想线段BG和AE的数量关系是；（2）将正方形DEFG绕点D逆时针方向旋转)3600(︒≤<︒αα，①判断（1）中的结论是否仍然成立？请利用图2证明你的结论；②若4==DEBC，当AE取最大值时，求AF的值．图1 图2ABEF图AB CEF图ABCEF图3FGED CAB BACDEGF。

度分秒的换算（北京习题集）（教师版）一．选择题（共5小题）1．（2019秋•房山区期末）把2.36︒用度、分、秒表示，正确的是( )A ．22136︒'''B ．21836︒'''C ．23060︒'''D ．236︒'''2．（2017秋•石景山区期末）若90C ∠=︒，2530A '∠=︒，则C A ∠-∠的结果是( )A ．7530'︒B ．7430'︒C ．6530'︒D ．6430'︒3．（2017•门头沟区二模）将284231︒'''保留到“'”为( )A ．2842︒'B ．2843︒'C ．284230︒'''D ．2900︒'4．（2016•朝阳区校级模拟）下面等式成立的是( )A ．83.58350︒=︒'B ．37123637.48︒'''=︒C ．24242424.44︒'''=︒D ．41.254115︒=︒' 5．（2009秋•门头沟区期末）把2.36︒用度、分、秒表示正确的是( )A ．236︒'''B ．2306︒'''C ．2216︒'''D ．22136︒'''二．填空题（共8小题）6．（2019秋•怀柔区期末）若4730α∠=︒'，则90α︒-∠= ．7．（2019秋•顺义区期末）65.24︒= 度 分 秒．8．（2019秋•延庆区期末）把5636︒'换算成度的结果是 ．9．（2019秋•丰台区期末）计算：1805218'︒-︒= ．10．（2019秋•门头沟区期末）计算：1807248︒-︒'= ．11．（2019秋•海淀区期末）计算：48396731︒'+︒'= ．12．（2019秋•平谷区期末）计算：901835'︒-︒= ．13．（2019秋•石景山区期末）将2036︒'换算成度为 ︒．三．解答题（共2小题）14．（2014秋•西城区校级期末）计算：（1）1820α=︒'，630β=︒'，求αβ+；（2）42483625︒'+︒'= ︒ '．15．（2013秋•大兴区期末）计算：38493︒'⨯．度分秒的换算（北京习题集）（教师版）参考答案与试题解析一．选择题（共5小题）1．（2019秋•房山区期末）把2.36︒用度、分、秒表示，正确的是()A．22136︒'''D．236︒'''︒'''C．23060︒'''B．21836【分析】根据大单位化小单位除以进率，可得答案．【解答】解：2.3620.36602210.66022136︒=︒+⨯'=︒'+⨯''=︒'''，故选：A．【点评】此题主要考查度、分、秒的转化运算，进行度、分、秒的转化运算，注意以60为进制．2．（2017秋•石景山区期末）若90C∠-∠的结果是()∠=︒，则C AA'∠=︒，2530A．7530'︒︒D．6430'︒B．7430'︒C．6530'【分析】度、分、秒之间是60进制．【解答】解：9025306430∠-∠=︒-︒=︒．C A''故选：D．【点评】考查了度分秒的换算．度、分、秒之间是60进制，将高级单位化为低级单位时，乘以60，反之，将低级单位转化为高级单位时除以60．同时，在进行度、分、秒的运算时也应注意借位和进位的方法．3．（2017•门头沟区二模）将284231︒'''保留到“'”为()A．2842︒'''D．2900︒'︒'C．284230︒'B．2843【分析】根据小单位化大单位除以进率，可得答案．【解答】解：31600.52÷≈∴︒'''=︒'≈︒'，2842312842.522843故选：B．【点评】本题考查了度分秒的换算，利用小单位化大单位除以进率是解题关键．4．（2016•朝阳区校级模拟）下面等式成立的是()A．83.58350︒=︒'B．37123637.48︒'''=︒C．24242424.44︒=︒'︒'''=︒D．41.254115【分析】进行度、分、秒的加法、减法计算，注意以60为进制．【解答】解：A、83.58350︒=︒'，错误；B、37123637.48︒'''=︒，错误；︒'''=︒，错误；C、24242424.44D 、41.254115︒=︒'，正确．故选：D ．【点评】此类题是进行度、分、秒的加法、减法计算，相对比较简单，注意以60为进制即可．5．（2009秋•门头沟区期末）把2.36︒用度、分、秒表示正确的是( )A ．236︒'''B ．2306︒'''C ．2216︒'''D ．22136︒'''【分析】进行度、分、秒的转化运算，注意以60为进制．【解答】解：根据角的换算可得2.3620.3660︒=︒+⨯'221.6=︒+'24210.660=︒+'+⨯''22136=︒'''．故选：D ．【点评】此题主要考查度、分、秒的转化运算，相对比较简单，注意以60为进制．二．填空题（共8小题）6．（2019秋•怀柔区期末）若4730α∠=︒'，则90α︒-∠= 42.5︒ ．【分析】根据度分秒的换算，即可得到结果．【解答】解：4730α∠=︒'，90904730423042.5α∴︒-∠=︒-︒'=︒'=︒，故答案为：42.5︒．【点评】本题考查的是度分秒的换算以及余角的概念，若两个角的和为90︒，则这两个角互余．7．（2019秋•顺义区期末）65.24︒= 65 度 分 秒．【分析】根据度、分、秒是60进制，把小数部分乘以60，逐次计算即可得解．【解答】解：65.24651424︒=︒'''．故答案为：65，14，24．【点评】本题考查了度分秒的换算，注意度、分、秒以60为进制即可．8．（2019秋•延庆区期末）把5636︒'换算成度的结果是 56.6︒ ．【分析】首先把36'除以60化成度，再加到56︒上即可．【解答】解：5636︒'，56(3660)=︒+÷︒，56.6=︒．【点评】此题主要考查了度分秒的换算，1度60=分，即160︒='，1分60=秒，即160'=''．9．（2019秋•丰台区期末）计算：1805218'︒-︒= 12742︒' ．【分析】首先把180︒化为17960︒'，然后进行计算即可．【解答】解：180521817960521812742''︒-︒=︒'-︒=︒'，故答案为：12742︒'．【点评】此类题考查了度、分、秒的换算，是角度计算中的一个难点，注意以60为进制即可．10．（2019秋•门头沟区期末）计算：1807248︒-︒'= 10712︒' ．【分析】直接利用度分秒的转化将原式变形，进而计算得出答案．【解答】解：1807248179607248︒-︒'=︒'-︒'10712=︒'．故答案为：10712︒'．【点评】此题主要考查了度分秒的换算，正确进行度分秒的转化是解题关键．11．（2019秋•海淀区期末）计算：48396731︒'+︒'= 11610'︒ ．【分析】根据度、分、秒的进制为60直接计算即可．【解答】解：393170110'+'='=︒'，故4839673111610'︒'+︒'=︒．故答案为：11610'︒．【点评】本题考查了角的运算，涉及到度、分、秒的进制，本题是道很基础的习题，认真计算即可得解．12．（2019秋•平谷区期末）计算：901835'︒-︒= 7125︒' ．【分析】根据度分秒的计算法则直接计算即可，注意度分秒间的进率是60．【解答】解：9018357125'︒-︒=︒'．故答案是：7125︒'．【点评】本题考查了度分秒的换算，相同单位相减，不够减时向上一单位借一当60再减．13．（2019秋•石景山区期末）将2036︒'换算成度为 20.6 ︒．【分析】依据度分秒的换算，即可得到计算结果．【解答】解：360.6'=︒，203620.6∴︒'=︒，故答案为：20.6．【点评】本题主要考查了度分秒的换算，度、分、秒是常用的角的度量单位．1度60=分，即160︒='，1分60=秒，即160'=''．三．解答题（共2小题）14．（2014秋•西城区校级期末）计算：（1）1820α=︒'，630β=︒'，求αβ+；（2）42483625︒'+︒'= 79 ︒ '．【分析】（1）根据度分秒的加法，度加度，分加分，满60向上一单位近1，可得答案；（2）根据度分秒的加法，度加度，分加分，满60向上一单位近1，可得答案．【解答】解：（1）由1820α=︒'，630β=︒'，得182********αβ+=︒'+︒'=︒'；（2）4248362578737913︒'+︒'=︒'=︒'，故答案为：79，13．【点评】本题考查了度分秒的换算，度分秒的加法利用了度加度，分加分，满60向上一单位近1．15．（2013秋•大兴区期末）计算：38493︒'⨯．【分析】把度分分别乘以3，再满60进1，即可得出答案．【解答】解：原式383493=︒⨯+'⨯114147=︒'11627=︒'．【点评】本题考查了度分秒之间的换算的应用，注意：160︒='，160'=''．。

2023北京初三二模数学汇编 二次函数的图象和性质1．（2023·北京朝阳·统考二模）在平面直角坐标系xOy 中，点()11,y −在抛物线2y x ax =−上． (1)求1y 的值（用含a 的式子表示）； (2)若1a <−，试说明：10y <；(3)点()21,y ，()32,a y −在该抛物线上，若1y ，2y ，3y 中只有一个为负数，求α的取值范围．2．（2023·北京海淀·统考二模）在平面直角坐标系xOy 中，已知抛物线()220y ax bx a a =+++>过点()1,42a +．(1)求该抛物线的顶点坐标；(2)过该抛物线与y 轴的交点作y 轴的垂线l ，将抛物线在y 轴右侧的部分沿直线l 翻折，其余部分保持不变，得到图形G ，()11,M a y −−，()21,N a y −+是图形G 上的点，设12t y y =+． ①当1a =时，求t 的值； ②若69t ≤≤，求a 的取值范围．3．（2023·北京顺义·统考二模）在平面直角坐标系xOy 中，已知抛物线()22230y ax a x a =−−≠．(1)求该抛物线的对称轴（用含a 的式子表示）； (2)若1a =，当23x −<<时，求y 的取值范围；(3)已知()121,A a y −，()2,B a y ，()32,C a y +为该抛物线上的点，若132y y y <<，求a 的取值范围．4．（2023·北京平谷·统考二模）已知抛物线22y x tx =−+，若点()11,P y −，2,2t Q y ⎛⎫ ⎪⎝⎭，()3,M m y 在抛物线上．(1)该抛物线的对称轴为______（用含t 的式子表示）； (2)若当2m =时，30=y ，则t 的值为______；(3)若对于23m ≤≤时，都有132y y y <<，求t 的取值范围．5．（2023·北京大兴·统考二模）在平面直角坐标系xOy 中，点(2,1)在抛物线21(0)y ax bx a =++>上． (1)求抛物线的对称轴；(2)已知点0(,)A x m ，点(3,)B n 在抛物线上，若对于01t x t ≤≤+，都有m n <，求t 的取值范围．6．（2023·北京东城·统考二模）在平面直角坐标系xOy 中，抛物线()210y ax bx a =++≠的对称轴是直线3x =．(1)求出该抛物线的顶点坐标（用含a 的式子表示）；(2)当0a >时，对于任意的正数t ，若点()()123,,32,t y t y −+在该抛物线上，则1y _________2y （填“>”“<”或“=”）；(3)已知点()()0,3,7,3A B ．若该抛物线与线段AB 恰有一个公共点，求a 的取值范围．7．（2023·北京西城·统考二模）在平面直角坐标系xOy 中，点()11,x y ，()22,x y 都在抛物线()2280y ax ax a =−+<上，且112x −<<，217m x m −<<+．(1)当2m =−时，比较1y ，2y 的大小关系，并说明理由； (2)若存在1x ，2x ，满足12y y =，求m 的取值范围．8．（2023·北京昌平·统考二模）在平面直角坐标系xOy 中，点(21)()a m b n +，，，是抛物线222(00)y ax a x c a c =−+≠>，上的点．(1)当1a =时，求抛物线对称轴，并直接写出m 与c 大小关系； (2)若对于任意的24b ≤≤，都有m c n >>，求a 的取值范围．9．（2023·北京房山·统考二模）平面直角坐标系xOy 中，抛物线243y ax x a =−+的对称轴为直线x n =．(1)若抛物线经过点()10，，求a 和n 的值； (2)若抛物线上存在两点()1,A x m 和()2,1B x m +，1x n =． ①判断抛物线的开口方向，并说明理由； ②若21||1x x −≤，求a 的取值范围 ．1,2，512a ≤≤）将点(1,4a123,3y y ==，即可求解；②22y ax bx a =+++与y 轴交于点()0,2a +，抛物线在y 轴右侧的部分关于直线2y a =+翻折可得222y ax ax a =−−++()0x >，()11,M a y −−在对称轴的左侧，()11,M a y −−，()21,N a y −+关于=1x −对称，分01a <≤，1a >，分别求得1y ，2y ，根据题意解不等式即可求解． 【详解】（1）解：将点()1,42a +代入22y ax bx a =+++中，得242a b a a +++=+ 解得：2b a =∴抛物线解析式为()222212y ax ax a a x =+++=++ ∴对称轴为直线=1x −，顶点为1,2，（2）①当1a =时，223y x x =++， 当0x =时，3y =，∴抛物线与y 轴交点为()0,3，∵()11,M a y −−，()21,N a y −+是图形G 上的点， 即()()122,,0,M y N y − ∴14433y =−+=，23y = ∴12336t y y =+=+=；②22y ax bx a =+++，当0x =时，2y a =+， ∴22y ax bx a =+++与y 轴交于点()0,2a +，∴抛物线在y 轴右侧的部分关于直线2y a =+翻折可得222y ax ax a =−−++()0x > ∵对称轴为直线=1x −∴()11,M a y −−在对称轴的左侧，∴()()23112122y a a a a a a =−−+−−++=+， ∵()11,M a y −−，()21,N a y −+关于=1x −对称∴当110a −<−+≤，即01a <≤时，即3212y y a ==+ ∴31224t y y a =+=+∵01a <≤ ∴6t ≤，当10a −+>，即1a >时，()()232121222y a a a a a a a =−−+−−+++=−++， ∴1224t y y a =+=+， ∵69t ≤≤， ∴6249a ≤+≤，【点睛】本题考查了二次函数的性质，熟练掌握二次函数的性质是解题的关键．3．(1)直线x a = (2)45y −≤< (3)1a <−【分析】（1）根据对称轴公式即可求解；（2）根据23x −<<，2x =−比3x =距离对称轴远，分别求得（3）根据题意得出()2,B a y 为抛物线的顶点，轴的左侧时，当()121,A a y −在对称轴的右侧时，列出不等式，解不等式即可求解．【详解】（1）解：抛物线(2223y ax a x a =−−≠抛物线的对称轴为m c >，22a a +∴<22a a ∴<c n <， 2b a ∴>，24b ≤≤2a ∴>；②当12−≤m c >，22a a +∴≥22a a ∴≥12a ∴−≤③当a <−m c >，22a a +∴<22a a ∴<c n >，24b ≤≤1a ∴<，12a ∴<−综上所述，【点睛】本题主要考查了二次函数的图象与性质，熟练掌握二次函数的图象与性质，采用分类讨论的思想。

2022-2023学年北京市顺义区中考数学专项突破仿真模拟试题（一模）一、选一选（共13小题；每小题3分,共39分）1.一个直角三角形有两条边长为3，4，则较小的锐角约为()A.37︒B.41︒C.37︒或41︒D.以上答案均不对2.已知⊙O 的半径为5，点P 到圆心O 的距离为6，那么点P 与⊙O 的地位关系是()A.点P 在⊙O 上B.点P 在⊙O 内C.点P 在⊙O 外D.无法确定3.若⊙O 1、⊙O 2的半径分别为4和6，圆心距O 1O 2=8，则⊙O 1与⊙O 2的地位关系是（）A.内切B.相交C.外切D.外离4.在△ABC 中，∠C=90°，∠A=72°，AB=10，则边AC 的长约为（到0.1）（）A.9.1B.9.5C.3.1D.3.55.已知抛物线y=﹣x 2+1的顶点为P ，点A 是象限内该二次函数图象上一点，过点A 作x 轴的平行线交二次函数图象于点B ，分别过点B 、A 作x 轴的垂线，垂足分别为C 、D ，连结PA 、PD ，PD 交AB 于点E ，△PAD 与△PEA 类似吗？（）A.一直不类似B.一直类似C.只要AB=AD 时类似D.无法确定6.已知⊙O 的半径为r ，圆心O 到直线l 的距离为d ．若直线l 与⊙O 有交点，则下列结论正确的是（）A.d＝r B.0≤d≤r C.d≥r D.d＜r 7.如图是二次函数2y=ax +bx+c 的部分图象，由图象可知不等式2ax +bx+c<0的解集是【】A.1<x<5- B.x>5 C.x<1-且x>5 D.x ＜－1或x ＞58.已知二次函数y=（x﹣h）2+1（h 为常数），在自变量x 的值满足1≤x≤3的情况下，与其对应的函数值y 的最小值为5，则h 的值为（）A.1或﹣5 B.﹣1或5 C.1或﹣3 D.1或39.已知函数y 1=4x ，二次函数y 2=2x 2+2，在实数范围内，对于x 的同一个值，这两个函数所对应的函数值为y 1与y 2，则下列关系正确的是（）A.y 1＞y 2 B.y 1≥y 2 C.y 1＜y 2 D.y 1≤y 210.如图，半圆O 的半径OA ＝4，P 是OA 延伸线上一点，线段OP 的垂直平分线分别交OP 、半圆O 于B 、C 两点，射线PC 交半圆O 于点D ．设PA ＝x ，CD ＝y ，则能表示y 与x 的函数关系的图象是（）A. B. C. D.11.若二次函数2y x bx =+的图象的对称轴是点(2,0)且平行于y 轴的直线，则关于x 的方程25x bx +=的解为（）．A.10x =，24x = B.11x =，25x = C.11x =，25x =- D.11x =-，25x =12.如图为二次函数y ＝ax 2＋bx ＋c 的图象，在下列说法中：①ac<0；②方程ax 2＋bx ＋c ＝0的根是x 1＝－1，x 2＝3；③a ＋b ＋c>0；④当x>1时，y 随x 的增大而增大．正确的有：_______．13.如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．若AC ，BC =2，则sin ∠ACD 的值为（）A.3B.255 C.2 D.23二、填空题（共10题；共30分）14.已知抛物线y=x 2﹣4x+3，如果点P(0，5)与点Q 关于该抛物线的对称轴对称，那么点Q 的坐标是_____．15.将函数y ＝x 2的图象向右平移2个单位得函数y 1的图象，将y 与y 1合构成新图象，直线y ＝m 被新图象依次截得三段的长相等，则m ＝___________16.已知抛物线y=﹣12x 2﹣3x 点（﹣2，m ），那么m=________．17.已知圆的半径是6cm ，则120°的圆心角所对的弧长是_____cm ．18.一个扇形的面积为6πcm 2，弧长为πcm ，则该扇形的半径为___．19.在平面直角坐标系中，将函数y=﹣2x 2的图象先向右平移1个单位长度，再向上平移5个单位长度，所得图象的函数表达式是_____．20.如图，CA ⊥AB ，DB ⊥AB ，已知AC=2，AB=6，点P 射线BD 上一动点，以CP 为直径作⊙O ，点P 运动时，若⊙O 与线段AB 有公共点，则BP 值为_______．21.已知函数()2321y k x x =-++的图象与x 轴有交点，则k 的取值范围为______．22.某服装店购进单价为15元的童装若干件，一段工夫后发现：当价为25元时平均每天能售出8件，而当价每降低1元，平均每天能多售出2件.当每件的定价为_______元时，该服装店平均每天的利润.23.△OAB 是以正多边形相邻的两个顶点A，B 与它的O 为顶点的三角形，若△OAB 的一个内角为70°，则该正多边形的边数为_____．三、解答题（共5题；共51分）24.如图，⊙O 的直径AB 垂直弦CD 于点E ，点F 在AB 的延伸线上，且∠BCF ＝∠A ．（1）求证：直线CF 是⊙O 的切线；（2）若⊙O 的半径为5，DB ＝4.求sin ∠D 的值．25.如图，AB 是⊙O 的直径，AC 是弦，半径OD ⊥AC 于点E ，过点D 的切线与BA 延伸线交于点F ．(1)求证：∠CDB=∠BFD ；(2)若AB=10，AC=8，求DF 的长．26.水利部门为加强防汛工作，决定对某水库大坝进行加固，大坝的横截面是梯形ABCD.如图所示，已知迎水坡面AB 的长为16米，∠B=600，背水坡面CD 的长为163坝的横截面积为梯形ABED，CE的长为8米．（1）已知需加固的大坝长为150米，求需求填土石方多少立方米？（2）求加固后的大坝背水坡面DE的坡度．27.如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，DE⊥AD，交AB于点E，AE为⊙O的直径．（1）判断BC与⊙O的地位关系，并证明你的结论；（2）求证：△ABD∽△DBE；（3）若co=3，AE=4，求CD．28.如图1，二次函数y1=（x﹣2）（x﹣4）的图象与x轴交于A、B两点（点A在点B的左侧），其对称轴l与x轴交于点C，它的顶点为点D．（1）写出点D的坐标．（2）点P在对称轴l上，位于点C上方，且CP=2CD，以P为顶点的二次函数y2=ax2+bx+c （a≠0）的图象过点A．①试阐明二次函数y2=ax2+bx+c（a≠0）的图象过点B；②点R在二次函数y1=（x﹣2）（x﹣4）的图象上，到x轴的距离为d，当点R的坐标为时，二次函数y2=ax2+bx+c（a≠0）的图象上有且只要三个点到x轴的距离等于2d；③如图2，已知0＜m＜2，过点M（0，m）作x轴的平行线，分别交二次函数y1=（x﹣2）（x﹣4）、y2=ax2+bx+c（a≠0）的图象于点E、F、G、H（点E、G在对称轴l左侧），过点H 作x轴的垂线，垂足为点N，交二次函数y1=（x﹣2）（x﹣4）的图象于点Q，若△GHN∽△EHQ，求实数m的值．2022-2023学年北京市顺义区中考数学专项突破仿真模拟试题（一模）一、选一选（共13小题；每小题3分,共39分）1.一个直角三角形有两条边长为3，4，则较小的锐角约为()A.37︒B.41︒C.37︒或41︒D.以上答案均不对【正确答案】C【详解】试题解析：①若3、4是直角边，∵两直角边为3，4，∴斜边长=5，∴较小的锐角所对的直角边为3，则其正弦值为3 5；②若斜边长为4，则较小边≈2.65，∴较小边所对锐角正弦值约=2.654=0.6625，利用计算器求得角约为37°或41°．故选C．2.已知⊙O的半径为5，点P到圆心O的距离为6，那么点P与⊙O的地位关系是()A.点P在⊙O上B.点P在⊙O内C.点P在⊙O外D.无法确定【正确答案】C【详解】试题分析：由于OP=6＞5，所以点P与⊙O的地位关系是点在圆外．故选C．考点：点与圆的地位关系．3.若⊙O 1、⊙O 2的半径分别为4和6，圆心距O 1O 2=8，则⊙O 1与⊙O 2的地位关系是（）A.内切B.相交C.外切D.外离【正确答案】B 【详解】试题分析：⊙O 1、⊙O 2的直径分别为4和6，圆心距O 1O 2=2，⊙O 1、⊙O 2的半径之和为5，只差为1，而1<O 1O 2=2<5,所以两圆相交考点：两圆的地位关系点评：考查两圆的地位关系，利用两圆的圆心距和两圆的半径之差或者之和，来判断两圆的地位4.在△ABC 中，∠C=90°，∠A=72°，AB=10，则边AC 的长约为（到0.1）（）A.9.1B.9.5C.3.1D.3.5【正确答案】C 【详解】分析：在Rt △ABC 中，根据三角函数的定义，易得AB 、AC 及∠A 的关系，进而计算可得答案．解答：解：根据题意在Rt △ABC 中，有cosA=BC AB ，sinA=；则AC=AB?cosA=10×cos72°≈3.1；故选C ．5.已知抛物线y=﹣x 2+1的顶点为P ，点A 是象限内该二次函数图象上一点，过点A 作x 轴的平行线交二次函数图象于点B ，分别过点B 、A 作x 轴的垂线，垂足分别为C 、D ，连结PA 、PD ，PD 交AB 于点E ，△PAD 与△PEA 类似吗？（）A.一直不类似B.一直类似C.只要AB=AD 时类似D.无法确定【正确答案】B 【详解】试题分析：设A （x ，-x 2+1）根据题意可求出PA 、PD 、PE 的值，从而得出PE PA PA PD =，又∠APE=∠DPA ，因此，△PAD ∽△PEA.故选B.考点:二次函数综合题.6.已知⊙O 的半径为r ，圆心O 到直线l 的距离为d ．若直线l 与⊙O 有交点，则下列结论正确的是（）A.d ＝rB.0≤d≤rC.d≥rD.d ＜r【正确答案】B 【详解】试题分析：圆与直线有交点，即可能为1个交点或2个交点，当1d r ==时，圆与直线相切，即有一个交点，当1d r ==时，有两个交点考点：圆与直线的关系点评：圆与直线有相交、相切、相离三种关系，其中相交、相切有交点，即当点与直线距离小于或者等于半径时，圆与直线有交点7.如图是二次函数2y=ax +bx+c 的部分图象，由图象可知不等式2ax +bx+c<0的解集是【】A.1<x<5- B.x>5 C.x<1-且x>5 D.x ＜－1或x ＞5【正确答案】D 【详解】利用二次函数的对称性，可得出图象与x 轴的另一个交点坐标，图象可得出2ax+bx+c<0的解集：由图象得：对称轴是x=2，其中一个点的坐标为（5，0），∴图象与x轴的另一个交点坐标为（－1，0）．ax+bx+c<0的解集即是y＜0的解集，由图象可知：2∴x＜－1或x＞5．故选D．8.已知二次函数y=（x﹣h）2+1（h为常数），在自变量x的值满足1≤x≤3的情况下，与其对应的函数值y的最小值为5，则h的值为（）A.1或﹣5B.﹣1或5C.1或﹣3D.1或3【正确答案】B【分析】讨论对称轴的不同地位，可求出结果．【详解】∴①若h＜1≤x≤3，x=1时，y取得最小值5，可得：（1﹣h）2+1=5，解得：h=﹣1或h=3（舍）；②若1≤x≤3＜h，当x=3时，y取得最小值5，可得：（3﹣h）2+1=5，解得：h=5或h=1（舍）．综上，h的值为﹣1或5，故选B．本题次要考查二次函数的性质和最值，根据二次函数的性质和最值分类讨论是解题的关键．由解析式可知该函数在x=h时取得最小值1、x＞h时，y随x的增大而增大、当x＜h 时，y随x的增大而减小，根据1≤x≤3时，函数的最小值为5可分如下两种情况：①若h ＜1≤x≤3，x=1时，y取得最小值5；②若1≤x≤3＜h，当x=3时，y取得最小值5，分别列出关于h的方程求解即可．9.已知函数y1=4x，二次函数y2=2x2+2，在实数范围内，对于x的同一个值，这两个函数所对应的函数值为y1与y2，则下列关系正确的是（）A.y1＞y2B.y1≥y2C.y1＜y2D.y1≤y2【正确答案】D【详解】试题解析：由2422y xy x ⎧⎨+⎩＝＝消去y 得到：x 2-2x+1=0，∵△=0，∴直线y=4x 与抛物线y=2x 2+2只要一个交点，如图所示，观察图象可知：y 1≤y 2，故选D．10.如图，半圆O 的半径OA ＝4，P 是OA 延伸线上一点，线段OP 的垂直平分线分别交OP 、半圆O 于B 、C 两点，射线PC 交半圆O 于点D ．设PA ＝x ，CD ＝y ，则能表示y 与x 的函数关系的图象是（）A.B.C.D.【正确答案】A【详解】试题解析：作OE ⊥CD ，垂足为E ，如图1，则CE=12CD=12y ，∵∠P=∠P ，∠PBC=∠PEO=90°，∴△PBC ∽△PEO ，∴PB PC PE OP=，而PB=12OP=12（x+4），PE=PC+CE=4+12y ，∴44244+2x y x ++＝，∴y=14x 2+2x-4（-4＜x ＜4）；故选A.11.若二次函数2y x bx =+的图象的对称轴是点(2,0)且平行于y 轴的直线，则关于x 的方程25x bx +=的解为（）．A.10x =，24x = B.11x =，25x = C.11x =，25x =- D.11x =-，25x =【正确答案】D【详解】∵二次函数y=x 2+bx 的图象的对称轴是点(2，0)且平行于y 轴的直线，∴抛物线的对称轴为直线x=2，则−2b a =−2b =2，解得：b=−4，∴x 2+bx=5即为x 2−4x−5=0，则(x−5)(x+1)=0，解得：x 1=5，x 2=−1.故选D.本题考查了抛物线与x 轴的交点：把二次函数y=ax 2+bx+c （a 、b 、c 是常数，a≠0）与x 轴的交点坐标成绩转化为关于x 的一元二次方程的成绩.12.如图为二次函数y ＝ax 2＋bx ＋c 的图象，在下列说法中：①ac<0；②方程ax 2＋bx ＋c ＝0的根是x 1＝－1，x 2＝3；③a ＋b ＋c>0；④当x>1时，y 随x 的增大而增大．正确的有：_______．【正确答案】②④【详解】试题解析：根据图象可得0,0a c ><，则0ac <，故①正确.二次函数与x 轴的交点是()1,0-和()3,0,则方程20ax bx c ++=的根为121,3x x =-=，故②正确.当1x =时，0y a b c =++<，故③错误.对称轴是1x =，当1x >时，y 随x 的增大而增大.故④正确.故答案为①②④13.如图，在Rt △ABC 中，∠ACB =90°，CD ⊥AB ，垂足为D ．若AC，BC =2，则sin ∠ACD 的值为（）A.53 B.255 C.52 D.23【正确答案】A【分析】在直角△ABC 中，根据勾股定理即可求得AB ，而∠B ＝∠ACD ，即可把求sin ∠ACD 转化为求si ．【详解】在直角△ABC 中，根据勾股定理可得：AB 222252AC BC =+=+=（）3．∵∠B +∠BCD ＝90°，∠ACD +∠BCD ＝90°，∴∠B ＝∠ACD ，∴sin ∠ACD ＝sin ∠B 53AC AB ==．故选A ．本题考查了解直角三角形中三角函数的运用，要纯熟掌握好边角之间的关系，难度适中．二、填空题（共10题；共30分）14.已知抛物线y=x 2﹣4x+3，如果点P(0，5)与点Q 关于该抛物线的对称轴对称，那么点Q 的坐标是_____．【正确答案】（4，5）．【分析】首先确定抛物线的对称轴，然后根据对称点的性质解题即可．【详解】∵y=x 2﹣4x+3的对称轴为x=2，∴点P （0，5）关于该抛物线的对称轴对称点Q 的坐标为（4，5），故答案为（4，5）．15.将函数y ＝x 2的图象向右平移2个单位得函数y 1的图象，将y 与y 1合构成新图象，直线y ＝m 被新图象依次截得三段的长相等，则m ＝___________【正确答案】144m =或【详解】试题解析：∵二次函数y=x 2的图象向右平移2个单位，∴平移后的解析式为：y=（x-2）2，把y=m代入y=x2得m=x2，解得，把y=m代入y=（x-2）2得m=（x-2）2，解得，当0＜m＜1-（），解得m=1 4，当m＞1时，则-（），解得m=4，故答案为14或4．16.已知抛物线y=﹣12x2﹣3x点（﹣2，m），那么m=________．【正确答案】4【详解】试题解析：∵y=-12x2-3x点（-2，m），∴m=-12×22-3×（-2）=4，故答案为4．17.已知圆的半径是6cm，则120°的圆心角所对的弧长是_____cm．【正确答案】4π【分析】直接利用扇形的弧长公式计算即可得出结论．【详解】解：由题意知，r=6cm，n=120，∴12064180180n rlπππ⨯===（cm），故4π．此题次要考查了扇形的弧长公式，解本题的关键是熟记扇形的弧长公式．18.一个扇形的面积为6πcm2，弧长为πcm，则该扇形的半径为___．【正确答案】12cm.【详解】试题解析：设半径是r，∵一个扇形的弧长是πcm，扇形的面积为6πcm2，∴6π=12×π×r，∴r=12．考点：1.扇形面积的计算；2.弧长的计算．19.在平面直角坐标系中，将函数y=﹣2x2的图象先向右平移1个单位长度，再向上平移5个单位长度，所得图象的函数表达式是_____．【正确答案】y=2（x﹣1）2+5．【详解】试题分析：由“左加右减”的准绳可知，抛物线y=﹣2x2的图象向右平移1个单位所得函数图象的关系式是：y=﹣2（x﹣1）2；由“上加下减”的准绳可知，抛物线y=﹣2（x﹣1）2的图象向上平移5个单位长度所得函数图象的关系式是：y=2（x﹣1）2+5．考点：二次函数图象与几何变换．20.如图，CA⊥AB，DB⊥AB，已知AC=2，AB=6，点P射线BD上一动点，以CP为直径作⊙O，点P运动时，若⊙O与线段AB有公共点，则BP值为_______．【正确答案】92．【详解】试题分析：首先判断当AB与⊙O相切时，PB的值，设AB与⊙O相切于E，连接OE，则OE⊥AB，过点C作CF⊥PB于F，由CA⊥AB，DB⊥AB，得到AC∥OE∥PB，四边形ABPC是矩形，证得CF=AB=6，在直角三角形PCF中，由勾股定理列方程求解．试题解析：当AB与⊙O相切时，PB的值，如图，设AB与⊙O相切于E，连接OE，则OE⊥AB，过点C作CF⊥PB于F，∵CA ⊥AB ，DB ⊥AB ，∴AC ∥OE ∥PB ，四边形ABPC 是矩形，∴CF=AB=6，∵CO=OP ，∴AE=BE ，设PB=x ，则PC=2OE=2+x ，PF=x-2，∴（x+2）2=（x-2）2+62，解得；x=92，∴BP 值为：92．考点：直线与圆的地位关系．21.已知函数()2321y k x x =-++的图象与x 轴有交点，则k 的取值范围为______．【正确答案】k ≤4【分析】分为两种情况：①当k -3≠0时，（k -3）x 2+2x +1=0，求出Δ=b 2-4ac =-4k +16≥0的解集即可；②当k -3=0时，得到函数y =2x +1，与x 轴有交点；即可得到答案．【详解】解：①当k -3≠0时，（k -3）x 2+2x +1=0，Δ=b 2-4ac =22-4（k -3）×1=-4k +16≥0，解得：k ≤4；②当k -3=0时，y =2x +1，与x 轴有交点；故k 的取值范围是k ≤4，故k ≤4．本题次要考查对抛物线与x 轴的交点，根的判别式，函数的性质等知识点的理解和掌握，能进行分类求出每种情况的k是解此题的关键．22.某服装店购进单价为15元的童装若干件，一段工夫后发现：当价为25元时平均每天能售出8件，而当价每降低1元，平均每天能多售出2件.当每件的定价为_______元时，该服装店平均每天的利润.【正确答案】22【详解】试题分析：设定价为x元时，利润为w元，由题意建立w与x的二次函数关系：w=（x-15）（25-x2×4+8）,化简得：w=2288870x x-+-，∵-2<0,∴当x=2ba-=884=22时，w有值,∴当每件的定价为22元时，该服装店平均每天的利润．考点：利用二次函数处理实践成绩．．23.△OAB是以正多边形相邻的两个顶点A，B与它的O为顶点的三角形，若△OAB的一个内角为70°，则该正多边形的边数为_____．【正确答案】9【详解】分两种情况讨论：若∠OAB＝∠OBA＝70°，则∠BOA＝40°，边数为：36040＝9；若∠BOA＝70°，则边数为：36070不为整数，故不存在．综上所述，边数为9．三、解答题（共5题；共51分）24.如图，⊙O的直径AB垂直弦CD于点E，点F在AB的延伸线上，且∠BCF＝∠A．（1）求证：直线CF是⊙O的切线；（2）若⊙O的半径为5，DB＝4.求sin∠D的值．【正确答案】（1）证明见解析；（2）2 5.【详解】试题分析：（1）连接OC，由OA=OA可知∠ACO=∠A，再根据∠FCB=∠A可知∠ACO=∠FCB，由于AB是⊙O的直径，所以∠ACO+∠OCB=90°故∠FCB+∠OCB=90°故可得出结论；（2）由AB 是⊙O 的直径，CD ⊥AB 可知试题解析:（1）连接OC ，∵OA=OC ，∴∠ACO=∠A ，又∵∠FCB=∠A∴∠ACO=∠FCB ，又∵AB 是⊙O 的直径∴∠ACO+∠OCB=90°，∠FCB+∠OCB=90°∴直线CF 为⊙O 的切线，（2）∵AB 是⊙O 直径∴∠ACB=90°∵DC ⊥AB∴ BCBD =∴BC=BD ，∠A=∠D ∴42sin sin 105BC D A AB ∠=∠===考点:1.切线的判定；2.圆周角定理；3.解直角三角形.25.如图，AB 是⊙O 的直径，AC 是弦，半径OD ⊥AC 于点E ，过点D 的切线与BA 延伸线交于点F ．(1)求证：∠CDB=∠BFD ；(2)若AB=10，AC=8，求DF 的长．【正确答案】（1）证明见解析（2）203【分析】（1）根据切线的性质得到DF ⊥OD ，由于OD ⊥AC ，推出DF ∥AC ，根据平行线的性质得到∠CAB=∠BFD ，再根据圆周角定理即可得到结论；（2）利用垂径定理得出AE 的长，再利用类似三角形的判定与性质得出DF 的长．【详解】解：（1）∵DF 与⊙O 相切，D 为切点，∴DF ⊥OD ，∵OD ⊥AC ，∴DF ∥AC ，∴∠CAB=∠BFD ，∵∠CAB=∠CDB ，∴∠CDB=∠BFD ；（2）∵半径OD 垂直于弦AC 于点E ，AC=8，∴AE=12AC=12×8＝4，∵AB 是⊙O 的直径，∴OA=OD=12AB=12×10=5，在Rt △AEO 中，222254OA AE -=-=3，∵AC ∥DF ，∴△OAE ∽△OFD ，∴OE AE OD DF ＝，∴34=5DF ，∴DF=203．本题考查切线的性质、圆周角定理、垂径定理、平行线的判定与性质、类似三角形的判定与性质、勾股定理等知识，纯熟掌握相关知识的联系与运用是解答的关键.26.水利部门为加强防汛工作，决定对某水库大坝进行加固，大坝的横截面是梯形ABCD.如图所示，已知迎水坡面AB 的长为16米，∠B=600，背水坡面CD 的长为坝的横截面积为梯形ABED ，CE 的长为8米．（1）已知需加固的大坝长为150米，求需求填土石方多少立方米？（2）求加固后的大坝背水坡面DE 的坡度．【正确答案】解：（1）需求填土石方150⨯.（2）加固后的大坝背水坡面DE 的坡度为34.【分析】（1）分别过A 、D 作下底的垂线，设垂足为F 、G ．在Rt △ABF 中，已知坡面长和坡角的度数，可求得铅直高度AF 的值，也就得到了DG 的长；以CE 为底，DG 为高即可求出△CED 的面积，再乘以大坝的长度，即为所需的填方体积.（2）在Rt △CDG 中，由勾股定理求CG 的长，即可得到GE 的长；Rt △DEG 中，根据DG 、GE 的长即可求得坡角的正切值，即坡面DE 的坡比.【详解】解：（1）如图，分别过A 、D 作AF ⊥BC ，DG ⊥BC ，垂点分别为F 、G ．在Rt △ABF 中，AB=16米，∠B=60°，AF sin B AB∠=，∴3AF 162=⨯=，即DG=又∵CE=8，∴11822DCE S CE DG ∆=⋅⋅=⨯⨯=又∵需加固的大坝长为150，∴需求填方.150⨯答：需求填土石方150⨯.（2）在Rt △DGC 中，DC=，DG=，∴GC 24==.∴GE=GC+CE=32.∴DE 的坡度833324DG i GE ===.答：加固后的大坝背水坡面DE 的坡度为4.27.如图，在△ABC 中，∠C=90°，∠BAC 的平分线交BC 于点D ，DE ⊥AD ，交AB 于点E ，AE 为⊙O 的直径．（1）判断BC 与⊙O 的地位关系，并证明你的结论；（2）求证：△ABD ∽△DBE ；（3）若co=223，AE=4，求CD ．【正确答案】（1）BC 与⊙O 相切；（2）证明见解析；（3）423．【详解】试题分析：（1）结论：BC 与⊙O 相切，连接OD 只需证明OD ∥AC 即可．（2）欲证明△ABD ∽△DBE ，只需证明∠BDE=∠DAB 即可．（3）在Rt △ODB 中，由co=BD OB =223，设BD=，OB=3k ，利用勾股定理列出方程求出k ，再利用DO ∥AC ，得BD BO CD AO =列出方程即可处理成绩．试题解析：（1）结论：BC 与⊙O 相切．证明：如图连接OD ．∵OA=OD ，∴∠OAD=∠ODA ，∵AD 平分∠CAB ，∴∠CAD=∠DAB ，∴∠CAD=∠ADO ，∴AC ∥OD ，∵AC ⊥BC ，∴OD ⊥BC ，∴BC 是⊙O 的切线．（2）∵BC 是⊙O 切线，∴∠ODB=90°，∴∠BDE+∠ODE=90°，∵AE 是直径，∴∠ADE=90°，∴∠DAE+∠AED=90°，∵OD=OE ，∴∠ODE=∠OED ，∴∠BDE=∠DAB ，∵∠B=∠B ，∴△ABD ∽△DBE ．（3）在Rt △ODB 中，∵co=BD OB =223，设BD=k ，OB=3k ，∵OD 2+BD 2=OB 2，∴4+8k 2=9k 2，∴k=2，∴BO=6，BD=DO ∥AC ，∴BD BO CD AO =，∴62CD =，∴CD=3．考点：圆的综合题；探求型．28.如图1，二次函数y 1=（x ﹣2）（x ﹣4）的图象与x 轴交于A 、B 两点（点A 在点B 的左侧），其对称轴l 与x 轴交于点C ，它的顶点为点D ．（1）写出点D 的坐标．（2）点P 在对称轴l 上，位于点C 上方，且CP=2CD ，以P 为顶点的二次函数y 2=ax 2+bx+c （a≠0）的图象过点A ．①试阐明二次函数y 2=ax 2+bx+c （a≠0）的图象过点B ；②点R 在二次函数y 1=（x ﹣2）（x ﹣4）的图象上，到x 轴的距离为d ，当点R 的坐标为时，二次函数y 2=ax 2+bx+c （a≠0）的图象上有且只要三个点到x 轴的距离等于2d ；③如图2，已知0＜m ＜2，过点M （0，m ）作x 轴的平行线，分别交二次函数y 1=（x ﹣2）（x ﹣4）、y 2=ax 2+bx+c （a≠0）的图象于点E 、F 、G 、H （点E 、G 在对称轴l 左侧），过点H 作x 轴的垂线，垂足为点N ，交二次函数y 1=（x ﹣2）（x ﹣4）的图象于点Q ，若△GHN ∽△EHQ ，求实数m 的值．【正确答案】（1）（3，﹣1）；（2）①证明见解析；②（32，1）、（2，1）或（3，﹣1）；③当△GHN ∽△EHQ ，实数m 的值为1．【详解】试题分析：（1）利用配方法将二次函数1y =（x ﹣2）（x ﹣4）变形为顶点式，由此即可得出结论；（2）①由点P 在对称轴l 上，可得出二次函数22y ax bx c =++的图象的对称轴为直线l ，再点A 、B 关于对称轴l 对称，二次函数22y ax bx c =++（a ≠0）的图象过点A ，即可得出二次函数22y ax bx c =++（a ≠0）的图象过点B ；②由二次函数22y ax bx c =++（a ≠0）的图象上有且只要三个点到x 轴的距离等于2d ，即可得出d =1，再令二次函数1y =（x ﹣2）（x ﹣4）中y 1=±1求出x 值，即可得出结论；③设N （n ，0），则H （n ，﹣2（n ﹣2）（n ﹣4）），Q （n ，（n ﹣2）（n ﹣4）），由此即可得出22213HN HQ ==+，根据类似三角形的性质即可得出23HN HG HQ HE ==，再根据对称性可得出12KG KE =，设KG =t （t ＞0），则G 的坐标为（3﹣t ，m ），E 的坐标为（3﹣2t ，m ），由此即可得出关于m 、t 的二元方程组，解方程组即可求出m 值．试题解析：（1）∵1y =（x ﹣2）（x ﹣4）=268x x -+=2(3)1x --，∴顶点D 的坐标为（3，﹣1）．故答案为（3，﹣1）．（2）①∵点P 在对称轴l 上，位于点C 上方，且CP =2CD ，∴点P 的坐标为（3，2），∴二次函数1y =（x ﹣2）（x ﹣4）与22y ax bx c =++的图象的对称轴均为x =3，∵点A 、B 关于直线x =3对称，∴二次函数22y ax bx c =++（a ≠0）的图象过点B ．②∵二次函数22y ax bx c =++的顶点坐标P （3，2），且图象上有且只要三个点到x 轴的距离等于2d ，∴2d =2，解得：d =1．令1y =（x ﹣2）（x ﹣4）=268x x -+中y 1=±1，即268x x -+=±1，解得：x 1=3，x 2=3+，x 3=3，∴点R的坐标为（3-，1）、（3+，1）或（3，﹣1）．故答案为（3，1）、（3，1）或（3，﹣1）．③设过点M 平行x 轴的直线交对称轴l 于点K ，直线l 也是二次函数22y ax bx c =++（a ≠0）的图象的对称轴．∵二次函数22y ax bx c =++过点A 、B ，且顶点坐标为P （3，2），∴二次函数2y =﹣2（x ﹣2）（x ﹣4）．设N （n ，0），则H （n ，﹣2（n ﹣2）（n ﹣4）），Q （n ，（n ﹣2）（n ﹣4）），∴HN =2（n ﹣2）（n ﹣4），QN =（n ﹣2）（n ﹣4），∴HN QN =2，即22213HN HQ ==+．∵△GHN ∽△EHQ ，∴23HN HG HQ HE ==．∵G 、H 关于直线l 对称，∴KG =KH =12HG ，∴12KG KE =．设KG =t （t ＞0），则G 的坐标为（3﹣t ，m ），E 的坐标为（3﹣2t ，m ），由题意得：2(32)(34)(322)(324)t t m t t m -----=⎧⎨----=⎩，解得：221t m ⎧=⎪⎨⎪=⎩或221t m ⎧=-⎪⎨⎪=⎩（舍去）．故当△GHN ∽△EHQ ，实数m 的值为1．2022-2023学年北京市顺义区中考数学专项突破仿真模拟试题（二模）第I 卷（选一选）评卷人得分一、单选题1．下列几何体中，其侧面展开图为扇形的是()A ．B ．C ．D ．2．2020年6月23日，我国成功发射北斗系统第5颗导航卫星，暨北斗三号一颗全球组网卫星，该卫星驻守在我们上方36000公里的天疆数36000用科学记数法表示为（）A ．33610⨯B ．33.610⨯C ．43.610⨯D ．50.3610⨯3．下列图形中，既是轴对称图形又是对称图形的是（）A ．B ．C ．D ．4．实数a ，b ，c 在数轴上对应点的位置如图所示，若a c =，则下列结论中正确的是（）A ．0a c +>B ．0a b ->C ．a b >D ．0ab >5．如图，AB CD ∥，30A ∠=︒，DA 平分∠CDE ，则∠DEB 的度数为（）A ．75°B ．60°C ．45°D ．30°6．方程2102x x -=-的解是（）A ．4B ．3C ．2D ．17．已知三个点()11,x y ，()22,x y ，()33,x y 在反比例函数2y x =的图象上，其中1230x x x <<<，下列结论中正确的是（）A ．2130y y y <<<B ．1230y y y <<<C ．3210y y y <<<D ．3120y y y <<<8．某超市的某种蔬菜一周内每天的进价与售价信息和实际每天的量情况如图表所示，则下列推断不合理的是（）该种蔬菜一周内实际量表（单位：斤）日期周一周二周三周四周五周六周日量30403530506050A ．该种蔬菜周一的利润最小B ．该种蔬菜周日的利润C ．该种蔬菜一周中每天的售价组成的这组数据的众数是4D ．该种蔬菜一周中每天进价组成的这组数据的中位数是3第II 卷（非选一选）评卷人得分二、填空题9．若分式21x x -+的值为0，则x 的值是______．10．一个正多边形的内角和为720︒，则这个多边形的外角的度数为______．11．已知a b <，且a 、b 为两个连续的整数，则a +b ＝_____．12．如果关于x 的方程240x x m ++=有实数根，那么m 的取值范围是______．13．如图，AD ，BE 是ABC 的两条高线，只需添加一个条件即可证明ADC BEC △△≌（不添加其它字母及辅助线），这个条件可以是______（写出一个即可）．14．柳州市某校的生物兴趣小组在老师的指导下进行了多项有意义的生物研究并取得成果．下面是这个兴趣小组在相同的实验条件下，对某植物种子发芽率进行研究时所得到的数据：种子数n307513021048085612502300发芽数m287212520045781411872185发芽频率mn 0.93330.96000.96150.95240.95210.95090.94960.9500依据上面的数据可以估计，这种植物种子在该实验条件下发芽的概率约是_____（结果到0.01）．15．幻方历史悠久，传说最早出现在夏禹时代的“洛书”．把洛书用今天的数学符号翻译出来，就是一个三阶幻方．将数字1～9分别填入如图所示的幻方中，要求每一横行，每一竖行以及两条对角线上的数字之和都是15，则a 的值为____________．16．某中学为积极开展校园足球运动，计划购买A 和B 两种品牌的足球，已知一个A 品牌足球价格为120元，一个B 品牌足球价格为150元．学校准备用3000元购买这两种足球（两种足球都买），并且3000元全部用完，则该校共有______种购买．评卷人得分三、解答题17(0184cos 45212︒+---．18．解不等式组：5241,13 1.42x x x x +≥-⎧⎪⎨+->+⎪⎩19．已知2320x x +-=，求代数式()()()22223x y x y x x y +---+的值．20．已知：如图，直线l 和l 外一点P．求作：直线PQ ，使得PQ l ∥．作法：①在直线l 上任取一点A ，连接PA ，以点A 为圆心，PA 的长为半径画弧，交直线l 于点B ；②分别以点P ，B 为圆心，PA 的长为半径画弧，两弧交于点Q （不与点A 重合）；③作直线PQ ．所以直线PQ 就是所求作的直线．(1)使用直尺和圆规，依作法补全图形（保留作图痕迹）；(2)完成下面的证明．证明：连接BQ ．∵AB BQ PQ PA ===，∴四边形PABQ 是______，（__________）（填推理依据）．∴PQ AB ∥（__________）（填推理依据）．即PQ l ∥．21．如图，在ABC 中，AB AC =，AD 为BC 边上的中线，点E 为AD 的中点，过点A 作AF BC ∥，交BE 的延长线于点F ，连接CF ．(1)求证：四边形ADCF 为矩形；(2)若12BC =，4sin 5ACB ∠=，求EF 的长．22．在平面直角坐标系xOy 中，直线l ：4y kx k =-+与函数()0m y x x =>的图象交于点()1,4A ．(1)求m 的值；(2)横、纵坐标都是整数的点叫做整点．记直线l 与函数()0m y x x=>的图象所围成的区域（不含边界）为W ．点(),1B n （4n ≥，n 为整数）在直线l 上．①当5n =时，求k 的值，并写出区域W 内的整点个数；②当区域W 内恰有5个整点时，直接写出n 和k 的值．23．如图，ABC 内接于O ，AB 是O 的直径，点D 在AB 的延长线上，且BCD A ∠=∠，点E 为AC 的中点，连接OE 并延长与DC 的延长线交于点F ．(1)求证：CD 是O 的切线；(2)若4CD =，1tan 2A =，求CF 的长．24．如图是某抛物线形拱桥的截面图．某数学小组对这座拱桥很感兴趣，他们利用测量工具=米，点E到拱桥顶面的垂直测出水面AB的宽为8米．设AB上的点E到点A的距离AE x=米．距离EF y通过取点、测量，数学小组的同学得到了x与y的几组值，如下表：x（米）012345678y（米）0 1.753 3.754 3.753 1.750(1)拱桥顶面离水面AB的高度为______米；(2)请你帮助该数学小组建立平面直角坐标系，描出上表中各对对应值为坐标的点，并用平滑的曲线连接；(3)测量后的某，由于降雨原因，水面比测量时上升1米．现有一游船（截面为矩形）宽度为4米，船顶到水面的高度为2米．要求游船从拱桥下面通过时，船顶到拱桥顶面的距离应大于0.5米．所画图象，请判断该游船是否能通过：______（填写“能”或“不能”）．25．为整体提升学生的综合素质，某中学利用课后服务时间，对八年级300名学生全员开设了A，B，C三类课程，一个学期的课程学习，学校想了解学生课程学习，从中随机抽取20名学生进行了检测，获得了他们的成绩（百分制），并对数据（成绩）进行整理、描述和分析．这20名学生A，B，C三类课程的成绩情况统计图如下：(1)①学生甲A 类课程的成绩是98分，则该生C 类课程的成绩是______分；②学生乙C 类课程的成绩是45分，则该生三类课程的平均成绩是______分；(2)补全这20名学生B 类课程成绩的频数分布直方图；（数据分成7组：3040x ≤<，4050x ≤<，5060x ≤<，6070x ≤<，7080x ≤<，8090x ≤<，90100x ≤≤）．(3)若成绩在85分及以上为，估计该校八年级学生A 类课程成绩的人数．26．在平面直角坐标系xOy 中，已知抛物线2y x mx n =++．(1)当3m =-时，①求抛物线的对称轴；②若点()11,A y ，()22,B x y 都在抛物线上，且21y y <，求2x 的取值范围；(2)已知点()1,1P -，将点P 向右平移3个单位长度，得到点Q ．当2n =时，若抛物线与线段PQ 恰有一个公共点，函数图象，求m 的取值范围．27．如图，在ABC 中，90ACB ∠=︒，AC BC =，P ，D 为射线AB 上两点（点D 在点P 的左侧），且PD BC =，连接CP ．以P 为，将线段PD 逆时针旋转()0180n n ︒<<得线段PE ．(1)如图1，当四边形ACPE 是平行四边形时，画出图形，并直接写出n 的值；。

顺义区2024年初中学业水平考试综合练习（二）数学答案及评分参考二、填空题（本题共16分，每小题2分）9．4x ≥ ； 10．22(1)x − ； 11．51x y x y +=⎧⎨−=−⎩（答案不唯一）； 12．0k >；13．<； 14．30︒； 15．4003π； 16．8． 三、解答题（共68分，第17-19题，每题5分，第20-21题，每题6分，第22-23题，每题5分，第24题6分，第25题5分，第26题6分，第27-28题每题7分）17．解：13tan 3021−−+−1312=+−…………………………………………………………4分 12= …………………………………………………………………………5分 18．解：解不等式：342x x ≥−2x −≥−2x ≤…………………………………………………………………………4分正整数解是2,1x =………………………………………………………………………. 5分19．（1）证明：∵a = 1，b = k ，c = -4，∴222=b 44416ac k k ∆−=+⨯=+∵20k ≥∴2160k ∆=+>∴方程总有两个不相等实数根 ……………………………………………….……2分（2） 将x =1代入方程，解得k =3 …………………………………………………………3分将k =3代入方程得到2340x x +−=解得121,4x x ==−所以方程的另一个根是-4.…………………………………………………………..…5分20．（1）证明：∵四边形ABCD 是平行四边形，∴AB =CD ，AB ∥CD.∵DE =CD ，∴AB =DE .又 ∵AB ∥DE ，∴四边形ABDE 是平行四边形. ……………………………………………………2分 ∵BD ⊥CD ，∴∠BDE =90︒∴四边形ABDE 是矩形 .……………………………………………………………3分 （2）解：连接AC∵DE =CD ，CD =1，∴DE =CD=1∴CE=2∵BD ⊥CD ，∴∠BDC =90︒，∵∠BCD =60︒,在Rt △BDC 中，∠BDC =90︒,∵CD =1，tan ∠BCD∴BD∵四边形ABDE 是矩形∴AE =BDE =90︒，在Rt △AEC 中，∠E =90︒,∴AC……………………………………………………………………………6分21.解：设球网同侧的单、双打后发球线间的距离是12x cm ，则中线同侧的单、双打边线间的距离是7x cm. …………………………………………………………………………1分 由题意可得 ()1180244425101444120x x ++⨯=++⨯+ ……………………………4分 解得6x =……………………………………………………………………………….……5分 1272x =…………………………………………………………………………………6分 答：球网同侧的单、双打后发球线间的距离是72 cm.22．解：（1）将A （1，3）分别代入k y x =，y x b =+ 解得3,2k b ==………………………………………………………………..…3分（2） 3.n > ……………………………………………………………………………….5分 23.解：（1）7.6m =…………………………………………………………………………1分（3）12p p >…………………………………………………………………………………2分理由：男生这一周体育锻炼时长平均数是7.4，中位数是7.6，7.67.4,>则156213p =++=；女生这一周体育锻炼时长平均数是7，中位数是6.8，说明有超过一半的女生体育锻炼时长低于平均数，即213p <,12.p p >所以 …………………………………………………3分 E D C B A（3）112259925⨯=人………………………………………………………………………5分答：估计该校所有男生中一周体育锻炼时间不低于8小时的有99人．24．（1）证明：连接OC．∵CF是⊙O的切线，∴∠OCF=∠OCB+∠DCF=90︒，∴∠DCF=90︒−∠OCB.∵EF⊥AB于E,∴∠FEB=90︒,在Rt△EBD中，∴∠EBD+∠EDB=90︒,∴∠EDB=90︒−∠EBD.又∵BC、EF交于点D,∴∠CDF=∠EDB,∴∠CDF=90︒−∠EBD.∵OC=OB，∴∠EBD=∠OCB,∴∠DCF=∠CDF……………………………………………………………..3分（2）∵AB是⊙O的直径，∴∠ACB=∠ACO+∠OCB=90︒,又∵∠OCF=∠DCF+∠OCB=90︒，∴∠ACO=∠DCF.∵OA=OC，∠DCF=∠CDF，∴∠ACO=∠OAC=∠DCF=∠CDF，∴△FCD∽△OCA∵3cos=5CDF∠,∠OAC=∠DCF =∠CDF,∴3 cos=5OAC∠.∵半径是5，∴AB=10.在Rt△ABC中，∠ACB=90︒,∴3 cos=5ACOACAB=∠，∴AC=6，BC=8. ∵D为BC中点,A B∴CD =BD =4,∵△FCD ∽△OCA . ∴=CD CF CA CO即4=65CF ∴10=3CF …………………………………………………………………………..……6分 25.（1）……………………………………………………………………………………2分（2）30.0（不唯一）； ………………………………………………………………………3分（3）44（不唯一）．…………………………………………………………………………. 5分26．解：（1）∵当m =2时，2m =4，3-m =1, 12y y =．∴抛物线2y x bx c =++经过（4，y 1）和（1，y 2）， ∴抛物线对称轴为5=-22b x =．……………………………………………1分 ∴ -5b =………………………………………………………………………2分（2）依题意，点1(2,)m y ，2(3,)m y −在抛物线2y x bx c =++上．∵1m >∴32m m −<.∵ 抛物线开口向上，对称轴为直线2b x =−， ∴ 当2b x ≤−时，y 随x 的增大而减小；当2b x ≥−时，y 随x 的增大而增大， 当32b m −≤−时，都有12y y >.若12y y =时，3222b m m −+−=. 当3322b m m +−<−<时，都有12y y >. ∴322b m +−<时，都有12y y >. ∴3b m >−−，∵1m >，∴34m −−<−∴当4b ≥−时，对于1m >都有12y y >. 当3222m b m +≤−≤时，12y y <，不合题意，舍去. 当22b m −>时，12y y <，不合题意，舍去. 综上所述，b 的取值范围是4b ≥−.……………………………………………6分27.解：（1）…………………………………………1分（2）证明：∵线段DA 绕点D 顺时针旋转α，得到线段DE∴∠ADE =α∵∠BAC =α ∴∠BAC =∠ADE ∴DE ∥AB∴ FE GE =DF BD ∵DF =BD∴EF =GE∴BG =2DE ………………………………4分（3）CH =CF证明：过点F 作FM ∥AB ，交AC 于点M∴∠BAM =∠FMA ，∵∠ADB =∠FDM ，DF =BD∴△ADB ≌△MDF∴AB =MF ，AD =MD∵AB =AC∴AC = MFBB∵BG =2DE ，AM =2AD ，且AD =DE∴BG =AM∴AB -AG =AC -AM即AG =CM∵AH =AG∴AH =CM∵FM ∥AB∴∠HAC =∠FMC∴△HAC ≌△CMF∴CH =CF …………………………………………7分28. （1）C 2，C 3………………………………………………………………………2分（2）∵D (-1,0)，⊙D 的半径为2， P 为⊙D 的关联点 ∴OE =3，OF =1，点P 在直线y 上，当OP = OE =3时，∴点P 1的横坐标是32−，P 4的横坐标是32，点P 在直线y 上，当OP = OF =1时，∴点P 2的横坐标是12−，P 3的横坐标是12，∴点P 的横坐标的取值范围是3122p x −≤≤−或1322p x ≤≤………………………5分 （3）-6≤t ≤6.…………………………………………7分。

2023北京初三二模数学汇编圆（下）章节综合 一、单选题1．（2023·北京昌平·统考二模）船航行的海岸附近有暗礁，为了使船不触上暗礁，可以在暗礁的两侧建立两座灯塔.只要留心从船上到两个灯塔间的角度不超过一定的大小，就不用担心触礁.如图所示的网格是正方形网格，点,,,,,,A B C D P M N 是网格线交点，当船航行到点P 的位置时，此时与两个灯塔,M N 间的角度（MPN ∠的大小）一定无触礁危险.那么，对于,,,A B C D 四个位置，船处于___________时，也一定无触礁危险.（ ）A ．位置AB ．位置BC ．位置CD ．位置D2．（2023·北京大兴·统考二模）在平面直角坐标系xOy 中，已知点(,0)A r −，(,0)B r ．点P 为平面内一点（不与点A ，点B 重合），若ABP 是以线段AB 为斜边的直角三角形，则称点P 为线段AB 的直点．(1)若1r =，①在点111(,)22P −，2(0,1)P ，3(1,1)P −−这三个点中，点________是线段AB 的直点； ②点P 为线段AB 的直点，点(1,1)C −，求CP 的取值范围；(2)点D 在直线1y x =−上，若点D 的横坐标D x 满足24D x <<，点P 为线段AB 的直点，且1DP =，直接写出r 的取值范围．为O的直径，为O上一点，(1)求证：EH是O的切线；(2)AE与O的交点为F，连接并延长与O相交于点D H∠=∠．4．（2023·北京大兴·统考二模）如图，是O的直径，点是O上一点，交O于点D作DE AC⊥交E．(1)求证：直线DE是O的切线；(2)延长AB与直线DE交于点F5．（2023·北京顺义·统考二模）如图，分别与O相切于是O的直径．(1)求证：12BAC APB ∠=∠(2)连接PO交O于点D，若AC6．（2023·北京东城·统考二模）已知：如图，点和O．求作：直线PA，使得PA与O相切于点长为半径作B ，与O 相交，其中一个交点为点使用直尺和圆规，依作法补全图形（保留作图痕迹）；的中点．连接OA ．为B 的直径，OAP =_________PA ．在O 上，是O 的切线（2023·北京昌平Q 是直线l 上一点，将线段是点P 关于直线 点123(1,1),(1,0),(1,2)K K K −中是点P 关于x 轴和点Q 的“双垂点”的是___________；(2)若点()0,5Q ，点,P K 是直线3y x 上的点，点K 是点P 关于y 轴和点Q 的“双垂点”，求(3)点P 在以(0,)t 为圆心，1为半径的圆M 上，直线:2l y x =+，若圆M 上存在点K 是点P 关于直线Q 的“双垂点”，直接写出t 的取值范围.8．（2023·北京海淀·统考二模）如图，P 为O 外一点，PA ，PB 是O 的切线，A ，B 为切点，点O 上，连接OA ，OC ，AC ．(1)求证：2AOC PAC ∠=∠(2)连接OB ，若AC OB ∥，O 的半径为9．（2023·北京平谷·统考二模）如图，为O 的直径，为O 上一点，过点作O 的切线，交的中点，连结并延长交O 于点D ，连结(1)求证：D EBC ∠=∠；(2)若1tan 2∠=D ，2BC =，求10．（2023·北京朝阳·统考二模）在平面直角坐标系(),a b 变换为点(),a b a b −+，形．，若O 的变换图形与直线统考二模）在平面直角坐标系可以重合），满足(1)如图1所示，已知，点()02A ，，点()32B ，． ①在点()()()123011141P P P −，，，，，中，是线段AB 的“对称平衡点”的是___________； ②线段AB 上是否存在线段AB 的“对称平衡点”？若存在，请求出符合要求的 “对称平衡点”的横坐标的范围，若不存在，请说明理由；(2)如图2，以点()02A ，为圆心，1为半径作A ．坐标系内的点C 满足2AC =，再以点C 为圆心，1为半径作C ，若C 上存在A 的“对称平衡点”，直接写出C 点纵坐标C y 的取值范围．12．（2023·北京东城·统考二模）如图，O 的直径AB 与弦CD 相交于点E ，且CE DE =，点F 在AB 的延长线上，连接,,OC DF F C ∠=∠．(1)求证：DF 是O 的切线；(2)若2,2OE BE BF ==，求O 半径的长．13．（2023·北京顺义·统考二模）在平面直角坐标系xOy 中，已知点P ，直线l 与图形G ．连接点P 与图形G 上任意一点Q ，取PQ 的中点M ，点M 关于直线l 的对称点为N ，所有的对称点组成的图形W 称为图形G 关于点P 及直线l 的“对应图形”．已知点()4,0A ．(1)对于直线:l x a =，若直线y x =−−24关于点A 及直线l 的“对应图形”与直线y x =−−24的交点在x 轴的上方，求a 的取值范围；(2)已知点()0,4B ，()4,0C −，()6,4D ，直线:1l x =−，T 的圆心(),0T t ，半径为2．若存在T 关于点D 及直线l 的“对应图形”与ABC 的边有交点，直接写出t 的取值范围．14．（2023·北京房山·统考二模）如图，A ，B ，C 三点在O 上，直径BD 平分ABC ∠，过点D 作DE AB ∥交弦BC 于点E ，在BC 的延长线上取一点F ，使得BFD ADB ∠=∠．(1)求证：DF 是O 的切线；(2)若4=AD ，5DE =，求DF 的长．15．（2023·北京西城·统考二模）在平面直角坐标系xOy 中，给定圆C 和点P ，若过点P 最多可以作出k 条不同的直线，且这些直线被圆C 所截得的线段长度为正整数，则称点P 关于圆C 的特征值为k ．已知圆O 的半径为2，(1)若点M 的坐标为()11，，则经过点M 的直线被圆O 截得的弦长的最小值为___________，点M 关于圆O 的特征值为___________；(2)直线y x b =+分别与x ，y 轴交于点A ，B ，若线段AB 上总存在关于圆O 的特征值为4的点，求b 的取值范围；(3)点T 是x 轴正半轴上一点，圆T 的半径为1，点R ，S 分别在圆O 与圆T 上，点R 关于圆T 的特征值记为r ，点S 关于圆O 的特征值记为s ．当点T 在x 轴正轴上运动时，若存在点R ，S ，使得3r s +=，直接写出点T 的横坐标t 的取值范围．16．（2023·北京西城·统考二模）如图，以菱形ABCD 的边AD 为直径作O 交AB 于点E ，连接DB 交O 于点M F ，是BC 上的一点，且BF BE =，连接DF ．(1)求证：DM BM =；(2)求证：DF 是O 的切线．17．（2023·北京昌平·统考二模）如图，AB 是O 直径，C 是O 上一点，过点A 作直线PA ，使PAC ABC ∠=∠．(1)求证：PA是O的切线；(2)点D是弧BC中点，连接由网格可知，点O是MN和MP垂直平分线的交点，△的外接圆的圆心，即点O是MNP22==+=，OM OB125∴点M在MNP△的外接圆上，∴MPN MBN∠=∠，∴船处于位置B时，也一定无触礁危险，∵1r =，∴点()()1010A B −，，，． ∵点P 为线段AB 的直点，∴点P 在O 上．∴点111(,)22P −，2(0,1)P ，3(1,1)P −−这三个点中，故答案为：2P ；②情况1：连接CO 交O 于点P ，此时CP )(1,0A −，，， 1OA CA AO =，，交O 于点P ，的取值范围是21CP −≤2CP ≤+为线段AB 的直点，为直径的O 上，DP当2x =时，211y =−=，∴11,D E =在1Rt D OE 中，221125D O =+=，∵111D P =,∴151OP =−；过点2P 作2PG x ⊥轴于点G ，过点2D 作2D ∴四边形2D FGH 是矩形，22D HP 为等腰直角三角形，∴,,HG D F D H FG ==，即23D F =2OP G Rt 中，取值范围是【点睛】本题考查了圆的有关知识，一次函数的性质，掌握圆的相关性质、勾股定理等知识，灵活运用数形结合思想和分类讨论思想思考问题．(1)见解析是O的半径，是O的切线；（2）证明：如图，连接OC∠，∵AC平分EAH∠=∠，∴EAC CAH∴FC CB=，【点睛】本题考查了切线的判定，平行线的判定，圆心角、弧、弦的关系，圆周角定理等知识，作出合适的辅助线，灵活运用相关性质定理是解题的关键．4．(1)见解析 (2)2 【分析】（1）连接OD ，证OD AE ∥，由已知DE AE ⊥，得出DE OD ，即可得出结论；（2）连接BC 交OD 于点H ，证明四边形CEDH 为矩形，得出,HC FE ∥HC DE BH ==，再证明ABC F ∠=∠，求出BC 的长即可得出结论．【详解】（1）连接OD ．∵AD 平分CAB ∠，∴BAD CAD ∠=∠．∵OD OA =，∴ODA OAD ∠=∠，∴ODA CAD ∠=∠，∴OD AE ∥，∴180E ODE ∠+∠=︒．∵DE AC ⊥．∴90E ∠=︒，∴90ODE ∠=︒，∴OD EF ⊥．又∵点D 在O 上，∴直线DE 是O 的切线．（2）连接BC 交OD 于点H ，如图．∵AB 为直径，∴90ACB ∠=︒，∴90BCE ∠=︒．为O的切线，∠=∠=12∠+∠3BAC，︒，，（2）解：∵AC 是O 的直径，∴90ABC ∠=︒，∵6AC =，4cos 5BAC ∠=，∴424cos 655AB AC BAC =⋅∠=⨯=，2246⎛=−是O 的切线．（2）证明：由作法可知，点∵OP 为B 的直径，∴90OAP ∠=︒（直径所对的圆周角是直角）∴OA PA ⊥．∵点A 在O 上，是O 的切线（切线的判定定理）故答案为：90；直径所对的圆周角是直角；切线的判定定理． 【点睛】本题主要考查了切线的判定定理，圆周角定理，线段垂直平分线的尺规作图等等，灵活运用所学知识是解题的关键．7．(1)12,K K(2)()1,2P −(3)242t −≤≤+3yx 上的点，则点3y x 上，P Q P K '⊥，别作于点C ，证明QP A KP C ''≌，设3,(P m m '−+3y x ，求得求得()1,2P −；）根据新定义可得K 的轨迹与直线2y x =+垂直，在M ，得K 点落在的轨迹所在直线k 与M 相切时，t 取得最大值，根据题意画出图形，求得t 的最大值，同理可得最小值.）解：如图所示，故答案为：12,K K ．（2）解：根据题意，点P 是直线3yx 上的点，则点P 关于y 轴的对称点在直线3y x =−+上， 由题意可得，点K 在直线3y x 上，P Q P K ''=且P Q P K ''⊥，如图所示，作P A y '⊥轴于点A ，分别作P C x '⊥轴，KC y ⊥轴，KC 交y 轴于点B ，P C '与KC 交于点C ，∴四边形ABCP '为矩形，∵90QP K AP C ''∠=∠=︒∴QP A KP C ''=∠∠又∵,90P Q P K QAP KCP ''''=∠=∠=︒∴QP A KP C ''≌∴,P A P C QA KC ''==∴四边形ABCP '为正方形，设3,()P m m '−+∴(03)(23,,,)A m C m m −+−+∵5(3)2QA KC m m ==−−+=+∴(223)K m −−+，3y x 中，在M 与M 相切时， ∵()0,M t ，关于直线2y x =+对称，∴()2,2M t '−如图所示，当K 刚好在直线2y x =+上时，，依题意，QP K '是等腰直角三角形，∵直线l 与直线k 垂直，且过点()1,3K ∴直线k 的解析式为4y x =−+∵1r =∴42t =+，同理可得2t =−，综上所述，242t −≤≤+．【点睛】本题考查了几何新定义，理解新定义中8．(1)见解析(2)10AP =【分析】（1）根据切线的性质得出PAO ∠形的性质，三角形内角和定理得出AOC ∠（2）延长AC 交PB 于点D ，过O 作OE 是O 的切线，OAC ，90OAC =︒−∠ ∴132AE EC AC ===，∵5AO = 在Rt AEO △中，EO AO =是O的切线，=−PD PB中，2=AP PD)24−，为O的切线，Rt AEB 中，∵12BF AE =【点睛】本题考查了切线的性质，圆周角定理，正切函数的定义，直角三角形的性质，解题的关键是灵活运用所学知识解决问题．．(1)①(3,3，可得O 的变2k +与O 的变换图形相切时的【详解】（∴点()3,0故答案为：②设直线按定义操作：∴O 的变换图形是以原点为圆心，半径为又∵直线y =∴直线y kx =如图，点(A 当直线y kx =与O 的变换图形相切于点42AB OA ==−=∴ABO 是等腰直角三角形，45BAO ∠=∴AOC 是等腰直角三角形，OA OC ==∴此时直线22k =，解得：1k =，同理，当直线与O 的变换图形相切于∴若O 的变换图形与直线2y kx =+ 【点睛】本题考查了新定义，一次函数的应用，圆的基本概念，切线的性质，两点间的距离公式，勾股定理等知识，正确理解变换图形的定义，能够准确表示出变换点的坐标是解题的关键．∴线段AB 的“对称平衡点”的是1P ，故答案为：1P ，3P ；②不存在设P 为线段AB 上任意一点，则它与线段33PA PB ≤≤，点P 关于x 轴的对称点为P '，它到线段即若M N ，是线段AB 上的任意两点，上不存在A 的“对称平衡点，O 上存在A 的“对称平衡点∵()()0,2,0,0A O∵CE DE =，AB 是O 的直径，∴AB CD ⊥，∴90DEF ∠=︒，∴90F EDF ∠+∠=︒，∵OC OD =，∴OCD ODC ∠=∠，∵F C ∠=∠，∴F ODC ∠=∠，是O 的半径，是O 的切线；）解：由题意可设OEEOD OD =ODF △中，4=，即O 的半径为）根据题意，先画出图形，由T 的圆心，T 关于点，根据新定义求得中点坐标，再关于对称，根据直线与圆的位置关系，即可求解．）解：如图所示，直线y x =−−22x =−，上的任意一点所成的线段的中点，即为直线E F '（2）T 的圆心(),0T t ，半径为2，T 关于点则T '是以604,22t ++⎛⎫ ⎪⎝⎭为圆心，半径为1， 作T '关于=1x −的对称的圆M ，则此圆是以 ∵点()4,0A ，()0,4B ，()4,0C −，∴直线BC 的解析式为4y x =+，当2y =时，2x =−，直线AB 的解析式为4y x =−+，当2y =时，2x =，∵M 与ABC 的边有交点，当M 在BC 的左侧，与BC 相切时，M 到()2,2−的距离为()2252t −+=−−， 解得：226t =−，当M 在BC 的右侧，与()22−=当M 在AB 2=2t −−解得：14t =−当M 在AB 2=2t +−解得：14t =−结合图形可知：【点睛】本题考查了几何新定义，一次函数的性质，直线与圆的位置关系，熟练掌握新定义，中点坐标公是O 的直径，得90，所以90 ，又因为90°，即90FDB ∠，即可由切线的判定定理得出结论．90，由BD ABC ，AD 4 ，由勾股定理可求得，根据平行线的性质与解平分线定义得出，所以EB 由勾股定理可得DB =，再FDB DCB ∽，得DF DC ∵BD 平分ABC ∠，∴12∠=∠，∵BD 是O 的直径，∴90A ∠=，∴190ADB ∠∠+= ，ADB ∠，1∠=∠90，，是O 的半径，是O 的切线．）解：连接DC ∵BD 是O 的直径，∴90DCB ∠=，∵BD 平分ABC ∠，4=AD ，∴4DC DA == ，∵5DE =，2DE DC −90，2∠∴FDB DCB ∽DF DB DC CB = 4548DF = 25DF =【点睛】本题考查角平分线的性质，圆周角定理的推论，切线的判定，相似三角形的判定与性质，勾股定的直线与O交于E，由勾股定理可得当重合时，OH，再由被圆O的特征值为3；的特征值为4的所有点都在以的直线与O交于E22OE OH−最小，（2）解：设点G 是圆O 的特征值为由（1）可知经过一点G 且弦长为∵特征值要保证为4，∴经过点G 且弦长为2的直线有且只有∴经过点G 的直线被圆O 截得的弦长的最小值为∵22213−=，∵直线y x b =+分别与x ，y 轴交于点∴()0A b −，，()0B b ，， ∴OA OB b ==，∴45OBH ∠=︒当0b >时，∵线段AB 上总存在关于圆O 的特征值为如图3-2所示，当以O为圆心，综上所述，当37 222t−≤≤【点睛】本题主要考查了垂径定理，圆与圆的位置关系，切线的性质，坐标与图形，勾股定理，一次函数与几何等等，正确理解题意找到对应点的轨迹是解题的关键．16．(1)见解析；(2)见解析【分析】（1）根据直径所对的圆周角是直角及菱形的性质得到点M 是BD 的中点即可解答；（2）根据菱形的性质及全等三角形的判定得到DBE DBF ≌，再根据全等三角形的性质得到90BFD DEB ∠=∠=︒，最后利用四边形的内角和及切线的判定即可解答．【详解】（1）解：连接AM ，∵AD 为O 的直径，∴90AMD ∠=︒，∴AM BD ⊥，∵四边形ABCD 是菱形，∴AD AB =，∴点M 是BD 的中点，∴DM BM =；（2）解：连接DE ，∵四边形ABCD 是菱形，∴DBE DBF ∠=∠，180DAB ABC ∠+∠=︒，∴在DBE 和DBF ，∴()DBE DBF SAS ≌DEB DFB ∠=∠，AD 是O 的直径，90AED DEB ∠=∠=90BFD DEB ∠=∠=180DAB ABC ∠+∠=∴在四边形ABFD 90=︒，是O 的切线．【点睛】本题考查了菱形的性质，直角所对的圆周角是形的判定与性质，掌握菱形的性质是解题的关键．见解析【分析】（1）首先根据直径的性质得到是O 的切线；）首先根据题意画出图形，然后根据三角函数得到，5OD =，然后根据垂径定理得到253=，即可求解．是O 直径，︒，是O 直径，是O 的切线；）如图所示，。