
第一章 线性方程组的解法
求解线性方程组是科学研究和工程应用中最普遍和最重要的问题,超过75%的科学研究和工程应用中的数学问题,在某一阶段都与线性方程组的求解有关.本章介绍求解线性方程组的消元法及其矩阵形式.
引例 交通流量问题
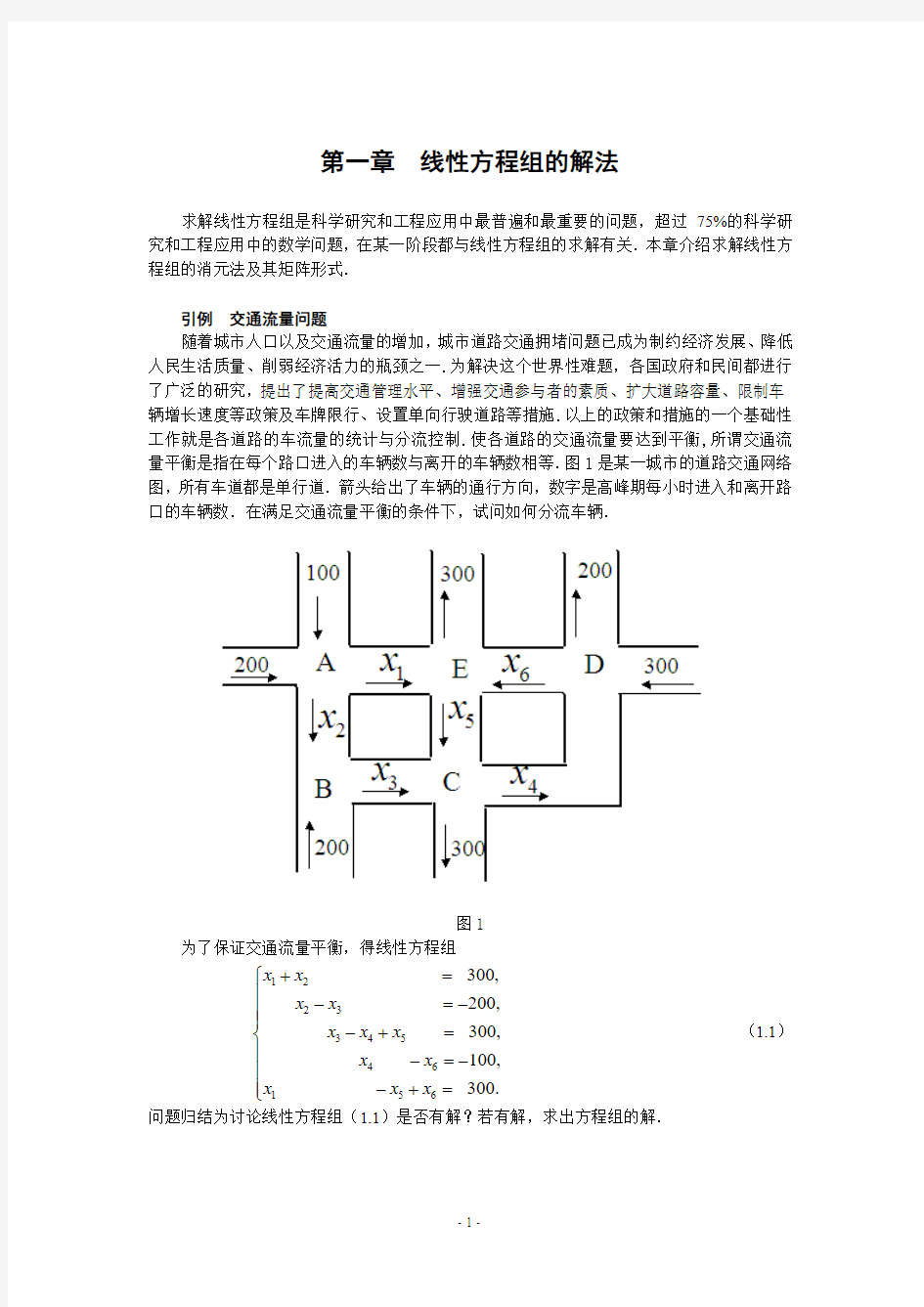
随着城市人口以及交通流量的增加,城市道路交通拥堵问题已成为制约经济发展、降低人民生活质量、削弱经济活力的瓶颈之一.为解决这个世界性难题,各国政府和民间都进行了广泛的研究,提出了提高交通管理水平、增强交通参与者的素质、扩大道路容量、限制车辆增长速度等政策及车牌限行、设置单向行驶道路等措施.以上的政策和措施的一个基础性工作就是各道路的车流量的统计与分流控制.使各道路的交通流量要达到平衡,所谓交通流量平衡是指在每个路口进入的车辆数与离开的车辆数相等.图1是某一城市的道路交通网络图,所有车道都是单行道.箭头给出了车辆的通行方向,数字是高峰期每小时进入和离开路口的车辆数.在满足交通流量平衡的条件下,试问如何分流车辆.
图1
为了保证交通流量平衡,得线性方程组
12
23345461
56300,200,300,100,300.x x x x x x x x x x x x +=??-=-??
-+=?
?-=-??-+=? (1.1) 问题归结为讨论线性方程组(1.1)是否有解?若有解,求出方程组的解.
第一节 线性方程组的消元法
一、线性方程组的概念
设12,,,n x x x L 为实未知量,12,,,,n a a a b L 为实数,n 为正整数.方程
1122n n a x a x a x b +++=L
称为含未知量12,,,n x x x L 的线性方程.由m 个含未知量12,,,n x x x L 的线性方程组成的方程组
1111221121122222
1122,,,
n n n n m m mn n m a x a x a x b a x a x a x b a x a x a x b +++=??+++=????+++=?L L L L L L L L L L L L L L (1.2)
称为n 元线性方程组,其中,(1,2,,;1,2,,)ij i a b i m j n ==L L 为实数.若
1122,,,n n x c x c x c ===L (1.3)
使(1.2)中的每一个方程都成立,则称(1.3)为方程组(1.2)的解.
如果线性方程组(1.2)有解,则称方程组(1.2)是相容的;否则,称方程组(1.2)是不相容的.
线性方程组解的全体所构成的集合称为该线性方程组的解集.显然,如果线性方程组不相容,其解集必为空集.能表示线性方程组全部解的表达式称为方程组的通解或一般解. 具有相同解集的线性方程组称为同解方程组或等价方程组.
二、线性方程组的消元法
中学所学的解线性方程组的消元法是求解线性方程组简单有效的方法.现在我们回忆消元法的过程.
例1 利用消元法求解线性方程组
121223,(1)45 6.
(2)
x x x x +=??
+=?
解 将方程(1)乘以4-加到方程(2)上,得等价方程组
122
23,(3)
3 6.(4)x x x +=??
-=-? 由方程(4)解得22x =,再代入方程(3),得11x =-,则原方程组的解为121,2x x =-=.该方程组有唯一解.
例2 利用消元法求解线性方程组
(I )1231231235675,(1)4845,
(2)3639.
(3)x x x x x x x x x ++=??
++=??++=?; (II )1231231
231,
(1)23,
(2)5811.(3)
x x x x x x x x x ++=??
+-=??+-=? 解 (I )方程(3)的两边乘以不为零的常数
1
3
,得 1231231
235675,(4)4845,(5)2 3.(6)
x x x x x x x x x ++=??
++=??++=? 交换方程(4)与(6)的位置,得
1231231
2323,
(7)4845,(8)567 5.
(9)x x x x x x x x x ++=??
++=??++=? 方程(7)乘以4-加到方程(8)上;方程(7)乘以5-加到方程(9)上,得
1232323,(10)07,(11)4210.
(12)x x x x x ++=??
=-?
?-+=-?
交换方程(11)与(12)的位置,得
1232323,
(13)4210,(14)07.(15)
x x x x x ++=??
-+=-??=-?
方程(15)是矛盾方程,则方程组(I )无解.
(II )方程(1)乘以1-加到方程(2)上;方程(1)乘以5-加到方程(3)上,得
12323231,(4)22,(5)36 6.(6)x x x x x x x ++=??
-=?
?-=?
方程(5)乘以3-加到方程(6)上,得
123231,(7)22,(8)00.(9)
x x x x x ++=??
-=?
?=?
解得
??
?+=--=,22,
1332
31x x x x 令3x c =,得方程组的通解为
???
??=+=--=,,22,133
21c x c x c x 其中c 为任意常数.此时方程组有无穷多解.
总结例1与例2,我们发现利用消元法求解线性方程组的过程,本质上是对线性方程组的方程进行下列三种变换:
(1)交换任意两个方程的位置;
(2)某一方程两边乘以不为零的常数; (3)把某一方程的倍数加到另一方程上去. 上述三种变换称为线性方程组的同解变换.
另外,我们还可以看到,线性方程组可能无解、可能有解,在有解时可能是唯一解或无穷多解,关于这方面的更深入的研究可参考下一节与第三章第六节.
思 考 题 一
1. 在例1与例2中,细心的读者会发现,这里用消元法求解线性方程组与中学所介绍的形 式上有所不同,您能指出它们各自的优点所在吗? 2.线性方程组的解与未知量的符号表示有关吗? 3.给定方程组??
?=+=+.654,32y x y x 将每个方程交换未知量x 与y 的位置,得方程组??
?=+=+.
645,
32y x y x 试问这两个方程组同解吗?
第二节 矩阵及其初等行变换
一、矩阵
例3 利用消元法求解线性方程组
23,(1)45 6.
(2)x y x y +=??
+=?
解 将方程(1)乘以4-加到方程(2)上,得
23,(3)3 6.
(4)
x y y +=??
-=-?
由方程(4)解得2y =,代入方程(3),得1x =-,则原方程组的解1,2x y =-=. 仔细比较例1和例3两个方程组,我们发现线性方程组的解是由未知量系数ij a 和方程右边的常数j b 所决定,而与线性方程组的未知量用哪个符号表示无关.鉴于此,在讨论线
性方程组(1.2)的求解时,我们可以舍弃未知量(但把未知量牢记于心中),建立方程组(1.2)与m 行1n +列的数表
11121121222212n n m m mn m a a a b a a a b a a a b ??
?
?
?
?
??
L M L
M M M M M M L M (1.4)
的一一对应关系:该数表的第(1,2,,)j j n =L 列是未知量j x 前的系数,第1n +列是方程右边的常数i b (1,2,,)i m =L ;第i 行代表方程组(1.2)的第i 个方程.我们称该数表为方程组(1.2)的增广矩阵,简记为B .而把数表
111212122212n n m m mn a a a a a a a a a ??
?
?
?
???
L L
M M M L (1.5) 称为方程组(1.2)的系数矩阵,简记为A . 例4 写出线性方程组
12312321231,,x x x x x x x x x λλλλλ
?++=?
++=??++=? 的系数矩阵与增广矩阵.
解 方程组的系数矩阵与增广矩阵分别为
111111A λλλ??
?
= ? ?
??
;21111111B λλλλλ?? ?= ? ???M M M .
以上讨论启发我们,为了简化线性方程组的求解,在代数上给出了数表——矩阵的概
念.(名词“矩阵(Matrix )”是由Sylvester 首先使用的)
定义1 由n m ?个数(1,2,;1,2,)ij a i m j n ==L L 排成的m 行n 列的数表
111212122212n n m m mn a a a a a a a a a ??
? ?
?
???
L
L M M M L 称为m 行n 列矩阵,简称n m ?矩阵,其中ij a 称为矩阵A 的第i 行第j 列的元素.n m ?矩阵可以表示为()ij m n a ?,一般用大写的英文字母,,,A B C L 等表示矩阵.
元素为实数的矩阵称为实矩阵,元素为复数的矩阵称为复矩阵.本书如无特殊声明,所讨论的矩阵都是指实矩阵.
二、矩阵的初等行变换
矩阵的初等行变换起源于求解线性方程组的消元法.由方程组的同解变换可知,对线性方程组作同解变换相当于对方程组的增广矩阵的行作相应的变换.由此有 定义2 以下对矩阵的三种变换称为矩阵的初等行变换: (1)交换矩阵两行的位置;
(2)不为零的数k 乘以矩阵的某一行中所有元素;
(3)将矩阵的某一行乘以数k 加到另一行上去.
为了说明方便,通常用i r 表示矩阵的第i 行.用i j r r ?表示交换矩阵的第i 行与第j 行;用i r k ?表示数k 乘以矩阵的第i 行;用j i r kr +表示数k 乘以矩阵的第i 行加到第j 行上去.
定义3 若矩阵A 经过有限次初等行变换变成矩阵B ,则称矩阵A 与B 行等价,记作
r A B ??→.
下面介绍消元法的矩阵形式。
例5 利用矩阵的初等行变换求解线性方程组
1212
23,
45 6.x x x x +=??
+=? 解 方程组的增广矩阵
2141123123456036r r B B -????
=???→= ? ?--????
M M M M ,
得同解方程组
122
23,
36,x x x +=??
-=-? (1.6) 由第2个方程解得22x =,代入第1个方程,得11x =-,则方程组的解为121,2x x =-=. 消元法的代入过程也可以对增广矩阵作初等行变换来代替.要在(1.6)的第2个方程解出2x ,则2x 的系数必须为1.将(1.6)的第2个方程两边乘以1
3
-
,得 12223,
2,x x x +=??
=?
(1.7)
得到(1.7)的过程相当于
21()3
123123036012r
r B ?-????→???→ ? ?--????M M M M .
将2x 代入(1.7)的第1个方程,即将(1.7)的第1个方程中2x 的系数化为零,只需将(1.7)的第2个方程两边乘以2-加到第1个方程上去,得方程组的解
121,
2.
x x =-??
=? (1.8) 得到(1.8)的过程相当于
1222123101012012r
r r B B --????→???→= ? ?????
M M M M ,
从而得方程组的解121,2x x =-=.
现在我们可以给出例5的完整求解过程了.方程组的增广矩阵
22112
(3)
42123123101456036012r r r r r B ÷----??????=???→???→ ? ? ?--??????
M M M M M M ,
从而得方程组的解121,2x x =-=.
一般地,消元法是由两个步骤所构成.第一个步骤是消元过程,在例5中得到矩阵1B ,称为矩阵B 的行阶梯形,其特点是:非零行的第一个非零元素的列标随着行标的增加而严
格增加.如下列矩阵
1232131213101010105,0015,0015000000000000A A A ?????? ? ? ?
=-=-= ? ? ? ? ? ???????
(1.9)
都是行阶梯形矩阵.第二个步骤是代入过程,在例5中得到矩阵2B ,称为矩阵B 的行最简形,其特点是:它是特殊的行阶梯形矩阵,且非零行的第一个非零元素为1,而该元素所在列的其他元素全为0.如(1.9)中的3A 是行最简形矩阵.
例6 利用初等行变换,将矩阵
111112422513A ??
?=-- ? ?-??
化成行阶梯形矩阵和行最简形矩阵.
解 21
312111111111242033325130331r r r r A +-???? ? ?=--???→- ? ? ? ?--????32111103330002r r -?? ????→- ? ?-??
, 最后一个矩阵即为行阶梯形矩阵,进一步,
13
323212(2)
3
111111101020011101100110000100010001r r r r r r r r A -÷--÷-??????
? ? ?
???→-???→-???→- ? ? ? ? ? ???????
,
最后一个矩阵即为行最简形矩阵.
总结例6利用初等行变换将矩阵化成行阶梯形矩阵和行最简形矩阵的方法,有
定理1 任何一个矩阵都可经有限次初等行变换变成行阶梯形矩阵和行最简形矩阵.
证 设()ij A a =为m n ?矩阵,对A 的行数m 利用数学归纳法.
1m =时该矩阵为行阶梯形.不妨设110a ≠,作行变换111
1
r a ?
,则矩阵化为行最简形. 设1m s =-结论成立.当m s =时,不妨设110a ≠,有
1
1
11
11121311112
1312122232222322,3,,31
3233332
3331
2
323000i i n n a r r n n a i s
n n s s s sn s s sn a a a a a a a a a a a a b b b A a a a a b b b a a a a b b b -=????
? ?
? ? ? ?=????→ ?
?
? ? ? ?????
.
矩阵()(2,3,,;2,3,,)ij B b i s j n === 为(1)(1)s n -?-矩阵,由归纳假设,知B 可化为行阶梯形矩阵,从而A 也可化为行阶梯形矩阵.
由归纳假设,知B 可化为行最简形矩阵,有
1112131411,11242,12343,13,101000010
0000100000
000000000
00t t n t n t n r
t t tn a a a a a a a c c c c c c A c c ++++??
?
? ?
?
???→ ?
? ? ?
? ??
? ,
11111141,11242,12343,1
3,2,3,,1
,11
0000100001000001000000
0000
0000
00j j t n t n t n r a r j t
r a t t tn c c c c c c c c c c c +++-=?+??
?
? ?
? ???????→
?
? ? ?
? ??
?
,
得A 的行最简形矩阵.
要注意的是,矩阵的行阶梯形矩阵一般不唯一,而矩阵的行最简形矩阵是唯一的. 注 由例5可得,利用初等行变换求解线性方程组的方法(也称为Gauss-Jordan 消元法),其步骤是:
(1)写出线性方程组的增广矩阵;
(2)将增广矩阵用初等行变换化成行阶梯形(等价于消元法的消元过程);
(3)判断线性方程组是否有解.如果行阶梯形的最后一个非零行代表矛盾方程00≠=d ,则方程组无解;否则线性方程组有解,并进行下一步;
(4)将行阶梯形矩阵用初等行变换化成行最简形矩阵(等价于代入过程); (5)由行最简形矩阵得线性方程组的解.
例7 利用Gauss-Jordan 消元法求解线性方程组
??????
?-=---=+--=+++-=-+-.4246,322,02,1223
2143214
3214321x x x x x x x x x x x x x x x 解 对方程组的增广矩阵进行初等行变换化为行阶梯形:
13
4122112
111223112101121011223211216420
43210
2r r r B ??-----????
? ?-- ? ?=
???→
?
?-----
? ?------????
M M M M M M M
M
213141
23112230003
3015670156
7r r r r r r +-----??
?-
????→ ?
-
?-??M M M M
23342
1311223015670001100000r r r r r ??----??
?-
?
???→ ?- ???
M
M M M
——行阶梯形 其最后一个非零行对应的不是矛盾方程,则方程组有解. 进一步,
13
2326112010150100011000
00r r r r B -+---?? ? ????→
?
-
???M M M M
1210
3000
1501000110
0000r r +?? ? ?
???→
?- ???
M M M M
——行最简形 得对应的方程组为
??
?
??-==+=+.1,15,0343231x x x x x 解得
???
??-=+-=-=,1,15,34
3231x x x x x 其中3x 为自由变量.令3x k =,则方程组的通解为
12
343,51,,1,
x k x k x k x =-??=-+??
=??=-?其中k 为任意常数. 例8 利用Gauss-Jordan 消元法求解线性方程组
???
??=-+=-+-=++.
352,242,
1321
321321x x x x x x x x x 解 方程组的增广矩阵
21
312111111111242033325130331r r r r B +-???? ? ?=--???→- ? ? ? ?--????M M M M M M 32111103330002r r -??
????→- ? ?-??
M M M ,
因为20-=,矛盾,所以方程组无解.
参考例5、例7、例8,对线性方程组有如下重要结论:
定理 2 对于n 元线性方程组,当增广矩阵的行阶梯形最后一个非零行代表矛盾方程时,则方程组无解;否则方程组有解,且
(1)当增广矩阵的行阶梯形有n 个非零行时,方程组有唯一解;
(2)当增广矩阵的行阶梯形少于n 个非零行时,方程组有无穷多解.
思 考 题 二
1.为什么说对线性方程组作同解变换相当于对该方程组的增广矩阵作相应的初等行变换? 2.比较行阶梯形矩阵与行最简形矩阵的相同点与不同点. 3.回忆利用Gauss-Jordan 消元法求解线性方程组的过程.
4.怎样判别线性方程组有解或无解?在有解时是唯一解还是无穷多解?除了这三种情形, 线性方程组的解还有其它情形吗?
第三节 应用举例
一、引例解答
(1.1)的增广矩阵
1100003001
00011
3000110002000
100
1100
011103000
010112000001011000
0010110010
00113000
000
00r
B -????
?
?
--- ? ? ? ?=→-- ?
?
---- ? ? ? ?-?
???
M M M M M M M M M M ,
由定理2得方程组有无穷多解,且方程组的通解为
1122
123124
25162300,,
200,
100,,,
x k k x k k x k k x k x k x k =-+??=-+??=-++??
=-??=?=??其中12,k k 为任意常数. 要注意的是,方程组的解不一定都是实际问题的解.由未知量的实际意义,应满足
1122
123124
251623000,
0,
2000,
1000,0,0,
x k k x k k x k k x k x k x k =-+≥??=-+≥??=-++≥??
=-≥??=≥?=≥?? 即有12,k k 还需满足2120300,100k k k ≤-≤≥的非负整数.
二、化学方程式的平衡
当丙烷(C 3H 8)气体燃烧时,会产生二氧化碳和水,该反应的化学反应式具有下列反应式
C 3H 8+O 2→CO 2+H 2O ,
试平衡此化学反应式。
为了使反应式平衡,选取适当的4321,,,x x x x ,使得
1x C 3H 8+2x O 2→3x CO 2+4x H 2O .
由质量守恒定律,对碳原子,有313x x =;同理,对氢原子,有4128x x =;对氧原子,有
43222x x x +=.从而得线性方程组
??
?
??=--=-=-,
022,028,0343241
3
1x x x x x x x 方程组的通解为k x k x k x k x 4,3,5,4321====.取1=k ,则化学反应式为
C 3H 8+5O 2→3CO 2+4H 2O .
三、封闭的列昂惕夫(Wassily Leontief)投入-产出模型 设某个封闭的产业链有n 个工厂生产n 种不同的产品,每个工厂需要投入自己的产品和其它工厂的产品.所谓封闭,是指每个工厂需要的产品该产业链内部可以提供,而不需要其它产业链提供.试问在满足总需求的条件下,每个工厂的产出各是多少?
令j x 表示第j 个工厂的产出量,ij a 表示第j 个工厂生产一个单位产品,需要投入第i 个工厂的产品数量(,1,2,,i j n =L ).此处一个单位的投入或产出,是指价值为1元人民币的产品.
由于产业链的封闭,第j 个工厂的总投入等于第j 个工厂的产出,则
11111221221122221122,,,
n n n n
n n n nn n x a x a x a x x a x a x a x x a x a x a x =+++??=+++??
??=+++?L L L L L L L L L L L L L L (1.10) 问题转化为求(1.10)的非负整数解.(1.10)可以化为
111122121122221122(1)0,(1)0,(1)0.
n n n n
n n nn n a x a x a x a x a x a x a x a x a x -+++=??+-++=??
??+++-=?L L L L L L L L L L L L L L L L (1.11) 现给出4n =时,各个工厂相互之间的需求有向图(图2).
图2
我们得到线性方程组
12341234
12342341
1110,248413110,448411310,44481150.
428x x x x x x x x x x x x x x x ?-+++=??
?-++=??
?+-+=???+-=?
方程组的增广矩阵
1
1112601000248423131139
00
100448446113119
00010444823
1150
000000428r B ??-?
?
?-
?
? ? ?- ?
?-
?=→
?
? ?-
?
-
? ? ?
? ?-??
?
?
M M M M M M M M , 得方程组的解为142623x x =
,243946x x =,3419
23x x =,其中4x 为自由变量.令4x k =,得方程组的通解为12623x k =,23946x k =,319
23
x k =,4x k =.所以四个工厂的产出量分别
为52,39,38,46m m m m ,其中m 为非负整数.
习 题 一 (A )
1.用消元法解下列线性方程组:
(1)?????=++=++=++.5432,9753,432321321321x x x x x x x x x (2)???
??=++--=++-=++-.
552,12,124321
43214321x x x x x x x x x x x x
(3)???????=+=+-=--=+-.05,3523,22,1231321321321x x x x x x x x x x x (4)???????=-++=+-+-=-++-=+-.
23,0243,6332,322432143214
32142
1x x x x x x x x x x x x x x x
2.用初等行变换将下列矩阵化成行阶梯形矩阵和行最简形矩阵:
(1)????? ??--122212221 (2)?????
??--324423211123
(3)?????
??--211132 (4)??????
?
?
?-34
624216311230211111
3.用初等行变换解下列线性方程组:
(1)?????=+-=+-=++.3,1142,53332321321x x x x x x x x (2)???
??=+++=+++=++-.2222,2562,
1344321
43214321x x x x x x x x x x x x
(3)???????-=--=+-=-+=-+-.1837,4,133,
443243243242
14321x x x x x x x x x x x x x (4)???????=+++-=+++-=+++-=+++-.
1224,9138436,354236,232254321543215432154321x x x x x x x x x x x x x x x x x x x x
(B )
1.当λ为何值时,线性方程组???
??=++=++=++2321321321,,1λ
λλλx x x x x x x x x 有无穷多解,并求解.
2.试讨论平面上两条直线相交、重合、平行不重合的条件. 3.(联合收入问题)已知三家公司A 、B 、C 具有如下图所示的股份关系,即A 公司掌握C 公司50%的股份,C 公司掌握A 公司30%的股份,而A 公司70%的股份不受另外两家公司控制等等.
3
现设A 、B 和C 公司各自的营业净收入分别是12万元、10万元、8万元,每家公司的联合收入是其净收入加上其它公司的股份按比例的提成收入.试确定各公司的联合收入及实际收入.
0.5 B A C 0.2 0.7 0.7
0.2
0.3 0.3 0.1
线性方程组的解法 1 引言 在科学研究和大型工程设计中出现了越来越多的数学问题,而这些问题往往需要求数值解。在进行数值求解时,经离散后,常常归结为求解形如Ax= b的大型线性方程组。而如插值公式,拟合公式等的建立,微分方程差分格式的构造等,均可归结为求解线性方程组的问题.在工程技术的科学计算中,线性方程组的求解也是最基本的工作之一.因此,线性方程组的解法一直是科学和工程计算中研究最为普遍的问题,它在数值分析中占有极其重要的地位。20世纪50年代至70年代,由于电子计算机的发展,人们开始考虑和研究在计算机上用迭代法求线性方程组Ax =b的近似解,用某种极限过程去逐渐逼近精确解,并发展了许多非常有效的迭代方法,迭代法具有需要计算机存储单元少、程序设计简单、原始系数矩阵在计算过程中始终不变等优点。例如Jacobi方法、Gauss—Seidel 方法、SOR方法、SSOR 方法,这几种迭代方法是最常用的一阶线性定常迭代法。 2 主要算法 20世纪50年代至70年代,人们开始考虑和研究用迭代法求解线性方程组。 Ax = b (1) 的近似解,发展了许多有效的方法,其中有Jacobi方法、Gauss—Seidel方法,SOR方法、SSOR方法,这几种迭代方法均属一阶线性定常迭代法,即若系数矩阵A的一个分裂:A =M-N ;M 为可逆矩阵,线性方程组(1)化为: (M-N)X =b; →M X = NX + b; →X= M -1NX+ M-1b 得到迭代方法的一般公式: X(k+1)=HX(k)+d (2) 其中:H =MN-1,d=M-1b,对任意初始向量X(0) 一阶定常迭代法收敛的充分必要条件是: 迭代矩H的谱半径小于1,即ρ(H) < 1;又因为对于任何矩阵范数恒有ρ(H)≤‖H‖,故又可得到收敛的一个充分条件为:‖H‖< 1。 2.1 Jacobi迭代法 若D为A的对角素构成的对角矩阵,且对角线元素全不为零。系数矩阵A的一个分解:A =
求解线性方程组的直接解法 5.2LU分解 ① Gauss消去法实现了LU分解 顺序消元结束时的上三角矩阵U和所用的乘数,严格下三角矩阵。 将下三角矩阵的对角元改成1,记为L,则有A=LU, 这事实是一般的,我们不难从消去的第k个元素时的矩阵k行及k列元素的 历史得到这一点.因为从消元的历史有 u kj=a kj-m k1u1j- m k2u2j -…- m k,k-1u k-1,j, j=k,k+1,…,n m ik=(a ik-m i1u1k- m i2u2k -…-m i,k-1u k-1,k>/u kk i=k+1,k+2,…,n 于是a kj=m k1u1j+m k2u2j+…+m k,k-1u k-1,j+u kj, j=k,k+1,…,n a ik=m i1u1k+m i2u2k+…+m i,k-1u k-1,k+m ik u kk i=k+1,k+2,…,n 从前面两个式子我们可以直接计算L和U(见下段>.将矩阵分解为单位下 三角矩阵和上三角矩阵之积称为矩阵的LU分解.顺序消元实现了LU分 解,同时还求出了g, Lg=b的解. ②直接LU分解 上段我们得到(l ij=m ij> u kj=a kj-l k1u1j-l k2u2j -…- l k,k-1u k-1,j, j=k,k+1,…,n l ik=(a ik-l i1u1k-l i2u2k -…-l i,k-1u k-1,k>/u kk i=k+1,k+2,…,n 2 诸元素对应乘积,只不过算L的元素时还要除以同列对角元.这一规律很 容易记住.可写成算法(L和U可存放于A>: for k=1:n-1 for j=k:n u kj=a kj-l k1u1j-l k2u2j -…- l k,k-1u k-1,j end for i=k+1:n l ik=(a ik-l i1u1k-l i2u2k -…-l i,k-1u k-1,k>/u kk end end 这一算法也叫Gauss消去法的紧凑格式,可一次算得L,U的元素,不需逐步 计算存储.
解线性方程组的直接解法 一、实验目的及要求 关于线性方程组的数值解法一般分为两大类:直接法与迭代法。直接法是在没有舍入误差的情况下,通过有限步运算来求方程组解的方法。通过本次试验的学习,应该掌握各种直接法,如:高斯列主元消去法,LU分解法和平方根法等算法的基本思想和原理,了解它们各自的优缺点及适用范围。 二、相关理论知识 求解线性方程组的直接方法有以下几种: 1、利用左除运算符直接求解 线性方程组为b x\ =即可。 A Ax=,则输入b 2、列主元的高斯消元法 程序流程图: 输入系数矩阵A,向量b,输出线性方程组的解x。 根据矩阵的秩判断是否有解,若无解停止;否则,顺序进行; 对于1 p :1- =n 选择第p列中最大元,并且交换行; 消元计算; 回代求解。(此部分可以参看课本第150页相关算法) 3、利用矩阵的分解求解线性方程组 (1)LU分解 调用matlab中的函数lu即可,调用格式如下: [L,U]=lu(A) 注意:L往往不是一个下三角,但是可以经过行的变换化为单位下三角。 (2)平方根法
调用matlab 中的函数chol 即可,调用格式如下: R=chol (A ) 输出的是一个上三角矩阵R ,使得R R A T =。 三、研究、解答以下问题 问题1、先将矩阵A 进行楚列斯基分解,然后解方程组b Ax =(即利用平方根法求解线性方程组,直接调用函数): ??????? ??--------=19631699723723312312A ,?????? ? ??-=71636b 解答: 程序: A=[12 -3 2 1;-3 23 -7 -3;2 -7 99 -6;1 -3 -6 19]; R=chol(A) b=[6 3 -16 7]'; y=inv(R')*b %y=R'\b x=inv(R)*y %x=R\y 结果: R =3.4641 -0.8660 0.5774 0.2887 0 4.7170 -1.3780 -0.5830 0 0 9.8371 -0.7085 0 0 0 4.2514 y =1.7321 0.9540 -1.5945 1.3940 x =0.5463 0.2023 -0.1385 0.3279 问题 2、先将矩阵A 进行LU 分解,然后解方程组b Ax =(直接调用函数): ?????????? ??----=8162517623158765211331056897031354376231A ,????????? ? ??-=715513252b
线性方程组的解法及其应用 The solution of linear equation and its application 专业:测控技术与仪器 班级: 2010-1班 作者:刘颖 学号: 20100310110105
摘要 线性方程组是线性代数的一个重要组成部分,也在现实生产生活中有着广泛的运用,在电子工程、软件开发、人员管理、交通运输等领域都起着重要的作用。在一些学科领域的研究中,线性方程组也有着不可撼动的辅助性作用,在实验和调查后期利用线性方程组对大量的数据进行处理是很方便简捷的选择。本文主要围绕如何解线性方程组来进行讲解,对于不同类型的线性方程组的不同方法,并简述线性方程组的一些实际应用。 关键词: 齐次线性方程组,非齐次线性方程组,克莱姆法则,消元法,矩阵,矩阵的秩,特解,通解。
Abstract Linear equations linear algebra is one of the important component parts, and in real life has extensive production use,and it plays an important role in electronic engineering, software development, personnel management, transportation, etc. In some discipline study, it also has the reigns of linear equations of the auxiliary function.In experiment and survey using the linear equations of the late on the data processing is very convenient simple choice. This article, focusing on how to solve linear equations to explain, for different types of linear equations of different methods, and briefly introduces some of the practical application of linear equations. Keywords: Homogeneous linear equations, Non homogeneous linear equation,Clem’s law,Elimination method,Matrix,Rank of matrix,Special solution,General solution.
第2章 解线性方程组的直接解法 §0 引言 11112211211222221122n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b +++=??+++=??? ?+++=?L L L L 1112121 22212112,(,,,),()n n T T n n n n nn a a a a a a A x x x x b b b a a a ??????===??? ??? ? ?L L L L L L L Ax b = 若A 非奇异,即det()0A ≠,方程组Ax b =有唯一解。由 Cramer 法则,其解 det(),1,2,,det() i i A x i n A = =L 其中i A 为用b 代替A 中第i 列所得的矩阵。当n 大时, 1n +个行列式计算量相当大,实际计算不现实。 121212(,)12det()(1)n n n i i i i i i n i i i A a a a τ=-∑L L L §1 Gauss 消去法 (I )Gauss 消去法的例子 (1)1231123 212336 ()123315()18315() x x x E x x x E x x x E ++=??-+=??-+-=-? 2131()12(),()(18)()E E E E -?--? (2) 12312342356 ()15957()211793()x x x E x x E x x E ++=?? --=-??+=?
方程组13()()E E -与方程组145(),(),()E E E 同解 541 ()21( )()15 E E --得 (3)1231234366()15957()3() x x x E x x E x E ++=?? --=-??=? 由(3)得3 213,2,1x x x === 123(,,)(1,2,3)T T x x x = (3)的系数矩阵为11 10159001????--?????? ,上三角 矩阵。 (II )Gauss 消去法,矩阵三角分解 Ax b = 1112 11,12122 22,112 ,1 n n n n n n nn n n a a a a a a a a A b a a a a +++????????=?????????? L M L M L L M M L M 令(1) ,1,2,,;1,2,,,1ij ij a a i n j n n ===+L L (1)(1)A b A b ??=?? ???? 第1次消去 (1) 110a ≠, 令 (1)1 1(1)11 , 2,3,,i i a l i n a ==L 作运算:11()()i i i l E E E -+→ i E 表示第i 个方程(第i 行) 2,3,,i n =L (2)(1)(1) 111110 2,3,,i i i a a l a i n =-==L
本科毕业论文 ( 2010 届) 题目线性方程组的直接解法及matlab的实现 学院数学与信息工程学院 专业数学与应用数学 班级2006级数学1 班 学号0604010127 学生姓名胡婷婷 指导教师王洁 完成日期2010年5月
摘要 随着科技技术的发展及人类对自然界的不断探索模拟.在自然科学和工程问题中的很多问题的解决常常归结为线性代数问题! 本文的主要内容是对线性方程组求解方法的探讨,主要介绍了四种求解线性方程组的方法,第一种是教科书上常见的消元法,我们称之为基本法.第二种方法是标准上三角形求解法,即将增广矩阵经过初等变换后化成标准上三角形,然后求解.它改进了一般教科书上的常见方法,与常见方法比较有如下优点:1)规范了自由未知量的选取;2)只用矩阵运算;3)减少了计算量.第三种方法是对特定的方程组(系数矩阵A为n阶对称正定矩阵,且A的顺序主子式均不为零.)的求解方法进行描述,并且为这种线性方程的求解提供了固定的公式化的方法.第四种方法是对现在实际问题中常常会遇到的系数矩阵为三对角矩阵的方程组的求解方法.同时给出这几种方法的数值解法(matlab程序),由于运用电脑软件求解,所以必须考虑计算方法的时间、空间上的效率以及算法的数值稳定性问题,所以针对不同类型的线性方程组有不同的解法.但是,基本的方法可以归结为两大类,即直接法和迭代法. 关键词 高斯消去法;三角分解法;乔莱斯基分解法;追赶法
Abstract Systems of linear equations are associated with many problems in engineering and scinence ,as well as with applications of mathematics to the social sciences and the quantitative study of business and economic problems. The main content of this article is the method for solving linear equations, we introduce four methods for solving linear equations in this paper. The first is the elimination method which is commonly found in textbooks, and we call the Basic Law. The second method is Standard on the triangle Solution, that first change Augmented matrix into standards in primary triangle, and then solving. It improves the general textbook on common methods, compared with the common method has the following advantages:1) Specification of the free choice of unknowns; 2)Only matrix operations;3) Reduce the computation. The third method describes a way to solve a Specific equations(N coefficient matrix A is symmetric positive definite matrix, and A are not zero-order principal minor), And for this linear equation provides a fixed formulaic approach. The fourth method is to present practical problems often encountered in the coefficient matrix is tridiagonal matrix method for solving the equations. These methods are given numerical solution of (matlab program), As the use of computer software to solve, it is necessary to consider ways of computing time and space efficiency and numerical stability of algorithms, Therefore, different types of linear equations have a different solution. However, the basic method can be classified into two categories, namely direct methods and iterative methods. Key words Gaussian elimination; Triangular decomposition; Cholesky decomposition method; Thomas algorithm
浅析线性方程组的平方根解法 在求解线性方程组时, 直接解法有顺序高斯消元法、列主元高斯消元法、全主元高斯消元法、高斯约当消元法、消元形式的追赶法、LU分解法、矩阵形式的追赶法,当我们遇到对称正定线性方程组时,我们就要用到平方根法(对称LLT 分解法)来求解,为了熟悉和熟练运用平方根法求解线性方程组,下面对运用平方根法求解线性方程组进行解析。一、运用平方根法求解线性方程组涉及到的定理及定义 我们在运用平方根法求解线性方程组时,要判定线性方程组Ax=b 的系数矩阵A 是否是对称正定矩阵,那么我们就要了解正定矩阵的性质和如下定理及定义: 1、由线性代数知,正定矩阵具有如下性质: 1)正定矩阵A 是非奇异的 2)正定矩阵A的任一主子矩阵也必为正定矩阵 3)正定矩阵A的主对角元素均为正数 4)正定矩阵A 的特征值均大于零 5)正定矩阵A的行列式必为正数 定义一线性方程组Ax=b的系数矩阵A是对称正定矩阵,那么Ax=b是对称正定线性方程组。 定义二如果方阵A满足A=AT那么A是对称阵。 2.1.4 平方根法和改进的平方根法 如果A是n阶对称矩阵,由定理2还可得如下分解定理: 定理2若A为n阶对称矩阵,且A的各阶顺序主子式都不为零,则A可惟一分解为:A= LDLT,其中L为单位下三角阵,D为对角阵。 证明因为A的各阶顺序主子式都不为零,所以A可惟一分解为:A= LU 因为,所以可将U 分解为:
i DU i 其中D 为对角矩阵,Ui 为单位上三角阵?于是:A = LDU 仁L(DUI) 因为A 为对称矩阵,所以,A = AT = UITDTL 七U 仃(DLT),由A 的LU 分解的惟一 性即得:L = UIT,即 Ui = LT ,故 A = LDLT 工程技术中的许多实际问题所归结出的线性方程组,其系数矩阵常有对称正定 性,对于具有此类特殊性质的系数矩阵,利用矩阵的三角分解法求解是一种较好 的有效方法,这就是对称正定矩阵方程组的平方根法及改进的平方根法, 这种方 法目前在计算机上已被广泛应用。 定理3对称矩阵A 为正定的充分必要条件是A 的各阶顺序主子式大于零。 2对称正定矩阵的三角分解 定理(Cholesky 分解)设A 为n 阶对称正定矩阵,则存在惟一的主对角线元素 都是正数的下三角阵L ,使得:A = LLT 。 分解式A = LLT 称为正定矩阵的Cholesky 分解,利用Cholesky 分解来求解系数 矩阵为对称正定矩阵的方程组AX ^ b 的方法称为平方根法。 设A 为4阶对称正定矩阵,则由定理 4 知,A = LLT ,即: a ii a i2 a i3 a i4 l ii 0 0 0 l ii l 2i l 3i l 4i a 21 a 22 a 23 a 24 l 2i l 22 0 0 0 l 22 l 32 l 42 a 3i a 32 a 33 a 34 l 3i l 32 l 33 0 0 l 33 l 43 a 4i a 42 a 43 a 44 l 4i l 42 l 43 144 l 44 将右端矩阵相乘, 并令两端矩阵的元素相等, 于是不难算得矩阵 L 的元素的计算 公式为: 平方根法的计算框图见图 用平方根法求解系数矩阵对称正定的线性方程组时,计算过程是数值稳定 U ii U 22 U l2 U in U ii 1 U nn U 2n U 22 U nn
目录 摘要................................................................................... I Abstract. ............................................................................. II 第一章绪论............................................................................ I 1.1引言 (1) 1.2线性方程组解的求解方法的研究现状 (1) 1.3本文对线性方程组解法的研究结构 (1) 第二章线性方程组理论基础 (2) 2.1 线性方程组概念 (2) 2.2 线性方程组的解的情况分析 (2) 2.3 齐次线性方程组解的结构 (4) 2.4非齐次线性方程组解的结构 (4) 第三章线性方程组的数值解 (5) 3.1 迭代法 (5) 3.1.1 Jacobi方法 (6) 3.2.2 高斯-赛德尔方法 (8) 第四章全文总结和展望 (10) 4.1 全文总结 (10) 4.2 未来展望 (10) 参考文献 (11) 致谢................................................................. 错误!未定义书签。
线性方程组的求解方法 学生:指导教师: 摘要:本文在对线性方程组解的结构的研究背景与意义分析的基础上,对线性方程组的求解方法的研究现状进行了介绍,之后针对线性方程组展开了研究,包括线性方程组的概念、线性方程组的求解方法以及线性方程组的作用等,在对线性方程组有了全面的认识后,基于线性方程组解的结构展开了研究,包括线性方程组解的基本定理,齐次和非齐次线性方程组解的结构形式,以及齐次和非齐次线性方程组解的结构,我们用迭代法中最常用的Jacobi方法中的相似上三角矩阵定理和迭代法中的收敛性讨论线性方程组的数值解法,并用高斯-赛德尔方法进行验证。得到线性方程组的数值解的一般方法。最后,对全文进行了总结和展望。 关键词:线性方程组;数值解;迭代法;Jacobi方法;高斯-赛德尔方法
本科实验报告 课程名称:数值计算方法B 实验项目:线性方程组的直接解法 最小二乘拟合多项式 实验地点:ZSA401 专业班级:学号:201000 学生姓名: 指导教师:李志 2012年4月13日
线性方程组的直接解法 一、实验目的和要求 实验目的:合理利用Gauss 消元法、LU 分解法或追赶法求解方程组。 实验要求:利用高斯消元法,LU 分解法或追赶法进行编程,求解题中所给的方程组。 二、实验内容和原理 实验内容:合理利用Gauss 消元法、LU 分解法或追赶法求解下列方程组: ① ?? ?? ? ?????=????????????????????13814142210321321x x x ②??? ? ?? ??????=????????????????????? ?? ? ??--?-2178.4617.5911212592.1121130.6291.513 14 .59103.043 2115x x x x ③?? ??? ??? ? ???????----=????????????????????????????????-55572112112112121 n n x x x x (n=5,10,100,…) 实验原理:这个实验我选用的是高斯消元法。高斯消元法:先按照 L ik =a ik^(k-1)/a kk^(k-1) , a ij^(k)=a ij^(k-1)-l ik a kj^(k-1) [其中k=1,2,…,n-1;i=k+1,k+2,…,n;j=k+1,k+2,…,n+1] 将方程组变为上三角矩阵,再经过回代,即可求解出方程组的解。 三.计算公式 通过消元、再回代的求解方法称为高斯消元法。特点是始终消去主对角线 下方的元素。 四、操作方法与实验步骤 #include "Stdio.h" #define N 3 main() { double a[N][N+1],b[N]; int i,j,k,x=0; for(i=0;i 第2章线性方程组的直接解法 2.1实验目的 理解线性方程组计算机解法中的直接解法的求解过程和特点,学习科学计算的方法和简单的编程技术。 2.2概念与结论 1. n阶线性方程组 如果未知量的个数为 n ,而且关于这些未知量x1,x2, …,x n的幂次都是一次的(线性的)那末, n 个方程 a11x1+a12x2+ … +a1n x n=b1 ┆┆┆ (1) a n1x1+a n2x2+ … +a nn x n= b n 构成一个含n个未知量的线性方程组,称为n阶线性方程组。其中,系数a11,…,a1n,a21, …,a2n, …,a n1, …,a nn 和b1, …,b n都是给定的常数。 方程组(1)也常用矩阵的形式表示,写为 Ax=b 其中,A是由系数按次序排列构成的一个n阶矩阵,称为方程组的系数矩阵,x和b都是n维向量,b称为方程组的右端向量。 2. n阶线性方程组的解 使方程组(1)中每一个方程都成立的一组数x1*,x2*, …,x n*称为式(1)的解,把它记为向量的形式,称为解向量. 3.一些特殊的线性方程组 1) 上三角方程组 2) 三对角方程组 ? ? ? ? ? ? ? ? ? ? ? ? = ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? - - - - - n n nn n n n n n n n n b b b x x x a a a a a a a a a a a a 2 1 2 1 1 1 1 2 1 2 23 22 1 1 1 13 12 11 4.矩阵的Doolittle 分解 5.Doolittle 分解的紧凑格式 6.矩阵的Crout 分解 ????????? ? ??=?????????? ???????????? ? ?--n n n n n n d d d x x x b a c b c b a c b a c b 21 2111333 22211???? ?? ? ? ???????? ??=??????? ??nn n n n n nn n n n n u u u u u u l l l a a a a a a a a a 222 11211 2 1 21 2 1 2222111211111 ???? ?? ? ? ???????? ??=??????? ??11 1 21122 1 2221 11 2 1 2222111211 n n nn n n nn n n n n u u u l l l l l l a a a a a a a a a ????? ?? ? ??nn n n n n n n u l l l u u l l u u u l u u u u 3 2 1 333323122322211131211 第2章 解线性方程组的直接解法 §0 引言 11112211211222221122n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b +++=??+++=????++ +=? 1112121 22212112,(,,,),()n n T T n n n n nn a a a a a a A x x x x b b b a a a ??????===???????? Ax b = 若A 非奇异,即det()0A ≠,方程组Ax b =有唯一解。由 Cramer 法则,其解 det(),1,2,,det()i i A x i n A == 其中i A 为用b 代替A 中第i 列所得的矩阵。当n 大时, 1n +个行列式计算量相当大,实际计算不现实。 121212(,)12det()(1)n n n i i i i i i n i i i A a a a τ=-∑ §1 Gauss 消去法 (I )Gauss 消去法的例子 (1)1231123212336()123315()18315()x x x E x x x E x x x E ++=??-+=??-+-=-? 2131()12(),()(18)()E E E E -?--? (2) 12312342356()15957()211793()x x x E x x E x x E ++=??--=-??+=? 方程组13()()E E -与方程组145(),(),()E E E 同解 541 ()21()()15E E --得 (3)1231234366 () 15957() 3() x x x E x x E x E ++=??--=-??=? 由(3)得3213,2,1x x x === 123(,,)(1,2,3)T T x x x = (3)的系数矩阵为11 10159001?? ?? --?????? ,上三角 矩阵。 (II )Gauss 消去法,矩阵三角分解 Ax b = 111211,1 212222,1 12,1 n n n n n n nn n n a a a a a a a a A b a a a a +++????????=?????????? 令(1) ,1,2,,;1,2,,,1 ij ij a a i n j n n ===+ (1)(1)A b A b ??=?????? 第1次消去 (1) 110a ≠, 令 (1) 1 1(1)11 ,2,3,,i i a l i n a == 作运算:11()()i i i l E E E -+→ i E 表示第i 个方程(第i 行) 2,3,,i n = (2)(1)(1) 1111102,3,,i i i a a l a i n =-== 第4章 线性方程组的直接解法 本章主要内容 线性方程组的直接解法——消元法(高斯消元法、主元消元法). 矩阵的三角分解法( Doolittle 分解、Crout 分解、 LDU 分解) 紧凑格式 改进平方根法. 本章重点、难点 一、消元法(高斯消元法、列主元消元法) 本章求解的是n 阶线性方程组Ax=b 的(即方程的个数和未知量的个数相等的线性方程组) ?????????=+???++????????????? ??=+???++=+???++n n nn n n n n n b x a x a x a b x a x a x a b x a x a x a 22112 3222212111212111 1. 高斯消元法 ①高斯消元法的基本思想:通过对线性方程组Ax=b 的进行同解消元变换(也可以用矩阵的初等行变换法进行线性方程组的消元变换),将线性方程组化为上三角形方程组,然后用回代法求出此线性方程组的解。 ②高斯消元法计算公式: ????? ? ? ????????--=-=--==? ????? ????? ???? +=-=-=====-+=------------∑)1,..., 2,1()1,..., 2,1(,...,1,,,,...,2,1) ,...,2,1,(,) 1(1)1()1()1() 1() 1()1() 1()1()() 1()1()1()1()(,)0()0(n n i a x a b x n n i a b x n k j i b a a b b a a a a a n k n j i b b a a i ii n i j j i ij i i i n nn n n n k k k kk k ik k i k i k kj k kk k ik k ij k ij i i ij ij 对回代公式: 消元公式: 线性方程组的几种解法 线性方程组形式如下: 常记为矩阵形式 其中 一、高斯消元法 高斯(Gauss)消元法的基本思想是:通过一系列的加减消元运算,也就是代数中的加减消去法,将方程组化为上三角矩阵;然后,再逐一回代求解出x 向量。现举例说明如下: (一)消元过程 第一步:将(1)/3使x 1的系数化为1 得 再将(2)、(3)式中x 1的系数都化为零,即由(2)-2×(1)(1) 得 )1(32)2( (03) 4 32=+x x )1(321)1(......23132=++ x x x 由(3)-4×(1)(1) 得 第二步:将(2)(1) 除以2/3,使x 2系数化为1,得 再将(3)(1) 式中x 2系数化为零,即 由(3)(1) -(-14/3)*(2)(2) ,得 第三步:将(3)(2) 除以18/3,使x 3系数化为1,得 经消元后,得到如下三角代数方程组: (二)回代过程 由(3)(3) 得 x 3=1, 将x 3代入(2)(2) 得x 2=-2, 将x 2 、x 3代入(1)(1) 得x 2=1 所以,本题解为[x]=[1,2,-1]T (三)、用矩阵演示进行消元过程 第一步: 先将方程写成增广矩阵的形式 第二步:然后对矩阵进行初等行变换 初等行变换包含如下操作 (1) 将某行同乘或同除一个非零实数 ) 3(3)3(......1-=x )2(3)3( (63) 18-=x ) 2(32) 2(......02=+x x ) 1(32)3( (63) 10 314-=-- x x (2)将某行加入到另一行 (3)将任意两行互换 第三步:将增广矩阵变换成上三角矩阵,即主对角线全为1,左下三角矩阵全为0,形式如下: 示例: (四)高斯消元的公式 综合以上讨论,不难看出,高斯消元法解方程组的公式为 1.消元 (1)令 a ij(1) = a ij , (i,j=1,2,3,…,n) b i(1) =b i , (i=1,2,3,…,n) (2)对k=1到n-1,若a kk(k)≠0,进行 l ik = a ik(k) / a kk(k) , (i=k+1,k+2,…,n) a ij(k+1) = a ij(k) - l ik * a kj(k), (i,j= k+1,k+2,…,n) b i(k+1) = b i(k) - l ik * b k(k), (i= k+1,k+2,…,n) 2.回代 若a nn(n) ≠0 x n = b n(n) / a nn(n) x i = (b i(i) – sgm(a ij(i) * x j)/- a ii(i),(i = n-1,n-2,…,1),( j = i+1,i+2,…,n ) (五)高斯消元法的条件 消元过程要求a ii(i) ≠0 (i=1,2,…,n),回代过程则进一步要求a nn(n) ≠0,但就方程组Ax=b 讲,a ii(i)是否等于0时无法事先看出来的。 注意A的顺序主子式D i(i=1,2,…,n),在消元的过程中不变,这是因为消元所作的变换是“将某行的若干倍加到另一行”。若高斯消元法的过程进行了k-1步(a ii(i) ≠0,i 实验五 线性方程组的直接解法 一、实验内容 1、用列主元素法求解方程组 15 123459.170.31059.43146.785.291 6.3112111.295221211x x x x -?????????????--??????=?????????????? ???? 并计算误差b-Ax ,分析结果的好坏; 2、 用改进Cholesky 方法求对称正定阵线性方程组 1234248.72171013.741090.7x x x -????????????-=????????????-?????? 并计算误差b-Ax ,分析结果的好坏; 3、 用追赶法解方程组 123421006132010121000351x x x x -????????????--??????=??????--??????-???? ?? 二、要求 1、 对上述三个方程组分别利用Gauss 列主元消去法;Cholesky 方法;追赶法求解(选择其一); 2、 应用结构程序设计编出通用程序; 3、 比较计算结果,分析数值解误差的原因; 三、目的和意义 1、通过该课题的实验,体会模块化结构程序设计方法的优点; 2、运用所学的计算方法,解决各类线性方程组的直接算法; 3、提高分析和解决问题的能力,做到学以致用; 4、 通过三对角形线性方程组的解法,体会稀疏线性方程组解法的特点。 四、实验学时:2学时 五、实验步骤: 1.进入matlab 开发环境; 2.根据实验内容和要求编写程序; 3.调试程序; 4.运行程序; 5.撰写报告,讨论分析实验结果. 六、程序 1、Gauss列主元素消去法 function x=Gauss_pivot(A,b) %用Gauss列主元素法求解线性方程组Ax=b %x是未知向量 n=length(b); x=zeros(n,1); c=zeros(1,n); d1=0; %消元计算 for i=1:n-1 max=abs(A(i,i)); m=i; for j=i+1:n if max 数值分析讲义 第三章线性方程组的解法 §3.0 引言 §3.1 雅可比(Jacobi)迭代法 §3.2 高斯-塞德尔(Gauss-Seidel)迭代法 §3.3 超松驰迭代法§3.7 三角分解法 §3.4 迭代法的收敛性§3.8 追赶法 §3.5 高斯消去法§3.9 其它应用 §3.6 高斯主元素消去法§3.10 误差分析 §3 作业讲评3 §3.11 总结 §3.0 引言 重要性:解线性代数方程组的有效方法在计算数学和科学计算中具有特殊的地位和作用.如弹性力学、电路分析、热传导和振动、以及社会科学及定量分析商业经济中的各种问题. 分类:线性方程组的解法可分为直接法和迭代法两种方法. (a) 直接法:对于给定的方程组,在没有舍入误差的假设下,能在预定的运算次数内求得精确解.最基本的直接法是Gauss消去法,重要的直接法全都受到Gauss消去法的启发.计算代价高. (b) 迭代法:基于一定的递推格式,产生逼近方程组精确解的近似序列.收敛性是其为迭代法的前提,此外,存在收敛速度与误差估计问题.简单实用,诱人. §3.1 雅可比Jacobi 迭代法 (AX =b ) 1 基本思想: 与解f (x )=0 的不动点迭代相类似,将AX =b 改写为X =BX +f 的形式,建立雅可比方法的迭代格式:X k +1=BX (k )+f ,其中,B 称为迭代矩阵.其计算精度可控,特别适用于求解系数为大型稀疏矩阵(sparse matrices)的方程组. 2 问题: (a) 如何建立迭代格式? (b) 向量序列{X k }是否收敛以及收敛条件? 3 例题分析: 考虑解方程组??? ??=+--=-+-=--2.453.82102 .72103 21321321x x x x x x x x x (1) 其准确解为X *={1, 1.2, 1.3}. 建立与式(1)相等价的形式: ??? ??++=++=++=84.02.01.083.02.01.072 .02.01.02 13312321x x x x x x x x x (2) 据此建立迭代公式: ?????++=++=++=+++84 .02.01.083.02.01.072.02.01.0)(2)(1)1(3 )(3 )(1)1(23)(2)1(1k k k k k k k k k x x x x x x x x x (3) 取迭代初值0) 0(3 )0(2)0(1===x x x ,迭代结果如下表. JocabiMethodP31.cpp 求线性方程组的方法 摘要:线性方程组是线性代数的一个重要组成部分,也在现实生活中有着广泛的运用,在电子工程、软件开发、人员管理、交通运输等领域都起着重要作用。在一些学科领域的研究中,线性方程组也有着不可撼动的辅助性作用,在实验和调查后期利用线性方程组对大量的数据处理是很方便简洁的选择。本文主要围绕如何解线性方程组来进行讲解,对于不同类型的线性方程组的不同方法,并简述线性方程组的一些实际应用。 关键词:齐次线性方程组,非齐次线性方程组,克莱姆法则,消元法,矩阵,矩阵的秩,特解,通解。 英文题目 The solution of linear equation Linear equations linear algebra is one of the important component parts, and in real life has extensive production use,and it plays an important role in electronic engineering, software development, personnel management, transportation, etc. In some discipline study, it also has the reigns of linear equations of the auxiliary function.In experiment and survey using the linear equations of the late on the data processing is very convenient simple choice.线性方程组的直接解法
解线性方程组直解法
线性方程组的直接解法
线性方程组的几种求解方法
线性方程组的直接解法
数值分析讲义——线性方程组的解法
线性方程组的理论和解法