
空间向量在立体几何中的应用
【考纲说明】
1.能够利用共线向量、共面向量、空间向量基本定理证明共线、共面、平行及垂直问题;
2.会利用空间向量的坐标运算、两点间的距离公式、夹角公式等解决平行、垂直、长度、角、距离等问题;
3.培养用向量的相关知识思考问题和解决问题的能力;
【知识梳理】
一、空间向量的运算 1、向量的几何运算 (1)向量的数量积:
已知向量 ,则 叫做 的数量积,记作 ,即 空间向量数量积的性质:① ;
② ;
③
.
(2)向量共线定理:向量()
0a a ≠r
r r 与b r 共线,当且仅当有唯一一个实数λ,使b a λ=r r .
2、向量的坐标运算 (1)若
,
,则
.
一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。
(2)若 , ,则 ,
,
,
;
,
.
(3)夹角公式:
(4)两点间的距离公式:若,,则
二、空间向量在立体几何中的应用
2.利用空间向量证明平行问题
对于平行问题,一般是利用共线向量和共面向量定理进行证明.
3.利用空间向量证明垂直问题
对于垂直问题,一般是利用进行证明;
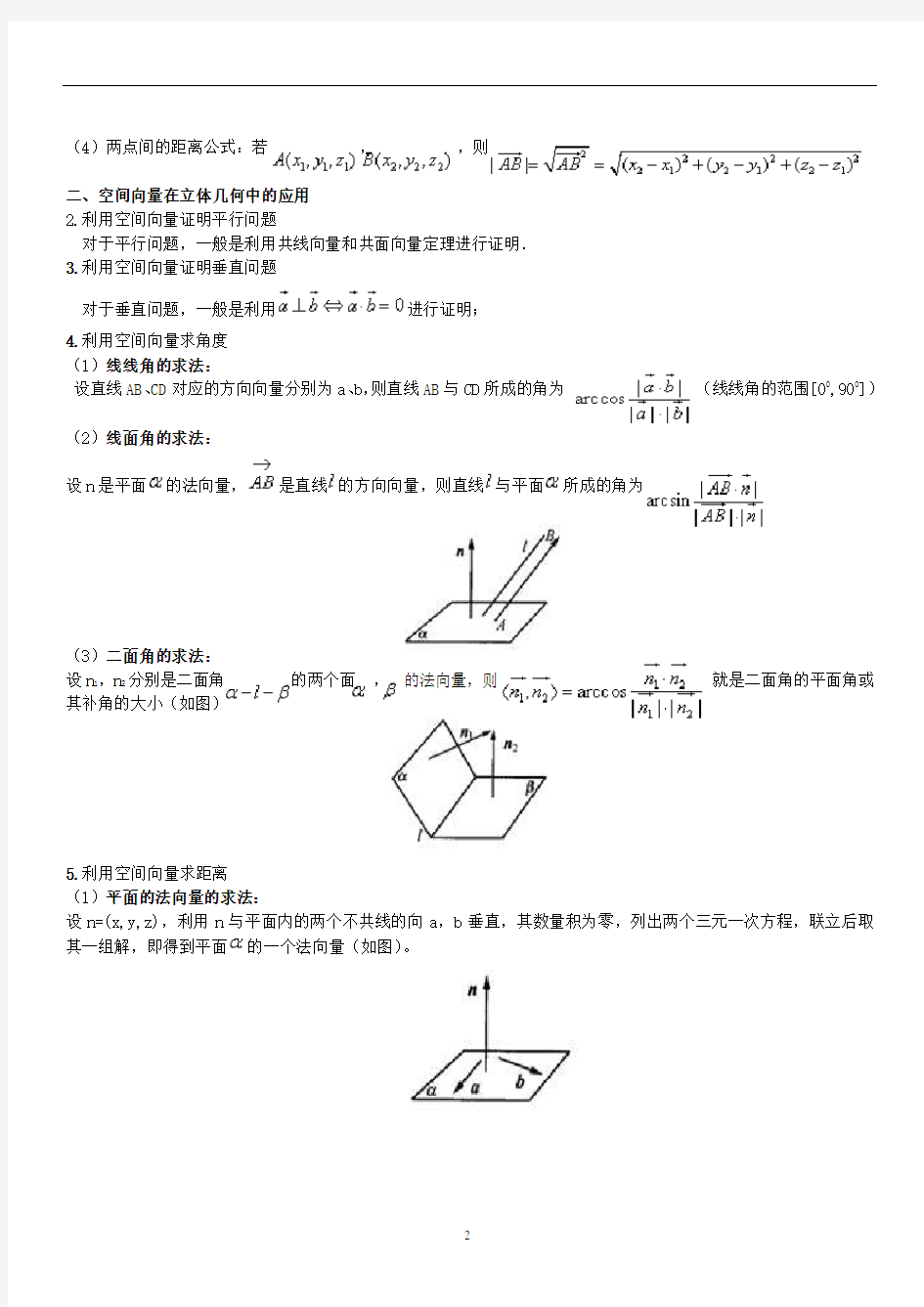
4.利用空间向量求角度
(1)线线角的求法:
设直线AB、CD对应的方向向量分别为a、b,则直线AB与CD所成的角为(线线角的范围[00,900])(2)线面角的求法:
设n是平面的法向量,是直线的方向向量,则直线与平面所成的角为
(3)二面角的求法:
设n1,n2分别是二面角的两个面,的法向量,则就是二面角的平面角或其补角的大小(如图)
5.利用空间向量求距离
(1)平面的法向量的求法:
设n=(x,y,z),利用n与平面内的两个不共线的向a,b垂直,其数量积为零,列出两个三元一次方程,联立后取其一组解,即得到平面的一个法向量(如图)。
(2)利用法向量求空间距离
(a)点A到平面的距离:,其中,是平面的法向量。
(b)直线与平面之间的距离:,其中,是平面的法向量。
(c)两平行平面之间的距离:,其中,是平面的法向量。
【经典例题】
【例1】(2010全国卷1理)正方体ABCD-
1111
A B C D中,B
1
B与平面AC
1
D所成角的余弦值为()(A)
2
3
(B)
3
3
(C)
2
3
(D)
6
3
【解析】D
【例2】(2010全国卷2文)已知三棱锥S ABC
-中,底面ABC为边长等于2的等边三角形,SA垂直于底面ABC,SA=3,那么直线AB与平面SBC所成角的正弦值为()
(A)
3
(B)
5
(C)
7
(D)
3
4
【解析】D
【例3】(2012全国卷)三棱柱
111
ABC A B C
-中,底面边长和侧棱长都相等,
11
60
BAA CAA
∠=∠=o,则异面直线
1
AB与
1
BC所成角的余弦值为____________。
【解析】
6
6
A
B
C
S
E
F
【例4】(2012重庆)如图,在直三棱柱ABC-A 1B 1C 1中,AB=4,AC=BC=3,D 为AB 的中点。
(Ⅰ)求异面直线CC 1和AB 的距离;
(Ⅱ)若AB 1⊥A 1C ,求二面角A 1—CD —B 1的平面角的余弦值。
【解析】5 3
1
【例5】(2012江苏)如图,在直三棱柱111ABC A B C -中,1111A B AC =,D E ,
分别是棱1BC CC ,上的点(点D 不同于点C ),且AD DE F ⊥,为11B C 的中点. 1B 求证:(1)平面ADE ⊥平面11BCC B ;
(2)直线1//A F 平面ADE .
【例6】(2012山东)在如图所示的几何体中,四边形ABCD 是等腰梯形,AB ∥CD ,∠DAB=60°,FC ⊥平面ABCD ,AE ⊥BD ,CB=CD=CF .
(Ⅰ)求证:BD ⊥平面AED ;
(Ⅱ)求二面角F-BD-C 的余弦值. 错误!未指定书签。
【解析】二面角F-BD-C 的余弦值为5
5.
【例7】(2012江西)在三棱柱111ABC A B C -中,已知15AB AC AA ===,4BC =,点1A 在底面ABC 的投
影是线段BC 的中点O 。
(1)证明在侧棱1AA 上存在一点E ,使得OE ⊥平面11BB C C ,并求出AE 的长; (2)求平面11A B C 与平面11BB C C 夹角的余弦值。
【解析】55,10
30
B 1
C 1
O A
C
B
A 1
1A
1C
F
E
C
D A
B
P A
B
C
E
D 【例8】(2012湖南)四棱锥P-ABCD 中,PA ⊥平面ABCD ,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,
E 是CD 的中点. (Ⅰ)证明:CD ⊥平面PAE ;
(Ⅱ)若直线PB 与平面PAE 所成的角和PB 与平面ABCD 所成的角相等,求四棱锥P-ABCD 的体积.
【解析】11851285
1633515V S PA =??=??=
【例9】(2012广东)如图所示,在四棱锥P ABCD -中,AB ⊥平面PAD ,//,AB CD PD AD =,E 是PB 中点,F 是DC 上的点,且1
2
DF AB =
,PH 为PAD ?中AD 边上的高。 (1)证明:PH ⊥平面ABCD ;
(2)若1,2,1PH AD FC ===,求三棱锥E BCF -的体积; (3)证明:EF ⊥平面PAB .
【解析】三棱锥E BCF -的体积111112123326212
BCF V S h FC AD h ?=
?=????=???= 【例10】(2012新课标)如图,直三棱柱ABC -A 1B 1C 1中,AC=BC=2
1
AA 1,D 是棱AA 1的中点,DC 1⊥BD . (1)证明:DC 1⊥BC ;
(2)求二面角A 1-BD -C 1的大小.
【解析】二面角11C BD A --的大小为30?
【例11】如图所示,在四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥平面ABCD 点E 在线段PC 上,PC ⊥平面BDE .
(1)证明:BD ⊥平面PAC ;
(2)若1PA =,2AD =,求二面角B PC A --的正切值.
【解析】二面角B PC A --的平面角的正切值为3
【例12】(2012天津)如图,在四棱锥P ABCD -中,PA 丄平面ABCD ,AC 丄AD ,AB 丄BC ,0
=45ABC ∠,
D
A 1
C
A
C 1
==2PA AD ,=1AC . (Ⅰ)证明PC 丄AD ;
(Ⅱ)求二面角A PC D --的正弦值;
(Ⅲ)设E 为棱PA 上的点,满足异面直线BE 与CD 所成的角为030,求AE 的长. 【解析】630,10
10
【课堂练习】
1、(2012上海)若)1,2(-=n 是直线l 的一个法向量,则l 的倾斜角的大小为 (用反三角函数值表示)
2、(2012四川)如图,在正方体1111ABCD A B C D -中,M 、N 分别是CD 、1CC 的中点,则异面直线1A M 与DN 所成角的大小是____________。
3、(2012全国卷)如图,四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥底面ABCD ,22AC =2PA =,
E 是PC 上的一点,2PE EC =。 (Ⅰ)证明:PC ⊥平面BED ;
(Ⅱ)设二面角A PB C --为90o
,求PD 与平面PBC 所成角的大小。
4、(2010辽宁理)已知三棱锥P -ABC 中,PA ⊥ABC ,AB ⊥AC ,PA=AC=?AB ,N 为AB 上一点,AB=4AN,M,S 分别为PB,BC 的中点.
(Ⅰ)证明:CM ⊥SN ;
(Ⅱ)求SN 与平面CMN 所成角的大小.
5、(2010辽宁文)如图,棱柱111ABC A B C -的侧面11BCC B 是菱形,11B C A B ⊥
N M
B 1
A 1
C 1
D 1
B
D E D
A P
(Ⅰ)证明:平面1AB C ⊥平面11A BC ;
(Ⅱ)设D 是11A C 上的点,且1//A B 平面1B CD ,求11:A D DC 的值.
6、(2010全国文)如图,直三棱柱ABC-A 1B 1C 1 中,AC=BC , AA 1=AB ,D 为BB 1的中点,E 为AB 1上的一点,AE=3 EB 1
(Ⅰ)证明:DE 为异面直线AB 1与CD 的公垂线;
(Ⅱ)设异面直线AB 1与CD 的夹角为45°,求二面角A 1-AC 1-B 1的大小
7、(2010江西理)如图△BCD 与△MCD 都是边长为2的正三角形,平面MCD ⊥平面BCD ,AB ⊥平面BCD ,23AB =。 (1) 求点A 到平面MBC 的距离;
(2) 求平面ACM 与平面BCD 所成二面角的正弦值。 8、(2010重庆文)四棱锥P ABCD -中,底面ABCD 为矩形,PA ⊥底面
C
B
A D
E P
ABCD ,2PA AB ==E 是棱PB 的中点.
(Ⅰ)证明:AE ⊥平面PBC ;
(Ⅱ)若1AD =,求二面角B EC D --的平面角的余弦值.
9、(2010浙江文)如图,在平行四边形ABCD 中,AB=2BC ,∠ABC=120°。E 为线段AB 的中点,将△ADE 沿直线DE 翻折成△A ’DE ,使平面A ’DE ⊥平面BCD ,F 为线段A ’C 的中点。 (Ⅰ)求证:BF ∥平面A ’DE ;
(Ⅱ)设M 为线段DE 的中点,求直线FM 与平面A ’DE 所成角的余弦值。
10、(2010重庆理)四棱锥P-ABCD 中,底面ABCD 为矩形,PA ⊥底面ABCD ,6,点E 是棱PB 的中点。 (1)求直线AD 与平面PBC 的距离;
(2)若3A-EC-D 的平面角的余弦值。
11、(2010北京理)如图,正方形ABCD 和四边形ACEF 所在的平面互相垂直,CE ⊥AC,EF ∥AC,AB=2,CE=EF=1. (Ⅰ)求证:AF ∥平面BDE ; (Ⅱ)求证:CF ⊥平面BDE ; (Ⅲ)求二面角A-BE-D 的大小。
12、如图,弧AEC 是半径为a 的半圆,AC 为直径,点E 为弧AC 的中点,
点B 和
点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB=a5
(1)证明:EB⊥FD
(2)求点B到平面FED的距离.
13、(2010江苏卷)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,PD=DC=BC=1,AB=2,AB∥DC,∠BCD=900。
(1)求证:PC⊥BC;
(2)求点A到平面PBC的距离。
14、(2012上海)如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥底面ABCD,E是PC的中点.已知AB=2,AD=22,PA=2.求:(1)三角形PCD的面积;
(2)异面直线BC与AE所成的角的大小.
15、(2012四川)如图,在三棱锥P ABC
-中,90
APB
∠=o,60
PAB
∠=o,AB BC CA
==,平面PAB⊥平面ABC。(Ⅰ)求直线PC与平面ABC所成角的大小;
(Ⅱ)求二面角B AP C
--的大小。
16、(2012安徽)长方体
1
1
1
1
D
C
B
A
ABCD-中,底面
1
1
1
1
D
C
B
A是正方形,O是BD的中点,E是棱
1
AA上任意一点。
C
P
16题图
D
C
(Ⅰ)证明:BD 1EC ⊥ ;
(Ⅱ)如果AB =2,AE =2,1EC OE ⊥,求1AA 的长。
17、(2012北京文)如图1,在Rt ABC ?中,90C ∠=o ,,D E 分别为,AC AB 的中点,点F 为线段CD 上的一点,将ADE ?沿DE 折起到1A DE ?的位置,使1A F CD ⊥,如图2。 (Ⅰ)求证://DE 平面1A CB ;(Ⅱ)求证:1A F BE ⊥;
(Ⅲ)线段1A B 上是否存在点Q ,使1
AC ⊥平面DEQ ?说明理由。 18、(2012湖南)如图6,在四棱锥P-ABCD 中,PA ⊥平面ABCD ,底面ABCD 是等腰梯形,AD ∥BC ,AC ⊥BD. (Ⅰ)证明:BD ⊥PC ;
(Ⅱ)若AD=4,BC=2,直线PD 与平面PAC 所成的角为30°,求四棱锥P-ABCD 的体积.
19、如图,在三棱锥P ABC -中,PA ⊥底面ABC ,D 是PC 的中点,已知∠BAC =
2
π
,2AB =,23AC =,2PA =,求:
(1)三棱锥P ABC -的体积
图2图1F
E
B
E
D C
B C
D
A 1
A
F
M
A B
D
C
O
(2)异面直线BC 与AD 所成的角的大小(结果用反三角函数值表示)
20、(2008安徽文)如图,在四棱锥O ABCD -中,底面ABCD 四边长为1的 菱形,4
ABC π
∠=
, OA ABCD ⊥底面,
2OA =,M 为OA 的中点。
(Ⅰ)求异面直线AB 与MD 所成角的大小; (Ⅱ)求点B 到平面OCD 的距离。
【课后作业】
1. (2008全国Ⅱ)如图,正四棱柱1111ABCD A B C D -中,124AA AB ==,点E 在1CC 上且EC E C 31=. (Ⅰ)证明:1AC ⊥平面BED ;
(Ⅱ)求二面角1A DE B --的大小.
2、(2008湖南)四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,PA ⊥底面ABCD ,
PA =2.
(Ⅰ)证明:平面PBE ⊥平面PAB ;
(Ⅱ)求平面PAD 和平面PBE 所成二面角(锐角)的大小.
A B C D E A 1
B 1
C 1
D 1
3、(2008福建)如图,在四棱锥P-ABCD 中,则面PAD ⊥底面 ABCD ,侧棱PA =PD =2,底面ABCD 为直角梯形, 其中BC ∥ AD ,AB ⊥AD ,AD =2AB =2BC =2,O 为AD 中点.
(Ⅰ)求证:PO ⊥平面ABCD ;(Ⅱ)求异面直线PD 与CD 所成角的大小; (Ⅲ)线段AD 上是否存在点Q ,使得它到平面PCD 的距离为3?
若存在,求出
AQ
QD
的值;若不存在,请说明理由.
4、(2008海南、宁夏理)如图,已知点P 在正方体ABCD -A 1B 1C 1D 1的对角线BD 1上,∠PDA=60°。 (1)求DP 与CC 1所成角的大小;(2)求DP 与平面AA 1D 1D 所成角的大小。
5、(2005湖南文、理)如图1,已知ABCD 是上、下底边长分别为2和6,高为3的等腰梯形,将它沿对称轴OO 1
折成直二面角,如图2。(Ⅰ)证明:AC ⊥BO 1; (Ⅱ)求二面角O -AC -O 1的大小。
B 1
C 1
D 1
A 1
C
D P C
D
O 1
C
O 1
D
6、(2007安徽文、理)如图,在六面体1111D C B A ABCD -中,四边形ABCD 是边长为2的正方形,四边形1111D C B A 是边长为1的正方形,⊥1DD 平面1111D C B A ,⊥1DD 平面ABCD ,DD 1=2。 (Ⅰ)求证:11C A 与AC 共面,11D B 与BD 共面. (Ⅱ)求证:平面;1111BDD B ACC A 平面⊥ (Ⅲ)求二面角C BB A --1的大小.
7、(2007海南)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°,O 为BC 中点. (Ⅰ)证明:SO ⊥平面ABC ;
(Ⅱ)求二面角A SC B --的余弦值.
8、(2007四川理)如图,PCBM 是直角梯形,∠PCB =90°,PM ∥BC ,PM =1,BC =2,又AC =1,∠ACB =120°,AB ⊥PC ,直线AM 与直线PC 所成的角为60°.
(Ⅰ)求证:平面PAC ⊥平面ABC ; (Ⅱ)求二面角B AC M --的大小; (Ⅲ)求三棱锥MAC P -的体积.
O
S B A C
9、(2006全国Ⅰ卷)如图,1l 、2l 是互相垂直的异面直线,MN 是它们的公垂线段.点A 、B 在1l 上,C 在2l 上,
AM MB MN ==。 (Ⅰ)证明AC ⊥NB ;
(Ⅱ)若60O
ACB ∠=,求NB 与平面ABC 所成角的余弦值。
10、(2006福建文、理)如图,四面体ABCD 中,O 、E 分别是BD 、BC 的中点,2, 2.CA CB CD BD AB AD ======
(I )求证:AO ⊥平面BCD ; (II )求异面直线AB 与CD 所成角的大小;
(III )求点E 到平面ACD 的距离。
11、(2010福建文)如图,在长方体ABCD – A 1B 1C 1D 1中,E ,H 分别是棱A 1B 1,D 1C 1上的点(点E 与B 1不重合),且EH//A 1D 1。过EH 的平面与棱BB 1,CC 1相交,交点分别为F ,G 。 (I )证明:AD//平面EFGH ;
(II )设AB=2AA 1=2a 。在长方体ABCD-A 1B 1C 1D 1内随机选取一点,记该点取自于几何体A 1ABFE – D 1DCGH 内的概率为p 。当点E ,F 分别在棱A 1B 1, B 1B 上运动且满足EF=a 时,求p 的最小值。
D
O
A
B
M
N
C
l 2
l 1
H
12、如图,四棱锥P ABCD -的底面是正方形,PD ABCD ⊥底面,点E 在棱PB 上. (Ⅰ)求证:平面AEC PDB ⊥平面; (Ⅱ)当2PD AB =且E 为PB 的中点时,求AE 与平面PDB 所成的角的大小.
13、在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥平面ABCD ,4PA AD ==,2AB =. 以AC 的中点O 为球心、AC 为直径的球面交PD 于点M ,交PC 于点N .
(1)求证:平面ABM ⊥平面PCD ; (2)求直线CD 与平面ACM 所成的角的大小;
(3)求点N 到平面ACM 的距离.
y
z
D M
P A
g N
14、如图4,在正三棱柱111ABC A B C -中,2AB AA =。D 是11A B 的中点,点E 在11A C 上,且DE AE ⊥。
(1)证明平面ADE ⊥平面11ACC A
(2)求直线AD 和平面ABC 所成角的正弦值。
【参考答案】
【课堂练习】
1、2arctan
2、90o
3、30o
4、SN 与面CMN 所成角为45°
5、A 1D :DC 1=1.
6、略
7、
5152
. 8、略 9、略 10、21 11、二面角A BE D --的大小为6π. 12、21214 13、点A 到平面PBC
14、异面直线BC 与AE 所成的角的大小是4π
15、直线PC 二面角B AP C --的大小为arctan 2与平面ABC
所成的角的大小为arctan
13
16
、1111
AC AE AA AO EA =?=?= 17、略
18、四棱锥P ABCD -的体积为11
941233
V S PA =
??=??=. 19、略 20、(1)AB 与MD 所成角的大小为3
π (2) 点B 到平面OCD 的距离为23
【课后作业】
1、二面角1A DE B --
的大小为arccos
42
. 2、平面PAD 和平面PBE
所成二面角(锐角)的大小是arccos
5
3、(Ⅱ)异面直线PB 与CD 所成的角是
(Ⅲ)存在点Q 满足题意,此时
1
3
AQ QD =. 4、(1)DP 与CC '所成的角为45o
.(2)DP 与平面AA D D ''所成的角为30o
. 5、cos <=cos θ,1BO .4
3|
|||11=?BO n
6、.5
11---∴的余弦为二面角C BB A 7、(Ⅱ)二面角A SC B --
8、(Ⅱ)二面角M AC B --
的平面角大小为
(Ⅲ)11111326212
P MAC A PCM V V PC PM h --===???=???=u u u r u u u u r 9、cos ∠NBH=
63
10、(Ⅱ)异面直线AB 与CD 所成角的大小.4
2
arccos
(Ⅲ)点E 到平面ACD 的距离为7
21.
11、略 12、AE 与平面PDB 所成的角的大小为45?
.
13、所求角的大小为,所求距离为5h 9= 14、线AD 和平面AB C 1所成角的正弦值为5
10
。
1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD,点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4. (1)求证:M为PB的中点; (2)求二面角B﹣PD﹣A的大小; (3)求直线MC与平面BDP所成角的正弦值. 【分析】(1)设AC∩BD=O,则O为BD的中点,连接OM,利用线面平行的性质证明OM∥PD,再由平行线截线段成比例可得M为PB的中点; (2)取AD中点G,可得PG⊥AD,再由面面垂直的性质可得PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,再证明OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,求出平面PBD与平面PAD的一个法向量,由两法向量所成角的大小可得二面角B﹣PD﹣A的大小;(3)求出的坐标,由与平面PBD的法向量所成角的余弦值的绝对值可得直线MC与平面BDP所成角的正弦值. 【解答】(1)证明:如图,设AC∩BD=O, ∵ABCD为正方形,∴O为BD的中点,连接OM, ∵PD∥平面MAC,PD?平面PBD,平面PBD∩平面AMC=OM, ∴PD∥OM,则,即M为PB的中点; (2)解:取AD中点G, ∵PA=PD,∴PG⊥AD, ∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, ∴PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG, 由G是AD的中点,O是AC的中点,可得OG∥DC,则OG⊥AD. 以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系, 由PA=PD=,AB=4,得D(2,0,0),A(﹣2,0,0),P(0,0,),C(2,
空间向量在立体几何中的应用 【知识网络】 空间向量的定义与运算 空间向量运 算几何意义 空间向量的坐标表示及运算 应用空间向量的运算解决立几问题 证明平行、垂直 求空间角与距离 【考点梳理】 要点一、空间向量 1.空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。要点诠释: ⑴空间的一个平移就是一个向量。 ⑵向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量。相等向量只考虑其定义要素:方向,大小。 ⑶空间的两个向量可用同一平面内的两条有向线段来表示。2.共线向量 (1)定义:如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共 线向量或平行向量.a 平行于b 记作b a //.当我们说向量a 、b 共线(或a //b )时,表示a 、b 的有向线段所在的直线可能是同一直线,也可能是平行直线. (2)共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 的充要条件是存在实数λ,使a =λb 。 3.向量的数量积 (1)定义:已知向量,a b ,则||||cos ,a b a b ??<> 叫做,a b 的数量积,记作a b ? ,即a b ?= ||||cos ,a b a b ??<> 。 (2)空间向量数量积的性质: ①||cos ,a e a a e ?=<> ;②0a b a b ⊥??= ;③2||a a a =? . (3)空间向量数量积运算律: ①()()()a b a b a b λλλ?=?=? ;②a b b a ?=? (交换律);③()a b c a b a c ?+=?+? (分配律)。
4.空间向量基本定理 如果三个向量,,a b c 不共面,那么对空间任一向量p ,存在一个唯一的有序实数组,,x y z ,使p xa yb zc =++ 。若三向量,,a b c 不共面,我们把{,,}a b c 叫做空间的一个基底,,,a b c 叫 做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。 5.空间直角坐标系: (1)若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位正交基底,用 {,,}i j k 表示; (2)在空间选定一点O 和一个单位正交基底{,,}i j k ,以点O 为原点,分别以,,i j k 的方向为正方向建立三条数轴:x 轴、y 轴、z 轴,它们都叫坐标轴.我们称建立了一个空间直角 坐标系O xyz -,点O 叫原点,向量,,i j k 都叫坐标向量.通过每两个坐标轴的平面叫坐标平面,分别称为xOy 平面,yOz 平面,zOx 平面; 6.空间直角坐标系中的坐标 在空间直角坐标系O xyz -中,对空间任一点A ,存在唯一的有序实数组(,,)x y z ,使 OA xi yj zk =++ ,有序实数组(,,)x y z 叫作向量A 在空间直角坐标系O xyz -中的坐标,记 作(,,)A x y z ,x 叫横坐标,y 叫纵坐标,z 叫竖坐标. 7.空间向量的直角坐标运算律: (1)若111(,,)A x y z ,222(,,)B x y z ,则212121(,,)AB x x y y z z =--- . 一个向量在直角坐标系中的坐标等于表示这个向量的有向线段的终点的坐标减去起点的坐标。 (2)若123(,,)a a a a = ,123(,,)b b b b = ,则 112233(,,)a b a b a b a b +=+++ ,112233(,,)a b a b a b a b -=--- ,123(,,)()a a a a R λλλλλ=∈ ,112233a b a b a b a b ?=++ ,112233//,,()a b a b a b a b R λλλλ?===∈ ,1122330a b a b a b a b ⊥?++= ; ||a == ||b == . 夹角公式:cos ||||a b a b a b ??==? .
向量法解立体几何 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系 线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离
点()111,,P x y z 与()222,,Q x y z 的 距离为PQ =u u u r 2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离: 方法:在直线上取一点(),Q x y , 则向量PQ u u u r 在法向量(),n A B =上的射影 PQ n n ?u u u r = 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ u u u r , 计算平面α的法向量n , 计算PQ u u u r 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤: ① 先求线的方向向量与面的法向量的夹角,若为锐角角即可,若为钝角,则取其补角; ②再求其余角,即是线面的夹角. 3.面面夹角(二面角) 若两面的法向量一进一出,则二面角等于两法向量的夹角;法
10 第七部分 立体几何与空间向量 一、知识梳理 (一)基本知识梳理:见《步步高》文科P123—124 ;理科P135—137 . (二)要点梳理: 1。平面的基本性质是高考中立体几何的重点容.要掌握平面的基本性质,特别注意:不共线的三点确定一个平面.考察点和平面的位置关系时,要注意讨论点在平面的同侧还是两侧,会根据不同的情况作出相应的图形. [例]已知线段AB 长为3,A 、B 两点到平面α的距离分别为1与2,则AB 所在直线与平面α所成角的大小为_____; 解析:要注意到点A 、B 是平面α同侧还是在平面α的两侧的情况.当A 、B 在平面α的同侧时,AB 所在直线与平面α所成角大小为31arcsin ;当A 、B 在平面α的两侧时,AB 所在直线与平面α所成角为 2 π. 2。线面关系中三类平行的共同点是“无公共点”;三类垂直的共同点是“成角90°”.线面平行、面面平行,最终化归为线线平行;线面垂直、面面垂直,最终化归为线线垂直. [例]已知平面βα,,直线b a ,.有下列命题:(1) βαβα////a a ?????;(2)αββα//a a ?? ?? ⊥⊥ (3)βαβα////??????⊥⊥b a b a ;(4)βαβα////??? ? ?? ??b a b a .其中正确的命题序号是______. 解析:立体几何中的符号语言所描述的问题是高考命题中的重点,基本上每年的高考在选择或填空题中都会有涉及,要充分理解符号语言所体现的几何意义.(1)体现的是两平面平行的一个性质:若两平面平行,则一个平面的任一直线与另一平面平行.(2)要注意的是直线a 可能在平面α.(3)注意到直线与平面之间的关系:若两平行直线中的一条与一个平面垂直,则另一条也与这个平面垂直.且垂直于同一直线的两个平面平行.(4)根据两平面平行的判定知,一个平面两相交直线与另一个平面平行,两平面才平行.由此知:正确的命题是(1)与(3). 3。直线与平面所成角的围是]2, 0[π ;两异面直线所成角的围是]2 ,0(π .一般情况下,求二面角往往是指定 的二面角,若是求两平面所成二面角只要求出它们的锐角(直角)情况即可. [例]设A 、B 、C 、D 分别表示下列角的取值围:(1)A 是直线倾斜角的取值围;(2)B 是锐角;(3)C 是直线与平面所成角的取值围;(4)D 是两异面直线所成角的取值围.用“?”把集合A 、B 、C 、D 连接起来得到___. (答案:A C D B ???) 4。立体几何中的计算主要是角、距离、体积、面积的计算.两异面直线所成角、直线与平面所成角的计算是重点.求两异面直线所成角可以利用平移的方法将角转化到三角形中去求解,也可以利用空间向量的方法,特别要注意的是两异面直线所成角的围.当求出的余弦值为a 时,其所成角的大小应为||arccos a . [例]正方体ABCD -A 1B 1C 1D 1中,E 是AB 中点,则异面直线DE 与BD 1所成角的大小为_____. (答案:515 arccos ) 特别需要注意的是:两向量所成的角是两向量方向所成的角,它与两向量所在的异面直线所成角的概念是 不一样的.本题中的向量1BD 与所成的角大小是两异面直线DE 与BD 1所成角的补角. 5。直线与平面所成角的求解过程中,要抓住直线在平面上的射影,转化到直角三角形中去求解.点到平面的距离的求解可以利用垂线法,也可以利用三棱锥的体积转化. C A 1 B 1 C 1 E
已知两异面直线 b a,,,,, A B a C D b ∈∈,则异面直线所成的角θ为:cos AB CD AB CD θ? = u u u r u u u r u u u r u u u r 例题 【空间向量基本定理】 例1.已知矩形ABCD,P为平面ABCD外一点,且PA⊥平面ABCD,M、N分别为PC、PD上的点,且M分成定比2,N分PD成定比1,求满足的实数x、y、z的值。 分析;结合图形,从向量出发,利用向量运算法则不断进行分解,直到全部向量都用、、表示出来,即可求出x、y、z的值。 如图所示,取PC的中点E,连接NE,则。 点评:选定空间不共面的三个向量作基向量,并用它们表示出指定的向量,是用向量解决立体几何问题的一项基本功,要结合已知和所求,观察图形,联想相关的运算法则和公式等,就近表示所需向量。再对照目标,将不符合目标要求的向量当作新的所需向量,如此继续下去,直到所有向量都符合目标要求为止,这就是向量的分解。有分解才有组合,组合是分解的表现形式。空间向量基本定理恰好说明,用空间三个不共面的向量组可以表示出空间任意一个向量,而且a,b,c的系数是惟一的。 【利用空间向量证明平行、垂直问题】 例2.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB于点F。 (1)证明:PA方形ABCD—中,E、F分别是,的中点,求:(1)异面直线AE与CF所成角的余弦值; (2)二面角C—AE—F的余弦值的大小。
点评:(1)两条异面直线所成的角可以借助这两条直线的方向向量的夹角求得,即。 (2)直线与平面所成的角主要可以通过直线的方向向量与平面的法向量的夹角求得,即 或 (3)二面角的大小可以通过该二面角的两个面的法向量的夹角求得,它等于两法向量的夹角或其补角。 【用空间向量求距离】 例4.长方体ABCD —中,AB=4,AD=6,,M 是A 1C 1的中点,P 在线段BC 上,且|CP|=2,Q 是DD 1的中点, 求: (1)异面直线AM 与PQ 所成角的余弦值; (2)M 到直线PQ 的距离; (3)M 到平面AB 1P 的距离。 本题用纯几何方法求解有一定难度,因此考虑建立空间直角坐标系,运用向量坐标法来解决。利用向量的模和夹角求空间的线段长和两直线的夹角,在新高考试题中已多次出现,但是利用向量的数量积来求空间的线与线之间的夹角和距离,线与面、面与面之间所成的角和距离还涉及不深,随着新教材的推广使用,这一系列问题必将成为高考命题的一个新的热点。现列出几类问题的解决方法。 (1)平面的法向量的求法:设,利用n 与平面内的两个向量a ,b 垂直,其数量积为零,列出两个三元 一次方程,联立后取其一组解。 (2)线面角的求法:设n 是平面的一个法向量,AB 是平面 的斜线l 的一个方向向量,则直线与平面 所成 角为n AB n AB ??= θθsin 则 (3)二面角的求法:①AB,CD 分别是二面角 的两个面内与棱l 垂直的异面直线,则二面角的大小为
空间向量与立体几何 1, 如图,在四棱锥V-ABCD中,底面ABCD是正方形,侧面VAD是正三角形,平面VADL底面ABC (1)证明AB丄平面VAD (2)求面VAD与面VDB所成的二面角的大小 2, 如图所示,在四棱锥P—ABCD中,底面ABCD为矩形,侧棱PA丄底面ABCD AB骑, BC=1 , PA=2, E为PD的中点. (1)求直线AC与PB所成角的余弦值; (2)在侧面PAB内找一点N使NE!平面PAC并求出N点到AB和AP的距 离.(易错点,建系后,关于N点的坐标的设法,也是自己的弱项)
3. 如图,在长方体 ABCD-ABCD 中,AD=AA=1, AB=2,点E 在棱 AB 上移动. 证明:DE 丄AD; 当E 为AB 的中点时,求点 A 到面ECD 的距离; 7T AE 等于何值时,二面角 D — EC- D 的大小为-(易错点:在找平面DEC 的法向量的时候,本 来法向量就己经存在了 ,就不必要再去找,但是我认为去找应该没有错吧 ,但法向量找出来了 , 和 那个己经存在的法向量有很大的差别 ,而且,计算结果很得杂,到底问题出在哪里?) 4. 如图,直四棱柱 ABCD — A I B I C I D I 中,底面ABCD 是等腰梯形,AB // CD , AB = 2DC =2, E 为BD i 的中点,F 为AB 的中点,/ DAB = 60° (1)求证:EF //平面 ADD 1A 1; ⑵若BB 1 ~2-,求A 1F 与平面DEF 所成角的正弦值. N : 5 题到 11 题都是运用基底思想解题 5. 空间四边形 ABCD 中, AB=BC=CD AB 丄BC, BC 丄CD , AB 与CD 成60度角,求AD 与BC 所 成角的大小。 (1) (2) (3) A B
向量法解立体几何 引言 立体几何的计算和证明常常涉及到二大问题:一是位置关系,它主要包括线线垂直,线面垂直,线线平行,线面平行;二是度量问题,它主要包括点到线、点到面的距离,线线、线面所成角,面面所成角等。教材上讲的比较多的主要是用向量证明线线、线面垂直及计算线线角,而如何用向量证明线面平行,计算点到平面的距离、线面角及面面角的例题不多,给老师对这部分内容的教学及学生解有关这部分内容的题目造成一定的困难,下面主要就这几方面问题谈一下自己的想法,起到一个抛砖引玉的作用。 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系
线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离 点()111,,P x y z 与()222,,Q x y z 的 距离为(PQ x =2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离: 方法:在直线上取一点(),Q x y , 则向量PQ 在法向量 (),n A B =上的射影PQ n n ?= 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ , 计算平面α的法向量n , 计算PQ 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤:
空间向量与立体几何 一、知识网络: 二.考纲要求: (1)空间向量及其运算 ① 经历向量及其运算由平面向空间推广的过程; ② 了解空间向量的概念,了解空间向量的基本定理及其意义,掌握空间向量的正交分解及其坐标表示; ③ 掌握空间向量的线性运算及其坐标表示; ④ 掌握空间向量的数量积及其坐标表示,能运用向量的数量积判断向量的共线与垂直。 (2)空间向量的应用 ① 理解直线的方向向量与平面的法向量; ② 能用向量语言表述线线、线面、面面的垂直、平行关系; ③ 能用向量方法证明有关线、面位置关系的一些定理(包括三垂线定理); ④ 能用向量方法解决线线、线面、面面的夹角的计算问题,体会向量方法在研究几何问题中的作用。 三、命题走向 本章内容主要涉及空间向量的坐标及运算、空间向量的应用。本章是立体几何的核心内容,高考对本章的考查形式为:以客观题形式考查空间向量的概念和运算,结合主观题借助空间向量求夹角和距离。 预测10年高考对本章内容的考查将侧重于向量的应用,尤其是求夹角、求距离,教材上淡化了利用空间关系找角、找距离这方面的讲解,加大了向量的应用,因此作为立体几何解答题,用向量法处
理角和距离将是主要方法,在复习时应加大这方面的训练力度。 第一课时 空间向量及其运算 一、复习目标:1.理解空间向量的概念;掌握空间向量的加法、减法和数乘; 2.了解空间向量的基本定理; 3.掌握空间向量的数量积的定义及其性质;理解空间向量的夹角的概念;掌握空间向量的数量积的概念、性质和运算律;了解空间向量的数量积的几何意义;能用向量的数量积判断向量的共线与垂直。 二、重难点:理解空间向量的概念;掌握空间向量的运算方法 三、教学方法:探析类比归纳,讲练结合 四、教学过程 (一)、谈最新考纲要求及新课标高考命题考查情况,促使积极参与。 学生阅读复资P128页,教师点评,增强目标和参与意识。 (二)、知识梳理,方法定位。(学生完成复资P128页填空题,教师准对问题讲评)。 1.空间向量的概念 向量:在空间,我们把具有大小和方向的量叫做向量。如位移、速度、力等。 相等向量:长度相等且方向相同的向量叫做相等向量。 表示方法:用有向线段表示,并且同向且等长的有向线段表示同一向量或相等的向量。 说明:①由相等向量的概念可知,一个向量在空间平移到任何位置,仍与原来的向量相等,用同向且等长的有向线段表示;②平面向量仅限于研究同一平面内的平移,而空间向量研究的是空间的平移。 2.向量运算和运算率 说明:①引导学生利用右图验证加法交换率,然后推广到首尾相接的若干向量之和;②向量加法的平行四边形法则在空间仍成立。 3.平行向量(共线向量):如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向量 叫做共线向量或平行向量。a 平行于b 记作a ∥b 。 注意:当我们说a 、b 共线时,对应的有向线段所在直线可能是同一直线,也可能是平行直线;当 我们说a 、b 平行时,也具有同样的意义。 共线向量定理:对空间任意两个向量a (a ≠)、b ,a ∥b 的充要条件是存在实数λ使b =λa (1)对于确定的λ和a ,b =λa 表示空间与a 平行或共线,长度为 |λa |,当λ>0时与a 同向, 当λ<0时与a 反向的所有向量。 (3)若直线l ∥a ,l A ∈,P 为l 上任一点,O 为空间任一点,下面根据上述定理来推导的表达式。
空间向量在立体几何中的应用 【重要知识】 一、求平面法向量的方法与步骤: 1、选向量:求平面的法向量时,要选取两个相交的向量,如, 2、设坐标:设平面法向量的坐标为),,(z y x = 3、解方程:联立方程组?????=?=?0 0,并解方程组 4、定结论:求出的法向量中三个坐标不就是具体的数值,而就是比例关系。设定某个坐标为常 数得到其她坐标 二、利用向量求空间角: 1、求异面直线所成的角: 设b a ,为异面直线,点C A ,为a 上任意两点,点D B ,为b 上任意两点,b a ,所成的角为θ, 则=θcos 【注】由于异面直线所成的角θ的范围就是:?≤=<21,n n θ或><-21,n n π, 其中21,cos n n < 三、利用向量求空间距离: 1、求点到平面的距离 设平面α的法向量为,,α?A α∈B ,则点A 到平面α 2、求两条异面直线的距离
设21,l l 就是两条异面直线,n 就是公垂线段AB 的方向向量,D C ,分别为21,l l 上的任意两点,则21l l 与的距离为n n CD AB ?= 【重要题型】 1、(2012广东,理)如图所示,在四棱锥ABCD P -中,底面ABCD 为矩形,ABCD PA 平面⊥,点E 在线段PC 上,BDE PC 平面⊥ (1)证明:PAC BD 平面⊥ (2)若2,1==AD PA ,求二面角A PC B --的正切值 2、(2013广东,理)如图①,在等腰三角形ABC 中,?=∠90A ,6=BC ,E D ,分别就是AB AC ,上的 点,2==BE CD ,O 为BC 的中点。将ADE ?沿 DE 折起,得到如图②所示的四棱锥BCDE A -',其中 3='O A 。 (1)证明:BCDE O A 平面⊥' (2)求二面角B CD A --'的平面角的余弦值 3、(2009广东,理)如图,已知正方体 1111D C B A ABCD -的棱长为2,点 E 就是正方形11B BCC 的中心,点 G F ,分别就是棱11D C 、1AA 的中 点,设,1E 1G 分别就是点G E ,在平面11D DCC 内的正投影。 (1)求以E 为顶点,以四边形FGAE 在平面11D DCC 内的正投影为底面边界的棱锥的体积; (2)证明:直线11FEE FG 平面⊥; (3)求异面直线11G E 与EA 所成角的正弦值。
立体几何空间向量练习 1.在边长是2的正方体ABCD﹣A1B1C1D1中,E,F分别为AB,A1C的中点.应用空间向量方法求解下列问题. (1)求EF的长 (2)证明:EF∥平面AA1D1D; (3)证明:EF⊥平面A1CD. 2.如图,在直三棱柱A1B1C1﹣ABC中,AB⊥AC,AB=AC=2,AA1=4,点D是BC的中点.(1)求异面直线A 1B与C1D所成角的余弦值; (2)求平面ADC1与平面A1BA所成的锐二面角(是指不超过90°的 角)的余弦值.
3.如图所示,在四棱锥P﹣ABCD中,底面ABCD为矩形,P A⊥平面ABCD,点E在线段PC上,PC⊥平面BDE,设P A=1,AD=2. (1)求平面BPC的法向量; (2)求二面角B﹣PC﹣A的正切值. 4.如图,在长方体ABCD﹣A1B1C1D1中,M为BB1上一点,已知 BM=2,CD=3,AD=4,AA1=5. (1)求直线A1C和平面ABCD的夹角; (2)求点A到平面A1MC的距离.
5.如图,在四棱锥P﹣ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB ∥CD,AB=2,AD=CD=1,E是PB的中点. (1)求证:平面EAC⊥平面PBC; (2)若二面角P﹣AC﹣E的余弦值为, 求直线P A与平面EAC所成角的正弦值. 6.如图,在正三棱柱ABC﹣A1B1C1中,D为AC的中点. (1)证明:AB1∥平面BC1D; (2)证明:BD⊥平面AA1C1C; (3)若AA1=AB,求直线BC1与平面AA1C1C所成角的正弦值.
7.如图,四棱锥P﹣ABCD的底面为正方形,PD⊥底面ABCD.设平面P AD与平面PBC的交线为l. (1)证明:l⊥平面PDC; (2)已知PD=AD=1,Q为l上的点,QB=, 求PB与平面QCD所成角的正弦值. 8.如图,在正方体ABCD﹣A1B1C1D1中,E为BB1的中点. (Ⅰ)求证:BC1∥平面AD1E; (Ⅱ)求直线AA1与平面AD1E所成角的正弦值.
空间向量与立体几何知识点归纳总结 一.知识要点。 1. 空间向量的概念:在空间,我们把具有大小和方向的量叫做向量。 注:(1)向量一般用有向线段表示同向等长的有向线段表示同一或相等 的向量。 (2)向量具有平移不变性 2. 空间向量的运算。 定义:与平面向量运算一样,空间向量的加法、减法与数乘运算如下(如图)。 OB OA AB a b =+=+u u u r u u u r u u u r v r ;BA OA OB a b =-=-u u u r u u u r u u u r r r ;()OP a R λλ=∈u u u r r 运算律:⑴加法交换律:a b b a ? ??ρ+=+ ⑵加法结合律:)()(c b a c b a ? ???ρ?++=++ ⑶数乘分配律:b a b a ? ???λλλ+=+)( 运算法则:三角形法则、平行四边形法则、平行六面体法则 3. 共线向量。 (1)如果表示空间向量的有向线段所在的直线平行或重合,那么这些向 量也叫做共线向量或平行向量,a ρ 平行于b ρ,记作b a ρ?//。 (2)共线向量定理:空间任意两个向量a ρ、b ρ (b ρ≠0ρ), a ρ b ρa ρb ρλ=)1(=++=y x y x 其中 a ± 共面向量 (1)定义:一般地,能平移到同一平面内的向量叫做共面向量。 说明:空间任意的两向量都是共面的。
(2)共面向量定理:如果两个向量,a b r r 不共线,p r 与向量,a b r r 共面的条件 是存在实数,x y 使p xa yb =+r r r 。 (3)四点共面:若A 、B 、C 、P 四点共面<=>y x AP += <=>)1(=++++=z y x OC z OB y OA x OP 其中 5. 空间向量基本定理:如果三个向量,,a b c r r r 不共面,那么对空间任一向量 p r ,存在一个唯一的有序实数组,,x y z ,使p xa yb zc =++r r r r 。 若三向量,,a b c r r r 不共面,我们把{,,}a b c r r r 叫做空间的一个基底,,,a b c r r r 叫 做基向量,空间任意三个不共面的向量都可以构成空间的一个基底。 推论:设,,,O A B C 是不共面的四点,则对空间任一点P ,都存在唯一的三 个有序实数,,x y z ,使OP xOA yOB zOC =++u u u r u u u r u u u r u u u r 。 6. 空间向量的直角坐标系: (1)空间直角坐标系中的坐标: 在空间直角坐标系O xyz -中,对空间任一点A ,存在唯一的有序实数组 (,,)x y z ,使++=,有序实数组(,,)x y z 叫作向量A 在空间直角坐 标系O xyz -中的坐标,记作(,,)A x y z ,x 叫横坐标,y 叫纵坐标,z 叫竖坐标。 注:①点A (x,y,z )关于x 轴的的对称点为(x,-y,-z),关于xoy 平面的对称点为(x,y,-z).即点关于什么轴/平面对称,什么坐标不变,其余的分坐标均相反。②在y 轴上的点设为(0,y,0),在平面yOz 中的点设为(0,y,z) (2)若空间的一个基底的三个基向量互相垂直,且长为1,这个基底叫单位 正交基底,用{,,}i j k r r r 表示。空间中任一向量k z j y i x a ++==(x,y,z ) (3)空间向量的直角坐标运算律: ①若123(,,)a a a a =r ,123(,,)b b b b =r ,则112233(,,)a b a b a b a b +=+++r r ,
. 1.如图,在四棱锥P﹣ABCD中,底面ABCD为正方形,平面PAD⊥平面ABCD, 点M在线段PB上,PD∥平面MAC,PA=PD=,AB=4. 的中点;PB(1)求证:M为 的大小;A2)求二面角B﹣PD﹣( 所成角的正弦值.BDP(3)求直线MC与平面 【分析】(1)设AC∩BD=O,则O为BD的中点,连接OM,利用线面平行的性质证明OM∥PD,再由平行线截线段成比例可得M为PB的中点; (2)取AD中点G,可得PG⊥AD,再由面面垂直的性质可得PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG,再证明OG⊥AD.以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系,求出平面PBD与平面PAD的一个法向量,由两法向量所成角的大小可得二面角B﹣PD﹣A的大小; (3)求出的坐标,由与平面PBD的法向量所成角的余弦值的绝对值可得直线MC与平面BDP所成角的正弦值. 【解答】(1)证明:如图,设AC∩BD=O,
∵ABCD为正方形,∴O为BD的中点,连接OM, ∵PD∥平面MAC,PD?平面PBD,平面PBD∩平面AMC=OM, ∴PD∥OM,则,即M为PB的中点; (2)解:取AD中点G, . . ∵PA=PD,∴PG⊥AD, ∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD, ∴PG⊥平面ABCD,则PG⊥AD,连接OG,则PG⊥OG, 由G是AD的中点,O是AC的中点,可得OG∥DC,则OG⊥AD. 以G为坐标原点,分别以GD、GO、GP所在直线为x、y、z轴距离空间直角坐标系, 由PA=PD=,AB=4,得D(2,0,0),A(﹣2,0,0),P(0,0,),C (2,4,0),B(﹣2,4,0),M(﹣1,2,), ,.
立体几何空间向量知识点总结 知识网络: 知识点拨: 1、空间向量的概念及其运算与平面向量类似,向量加、减法的平行四边形法则,三角形法则以及相关的运算律仍然成立.空间向量的数量积运算、共线向量定理、共面向量定理都是平面向量在空间中的推广,空间向量基本定理则是向量由二维到三维的推广. 2、当a 、b 为非零向量时.0a b a b ?=?⊥是数形结合的纽带之一,这是运用空间向量研究线线、线面、面面垂直的关键,通常可以与向量的运算法则、有关运算律联系来解决垂直的论证问题. 3、公式cos ,a b a b a b ?<>= ?是应用空间向量求空间中各种角的基础,用这个公式可以求两异面直线所成的角(但要注意两异面直线所成角与两向量的夹角在取值围上的区别),再结合平面的法向量,可以求直线与平面所成的角和二面角等. 4、直线的方向向量与平面的法向量是用来描述空间中直线和平面的相对位置的重要概念,通过研究方向向量与法向量之间的关系,可以确定直线与直线、直线与平面、平面与平面等的位置关系以及有关的计算问题. 5、用空间向量判断空间中的位置关系的常用方法 (1)线线平行 证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2)线线垂直 证明两条直线垂直,只需证明两条直线的方向向量垂直,即0a b a b ?=?⊥.
(3)线面平行 用向量证明线面平行的方法主要有: ①证明直线的方向向量与平面的法向量垂直; ②证明可在平面找到一个向量与直线方向向量是共线向量; ③利用共面向量定理,即证明可在平面找到两不共线向量来线性表示直线的方向向量.(4)线面垂直 用向量证明线面垂直的方法主要有: ①证明直线方向向量与平面法向量平行; ②利用线面垂直的判定定理转化为线线垂直问题. (5)面面平行 ①证明两个平面的法向量平行(即是共线向量); ②转化为线面平行、线线平行问题. (6)面面垂直 ①证明两个平面的法向量互相垂直; ②转化为线面垂直、线线垂直问题. 6、运用空间向量求空间角 (1)求两异面直线所成角 利用公式cos, a b a b a b ? <>= ? , 但务必注意两异面直线所成角θ的围是 0, 2 π ?? ???, 故实质上应有:cos cos,a b θ=<> . (2)求线面角 求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量,通过数量积求出直线与平面所成角;另一种方法是借助平面的法向量,先求出直线方向向量与平面法向量的夹角φ,即可求出直线与平面所成的角θ,其关系是sinθ=| cosφ|.(3)求二面角 用向量法求二面角也有两种方法:一种方法是利用平面角的定义,在两个面先求出与棱垂直的两条直线对应的方向向量,然后求出这两个方向向量的夹角,由此可求出二面角的大小;另一种方法是转化为求二面角的两个面的法向量的夹角,它与二面角的大小相等或互补.7、运用空间向量求空间距离 空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离. (1)点与点的距离 点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模. (2)点与面的距离 点面距离的求解步骤是: ①求出该平面的一个法向量; ②求出从该点出发的平面的任一条斜线段对应的向量; ③求出法向量与斜线段向量的数量积的绝对值再除以法向量的模,即得要求的点面距离. 备考建议:
微专题64 利用空间向量解立体几何问题 一、基础知识 (一)刻画直线与平面方向的向量 1、直线:用直线的方向向量刻画直线的方向问题,而方向向量可由直线上的两个点来确定 例如:()()2,4,6,3,0,2A B ,则直线AB 的方向向量为()1,4,4AB =-- 2、平面:用平面的法向量来刻画平面的倾斜程度,何为法向量?与平面α垂直的直线称为平面α的法线,法线的方向向量就是平面α的法向量,如何求出指定平面的法向量呢? (1)所需条件:平面上的两条不平行的直线 (2)求法:(先设再求)设平面α的法向量为(),,n x y z =,若平面上所选两条直线的方向向量分别为()()111222,,,,,a x y z b x y z ==,则可列出方程组: 1112220 x y z x y x y z x y z z ++=?? ++=? 解出,,x y z 的比值即可 例如:()()1,2,0,2,1,3a b ==,求,a b 所在平面的法向量 解:设(),,n x y z =,则有20230x y x y z +=??++=? ,解得:2x y z y =-??=? ::2:1:1x y z ∴=- ()2,1,1n ∴=- (二)空间向量可解决的立体几何问题(用,a b 表示直线,a b 的方向向量,用,m n 表示平面 ,αβ的法向量) 1、判定类 (1)线面平行:a b a b ?∥∥ (2)线面垂直:a b a b ⊥?⊥ (3)面面平行:m n αβ?∥∥ (4)面面垂直:m n αβ⊥?⊥ 2、计算类: (1)两直线所成角:cos cos ,a b a b a b θ?==
用空间向量判断空间中的位置关系的常用方法 (1)线线平行 证明两条直线平行,只需证明两条直线的方向向量是共线向量. (2)线线垂直 证明两条直线垂直,只需证明两条直线的方向向量垂直,即0a b a b ?=?⊥. (3)线面平行 用向量证明线面平行的方法主要有: ①证明直线的方向向量与平面的法向量垂直; ②证明可在平面内找到一个向量与直线方向向量是共线向量; ③利用共面向量定理,即证明可在平面内找到两不共线向量来线性表示直线的方向向量. (4)线面垂直 用向量证明线面垂直的方法主要有: ①证明直线方向向量与平面法向量平行; ②利用线面垂直的判定定理转化为线线垂直问题. (5)面面平行 ①证明两个平面的法向量平行(即是共线向量); ②转化为线面平行、线线平行问题. (6)面面垂直 ①证明两个平面的法向量互相垂直; ②转化为线面垂直、线线垂直问题. 6、运用空间向量求空间角 (1)求两异面直线所成角 利用公式cos ,a b a b a b ?<>= ?, 但务必注意两异面直线所成角θ的范围是0,2π?? ? ??, 故实质上应有:cos cos ,a b θ=<> . (2)求线面角 求直线与平面所成角时,一种方法是先求出直线及射影直线的方向向量,通过数量积求出直线与平面所成角;另一种方法是借助平面的法向量,先求出直线方向向量与平面法向量的夹角φ,即可求出直线与平面所成的角θ,其关系是sin θ=| cos φ|. (3)求二面角 用向量法求二面角也有两种方法:一种方法是利用平面角的定义,在两个面内先求出与棱垂直的两条直线对应的方向向量,然后求出这两个方向向量的夹角,由此可求出二面角的大小;另一种方法是转化为求二面角的两个面的法向量的夹角,它与二面角的大小相等或互补. 7、运用空间向量求空间距离 空间中的各种距离一般都可以转化为求点与点、点与线、点与面的距离. (1)点与点的距离 点与点之间的距离就是这两点间线段的长度,因此也就是这两点对应向量的模. (2)点与面的距离 点面距离的求解步骤是: ①求出该平面的一个法向量;
空间向量与立体几何典型例题 一、选择题: 1.(2008全国Ⅰ卷理)已知三棱柱111ABC A B C -的侧棱与底面边长都相等,1A 在底面ABC 内的射影为ABC △的中心,则1AB 与底面ABC 所成角的正弦值等于( C ) A. 13 D.2 3 1、解:C.由题意知三棱锥1A ABC -为正四面体,设棱长为a , 则1AB =, 棱柱的高 1 3AO a ===(即点1B 到底面ABC 的距离),故1AB 与底面ABC 所成角的正弦值为113 AO AB =、 另解:设1,,AB AC AA u u u r u u u r u u u r 为空间向量的一组基底,1,,AB AC AA u u u r u u u r u u u r 的两两间的夹角为0 60 长度均为a ,平面ABC 的法向量为111133 OA AA AB AC =--u u u r u u u r u u u r u u u r ,11AB AB AA =+u u u r u u u r u u u r 211112,,33 OA AB a OA AB ?===u u u r u u u r u u u r u u u r 则1AB 与底面ABC 所成角的正弦值为11 1 1OA AB AO AB ?=u u u u r u u u r u u u r u u u r 、 二、填空题: 1.(2008全国Ⅰ卷理)等边三角形ABC 与正方形ABDE 有一公共边AB ,二面角C AB D -- M N ,分别就是AC BC ,的中点,则EM AN ,所成角的余弦值等于 6 1 . 1、答案: 1 6 、设2AB =,作CO ABDE ⊥面, OH AB ⊥,则CH AB ⊥,CHO ∠为二面角C AB D -- cos 1CH OH CH CHO ==?∠=,结合等边三角形ABC 与正方形ABDE 可知此四棱锥为正四棱锥,则AN EM ==11(),22AN AC AB EM AC AE =+=-u u u r u u u r u u u r u u u u r u u u r u u u r , 11()()22AN EM AB AC AC AE ?=+?-=u u u r u u u u r u u u r u u u r u u u r 12 故EM AN ,所成角的余弦值1 6 AN EM AN EM ?=u u u r u u u u r u u u r u u u u r 另解:以O 为坐标原点,建立如图所示的直角坐标系, 则点(1,1,0),(1,1,0),(1,1,0),A B E C ----, 1111(,,(,,)222222 M N ---,
向量法解立体几何 一、基本工具 1.数量积: cos a b a b θ?= 2.射影公式:向量a 在b 上的射影为 a b b ? 3.直线0Ax By C ++=的法向量为 (),A B ,方向向量为 (),B A - 4.平面的法向量(略) 二、用向量法解空间位置关系 1.平行关系 线线平行?两线的方向向量平行 线面平行?线的方向向量与面的法向量垂直 面面平行?两面的法向量平行 2.垂直关系 线线垂直(共面与异面)?两线的方向向量垂直 线面垂直?线与面的法向量平行 面面垂直?两面的法向量垂直 三、用向量法解空间距离 1.点点距离 点()111,,P x y z 与()222,,Q x y z 的 距离为(PQ x =2.点线距离 求点()00,P x y 到直线:l 0Ax By C ++=的距离:
方法:在直线上取一点(),Q x y , 则向量PQ 在法向量(),n A B =上的射影PQ n n ? = 即为点P 到l 的距离. 3.点面距离 求点()00,P x y 到平面α的距离: 方法:在平面α上去一点(),Q x y ,得向量PQ , 计算平面α的法向量n , 计算PQ 在α上的射影,即为点P 到面α的距离. 四、用向量法解空间角 1.线线夹角(共面与异面) 线线夹角?两线的方向向量的夹角或夹角的补角 2.线面夹角 求线面夹角的步骤: ① 先求线的方向向量与面的法向量的夹角,若为锐角角即可,若为钝角,则取其补角; ②再求其余角,即是线面的夹角. 3.面面夹角(二面角) 若两面的法向量一进一出,则二面角等于两法向量的夹角;法向量同进同出,则二面角等于法向量的夹角的补角.