
第十二章 结构方程分析
1 1.1 结构方程的表述
2 测度模型的目的是为了检验测度工具的有效性。结构方程模型在测度模型的基础上
3 进一步对变量之间的因果关系进行假设,所以是测度模型与因果模型的一个综合。读者已
4 经在范文中见过这种模型。我们在测度模型的基础上来看结构模型与其相同与不同的地
5 方。
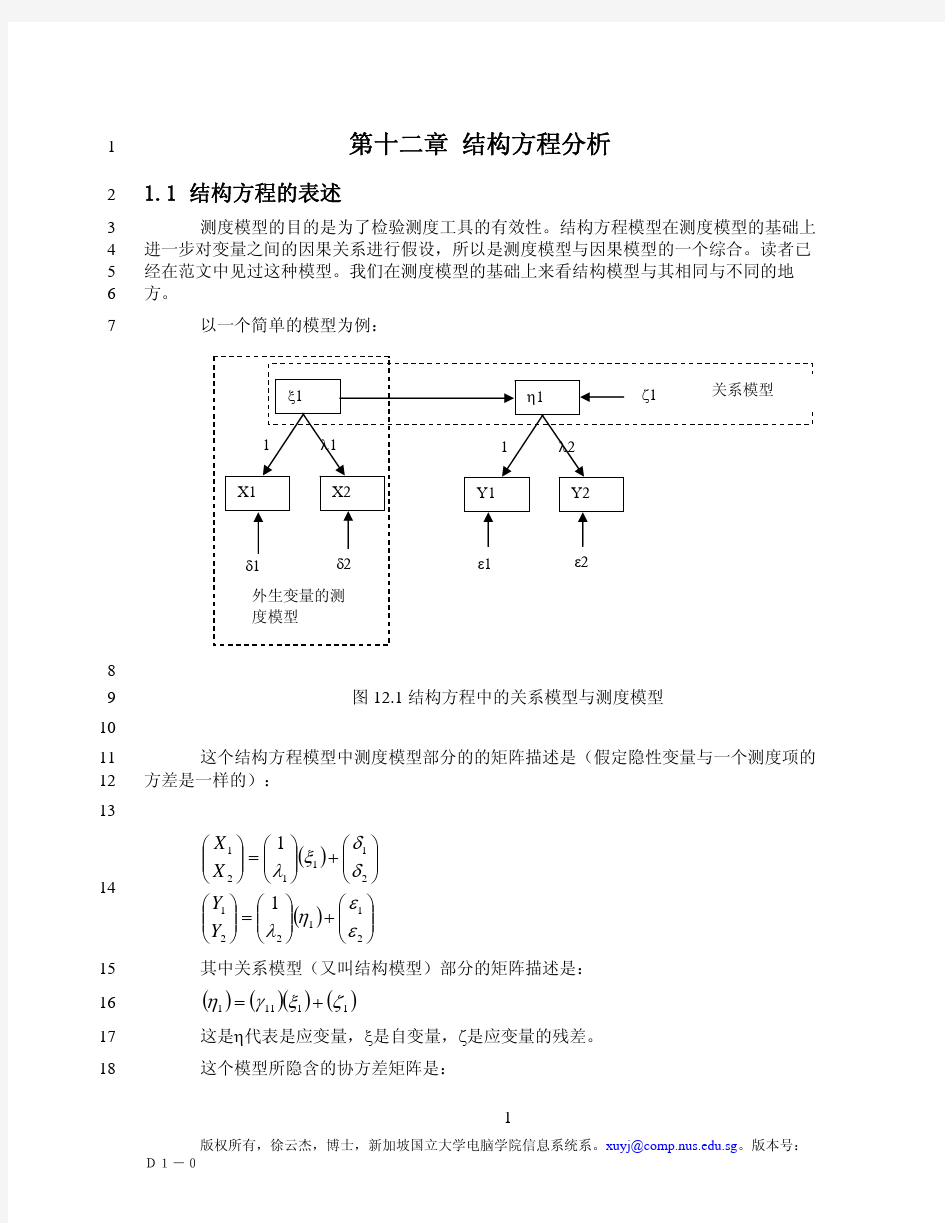
6 以一个简单的模型为例:
7
8 图12.1 结构方程中的关系模型与测度模型
9
10 这个结构方程模型中测度模型部分的的矩阵描述是(假定隐性变量与一个测度项的
11 方差是一样的):
12
13
()()???
?????+????????=???????????
?????+????????=????????21122121112111εεηλδδξλY Y X X
14
其中关系模型(又叫结构模型)部分的矩阵描述是:
15 ()()()()11111ζξγη+=
16 这是η代表是应变量,ξ是自变量,ζ是应变量的残差。 17 这个模型所隐含的协方差矩阵是:
18
??
?
?
??
????????+++++++=)()()()()()()(2112111111112111111111111121111211112
11221111211211111211δφλφλφγλλφγλδφφγλφγεψφγλψφγλεψφγVar Var Var Var θΣ1
所以,要求解的参数是:
2 ()1111111121 ))())( 'ψδδεεφγλλ22Var(Var Var(Var =θ
3 虽然没有明确表示出来,这个模型也假定残差之间的相关系数为零,残差与因子是
4 独立的。这个求解的过程也就是求解参数、使得Σ
? 与Σ或者其样本S 尽量拟合的过程。 5 这个模型可以观察到的样本的协方差矩阵是:
6
?
???
?
??
??????
?=)(),(),(),()
(),(),()(),()(2122212121112121X Var X X Cov Y X Cov Y X Cov X Var Y X Cov Y X Cov Y Var Y Y Cov Y Var S 7
在S 中, 我们有1/2×4×5=9个已知量,我们也有9个未知数在Σ
?中。可以验证一8 个唯一的解存在。如果我们的未知数再多一个,这个模型就是无解的(under identified)。
9 一般地,一个结构方程往往被描述成三个部分: 10 外生变量的测度模型:
11
ξξ'
Φ δδ'Θ ΘΦΛΛΣδ
ξΛX δδ'X X XX X ==+=+=
12
内生变量的测度模型:
13
ηη'
Ψ εε'Θ ΘεΨΛΛΣε
ηΛY ε'Y Y YY Y ==+=+=
14
结构模型:
15 ζΓξΒηη++=
16 这组模型表明,在一组因果关系所组成的方程系统中,一个内生变量即可以是自变
17 量,也可以是应变量。我们把所有受一个方程系统中其它变量影响的变量叫作内生变量,18 把所有不受其它变量影响的叫作外生变量。如果没有明确的指定,在一般情况下,我们假19 定残差之间、残差与因子之间是独立的;我们也假定外生变量之间可以自由相关,但外生
20
变量与内生变量之间、内生变量内部除了理论模型假设的关系外不存在其它关系(也即其1 它的关系是独立的)。所以,这三个部分综合在一起可以描述成:
2 ???
?
????=XX XY
XY YY
ΣΣ
ΣΣθΣ)( 3 其中ΣYY 是内生变量的协方差矩阵估计,ΣXX 是外生变量的协方差矩阵估计,ΣXY 是
4 内生变量与外生变量之间的协方差矩阵估计。正如前面的例子一样,我们可以根据一个理
5 论模型来确定各个子矩阵(比如用ΛX 来描述测度项因子关系,用Γ来表述内生变量与外生
6 变量之间的因果关系,用Β来表示内生变量之间的因果关系)来得到各个协方差矩阵的估
7 计。有了)(θΣ的具体形式,我们就可以用估计方法进行拟合。
8 至此,我们对所用到的符号作一个总结。对于那些想对结构方程有深入理解的读者
9 来讲,熟记这些符号是直接阅读结构方程专业论文所不可缺少的。
10
11 表12.1 结构模型中的矩阵符号
12
希腊字母 矩阵符号 矩阵元素 LISRE 程序中
的代码
直观解释
测度模型
Lambda-X ΛX
λx LX 外生变量与测度项的回归系数矩阵,又叫内生变量的因子载荷
Lambda-Y Λy
λy
LY 内生变量与测度项的回归系数矩阵,内生变量的因子载荷
Theta delta
Θδθδ
TD
外生变量的残差协方差矩阵(当我们假定残差之间有相关性是,残差是一个矩阵)
Theta epsilon Θεθε TE 内生变量的残差协方差矩阵 关系模型
Gamma Γ
γ GA 外生变量与内生变量之间的回归系数矩阵
Beta Β β BE 内生变量与内生变量之间的回归系数矩阵
Phi Φ φ PH 外生变量之间的协方差矩阵 Psi
Ψ ψ PS 内生变量之间的协方差矩阵 Xi (Ksi) -- ξ -- 一列(个)外生变量 Eta -- η -- 一列(个)内生变量
Zeta
--
ζ
--
一列(个)内生变量的残差
13 我们来描述一个更为复杂的模型:
14
1 图12.
2 一个结构方程的路径图
2
3 在这个模型中,首先,我们有两个外生变量与两个内生变量:
4
????????=????
???
?===??????
??=???
?
????=2221112221121112121 ,),()(, ,???φφξξφξηηξξΨΦηξCov V
5
在测度模型中,各个矩阵可以表示成:
6
????
?????
??????
?????====????
???????????
?????====?
??????????????????
?=????
????
????
???
?????=)(00000)(0000)(000)
(00)(0),Cov()( , )(00000)(0000)(000)(0
0)(0),Cov()( 000000 ,000000 6655443322211211116
543216655443322211211116543216252423121116252423121
11
2
121εεεεεθεεθεεεεεεεδδδδδθδδθδδδδδδδλλλλλλλλλλλληηξξεεδδV V V V V V V V V V V V y y y y y y x x x x x x εδY X ΘΘΛΛ 1
以上的矩阵包含了所有需要估计的未知变量,而其它为零的元素则不用估计,因为
2 我们假设(确切地讲是约束)它们为零。细心的读者会注意到,我们忘记了把 λx11、
3 λx42、λy11、λy42约束为1,或者把φ11、φ22、?11、?22约束为1。这样的约束在估计过程中
4 是必要的。以上的矩阵只是表示了一种很可能的未知参数集合。有时候,比如说,研究者
5 要看看X1与X2之间的残差是否有相关性,他可以不约束θδ21为零,而是允许它自由取一
6 个估算的值;这时,我们就多了一个未知的参数。
7 在关系模型中,包含未知参数的矩阵是:
8
???
?????=????????=000 ,0 212112112
121βγγγηηξξΒΓ
9
有了这些矩阵,我们就可以根据式子(?)描述预测中的内生变量与外生变量之内
10
与之间的协方差矩阵。对过参数优化,我们可以得到对样本协方差矩阵的最优估计。这就11 是结构方程求解的过程。
12
1
1.2结构方程求解
2
我们不对结构方程的求解或拟合进行细述。与在检验性因子分析中一样,在结构方3
4
程拟合的过程中存在着多解、唯一解、或无解的情况。只有有解的情况在实际研究中是有
用的。无解的情况意味着对数过多,或者已知的信息太少,比如测度项个数过少。无解也5
6
可能因为一个模型局部的关系过于复杂,局部无解导致整体无解。
7
在对模型进行拟合时,最常用的还是极大似然估计。测度项也被要求符合多元正态
分布。所以对原始数据的正态性检验是必要的。有时候,一个模型在拟合的过程中可能不8
9
收敛。这可能是模型的问题,比如模型过于复杂,或者模型描述中的错误(比如有个因子
10
只有一个测度项,同时我们要求估计这个测度项的残差)。这也可能是数据问题,比如几
11
列数据(测度项)之间是线性相关的。样本过小也会导致无法收敛。一般,在行为研究
12
中,样本量最好在200以上。小于150的研究在现在很难被接收。当然样本量的大小也因
13
模型的复杂程度不同而不同。一般,样本量应该是测度项个数的至少5倍,理想的情况是
10倍以上。
14
1.3SIMPLIS编程
15
16
在实际科研中,知道结构方程的原理的目的是为了能够采用合理的步骤进行实际模
17
型拟合。可以进行结构方程建模并拟合的统计软件有很多,比如LISREL、AMOS、
18
EQS、MPLUS等。其中最常用的是LISREL。在LISREL这个软件中有三种编程语言:19
PRELIS是用来作数据处理或简单运算,比如作一些回归分析、计算一个样本的协方差矩阵;LISREL是一种矩阵编程语言,它用矩阵的方式来定义我们在前面提到的测度项与构
20
21
件、构件之间的关系,然后采用一个估计方法(比如极大似然估计)进行模型拟合;
22
SIMPLIS是一种简化的结构方程编程语言,适合行为研究者用。我们以SIMPLIS为例来说明如何进行结构方程建模。
23
24
以范文一中的文档相关度为例,我们的理论模型是:
1
图12.3 范文一的理论模型
2
3
这是一个不算复杂的模型,只有一个应变量。其相关的关系模型可以用PRELIS表4
示成:
5
6
Title Relational Model for Relevance Judgment (relevance.spj)
!Define data file with command: Raw Data from File Raw Data from File 'formal242.psf'
!Define latent variables with command: Latent Variables
Latent Variables topicality novelty understandability reliability scope
relevance
!Define measurement model and structural model in ‘Relationship’ section
Relationships
!Measurement model
topic1 = topicality
topic2 = topicality
topic3 = topicality
topic4 = topicality
novel1 = novelty
novel2 = novelty
novel3 = novelty
!novel4 = novelty
under1 = understandability
under2 = understandability
under3 = understandability
reliab1 = reliability
reliab2 = reliability
reliab3 = reliability
reliab4 = reliability
sco1r = scope
sco2r = scope
sco3r = scope
!sco4r = scope
ri1 = relevance
!ri2 = relevance
ri3 = relevance
ri4 = relevance
ri5 = relevance
!Relational model
relevance= topicality novelty reliability understandability scope
!Request for diagram output
Path Diagram
!Specify model fitting parameters such as Iteration and Method of Estimation Iterations = 250
Method of Estimation: Maximum Likelihood
End of Problem
1
2
以上的程序可以说是不言自明的。与结构模型相比,我们只需要增加一行就得到了
关系模型。按Run LISREL图标()进行拟合之后,我们得到标准化后的解如下图:
3
4
1
图12.4 范文一的理论模型的拟合结果
2
3
选择T-Values显式模型,我们也同时可以得到假设检验的基本结果:
4
1
图12.5 范文一的理论模型的拟合结果的显著性
2
3
这表明从Scope到Relevance的假设不被支持。这个图与前图最明显的不同是测度4
5
项ri1没有一个从因子到测度项的箭头,这是因为在LISREL中内生变量的方差被默认为6
第一个测度项的方差。如果有需要,研究者也可以把应变量的方差设为其中任何一个(被7
认为比较好的)测度项的方差。相反,对于外生变量,其方差被默认为零。研究者也可能8
根据需要设定外生变量的方差等于某个测度项的方差。
虽然图形输出给了我们最基本的结果,我们可以从输出文件中得到更多信息。对于9
10
这个例子,我们对输出文件作以下注解。
11
注:程序部分
The following lines were read from file F:\methodologybook\9-
sem\example\relevance.SPJ:
Title Relational Model for Relevance Judgment
!Define data file with command: Raw Data from File
Raw Data from File 'formal242.psf'
!Define latent variables with command: Latent Variables
Latent Variables topicality novelty understandability reliability scope
relevance
!Define measurement model and structural model in Relationship section
Relationships
!Measurement model
topic1 = topicality
topic2 = topicality
topic3 = topicality
topic4 = topicality
novel1 = novelty
novel2 = novelty
novel3 = novelty
!novel4 = novelty
under1 = understandability
under2 = understandability
under3 = understandability
reliab1 = reliability
reliab2 = reliability
reliab3 = reliability
reliab4 = reliability
sco1r = scope
sco2r = scope
sco3r = scope
!sco4r = scope
ri1 = relevance
!ri2 = relevance
ri3 = relevance
ri4 = relevance
ri5 = relevance
!Relational model
relevance= topicality novelty reliability understandability scope
!Request for diagram output
Path Diagram
!Specify model fitting parameters such as Iteration and Method of Estimation
Iterations = 250
Method of Estimation: Maximum Likelihood
End of Problem
注:计算结果从这里开始
Sample Size = 242
Relational Model for Relevance Judgment
注:包含所有测度项的协方差矩阵。这是一个实际数据中的协方差矩阵,不是拟合的矩阵。有些方法专家这为一定要在论文中报告这个矩阵。但在实际发表的文章中,报告这个矩阵的并不多(可能是因为篇幅限制)。
Covariance Matrix
ri1 ri3 ri4 ri5 topic1 topic2 -------- -------- -------- -------- -------- --------
ri1 1.83
ri3 1.12 1.97
ri4 1.04 1.36 1.66
ri5 0.95 1.16 1.23 1.69
topic1 0.86 0.89 0.76 0.70 1.88
topic2 0.91 0.77 0.66 0.75 1.47 2.18
topic3 0.85 0.85 0.71 0.85 1.47 1.68
topic4 0.90 0.79 0.70 0.75 1.30 1.37
novel1 0.60 0.75 0.72 0.67 0.51 0.29
novel2 0.42 0.34 0.37 0.51 0.27 0.16
novel3 0.51 0.52 0.55 0.61 0.46 0.22
under1 0.38 0.84 0.45 0.46 0.49 0.48
under2 0.20 0.67 0.33 0.32 0.32 0.25
under3 0.23 0.59 0.36 0.40 0.34 0.27
reliab1 0.63 0.62 0.59 0.68 0.61 0.79
reliab2 0.53 0.48 0.47 0.53 0.65 0.79
reliab3 0.63 0.58 0.56 0.65 0.64 0.74
reliab4 0.49 0.48 0.42 0.50 0.61 0.70
sco1r 0.28 0.36 0.25 0.19 0.27 0.29
sco2r 0.54 0.56 0.40 0.36 0.46 0.46
sco3r 0.55 0.45 0.48 0.40 0.35 0.33
Covariance Matrix
topic3 topic4 novel1 novel2 novel3 under1 -------- -------- -------- -------- -------- --------
topic3 2.19
topic4 1.47 1.98
novel1 0.33 0.45 1.93
novel2 0.27 0.21 0.90 2.19
novel3 0.30 0.48 1.28 1.18 2.12
under1 0.49 0.30 0.22 0.08 0.13 1.92
under2 0.24 0.20 0.10 -0.05 0.04 1.42
under3 0.29 0.14 0.12 0.08 0.14 1.38
reliab1 0.72 0.69 0.31 0.17 0.26 0.43
reliab2 0.76 0.66 0.22 0.19 0.26 0.42
reliab3 0.71 0.68 0.38 0.18 0.31 0.36
reliab4 0.71 0.60 0.27 0.13 0.16 0.48
sco1r 0.28 0.37 0.04 0.22 0.11 0.36
sco2r 0.38 0.49 0.27 0.09 0.32 0.39
sco3r 0.44 0.51 0.18 -0.02 0.12 0.34
Covariance Matrix
under2 under3 reliab1 reliab2 reliab3 reliab4 -------- -------- -------- -------- -------- --------
under2 1.91
under3 1.32 1.63
reliab1 0.26 0.31 1.21
reliab2 0.22 0.32 0.85 1.04
reliab3 0.27 0.32 0.87 0.84 1.17
reliab4 0.39 0.42 0.77 0.82 0.88 1.17
sco1r 0.26 0.27 0.17 0.18 0.15 0.17
sco2r 0.20 0.25 0.29 0.31 0.31 0.32
sco3r 0.12 0.24 0.29 0.22 0.26 0.21
Covariance Matrix
sco1r sco2r sco3r
-------- -------- --------
sco1r 2.17
sco2r 1.37 1.94
sco3r 1.21 1.13 2.08
注:以下报告每个测度项未经标准化的因子载荷与解释的方差。
Relational Model for Relevance Judgment Number of Iterations = 11
LISREL Estimates (Maximum Likelihood)
Measurement Equations
ri1 = 0.94*relevanc, Errorvar.= 0.94 , R2 = 0.49
(0.095)
9.86
ri3 = 1.17*relevanc, Errorvar.= 0.60 , R2 = 0.70
(0.099) (0.073)
11.85 8.19
ri4 = 1.13*relevanc, Errorvar.= 0.37 , R2 = 0.78
(0.092) (0.055)
12.38 6.80
ri5 = 1.05*relevanc, Errorvar.= 0.58 , R2 = 0.66
(0.091) (0.067)
11.54 8.68
topic1 = 1.15*topicali, Errorvar.= 0.55 , R2 = 0.70
(0.073) (0.065)
15.71 8.53
topic2 = 1.27*topicali, Errorvar.= 0.57 , R2 = 0.74
(0.078) (0.071)
16.29 8.08
topic3 = 1.30*topicali, Errorvar.= 0.50 , R2 = 0.77
(0.077) (0.067)
16.88 7.50
topic4 = 1.12*topicali, Errorvar.= 0.72 , R2 = 0.63
(0.077) (0.079)
14.50 9.22
novel1 = 1.07*novelty, Errorvar.= 0.79 , R2 = 0.59
(0.087) (0.12)
12.27 6.72
novel2 = 0.91*novelty, Errorvar.= 1.36 , R2 = 0.38
(0.095) (0.14)
9.60 9.39
novel3 = 1.21*novelty, Errorvar.= 0.65 , R2 = 0.69
(0.090) (0.13)
13.42 4.93
under1 = 1.23*understa, Errorvar.= 0.40 , R2 = 0.79
(0.073) (0.064)
16.96 6.28
under2 = 1.16*understa, Errorvar.= 0.57 , R2 = 0.70
(0.075) (0.070)
15.53 8.14
under3 = 1.13*understa, Errorvar.= 0.36 , R2 = 0.78
(0.067) (0.055)
16.80 6.54
reliab1 = 0.91*reliabil, Errorvar.= 0.37 , R2 = 0.69
(0.059) (0.042)
15.53 8.91
reliab2 = 0.91*reliabil, Errorvar.= 0.21 , R2 = 0.80
(0.052) (0.029)
17.40 7.32
reliab3 = 0.95*reliabil, Errorvar.= 0.28 , R2 = 0.76
(0.056) (0.035)
16.78 7.98
reliab4 = 0.90*reliabil, Errorvar.= 0.37 , R2 = 0.69
(0.058) (0.041)
15.46 8.95
sco1r = 1.18*scope, Errorvar.= 0.78 , R2 = 0.64
(0.089) (0.12)
13.33 6.43
sco2r = 1.16*scope, Errorvar.= 0.60 , R2 = 0.69
(0.083) (0.11)
13.91 5.54
sco3r = 1.00*scope, Errorvar.= 1.08 , R2 = 0.48
(0.089) (0.12)
11.30 8.80
注:结构方程的解,包括“回归”系数、每个系数的标准差、T值、与R2。
Structural Equations
relevanc = 0.31*topicali + 0.32*novelty + 0.17*understa + 0.18*reliabil +
0.10*scope, Errorvar.= 0.48 , R2 = 0.52
(0.078) (0.065) (0.060) (0.077)
(0.061) (0.086)
4.00 4.94 2.81 2.37 1.66
5.56
注:外生变量的相关系数矩阵,包括标准差与T值。
Correlation Matrix of Independent Variables
topicali novelty understa reliabil scope
-------- -------- -------- -------- --------
topicali 1.00
novelty 0.25 1.00
(0.07)
3.58
understa 0.23 0.09 1.00
(0.07) (0.07)
3.46 1.18
reliabil 0.62 0.25 0.33 1.00
(0.05) (0.07) (0.06)
13.73 3.50 5.15
scope 0.28 0.14 0.21 0.24 1.00
(0.07) (0.08) (0.07) (0.07)
3.99 1.83 3.00 3.38
注:所有隐性变量之间的相关系数矩阵
Covariance Matrix of Latent Variables
relevanc topicali novelty understa reliabil scope -------- -------- -------- -------- -------- --------
relevanc 1.00
topicali 0.57 1.00
novelty 0.47 0.25 1.00
understa 0.35 0.23 0.09 1.00
reliabil 0.54 0.62 0.25 0.33 1.00
scope 0.31 0.28 0.14 0.21 0.24 1.00 注:模型拟合度。我们可以从中选取需报告的指标。
Goodness of Fit Statistics
Degrees of Freedom = 174
Minimum Fit Function Chi-Square = 274.00 (P = 0.00)
Normal Theory Weighted Least Squares Chi-Square = 272.19 (P = 0.00)
Estimated Non-centrality Parameter (NCP) = 98.19
90 Percent Confidence Interval for NCP = (57.35 ; 146.97)
Minimum Fit Function Value = 1.14
Population Discrepancy Function Value (F0) = 0.41
90 Percent Confidence Interval for F0 = (0.24 ; 0.61)
Root Mean Square Error of Approximation (RMSEA) = 0.048
90 Percent Confidence Interval for RMSEA = (0.037 ; 0.059)
P-Value for Test of Close Fit (RMSEA < 0.05) = 0.58
Expected Cross-Validation Index (ECVI) = 1.60
90 Percent Confidence Interval for ECVI = (1.43 ; 1.80)
ECVI for Saturated Model = 1.92
ECVI for Independence Model = 26.33
Chi-Square for Independence Model with 210 Degrees of Freedom = 6304.19
Independence AIC = 6346.19
Model AIC = 386.19
Saturated AIC = 462.00
Independence CAIC = 6440.46
Model CAIC = 642.06
Saturated CAIC = 1498.94
Normed Fit Index (NFI) = 0.96
Non-Normed Fit Index (NNFI) = 0.98
Parsimony Normed Fit Index (PNFI) = 0.79
Comparative Fit Index (CFI) = 0.98
Incremental Fit Index (IFI) = 0.98
Relative Fit Index (RFI) = 0.95
Critical N (CN) = 194.78
Root Mean Square Residual (RMR) = 0.090
Standardized RMR = 0.049
Goodness of Fit Index (GFI) = 0.90
Adjusted Goodness of Fit Index (AGFI) = 0.87
Parsimony Goodness of Fit Index (PGFI) = 0.68
注:LISREL会自动建议一些添加以后可能会显著地增加模型拟合度的关系。但这种建议是事后的而不是事先的。
The Modification Indices Suggest to Add an Error Covariance
Between and Decrease in Chi-Square New Estimate
ri5 ri3 9.1 -0.18
novel3 novel2 11.7 0.57
reliab4 reliab1 8.1 -0.09
sco1r novel2 10.1 0.27
Time used: 0.156 Seconds
1
1.4结果与分析
2
3
模型在拟合之后,其拟合度的指标与指标的经验法则与在测度模型中的解释是一致4
的,我们不作重复。需要指出的是,如果模型的拟合度可以接受,这并不意味着当前的模5
型是正确的。实际上,如果我们反转两个变量之间的因果关系,我们往往可以得到一个的拟合度。所以拟合度与模型的理论合理性是两回事。但是,充分的拟合度是进行假设检验6
7
的前提。
8
1.5多层因子分析
9
在社会研究中,有一些心理变量往往是相当复杂的,它们是很多心理现象的综合,
10
11
比如信任度、忠诚度、满意度。举例来讲,我们信任一个人往往有几种不同的情况:他有12
能力做你想要他做的事、他对你有爱心愿意尽力帮你做事(不管他能力如何)、他言出必13
行。要注意当一个人可信任时这三方面虽然不一定要同时出现,却常常同时出现,所以这14
三方面具有高度相关性。这种心理认识因为综合了很多因素而具有多维性,它不再是一个15
单维的变量。从语义的角度来看,在语言的演化过程中,我们用一个语义上相当丰富的词16
“信任”来综合表示这种认识。可以粗略地认为,一个字典中有很多相关语义的单词在实17
际使用中,使用者可能同时意指其中多方面,从而使这个变量成为一个多维的变量。在心18
理学中,常见的这一类变量还有态度、情感、动机、能力、形象等等。
从因子分析的角度看,一个第二层的因子的各个维度也是一个因子,这些子因子可
19
20
能用多个测度项来测量。如同因子是测度项的因、测度项是果,高层的因子是因、子因子是果。所以,在一个多维的因子结构中,中间的因子即是因、又是果。以文档的相关度为
21
22
例,如果我们假定Topicality、Novelty、Reliability是Relevance是三个子因子,双层因子23
分析(second-order CFA)的关系可以图示为:
1 图12.6 多层因子分析的结构模型
2
3 要注意,在这个关系中,Relevance 本身是没有测度项的,它把它的子因子当作测
4 度项,而它的子因子是有测度项的。因为子因子们即是因(测度项的因),又是果(高层
5 因子的果),所以它们也会有残差项。上图中没有标记子因子的残差。中层的因子具有残
6 差是多层因子分析与一般测度模型不同的一个地方。中层因子因为担当果的角色,所以整
7 体上是内生变量,它与高层因子的关系可以表示成:
8
()????
??????+??????????=??????????Γ3211312111321 ζζζξγγγηηηζ
ξη 9
ξ1是第二层因子,η1、η2、η3、是Topicality 、Novelty 、Reliability 。这种关系告诉
10 我们多层因子分析已经不是全自变量的简单测度模型,在数学上它更象是一个完整的结构11 模型,只不过只有一个外生变量ξ1、有多个内生变量η1、η2、η3罢了。
12
1
以上的模型认为Topicality、Novelty、Reliability是Relevance是三个子因子2
没有经过严密的理论论证,所以只可以当作一个演示性例子来看。我们来看这个例子的拟3
合结果。首先,SIMPLIS的程序是这样的:
Title Measurement Model for Relevance Judgment
!Define data file with command: Raw Data from File Raw Data from File 'formal242.psf'
!Define latent variables with command: Latent Variables
Latent Variables topicality novelty understandability reliability scope
relevance
!Define measurement model and structural model in Relationship section
Relationships
!Measurement model
topic1 = 1*topicality
topicality -> topic2 topic3 topic4
novel1 = 1*novelty
novelty -> novel2 novel3
reliab1 = 1*reliability
reliability -> reliab2 reliab3 reliab4
!Define relevance as a second-order factor
topicality novelty reliability = relevance
!Request for diagram output
Path Diagram
!Specify model fitting parameters such as Iteration and Method of Estimation Iterations = 250
Method of Estimation: Maximum Likelihood
Options RS SS SC
End of Problem
4
5
我们不详细报告输出文件。这个模型拟合的得到:
1
图12.7 多层因子分析的按惯例结果
2
3
我们可以看到第二层因子的方差被默认为1。以上的程序设第一层因子的方差为第4
一个测度项的方差。
5
从这个结果可以看出Novelty的载荷很小(0.3)。在实际研究中,这表明这三个子6
因子可能不够成一个高层因子的三个表征。如同在单层的因子分析中一样,我们也希望在7
8
高层因子分析中看到聚合与区别有效性,而这个例子不满足聚合有效性。这个例子也提出了一个和理论与实证研究同时相关的问题:什么时候一组因子可以被看作是一个更高级因9
10
子的子因子?什么时候我们需要把这样一组因子看作相关、但“各自为政”的一组因子?
11
我们把这个问题留给读者去思考。
1.6两个外生变量的因果强度比较
12
有时候,研究者相比较两个自变量对一个应变量的作用的大小。比如说,在文档13
Relevance评估中,作者认为Topicality与Novelty同等重要,这样的假设要如何测试呢?
14
我们的思路还是约束测试。我们建立两个模型:一个是自由模型,两个自
1
2
变量到应变量的系数可以自由变化;一个是约束模型,这两个系数必需一致。我们然后比3
较两个模型的拟合度与自由度差异,并由此得到差异的显著性。我们在前面已经看到了自4
由模型的输出。我们的约束模型是:
Titel Constrained test for two IVs' effect on one DV Raw Data from File 'formal242.psf'
Latent Variables topicali novelty understa reliabil scope relevance
Relationships
topic1 topic2 topic3 topic4 = topicali
novel1 novel2 novel3 = novelty
under1 under2 under3 = understa
reliab1 reliab2 reliab3 reliab4 = reliabil
sco1r sco2r sco3r = scope
ri1 ri3 ri4 ri5 = relevance
relevance = topicali novelty understa reliabil scope
Set Path topicali->relevance Equal novelty->relevance
Path Diagram
End of Problem
5
6
7
图12.8 同一模型中对系数的约束
8
9
比较这两个模型,?χ2=272.24-272.19=0.05,?dof=1,p=.82。所以,我们的数据支10
持我们的假设:这两个变量对Relevance的影响是一样的。当然,这个例子是演示性的,11
对于这样的假设我们没有足够的理论根据。
晶体结构分析的历史发展 (一)X射线晶体学的诞生 1895年11月8日德国维尔茨堡大学物理研究所所长伦琴发现了X射线。自X射线发现后,物理学家对X射线进行了一系列重要的实验,探明了它的许多性能。根据狭缝的衍射实验,索末菲(Som-merfeld)教授指出,X射线如是一种电磁波的话,它的波长应当在1埃上下。 在发现X射线的同时,经典结晶学有了很大的进展,230个空间群的推引工作使晶体构造的几何理论全部完成。当时虽没有办法测定晶胞的形状和大小以及原子在晶胞中的分布,但对晶体结构已可臆测。根据当时已知的原子量、分子量、阿伏伽德罗常数和晶体的密度,可以估计晶体中一个原子或一个分子所占的容积,晶体中原子间距离约1—2埃。1912年,劳厄(Laue)是索末菲手下的一个讲师,他对光的干涉现象很感兴趣。刚巧厄瓦耳(P.Ewald)正随索末菲进行结晶光学方面的论文,科学的交流使劳厄产生了一种极为重要的科学思想:晶体可以用作X射线的立体衍射光栅,而X射线又可用作量度晶体中原子位置的工具。刚从伦琴那里取得博士学位的弗里德里克(W.Friedrich)和尼平(P.Knipping)亦在索末菲教授处工作,他们自告奋勇地进行劳厄推测的衍射实验。他们使用了伦琴提供的X射线管和范克罗斯(Von.Groth)提供的晶体,最先对五水合硫酸铜晶体进行了实验,费了很多周折得到了衍射点,初步证实了劳厄的预见。后来他们对辉锌矿、铜、氯化钠、黄铁矿、沸石和氯化亚铜等立方晶体进行实验,都得到了正面的结果,为了解释这些衍射结果,劳厄提出了著名的劳厄方程。劳厄的发现导致了X射线晶体学和X射线光谱学这二门新学科的诞生。 劳厄设计的实验虽取得了正面的结果,但X射线晶体学和X射线光谱学成为新学科是一些得力科学家共同努力的结果。布拉格父子(W.H.Bragg,W.L.Bragg)、莫塞莱(Moseley)、达尔文(Darwin)完成了主要的工作,通过他们的工作认识到X射线具有波粒二重性;X射线中除了连续光谱外,还有波长取决于阴极材料的特征光谱,发现了X射线特征光谱频率和元素在周期表中序数之间的规律;提出了镶嵌和完整晶体的强度公式,热运动使衍射线变弱的效应,发展了X射线衍射理论。W·L·布拉格在衍射实验中发现,晶体中显得有一系列原子面在反射X射线。他从劳厄方程引出了布拉格方程,并从KCl和NaCl的劳厄衍射图引出了晶体中的原子排列方式,W·L·布拉格在劳厄发现的基础上开创了X射线晶体结构分析工作。 伦琴在1901年由于发现X射线成为世界上第一个诺贝尔物理奖获得者,而劳厄由于发现X射线的晶体衍射效应也在1914年获得了诺贝尔物理奖。 (二)X射线晶体结构分析促进了化学发展 W·L·布拉格开创的X射线晶体结构分析工作把X射线衍射效应和化学联系在一起。当NaCl等晶体结构被测定后,使化学家恍然大悟,NaCl的晶体结构中没有用NaCl表示的分子集团,而是等量的Na+离子和Cl-离子棋盘交叉地成为三维结构。当时X射线结构分析中的位相问题是通过强度数据和强度公式用试差法来解决的,只能测定含二三十个参数的结构,这些结构虽简单,但使无机物的结构化学有了真正的开始。 从1934年起,帕特孙(Patterson)法和其他应用付里叶级数的方法相继提出,位相问题可通过帕特孙函数找出重原子的位置来解决,使X射线晶体结构分析摆脱了试差法。1940年后计算机的使用,使X射线晶体结构分析能测定含重原子的复杂的化合物的结构。X射线晶体结构分析不但印证了有机物的经典结构化学,也为有机物积累了丰富的立体化学数据,
结构方程模型(Structural Equation Modeling,SEM) 20世纪——主流统计方法技术:因素分析回归分析 20世纪70年代:结构方程模型时代正式来临 结构方程模型是一门基于统计分析技术的研究方法学,它主要用于解决社会科学研究中的多变量问题,用来处理复杂的多变量研究数据的探究与分析。在社会科学及经济、市场、管理等研究领域,有时需处理多个原因、多个结果的关系,或者会碰到不可直接观测的变量(即潜变量),这些都是传统的统计方法不能很好解决的问题。SEM能够对抽象的概念进行估计与检定,而且能够同时进行潜在变量的估计与复杂自变量/因变量预测模型的参数估计。 结构方程模型是一种非常通用的、主要的线形统计建模技术,广泛应用于心理学、经济学、社会学、行为科学等领域的研究。实际上,它是计量经济学、计量社会学与计量心理学等领域的统计分析方法的综合。多元回归、因子分析和通径分析等方法都只是结构方程模型中的一种特例。 结构方程模型是利用联立方程组求解,它没有很严格的假定限制条件,同时允许自变量和因变量存在测量误差。在许多科学领域的研究中,有些变量并不能直接测量。实际上,这些变量基本上是人们为了理解和研究某类目的而建立的假设概念,对于它们并不存在直接测量的操作方法。人们可以找到一些可观察的变量作为这些潜在变量的“标识”,然而这些潜在变量的观察标识总是包含了大量的测量误差。在统计分析中,即使是对那些可以测量的变量,也总是不断受到测量误差问题的侵扰。自变量测量误差的发生会导致常规回归模型参数估计产生偏差。虽然传统的因子分析允许对潜在变量设立多元标识,也可处理测量误差,但是,它不能分析因子之间的关系。只有结构方程模型即能够使研究人员在分析中处理测量误差,又可分析潜在变量之间的结构关系。 简单而言,与传统的回归分析不同,结构方程分析能同时处理多个因变量,并可比较及评价不同的理论模型。与传统的探索性因子分析不同,在结构方程模型中,我们可以提出一个特定的因子结构,并检验它是否吻合数据。通过结构方程多组分析,我们可以了解不同组别内各变量的关系是否保持不变,各因子的均值是否有显著差异。” 目前,已经有多种软件可以处理SEM,包括:LISREL,AMOS, EQS, Mplus. 结构方程模型包括测量方程(LV和MV之间关系的方程,外部关系)和结构方程(LV之间关系的方程,内部关系),以ACSI模型为例,具体形式如下:
浅谈有关晶体结构的分 析和计算 Revised as of 23 November 2020
浅谈有关晶体结构的分析和计算 摘要:晶体结构的分析和计算是历年全国高考化学试卷中三个选做题之一,本文从晶体结构的粒子数和化学式的确定,晶体中化学键数的确定和晶体的空间结构的计算等方面,探讨有关晶体结构的分析和计算的必要性。 关键词:晶体、结构、计算、晶胞 在全国统一高考化学试卷中,有三个题目是现行中学化学教材中选学内容,它们分别《化学与生活》、《有机化学基础》和《物质结构与性质》。虽然三个题目在高考时只需选做一题,由于是选学内容,学生对选学内容往往重视不够,所以在高考时学生对这部分题目得分不够理想。笔者对有关晶体结构的分析和计算进行简单的归纳总结,或许对学生学习有关晶体结构分析和计算有所帮助,若有不妥这处,敬请同仁批评指正。 一、有关晶体结构的粒子数和化学式确定 (一)、常见晶体结构的类型 1、原子晶体 (1)金刚石晶体中微粒分布: ①、每个碳原子与4个碳原子以共价键结合,形成正四面体结构。 ②、键角均为109°28′。 ③、最小碳环由6个碳组成并且六个碳原子不在同一平面内。 ④、每个碳原子参与4条C-C 键的形成,碳原子与C-C 键之比为1:2。 (2)二氧化硅晶体中微粒分布 ①、每个硅原子与4个氧原子以共价键结合,形成正四面体结构。 ②、每个正四面体占有1个Si ,4个“2 1氧”,n(Si):n(O)=1:2。 ③、最小环上有12个原子,即:6个氧原子和6个硅原子.
2、分子晶体:干冰(CO 2)晶体中微粒分布 ①、8个CO 2分子构成立方体并且在6个面心又各占据1个CO 2分子。 ②、每个CO 2分子周围等距离紧邻的CO 2分子有12个。 3、离子晶体 (1)、NaCl 型晶体中微粒分布 ①、每个Na +(Cl -)周围等距离且紧邻的Cl -(Na +)有6个。每 个Na +周围等距离紧邻的Na +有12个。 ②、每个晶胞中含4个Na +和4个Cl -。 (2)、CsCl 型晶体中微粒分布 ①、每个Cs +周围等距离且紧邻的Cl -有8个,每个Cs +(Cl -) 周围等距离且紧邻的Cs +(Cl -)有6个。 ②、如图为8个晶胞,每个晶胞中含有1个Cs +和1个Cl - 。 3、金属晶体 (1)、简单立方晶胞:典型代表Po ,空间利用率52%,配位数为6 (2)、体心立方晶胞(钾型):典型代表Na 、K 、Fe ,空间利用率60%,配位数为8。 (3)、六方最密堆积(镁型):典型代表Mg 、Zn 、Ti ,空间利用率74%,配位数为12。 (4)、面心立方晶胞(铜型):典型代表Cu 、Ag 、Au ,空间利用率74%,配位数为12。 (二)、晶胞中微粒的计算方法——均摊法 1、概念:均摊法是指每个图形平均拥有的粒子数目,如某个粒子为n 个晶胞所共有,则 该粒子有n 1属于一个晶胞。 2、解题思路:首先应分析晶胞的结构(该晶胞属于那种类型),然后利用“均摊法”解题。
数值分析期末复习资料
数值分析期末复习 题型:一、填空 二、判断 三、解答(计算) 四、证明 第一章 误差与有效数字 一、 有效数字 1、 定义:若近似值x*的误差限是某一位的半个单位,该位到x*的第一位非零数字共有n 位,就说 x*有n 位有效数字。 2、 两点理解: (1) 四舍五入的一定是有效数字 (2) 绝对误差不会超过末位数字的半个单位eg. 3、 定理1(P6):若x*具有n 位有效数字,则其相对误差限为 4、 考点: (1)计算有效数字位数:一个根据定义理解,一个根据定理1(P7例题3) 二、 避免误差危害原则 1、 原则: (1) 避免大数吃小数(方法:从小到大相加;利用韦达定理:x1*x2= c / a ) (2) 避免相近数相减(方法:有理化)eg. 或 (3) 减少运算次数(方法:秦九韶算法)eg.P20习题14 三、 数值运算的误差估计 1、 公式: (1) 一元函数:|ε*( f (x *))| ≈ | f ’(x *)|·|ε*(x )|或其变形公式求相对误差(两边同时 除以f (x *)) eg.P19习题1、2、5 (2) 多元函数(P8)eg. P8例4,P19习题4 *(1) 11 102n r a ε--≤?;x εx εx εx ++=-+();1ln ln ln ??? ? ??+=-+x εx εx x cos 1-2sin 22x =
第二章 插值法 一、 插值条件 1、 定义:在区间[a,b]上,给定n+1个点,a ≤x 0<x 1<…<x n ≤b 的函数值 yi=f(xi),求次数不超过n 的多项式P(x),使 2、 定理:满足插值条件、n+1个点、点互异、多项式次数≤n 的P(x)存在且唯一 二、 拉格朗日插值及其余项 1、 n 次插值基函数表达式(P26(2.8)) 2、 插值多项式表达式(P26(2.9)) 3、 插值余项(P26(2.12)):用于误差估计 4、 插值基函数性质(P27(2.17及2.18))eg.P28例1 三、 差商(均差)及牛顿插值多项式 1、 差商性质(P30): (1) 可表示为函数值的线性组合 (2) 差商的对称性:差商与节点的排列次序无关 (3) 均差与导数的关系(P31(3.5)) 2、 均差表计算及牛顿插值多项式 四、埃尔米特插值(书P36) 两种解法: (1) 用定义做:设P 3(x)=ax 3+bx 2+cx+d ,将已知条件代入求解(4个条件:节点函数值、导数值相 等各2个) (2) 牛顿法(借助差商):重节点eg.P49习题14 五、三次样条插值定义 n i y x P i i n ,,2,1,0)( ==
几种常见晶体结构分析文档编制序号:[KK8UY-LL9IO69-TTO6M3-MTOL89-FTT688]
几种常见晶体结构分析 河北省宣化县第一中学 栾春武 邮编 075131 栾春武:中学高级教师,张家口市中级职称评委会委员。河北省化学学会会员。市骨干教师、市优秀班主任、模范教师、优秀共产党员、劳动模范、县十佳班主任。 联系电话: E-mail : 一、氯化钠、氯化铯晶体——离子晶体 由于离子键无饱和性与方向性,所以离子晶体中无单个分子存在。阴阳离子在晶体中按一定的规则排列,使整个晶体不显电性且能量最低。离子的配位数分析如下: 离子数目的计算:在每一个结构单元(晶胞)中,处于不同位置的微粒在该单元中所占的份额也有所不同,一般的规律是:顶点上的微粒属于该 单元中所占的份额为18,棱上的微粒属于该单元中所占的份额为1 4,面上 的微粒属于该单元中所占的份额为1 2,中心位置上(嚷里边)的微粒才完 全属于该单元,即所占的份额为1。 1.氯化钠晶体中每个Na +周围有6个Cl -,每个Cl -周围有6个Na +,与一个Na +距离最近且相等的Cl -围成的空间构型为正八面体。每个Na +周围与其最近且距离相等的Na +有12个。见图1。 图1 图2 NaCl
晶胞中平均Cl-个数:8×1 8 + 6× 1 2 = 4;晶胞中平均Na+个数:1 + 12×1 4 = 4 因此NaCl的一个晶胞中含有4个NaCl(4个Na+和4个Cl-)。 2.氯化铯晶体中每个Cs+周围有8个Cl-,每个Cl-周围有8个Cs+,与一个Cs+距离最近且相等的Cs+有6个。 晶胞中平均Cs+个数:1;晶胞中平均Cl-个数:8×1 8 = 1。 因此CsCl的一个晶胞中含有1个CsCl(1个Cs+和1个Cl-)。 二、金刚石、二氧化硅——原子晶体 1.金刚石是一种正四面体的空间网状结构。每个C 原子以共价键与4个C原子紧邻,因而整个晶体中无单 个分子存在。由共价键构成的最小环结构中有6个碳原 子,不在同一个平面上,每个C原子被12个六元环共用,每C—C键共6 个环,因此六元环中的平均C原子数为6× 1 12 = 1 2 ,平均C—C键数为 6×1 6 = 1。 C原子数: C—C键键数= 1:2; C原子数: 六元环数= 1:2。 2.二氧化硅晶体结构与金刚石相似,C被Si代替,C与C之间插 氧,即为SiO 2晶体,则SiO 2 晶体中最小环为12环(6个Si,6个O), 图3 CsCl 晶 图4 金刚石晶
数值分析讲义 第三章线性方程组的解法 §3.0 引言 §3.1 雅可比(Jacobi)迭代法 §3.2 高斯-塞德尔(Gauss-Seidel)迭代法 §3.3 超松驰迭代法§3.7 三角分解法 §3.4 迭代法的收敛性§3.8 追赶法 §3.5 高斯消去法§3.9 其它应用 §3.6 高斯主元素消去法§3.10 误差分析 §3 作业讲评3 §3.11 总结
§3.0 引言 重要性:解线性代数方程组的有效方法在计算数学和科学计算中具有特殊的地位和作用.如弹性力学、电路分析、热传导和振动、以及社会科学及定量分析商业经济中的各种问题. 分类:线性方程组的解法可分为直接法和迭代法两种方法. (a) 直接法:对于给定的方程组,在没有舍入误差的假设下,能在预定的运算次数内求得精确解.最基本的直接法是Gauss消去法,重要的直接法全都受到Gauss消去法的启发.计算代价高. (b) 迭代法:基于一定的递推格式,产生逼近方程组精确解的近似序列.收敛性是其为迭代法的前提,此外,存在收敛速度与误差估计问题.简单实用,诱人.
§3.1 雅可比Jacobi 迭代法 (AX =b ) 1 基本思想: 与解f (x )=0 的不动点迭代相类似,将AX =b 改写为X =BX +f 的形式,建立雅可比方法的迭代格式:X k +1=BX (k )+f ,其中,B 称为迭代矩阵.其计算精度可控,特别适用于求解系数为大型稀疏矩阵(sparse matrices)的方程组. 2 问题: (a) 如何建立迭代格式? (b) 向量序列{X k }是否收敛以及收敛条件? 3 例题分析: 考虑解方程组??? ??=+--=-+-=--2.453.82102 .72103 21321321x x x x x x x x x (1) 其准确解为X *={1, 1.2, 1.3}. 建立与式(1)相等价的形式: ??? ??++=++=++=84.02.01.083.02.01.072 .02.01.02 13312321x x x x x x x x x (2) 据此建立迭代公式: ?????++=++=++=+++84 .02.01.083.02.01.072.02.01.0)(2)(1)1(3 )(3 )(1)1(23)(2)1(1k k k k k k k k k x x x x x x x x x (3) 取迭代初值0) 0(3 )0(2)0(1===x x x ,迭代结果如下表. JocabiMethodP31.cpp
几种典型晶体结构的特点分析 徐寿坤 有关晶体结构的知识是高中化学中的一个难点,它能很好地考查同学们的观察能力和三维想像能力,而且又很容易与数学、物理特别是立体几何知识相结合,是近年高考的热点之一。熟练掌握NaCl 、CsCl 、CO 2、SiO 2、金刚石、石墨、C 60等晶体结构特点,理解和掌握一些重要的分析方法与原则,就能顺利地解答此类问题。 通常采用均摊法来分析这些晶体的结构特点。均摊法的根本原则是:晶胞任意位置上的原子如果是被n 个晶胞所共有,则每个晶胞只能分得这个原子的1/n 。 1. 氯化钠晶体 由下图氯化钠晶体结构模型可得:每个Na +紧邻6个- Cl ,每个- Cl 紧邻6个+ Na (上、下、左、右、前、后),这6个离子构成一个正八面体。设紧邻的Na +-a ,每个Na +与12个Na +等距离紧邻(同层4个、上层4个、下层4个),距离为a 2。由均摊法可得:该晶胞中所拥有的Na +数为4216818=?+? ,-Cl 数为44 1 121=?+,晶体中Na +数与Cl -数之比为1:1 2. 氯化铯晶体 每个Cs +紧邻8个-Cl -紧邻8个Cs +,这8个离子构成一个正立方体。设紧邻 的Cs +与Cs +间的距离为 a 2 3 ,则每个Cs +与6个Cs +等距离紧邻(上、下、左、右、前、后)。在如下图的晶胞中Cs +数为812 164112818=+?+?+?,- Cl 在晶胞内其数目为8, 晶体中的+Cs 数与- Cl 数之比为1:1,则此晶胞中含有8个CsCl 结构单元。
3. 干冰 每个CO 2分子紧邻12个CO 2分子(同层4个、上层4个、下层4个),则此晶胞中的CO 2分子数为42 1 6818=?+? 。 4. 金刚石晶体 每个C 原子与4个C 原子紧邻成键,由5个C 原子形成正四面体结构单元,C-C 键的夹角为'28109?。晶体中的最小环为六元环,每个C 原子被12个六元环共有,每个C-C 键被6个六元环共有,每个环所拥有的C 原子数为211216=?,拥有的C-C 键数为16 1 6=?,则C 原子数与C-C 键数之比为 2:11:2 1 =。 5. 二氧化硅晶体 每个Si 原子与4个O 原子紧邻成键,每个O 原子与2个Si 原子紧邻成键。晶体中的
几种常见晶体结构分析 河北省宣化县第一中学 栾春武 邮编 075131 栾春武:中学高级教师,张家口市中级职称评委会委员。河北省化学学会会员。市骨干教师、市优秀班主任、模范教师、优秀共产党员、劳动模范、县十佳班主任。 联系电话::: 一、氯化钠、氯化铯晶体——离子晶体 由于离子键无饱和性与方向性,所以离子晶体中无单个分子存在。阴阳离子在晶体中按一定的规则排列,使整个晶体不显电性且能量最低。离子的配位数分析如下: 离子数目的计算:在每一个结构单元(晶胞) 中,处于不同位置的微粒在该单元中所占的份额也有 所不同,一般的规律是:顶点上的微粒属于该单元中 所占的份额为18 ,棱上的微粒属于该单元中所占的份额为14,面上的微粒属于该单元中所占的份额为12 ,中心位置上(嚷里边)的微粒才完全属于该单元,即所占的份额为1。 1.氯化钠晶体中每个Na +周围有6个C l -,每个Cl -周围有6个Na +,与一个Na +距离最近且相等的 Cl -围成的空间构型为正八面体。每个N a +周围与其最近且距离相等的Na + 有12个。见图1。 晶胞中平均Cl -个数:8×18 + 6×12 = 4;晶胞中平均Na +个数:1 + 12×14 = 4 因此NaCl 的一个晶胞中含有4个NaCl (4个Na +和4个Cl -)。 2.氯化铯晶体中每个Cs +周围有8个Cl -,每个Cl -周围有8个Cs +,与 一个Cs +距离最近且相等的Cs +有6个。晶胞中平均Cs +个数:1;晶胞中平 均Cl -个数:8×18 = 1。 因此CsCl 的一个晶胞中含有1个CsCl (1个Cs +和1个Cl -)。 二、金刚石、二氧化硅——原子晶体 1.金刚石是一种正四面体的空间网状结构。每个C 原子以共价键与4 个C 原子紧邻,因而整个晶体中无单个分子存在。由共价键构成的最小 环结构中有6个碳原子,不在同一个平面上,每个C 原子被12个六元环 共用,每C —C 键共6个环,因此六元环中的平均C 原子数为6× 112 = 12 ,平均C —C 键数为6×16 = 1。 C 原子数: C —C 键键数 = 1:2; C 原子数: 六元环数 = 1:2。 2.二氧化硅晶体结构与金刚石相似,C 被Si 代替,C 与C 之间插氧,即为SiO 2晶体,则SiO 2晶体中最小环为12环(6个Si ,6个O ), 最小环的平均Si 原子个数:6×112 = 12;平均O 原子个数:6×16 = 1。 即Si : O = 1 : 2,用SiO 2表示。 在SiO 2晶体中每个Si 原子周围有4个氧原子,同时每个氧原子结合2个硅原子。一个Si 原子可形 图 1 图 2 NaCl 晶体 图3 CsCl 晶体 图4 金刚石晶体
一 实验目的 1.掌握求解线性方程组的高斯消元法及列主元素法; 2. 掌握求解线性方程组的克劳特法; 3. 掌握求解线性方程组的平方根法。 二 实验内容 1.用高斯消元法求解方程组(精度要求为610-=ε): 1231231 233272212240x x x x x x x x x -+=??-+-=-??-+=? 2.用克劳特法求解上述方程组(精度要求为610-=ε)。 3. 用平方根法求解上述方程组(精度要求为610-=ε)。 4. 用列主元素法求解方程组(精度要求为610-=ε): 1231231 233432222325x x x x x x x x x -+=??-+-=??--=-? 三 实验步骤(算法)与结果 1. 程序代码(Python3.6): import numpy as np def Gauss(A,b): n=len(b) for i in range(n-1): if A[i,i]!=0: for j in range(i+1,n): m=-A[j,i]/A[i,i] A[j,i:n]=A[j,i:n]+m*A[i,i:n] b[j]=b[j]+m*b[i] for k in range(n-1,-1,-1): b[k]=(b[k]-sum(A[k,(k+1):n]*b[(k+1):n]))/A[k,k]
print(b) 运行函数: >>> A=np.array([[3,-1,2],[-1,2,-2],[2,-2,4]],dtype=np.float) >>> b=np.array([7,-1,0],dtype=np.float) >>> x=Gauss(A,b) 输出: 结果:解得原方程的解为x1=3.5,x2=-1,x3=-2.25 2 程序代码(Python3.6): import numpy as np A=np.array([[3,-1,2],[-1,2,-2],[2,-2,4]],dtype=float) L=np.array([[1,0,0],[0,1,0],[0,0,1]],dtype=float) U=np.array([[0,0,0],[0,0,0],[0,0,0]],dtype=float) b=np.array([7,-1,0],dtype=float) y=np.array([0,0,0],dtype=float) x=np.array([0,0,0],dtype=float) def LU(A): n=len(A[0]) i=0 while i *4 1* 3 2* 13* 3 4* 1 51()1021()1021()1021()1021()102 x x x x x εεεεε-----=?=?=?=?=? *** 124***1244333 (1)()()()() 1111010102221.0510x x x x x x εεεε----++=++=?+?+?=? *** 123*********123231132143 (2)() ()()() 111 1.10210.031100.031385.610 1.1021385.610222 0.215 x x x x x x x x x x x x εεεε---=++=???+???+???≈ ** 24**** 24422 *4 33 5 (3)(/) ()() 11 0.0311056.430102256.43056.430 10x x x x x x x εεε---+≈ ??+??= ?= 5计算球体积要使相对误差限为1,问度量半径R 时允许的相对误差限是多少? 解:球体体积为343 V R π= 则何种函数的条件数为 2 3'4343 p R V R R C V R ππ===g g (*)(*)3(*)r p r r V C R R εεε∴≈=g 又(*)1r V ε=Q %1 晶体结构解析基本步骤 Steps to Crystallographic Solution (基于SHELXL97结构解析程序的SHELXTL软件,尚需WINGX和DIAMOND程序配合) 注意:每一个晶体数据必须在数据所在的目录(E:\STRUCT)下建立一子目录(如E:\STRUCT\AAA),并将最初的数据备份一份于AAA目录下的子目录ORIG,形成如右图所示的树形结构。 一. 准备 1. 对IP收录的数据, 检查是否有inf、dat和f2(设为, 并更名为文件; 对CCD收录的数据, 检查是否有同名的p4p和hkl(设为文件 2. 对IP收录的数据, 用EDIT或记事本打开dat或inf文件, 并于记录本上记录下相关数据(下面所说的记录均指记录于记录本上): ⊕从% crystal data项中,记下晶胞参数及标准偏差(cell);晶体大小(crystal size);颜色(crystal color);形状(crystal habit);测量温度(experiment temperature); ⊕从 total reflections项中,记下总点数;从R merge项中,记下Rint=. % (IP收录者常将衍射数据转化为独立衍射点后传给我们); ⊕从unique reflections项中,记下独立点数 对CCD收录的数据, 用EDIT或记事本打开P4P文件, 并于记录下相关数据: ⊕从CELL和CELLSD项中,记下晶胞参数及标准偏差; ⊕从CCOLOR项中,记下晶体颜色; 总点数;从CSIZE项中,记下晶体大小; ⊕从BRAVAIS和SYMM项中,记下BRAVAIS点阵型式和LAUE群 3. 双击桌面的SHELXTL图标(打开程序), 呈 4. New, 先在“查找范围”选择数据所在的文件夹(如E:\STRUCT\AAA), 并选择衍射点数据文件(如,单击Project Open,最后在“project name”中给一个易于记忆和区分的任务名称(如050925-znbpy). 下次要处理同一结构时, 则只需Project 在任务项中选择050925-znbpy便可 5. 单击XPREP , 屏幕将显示DOS式的选择菜单: ⊕对IP收录的数据, 输入晶胞参数后回车(下记为 数值分析期末复习 题型:一、填空 二、判断 三、解答(计算) 四、证明 第一章 误差与有效数字 一、 有效数字 1、 定义:若近似值x*的误差限是某一位的半个单位,该位到x*的第一位非零 数字共有n 位,就说x*有n 位有效数字。 2、 两点理解: (1) 四舍五入的一定是有效数字 (2) 绝对误差不会超过末位数字的半个单位eg. 3、 定理1(P6):若x*具有n 位有效数字,则其相对误差限为 4、 考点: (1)计算有效数字位数:一个根据定义理解,一个根据定理1(P7例题3) 二、 避免误差危害原则 1、 原则: (1) 避免大数吃小数(方法:从小到大相加;利用韦达定理:x1*x2= c / a ) (2) 避免相近数相减(方法:有理化)eg. 或 (3) 减少运算次数(方法:秦九韶算法)eg.P20习题14 三、 数值运算的误差估计 1、 公式: (1) 一元函数:|ε*( f (x *))| ≈ | f ’(x *)|·|ε*(x )|或其变形公式求相对误差 (两边同时除以f (x *)) eg.P19习题1、2、5 (2) 多元函数(P8)eg. P8例4,P19习题4 第二章 插值法 一、 插值条件 1、 定义:在区间[a,b]上,给定n+1个点,a ≤x 0<x 1<…<x n ≤b 的函数值 yi=f(xi),求次数不超过n 的多项式P(x),使 2、 定理:满足插值条件、n+1个点、点互异、多项式次数≤n 的P(x)存在且唯一 二、 拉格朗日插值及其余项 1、 n 次插值基函数表达式(P26(2.8)) 2、 插值多项式表达式(P26(2.9)) 3、 插值余项(P26(2.12)):用于误差估计 *(1) 11 102n r a ε--≤?;x εx εx εx ++=-+();1ln ln ln ??? ? ??+=-+x εx εx x cos 1-2sin 22x =n i y x P i i n ,,2,1,0)( == 概念: 结构方程建模(Structural Equation Modeling. 简称SEM) 是一种综合运用多元回归分析、路径分析和确认型因子分析方法而形成的一种统计数据分析工具,是基于变量的协方差矩阵来分析变量之间关系得一种统计方法,也称为协方差结构分析。它既能够分析处理测量误差,又可分析潜在变量之间的结构关系。 特点: 1.同时处理多个因变量 结构方程分析可同时考虑并处理多个因变量。在回归分析或路径分析中,即使统计结果的图表中展示多个因变量,在计算回归系数或路径系数时,仍是对每个因变量逐一计算。所以图表看似对多个因变量同时考虑,但在计算对某一个因变量的影响或关系时,都忽略了其他因变量的存在及其影响。 2.容许自变量和因变量含测量误差 态度、行为等变量,往往含有误差,也不能简单地用单一指标测量。结构方程分析容许自变量和因变量均含测量误差。变量也可用多个指标测量。用传统方法计算的潜变量间相关系数与用结构方程分析计算的潜变量间相关系数,可能相差很大。 3.同时估计因子结构和因子关系 假设要了解潜变量之间的相关程度,每个潜变量者用多个指标或题目测量,一个常用的做法是对每个潜变量先用因子分析计算潜变量(即 因子)与题目的关系(即因子负荷),进而得到因子得分,作为潜变量的观测值,然后再计算因子得分,作为潜变量之间的相关系数。这是两个独立的步骤。在结构方程中,这两步同时进行,即因子与题目之间的关系和因子与因子之间的关系同时考虑。 4.容许更大弹性的测量模型 传统上,只容许每一题目(指标)从属于单一因子,但结构方程分析容许更加复杂的模型。例如,我们用英语书写的数学试题,去测量学生的数学能力,则测验得分(指标)既从属于数学因子,也从属于英语因子(因为得分也反映英语能力)。传统因子分析难以处理一个指标从属多个因子或者考虑高阶因子等有比较复杂的从属关系的模型。 5.估计整个模型的拟合程度 在传统路径分析中,只能估计每一路径(变量间关系)的强弱。在结构方程分析中,除了上述参数的估计外,还可以计算不同模型对同一个样本数据的整体拟合程度,从而判断哪一个模型更接近数据所呈现的关系。 友情提示:本资料代表个人观点,如有帮助请下载,谢谢您的浏览!晶体结构解析基本步骤
数值分析期末复习资料-福大研究生版
结构方程模型的概念和特点