高考数列专题复习

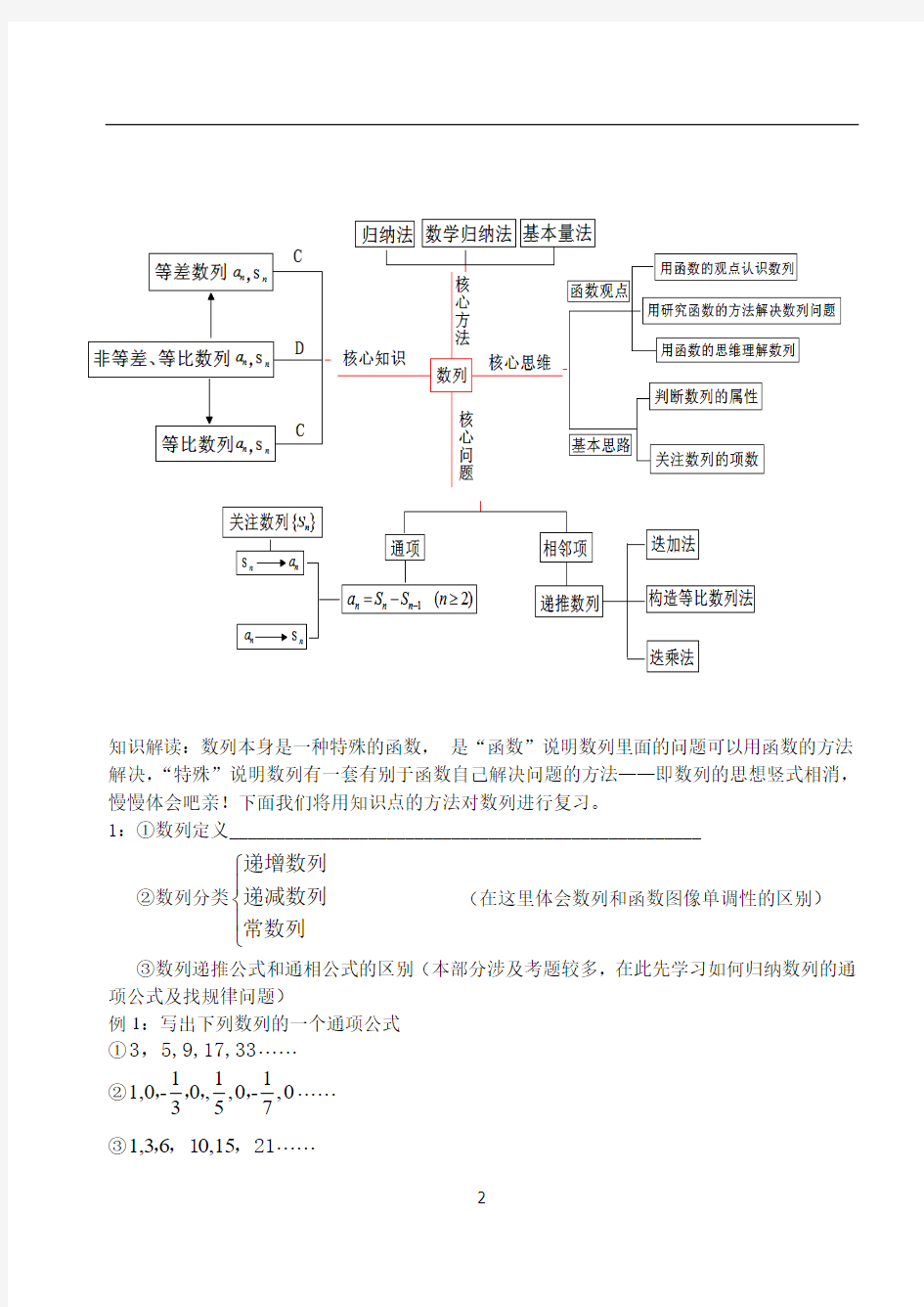
高中数列专题复习

李小楠编写思维导图

知识解读：数列本身是一种特殊的函数， 是“函数”说明数列里面的问题可以用函数的方法解决，“特殊”说明数列有一套有别于函数自己解决问题的方法——即数列的思想竖式相消，慢慢体会吧亲！下面我们将用知识点的方法对数列进行复习。

1：①数列定义___________________________________________________

②数列分类??

???

递增数列递减数列常数列 （在这里体会数列和函数图像单调性的区别）

③数列递推公式和通相公式的区别（本部分涉及考题较多，在此先学习如何归纳数列的通项公式及找规律问题）

例1：写出下列数列的一个通项公式 ①??????3，5,9,17,33

②1111,0-0,,0-,0357

??????，

，，， ③1,360,15??????，

，1，21

例2．

①将正奇数排列如下表其中第i 行第j 个数表示

ij a ),(**N j N i ∈∈，例如

932=a ，若2009ij a =，则=+j i ．

答案 60

②如图，在直角坐标系中,一质点从原点出发,沿图示箭头方向每秒钟移动一个单位,问第2008秒时质点所在的位置坐标是

答案：（-31，7）

小结：此类题目在高考中日趋流行，没有固定的通法通解。一般步骤是先多列几项找一个规律，对于数据较多的可以考察它的周期或者相邻两项之间的关系（递推关系）进而找出通项公式。此类题目大多是意会，少数是言传，附件里有后备例题，慢慢悟吧！悟懂了数学能力就提高一大节。

2：同一数列中n n a s ，的关系____________________________

（本知识存在有两个用处①利用式子统一变量，换成只有n a 或者n s 的式子进行求解②利用此

1 3 5 7

9 11

13 15 17 19

……

式子求数列n a ，n s 的最大最小项) 例1：求下列数列的通项公式 ①2n s =23n n + ②n s =31n +

③2

n (1)s =

(0)4

n n a a +>

例2：已知等差数列{}n a 的通项为*172,n a n n N =-∈，则使得n S 最大的n 的值是？、

3：等差等比知识回顾

亲，上面所列的东西是数列本章需要记忆（常用）的东西，牢记可以提高做提速噢，练习以下热热身

①已知等差数列}{n a 中，12497,1,16a a a a 则==+的值是 ( )

A.15

B.30

C.31

D.64

②在各项都为正数的等比数列｛a n ｝中，首项a 1=3 ，前三项和为21，则a 3+ a 4+ a 5=( )

A.33

B.72

C.84

D.189 ③已知等差数列{}n a 的公差为2,若431,,a a a 成等比数列, 则2a = ( ) A.–4 B.–6 C.–8 D.–10 ④如果数列}{n a 是等差数列，则( ) A.5481a a a a +>+ B.5481a a a a +=+ C.5481a a a a +<+ D.5481a a a a =

4：数列的通项公式（很多高考大题的第一问）

方法1：利用定义（已知等差等比或者能配凑成等差等比）

例1：等差数列{}n a 是递增数列，前n 项和为n S ，且931,,a a a 成等比数列，2

5

5a S =．求数列{}n a 的通项公式

方法2：公式法

若已知数列的前n 项和n S 与n a 的关系，求数列{}n a 的通项n a 可用公式

??

?≥???????-=????????????????=-2

1

11n S S n S a n n n 求解 例2：(1)已知数列{}n a 的前n 项和n S 满足1,)1(2≥-+=n a S n n n ．求数列{}n a 的通项公式

(2) 设n S 是数列{}n a 的前n 项和，11=a ，)2(212

≥??? ?

?-=n S a S n n n .

⑴求{}n a 的通项；

⑵设1

2+=n S b n

n ，求数列{}n b 的前n 项和n T .

方法3：递推公式

类型一：)(1n f a a n n +=+（迭加法或迭代法） 例3：已知数列{}n a 满足2

1

1=a ，n a a n n +=+1，求n a

练习1：已知数列{}n a 中，)2(12,211≥-+==-n n a a a n n ，求数列{}n a 的通项公式；

类型二：n n a n f a )(1=+（累乘法） 例4：已知数列{}n a 满足321=a ，n n a n n

a 1

1+=

+，求n a

练习2：已知数列{}n a 满足：111

(2),21

n n a n n a a n --=≥=+，求求数列{}n a 的通项公式；

类型三：q pa a n n +=+1（待定系数法）构造新数列

例5：已知数列{}n a 中，11=a ，321+=+n n a a ，求n a

知识点巩固：

①数列{a n }满足a 1=1，a n =2

1

a 1-n +1（n ≥2），求数列{a n }的通项公式

②数列{a n }满足a 1=1，0731=-++n n a a ,求数列{a n }的通项公式

③已知数列{}n a 满足11=a ，且132n n a a +=+，求n a

④已知数列{}n a 满足321=a ，n n a n n

a 1

1+=

+，求n a

5：证明数列是等差或等比数列

1)证明数列等差

例1、已知n S 为等差数列{}n a 的前n 项和，)(+∈=N n n

S b n

n .求证：数列{}n b 是等差数列.

例2、已知数列{a n }的前n 项和为S n ，且满足a n +2S n ·S n －1=0（n ≥2），a 1=2

1. 求证：{

n

S 1

}是等差数列；

2）证明数列等比

例1、设{a n }是等差数列，b n ＝n

a ??

?

??21，求证：数列{b n }是等比数列；

例2、数列{a n }的前n 项和为S n ，数列{b n }中，若a n +S n =n .设c n =a n －1，求证：数列{c n }是等比数列；

例3、已知n S 为数列{}n a 的前n 项和，11=a ，24+=n n a S .

⑴设数列{}n b 中，n n n a a b 21-=+，求证：{}n b 是等比数列；

⑵设数列{}n c 中，n

n n a

c 2

=，求证：{}n c 是等差数列；⑶求数列{}n a 的通项公式及前n 项和.

例4、已知数列{}n a 满足*12211,3,32().n n n a a a a a n N ++===-∈ ⑴证明：数列{}1n n a a +-是等比数列； ⑵求数列{}n a 的通项公式；

⑶若数列{}n b 满足12111*44...4(1)(),n n b b b b n a n N ---=+∈证明{}n b 是等差数列.

6：数列求和

方法1：公式法

例1：已知数列12-=n a n ，求n S

方法2：分组求和

例2：已知数列n n n a 2+=，求n S

方法3：错位相减——适用于通项为等差乘以等比类型 例3：已知数列n n n a 2?=，求n S

方法4：裂项相消——常见裂项公式

1

(1)

n n =

+111

n n -

+,

])

2)(1(1

)1(1[21)2)(1(1++-+=+-=

n n n n n n n a n

1(21)(21)n n =-+11122121n n ??

- ?-+??

例4：已知数列)

1(1

+=

n n a n ，求n S

方法5：倒序相加法，

例5、设2

2

1)(x x x f +=，求：

⑵ )4()3()2()()()(1

11f f f f f f +++++；

⑵).2010()2009

()2()()()()(21312009120101f f f f f f f ++++++++ 7：数列中的最值问题

例1、数列{}n a 中，492-=n a n ，当数列{}n a 的前n 项和n S 取得最小值时，=n .

例2、已知n S 为等差数列{}n a 的前n 项和，.16,2541==a a 当n 为何值时，n S 取得最大值；

例3、数列{}n a 中，12832+-=n n a n ，求n a 取最小值时n 的值.

例4、数列{}n a 中，22+-=n n a n ，求数列{}n a 的最大项和最小项.

例5、设数列{}n a 的前n 项和为n S ．已知1a a =，13n n n a S +=+，*n ∈N ． （Ⅰ）设3n n n b S =-，求数列{}n b 的通项公式； （Ⅱ）若1n n a a +≥，*n ∈N ，求a 的取值范围．

8：高考真题解答

1．在公差为d 的等差数列}{n a 中,已知101

=a ,且3215,22,a a a +成等比数列.

(1)求n a d ,; (2)若0

2．等差数列

{}n a 的前n 项和为n S ,已知232=S a ,且124,,S S S 成等比数列,求{}n a 的通项式.

3．（2013年高考江西卷（理））正项数列{a n }的前项和{a n }满足:2

22(1)()0n

n s n n s n n -+--+=

(1)求数列{a n }的通项公式a n ; (2)令22

1(2)n n b n a

+=+,数列{b n }的前n 项和为n T .证明:对于任意的*

n N ∈,都有564n T < 4.已知

{}

n a 是等差数列,其前n 项和为n S ,

{}

n b 是等比数列,且

114444,27,=10a b a b S b =+=-.

(I)求数列{}n a 与{}n b 的通项公式; (II)记1122=++

+n n n T a b a b a b (*n N ∈)证明:*118(,2)n n n T a b n N n ---=∈>.

5.设数列{}n a 的前n 项和为n S ,数列{}n S 的前n 项和为n T ,满足22n n T S n =-,n ∈*N .

(Ⅰ)求1a 的值;

(Ⅱ)求数列{}n a 的通项公式.

6.已知等比数列{}n a 的各项均为正数，且

2

12326231,9a a a a a +==． （I ）求数列

{}n a 的通项公式．

（II ）设

31323log log log n n b a a a =++

+，求数列1

{}

n b 的前n 项和．

数列高考试题汇编

1.【2014·全国卷Ⅱ（文5）】等差数列{}n a 的公差为2，若2a ，4a ，8a 成等比数列，则{}n a 的前n 项和n S =

（A ） ()1n n + （B ）()1n n - （C ）

()12

n n + (D)

()12

n n -

2.【2014·全国大纲卷（理10）】等比数列{}n a 中，452,5a a ==，则数列{lg }n a 的前8项和等于 （ ）

A ．6

B ．5

C ．4

D ．3

3.【2014·全国大纲卷（文8）】设等比数列{a n }的前n 项和为S n ，若S 2=3，S 4=15，则S 6=( ) A. 31 B. 32 C. 63 D. 64

4.【2014·北京卷（理5）】设{}n a 是公比为q 的等比数列，则"1"q >是"{}"n a 为递增数列的（ ）

.A 充分且不必要条件 .B 必要且不充分条件 .C 充分必要条件 .D 既不充分也不必要条件

5.【2014·天津卷（文5）】设{}n a 是首项为1a ，公差为-1的等差数列，n S 为其前n 项和.若

124,,S S S 成等比数列，则1a =（ ）

（A ）2 （B ）-2 （C ）

12 （D ）12

- 6.【2014·福建卷（理3）】等差数列{}n a 的前n 项和n S ，若132,12a S ==，则6a =( )

.8A .10B .12C .14D

7.【2014·辽宁卷（文9）】设等差数列{}n a 的公差为d ，若数列1{2}n a a

为递减数列，则（ ） A ．0d > B ．0d < C ．10a d > D ．10a d <

8.【2014·陕西卷（理文4）】根据右边框图，对大于2的整数N ， 得出数列的通项公式是（ ）

.2n Aa n = .2(1)n B a n =-

.2n n C a = 1.2n n D a -=

9.【2014·重庆卷（理2）】对任意等比数列{}n a ,下列说法一定正确的是（ ）

139.,,A a a a 成等比数列 236.,,B a a a 成等比数列 248.,,C a a a 成等比数列 369.,,D a a a 成等比数列

10.【2014·重庆卷（文2）】在等差数列{}n a 中,1352,10a a a =+=，则7a =（ ）

.5A .8B .10C .14D

11.【2014·全国卷Ⅱ（文16）】数列{}n a 满足1+n a =

n a -11

，2a =2，则1

a =_________. 12.【2014·安徽卷（理12）】数列{}a n 是等差数列，若1a 1+，3a 3+，5a 5+构成公比为q 的等比数列，则q =________.

13.【2014·安徽卷（文12）】如图，在等腰直角三角形ABC

A

A 2

中，斜边BC =A 作BC 的垂线，垂足为1A ；过点1A 作AC 的垂线，垂足为2A ；过点

2A 作1A C

的垂线，垂足为3A ；…，以此类推，设1BA a =，12AA a =，123A A a =，…，567A A a =，

则7a =_____ ___.

14.【2014·北京卷（理12）】若等差数列{}n a 满足7890a a a ++>，7100a a +<，则当

n =________时{}n a 的前n 项和最大.

15.【2014·天津卷（理11）】设{}n a 是首项为1a ，公差为-1的等差数列，n S 为其前n 项和.若124,,S S S 成等比数列，则1a 的值为__________.

16.【2014·江西卷（文13）】在等差数列{}n a 中，17a =，公差为d ，前n 项和为n S ，当且仅当8n =时n S 取最大值，则d 的取值范围_________.

17.【2014·广东卷（理13）】若等比数列{}n a 的各项均为正数，且512911102e a a a a =+，则

1220ln ln ln a a a +++= 。

18.【2014·广东卷（文13）】等比数列{}n a 的各项均为正数且154a a =，则

2122232425log log log log log a a a a a ++++ ＝ .

高考数列专题练习精选文档

高考数列专题练习精选 文档 TTMS system office room 【TTMS16H-TTMS2A-TTMS8Q8-

1..等比数列}{n a 为递增数列，且,324=a 9 20 53= +a a ，数列2log 3n n a b =(n ∈N ※) （1）求数列}{n b 的前n 项和n S ； （2）122221-++++=n b b b b T n ，求使0>n T 成立的最小值n ． 2．已知数列{ n a }、{ n b }满足：112 1 ,1,41n n n n n b a a b b a +=+==-. (1)求1,234,,b b b b ; (2)求数列{ n b }的通项公式； (3)设1223341...n n n S a a a a a a a a +=++++，求实数a 为何值时4n n aS b <恒成立 3．在数列{}n a 中，n S 为其前n 项和，满足2,(,*)n n S ka n n k R n N =∈∈+-． （I ）若1k =，求数列{}n a 的通项公式； （II ）若数列{21}n a n --为公比不为1的等比数列，且1>k ，求n S ． 4．已知等差数列{}n a 满足：37a =，5726a a +=，{}n a 的前n 项和为n S ． （Ⅰ）求n a 及n S ； （Ⅱ）令b n = 2 1 1 n a -（*n ∈N ），求数列{}n b 的前n 项和n T 。 5，已知递增的等比数列{}n a 满足234328,2a a a a ++=+且是24,a a 的等差中项。 （Ⅰ）求数列{}n a 的通项公式； （Ⅱ）若n n n S a b ,12log +=是数列{}n n a b 的前n 项和，求.n S 6．已知数列{}n a 中，14a =，12(1)n n a a n +=-+，（1）求证：数列{}2n a n -为等比数列。 （2）设数列{}n a 的前n 项和为n S ，若22n n S a n ≥+，求正整数列n 的最小值。 7．已知数列{}n a 的前n 项和为n S ，若1 1 2,.n n n n n n a S a n b a a +-=+=且 （1）求证：{1}n a -为等比数列；

最全高考复习数列专题及练习答案详解

高考复习数列专题： 数 列(参考答案附后) 第一节 数列的概念与数列的简单表示 一、选择题 1．已知数列{}a n 对任意的p ，q ∈N * 满足a p ＋q ＝a p ＋a q ，且a 2＝－ 6，那么a 10＝( ) A ．－165 B ．－33 C ．－30 D ．－21 2．在数列{a n }中，a 1＝2，a n ＋1＝a n ＋ln(1＋1 n )，则a n ＝( ) A ．2＋ln n B ．2＋(n －1)ln n C ．2＋n ln n D ．1＋n ＋ln n 3．若数列{a n }的前n 项积为n 2 ，那么当n ≥2时，{a n }的通项公式为( ) A ．a n ＝2n －1 B ．a n ＝n 2 C ．a n ＝ n ＋12 n 2 D ．a n ＝ n 2n －1 2 4．在数列{a n }中，a n ＋1＝a n ＋2＋a n ，a 1＝2，a 2＝5，则a 6的值是( ) A ．－3 B ．－11 C ．－5 D ．19 5．已知数列{a n }中，a n ＝n －79n －80 (n ∈N *)，则在数列{a n }的前50 项中最小项和最大项分别是( ) A ．a 1，a 50 B ．a 1，a 8 C ．a 8，a 9 D ．a 9， a 50 二、填空题 6．若数列{}a n 的前n 项和S n ＝n 2 －10n (n ＝1,2,3，…)，则此数

列的通项公式为________；数列{}na n 中数值最小的项是第__________项． 7．数列35，12，511，37，7 17，…的一个通项公式是 ___________________________． 8．设数列{a n }中，a 1＝2，a n ＋1＝a n ＋n ＋1，则通项a n ＝__________. 三、解答题 9．如果数列{}a n 的前n 项和为S n ＝3 2a n －3，求这个数列的通项 公式． 10．已知{a n }是正数组成的数列，a 1＝1，且点(a n ，a n ＋1)(n ∈N ＋ )在函数y ＝x 2 ＋1的图象上． (1)求数列{a n }的通项公式； (2)若列数{b n }满足b 1＝1，b n ＋1＝b n ＋2a n ，求证：b n ·b n ＋2＜b 2 n ＋1.

高考数学《数列》大题训练50题含答案解析

一．解答题（共30小题） 1．（2012?上海）已知数列{a n}、{b n}、{c n}满足．（1）设c n=3n+6，{a n}是公差为3的等差数列．当b1=1时，求b2、b3的值； （2）设，．求正整数k，使得对一切n∈N*，均有b n≥b k； （3）设，．当b1=1时，求数列{b n}的通项公式． 2．（2011?重庆）设{a n}是公比为正数的等比数列a1=2，a3=a2+4． （Ⅰ）求{a n}的通项公式； ( （Ⅱ）设{b n}是首项为1，公差为2的等差数列，求数列{a n+b n}的前n项和S n． 3．（2011?重庆）设实数数列{a n}的前n项和S n满足S n+1=a n+1S n（n∈N*）． （Ⅰ）若a1，S2，﹣2a2成等比数列，求S2和a3． （Ⅱ）求证：对k≥3有0≤a k≤． 4．（2011?浙江）已知公差不为0的等差数列{a n}的首项a1为a（a∈R）设数列的前n 项和为S n，且，，成等比数列． （Ⅰ）求数列{a n}的通项公式及S n； ` （Ⅱ）记A n=+++…+，B n=++…+，当a≥2时，试比较A n与B n的大小． 5．（2011?上海）已知数列{a n}和{b n}的通项公式分别为a n=3n+6，b n=2n+7（n∈N*）．将集合{x|x=a n，n∈N*}∪{x|x=b n，n∈N*}中的元素从小到大依次排列，构成数列c1，c2，

（1）写出c1，c2，c3，c4； （2）求证：在数列{c n}中，但不在数列{b n}中的项恰为a2，a4，…，a2n，…； （3）求数列{c n}的通项公式． 6．（2011?辽宁）已知等差数列{a n}满足a2=0，a6+a8=﹣10 * （I）求数列{a n}的通项公式； （II）求数列{}的前n项和． 7．（2011?江西）（1）已知两个等比数列{a n}，{b n}，满足a1=a（a＞0），b1﹣a1=1，b2﹣a2=2，b3﹣a3=3，若数列{a n}唯一，求a的值； （2）是否存在两个等比数列{a n}，{b n}，使得b1﹣a1，b2﹣a2，b3﹣a3．b4﹣a4成公差不为0的等差数列若存在，求{a n}，{b n}的通项公式；若不存在，说明理由． 8．（2011?湖北）成等差数列的三个正数的和等于15，并且这三个数分别加上2、5、13后成为等比数列{b n}中的b3、b4、b5． （I）求数列{b n}的通项公式； ] （II）数列{b n}的前n项和为S n，求证：数列{S n+}是等比数列． 9．（2011?广东）设b＞0，数列{a n}满足a1=b，a n=（n≥2） （1）求数列{a n}的通项公式； （4）证明：对于一切正整数n，2a n≤b n+1+1．

高考数学数列题型专题汇总

高考数学数列题型专题 汇总 公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]

高考数学数列题型专题汇总 一、选择题 1、已知无穷等比数列{}n a 的公比为q ，前n 项和为n S ，且S S n n =∞ →lim .下列 条件中，使得()*∈q a （B ）6.07.0,01-<<-q a （D ）7.08.0,01-<<-

A ．{}n S 是等差数列 B ．2{}n S 是等差数列 C ．{}n d 是等差数列 D ．2{}n d 是等差数列 【答案】A 二、填空题 1、已知{}n a 为等差数列，n S 为其前n 项和，若16a =，350a a +=，则 6=S _______.. 【答案】6 2、无穷数列{}n a 由k 个不同的数组成，n S 为{}n a 的前n 项和.若对任意 *∈N n ，{}3,2∈n S ，则k 的最大值为________. 【答案】4 3、设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2a n 的最大值 为 . 【答案】64 4、设数列{a n }的前n 项和为S n .若S 2=4，a n +1=2S n +1，n ∈N *，则 a 1= ，S 5= . 【答案】1 121

高考数列专题练习(精选课件)

高考数列专题练习 数列综合题 １．已知等差数列{}n a 满足：3 7a =，5726a a +=,{}n a 的前n 项 和为n S . ?（Ⅰ）求n a 及n S ； ?（Ⅱ）令b n = 21 1 n a -(*n ∈N ）,求数列{}n b 的前n 项和n T 。 2.已知递增的等比数列{}n a 满足234328,2a a a a ++=+且是2 4 ,a a 的 等差中项。 ?(Ⅰ)求数列{}n a 的通项公式; ?（Ⅱ）若n n n S a b ,12log +=是数列{}n n a b 的前n 项和,求.n S 3.等比数列}{n a 为递增数列，且, 3 24=a 9 2053= +a a ,数列 2 log 3n n a b =（n ∈N ※ ) （1）求数列}{n b 的前n 项和n S ； （2）12 22 21-++++=n b b b b T n ，求使0>n T 成立的最小值n . 4.已知数列{ n a ｝、{ n b ｝满足：112 1,1,4 1n n n n n b a a b b a +=+== -. (１）求1,2 3 4 ,,b b b b ; （2)求数列{ n b ｝的通项公式； (３）设1223341...n n n S a a a a a a a a +=++++，求实数a 为何值时4n n aS b <

恒成立 5．在数列{}n a 中，n S 为其前n 项和,满足 2,(,*)n n S ka n n k R n N =∈∈+-。 (I)若1k =，求数列{}n a 的通项公式； （II)若数列{21}n a n --为公比不为1的等比数列，且1>k ,求n S . 6.已知数列{}n a 中，1 4a =，12(1)n n a a n +=-+,(1）求证：数列 {}2n a n -为等比数列。 （２)设数列{}n a 的前n 项和为n S ,若22n n S a n ≥+，求正整数列 n 的最小值。? 7．已知数列{}n a 的前n 项和为n S ,若1 12,.n n n n n n a S a n b a a +-=+=且 ?（1)求证:{1}n a -为等比数列； (2)求数列{}n b 的前n 项和. 8．已知数列{}n a 中，113 a =,当2n ≥时,其前n 项和n S 满足 2 221 n n n S a S = -. （1）求n S 的表达； （2）求数列{}n a 的通项公式； 9．已知数列{}n a 的首项135 a =，1 231+= +n n n a a a ,其中*∈N n . （1）求证:数列11n a ?? -???? 为等比数列; （2)记12111n n S a a a = ++，若100n S <，求最大的正整数n .

高考数列专题总结(全是精华)

数列专题复习（0929） 一、证明等差等比数列 1． 等差数列的证明方法： （1）定义法：1n n a a d +-=(常数) （2）等差中项法：112(2)n n n a a a n +-+=≥ 2．等比数列的证明方法： （1）定义法： 1 n n a q a +=(常数) （2）等比中项法：211(2)n n n a a a n +-=≥ 例1.设｛a n ｝为等差数列，S n 为数列｛a n ｝的前n 项和，已知S 7＝7，S 15＝75， T n 为数列｛n S n ｝的前n 项和，求T n ． 解：设等差数列｛a n ｝的公差为d ，则 S n =na 1＋21 n （n －1）d ．∴S 7＝7，S 15＝75，∴???=+=+,7510515,721711d a d a 即???=+=+,57,1311d a d a 解得a 1＝－2，d ＝1．∴n S n ＝a 1＋21（n －1）d ＝－2＋21 （n －1）． ∵ 2111=-++n S n S n n ，∴数列｛n S n ｝是等差数列，其首项为－2，公差为2 1 ， ∴T n ＝ 41n 2－4 9n ． 例2．设数列{a n }的首项a 1=1，前n 项和S n 满足关系式： 3tS n －（2t +3）S n －1=3t （t >0，n =2，3，4，…） 求证：数列{a n }是等比数列； 解：（1）由a 1=S 1=1，S 2=1+a 2，得a 2=t t a a t t 323,32312+= + 又3tS n －（2t +3）S n －1=3t ① 3tS n －1－（2t +3）S n －2=3t ② ①－②得3ta n －（2t +3）a n －1=0 ∴t t a a n n 33 21+= -，（n =2，3，…） 所以{a n }是一个首项为1，公比为 t t 33 2+的等比数列. 练习：已知a 1=2，点(a n ,a n+1)在函数f (x )=x 2+2x 的图象上，其中=1，2，3，… （1） 证明数列｛lg(1+a n )｝是等比数列； （2） 设T n =(1+a 1) (1+a 2) …(1+a n )，求T n 及数列｛a n ｝的通项； 答案 .(2) 21 3 n n T -=,21 3 1n n a -=-; 二．通项的求法 （1）利用等差等比的通项公式 (2)累加法：1()n n a a f n +-= 例3．已知数列{}n a 满足211=a ，n n a a n n ++=+211，求n a 。 解：由条件知：1 1 1)1(112 1+-=+=+= -+n n n n n n a a n n 分别令)1(,,3,2,1-??????=n n ，代入上式得)1(-n 个等式累加之，即 )()()()(1342312--+??????+-+-+-n n a a a a a a a a )111()4131()3121()211(n n --+??????+-+-+-=所以n a a n 1 11-=- 211=a ，n n a n 1231121-=-+=∴ （3）构造等差或等比 1n n a pa q +=+或1()n n a pa f n +=+ 例4．已知数列{}n a 满足* 111,21().n n a a a n N +==+∈ 求数列{}n a 的通项公式； 解：*121(),n n a a n N +=+∈ 112(1),n n a a +∴+=+ {}1n a ∴+是以112a +=为首项，2为公比的等比数列。 12.n n a ∴+= 即 *21().n n a n N =-∈

高考数学数列大题专题

高考数学数列大题专题 1. 已知等比数列432,,,}{a a a a n 中分别是某等差数列的第5项、第3项、第2项，且1,641≠=q a 公比 （Ⅰ）求n a ；（Ⅱ）设n n a b 2log =，求数列.|}{|n n T n b 项和的前 2.已知数列}{n a 满足递推式)2(121≥+=-n a a n n ，其中.154=a （Ⅰ）求321,,a a a ； （Ⅱ）求数列}{n a 的通项公式； （Ⅲ）求数列}{n a 的前n 项和n S 3．已知数列{}n a 的前n 项和为n S ，且有12a =，11353n n n n S a a S --=-+(2)n ≥ （1）求数列n a 的通项公式； （2）若(21)n n b n a =-，求数列n a 的前n 项的和n T 。 4.已知数列{n a }满足11=a ，且),2(22*1N n n a a n n n ∈≥+=-且． （Ⅰ）求2a ，3a ；（Ⅱ）证明数列{n n a 2}是等差数列； （Ⅲ）求数列{n a }的前n 项之和n S

5.已知数列{}n a 满足31=a ，1211-=--n n n a a a . （1）求2a ，3a ，4a ； （2）求证：数列11n a ??? ?-?? 是等差数列，并写出{}n a 的一个通项。 622,,4,21121+=-===++n n n n n b b a a b a a . 求证： ⑴数列{b n +2}是公比为2的等比数列； ⑵n a n n 221-=+； ⑶4)1(2221-+-=++++n n a a a n n Λ. 7. .已知各项都不相等的等差数列}{n a 的前六项和为60，且2116a a a 和为 的等比中项. （1）求数列}{n a 的通项公式n n S n a 项和及前； （2）若数列}1{,3),(}{11n n n n n b b N n a b b b 求数列且满足=∈=-*+的前n 项和T n .

高考数列专题讲解(含答案)

数列 题型一、数列的综合问题 【例1】已知首项为32的等比数列{a n }不是递减数列，其前n 项和为S n (n ∈N *)，且 S 3＋a 3，S 5＋a 5，S 4＋a 4成等差数列. (1)求数列{a n }的通项公式； (2)设T n ＝S n －1S n (n ∈N *)，求数列{T n }的最大项的值与最小项的值. 解 (1)设等比数列{a n }的公比为q ， 因为S 3＋a 3，S 5＋a 5，S 4＋a 4成等差数列， 所以S 5＋a 5－S 3－a 3＝S 4＋a 4－S 5－a 5，即4a 5＝a 3， 于是q 2＝a 5a 3 ＝14. 又{a n }不是递减数列且a 1＝32，所以q ＝－12. 故等比数列{a n }的通项公式为a n ＝32×? ?? ??－12n －1 ＝(－1)n －1·32n . (2)由(1)得S n ＝1－? ????－12n ＝?????1＋12n ，n 为奇数，1－12n ，n 为偶数， 当n 为奇数时，S n 随n 的增大而减小， 所以1S n －1S n ≥S 2－1S 2 ＝34－43＝－712.

综上，对于n ∈N *，总有－712≤S n －1S n ≤56. 所以数列{T n }最大项的值为56，最小项的值为－712. 【分析】解决等差数列与等比数列的综合问题，既要善于综合运用等差数列与等比数列的相关知识求解，更要善于根据具体问题情境具体分析，寻找解题的突破口. 【即时应用】已知数列{a n }是公差不为零的等差数列，其前n 项和为S n ，满足S 5－2a 2＝25，且a 1，a 4，a 13恰为等比数列{b n }的前三项. (1)求数列{a n }，{b n }的通项公式； (2)设T n 是数列??????????1a n a n ＋1的前n 项和，是否存在k ∈N *，使得等式1－2T k ＝1b k 成立？若存在，求出k 的值；若不存在，请说明理由. 解 (1)设等差数列{a n }的公差为d (d ≠0)， ∴?????? ????5a 1＋5×42d －2（a 1＋d ）＝25，（a 1＋3d ）2＝a 1（a 1＋12d ）， 解得a 1＝3，d ＝2，∴a n ＝2n ＋1. ∵b 1＝a 1＝3，b 2＝a 4＝9， ∴等比数列{b n }的公比q ＝3，∴b n ＝3n . (2)不存在.理由如下： ∵1a n a n ＋1＝1（2n ＋1）（2n ＋3）＝12? ?? ??12n ＋1－12n ＋3， ∴T n ＝12???? ??? ????13－15＋? ????15－17＋…＋? ????12n ＋1－12n ＋3 ＝12? ?? ??13－12n ＋3， ∴1－2T k ＝23＋12k ＋3 (k ∈N *)， 易知数列?????? ????12k ＋3为单调递减数列， ∴23<1－2T k ≤1315，又1b k ＝13k ∈? ????0，13，

(word完整版)全国高考数列大题专题.doc

高考中的数列—最后一讲 （内部资料勿外传）1．已知数列 {a n} 、 {b n} 、 {c n} 足． （ 1） c n=3n+6， {a n} 是公差 3 的等差数列．当b1 =1 ，求 b2、 b3的； （ 2），．求正整数 k，使得一切 * n∈N，均有 b n≥b；k （ 3），．当b1=1，求数列{b n}的通公式．2． {a } 是公比正数的等比数列 a =2， a =a +4． n 13 2 （Ⅰ）求 {a n} 的通公式； （Ⅱ） {b n } 是首 1，公差 2 的等差数列，求数列 n n n {a +b } 的前 n 和 S ． 3．已知公差不0 的等差数列 {a n} 的首 a1a（ a∈R）数列的前n 和 S n，且，，成等比数列． 矚 慫润厲钐瘗睞枥庑赖。 （Ⅰ）求数列 {a n} 的通公式及S n； （Ⅱ） A n=+++?+，B n=++?+，当a≥2，比 A n与 B n的大小． 4．已知等差数列 {a } 足 a =0， a +a = 10 n 2 6 8 （ I）求数列 {a n} 的通公式； （ II ）求数列 { } 的前 n 和． 5．成等差数列的三个正数的和等于15，并且三个数分加上2、5、 13 后成等比数列{b n} 中的 b3、 b4、 b5． 聞 創沟燴鐺險爱氇谴净。 （I）求数列 {b n} 的通公式； （II ）数列 {b n} 的前 n 和 S n，求：数列 {S n+ } 是等比数列． 6．在数 1 和 100 之插入 n 个数，使得 n+2 个数构成增的等比数列，将n+2个数的乘作T n，再令 a n=lgT n，

(完整版)高考数列专题复习

专题数列知识网络

专题训练 一．选择题 1.设数列{}n a的前n项和 2 n S n =，则 8 a的值为 （A） 15 (B) 16 (C) 49 （D）64 2.设等差数列 {} n a 的前n项和为n S,若111 a=-, 46 6 a a +=-,则当 n S取最小值时,n 等于 A.6 B.7 C.8 D.9 3.如果等差数列 {} n a 中，34512 a a a ++=，那么 127 ... a a a +++= （A）14 （B）21 （C）28 （D）35 4.已知等比数列{m a}中，各项都是正数，且1a，32 1 ,2 2 a a 成等差数列，则 910 78 a a a a + = + A.12 + B. 12 - C. 322 +D322 - 5.在等比数列 {} n a 中，11 a=，公比1 q≠ .若12345 m a a a a a a =，则m= （A）9 （B）10 （C）11 （D）12

6.等比数列 {} n a 中，15252||1,8,, a a a a a ==->则 n a = A ．1 (2)n -- B ．1 (2)n --- C ．(2)n - D ．(2)n -- 7.设{n a }是由正数组成的等比数列，n S 为其前n 项和，已知24a a =1, 37 S =, 则 5S = （A ）152 (B)314 (C)33 4 (D)172 8.设 n S 为等比数列{}n a 的前n 项和，已知3432S a =-，2332 S a =-，则公比q = （A ）3 （B ）4 （C ）5 （D ）6 9.（文）设{}n a 是等比数列，则“123a a a <<”是数列{}n a 是递增数列的 （A ）充分而不必要条件 (B)必要而不充分条件、 （C ）充分必要条件 （D ）既不充分也不必要条件 （理）设{}n a 是首项大于零的等比数列，则“12 a a <”是“数列{}n a 是递增数列”的 （A ）充分而不必要条件 (B)必要而不充分条件 (C)充分必要条件 (D)既不充分也不必要条件 10.已知{ n a }是首项为1的等比数列，n S 是{n a }的前n 项和，且36 9S S =。则数列 n 1a ?? ?? ??的前5项和为 （A ）158或5 （B ）3116或5 （C ）3116 （D ）15 8 11.设n S 为等比数列{}n a 的前n 项和，2580a a +=，则5 2S S = （A ）11 （B ）5 （C ）8- （D ）11- 12.设{}n a 是任意等比数列，它的前n 项和，前2n 项和与前3n 项和分别为,,X Y Z ，则下列等式中恒成立的是

高考数列大题专题精选

高考数列大题专题 （内部资料勿外 传） 1．已知数列{a n}、{b n}、{c n}满足． （1）设c n=3n+6，{a n}是公差为3的等差数列．当b1=1时，求b2、b3的值； （2）设，．求正整数k，使得对一切n∈N*，均有b n≥b k； （3）设，．当b1=1时，求数列{b n}的通项公式． 2．设{a n}是公比为正数的等比数列a1=2，a3=a2+4． （Ⅰ）求{a n}的通项公式； （Ⅱ）设{b n}是首项为1，公差为2的等差数列，求数列{a n+b n}的前n项和S n． 3．已知公差不为0的等差数列{a n}的首项a1为a（a∈R）设数列的前n项和为S n，且，，成等比数列． （Ⅰ）求数列{a n}的通项公式及S n； （Ⅱ）记A n=+++…+，B n=++…+，当a≥2时，试比较A n与B n的大小． 4．已知等差数列{a n}满足a2=0，a6+a8=﹣10

（I）求数列{a n}的通项公式； （II）求数列{}的前n项和． 5．成等差数列的三个正数的和等于15，并且这三个数分别加上2、5、13后成为等比数列{b n}中的b3、b4、b5． （I）求数列{b n}的通项公式； （II）数列{b n}的前n项和为S n，求证：数列{S n+}是等比数列． 6．在数1 和100之间插入n个实数，使得这n+2个数构成递增的等比数列，将这n+2个数的乘积计作T n，再令a n=lgT n ，n≥1． （I）求数列{a n}的通项公式； （Ⅱ）设b n=tana n?tana n+1，求数列{b n}的前n项和S n． 7.设a1，d为实数，首项为a1，公差为d的等差数列{a n}的前n项和为S n，满足S5S6+15=0． （Ⅰ）若S5=5，求S6及a1； （Ⅱ）求d的取值范围． 8．已知等差数列{a n}的前3项和为6，前8项和为﹣4． （Ⅰ）求数列{a n}的通项公式； （Ⅱ）设b n=（4﹣a n）q n﹣1（q≠0，n∈N*），求数列{b n}的前n项和S n．

高考数列专题总结(全是精华)

数列专题复习（0929） 一、证明等差等比数列 1． 等差数列的证明方法： （1）定义法：1n n a a d +-=(常数) （2）等差中项法：112(2)n n n a a a n +-+=≥ 2．等比数列的证明方法： （1）定义法： 1 n n a q a +=(常数) （2）等比中项法：211(2)n n n a a a n +-=≥ 例1.设｛a n ｝为等差数列，S n 为数列｛a n ｝的前n 项和，已知S 7＝7，S 15＝75， T n 为数列｛ n S n ｝的前n 项和，求T n ． 解：设等差数列｛a n ｝的公差为d ，则 S n =na 1＋21 n （n －1）d ．∴S 7＝7，S 15＝75，∴???=+=+,7510515,721711d a d a 即???=+=+,57,131 1d a d a 解得a 1＝－2，d ＝1．∴ n S n ＝a 1＋21（n －1）d ＝－2＋21 （n －1）． ∵ 2111=-++n S n S n n ，∴数列｛n S n ｝是等差数列，其首项为－2，公差为21 ， ∴T n ＝ 41n 2－4 9 n ． 例2．设数列{a n }的首项a 1=1，前n 项和S n 满足关系式： 3tS n －（2t +3）S n －1=3t （t >0，n =2，3，4，…） 求证：数列{a n }是等比数列； 解：（1）由a 1=S 1=1，S 2=1+a 2，得a 2=t t a a t t 323,32312+= + 又3tS n －（2t +3）S n －1=3t ① 3tS n －1－（2t +3）S n －2=3t ② ①－②得3ta n －（2t +3）a n －1=0 ∴ t t a a n n 33 21+= -，（n =2，3，…） 所以{a n }是一个首项为1，公比为t t 33 2+的等比数列. 练习：已知a 1=2，点(a n ,a n+1)在函数f (x )=x 2+2x 的图象上，其中=1，2，3，… （1） 证明数列｛lg(1+a n )｝是等比数列； （2） 设T n =(1+a 1) (1+a 2) …(1+a n )，求T n 及数列｛a n ｝的通项； 答案 .(2) 2 1 3n n T -=,2 1 31n n a -=-; 二．通项的求法 （1）利用等差等比的通项公式 (2)累加法：1()n n a a f n +-= 例3．已知数列{}n a 满足211=a ，n n a a n n ++=+211，求n a 。 解：由条件知：1 1 1)1(112 1+-=+=+= -+n n n n n n a a n n 分别令)1(,,3,2,1-??????=n n ，代入上式得)1(-n 个等式累加之，即 )()()()(1342312--+??????+-+-+-n n a a a a a a a a )111()4131()3121()211(n n --+??????+-+-+-=所以n a a n 1 11-=- 211=a ，n n a n 1231121-=-+=∴ （3）构造等差或等比 1n n a pa q +=+或1()n n a pa f n +=+ 例4．已知数列{}n a 满足*111,21().n n a a a n N +==+∈ 求数列{}n a 的通项公式； 解：* 121(),n n a a n N +=+∈ 112(1),n n a a +∴+=+ {}1n a ∴+是以112a +=为首项，2为公比的等比数列。 12.n n a ∴+= 即 *21().n n a n N =-∈ 例5．已知数列{}n a 中，11a =,1111 ()22 n n n a a ++=+，求n a . 解：在1111 ()22 n n n a a ++= +两边乘以12+n 得：112(2)1n n n n a a ++?=?+ 令2n n n b a =?，则11n n b b +-=,解之得：111n b b n n =+-=-,所以1 22 n n n n b n a -= =.

2020年高考数学 大题专项练习 数列 三(15题含答案解析)

2020年高考数学 大题专项练习 数列 三 1.已知数列{a n }满足a n+1=λa n +2n (n ∈N *，λ∈R)，且a 1=2． (1)若λ=1，求数列{a n }的通项公式； (2)若λ=2，证明数列{n n a 2 }是等差数列，并求数列{a n }的前n 项和S n ． 2.设数列{}的前项和为 .已知=4，=2+1，.（1）求通项公式 ；（2）求数列{}的前项和. 3.已知数列{a n }是等差数列，a 2=6，前n 项和为S n ，数列{b n }是等比数列，b 2=2，a 1b 3=12，S 3＋b 1=19. (1)求{a n }，{b n }的通项公式； (2)求数列{b n cos(a n π)}的前n 项和T n .

4.设等差数列{a n }的前n 项和为S n ，且a 5＋a 13=34，S 3=9. (1)求数列{a n }的通项公式及前n 项和公式； (2)设数列{b n }的通项公式为b n =，问：是否存在正整数t ，使得b 1，b 2，b m (m≥3，m an an ＋t ∈N)成等差数列？若存在，求出t 和m 的值；若不存在，请说明理由． 5.已知数列满足：，。数列的前n 项和为,且 .⑴求数列、的通项公式；⑵令数列满足，求其前n 项和为 6.已知{a n }是递增数列，其前n 项和为S n ，a 1>1，且10S n =(2a n ＋1)(a n ＋2)，n ∈N *. (1)求数列{a n }的通项a n ； (2)是否存在m ，n ，k ∈N *，使得2(a m ＋a n )=a k 成立？若存在，写出一组符合条件的m ，n ，k 的值；若不存在，请说明理由．

高三数列专题练习30道带答案

高三数列专题训练二 学校:___________姓名：___________班级：___________考号：___________ 一、解答题 1．在公差不为零的等差数列{}n a 中，已知23a =，且137a a a 、、成等比数列． （1）求数列{}n a 的通项公式； （2）设数列{}n a 的前n 项和为n S ，记，求数列{}n b 的前n 项和n T ． 2．已知等差数列{}n a 的前n 项和为n S ，公差,50,053=+≠S S d 且1341,,a a a 成等比数列. （Ⅰ）求数列{}n a 的通项公式； 1，公比为3的等比数列，求数列{}n b 的前n 项和n T . 3．设等比数列{}n a 的前n 项和为n S ，，2S ，3S 成等差数列，数列{}n b 满足2n b n =． （1）求数列{}n a 的通项公式； （2）设n n n c a b =?，若对任意*n N ∈，求λ的取值范围． 4．已知等差数列{n a }的公差2d =，其前n 项和为n S ，且等比数列{n b }满足11b a =， 24b a =，313b a =． （Ⅰ）求数列{n a }的通项公式和数列{n b }的前n 项和n B ； （Ⅱ）记数列的前n 项和为n T ，求n T ． 5．设数列{}n a 的前n 项和为n S ，且满足()21,2,3,n n S a n =-=． （1）求数列{}n a 的通项公式； （2）若数列{}n b 满足11b =，且1n n n b b a +=+，求数列{}n b 的通项公式； （3）设()3n n c n b =-，求数列{}n c 的前n 项和n T ．

全国卷数列高考题汇总附答案

数列专题 高考真题 (2014·I) 17. (本小题满分12分) 已知数列{}的前项和为，=1， ， ，其中为常数. （Ⅰ）证明：； （Ⅱ）是否存在，使得{}为等差数列并说明理由. (2014·II) 17.（本小题满分12分） 已知数列 满足=1， . （Ⅰ）证明是等比数列，并求 的通项公式； （Ⅱ）证明： . (2015·I)（17）（本小题满分12分） 为数列的前项和.已知， （Ⅰ）求的通项公式： （Ⅱ）设 ,求数列 的前项和。 (2015·I I)（4）等比数列 满足 ，135a a a ++ =21，则357a a a ++= ( )

（A ）21 （B ）42 （C ）63 （D ）84 (2015·I I)（16）设n S 是数列{}n a 的前n 项和，且11a =-，11n n n a S S ++=，则n S =________． (2016·I)（3）已知等差数列 前9项的和为27， ，则 （A ）100 （B ）99 （C ）98 （D ）97 (2016·I)（15）设等比数列满足 的最大值为 __________。 (2016·II)（17）（本题满分12分） S n 为等差数列的前项和，且=1 ，=28 记 ，其中表示不超过的最大整数， 如 . （I ）求，， ； （II ）求数列的前1 000项和. (2016·III)（12）定义“规范01数列” 如下： 共有项，其中项为0，项为1，且对任意， 中0的个数不少于1的个数.若 ，则不同的“规范01数列”共有 （A ）18个 （B ）16个 （C ）14个 （D ）12个 (2016·III)（17）（本小题满分12分） 已知数列的前项和 ，其中 （I ）证明是等比数列，并求其通项公式； （II ）若 ，求. (2017·I)4．记n S 为等差数列{}n a 的前n 项和．若4524a a +=，648S =，则{}n a 的公差为 A ．1 B ．2 C ．4 D ．8 (2017·I)12．几位大学生响应国家的创业号召，开发了一款应用软件。为激发大家学习数学的兴趣，他们推出了“解数学题获取软件激活码”的活动.这款软件的激活码为下面数学问题的答案：已知数列

高考数列专项大题与答案

高考数列专项大题与答 案 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN

高考数列大题专项 1.（北京卷）设数列{a n }的首项a 1=a ≠41，且 11 为偶数21 为奇数 4n n n a n a a n +???=??+??, 记 211 4n n b a -=- ，n ＝＝l ， 2，3，…·． （I ）求a 2，a 3； （II ）判断数列{b n }是否为等比数列，并证明你的结论； （III ）求123lim() n n b b b b →∞ +++ +． 2.（北京卷）数列{a n }的前n 项和为S n ，且a 1=1， 11 3n n a S +=，n =1，2，3，……，求 （I ）a 2，a 3，a 4的值及数列{a n }的通项公式； （II ）2462n a a a a +++ +的值. 3．（福建卷）已知{n a }是公比为q 的等比数列，且231,,a a a 成等差数列. （Ⅰ）求q 的值； （Ⅱ）设{ n b }是以2为首项，q 为公差的等差数列，其前n 项和为S n ，当n ≥2时，比较S n 与b n 的 大小，并说明理由.

4. （福建卷）已知数列{a n }满足a 1=a , a n+1=1+n a 1 我们知道当a 取不同的值时，得到不同的数列，如 当a =1时，得到无穷数列：. 0,1,21:,21;,35,23,2,1---=得到有穷数列时当a （Ⅰ）求当a 为何值时a 4=0； （Ⅱ）设数列{b n }满足b 1=－1, b n+1=) (11 +∈-N n b n ，求证a 取数列{b n }中的任一个数，都可以得到一个有穷数列{a n }； （Ⅲ）若)4(223 ≥<

2019年高考专题：数列试题及答案

2019年高考专题：数列 1．【2019年高考全国III 卷文数】已知各项均为正数的等比数列{}n a 的前4项和为15，且53134a a a =+，则3a =（ ） A ．16 B ．8 C ．4 D ．2 【解析】设正数的等比数列{a n }的公比为q ，则23111142 1111534a a q a q a q a q a q a ?+++=?=+?， 解得11,2 a q =??=?，2 314a a q ∴==，故选C ． 2．【2019年高考全国I 卷文数】记S n 为等比数列{a n }的前n 项和.若133 14 a S ==，，则S 4=___________． 【解析】设等比数列的公比为q ，由已知22 3111314S a a q a q q q =++=++= ，即2 104 q q ++=. 解得12q =-，所以4 4 1411()(1)521181()2 a q S q -- -= ==---． 3．【2019年高考全国III 卷文数】记n S 为等差数列{}n a 的前n 项和，若375,13a a ==，则10S = ___________. 【解析】设等差数列{}n a 的公差为d ，根据题意可得 317 125,613a a d a a d =+=??=+=?得11,2a d =??=? 101 109109 101012100.22S a d ??∴=+=?+?= 4．【2019年高考江苏卷】已知数列* {}()n a n ∈N 是等差数列， n S 是其前n 项和.若25890,27a a a S +==，则8S 的值是__________． 【解析】由题意可得：()()()25811191470 98 9272a a a a d a d a d S a d ?+=++++=? ??=+=?? ， 解得：152 a d =-??=?，则8187 840282162S a d ?=+=-+?=.

高考数学数列大题专题训练

高考数学数列大题专题训练 命题：郭治击 审题：钟世美 参考答案 1.解：（Ⅰ）设221,,,+n t t t 构成等比数列，其中100,121==+n t t ，则 2121++????=n n n t t t t T ① 1212t t t t T n n n ???=+?+ ② ①×②并利用)21(,102213+≤≤=?=?+-+n i t t t t n i n i ，得 （Ⅱ）由题意和（Ⅰ）中计算结果，知 另一方面，利用 得 所以 2.解：（Ⅰ）0，1，2，1，0是一具满足条件的E 数列A 5。 （答案不唯一，0，1，0，1，0也是一个满足条件的E 的数列A 5） （Ⅱ）必要性：因为E 数列A 5是递增数列， 所以)1999,,2,1(11 ==-+k a a k k . 所以A 5是首项为12，公差为1的等差数列. 所以a 2000=12+（2000—1）×1=2011. 充分性，由于a 2000—a 1000≤1， a 2000—a 1000≤1 …… a 2—a 1≤1 所以a 2000—a≤19999，即a 2000≤a 1+1999.

又因为a 1=12，a 2000=2011, 所以a 2000=a 1+1999. n n n A k a a 即),1999,,2,1(011 =>=-+是递增数列. 综上，结论得证。 （Ⅲ）令.1),1,,2,1(011±=-=>=-=+A k k k c n k a a c 则 因为2111112 c c a a c a a ++=++= …… 所以13211)3()2()1()(-++-+-+-+=n n c c n c n c n na A S 因为).1,,1(1,1-=-±=n k c c k k 为偶数所以 所以)1()2)(1()1)(1*21n c n c n c -++--+-- 为偶数, 所以要使2 )1(,0)(-=n n A S n 必须使为偶数, 即4整除*)(144),1(N m m n m n n n ∈+==-或亦即. 当 ,1,0,*)(14241414-===∈+=--+k k k n a a a A E N m m n 的项满足数列时14=k a ),,2,1(m k =时，有;0)(,01==n A S a 当n A E N m m n 数列时,*)(14∈+=的项满足，,1,0243314-===---k k k a a a 当)1(,)(3424-∈+=+=m n N m m n m n 时或不能被4整除，此时不存在E 数列A n ， 使得.0)(,01 ==n A S a 3.