
习题13-1图
*第13章 动力学普遍方程 和第二类拉格朗日方程
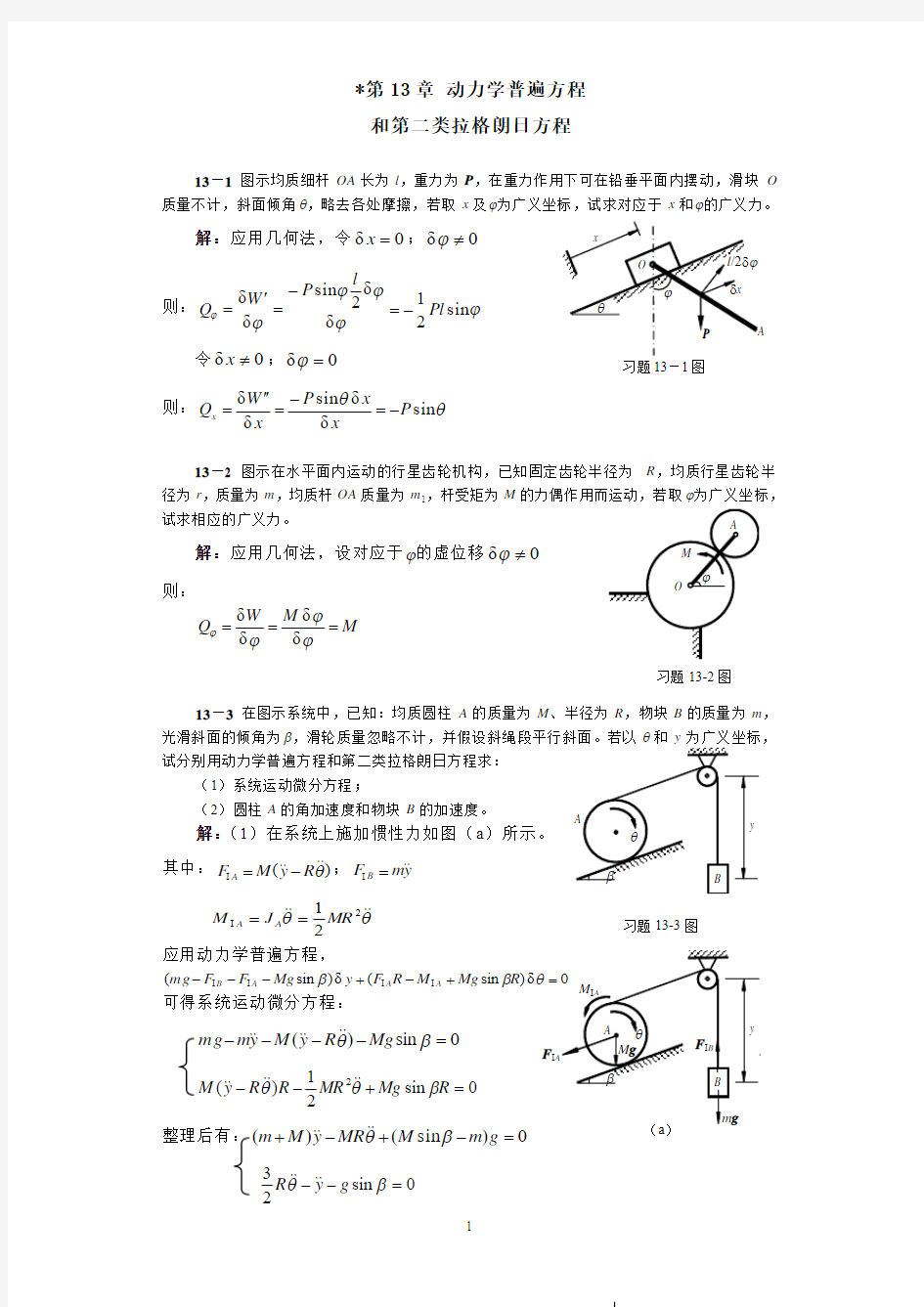
13-1 图示均质细杆OA 长为l ,重力为P ,在重力作用下可在铅垂平面内摆动,滑块O 质量不计,斜面倾角θ,略去各处摩擦,若取x 及?为广义坐标,试求对应于x 和?的广义力。
解:应用几何法,令0δ=x ;0δ≠?
则:??????sin 2
1δδ2sin δδPl l
P W Q -=-='= 令0δ≠x ;0δ=? 则:θθsin δδsin δδP x
x
P x W Q x -=-=''=
13-2 图示在水平面内运动的行星齿轮机构,已知固定齿轮半径为R ,均质行星齿轮半径为r ,质量为m ,均质杆OA 质量为m 1,杆受矩为M 的力偶作用而运动,若取?为广义坐标,试求相应的广义力。
解:应用几何法,设对应于?的虚位移0δ≠? 则:
M M W Q ===
?
???δδδδ
13-3 在图示系统中,已知:均质圆柱A 的质量为M 、半径为R ,物块B 的质量为m ,光滑斜面的倾角为β,滑轮质量忽略不计,并假设斜绳段平行斜面。若以θ 和y 为广义坐标,试分别用动力学普遍方程和第二类拉格朗日方程求:
(1)系统运动微分方程;
(2)圆柱A 的角加速度和物块B 的加速度。
解:(1)在系统上施加惯性力如图(a )所示。
其中:)(I θ R y M F A -=;y m F B
=I θ
θ
2I 2
1MR J M A A == 应用动力学普遍方程,
δ)sin (δ)sin (I I I I =+-+--
-θββR Mg M R F y Mg F F mg A A A B 可得系统运动微分方程:
0sin )(=----βθMg R y
M y m mg 0sin 2
1)(2=+--R Mg MR R R y
M βθθ 整理后有:0)sin ()(=-+-+g m M MR y
M m βθ 0sin 2
3=--βθg y
R
习题13-2图
习题13-3图
F I
应用第二类拉格朗日方程:
2222)(2
1212121θθ R y M MR y m T -+?+=
;)(sin θβR y Mg mgy V -+-= =-=V T L 2222)(2
1212121θθ R y M MR y m -+?+)(sin θβR y Mg mgy --+ )(d d θ R y
M y m y L t -+=??;βsin Mg mg y
L -=?? 0d d =??-??y L y L t ;0)sin ()(=-+-+g m M MR y M m βθ (a ) )(21d d 2θθθ R y RM MR L t --=??;R Mg L βθsin =?? 0d d =??-??θθL L t
;0sin 2
3=--βθg y R (b ) (2)求圆柱A 的角加速度和物块B 的加速度。
由式(b )得:βθsin 2
3g R y
-=
代入式(a )
,有 0)sin ()sin 2
3)((=-+--+g m M MR g R M m βθβθ 解得:R
m M mg A )3()sin 1(2++==βθ
α ;m M g
M m g m M mg y a B 3)sin 3(sin 3)sin 1(3+-=
-++==βββ
13-4 在图示系统中,已知滑块A 的质量为M ,至于光滑水平面上,其上作用有水平力F ,均质杆AB 长2b ,质量为m ,若选取x 和θ 作为系统的广义坐标,试建立系统运动微分方程。
解:应用第二类拉格朗日方程。对应于 广义坐标x 和θ的广义力分别为:
F Q x =;θθsin mgb Q -=
杆AB 质心C 的速度为:
2
2
)sin ()cos (θθθθ b b x
v C ++= 系统的动能为:
)cos 2(2
141212*********θθθθ b b x x m b m x
M T +++?+=
)sin cos (d d 2θθθθ -++=??mb x
m x M x T t ;0=??x
T x Q x T x T t =??-?? d d ;0sin cos )(2=--++F mb mb x M m θθθθ (a ) )sin cos (31d d 22θθθθθθ x x mb mb mb T t -++=??;θθθ x mb T sin -=?? θθθQ T T t
=??-?? d d ;0sin cos 3
42=++θθθgb x b b (b ) 式(a )、(b )即为系统运动微分方程。
习题13-4图
13-5 在图示系统中,已知:均质圆轮A 的质量为M 、半径为r ,摆球B 的质量为m 、摆长为b ,弹簧刚度为k ,弹簧及刚杆AB 质量不计,圆盘在水平面上作纯滚动。若选取? 和
θ 作为系统的广义坐标,设? = 0时弹簧为原长。试分别用动力学普遍方程和第二类拉格朗日
方程建立系统运动微分方程。
解:(1)在系统上施加惯性力如图(a
其中惯性力为:? Mr F A =I ;?? 2I 2
1Mr J M A A == ? mr F B =e I ;θ mb F B =t r I ;2n r I θ mb F B = 应用动力学普遍方程,
δ)sin cos (n r
I t r I e
I I I =+-----?θθr F r F r F Fr M r F B B B A A 0δ)cos sin (t r I e I =---θθθb F F mg B B
可得系统运动微分方程(F = kr ?):
0)sin cos ()2
3(2=-+++θθθθ??
mb kr r m M 0sin cos =++θ
θ?
θmg mb mr 整理后有:
02)sin cos (2)23(2=+-++?θθθθ?
kr mb r m M 0sin cos =++θθ?
θmg mb mr 应用第二类拉格朗日方程:
])sin ()cos [(2
12121)(2122222θθθθ???
b b r m Mr r M T +++?+=
; 2)(21
cos ?θr k b mg V +-=
=-=V T L ])(cos 2)[(2
1)(4
3222θθθ
??? b rb r m r M +++2)(2
1cos ?θr k b mg -+ )sin cos (23d d 222θθθθ??
? -++=??mrb mr Mr L t ;??
2kr L -=?? 0d d =??-????L L t ;02)sin cos (2)32(2=+-++?θθθθ?kr mb r M m (a ) )sin cos (d d 2θ?θθ?θθ -+=??mbr mb L t ;b mg mrb L θθθ?θsin sin --=?? 0d d =??-??θ
θL L t
;0sin cos =++θθ?θmg mb mr (b ) 式(a )、(b )即为系统运动微分方程。
13-6 图示系统由摆长为l 、质量为m 的摆锤和两根弹簧刚度为k 的弹簧组成,弹簧、滑块A 及刚杆AB 的质量均不计,水平面光滑。若选取x 和θ 作为系统的广义坐标,试用第二类拉格朗日方程建立系统运动微分方程。
习题13-5图
解:摆锤B 的速度为:22)sin ()cos (θθ
θθ l l x v B ++= 系统的动能、势能分别为:
)cos 2(2
1222θθθ l l x x
m T ++=
;2cos kx mgl V +-=θ =-=V T L )cos 2(2
1222θθθ l l x x m ++2cos kx mgl -+θ )sin cos (d d 2θθθθ -+=??ml x m x L t ;kx x L 2-=?? 0d d =??-??x L x L t ;02sin cos 2=+-+kx ml ml x m θθθθ (a ) )sin cos (d d 2θθθθθ x x ml ml L t -+=??;θθθθsin sin mgl x ml L --=?? 0d d =??-??θ
θL L t
;0sin cos 2=++θθθmgl x ml ml (b ) 式(a )、(b )即为系统运动微分方程。
13-7 在图示系统中,已知:物块A 质量为m ,均质圆柱B 质量为M 、半径为r ,弹簧刚度为k ,自然长度为d ,圆柱B 相对于物块A 作纯滚动,物块A 沿光滑水平面运动。若选取x 和? 作为系统的广义坐标,试用第二类拉格朗日方程建立系统运动微分方程。
解:系统的动能、势能分别为:
2222)(2
1
4121?? r x M Mr x
m T +++=; 22)(21)(21?r k d x k V +-= V T L -=
)(d d ? r x M x m x L t ++=??;)(d x k x L
--=??
0d d =??-??x L
x
L t ;0)()(=-+++d x k Mr x
M m ? (a ) )(21
d d 2???
r x
Mr Mr L t ++=??;?θ2kr L -=?? 0d d =??-???
?L L t ;023
=++??kr Mr x
M (b ) 式(a )、(b )即为系统运动微分方程。
13-8 在图示系统中,已知:摆球B 的质量为m 、摆长为b ,弹簧的刚度系数为k ,其他物体质量不计。若选取y (从点A 的静平衡位置算起)和θ 作为系统的广义坐标,试用第二类拉格朗日方程建立系统运动微分方程。
解:应用第二类拉格朗日方程: )sin 2(2
1222θθθ b y b y
m T +-=;221cos ky mgb V +-=θ V T L -=
习题13-7图
B
)cos sin (d d 2θθθθ +-=??mb y
m y L t ;ky y
L -=?? 0d d =??-??y L y L t ;0cos sin 2=+--ky mb mb y m θθθθ (a ) )cos sin (d d 2θθθθθ y y mb mb L t +-=??;θθθθ
sin cos mgb y mb L --=?? 0d d =??-??θ
θL L t
;0sin sin =+-θθθg y b (b ) 式(a )、(b )即为系统运动微分方程。
13-9 重力为P 1的楔块B 放在光滑水平面上,铅直杆重力P 2,均质圆盘重力P 3,如图所示。在楔块上作用一水平力F 。若圆盘在楔块斜面上作纯滚动,斜面与水平面的夹角为β,
试求楔块的加速度。
解:此系统只有一个自由度,若选取x
为广义坐标,应用第二类拉格朗日方程:
2322232
121)sin (4121O O v g
P P r v r g P x g P T +++=
β 如图所示圆盘的速度瞬心在点D ,且x
v B =, 则:ββ
β
t an cos sin x
r r v v B O ==
22322
232
1tan 21cos 4121x g
P P x g P x g P T ββ+++= βtan )(δδ)(δ3232P P F x
r P P x F Q O
x +-=+-=
;(βt a n δδx r O =)
x g
P P x g P x g P x T t ββ2
322
31tan cos 2d d +++=??;0=??x T x Q x T x T t =??-?? d d ;ββ
ββtan )(cos 2sin )(2cos 2322
23
2321P P F x g P P P P +-=+++
)sin 21()sin cos (2cos ]tan )([22
3
2221232βββββ++++-==P P P P P F g x a
13-10 在图示系统中,已知:均质杆AB 质量为m 、长为b ,光滑斜面的倾角为β,滚轮A 的质量不计。若选取x 和? 作为系统的广义坐标,试用第二类拉格朗日方程建立系统运动微分方程。
解:杆AB 质心的速度为: 22)]sin(2
[)]cos(2[?β??β?-+--= b b x v C 系统的动能、势能分别为:
22222
12
121]4)cos([21???β? mb b b x x
m T ?++--=
13-9图
?βcos 2
sin b
mg
mgx V --= =-=V T L 22222
24
1]4)cos([21???β?
mb b b x x m ++--?βcos 2sin b mg mgx ++ ])sin()cos([2d d
2??β?β? -+--=??b m x m x L t ;βsin mg x L
=??
0d d =??-??x L x L t ;0sin )sin(2
)cos(22=-----β??β??βmg b
m b m x m (a )
])sin()cos([2
124d d 22??β?β??? x x
b
m b m b m L t -+--+=??; ???β?sin 2
)sin(2b
mg x
b m L ---=?? 0d d =??-???
?L L t ;0sin 21
)cos(21312=+--??β?mgb x
mb mb (b ) 式(a )、(b )即为系统运动微分方程。
13-11 系统由定滑轮A 和动滑轮B 以及三个重物组成,如图所示。重物M 1,M 2,M 3
的质量分别是m 1,m 2,m 3,且m 1< m 2+m 3,m 2>m 3
试求欲使M 1下降,质量m 1,m 2和m 3之间的关系。
解:选取广义坐标x 1、x 2如图所示。
22132212211)(2
1)(2121x x m x x m x m T ++-+=
)()(21321211x x g m x x g m gx m V ++-+-=
V T L -=
)()(d d 213212111x x m x x m x m x L t ++-+=??;g m g m g m x L
3211
--=??
0d d 1
1=??-??x L x L t 0)()()(3212231321=----+++g m m m x
m m x m m m (a ) )()(d d 2132122x x m x x m x L t ++--=??;g m g m x L
322-=??
0d d 22=??-??x L
x
L t ;0)()()(32223123=--++-g m m x
m m x m m (b ) 由式(b )可得:3
21322))((m m g x
m m x ++-= ,将此式代入式(a ),得:
0)()()()(32113
22231321=---++--++g m m m g x
m m m m x m m m g m m m m m m m x
m m m m m m m )])(()[(])())([(32321223122332321+--+-=--+++ g m m m m m m x
m m m m m m )4()4(3231211312321-+=++ 当x 1 > 0时,有04323121>-+m m m m m m ,即:3
23
214m m m m m +>
习题13-11图
13-12 图示系统由均质圆柱和平板AB 组成,圆柱体重力为P 、半径为R ,平板AB 重力为Q ,AC 与BD 两悬绳相互平行,AC =BD =l ,且圆柱相对于平板只滚不滑。试用第二类拉格朗日方程求该系统在平衡位置附近作微摆动的运动微分方程。
解:圆柱O 质心的速度为:
r v v v +=A O
2112112)sin ()cos (?????
l l R v O ++= 系统的动能、势能分别为:
)cos 2(21212121212121222222212??????? l Rl R g
P R g P l g Q T ++?+??+?=
11cos cos ??Pl Ql V --=
V T L -=
)sin cos (d d 1211212121???????
? -++=??Rl g
P
l g P l g Q L t ; 11211sin )(sin ????
?l Q P Rl g
P
L +--=?? ;0d d 11=??-????L L t 0sin )(cos 11212=++++????l Q P Rl g
P
l g P Q (a ) )sin cos (2d d 1211122222?????
?? -++=??Rl g P
g PR g PR L t ;02=???L 0d d 22=??-????L L t ;0)sin cos (231211122=-+????? Rl g
P g PR (b ) 系统作微摆动时,忽略高阶小量,则式(a )、(b )为:
0)(1212=+++
+???l Q P Rl g P l g P Q 023122=+?? Rl g
P g PR 习题13-12图
B
第五章 习题 5—2 试用力法计算下列结构,并会出弯矩图。 解:1.判断超静定次数:n=1 2. 确定(选择)基本结构。 3.写出变形(位移)条件: (a ) 根据叠加原理,式(a )可写成 (b ) 4 .建立力法基本方程 将? 11 = 11 x 1代入(b)得 F P A B C l/2 l/2 (a) F P X 1 X 1=1 M 1图 基本体系 M P 图 l F P F P l /2 1=?0 1111=?+?=?P
(c ) 5. 计算系数和常数项 EI l l l l EI 332)21(1311= ???=δ 6. 将d11、 ?11代入力法方程式(c ) 7.作弯矩图 3FP P l /16 1111=?+P X δEI l F l F l l l F l l EI P P P P 4852322212312221(13 1= ???+????=?) (1651111↑=?-=P P F X δp M X M M +=116 32165l F l F l F M P P P A = -?=
解:1.判断超静定次数:n=1 2. 确定(选择)基本结构。 3.写出变形(位移)条件: (a ) 根据叠加原理,式(a )可写成 (b ) 4 .建立力法基本方程 将?11 = 11 x 1代入(b)得 (c ) EI 2 EI 1 F P A B X 1 X 1=1 F P C (b) M 1图 基本体系 M P 图 l F P (l -a ) 1=?0 1111=?+?=?P 0 1111=?+P X δ
5. 计算系数和常数项 1 33)3221(1)]332()(21)332()(21[13 2331211EI a EI a l a a a EI a l a a l l a a a l EI + -=???++??-?++??-?= δ2 2216)2()(]3 )(2)(213)()(21 [1EI a l a l F a l F a a l a l F a a l EI P P P P +--= -??-?+-??-?=? 6. 将d11、 ?11代入力法方程式(c ) 31 23 3 231)1(322a I I l a al l F X P --+-= 7.作弯矩图 (d )解: 超静定次数为2 选择基本结构如图(1)所示力法典型方程为: d 11X 1+d 12X 2+△1P =0 d 21X 1 + d 22X 2+△2P =0 计算系数和常数项,为此作作出X 1=1、X 2=1和荷载单独作用下的弯矩图如(2)(3)(4)所示计 p M X M M +=1 1(a)
第一章 单自由度系统 1.1 总结求单自由度系统固有频率的方法和步骤。 单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法和能量守恒定理法。 1、 牛顿第二定律法 适用范围:所有的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析,得到系统所受的合力; (2) 利用牛顿第二定律∑=F x m && ,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 2、 动量距定理法 适用范围:绕定轴转动的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析和动量距分析; (2) 利用动量距定理J ∑=M θ &&,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 和势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程 θθ ??- ???L L dt )(&=0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 4、 能量守恒定理法 适用范围:所有无阻尼的单自由度保守系统的振动。 解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 和势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即 0) (=+dt U T d ,进一步得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1.2 叙述用衰减法求单自由度系统阻尼比的方法和步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法和共振法。 方法一:衰减曲线法。 求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期和相邻波峰和波谷的幅值i A 、1+i A 。 (2)由对数衰减率定义 )ln( 1 +=i i A A δ, 进一步推导有 2 12ζ πζδ-= ,
宁波大学 学校 102 条目的4类题型式样及交稿式样 1. 选择题 题号:10211001 分值:3分 难度系数等级:1 一弹簧振子,物体的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动。当物体通过平衡位置且向规定的正方向运动时开始计时。则其振动方程为: (A) )21/(cos π+=t m k A x ; (B) )2 1/cos(π-=t m k A x ; (C) )2 1/cos(π-=t k m A x ; (D) t m /k A x cos =。 [ ] 答案:(B ) 题号:10211002 分值:3分 难度系数等级:1 一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。将它们拿到月球上去,相应的周期分别为1T '和2T '。则有 (A) 11T T >'且22T T >'; (B) 11T T <'且22T T <'; (C) 11T T ='且22T T ='; (D) 11T T ='且22T T >'。 [ ] 答案:(D ) 题号:10212003 分值:3分 难度系数等级:2 两个质量分别为1m 、2m 并由一轻弹簧的两端连结着的小球放在光滑的水平桌面上。当1m 固定时,2m 的振动频率为2ν,当2m 固定时,1m 的振动频率1ν为: (A )2ν ; (B ) 122m m ν ; (C )221m m ν ; (D )ν [ ] 答案:(D ) 题号:10212004 分值:3分 难度系数等级:2
1l ?=22l ?,两弹簧振子的周期之比T 1:T 2为 (A )2; (B )2; (C ) 2 1 ; (D )2/1。 [ ] 答案:(B ) 题号:10212005 分值:3分 难度系数等级:2 同一弹簧振子悬挂相同的质量,分别按如图(a )、(b )、(c )所示的三种方式放置,摩擦力都忽略不计,它们的振动周期分别为 a T 、 b T 、 c T ,则三者之间的关系为 (A )a b c T T T == ; (B )a b c T T T => ; (C )a b c T T T >> ; (D )a b c T T T << 。 [ ] 答案:(A ) 题号:10213006 分值:3分 难度系数等级:3 如图所示,质量为m 的物体由劲度系数为k 1和k 2的两个轻弹簧连接在水平光滑导轨上作微小振动,则该系统的振动周期为 (A) T = ; (B) 2T = ; (C) 2T =; (D) 2T =。 [ ] 答案:(B ) 题号:10213007 分值:3分 难度系数等级:3 如图所示,质量为m 的物体,由劲度系数为k 1和k 2的两个轻弹簧连接到固定端,在水平光滑导轨上作微小振动,其振动频率为 (B) m k k 212+π=ν; (B) m k k 2 121+π=ν ; (C) 212121k mk k k +π= ν ; (D) ) (21 2121k k m k k +π=ν 。 [ ] (a ) (b ) (c )
1 : 图 a 桁 架, 力 法 基 本 结 构 如 图 b ,力 法 典 型 方 程 中 的 系 数 为 :( ) 3. 2:图示结构用力矩分配法计算时,结点A 的约束力矩(不平衡 力矩)为(以顺时针转为正) ( ) 4.3Pl/16 3:图示桁架1,2杆内力为: 4. 4:连续梁和 M 图如图所示,则支座B 的竖向反力 F By 是:
4.17.07(↑) 5:用常应变三角形单元分析平面问题时,单元之间()。 3.应变、位移均不连续; 6:图示体系的几何组成为 1.几何不变,无多余联系; 7:超静定结构在荷载作用下的内力和位移计算中,各杆的刚度为() 4.内力计算可用相对值,位移计算须用绝对值 8:图示结构用力矩分配法计算时,结点A之杆AB的分配系数
μAB 为(各杆 EI= 常数)( ) 4.1/7 9:有限元分析中的应力矩阵是两组量之间的变换矩阵,这两组量是( )。 4.单元结点位移与单元应力 10:图示结构用位移法计算时,其基本未知量数目为( ) 4.角位移=3,线位移=2 11:图示结构,各柱EI=常数,用位移法计算时,基本未知量数 目是( ) 3.6 12:图示结构两杆长均为d,EI=常数。则A 点的垂直位移为( ) 4.qd 4/6EI (↓) 13:图示桁架,各杆EA 为常数,除支座链杆外,零杆数为:
1.四 根 ; 14:图示结构,各杆线刚度均为i,用力矩分配法计算时,分配 系数μAB 为( ) 2. 15:在位移法中,将铰接端的角位移,滑动支撑端的线位移作为基本未知量: 3.可以,但不必; 1:用图乘法求位移的必要条件之一是:( ) 2.结构可分为等截面直杆段; 2:由于静定结构内力仅由平衡条件决定,故在温度改变作用下静定结构将( ) 2.不产生内力 3:图示结构,各杆EI=常数,欲使结点B 的转角为零,比值P1/P2应 为( ) 2.1
第一章 单自由度系统 1、1 总结求单自由度系统固有频率的方法与步骤。 单自由度系统固有频率求法有:牛顿第二定律法、动量距定理法、拉格朗日方程法与能量守恒定理法。 1、 牛顿第二定律法 适用范围:所有的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析,得到系统所受的合力; (2) 利用牛顿第二定律∑=F x m && ,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 2、 动量距定理法 适用范围:绕定轴转动的单自由度系统的振动。 解题步骤:(1) 对系统进行受力分析与动量距分析; (2) 利用动量距定理J ∑=M θ &&,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 3、 拉格朗日方程法: 适用范围:所有的单自由度系统的振动。 解题步骤:(1)设系统的广义坐标为θ,写出系统对于坐标θ的动能T 与势能U 的表达式;进一步写求出拉格朗日函数的表达式:L=T-U ; (2)由格朗日方程 θθ ??- ???L L dt )(&=0,得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 4、 能量守恒定理法 适用范围:所有无阻尼的单自由度保守系统的振动。 解题步骤:(1)对系统进行运动分析、选广义坐标、写出在该坐标下系统的动能T 与势能U 的表达式;进一步写出机械能守恒定理的表达式 T+U=Const (2)将能量守恒定理T+U=Const 对时间求导得零,即 0) (=+dt U T d ,进一步得到系统的运动微分方程; (3) 求解该方程所对应的特征方程的特征根,得到该系统的固有频率。 1、2 叙述用衰减法求单自由度系统阻尼比的方法与步骤。 用衰减法求单自由度系统阻尼比的方法有两个:衰减曲线法与共振法。 方法一:衰减曲线法。 求解步骤:(1)利用试验测得单自由度系统的衰减振动曲线,并测得周期与相邻波峰与波谷的幅值i A 、1+i A 。 (2)由对数衰减率定义 )ln( 1 +=i i A A δ, 进一步推导有 2 12ζ πζδ-= ,
第三章 多自由度系统 试求图3-10所示系统在平衡位置附近作微振动的振动方程。 图3-10 解:(1)系统自由度、广义坐标 图示系统自由度N=2,选x1、x2和x3为广义坐标; (2)系统运动微分方程 根据牛顿第二定律,建立系统运动微分方程如下: ;)(;)()(;)(3 4233332625323122222121111x K x x K x m x K x K x x K x x K x m x x K x K x m ---=------=---=&&&&&& 整理如下 ; 0)(;0)(;0)(3432333332653212222212111=++-=-++++-=-++x K K x K x m x K x K K K K x K x m x K x K K x m &&&&&& 写成矩阵形式 ;000)(0)(0) (0 0000321433365322221321321 ?? ????????=????????????????????+--+++--++????????????????????x x x K K K K K K K K K K K K x x x m m m &&&&&&(1) (3)系统特征方程 设)sin(,)sin(,)sin(332211?ω?ω?ω+=+=+=t A x t A x t A x 代入系统运动微分方程(1)得系统特征方程 ;000)(0)(0)(321234333 2 26532222121?? ????????=????????????????????-+---+++---+A A A m K K K K m K K K K K K m K K ωωω(2) (4)系统频率方程 系统特征方程(2)有非零解的充要条件是其系数行列式等于零, 即 ;0) (0)(0)(234333226532222121=-+---+++---+ωωωm K K K K m K K K K K K m K K 展开得系统频率方程
102简谐运动的动力学方程 1. 选择题 1,一弹簧振子,物体的质量为m ,弹簧的劲度系数为k ,该振子作振幅为A 的简谐振动。当物体通过平衡位置且向规定的正方向运动时开始计时。则其振动方程为: (A) )2 1/(cos π+=t m k A x ; (B) )21/cos(π-=t m k A x ; (C) )2 1/cos( π-=t k m A x ; (D) t m /k A x cos =。 [ ] 2,一个弹簧振子和一个单摆(只考虑小幅度摆动),在地面上的固有振动周期分别为T 1和T 2。将它们拿到月球上去,相应的周期分别为1T '和2T '。则有 (A) 11T T >'且22T T >'; (B) 11T T <'且22T T <'; (C) 11T T ='且22T T ='; (D) 11T T ='且22T T >'。 [ ] 3,两个质量分别为1m 、2m 并由一轻弹簧的两端连结着的小球放在光滑的水平桌面上。当1m 固定时,2m 的振动频率为2ν,当2m 固定时,1m 的振动频率1ν为: (A )2ν ; (B )122 m m ν ; (C )221 m m ν ; (D )2 ν [ ] 4,两个质量相同的物体分别挂在两个不同的弹簧下端,弹簧的伸长分别为1l ?和2l ?,且1l ?=22l ?,两弹簧振子的周期之比T 1:T 2为 (A )2; (B ) 2; (C ) 2 1; (D )2/1。 [ ] 5,同一弹簧振子悬挂相同的质量,分别按如图(a )、(b )、(c )所示的三种方式放置,摩擦力 都忽略不计,它们的振动周期分别为a T 、 b T 、 c T ,则三者之间的关系为 (A )a b c T T T == ; (B )a b c T T T => ; (C ) a b c T T T >> ; (D )a b c T T T << 。 [ ] 6,如图所示,质量为m 的物体由劲度系数为k 1和k 2的两个轻弹簧连接在水平光滑导轨上作微小振动,则该系统的振动周期为 (A) T = ; (B) 2T = ; (a ) (b ) (c )
《结构力学》作业参考答案 一、判断题(将判断结果填入括弧内,以 √表示正确 ,以 × 表示错误。) 1.图示桁架结构中有3个杆件轴力为0 。(×) 2.图示悬臂梁截面A 的弯矩值是ql 2。 (×) l l 3.静定多跨梁中基本部分、附属部分的划分与所承受的荷载无关。(√ ) 4.一般来说静定多跨梁的计算是先计算基本部分后计算附属部分。(× ) 5.用平衡条件能求出全部内力的结构是静定结构。( √ ) 6.求桁架内力时截面法所截取的隔离体包含两个或两个以上的结点。(√ ) 7.超静定结构的力法基本结构不是唯一的。(√) 8.在桁架结构中,杆件内力不是只有轴力。(×) 9.超静定结构由于支座位移可以产生内力。 (√ ) 10.超静定结构的内力与材料的性质无关。(× ) 11.力法典型方程的等号右端项不一定为0。 (√ ) 12.计算超静定结构的位移时,虚设力状态可以在力法的基本结构上设。(√) 13.用力矩分配法计算结构时,汇交于每一结点各杆端分配系数总和为1,则表明分配系 数的计算无错误。 (× ) 14.力矩分配法适用于所有超静定结构的计算。(×) 15.当AB 杆件刚度系数i S AB 3 时,杆件的B 端为定向支座。 (×)
二、单项选择题(在每小题的四个备选答案中选出一个正确答案,并将其代号填在题干后面的括号内。不选、错选或多选者,该题无分。) 1.图示简支梁中间截面的弯矩为( A ) q l A . 82ql B . 42ql C . 22 ql D . 2ql 2.超静定结构在荷载作用下产生的内力与刚度(B ) A . 无关 B . 相对值有关 C . 绝对值有关 D . 相对值绝对值都有关 3.超静定结构的超静定次数等于结构中(B ) A .约束的数目 B .多余约束的数目 C .结点数 D .杆件数 4.力法典型方程是根据以下哪个条件得到的(C )。 A .结构的平衡条件 B .结构的物理条件 C .多余约束处的位移协调条件 D .同时满足A 、B 两个条件 5. 图示对称结构作用反对称荷载,杆件EI 为常量,利用对称性简化后的一半结构为(A )。 6.超静定结构产生内力的原因有(D ) A .荷载作用与温度变化 B .支座位移 C .制造误差 D .以上四种原因
习题13-1图 *第13章 动力学普遍方程 和第二类拉格朗日方程 13-1 图示均质细杆OA 长为l ,重力为P ,在重力作用下可在铅垂平面内摆动,滑块O 质量不计,斜面倾角θ,略去各处摩擦,若取x 及?为广义坐标,试求对应于x 和?的广义力。 解:应用几何法,令0δ=x ;0δ≠? 则:??????sin 2 1δδ2sin δδPl l P W Q -=-='= 令0δ≠x ;0δ=? 则:θθsin δδsin δδP x x P x W Q x -=-=''= 13-2 图示在水平面内运动的行星齿轮机构,已知固定齿轮半径为R ,均质行星齿轮半径为r ,质量为m ,均质杆OA 质量为m 1,杆受矩为M 的力偶作用而运动,若取?为广义坐标,试求相应的广义力。 解:应用几何法,设对应于?的虚位移0δ≠? 则: M M W Q === ? ???δδδδ 13-3 在图示系统中,已知:均质圆柱A 的质量为M 、半径为R ,物块B 的质量为m ,光滑斜面的倾角为β,滑轮质量忽略不计,并假设斜绳段平行斜面。若以θ 和y 为广义坐标,试分别用动力学普遍方程和第二类拉格朗日方程求: (1)系统运动微分方程; (2)圆柱A 的角加速度和物块B 的加速度。 解:(1)在系统上施加惯性力如图(a )所示。 其中:)(I θ R y M F A -=;y m F B =I θ θ 2I 2 1MR J M A A == 应用动力学普遍方程, δ)sin (δ)sin (I I I I =+-+-- -θββR Mg M R F y Mg F F mg A A A B 可得系统运动微分方程: 0sin )(=----βθMg R y M y m mg 0sin 2 1)(2=+--R Mg MR R R y M βθθ 整理后有:0)sin ()(=-+-+g m M MR y M m βθ 0sin 2 3=--βθg y R 应用第二类拉格朗日方程: 习题13-2图 习题13-3图 F I
第十六章结构动力学 【例16-1】不计杆件分布质量和轴向变形,确定图16-6 所示刚架的动力自由度。 图16-6 【解】各刚架的自由度确定如图中所示。这里要注意以下两点: 1.在确定刚架的自由度时,引用受弯直杆上任意两点之间的距离保持不变的假定。根据这个假定并加入最少数量的链杆以限制刚架上所有质量的位置,则刚架的自由度数目即等于所加链杆数目。 2.集中质量的质点数并不一定等于体系的自由度数,而根据自由度的定义及问题的具体情形确定。
【例16-2】 试用柔度法建立图16-7a 所示单自由度体系,受均布动荷载)t (q 作用的运动方程。 【解】本题特点是,动荷载不是作用在质量上的集中荷载。对于非质量处的集中动荷载的情况,在建立运动方程时,一般采用柔度法较为方便。 设图a 质量任一时刻沿自由度方向的位移为y (向下为正)。把惯性力I 、阻尼力R 及动荷载)(t P ,均看作是一个静荷载,则在其作用下体系在质量处的位移y ,由叠加原理(见图b 、c 、d 及e ),则 )(R I y P D I P +δ+?=?+?+?= 式中,)t (q EI 38454P =?,EI 483 =δ。将它们代入上式,并注意到y m I -=,y c R -=,得 )(48)(38453 4y c y m EI t q EI y --+= 图16-7 经整理后可得 )(t P ky y c y m E =++ 式中,3EI 481k =δ= ,)(8 5)(t q k t P P E =?= )(t P E 称为等效动荷载或等效干扰力。其含义为:)(t P E 直接作用于质量上所产生的位移和 实际动荷载引起的位移相等。图a 的相当体系如图f 所示。 【例16-3】 图16-8a 为刚性外伸梁,C 处为弹性支座,其刚度系数为k ,梁端点A 、D 处分别有m 和 3 m 质量,端点D 处装有阻尼器c ,同时梁BD 段受有均布动荷载)t (q 作用,试建立刚性梁的运动方程。 【解】 因为梁是刚性的,这个体系仅有一个自由度,故它的动力响应可由一个运动方程来表达,方程可以用直接平衡法来建立。 这个单自由度体系可能产生的位移形式如图b 所示,可以用铰B 的运动)t (α作为基本
论简谐运动动力学与运动学公式的统一 ——用导数、微积分知识推导简谐运动的运动学与动力学公式 【摘要】本文通过简谐运动与数学知识的联系,用导数、微积分的知识推导简谐运动的动力学、运动学公式。 【研究背景】本人通过对《物理》选修3-4第十一章简谐运动的学习,了解了简谐运动的运动学与动力学性质。但是书中并未给出其具体的证明过程,于是对其开展研究。 【正文】根据简谐运动的定义,如果质点的位移与时间的关系遵从正弦函数规律,即它的振动图像(x-t图像)是正弦函数图像,这样的运动叫做简谐运动。接下来我们来证明做简谐运动的质点一定受到随位移均匀变化的合力。 由定义可知,质点的位移随时间变化关系 x=A sin(ωt+φ)(1) 对时间求导,即可得到速度随时间变化关系 v=dx =Aωcos(ωt+φ)(2) dt 再次求导,可得加速度随时间变化关系 =?Aω2sin(ωt+φ)(3) a=dv dt 由牛顿第二定律,可得质点所受合力为 F=ma(4) 联立(3)(4)可得 F=?mAω2sin(ωt+φ)(5) 将(1)代入(5)得 F=?mω2x(6)
上式中,m 与ω都是常数,从而写成 F =?kx (7) 这就证明了做简谐运动的质点一定受到随位移均匀变化的合力,同时联立(6)(7)得 ω= k m (8) 根据周期公式T = 2πω可得 T =2π m k 以上便是简谐运动的周期公式 既然做简谐运动的质点一定受到随位移均匀变化的合力,那么如果一个质点受到随位移均匀变化的合力,是否做简谐运动。答案是肯定的,接下来,我们给出证明。 由简谐运动的运动学公式,得到其所受合力随位移的变化关系 F =?kx (1) 由牛顿第二定律得 F =ma (2) 联立(1)(2)得 a =?k m x (3) 对(3)进行积分可得速度的平方随位移的变化关系 v 2=2 ?k m x 0x dx +C =?k m x 2+C (4) 假设质点处于平衡位置时的速度为v 0,则 当x=0时,有C =v 02 (5)
《结构力学》计算题61.求下图所示刚架的弯矩图。 a a 62.用结点法或截面法求图示桁架各杆的轴力。 63.请用叠加法作下图所示静定梁的M图。 64.作图示三铰刚架的弯矩图。 65.作图示刚架的弯矩图。
66. 用机动法作下图中E M 、L QB F 、R QB F 的影响线。 1m 2m 2m Fp 1 =1m E B A 2m C D 67. 作图示结构F M 、QF F 的影响线。 68. 用机动法作图示结构影响线L QB F F M ,。 69. 用机动法作图示结构R QB C F M ,的影响线。 70. 作图示结构QB F 、E M 、QE F 的影响线。
71. 用力法作下图所示刚架的弯矩图。 l B D P A C l l EI =常数 72. 用力法求作下图所示刚架的M 图。 73. 利用力法计算图示结构,作弯矩图。 74. 用力法求作下图所示结构的M 图,EI=常数。 75. 用力法计算下图所示刚架,作M 图。
76. 77. 78. 79. 80. 81. 82.
83. 84. 85.
答案 取整体为研究对象,由 0A M =,得 2220yB xB aF aF qa +-= (1)(2分) 取BC 部分为研究对象,由 0C M =∑,得 yB xB aF aF =,即yB xB F F =(2)(2分) 由(1)、(2)联立解得2 3 xB yB F F qa ==(2分) 由 0x F =∑有 20xA xB F qa F +-= 解得 4 3xA F qa =-(1分) 由0y F =∑有 0yA yB F F += 解得 2 3 yA yB F F qa =-=-(1分) 则222 4222333 D yB xB M aF aF qa qa qa =-=-=()(2分) 弯矩图(3分) 62. 解:(1)判断零杆(12根)。(4分) (2)节点法进行内力计算,结果如图。每个内力3分(3×3=9分) 63. 解:
第九章 结构动力计算 一、是非题 1、结构计算中,大小、方向随时间变化的荷载必须按动荷载考虑。 2、忽略直杆的轴向变形,图示结构的动力自由度为4个。 3、仅在恢复力作用下的振动称为自由振动。 4、单自由度体系其它参数不变,只有刚度EI 增大到原来的2倍,则周期比原来的周期减小1/2。 5、图 a 体 系 的 自 振 频 率 比 图 b 的 小 。 l /2 l /2 l /2 l /2 (a)(b) 6、单 自 由 度 体 系 如 图 ,W =98 .kN ,欲 使 顶 端 产 生 水 平 位 移 ?=001 .m ,需 加 水 平 力 P =16kN ,则 体 系 的 自 振 频 率 ω=-40s 1 。 ? 7、结构在动力荷载作用下,其动内力 与动位移仅与动力荷载的变化规律有关。 8、由于阻尼的存在,任何振动都不会长期继续下去。 9、桁 架 ABC 在 C 结 点 处 有 重 物 W ,杆 重 不 计 , EA 为 常 数 ,在 C 点 的 竖 向 初 位 移 干 扰 下 ,W 将 作 竖 向 自 由 振 动 。 A C 10、不 计 阻 尼 时 ,图 示 体 系 的 运 动 方 程 为 : m m X X h EI EI EI EI X X P t 00148242424012312????????????+--????????????=?????? () 二、选择题 1、图 示 体 系 ,质 点 的 运 动 方 程 为 :
A .()()()y l P s in m y EI =-77683θ t /; B .()()m y EI y l P s in /+=19273 θ t ; C .()()m y EI y l P s in /+=38473θ t ; D .()()()y l P s in m y EI =-7963θ t / 。 l l 0.50.5 2、在 图 示 结 构 中 ,若 要 使 其 自 振 频 率 ω增 大 ,可 以 A .增 大 P ; B .增 大 m ; C .增 大 E I ; D .增 大 l 。 l t ) 3、单 自 由 度 体 系 自 由 振 动 的 振 幅 取 决 于 : A .初 位 移 ; B .初 速 度 ; C .初 位 移 、初 速 度 与 质 量 ; D .初 位 移 、初 速 度 与 结 构 自 振 频 率 。 4、考 虑 阻 尼 比 不 考 虑 阻 尼 时 结 构 的 自 振 频 率 : A .大 ; B .小 ; C .相 同 ; D .不 定 ,取 决 于 阻 尼 性 质 。 5、已 知 一 单 自 由 度 体 系 的 阻 尼 比 ξ=12.,则 该 体 系 自 由 振 动 时 的 位 移 时 程 曲 线 的 形 状 可 能 为 : D. C. B. A. 6、图 a 所 示 梁 ,梁 重 不 计 ,其 自 振 频 率 () ω=76873 EI ml /;今 在 集 中 质 量 处 添 加 弹 性 支 承 ,如 图 b 所 示 ,则 该 体 系 的 自 振 频 率 ω为 : A .() 76873 EI ml k m //+; B . ()76873EI ml k m //-; C .()76873 EI ml k m //-; D . () 76873 EI ml k m //+ 。 l l /2 /2 l l /2 /2(a)(b) 7、图 示 结 构 ,不 计 阻 尼 与 杆 件 质 量 ,若 要 其 发 生 共 振 ,θ 应 等 于 A . 23k m ; B .k m 3;
简谐运动的动力学条件和周期公式的推导 [摘要]:本文从简谐运动的概念出发,用数学知识,推理出了简谐运动的动力学条件及弹簧振子的周期公式、单摆做小角度摆动的周期。从逻辑上对机械振动一章的知识有了一个整体的认识。 [关键词]:简谐运动,动力学条件,周期公式,弹簧振子,单摆 [正文] 课程标准实验教科书《物理》3—4第十一章从运动学的角度对简谐运动进行了定义,恰好从数学课上学生也学到了关于导数的知识。这就为构造简谐运动的逻辑提供了条件,通过这样的一个逻辑构造,可以让学生体会数学在物理学中的应用。同时,也可以让学生充分体会物理学逻辑上的统一美。激发学生学习物理,从理论上探究物理问题的兴趣和决心。 如果质点的位移与时间的关系遵从正弦的规律,即它的振动图象(x —t 图象)是一条正弦,这样的运动叫做简谐运动。 由定义可知,质点的位移时间关系为 ()?ω+=t A x sin (1) 对时间求导数可得速度随时间变化的规律: ()?ωω+==t A dt dx v cos ………………(2) 再次对埋单求导数可得加速度随时间变化的规律: ()?ωω+-==t A dt dv a sin 2………………(3) 由牛顿第二定律可知,质点受到的合力为: ma F = (4) 由(3)(4)可知: ()?ωω+-=t mA F sin 2 (5) 将(1)式代入(5)式可得: x m F 2ω-= (6) 上式中,m 和ω都是常数,从而可以写成下面的形式 kx F -= (7) 其中2 ωm k =,至此得到了质点做简谐运动的动力学条件:质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置。 对于的弹簧振子来说,(7)式中的k 表示弹簧的劲度系数,对比(6)式可知k m =2ω,
第2章平面体系的几何构造分析典型例题 1. 对图 2.1a体系作几何组成分析。 图2.1 分析:图2.1a等效图2.1b(去掉二元体)。 对象:刚片Ⅰ、Ⅱ和Ⅲ; 联系:刚片Ⅰ、Ⅲ有虚铰A(杆、2);刚片Ⅱ、Ⅲ有虚铰C(无穷远)(杆3、4);刚片Ⅰ、Ⅱ有虚铰B(杆5、6); 结论:三铰共线,几何瞬变体系。 2. 对图2.2a体系作几何组成分析。 图2.1 分析:去掉二元体(杆12、杆34和杆56图2.1b),等效图2.1c。 对象:刚片Ⅰ和Ⅱ; 联系:三杆:7、8和9; 结论:三铰不共线,无多余约束的几何不变体系。
3. 对图2.3a体系作几何组成分析。 图2.3 分析:图2.3a 对象:刚片Ⅰ(三角形原则)和大地Ⅱ; 联系:铰A和杆1; 结论:无多余约束的几何不变体系。 对象:刚片Ⅲ(三角形原则)和大地Ⅱ; 联系:杆2、3和4; 结论:无多余约束的几何不变体系。 第3章静定结构的受力分析典型题
1. 求图3.1结构的内力图。 图3.1 解(1)支座反力(单位:kN) 由整体平衡,得=100.= 66.67,=-66.67.(2)内力(单位:kN.m制) 取AD为脱离体: ,,; ,,。取结点D为脱离体: ,, 取BE为脱离体: ,,。
取结点E为脱离体: ,, (3)内力图见图3.1b~d。 2. 判断图 3.2a和b桁架中的零杆。 图3.2 分析: 判断桁架零杆的常用方法是找出桁架中的L型结点和T型结点。如果这两种结点上无荷载作用.那么L型纪点的两杆及T型结点的非共线杆均为零杆。 解:图3.2a: 考察结点C、D、E、I、K、L,这些结点均为T型结点,且没有荷载作用,故杆件CG、DJ、EH、IJ、KH、LF 均为零杆。 考察结点G和H,这两个结点上的两竖向链杆均已判断为零杆,故这两个结点的受力也已成为T型结点的情形.由于没有荷载作用,故杆件AG、BH也为零杆。 整个结构共有8根零杆.如图3.2c虚线所示。 图3.2b: 考察结点D,为“K”型结点且无荷载作用,故;对称结构对称荷载(A支座处的水平反力为零),有 ,故杆件DE和DF必为零杆。
年《结构动力学》复习题
————————————————————————————————作者:————————————————————————————————日期:
2016年《结构动力学》复习题 一、(概念题) (1) (填空题)某等效单自由度振动系统具有下列参数:17.5m kg =,70/k N cm =,阻尼比 0.2ξ=, 则系统的固有频率ω为 rad/s ,等效阻尼系数c 为 N. s/m 。 (2) (填空题)某振动系统具有下列参数:17.5m kg =,70/k N cm =,0.7/c N s cm =?,则系统的固有频率ω为 ,阻尼比ξ为 ,衰减系数n 为 。 (3) (简单计算题)一弹簧悬挂某质量块,弹簧产生了静变形mm 4=?st ,试确定系统作自由振动的固有频率 (重力加速度取2s m /10=g )。(10分) (4) (填空题)当系统受简谐力作用发生共振时,系统所受的外力是由 来平衡。 (5) (问答题)某单自由度系统具有非线性的弹簧,其运动方程为:()()mx cx f x F t ++=,能否用杜哈美积分计算该系统的受迫振动响应?并说明理由。 (6) (填空题)同种材料的弦承受相同的张力,如果长度增加到原来的4倍,截面积减小到原来的4倍,则作该弦横向振动的各阶固有频率将 。 (7) (填空题)图示两个系统,已知各质点的质量 i m ,刚架的质量不计,忽略杆的轴向变形,试分别确定两系统的动力自由度: (1) n = ; (2) n = 。 (8) (作图题) 0.1ξ=时单自由度系统受迫振动的相频曲线如图所示,其中ω为系统的固有频 率,p 为激振力的频率,?为位移响应滞后于激振力的相位角。试大致绘出0.05ξ=和0.2ξ=时相频曲线的形状。 (9) (问答题)模态分析法能否求解多自由度系统的弹塑性地震响应?并说明理由。 (10) (选择题) 对于一个单自由度系统而言,其临界阻尼与系统的固有特性参数 ,与 系统所受的阻尼力 。 (a) 有关,有关;(b) 无关,无关;(c) 有关,无关;(d) 无关,有关 1 m 2 m 3 m ( 2 m 3 m ( 1 m ω p ? 10.1 ξ=π 2 π
《结构动力学》考试复习题 一、(概念题) (1) (填空题)某等效单自由度振动系统具有下列参数:17.5m kg =,70/k N cm =,阻尼比 0.2ξ=, 则系统的固有频率ω为 rad/s ,等效阻尼系数c 为 N. s/m 。 (2) (填空题)某振动系统具有下列参数:17.5m kg =,70/k N cm =,0.7/c N s cm =?,则系统的固有频率ω为 ,阻尼比ξ为 ,对数衰减率n 为 。 (3) (简单计算题)一弹簧悬挂某质量块,弹簧产生了静变形mm 4=?st ,试确定系统作自由振动的固有频率 (重力加速度取2s m /10=g )。(10分) (4) (填空题)当系统受简谐力作用发生共振时,系统所受的外力是由 来平衡。 (5) (问答题)某单自由度系统具有非线性的弹簧,其运动方程为:()()mx cx f x F t ++= ,能否用杜哈美积分计算该系统的受迫振动响应?并说明理由。 (6) (填空题)同种材料的弦承受相同的张力,如果长度增加到原来的4倍,截面积减小到原来的4倍,则作该弦横向振动的各阶固有频率将 。 (7) (填空题)图示两个系统,已知各质点的质量 i m ,刚架的质量不计,忽略杆的轴向变形,试分别确定两系统的动力自由度: (1) n = ; (2) n = 。 (8) (作图题) 0.1ξ=时单自由度系统受迫振动的相频曲线如图所示,其中ω为系统的固有频 率,p 为激振力的频率,?为位移响应滞后于激振力的相位角。试大致绘出0.05ξ=和0.2ξ=时相频曲线的形状。 (9) (问答题)模态分析法能否求解多自由度系统的弹塑性地震响应?并说明理由。 (10) (选择题) 对于一个单自由度系统而言,其临界阻尼与系统的固有特性参数 ,与 系统所受的阻尼力 。 (a) 有关,有关;(b) 无关,无关;(c) 有关,无关;(d) 无关,有关 2 ω p π π
2016年《结构动力学》复习题 一、(概念题) (1) (填空题)某等效单自由度振动系统具有下列参数:17.5m kg =,70/k N cm =,阻尼比 0.2ξ=, 则系统的固有频率ω为 rad/s ,等效阻尼系数c 为 N. s/m 。 (2) (填空题)某振动系统具有下列参数:17.5m kg =,70/k N cm =,0.7/c N s cm =?,则系统的固有频率ω为 ,阻尼比ξ为 ,衰减系数n 为 。 (3) (简单计算题)一弹簧悬挂某质量块,弹簧产生了静变形mm 4=?st ,试确定系统作自由振动的固有频率 (重力加速度取2s m /10=g )。(10分) (4) (填空题)当系统受简谐力作用发生共振时,系统所受的外力是由 来平衡。 (5) (问答题)某单自由度系统具有非线性的弹簧,其运动方程为:()()mx cx f x F t ++=&&&,能否用杜哈美积分计算该系统的受迫振动响应?并说明理由。 (6) (填空题)同种材料的弦承受相同的张力,如果长度增加到原来的4倍,截面积减小到原来的4倍,则作该弦横向振动的各阶固有频率将 。 (7) (填空题)图示两个系统,已知各质点的质量 i m ,刚架的质量不计,忽略杆的轴向变形,试分别确定两系统的动力自由度: (1) n = ; (2) n = 。 (8) (作图题) 0.1ξ=时单自由度系统受迫振动的相频曲线如图所示,其中ω为系统的固有频率,p 为激振力的频率,?为位移响应滞后于激振力的相位角。试大致绘出0.05ξ= 0.2ξ=时相频曲线的形状。 (9) (问答题)的弹塑性地震响应?并说明理由。 (10) (选择题) 对于一个单自由度系统而言, 其临界阻尼与系统的固有特性参数 ,与系统所受的阻尼力 。 (a) 有关,有关;(b) 无关,无关;(c) 有关,无关;(d) 无关,有关 二、(计算题) (1) 图示两个系统,已知EI 和M ,弹簧刚度316k EI l =,不计梁的质量,试确定:(1) 简支梁的等效刚度L k ;(2) 两个系统的等效刚度 a k 和 b k ;(3) 两个系统 的固有频率a ω和b ω。 (2) 水平刚杆 AB 可绕 铰链A 作微幅旋转振动,在杆的中点固定一个质量为m 的物块,设弹簧刚度为k ,杆长为l ,杆的质量不计。(1) 以杆AB 的转角θ为自由度求系统的动能和势能;(2) 建立系统的运动方程;(3) 求固
结构动力学习题参考答案
2.3一根刚梁AB ,用力在弹簧BC 上去激励它,其C 点的运动规定为Z (t ),如图P2. 3. 按B 点的垂直运动u 来确定系统的运动方程,假定运动是微小的。 解:以在重力作用下的平衡位置作为基准点,则方程建立时不考虑重力。根据 达朗贝尔原理,通过对A 点取矩建立平衡方程,刚体上作用有弹簧弹力1s f , 2s f , 以及阻尼力D f ,惯性力2M 。B 点的垂直位移是u ,则有几何关系知2/L 处的位移为2/u 。 根据位移图和受力图可得: 02 221=?-?+? +L f L f L f M s D s I 其中 . 22221.... 221) (21 23 1 31u c f u z k f u k u R f u m L L u m L M D s s I =-==?=== 代入○ 1式得: 0 )(L 4 1 41ML 3121...=--++L u z k u k u cL u 合并化简得: )(12)123(3M 4221. .. t Z k u k k u c u =+++ 2.5 系统如图P2.5 , 确定按下形式的运动方程:)(. ..t P ku u c u m u =++。其中u 为 E 点的垂直运动。假定薄刚杆AE 的质量为M,其转动很小。
解:根据牛顿定律,运动几何关系,对B 点取矩得 L u L m mL L u k L u c L L t f p 4 3 )4(1214343854)(.. 22.0? ??????+=??-?-?? 化简合并得: ) ()()(845 .,3,3,M 7)(8 45 337. ... .. t P ku u c u m t P L t f P K k C c m L t f P ku u c u M u u O O =++===== ++得令 2.13 一根均匀杆,图P2.13 其单位体积质量密度ρ,并具有顶部质量M ,应 用假定法L x x =()ψ来推导该系统轴向自由振动的运动方程。假定=AE 常数。 解: ) ()()(),(t u L x t u x t x u = =ψ 由虚功原理,有: 0W V W =+-惯非保守δδδ ① 其中非保守力为端部集中力)(t P ,惯性力包括顶部质量M 和均匀杆的所受的惯性力,计算如下: