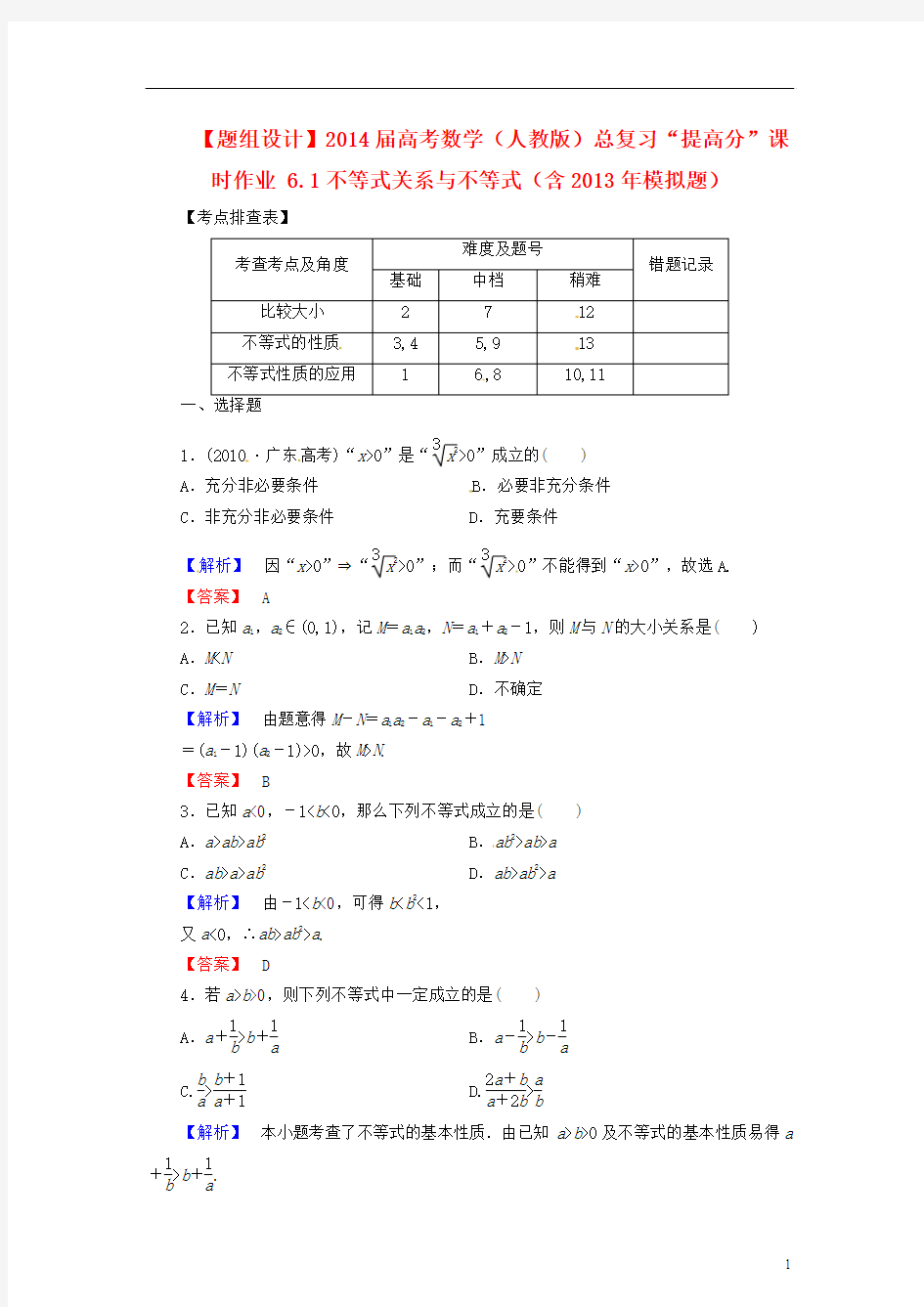
x +y +1xy ≤1x +1
y
+xy ?xy (x +y )+1≤y +x +(xy )2.
将上式中的右式减左式,得
[y +x +(xy )2
]-[xy (x +y )+1]=[(xy )2
-1]-[xy (x +y )-(x +y )]=(xy +1)(xy -1)-(x +y )(xy -1)=(xy -1)(xy -x -y +1)=(xy -1)(x -1)(y -1).
既然x ≥1,y ≥1,所以(xy -1)(x -1)(y -1)≥0,从而所要证明的不等式成立. (2)设log a b =x ,log b c =y ,由对数的换底公式得 log c a =1xy ,log b a =1x ,log c b =1
y
,log a c =xy .
于是,所要证明的不等式即为
x +y +1xy ≤1x +1
y
+xy
其中x =log a b ≥1,y =log b c ≥1.故由(1)可知所要证明的不等式成立.
高考数学真题分类汇编专题不等式理科及答案
专题七 不等式 1.【2015高考四川,理9】如果函数()()()()21 281002 f x m x n x m n = -+-+≥≥, 在区间122?????? ,上单调递减,则mn 的最大值为( ) (A )16 (B )18 (C )25 (D )812 【答案】B 【解析】 2m ≠时,抛物线的对称轴为82n x m -=--.据题意,当2m >时,8 22 n m --≥-即212m n +≤ .26,182 m n mn +≤ ≤∴≤Q .由2m n =且212m n +=得3,6m n ==.当2m <时,抛物线开口向下,据题意得,81 22 n m -- ≤-即218m n +≤ .281 9,22 n m mn +≤ ≤∴≤Q .由2n m =且218m n +=得92m =>,故应舍去.要使得mn 取得最大值,应有218m n +=(2,8)m n <>.所以 (182)(1828)816mn n n =-<-??=,所以最大值为18.选B.. 【考点定位】函数与不等式的综合应用. 【名师点睛】首先弄清抛物线的开口方向和对称轴,结合所给单调区间找到m 、n 满足的条件,然后利用基本不等式求解.本题将函数的单调性与基本不等式结合考查,检测了学生综合运用知识解题的能力.在知识的交汇点命题,这是高考的一个方向,这类题往往以中高档题的形式出现. 2.【2015高考北京,理2】若x ,y 满足010x y x y x -?? +??? ≤, ≤,≥,则2z x y =+的最大值为( ) A .0 B .1 C . 3 2 D .2 【答案】D 【解析】如图,先画出可行域,由于2z x y = +,则11 22 y x z =- +,令0Z =,作直线1 2 y x =- ,在可行域中作平行线,得最优解(0,1),此时直线的截距最大,Z 取
高考数学复习专题 基本不等式 (文 精讲)
专题7.3 基本不等式 【核心素养分析】 1.了解基本不等式的证明过程; 2.会用基本不等式解决简单的最大(小)值问题. 【知识梳理】 知识点一 基本不等式ab ≤ a +b 2 (1)基本不等式成立的条件:a >0,b >0. (2)等号成立的条件:当且仅当a =b . 知识点二 几个重要的不等式 (1)a 2+b 2≥2ab (a ,b ∈R);(2)b a +a b ≥2(a ,b 同号); (3)ab ≤????a +b 22(a ,b ∈R);(4)????a +b 22≤a 2 +b 2 2(a ,b ∈R); (5)2ab a +b ≤ab ≤a +b 2≤ a 2+ b 2 2 (a >0,b >0). 知识点三 算术平均数与几何平均数 设a >0,b >0,则a ,b 的算术平均数为a +b 2,几何平均数为ab ,基本不等式可叙述为:两个正数的 算术平均数不小于它们的几何平均数. 知识点四 利用基本不等式求最值问题 已知x >0,y >0,则 (1)如果xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p (简记:积定和最小). (2)如果x +y 是定值q ,那么当且仅当x =y 时,xy 有最大值是q 2 4(简记:和定积最大). 【特别提醒】 1.此结论应用的前提是“一正”“二定”“三相等”.“一正”指正数,“二定”指求最值时和或积为定值,“三相等”指等号成立. 2.连续使用基本不等式时,牢记等号要同时成立. 【典例剖析】 高频 考点一 利用基本不等式求最值 【例1】【2020·江苏卷】已知22451(,)x y y x y +=∈R ,则22x y +的最小值是 ▲ .
(完整版)高考数学-基本不等式(知识点归纳)
高中数学基本不等式的巧用 一.基本不等式 1.(1)若R b a ∈,,则ab b a 22 2 ≥+ (2)若R b a ∈,,则2 2 2b a ab +≤(当且仅当b a =时取“=”) 2. (1)若*,R b a ∈,则ab b a ≥+2 (2)若* ,R b a ∈,则ab b a 2≥+(当且仅当b a =时取“=” ) (3)若* ,R b a ∈,则2 2?? ? ??+≤b a ab (当且仅当b a =时取“=”) 3.若0x >,则12x x + ≥ (当且仅当1x =时取 “=”);若0x <,则1 2x x +≤- (当且仅当1x =-时取“=”) 若0x ≠,则11122-2x x x x x x +≥+≥+≤即或 (当且仅当b a =时取“=”) 3.若0>ab ,则2≥+a b b a (当且仅当b a =时取“=”) 若0ab ≠,则 22-2a b a b a b b a b a b a +≥+≥+≤即或 (当且仅当b a =时取“=” ) 4.若R b a ∈,,则2 )2( 2 22b a b a +≤ +(当且仅当b a =时取“=”) 注:(1)当两个正数的积为定植时,可以求它们的和的最小值,当两个正数的和为定植时,可以求它们的 积的最小值,正所谓“积定和最小,和定积最大”. (2)求最值的条件“一正,二定,三取等” (3)均值定理在求最值、比较大小、求变量的取值范围、证明不等式、解决实际问题方面有广泛的应用. 应用一:求最值 例1:求下列函数的值域 (1)y =3x 2 +12x 2 (2)y =x +1x 解:(1)y =3x 2 +12x 2 ≥2 3x 2 ·12x 2 = 6 ∴值域为[ 6 ,+∞) (2)当x >0时,y =x +1 x ≥2 x ·1 x =2; 当x <0时, y =x +1x = -(- x -1 x )≤-2 x ·1 x =-2 ∴值域为(-∞,-2]∪[2,+∞) 解题技巧: 技巧一:凑项 例1:已知5 4x < ,求函数14245 y x x =-+-的最大值。 解:因450x -<,所以首先要“调整”符号,又1 (42)45 x x --g 不是常数,所以对42x -要进行拆、凑项, 5,5404x x <∴->Q ,11425434554y x x x x ??∴=-+=--++ ?--? ?231≤-+= 当且仅当1 5454x x -= -,即1x =时,上式等号成立,故当1x =时,max 1y =。
高考数学不等式知识点总结及解题思路方法
高考数学不等式知识点总结及解题思路方法 考试内容: 不等式.不等式的基本性质.不等式的证明.不等式的解法.含绝对值的不等式. 考试要求: (1)理解不等式的性质及其证明. (2)掌握两个(不扩展到三个)正数的算术平均数不小于它们的几何平均数的定理,并会简单的应用. (3)掌握分析法、综合法、比较法证明简单的不等式. (4)掌握简单不等式的解法. (5)理解不等式│a│-│b│≤│a+b│≤│a│+│b│ §06. 不等式知识要点 1.不等式的基本概念 (1)不等(等)号的定义:. - = < ? a< ? b ? > > - = - b ; 0b ; a a a b b a b a (2)不等式的分类:绝对不等式;条件不等式;矛盾不等式. (3)同向不等式与异向不等式. (4)同解不等式与不等式的同解变形. 2.不等式的基本性质 (1)a >(对称性) ? a< b b (2)c ? > >,(传递性) a> c a b b (3)c + ? > >(加法单调性) c a+ a b b (4)d + > >,(同向不等式相加) a+ > ? d b c a c b
(5)d b c a d c b a ->-?<>,(异向不等式相减) (6)bc ac c b a >?>>0,. (7)bc ac c b a 0,(乘法单调性) (8)bd ac d c b a >?>>>>0,0(同向不等式相乘) (9)0,0a b a b c d c d >><(异向不等式相除) 11(10),0a b ab a b >>?<(倒数关系) (11))1,(0>∈>?>>n Z n b a b a n n 且(平方法则) (12))1,(0>∈>?>>n Z n b a b a n n 且(开方法则) 3.几个重要不等式 (1)0,0||,2≥≥∈a a R a 则若 (2))2||2(2,2222ab ab b a ab b a R b a ≥≥+≥+∈+或则、若(当仅当a=b 时取等号) (3)如果a ,b 都是正数,那么 .2a b +(当仅当a=b 时取等号) 极值定理:若,,,,x y R x y S xy P +∈+==则: ○ 1如果P 是定值, 那么当x=y 时,S 的值最小; ○ 2如果S 是定值, 那么当x =y 时,P 的值最大. 利用极值定理求最值的必要条件: 一正、二定、三相等 . ,3a b c a b c R +++∈≥(4)若、、则a=b=c 时取等号) 0,2b a ab a b >+≥(5)若则(当仅当a=b 时取等号) 2222(6)0||; ||a x a x a x a x a x a x a a x a >>?>?<->
2018年高考数学总复习 基本不等式及其应用
第二节基本不等式及其应用 考纲解读 1. 了解基本不等式错误!未找到引用源。的证明过程. 2. 会用基本不等式解决简单的最大(小)值问题. 3. 利用基本不等式证明不等式. 命题趋势探究 基本不等式是不等式中的重要内容,也是历年高考重点考查的知识点之一,其应用范围涉及高中数学的很多章节,且常考常新,但考查内容却无外乎大小判断、求最值和求最值范围等问题. 预测2019年本专题在高考中主要考查基本不等式求最值、大小判断,求取值范围问题. 本专题知识的考查综合性较强,解答题一般为较难题目,每年分值为58分. 知识点精讲 1. 几个重要的不等式 (1)错误!未找到引用源。 (2)基本不等式:如果错误!未找到引用源。,则错误!未找到引用源。(当且仅当“错误!未找到引用源。”时取“”). 特例:错误!未找到引用源。同号. (3)其他变形: ①错误!未找到引用源。(沟通两和错误!未找到引用源。与两平方和错误!未找到引用源。的不等关系式) ②错误!未找到引用源。(沟通两积错误!未找到引用源。与两平方和错误!未找到引用源。的不等关系式) ③错误!未找到引用源。(沟通两积错误!未找到引用源。与两和错误!未找到引用源。的不等关系式) ④重要不等式串:错误!未找到引用源。即 调和平均值几何平均值算数平均值平方平均值(注意等号成立的条件). 2. 均值定理 已知错误!未找到引用源。. (1)如果错误!未找到引用源。(定值),则错误!未找到引用源。(当且仅当“错误!未找到引用源。”时取“=”).即“和为定值,积有最大值”. (2)如果错误!未找到引用源。(定值),则错误!未找到引用源。(当且仅当“错误!未找到引用源。”时取“=”).即积为定值,和有最小值”. 题型归纳及思路提示 题型91 基本不等式及其应用 思路提示 熟记基本不等式成立的条件,合理选择基本不等式的形式解题,要注意对不等式等号是否成立进行验证. 例7.5“错误!未找到引用源。”是“错误!未找到引用源。”的() A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
高考数学真题分类汇编专题不等式理科及答案
高考数学真题分类汇编专题不等式理科及答案 Coca-cola standardization office【ZZ5AB-ZZSYT-ZZ2C-ZZ682T-ZZT18】
专题七 不等式 1.【2015高考四川,理9】如果函数()()()()21 281002 f x m x n x m n = -+-+≥≥, 在区间122?? ???? ,上单调递减,则mn 的最大值为( ) (A )16 (B )18 (C )25 (D )812 【答案】B 【解析】 2m ≠时,抛物线的对称轴为82n x m -=- -.据题意,当2m >时,8 22 n m --≥-即212m n +≤.226,182 m n m n mn +?≤ ≤∴≤.由2m n =且212m n +=得3,6m n ==.当2m <时,抛物线开口向下,据题意得,81 22 n m -- ≤-即218m n +≤.281 29,22 n m n m mn +?≤ ≤∴≤.由2n m =且218m n +=得92m =>,故应舍去.要使得mn 取得最大值,应有218m n +=(2,8)m n <>.所以 (182)(1828)816mn n n =-<-??=,所以最大值为18.选B.. 【考点定位】函数与不等式的综合应用. 【名师点睛】首先弄清抛物线的开口方向和对称轴,结合所给单调区间找到m 、n 满足的条件,然后利用基本不等式求解.本题将函数的单调性与基本不等式结合考查,检测了学生综合运用知识解题的能力.在知识的交汇点命题,这是高考的一个方向,这类题往往以中高档题的形式出现. 2.【2015高考北京,理2】若x ,y 满足010x y x y x -?? +??? ≤, ≤,≥,则2z x y =+的最大值为 ( ) A .0 B .1 C .32 D .2 【答案】D
基本不等式-高考数学知识点总结-高考数学真题复习
§7.4 基本不等式 2014高考会这样考 1.利用基本不等式求最值、证明不等式;2.利用基本不等式解决实际问题. 复习备考要这样做 1.注意基本不等式求最值的条件;2.在复习过程中注意转化与化归思想、分类讨论思想的应用. 1. 基本不等式≤ab a +b 2 (1)基本不等式成立的条件:a >0,b >0. (2)等号成立的条件:当且仅当a =b 时取等号.2. 几个重要的不等式 (1)a 2+b 2≥2ab (a ,b ∈R ).(2)+≥2(a ,b 同号). b a a b (3)ab ≤ 2 (a ,b ∈R ). (a +b 2)(4) ≥2 (a ,b ∈R ). a 2+ b 22 (a +b 2)3. 算术平均数与几何平均数 设a >0,b >0,则a ,b 的算术平均数为,几何平均数为,基本不等式可叙述为:a +b 2ab 两个正数的算术平均数不小于它们的几何平均数.4. 利用基本不等式求最值问题 已知x >0,y >0,则
(1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2.(简记:积定和最p 小) (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值是.(简记:和定积最大)p 2 4[难点正本 疑点清源] 1. 在应用基本不等式求最值时,要把握不等式成立的三个条件,就是“一正——各项均为 正;二定——积或和为定值;三相等——等号能否取得”,若忽略了某个条件,就会出现错误. 2. 运用公式解题时,既要掌握公式的正用,也要注意公式的逆用,例如a 2+b 2≥2ab 逆用 就是ab ≤ ;≥ (a ,b >0)逆用就是ab ≤ 2 (a ,b >0)等.还要注意“添、 a 2+ b 2 2 a +b 2ab (a +b 2)拆项”技巧和公式等号成立的条件等. 3. 对使用基本不等式时等号取不到的情况,可考虑使用函数y =x +(m >0)的单调性. m x 1. 若x >0,y >0,且x +y =18,则xy 的最大值是________. 答案 81 解析 由于x >0,y >0,则x +y ≥2, xy 所以xy ≤ 2 =81, (x +y 2)当且仅当x =y =9时,xy 取到最大值81. 2. 已知t >0,则函数y = 的最小值为________. t 2-4t +1 t 答案 -2
2020年高考数学复习题:基本不等式及其应用
基本不等式及其应用 [基础训练] 1.下列结论中正确的个数是( ) ①若a >0,则a 2 +1 a 的最小值是2a ; ②函数f (x )=sin 2x 3+cos 2x 的最大值是2; ③函数f (x )=x +1 x 的值域是[2,+∞); ④对任意的实数a ,b 均有a 2+b 2≥-2ab ,其中等号成立的条件是a =-b . A .0 B .1 C .2 D .3 : 答案:B 解析:①错误:设f (a )=a 2 +1 a ,其中a 是自变量,2a 也是变化的,不能说2a 是f (a )的最小值; ②错误:f (x )=sin 2x 3+cos 2 x ≤sin 2x +3+cos 2x 2 =2, 当且仅当sin 2x =3+cos 2x 时等号成立,此方程无解, ∴等号取不到,2不是f (x )的最大值; ③错误:当x >0时,x +1 x ≥2 x ·1x =2, 当且仅当x =1 x ,即x =1时等号成立; 当x <0时,-x >0,x +1 x =-? ?? ??-x +1-x ≤-2 -x ·1 -x =-2, ¥ 当且仅当-x =-1 x ,即x =-1时等号成立. ∴f (x )=x +1 x 的值域是(-∞,-2]∪[2,+∞); ④正确:利用作差法进行判断.
∵a 2+b 2+2ab =(a +b )2≥0,∴a 2+b 2≥-2ab , 其中等号成立的条件是a +b =0,即a =-b . 2.[2019河北张家口模拟]已知a +2b =2,且a >1,b >0,则 2 a -1+1 b 的最小值为( ) A .4 B .5 C .6 D .8 答案:D 解析:因为a >1,b >0,且a +2b =2, \ 所以a -1>0,(a -1)+2b =1, 所以2a -1+1b =? ????2 a -1+1 b ·[(a -1)+2b ] =4+4b a -1 +a -1b ≥4+2 4b a -1·a -1 b =8, 当且仅当4b a -1=a -1 b 时等号成立, 所以2a -1 +1b 的最小值是8,故选D. 3.若2x +2y =1,则x +y 的取值范围是( ) A .[0,2] B .[-2,0] C .[-2,+∞) D .(-∞,-2] ! 答案:D 解析:∵2x +2y ≥22x ·2y =22x +y (当且仅当2x =2y 时等号成立), ∴2 x +y ≤12,∴2x +y ≤14, 得x +y ≤-2.故选D. 4.已知x >0,y >0,且4xy -x -2y =4,则xy 的最小值为( ) B .2 2 D .2 答案:D 解析:∵x >0,y >0,x +2y ≥22xy , ∴4xy -(x +2y )≤4xy -22xy , ∴4≤4xy -22xy ,
高中数学不等式知识点总结
弹性学制数学讲义 不等式(4课时) ★知识梳理 1、不等式的基本性质 ①(对称性)a b b a >?> ②(传递性),a b b c a c >>?> ③(可加性)a b a c b c >?+>+ (同向可加性)d b c a d c b a +>+?>>, (异向可减性)d b c a d c b a ->-?<>, ④(可积性)bc ac c b a >?>>0, bc ac c b a 0, ⑤(同向正数可乘性)0,0a b c d ac bd >>>>?> (异向正数可除性)0,0a b a b c d c d >>< ⑥(平方法则) 0(,1)n n a b a b n N n >>?>∈>且 ⑦(开方法则)0(,1)n n a b a b n N n >>?>∈>且 ⑧(倒数法则) b a b a b a b a 110;110>?<<> 2、几个重要不等式 ①()222a b ab a b R +≥∈,,(当且仅当a b =时取""=号). 变形公式:22 .2a b ab +≤ ②(基本不等式) 2a b ab +≥ ()a b R +∈,,(当且仅当a b =时取到等号). 变形公式: 2a b a b +≥ 2 .2a b ab +??≤ ??? 用基本不等式求最值时(积定和最小,和定积最大),要注意满足三个条件“一正、二定、
三相等”. ③(三个正数的算术—几何平均不等式) 33a b c abc ++≥()a b c R +∈、、(当且仅当a b c ==时取到等号). ④()222a b c ab bc ca a b R ++≥++∈, (当且仅当a b c ==时取到等号). ⑤ 3333(0,0,0)a b c abc a b c ++≥>>> (当且仅当a b c ==时取到等号). ⑥0,2b a ab a b >+≥若则(当仅当a=b 时取等号) 0,2b a ab a b <+≤-若则(当仅当a=b 时取等号) ⑦b a n b n a m a m b a b <++<<++<1,(其中000)a b m n >>>>,, 规律:小于1同加则变大,大于1同加则变小. ⑧220;a x a x a x a x a >>?>?<->当时,或 22. x a x a a x a
高考数学不等式专题
基本不等式专题 一、知识点总结 1、基本不等式原始形式 (1)若R b a ∈,,则ab b a 22 2 ≥+ (2)若R b a ∈,,则2 2 2b a ab +≤ 2、基本不等式一般形式(均值不等式) 若*,R b a ∈,则ab b a 2≥+ 3、基本不等式的两个重要变形 (1)若* ,R b a ∈,则ab b a ≥+2(2)若*,R b a ∈,则2 2? ? ? ??+≤b a ab 总结:当两个正数的积为定植时,它们的和有最小值; 5、常用结论 (1)若0x >,则1 2x x +≥ (当且仅当1x =时取“=”) (2)若0x <,则1 2x x +≤- (当且仅当1x =-时取“=”) (3)若0>ab ,则2≥+a b b a (当且仅当 b a =时取“=”) (4)若R b a ∈,,则2 )2(222b a b a ab +≤ +≤ (5)若*,R b a ∈,则22111 22b a b a ab b a +≤+≤≤+ (6),、、)(3 33 333 3 3 +∈++≤?≥++R c b a c b a abc abc c b a 当且仅当a = b = c 时,“=”号成立; (7))(333 3+ ∈?? ? ??++≤?≥++R c b a c b a abc abc c b a 、、 ,当且仅当a = b = c 时, “ =”号成立. (1)若,,,a b c d R ∈,则22222()()()a b c d ac bd ++≥+ (2)若123123,,,,,a a a b b b R ∈,则有: 22222221231123112233()()()a a a b b b a b a b a b ++++≥++
2014届高考数学知识点总复习教案一元二次不等式及其解法
第2讲 一元二次不等式及其解法 A 级 基础演练 (时间:30分钟 满分:55分) 一、选择题(每小题5分,共20分) 1.(2012·南通二模)已知f (x )=????? x 2 ,x ≥0, -x 2+3x ,x <0, 则不等式f (x )2,因此x <0. 综上,x <4.故f (x )3.设a >0,不等式-c 0,∴-b +c a 0的解集是 ( ). A .(0,1)∪(2,+∞) B .(-2,1)∪(2,+∞) C .(2,+∞) D .(-2,2) 解析 原不等式等价于??? x 2-2>0,log 2x >0或??? x 2 -2<0, log 2x <0. ∴x >2或00的解集为? ???? -13,12,则不 等式-cx 2+2x -a >0的解集为________. 解析 由ax 2+2x +c >0的解集为? ???? -13,12知a <0,且-13,12为方程ax 2+2x +c =0的两个根,由根与系数的关系得-13+12=-2a ,-13×12=c a ,解得a =-12,c =2,∴-cx 2+2x -a >0,即2x 2-2x -12<0,其解集为(-2,3). 答案 (-2,3) 6.在实数集上定义运算?:x ?y =x (1-y ),若不等式(x -a )?(x +a )<1对任意实数x 恒成立,则实数a 的取值范围是________.
2017-18全国卷高考真题 数学 不等式选修专题
2017-2018全国卷I -Ⅲ高考真题 数学 不等式选修专题 1.(2017全国卷I,文/理.23)(10分) [选修4—5:不等式选讲](10分) 已知函数f (x )=–x 2+ax +4,g (x )=│x +1│+│x –1│. (1)当a =1时,求不等式f (x )≥g (x )的解集; (2)若不等式f (x )≥g (x )的解集包含[–1,1],求a 的取值范围. 【答案解析】 解:(1)当1a =时,()24f x x x =-++,是开口向下,对称轴12 x = 的二次函数. ()211121121x x g x x x x x >??=++-=-??-<-?,,≤x ≤,, 当(1,)x ∈+∞时,令242x x x -++= ,解得x =()g x 在()1+∞, 上单调递增,()f x 在()1+∞,上单调递减 ∴此时()()f x g x ≥ 解集为1? ?? . 当[]11x ∈-, 时,()2g x =,()()12f x f -=≥. 当()1x ∈-∞-, 时,()g x 单调递减,()f x 单调递增,且()()112g f -=-=. 综上所述,()()f x g x ≥ 解集1?-??? . (2)依题意得:242x ax -++≥在[]11-, 恒成立. 即220x ax --≤在[]11-, 恒成立. 则只须()()2211201120 a a ?-?-??----??≤≤,解出:11a -≤≤. 故a 取值范围是[]11-, .
2.(2017全国卷Ⅱ,文/理.23)(10分) [选修4-5:不等式选讲](10分) 已知0a >,222ba b +==2.证明: (1)()22()4a b a b ++≥; (2)2a b +≤. 【答案解析】 3.(2017全国卷Ⅱ,文/理.23)(10分) [选修4—5:不等式选讲](10分) 已知函数f (x )=│x +1│–│x –2│. (1)求不等式f (x )≥1的解集; (2)若不等式f (x )≥x 2–x +m 的解集非空,求m 的取值范围. 【答案解析】 解:(1)()|1||2|f x x x =+--可等价为()3,121,123,2--??=--<
2019高考数学不等式:基本不等式
基本不等式 【考点梳理】 1.基本不等式ab ≤ a +b 2 (1)基本不等式成立的条件:a >0,b >0. (2)等号成立的条件:当且仅当a =b . 2.几个重要的不等式 (1)a 2 +b 2 ≥2ab (a ,b ∈R ); (2)b a +a b ≥2(a ,b 同号且不为零); (3)ab ≤? ?? ??a +b 22(a ,b ∈R ); (4)? ?? ??a +b 22≤a 2 +b 2 2(a ,b ∈R ). 3.算术平均数与几何平均数 设a >0,b >0,则a ,b 的算术平均数为 a +b 2 ,几何平均数为ab ,基本不等式可叙述为: 两个正数的算术平均数不小于它们的几何平均数. 4.利用基本不等式求最值问题 已知x >0,y >0,则 (1)如果xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p (简记:积定和最小). (2)如果x +y 是定值q ,那么当且仅当x =y 时,xy 有最大值是q 2 4(简记:和定积最大). 【考点突破】 考点一、配凑法求最值 【例1】(1)若x < 54,则f (x )=4x -2+145 x -的最大值为________. (2)函数y = x -1 x +3+x -1 的最大值为________. [答案] (1) 1 (2) 1 5 [解析] (1)因为x <5 4 ,所以5-4x >0,
=-2+3=1. 当且仅当5-4x =1 5-4x ,即x =1时,等号成立. 故f (x )=4x -2+1 4x -5的最大值为1. (2)令t =x -1≥0,则x =t 2 +1, 所以y = t t 2 +1+3+t = t t 2 +t +4 . 当t =0,即x =1时,y =0; 当t >0,即x >1时,y = 1 t +4t +1 , 因为t +4 t ≥24=4(当且仅当t =2时取等号), 所以y = 1t +4t +1 ≤1 5, 即y 的最大值为1 5(当t =2,即x =5时y 取得最大值). 【类题通法】 1.应用基本不等式解题一定要注意应用的前提:“一正”“二定”“三相等”.所谓“一正”是指正数,“二定”是指应用基本不等式求最值时,和或积为定值,“三相等”是指满足等号成立的条件. 2.在利用基本不等式求最值时,要根据式子的特征灵活变形,配凑出积、和为常数的形式,然后再利用基本不等式. 【对点训练】 1.若函数f (x )=x + 1 x -2 (x >2)在x =a 处取最小值,则a 等于( ) A .1+2 B .1+3 C .3 D .4 [答案] C [解析] 当x >2时,x -2>0,f (x )=(x -2)+ 1 x -2 +2≥2(x -2)× 1 x -2 +2=4,当
高考数学专题练习:不等式与线性规划
高考数学专题练习:不等式与线性规划 1。若不等式(-2)n a -3n -1-(-2)n <0对任意正整数n 恒成立,则实数a 的取值范围是( ) A 。? ? ???1,43 B 。? ???? 12,43 C 。? ? ???1,74 D 。? ?? ??12,74 答案 D 解析 当n 为奇数时,要满足2n (1-a )<3n -1恒成立, 即1-a <13× ? ????32n 恒成立,只需1-a <13×? ????321,解得a >1 2; 当n 为偶数时,要满足2n (a -1)<3n -1恒成立, 即a -1<13× ? ????32n 恒成立,只需a -1<13×? ????322,解得a <7 4。 综上,12<a <7 4,故选D 。 2。已知a >0,b >0,且a ≠1,b ≠1,若log a b >1,则( ) A 。(a -1)(b -1)<0 B 。(a -1)(a -b )>0 C 。(b -1)(b -a )<0 D 。(b -1)(b -a )>0 答案 D 解析 取a =2,b =4,则(a -1)(b -1)=3>0,排除A ;则(a -1)(a -b )=-2<0,排除B ;(b -1)(b -a )=6>0,排除C,故选D 。 3。设函数f (x )=??? x 2-4x +6,x ≥0, x +6,x <0,则不等式f (x )>f (1)的解集是( ) A 。(-3,1)∪(3,+∞) B 。(-3,1)∪(2,+∞) C 。(-1,1)∪(3,+∞) D 。(-∞,-3)∪(1,3) 答案 A 解析 f (1)=3。由题意得??? x ≥0,x 2-4x +6>3或??? x <0, x +6>3, 解得-33。 4。 若a ,b ,c 为实数,则下列命题为真命题的是( ) A 。若a >b ,则ac 2>bc 2 B 。若a <b <0,则a 2>ab >b 2
高考数学复习+不等式选讲大题-(文)
专题十五不等式选讲大题 (一)命题特点和预测: 分析近8年全国新课标1不等式选讲大题,发现8年8考,主要考查绝对值不等式的解法(出现频率太高了,应当高度重视)、不等式恒成立或有解求参数的范围,考查利用不等式的性质、基本不等式、绝对值不等式性质求最值或证明不等式,难度为基础题.2019年不等式选讲大题仍将主要考查绝对值不等式的解法(出现频率太高了,应当高度重视)、不等式恒成立或有解求参数的范围,考查利用不等式的性质、基本不等式、绝对值不等式性质求最值或证明不等式,难度为基础题. (二)历年试题比较: . 时,求不等式 时不等式成立,求的取值范围. 已知函数, 的解集; 的解集包含
已知函数 ?并说明文由 ( )≤ 【解析与点睛】 (2018年)【解析】(1)当时,,即 故不等式的解集为. (2)当时成立等价于当时成立.若,则当时;
若,的解集为,所以,故. 综上,的取值范围为. (2017年)【解析】 x>时,①式化为,从而. 当1 【名师点睛】零点分段法是解答绝对值不等式问题常用的方法,也可以将绝对值函数转化为分段函数,借助图象解题. (2016年)【解析】(I) y=的图像如图所示. f ) (x
(II )由)(x f 的表达式及图像,当1)(=x f 时,可得1=x 或3=x ; 当1)(-=x f 时,可得3 1 = x 或5=x , 故1)(>x f 的解集为{} 31<x f 的解集为 . 【名师点睛】不等式选讲多以绝对值不等式为载体命制试题,主要涉及图像、解不等式、由不等式恒成立求参数范围等.解决此类问题通常转换为分段函数求解,注意不等式的解集一定要写成集合的形式. 以△ABC 的面积为22 (1)3 a +. 由题设得 22 (1)3 a +>6,解得2a >.
高考数学之基本不等式
基本不等式 基础梳理 1.基本不等式:ab ≤a +b 2 (1)基本不等式成立的条件:a >0,b >0. (2)等号成立的条件:当且仅当a =b 时取等号. 2.几个重要的不等式 (1)a 2+b 2≥2ab (a ,b ∈R ); (2)b a +a b ≥2(a ,b 同号); (3)ab ≤????a +b 22(a ,b ∈R ); (4)a 2+b 22≥????a +b 22(a ,b ∈R ). 3.算术平均数与几何平均数 设a >0,b >0,则a ,b 的算术平均数为 a + b 2,几何平均数为ab ,基本不等式可叙述为两个正数的算术平均数大于或等于它的几何平均数. 4.利用基本不等式求最值问题 已知x >0,y >0,则 (1)如果积xy 是定值p ,那么当且仅当x =y 时,x +y 有最小值是2p .(简记:积定和最小) (2)如果和x +y 是定值p ,那么当且仅当x =y 时,xy 有最大值是p 24.(简记:和定积最大) 一个技巧 22 ab ≤????a +b 22(a ,b >0)等.还要注意“添、拆项”技巧和公式等号成立的条件等. 两个变形 (1)a 2+b 22≥????a +b 22≥ab (a ,b ∈R ,当且仅当a =b 时取等号); a +b 这两个不等式链用处很大,注意掌握它们.
三个注意 (1)使用基本不等式求最值,其失误的真正原因是其存在前提“一正、二定、三相等”的忽视.要利用基本不等式求最值,这三个条件缺一不可. (2)在运用基本不等式时,要特别注意“拆”“拼”“凑”等技巧,使其满足基本不等式中“正”“定”“等”的条件. (3)连续使用公式时取等号的条件很严格,要求同时满足任何一次的字母取值存在且一致. 双基自测 1.(人教A 版教材习题改编)函数y =x +1x (x >0)的值域为( ). A .(-∞,-2]∪[2,+∞) B .(0,+∞) C .[2,+∞) D .(2,+∞) 解析 ∵x >0,∴y =x +1x ≥2, 当且仅当x =1时取等号. 答案 C 2.下列不等式:①a 2+1>2a ;②a +b ab ≤2;③x 2+1x 2+1≥1,其中正确的个数是( ). A .0 B .1 C .2 D .3 解析 ①②不正确,③正确,x 2+1x 2+1=(x 2+1)+1x 2+1 -1≥2-1=1. 答案 B 3.若a >0,b >0,且a +2b -2=0,则ab 的最大值为( ). A.12 B .1 C .2 D .4 解析 ∵a >0,b >0,a +2b =2, ∴a +2b =2≥22ab ,即ab ≤12 . 答案 A 4.(2011·重庆)若函数f (x )=x +1x -2 (x >2)在x =a 处取最小值,则a =( ). A .1+ 2 B .1+ 3 C .3 D .4 解析 当x >2时,x -2>0,f (x )=(x -2)+1x -2 +2≥2 (x -2)×1x -2+2=4,当且仅当x -2=1x -2 (x >2),即x =3时取等号,即当f (x )取得最小值时,x =3,即a =3. 答案 C 5.已知t >0,则函数y =t 2-4t +1t 的最小值为________. 解析 ∵t >0,∴y =t 2-4t +1t =t +1t -4≥2-4=-2,当且仅当t =1时取等号. 答案 -2
必修五不等式知识点总结
不等式总结 一、不等式的主要性质: (1)对称性:a b b a (2)传递性:c a c b b a >?>>, (3)加法法则:c b c a b a +>+?>; d b c a d c b a +>+?>>, (4)乘法法则:bc ac c b a >?>>0,; bc ac c b a 0, bd ac d c b a >?>>>>0,0 (5)倒数法则:b a a b b a 110,> (6)乘方法则:)1*(0>∈>?>>n N n b a b a n n 且 (7)开方法则:)1*(0>∈>?>>n N n b a b a n n 且 二、一元二次不等式02>++c bx ax 和)0(02≠<++a c bx ax 及其解法 有两相异实根 有两相等实根注意:一般常用因式分解法、求根公式法求解一元二次不等式 顺口溜:在二次项系数为正的前提下:大于型取两边,小于型取中间
三、均值不等式 1.均值不等式:如果a,b 是正数,那么 ).""(2 号时取当且仅当==≥+b a ab b a 2、使用均值不等式的条件:一正、二定、三相等 3、平均不等式:平方平均≥算术平均≥几何平均≥调和平均(a 、b 为正数),即 2 112a b a b ++(当a = b 时取等) 四、含有绝对值的不等式 1.绝对值的几何意义:||x 是指数轴上点x 到原点的距离;12||x x -是指数轴上12,x x 两点间的距离 2、则不等式:如果,0>a a x a x a x -<><=>>或|| a x a x a x -≤≥<=>≥或|| a x a a x <<-<=><|| a x a a x ≤≤-<=>≤|| 3.当0c >时, ||ax b c ax b c +>?+>或ax b c +<-, ||ax b c c ax b c +?∈,||ax b c x φ+?-<<,|| (0)x a a x a >>?>或x a <-. (2)定义法:零点分段法;(3)平方法:不等式两边都是非负时,两边同时平方. 五、其他常见不等式形式总结:
2018年高考数学—不等式专题
不等式 (必修5P80A3改编)若关于x 的一元二次方程x 2-(m +1)x -m =0有两个不相等的实数根,则m 的取值范围是________. 解析 由题意知Δ=[(m +1)]2+4m >0.即m 2+6m +1>0, 解得m >-3+22或m <-3-2 2. 答案 (-∞,-3-22)∪(-3+22,+∞) (2016·全国Ⅱ卷)若x ,y 满足约束条件???x -y +1≥0, x +y -3≥0,x -3≤0, 则 z =x -2y 的最小值为 ________. 解析 画出可行域,数形结合可知目标函数的最小值在直线x =3与直线x -y +1=0的交点(3,4)处取得,代入目标函数z =x -2y 得到-5. 答案 -5 (2016·全国Ⅲ卷)设x ,y 满足约束条件???2x -y +1≥0, x -2y -1≤0,x ≤1, 则z =2x +3y -5的最小值为_____. 解析 画出不等式组表示的平面区域如图中阴影部分所示.由题意可知, 当直线y =-23x +53+z 3过点A (-1,-1)时,z 取得最小值,即z min =2×(-1)+3×(-1)-5=-10.
(2017·西安检测)已知变量x ,y 满足???2x -y ≤0, x -2y +3≥0,x ≥0, 则z =(2)2x +y 的最大值为________. 解析 作出不等式组所表示的平面区域,如图阴影部分所示.令m =2x +y ,由图象可知当直线y =-2x +m 经过点A 时,直线y =-2x +m 的纵截距最大,此时m 最大,故z 最大.由?????2x -y =0,x -2y +3=0,解得?????x =1,y =2, 即A (1,2).代入目标函数z =(2)2x +y 得,z =(2)2×1+2=4. 答案 4 (2016·北京卷)若x ,y 满足???2x -y ≤0,x +y ≤3,x ≥0, 则2x +y 的最大值为( ) A.0 B.3 C.4 D.5 解析 画出可行域,如图中阴影部分所示, 令z =2x +y ,则y =-2x +z ,当直线y =-2x +z 过点A (1,2)时,z 最大,z max =4. 答案 C (2016·山东卷)若变量x ,y 满足???x +y ≤2, 2x -3y ≤9,x ≥0, 则x 2+y 2的最大值是( )