
求几何体外接球半径一法
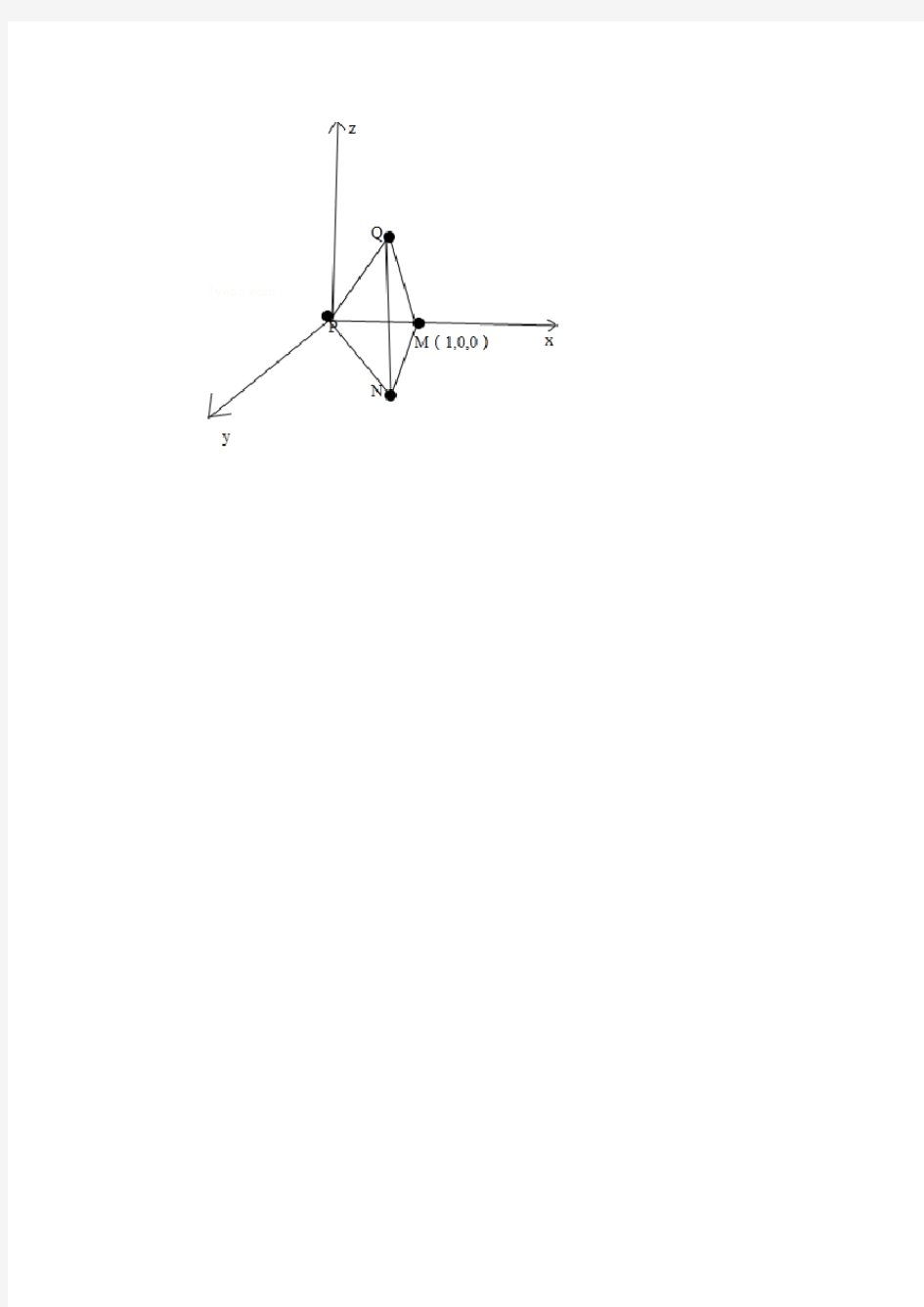
(2014春?铁岭月考)空间中一点P出发的三条射线PA,PB,PC,两两所成的角为60°,在射线PA,PB,PC上分别取点M,N,Q,使PM=1,PN=2,PQ=3,则三棱锥P﹣MNQ 的外接球表面积是10π.
考
点:
球内接多面体;棱柱、棱锥、棱台的体积.
专
题:
空间位置关系与距离;球.
分析:以P为坐标原点,PA所在直线为x轴,建立直角坐标系,设球心为O,则OP=OM=ON=OQ,列出等式,求出球的半径的平方,然后根据球的表面积公式解答即可.
解答:解:以P为坐标原点,PA所在直线为x轴,建立直角坐标系,则P(0,0,0),M(1,0,0),N(1,,0)
求得Q();
设球心为O,则OP=OM=ON=OQ,
∴x2+y2+z2=(x﹣1)2+y2+z2=
=
解得x=,,,
∴外接球半径的平方R2==
∴外接球的表面积S=4π×=10π.
故答案为:10π.
多面体外接球半径常见求法 知识回顾: 定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。 定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球。 球心到截面的距离d 与球半径R 及截面的半径r 有以下关系: . 球面被经过球心的平面截得的圆叫 .被不经过球心的平面截得的圆叫 球的表面积表面积S = ;球的体积V = . 球与棱柱的组合体问题 1. 正方体的内切球: 球与正方体的每个面都相切,切点为每个面的中心,显然球心为正方体的中心。设正方体的棱长为a ,球半径为R 。 如图3,截面图为正方形EFGH 的内切圆,得2 a R =; 2. 与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,如图4作截面图,圆O 为正方形EFGH 的外接圆,易得a R 2 2=。 3. 正方体的外接球:正方体的八个顶点都在球面上,如图5,以对角面1AA 作截面图得,圆O 为矩形C C AA 11的外接圆,易得a O A R 2 31==。 一、公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为 98 ,底面周长为3,则这个球的体积为 . 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式. 图3 图4 图5
二、多面体几何性质法 例2 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π 小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 三、补形法 例3 ,则其外接球的表面积是 . 小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2R = 变式1:三棱锥O ABC -中,,,OA OB OC 两两垂直,且22OA OB OC a ===,则三棱锥O ABC -外接球的表面积为( ) A .26a π B .29a π C .212a π D .2 24a π 四、寻求轴截面圆半径法 例4 正四棱锥S ABCD - S A B C D 、、、、都在同一球面上,则此球的体积为 . 而把立体几何问题转化为平面几何问题来研究.这种等价转化的数学思 想方 法值得我们学习. 变式1:求棱长为 a 的正四面体 P – ABC 的外接球的表面积 C D A B S O 1图3
空间几何体的内切球与外接球问题 1.[2016·全国卷Ⅱ] 体积为8的正方体的顶点都在同一球面上,则该球的表面积为( ) A .12π B.32 3 π C .8π D .4π [解析]A 因为正方体的体积为8,所以正方体的体对角线长为23,所以正方体的外接球的半径为3,所以球的表面积为4π·(3)2=12π. 2.[2016·全国卷Ⅲ] 在封闭的直三棱柱ABC - A 1B 1C 1内有一个体积为V 的球.若AB ⊥BC ,AB =6,BC =8,AA 1=3,则V 的最大值是( ) A .4π B.9π2 C .6π D.32π 3 [解析]B 当球与三侧面相切时,设球的半径为r 1,∵AB ⊥BC ,AB =6,BC =8,∴8-r 1+6-r 1=10,解得r 1=2,不合题意;当球与直三棱柱的上、下底面相切时,设球的半径为r 2, 则2r 2=3,即r 2=32.∴球的最大半径为32,故V 的最大值为43π×????323=92 π. 3.[2016·郑州模拟] 在平行四边形ABCD 中,∠CBA =120°,AD =4,对角线BD =23,将其沿对角线BD 折起,使平面ABD ⊥平面BCD ,若四面体ABCD 的顶点在同一球面上,则该球的体积为________. 答案:2053 π;解析:因为∠CBA =120°,所以∠DAB =60°,在三角形ABD 中,由余弦 定理得(23)2=42+AB 2-2×4·AB ·cos 60°,解得AB =2,所以AB ⊥BD .折起后平面ABD ⊥平面BCD ,即有AB ⊥平面BCD ,如图所示,可知A ,B ,C ,D 可看作一个长方体中的四个顶点,长方体的体对角线AC 就是四面体ABCD 外接球的直径,易知AC =22+42=25, 所以球的体积为205 3 π. 4.[2016·山西右玉一中模拟] 球O 的球面上有四点S ,A ,B ,C ,其中O ,A ,B ,C 四点共面,△ABC 是边长为2的正三角形,平面SAB ⊥平面ABC ,则棱锥S-ABC 的体积的最大 值为( ) A . 3 3 B . 3 C .2 3 D .4 选A ;[解析] (1)由于平面SAB ⊥平面ABC ,所以点S 在平面ABC 上的射影H 落在AB 上,根据球的对称性可知,当S 在“最高点”,即H 为AB 的中点时,SH 最大,此时棱锥S -ABC 的体积最大. 因为△ABC 是边长为2的正三角形,所以球的半径r =OC =23CH =23×32×2=23 3 . 在Rt △SHO 中,OH =12OC =3 3 ,
多面体外接球半径常见的5种求法 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 多面体几何性质法 例1 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π 解 设正四棱柱的底面边长为x ,外接球的半径为R ,则有2416x =,解得2x =. ∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C. 小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例2 ,则其外接球的表面积是 . 解 正方体,于是正方体的外接球就是三棱锥的外接球. 设其外接球的半径为R ,则有( ) 2 2 2 2 29R =++=.∴294 R = . 故其外接球的表面积249S R ππ==. 小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2R = 寻求轴截面圆半径法 例3 正四棱锥S ABCD - S A B C D 、、、、都在同一球面上,则此球的体积为 . 解 设正四棱锥的底面中心为1O ,外接球的球心为O ,如图1所示.∴ 由球的截面的性质,可得1OO ABCD ⊥平面. 又1SO ABCD ⊥平面,∴球心O 必在1SO 所在的直线上. ∴ASC ?的外接圆就是外接球的一个轴截面圆,外接圆的半径就是外接球 的半径. 在ASC ? 中,由2SA SC AC ===,得222SA SC AC +=. ∴ASC AC ??是以为斜边的Rt . ∴ 12AC =是外接圆的半径,也是外接球的半径.故43 V π =球. 小结 根据题意,我们可以选择最佳角度找出含有正棱锥特征元素的外接球的一个轴截面圆, C D A B S O 1图3
多面体外接球、内切球半径常见的 5种求法 欧阳光明(2021.03.07) 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98 ,底面周长为3,则这个球的体积为. 解 设正六棱柱的底面边长为x ,高为h ,则有263,1,296,84x x x h h =??=??∴??=???=?? ∴正六棱柱的底面圆的半径12r = ,球心到底面的距离d =. ∴外接球的半径1R ==.43V π∴=球. 小结本题是运用公式222R r d =+求球的半径的,该公式是求球
的半径的常用公式. 多面体几何性质法 例2 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π 解 设正四棱柱的底面边长为x ,外接球的半径为R ,则有2416x =,解得2x =. ∴2R R ==∴= .∴这个球的表面积是 2424R ππ=.选C. 小结本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例3 ,则其外接球的表面积是. 解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三 的正方体,于是正方体的外接球就是三棱锥的外接球. 设其外接球的半径为R ,则有()222 229R =++=.∴294 R =. 故其外接球的表面积249S R ππ==. 小结一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长
高中数学课题研究 几何体与球切、接的问题 纵观近几年高考对于组合体的考查,与球相关的外接与内切问题是高考命题的热点之一.高考命题小题综合化倾向尤为明显,要求学生有较强的空间想象能力和准确的计算能力,才能顺利解答.从实际教学来看,这部分知识学生掌握较为薄弱、认识较为模糊,看到就头疼的题目.分析原因,除了这类题目的入手确实不易之外,主要是学生没有形成解题的模式和套路,以至于遇到类似的题目便产生畏惧心理. 下面结合近几年高考题对球与几何体的切接问题作深入的探究,以便更好地把握高考命题的趋势和高考的命题思路,力争在这部分内容不失分.从近几年全国高考命题来看,这部分内容以选择题、填空题为主,大题很少见. 首先明确定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。 定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多面体,这个球是这个多面体的内切球. 1 球与柱体的切接 规则的柱体,如正方体、长方体、正棱柱等能够和球进行充分的组合,以外接和内切两种形态进行结合,通过球的半径和棱柱的棱产生联系,然后考查几何体的体积或者表面积等相关问题. 1.1 球与正方体 如图所示,正方体1111ABCD A B C D -,设正方体的棱长为a ,,,,E F H G 为棱的中点,O 为球的球心.常见组合方式有三类:一是球为正方体的内切球,截面图为正方形EFGH 和其内切圆,则2a OJ r ==;二 是与正方体各棱相切的球,截面图为正方形EFGH 和其外接圆,则GO R a ==;三是球为正方体的 外接球,截面图为长方形11ACA C 和其外接圆,则12 A O R a '==.通过这三种类型可以发现,解决正方体与球的组合问题,常用工具是截面图,即根据组合的形式找到两个几何体的轴截面,通过两个截面图的位置关系,确定好正方体的棱与球的半径的关系,进而将空间问题转化为平面问题.
多面体外接球半径常见的几种求法
————————————————————————————————作者:————————————————————————————————日期: ?
多面体外接球半径常见的几种求法 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9 8 ,底面周长为3,则这个球的体积为 . 解 设正六棱柱的底面边长为x ,高为h ,则有 263,1,2936,38 4x x x h h =?? =?? ∴?? =???=??. ∴正六棱柱的底面圆的半径12r =,球心到底面的距离3 2 d =.∴外接球的半径221R r d =+=.43 V π ∴= 球. 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式. 多面体几何性质法 例2 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A .16π B.20π C.24π D.32π
解 设正四棱柱的底面边长为x ,外接球的半径为R ,则有 2416x =,解得2x =. ∴222222426,6R R =++=∴= .∴这个球的表面积是 2424R ππ=.选C. 小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例3 若三棱锥的三个侧面两两垂直,且侧棱长均为3,则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直,∴把这个三棱锥可以补成一个棱长为3的正方体,于是正方体的外接球就是三棱锥的外接球. 设其外接球的半径为R ,则有()()()()2 2 2 2 23339R =++=.∴ 294 R = . 故其外接球的表面积249S R ππ==. 小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为 R ,则有2222R a b c =++.
精品文档 多面体外接球半径常见的5种求法 文/郭军平 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98 ,底面周长为3,则这个球的体积为 . 解 设正六棱柱的底面边长为x ,高为h ,则有263,1,296,8 4x x x h h =??=??∴??=???=?? ∴正六棱柱的底面圆的半径12 r = ,球心到底面的距离2d =. ∴外接球的半径1R ==.43 V π∴=球. 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式. 多面体几何性质法 例2 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π 解 设正四棱柱的底面边长为x ,外接球的半径为R ,则有2416x =,解得2x =. ∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C. 小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例3 若三棱锥的三个侧面两两垂直, 则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直, ∴把这个三棱锥可以补成一个棱长为. 设其外接球的半径为R ,则有( ) 222229R = ++=.∴294R =. 故其外接球的表面积249S R ππ==. 小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就
空间几何体的外接球 类型一: 长方体模型一(三条线两两垂直,不找球心的位置即可求出球半径) c a b C P A B a b c 图2 P C B A a b c 图3 C B P A a b c P C O 2 B A 方法:找三条两两垂直的线段,直接用公式2 2 2 2 )2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( ) A .π16 B .π20 C .π24 D .π32 (2)若三棱锥ABC S -的三条侧棱两两垂直,且2=SA ,4==SC SB ,则该三棱锥的外接球半径为( ) A.3 B.6 C.36 D.9 (3)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 (4)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱23SA =,则正三棱锥ABC S -外接球的表面积是 (5)如果三棱锥的三个侧面两两垂直,它们的面积分别为6、4、3,那么它的外接球的表面积是 (6)已知某几何体的三视图如图所示,三视图是腰长为1的等腰直角三角形和边长为 1的正方形,则该几何体外接球的体积为 长方体模型二:(一条直线垂直于一个平面) 1.题设:如图5,⊥PA 平面ABC 解题步骤: 第一步:将ABC ?画在小圆面上,A 为小圆直径的一个端点,作小圆的直 径AD ,连接PD ,则PD 必过球心O ; 第二步:1O 为ABC ?的外心,所以⊥1OO 平面ABC ,算出小圆1O 的半 径r D O =1(三角形的外接圆直径算法:利用正弦定理,得 r C c B b A a 2sin sin sin ===),PA OO 211=; 第三步:利用勾股定理求三棱锥的外接球半径:①2 22)2()2(r PA R +=?22)2(2r PA R += ; ②2 12 2OO r R +=?2 12OO r R += 图5 A D P O 1O C B
多面体外接球、内切球半径常见的5种求法 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为98 ,底面周长为3,则这个球的体积为 . 解 设正六棱柱的底面边长为x ,高为h ,则有263,1,296,8 x x h h =??=??∴??=??=?? ∴正六棱柱的底面圆的半径12 r = ,球心到底面的距离d =. ∴外接球的半径1R ==.43 V π∴=球. 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式. 多面体几何性质法 例2 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是 A.16π B.20π C.24π D.32π 解 设正四棱柱的底面边长为x ,外接球的半径为R ,则有2416x =,解得2x =. ∴2R R ==∴= .∴这个球的表面积是2424R ππ=.选C. 小结 本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例3 若三棱锥的三个侧棱两两垂直, ,则其外接球的表面积是 . 解 据题意可知,该三棱锥的三条侧棱两两垂直, ∴把这个三棱锥可以补成一个棱长为. 设其外接球的半径为R ,则有( ) 222229R = ++=.∴294R =. 故其外接球的表面积249S R ππ==. 小结 一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为a b c 、、,则就可以将这个三棱锥补成一个长方体,于是长方体的体对角线的长就是该三棱锥的外接球的直径.设其外接球的半径为R ,则有2R =
多面体外接球、内切球半径常见的5种求法 如果一个多面体的各个顶点都在同一个球面上,那么称这个多面体是球的内接多面体,这个球称为多面体的外接球.有关多面体外接球的问题,是立体几何的一个重点,也是高考考查的一个热点.研究多面体的外接球问题,既要运用多面体的知识,又要运用球的知识,并且还要特别注意多面体的有关几何元素与球的半径之间的关系,而多面体外接球半径的求法在解题中往往会起到至关重要的作用. 公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同一个球面上,且该六棱柱的体积为9,底面周长为3,则这个球的体积为 8 T 6x=3,T 1 I ' I x =— 解设正六棱柱的底面边长为x,咼为h,则有丿9 V3 2 2’ _=6汉——xh, 石 8 4 小一x/3 ???正六棱柱的底面圆的半径r =-,球心到底面的距离d二上3.二外接球的半径 2 2 R=、r2d2「=1. . V球二—. 3 小结本题是运用公式R2-r2 d2求球的半径的,该公式是求球的半径的常用公式. 多面体几何性质法 例2已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表 面积是 A. 16二 B. 20 二 C. 24 二 D. 32 二 解设正四棱柱的底面边长为x ,外接球的半径为R,则有4x2 = 16,解得x = 2. 二2R = J22+22+42=2屈,二R = T6. ???这个球的表面积是4兀R2=24兀.选C. 小结本题是运用“正四棱柱的体对角线的长等于其外接球的直径”这一性质来求解的. 补形法 例3若三棱锥的三个侧棱两两垂直,且侧棱长均为.3,则其外接球的表面积是. 解据题意可知,该三棱锥的三条侧棱两两垂直,I把这个三棱锥可以补成一个棱长 为3的正方体,于是正方体的外接球就是三棱锥的外接球 设其外接球的半径为R,则有(2R f =(応行(亦丫+(73$ =9.二R2=9. 4 故其外接球的表面积S =4二R2=9二. 小结一般地,若一个三棱锥的三条侧棱两两垂直,且其长度分别为 a b、c,则就
几何体外接球常用结论及方法(如何求几何体的外接球半径) 一、在涉及球的问题中,经常用到结论: (1)在三棱锥P ABC -中,PA PB ⊥,PA PC ⊥,PB PC ⊥,则该三棱锥外接球半径 2R = (2倍. (3)直角三角形的三角形外接圆的半径等于斜边的一半. (4)一般的三角形ABC 可由正弦定理:2sin sin sin a b c R A B C ===(R 为外接圆半径)求得外接圆半径,内切圆的半径通过:12 S C r =?多边形多边形的周长(r 为内切圆的半径)求得. (5)已知三棱锥P ABC -,PA ⊥面ABC ,若PA a =,ABC △的外接圆半径为r ,则该三棱锥 P ABC -的外接球半径为()()22222R r a =+. (6)正方体的外接球、内切球、棱切球的直径分别为正方体的体对角线长2R =、棱长2R a =、 面对角线长2R =. (7)在四面体P ABC -,若90APC ∠=?,90ABC ∠=?,则四面体P ABC -的外接球的直径是 AC . (8)对于正棱锥的外接球的半径计算,也可借用几何法求出.如针对正三棱锥V ABC -,可根据平 面几何中射影定理22VA VO VH Rh '=?=(h 为正三棱锥的高,VA 为侧棱长,即正棱锥侧棱长的平方等于正棱锥的高与外接球直径的乘积. (9)正四面体的高、外接球的半径与内切球的半径之间关系: ①高:a h 36=;②球心把高分成3:1;③内切球半径:a 126;外接球半径:a 4 6. (10)有内切球的多面体的内切球的半径计算方法:13V S r =全 . (11)三棱锥的两个侧面互相垂直,已知两个相互垂直的面的外接圆半径的长及其公共棱的长度的情 形:已知三棱锥A BCD -中,面ABD ⊥面BCD ,且ABD ?,BCD ?的外接圆半径分别记为12,r r ,公共棱BD a =,则该三棱锥的外接球半径满足:()()()222 212222R r r a =+- 证明:分别在ABD ?,BCD ?所在的圆面上调整这两个三角形的开关,如图
八个有趣模型——搞定空间几何体的外接球与内切球 类型一、墙角模型(三条线两个垂直,不找球心的位置即可求出球半径) 图2 图3 图4 方法:找三条两两垂直的线段,直接用公式2 2 2 2 )2(c b a R ++=,即2222c b a R ++=,求出R 例1 (1)已知各顶点都在同一球面上的正四棱柱的高为4,体积为16,则这个球的表面积是( C ) A .π16 B .π20 C .π24 D .π32 (2)若三棱锥的三个侧面两垂直,且侧棱长均为3,则其外接球的表面积是 π9 解:(1)162 ==h a V ,2=a ,24164442 2 2 2 =++=++=h a a R ,π24=S ,选C ; (2 )933342 =++=R ,ππ942 ==R S (3)在正三棱锥S ABC -中,M N 、分别是棱SC BC 、的中点,且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 。π36 解:引理:正三棱锥的对棱互垂直。证明如下: 如图(3)-1,取BC AB ,的中点E D ,,连接CD AE ,,CD AE ,交于H ,连接SH ,则H 是底面正三角形ABC 的中心,∴⊥SH 平面ABC ,∴AB SH ⊥, BC AC =,BD AD =,∴AB CD ⊥,∴⊥AB 平面SCD , ∴SC AB ⊥,同理:SA BC ⊥,SB AC ⊥,即正三棱锥的对棱互垂直, 本题图如图(3)-2, MN AM ⊥,MN SB //, ∴SB AM ⊥, SB AC ⊥,∴⊥SB 平面SAC , ∴SA SB ⊥,SC SB ⊥, SA SB ⊥,SA BC ⊥, ∴⊥SA 平面SBC ,∴SC SA ⊥, 故三棱锥ABC S -的三棱条侧棱两两互相垂直, ∴36)32()32()32()2(2222 =++=R ,即3642=R , ∴正三棱锥ABC S -外接球的表面积是π36 (3)题-1 A (3)题-2 A
αR P d r O O'第二讲 几何体的外接球和内切球问题 ※基础知识: 1.常见平面图形:正方形,长方形,正三角形的外接圆和内切圆 长方形(正方形)的外接圆半径为对角线长的一半,正方形的内切圆半径为边长的一半; 正三角形的内切圆半径:36a 外接圆半径:33a 三角形面积:234 a 正三角形三心合一,三线合一,心把高分为2:1两部分。 2.球的概念: 概念1:与定点距离等于或小于定长的点的集合,叫做球体,简称球.,定长叫球的半径; 与定点距离等于定长的点的集合叫做球面.一个球或球面用表示它的球心的字母表示,例如球O 或O e . 概念2:半圆以它的直径为旋转轴,旋转所成的曲面叫做球面,球面所围成的几何体叫做球体,简称球。 3.球的截面: 用一平面α去截一个球O ,设OO '是平面α的垂线段,O '为垂足,且 OO d '=,所得的截面是以球心在截面内的射影为圆心,以22r R d =-为半 径的一个圆,截面是一个圆面. 球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆. 4.空间几何体外接球、内切球的概念: 定义1:若一个多面体的各顶点都在一个球的球面上,则称这个多面体是这个球的内接多面体,这个球是这个多面体的外接球。 定义2:若一个多面体的各面都与一个球的球面相切, 则称这个多面体是这个球的外切多
面体,这个球是这个多面体的内切球。 长方体的外接球 正方体的内切球 5.外接球和内切球性质: (1)内切球球心到多面体各面的距离均相等,外接球球心到多面体各顶点的距离均相等。 (2)正多面体的内切球和外接球的球心重合。 (3)正棱锥的内切球和外接球球心都在高线上,但不重合。 (4)基本方法:构造三角形利用相似比和勾股定理。 (5)体积分割是求内切球半径的通用做法。 6.公式:球的表面积公式:24S R π=;球的体积公式:343 V R π= 长方体的外接球半径公式:2 2 22c b a R ++=,其中,,a b c 分别为长方体共顶点的3条棱长 正棱锥的外接球半径公式:2 ,2a R h = 2侧棱=2R h ?外正棱锥,其中a 为侧棱长,h 为正棱锥的高 正棱柱的外接球球心在两底面中心连线的中点处。 ※典型例题: 题型一:球的概念 例1. (1)已知球的直径为8cm ,那么它的表面积为__________,体积为___________
3 3 空间几何体的外接球与内切球(一) 第一讲 柱体背景的模型 类型一、墙角模型(三条棱两两垂直,不找球心的位置即可求出球半径) 侧 1-1 侧 1-2 侧 1-3 侧 1-4 方法:找三条两两垂直的线段,直接用公式(2R )2 = a 2 + b 2 + c 2 ,即2R = ,求出 R 例 1 ( 1) 已知各顶点都在同一球面上的正四棱柱的高为 4 , 体积为 16 , 则这个球的表面积是 ( C ) A .16 B . 20 C . 24 D . 32 解: V = a 2 h = 16 , a = 2 , 4R 2 = a 2 + a 2 + h 2 = 4 + 4 + 16 = 24 , S = 24 ,选 C ; (2) 若三棱锥的三个侧面两两垂直,且侧棱长均为 , 则 其 外 接 球 的 表 面 积 是 9 解: 4R 2 = 3 + 3 + 3 = 9 , S = 4R 2 = 9; (3) 在正三棱锥 S - ABC 中, M 、N 分别是棱 SC 、BC 的中点,且 AM ⊥ MN ,若侧棱 SA = 2 ,则 正三棱锥 S - ABC 外接球的表面积是 . 36 S 解:引理:正三棱锥的对棱互相垂直.证明如下:如图(3)-1, 取 AB , BC 的中点 D , E ,连接 AE , CD , AE , CD 交于 H ,连接 SH , 则 H 是底面正三角形 ABC 的中心, ∴ SH ⊥ 平面 ABC ,∴ SH ⊥ AB , A C D H E B AC = BC , AD = BD ,∴ CD ⊥ AB ,∴ AB ⊥ 平面 SCD , ∴ AB ⊥ SC ,同理: BC ⊥ SA , AC ⊥ SB ,即正三棱锥的对棱互垂直, 本题图如图(3)-2, AM ⊥ MN , SB // MN , ∴ AM ⊥ SB , AC ⊥ SB ,∴ SB ⊥ 平面 SAC , ∴ SB ⊥ SA , SB ⊥ SC , SB ⊥ SA , BC ⊥ SA , A ∴ SA ⊥ 平面 SBC ,∴ SA ⊥ SC , 故三棱锥 S - ABC 的三棱条侧棱两两互相垂直, (3)侧-1(侧侧侧 S M C N B (3)侧-2侧侧侧侧侧 P c B b a C A P c C b A a B P c C b A a B P c A a b C B a 2 + b 2 + c 2
简单几何体外接球半径的求法 一、补成正方体或长方体型 有三维垂直的条件或者正四面体或者三对相对棱分别相等的三棱锥。 练习:1、三棱锥P-ABC中,PA,PB,PC两两垂直,长度 2,则其外接球半径为。 分别为3,5,2 2,则其外接球表面积为。 2、正四面体棱长为2 3、已知三棱锥A-BCD的三对相对棱分别长为5 , 13, 10 , 则其外接球表面积为。 二、补成圆柱型 底面有外接圆的直棱柱都可以补成圆柱求外接球半径。 练习:1、三棱锥P-ABC中,PA垂直于底面ABC, 120,PA=3, AB=BC=2,∠B=0 其外接球表面积为。 2、三棱锥P-ABC中,PC垂直于底面ABC,
AB=3,BC=23,∠B=060, 其外接球表面积为π28,则PC=。 三、正棱锥型 外接球球心在正棱锥高所在直线上,在直角三角形中求解。 练习:1、如图,正三棱锥A-BCD 底面边长BC=6,高AH=8,则其 外接球表面积为。 2、正四棱锥底面边长为4,侧棱长为112 ,则其外接球表面积为。 四、面面垂直型 找出互相垂直的这两个面的外心21,O O ,分别过21,O O 作所在平面的垂线21,l l ,21,l l 的交点即为外接球的球心。在直角三角形中求外接球的半径。 练习:1、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ和PBC Δ都是边长为6的正三角形, 则其外接球半径为。
2、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ是斜边为BC 的直角三角形,PBC Δ是边长为6的正三角形,则其外接球半径为。 3、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ是斜边为AB 的直角三角形,AC=4,PBC Δ是边长为6的正三角形,则其外接球半径为。 4、四棱锥P-ABCD 中,面PBC 垂直于面ABCD ,其中PBC Δ都是边长为6的正三角形,底面ABCD 是矩形, AB=8,则其外接球半径为。
【知识要点】 求几何体外接球的半径一般有两种方法:模型法和解三角形法. 模型法就是把几何体放在长方体中,使几何体的顶点和长方体的若干个顶点重合,则几何体的外接球.如果已知中有多个垂直关系,可以考虑用此种方法. 解三角形法就是找到球心O 和截面圆的圆心O ',找到OO '、球的半径OA 、截面圆的半径O A '确定的Rt OO A '?,再解Rt OO A '?求出球的半径OA . 【方法讲评】 【例1】已知四面体中, , , , 平面 ,则四面体 外 接球的表面积为__. 【点评】(1)本题看起来没有三条直线相交于一点且两两垂直的模型,但是通过推理分析得到了 PA PB PC 、、两两垂直,所以可以采用模型法来求几何体外接球的半径. (2)利用模型法解答时,一定 要保证几何体的所有顶点都和长方体的顶点重合,这才能保证几何体的外接球和长方体的外接球是同一个. 【反馈检测1
上,则球的体积为___________. 3 【点评】(1)由于本题的几何体不宜放在长方体模型中,所以用解三角形法解答. (2)利用解三角形法求几何体外接球的半径,先要找到球心O 的位置,要找球心O 的位置,没有固定的规律,要结合几何体的特征,发挥自己的空间想象力分析,本题由于是直三棱柱,所以球心在上下底面外接圆圆心连线的中点,如果是其它的几何体就不是这个位置了. 找到球心O 的位置后,再确定截面圆的圆心1O 位置,再表示出球心O 到截面圆圆心1O 的距离1OO ,这个是难点,要结合几何图形分析.最后是解1Rt OO A ?,求出球的半径R . (2)如果几何体底面是三角形,求截面圆的半径r ,一般利用正弦定理
简单几何体外接球半径的 求法 一、补成正方体或长方体型 有三维垂直的条件或者正四面体或者三对相对棱分别相等的三棱锥。 练习:1、三棱锥P-ABC中,PA,PB,PC两两垂直,长度 分别为3,5,2 2 ,则其外接球半径为。 2、正四面体棱长为2 2 ,则其外接球表面积为。 3、已知三棱锥A-BCD的三对相对棱分别长为13, 10, 5 ,则其外接球表面积为。 二、补成圆柱型底面有外接圆的直棱柱都可以补成圆柱求外接球半径。练习:1、三棱锥P-ABC中,PA垂直于底面ABC,AB=BC=2,∠ B=1200,PA=3,其外接球表面积为。 2、三棱锥P-ABC中,PC垂直于底面ABC,
AB= 3,BC=2 3,∠ B=600,其外接球表面积为28π,则PC=。 三、正棱锥型外接球球心在正棱锥高所在直线上,在直角三角形中求解。练习: 1、如图,正三棱锥A-BCD 底面边长BC=6,高AH=8,则其外接球表面积为。 2、正四棱锥底面边长为4,侧棱长为2 11 则其外接球表面积为。 四、面面垂直型 找出互相垂直的这两个面的外心O1,O2 ,分别过O1,O2 作所在平面的垂线l1, l 2 ,l1 ,l 2的交点即为外接球的球心。在直角三角形中求外接球的半径。 练习:1、三棱锥P-ABC中,面PBC垂直于面ABC,ΔABC 和ΔPBC 都是边长为6 的正三角形,则其外接球半径为。
ΔPBC 是边长为6 的2、三棱锥P-ABC中,面PBC垂直于面ABC,ΔABC 是斜边为BC 的直角三角形,正三角 形,则其外接球半径为。 ΔABC 是斜边为AB 的直角三角形,AC=4,ΔPBC 是边长3、三棱锥P-ABC中,面PBC垂直于面ABC,为 6 的正三角形,则其外接球半径为。 4、四棱锥P-ABCD中,面PBC垂直于面ABCD,其中ΔPBC 都是边长为6 的正三角形, 底面ABCD 是矩形,AB=8,则其外接球半径为。
四面体外接球的球心、半径求法 在立体几何中,几何体外接球是一个常考的知识点,对于学生来说这是一个难点,一方面图形不会画,另一方面在画出图形的情况下无从下手,不知道球心在什么位置,半径是多少而无法解题。 本文章在给出图形的情况下解决球心位置、半径大小的问题。 一、出现“墙角”结构利用补形知识,联系长方体。 【原理】:长方体中从一个顶点出发的三条棱长分别为c b a ,,,则体对角线长为 2 2 2 c b a l ++=,几何体的外接球直径R 2为体对角线长l 即2 2 22c b a R ++= 【例题】:在四面体ABCD 中,共顶点的三条棱两两垂直,其长度分别为3,61,,若该四面体的四个顶点在一个球面上,求这个球的表面积。 解: 因为:长方体外接球的直径为长方体的体对角线长 所以:四面体外接球的直径为AE 的长 即:22224AD AC AB R ++= 1663142 2 22=++=R 所以2=R 球的表面积为ππ1642==R S 二、出现两个垂直关系,利用直角三角形结论。 【原理】:直角三角形斜边中线等于斜边一半。球心为直角三角形斜边中点。 【例题】:已知三棱锥的四个顶点都在球O 的球面上,BC AB ⊥且7=PA , 5=PB ,51=PC ,10=AC ,求球O 的体积。 解:BC AB ⊥且7=PA ,5=PB ,51=PC ,10=AC , A C D B E
因为22 210517=+ 所以知222PC PA AC += 所以 PC PA ⊥ 所以可得图形为: 在ABC Rt ?中斜边为AC 在PAC Rt ?中斜边为AC 取斜边的中点O , 在ABC Rt ?中OC OB OA == 在PAC Rt ?中OC OB OP == 所以在几何体中OA OC OB OP ===,即O 为该四面体的外接球的球心 52 1 == AC R 所以该外接球的体积为3 500343π π==R V 【总结】斜边一般为四面体中除了直角顶点以外的两个点连线。 三、出现多个垂直关系时建立空间直角坐标系,利用向量知识求解 【例题】:已知在三棱锥BCD A -中,ABC AD 面⊥,?=∠120BAC , 2===AC AD AB ,求该棱锥的外接球半径。 解:由已知建立空间直角坐标系 )000(,,A )002(,,B )200(,,D )031(,,-C 由平面知识得 设球心坐标为),,(z y x O 则DO CO BO AO ===,由空间两点间距离公式知 222222)2(z y x z y x ++-=++ 222222)2(-++=++z y x z y x 222222)3()1(z y x z y x +-+-=++ O A B C P A B C D z x y
多面体外接球半径常见的5种求法 一、公式法 例1 一个六棱柱的底面是正六边形,其侧棱垂直于底面,已知该六棱柱的顶点都在同 一个球面上,且该六棱柱的体积为9 8 ,底面周长为3,则这个球的体积为 . 解 设正六棱柱的底面边长为x ,高为h ,则有263,1,296,84x x x h h =?? =?? ∴?? =???=?? ∴正六棱柱的底面圆的半径1 2 r = ,球心到底面的距离2d =. ∴外接球的半径 1R ==.43 V π ∴= 球. 小结 本题是运用公式222R r d =+求球的半径的,该公式是求球的半径的常用公式. 二、多面体几何性质法 例1 (2006年广东高考题)若棱长为3的正方体的顶点都在同一球面上,则该球的表面积为 . 解析:要求球的表面积,只要知道球的半径即可.因为正方体内接于球,所以它的体对角线正好为球的直径,因此,求球的半径可转化为先求正方体的体对角线长,再计算半径.故表面积为27π. 例2 一个正方体的各顶点均在同一球的球面上,若该正方体的表面积为24,则该球的体积为 . 解析:要求球的体积,还是先得求出球的半径,而球的直径正好是正方体的体对角线, 因此,由正方体表面积可求出棱长,从而求出正方体的体对角线是 . 故该球的体积为. 例3 (2007年天津高考题)一个长方体的各顶点均在同一球面上,且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为 . 解析:关键是求出球的半径,因为长方体内接于球,所以它的体对角线正好为球的直径。 长方体体对角线长为14π. 例4、(2006年全国卷I ) 已知各顶点都在同一个球面上的正四棱柱的高为4,体积为16,则这个球的表面积是
文科常见的简单几何体外接球半径的求法 一、补成正方体或长方体型 有三维垂直的条件或者正四面体或者三对相对棱分别相等的三棱锥。 练习:1、三棱锥P-ABC中,PA,PB,PC两两垂直,长度 2,则其外接球半径为。 分别为3,5,2 2,则其外接球表面积为。 2、正四面体棱长为2 3、已知三棱锥A-BCD的三对相对棱分别长为5 13, , , 10 则其外接球表面积为。 二、补成圆柱型 底面有外接圆的直棱柱都可以补成圆柱求外接球半径。 练习:1、三棱锥P-ABC中,PA垂直于底面ABC, 120,PA=3, AB=BC=2,∠B=0 其外接球表面积为。 2、三棱锥P-ABC中,PC垂直于底面ABC, 60, AB=3,BC=23,∠B=0
其外接球表面积为π28,则PC=。 三、正棱锥型 外接球球心在正棱锥高所在直线上,在直角三角形中求解。 练习:1、如图,正三棱锥A-BCD 底面边长BC=6,高AH=8,则其 外接球表面积为。 2、正四棱锥底面边长为4,侧棱长为112 ,则其外接球表面积为。 四、面面垂直型 找出互相垂直的这两个面的外心21,O O ,分别过21,O O 作所在平面的垂线21,l l ,21,l l 的交点即为外接球的球心。在直角三角形中求外接球的半径。 练习:1、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ和PBC Δ都是边长为6的正三角形, 则其外接球半径为。
2、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ是斜边为BC 的直角三角形,PBC Δ是边长为6的正三角形,则其外接球半径为。 3、三棱锥P-ABC 中,面PBC 垂直于面ABC , ABC Δ是斜边为AB 的直角三角形,AC=4,PBC Δ是边长为6的正三角形,则其外接球半径为。 4、四棱锥P-ABCD 中,面PBC 垂直于面ABCD ,其中PBC Δ都是边长为6的正三角形,底面ABCD 是矩形, AB=8,则其外接球半径为。