
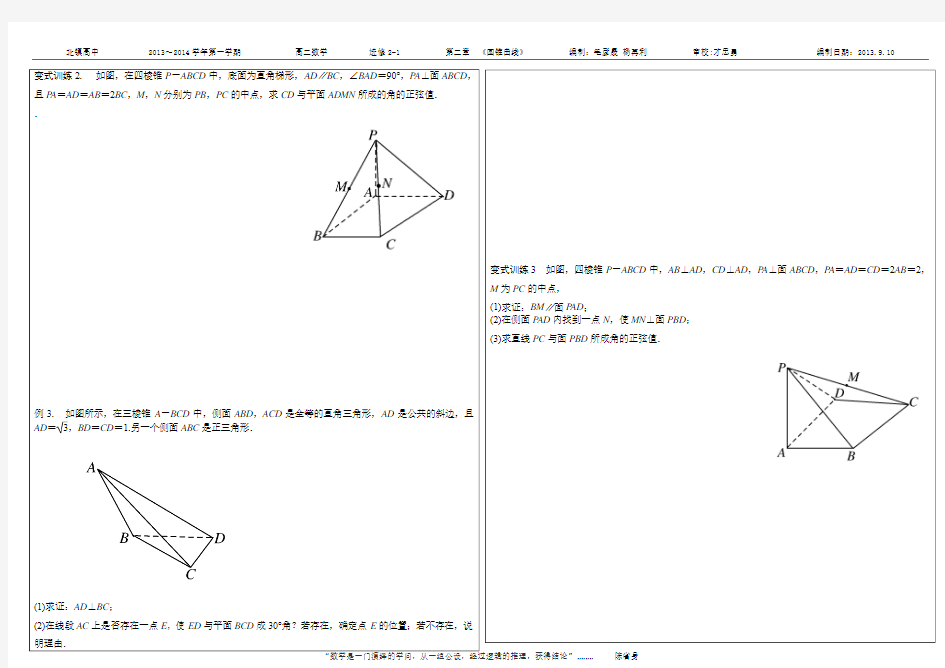
北镇高中 2013~2014学年第一学期高二数学选修2-1 第二章《圆锥曲线》编制:毛彦晟杨再利审校:才忠勇编制日期:2013.9.10
北镇高中 2013~2014学年第一学期高二数学选修2-1 第二章《圆锥曲线》编制:毛彦晟杨再利审校:才忠勇编制日期:2013.9.10
是全等的直角三角形,AD是公共的斜边,且
AD⊥BC;
AC上是否存在一点E,使ED与平面
内所有直线所成的角中最小的角是()
A与面ABC所成的角为()
AB的长度为________.
与侧面ACC1A1所成角的正弦值为
,且AC=BC=BD=2AE,M为AB的
平面上两直线的夹角求法解析 一、内容概述 在2004年审定的人教A和B版教材中,平面两条直线的夹角概念与相应问题没有涉及到.但是,该问题完全可以作为三角恒等式中两角差的正切公式: ,平面向量中直线法向量夹角的余弦及直线方向向量夹角的余弦的应用来进行考查. 二、基本概念 ①平面上直线方程的两种常用表示: 直线的点斜式方程:; 直线的一般式方程:不全为. ②平面上两条相交直线夹角的概念: 平面上两条相交直线,所成四个角中的最小角,叫做两条直线的夹角. ③平面上两条直线所成角的范围: 如果两条直线平行或重合,规定它们所成的角为; 如果两条直线垂直,规定它们的夹角为; 如果两条直线相交且互不垂直,则两直线的夹角范围为. ④平面上直线的方向向量: 基线与平面上一条直线平行或重合的向量,叫做直线的方向向量; 直线点斜式方程的一个方向向量为. ⑤平面上直线的法向量: 基线与平面上一直线垂直的向量,叫做直线的法向量; 直线的一般式方程不全为的一个法向量为.
三、理论推导 1.已知倾斜角,根据两角差的正切公式求两直线夹角. 证明:如下图所示,在平面直角坐标系中,直线的倾斜角为,直线的倾斜角为. 假设为直线,所成的一角,显然,则,由公式得: 又因为平面上两条相交且互不垂直的直线夹角范围是,所以.从而得: 即,平面上直线与直线的夹角. 2.已知直线的一般式方程,运用直线法向量夹角余弦求平面上两直线夹角.
证明:如下图所示,在平面直角坐标系中,直线的一般式方程为 ,一法向量;直线的一般式方程为,一法向量. 假设为直线,所成的一角,显然(左图)或(右图)由法向量夹角的余弦得: 又因为平面上两条相交且互不垂直的直线夹角范围是,所以.从而得: 即,平面上直线与直线的夹角. 3.已知直线的点斜式方程,利用直线方向向量夹角余弦求平面上两直线夹角. 证明:如下图所示,在平面直角坐标系中,直线的点斜式方程为,一方向向量;直线的点斜式方程为,一方向向量.
直线与平面的夹角 学案 编制单位 临朐第二中学 编制人 谢文利 审核人 (董洪安) 编号 学习目标 ①理解掌握直线和平面所成的角定义 ②初步掌握求直线和平面所成角的方法和步骤 重点难点 (1)直线和平面所成的角的定义的生成. (2)求直线和平面所成的角的方法步骤. (3)初步掌握公式 12 cos cos cos θθθ=?及公式的应用. 知识链接(新宋体4号) 1、直线和平面的位置关系有哪几种? (1)直线在平面内 (2)直线和平面平行 (3)直线和平面相交 2、平面的斜线及斜线在平面内的射影的定义: 学习过程 一、课内探究 问题1:平面的斜线和平面内的直线所成的最小角 问题2:θθθ、、21三个角之间的关系. 二、典例剖析 (一)定义法求斜线与平面所成的角
例1:在单位正方体1111 ABCD A B C D -中,试求直线 1 BD 与平面ABCD 所成的角. 跟踪训练: 在单位正方体 1111 ABCD A B C D -中,求直线 11 A C 与截面 11 ABC D 所成的角. . 向量法求斜线与平面所成的角 例2、已知正三棱柱ABC-A 1B 1 C 1中,AB=AA 1,求直线CB 1与平面AA 1B 1B 所成角的正弦值。 跟踪训练:
在正四面体ABCD中,AD=1,求AD与平面BCD所成的角; 公式法求斜线与平面所成的角 例3:如图,已知AB为平面α的一条斜线,B为斜足,AOα ⊥,O为垂足,BC为α内的一条 直线, 60,45 ABC OBC ∠=?∠=?,求斜线AB和平面α所成的角. 跟踪训练: 已知平行六面体ABCD—A1B1C1D1的底面是边长为a的菱形,O为菱形ABCD的中心, ∠BAD=∠BAA1=∠DAA1=600, 1 3 2 AA a = ,求证:A1O⊥平面ABCD。
自学检测 平面的一条斜线段长是它在平面上射影长的1、 2血 A 3 B、3 一条直线与平面:所成的角为30°,则它和平面3倍,则这条斜线段与平面所成角的余弦值是(2 3、 C 2 D 3 a内所有直线所成的角中最小的角是( A、300 B、600 C 900 PA、PB PC是由P点出发的三条射线,两两夹角均为60°,则直线PC与平面PAB所成角的余弦值是 B、 600 D、1500 323直线与平面的夹角 教学目标 1. 掌握直线和平面夹角的定义,会用定义、三余弦公式、法向量求线面角。 2. 自主教学、合作交流,探究向量法解决直线和平面夹角的规律方法。 3. 体验向量法解决立体几何问题的乐趣。 自学指导 预习课本106页至107页,填写下列内容: 1. 斜线与平面夹角的定义:斜线和它在平面内的_________ 所成的角。 2. 斜线与平面夹角的范围是_______ ;直线与平面夹角范围是________ 。 两异面直线夹角的范围_______ ;两非零向量夹角的范围是________ 。 3. 三余弦公式cos 丁-cos n *cosn 中,和v2分另寸是_________________________ 所成的角、_________________ 所成的角、 ____________________ 所成的角;寸严和二2的范围分别是__________ 、 ________ 、____________ 。问题1 :三棱锥P-ABC, P从面ABC / ACB=90 ,你能找到三余弦公式cosT =cosB?co的2中日,也和日2吗? 问题2:如果COST -cos二?cosn中R =90°,你能得出什么结论?和三垂线定理有何关系? 问题3: PA, PB, PC是从P点出发的三条射线,每两条射线的夹角均为60°,若/ APB的角平分线为AD, 那么在COST -COST1 *cos^2中,v,3禾口m分另U对应的角是______ 、__________ 、_________ ,直线PC 与平面PAB所成角的余弦值为_______________________ 。 冋题4:你能用三余弦公式COST -COSH ?COST2证明教材P107的例题吗
3.2.3直线与平面的夹角 3.2.4二面角及其度量 学习目标 1.理解斜线和平面所成的角的定义,体会夹角定义的唯一性、合理性.2.会求直线与平面的夹角θ.3.掌握二面角的概念,二面角的平面角的定义,会找一些简单图形中的二面角的平面角.4.掌握求二面角的基本方法、步骤. 知识点一直线与平面所成的角 1.直线与平面所成的角 2.最小角定理 知识点二二面角及理解 1.二面角的概念 (1)二面角的定义:平面内的一条直线把平面分成两部分,其中的每一部分都叫做半平面.从一条直线出发的两个半平面所组成的图形叫做二面角.如图所示,其中,直线l叫做二面角的棱,每个半平面叫做二面角的面,如图中的α,β.
(2)二面角的记法:棱为l ,两个面分别为α,β的二面角,记作α—l —β.如图,A ∈α,B ∈β,二面角也可以记作A —l —B ,也可记作2∠l . (3)二面角的平面角:在二面角α—l —β的棱上任取一点O ,在两半平面内分别作射线OA ⊥l ,OB ⊥l ,则∠AOB 叫做二面角α—l —β的平面角,如图所示.由等角定理知,这个平面角与点O 在l 上的位置无关. (4)直二面角:平面角是直角的二面角叫做直二面角. (5)二面角的范围是[0°,180°]. 2.用向量夹角来确定二面角性质及其度量的方法 (1)如图,分别在二面角α—l —β的面α,β内,并沿α,β延伸的方向,作向量n 1⊥l ,n 2⊥l ,则〈n 1,n 2〉等于该二面角的平面角. (2)如图,设m 1⊥α,m 2⊥β,则角〈m 1,m 2〉与该二面角大小相等或互补. 1.直线与平面所成的角α与该直线的方向向量与平面的法向量的夹角β互余.( × ) 2.二面角的大小范围是??? ?0,π 2.( × ) 3.二面角的大小等于其两个半平面的法向量的夹角的大小.( × ) 题型一 求直线与平面的夹角 例1 已知正三棱柱ABC-A 1B 1C 1的底面边长为a ,侧棱长为2a ,求AC 1与侧面ABB 1A 1所成的角. 解 建立如图所示的空间直角坐标系Axyz ,
高中数学-直线与平面的夹角练习 课后导练 基础达标 1.直线a与平面α内任一条线所成最小的角为θ,a是平面α的斜线,b是平面α内与a 异面的任意直线,则a与b所成的角() π A.最小值为θ,最大值为π-θ B.最小值为θ,最大值为 2 π C.最小值为θ,无最大值 D.无最小值,最大值为 2 答案:B 2.如右图所示,在正方体ABCD-A1B1C1D1中,求直线A1C1与平面ABC1D1所成的角 () A.30° B.60° C.45° D.90° 答案:A 3.正方体ABCD-A1B1C1D1中,A1B和面BB1D1D所成的角为() A.15° B.45° C.60° D.30° 答案:D 4.如左下图,正方体ABCD-A1B1C1D1中,E是CC1的中点,求BE与平面B1BD所成角的余弦值________________. 15 答案: 5 5.如右上图,S是△ABC所在平面外一点,SA,SB,SC两两垂直,判断△ABC的形状_________. 答案:锐角三角形 6.四面体S-ABC中,SA、SB、SC两两垂直,∠SBA=45°,∠SBC=60°,M为AB的中点,求:(1)BC与平面SAB所成的角; (2)SC与平面ABC所成角的正弦值. 解析:(1)如右图,∵SA、SB、SC两两垂直,
∴SC⊥面SAB. ∴∠CBS 是BC 与平面SAB 所成的角. ∵∠CBS=60°, ∴BC 与平面SAB 所成的角为60°. (2)连结MC,在Rt△ASB 中,∠SBA=45°,则SM⊥AB. 又SC⊥面SAB, ∴SC⊥AB, ∴AB⊥面SMC.过S 作SO⊥MC 于点O,则SO⊥AB, ∴SO⊥面ABC, ∴∠ SCM 是SC 与平面ABC 所成的角. 设SB=a,则SC=3a,SM= 2 2a, 在Rt△CSM 中,CM= 2 14a, ∴sin∠SCM= 7 7 =MC SM . 7.在Rt△ABC 中,∠A=90°,AB=3,AC=4,PA 是平面ABC 的斜线,∠PAB=∠PAC=60°, (1)求PA 与平面ABC 所成角的大小; (2)PA 的长等于多少时,点P 在平面ABC 上的射影O 恰好在BC 边上? 解:(1)如右图,过P 作PO⊥平面ABC 于O,则∠PAO 为PA 与平面ABC 所成的角, 易证AO 为∠BAC 的平分线,则∠OAB=45°. 由公式cosθ=cosθ1·cosθ2可得 cos∠PAO= OAB PAB ∠∠cos cos =22 45 cos 60cos =ο ο, ∴∠PAO=45°. ∴PA 与平面ABC 所成的角为45°.
§14.3空间直线与平面的位置关系(夹角) 【知识解读】 1、线面平行的判定定理:如果不在一个平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行. 2、线面平行的性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行. 3、平行平面:如果两个平面没有公共点,那么这两个平面互相平行. 4、推论:如果一个平面内有两条相交直线分别平行于另一个平面内的两条相交直线,那么这两个平面互相平行. 5、平行平面的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行. 6、面面平行的另一性质:如果两个平面平行,那么其中一个平面内的直线都平行于另一个平面. 7、线面角--直线l与其在平面 上的射影所成的锐角称为直线与平面所成的角
F E D C B A 【例题讲解】 例1、简述下列问题的结论,并画图说明: (1)直线?a 平面α,直线A a b = ,则b 和α的位置关系如何? (2)直线α?a ,直线a b //,则直线b 和α的位置关系如何? 例2、已知:空间四边形A B C D 中,,E F 分别是,AB AD 的中点,求证://EF BCD 平面. 例3、两个全等的正方形ABCD 和ABEF 所在平面相交于AB ,M ∈AC ,N ∈FB ,且AM =FN ,求证MN ∥平面BCE _ C _ B
B M H S C A A 例4、在正方体中,棱长为a .求:(1)直线1AB 与面1111D C B A 所成的角;(2)直线1DB 与面1111D C B A ; 例5、四面体ABCS 中,SA,SB,SC 两两垂直,∠SBA=45°, ∠SBC=60°, M 为 AB 的中点, 求(1)BC 与平面SAB 所成的角。(2)SC 与平面ABC 所成的角。 例6、如图,几何体ABCDE 中,△ABC 是正三角形,EA 和DC 都垂直于平面ABC ,且 a AB EA 2==,a DC =,F 、G 分别为EB 和AB 的中点.(1)求证:FD ∥平面ABC ;(2) 求证:AF ⊥BD ; 1111D C B A ABCD -
3.2.3直线与平面的夹角教学设计 [学习目标] 1.了解直线与平面的夹角的三种情况,理解斜线和平面所成角的概念. 2.了解三个角θ,θ1,θ2的意义,会利用公式cos θ=cos θ1·cos θ2求平面的斜线与平面内的直线的夹角. [知识回顾] 怎样求两条异面直线所成的角? (1)_______________________________________________________; (2)________________________________________________________. [预习导引] 1.线线角、线面角的关系式 如图所示,已知OA是平面α的斜线段,O是斜足,线段AB垂直于α,B为垂足,则直线OB是斜线OA在平面α内的正射影.设OM是α内通过点O的任一条直线,OA与OB所成的角为θ1,OB与OM所成的角为θ2,OA与OM所成的角为θ,则θ,θ1,θ2之间的关系为____________________ 在上述公式中,因为______________________,又因为θ1和θ都是锐角,所以θ1≤θ. 2.最小角定理 _____和它在平面内的_____所成的角是斜线和这个平面内所有直线所成角中_____.3.直线与平面的夹角 (1)如果一条直线与一个平面垂直,这条直线与平面的夹角为_____. (2)如果一条直线与一个平面平行或在平面内,这条直线与平面的夹角为_____. (3)斜线和它在平面内的__________叫做斜线和平面所成的角(或斜线和平面的夹角).【设计意图】重点强调斜线的射影是过垂足和斜足的直线.教师可在此处多设计几个图形,让学生练习辨别垂线,斜线及其射影. [典型例题] 知识点一用定义求线面角 例1在正四面体ABCD中,E为棱AD中点,连CE,求CE和平面BCD所成角的正弦值. 变式1如图所示,在四棱锥P-ABCD中,底面ABCD是正方形,PD⊥平面ABCD. PD=DC,E是PC的中点.求EB与平面ABCD夹角的余弦值. 方法小结:_____________________________________________________________ _______________________________________________________________________. 【设计意图】教师用问题引导学生一步步分析如何作出斜线与平面所成的角,培养学生思维的条理性. 知识点二由公式cosθ=cosθ1·cosθ2求线面角 例2已知平行六面体ABCD-A1B1C1D1的底面是边长为a的菱形,O为菱形ABCD
3.2.3直线与平面的夹角 教学目标 1.掌握直线和平面夹角的定义,会用定义、三余弦公式、法向量求线面角。 2.自主教学、合作交流,探究向量法解决直线和平面夹角的规律方法。 3.体验向量法解决立体几何问题的乐趣。 自学指导 预习课本106页至107页,填写下列内容: 1.斜线与平面夹角的定义:斜线和它在平面内的所成的角。 2.斜线与平面夹角的范围是;直线与平面夹角范围是。 两异面直线夹角的范围;两非零向量夹角的范围是。 3.三余弦公式21cos cos cos θθθ?=中,21,θθθ和分别是所成的角、 所成的角、所成的角;21,θθθ和的范围分别是、、。 问题1:三棱锥P-ABC ,PA ⊥面ABC ,∠ACB=90°,你能找到三余弦公式21cos cos cos θθθ?=中21,θθθ和吗? 问题2:如果21cos cos cos θθθ?=中0290θ=,你能得出什么结论?和三垂线定理有何关系? 问题3:PC PB PA ,,是从P 点出发的三条射线,每两条射线的夹角均为0 60,若∠APB 的角平分线为AD ,那么在21cos cos cos θθθ?=中,21,θθθ和分别对应的角是、、,直线PC 与平面PAB 所成角的余弦值为 。 问题4:你能用三余弦公式21cos cos cos θθθ?=证明教材P107的例题吗 自学检测 1、平面的一条斜线段长是它在平面上射影长的3倍,则这条斜线段与平面所成角的余弦值是( ) A 、13 B C 、2- D 、23 2、一条直线与平面α所成的角为30°,则它和平面α内所有直线所成的角中最小的角是( ) A 、300 B 、600 C 、900 D 、1500 3、PA 、PB 、PC 是由P 点出发的三条射线,两两夹角均为60°,则直线PC 与平面PAB 所成角的余弦值是( )
3.2.3直线与平面的夹角 一、复习回顾:(3分钟) 1、直线和平面的位置关系; 2、直线在平面内的正射影; 3、空间两条直线所成的角。 二、概念形成(15分钟) 一条直线与一个平面垂直,我们规定这条直线与平面的夹角为 一条直线与一个平面平行或在平面内,我们规定这条直线与平面的夹角为 。 下面我们研究一条斜线与平面的夹角 1、如图,OA 是平面的斜线段,,斜足为 ,α⊥AB 垂足为 ,则斜线段OA 在平面内的正射影为 。 2、如图,OM 是平面内过点O 的任意一条直线,OA 与OB 所成的角 OB 与OM 所成 的角 OA 与OM 所成的角 3、考察θ、1θ、2θ之间的关系: 在直线OM 上取单位向量m ,则m BA ⊥,即=?m BA 因为+=,所以?= 因此m OA ?=m OB ? 2θθ=, =θcos = 所以 21cos cos cos θθθ= 探究:在上式中,θθ和1的大小关系 得到结论:斜线和它在平面内的射影所成的角,是斜线和这个平面内所有直线所成角中 最小的角。 定义:斜线和平面所成的角 (或称斜线和平面的 夹角)
练习: 1、已知平面内的一条直线与平面的一条斜线的夹角为?60,这条直线与斜线在平面内的射影的夹角为?45,求斜线和平面所成的角的大小。 2、已知正方体1111D C B A ABCD -中,写出对角线1BD 分别与平面AC 、平面1BA 、平面1BC 所成的角,并求这些角的余弦值。 三、概念深化 如图,设向量在平面α内的射影为//B A ,且直线AB 的夹角为θ,则 例题1 BAC ∠在平面α内,过该角的顶点P 引平面α的斜线AP ,且使PAC PAB ∠=∠, 求证:斜线AP 在平面α内的射影平分BAC ∠
直线与平面的夹角 一、基础过关 1.平面的一条斜线和这个平面所成角θ的范围是 ( ) A .0°<θ<90° B .0°≤θ<90° C .0°<θ≤90° D .0°<θ<180° 2.正方体ABCD —A 1B 1C 1D 1中,B 1C 与平面ABCD 所成的角是 ( ) A .90° B .30° C .45° D .60° 3.正四面体ABCD 中棱AB 与底面BCD 所成角的余弦值为 ( ) A.12 B.13 C.33 D. 3 4.在三棱柱ABC —A 1B 1C 1中,底面是棱长为1的正三角形,侧棱AA 1⊥底面ABC ,点D 在棱BB 1上,且BD =1,若AD 与平面AA 1C 1C 所成的角为α,则sin α的值是 ( ) A.32 B.22 C.104 D.64 5.正方体ABCD -A 1B 1C 1D 1中,BB 1与平面ACD 1所成角的余弦值为 ( ) A.23 B.33 C.23 D.63 6.如果平面的一条斜线与它在这个平面上的射影的方向向量分别是a =(1,0,1),b =(0,1,1),那么这条斜线与平面所成的角是________. 二、能力提升 7.已知三棱锥S -ABC 中,底面ABC 为边长等于2的等边三角形,SA 垂直于底面ABC ,SA =3,那么直线AB 与平面SBC 所成角的正弦值为 ( ) A.34 B.54 C.74 D.34 8.如图,∠BOC 在平面α内,OA 是平面α的一条斜线,若∠AOB = ∠AOC =60°,OA =OB =OC =a ,BC =2a ,OA 与平面α所成的 角为________. 9.在正三棱柱ABC —A 1B 1C 1中侧棱长为2,底面边长为1,则BC 1 与侧面ACC 1A 1所成的角是__________________________. 10.在正四面体ABCD 中,E 为棱AD 的中点,连接CE ,求CE 和平面BCD 所成角的正弦值.
3.2.3直线与平面的夹角 教学目标 1.掌握直线和平面夹角的定义,会用定义、三余弦公式、法向量求线面角。 2.自主教学、合作交流,探究向量法解决直线和平面夹角的规律方法。 3.体验向量法解决立体几何问题的乐趣。 自学指导 预习课本106页至107页,填写下列内容: 1.斜线与平面夹角的定义:斜线和它在平面内的 所成的角。 2.斜线与平面夹角的范围是 ;直线与平面夹角范围是 。 两异面直线夹角的范围 ;两非零向量夹角的范围是 。 3.三余弦公式21cos cos cos θθθ?=中,21,θθθ和分别是 所成的角、 所成的角、 所成的角;21,θθθ和的范围分别是 、 、 。 问题1:三棱锥P-ABC ,PA ⊥面ABC ,∠ACB=90°,你能找到三余弦公式21cos cos cos θθθ?=中2 1,θθθ和吗? 问题2:如果21cos cos cos θθθ?=中0290θ=,你能得出什么结论?和三垂线定理有何关系? 问题3:PC PB PA ,,是从P 点出发的三条射线,每两条射线的夹角均为0 60,若∠APB 的角平分线为AD ,那么在21cos cos cos θθθ?=中,21,θθθ和分别对应的角是 、 、 ,直线PC 与平面PAB 所成角的余弦值为 。 问题4:你能用三余弦公式21cos cos cos θθθ?=证明教材P107的例题吗
自学检测 1、平面的一条斜线段长是它在平面上射影长的3倍,则这条斜线段与平面所成角的余弦值是() A、1 3B C 、 - D、 2 3 2、一条直线与平面α所成的角为30°,则它和平面α内所有直线所成的角中最小的角是() A、300 B、600 C、900 D、1500 3、PA、PB、PC是由P点出发的三条射线,两两夹角均为60°,则直线PC与平面PAB所成角的余弦值是() A、1 2B 、C 、D、 4、在长方体ABCD-A1B1C1D1中,AB=3,AD=4,AA1=5,体对角线BD1分别与平面AC、平面BA1、平面BC1所成角的余弦值为、、 例题探究 例1、在正方体AC1中,试求(1)直线A1B与平面ABCD所成的角。(2)直线A1B与平面BCC1B1所成的角 (3)直线A1B与平面A1B1CD所成的角
第二章 空间向量与立体几何 第五节 夹角的计算 第11课时 5.3直线与平面的夹角 【课堂互动】 新知1 直线与平面垂直 例1. 如图,在四棱锥V ABCD -中,底面ABCD 是正方形,侧面VAD 是正三角形, 平面VAD ⊥底面 证明:AB ⊥平面VAD ; 笔记: 新知2直线与平面的夹角 例2在棱长为a 的正方体''''ABCD A B C D - 求直线AD 与平面' B EDF 所成的角, 笔记: 【堂中精炼】 3. 对空间任意两个向量b a o b b a //),(,≠ A .= B .-= C .λ= D .λ= 4.已知向量与则),2,1,1(),1,2,0(--==的夹角为 ( ) A .0° B .45° C .90° D .180° 5. 正方体ABCD —A 1B 1C 1D 1中,E ,F 分别为AB ,C 1D 1的中点,则A 1B 1与平面A 1EF 所成角 的正切值为( ) A .2 B . C .1 D . 6空间四边形OABC 中,OB OC =,3 AOB AOC π ∠=∠= ,则cos <,OA BC >的 值是( ) A 21 B 2 2 C -21 D 0 7. 如果与直线l 共线的非零向量与平面α的法向量所成的角为θ,那么直线l 与平面 α所成的角则为 8若00≤θ<900,则直线l 与平面α所成的角为900-θ;若900≤θ≤1800 ,则直线l 与平面α所成的角为 点睛:由, 0=?得 AB VA ⊥,又A B A ⊥,因而AB 与平面VAD 内两条相交直线 VA ,AD 都垂直 ∴AB ⊥平面VAD 点睛:设 AB 是平面α的 斜线,且 ,B BC α∈是 斜线 AB 在平面α内的 射影,则斜线 AB 与平面 α 所成的角为 arccos AB BC AB BC ?? 。 x
3.2.3直线与平面的夹角 一、选择题 1.已知平面α内的角∠APB =60°,射线PC 与P A 、PB 所成角均为135°,则PC 与平面α所成角的余弦值是( ) A .-6 3 B. 6 3 C. 3 3 D .- 33 [答案] B [解析] 由三余弦公式知cos45°=cos α·cos30°, ∴cos α= 6 3 . 2.三棱锥P —ABC 的底面是以AC 为斜边的直角三角形,顶点P 在底面的射影恰好是△ABC 的外心,P A =AB =1,BC =2,则PB 与底面ABC 所成角为( ) A .60° B .30° C .45° D .90° [答案] B [解析] 由AB =1,BC =2,知AC =3,∴OA =3 2 , 又∵P A =1,PQ ⊥AC ,∴PO =12, ∵OB =OA = 32,∴tan θ=3 3 .∴应选B. 3.正方体ABCD —A 1B 1C 1D 1中,直线BC 1与平面A 1BD 所成角的正弦值是( ) A.2 4 B.23 C.6 3 D.32 [答案] C [解析] 由计算得sin θ= 2 3 .故选C. 4.在三棱锥P —ABC 中,AB ⊥BC ,AB =BC =1 2P A ,点O 、D 分别是AC 、PC 的中点, OP ⊥底面ABC ,则直线OD 与平面PBC 所成角的正弦值为( ) A.216 B.833 C. 21060 D. 21030
[答案] D [解析] 以O 为原点,射线OA 、OB 、OP 为x 、y 、z 轴建立空间 直角坐标系,如图,设AB =a ,则OP = 72a ,OD →=(-24a,0,14 4 a ),可求得平面PBC 的法向量为n =(-1,-1, 1 7 ), ∴cos(OD → ,n )=OD →·n |OD → ||n | =21030, 设OD → 与面PBC 的角为θ,则sin θ=21030 ,故选D. 5.若直线l 与平面α所成角为π 3,直线a 在平面α内,且与直线l 异面,则直线l 与直 线a 所成角的取值范围是( ) A.? ???0,2π 3 B.????π3,2π3 C.????π2,2π3 D.????π3,π2 [答案] D 6.如果平面的一条斜线段长是它在这个平面上的射影长的3倍,那么斜线段与平面所成角的余弦值为( ) A.13 B.223 C. 2 2 D.23 [答案] A 7.如图,正方体AC 1中,BC 1与对角面BB 1D 1D 所成的角是( ) A .∠C 1BB 1 B .∠C 1BD C .∠C 1BD 1 D .∠C 1BO [答案] D [解析] 由三垂线定理得,OB 为BC 1在平面BB 1D 1D 上的射影.故选D. 8.在棱长为1的正方体ABCD —A 1B 1C 1D 1中,E 为CC 1的中点,则直线A 1B 与平面BDE 所成的角为( ) A.π 6 B.π3
直线与平面的夹角 课时目标 1、理解直线与平面所成角的概念;(重点) 2、能够利用定义计算直线与平面所成的角; 3、理解最小角定理。(难点) 4、会简单应用最小角定理求线面角 5、提高分析能力、化归能力和空间想象能力 情境导入 1、直线和平面存在哪几种位置关系? 2、我们该如何刻画直线相对于平面的倾斜程度? 探索新知:目标一 任务一:学习线面角的概念。 任务二:确定线面角的取值范围 任务三:思考探索,如果两条直线与一个平面所成的角相等,那么这两条直线一定平行吗? 任务四:找寻生活中的线面夹角 任务五: 小组讨论,归纳找线面夹角的步骤 知识巩固:目标二 例1:如图所示,等腰△ ABC的顶点A在平面α外,底边BC在平面α内,已知底边长BC=16,腰长AB=17,又知点A到平面α的垂线段AD=10.求 (1)等腰△ ABC的高AE的长; (2)斜线AE和平面α所成的角的正弦值 . 能力提升 1、若斜线段AB与它在平面α内射影的长比值是2:1,那么AB与平面α的夹角是() A、30° B、45° C、60° D、90°: 2、从平面外一点P,引平面α的垂线段PO和斜线段PA,且PO=3cm,PA=6cm.求斜线PA与平面α所成角的大小. 3、如图所示,长方体ABCD-EFGH中,高AE=4cm,底面是边长为3cm的正方形,求对角线BH与底面ABCD 所成的角的正切值 归纳小结 知识点 思想方法 观察猜想:目标三 问题1:斜线与平面所成的角与斜线和平面内的其它直线所成的角的是怎样的大小关系? 诱思探究,分组讨论 研究角,往往把角放在直角三角形中去研究,请同学们分组研究我们刚才所猜想的结果是否正确? 问题2:斜线和射影所成的角,是这条斜线和这个平面内的任一直线所成的角中最小的角吗? .
§3.2.3利用向量法求直线与平面所成的角 一、储备 (一)、学习目标 1.使学生学会求直线与平面所成的角; 2.使学生能够应用向量方法解决一些简单的立体几何问题; 3.使学生的分析与推理能力和空间想象能力得到提高. (二)、课前准备 向量的有关知识: (1)两向量数量积的定义:><=?,cos |||| (2)两向量夹角公式:| |||,cos b a >= < (3)平面的法向量:与平面垂直的向量 知识点1:面直线所成的角(范围:]2 ,0(π θ∈) 问题1: 当a 与b 的夹角不大于90°时,异面直线a 、b 所成 的角θ与 和 的夹角的关系? 问题 2:与的夹角大于90°时, ,异面直线a 、b 所成的角θ与 和的夹角的关系? 结论:异面直线a 、b 所成的角的余弦值为|,cos |cos n m =><=θ 知识点2:二面角(范围:],0[πθ∈) ①方向向量法:将二面角转化为二面角的两个面的方向向量(在二面角的面内且垂直于二面角的棱)的夹角。如图,设二面角αβα?⊥?⊥CD l CD AB l AB ,,,.
x y 二、导学 直线与平面所成的角(范围:]2 ,0[π θ∈) 思考:设平面α的法向量为,则><,与θ的关系? 例1、如图,正三棱柱1 11C B A ABC -的底面边长为a ,侧棱长为a 2,求1AC 和 B B AA 11面所成角的正弦值. 分析:直线与平面所成的角步骤: 1. 求出平面的法向量 2. 求出直线的方向向量 3. 求以上两个向量的夹角,(锐角)其余角为所求角 解:如图建立空间直角坐标系xyz A -,则),0,,0(),2,0,0(1a a == )2,2 1 ,23(1a a a AC - = 设平面B B AA 11的法向量为),,(z y x = 由?? ?==????==??????=?=?00 002001z y ay az AB n AA 取1=x ,)0,0,1(=∴ 21323,cos 2 2 111-=-= >= <∴a a AC ∴1AC 和B B AA 11面所成角的正弦值2 1 . 练习:正方体1111D C B A ABCD -的棱长为1,点E 、F 分别为CD 、1DD 的中点.求直线11C B 与平面C AB 1所成的角的正弦值. 11(,)2AC a =-