
五点法作图应用
1. 知识点:
函数y=sinx 的图象上有五个重要的点(0,0),)1,2(π,(π,0),)1,2
3(-π
,
(2π,0)
把函数y=sinx 的图象经过伸缩(左右、上下)得到y=Asin(ωx+φ)的图
象。这时前面的五个点(0,0),)1,2(π(π,0),)1,2
3(-π
,(2π,0)依次变为
)0,(ω?-,),2(A ω?ωπ-,)0,(ω?ωπ-,),3(A --ω?ωπ,)0,2(ω
?ωπ- (这五个点的横坐标可以通过令ωx+φ分别等于0, 2
π
,π,23π,2π解出x ,
进一步求出相应的纵坐标)
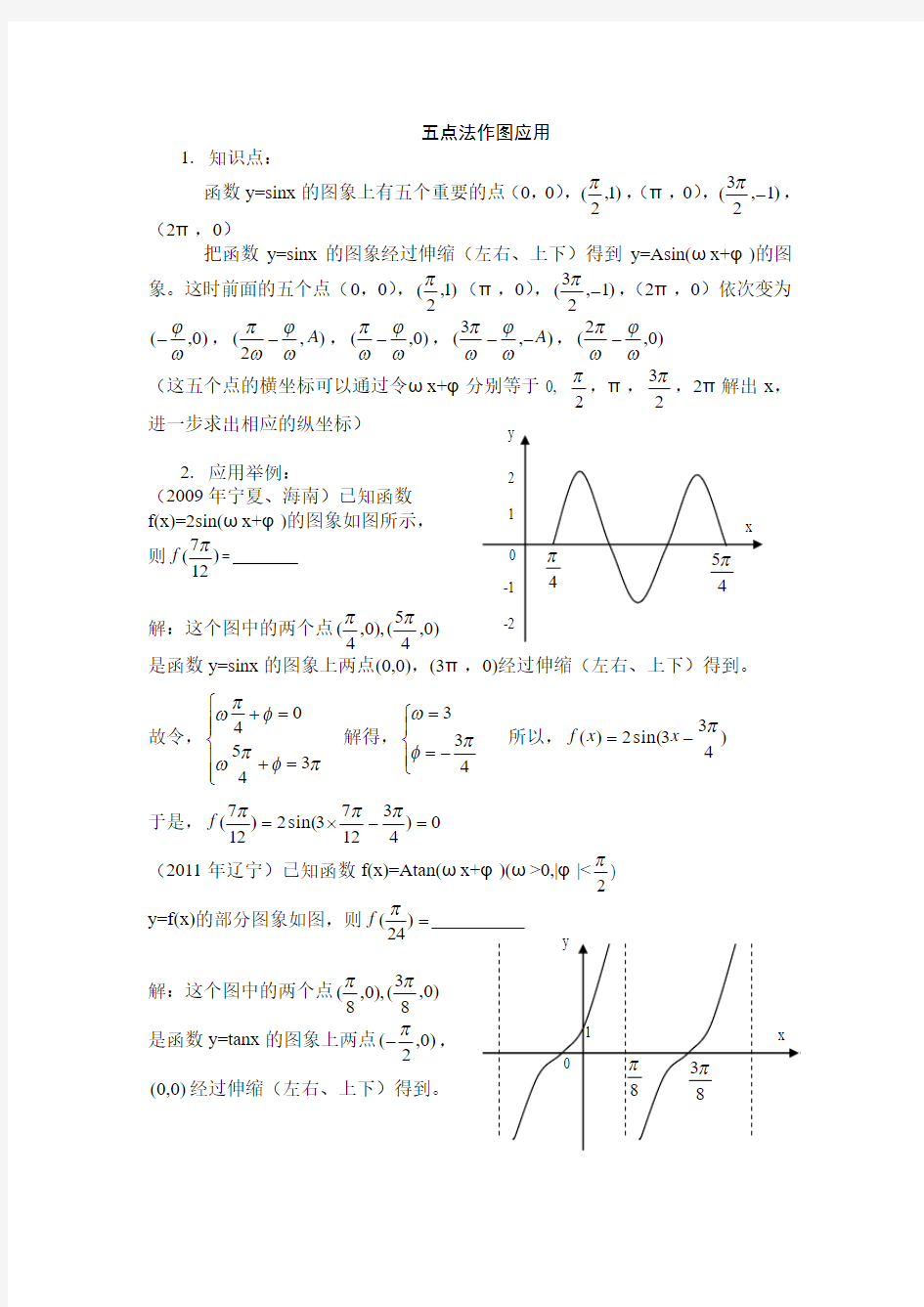
2. 应用举例: (2009年宁夏、海南)已知函数
f(x)=2sin(ωx+φ)的图象如图所示, 则)12
7(π
f =
解:这个图中的两个点)0,4
5(),0,4(ππ 是函数y=sinx 的图象上两点(0,0),(3π,0)经过伸缩(左右、上下)得到。
故令,???????=+=+πφπωφπ
ω34
504 解得,???
??-==433π
φω 所以,)433sin(2)(π-=x x f 于是,0)4
31273sin(2)127(
=-?=πππf (2011年辽宁)已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<2
π
) y=f(x)的部分图象如图,则=)24
(π
f
解:这个图中的两个点)0,83(),0,8(π
π
是函数y=tanx 的图象上两点)0,2
(π
-
,
)0,0(经过伸缩(左右、上下)得到。
故令,???????=+-=+0832
8φπωπφπ
ω 解得,?????-==432πφω
所以,)4
2tan()43tan()(ππ+=-
=x A x A x f 又因为图象经过(0,1)点,所以14
tan )0(===A A f π
于是,)4
2tan()(π
+=x x f ,所以3)4
24
2tan()24
(
=+
?
=π
π
π
f
正弦函数图象 梁翠琼 一、教学目标: 1.知识与技能的掌握 (1)学会用列表、描点、连线的方法作出正弦函数的图象; (2)掌握五点法作正弦函数的简图; (3)掌握形如sin y k x b =+的函数图象简图的画法。 2.过程与方法的思考 (1)学会画图的一般步骤,培养动手能力; (2)会用“五点法”画正弦函数。 3.情感态度与价值观的培养 通过本节课的学习学会善于寻找,观察数学知识之间的内在联系.培养学生从特殊到一般与从一般到特殊的辩证思想方法。 二、重点和难点: 1.用列表、描点、连线的方法作出正弦函数的图象以及利用五点法画正弦函数的简图为本节课的教学重点; 2.用五点法画形如sin y k x b =+的函数图象简图。 三、学习过程 1. 情境导入 问题一:如何画一般函数的图象? 学生思考回答作图步骤:(Ⅰ)列表; (Ⅱ)描点 (Ⅲ)连线。 问题二:那我们能否通过描点法画正弦函数在[0,2]π内的图像, 教师与学生一起尝试描点法画图. 描点法在取函数值时,取得点越多,画出的函数图象就会越准确。 2.学导结合 (1)描点法画图: 列表------- 描点---- 连线 6 π 3 π2 π 3 2π6 5ππ 67π34π23π35π6 11ππ 20 2 12 30 1 2 1-2 3 - 2 12 30 2 1-23 -1-x y [] π2,0,sin ∈=x x y
(2)如何作正弦函数y =Sinx, x ∈R 的图象呢? 学生思考,老师点拨. 因为终边相同的角的三角函数值相同,所以 sin ,[2,2(1)),,0y x x k k k Z k ππ=∈+∈≠的图像,与函数 sin ,[0,2)y x x π=∈一致.于是我们 只要将sin ,[0,2)y x x π=∈的图像像左向右平行移动(每次2π个单位长度)就可以得到正弦函数y =Sinx ,x ∈R 的图象 (3)探究深化 ①“五点法”作简图: 教师提出问题:观察y=Sinx ,x ∈[0,2π]的图象,在作图连线过程中起关键作用的是哪几个点? 能否利用这些点作出正弦函数的简图? 引导学生得到五个关键点。 学生回答:关键五点:(0,0)、(2 π ,1)、(π,0)、 (32π ,-1)、(2π,0)。 教师总结:事实上,只要指出这五个点,y=Sinx ,x ∈[0,2π]的图象形状就基本定位了。因此在精确度要求不高时,我们就常先找出这五个关键点,然后用光滑的曲线将它们连结起来,就得到函数的简图,这种作图的方法称为“五点法”作图。 注:五个关键点中,重点应突出点的横坐标,纵坐标即相应函数值; 画简图时应掌握曲线的形状及弯曲的“方向”。
学习奥数的优点 1、激发学生对数学学习的兴趣,更容易让学生体验成功,树立自信。 2、训练学生良好的数学思维习惯和思维品质。要使经过奥数训练的学生,思维更敏捷,考虑问题比别人更深层次。 3、锻炼学生优良的意志品质。可以培养持之以恒的耐心和克服困难的信心, 以及战胜难题的勇气。可以养成坚韧不拔的毅力 4、获得扎实的数学基本功,发挥创新精神和创造力的最大空间。 第二十二周作图法解题 专题简析: 用作图的方法把应用题的数量关系提示出来,使题意形象具体, 一目了然,以便较快地找到解题的途径,它对解答条件隐蔽、复杂疑 难的应用题,能起化难为易的作用。 在解答已知一个数或者几个数的和差、倍差及相互之间的关系, 求其中一个数或者几个数问题等应用题时,我们可以抓住题中给出的 数量关系,借助线段图进行分析,从而列出算式。
例题1 五(1)班的男生人数和女生人数同样多。抽去18名男生和26名女生参加合唱队后,剩下的男生人数是女生的3倍。五(1)班原有男、女生各多少人? 分析根据题意作出示意图: 从图中可以看出,由于女生比男生多抽去26-18=8名去合唱队,所以,剩下的男生人数是女生人数的3倍,而这8名同学正好相当于剩下女生人数的2倍,剩下的女生人数有8÷2=4名,原来女生人数是26+4=30名。 练习一 1,两根电线一样长,第一根剪去50厘米,第二根剪去180厘米后,剩下部分,第一根是第二根长度的3倍。这两根电线原来共长多少厘米? 2,甲、乙两筐水果个数一样多,从第一筐中取出31个,第二筐中取出19个后,第二筐剩下的个数是第一筐的4倍。原来两筐水果各有多少个? 3,哥哥现存的钱是弟弟的5倍,如果哥哥再存20元,弟弟再存100元,二人的存款正好相等。哥哥原来存有多少钱?
五点法作图应用 1. 知识点: 函数y=sinx 的图象上有五个重要的点(0,0),)1,2(π,(π,0),)1,2 3(-π , (2π,0) 把函数y=sinx 的图象经过伸缩(左右、上下)得到y=Asin(ωx+φ)的图 象。这时前面的五个点(0,0),)1,2(π(π,0),)1,2 3(-π ,(2π,0)依次变为 )0,(ω?-,),2(A ω?ωπ-,)0,(ω?ωπ-,),3(A --ω?ωπ,)0,2(ω ?ωπ- (这五个点的横坐标可以通过令ωx+φ分别等于0, 2 π ,π,23π,2π解出x , 进一步求出相应的纵坐标) 2. 应用举例: (2009年宁夏、海南)已知函数 f(x)=2sin(ωx+φ)的图象如图所示, 则)12 7(π f = 解:这个图中的两个点)0,4 5(),0,4(ππ 是函数y=sinx 的图象上两点(0,0),(3π,0)经过伸缩(左右、上下)得到。 故令,???????=+=+πφπωφπ ω34 504 解得,??? ??-==433π φω 所以,)433sin(2)(π-=x x f 于是,0)4 31273sin(2)127( =-?=πππf (2011年辽宁)已知函数f(x)=Atan(ωx+φ)(ω>0,|φ|<2 π ) y=f(x)的部分图象如图,则=)24 (π f 解:这个图中的两个点)0,83(),0,8(π π 是函数y=tanx 的图象上两点)0,2 (π - , )0,0(经过伸缩(左右、上下)得到。
故令,???????=+-=+0832 8φπωπφπ ω 解得,?????-==432πφω 所以,)4 2tan()43tan()(ππ+=- =x A x A x f 又因为图象经过(0,1)点,所以14 tan )0(===A A f π 于是,)4 2tan()(π +=x x f ,所以3)4 24 2tan()24 ( =+ ? =π π π f
尺规作图五点定椭圆的 方法 -CAL-FENGHAI.-(YICAI)-Company One1
尺规作图五点定椭圆的方法 徐文平 (东南大学南京210096) 摘要:已知椭圆上五点,通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤,尺规作图完成椭圆作图。 椭圆在开普勒行星运行三定律中扮演了重要角色,在机械制图和土木工程领域中也有重要运用。利用几何画板和cad软件,依据任意五个点的椭圆尺规作图,具有重要意义。 一、引言 在几何画板和cad软件中,任意五个点作椭圆,具有意义。五点定椭圆在卫星轨道,机械制图和土木工程中是有重要用途。 第一步,通过五点寻找椭圆圆心 第二步,确定椭圆坐标x、y主轴方向 第三步、确定椭圆的长轴a和短轴b 1)大狗熊定理1:二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。如图1,椭圆内接四边形KLMN,对边线KN与LM交于A,对边线KL与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN 交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD= 2/AB。双曲线和抛物线也具有同样性质。 2)命题1:已知椭圆的斜向割线AB,作一条过椭圆圆心O点的任意割线JK, JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB 就是椭圆的切线。 证明:由于割线JK的切线交点极点在无穷远,利用定理1,可以快速证明这 个命题。
定理2:圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。 命题3(高斯定理):已知椭圆外一点P,过P点作PAB与PCD二条任意椭圆割线,AD、CB交于Q点,AC、BD延长交于R,连线QR与椭圆交于S、T 两点,PS、PT就是椭圆的切线。 图 3 二、通过五点寻找椭圆圆心 原理:通过已知五点,作椭圆切线,获得割线的极点,将割线的极点和割线中点连接并延伸,必定通过椭圆的圆心。 图 4 问题1:只有五点,没有坐标轴和原点,椭圆斜的,割线PQ的切线极点如何办
尺规作图五点定椭圆的方法 徐文平 (东南大学南京210096) 摘要:已知椭圆上五点,通过确定椭圆圆心、椭圆主轴方向和椭圆长轴短轴位置等三个步骤,尺规作图完成椭圆作图。 椭圆在开普勒行星运行三定律中扮演了重要角色,在机械制图和土木工程领域中也有重要运用。利用几何画板和cad软件,依据任意五个点的椭圆尺规作图,具有重要意义。 一、引言 在几何画板和cad软件中,任意五个点作椭圆,具有意义。五点定椭圆在卫星轨道,机械制图和土木工程中是有重要用途。 第一步,通过五点寻找椭圆圆心 第二步,确定椭圆坐标x、y主轴方向 第三步、确定椭圆的长轴a和短轴b 1)大狗熊定理1:二次圆锥曲线内接四边形的对边延伸线两交点调和分割对角线两极点。如图1,椭圆内接四边形KLMN,对边线KN与LM交于A,对边线KL与NM交于B,对角线KM的极点为C,对角线LN的极点为D,KM与LN交于Q点,则A、B、C、D四点共线,且AB调和分割CD,即1/AC+1/AD=2/AB。双曲线和抛物线也具有同样性质。 2)命题1:已知椭圆的斜向割线AB,作一条过椭圆圆心O点的任意割线JK,JA、BK交于E点,JB、AK交于F点,确定EF的中点N点,连线NA、NB就是椭圆的切线。 证明:由于割线JK的切线交点极点在无穷远,利用定理1,可以快速证明这个命题。
定理2:圆锥曲线的内接完全四点形的对边三点形是圆锥曲线的自配极三点形。 命题3(高斯定理):已知椭圆外一点P,过P点作PAB与PCD二条任意椭圆割线,AD、CB交于Q点,AC、BD延长交于R,连线QR与椭圆交于S、T两点,PS、PT就是椭圆的切线。 图 3 二、通过五点寻找椭圆圆心 原理:通过已知五点,作椭圆切线,获得割线的极点,将割线的极点和割线中点连接并延伸,必定通过椭圆的圆心。 图 4 问题1:只有五点,没有坐标轴和原点,椭圆斜的,割线PQ的切线极点如何办? 切线方法:帕斯卡定理(五点+ 一个切点二次)做切线,或者如图5方法作切线。 图 5
五点作图法求三角函数解析式教师版 例1.用“五点作图法”画函数f(x)=A sin(ωx+φ)(A>0,ω>0,|φ|<)在一个周期内的图象时,某同学列表并填入的数据如下: (1)求x1、x2的值及f(x)的表达式; (2)已知函数g(x)是将函数f(x)的图象向右平移个单位所得,若 ,求g(x0)的值. 【分析】(1)根据五点法作图,求出A,ω和φ的值即可得到结论 (2)求出g(x)解析式,结合f(x0)=1的值,求出x0=,代入求解即可 【解答】解:(1)函数的周期T=﹣=π, 即,得ω=2, 函数的最大值为2,即A=2, 则f(x)=2sin(2x+φ), 由五点对应法,得2×+φ=0,得φ=﹣, 则f(x)=2sin(2x﹣), 2x1﹣=,得x1=,由2x2﹣=,得x2=. (2)g(x)是将函数f(x)的图象向右平移个单位所得, 即g(x)=2sin[2(x﹣)﹣]=2sin(2x﹣)=﹣2cos2x, 若,则2sin(2x0﹣)=1, 即sin(2x0﹣)=, ∵0<x0<,∴﹣<2x0﹣<,
∴2x0﹣=,得x0=, 即g(x0)=g()=﹣2cos(2×)=﹣2cos=0. 【点评】本题主要考查三角函数的图象和性质,根据五点作图法求出函数解析式以及利用三角函数的变换关系是解决本题的关键. 练习1.函数f(x)=A sin(ωx+φ)+h(A>0,ω>0,|φ|<π),在同一个周期内,当时,y有最大值4,当时,y有最小值2. (1)求f(x)解析式; (2)求f(x)的递增区间; (3)若x∈[0,],求g(x)=f(x+)﹣4λcos x的最小值. 【分析】(1)由,可求A,h,利用周期公式可求ω,由(,4)为五点作图法第二点,可求φ,可求f(x)解析式. (2)由,解得单调递增间. (3)由(1)知可求g(x)的解析式,由,可得cos x∈[0,1],根据λ的范围分类讨论即可求得最小值. 【解答】(本题满分为12分) 解:(1)∵由,得A=1,h=3, ∴=,可得T=π,ω=2, ∵由(,4)为五点作图法第二点,, ∴f(x)=sin(2x+)+3,………………………(3分) (2)由, 得:﹣+kπ≤x≤+kπ,k∈Z, 可得单调递增间为:.………………………(6分)(3)由(1)知, 所以:g(x)=f(x+)﹣4λcos x
五点法作图 例1、(l )利用“五点法”作函数)3 2sin(π -=x y 的图象,并指出这个函数的振幅、 周期和初相. (2)怎样由x y sin =的图象得到)3 2sin(π -=x y 的图象? 分析: 令3 2π -=x t ,找出t y sin =图象的五个关键点对应的x 值. 解:(1)列表: 描点:( 6 ,0),(12,2),(3,0),(12,-2),(6,0)。 用光滑的曲线将它们连结起来,就得到函数)3 2sin(π -=x y 在一个周期内的简图(图 1).把这个简图利用函数的周期性向左、右扩展,就得到函数)3 2sin(2π -=x y 的简图. 振幅2=A ,周期ππ==22T ,初相.3 π?-= (2)解法一 ①把函数x y sin =的图象上所有点向右平移3 π个单位,得到函数)3sin(π -=x y 的图 象;②把函数)3sin(π-=x y 图象上所有点的根坐标缩短到原来的2 1 (纵坐标不变),得到 函数)32sin(π-=x y 的图象;③把函数)3 2sin(π -=x y 图象上所有的点的纵坐标伸长到原 来的2倍(横坐标不变),就得到函数) 3 2sin(2π -=x y 的图象见 图1. 解法二 ①把函数x y sin =的图象上所有的点的横坐标缩短到原来的 2 1 (纵坐标不变),得到函数x y 2sin =的图象;②把函数x y 2sin =图象上所有的点向右平移 6 π 个单位,得到函数 图1
)3 2sin(π - =x y 的图象;③把函数)3 2sin(π - =x y 的图象上所有的点的纵坐标伸长到原来 的2倍(根坐标不变),就得到函数)3 2sin(2π - =x y 的图象见图1. 小结:函数图象变换中,横向变换是对x 变化的反映,纵向变换是对y 变化的反映.