
第2章 线性时不变连续系统的时域分析
2.1 学习要求
(1)会建立描述系统激励与响应关系的微分方程;
(2)深刻理解系统的完全响应可分解为:零输入响应与零状态响应,自由响应与强迫响应,瞬态响应与稳态响应;
(3)深刻理解系统的零输入线性与零状态线性,并根据关系求解相关的响应;
(4)会根据系统微分方程和初始条件求解上述几种响应;
(5)深刻理解单位冲激响应的意义,并会求解;
(6)深刻理解系统起始状态与初始状态的区别,会根据系统微分方程和输入判断0时刻的跳变情况;
(7)理解卷积运算在信号与系统中的物理意义和运算规律,会计算信号的卷积。;
2.2 本章重点
(1)系统(电子、机械)数学模型(微分方程)的建立;
(2)用时域经典法求系统的响应;
(3)系统的单位冲激响应及其求解;
(4)卷积的定义、性质及运算,特别是()t δ函数形式与其它信号的卷积;
(5)利用零输入线性与零状态线性,求解系统的响应。
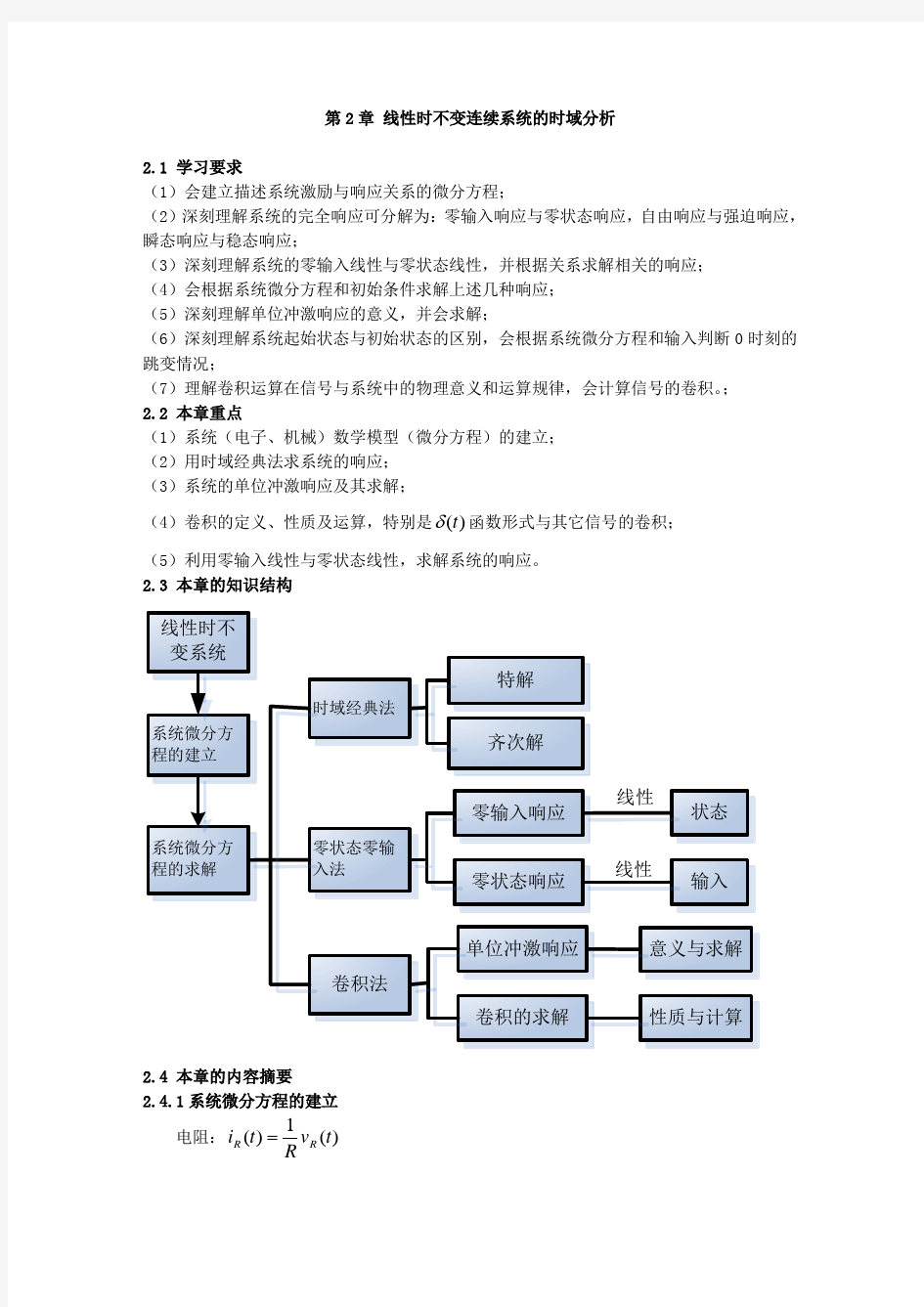
2.3 本章的知识结构
2.4 本章的内容摘要
2.4.1系统微分方程的建立
电阻:)(1)(t v R
t i R R =
电感:dt t di L
t v L L )()(= )(d )(1)(0t i v L
t i L t L L +=?∞-ττ 电容:dt t dv C
t i C C )()(= ?+=t t L C C t i i C
t v 0)(d )(1)(0ττ 2.4.2 系统微分方程的求解
齐次解和特解。
齐次解为满足齐次方程
t n t t h e c e c e c t y 32121)(λλλ+???++=
当特征根有重根时,如1λ有k 重根,则响应于1λ的重根部分将有k 项,形如
t k t k t k t k h e c te c e t c e t c t y 111112211)(λλλλ++???++=---
当特征根有一对单复根,即bi a +=2,1λ,则微分方程的齐次解
bt e c bt e c t y at at h sin cos )(21+=
当特征根有一对m 重复根,即共有m 重ib a ±=2,1λ的复根,则微分方程的齐次解
bt e t c bt te c bt c t y at m m at h cos cos cos )(121-+???++=
bt e t d bt te d bt e d at m m at at sin sin sin 121-+???+++
特解的函数形式与激励函数的形式有关。
注:(1)表中、是待定系数。
(2)若)(t x 由几种激励组合而成,则特解也为其相应的组合。
(3)若表中所列特解与齐次解重复,则应在特解中增加一项:t 倍乘表中特解。假如这种重
复形式有k 次(特征为k 次),则依次增加倍乘t ,2t ,…,k t 诸项。
2.4.3起始点的跳变-从-0到+0状态的转换
在系统分析中,定义响应区间为确定激励信号)(t x 加入后系统的状态变化区间。一般激励)(t x 都是从0=t 时刻加入,此时系统的响应区间定义为∞≤≤+t 0。当系统用微分方程表示时,系统从-0到+0状态有没有跳变取决于微分方程右端自由项是否包含)(t δ及其各阶导数项。如果包含有)(t δ及其各阶导数项,说明相应的-0到+0状态发生了跳变,即)0()0(-+≠y y 或)0()0(''-+≠y y 等等。这时为确定)0(+y 、)0('+y 等状态,可以用冲激函数匹配法。
2.4.4系统的零输入响应与零状态响应
(1)零输入响应
系统的零输入响应是当系统没有外加激励信号时的响应。
零输入响应)(t y zi 是满足
0)()()()(0)1(1)1(1)(=++???++--t y a t y a t y a t y a n n n n
及起始状态)0()(-k y )110(-???=,n ,,
k 的解,它是齐次解的一部分 ∑==n
k t zik zi k e c t y 1
)(α
由于没有外界激励作用,因而系统的状态不会发生跳变,)0()0()()(+-=k k y y ,所以)(t y zi 中的常数zik c 可由)0()(-k y 确定。
(2)零状态响应
所谓零状态,是指系统没有初始储能,系统的起始状态为零,即
0)0()0()0()1()1(===-=----n y y y
这时仅由系统的外加激励所产生的响应称为零状态响应)(t y zs 。
零状态响应)(t y zs 由起始状态为零时的方程
?????????-???==++???++=++???++------1100
)0()()()()()()()()()(011101111,n ,,k y t x b t x b dt t x d b dt t x d b t y a dt t dy a dt t y d a dt t y d a k m m m m n n n n n n 所确定。
系统的零状态响应)(t y zs 为
)()()(t y t y t y zsp zsh zs +=
其中)(t y zsh 和)(t y zsp 分别为齐次解和特解。
系统的线性:
条件1 系统响应可以分解为零输入响应与零状态响应之和。
条件2 零输入线性,即零输入响应与初始状态)0(-x 或)0(+x 之间满足线性特性。 条件3 零状态线性,即零状态响应与激励之间满足线性特性。
2.2.5连续时间系统的冲激响应与阶跃响应
(1)冲激响应
系统在单位冲激信号)(t δ作用下产生的零状态响应,称为单位冲激响应,简称冲激响应,用)(t h 表示。亦即,冲激响应是激励为单位冲激信号)(t δ时系统的零状态响应。
在时域中,子系统级联时,总的冲激响应等于子系统冲激响应的卷积。
因果系统的冲激响应为0)(=t h 0 (2)阶跃响应 一线性时不变系统,当其初始状态为零时,输入为单位阶跃函数所引起的响应称为单位阶跃响应,简称阶跃响应,用)(t g 表示。阶跃响应是激励为单位阶跃函数)(t u 时,系统的零状态响应 阶跃响应)(t g 与冲激响应)(t h 之间的关系为 ττd h t g t ?∞-=)()( 或 )()(t g dt d t h = 2.2.6 卷积积分 (1)卷积积分的概念 一般情况下,如有两个信号)(1t f 和)(2t f 做运算 τττd )()()(21?∞ ∞--=t f f t y 此运算定义为)(1t f 和)(2t f 的卷积(Convolution),简记为 )()()(21t f t f t y *= 或 )()()(21t f t f t y ?= (2)卷积积分的图解法 用图解法能直观地说明卷积积分的计算过程,而且便于理解卷积的概念。两个信号)(1t f 和)(2t f 的卷积运算可通过以下几个步骤来完成: 第一步,画出)(1t f 和)(2t f 波形,将波形图中的t 轴改换成τ轴,分别得到)(1τf 和)(2τf 的波形。 第二步,将)(2τf )波形以纵轴为中心轴翻转180°,得到)(2τ-f 波形。 第三步,给定一个t 值,将)(2τ-f 波形沿τ轴平移t 。在0 第四步,将)(1τf 和)(2τ-t f 相乘,得到卷积积分式中的被积函数)()(21ττ-t f f 。 第五步,计算乘积信号)()(21ττ-t f f 波形与τ轴之间包含的净面积。 第六步,令变量t 在),(+∞-∞范围内变化,重复第三、四、五步操作,最终得到卷积信号)()(21t f t f *。 (3)卷积运算的性质 性质1 乘法运算中的交换律、结合律和结合律适应于卷积运算 交换律 )()()()(1221t f t f t f t f *=* 结合律)()]()([)]()([)(321321t f t f t f t f t f t f **=** 分配律)()()()()]()([)(3121321t f t f t f t f t f t f t f *+*=+* 性质2 信号与奇异信号的卷积 信号与冲激信号的卷积等于信号本身,即 )()()(t f t t f =*δ )()()(00t t f t t t f -=-*δ 信号)(t f 与冲激偶)('t δ的卷积等于)(t f 的导函数,即 )()()(''t f t t f =*δ 信号)(t f 与阶跃信号)(t u 的卷积等于信号)(t f 的积分,即 ττd f t u t f t ?∞-==*)()()( 性质3 卷积的微分与积分 如果)()()(21t f t f t y *=,则有)()()()()(2'1'21't f t f t f t f t y *=*= 如果)()()(21t f t f t y *=,则 ???∞-∞-∞-*=*=t t t d f t f d f t f d y λλλλλλ)()()()()(1221。 设)()()(21t f t f t y *=,则有)()()()(2)(1)(t f t f t y j i j i -*= 2.2.7 用卷积积分法求系统的零状态响应 对于任一时刻t 系统的零状态响应为?-= t zs d t h x t y 0)()()(τττ 2.2.8 相关 如果)(1t f 和)(2t f 是两个能量有限的信号,且均为实函数,则它们之间的相关函数(又称为互相关函数)定义为 121212()()()()()d R f t f t dt f t f t t τττ+∞ ∞-∞-∞ =-=+?? 和212112()()()()()R f t f t dt f t f t dt τττ+∞+∞ -∞-∞=-=+?? 互相关性质:)()(2112ττ-=R R 。 当)(1t f 和)(2t f 是同一个信号时,即)()()(21t f t f t f ==,则它们之间的相关函数(又称为自相关函数)定义为 ()()()()()R f t f t dt f t f t dt τττ+∞ +∞-∞-∞=-=+?? 自相关函数性质: (1))()(ττ-=R R (2)0=t 时,相关性最强,()0R 最大。 如果)(1t f 和)(2t f 是功率有限信号,且均为实函数,那么互相关函数定义为 ?-∞→-=21 212112)()(1lim )(dt t f t f T R T ττ 和?? ??? ?-=?-∞→221221d )()(1lim )(T T T t t f t f T R ττ 自相关函数定义为 ?-∞→-=21 2 1)()(1lim )(dt t f t f T R T ττ 2.2.9用算子符号表示微分方程 (1)算子符号的基本性质 和积分用下述算子符号表示 dt d p = ?∞-=t d p τ)(1 式中,p 称为微分算子,p 1称为微分逆算子或积分算子。这样,可以应用微分或积分算子简化表示微分和积分运算。 例如 )()(t x dt d t pf = )()(t x dt d t f p n n = ?∞-=t d x t f p ττ)()(1 对于微分方程式(2-4)则可表示为 )()()()(0111t y a t py a t y p a t y p a n n n n ++???++-- )()()()(0111t x b t px b t x p b t x p b m m m m ++???++=-- 性质1 以p 的正幂多项式出现的运算式,在形式上可以像代数多项式那样进行展开和因式分解。性质2 设A (p )和B (p )是p 的正幂多项式,则 )()()()()()(t x p A p B t x p B p A = 性质3 微分算子方程等号两边p 的公因式不能随便消去。 性质4 算子的乘除顺序不可以随意颠倒。 (2)用算子符号建立微分方程 对于LTI 连续系统,其输入输出方程是线性、常系数微分方程,用输入-输出法描述系统时,由式(2-62)可得出输入激励与输出响应之间的关系是 )()()()(t x p D p N t y = 其中 =)(p N 0111a p a p a p a n n n n ++???++-- =)(p D 0111b p b p b p b m m m m ++???++-- 令) ()()(p D p N p H =,)(p H 代表了系统将输入转变为输出的作用,或系统对输入的传输作用,故称)(p H 为响应)(t y 对激励)(t f 的传输算子或系统的传输算子。 2.5典型考试试题解析 题1、 已知系统微分方程为()()d 2d y t y t f (t )t +=,若01y()+=,sin2f (t )tu(t )=,解得全响应为( )2524544t y t e (t )-=+- ,t ≥0。 全响应中2454 (t )- 为( ) (a )零输入响应分量 (b)零状态响应分量 (c)自由响应分量 (d)稳态响应分量 答案:(d ) 分析:响应中2454 (t )- 不含齐次解254t e -,所以答案(a)(b)(c)都不是 题2、两线性时不变系统分别为S1和S2,初始状态均为零。将激励信号()f t 先通过S1再通过S2,得到响应1()y t ;将激励信号()f t 先通过S2再通过S1,得到响应2()y t 。则1()y t 与2()y t 的关系为_________________。 答案:12()()y t y t = 分析:该题是考查级联系统的交换率:两级联系统交换保持不变 题3、计算 d ()[()*]d d t f t t t t δτ-∞ -?,其中“*”表示卷积。 解: d ()d ()[()*]d ()*d d d t t f t f t t t t t t t δτδτ-∞-∞-=-?? ()*()t f t δτ=-()f t τ=- 题4、已知信号1()x t 和2()x t 如图4所示 图4 试计算12()()()x t x t x t =*,并画出()x t 的波形。 2()x t t 3101-3-22-11 1 解:12()()()x t x t x t =*[]1()*(2)(2)x t t t δδ=++- 11(2)(2)x t x t =++- 波形如下图: 题5、 已知)()(),()(21t u e t f t u t f at -==,可以求得=)(*)(21t f t f ( ) (a) (1)()at e u t -- (b)()at e u t - (c)1(1)()at e u t a -- (d) 1()at e u t a - 答案(c) 分析:采用卷积的定义,直接积分求得 题6、[()*()]t d e u t u t dt -=_________________。 答案:()t e u t - 分析:采用卷积的微分性质:[()*()]()*()()*()()t t t t d d e u t u t e u t u t e u t t e u t dt dt δ----=== 题7、 一起始储能为零的系统,当输入为()u t 时,系统响应为3()t e u t -,则当输入为()t δ时, 系统的响应为 。 答案:3()3()t t e u t δ-- 分析:线性系统的微分特性的33()()3()t t d e u t t e u t dt δ--=- 题8、一线性时不变系统在相同的初始状态下,当激励为()x t 时,其全响应为)2cos(21t e y t +=-; 当激励为2()x t 时,其全响应为 )2cos(2)(2t t e y t +=-。试求在同样初始条件下,激励为4()x t 时 系统的全响应。 解: )2cos(2)()()(111t e t y t y t y t zi zs +=+=- (1) )2cos(2)()()(222t e t y t y t y t zi zs +=+=- (2) ∵)()(1t x t x =,)(2)(2t x t x =,两种输入的初始条件一样 ∴)(2)(12t y t y zs zs =,)()(12t y t y zi zi = (3) 根据(1)(2)(3)式,可得 ?????+-==--) 2cos()(3)(11t e t y e t y t zs t zi ∵)(4)(3t x t x =,初始条件不变 ∴)(4)(13t y t y zs zs =,)()(13t y t y zi zi = )()]2cos(4[3))2cos((4)()(4)()()(11333t u t e e t e t y t y t y t y t y t t t zi zs zi zs +-=++-=+=+=--- 2.6本章习题全解 2.1如题图2-1所示机械位移系统,质量为m 的刚体一端由弹簧牵引,弹簧的另一端固定在壁上,弹簧的刚度系数为k 。刚体与地面间的摩擦系数为f ,外加牵引力为)(t F S ,求外加牵引力)(t F S 与刚体运动速度)(t v 间的关系。 题图2-1 解:由机械系统元件特性,拉力k F 与位移x 成正比,即k F kx = 又()()t x t v d ττ-∞=? 所以,()()()t k F t kx t k v d ττ-∞==? 刚体在光滑表面滑动,摩擦力与速度成正比,即()()f F t fv t = 根据牛顿第二定律以及整个系统力平衡的达朗贝尔原理,可得 ()()()()t s d F t fv t k v d m v t dt ττ-∞--=? 整理得22()()()()s d d d m v t f v t kv t F t dt dt dt --= 2.2题图2-2所示电路,输入激励是电流源)(t i s ,试列出电流)(t i L 及1R 上电压)(1t u 为输出响应变量的方程式。 题图2-2 解:由电路的基尔霍夫电流定律可得:()()()C L S i t i t i t += (1) 根据电容特性,()()C C d i t C u t dt = (2) 由电路的基尔霍夫电压定律可得:12()()()()C C L L d u t R i t L i t R i t dt +=+ (3) 将21()()()()C L L C d u t L i t R i t R i t dt =+-代入(2)得 2212()()()()C L L C d d d i t LC i t R C i t R C i t dt dt dt =+-(4) ()()()C S L i t i t i t =-代入(4)得, 22112()()()()()()S L L L S L d d d d i t i t LC i t R C i t R C i t R C i t dt dt dt dt -=+-+ 整理得,21 212()11()()()()()L L L S S R R R d d d i t i t i t i t i t dt L dt LC L dt LC +++=+ (5) 将111()()(()())C S L u t i t R i t i t R ==-,即11 ()()()L S u t i t i t R =-代入(5)得 21121112111()()()()11(())(())(())()()S S S S S u t R R u t u t R d d d i t i t i t i t i t dt R L dt R LC R L dt LC +-+-+-=+ 整理得,22 1211211122()()()()()()S S R R u t R R d d d u t u t R i t i t dt L LC dt L dt +++=-- 2.3某连续系统的输入输出方程为 )(')(4)('3)("2t x t y t y t y =++已知)()(t u t x =,1)0(=-y ,1)0('=-y ,试计算)0(+y 和)0('+y 值。 解:将输入代入系统方程可得()t t y t y t y δ=++)(4)('3)("2 采用冲激函数匹配法求)0(+y 和)0(' +y 方程右端的冲激函数项最高阶数为()t δ,设 ()()()t u b t a t y ?+=''δ, 则有:()()()()t u at t y t u a t y ?=?=',,将其代入原系方程,得 ()()()()()t t u at t u a t u b t a δδ=?+?+?+4322 所以2 1=a ()()()()1 00231210210===+='+='∴-+-+y y y y 2.4 已知描述某线性时不变连续系统的微分方程如下, )(3)()(4)(4)(2 2t x t x dt d t y t y dt d t y dt d +=++, 1)0(=-y ,2)0(=-y ,)()(t u e t x t -=,试求其完全响应。 解:(1)求齐次解()t y h 特征方程为:0442 =++αα 特征根为:221==αα 所以,()()t h e t C C t y 221-+= (2)求特解()t y p ()()()t p t p e t y A t Ae t y --=∴=>=220:特解为:代入原方程得:设特解为 (3)全响应()()()()t t p h e e t C C t y t y t y --++=+=2221 将()()t f t e u t -=代入系统方程得 ()t t u e t y t y dt d t y dt d t δ+=++-)(2)(4)(4)(22 (1) ()()()()()()() ()()()()(), 1003 0,1001 ,)1(,:==∴='+'='∴=?=?='?+=''-++-+y y y y y a t u at t y t u a t y t u b t a t y 得将其代入式则设δ 将初始条件代入()()()()t t p h e e t C C t y t y t y --++=+=2221 得:3,121=-=C C 所以全响应为:()()()()0, 2312>++-=+=--t e e t t y t y t y t t p h 2.5 已知描述某线性时不变连续系统的微分方程为 )(3)()(2)(3)(22t x t x dt d t y t y dt d t y dt d +=++, 当激励为)()(t u e t x t -=时,系统的完全响应为t t e e t t y 22)32()(---+=,0≥t 。试求其零输入响应、零状态响应、自由响应和强迫响应。 解:由全响应得初始条件1)0(=-y ,3)0(='-y (1)求零输入响应 )(t y zi 特征方程为0232=++λλ, 特征根为1-=λ,2-=λ 所以t zi t zi zi e C e C t y 221)(--+= t zi t zi zi e C e C t y 2212)(----=' 代入初始条件1)0(=-y ,3)0(='-y ,解得51 =zi C ,42-=zi C 所以, 0,45)(2≥-=--t e e t y t t zi (2)求零状态响应)(t y zs 0,2)22()45(]2)32[()()()(222≥+-=---+=-=------t e e t e e e e t t y t y t y t t t t t t zi zs (3) 2.6 已知某线性时不变系统的方程式为 0)(2)(3)(≥=+t t x t y t y dt d 试求系统的冲激响应h(t)。 解:方程右端的冲激函数项最高阶数为()t δ,设 ()()()t u b t a t h ?+='δ, 则有:()()t u a t h ?=,将其代入原系方程,得6,2-==b a ()()()()()0 2220,02 20033>=∴==≥==+=∴-+--+t e t h A h t Ae t h h h t t h 得,代入将:而方程的齐次解为 2.7若描述系统的微分方程为 )(2)(21)(2)(3)("''t x t x t y t y t y += ++ 试求系统的阶跃响应。 解:由题可知: ()()()()()()()()()() ()()()()()()()()()()()()()()()t u e e t h A A A A h A A h e A e A t h a a a a t h a h h b h h b a t u a t h t u b t a t h t u c t b t a t h t t t h t h t h t t t t ??? ? ?+-=?????==?????+===='+=-=-==++?? ???=+'==+'='==?=?+='?++'=''+'=+'+''--++---+-+2323-1210--22101 ,2023210021002 1 ) 1(,,122 1232212121221212所以:,所以齐次解:特征根为:,的齐次方程为:又知所以:得:将其代入方程所以:由冲激匹配法设:δδδδδ 阶跃响应:()()()=?? ? ??+-==??∞---∞-ττττττd u e e d h t g t t 232 2.8已知某线性时不变(LTI)系统如题图 2.8所示。已知图中)1()(1-=t t h δ,)3()()(2--=t u t u t h ,)1()()(--=t u t u t x ,试求该系统的冲激响应)(t h 。 题图2.8 解:利用系统串联与系统并联的冲激响应求解 ()()()()[]() ()()()[]()()[] ()()[]()()[]()()[] 322111*********---+---+--=--*-*-+-+=+*++=t u t u t u t u t u t u t u t u t t t t h t h t h t h t h δδδ 2.9 设系统的微分方程表示为)()(6)('5)("t u e t y t y t y t -=++,求使完全响应为)(t u Ce t -时的系统起始状态_)0(y 和_)0('y ,并确定常数C 。 解:引入微分算子,则原微分方程可变换为: ()()()()()()()()()()()()()t u e e e t p p p t p p p t y t p t y p p t t t zs ?? ????+-=????? ???????+++-+=+++=+=++---32221213212112132111 165δδδ则零状态响应为:又由原微分方程知特征根为:3,221-=-=αα 所以:()03221>+=--t e A e A t y t t zi ()()()()() ()()()()()()2132002 1002 1,1,2121212121213232211-=--='='=+==-===?? ????+-++=+==+-+-------A A y y A A y y A A C t u e e e t u e A e A t y t y t u e C t y zi zi t t t t t zs zi t 所以起始状态:所以:全响应为: 2.10 已知某连续系统的微分方程为 )(6)('2)(6)('5)("t x t x t y t y t y +=++若系统的初始条件1)0(=-y 和 0)0('=-y , 输入信号)()1()(t u e t x t -+=,求系统的零输入响应)(t y zi ,零状态响应)(t y zs 和完全响应)(t y 。 (1)零输入响应)(t y zi 满足方程 0)(6)(5)(=+'+''t y t y t y zi zi zi 其+0值 1)0()0()0(===--+y y y zi zi 0)0()0()0(='='='--+y y y zi zi 方程特征根21-=λ,31-=λ,故零输入响应 t zi t zi zi e C e C t y 3221)(--+= 将初始值代入上式及其导数,得 1)0(21=+=+zi zi zi C C y 032)0(21=--='+zi zi zi C C y 由上式解得31=zi C ,22-=zi C ,所以 0,23)(32≥-=--t e e t y t t zi (2)零状态响应)(t y zs 是初始状态为零,且)()1()(t u e t x t -+=时,原微分方程的解,即)(t y zs 满足方程 )()1(6)](2)([2)(6)(5)(t u e t t u e t y t y t y t t zs zs zs --+++-=+'+''δ 即 )(4)()64()(6)(5)(t t u e t y t y t y t zs zs zs δ++=+'+''- 及初始状态0)0()0(='=--zs zs y y 。先求)0(+zs y 和)0(+'zs y ,由于上式等号右端含有)(t δ, 令 )()()(0t r t a t y zs +=''δ 积分(从∞-到t )得 )()(1t r t y zs =' )()(2t r t y zs = 将)(t y zs ''、)(t y zs '和)(t y zs 代入微分方程可求得4=a 。 对以上三式等号两端从-0到+0积分,并考虑到0)(000=?+-dt t r ,0)(001=?+ - dt t r ,可求得 4)0()0(=='-'-+a y y zs zs 0)0()0(=--+zs zs y y 解上式,得4)0(='+zs y ,0)0(=+zs y 。 对于0>t ,微分方程可写为 64)(6)(5)(+=+'+''-t zs zs zs e t y t y t y 不难求得其齐次解为t zi t zi e C e C 3221--+,其特解为12+-t e 。于是有 12)(3221+++=---t t zi t zi zs e e C e C t y 将初始值代入上式及其导数,得 03)0(21=++=+zi zi zs C C y 4232)0(21=---='+zi zi zs C C y 由上式可求得31-=zi C ,02=zi C ,所以系统的零状态响应为 0,123)(2≥++-=--t e e t y t t zs (3)全响应)(t y ,1220,12323) ()()(3232≥++-=≥++-+-=+=------t e e t e e e e t y t y t y t t t t t t zs zi 2.11已知一线性时不变系统,在相同初始条件下, 当激励为)(t e 时,其全响应为 )]()]2sin(2[)(31t u t e t y t +=-; 当激励为)(2t e 时,其全响应为 )]()]2sin(2[)(32t u t e t y t +=- 求:(1)初始条件不变,当激励为 )(0t t e -时的全响应)(3t y ,0t 为大于零的实常数。 (2)初始条件增大1倍,当激励为)(5.0t e 时的全响应)(4t y 。 解:系统的全响应是由零输入响应和零状态响应组成的,零输入响应与系统的状态呈线性关系,零状态响应与系统的输入呈线性时不变关系。 设 3111()()()[2sin(2)]()t zs zi y t y t y t e t u t -=+=+ (1) 则根据零状态响应线性可得 3211()2()()[2sin(2)]()t zs zi y t y t y t e t u t -=+=+ (2) 联立(1)、(2)得 31()[sin(2)]()t zs y t e t u t -=-+ 31()3()t zi y t e u t -= (1)初始条件不变,激励为 )(0t t e -时, 则331()()3()t zi zi y t y t e u t -== 03()31000()()[sin(22)]()t t zs zs y t y t t e t t u t t --=-=-+-- 03()333300()()()3()[sin(22)]()t t t zs zi y t y t y t e u t e t t u t t ---=+=+-+-- (2)初始条件增大1倍,当激励为)(5.0t e 时 341()2()6()t zi zi y t y t e u t -== 3()41()0.5()0.5[sin(2)]()t zs zs y t y t e t u t -==-+ 3444()()() 5.5()0.5sin(2)]()t zs zi y t y t y t e u t t u t -=+=+ 2.12 求下列各函数)(1t f 和)(2t f 的卷积)()()(t f t f t y *= (1))(e )(1t u A t f t ?-=α 和 t C t f 02sin )(ω= (2))()(1t u t f = 和 )()(2t u e t f at -= (3))()(1t t f δ= 和 )45cos()(2 +=t t f ω (4))]1()()[1()(1--+=t u t u t t f 和 )2()1()(2---=t u t u t f (5))cos()(1t t f ω= 和 )1()1()(2--+=t t t f δδ (6))2()(1-=t u t f ,)1()(2--=t u e t f t 解:(1) ()()()()()()()()()t u t t e AC d e e j e AC d e e j e ACe d e e AC d t u e AC t f t f t t j j t t j j t t t 1 cos sin 22sin sin 20000021+-+=-=-=?=-?=*--+---∞ -∞∞---????ααττττωτττωαταταατταταατατα(2) ()()()()()()()()()() ()t u e t u e t d e t d u e t d u e dt t du t f t f t t t t t αααταταταααδτδττδττ---∞--∞---=??????-*=*=*=??????*=*???1111021 (3)()()()()() o o t t t t f t f 45cos 45cos 21+=+*=*ωωδ (4) ()()()()()[]()()[] ()()()[]}{()()[] ()()()()[]()()()()[]()() ()()?????????><<++-<<-<=-??? ??--+-++-+-??? ? ??-=---*?? ????-???? ??-+-???? ??+=---*?? ????+++=---*--+=---*--+=*???∞-30322322121210323212212122112322211121112111222222 1021t t t t t t t t u t t u t t t u t t t t u t t t u t t t t d d t t d u u t u t u t u t u t t f t f t t t δδδδττττδδττττ (5)()()()()()[]()[]()[]1cos 1cos 11cos 21--+=--+*=*t t t t t t f t f ωωδδω (6)τττττττd )1()2(d )()()()()(2121??∞ ∞--∞∞----=-= *=t u e u t f f t f t f t y t 当21≤+t 即1≤t 时, 22222d d d )(--∞--∞-∞-∞--=?-=-===???t t t t t e e e e e e e e t y τττττττ 当21>+t 即1>t 时, 11111d d d )(---∞---∞-∞+-∞+--=?-=-===???e e e e e e e e t y t t t t t t t t τττττττ 故有)1()1()(12----=--t u e t u e t y t 2.13已知某线性时不变系统数学模型为 )()(2)('3)("t x t y t y t y =++ 且0)0(=h ,1)0('=h ,试用卷积积分法求当输入激励为)()(t u e t f t ?=-的零状态响应。 解:冲激响应满足? ??='==+'+''--0)0()0()()(2)(3)(h h t t h t h t h δ 不难求得其+0值分别为 0)0(=+h 1)0(='+h 特征方程为 0232=++λλ 其特征根11-=λ,22-=λ。故系统的冲激响应 0,)(221>+=--t e C e C t h t t 将初始条件0)0(=+h ,1)0(='+h 代入上式,得 11=C ,12-=C 所以)()()(2t u e e t h t t ---=,由此0)0(=h ,故)(t h 不含)(t δ。 零状态响应)(t y zs 是冲激响应)(t h 与激励)(t x 的卷积积分,即 ) (])1[()()()()()()()(20)(02)(2t u e e t d e e d e e e d t u e u e e t f t h t y t t t t t t t t zs -----------∞ ∞----+=-=-=--=*=???ττττττττττττ 2.14某LTI 连续系统有A 、B 、C 三部分组成,如题图2.14所示。已知子系统A 的冲激响应 )(2 1)(4t e t h t A ε-= 子系统B 和C 的阶跃响应分别为 )()1()(t u e t g t B --=,)(2)(3t u e t g t C -= 信号与系统期末考试试题 一、选择题(共10题,每题3分 ,共30分,每题给出四个答案,其中只有一个正确的) 1、 卷积f 1(k+5)*f 2(k-3) 等于 。 (A )f 1(k)*f 2(k) (B )f 1(k)*f 2(k-8)(C )f 1(k)*f 2(k+8)(D )f 1(k+3)*f 2(k-3) 2、 积分 dt t t ? ∞ ∞ --+)21()2(δ等于 。 (A )1.25(B )2.5(C )3(D )5 3、 序列f(k)=-u(-k)的z 变换等于 。 (A ) 1-z z (B )-1-z z (C )11-z (D )1 1--z 4、 若y(t)=f(t)*h(t),则f(2t)*h(2t)等于 。 (A ) )2(41t y (B ))2(21t y (C ))4(41t y (D ))4(2 1 t y 5、 已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时,系 统的零状态响应y f (t)等于 (A )(-9e -t +12e -2t )u(t) (B )(3-9e -t +12e -2t )u(t) (C ))(t δ+(-6e -t +8e -2t )u(t) (D )3)(t δ +(-9e -t +12e -2t )u(t) 6、 连续周期信号的频谱具有 (A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 7、 周期序列2)455.1(0 +k COS π的 周期N 等于 (A ) 1(B )2(C )3(D )4 8、序列和 ()∑∞ -∞ =-k k 1δ等于 (A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()s e s s s F 22 12-+= 的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u te t f t 的单边拉氏变换()s F 等于 ()A ()()()232372+++-s e s s ()() 2 23+-s e B s 第一章作业参考答案: 1.18求下列积分值: (a )解: 26 242)2()2(2)()0()2()(2)()()]2(2)([)()]2(2)()[23(4 4 44 4 4 4 4 4 4 2 =+=-+=-+=-+=-+++????? -----dt t x dt t x dt t t x dt t t x dt t t t x dt t t t t δδδδδδδδ (b) 解: 6 510)2()2()()0()5()5()2()()()()5()()]2()()5([)()]2()()5()[1(4 4 44 44 4 4 4 4 4 4 2 =++=-+++-=-+++=-+++=-++++?????? ------dt t x dt t x dt t x dt t t x dt t t x dt t t x dt t t t t x dt t t t t δδδδδδδδδδδδ(C )解: 1 )2 ()cos 1()2 ()cos 1(2=--=- -? ?-- π π ππ π π δπ δdt t dt t t (d )解: 4 2 312121231)(cos )23()(cos )2()(cos )2()(cos )23()(cos )1(200 222=++++-+-=++-+- =+????? -----ππππδπδπδπδπδπ ππππππ π dt t x dt t x dt t x dt t x dt t t 1.19解: 1.21 判断下列每个信号是否周期的?如果是周期的,是求它的基波周期。 (a )解: 3 2,/23) cos(2)43cos(200π πω?ωπ= ==+=+T T t t 基波周期为:是周期信号 (b)解: e e e T e e e t j T t j T j T j t j T t j ) 1() 1)(()1() 1)((12--±±±--±====ππππππ,时,当 是周期信号,基波周期是 T 0=2 (c)解: 互质与是有理数,且74,7 4 2782) 2cos()278cos(==Ω+Ω=+ππππn n 所以原式是周期信号,基波周期N 0=7. (d)解: 不是有理数,,812412cos 4 cos π ππ==ΩΩ=n n 所以原式不是周期信号 (e )解: 。 有为整数, 其中则令][][4/,)4/(4`, `]}41[`]4[{]} 41[]4[{][,]} 41[]4[{][:n x N n x N N k k k n k n k N n k N n N n x k n k n n x k k k =+-=----= --+--+= +----= ∑∑∑∞ -∞ =∞ -∞=∞ -∞ =δδδδδδ 所以原式是周期信号,基波周期N 0=4. (f )解: 1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号? 图1-1 图1-2 解 信号分类如下: ??? ?? ? ????--???--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号; (e )离散信号,数字信号; (f )离散信号,数字信号。 1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ; (4)为任意值)(00)sin(ωωn ; (5)2 21??? ??。 解 由1-1题的分析可知: (1)连续信号; (2)离散信号; (3)离散信号,数字信号; (4)离散信号; (5)离散信号。 1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -; (2)j10t e ; (3)2)]8t (5sin [; (4)[]为整数)(n )T nT t (u )nT t (u )1(0 n n ∑∞ =-----。 解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各 分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。 (1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15 T 2π=。由于 5π 2.1 引言 连续时间系统处理连续时间信号,通常用微分方程来描述这类系统,也就是系统的输入输出之间通过他们时间函数及其对时间t的各阶导数的线性组合联系起来。 输入与输出只用一个高阶的微分方程相联系,而且不研究内部其他信号的变化,这种描述系统的方法称为输入——输出法。 此处的分析方法有很多,其中时域分析法不通过任何变换,直接求微分方程,这种方法直观,物理概念清楚,是学习各类变换域分析方法的基础。系统时域分析法包含两方面内容,一是微分方程的求解,另一是已知系统单位冲激响应,将冲激响应与输入激励信号进行卷积,求出系统的输出响应。其中第一种方法在高等数学中有详细的解释,在这里主要是解释其物理含义,并建立零输入响应和零状态响应两个重要的基本概念。虽然卷积只能用于系统的零状态响应,但他的物理概念明确。。。。。。。。。。。主要的是卷积是时域和频域之间的纽带,通过它把变换域分析赋以清晰的物理概念。 2.2 微分方程的建立与求解 激励信号为e(t),系统响应为r(t)。 由时域经典解法,方程式的完全解由两部分组成:齐次解与特解。齐次解解法: 代入: 化简为: 特征根为: 所以微分方程的齐次解为: 其中常数A由初始条件决定。 如果有重根,即: a1相应于重根部分有k项: 特解解法:特解rp(t)的函数形式与激励函数有关,将激励e(t)代入方程式,求特解方程的待定系数,即可给出特解。 完全解: 一般需要给出初始条件才能求解系数 因此可以求出常数A a值构成的矩阵称为范德蒙德矩阵. 齐次解表示系统的自由响应,特征根表示系统的“固有频率”,特解称为系统的强迫响应,强迫响应只与激励函数的形式有关。 r(t) = rh(t) + rp(t) 2.3 起始点的跳变从0-到0+ 《信号与系统》复习题 1. 已知f(t)如图所示,求f(-3t-2)。 2. 已知f(t),为求f(t0-at),应按下列哪种运算求得正确结果?(t0和a 都为正值) 3.已知f(5-2t)的波形如图,试画出f(t)的波形。 解题思路:f(5-2t)?????→?=倍 展宽乘22/1a f(5-2×2t)= f(5-t) ??→?反转f(5+t)??→?5 右移 f(5+t-5)= f(t) 4.计算下列函数值。 (1) dt t t u t t )2(0 0--?+∞ ∞-) (δ (2) dt t t u t t )2(0 --?+∞ ∞-) (δ (3) dt t t e t ?+∞ ∞ --++)(2)(δ 5.已知离散系统框图,写出差分方程。 解:2个延迟单元为二阶系统,设左边延迟单元输入为x(k) 左○ ∑:x(k)=f(k)-a 0*x(k-2)- a 1*x(k-1)→ x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) 右○ ∑: y(k)= b 2*x(k)- b 0*x(k-2) (2) 为消去x(k),将y(k)按(1)式移位。 a 1*y(k-1)= b 2* a 1*x(k-1)+ b 0* a 1*x(k-3) (3) a 0*y(k-2)= b 2* a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2)、(3)、(4)三式相加:y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*[x(k)+ a 1*x(k-1)+a 0*x(k-2)]- b 0*[x(k-2)+a 1*x(k-3)+a 0*x(k-4)] ∴ y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*f(k)- b 0*f(k-2)═>差分方程 6.绘出下列系统的仿真框图。 )()()()()(10012 2t e dt d b t e b t r a t r dt d a t r dt d +=++ 7.判断下列系统是否为线性系统。 (2) 8.求下列微分方程描述的系统冲激响应和阶跃响应。 )(2)(3)(t e dt d t r t r dt d =+ 第1章 习题答案 1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号? 解: ① 连续信号:图(a )、(c )、(d ); ② 离散信号:图(b ); ③ 周期信号:图(d ); ④ 非周期信号:图(a )、(b )、(c ); ⑤有始信号:图(a )、(b )、(c )。 1-2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。 解: 设T 为此系统的运算子,由已知条件可知: y(t)=T[f(t)]=|f(t)|,以下分别判定此系统的线性和时不变性。 ① 线性 1)可加性 不失一般性,设f(t)=f 1(t)+f 2(t),则 y 1(t)=T[f 1(t)]=|f 1(t)|,y 2(t)=T[f 2(t)]=|f 2(t)|,y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|,而 |f 1(t)|+|f 2(t)|≠|f 1(t)+f 2(t)| 即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下,不存在f 1(t)+f 2(t)→y 1(t)+y 2(t),因此系统不具备可加性。 由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。 2)齐次性 由已知条件,y(t)=T[f(t)]=|f(t)|,则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) (其中a 为任一常数) 即在f(t)→y(t)前提下,不存在af(t)→ay(t),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。 ② 时不变特性 由已知条件y(t)=T[f(t)]=|f(t)|,则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|, 即由f(t)→y(t),可推出f(t-t 0)→y(t-t 0),因此,此系统具备时不变特性。 依据上述①、②两点,可判定此系统为一非线性时不变系统。 1-3 判定下列方程所表示系统的性质: )()()]([)()(3)(2)(2)()()2()()(3)(2)()()()()() (2''''''''0t f t y t y d t f t y t ty t y c t f t f t y t y t y b dx x f dt t df t y a t =+=++-+=+++=? 解:(a )① 线性 1)可加性 由 ?+=t dx x f dt t df t y 0)()()(可得?????→+=→+=??t t t y t f dx x f dt t df t y t y t f dx x f dt t df t y 01122011111)()()()()()()()()()(即即 则 ???+++=+++=+t t t dx x f x f t f t f dt d dx x f dt t df dx x f dt t df t y t y 0212102201121)]()([)]()([)()()()()()( 即在)()()()()()()()(21212211t y t y t f t f t y t f t y t f ++前提下,有、→→→,因此系统具备可加性。 2)齐次性 由)()(t y t f →即?+=t dx x f dt t df t y 0)()()(,设a 为任一常数,可得 )(])()([)()()]([)]([000t ay dx x f dt t df a dx x f a dt t df a dx x af t af dt d t t t =+=+=+??? 即)()(t ay t af →,因此,此系统亦具备齐次性。 由上述1)、2)两点,可判定此系统为一线性系统。 2-1 绘出下列各时间函数的波形图。 (1)1()(1)f t tu t =- (2) 2()[()(1)](1) f t t u t u t u t =--+- (3)3()(1)[()(1)]f t t u t u t =---- (4)4()[(2)(3)]f t t u t u t =--- (5)5()(2)[(2)(3)]f t t u t u t =---- (6)6()()2(1)(2)f t u t u t u t =--+- 解: 2-5 已知()f t 波形如图题2-5所示,试画出下列信号的波形图。 t 图 题2-5 (3)3()(36) f t f t =+ (5)51 1()3 6f t f t ??= -- ? ?? 解: t t 2-6 已知()f t 波形如图题2-6所示,试画出下列信号的波形图。 图 题2-6 (4)4()(2)(2)f t f t u t =-- (6)6()(1)[()(2)]f t f t u t u t =--- 解: 2-7 计算下列各式。 (1) 0()() f t t t δ+ (2)00()()d f t t t t t δ∞ -∞ +-? (3)2 4 e (3)d t t t δ-+? (4)0 e sin (1)d t t t t δ∞ -+? (5) d [ e ()] d t t t δ- (6)0()()d f t t t t δ∞ -∞ -? (7)0()()d f t t t t δ∞ -∞ -? (8)00()d 2t t t u t t δ∞ -∞ ??-- ?? ? ? (9)00()(2)d t t u t t t δ∞ -∞ --? (10)(e )(2)d t t t t δ∞ -∞ ++? (11)(sin )d 6t t t t δ∞ -∞ π? ?+- ???? (12) j 0e [()()]d t t t t t Ωδδ∞ --∞ --? 解:(1) 原式0()()f t t δ= 信科0801《信号与系统》复习参考练习题一、单项选择题: 14、已知连续时间信号,) 2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。200 rad /s C 。100 rad /s D 。50 rad /s f如下图(a)所示,其反转右移的信号f1(t) 是() 15、已知信号)(t f如下图所示,其表达式是() 16、已知信号)(1t A、ε(t)+2ε(t-2)-ε(t-3) B、ε(t-1)+ε(t-2)-2ε(t-3) C、ε(t)+ε(t-2)-ε(t-3) D、ε(t-1)+ε(t-2)-ε(t-3) 17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是() A、f(-t+1) B、f(t+1) C、f(-2t+1) D、f(-t/2+1) 18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是( ) 19。信号)2(4sin 3)2(4cos 2)(++-=t t t f π π 与冲激函数)2(-t δ之积为( ) A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ ,则该系统是()>-系统的系统函数.已知2]Re[,6 51)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统 C 、因果稳定系统 D 、非因果不稳定系统 21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( ) A 、常数 B 、 实数 C 、复数 D 、实数+复数 22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( ) A 、阶跃信号 B 、正弦信号 C 、冲激信号 D 、斜升信号 1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11))]7()()[6sin()(--=k k k k f εεπ (12) )]()3([2)(k k k f k ---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2) )2()1(2)()(-+--=t r t r t r t f (5) )2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11) )]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。 1-4 写出图1-4所示各序列的闭合形式表达式。 1-5 判别下列各序列是否为周期性的。如果是,确定其周期。 (2))63cos()443cos()(2ππππ+++=k k k f (5))sin(2cos 3)(5t t t f π+= 解: 1-6 已知信号)(t f 的波形如图1-5所示,画出下列各函数的波形。 (1))()1(t t f ε- (2))1()1(--t t f ε (5) )21(t f - (6))25.0(-t f (7)dt t df ) ( (8)dx x f t ?∞-)( 解:各信号波形为 专业课习题解析课程 第1讲 第一章 信号与系统 (一) 专业课习题解析课程 第2讲 第一章 信号与系统 (二) 1-1画出下列各信号的波形【式中)()(t t t r ε=】为斜升函数。 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 解:各信号波形为 (2)∞<<-∞=-t e t f t ,)( (3))()sin()(t t t f επ= (4))(sin )(t t f ε= (5))(sin )(t r t f = (7))(2)(k t f k ε= (10))(])1(1[)(k k f k ε-+= 1-2 画出下列各信号的波形[式中)()(t t t r ε=为斜升函数]。 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2))2()1(2)()(-+--=t r t r t r t f (5))2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11) )]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 解:各信号波形为 (1))2()1(3)1(2)(-+--+=t t t t f εεε (2) )2()1(2)()(-+--=t r t r t r t f (5) )2()2()(t t r t f -=ε (8))]5()([)(--=k k k k f εε (11) )]7()()[6sin()(--=k k k k f εεπ (12))]()3([2)(k k k f k ---=εε 1-3 写出图1-3所示各波形的表达式。 第一章信号与系统 本章学习要求 (1)了解信号与系统的基本概念;信号的不同类型与特点;系统的类型与特点; (2)熟悉离散时间信号的基本表示方法; (3)掌握正弦序列周期性的定义和判断; (4)深刻理解能量信号、功率信号的定义和判断; (5)掌握信号的基本运算(变换)方法; (6)深刻理解冲激信号、阶跃信号的定义、特点及相互关系;理解冲激函数的广义函数定义;掌握冲激函数的基本性质;冲激函数的微积分; (7)熟悉系统的数学模型和描述方法 (8)了解系统的基本分析方法;掌握系统的基本特性及其判断 本章重点 (1)离散时间信号的表示; (2)离散周期序列的判断、周期的计算; (3)能量信号的定义、判断;功率信号的定义、判断; (4)信号的加法、乘法;信号的反转、平移;信号的尺度变换; (5)阶跃函数的极限定义、冲激函数的极限定义;阶跃函数与冲激函数的关系; (6)冲激函数的广义函数定义;冲激函数的导数与积分;冲激函数的性质; (7)连续系统和离散系统的数学模型;系统的表示方法; (8)线性时不变系统的基本特性;线性、时不变性的判断。 1.1 绪言 什么是信号?什么是系统?为什么把这两个概念连在一起?信号、系统能不能相互独立而存在? 一、信号的概念 1. 消息(message): 人们常常把来自外界的各种报道统称为消息。 2. 信息(information): 通常把消息中有意义的内容称为信息。 本课程中对“信息”和“消息”两词不加严格区分。 3. 信号(signal): 信号是信息的载体。通过信号传递信息。 为了有效地传播和利用信息,常常需要将信息转换成便于传输和处理的信号,由此再次说明“信号是信息的载体,信息是信号的内涵”。 信号我们并不陌生,如刚才铃声—声信号,表示该上课了;十字路口的红绿灯—光信号,指挥交通;电视机天线接受的电视信息—电信号;广告牌上的文字、图象信号等等。 二、系统的概念 信号的产生、传输和处理需要一定的物理装置,这样的物理装置常称为系统。一般而言,系统(system)是指若干相互关联的事物组合而成具有特定功能的整体。 如手机(可以用手机举例)、电视机、通信网、计算机网等都可以看成系统。它们所传送的语音、音乐、图象、文字等都可以看成信号。信号的概念与系统的概念常常紧密地联系在一起。 系统的基本作用是对输入信号进行加工和处理,将其转换为所需要的输出信号,如图1所示。 图1 从系统的角度出发,系统理论包括系统的分析与综合两个方面。简单地说,系统分析是对已知的系统做各种特性的分析;系统综合又称系统的设计或实现,它是指根据需要去设计构成满足性能要求的系统。 通常,系统分析是针对已有的系统,系统综合往往意味着做出新系统。显然,前者属于认识世界的问题,后者则是改造世界的问题,且是人们追求的最终目的。一般来说,系统分析是系统综合的基础,只有精于分析,才能善于综合。本课程主要侧重于系统分析。 三、信号与系统概念无处不在 信息科学已渗透到所有现代自然科学和社会科学领域,因此可以说信号与系统在当今社会无处不在,大致列举的应用领域如下: ?工业监控、生产调度、质量分析、资源遥感、地震预报 ?人工智能、高效农业、交通监控 ?宇宙探测、军事侦察、武器技术、安全报警、指挥系统 ?经济预测、财务统计、市场信息、股市分析 ?电子出版、新闻传媒、影视制作 ?远程教育、远程医疗、远程会议 ?虚拟仪器、虚拟手术 如对于通讯: ?古老通讯方式:烽火、旗语、信号灯 ?近代通讯方式:电报、电话、无线通讯 《信号与系统》复习题 1.已知 f(t) 如图所示,求f(-3t-2) 。 2.已知 f(t) ,为求 f(t0-at) ,应按下列哪种运算求得正确结果?(t0 和 a 都为正值) 3.已知 f(5-2t) 的波形如图,试画出f(t) 的波形。 解题思路:f(5-2t)乘a 1 / 2展宽 2倍f(5-2 × 2t)= f(5-t) 反转 右移 5 f(5+t) f(5+t-5)= f(t) 4.计算下列函数值。 ( 1) ( 2) ( t ) t 0 )dt t 0 u(t 2 (t t 0)u(t 2t 0 )dt ( 3) (e t t ) (t 2)dt 5.已知离散系统框图,写出差分方程。 解: 2 个延迟单元为二阶系统,设左边延迟单元输入为 x(k) ∑ 0 1 1) → 左○ :x(k)=f(k)-a *x(k-2)- a*x(k- x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) ∑ y(k)= b 2*x(k)- b 0*x(k-2) (2) 右○ : 为消去 x(k) ,将 y(k) 按( 1)式移位。 a 1*y(k-1)= b 2 * a 1*x(k-1)+ b * a 1*x(k-3) (3) a 0*y(k-2)= b 2 * a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2) 、( 3)、( 4)三式相加: y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b *[x(k)+ a 1 *x(k-1)+a *x(k-2)]- b *[x(k-2)+a 1*x(k-3)+a *x(k-4)] 2 0 0 0 ∴ y(k)+ a 1 *y(k-1)+ a *y(k-2)= b 2 *f(k)- b *f(k-2) ═ >差分方程 1. 系统的激励是)t (e ,响应为)t (r ,若满足dt ) t (de )t (r = ,则该系统为 线性、时不变、因果。(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+?∞ ∞-δ的值为 5 。 3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频 分量 主要影响脉冲的跳变沿。 4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。 5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统 幅频特性为 一常数相频特性为_一过原点的直线(群时延)。 6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。 7. 若信号的3s F(s)= (s+4)(s+2) ,求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。 8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。 9. 已知信号的频谱函数是)) 00(()j (F ωωδωωδω--+=,则其时间信号f(t)为 01 sin()t j ωπ 。 10. 若信号f(t)的2 11 )s (s )s (F +-=,则其初始值=+)(f 0 1 。 二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。(每小题2分,共10分) 1.单位冲激函数总是满足)()(t t -=δδ ( √ ) 2.满足绝对可积条件∞ 第1章 习题答案 1-1 题1-1图所示信号中,哪些是连续信号?哪些是离散信号?哪些是周期信号?哪些是非周期信号?哪些是有始信号? 解: ① 连续信号:图(a )、(c )、(d ); ② 离散信号:图(b ); ③ 周期信号:图(d ); ④ 非周期信号:图(a )、(b )、(c ); ⑤有始信号:图(a )、(b )、(c )。 1-2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|,试判定该系统是否为线性时不变系统。 解: 设T 为此系统的运算子,由已知条件可知: y(t)=T[f(t)]=|f(t)|,以下分别判定此系统的线性和时不变性。 ① 线性 1)可加性 不失一般性,设f(t)=f 1(t)+f 2(t),则 y 1(t)=T[f 1(t)]=|f 1(t)|,y 2(t)=T[f 2(t)]=|f 2(t)|,y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|,而 |f 1(t)|+|f 2(t)|≠|f 1(t)+f 2(t)| 即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下,不存在f 1(t)+f 2(t)→y 1(t)+y 2(t),因此系统不具备可加性。 由此,即足以判定此系统为一非线性系统,而不需在判定系统是否具备齐次性特性。 2)齐次性 由已知条件,y(t)=T[f(t)]=|f(t)|,则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) (其中a 为任一常数) 即在f(t)→y(t)前提下,不存在af(t)→ay(t),此系统不具备齐次性,由此亦可判定此系统为一非线性系统。 ② 时不变特性 由已知条件y(t)=T[f(t)]=|f(t)|,则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|, 即由f(t)→y(t),可推出f(t-t 0)→y(t-t 0),因此,此系统具备时不变特性。 依据上述①、②两点,可判定此系统为一非线性时不变系统。 1-3 判定下列方程所表示系统的性质: 解:(a )① 线性 1)可加性 由 ?+=t dx x f dt t df t y 0)()()(可得?????→+=→+=??t t t y t f dx x f dt t df t y t y t f dx x f dt t df t y 01122011111) ()()()()()()()()()(即即 则 即在)()()()()()()()(21212211t y t y t f t f t y t f t y t f ++前提下,有、→→→,因此系统具备可加性。 2)齐次性 由)()(t y t f →即?+=t dx x f dt t df t y 0)()()(,设a 为任一常数,可得 即)()(t ay t af →,因此,此系统亦具备齐次性。 由上述1)、2)两点,可判定此系统为一线性系统。 ② 时不变性 )()(t y t f → 具体表现为:?+=t dx x f dt t df t y 0)()()( 将方程中得f(t)换成f(t-t 0)、y(t)换成y(t-t 0)(t 0为大于0的常数), 第二章 作业答案 2–1 已知描述某LTI 连续系统的微分方程和系统的初始状态如下,试求此系统的零输入响应。 (1))()(2)(2)(3)(t e t e t y t y t y +'=+'+'' 2)0(=-y ,1)0(-='-y 解: 根据微分方程,可知特征方程为: 0)2)(1(0232=++?=++λλλλ 所以,其特征根为: 1, 221-=-=λλ 所以,零输入响应可设为:0)(221≥+=--t e C e C t y t t zi 又因为 ???=-=??? ?-=--='=+=--31 12)0(2)0(2 1 2121C C C C y C C y 所以,03)(2≥-=--t e e t y t t zi (2))(2)()(6)(5)(t e t e t y t y t y -'=+'+'' ?1)0()0(=='--y y 。 解: 根据微分方程,可知特征方程为: 0)3)(2(0652=++?=++λλλλ 所以,其特征根为: 3, 221-=-=λλ 所以,零输入响应可设为:0)(3221≥+=--t e C e C t y t t zi 又因为 ???-==??? ?=--='=+=--3 4 132)0(1)0(21 2121C C C C y C C y 所以,034)(32≥-=--t e e t y t t zi 2–2 某L TI 连续系统的微分方程为)(3)()(2)(3)(t e t e t y t y t y +'=+'+'' 已知1)0(=-y ,2)0(='-y ,试求: (1) 系统的零输入响应)(t y zi ; (2) 输入)()(t t e ε=时,系统的零状态响应)(t y zs 和全响应)(t y 。 解: (1)根据微分方程,可知特征方程为: 0)2)(1(0232=++?=++λλλλ 所以,其特征根为: 1, 221-=-=λλ 所以,零输入响应可设为:0)(221≥+=--t e C e C t y t t zi 又因为 ???=-=??? ?=--='=+=--43 22)0(1)0(2 12121C C C C y C C y 所以,034)(2≥-=--t e e t y t t zi ? (2) 可设零状态响应为:0)(221>++=--t p e C e C t y t x t x zs 其中p 为特解,由激励信号和系统方程确定。 因为)()(t t e ε= 所以,p 为常数,根据系统方程可知,23=p 。 于是,零状态响应可设为为:02 3)(221>++=--t e C e C t y t x t x zs 将上式代入原方程中,比较方程两边的系数,可得到 信号与系统复习题含答 案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】 (C )) (t δ+(-6e -t +8e -2t )u(t) (D )3) (t δ +(-9e -t +12e -2t )u(t) 6、 连续周期信号的频谱具有 (A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性 7、 周期序列2)455.1(0+k COS π的 周期N 等 于 (A) 1 (B )2 (C )3 (D ) 4 8、序列和() ∑∞ -∞=-k k 1δ等于 (A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换 ()s e s s s F 2212-+= 的愿函数等于 10、信号 ()()23-=-t u te t f t 的单边拉氏变换()s F 等于 二、填空题(共9小题,每空3分,共30分) 1、 卷积和[() k+1 u(k+1)]*)1(k -δ=______________________ __ 2、 单边z 变换F(z)= 12-z z 的原序列 f(k)=______________________ 3、 已知函数f(t)的单边拉普拉斯变换 F(s)=1+s s ,则函数y(t)=3e -2t ·f(3t)的单边拉 普拉斯变换 Y(s)=_________________________ 4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换 f(t)=__________________ 5、 单边拉普拉斯变换 s s s s s F +++= 221 3)(的原函数 f(t)=__________________________ 6、 已知某离散系统的差分方程为 ) 1(2)()2()1()(2-+=----k f k f k y k y k y ,则系统的单位序列响应 h(k)=_______________________ 7、 已知信号f(t)的单边拉氏变换是F(s),则信号 ? -=2 )()(t dx x f t y 的单边拉氏变换 Y(s)=______________________________ 8、描述某连续系统方程为 该系统的冲激响应h(t)= 9、写出拉氏变换的结果()=t u 66 ,=k t 22 三(8分)已知信号 ()()()???? ?><==?./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(), dt t df t s = 求? ?? ??2ωs 的傅里叶逆变换。 四、(10分)如图所示信号 ()t f ,其傅里叶变换 ()()[]t f jw F F =,求(1) ()0F (2) ()?∞ ∞-dw jw F 五、(12)分别求出像函数()25232 +-= z z z z F 在下列 三种收敛域下所对应的序列 (1)2?z (2) 5 .0?z (3)2 5.0??z 六、(10分)某LTI 系统的系统函数 ()1222 ++= s s s s H ,已知初始状态 ()(),20,00=='=--y y 激励()(),t u t f =求该系统 的完全响应。 试题三 一、单项选择题(在每小题的四个备选答案中,选出一个正确答案,并将正确答案的序号填在题干的括号内。每小题3分,共30分) 1.设:如图—1所示信号。 则:信号f(t)的数学表示式为( )。 (A)f(t)=t ε(t)-t ε(t-1) (B)f(t)=t ε(t)-(t-1)ε(t-1) (C)f(t)=(1-t)ε(t)-(t-1)ε(t-1) (D)f(t)=(1+t)ε(t)-(t+1)ε(t+1) 2.设:两信号f 1(t)和f 2(t)如图—2。则:f 1(t)与f 2(t)间变换关系为( )。 (A)f 2(t)=f 1(2 1t+3) (B)f 2(t)=f 1(3+2t) (C)f 2(t)=f 1(5+2t) (D)f 2(t)=f 1(5+2 1t) 3.已知:f(t)=SgN(t)的傅里叶变换为F(j ω)=ω j 2, 则:F 1(j ω)=j πSgN(ω)的傅里叶反变换f 1(t)为( )。 (A)f 1(t)=t 1 (B)f 1(t)=-t 2 (C)f 1(t)=-t 1 (D)f 1(t)=t 2 4.周期性非正弦连续时间信号的频谱,其特点为( )。 (A)频谱是连续的,收敛的 (B)频谱是离散的,谐波的,周期的 (C)频谱是离散的,谐波的,收敛的 (D)频谱是连续的,周期的 5.设:二端口网络N 可用A 参数矩阵{a ij }表示,其出 端与入端特性阻抗为Z c2、Z c1,后接载Z L ,电源? U s 的频率为ωs ,内阻抗为Z s 。则:特性阻抗Z c1、Z c2仅与 ( )有关。 (A){a ij },Z L (B){a ij },Z L ,Z s (C){a ij },ωs , *U s (D){a ij } 6.设:f(t)?F(j ω) 则:f 1(t)=f(at+b) ?F 1(j ω)为( ) (A)F 1(j ω)=aF(j a ω)e -jb ω (B)F 1(j ω)=a 1 F(j a ω)e -jb ω 信号与系统 考试方式:闭卷 考试题型:1、简答题(5个小题),占30分;计算题(7个大题),占70分。 一、简答题: 1.dt t df t f x e t y t ) ()()0()(+=-其中x(0)是初始状态, 为全响应,为激励,)()(t y t f 试回答该系统是否是线性的?[答案:非线性] 2.)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的,是时 变的还是非时变的?[答案:线性时变的] 3.已知有限频带信号)(t f 的最高频率为100Hz ,若对)3(*)2(t f t f 进行时域取样, 求最小取样频率s f =?[答案:400s f Hz =] 4.简述无失真传输的理想条件。[答案:系统的幅频特性为一常数,而相频特性为通过原点的直线] 5.求[]?∞ ∞ --+dt t t e t )()('2δδ的值。[答案:3] 6.已知)()(ωj F t f ?,求信号)52(-t f 的傅立叶变换。 [答案:521(25)()22 j f t e F j ωω --?] 7.已知)(t f 的波形图如图所示,画出)2()2(t t f --ε的波形。 [答案: ] 8.已知线性时不变系统,当输入)()()(3t e e t x t t ε--+=时,其零状态响应为 )()22()(4t e e t y t t ε--+=,求系统的频率响应。[答案:()) 4)(2(52)3(++++ωωωωj j j j ] 9.求象函数2 ) 1(3 2)(++=s s s F ,的初值)0(+f 和终值)(∞f 。 [答案:)0(+f =2,0)(=∞f ] 10.若LTI 离散系统的阶跃响应为)(k g ,求其单位序列响应。 其中:)()2 1 ()(k k g k ε=。 [答案:1111 ()()(1)()()()(1)()()(1)222 k k k h k g k g k k k k k εεδε-=--=--=--] 11.已知()1 1 , 0,1,20 , k f k else ==??? ,()2 1 , 0,1,2,3 0 , k k f k else -==??? 设()()()12f k f k f k =*,求()3?f =。[答案:3] 12.描述某离散系统的差分方程为()()()122()y k y k y k f k +---= 求该系统的单位序列响应()h k 。[答案:21()[(2)]()33 k h k k ε=-+] 13.已知函数()f t 的单边拉普拉斯变换为()1 s F s s =+,求函数()()233t y t e f t -=的单边拉普 拉斯变换。[答案:()2 5 Y s s s = ++] 14.已知()()12f t f t 、的波形如下图,求()()()12f t f t f t =*(可直接画出图形)信号与系统期末考试试题(有答案的)
信号与系统习题解答 (1)
(精品)信号与系统课后习题与解答第一章
信号与系统第二章
信号与系统习题答案
信号与系统课后习题答案—第1章
信号与系统第二章答案
信号与系统试题附答案
信号与系统第一章答案
信号与线性系统分析吴大正_第四版第一章习题答案
第1章 信号与系统
(完整版)信号与系统习题答案.docx
信号与系统复习题及答案
信号与系统课后习题答案—第章
信号与系统作业作业1第二章答案
信号与系统复习题含答案完整版
信号与系统试题库史上最全内含答案)