
平面向量的概念与线性运算
基础巩固强化
1.(文)(2011·广西六校联考、北京石景山检测)已知O 是△ABC 所在平面内一点,D 为BC 边中点,且2OA →+OB →+OC →
=0,那么( )
A.AO →=OD →
B.AO →=2OD →
C.AO →=3OD → D .2AO →=OD →
[答案] A
[解析] ∵OB →+OC →=2OD →
, ∴2OA →+2OD →=0,∴AO →=OD →.
(理)(2012·珠海调研)已知△ABC 及其平面内点M 满足MA →+MB →
+MC →=0,若存在实数m 使得AB →+AC →=mAM →
成立,则m 等于( )
A .2
B .3
C .4
D .5 [答案] B
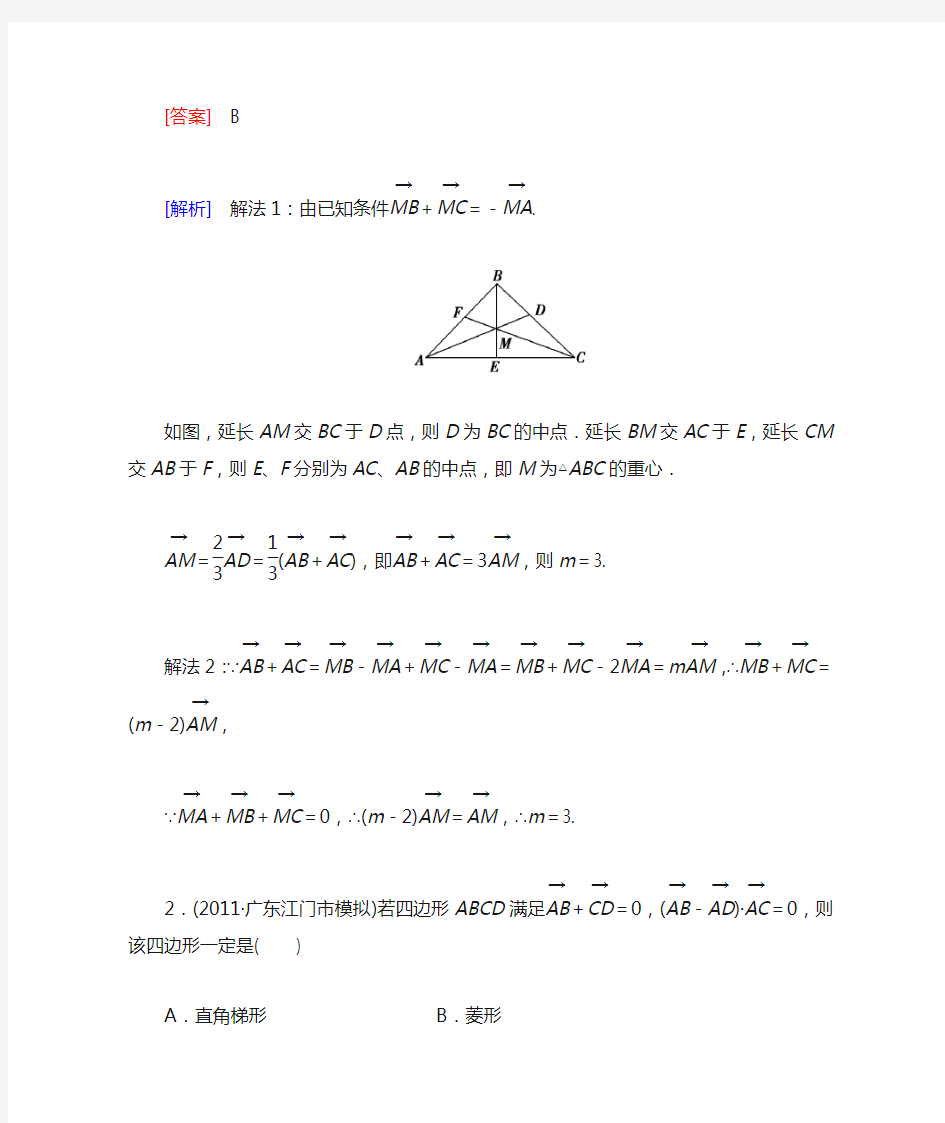
[解析] 解法1:由已知条件MB →+MC →=-MA →
.
如图,延长AM 交BC 于D 点,则D 为BC 的中点.延长BM 交AC 于E ,延长CM 交AB 于F ,则E 、F 分别为AC 、AB 的中点,即M 为△ABC 的重心.
AM →=23AD →=13(AB →+AC →),即AB →+AC →=3AM →
,则m =3.
解法2:∵AB →+AC →=MB →-MA →+MC →-MA →=MB →+MC →-2MA →
=mAM →,∴MB →+MC →=(m -2)AM →,
∵MA →+MB →+MC →=0,∴(m -2)AM →=AM →
,∴m =3.
2.(2011·广东江门市模拟)若四边形ABCD 满足AB →+CD →=0,(AB →
-AD →)·AC →=0,则该四边形一定是( )
A .直角梯形
B .菱形
C .矩形
D .正方形
[答案] B
[解析] 由AB →+CD →=0知,AB →=DC →
,
即AB =CD ,AB ∥CD .∴四边形ABCD 是平行四边形. 又(AB →-AD →)·AC →=0,∴DB →·AC →=0,即AC ⊥BD , 因此四边形ABCD 是菱形,故选B.
3.(文)如图所示,在△ABC 中,BD →=12DC →,AE →=3ED →,若AB →=a ,AC →=b ,则BE →
等于( )
A.13a +13b B .-12a +14b C.12a +14b D .-13a +13b [答案] B
[解析] ∵AE →=3ED →,∴ED →=14AD →
, ∵BD →=12DC →,∴BD →=13BC →,
∴BE →=BD →-ED →=BD →-14AD →=BD →-14(AB →+BD →) =34BD →-14AB →=14BC →-14AB → =14AC →-12AB →=14b -12a .
(理)在平行四边形ABCD 中,AC 与BD 交于点O ,E 是线段OD 的中点,AE 的延长线与CD 交于点F .若AC →=a ,BD →=b ,则AF →
=( )
A.14a +1
2b
B.13a +23b
C.12a +14b
D.23a +13b
[答案] D
[解析] 由条件易知,DF →=13DC →
,
∴AF →=AC →+CF →=a +23CD →=a +13(b -a )=23a +1
3b .故选D. 4.(2011·广东文)已知向量a =(1,2),b =(1,0),c =(3,4).若λ为实数,(a +λb )∥c ,则λ=( )
A.14
B.12 C .1 D .2
[答案] B
[解析] a +λb =(1,2)+λ(1,0)=(1+λ,2),因为(a +λb )∥c ,所以4+4λ-6=0,所以λ=1
2.
5.(文)(2011·惠州模拟)在△ABC 中,已知D 是AB 边上一点,若AD →=2DB →,CD →=λCA →+μCB →,则μ
λ的值为( )
A .1 B.12 C .2 D.13 [答案] C
[解析] CD →=CA →+AD →=CA →+23AB →
=CA →+23(CB →-CA →)=13CA →+23CB →, ∴λ=13,μ=23,∴μλ=2.
(理)(2011·厦门模拟)已知点M 在平面ABC 内,并且对空间任一点O ,OM →=xOA →+12OB →+13OC →
,则x 的值为( )
A .0 B.1
3 C.12 D.16
[答案] D
[解析] ∵x +12+13=1,∴x =1
6.
6.设OA →=e 1,OB →
=e 2,若e 1与e 2不共线,且点P 在线段AB 上,|AP | |P B |=4,如图所示,则OP →
=( )
A.15e 1-25e 2
B.25e 1+15e 2
C.15e 1+45e 2
D.25e 1-15e 2 [答案] C
[解析] AP →=4PB →,∴AB →=AP →+PB →=5PB →
, OP →=OB →+BP →=OB →-15AB →
=OB →-15(OB →-OA →)=45OB →+15OA →=15e 1+45e 2. 7.(文)
(2011·山东济南市调研)如图,在△ABC 中,AN →=13NC →
,P 是BN 上的一点,若AP →=mAB →+211AC →
,则实数m 的值为________.
[答案] 3
11
[解析] (如图)因为AP →=AB →+BP →
=AB →+kBN →=AB →+k (AN →-AB →) =AB →+k (14AC →-AB →) =(1-k )AB →+k 4AC →
, 所以1-k =m ,且k 4=2
11, 解得k =811,m =3
11.
(理)(2011·聊城模拟)在平行四边形ABCD 中,E 和F 分别是边CD 和BC 的中点,若AC →=λAE →+μAF →,其中, λ,μ∈R ,则λ+μ=________.
[答案] 4
3 [解析]
如图,∵四边形ABCD 是平行四边形,且E 、F 分别为CD 、BC
中点.
∴AC →=AD →+AB → =(AE →-DE →)+(AF →-BF →)
=(AE →+AF →)-12(DC →+BC →)=(AE →+AF →)-12AC →, ∴AC →=23(AE →+AF →), ∴λ=μ=23,∴λ+μ=4
3.
8.(文)(2011·合肥模拟)在平面直角坐标系中,O 为坐标原点,A 、B 、C 三点满足OC →=23OA →+13OB →,则|AC →
|
|AB →|
=________.
[答案] 1
3
[解析] ∵OC →=23OA →+13OB →,23+1
3=1, ∴A 、B 、C 三点共线,
∵AC →=OC →-OA →=13OB →-13OA →=13AB →, ∴|AC →||AB →|
=13. (理)(2012·四川文)设a 、b 都是非零向量,下列四个条件中,使
a
|a |=b
|b |
成立的充分条件是( )
A .|a |=|b |且a ∥b
B .a =-b
C .a ∥b
D .a =2b
[答案] D
[解析] 对于A ,|a |=|b |,且a ∥b ,可知a 与b 共线,若反向,则不能满足结论a |a |=b
|b |,对于B 选项,两向量反向,而C 选项a ∥b ,
同样若反向不能满足.而D 项显然满足,故选D.
[点评] 注意到a |a |是与a 同向的单位向量,b
|b |是与b 同向的单位
向量,故a |a |=b
|b |
?a 与b 同向.
9.(2012·东北三省四市联考)在△ABC 中,AB =2AC =2,AB →·AC →
=-1,若AO →=x 1AB →+x 2AC →
(O 是△ABC 的外心),则x 1+x 2的值为________.
[答案] 13
6
[解析] O 为△ABC 的外心,AO →=x 1AB →+x 2AC →,AO →·AB →=x 1AB →·AB →
+x 2AC →·AB →,由向量数量积的几何意义,AO →·AB →=12|AB →|2=2,∴4x 1-x 2=2,①
又AO →·AC →=x 1AB →·AC →+x 2AC →·AC →,∴-x 1+x 2=1
2,② 联立①②,解得x 1=56,x 2=43,∴x 1+x 2=136.
10.(文)如图,在平行四边形ABCD 中,M 、N 分别为DC 、BC 的中点,已知AM →=c ,AN →=d ,试用c 、d 表示AB →、AD →
.
[解析] 解法一:AD →=AM →-DM →=c -12AB →
,① AB →=AN →-BN →=d -12AD →
,② 由①②得AB →=2
3(2d -c ), AD →=2
3(2c -d ).
解法二:设AB →=a ,AD →
=b ,因为M 、N 分别为CD 、BC 的中点,所以BN →=12b ,DM →=1
2a ,于是有:
?????
c =b +12a ,
d =a +12b ,
解得???
??
a =23(2d -c ),
b =23(2
c -
d ),
即AB →=23(2d -c ),AD →=2
3(2c -d ).
(理)如图,在△ABC 中,AM AB =1 3,AN AC =1 4,BN 与CM 交于P 点,且AB →=a ,AC →=b ,用a ,b 表示AP →.
[分析] 由已知条件可求AM →、AN →
,∵BN 与CM 相交于点P ,∴B 、P 、N 共线,C 、P 、M 共线,因此,可以设PN →=λBN →,PM →=μCM →
,利用同一向量的两种a ,b 的线性表示及a 、b 不共线求解;也可以设BP →=λBN →,用a 、b ,λ来表示CP →与CM →,利用CP →与CM →
共线及a 、b 不共线求解.解题方法很多,但无论什么方法,都要抓住“共线”来作文章.
[解析] 由题意知:AM →=13AB →=13a ,AN →=14AC →=14b ,BN →=AN →-AB →
=1
4b -a ,CM →=AM →-AC →=13a -b .
设PN →=λBN →,PM →=μCM →,则PN →=λ4b -λa ,PM →=μ
3a -μb . ∴AP →=AN →-PN →=14b -(λ
4b -λa )=λa +1-λ4b , AP →=AM →-PM →=13a -(μ
3a -μb )=1-μ3
a +μ
b ,
∴λa +1-λ4b =1-μ3a +μb ,而a ,b 不共线.∴λ=1-μ3且1-λ4=
μ.∴λ=311.因此AP →=311a +2
11b .
能力拓展提升
11.(2011·山东青岛质检)在数列{a n }中,a n +1=a n +a (n ∈N *,a 为常数),若平面上的三个不共线的非零向量OA →,OB →,OC →满足OC →=a 1OA →+a 2010OB →,三点A 、B 、C 共线且该直线不过O 点,则S 2010等于( )
A .1005
B .1006
C .2010
D .2012
[答案] A
[解析] 由题意知,a 1+a 2010=1, 又数列{a n }为等差数列,
所以S 2010=a 1+a 2010
2
×2010=1005,故选A. 12.(文)(2011·安徽安庆模拟)已知点P 是△ABC 所在平面内一点,且满足3P A →+5PB →+2PC →
=0,设△ABC 的面积为S ,则△P AC 的面积为( )
A.34S
B.23S
C.12S
D.25S [答案] C [分析]
由系数3+2=5,可将条件式变形为3(P A →+PB →)+2(PB →+PC →
)=0,故可先构造出P A →+PB →与PB →+PC →
,假设P 为P ′点,取AB 、BC 中点M 、N ,则PM →=12(P A →+PB →),PN →=12(PB →+PC →),条件式即转化为PM →
与PN →
的关系.
[解析] 设AB ,BC 的中点分别为M ,N , 则PM →=12(P A →+PB →), PN →=12(PB →+PC →), ∵3P A →+5PB →+2PC →
=0, ∴3(P A →+PB →)=-2(PB →+PC →),
∴3PM →=-2PN →
,即点P 在中位线MN 上, ∴△P AC 的面积为△ABC 面积的一半,故选C.
(理)(2011·东北三校联考)在△ABC 中,点P 是AB 上的一点,且CP →
=23CA →+13CB →,Q 是BC 的中点,AQ 与CP 的交点为M ,又CM →=tCP →,
则t 的值为( )
A.12
B.23
C.34
D.45
[答案] C
[解析] ∵CP →=23CA →+13CB →
,
∴3CP →=2CA →+CB →,即2CP →-2CA →=CB →-CP →,
∴2AP →=PB →,
因此P 为AB 的一个三等分点,如图所示. ∵A ,M ,Q 三点共线, ∴CM →=xCQ →+(1-x )CA → =x 2CB →
+(x -1)AC →(0 ∵CB →=AB →-AC →,∴CM →=x 2AB →+(x 2-1)AC →. ∵CP →=CA →-P A →=-AC →+13AB →, 且CM →=tCP → (0 ∴x 2AB →+(x 2-1)AC →=t (-AC →+13AB →), ∴x 2=t 3且x 2-1=-t ,解得t =3 4,故选C. 13.已知点A (2,3),C (0,1),且AB →=-2BC → ,则点B 的坐标为________. [答案] (-2,-1) [解析] 设点B 的坐标为(x ,y ),则有AB →=(x -2,y -3),BC → =(-x,1-y ),因为AB →=-2BC →, 所以????? x -2=2x ,y -3=-2(1-y ), 解得x =-2,y =-1. 14.已知D 为三角形ABC 的边BC 的中点,点P 满足P A →+BP →+CP →=0,AP →=λPD → ,则实数λ的值为________. [答案] -2 [解析] 如图,∵D 是BC 中点,将△ABC 补成平行四边形ABQC ,则Q 在AD 的延长线上,且|AQ |=2|AD |=2|DP |,∵P A →+BP →+CP →=BA →+CP →=0,∴BA →=PC →, 又BA →=QC → ,∴P 与Q 重合, 又∵AP →=λPD →=-2PD → ,∴λ=-2. 15.(文)已知四点A (x,0)、B (2x,1)、C (2,x )、D (6,2x ). (1)求实数x ,使两向量AB →、CD → 共线. (2)当两向量AB →与CD → 共线时,A 、B 、C 、D 四点是否在同一条直线上? [解析] (1)AB →=(x,1),CD → =(4,x ). ∵AB →∥CD →, ∴x 2-4=0,即x =±2. (2)当x =±2时,AB →∥CD →. 当x =-2时,BC →=(6,-3),AB → =(-2,1), ∴AB →∥BC → .此时A 、B 、C 三点共线, 从而,当x =-2时,A 、B 、C 、D 四点在同一条直线上. 但x =2时,A 、B 、C 、D 四点不共线. (理)(2011·济南模拟)已知△ABC 中,AB →=a ,AC → =b ,对于平面ABC 上任意一点O ,动点P 满足OP →=OA → +λa +λb ,则动点P 的轨迹是什么?其轨迹是否过定点,并说明理由. [解析] 依题意,由OP →=OA → +λa +λb , 得OP →-OA → =λ(a +b ), 即AP →=λ(AB →+AC →). 如图,以AB ,AC 为邻边作平行四边形ABDC ,对角线交于O , 则AP →=λAD →, ∴A 、P 、D 三点共线, 即P 点的轨迹是AD 所在的直线,由图可知P 点轨迹必过△ABC 边BC 的中点(或△ABC 的重心). 16.已知a =(2x -y +1,x +y -2),b =(2,-2). (1)当x 、y 为何值时,a 与b 共线? (2)是否存在实数x 、y ,使得a ⊥b ,且|a |=|b |?若存在,求出xy 的值;若不存在,说明理由. [解析] (1)∵a 与b 共线, ∴存在非零实数λ使得a =λb , ∴????? 2x -y +1=2λ, x +y -2=-2λ, ???? x =1 3,y ∈R . (2)由a ⊥b ?(2x -y +1)×2+(x +y -2)×(-2)=0?x -2y +3=0.① 由|a |=|b |?(2x -y +1)2+(x +y -2)2=8.② 由①②解得??? ?? x =-1,y =1, 或????? x =53, y =73. ∴xy =-1或xy =35 9. 1.设平面内有四边形ABCD 和点O ,若OA →=a ,OB →=b ,OC → =c ,OD → =d ,且a +c =b +d ,则四边形ABCD 为( ) A .菱形 B .梯形 C .矩形 D .平行四边形 [答案] D [解析] 解法一:设AC 的中点为G ,则OB →+OD → =b +d =a +c =OA →+OC →=2OG → ,∴G 为BD 的中点,∴四边形ABCD 的两对角线互相平分,∴四边形ABCD 为平行四边形. 解法二:AB →=OB →-OA → =b -a , CD →=OD →-OC →=d -c =-(b -a )=-AB →, ∴AB 綊CD ,∴四边形ABCD 为平行四边形. 2.(2011·银川模拟)已知a 、b 是两个不共线的向量,AB → =λa +b ,AC → =a +μb (λ,μ∈R ),那么A 、B 、C 三点共线的充要条件是( ) A .λ+μ=2 B .λ-μ=1 C .λμ=-1 D .λμ=1 [答案] D [解析] ∵A 、B 、C 三点共线,∴AB →与AC → 共线, ∴存在t ∈R ,使AB →=tAC → , ∴λa +b =t (a +μb )=t a +tμb , ∵a ,b 不共线,∴? ???? λ=t , 1=tμ,即λμ=1. 3.设两个非零向量a 与b 不共线, (1)若AB →=a +b ,BC →=2a +8b ,CD → =3(a -b ).求证:A 、B 、D 三点共线; (2)试确定实数k ,使k a +b 和a +k b 共线. [解析] (1)证明:∵AB →=a +b ,BC →=2a +8b ,CD → =3(a -b ), ∴BD →=BC →+CD → =2a +8b +3(a -b ) =5(a +b )=5AB → . ∴AB →、BD → 共线, 又它们有公共点B ,∴A 、B 、D 三点共线. (2)∵k a +b 与a +k b 共线, ∴存在实数λ,使k a +b =λ(a +k b ), ∴(k -λ)a =(λk -1)b . ∵a 、b 是不共线的两个非零向量, ∴k -λ=λk -1=0,∴k 2-1=0.∴k =±1. 4.已知点O (0,0)、A (1,2)、B (4,5),向量OP →=OA →+tAB →. (1)t 为何值时,点P 在x 轴上? (2)t 为何值时,点P 在第二象限? (3)四边形ABPO 能否为平行四边形?若能,求出t 的值;若不能,说明理由; (4)求点P 的轨迹方程. [解析] ∵OP →=OA →+tAB → =(1,2)+t (3,3) =(1+3t,2+3t ), ∴P (1+3t,2+3t ). (1)∵P 在x 轴上,∴2+3t =0即t =-2 3. (2)由题意得? ???? 1+3t <0,2+3t >0,∴-23 =(1+3t,2+3t ). 若四边形ABPO 为平行四边形,则AB →=OP → , ∴? ???? 1+3t =3,2+3t =3,而上述方程组无解, ∴四边形ABPO 不可能为平行四边形. (4)∵OP → =(1+3t,2+3t ), 教学过程 课堂导入 以前台胞春节期间来大陆探亲,乘飞机先从台北到香港,再从香港到上海.20XX年7月4日,两岸直航包机启航.若台北到香港的位移用向量a表示,香港到上海的位移用向量b表示,台北到上海的位移用向量c表示.想一想,向量a、b、c有何关系? 复习预习 1.我们已经学习过位移、速度、力等,你能总结出它们的特点吗?特点为________________________________. 2.在学习三角函数线时,我们已经学习过有向线段了,你还记得吗? 所谓有向线段就是________________________,三角函数线都是_____________. 知识讲解 考点1 向量的有关概念 考点2 向量的线性运算 向量运算定义法则(或几何意义)运算律 加法求两个向量和的运算(1)交换律:a+b=b+a (2)结合律:(a+b)+c=a +(b+c) 减法求a与b的相反向量-b的 和的运算叫做a与b的差 a-b=a+(-b) 数乘求实数λ与向量a的积的运 算 (1)|λa|=|λ||a| (2)当λ>0时,λa与a的方向相同; 当λ<0时,λa与a的方向相反;当λ =0时,λa=0 λ(μa)=(λμ) a (λ+μ)a=λa+μa λ(a+b)=λa+λb 考点3 共线向量定理 向量a(a≠0)与b共线的充要条件是存在唯一一个实数λ,使得b=λa. 例题精析 【例题1】 【题干】设a0为单位向量,①若a为平面内的某个向量,则a=|a|a0;②若a与a0平行,则a=|a|a0; ③若a与a0平行且|a|=1,则a=a0.上述命题中,假命题的个数是() A.0 B.1 C.2 D.3 【答案】D 【解析】向量是既有大小又有方向的量,a与|a|a0的模相同,但方向不一定相同,故①是假命题;若a与a0平行,则a与a0的方向有两种情况:一是同向,二是反向,反向时a=-|a|a0,故②③也是假命题.综上所述,假命题的个数是3. 【例题2】 【题干】如图,在△OAB中,延长BA到C,使AC=BA,在OB上取点D,使DB=13OB.设OA=a,OB=b,用a,b表示向量OC,DC. 平面向量的概念与线性运算知识点 一.平面向量的有关概念 1.向量:既有大小,又有方向的量. 2.数量:只有大小,没有方向的量. 3.有向线段的三要素:起点、方向、长度. 4.零向量:长度为0的向量. 5.单位向量:长度等于1个单位的向量. 6.平行向量(共线向量):方向相同或相反的非零向量.零向量与任一向量平行. 注:任一组平平行向量都可以平移到同一直线上 7.相等向量:长度相等且方向相同的向量. 8.相反向量:长度相等且方向相反的向量 二.向量的表示法 1.字母表示法:如:a ,AB 等 2.几何表示法:用一条有向线段表示向量 3.代数表示法:在平面直角坐标系中,设向量OA 的起点O是坐标原点,终点坐标是(x ,y ),则(x ,y )称为OA 的坐标,记作:OA =(x ,y ) 三.向量的运算 1.向量加法运算: ⑴三角形法则的特点:首尾相连. ⑵平行四边形法则的特点:共起点. ⑶三角形不等式:a b a b a b -≤+≤+. ⑷运算性质:①交换律:a b b a +=+;②结合律:()()a b c a b c ++=++; ③00a a a +=+=. b a C B A a b C C -=A -AB =B ⑸坐标运算:设()11,a x y =,()22,b x y =,则()1212,a b x x y y +=++. 2.向量减法运算: ⑴三角形法则的特点:共起点,连终点,方向指向被减向量. ⑵坐标运算:设()11,a x y =,()22,b x y =,则()1212,a b x x y y -=--. 设A 、B 两点的坐标分别为()11,x y ,()22,x y ,则()1212,x x y y AB =--. 3.向量数乘运算: ⑴实数λ与向量a 的积是一个向量的运算叫做向量的数乘,记作a λ. ①a a λλ=; ②当0λ>时,a λ的方向与a 的方向相同;当0λ<时,a λ的方向与a 的方向相反;当0λ=时,0a λ=. ⑵运算律:①()()a a λμλμ=;②()a a a λμλμ+=+;③()a b a b λλλ+=+. ⑶坐标运算:设(),a x y =,则()(),,a x y x y λλλλ==. 4.向量共线定理: 向量()0a a ≠与b 共线,当且仅当有唯一一个实数λ,使b a λ=. 设()11,a x y =,()22,b x y =,其中0b ≠,则当且仅当12210x y x y -=时,向量a 、() 0b b ≠共线. 四.跟踪训练 1.=++++( ) A . B .0 C . D . 2.给出命题 (1)零向量的长度为零,方向是任意的.(2)若a ,b 都是单位向量,则a =b . (3)向量AB 与向量BA 相等.(4)若非零向量AB 与CD 是共线向量,则A ,B ,C ,D 四点共线. 以上命题中,正确命题序号是 A.(1) B.(2) C.(1)和(3) D.(1)和(4) 3.在四边形ABCD 中,如果0AB CD =,AB DC =,那么四边形ABCD 的形状是 A.矩形 B.菱形 C.正方形 D.直角梯形 4.如图,在△ABC 中,AD 、BE 、CF 分别是BC 、CA 、AB 上的中线,它们交于点 G ,则下列各等式中不正确的是 用心 爱心 专心 - 1 - 课题:3.1.1空间向量的线性运算 设计人: 审核人: 班级: 组名: 姓名: 日期: 典型例题 例1.已知平行六面体''''D C B A ABCD -(如图),以图中一对顶点构造向量,使 它们分别等于: ; ⑴BC AB + ;⑵'AA AD AB ++ '2 1CC AD AB + +⑶ .⑷ )'(3 1AA AD AB ++ (5)D D AB BC → → → '-+ 1(6)()2 A B A D D D B C → → → → '++ - (7)AB BC C C C D D A → → → → → '''''++++ 例3.已知平行六面ABCD-A1B1C1D1 ,求满足下列各式的x 的值。 11111 )3(2 )2(AC x AD AB AC AC x BD AD =++=-x C D A AB =++1111 )1( 1 C C ' D ' A ' B ' D A )(21,,.2→ →→+=BC AD MN CD AB ABCD N M 求证:的中点, 的棱分别是四面体例D C B A N M 用心 爱心 专心 - 2 - 四.当堂检测 1.在三棱柱111ABC A B C -中,设M 、N 分别为1,BB AC 的中点,则MN 等于( ) A .11()2A C A B B B ++ B .111111()2 B A B C C C ++ C .11()2A C C B B B ++ D .11()2 B B B A B C -- 2.若A 、B 、C 、D 为空间四个不同的点,则下列各式为零向量的是 ( )①22AB BC CD DC +++ ②2233AB BC CD DA AC ++++ ③AB CA BD ++ ④AB CB CD AD -+- A .①② B .②③ C .②④ D .①④ 3.在空间四边形ABCD 中,点M 、G 分别是BC 、CD 边的中点,化简 4. 如图,在三棱柱111C B A ABC -中,M 是1BB 的中点, 化简下列各式,并在图中标出化简得到的向量: (1)1 BA CB +; (2)1 21AA CB AC + +; (3)CB AC AA --1 五.课后练习 1.四棱锥P-ABCD 的底面ABCD 为平行四边形,,,AB a AD b AP c === ,E 为PC 中点, 则向量C E = _______________________; 2.已知长方体 1111 ABC D A B C D -,化简向量表达式 1CB AC AD AA +++= _____________; 3. 1(1) ()2 1(2) ()2 AB BC BD AG AB AC ++-+ a b AD c a ,b,c C D ,. ABC D AB BC AC BD == 空间四边形中,,=,,试用来表示, 2.2《平面向量的线性运算》教学设计 【教学目标】 1.掌握向量的加、减法运算,并理解其几何意义; 2.会用向量加、减的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力; 3.通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法; 4.掌握实数与向量的积的定义以及实数与向量的积的三条运算律,会利用实数与向量的积的运算律进行有关的计算; 5.理解两个向量平行的充要条件,能根据条件判断两个向量是否平行; 6.通过对实数与向量的积的学习培养学生的观察、分析、归纳、抽象的思维能力,了解事物运动变化的辩证思想. 【导入新课】 设置情景: 1、 复习:向量的定义以及有关概念 强调:向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此,我们研究的向量是与起点无关的自由向量,即任何向量可以在不改变它的方向和大小的前提下,移到任何位置 2、 情景设置: (1)某人从A 到B ,再从B 按原方向到C , 则两次的位移和:AC BC AB =+ (2)若上题改为从A 到B ,再从B 按反方向到C , 则两次的位移和:=+ (3)某车从A 到B ,再从B 改变方向到C , 则两次的位移和:=+ (4)船速为AB ,水速为,则两速度和:AC =+ 新授课阶段 一、向量的加法 A B C A C A B C O A a a a b b b 1.向量的加法:求两个向量和的运算,叫做向量的加法. 2.三角形法则(“首尾相接,首尾 连”) 如图,已知向量a 、b.在平面内任取一点A ,作AB =a ,BC =b,则向量AC 叫做a 与b的和,记作a +b,即 a +bAC BC AB =+=,规定: a + 0-= 0 + a. 探究:(1)两相向量的和仍是一个向量; (2)当向量a 与b 不共线时,a +b 的方向不同向,且|a +b |<|a |+|b |; (3)当a 与b 同向时,则a +b 、a 、b 同向,且|a +b |=|a |+|b |,当a 与b 反向时,若|a |>|b |,则a +b 的方向与a 相同,且 |a +b |=|a |-|b |;若|a |<|b |,则a +b 的方向与b 相同,且|a +b|=|b |-|a |. (4)“向量平移”(自由向量):使前一个向量的终点为后一个向量的起点,可以推广到n 个向量连加. 例1 已知向量a 、b ,求作向量a +b . 作法:在平面内取一点,作a OA = b AB =,则b a OB +=. 4.加法的交换律和平行四边形法则 问题:上题中b +a 的结果与a +b 是否相同? 验证结果相同 从而得到:1)向量加法的平行四边形法则(对于两个向量共线不适应); A B C a +b a +b a a b b a b b aa 向量的加法;向量的减法;向量的数乘. 教学目标 通过经历向量加法的探究,掌握向量加法概念,结合物理学实际理解向量加法的意义。能 熟练地掌握向量加法的平行四边形法则和三角形法则, 并能作出已知两向量的和向量。 通 过探究活动,掌握向量减法概念,理解两个向量的减法就是转化为加法来进行,掌握相反 向量。 教学重点 向量的加减法的运算。 〔 _____________ ! 教学难点 教学过程 」、导入 高考对本内容的考查主要以选择题或者是填空题的形式来出题, 一般难度不 大,属于简单题 二、知识讲解 I 考)向量加量加三法形法则 在定义中所给出的求象量和的方法就是向量加法的三角形法则。 运用这一法则时 要特别注意“首尾相接”,即第二个向量要以第一个向量的终点为起点, 则由第 一个向量的起点指向第二个向量的终点的向量即为和向量。 0位移的合成可以看 作向量加法三角形法则的物理模型。 知识点 向量的加减法的几何意义 。 【知识导图】 (2)平行四边形法则 以同一点0为起点的两个已知向量 A.B为邻边作平行四边形,则以0为起点的对角线0C就是a与b 的和。我们把这种作两个向量和的方法叫做向量加法的平行四边形法则。 由于方向反转两次仍法法原来的方向,因此a和-:互为相反向量。 于是-(-a)=a。 我们规定,零向量的相反向量仍是零向量. ____________ __ 一「 4 ■+ , 4 4 任一向量与其相反向量的和是零向量,即 a (-a)二(-a)■ a =0。 TH 4 4 H ^4^4 所以,如果a,b是互为相反的向量,那么a二-b,b二-a,a ? b =0。 考点3实数与向量的积的运算律 设■, ^为实数,那么 ⑴,(七)=(」i)a; (2)(I 丄)a 虫;」a ; (3)(a b)八a ■ b. ■.斗、- ,4 _斗屮.4 特别地,我们有(- ’)a = ,a)二’(-a),,(a-b)二’a-'b。 ■H 屮 4 . 向量共线的等价条件是:如果a(a = 0)与b共线,那么有且只有一个实数?,使 ■I J b —■ a。 二、例题精析 类型一平面向量的坐标表示 例题知边长为1的正方形ABCD 中, AB与x轴正半轴成30°角.求点B和点D的坐标和 uuiv uuv AB与AD的坐标. 平面向量 一、向量的相关概念 1、向量的概念:既有大小又有方向的量,注意向量和数量的区别。向量常用有向线段来表示,注意不能说向量就是有向线段(向量可以平移)。如已知A (1,2),B (4,2),则把向量AB u u u r 按向量a r =(-1,3)平移后得到的向量是_____(3,0) 2、向量的表示方法:用有向线段来表示向量. 起点在前,终点在后。有向线段的长度表示向量的大小,用_____箭头所指的方向____表示向量的方向.用字母a ,b ,…或用AB ,BC ,…表示 (1) 模:向量的长度叫向量的模,记作|a |或|AB |. (2)零向量:长度为0的向量叫零向量,记作:0,注意零向量的方向是任意的; (3)单位向量:长度为一个单位长度的向量叫做单位向量(与AB u u u r 共线的单位向量是|| AB AB ±u u u r u u u r ); (4)相等向量:长度相等且方向相同的两个向量叫相等向量,相等向量有传递性。 (5)平行向量(也叫共线向量):方向相同或相反的非零向量a 、b 叫做平行向量,记作:a ∥b ,规定零向量和任何向量平行。提醒:①相等向量一定是共线向量,但共线向量不一定相等;②两个向量平行与与两条直线平行是不同的两个概念:两个向量平行包含两个向量共线, 但两条直线平行不包含两条直线重合;③平行向量无传递性!(因为有0r );④三点A B C 、、共线? AB AC u u u r u u u r 、共线; (6)相反向量:长度相等方向相反的向量叫做相反向量。a 的相反向量是-a 。零向量的相反向量时零向量。 二、向量的线性运算 1.向量的加法: (1)定义:求两个向量和的运算,叫做向量的加法. 如图,已知向量a ,b ,在平面内任取一点A ,作AB =u u u r a ,BC =u u u r b ,则向量AC 叫做a 与b 的和,记作a+b ,即 a+b AB BC AC =+=u u u r u u u r u u u r 。AB BC CD DE AE +++=u u u r u u u r u u u r u u u r u u u r 特殊情况:a b a b a+b b a a+ b (1)平行四边形法则三角形法则 C B D C B A 对于零向量与任一向量a ,有 a 00+=+ a = a (2)法则:____三角形法则_______,_____平行四边形法则______ (3)运算律:____ a +b =b +a ;_______,____(a +b )+c =a +(b +c )._______ 当a 、b 不共线时, 空间向量及其线性运算 学习目标: 1.运用类比方法,经历向量及其运算由平面向空间推广的过程; 2.了解空间向量的概念,掌握空间向量的线性运算及其性质; 3.理解空间向量共线的充要条件。 学习重点:空间向量的概念、空间向量的线性运算及其性质; 学习难点:空间向量的线性运算及其性质。 学习过程: 一、创设情景 1、平面向量的概念及其运算法则; 2、物体的受力情况分析(如右图)。 二、建构数学 1.空间向量的概念 在空间,我们把具有大小和方向的量叫做向量。 注:(1)空间的一个平移就是一个向量。 (2)向量一般用有向线段表示,同向等长的有向线段表示同一或相等的向量。 (3)空间的两个向量可用同一平面内的两条有向线段来表示。 2.空间向量的运算 定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下(如图) b a AB OA OB +=+= b a -=-= )(R a ∈=λλ 运算律: (1)加法交换律:a b b a +=+ (2)加法结合律:)()(c b a c b a ++=++ (3)数乘分配律:b a b a λλλ+=+)( 3.平行六面体 O 平行四边形ABCD 平移向量a 到D C B A ''''的轨迹所形成的几何体,叫做平行六面体,并 记作:ABCD -D C B A '''',它的六个面都是平行四边形,每个面的边叫做平行六面体的棱。 4.共线向量 与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向 量叫做共线向量或平行向量。a 平行于b 记作b a //。 当我们说向量a 、b 共线(或a //b )时,表示a 、b 的有向线段所在的直线可能是同一 直线,也可能是平行直线。 5.共线向量定理及其推论 共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 的充要条件是存在实数λ,使a =λb 。 推论:如果l 为经过已知点A 且平行于已知非零向量a 的直线,那么对于任意一点O , 点P 在直线l 上的充要条件是存在实数t 满足等式 t OA OP +=a ,其中向量a 叫做直线l 的 方向向量。 三、数学运用 1、如图,在三棱柱111C B A ABC -中,M 是1BB 的中点, 化简下列各式,并在图中标出化简得到的向量: (1)1BA CB +; (2)12 1 AA + +; (3)CB AC AA --1。 解:(1)11CA BA =+; (2)AM AA CB AC =+ +12 1 ; (3)11BA CB AC AA =--。 课 题:空间向量及其线性运算 教学目标: 1.运用类比方法,经历向量及其运算由平面向空间推广的过程; 2.了解空间向量的概念,掌握空间向量的线性运算及其性质; 3.理解空间向量共线的充要条件 教学重点:空间向量的概念、空间向量的线性运算及其性质; 教学难点:空间向量的线性运算及其性质。 教学过程: 一、创设情景 1、蚂蚁爬行的问题引入为什么要研究空间向量. 2、平面向量的概念及其运算法则; 二、建构数学 1.空间向量的概念: 在空间,我们把具有大小和方向的量叫做向量注:⑴空间的一个平移就是一个向量 ⑵向量一般用有向线段表示同向等长的有向线段表示同一或相等的向量 ⑶空间的两个向量可用同一平面内的两条有向线段来表示 2.空间向量的运算 定义:与平面向量运算一样,空间向量的加法、减法与数乘向量运算如下(如图) b a AB OA OB +=+= b a -=-= )(R a ∈=λλ 运算律: ⑴加法交换律:a b b a +=+ ⑵加法结合律:)()(c b a c b a ++=++ ⑶数乘分配律:b a b a λλλ+=+)( 3.平行六面体: 平行四边形ABCD 平移向量a 到D C B A ''''的轨迹所形成的几何体,叫做平行六面体,并记作:ABCD -D C B A '''',它的六个面都是平行四边形,每个面的边叫做平行六面体的棱。 4.共线向量 与平面向量一样,如果表示空间向量的有向线段所在的直线互相平行或重合,则这些向 量叫做共线向量或平行向量.a 平行于b 记作b a //. 当我们说向量a 、b 共线(或a //b )时,表示a 、b 的有向线段所在的直线可能是同 一直线,也可能是平行直线. 5.共线向量定理: 共线向量定理:空间任意两个向量a 、b (b ≠0 ),a //b 的充要条件是存在实数λ, 《平面向量的线性运算》复习教学设计 高中数学北师大版 西安交通大学第二附属中学 刘正伟 §5.1平面向量的线性运算 【教学目标】 知识与能力;过程与方法;情感、态度、价值观; 1.掌握向量加法,减法的运算,并理解其几何意义; 2.掌握向量数乘向量的运算及其几何意义,理解向量共线的充要条件; 了解向量共线的含义,理解向量共线判定和性质定理。 【教学重点、难点】 重点:理解并掌握向量的线性运算及向量共线的充要条件; 难点:向量的线性运算及向量共线的充要条件的应用。 【教具准备】 多媒体课件 【教学方法】 启发引导式;讲练结合 【教学设计】 (一).复习导入 问题:前面我们已经复习了的向量的有关概念,知道了向量是既有大小又有方向的量,物理中既有大小又有方向的量? 学生:速度,加速度,位移,力 力可以合成也可以分解,那么向量怎么运算 那么我们今天一起回顾向量的线性运算——板书课题 (二)知识要点 1.向量的线性运算 a 是一个非零向量,若存在一个实数λ.,使得 b =λa ,则向量b 与非零向量a 共线. 3.【知识拓展】 1.一般地,首尾顺次相接的多个向量的和等于从第一个向量起点指向最后一个向量终 点的向量,即A 1A 2→+A 2A 3→+A 3A 4→+…+A n -1A n ——→=A 1A n →,特别地,一个封闭图形,首尾连 接而成的向量和为零向量. 2.若P 为线段AB 的中点,O 为平面内任一点,则OP →=12 (OA →+OB →). 3.OA →=λOB →+μOC →(λ,μ为实数),点A ,B ,C 共线 λ+μ=1. 题型一 平面向量的线性运算 命题点1 向量的线性运算 例2 (1)在△ABC 中,AB →=c ,AC →=b ,若点D 满足BD →=2DC →,则AD →等于( ) 第三章空间向量与立体几何 §3.1空间向量及其运算 3.1.1 空间向量及其加减运算 师:这节课我们学习空间向量及其加减运算,请看学习目标。 学习目标:⒈理解空间向量的概念,掌握其表示方法; ⒉会用图形说明空间向量加法、减法、数乘向量及它们的运算律; ⒊能用空间向量的运算意义及运算律解决简单的立体几何中的问题. 师:在必修四第二章《平面向量》中,我们学习了平面向量的一些知识,现在我们一起来复习。(不要翻书) (在黑板或背投上呈现或边说边写) 1、在平面中,我们把具有__________________的量叫做平面向量; 2、平面向量的表示方法: ①几何表示法:_________________________ ②字母表示法:_________________________ (注意:向量手写体一定要带箭头) 3、平面向量的模表示_________________,记作____________ 4、一些特殊的平面向量: ①零向量:__________________________,记作___(零向量的方向具有任意性) ②单位向量:______________________________ (强调:都只限制了大小,不确定方向) ③相等向量:____________________________ ④相反向量:____________________________ 5、平面向量的加法: 6、平面向量的减法: 7、平面向量的数乘:实数λ与向量a的积是一个向量,记作λa,其长度和 方向规定如下: (1)|λa|=|λ||a| (2)当λ>0时,λa与a同向; 当λ<0时,λa与a反向; 当λ=0时,λa=0. 8、向量加法和数乘向量满足以下运算律 加法交换律:a+b=b+a 加法结合律:(a+b)+c=a+(b+c) 数乘分配律:λ(a+b)=λa+λb 数乘结合律:λ(aμ)=a) (λμ [师]:刚才我们复习了平面向量,那空间向量会是怎样,与平面向量有怎样的区别和联系呢?请同学们阅读书P84-P86.(5分钟) [师]:对比平面向量,我们得到空间向量的相关概念。(在刚复习的黑板或幻灯片上,只需将平面改成空间) [师]:空间向量与平面向量有什么联系? [生]:向量在空间中是可以平移的.空间任意两个向量都可以用同一平面内的两条有向线段表示.因此我们说空间任意两个向量是共面的.所以凡涉及 空间两个向量的问题,平面向量中有关结论仍适用于它们。 适用 (2)平行四边形法则 以同一点 O 为起点的两个已知向量 A.B 为邻边作平行四边形,则以 O 为起点的 对角线 OC 就是 a 与 b 的和。我们把这种作两个向量和的方法叫做向量加法的平 行四边形法则。 平面向量的线性运算 学习过程 知识点一:向量的加法 (1)定义已知非零向量,a b r r ,在平面内任取一点A ,作AB =a r ,BC =b r ,则向量AC 叫做a r 与b r 的和,记作a b +r r ,即a b +r r =AB +BC =AC . 求两个向量和的运算,叫做叫向量的加法.这种求向量和的方法,称为向量加法的三角形法则. 说明:①运用向量加法的三角形法则时,要特别注意“首尾相接”,即第二个向量要以第一个向量的终点为起点,则由第一个向量的起点指向第二个向量终点 的向量即为和向量. ②两个向量的和仍然是一个向量,其大小、方向可以由三角形法则确定. ③位移的合成可以看作向量加法三角形法则的物理模型. (2)向量加法的平行四边形法则 以点O 为起点作向量a OA = ,OB b =uu u r r ,以OA,OB 为邻边作OACB Y ,则以O 为起点的对角线所在向量OC uuu r 就是,a b r r 的和,记作a b +r r =OC uuu r 。 说明:①三角形法则适合于首尾相接的两向量求和,而平行四边形法则适合于同起点的两向量求和,但两共线向量求和时,则三角形法则较为合适. ②力的合成可以看作向量加法平行四边形法则的物理模型. ③对于零向量与任一向量00a a a a +=+=r r r r r r , (3)特殊位置关系的两向量的和 ①当向量a 与b 不共线时,a +b 的方向不同向,且|a +b |<|a |+|b |; ②当a 与b 同向时,则a +b 、a 、b 同向,且|a +b |=|a |+|b |, ③当a 与b 反向时,若|a |>|b |,则a +b 的方向与a 相同,且|a +b |=|a |-|b |;若|a |<|b |,则a +b 的方向与b 相同,且|a +b|=|b |-|a |. (4)向量加法的运算律 ①向量加法的交换律:a +b =b +a ②向量加法的结合律:(a +b ) +c =a + (b +c ) 知识点二:向量的减法 高中数学必修4《平面向量线性运算》教案 High school mathematics compulsory 4 "plane vector linear op eration" teaching plan 高中数学必修4《平面向量线性运算》教案前言:数学是研究数量、结构、变化、空间以及信息等概念的一门学科,从某种角度看属于形式科学的一种,在人类历史发展和社会生活中,数学发挥着不可替代的作用,是学习和研究现代科学技术必不可少的基本工具。本教案根据数学课程标准的要求和教学对象的特点,将教学诸要素有序安排,确定合适的教学方案的设想和计划、并以启迪发展学生智力为根本目的。便于学习和使用,本文档下载后内容可按需编辑修改及打印。 教学准备 教学目标 1、掌握向量的加法运算,并理解其几何意义; 2、会用向量加法的三角形法则和平行四边形法则作两个向量的和向量,培养数形结合解决问题的能力; 3、通过将向量运算与熟悉的数的运算进行类比,使学生掌握向量加法运算的交换律和结合律,并会用它们进行向量计算,渗透类比的数学方法; 教学重难点 教学重点:会用向量加法的三角形法则和平行四边形法则作两个向量的和向量. 教学难点:理解向量加法的定义. 教学工具 投影仪 教学过程 一、设置情景: 1、复习:向量的定义以及有关概念 强调:向量是既有大小又有方向的量.长度相等、方向相同的向量相等.因此,我们研究的向量是与起点无关的自由向量,即任何向量可以在不改变它的方向和大小的前提下,移到任何位置 从而,多个向量的加法运算可以按照任意的次序、任意的组合来进行. 三、应用举例: 例二(P94—95)略 练习:P95 四、小结 1、向量加法的几何意义; 2、交换律和结合律; §平面向量的线性运算 重难点:灵活运用向量加法的三角形法则和平行四边形法则解决向量加法的问题,利用交换律和结合律进行向量运算;灵活运用三角形法则和平行四边形法则作两个向量的差,以及求两个向量的差的问题;理解实数与向量的积的定义掌握实数与向量的积的运算律体会两向量共线的充要条件. 考纲要求:①掌握向量加法,减法的运算,并理解其几何意义. ②掌握向量数乘的运算及其意义。理解两个向量共线的含义. ③了解向量线性运算的性质及其几何意义. 经典例题:如图,已知点,,D E F 分别是ABC ?三边,,AB BC CA 的中点, 求证:0EA FB DC ++=. 当堂练习: 1.a 、b 为非零向量,且+=+||||||a b a b ,则 ( ) A .a 与b 方向相同 B .a =b C .a =-b D .a 与b 方向相反 2.设+++=()()AB CD BC DA a ,而b 是一非零向量,则下列各结论:①//a b ;② +=a b a ;③+=a b b ;④+<+a b a b ,其中正确的是 ( ) A .①② B .③④ C .②④ D .①③ 3.3.在△ABC 中,D 、E 、F 分别BC 、CA 、AB 的中点,点M 是△ABC 的重心,则 MC MB MA -+等于 ( ) A .O B .MD 4 C .MF 4 D .M E 4 4.已知向量b a 与反向,下列等式中成立的是 ( ) A .||||||b a b a -=- B .||||b a b a -=+ C .||||||b a b a -=+ D .||||||b a b a +=+ 5.若a b c =+化简3(2)2(3)2()a b b c a b +-+-+ ( ) A .a B .b C .c D . 以上都不对 6.已知四边形ABCD 是菱形,点P 在对角线AC 上(不包括端点A 、C ),则AP =( ) A .().(0,1)AB AD λλ+∈ B .2 ().(0, )AB BC λλ+∈ C . ().(0,1)AB AD λλ-∈ D . 2().(0, )2 AB BC λλ-∈ 7.已知==||||3OA a ,==||||3OB b ,∠AOB=60?,则+=||a b __________。 平面向量的线性运算教案 海伊教育学科教师辅导讲义 学员编号:年级:九年级课时数: 学员姓名:张鸿敬辅导科目:数学学科教师:高老师 课 题 平面向量的线性运算 授课时间:2013 年10月18日备课时间:2013 年10月16日 教学目 标1.通过经历向量加法的探究,掌握向量加法概念,结合物理学实际理解向量加法的意义。能熟练地掌握向量加法的平行四边形法则和三角形法则,并能作出已知两向量的和向量。 2.在应用活动中,理解向量加法满足交换律和结合律及表述两个运算律的几何意义。掌握有特殊位置关系的两个向量的和,比如共线向量、共起点向量、共终点向量等。 3.通过本节内容的学习,认识事物之间的相互转化,培养数学应用意识,体会数学在生活中的作用。培养类比、迁移、分类、归纳等能力。 4.通过探究活动,掌握向量减法概念,理解两个向量的减法就是转化为加法来进行,掌握相反向量。 5.学会分析问题和创造地解决问题。能熟练地掌握用三角形法则和平行四边形法则作出两向量的差向量。 6.通过经历探究数乘运算法则及几何意义的过程,掌握实数与向量积的定义,理解实数与向量积的几何意义,掌握实数与向量的积的运算律。 重点、难 点1.向量加法的运算及其几何意义。 2.对向量加法法则定义的理解。 3.向量的减法运算及其几何意义。 4.对向量减法定义的理解。 5.实数与向量积的意义。 6.实数与向量积的运算律。 7.两个向量共线的等价条件及其运用。 8.对向量共线的等价条件的理解运用。 授课方 法 联想质疑——交流研讨——归纳总结— —实践提高 教学过程 一、情景设置(知识导入) 二、探索研究 【知识点总结与归纳】 一、求若干个向量的和的模(或最值)的问题通常按下列步骤进行: (1)寻找或构造平行四边形,找出所求向量的关系式; (2)用已知长度的向量表示待求向量的模,有时还要利用模的重要性质。 二、1. 向量的加法定义 向量加法的定义:如图3,已知非零向量A.b,在平面内任取一点A,作AB=a,BC=b,则向量AC叫做a与b的和,记作a+b,即a+b=AB+BC=AC。 求两个向量和的运算,叫做向量的加法。 2. 向量加法的法则: (1)向量加法的三角形法则 在定义中所给出的求象量和的方法就是向量加法的三角形法则。运用这一法则时要特 向量的线性运算经典测试题及答案解析 一、选择题 1.若2a b c +=r r ,3a b c -=r r ,而且c r ≠0,a r 与r b 是( ) A .a r 与r b 是相等向量 B .a r 与r b 是平行向量 C .a r 与r b 方向相同,长度不等 D .a r 与r b 方向相反,长度相等 【答案】B 【解析】 【分析】 根据已知条件求得52a c =r r ,1b 2 c =-r r ,由此确定a r 与b r 位置和数量关系. 【详解】 解:由2a b c +=r r ,3a b c -=r r ,而且c r ≠0,得到:52a c =r r ,1b 2 c =-r r , 所以a r 与b r 方向相反,且|a r |=5|b r |. 观察选项,只有选项B 符合题意. 故选:B . 【点睛】 本题考查了平面向量的知识,属于基础题,注意对平面向量这一基础概念的熟练掌握. 2.下列命题中,真命题的个数为( ) ①方向相同 ②方向相反 ③有相等的模 ④ 方向相同 A .0 B .1 C .2 D .3 【答案】C 【解析】 【分析】 直接利用向量共线的基本性质逐一核对四个命题得答案. 【详解】 解:对于①,若,则 方向相同,①正确; 对于②,若,则方向相反,②正确; 对于③,若,则方向相反,但 的模不一定,③错误; 对于④,若 ,则 能推出 的方向相同,但 的方向相同,得到 ④错误. 所以正确命题的个数是2个,故选:C. 【点睛】 本题考查命题的真假判断与应用,考查了向量共线的基本性质,是基础题. 3.如图,已知向量a r ,b r ,c r ,那么下列结论正确的是( ) A .a b c +=r r r B .b c a +=r r r C .a c b +=r r r D .a c b +=-r r r 【答案】D 【解析】 【分析】 【详解】 由平行四边形法则,即可求得: 解:∵CA AB CB +=u u u r u u u r u u u r , 即a c b +=-r r r 故选D . 4.下列判断正确的是( ) A .0a a -=r r B .如果a b =r r ,那么a b =r r C .若向量a r 与b 均为单位向量,那么a b =r r D .对于非零向量b r ,如果()0a k b k =?≠r r ,那么//a b r r 【答案】D 【解析】 【分析】 根据向量的概念、性质以及向量的运算即可得出答案. 【详解】 A. -r r a a 等于0向量,而不是等于0,所以A 错误; B. 如果a b =r r ,说明两个向量长度相等,但是方向不一定相同,所以B 错误; C. 若向量a r 与b 均为单位向量,说明两个向量长度相等,但方向不一定相同,所以C 错误; D. 对于非零向量b r ,如果()0a k b k =?≠r r ,即可得到两个向量是共线向量,可得到//a b r r ,故D 正确. 故答案为D. 【点睛】 平面向量定义及线性运算练习题 一.选择题 1、下列说法正确的是( ) A 、数量可以比较大小,向量也可以比较大小. B 、方向不同的向量不能比较大小,但同向的可以比较大小. C 、向量的大小与方向有关. D 、向量的模可以比较大小. 2、给出下列六个命题: ①两个向量相等,则它们的起点相同,终点相同;②若||||a b =r r ,则a b =r r ; ③若AB DC =u u u r u u u r ,则四边形ABCD 是平行四边形; ④平行四边形ABCD 中,一定有AB DC =u u u r u u u r ; ⑤若m n =u r r ,n k =r r ,则m k =u r r ;⑥a b r r P ,b c r r P ,则a c r r P . 其中不正确的命题的个数为( )A 、2个 B 、3个 C 、4个 D 、5个 3、设O 是正方形ABCD 的中心,则向量,,,AO BO OC OD u u u r u u u r u u u r u u u r 是( ) A 、相等的向量 B 、平行的向量 C 、有相同起点的向量 D 、模相等的向量 4、判断下列各命题的真假: (1)向量AB u u u r 的长度与向量BA uu u r 的长度相等; (2)向量a r 与向量b r 平行,则a r 与b r 的方向相同或相反; (3)两个有共同起点的而且相等的向量,其终点必相同; (4)两个有共同终点的向量,一定是共线向量; (5)向量AB u u u r 和向量CD uuu r 是共线向量,则点A 、B 、C 、D 必在同一条直线上; (6)有向线段就是向量,向量就是有向线段. 其中假命题的个数为( ) A 、2个 B 、3个 C 、4个 D 、5个 5、若a r 为任一非零向量,b r 为模为1的向量,下列各式:①|a r |>|b r | ②a r ∥b r ③|a r |>0 ④|b r |=±1,其中正确的是( ) A 、①④ B 、③ C 、①②③ D 、②③ 6、下列命中,正确的是( ) A 、|a r |=|b r |?a r =b r B 、|a r |>|b r |?a r >b r 1.1 空间向量及其运算 1.1.1 空间向量及其线性运算 学习目标核心素养 1.理解空间向量的概念.(难点) 2.掌握空间向量的线性运算.(重点) 3.掌握共线向量定理、共面向量定理及推 论的应用.(重点、难点) 1.通过空间向量有关概念的学习,培养学生的 数学抽象核心素养. 2.借助向量的线性运算、共线向量及共面向量 的学习,提升学生的直观想象和逻辑推理的核 心素养. 国庆期间,某游客从上海世博园(O)游览结束后乘车到外滩(A)观赏黄浦江,然后抵达东方明珠(B)游玩,如图1,游客的实际位移是什么?可以用什么数学概念来表示这个过程? 图1 图2 如果游客还要登上东方明珠顶端(D)俯瞰上海美丽的夜景,如图2,那么他实际发生的位移是什么?又如何表示呢? 1.空间向量 (1)定义:在空间,具有大小和方向的量叫做空间向量. (2)长度或模:空间向量的大小. (3)表示方法: ①几何表示法:空间向量用有向线段表示; ②字母表示法:用字母a,b,c,…表示;若向量a的起点是A,终点是B,也可记作:AB → ,其模记为|a|或|AB → |. 2.几类常见的空间向量 名称方向模记法 零向量任意00 单位向量任意1 相反向量相反相等 a的相反向量:-a AB → 的相反向量:BA → 相等向量相同相等a=b 3.空间向量的线性运算 (1)向量的加法、减法 空间向量的 运算 加法OB→=OA→+OC→=a+b 减法CA→=OA→-OC→=a-b 加法运算律 ①交换律:a+b=b+a ②结合律:(a+b)+c=a+(b+c) ①定义:实数λ与空间向量a的乘积λa仍然是一个向量,称为向量的数乘运算. 当λ>0时,λa与向量a方向相同; 当λ<0时,λa与向量a方向相反; 当λ=0时,λa=0;λa的长度是a的长度的|λ|倍. ②运算律 a.结合律:λ(μa)=μ(λa)=(λμ)a. b.分配律:(λ+μ)a=λa+μa,λ(a+b)=λa+λb. 思考:向量运算的结果与向量起点的选择有关系吗? [提示]没有关系. 4.共线向量 (1)定义:表示若干空间向量的有向线段所在的直线互相平行或重合,则这些向量叫做共线向量或平行向量. (2)方向向量:在直线l上取非零向量a,与向量a平行的非零向量称为直线l的方向向量. 规定:零向量与任意向量平行,即对任意向量a,都有0∥a. (3)共线向量定理:对于空间任意两个向量a,b(b≠0),a∥b的充要条件是存在实数λ使a=λb. (4)如图,O是直线l上一点,在直线l上取非零向量a,则对于直线l上任意一点P,由数乘向量定义及向量共线的充要条件可知,存在实数λ,使得OP → =λa. 5.共面向量 (1)定义:平行于同一个平面的向量叫做共面向量. (2)共面向量定理:若两个向量a,b不共线,则向量p与向量a,b共面的充要条件是存《第一节平面向量的概念及其线性运算》教案
平面向量的概念与线性运算知识点
高中数学 空间向量的线性运算教案
人教A版高中数学《平面向量的线性运算》教学设计
平面向量线性运算教案
平面向量的基本概念及线性运算知识点
苏教版高中数学选修2-1《空间向量及其线性运算》教案
空间向量及其线性运算(教案)
平面向量的线性运算教学设计
数学选修空间向量及其运算教案
平面向量线性运算教案
高中数学
适用年级
高一
学科
适用区域 苏教版区域
课时时长(分钟)
2 课时
知识点 向量的加法;向量的减法;向量的数乘.
教学目标
通过经历向量加法的探究,掌握向量加法概念,结合物理学实际理解向量加法的意义。能 熟练地掌握向量加法的平行四边形法则和三角形法则,并能作出已知两向量的和向量。通 过探究活动,掌握向量减法概念,理解两个向量的减法就是转化为加法来进行,掌握相反 向量。
教学重点 向量的加减法的运算。
教学难点 向量的加减法的几何意义。
【知识导图】
教学过程
一、导入
高考对本内容的考查主要以选择题或者是填空题的形式来出题,一般难度不 大,属于简单题。
二、知识讲解
(考1)点向1量向加量法加的法三法角则形法则 在定义中所给出的求象量和的方法就是向量加法的三角形法则。运用这一法则时 要特别注意“首尾相接”,即第二个向量要以第一个向量的终点为起点,则由第一 个向量的起点指向第二个向量的终点的向量即为和向量。0 位移的合成可以看作 向量加法三角形法则的物理模型。
第1页/共9页
由考于点方2向反向转量两的次减仍法回法到则原来的方向,因此 a 和 a 互为相反向量。 于是 (a) a 。 我们规定,零向量的相反向量仍是零向量. 任一向量与其相反向量的和是零向量,即 a (a) (a) a 0 。 所以,如果 a, b 是互为相反的向量,那么 a= b,b= a, a b 0 。
考点 3 实数与向量的积的运算律 设 , 为实数,那么 (1) ( a) ()a ; (2) ( )a a a ; (3) (a b) a b . 特别地,我们有 ()a (a) (a) , (a b) a b 。 向量共线的等价条件是:如果 a(a 0) 与 b 共线,那么有且只有一个实数 ,使 b a。
三 、例题精析 类型一 平面向量的坐标表示
例题 1
已知边长为 1 的正方形 ABCD 中,AB 与 x 轴正半轴成 30°角.求点 B 和点 D 的坐标和 AB 与 AD 的坐标.
第2页/共9页最新平面向量的线性运算及练习
高中数学必修4《平面向量线性运算》教案
平面向量的线性运算随堂练习(答案)
平面向量的线性运算教案
向量的线性运算经典测试题及答案解析
平面向量定义及线性运算练习题
2020_2021学年新教材高中数学第1章空间向量与立体几何1.1空间向量及其运算1.1.