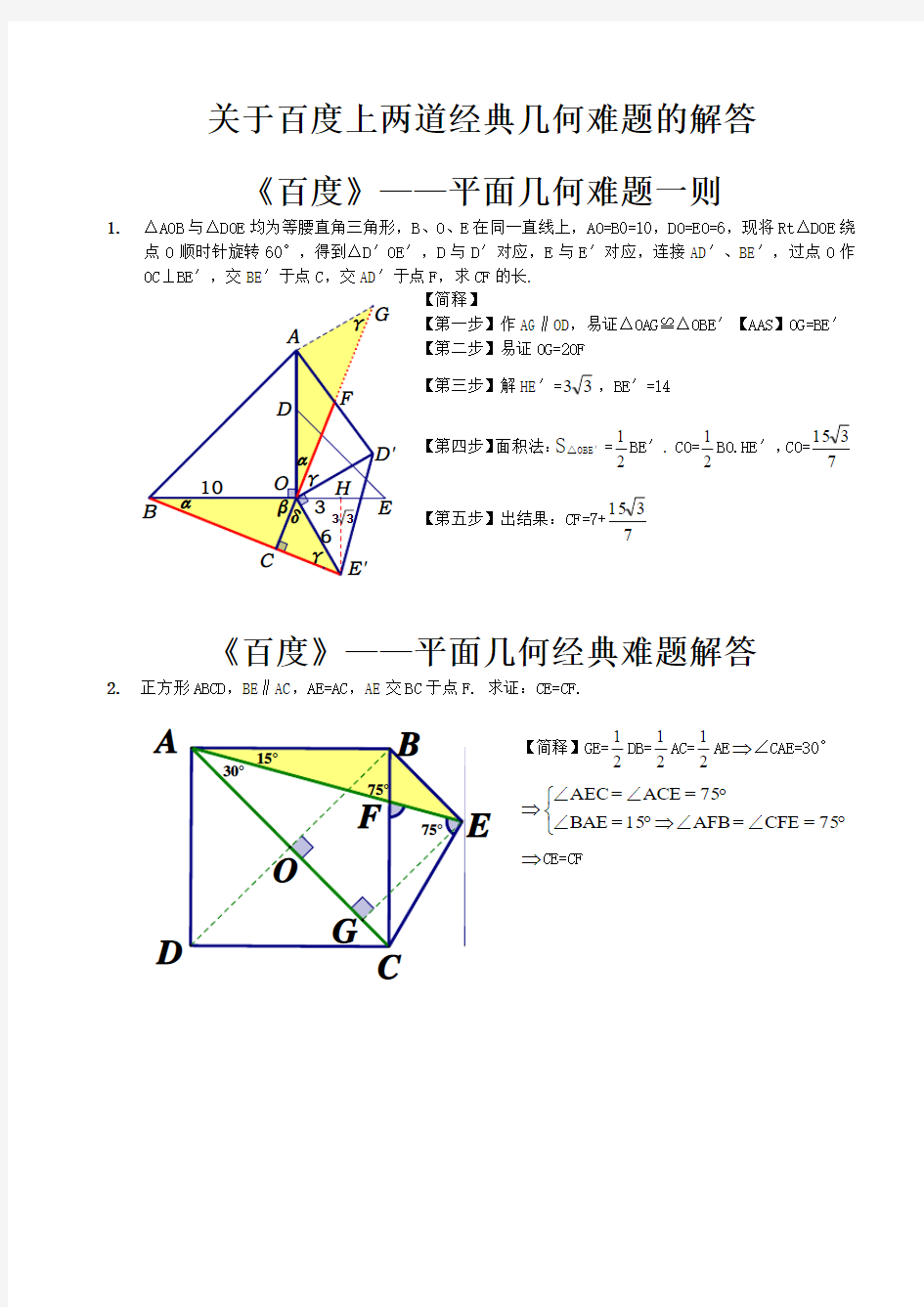
关于百度上两道经典几何难题的解答
《百度》——平面几何难题一则
1. △AOB 与△DOE 均为等腰直角三角形,B 、O 、E 在同一直线上,AO=B0=10,DO=EO=6,现将Rt △DOE 绕点O 顺时针旋转60°,得到△D ′OE ′,D 与D ′对应,E 与E ′对应,连接AD ′、BE ′,过点O 作OC ⊥BE ′,交BE ′于点C ,交AD ′于点F ,求CF 的长.
【简释】
【第一步】作AG ∥OD ,易证△OAG ≌△OBE ′【AAS 】OG=BE ′ 【第二步】易证OG=2OF
【第三步】解HE ′=33,BE ′=14 【第四步】面积法:S △OBE ′=21BE ′. CO=21BO.HE ′,CO=7315 【第五步】出结果:CF=7+
7315
《百度》——平面几何经典难题解答
2. 正方形ABCD ,BE ∥AC ,AE=AC ,AE 交BC 于点F. 求证:CE=CF.
【简释】GE=21DB=21AC=21AE ?∠CAE=30° ????
????75=CFE ∠=AFB ∠ 15=BAE ∠75=ACE ∠=AEC ∠ ?CE=CF
E D A
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第4 题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F . B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO .(初二) 第1题图 第2题图 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 第3题图 第4题图 F
几何图形的十大解法(30例) 一、 分割法 例:将两个相等的长方形重合在一起,求组合图形的面积。(单位:厘米) 解:将图形分割成两个全等的梯形。 S 组=(7-2+7)×2÷2×2=24(平方厘米) 例:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。 解:将图形分割成3个三角形。 S = 5×5÷2 + 5×8÷2 + (8-5)×5÷2 = 12.5+20+7.5 = 38(平方厘米) 例:左图中两个正方形的边长分别为8厘米和6厘米。求阴影部分面积。 解:将阴影部分分割成两个三角形。 S 阴 = 8×(8+6)÷2 + 8×6÷2 =56+24 = 80(平方厘米) 二、 添辅助线 例:已知正方形边长4厘米,A、B、C、D 是正方形边上的中点,P 是任意一点。 求阴影部分面积。 解:从P 点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。 S 阴 = 4×4÷2 = 8(平方厘米) 2 7
例:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行 四边形底20.4厘米,高8厘米。梯形下底是多少厘米? 解:因为添一条辅助线平行于三角形一条边,发现40平方 厘米是一个平行四边形。 所以梯形下底:40÷8=5(厘米) 例:平行四边形的面积是48平方厘米,BC 分别是这个平行四边形相邻两条边的中 点,连接A、B、C 得到4个三角形。求阴影部分的面积。 解:如图连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。 S 阴 = 48÷8×3 = 18(平方厘米) 三、 倍比法 例:已知:OC=2AO,S ABO =2㎡,求梯形ABCD 的面积。 解:因为OC = 2AO, 所以 S BOC = 2×2 = 4(㎡) S DOC = 4×2 = 8(㎡) S ABCD = 2+4×2+8 = 18(㎡) 例:已知:S 阴=8.75㎡ ,求下图梯形的面积。 解:因为 7.5÷2.5=3(倍) 所以 S 空 = 3 S 阴。 S = 8.75×(3+1)=35(㎡) B A C D O 7.5 2.5
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第 4题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延 B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
长线交MN于E、F.求证:∠DEN=∠F. 经典难题(二) 1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M. (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO.(初二) 第1题图第2题图 2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及 D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二) 3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题: 设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)
第3题图 第4题图 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典难题(三) 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二) 第1题图 第2题图 2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)
几何最值问题 一.选择题(共6小题) 1.(2015?孝感一模)如图,已知等边△ABC的边长为6,点D为AC的中点,点E为BC的中点,点P为BD上一点,则PE+PC的最小值为() 3 AE==3, . 2.(2014?鄂城区校级模拟)如图,在直角坐标系中有线段AB,AB=50cm,A、B到x轴的距离分别为10cm和40cm,B点到y轴的距离为30cm,现在在x轴、y轴上分别有动点P、Q,当四边形PABQ的周长最短时,则这个值为() 5050+50
LN=AS==40 MN==50 MN=MQ+QP+PN=BQ+QP+AP=50 =50 3.(2014秋?贵港期末)如图,AB⊥BC,AD⊥DC,∠BAD=110°,在BC、CD上分别找一点M、N,当△AMN周长最小时,∠MAN的度数为()
4.(2014?无锡模拟)如图,∠MON=90°,矩形ABCD的顶点A,B分别在OM、ON上,当B 在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=.运动过程中,当点D到点O的距离最大时,OA长度为() C OE=AE=AB=× AD=BC= DE= ADE==, =
DF=, OA=AD= 5.(2015?鞍山一模)如图,正方形ABCD的边长为4,点E在边BC上且CE=1,长为的线段MN在AC上运动,当四边形BMNE的周长最小时,则tan∠MBC的值是() C D ,连结,此时四 ,连结MN= =, =, ,
PC= PDC==. 6.(2015?江干区一模)如图,△ABC中,CA=CB,AB=6,CD=4,E是高线CD的中点,以CE 为半径⊙C.G是⊙C上一动点,P是AG中点,则DP的最大值为() C BG AD=BD=AB=3 CE=
世界数学十大未解难题 (其中“一至七”为七大“千僖难题”;附录“希尔伯特23个问题里尚未解决 的问题”) 一:P(多项式算法)问题对NP(非多项式算法)问题 在一个周六的晚上,你参加了一个盛大的晚会。由于感到局促不安,你想知道这一大厅中是否有你已经认识的人。你的主人向你提议说,你一定认识那位正在甜点盘附近角落的女士罗丝。不费一秒钟,你就能向那里扫视,并且发现你的主人是正确的。然而,如果没有这样的暗示,你就必须环顾整个大厅,一个个地审视每一个人,看是否有你认识的人。生成问题的一个解通常比验证一个给定的解时间花费要多得多。这是这种一般现象的一个例子。与此类似的是,如果某人告诉你,数 13,717,421可以写成两个较小的数的乘积,你可能不知道是否应该相信他,但是如果他告诉你它可以因子分解为3607乘上3803,那么你就可以用一个袖珍计算器容易验证这是对的。不管我们编写程序是否灵巧,判定一个答案是可以很快利用内部知识来验证,还是没有这样的提示而需要花费大量时间来求解,被看作逻辑和计算机科学中最突出的问题之一。它是斯蒂文·考克(StephenCook)于1971年陈述的。 二:霍奇(Hodge)猜想 二十世纪的数学家们发现了研究复杂对象的形状的强有力的办法。基本想法是问在怎样的程度上,我们可以把给定对象的形状通过把维数不断增加的简单几何营造块粘合在一起来形成。这种技巧是变得如此有用,使得它可以用许多不同的方式来推广;最终导至一些强有力的工具,使数学家在对他们研究中所遇到的形形色色的对象进行分类时取得巨大的进展。不幸的是,在这一推广中,程序的几何出发点变得模糊起来。在某种意义下,必须加上某些没有任何几何解释的部件。霍奇猜想断言,对于所谓射影代数簇这种特别完美的空间类型来说,称作霍奇闭链的部件实际上是称作代数闭链的几何部件的(有理线性)组合。 三:庞加莱(Poincare)猜想
专题10 几何最值问题【十二个基本问题】
1.如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为() A.61cm B.11cm C.13cm D.17cm 2.已知圆锥的底面半径为r=20cm,高h=20 15cm,现在有一只蚂蚁从底边上一点A出发.在侧面上爬行一周又回到A点,蚂蚁爬行的最短距离为________. 3.如图,在△ABC中,AB=3,AC=4,BC=5,P为边BC上一动点,PE⊥AB于E,PF⊥AC 于F,则EF的最小值为() A.2 B.C.D. 4.如图,在矩形ABCD中,AB=10,BC=5.若点M、N分别是线段AC,AB上的两个动点,
则BM+MN的最小值为() A.10 B.8 C.5 3 D.6 5.如图,一个长方体形的木柜放在墙角处(与墙面和地面均没有缝隙),有一只蚂蚁从柜角A处沿着木柜表面爬到柜角C处. (1)请你画出蚂蚁能够最快到达目的地的可能路径; (2)当AB=4,BC=4,CC=5时,求蚂蚁爬过的最短路径的长. (3)在(2)的条件下,求点B到最短路径的距离. 6.如图,已知P为∠AOB内任意一点,且∠AOB=30°,点P、P分别在OA、OB上,求作点P、P,使△PPP的周长最小,连接OP,若OP=10cm,求△PPP的周长. 7.如图,E,F是正方形ABCD的边AD上两个动点,满足AE=DF.连接CF交BD于点G,连接BE交AG于点H.若正方形的边长为2,则线段DH长度的最小值是________.
第7题 第8题 第9题 8.如图,在等腰Rt △ABC 中,∠BAC =90°,AB =AC ,BC =4 2,点D 是AC 边上一动点,连接 BD ,以AD 为直径的圆交BD 于点E ,则线段CE 长度的最小值为 . 9.如图,⊙O 的半径为1,弦AB =1,点P 为优弧(⌒)AB 上一动点,AC ⊥AP 交直线PB 于点C ,则△ABC 的最大面积是( ) A .1 2 B . 22 C . 32 D . 34 10.如图,已知抛物线y =-x +bx +c 与一直线相交于A (-1,0),C (2,3)两点,与y 轴交 于点N .其顶点为D . (1)抛物线及直线AC 的函数关系式; (2)设点M (3,m ),求使MN +MD 的值最小时m 的值; (3)若抛物线的对称轴与直线AC 相交于点B ,E 为直线AC 上的任意一点,过点E 作EF ∥BD 交抛物线于点F ,以B ,D ,E ,F 为顶点的四边形能否为平行四边形若能,求点E 的坐标;若不能,请说明理由; (4)若P 是抛物线上位于直线AC 上方的一个动点,求△APC 的面积的最大值.
尺规作图三大几何难 题
安溪六中校本课程之数学探秘 尺规作图三大几何问题 一、教学目标 1.让学生了解尺规作图三大几何问题如何产生的? 2.经历探索尺规作图三大几何问题如何解决的过程,进一步体会数学方法思想。 3.学生通过自主探究、合作交流体会尺规作图三大几何问题有什么教育价值? 二、问题背景 传说大约在公元前400年,古希腊的雅典流行疫病,为了消除灾难,人们向太阳神阿波罗求助,阿波罗提出要求,说必须将他神殿前的立方体祭坛的体积扩大1倍,否则疫病会继续流行。人们百思不得其解,不得不求教于当时最伟大的学者柏拉图,柏拉图也感到无能为力。这就是古希腊三大几何问题之一的倍立方体问题。用数学语言表达就是:已知一个立方体,求作一个立方体,使它的体积是已知立方体的两倍。另外两个著名问题是三等分任意角和化圆为方问题。古希腊三大几何问题既引人入胜,又十分困难。问题的妙处在于它们从形式上看非常简单,而实际上却有着深刻的内涵。它们都要求作图只能使用圆规和无刻度的直尺,而且只能有限次地使用直尺和圆规。但直尺和圆规所能作的基本图形只有:过两点画一条直线、作圆、作两条直线的交点、作两圆的交点、作一条直线与一个圆的交点。某个图形是可作的就是指从若干点出发,可以通过有限个上述基本图形复合得到。这一过程中隐含了近代代数学的思想。经过2000多年的艰苦探索,数学家们终于弄清楚了这3个古典难题是
“不可能用尺规完成的作图题”。认识到有些事情确实是不可能的,这是数学思想的一大飞跃。然而,一旦改变了作图的条件,问题则就会变成另外的样子。比如直尺上如果有了刻度,则倍立方体和三等分任意角就都是可作的了。数学家们在这些问题上又演绎出很多故事。直到最近,中国数学家和一位有志气的中学生,先后解决了美国著名几何学家佩多提出的关于“生锈圆规”(即半径固定的圆规)的两个作图问题,为尺规作图添了精彩的一笔。或描述如下: 这是三个作图题,只使用圆规和直尺求出下列问题的解,直到十九世纪被证实这是不可能的: 1.立方倍积,即求作一立方体的边,使该立方体的体积为给定立方体的两倍。 2.化圆为方,即作一正方形,使其与一给定的圆面积相等。 3.三等分角,即分一个给定的任意角为三个相等的部分。 三、问题探秘 1.立方倍积 关于立方倍积的问题有一个神话流传:当年希腊提洛斯(Delos)岛上瘟疫流行,居民恐惧也向岛上的守护神阿波罗(Apollo)祈祷,神庙里的预言修女告诉他们神的指示:“把神殿前的正立方形祭坛加到二倍,瘟疫就可以停止。”由此可见这神是很喜欢数学的。居民得到了这个指示后非常高兴,立刻动工做了一个新祭坛,使每一稜的长度都是旧祭坛稜长的二倍,但是瘟疫不但没停止,反而更形猖獗,使他们都又惊奇又惧怕。结果被一个学者指出了错误:「棱二倍起来体积就成了八倍,神所要的是二倍而不是八倍。」大家都觉得这个说法很对,於是改在神前并摆了与旧祭坛同形状同大小的两个祭坛,可是瘟
几何最值问题大一统 追本溯源化繁为简 目有千万而纲为一,枝叶繁多而本为一。纲举则目张,执本而末从。如果只在细枝末节上下功夫,费了力气却讨不了好。学习就是不断地归一,最终以一心一理贯通万事万物,则达自由无碍之化境矣(呵呵,这境界有点高,慢慢来)。 关于几何最值问题研究的老师很多,本人以前也有文章论述,本文在此基础上再次进行归纳总结,把各种知识、方法、思想、策略进行融合提炼、追本溯源、认祖归宗,以使解决此类问题时更加简单明晰。 一、基本图形 所有问题的老祖宗只有两个:①[定点到定点]:两点之间,线段最短;②[定点到定线]:点线之间,垂线段最短。 由此派生:③[定点到定点]:三角形两边之和大于第三边;④[定线到定线]:平行线之间,垂线段最短;⑤[定点到定圆]:点圆之间,点心线截距最短(长);⑥[定线到定圆]:线圆之间,心垂线截距最短;⑦[定圆到定圆]:圆圆之间,连心线截距最短(长)。余不赘述,下面仅举一例证明:[定点到定圆]:点圆之间,点心线截距最短(长)。 已知⊙O半径为r,AO=d,P是⊙O上一点,求AP的最大值和最小值。 证明:由“两点之间,线段最短”得AP≤AO+PO,AO≤AP+PO,得d-r≤AP≤d+r,AP最小时点P在B处,最大时点P在C处。即过圆心和定点的直线截得的线段AB、AC分别最小、最大值。(可用“三角形两边之和大于第三边”,其实质也是由“两点之间,线段最短”推得)。上面几种是解决相关问题的基本图形,所有的几何最值问题都是转化成上述基本图形解决的。
二、考试中出现的问题都是在基本图形的基础上进行变式,如圆与线这些图形不是直接给出,而是以符合一定条件的动点的形式确定的;再如过定点的直线与动点所在路径不相交而需要进行变换的。类型分三种情况:(1)直接包含基本图形;(2)动点路径待确定;(3)动线(定点)位置需变换。 (一)直接包含基本图形。 AD一定,所以D是定点,C是直线 的最短路径,求得当CD⊥AC时最短为 是定点,B'是动点,但题中未明确告知B'点的运动路径,所以需先确定B'点运动路径是什么图形,一般有直线与圆两类。此题中B'的路径是以为半径的圆弧,从而转化为定点到定圆的最短路径为AC-B'C=1。
几何问题解题思路 数量关系技巧包含了数学运算技巧和数字推理技巧两大部分,公务员考试数学运算是最为考生所头疼,其所占分值高并且难度也高。今天中公教育为考生整理了数量关系答题技巧中的几何问题解题思路,希望对考生有所帮助! 中公教育为考生整理了几何问题考点的解题思路和技巧,望考生注意以下几个方面。 第一个方面,几何基本公式: 三角形的面积=底×高÷2,长方形(正方形)的面积=长×宽,梯形的面积=(上底+下底)×高÷2,圆形的面积=π×半径的平方,长方体(正方体)的面积=长×宽×高,圆柱体的体积=底面积×高,圆锥体的面积=底面积×高÷3。 第二个方面,几何问题的“割补平移”思想。 中公教育提醒考生,当看到一个关于求解面积的问题,不要立刻套用公式去求解,这样做很可能走入误区,最后无法求解或不能快速求解。对于此类问题通常的使用的方法就是“辅助线法”即通过引入新的辅助线将图形分割或者补全为很容易得到的规则图形,从而快速求得面积。 第三个方面,几何极限理论。 平面图形:①周长一定,越趋近于圆,面积越大,②面积一定,越趋近于圆,周长越小; 立体图形:①表面积一定,越趋近于球,体积越大,②体积一定,越趋近于球,表面积越小。 实战例题: 【例题】半径为5厘米的三个圆弧围成如右图所示的区域,其中AB弧与AD弧为四分之一圆弧,而BCD弧是一个半圆弧,则此区域的面积是多少平方米? A.25
B.10+5л C.50 D.55 【中公教育解析】如下图:连接BD,作矩形BDMN,将下面的四分之一圆弧的半径画出来,可见该部分面积分为彩色的两部分。上面部分是半圆,下半部分是矩形面积减去2个四分之一圆,即矩形面积减半个圆形面积二部分之和,正好是矩形面积,即10×5=50平方厘米。故答案为C。 最新招考公告、备考资料就在辽宁事业单位考试网 https://www.doczj.com/doc/9613816528.html,/liaoning/
小学几何图形的九大方法 例1:将两个相等的长方形重合在一起,求组合图形的面积。(单位:厘米) 解:将图形分割成两个全等的梯形。S组=(7-2+7)×2÷2×2=24(平方厘米) 例2:下列两个正方形边长分别为8厘米和5厘米,求阴影部分面积。 解:将图形分割成3个三角形。S=5×5÷2+5×8÷2+(8-5)×5÷2=12.5+20+7.5=38(平方厘米) 例3:左图中两个正方形边长分别为8厘米和6厘米。求阴影部分面积。 解:将阴影部分分割成两个三角形。 S阴=8×(8+6)÷2+8×6÷2=56+24=80(平方厘米)
添加辅助线法 例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。求阴影部分面积。 解:从P点向4个定点添辅助线,由此看出,阴影部分面积和空白部分面积相等。S阴=4×4÷2=8(平方厘米) 例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方厘米,平行四边形底20.4厘米,高8厘米。梯形下底是多少厘米? 解:因为添一条辅助线平行于三角形一条边,发现40平方厘米是一个平行四边形。 所以梯形下底:40÷8=5(厘米) 例3:平行四边形的面积是48平方厘米,BC分别是这个平行四边形相邻两条边的中点,连接A、B、C得到4个三角形。求阴影部分的面积。
解:如果连接平行四边形各条边上的中点,可以看出空白部分占了整个平行四边形的八分之五,阴影部分占了八分之三。S阴=48÷8×3=18(平方厘米) 倍比法 例1:已知OC=2AO,SABO=2㎡,求梯形ABCD的面积。 解:因为OC=2AO,所以SBOC=2×2=4(㎡)SDOC=4×2=8(㎡)SABCD=2+4×2+8=18(㎡) 例2:已知S阴=8.75㎡,求下图梯形的面积。 解:因为7.5÷2.5=3(倍)所以S空=3S阴S=8.75×(3+1)=35(㎡) 例3:下图AB是AD的3倍,AC是AE的5倍,那么三角形
初三数学总复习辅导学习资料(6)——几何经典难题 1.已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF . 2.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 .求证:△PBC 是正三角形. 3.如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、 C 2、 D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2 C 2 D 2是正方形. 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . 5.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600 ,求证:AH =AO . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1
F 6.设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及 CD 分别交MN 于P 、Q .求证:AP =AQ . 7.如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作 两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ . 8.如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半. 9.如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于 10.如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF . E
中考数学几何最值问题解法 在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。 解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。下面通过近年全国各地中考的实例探讨其解法。 应用两点间线段最短的公理(含应用三角形的三边关系)求最值 典型例题: 例1. 如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为【】 A1B C. 55 D. 5 2 例2.在锐角三角形ABC中,BC=2 4,∠ABC=45°,BD平分∠ABC,M、N分别是BD、BC上的动点,则CM+MN 的最小值是▲ 。 例3.如图,圆柱底面半径为2cm,高为9cm π,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一棉线从A顺着圆柱侧面绕3圈到B,求棉线最短为▲ cm。
练习题: 1. 如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开 始经过4个侧面爬行一圈到达Q 点,则蚂蚁爬行的最短路径长为【 】 A.13cm B.12cm C.10cm D.8cm 2.如图,圆柱的底面周长为6cm ,AC 是底面圆的直径,高BC=6cm ,点P 是母线BC 上一点,且PC= 23 BC .一只蚂蚁从A 点出发沿着圆柱体的表面爬行到点P 的最短距离是【 】 A 、6 (4)π+㎝ B 、5cm C 、㎝ D 、7cm 3.如图所示,在边长为2的正三角形ABC 中,E 、F 、G 分别为AB 、AC 、BC 的中点,点P 为线段EF 上一个动点,连接BP 、GP ,则△BPG 的周长的最小值是 _ ▲ . 二、应用垂线段最短的性质求最值:典型例题: 例1. (2012山东莱芜4分)在△ABC 中,AB =AC =5,BC =6.若点P 在边AC 上移动,则BP 的最小值是 ▲ .
世界近代三大数学难题:哥德巴赫猜想 哥德巴赫1742年给欧拉的信中哥德巴赫提出了以下猜想:任一大于2的偶数都可写成两个质数之和。但是哥德巴赫自己无法证明它,于是就写信请教赫赫有名的大数学家欧拉帮忙证明,但是一直到死,欧拉也无法证明。因现今数学界已经不使用“1也是素数”这个约定,原初猜想的现代陈述为:任一大于5的整数都可写成三个质数之和。欧拉在回信中也提出另一等价版本,即任一大于2的偶数都可写成两个质数之和。今日常见的猜想陈述为欧拉的版本。把命题"任一充分大的偶数都可以表示成为一个素因子个数不超过a个的数与另一个素因子不超过b个的数之和"记作"a+b"。1966年陈景润证明了"1+2"成立,即"任一充分大的偶数都可以表示成二个素数的和,或是一个素数和一个半素数的和"。 今日常见的猜想陈述为欧拉的版本,即任一大于2的偶数都可写成两个素数之和,亦称为“强哥德巴赫猜想”或“关于偶数的哥德巴赫猜想”。 从关于偶数的哥德巴赫猜想,可推出:任一大于7的奇数都可写成三个质数之和的猜想。后者称为“弱哥德巴赫猜想”或“关于奇数的哥德巴赫猜想”。若关于偶数的哥德巴赫猜想是对的,则关于奇数的哥德巴赫猜想也会是对的。弱哥德巴赫猜想尚未完全解决,但1937年时前苏联数学家维诺格拉多夫已经证明充分大的奇质数都能写成三个质数的和,也称为“哥德巴赫-维诺格拉朵夫定理”或“三素数定理”。 猜想提出 1742年6月7日,哥德巴赫写信给欧拉,提出了著名的哥德巴赫猜想:随便取某一个奇数,比如77,可以把它写成三个素数之和,即77=53+17+7;再任取一个奇数,比如461,可以表示成461=449+7+5,也是三个素数之和,461还可以写成257+199+5,仍然是三个素数之和。例子多了,即发现“任何大于5的奇数都是三个素数之和。” 1742年6月30日欧拉给哥德巴赫回信。这个命题看来是正确的,但是他也给不出严格的证明。同时欧拉又提出了另一个命题:任何一个大于2的偶数都是两个素数之和。但是这个命题他也没能给予证明。 研究途径 研究偶数的哥德巴赫猜想的四个途径。这四个途径分别是:殆素数,例外集合,小变量的三素数定理以及几乎哥德巴赫问题。 殆素数
【2013年中考攻略】专题&几何最值问题解法探讨在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。 解决平面几何瑕值问题的常用的方法有:(1)应用两点间线段垠短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值; (5)应用其它知识求最值。下面通过近年全国各地中考的实例探讨其解法。一、应用两点间线段最短的公理(含应用三角形的三边关系)求最值: 1?(2012山东济南3分)如图,ZM0N二90° ,矩形ABCD的顶点A、B分别在边0M, 0N ±,当B在边 0N 上运动时,A随之在边0M上运动,矩形ABCD的形状保持不变,其中AB二2, BC二1,运动过程中,点D到点0的最大距离为【】 A* E 氏厉 U琴''D?j 2.(2012湖北鄂州3分)在锐角三角形ABC中,BC二4血,ZABC二45° , BD平分ZABC, M—N分别是BD、BC上的动点,则CM+MN的最小值是一▲ 3.(2011四川凉山5分)如图,圆柱底面半径为2c加,高为9/rcm,点A、 B分别是圆柱两底而圆周上的点,HA、B在同一母线上,用一?棉线从A顺着圆柱侧而绕3圈到B,求棉 线最短为▲ cm C
4. (2012四川眉山 3分)在△ABC 中,AB = 5, AC=3, AD 是BC 边上的中线,则AD 的収值范围是 5. (2012山东莱芜4分)在AABC 中,AB = AC=5, BC = 6.若点P 在 边AC 上移动,则BP 的垠小值是一 ▲ B C 6. (2012浙江台州4分)如图,菱形ABCD 中,AB 二2, ZA=120°,点P, Q, K 分别为线段BC, CD, BD ± 的任意一点,贝'J PK+QK 的最小值为【 7. (2012 江苏连云港 12 分)C 知梯形 ABCD, AD/7BC, AB 丄BC, AD = 1, AB=2, BC = 3, 二、应用垂线段最短的性质求最值: A. 1 B. 73 G / X
几何三大难题 如果不知道远溯古希腊前辈所建立和发展的概念、方法和结果,我们就不可能理解近50年来数学的目标,也不可能理解它的成就. Herm??nn Weyl § 1 问题的提出和解决 数学的心脏 数学是由什么组成的公理吗定义吗定理吗证明吗吗公式吗诚然,没有这些组成部分数学就不存在,它们都数数学的必要组成部分,但是,它们中间的任一个都不是数学的心脏.数学家存在的主要理由就是提出问题和解决问题.因此,数学的真正组成部分是问题和解.两千多年以来,数学就是在解决各种问题中进行的. 那么,什么样的问题是好问题呢对此希尔伯特有一段精彩的论述:“要想预先正确判断一个问题的价值是困难的,并且常常是不可能的;因为最终的判断取决于科学从该问题获得的收益,虽说如此,我们仍然要问:是否存在一个一般准则,可以借以鉴别好的数学问题,一个老的法国数学家曾经说过:一种数学理论应该这样清晰,使你能向大街上遇到的第一个人解释它.在此以前,这一理论不能认为是完善的.这里对数学理论所坚持的清晰性和易懂性,我想更应该把它作为一个数学问题堪称完善的要求.因为清楚地、易于理解的问题吸引着人们的兴趣,而复杂的问题却使我们望而却步.” “其次,为了具有吸引力,一个数学问题应该是困难的,但却不能是完全不可解决的,使我们白费力气.在通向哪隐藏的真理的曲折道路上,它应该是指引我们前进的一盏明灯,最终以成功的喜悦作为我们的报偿.” 在数学史上这样的例子是不胜枚举的.本章介绍的几何作图三大问题就是最着名的问题之一. 希腊古典时期数学发展的路线 希腊前300年的数学沿着三条不同的路线发展着.第一条是总结在欧几里得得《几何原本》中的材料.第二条路线是有关无穷小、极限以及求和过程的各种概念的发展,这些概念一直到近代,微积分诞生后才得以澄清.第三条路线是高等几何的发展,即园和直线以外的曲线以及球和平面以外的曲面的发展.令人惊奇的是,这种高等几何的大部分起源于解几何作图三大问题. 几何作图三大问题 古希腊人在几何学上提出着名的三大作图问题,它们是: ( 1) 三等分任意角. ( 2) 化园为方:求作一正方形,使其面积等于一已知园的面积.
几何图形的十大解法(30例) 一、分割法 例1:将两个相等的长方形重合在一起,求组合图形的 面积。(单位:厘米) 2 例2:下列两个正方形边长分别为8厘米和5厘米, 求阴影部分面积。 例3:左图中两个正方形的边长分别为8厘米和6厘米。 求阴影部分面积。 二、添辅助线 例1:已知正方形边长4厘米,A、B、C、D是正方形边上的中点,P是任意一点。求阴影部分面积。 C P D B A 例2:将下图平行四边形分成三角形和梯形两部分,它们面积相差40平方
厘米,平行四边形底20.4厘米,高8厘米。梯形下底是多少厘米? 例3:平行四边形的面积是48平方厘米,BC分别是 A 这个平行四边形相邻两条边的中点,连接A、 B B、C得到4个三角形。求阴影部分的面积。 C 三、倍比法 例1: A B 已知:OC=2AO,S ABO=2㎡,求梯形ABCD O 的面积。 例2:7.5 已知:S阴=8.75㎡,求下图梯形的面积。 2.5 例3: A 下图AB是AD的3倍,AC是AE的5倍, D E 那么三角形ABC的面积是三角形ADE的多少 倍? C 四、割补平移
例1: A B 已知:S阴=20㎡, EF为中位线 E F 求梯形ABCD的面积。 D C 例2:10 求左图面积(单位:厘米) 5 5 10 例3:把一个长方形的长和宽分别增加2 厘米,面积增加24平方厘米。 求原长方形的周长。 2 五、等量代换 例已知:AB平行于EC,求阴影部分面积。 8 E 10 D (单位:m) 例2:下图两个正方形边长分别是6分米、4分米。求阴影部分面积。 例3:已知三角形ABC的面积等于三角形AED的面积(形状大小都相同),
用” “?求解几何最值问题 江苏省睢宁县双沟中学赵光朋(221212) 通过恰当的途径,构建一元二次方程模型,在其有解的前提下,应用0≥?或?>0去探讨某些几何最值(或不等)问题,有时可收到条理清晰、简捷明快的解题效果.举例说明如下: 例1.当斜边一定时,求直角三角形周长的最大值. 分析:.当三角形的斜边c 一定时,两条直角边的和b a +与积ab 都可表示为周长l 与c 的代数式,由此想到以b a 、为实数根构造一元二次方程,再通过判别式?求解. 解:设直角三角形的两条直角边长分别为b a 、,斜边为c ,周长为l .则l c b a =++, c l b a -=+ (1).所以22)()(c l b a -=+,即222222c cl l b ab a +-=++.又222c b a =+, 所以222cl l ab -= (2).由(1)、(2)知b a 、是方程022)(22 =-+ --cl l x l c x 的两个实数根.所以02 24)]([22 ≥-?---=?cl l l c .整理,得022 2≥--c cl l ,求得c l )(21+≤,所以周长l 的最大值是 c )(21+. 点评:上述解法中,以三角形的斜边c 和周长l 表示两条直角边b a 和,并利用韦达定理构造一元二次方程,再巧用判别式“?” 化“相等”为“不等”,为求得周长的最大值疏通了渠道. 例2.三角形有一个内角为0 60,此角所对的边长为1,求证其余两边的和不大于2. 证明:如图1,ABC ?中,0 60=∠B ,1=AC .过A 作BC AD ⊥于D ,设x BD =,通过 ADC Rt ABD Rt ??和,得x AB 2=,x AD 3=,231x DC -=.令 2312x x x BC AB y -++=+=,整理,得关于x 的一元二次方程 0161222=-+-y xy x .由)1(1243622-?-=?y y 0≥,得 048122≥+-y ,所以,22≤≤-y ,y 的最大值为2,即其余两边的和不大于2. 点评:在此解法中,适时地引入变量y x 、,并将他们的关系用一个等式表达出来,为构造一元二次方程明确了目标,为应用”“?埋下了伏笔.更体现了几何问题代数化的转换思想. 例3.如图2,已知ABC ?的面积为S ,作一条直线l ∥BC ,且与AC AB 、分别交于 E D 、两点。记BED ?的面积为k ,证明:S k 4 1 ≤. 1 图l 2 图
三大几何难题 古希腊是世界数学史上浓墨重彩的一笔,希腊数学的成就是辉煌的,它为人类创造了巨大的精神财富。其中,几何是希腊数学研究的重心,柏拉图在他的柏拉图学院的大门上就写着“不懂几何的人,勿入此门”。历史上第一个公理化的演绎体系《几何原本》阐述的也基本上为几何内容。 古希腊的几何发展得如此繁荣,但有一个问题一直没有得到解决,那就是著名的尺规作图三大难题。它们分别是化圆为方、三等分任意角以及倍立方问题。这三个问题首先是“巧辨学派”提出并且研究的,但看上去很简单的三个问题,却困扰了数学家们两千多年之久。 这些问题的难处,是作图只能用直尺和圆规这两种工具,其中直尺是指只能画直线,而没有刻度的尺。在欧几里得的《几何原本》中对作图作了规定,只有圆和直线才被承认是可几何作图的,因此在这本书的巨大影响下,尺规作图便成为希腊几何学的金科玉律。并且,古代希腊人较重视规、矩在数学中训练思维和智力的作用,而忽视规矩的实用价值。因此,在作图中对规、矩的使用方法加以很多限制,在这里,就是要在有限的次数中解决这三个问题。化圆为方 圆和正方形都是常见的几何图形,人们自然会联想到可否作一个正方形和已知圆等积,这就是化圆为方问题。 三等分任意角 用尺规二等分一个角很容易就可以作出来,那么三等分角呢?三等分180,90角也很容易,但是60,45等这些一般角可以用尺规作出来吗? 倍立方 关于倍立方问题是起源于一个祭祀问题,第罗斯岛上流行着一种可怕的传染病,一时人心惶惶,不可终日.人们来到阿波罗神前,请求阿波罗神像的指示.阿波罗神给了祈求人这样一个指示:“神殿前有一个正方体祭坛,如果能不改变它的形状而把它的体积增加1倍,那么就能消灭传染病.”人们连夜赶造了一个长、宽、高都比正方体祭坛大一倍的祭坛,可是,那传染病传播得更加厉害了.人们又来到阿波罗神像前祈求.神说:“我要你们增加一倍的是祭坛的体积,你们把长、宽、高都增加1倍,祭坛的体积不是要比原来体积大7倍了吗?”人们绞尽脑汁想找出一个答案,可是始终没有人能解答这个难题. 由三大问题的起源,可以看出,化圆为方和三等分角是人们在已有知识的基础上,向更深层次,更一般的方向去思考、探索,这也是希腊数学的理论性的演绎推理与抽象性的表现。而倍立方则是起源于建筑的需要,这也反应了数学的发展是离不开现实社会的推动的。 三个几何难题提出后,有很多人都为之做了不懈的努力。可以说,但凡是数学史上称得上是数学家的人,都研究过这个问题。由三大难题引出的各种结论与发现也数不胜数,例如割圆曲线、阿基米德螺线等。但这些解法并没有完全遵从尺规作图的要求,因此也不算解决了三大难题。但是由19世纪所证出的三大几何难题的不可解,可以发现,只有冲破尺规的限制才能解决问题。正如很多事情,我们觉得无论如何也找不到解决的办法,就是因为有太多的枷锁罩在我们身上,只有打破这些桎梏,才会豁然开朗,找到一片新天地。 三大几何问题的真正解决是在19世纪解析几何创立之后,人们知道了直线与圆分别是二元一次方程和二元二次方程的轨迹,交点则是方程组的解,因此一个几何量是否能用尺规作出,则是它能否由已知量经过有限次加、减、乘、除、开平方运算得到。那么三大难题就可以转换成代数的语言来表示: 1化圆为方设圆的半径为一个单位,要作一面积等于单位圆的正方形,设这个正方形连长为x,则x2=π.集能否用尺规作出一条长为π的线段?
初中数学经典几何难题及答案
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) A P C D B A F G C E B O D
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正 方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC , M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . D 2 C 2 B 2 A 2 D 1 C 1 B 1 C D A A 1 A N F E C D M B
经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初 二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) · A D H E M C B O · G A O D B E C Q P N M
C G D E 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. · O Q P B D E C N M · A
几何最值问题解法探讨 在平面几何的动态问题中,当某几何元素在给定条件变动时,求某几何量(如线段的长度、图形的周长或面积、角的度数以及它们的和与差)的最大值或最小值问题,称为最值问题。 解决平面几何最值问题的常用的方法有:(1)应用两点间线段最短的公理(含应用三角形的三边关系)求最值;(2)应用垂线段最短的性质求最值;(3)应用轴对称的性质求最值;(4)应用二次函数求最值;(5)应用其它知识求最值。下面通过近年全国各地中考的实例探讨其解法。 一、应用两点间线段最短的公理(含应用三角形的三边关系)求最值: 典型例题: 例1. (2012山东济南3分)如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中, 点D到点O的最大距离为【】A 1B C5D.5 2 【答案】A。 【分析】如图,取AB的中点E,连接OE、DE、OD,∵OD≤OE+DE, AB=1。 ∴当O、D、E三点共线时,点D到点O的距离最大,此时,∵AB=2,BC=1,∴OE=AE=1 2 。故选A。 DE=OD 4,∠ABC=45°,BD平分∠ABC,M、N分别例2.(2012湖北鄂州3分)在锐角三角形ABC中,BC=2 是BD、BC上的动点,则CM+MN的最小值是▲ 。【答案】4。 【分析】如图,在BA上截取BE=BN,连接EM。∵∠ABC的平分线交AC于点D,∴∠EBM=∠NBM。 在△AME与△AMN中,∵BE=BN,∠EBM=∠NBM,BM=BM, ∴△BME≌△BMN(SAS)。∴ME=MN。∴CM+MN=CM+ME≥CE。 又∵CM+MN有最小值,∴当CE是点C到直线AB的距离时,CE取最小值。 ∵BC=ABC=45°,∴CE的最小值为450=4。∴CM+MN的最小值是4。 π,点A、B分别是圆柱两底面圆例3.(2011四川凉山5分)如图,圆柱底面半径为2cm,高为9cm 周上的点,且A、B在同一母线上,用一棉线从A顺着圆柱侧面绕3圈到B,求棉线最短为▲ cm。