
构造相似三角形解题的几种类型
⑴构造相似三角形求值;⑵构造相似三角形证角相等;⑶构造相似三角形证明等积式;⑷构造相似三角形证明线段的平方和、差、积;⑸构造相似三角形证明两线垂直
例1、(构造相似三角形求值)如图,已知梯形ABCD 中,AD ∥BC ,BC=3AD ,E 是腰AB 上一点.若△BCE 和四边形AECD 的面积分别为1S 和2S ,并且21S =32S ,求
AE
BE 的值
(延长两腰,构造相似三角形)
例2、(构造相似三角形证角相等)如图,在等边△ABC 的边BC 上取点D ,使DC BD =2
1,作CH ⊥AD ,H 为垂足,连接BH.求证:∠DBH=∠DAB
构造相似三角形证明等积式
(作BC 边上的高,由“三线合一”得到垂足即为中点.构造相似三角形;对△BDH 和△ADB ,有一个公共角,只需证夹它的两边对应成比例)
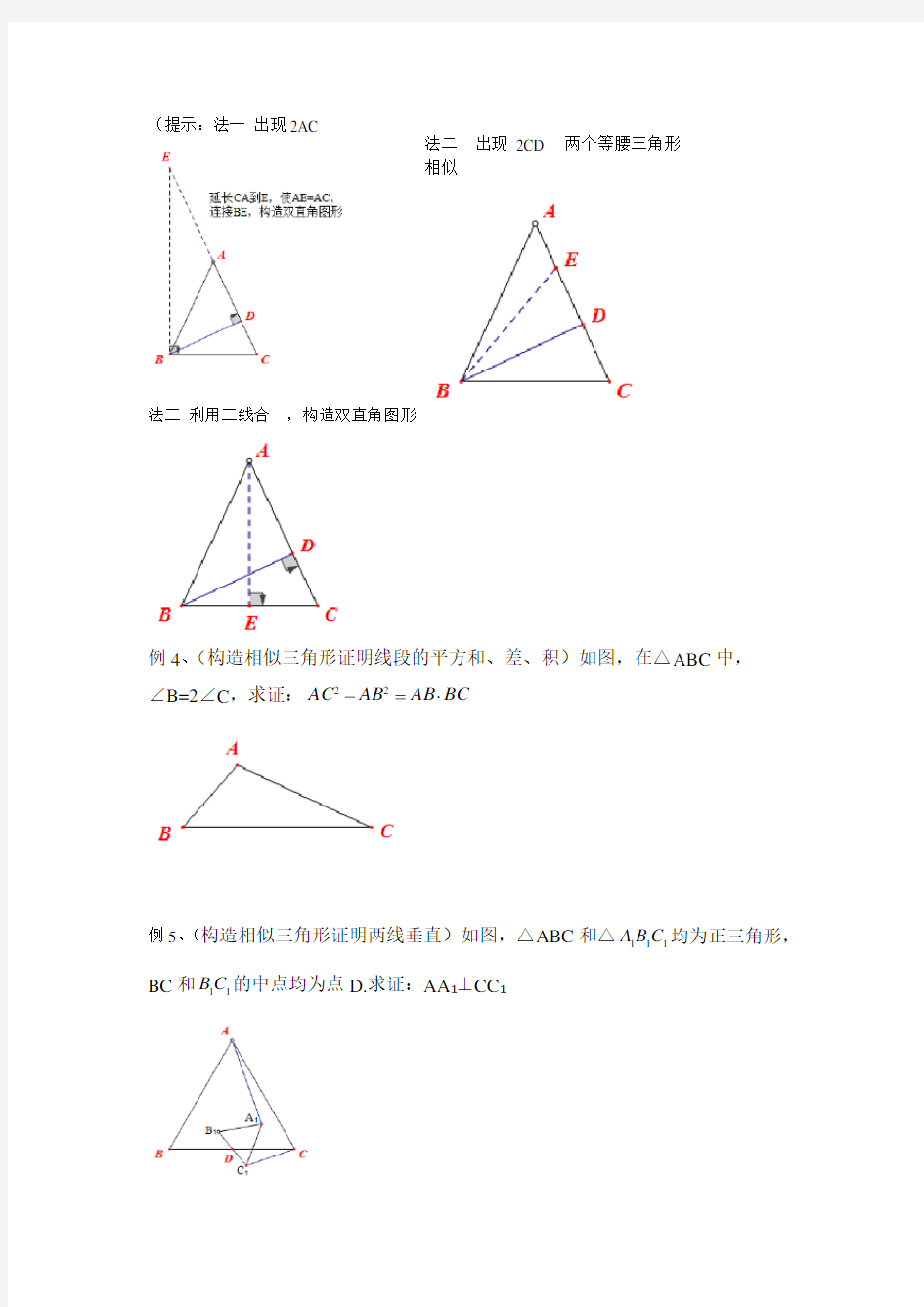
例3、(构造相似三角形证明等积式)在△ABC 中,已知AB=AC ,BD 为AC 边上的高.求证:CD AC BC ?=22
(提示:法一 出现
2AC
法三
利用三线合一,构造双直角图形
例4、(构造相似三角形证明线段的平方和、差、积)如图,在△ABC 中, ∠B=2∠C ,求证:BC AB AB AC ?=-22
例5、(构造相似三角形证明两线垂直)如图,△ABC 和△111C B A 均为正三角形,BC 和11C B 的中点均为点D.求证:AA ?⊥CC ?
法二 出现2CD 两个等腰三角形
相似
例6、⑴确定最值;⑵探索图形相似
如图①,在△ABC中,∠A=90°,BC=10,△ABC的面积为25.点D为AB 边上的任意一点(D不与A、B重合),过点D作DE∥BC,交AC于点E.设DE=x,以DE为折痕将△ADE翻折,使△ADE落在四边形BDCE所在平面内,所得的△A′DE与梯形DBCE重叠部分的面积记为y.
⑴用x表示△ADE的面积;
⑵当0<x≤5时,求y与x的函数关系式;
⑶当5<x<10时,求y与x的函数关系式;
⑷当x取何值时,y的值最大?最大值时多少?
巧构一线三直角解题 发表时间:2017-02-14T14:06:18.193Z 来源:《中小学教育》2017年2月第269期作者:鲍玉秀张刚 [导读] 教师在教学时要注意给学生创造机会,让学生学会找基本图形。 山东省淄博市周村区北郊中学255000;山东省淄博市修文外国语学校255000 教师在教学时要注意给学生创造机会,让学生学会找基本图形。通过基本图形的积累,学生在分析题目时,就能唤醒利用这些基本图形,并能直接解题。几何命题的证明方法很多,只要找到规律、找到模型,我们就可以“以不变应万变”,任何问题就能迎刃而解。所以说,模型建立是学好数学的秘密武器。 基本图形:如图1,B、D、C在一条直线上,∠B=∠ADE=∠C=90°。我们称这一图形为“一线三直角”模型,则△ABD∽△DCE(或 △ABD≌△DCE)。 点评:我们在教学中经常遇到此图形,只要见到一直角在一条直线上,我们可以构造两侧的直角三角形,利用相似三角形可以解决一类相关问题。当出现了有相等边的条件之后,相似就转化为全等了。综合性题目往往就会把相似和全等的转化作为出题的一种形式。本文将重点对这一基本图形进行探讨。 一、在旋转中出现一线三直角基本图形(全等) 如图,将AO绕点O按逆时针方向旋转90°,得到A’O。若点A的坐标为(a,b),则点A’的坐标为( )。 解析:过A点作AB⊥x轴,垂足为E,过A’作A’E’⊥x轴,则△A’OE≌△OAE,所以A’E’=OE=a,AE=OE’=b,所以A’的坐标为(-b,a)。 点评:教师在平时教学中就要注意基本图形的构造,为以后学习打下良好的基础。 变式:直线l1∥l2∥l3,且l1与l2的距离为1,l2与l3的距离为2。把一块含有45°角的直角三角形如图放置,顶点A、B、C恰好分别落在三条直线上,AC与直线l2交于点D,则线段BD的长度为()。 分析:∠AEC=90°,并在直线l3,此时我们可以构造一线三直角数学模型,△ADE与△BEC全等,所以DB=CE=3。 二、在折叠中构造一线三直角 如图,把矩形纸片OABC放入平面直角坐标系中,使OA、OC分别落在x轴、y轴上,连结OB,将纸片OABC沿OB折叠,使点A落在A’的位置。若OB= 5,tan∠BOC= ,则点A’的坐标是多少? 解析:因为OB= 5,tan∠BOC= ,OA=1,AB=2,△A’OD∽△A’BE。设OD=a,则A’E=2a, A’D= (a+1), DE=AB,2a+ (a+1)=2,解得a= ,所以A’的坐标(- ,)。 点评:此题是以矩形折叠为载体,如果利用常规方法勾股定理及全等计算很麻烦。如果构造一线三直角是非常简单的,过A’做AB的平行线,与BC、AO的延长线交于E、D, △A’OD∽△A’BE。设OD=a,则A’E=2a, A’D= (a+1),DE=AB,2a+ (a+1)=2,计算量相当简单。 三、画斜为直,找直线构造一线三直角 如图,在平面直角坐标系xoy中,点A的坐标是(-7,1),∠AOB=135°,OB=5。(1)求△AOB的面积。(2)求点B的坐标。 解析:设B(x,y),过B点作BF⊥x轴,过D点作x轴的平行线,与y轴交于G点,过A点作AC⊥CD。因为∠AOB=135°,AO=5 2,所以∠AOD=45°,AD=OD=5,所以△BOF≌△DOG≌△DCA,所以AD=OD=BO,AC=DG=OF,CD=OG=BF,所以△AOB的面积= ×5×5= ,所以x+y=7,1+y=x,所以x=4,y=3。 点评:这是一道一题多解的题,将∠AOB=135°转化为∠AOD=45°,构造等腰直角三角形,再构造模型一线三直角(全等)。 四、在圆中构造一线三直角 如图,在平面直角坐标系中,⊙P与x轴相切于点C,与y轴分别交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、E,连接DC并延长交y轴于点F。若点F的坐标为(0,1),点D的坐标为(6,-1)。(1)求证:DC=FC。(2)求直线AD的解析式。 解析:(1)由△OFC≌△GDC得到OC=CG,过点作DG⊥x轴,连接AC,因为AD为直径,所以∠AGD=90°,△OAG∽△CGD,所以DG∶GC=OG∶OA,所以1∶3=3∶OA,所以OA=9。 点评:从圆中找直角,利用直径得圆周角等于90°,问题便可迎刃而解。 基本图形的教学是初中几何教学的重点,也是难点,教师在平时教学中要注重基本图形的研究,要有足够的耐心等学生慢慢积累。学生的学习达到一定程度就会从复杂的图形中提炼出基本图形,才会出现解决问题时的灵感。
构造相似辅助线(1)——双垂直模型 6.在平面直角坐标系xOy中,点A的坐标为(2,1),正比例函数y=kx 的图象与线段OA的夹角是45°,求这个正比例函数的表达式. 7.在△ABC中,AB=,AC=4,BC=2,以AB为边在C点的异侧作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
8.在△ABC中,AC=BC,∠ACB=90°,点M是AC上的一点,点N是BC上的一点,沿着直线MN折叠,使得点C恰好落在边AB上的P点.求证:MC:NC=AP:PB. 9.如图,在直角坐标系中,矩形ABCO的边OA在x轴上,边OC在y 轴上,点B的坐标为(1,3),将矩形沿对角线AC翻折B点落在D 点的位置,且AD交y轴于点E.那么D点的坐标为() A. B. C. D.
10..已知,如图,直线y=﹣2x+2与坐标轴交于A、B两点.以AB为短边在第一象限做一个矩形ABCD,使得矩形的两边之比为1﹕2。求C、D两点的坐标。
6.答案:解:分两种情况 第一种情况,图象经过第一、三象限 过点A作AB⊥OA,交待求直线于点B,过点A作平行于y轴的直线交x轴于点C,过点B作BD⊥AC则由上可知:=90°由双垂直模型知:△OCA∽△ADB ∴ ∵A(2,1),=45°∴OC=2,AC=1,AO=AB ∴AD=OC=2,BD=AC=1 ∴D点坐标为(2,3)∴B点坐标为(1,3) ∴此时正比例函数表达式为:y=3x 第二种情况,图象经过第二、四象限 过点A作AB⊥OA,交待求直线于点B,过点A作平行于x轴的直线交y轴于点C,过点B作BD⊥AC 则由上可知:=90°由双垂直模型知:△OCA∽△ADB ∴
中考数学压轴题解题策略(3) 直角三角形的存在性问题解题策略 《挑战压轴题·中考数学》的作者上海马学斌 专题攻略 解直角三角形的存在性问题,一般分三步走,第一步寻找分类标准,第二步列方程,第三步解方程并验根. 一般情况下,按照直角顶点或者斜边分类,然后按照三角比或勾股定理列方程. 有时根据直角三角形斜边上的中线等于斜边的一半列方程更简便. 解直角三角形的问题,常常和相似三角形、三角比的问题联系在一起. 如果直角边与坐标轴不平行,那么过三个顶点作与坐标轴平行的直线,可以构造两个新的相似直角三角形,这样列比例方程比较简便. 在平面直角坐标系中,两点间的距离公式常常用到. 怎样画直角三角形的示意图呢?如果已知直角边,那么过直角边的两个端点画垂线,第三个顶点在垂线上;如果已知斜边,那么以斜边为直径画圆,直角顶点在圆上(不含直径的两个端点). 例题解析 例?如图1-1,在△ABC中,AB=AC=10,cos∠B=4 5 .D、E为线段BC上的两个 动点,且DE=3(E在D右边),运动初始时D和B重合,当E和C重合时运动停止.过E 作EF//AC交AB于F,连结DF.设BD=x,如果△BDF为直角三角形,求x的值. 图1-1 【解析】△BDF中,∠B是确定的锐角,那么按照直角顶点分类,直角三角形BDF存在两种情况.如果把夹∠B的两条边用含有x的式子表示出来,分两种情况列方程就可以了.如图1-2,作AH⊥BC,垂足为H,那么H是BC的中点. 在Rt△ABH中,AB=10,cos∠B=4 5 ,所以BH=8.所以BC=16. 由EF//AC,得BF BE BA BC =,即 3 1016 BF x+ =.所以BF= 5 (3) 8 x+. 图1-2 图1-3 图1-4
一、相似三角形中的动点问题 1.如图,在Rt△ ABC中,∠ACB=90°,AC=3,BC=4,过 点B作射线BB1∥AC.动点D 从点A 出发沿射线AC方向 以每秒5 个单位的速度运动,同时动点E 从点C沿射线 AC 方向以每秒3个单位的速度运动.过点D作DH⊥AB 于H,过点E作EF⊥ AC交射线BB1于F,G是EF中点, 连接DG.设点D 运动的时间为t 秒. (1)当t 为何值时,AD=AB,并求出此时DE的长度; (2)当△DEG与△ACB 相似时,求t 的值. 点P从A点出发,沿着AB以每秒4cm的速度向B点运 动;同时点Q从C点出发,沿CA以每秒3cm 的速度向A 点运动,当P点到达B点时,Q 点随之停止运动.设运动 的时间为x. (1)当x 为何值时,PQ∥ BC? (2)△APQ 与△CQB能否相似?若能,求出AP的长; 若不能说明理由. 2.如图,在△ ABC中,ABC=90°,AB=6m,BC=8m, 动点P 以2m/s 的速度从A 点出发,沿AC 向点C 移 动.同时,动点Q以1m/s的速度从C点出发,沿CB向 点B移动.当其中有一点到达终点时,它们都停止移 动.设移动的时间为t 秒. (1)① 当t=2.5s 时,求△ CPQ的面积; ② 求△ CPQ的面积S(平方米)关于时间t(秒)的函数 解析式; (2)在P,Q 移动的过程中,当△CPQ为等腰三角形 时,求出t 的值. 5.如图,在矩形ABCD 中,AB=12cm,BC=6cm,点P 沿 AB 边从A 开始向点B 以2cm/s 的速度移动;点Q 沿DA 边从点D开始向点A以1cm/s 的速度移动.如果P、Q 同 时出发,用t(s)表示移动的时间(0< t <6)。 (1)当t 为何值时,△ QAP为等腰直角三角形?(2) 当t 为何值时,以点Q、A、P 为顶点的三角形与△ABC 相似? 3.如图1,在Rt△ ABC中,ACB=90°,AC=6,BC=8, 点D 在边AB 上运动,DE 平分CDB交边BC 于点E, EM⊥ BD,垂足为M,EN⊥CD,垂足为N. (1)当AD=CD 时,求证:DE∥AC; (2)探究:AD 为何值时,△BME与△CNE相似? 二、构造相似辅助线——双垂直模型 6.在平面直角坐标系xOy 中,点A 的坐标为(2,1), 正比例函数y=kx 的图象与线段OA 的夹角是45°,求这个 正比例函数的表达式. 7.在△ABC中,AB= ,AC=4, BC=2,以AB 为边在 C点的异侧作△ABD,使△ABD 为等腰直角三角形, 4.如图所示,在△ ABC中,BA=BC=20cm,AC=30cm ,
解题技巧专题:等腰三角形中辅助线的作法 ——形成精准思维模式,快速解题 ◆类型一利用“三线合一”作辅助线 一、已知等腰作垂线(或中线、角平分线) 1.如图,在△ABC中,AB=AC,AE⊥BE于点E,且∠ABE=∠ABC.若BE=1,则BC的长为________. 2.如图,在△ABC中,AC=2AB,AD平分∠BAC交BC于点D,E是AD上一点,且EA=EC,连接EB,求证:EB⊥AB. 二、构造等腰三角形 3.如图,在△ABC中,BP平分∠BAC,且AP⊥BP于点P,连接CP.若△PBC的面积为2,则△ABC的面积为() A.3 B.4 C.5 D.6 4.如图,已知△ABC是等腰直角三角形,∠A=90°,BD平分∠ABC交AC于点D,CE⊥BD,交BD的延长线于点E.求证:BD=2CE.
◆类型二 巧用等腰直角三角形构造全等 5.如图,在△ABC 中,AC =BC ,∠C =90°,D 是AB 的中点,DE ⊥DF ,点E ,F 分别在AC ,BC 上.求证:DE =DF . ◆类型三 等腰(边)三角形中截长补短或作平行线构造全等 6.(2017·郑州校级月考)如图,过等边△ABC 的边AB 上一点P ,作PE ⊥AC 于点E ,Q 为BC 延长线上一点,且P A =CQ ,连 接PQ 交AC 于点D .若△ABC 的边长为6,则 DE 的长为【方法8】( ) A .2 B .3 C .4 D .不能确定 7.如图,在△ABC 中,AB =AC ,∠A =108°,BD 平分∠ABC 交AC 于点D .求证:BC =AB +CD . 参考答案与解析 1.2 2.证明:过点E 作EF ⊥AC 于点F .∵EA =EC ,∴AF =FC =12 AC .∵AC =2AB ,∴AF =AB .∵AD 平分∠BAC ,∴∠BAE =∠F AE .又∵AE =AE ,∴△ABE ≌△AFE (SAS),∴∠ABE =∠AFE =90°,∴EB ⊥AB .
相似三角形解题方法、技巧、步骤 一、相似、全等的关系 全等和相似是平面几何中研究直线形性质的两个重要方面,全等形是相似比为1的特殊相似形,相似形则是全等形的推广.因而学习相似形要随时与全等形作比较、明确它们之间的联系与区别;相似形的讨论又是以全等形的有关定理为基础. 二、相似三角形 (1)三角形相似的条件: ①;②;③. 三、两个三角形相似的六种图形: 只要能在复杂图形中辨认出上述基本图形,并能根据问题需要舔加适当的辅助线,构造出基本图形,从而使问题得以解决. 四、三角形相似的证题思路:判定两个三角形相似思路: 1)先找两对内角对应相等(对平行线型找平行线),因为这个条件最简单; 2)再而先找一对内角对应相等,且看夹角的两边是否对应成比例; 3)若无对应角相等,则只考虑三组对应边是否成比例; 找另一角两角对应相等,两三角形相似 找夹边对应成比例两边对应成比例且夹角 相等,两三角形相似 找夹角相等两边对应成比例且夹角相等,两三角形相似 找第三边也对应成比例三边对应 成比例,两三角形相似 找一个直角斜边、直角边对应成比例,两个直角三角形相似 找另一角两角对应相等,两三角形相似 找两边对应成比例判定定理1或判定定理 4 找顶角对应相等判定定理1 找底角对应相等判定定理1 找底和腰对应成比例判定定理3 e)相似形的传递性若△1∽△2,△2∽△3,则△1∽△3 五、“三点定形法”,即由有关线段的三个不同的端点来确定三角形的方法。具体做法是:先看比例式前项和后项所代表的两条线段的三个不同的端点能否分别确定一个三角形,若能,则只要证明这两个三角形相似就可以了,这叫做“横定”;若不能,再看每个比的前后两项的两条线段的两条线段的三个不同的端点能否分别确定一个三角形,则只要证明这两个三角形相似就行了,这叫做“竖定”。 有些学生在寻找条件遇到困难时,往往放弃了基本规律而去乱碰乱撞,乱添辅助线,这样反而使问题复杂化,效果并不好,应当运用基本规律去解决问题。 例1、已知:如图,ΔABC 中,CE ⊥AB,BF ⊥AC. 求证:BA AC AF AE = (判断“横定”还是“竖定”?) 例2、如图,CD 是Rt △ABC 的斜边AB 上的高,∠BAC 的 平分线分别交BC 、CD 于点E 、F ,AC ·AE=AF ·AB 吗? 说明理由。 分析方法: 1)先将积式______________ 2)______________(“横定”还是“竖定”?) 例1、 已知:如图,△ABC 中,∠ ACB=900 ,AB 的垂直平分线交AB 于D ,交BC 延长线于F 。 求证:CD 2 =DE ·DF 。 分析方法: 1)先将积式______________ 2)______________(“横定”还是“竖定”?) 六、过渡法(或叫代换法) 有些习题无论如何也构造不出相似三角形,这就要考虑灵活地运用“过渡”,其主要类型有三种,下面分情况说明. 1、 等量过渡法(等线段代换法) 遇到三点定形法无法解决欲证的问题时,即如果线段比例式中的四条线段都在图形中的同一条直线上,不能组成三角形,或四条线段虽然组成两个三角形,但这两个三角形并不相似,那就需要根据已知条件找到与比例式中某条线段相等的一条线段来代替这条线段,如果没有,可考虑添加简单的辅助线。然后再应用三点定形法确定相似三角形。只要代换得当,问题往往可以得到解决。当然,还要注意最后将代换的线段再代换回来。 例1:如图3,△ABC 中,AD 平分∠BAC , AD 的垂直平分线FE 交BC 的延长线于E .求证:DE 2=BE·CE . 分析: 2、 等比过渡法(等比代换法) 当用三点定形法不能确定三角形,同时也无等线段代换时,可以考虑用等比代换法,即考虑利用第三组线段的比为比例式搭桥,也就是通过对已知条件或图形的深入分析,找到与求证的结论中某个比相等的比,并进行代换,然后再用三点定形法来确定三角形。 例2:如图4,在△ABC 中,∠BAC=90°,AD ⊥BC ,E 是AC 的中点,ED 交AB 的延长线于点F . 求证:AB DF AC AF =. a)已知一对等b)己知两边对应成比 c)己知一个直d)有等腰关
题目 在凸四边形ABCD 中,60ABC ∠=?,AB BC =,30ADC ∠=?。 证明:222AD CD BD +=。 分析:待证结论让我们联想到勾股定理,需要通过添加辅助线将AD 、CD (作 为直角边)和BD (作为斜边)集中到一个直角三角形里。 图1 图2 证明1:如图1,过D 作DE DA ⊥,且使得ED CD =,连接AE 、CE 、AC 903060CDE ADE ADC ∠=∠-∠=?-?=? ∴CDE ?是等边三角形 ∴CE CD =,60DCE ∠=? 60ABC ∠=?,AB BC = ∴ABC ?是等边三角形 ∴AC BC =,60BCA ∠=? ∴ACE ACD DCE ACD BCA BCD ∠=∠+∠=∠+∠=∠ ∴ACE ?≌BCD ?(SAS ) ∴AE BD = 在Rt ADE ?中,222AD ED AE += ∴222AD CD BD += 评注:意外的是,添加辅助线后原图回到了一个经典(老)问题的图上—两个有公共顶点的等边三角形(不看AD ,试试?)!另外,也可以按如下方式作辅助线:如图2,过D 作DE DC ⊥,且使得ED AD =,连接CE 、AE 、AC (过程基本同证明1,不赘述)。 D B B D B D
图3 图4 证明2:如图3,过C 作CE CD ⊥,且使得CE AD =,连接DE 、BE 360360BCE ECD BCD ABC ADC BCD BAD ∠=?-∠-∠=?-∠-∠-∠=∠ BC BA = ∴BCE ?≌BAD ?(SAS ) ∴BE BD =,CBE ABD ∠=∠ ∴60DBE ABC ∠=∠=? ∴DBE ?是等边三角形 ∴ED BD = 在Rt DCE ?中,222CE CD ED += ∴222AD CD BD += 评注:明白作辅助线的初衷和目的后,问题解决将得心应手,也可以按如下方式作辅助线:如图4,过A 作AE AD ⊥,且使得AE CD =,连接DE 、BE (过程基本同证明2,不赘述)。 后记:1、证明1的图可以看成以CD 为边作等边三角形CDE ,证明2的图可以看成以BD 为边作等边三角形BDE ,你能理解为什么作等边三角形吗? 2、图1可以看成是将BCD ?绕点C 沿顺时针方向旋转60?到ACE ?,图3可以看成是将ABD ?绕点B 沿顺时针方向旋转60?到CBE ?,你能理解为什么旋转60?吗?其实,从旋转的视角来看待本题,过程将十分简洁:如图3,将ABD ?绕点B 沿顺时针方向旋转60?到CBE ?,连接DE ,易知DBE ?是等边三角形,故ED BD =, 由于D C E D B E C E B C D B A B C A D B C ∠=∠+∠+∠=∠+∠+∠603090=?+?=?(凹四边形),所以2 2 2 CE CD ED +=,从而2 2 2 AD CD BD +=。 相关题目如图,在ABC ?中,90ABC ∠=?,AB CB =,45DBE ∠=?D 、E 是AC 上两点。试证明:222 AD CE DE +=。 请务必督促孩子今晚进行独立思考,下午辅导课时在黑板上已抄过B B
勾股定理与勾股定理逆定理典型例题 类型一、勾股定理的构造应用 例1、如图,已知:在中,,,. 求:BC 的长. 思路点拨:由条件,想到构造含角的直角三角形 总结反思: 举一反三【变式1】已知:如图,∠B=∠D=90°,∠A=60°,AB=4,CD=2。求:四边形ABCD的面积。 【变式2】
类型二:方程的思想方法 例1、如图所示,已知△ABC 中,∠C=90°,∠A=60°, ,求、、的值。 思路点拨:由,再找出、的关系即可求出和的值 总结升华: 举一反三: 【变式1】如图,四边形ABCD 中,∠ACB=90O ,CD ⊥AB 于点D ,若AD=8,BD=2, 求CD 的长度。 【变式2 】C A
类型三:转化的思想方法 我们在求三角形的边或角,或进行推理论证时,常常作垂线,构造直角三角形,将问题转化为直角三角形问题来解决. 例1.如图所示,△ABC 是等腰直角三角形,AB=AC ,D 是斜边BC 的中点,E 、F 分别是AB 、AC 边上的点,且DE ⊥DF ,若BE=12,CF=5.求线段EF 的长。 思路点拨:现已知BE 、CF ,要求EF ,但这三条线段不在同一三角形中,所以关键是线段的转化,根据直角三角形的特征,三角形的中线有特殊的性质,不妨先连接AD . 总结升华: 【变式1】如图,已知:,,于P . 求证:. 【变式2】如图,ADC ?和BCE ?都是等边三角形, 30=∠ABC , 求证:2 22BC AB BD +=
3. 类型五:利用勾理作长为 的线段 例1. 作长为、、的线段。 思路点拨:由勾股定理得,直角边为1的等腰直角三角形,斜边长就等于 ,直角边为和1的直角三角形斜边长就是,类似地可作D C B A
第27章.相似——专训2:巧作平行线构造相似三角形 名师点金:解题时,往往会遇到要证的问题与相似三角形联系不上或者说图中根本不存在相似三角形的情况,做平行线构造相似三角形是这类几何证明题的一种重要方法.常作的平行线有以下几种:(1)由比例式作平行线;(2)有中点时,作中位线;(3)根据比例式,构造相似三角形. 巧连线段的中点构造相似三角形 1.如图,在△ABC 中,E ,F 是边BC 上的两个三等分点,D 是AC 的中点,BD 分别交AE ,AF 于点P ,Q ,求BP :PQ : QD. (第1题 ) 过顶点作平行线构造相似三角形 2.如图,在△ABC 中,AC =BC ,F 为底边AB 上一点,BF :AF =3:2,取CF 的中点D ,连接AD 并延长交BC 于点E ,求BE EC 的值. (第2题) 3.如图,已知△ABC 中,AD 为BC 边上中线,过C 任作一条直线交AD 于E ,交AB 于F ,求证:AE :ED=2AF :FB . (第3题 ) 过一边上的点作平行线构造相似三角形 4.如图,在△ABC 中,AB >AC ,在边AB 上取一点D ,在AC 上取一点E ,使AD =AE ,直线DE 和BC 的延长线交于点P.求证:BP CP =BD EC . (第4题 ) 过一点作平行线构造相似三角形 5.如图,在△ABC 中,点M 为AC 边的中点,点E 为AB 上一点,且AE =1 4 AB ,连接EM 并延 长交BC 的延长线于点D.求证:BC =2CD. 作辅助线的方法一: (第5题①) 作辅助线的方法二: (第5题②) 作辅助线的方法三: (第5题③) 作辅助线的方法四: (第5题④)
相似三角形解题思路赏析(3.29) 姓名_______ 评价 内容解读:人们在对两个物体或图形的形状和大小进行认识时,全等和相似的感知是伴生的.在数学上全等和相似是特殊与一般、共性与个性的关系,形状相同是二者的共性.全等形是相似比等于1时的相似形;同时我们应学会应用两个三角形相似的判定方法去解决问题。 例题讲解: 1、如图,在Rt △ABC 内有边长分别为,,a b c 的三个正方形,则,,a b c 满足的关系式是( ) A 、b a c =+ B 、b ac = C 、2 2 2 b a c =+ D 、22b a c == 2、已知矩形ABCD 的边长3cm 6cm AB BC ==,.某一时刻,动点M 从A 点出发沿AB 方向以1cm/s 的速度向B 点匀速运动;同时,动点N 从D 点出发沿DA 方向以2cm /s 的速度向A 点匀速运动,问:(1)经过多少时间,AMN △的面积等于矩形ABCD 面积的 1 9 ? (2)是否存在时刻t ,使以A M N ,,为顶点的三角形与ACD △ 相似?若存在,求t 的值;若不存在,请说明理由. 3、如图1,在Rt ABC △中,90BAC ∠=°,AD BC ⊥于点D ,点O 是AC 边上一点,连接BO 交AD 于F ,OE OB ⊥交BC 边于点E . (1)求证:ABF COE △∽△; (2)当O 为AC 边中点,2AC AB =时,如图2,求 OF OE 的值; (3)当O 为AC 边中点,AC n AB =时,请直接写出 OF OE 的值. 4、已知9023ABC AB BC AD BC P ∠===°,,,∥,为线段BD 上的动点,点Q 在射线AB 上,且满足PQ AD PC AB = (如图1所示). B A D E C O F 图2 B A C E D 图1 F
思想方法中考题型 一、方程思想 根据题意设适当的未知数,从已知和未知中寻求等量关系,构造出方程或方程组,从而使问题获解. 例1如图1,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,又知河宽CD为50米.现需从山顶A到河对岸点C拉一条笔直的缆绳AC,求缆绳AC的长(答案可带根号). 解:过A点作AB⊥CD交CD的延长线于点B,设AB=x 在Rt△ABC中,因为∠ACB=∠CAE=30°,所以AC=2ABC=2x,BC=3AB=3x 在Rt△ABD中,因为∠ADB=∠EAD=45°,所以DB=AB=x 因为CD=50,所以 解得x=25(1+3)。答:缆绳AC的长为() 5013 +米. 说明先得出边角之间的关系,再构造方程求解,这是直角三角形的边角关系应用的常见方法,应值得注意. 二、数形结合思想 将数量和图形巧妙结合来寻找解题思路 例2如图2,A、B、C表示建筑在一座比较险峻的名山上的三个缆车站的位置,AB、BC表示连接三个缆车站的钢缆。已知A、B、C所处位置的海拔高度分别为124m、400m、1100m,如图建立直角坐标系,即A(a,124)、B(b,400)、C(c, 1100),若直线AB的解析式为y=1 2x+4,直线BC与水平线BC1的交角为45°. ⑴分别求出A、B、C三个缆车站所在位置的坐标; ⑵求缆车从B站出发到达C站单向运行的距离(精确到1m). A(240,124)、B(792,400)、C(2192,1100);(2)7002≈990(米). 三、转化思想 抽象转化为具体,复杂转化为简单、未知转化为已知,通过变换迅速而合理的寻找和选择问题解决的途径和方法. 例3如图3,学校旗杆附近有一斜坡.小明准备测量学校旗杆AB的高度,他发现当斜坡正对着太阳时,旗杆AB的影子恰好落在水平地面和斜坡的坡面上,此时小明测得水平地面上的影长BC=20米,斜坡坡面上的影长CD=8米,太阳光线AD与水平地面成26°角,斜坡CD与水平地面成30°的角.求旗杆AB的高度(精确到1米).(tan26°=0.43) 解:延长AD、BC交于点E,过点D作DF⊥CE于F.则依据题意可知,∠E=°,∠DCE=°。 在Rt△CFD中,得DF=4,CF=43≈6.928, 在Rt△DFE中, 在Rt△ABE中, 答:旗杆AB的高度约为. 四、建模思想 所谓建模思想就是认真分析题意,将实际问题抽象、转化为数学问题,建立数学模型,再通过对数学模型的探索达到解决问题的目的. 例4如图4,MN表示一段高速公路的设计路线图.在点M测得点N在它的南偏东30°的方向.测得另一点A在它的南偏东60°的方向;取MN上另一点B,在点B测得点A在它的南偏东75°的方向.以点A为圆心,500m为半径的圆形区域为某居民区.已知MB=400m,通过计算回答:如果不改变方向,高速公路是否会穿过居民区? 解:过点A作AC⊥MN于点C.依题意,得∠AMC=60°-30°=30°,∠ABC=75°-30°=45°.设AC为x m, 图2 B A 图4 M 30° 60° 75° 北 北 N C 图1 F 图3 E D C B A
相似三角形之常用辅助线 在与相似有关的几何证明、计算的过程中,常常需要通过相似三角形,研究两条线段之间的比例关系,或者转移线段或角。而有些时候,这样的相似三角形在问题中,并不是十分明显。因此,我们需要 通过添加辅助线,构造相似三角形,进而证明所需的结论。 专题一、添加平行线构造“ A ”“X ”型 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原三角形相似. 定理的基本图形: 例1、平行四边形ABCD中, E为AB中点,AF: FA 1 : 2,求AG GC
变式练习: 如图,直线交厶ABC的BC,AB两边于D,E,与CA延长线交于F,若—;;=2,求BE:EA的比 值. 例3、BE^ AD,求证:EF- BO AC- DF 变式练习: 已知在△ ABC中,AD是/ BAC的平分线.求证: AB BD AC CD BD 例2、如图,直线交△ ABC的BC,AB两边于D,E,与CA延长线交于F,若 - DC FC =2,求BE:EA的比值. FA (本题有多种解法,多想想)
变式1、如图,△ ABC中,AB 说明:此题充分展示了添加辅助线,构造相似形的方法和技巧?在解题中方法要灵活,思路要开阔. 总结:(1)遇燕尾,作平行,构造.字一般行。 (2)引平行线应注意以下几点: 1)选点:一般选已知(或求证)中线段的比的前项或后项,在冋一直线的线段的端点作为引平行 线的点。 2)引平行线时尽量使较多已知线段、求证线段成比例。 专题二、作垂线构造相似直角三角形 基本图形 例1、如图, ABC 中,AB AC, BD AC,那么BC22CA CD吗?试说明理由?(用多种 构造相似基本恩图形,为解题打开一扇智慧之门 相似三角形问题解答时,常遇到或构造一个重要解题基本图形,这个基本图形构成元件非常简单,但是这个图形的解题内涵非常丰富,能为很多问题的破解提供强有力的方法支撑.一起走进这个基本图形. 一、认识基本图形 如图1,在△ABC中,点D,E分别是AB,AC上的点,且DE∥BC.则△ADE∽△ABC. 常见基本结论: 一“=”型比例式: AD:BD=AE:EC;AD:AB=AE:AC;AD:AE=BD:CE. 连“=”型比例式: AD:AB=AE:AC=DE:BC. 二、基本图形的解题应用 (一).直接应用型 1.1探求被截线段的长度 例1 (2019年四川内江市)如图2,在△ABC中,DE∥BC,AD=9,DB=3,CE=2,则AC的长为() A.6 B.7 C.8 D.9 解析:因为DE∥BC,所以=,即=,所以AE=6,所以AC=AE+EC=6+2=8. 所以选C. 点评:这是平行线分线段成比例定理的简易图形,是定理的一个重要缩影,更是解题的一个重要工具性图形,识记图形是基础,活用图形解题是根本,据图正确选择比例式是解题的关键. 1.2探求与截线平行线段的长度 例2 (2019年广西贺州市)如图3,在△ABC中,D,E分别是AB,AC边上的点,DE∥BC,若AD=2,AB=3,DE=4,则BC等于() A.5 B.6 C.7 D.8 解析: 因为DE∥BC,所以△ADE∽△ABC,所以=,即=,解得:BC=6,所以选B. 点评:基本图形中,当求与截线平行的线段长时,要转换解题思路,把平行线分线段成比例定理转型为“A”字型的三角形相似问题解决,这种转化思想很重要. 1.3探求非比例线段,非平行线段的线段的长度 例3 (2019年广西贵港市)如图4,在△ABC中,点D,E分别在AB,AC边上,DE∥BC,∠ACD=∠B,若AD=2BD,BC=6,则线段CD的长为() A.2B.3C.2D.5 解析:设AD=2x,BD=x,所以AB=3x,因为DE∥BC,所以△ADE∽△ABC,所以=,所以=,所以DE=4,=,因为∠ACD=∠B, ∠ADE=∠B,所以∠ADE=∠ACD,因为∠A=∠A,所以△ADE∽△ACD, 所以=,设AE=2y,AC=3y,所以=,所以AD=y, 所以=,所以CD=2,所以选:C. 点评:在“A”字型基本图形中解题,实现三个维度的目标:一是三角形相似,构造连等比例式;二是巧妙引进未知数表示未知线段,化抽象线段为具体表达线段,利于计算;三是依托基本图形为基础,提供新条件,为新三角形的相似奠基,为问题的最终解决搭桥. 1.4 甄别比例式 例4 (2019年浙江省杭州市)如图5,在△ABC中,点D,E分别在AB和AC上,DE∥BC,M 为BC边上一点(不与点B,C重合),连接AM交DE于点N,则() A.=B.=C.=D.= 构造等腰三角形解题的常见途径 等腰三角形是研究几何图形的基础,因此在许多几何问题中,常常需要构造等腰三角形才能使问题获解,那么如何构造等腰三角形呢?一般说来有以下几种途径: 一、利用角平分线+平行线,构造等腰三角形 当一个三角形中出现角平分线和平行线时,我们就可以寻找到等腰三角形.如图1①中,若AD 平分∠BAC ,AD ∥EC ,则△ACE 是等腰三角形;如图1②中,AD 平分∠BAC ,DE ∥AC ,则△ADE 是等腰三角形;如图1③中,AD 平分∠BAC ,CE ∥AB ,则△ACE 是等腰三角形;如图1④中,AD 平分∠BAC ,EF ∥AD ,则△AGE 是等腰三角形. 例1 如图2,△ABC 中,AB =AC ,在AC 上取点P ,过点P 作EF ⊥BC ,交BA 的延 长线于点E ,垂足为点F .求证:.AE =AP . 简析 要证.AE =AP ,可寻找一条角平分线与EF 平行,于是想到AB =AC ,则可以作AD 平分∠BAC ,所以AD ⊥BC ,而EF ⊥BC ,所以AD ∥EF ,所以可得到△AEP 是等腰三角形,故AE =AP . 例2 如图3 ,在△ABC 中,∠BAC 、∠BCA 的平分线相交于点O ,过点O 作DE ∥AC ,分别交AB 、BC 于点 D 、 E .试猜想线段AD 、CE 、DE 的数量关系,并说明你的猜想 C A B E D O 图3 图4 F C D E B A M 图2 F B A C D P E 图1 ① D ② C D C ④ F C D 理由. 简析 猜想:AD +CE =DE .理由如下:由于OA 、OC 分别是∠BAC 、∠BCA 的平分线,DE ∥AC ,所以△ADO 和△CEO 均是等腰三角形,则DO =DA ,EC =EO ,故AD +CE =DE . 例3 如图4,△ABC 中,AD 平分∠BAC ,E 、F 分别在BD 、AD 上,且DE =CD ,EF =AC .求证:EF ∥AB . 简析 由于这里要证明的是EF ∥AB ,而AD 平分∠BAC ,所以必须通过辅助线构造出平行线,这样就可以得到等腰三角形了,于是DE =CD 的提示下,相当于倍长中线,即延长AD 至M ,使DM =AD ,连结EM ,则可证得△MDE ≌△ADC ,所以ME =AC ,又EF =AC ,∠M =∠CAD ,所以∠M =∠EFM ,即∠CAD =∠EFM ,又因为AD 平分∠BAC ,所以∠BAD =∠EFD =∠CAD ,所以EF ∥AB . 二、利用角平分线+垂线,构造等腰三角形 当一个三角形中出现角平分线和垂线时,我们就可以寻找到等腰三角形.如图5中,若AD 平分∠BAC ,AD ⊥DC ,则△AEC 是等腰三角形. 例4 如图6,已知等腰R t△ABC 中,AB =AC ,∠BAC =90°,BF 平分∠ABC ,CD ⊥BD 交BF 的延长线于D .求证:BF =2CD . 简析 由BF 平分∠ABC ,CD ⊥BD ,并在图5的揭示之下,延长线BA 、CD 交于点E ,于是△BCE 是等腰三角形,并有ED =CD ,余下来的问题只需证明BF =CE ,而事实上,由∠BAC =90°,CD ⊥BD ,∠AFB =∠DFC ,得∠ABF =∠DCF ,而AB =AC ,所以△ABF ≌△ACE ,则BF =CE ,故BF =2CD . 三、利用转化倍角,构造等腰三角形 E 图5 A B C D 图6 B F D E C A 构造直角三角形巧解题 山东省博兴县锦秋街道清河学校 张海生 256500 有些几何题,若能仔细观察、把握特征、抓住本质、恰当地构造直角三角形进行转化,就会收到化难为易、事半功倍的效果.下面举例介绍构造直角三角形解题的若干常用方法,供同学们复习时参考. 一、利用已知直角构造直角三角形 例1:如图1,在四边形ABCD 中,∠A=060,∠B=∠D=090,AB=2,CD=1.则BC 和AD 的长分别为_______和_______. 解析:考虑到图中含有090和060的角,若延长AD 、BC 相交于E ,则可以构造出Rt △AEB 和Rt △CED ,易知∠E=030,从而可求出DE=3,AE=4,BE=23,故AD=4-3,BC=23-2. 二、利用勾股定理构造直角三角形 例2:如图2,在四边形ABCD 中,AB=AD=8,∠A=060,∠ADC=0150,已知四边形ABCD 的周长为32,求四边形ABCD 的面积. 解析:四边形ABCD 是一个不规则的四边形,要求其面积,可设法变成特殊的三角形求解.连接BD ,则△ABD 是等边三角形, △BDC 是直角三角形,由于AB=AD=BD=8,,求△ABD 的面积不难解决,关键是求△BDC 的面积.可运用周长和勾股定理联合求出DC ,从而求出△BDC 的面积. 解答:连接BD.∵AB=AD ,∠A=060,∴△ABD 是等边三角形. ∴∠ADB=060,BD=AD=AB=8. 因为∠ADC=0150,∴∠BDC=090, 故△BDC 是直角三角形, 因为四边形ABCD 的周长为32, AB=AD=8, ∴BC+DC=32-16=16,BC=16-DC. 在Rt △BDC 中,222BC DC BD =+, 即()222168DC DC -=+.解得DC=6. ∴248621=??=?B DC S .用勾股定理求出等边△ABD 的高为3482 3=?. 3163482 1=??=?A B D S .∴24316+=+=??B DC A B D A B CD S S S 四. 说明:⑴求不规则的图形面积应用割补法把图形分解为特殊的图形;⑴四边形中通过添加辅助线构造直角三角形;⑶边长为a 的等边三角形的高为a 23,面积为24 3a . 三、利用高构造直角三角形 例3:如图3,等腰△ABC 的底边长为8cm ,腰长为5cm ,一动点P 在底边上从B 向C 以0.25cm/s 的速度移动,请你探究:当P 运动几秒时,P 点与顶点A 的连线PA 与腰垂直. 解析:本题是一道探究性的动态问题,假设P 在某一时刻有PA ⊥AC ,此时P 点运动了几秒,这是解决问题的着手点.设BP=x ,PC=8-x ,在Rt △PAC 中,由于PA 不知道,无法建立关系式.考虑△ABC 是等腰三角形,如作底边上的高AD ,则可用x 的代数式表示AP ,用勾股定理便可求出x ,进而求出运动时间.当P 点运动到D 与C 之间时,也存在AP ⊥AB 的情况,故要分类 讨论. 解答:作底边BC 的高AD ,则AD ⊥BC ,垂足为D. 设BP=xcm ,PA ⊥AC. 图1 图2 图3 平行线及角平分线类相似 中考要求 重难点 1.相似定义,性质,判定,应用和位似 2.相似的判定和证明 3.相似比的转化 课前预习 上一节课我们知道了相似三角形的由来,那你是否知道其他跟金子塔有关的不可思议的事实呢? 不仅建造金字搭的技术中,表现了古埃及人的非凡的数学天才;而且,它本身的许多数据,也说明了古埃及人的数学才华,巧夺天工,比如,胡夫金字塔底面周长365米,恰好是一年的天娄;周长乘以2,正是赤道的时分度;搭高乘以10九次方,正是地球到太阳的距离;周长除以塔塔高的2倍,正是圆周率3.1415926……;塔的自重乘以10的15次方,正好是地球的重量;塔里放置的棺材內部尺寸,正好是几千年后希腊数学家华连哥拉斯发现华连哥拉斯数——345 ∶∶. 数学的趣味是无法言语的,同学们可以从身边的点滴去发现其中的奥秘. 例题精讲 模块一 平行线类相似问题 平行线类相似的基本模型有 ?模型一、二类综合题 【例1】 如图,在ABC △中,M 是AC 的中点,E 是AB 上一点,且1 4 AE AB = ,连接EM 并延长,交BC 的延长线于D ,则 BC CD =____ ___. M E C B A 【难度】3星 【解析】先介绍常规的解法: B C F E D M A B C F E D M A 如图,过点C 作DE 或AB 的平行线均可,不妨以左图为例来说明. 过点C 作//CF DE ,交AB 于点F . ∵AM MC =,//CF DE ∴AE EF = ∵14AE AB = ∴2BF EF = ∵//CF DE ∴ 2BC BF CD EF == 当然,过点M 、点E 作适当的平行线,均可作出此题,这里不再给出. 构造等腰三角形解题的辅助线做法 吕海艳 等腰三角形是一种特殊的三角形,常与全等三角形的相关知识结合在一起考查。在许多几何问题中,通常需要构造等腰三角形才能使问题获解。那么如何构造等腰三角形呢一般有以下四种方法: (1)依据平行线构造等腰三角形; (2)依据倍角关系构造等腰三角形; (3)依据角平分线+垂线构造等腰三角形; (4)依据120°角或60°角,常补形构造等边三角形。 1、依据平行线构造等腰三角形 例1:如图。△ABC中,AB=AB,E为AB上一点,F为AC延长线上一点,且BE=CF,EF交BC于D,求证DE=DF. [点拔]:若证DE=DF,则联想到D是EF的中点,中点的两旁容易构造全等三角形,方法是过E或F作平行线,构造X型的基本图形,只需证两个三角形全等即可。 " 证明:过E作EG∥AC交BC于G ∴∠1=∠ACB,∠2=∠F ∵AB=AC ∴∠B=∠ACB ∴∠1=∠B ∴BE=GE ∵BE=CF ∴GE=CF 在△EDG和△FDC中 ∠3=∠4 ∠2=∠F ( GE=CF ∴△EDG≌△FDC ∴DE=DF [评注]:此题过E作AC的平行线后,构造了等腰△BEG,从而达到转化线段的目的。 2、依据倍角关系构造等腰三角形 例2:如图。△ABC中,∠ABC=2∠C,AD是∠BAC的平分线 求证:AB+BD=AB [点拔]:在已知条件中出现了一个角是另一个角的2倍,可延长CB,构造等腰三角形,问题即可解决。 证明:延长CB至E,使BE=BA, 连接AE ( ∵BE=BA ∴∠BAE=∠E ∵∠ABC=2∠C, ∠ABC=∠E+∠BAE=2∠E ∴∠C=∠E AC=AE ∵AD平分∠BAC ∴∠1=∠2 ∴∠EAD=∠BAE+∠1=∠E+∠1=∠C+∠2=∠BDA ∴EA=ED ∵ED=EB+BD,EB=AB,AC=AE ∴AC=AB+BD …北师版数学九年级上册相似三角形---构造相似基本恩图形,为解题打开一扇智慧之门
构造等腰三角形解题的常见途径(新)
构造直角三角形来解题
平行线及角平分线类相似
构造等腰三角形解题的辅助线做法