
切线长定理、弦切角定理、切割线定理、相交弦定理
以及与圆有关的比例线段
[学习目标] 1.切线长概念
切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。 2.切线长定理
对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。
3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。
直线AB 切⊙O 于P ,PC 、PD 为弦,图中几个弦切角呢?(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。
5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。
6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。
7.与圆有关的比例线段 定理 图形 已知 结论 证法 相交弦定理
⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB .
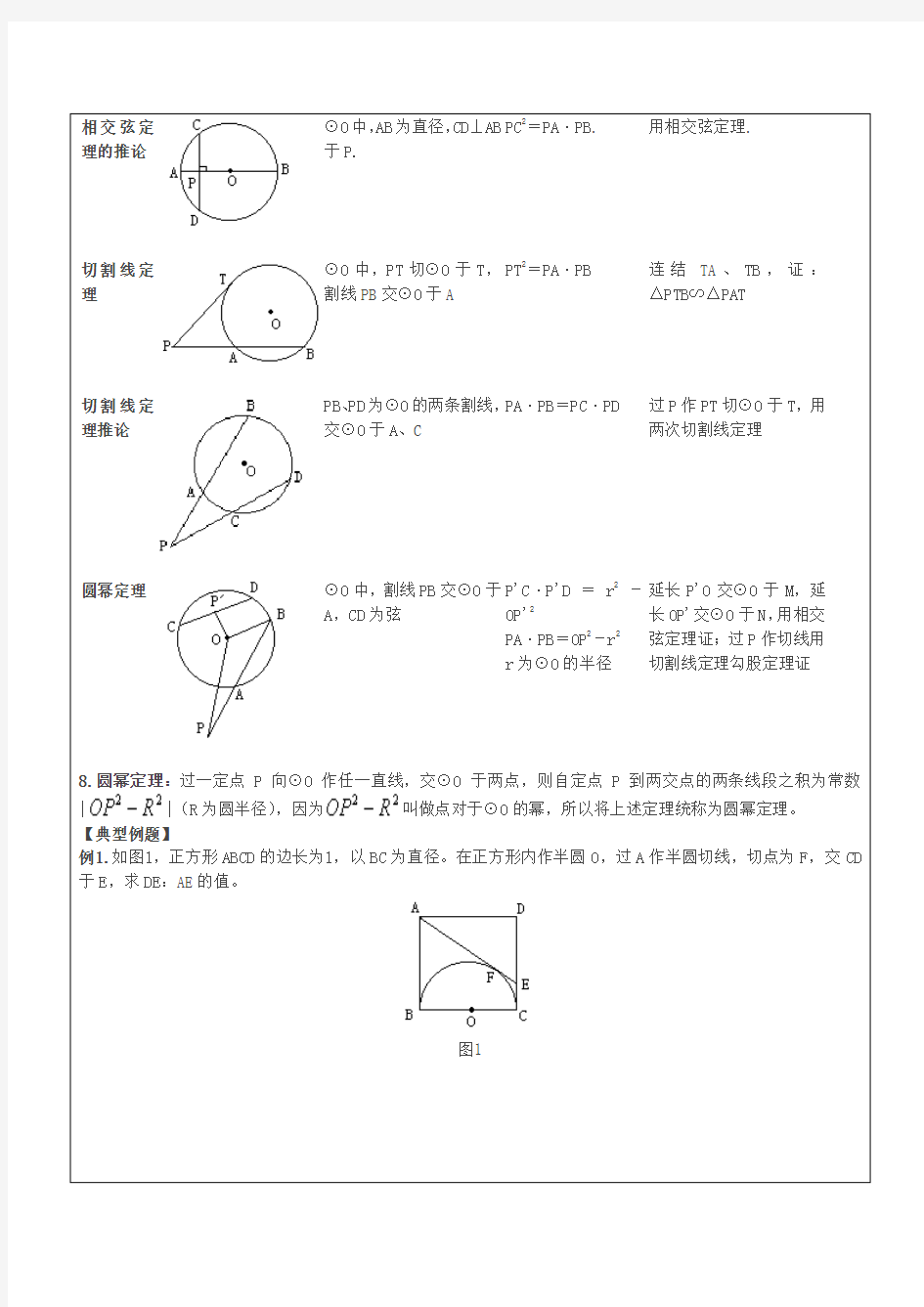
相交弦定理的推论
⊙O 中,AB 为直径,CD⊥AB 于P.
PC 2
=PA·PB . 用相交弦定理.
切割线定理
⊙O 中,PT 切⊙O 于T ,割线PB 交⊙O 于A
PT 2
=PA·PB 连结TA 、TB ,证:△PTB∽△PAT
切割线定理推论
PB 、PD 为⊙O 的两条割线,交⊙O 于A 、C
PA·PB=PC·PD 过P 作PT 切⊙O 于T ,用两次切割线定理
圆幂定理
⊙O 中,割线PB 交⊙O 于A ,CD 为弦 P'C·P'D =r 2
-OP'2
PA·PB=OP 2-r 2
r 为⊙O 的半径 延长P'O 交⊙O 于M ,延
长OP'交⊙O 于N ,用相交
弦定理证;过P 作切线用切割线定理勾股定理证
8.圆幂定理:过一定点P 向⊙O 作任一直线,交⊙O 于两点,则自定点P 到两交点的两条线段之积为常数||(R 为圆半径),因为叫做点对于⊙O 的幂,所以将上述定理统称为圆幂定理。 【典型例题】
例1.如图1,正方形ABCD 的边长为1,以BC 为直径。在正方形内作半圆O ,过A 作半圆切线,切点为F ,交CD 于E ,求DE :AE 的值。
图1
例2.⊙O中的两条弦AB与CD相交于E,若AE=6cm,BE=2cm,CD=7cm,那么CE=_________cm。
图2
例3.已知PA是圆的切线,PCB是圆的割线,则________。
例4.如图3,P是⊙O外一点,PC切⊙O于点C,PAB是⊙O的割线,交⊙O于A、B两点,如果PA:PB=1:4,PC=12cm,⊙O的半径为10cm,则圆心O到AB的距离是___________cm。
图3
例5.如图4,AB为⊙O的直径,过B点作⊙O的切线BC,OC交⊙O于点E,AE的延长线交BC于点D,(1)求证:;(2)若AB=BC=2厘米,求CE、CD的长。
图4
例6.如图5,AB为⊙O的直径,弦CD∥AB,AE切⊙O于A,交CD的延长线于E。
图5
求证:
例7.如图6,PA、PC切⊙O于A、C,PDB为割线。求证:AD·BC=CD·AB
图6
点悟:由结论AD·BC=CD·AB得,显然要证△PAD∽△PBA和△PCD∽△PBC
例8.如图7,在直角三角形ABC中,∠A=90°,以AB边为直径作⊙O,交斜边BC于点D,过D点作⊙O的切线交AC于E。
图7
求证:BC=2OE。
例9.如图8,在正方形ABCD中,AB=1,是以点B为圆心,AB长为半径的圆的一段弧。点E是边AD上的任
意一点(点E与点A、D不重合),过E作所在圆的切线,交边DC于点F,G为切点。
当∠DEF=45°时,求证点G为线段EF的中点;
图8
【模拟试题】
一、选择题
1.已知:PA、PB切⊙O于点A、B,连结AB,若AB=8,弦AB的弦心距3,则PA=()
A. B. C. 5 D. 8
2.下列图形一定有内切圆的是()
A.平行四边形
B.矩形
C.菱形
D.梯形
3.已知:如图1直线MN与⊙O相切于C,AB为直径,∠CAB=40°,则∠MCA的度数()
图1
A. 50°
B. 40°
C. 60°
D. 55°
4.圆内两弦相交,一弦长8cm且被交点平分,另一弦被交点分为1:4,则另一弦长为()
A. 8cm
B. 10cm
C. 12cm
D. 16cm
5.在△ABC中,D是BC边上的点,AD,BD=3cm,DC=4cm,如果E是AD的延长线与△ABC的外接圆的交点,那么DE长等于()
A. B.
C. D.
6. PT切⊙O于T,CT为直径,D为OC上一点,直线PD交⊙O于B和A,B在线段PD上,若CD=2,AD=3,BD=4,则PB等于()
A. 20
B. 10
C. 5
D.
二、填空题
7. AB、CD是⊙O切线,AB∥CD,EF是⊙O的切线,它和AB、CD分别交于E、F,则∠EOF=_____________度。
8.已知:⊙O和不在⊙O上的一点P,过P的直线交⊙O于A、B两点,若PA·PB=24,OP=5,则⊙O的半径长为_____________。
9.若PA为⊙O的切线,A为切点,PBC割线交⊙O于B、C,若BC=20,,则PC的长为_____________。
10.正△ABC内接于⊙O,M、N分别为AB、AC中点,延长MN交⊙O于点D,连结BD交AC于P,则
_____________。
三、解答题
11.如图2,△ABC中,AC=2cm,周长为8cm,F、K、N是△ABC与内切圆的切点,DE切⊙O于点M,且DE∥AC,求DE的长。
图2
12.如图3,已知P为⊙O的直径AB延长线上一点,PC切⊙O于C,CD⊥AB于D,求证:CB平分∠DCP。
图3
13.如图4,已知AD为⊙O的直径,AB是⊙O的切线,过B的割线BMN交AD的延长线于C,且BM=MN=NC,若AB,求⊙O的半径。
1、如图,BD为圆O的直径,直线ED为圆O的切线,A、C两点在圆上,AC平分∠BAD且交BD于F点.若∠ADE=19°,则∠AFB的度数为何?()
A、97°
B、104°
C、116°
D、142°
2、如图为△ABC和一圆的重迭情形,此圆与直线BC相切于C点,且与AC交于另一点D.若∠A=70°,∠B=60°,则错误!未找到引用源。的度数为何()
A、50°
B、60°
C、100°
D、120°
3、如图,CD是⊙O的切线,T为切点,A是错误!未找到引用源。上的一点,若∠TAB=100°,则∠BTD的度数为()
A、20°
B、40°
C、60°
D、80°
4、如图,四边形ABCD内接于⊙O,AB=BC.AT是⊙O的切线,∠BAT=55°,则∠D等于()
A、110°
B、115°
C、120°
D、125°
5、如图,直线AD与△ABC的外接圆相切于点A,若∠B=60°,则∠CAD等于()
A、30°
B、60°
C、90°
D、120°
6、如图,△ABC是⊙O的内接三角形,AD是⊙O的切线,点A为切点,∠ACB=60°,则∠DAB的度数是()
A、30°
B、45°
C、60°
D、120°
7、已知:如图,E是相交两圆⊙M和⊙N的一个交点,且ME⊥NE,AB为外公切线,切点分别为A,B连接AE,BE,则∠AEB的度数为()
A、145°
B、140°
C、135°
D、130°
8、如图,直线AB切⊙O于点A,割线BDC交⊙O于点D、C.若∠C=30°,∠B=20°,则∠ADC=()
A、70°
B、50°
C、30°
D、20°
9、如图,PA、PB、DE分别与⊙O相切,若∠P=40°,则∠DOE等于()度.
A、40
B、50
C、70
D、80
10、如图,P为半⊙O直径BA延长线上一点,PC切半⊙O于C,且PA:PC=2:3,则sin∠ACP的值为_______
11、如图AB是⊙O的直径,DE为⊙O的切线,切点为B,点C在⊙O上,若∠CBE=40°,则∠A的度数为( )
A、30°
B、40°
C、50°
D、60°
12、如图,△ABC内接于⊙O,BD切⊙O于点B,AB=AC,若∠CBD=40°,则∠ABC等于()
A、40°
B、50°
C、60°
D、70°
13、如图,AB、CD是⊙O的两条平行弦,BE∥AC交CD于E,过A点的切线交DC延长线于P,若AC= 32则PC?CE的值是()
A、18
B、6
C、62
D、93
14、如图,AB为⊙O的直径,C、D为⊙O上的点,直线MN切⊙O于C点,图中与∠BCN互余的角有()
A、1个
B、2个
C、3个
D、4个
15、点P是⊙O外一点,PA、PB分别切⊙O于点A、B,∠P=70°,点C是⊙O上的点(不与点A、B重合),则∠ACB等于()
A、70°
B、55°
C、70°或110°
D、55°或125°
16、如图,AB是⊙O的直径,DB、DE分别切⊙O于点B、C,若∠ACE=25°,则∠D的度数是()
A、50°
B、55°
C、60°
D、65°
17、如图,在⊙O中,AB是弦,AC是⊙O切线,过B点作BD⊥AC于D,BD交⊙O于E点,若AE平分∠BAD,则∠ABD的度数是()
A、30°
B、45°
C、50°
D、60°
二、填空题(共13小题)
18、如图,已知AD为⊙O的切线,⊙O的直径是AB=2,弦AC=1,则∠CAD=_________度.
19、已知⊙O中,错误!未找到引用源。的度数为70°,过点A的直线AC与⊙O相切,则弦切角∠BAC的度数为_________.
20、如图,AB切⊙O于C,AO交⊙O于D,AO的延长线交⊙O于E,若∠A=α,则∠ECB=_________(用含α的式子表示).
20题21题22题23题
21、如图,△ABC内接于圆⊙O,CT切⊙O于C,∠ABC=100°,∠BCT=40°,则∠AOB=___度.
22、如图,割线PAB过圆心O,PD切⊙O于D,C是错误!未找到引用源。上一点,∠PDA=20°,则∠C的度数是______度.
23、如图,PA、PB是⊙O的两条切线,A、B为切点,则∠ABO﹣错误!未找到引用源。∠ABP=
___.
24、如图,四边形ABED内接于⊙O,E是AD延长线上的一点,若∠AOC=122°,则∠B=_________度,
∠EDC=_________度.
25、如图,已知AB是⊙O的弦,AC切⊙O于点A,∠BAC=60°,则∠ADB的度数为_________度.
26、如图,AB为⊙O直径,CE切⊙O于点C,CD⊥AB,D为垂足,AB=12cm,∠B=30°,则∠ECB=_________度;CD=_________cm.
27、如图,已知AB是圆O的弦,AC是圆O的切线,∠BAC的平分线交圆O于D,连BD并延长交AC于点C,若∠DAC=40°,则∠B=_________度,∠ADC=_________度.
28、如图,PA切⊙O于A点,C是弧AB上任意一点,∠PAB=58°,则∠C的度数是_________度.
29、如图,EF切△ABC的外接圆于C,∠BAC=80°,那么∠BCE=_________度.
30、已知:如图,在⊙O中,AB是直径,四边形ABCD内接于⊙O,∠BCD=130°,过D点的切线PD与直线AB交于点P,则∠ADP的度数为_________.
1.垂径定理及推论: 如图:有五个元素,“知二可推三”;需记忆其中四个定理, 即“垂径定理”“中径定理”“弧径定理”“中垂定理”. 几何表达式举例: ∵ CD过圆心 ∵CD⊥AB 2.平行线夹弧定理: 圆的两条平行弦所夹的弧相等. 几何表达式举例: 3.“角、弦、弧、距”定理:(同圆或等圆中) “等角对等弦”;“等弦对等角”; “等角对等弧”;“等弧对等角”; “等弧对等弦”;“等弦对等(优,劣)弧”; “等弦对等弦心距”;“等弦心距对等弦”. 几何表达式举例: (1) ∵∠AOB=∠COD ∴ AB = CD (2) ∵ AB = CD ∴∠AOB=∠COD 4.圆周角定理及推论: (1)圆周角的度数等于它所对的弧的度数的一半; (2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图) (3)“等弧对等角”“等角对等弧”; (4)“直径对直角”“直角对直径”;(如图) (5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如 图) (1)(2)(3)(4) 几何表达式举例: (1)∵∠ACB=∠AOB ∴…………… (2)∵ AB是直径 ∴∠ACB=90° (3)∵∠ACB=90° ∴ AB是直径 (4)∵ CD=AD=BD ∴ΔABC是RtΔ 5.圆内接四边形性质定理: 圆内接四边形的对角互补,并且任何一个外 角都等于它的内对角. 几何表达式举例: ∵ ABCD是圆内接四边形 ∴∠CDE =∠ABC ∠C+∠A =180° 6.切线的判定与性质定理: 如图:有三个元素,“知二可推一”;需记忆其中四个定理. (1)经过半径的外端并且垂直于这条 半径的直线是圆的切线; (2)圆的切线垂直于经过切点的半径; ※(3)经过圆心且垂直于切线的直线必经过切点; ※(4)经过切点且垂直于切线的直线必经过圆心. 几何表达式举例: (1)∵OC是半径∵OC⊥AB ∴AB是切线 (2)∵OC是半径 ∵AB是切线 ∴OC⊥AB (3)…………… 7.切线长定理: 从圆外一点引圆的两条切线, 它们的切线长相等;圆心和这一 点的连线平分两条切线的夹角. 几何表达式举例: ∵ PA、PB是切线 ∴ PA=PB ∵PO过圆心 ∴∠APO =∠BPO 8.弦切角定理及其推论: 几何表达式举例:
蔡甸区常福中学九年级数学下册教学案 课题:几何计算专题复习--与圆有关的定理 第13周 主备人:袁劲梅 教研组长:向俊伟 审核人______ 授课人: 袁劲梅 授课时间2017.5.28 编号______ 学案 教案 一、课堂导入: 本节课我们学习几何知识里几个新的定理,进一步掌握这些定理的推导和灵活运用。 二、揭示目标: 学生齐读学习目标,了解本节课的学习内容及应达到的目标。 三、合作探究: 1、小组合作探究(讨论质疑) 学生合作完成该部分题目。①要求小组各成员都能不同程度的解答各题,先完成的帮助后进生,老师巡视了解学生的完成情况;②选代表上台讲解解法。 2、组间合作探究(交流释疑) 各组成员可随意请求质疑或发表不同解法; 四、归纳小结 总结:本节课学习了与圆有关的几个定理: 弦切角定理 切割线定理 射影定理 1、熟练掌握这些定理的推导过程; 2、通过这些定理结论,直接解题,提高解题速 一、考点分析 此题型为中考题中的第21题圆的综合题,主要考查圆与直角三角形、切线有关定理、三角函数、相似的计算,命题极为灵活,考查知识面广,有一定的难度。结合图形特征利用定理结论求线段的长度是必考的知识点。 二、学习目标 1、学习一些新的定理,并推导出结论。 2、能够灵活运用这些结论解决圆中线段的长,角的三角函数的计算。 三、课堂前置 如图:在⊙O 中,弦AB 、CD 相交于P, 求证:PA ·PB=PC ·PD 四、课堂新授 知识一:弦切角定理 如图,已知PC 为⊙O 的切线,PBA 为割线. 求证:∠1=∠A 例1:如图:PA 、PB 与⊙O 相切与A 、B 两点,C 为优弧AB 上的一点,若tan ∠ACB=2,则sin ∠APB 的值为______.
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 【课前测试】 1. PT 切⊙O 于T ,CT 为直径,D 为OC 上一点,直线PD 交⊙O 于B 和A ,B 在线段PD 上,若CD =2,AD =3,BD =4,则PB 等于( ) A. 20 B. 10 C. 5 D. 【知识点回顾】 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。 2.切线长定理 对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角:顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB 切⊙O 于P ,PC 、PD 为弦,图中几个弦切角呢?(四个) 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。 5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。 7.与圆有关的比例线段 定理 图形 已知 结论 证法 相交弦定理 ⊙O 中,AB 、CD 为弦,交于P. PA·PB=PC·PD . 连结AC 、BD ,证:△APC∽△DPB . 相交弦定理的推论 ⊙O 中,AB 为直径,CD⊥AB 于P. PC 2 =PA·PB . 用相交弦定理.
切线长定理、弦切角定理、切割线定理、相交弦定理 以及与圆有关的比例线段 1.切线长概念 切线长是在经过圆外一点的圆的切线上,这点和切点之间的线段的长度,“切线长”是切线上一条线段的长,具有数量的特征,而“切线”是一条直线,它不可以度量长度。 2.切线长定理 如图1对于切线长定理,应明确(1)若已知圆的两条切线相交,则切线长相等;(2)若已知两条切线平行,则圆上两个切点的连线为直径;(3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形;(4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补;(5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 3.弦切角(如图2):顶点在圆上,一边和圆相交,另一边和圆相切的角。 直线AB切⊙O于P,PC、PD为弦,图中几个弦切角呢?(四个)∠APC,∠APD,∠BPD,∠BPC 4.弦切角定理:弦切角等于其所夹的弧所对的圆周角。即如上图中∠APC=∠CDP等 证明:如图2,连接CD、OC、OP,因为∠CPO=∠PCO,所以∠COP=180?-2∠CPO而∠CPO=90?-∠APC,故∠COP=2∠5.弄清和圆有关的角:圆周角,圆心角,弦切角,圆内角,圆外角。 6.遇到圆的切线,可联想“角”弦切角,“线”切线的性质定理及切线长定理。 7.与圆有关的比例线段 定理图形已知结论证法 相交 弦定 理 ⊙O 中,AB、 CD为 弦,交于 P. PA·PB=PC·PD 连结AC、BD,∠C=∠B,∠A=∠D, 所以△APC∽△DPB 相交 弦定 理的 推论 ⊙O中, AB为直 径,C D⊥AB 于P. PC2=PA·PB 用相交弦定理. 切割 线定 理 ⊙O 中,PT切 ⊙O于T, 割线PB 交⊙O于 A PT2=PA·PB 连结TA、TB,则∠PTA=∠B(弦 切角等于同弧圆周角)所以 △PTA∽△PBT,所以 PT2=PA·PB 图1 图2
1.圆的周长C=2πr=πd 2.圆的面积S=πr2 3.扇形弧长l=nπr/180 4.扇形面积S=nπr2/360=rl/2 5.圆锥侧面积S=πrl 〖圆的定义〗 几何说:平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径。 轨迹说:平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆。 集合说:到定点的距离等于定长的点的集合叫做圆。 〖圆的相关量〗 圆周率:圆周长度与圆的直径长度的比叫做圆周率, 值是 3.141592653589793238462643383279502884197169399375105820974944 5923078164062862089986280348253421170679..., 通常用π表示,计算中常取3.14为它的近似值(但奥数常取3或3.1416)。 圆弧和弦:圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。 圆心角和圆周角:顶点在圆心上的角叫做圆心角。顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。 内心和外心:过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。 扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。圆锥侧面展开图是一个扇形。这个扇形的半径成为圆锥的母线。 〖圆和圆的相关量字母表示方法〗 圆—⊙半径—r 弧—⌒直径—d 扇形弧长/圆锥母线—l 周长—C 面积—S 〖圆和其他图形的位置关系〗 圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r。
费尔巴赫定理 费尔巴赫定理三角形的九点圆与内切圆内切,而与旁切圆外切。 此定理由德国数学家费尔巴赫(K·W·Feuerbach,1800—1834)于1822年提出。 费尔巴赫定理的证明 在不等边△ABC中,设O,H,I,Q,Ia分别表示△ABC的外心,垂心,内心,九点圆心和∠A所对的旁切圆圆心.s,R,r,ra分别表示△ABC的半周长,外接圆半径,内切圆半径和∠A 所对的旁切圆半径,BC=a,CA=b,AB=c. 易得∠HAO=|B-C|,∠HAI=∠OAI=|B-C|/2; AH=2R*cosA,AO=R,AI=√[(s-a)bc/s],AIa=√[sbc/(s-a)] 在△AHI中,由余弦定理可求得: HI^2=4R^2+4Rr+3r^2-s^2; 在△AHO中,由余弦定理可求得: HO^2=9R^2+8Rr+2r^2-2s^2; 在△AIO中,由余弦定理可求得: OI^2=R(R-2r). ∵九点圆心在线段HO的中点, ∴在△HIO中,由中线公式可求得. 4IQ^2=2(4R^2+4Rr+3r^2-s^2)+ 2(R^2-2Rr)-(9R^2+8Rr+2r^2-2s^2) =(R-2r)^2 故IQ=(R-2r)/2. 又△ABC的九点圆半径为R/2, 所以九点圆与内切圆的圆心距为 d=R/2-r=(R-2r)/2=IQ. 因此三角形的九点圆与内切圆内切。 在△AHIa中,由余弦定理可求得: IaH^2=4R^2+4Rr+r^2-s^2+2(ra)^2; 在△AOIa中,由余弦定理可求得: IaO^2=R(R+2ra). 在△HIaO中,由中线公式可求得. 4IaQ^2=2(4R^2+4Rr+r^2-s^2+2ra^2)+2(R^2+2Rra)-(9R^2+8Rr+2r^2-2s^2)=(R+2ra) ^2 故IaQ=(R+2ra)/2.
高图教育数学教研组卢老师专用 - 1 - 《圆》知识点及定理 一、圆的概念 集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合 轨迹形式的概念: 1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; (补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内?dr??点C在圆内; 2、点在圆上?dr??点B在圆上; 3、点在圆外?dr??点A在圆外; 三、直线与圆的位置关系 1、直线与圆相离?dr??无交点; 2、直线与圆相切?dr??有一个交点; 3、直线与圆相交?dr??有两个交点;
d r d=r rd 四、圆与圆的位置关系 外离(图1)?无交点?dRr??; 外切(图2)?有一个交点?dRr??; 相交(图3)?有两个交点?RrdRr????;内切(图4)?有一个交点?dRr??; 内含(图5)?无交点?dRr??; 图1rRd
五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即: ①AB是直径②ABCD?③CEDE?④弧BC?弧BD⑤弧AC?弧AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 即:在⊙O中,∵AB∥CD ∴弧AC?弧BD Rd rddCBAO图2rRd图Rd图dOEDCBA OCDAB. 高图教育数学教研组卢老师专用
弦切角定理 一、弦切角 1、弦切角定义:顶点在圆上,一边和圆相交,另一边和圆相切的角叫做(弦切角就是与弦所夹的角) 如右图所示,直线PT切圆O于点C,BC、AC为圆O的弦,∠TCB,∠TCA,∠PCA,∠PCB都为弦切角。 二、弦切角定理 1、弦切角定理:弦切角的度数等于它所夹的弧的圆心角的度数的一半 2、弦切角定理证明(分三种情况讨论): 已知:AC是⊙O的弦,AB是⊙O的切线,A为切点,弧是弦切角∠BAC所夹的弧. 求证:弦切角定理 ①圆心O在∠BAC的一边AC上 ∵AC为直径,AB切⊙O于A, ∴弧CmA=弧CA ∵为半圆, ∴∠CAB=90=弦CA所对的圆周角 ②圆心O在∠BAC的内部 过A作直径AD交⊙O于D,若在优弧m所对的劣弧上有一点E,连接EC、ED、EA ∴∠CED=∠CAD ∠DEA=∠DAB ∴∠CEA=∠CAB B ③圆心O在∠BAC的外部, 过A作直径AD交⊙O于D ∴∠CDA+∠CAD=∠CAB+∠CAD=90 ∴∠CDA=∠CAB 三、弦心角推论 1、推论内容:若两弦切角所夹的弧相等,则这两个弦切角也相等 2、应用: Eg.如图,ΔABC内接于⊙O,AB是⊙O直径,CD⊥AB于D,MN切⊙O于C 求证:AC平分∠MCD,BC平分∠NCD. 证明:∵AB是⊙O直径 ∴∠ACB=90 ∵CD⊥AB ∴∠ACD=∠B, ∵MN切⊙O于C ∴∠MCA=∠B, ∴∠MCA=∠ACD, 即AC平分∠MCD,
同理:BC平分∠NCD. 圆幂定理——相交弦定理 一、相交弦定理 1、相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等) 几何语言: ∵弦AB、CD交于点P ∴PA·PB=PC·PD(相交弦定理) 1、推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的 比例中项的概念:如果a、b、c三个量成连比例即a:b=b:c,b叫做a和c的比例中项。 2、性质:b2=a*c 几何语言: ∵AB是直径,CD垂直AB于点P ∴PC2=PA·PB(相交弦定理推论) 二、相交弦定理证明 证明:连结AC,BD 由的推论 得∠A=∠D,∠C=∠B(推论2: 同(等)弧所对圆周角相等) ∴△PAC∽△PDB, ∴PA∶PD=PC∶PB,PA·PB=PC·PD 圆幂定理——切割线定理 一、切割线定理 1、切割线定理:从圆外一点引圆的和,切线长是这点到割线与圆交点的两条线段长的 几何语言: ∵PT切⊙O于点T,PBA是⊙O的割线 ∴PT2=PA·PB(切割线定理) 2、推论:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 几何语言: ∵PBA,PDC是⊙O的割线 ∴PD·PC=PA·PB(切割线定理推论)/() 由上可知:PT2=PA·PB 即PT2=PC·PD 二、切割线定理证明 已知:如图ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T, 证明:PT2=PA·PB 证明:连接AT, BT ∵∠PTB=∠PAT() ∠P=∠P(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB:PT=PT:AP 即:PT2=PA·PB 圆幂定理——割线定理 一、割线定理
几何B级概念:(要求理解、会讲、会用,主要用于填空和选择题) 一基本概念:圆的几何定义和集合定义、弦、弦心距、弧、等弧、弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、三角形的内心、圆心角、圆周角、弦切角、圆的切线、圆的割线、两圆的内公切线、两圆的外公切线、两圆的内(外)公切线长、正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角. 二定理:
1.不在一直线上的三个点确定一个圆. 2.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆. 3.正n 边形的半径和边心距把正n 边形分为2n 个全等的直角三角形. 三 公式: 1.有关的计算:(1)圆的周长C=2πR ;(2)弧长L= 180 R n π;(3)圆的面积S=πR 2 . (4)扇形面积S 扇形 =LR 2 1 360R n 2=π; (5)弓形面积S 弓形 =扇形面积S AOB ±ΔAOB 的面积.(如图) 2.圆柱与圆锥的侧面展开图: (1)圆柱的侧面积:S 圆柱侧 =2πrh ; (r:底面半径;h:圆柱高) (2)圆锥的侧面积:S 圆锥侧 =LR 21 . (L=2πr ,R 是圆锥母线长;r 是底面半径) 四 常识: 1. 圆是轴对称和中心对称图形. 2. 圆心角的度数等于它所对弧的度数. 3. 三角形的外心 ? 两边中垂线的交点 ? 三角形的外接圆的圆心; 三角形的内心 ? 两内角平分线的交点 ? 三角形的内切圆的圆心. 4. 直线与圆的位置关系:(其中d 表示圆心到直线的距离;其中r 表示圆的半径) 直线与圆相交 ? d <r ; 直线与圆相切 ? d=r ; 直线与圆相离 ? d >r. 5. 圆与圆的位置关系:(其中d 表示圆心到圆心的距离,其中R 、r 表示两个圆的半径且R ≥r ) 两圆外离 ? d >R+r ; 两圆外切 ? d=R+r ; 两圆相交 ? R-r <d <R+r ; 两圆内切 ? d=R-r ; 两圆内含 ? d <R-r. 6.证直线与圆相切,常利用:“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线. 7.关于圆的常见辅助线:
圆幂定理 定义 圆幂=PO^2-R^2(该结论为欧拉公式) 所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。 割线定理:从圆外一点P引两条割线与圆分别交于A、B;C、D,则有PA·PB=PC·PD。 统一归纳:过任意不在圆上的一点P引两条直线L1、L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D(可重合),则有PA·PB=PC·PD。 相交弦定理 圆内的两条相交弦,被交点分成的两条线段长的积相等。(经过圆内一点引两条弦,各弦被这点所分成的两段的积相等) 相交弦说明 几何语言: 若弦AB、CD交于点P 则PA·PB=PC·PD(相交弦定理) 推论:如果弦与直径垂直相交,那么弦的一半是它分
直径所成的两条线段的例中项 几何语言: 若AB是直径,CD垂直AB于点P,则PC^2=PA·PB(相交弦定理推论) 切割线定理 定义 从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。是圆幂定理的一种。 几何语言: ∵PT切⊙O于点T,PBA是⊙O的割线 ∴PT的平方=PA·PB(切割线定理)推论: 从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等 几何语言: ∵PT是⊙O切线,PBA,PDC是⊙O的割线 ∴PD·PC=PA·PB(切割线定理推论)(割线定理) 由上可知:PT∧2(平方)=PA·PB=PC·PD 证明 切割线定理证明: 设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则 PT^2=PA·PB 证明:连接AT, BT ∵∠PTB=∠PAT(弦切角定理) ∠P=∠P(公共角) ∴△PBT∽△PTA(两角对应相等,两三角形相似) 则PB:PT=PT:AP 即:PT^2=PB·PA 割线定理 定义 从圆外一点引圆的两条割线,这一点到每条割线 与圆交点的距离的积相等。
初三数学中考复习《与圆有关几个定理》教学设计 一. 教学内容: 圆有关定理 1. 圆的内容包括:圆的有关概念和基本性质,直线和圆的位置关系,。 2. 主要定理: (1)垂径定理及其推论。 (2)圆心角、弧、弦、弦心距之间的关系定理。 (3)圆周角定理、弦切角定理及其推论。 (4)切线的性质 (5)切线判定定理 (5)切线长定理 二. 中考聚焦: 圆这一章六个定理圆的知识在中考中所占的比例大,题型多,常见的有填空题、选择题、计算题或证明题,近年还出现了一些圆的应用题及开放型问题、设计型问题,中考的压轴题都综合了圆的知识。 三. 知识框图: 圆的有关性质 圆的定义 点和圆的位置关系(这是重点) 不在同一直线上的三点确定一个圆 圆的有关性质 轴对称性—垂径定理(这是重点) 旋转不变性 圆心角、弧、弦、弦心距间的关系 圆心角定理 圆周角定理(这是重点) 圆内接四边形(这是重点) ? ? ? ? ? ? ? ? ? ? ? ? ? ?? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 直线和圆的位置关系 相离 相交 相切 切线的性质(这是重点) 切线的判定(这是重点) 弦切角(这是重点) 和圆有关的比例线段(这是重点难点) ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 四.重点知识讲解:
1.垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即: ①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 即:在⊙O 中,∵AB ∥CD 同步自测 1、已知 ⊙ O 中,弦AB 垂直于直径CD , 垂足为P ,AB=6,CP=1,则 ⊙ 的半径----。 2.已知 ⊙ O 的直径为10cm,A 是⊙ O 内一点,且OA=3cm,则 ⊙ O 中过点A 的最短弦 长=------------- cm 2.圆周角定理 1、圆周角定理:同弧所对的圆周角等于它所对的圆心的角的一半。 即:∵AOB ∠和ACB ∠是弧AB 所对的圆心角和圆周角 ∴2AOB ACB ∠=∠ 2、圆周角定理的推论: 推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧是等弧; B D
关于圆的几个定理 1. 四点共圆 1.1定义:若四边形ABCD 的四点同时共于一圆上,则称A ,B ,C ,D 四点共圆 基本性质:若凸四边形ABCD 是圆内接四边形,则其对角互补 1.2定义:若存在一点O 使OA=OB=OC=OD ,则A ,B ,C ,D 四点共圆 2.若干定理 圆幂定理是圆的相交弦定理、切割线定理、割线定理、切线长定理的统一形式。 相交弦定理:P 是圆内任一点,过P 作圆的两弦AB ,CD ,则PA PB PC PD ?=? (切)割线定理:P 是圆外任意一点,过P 任作圆的两割(切)线PAB ,PCD ,则 PA PB PC PD ?=? 圆幂定理:P 是圆O 所在平面上任意一点(可以在圆内,圆上,圆外),过点P 任作一直线交圆O 于A ,B 两点(A ,B 两点可以重合,也可以之一和P 重合), 圆O 半径为r ,则有:22||PA PB PO r ?=- 圆内接四边形判定方法 相交弦定理逆定理:如果四边形ABCD 的对角线AC ,BD 交于点P ,且满足 PA PC PB PD ?=?,则四边形ABCD 有一外接圆
切割线定理逆定理:如果凸四边形ABCD 一双对边AB 与DC 交于点P 且满足PA PC PB PD ?=?,则四边形ABCD 有一外接圆 射影定理:RTΔABC 中,BC 是斜边,AD 是斜边上的高,则 222(1)(2)(3)AD BD CD AB BD BC AC CD BC =?=?=? Miquel 定理:ΔABC 中,X ,Y ,Z 分别是直线AB ,BC ,AC 上的点,则 ,,共于一点AXZ BXY CYZ O 这样的点O 称为X ,Y ,Z 对于ΔABC 的Miquel 点 Simson 定理
托勒密定理 定理图 定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质. 定理的提出 一般几何教科书中的“托勒密定理”,实出自依巴谷(Hipparchus)之手,托勒密只是从他的书中摘出。 证明 一、(以下是推论的证明,托勒密定理可视作特殊情况。) 在任意四边形ABCD中,作△ABE使∠BAE=∠CAD ∠ABE=∠ ACD 因为△ABE∽△ACD 所以 BE/CD=AB/AC,即BE·AC=AB·CD (1) 而∠BAC=∠DAE,,∠ACB=∠ADE 所以△ABC∽△AED相似. BC/ED=AC/AD即ED·AC=BC·AD (2) (1)+(2),得 AC(BE+ED)=AB·CD+AD·BC 又因为BE+ED≥BD (仅在四边形ABCD是某圆的内接四边形时,等号成立,即“托勒密定理”) 所以命题得证 复数证明 用a、b、c、d分别表示四边形顶点A、B、C、D的复数,则AB、CD、AD、BC、AC、BD 的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。首先注意到复数恒等式:(a ? b)(c ? d) + (a ? d)(b ? c) = (a ? c)(b ? d) ,两边取模,运用三角不等式得。等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。四点不限于同一平面。平面上,托勒密不等式是三角不等式的反演形式。 二、设ABCD是圆内接四边形。在弦BC上,圆周角∠BAC = ∠BDC,而在AB上,∠ADB = ∠ACB。在AC上取一点K,使得∠ABK = ∠CBD;因为∠ABK + ∠CBK = ∠ABC = ∠CB D + ∠ABD,所以∠CBK = ∠ABD。因此△ABK与△DBC相似,同理也有△ABD ~ △KBC。
一些圆的性质及定理 圆的基本性质 平面上到定点距离等于定长的点的集合 周长2πr(滚一圈),面积πr2(微元法) 切、割、弦、角 切线长定理 1)若已知圆的两条切线相交,则切线长相等; 2)若已知两条切线平行,则圆上两个切点的连线为直径; 3)经过圆外一点引圆的两条切线,连结两个切点可得到一个等腰三角形; 4)经过圆外一点引圆的两条切线,切线的夹角与过切点的两个半径的夹角互补; 5)圆外一点与圆心的连线,平分过这点向圆引的两条切线所夹的角。 圆周角定理 圆周角定理指的是一条弧所对圆周角等于它所对圆心角的一半。(连接圆心和三点,利用等腰三角形。同时定理说明同一条弧所对的圆周角是相等的) 弦切角定理 弦切角等于它所夹的弧所对的圆心角的一半,等于它所夹的弧所对的圆周角。(利用切点半径垂直于切线和半径相等构成等腰三角形) 圆内角和相交弦定理 1)圆内角:圆的两条弦在圆内相交所成的角叫做圆内角。 2)相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等或经过圆内一点引两条弦,各弦被这点所分成的两线段的积相等。(对两个对顶圆内角作所在的三角形证相似) 切割线定理 切割线定理是指从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。(通过连接切点和割线与圆的交点,利用弦切角定理证明相似) 圆外角和割线定理 1)圆外角:过圆外一点作圆的两条割线所成的角叫做圆外角。 2)割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。 (过圆外角定点作圆切线,用两次切割线定理) 圆幂定理 过一定点P作直线交⊙O于两点,点P与两交点所成线段长度乘积等于|OP2-r2|。(该定理是相交弦、切割线和割线定理的统一,可以分情况一一证明) 圆和三角形 三角形内心和内切圆 1)内心:三个内角角分线交点,记I 内心到三边距离相等(AAS),记r 2)内切圆:以内心为圆心半径为r的圆 三边所在直线为内切圆切线。
关于圆的几个定理 1.四点共圆 1.1定义:若四边形ABCD的四点同时共于一圆上,则称A,B,C,D四点共圆基本性质:若凸四边形ABCD是圆内接四边形,则其对角互补 1.2定义:若存在一点O使OA=OB=OC=OD,则A,B,C,D四点共圆 2.若干定理 圆幂定理是圆的相交弦定理、切割线定理、割线定理、切线长定理的统一形式。相交弦定理:P是圆内任一点,过P作圆的两弦AB,CD,则PA PB PC PD ?=? (切)割线定理:P是圆外任意一点,过P任作圆的两割(切)线PAB,PCD,则 PA PB PC PD ?=?
圆幂定理:P 是圆O 所在平面上任意一点(可以在圆内,圆上,圆外),过点P 任作一直线交圆O 于A ,B 两点(A ,B 两点可以重合,也可以之一和P 重合), 圆O 半径为r ,则有:22||PA PB PO r ?=- 圆内接四边形判定方法 相交弦定理逆定理:如果四边形ABCD 的对角线AC ,BD 交于点P ,且满足 PA PC PB PD ?=?,则四边形ABCD 有一外接圆 切割线定理逆定理:如果凸四边形ABCD 一双对边AB 与DC 交于点P 且满足PA PC PB PD ?=?,则四边形ABCD 有一外接圆 射影定理:RTΔABC 中,BC 是斜边,AD 是斜边上的高,则 222(1)(2)(3)AD BD CD AB BD BC AC CD BC =?=?=? Miquel 定理:ΔABC 中,X ,Y ,Z 分别是直线AB ,BC ,AC 上的点,则
AXZ BXY CYZ O ,, 共于一点 这样的点O称为X,Y,Z对于ΔABC的Miquel点 Simson定理 P是ΔABC外接圆上一点,过点P作PD垂直BC,PE垂直于AB,同理PF 则D,E,F是共线的三点 直线DEF称为点P关于ΔABC的Simson线
《圆》知识点及定理 一、圆的概念 集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合; 2、圆的外部:可以看作是到定点的距离大于定长的点的集合; 3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念: 1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆; (补充)2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线); 3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线; 4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线; 5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。 二、点与圆的位置关系 1、点在圆内?d r ?点A在圆外; 三、直线与圆的位置关系 1、直线与圆相离?d r >?无交点; 2、直线与圆相切?d r =?有一个交点; 3、直线与圆相交?d r +; 外切(图2)?有一个交点?d R r =+; 相交(图3)?有两个交点?R r d R r -<<+; 内切(图4)?有一个交点?d R r =-; 内含(图5)?无交点?d R r <-; 五、垂径定理 垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。 推论 1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧; (2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧; (3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧 以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中 2个即可推出其它3个结论,即: ①AB是直径②AB CD ⊥③CE DE =④弧BC=弧BD⑤弧 AC=弧AD 中任意2个条件推出其他3个结论。 推论2:圆的两条平行弦所夹的弧相等。 即:在⊙O中,∵AB∥CD ∴弧AC=弧BD A 图4 图5 D --
初三数学圆的性质定理 1、圆的对称性:圆是轴对称图形,任一条直径所在的直线都是它的对称轴. 2、垂径定理:垂直于弦的直径平分弦,并且平分弦所对的两条弧. 3、垂径定理的推论:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧. 4、垂径定理的应用: ①用直尺和圆规平分一条弧. 作法是过圆心作弧所对弦的垂线,理由是垂径定理; ②在利用垂径定理计算或证明时,我们通常将其化为一个直角三角形的边和角,这 个特殊直角三角形的三边分别是半径、弦的一半和圆心到弦的垂线段. 例1、如图,已知以点 O为公共圆心的两个同心圆,大圆的弦 AD交小圆于 B、C. (1)求证: AB=CD (2)如果 AD=6cm, BC=4cm,求圆环的面积 . 1.圆周角定义:顶点在圆周上,并且两边都和圆相交的角叫做圆周角. 2.圆周角定理:同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的 圆心角的一半 . 3.推论:①同圆或等圆中,相等的圆周角所对的弧一定相等 . ②半圆(或直径) 所对圆周角是直角, 90°的圆周角所对的弦是直径 . ③如果三角形一边上的中线等于这条边的一半,那么这个三角形是直角三角形. 4.圆的内接四边形: ①定义:如果一个多边形的所有顶点都在同一圆上,这个多边形叫做圆内接多边形, 这个圆叫做这个多边形的外接圆. ②圆内接四边形的性质:圆内接四边形的对角互补. 例2、如图, AB是⊙ O的直径, BC是弦, OD⊥BC于 E,交 BC于 D.若 BC=8, ED=2,求⊙O的半径 . 解: 1、如图,已知 AB是⊙ O的直径,弦 CD⊥AB于点 P,CD=10cm,AP∶PB=1∶5,那么⊙ O的半径是( )
第二讲-圆的几个重要定理 中考要求 内容基本要求略高要求较高要求圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆;能 利用圆的有关概念解决简单问题 圆的性质知道圆的对称性,了解弧、弦、圆心 角的关系能用弧、弦、圆心角的关系解决简单 问题 能运用圆的性质解 决有关问题 圆周角了解圆周角与圆心角的关系;了解直 径所对的圆周角是直角会求圆周角的度数,能用圆周角的知 识解决与角有关的简单问题 能综合运用几何知 识解决与圆周角有 关的问题 知识点睛 一、圆周角定理 圆心角和圆周角 1.圆心角:顶点在圆心的角叫做圆心角.将整个圆分为360等份,每一份的弧对应1?的圆心角,我们也称这样的弧为1?的弧.圆心角的度数和它所对的弧的度数相等. 2.圆周角:顶点在圆上,并且两边都和圆相交的角叫做圆周角. 3.圆周角定理:一条弧所对的圆周角等于它所对的圆心角的一半. 推论1:同弧或等弧所对的圆周角相等;同圆或等圆中,相等的圆周角所对的弧相等. 推论2:半圆(或直径)所对的圆周角是直角,90?的圆周角所对的弦是直径. 推论3:如果三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形. 4.圆心角、弧、弦、弦心距之间的关系定理:在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦相等,所对的弦的弦心距相等. 推论:在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两条弦的弦心距中有一组量相等,那么它们所对应的其余各组量分别相等. 圆是平面几何中的一个重要内容.由于圆与直线型图形可组合成一些复杂的几何问题,所以它经常出现在数学竞赛中. 圆的基本性质有: ⑴直径所对的圆周角是直角. ⑵同弧所对的圆周角相等. ⑶经过圆心及一弦中点的直线垂直平分该弦. 二、圆心角、弧、弦、弦心距之间的关系 在同圆或等圆中,两个圆心角、两条弧、两条弦、两条弦的弦心距中有一组量相等,其它各组量都相等。 三、相交弦定理(选讲) 相交弦定理:圆内的两条相交弦被交点分成的两条线段长的乘积相等. 如图,弦AB和CD交于O ⊙内一点P,则PA PB PC PD ?=?. 2010年·暑假·短期班圆·第2讲·学生版page 1 of 8
初中圆的定理和公式汇总 1不在同一直线上的三点确定一个圆。 ①圆:由定点到定长点的集合叫做圆。符号⊙0 A B ②弦:连接圆上任意两点的线段叫做弦。弦:⌒ 经过圆心的弦叫直径 ③半径不同,圆心相同的两个圆叫做同心圆 同圆、等圆或半径相同的叫做等圆 两个完全重合的弧叫等弧 ④经过平面上一点可画无数个圆; 经平面上二点可画无数个圆; ⑤在三角形外画一个圆的圆心叫做此三角形的外心,此圆为三角形 的外接圆。 ⑥外心:三角形三条中垂线的交点。 ⑦三角形三个顶点在圆上,这个三角形叫圆的内接三角形。 2垂径定理:垂直于弦的直径平分这条弦并且平分弦所对的两条弧 推论1①平分弦(不是直径)的直径垂直于弦,并且平分弦所对的 两条弧 ②弦的垂直平分线经过圆心,并且平分弦所对的两条弧 ③平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另 一条弧 推论2圆的两条平行弦所夹的弧相等 3圆是以圆心为对称中心的中心对称图形
4圆是定点的距离等于定长的点的集合 5圆的内部可以看作是圆心的距离小于半径的点的集合 6圆的外部可以看作是圆心的距离大于半径的点的集合 7同圆或等圆的半径相等 8到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆 9定理在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦 相等,所对的弦的弦心距相等 10推论在同圆或等圆中,如果两个圆心角、两条弧、两条弦或两弦的弦心距中有一组量相等那么它们所对应的其余各组量都相等11定理圆的内接四边形的对角互补,并且任何一个外角都等于它的内对角 12①直线L和⊙O相交d<r ②直线L和⊙O相切d=r ③直线L和⊙O相离d>r 13切线的判定定理:经过半径的外端并且垂直于这条半径的直线是圆的切线 14切线的性质定理圆的切线垂直于经过切点的半径 15推论1经过圆心且垂直于切线的直线必经过切点 16推论2经过切点且垂直于切线的直线必经过圆心 17切线长定理从圆外一点引圆的两条切线,它们的切线长相等,圆心和这一点的连线平分两条切线的夹角
关于圆的定理 割线定理 割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆交 点的距离的积相等. 数学语言:从圆外一点L引两条割线与圆分别交于A、B、C、D 则有LA〃LB=LC〃LD=LT^2. 几何语言: ∵割线LDC和LBA交于圆O于ABCD点. ∴LA〃LB=LC〃LD=LT^2.如右图所示.(LT为切线) 切割线定理 切割线定理:从圆外一点引圆的切线和割线,切线长是这点 到割线与圆交点的两条线段长的比例中项。是圆幂定理的一种. 几何语言: ∵PT切⊙O于点T,PBA是⊙O的割线∴PT2=PA〃PB(切 割线定理). 推论:从圆外一点引圆的两条割线,这一点到每条割线与圆 的交点的两条线段长的积相等. 几何语言: ∵PT是⊙O切线,PBA,PDC是⊙O的割线∴PD〃PC=PA〃PB(切割线定理推论)(割线定理) 由上可知:PT2=PA〃PB=PC〃PD 相交弦定理 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等. 几何语言: ∵弦AB、CD交于点P.∴PA〃PB=PC〃PD(相交弦定理). 推论:如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例 中项. 几何语言: ∵AB是直径,CD⊥AB于点P.∴PC2=PA〃PB(相交弦定理推论). 弦切角定理 弦切角定理:弦切角等于它所夹的弧所对的圆周角.弦切角等于它所夹 的弧所对的圆心角的一半.两个弦切角所夹的弧相等,那么这两个弦切角也相等. 证明:如图2,AB为圆O的切线,因为BD是直径,所以内接三角形BCD 是直角三角形,其中∠DCB是直角. ∴∠BDC+∠1=90°.∵∠1+∠CBA=90°. ∴∠CBA=∠BDC. 射影定理 直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项,每一条直角边是这条直角边在斜边上的射影和斜边的比例中项. 概述图中,在Rt△ABC中,∠ACB=90°,CD是斜边AB上的高,则有射影定理如下:
圆幂定理 圆幂的定义:一点P 对半径R 的圆O 的幂定义如下:22OP R - 所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。 圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)及他们推论的统称。 相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。 如图,AB 、CD 为圆O 的两条任意弦。相交于点P ,连接AD 、BC ,则∠D=∠B , ∠A=∠C 。所以△APD ∽△BPC 。所以 A P P D A P B P P C P D P C B P =??=? 切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆焦点的两条线段长的比例中项。 如图,PT 为圆切线,PAB 为割线。连接TA ,TB ,则∠PTA=∠B (弦切角等于同弧圆周角)所以△PTA ∽△PBT ,所以 2 P T P A P T P A P B P B P T =?=?
割线定理:从圆外一点P 引两条割线与圆分别交于A.B.C.D 则有 PA·PB=PC·PD 。 这个证明就比较简单了。可以过P 做圆的切线,也可以连接CB 和AD 。证相似。 存在:P A P B P C P D ?=? 进一步升华(推论): 过任意在圆O 外的一点P 引一条直线L1与一条过圆心的直线L2,L1与圆交于A 、B (可重合,即切线),L2与圆交于C 、D 。则PA·PB=PC·PD 。若圆半径为r ,则 2 2 2 2 ()()||PC PD PO R PO R PO R PO R ?=-?+=-=-(一定要加绝对值,原因见下) 为定值。这个值称为点P 到圆O 的幂。(事实上所有的过P 点与圆相交的直线都满足这个值) 若点P 在圆内,类似可得定值为2222||R PO PO R -=- 故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝 对值。(这就是“圆幂”的由来)