
§4.4 三角函数的图象和性质
1. 用五点法作正弦函数和余弦函数的简图
正弦函数y =sin x ,x ∈[0,2π]的图象中,五个关键点是:(0,0),(π2,1),(π,0),(3π
2,-
1),(2π,0).
余弦函数y =cos x ,x ∈[0,2π]的图象中,五个关键点是:(0,1),(π2,0),(π,-1),(3π
2,
0),(2π,1).
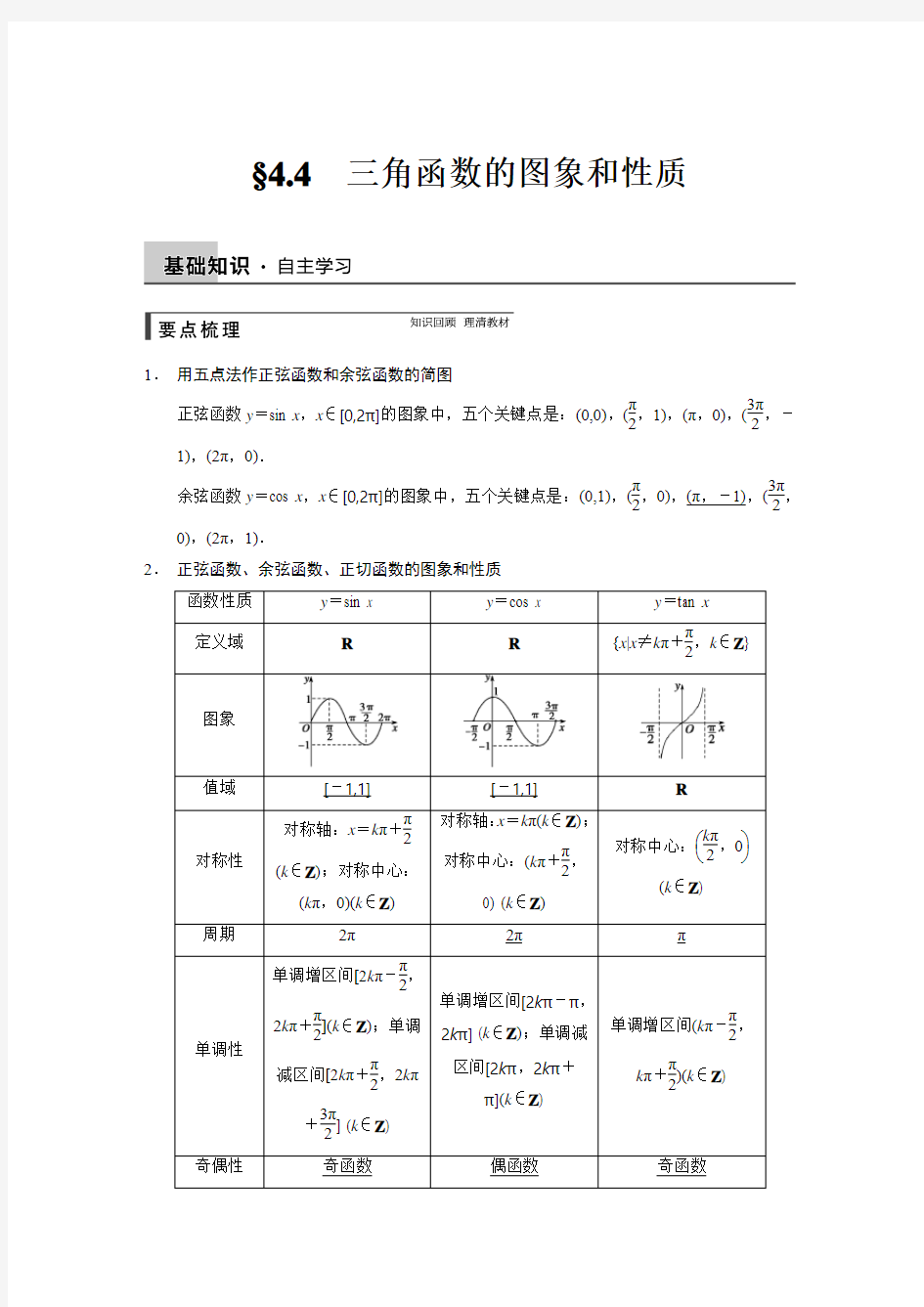
2. 正弦函数、余弦函数、正切函数的图象和性质
1. 判断下面结论是否正确(请在括号中打“√”或“×”)
(1)常数函数f (x )=a 是周期函数,它没有最小正周期. ( √ ) (2)y =sin x 在x ∈[0,π
2
]上是增函数.
( √ ) (3)y =cos x 在第一、二象限上是减函数. ( × ) (4)y =tan x 在整个定义域上是增函数. ( × ) (5)y =k sin x +1(x ∈R ),则y max =k +1. ( × ) (6)若sin x >
22,则x >π4
.
( × ) 2. (2012·福建)函数f (x )=sin ???
?x -π
4的图象的一条对称轴是
( )
A .x =π4
B .x =π2
C .x =-π4
D .x =-π
2
答案 C
解析 方法一 ∵正弦函数图象的对称轴过图象的最高点或最低点, 故令x -π4=k π+π2,k ∈Z ,∴x =k π+3π
4,k ∈Z .
取k =-1,则x =-π
4.
方法二 用验证法.
x =π
4时,y =sin ????π4-π4=0,不合题意,排除A ; x =π2时,y =sin ????π2-π4=2
2,不合题意,排除B ; x =-π
4
时,y =sin ????-π4-π4=-1,符合题意,C 项正确; x =-π2时,y =sin ????-π2-π4=-2
2
,不合题意,故D 项也不正确. 3. 若函数f (x )=sin ωx (ω>0)在区间????0,π3上单调递增,在区间???
?π3,π
2上单调递减,则ω等于
( )
A.23
B.3
2 C .2 D .
3 答案 B
解析 ∵f (x )=sin ωx (ω>0)过原点,
∴当0≤ωx ≤π2,即0≤x ≤π
2ω
时,y =sin ωx 是增函数;
当π2≤ωx ≤3π2,即π2ω≤x ≤3π
2ω时,y =sin ωx 是减函数. 由f (x )=sin ωx (ω>0)在????0,π
3上单调递增, 在????π3,π2上单调递减知,π2ω=π3,∴ω=3
2
. 4. (2013·湖北)将函数y =3cos x +sin x (x ∈R ) 的图象向左平移m (m >0)个单位长度后,所
得到的图象关于y 轴对称,则m 的最小值是 ( )
A.π12
B.π6
C.π3
D.5π6 答案 B
解析 y =3cos x +sin x =2sin(x +π3)向左平移m 个单位长度后得到y =2sin(x +π
3+m ),
它关于y 轴对称可得 sin(π
3
+m )=±1, ∴π3+m =k π+π2,k ∈Z ,∴m =k π+π
6,k ∈Z , ∵m >0,∴m 的最小值为π6
.
5. 函数y =lg sin 2x +9-x 2的定义域为________________.
答案 {x |-3≤x <-π2或0 2 } 解析 由????? sin 2x >0 9-x 2 ≥0, 得? ???? 2k π<2x <2k π+π,k ∈Z , -3≤x ≤3. ∴-3≤x <-π2或0 . ∴函数y =lg sin 2x +9-x 2的定义域为 {x |-3≤x <-π2或0 2 }. 题型一 求三角函数的定义域和最值 例1 (1)(2012·山东)函数y =2sin ???? πx 6-π3(0≤x ≤9)的最大值与最小值之和为( ) A .2- 3 B .0 C .-1 D .-1- 3 (2)函数y =1 tan x -1 的定义域为__________. 思维启迪 求函数的定义域可利用三角函数的图象或数轴;求函数最值或值域时要利用图象、三角变换、二次函数等知识. 答案 (1)A (2){x |x ≠π4+k π且x ≠π 2+k π,k ∈Z } 解析 (1)利用三角函数的性质先求出函数的最值. ∵0≤x ≤9,∴-π3≤π6x -π3≤7π 6, ∴sin ????π6x -π3∈??? ?-3 2,1. ∴y ∈[]-3,2,∴y max +y min =2- 3. (2)要使函数有意义,必须有????? tan x -1≠0x ≠π2 +k π,k ∈Z , 即??? x ≠π 4 +k π,k ∈Z x ≠π 2+k π,k ∈Z . 故函数的定义域为{x |x ≠π4+k π且x ≠π 2 +k π,k ∈Z }. 思维升华 (1)求三角函数的定义域实际上是解简单的三角不等式,常借助三角函数线或三角函数图象来求解. (2)求解三角函数的值域(最值)常见到以下几种类型的题目: ①形如y =a sin x +b cos x +c 的三角函数化为y =A sin(ωx +φ)+k 的形式,再求最值(值域); ②形如y =a sin 2x +b sin x +c 的三角函数,可先设sin x =t ,化为关于t 的二次函数求值域(最值); ③形如y =a sin x cos x +b (sin x ±cos x )+c 的三角函数,可先设t =sin x ±cos x ,化为关于t 的二次函数求值域(最值). (1)函数y =lg(sin x )+ cos x -1 2的定义域为________. (2)函数y =sin 2x +sin x -1的值域为 ( ) A .[-1,1] B .[-5 4,-1] C .[-5 4 ,1] D .[-1,5 4 ] 答案 (1){x |2k π 3 +2k π,k ∈Z } (2)C 解析 (1)要使函数有意义必须有???? ? sin x >0,cos x -1 2≥0, 即????? sin x >0,cos x ≥12,解得???? ? 2k π 3+2k π(k ∈Z ), ∴2k π 3 +2k π,k ∈Z , ∴函数的定义域为{x |2k π 3 +2k π,k ∈Z }. (2)y =sin 2x +sin x -1,令t =sin x ,则有y =t 2+t -1,t ∈[-1,1], 画出函数图象如图所示,从图象可以看出, 当t =-1 2及t =1时,函数取最值,代入y =t 2+t -1, 可得y ∈[-5 4 ,1]. 题型二 三角函数的单调性、周期性 例2 写出下列函数的单调区间及周期: (1)y =sin ? ???-2x +π 3;(2)y =|tan x |. 思维启迪 (1)化为y =-sin ????2x -π 3,再求单调区间及周期.(2)由y =tan x 的图象→y =|tan x |的图象→求单调性及周期. 解 (1)y =-sin ? ???2x -π 3, 它的增区间是y =sin ????2x -π 3的减区间, 它的减区间是y =sin ????2x -π 3的增区间. 由2k π-π2≤2x -π3≤2k π+π 2,k ∈Z , 得k π-π12≤x ≤k π+5π 12,k ∈Z . 由2k π+π2≤2x -π3≤2k π+3π 2 ,k ∈Z , 得k π+5π12≤x ≤k π+11π 12 ,k ∈Z . 故所给函数的减区间为????k π-π12,k π+5π 12,k ∈Z ; 增区间为????k π+5π12,k π+11π 12,k ∈Z . 最小正周期T =2π 2 =π. (2)观察图象可知,y =|tan x |的增区间是????k π,k π+π2,k ∈Z ,减区间是????k π-π2,k π,k ∈Z . 最小正周期T =π. 思维升华 (1)求形如y =A sin(ωx +φ)或y =A cos(ωx +φ)(其中,ω>0)的单调区间时,要视“ωx +φ”为一个整体,通过解不等式求解.但如果ω<0,那么一定先借助诱导公式将ω化为正数,防止把单调性弄错. (2)求函数的单调区间应遵循简单化原则,将解析式先化简,并注意复合函数单调性规律“同增异减”. (3)求含有绝对值的三角函数的单调性及周期时,通常要画出图象,结合图象判定. (2013·阜新模拟)求函数y =sin ????π3+4x +cos ? ???4x -π 6的周期、单调区间及最大、最小值. 解 ∵????π3+4x +????π6-4x =π 2, ∴cos ????4x -π6=cos ????π 6-4x =cos ??? ?π2-????π 3+4x =sin ??? ?π3+4x . ∴y =2sin ????4x +π3,周期T =2π4=π2 . 当-π2+2k π≤4x +π3≤π 2+2k π (k ∈Z )时,函数单调递增, ∴函数的递增区间为????-5π24+k π2,π24+k π 2 (k ∈Z ). 当π2+2k π≤4x +π3≤3π 2+2k π (k ∈Z )时,函数单调递减, ∴函数的递减区间为????π24+k π2,7π24+k π2(k ∈Z ). 当x =π24+k π 2 (k ∈Z )时,y max =2; 当x =-5π24+k π 2 (k ∈Z )时,y min =-2. 题型三 三角函数的奇偶性和对称性 例3 (1)已知f (x )=sin x +3cos x (x ∈R ),函数y =f (x +φ) ? ???|φ|≤π 2的图象关于直线x =0对 称,则φ的值为________. (2)如果函数y =3cos(2x +φ)的图象关于点???? 4π3,0中心对称,那么|φ|的最小值为( ) A.π6 B.π4 C.π3 D.π2 答案 (1)π 6 (2)A 解析 (1)f (x )=2sin ??? ?x +π3, y =f (x +φ)=2sin ????x +π 3+φ图象关于x =0对称, 即f (x +φ)为偶函数. ∴π3+φ=π2+k π,k ∈Z ,φ=k π+π 6,k ∈Z , 又∵|φ|≤π2,∴φ=π6 . (2)由题意得3cos ????2×4π3+φ=3cos ????2π 3+φ+2π =3cos ????2π 3+φ=0, ∴2π3+φ=k π+π 2 ,k ∈Z , ∴φ=k π-π6,k ∈Z ,取k =0,得|φ|的最小值为π6 . 思维升华 若f (x )=A sin(ωx +φ)为偶函数,则当x =0时,f (x )取得最大值或最小值. 若f (x )=A sin(ωx +φ)为奇函数,则当x =0时,f (x )=0. 如果求f (x )的对称轴,只需令ωx +φ=π 2+k π (k ∈Z ),求x . 如果求f (x )的对称中心的横坐标,只需令ωx +φ=k π (k ∈Z )即可. (1)若函数f (x )=sin ax +cos ax (a >0)的最小正周期为1,则它的图象的一个对 称中心为 ( ) A .(-π 8,0) B .(0,0) C .(-1 8 ,0) D .(1 8 ,0) (2)设函数y =sin(ωx +φ)(ω>0,φ∈(-π2,π2))的最小正周期为π,且其图象关于直线x = π 12对称,则在下面四个结论:①图象关于点(π4,0)对称;②图象关于点(π 3 ,0)对称;③在[0, π6]上是增函数;④在[-π 6,0]上是增函数中,所有正确结论的编号为________. 答案 (1)C (2)②④ 解析 (1)由条件得f (x )=2sin(ax +π4), 又函数的最小正周期为1,故2π a =1,∴a =2π, 故f (x )=2sin(2πx +π 4). 将x =-1 8代入得函数值为0. (2)∵T =π,∴ω=2. 又2×π12+φ=k π+π2(k ∈Z ),∴φ=k π+π 3(k ∈Z ). ∵φ∈(-π2,π2),∴φ=π3,∴y =sin(2x +π3), 由图象及性质可知②④正确. 三角函数的单调性、对称性 典例:(20分)(1)已知ω>0,函数f (x )=sin(ωx +π4)在(π 2 ,π)上单调递减,则ω的取值范围是( ) A .[12,5 4] B .[12,34] C .(0,1 2 ] D .(0,2] (2)已知函数f (x )=2cos(ωx +φ)+b 对任意实数x 有f (x +π4)=f (-x )成立,且f (π 8)=1,则实 数b 的值为 ( ) A .-1 B .3 C .-1或3 D .-3 (3)(2012·课标全国)已知ω>0,0<φ<π,直线x =π4和x =5π 4是函数f (x )=sin(ωx +φ)图象的两 条相邻的对称轴,则φ等于 ( ) A.π 4 B.π3 C.π2 D.3π4 (4)函数y =sin(ωx +φ)(ω>0且|φ|<π2)在区间[π6,2π 3 ]上单调递减,且函数值从1减小到-1, 那么此函数图象与y 轴交点的纵坐标为 ( ) A.12 B.22 C.32 D. 6+2 4 思维启迪 (1)(π2,π)为函数f (x )某个单调减区间的子集;(2)由f (x +π 4 )=f (-x )可得函数的对称 轴,应用函数在对称轴处的性质求解即可;(3)f (x )=sin(ωx +φ)图象相邻两条对称轴之间的距离是T 2;(4)可结合图象分析函数的单调性,周期性确定ω,φ. 解析 (1)由π2 4, 由题意知(π2ω+π4,πω+π4)?[π2,3π 2 ], ∴??? π2ω+π4≥π 2, πω+π4≤3π 2 ,∴12≤ω≤5 4 ,故选A. (2)由f (x +π4)=f (-x )可知函数f (x )=2cos(ωx +φ)+b 关于直线x =π 8对称,又函数f (x )在对 称轴处取得最值,故±2+b =1,∴b =-1或b =3. (3)利用三角函数的对称轴求得周期. 由题意得周期T =2???? 5π4-π4=2π, ∴2π=2π ω,即ω=1,∴f (x )=sin(x +φ), ∴f ????π4=sin ????π4+φ=±1, ∵0<φ<π,∴π4<φ+π4<5π4,∴φ+π4=π2,∴φ=π4 . (4)函数y =sin(ωx +φ)的最大值为1,最小值为-1,由该函数在区间[π6,2π 3]上单调递减, 且函数值从1减小到-1,可知2π3-π6=π2为半周期,则周期为π,ω=2πT =2π π=2,此时原 函数式为y =sin(2x +φ),又由函数y =sin(ωx +φ)的图象过点(π6,1),代入可得φ=π 6,因 此函数为y =sin(2x +π6),令x =0,可得y =1 2. 答案 (1)A (2)C (3)A (4)A 温馨提醒 (1)对于已知函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已 知的单调区间应为函数的单调区间的子集;其次,要确定已知函数的单调区间,从而利 用它们之间的关系可求解. (2)函数y =A sin(ωx +φ)+b 的图象与其对称轴的交点是最值点. 方法与技巧 1.讨论三角函数性质,应先把函数式化成y =A sin(ωx +φ)(ω>0)的形式. 2.函数y =A sin(ωx +φ)和y =A cos(ωx +φ)的最小正周期为2π |ω|,y =tan(ωx +φ)的最小正周期为 π|ω| . 3.对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t =ωx +φ,将其转化为研究y =sin t 的性质. 失误与防范 1.闭区间上最值或值域问题,首先要在定义域基础上分析单调性,含参数的最值问题,要讨论参数对最值的影响. 2.要注意求函数y =A sin(ωx +φ)的单调区间时ω的符号,尽量化成ω>0时的情况. A 组 专项基础训练 (时间:40分钟) 一、选择题 1. 下列函数中,周期为π且在[0,π 2 ]上是减函数的是 ( ) A .y =sin(x +π 4) B .y =cos(x +π 4) C .y =sin 2x D .y =cos 2x 答案 D 解析 对于函数y =cos 2x ,T =π, 当x ∈[0,π 2]时,2x ∈[0,π],y =cos 2x 是减函数. 2. (2012·湖南)函数f (x )=sin x -cos ??? ?x +π 6的值域为 ( ) A .[-2,2] B .[-3,3] C .[-1,1] D.? ?? ? - 32, 32 答案 B 解析 将函数化为y =A sin(ωx +φ)的形式后求解. ∵f (x )=sin x -cos ????x +π6 =sin x -cos x cos π6+sin x sin π 6 =sin x -32cos x +1 2 sin x =3?? ? ?32sin x -12cos x =3sin ????x -π 6(x ∈R ), ∴f (x )的值域为[-3,3]. 3. (2013·浙江)已知函数f (x )=A cos(ωx +φ)(A >0,ω>0,φ∈R ),则“f (x )是奇函数”是“φ= π 2 ”的 ( ) A .充分不必要条件 B .必要不充分条件 C .充分必要条件 D .既不充分也不必要条件 答案 B 解析 φ=π 2?f (x )=A cos ????ωx +π2=-A sin ωx 为奇函数, ∴“f (x )是奇函数”是“φ=π 2 ”的必要条件. 又f (x )=A cos(ωx +φ)是奇函数?f (0)=0?φ=π2+k π(k ∈Z )D /?φ=π 2. ∴“f (x )是奇函数”不是“φ=π 2”的充分条件. 4. 函数y =cos 2x +sin 2x ,x ∈R 的值域是 ( ) A .[0,1] B .[1 2,1] C .[-1,2] D .[0,2] 答案 A 解析 y =cos 2x +sin 2x =cos 2x +1-cos 2x 2=1+cos 2x 2. ∵cos 2x ∈[-1,1],∴y ∈[0,1]. 5. (2012·天津)将函数f (x )=sin ωx (其中ω>0)的图象向右平移π 4 个单位长度,所得图象经过点 ??? ?3π4,0,则ω的最小值是 ( ) A.13 B .1 C.53 D .2 答案 D 解析 根据题意平移后函数的解析式为y =sin ω????x -π4, 将????3π4,0代入得sin ωπ 2=0,则ω=2k ,k ∈Z ,且ω>0, 故ω的最小值为2. 二、填空题 6. 函数y =cos(π 4 -2x )的单调减区间为________. 答案 [k π+π8,k π+5π 8](k ∈Z ) 解析 由y =cos(π4-2x )=cos(2x -π 4)得 2k π≤2x -π 4≤2k π+π(k ∈Z ), 故k π+π8≤x ≤k π+5π 8 (k ∈Z ). 所以函数的单调减区间为[k π+π8,k π+5π 8 ](k ∈Z ). 7. 当-π2≤x ≤π 2 时,函数y =sin x +3cos x 的最大值为________,最小值为________. 答案 2 -1 解析 y =2sin(x +π3),-π6≤x +π3≤5π6, ∴-12≤sin(x +π 3)≤1,∴-1≤y ≤2, 故y max =2,y min =-1. 8. 已知函数f (x )=A tan(ωx +φ)(ω>0,|φ|<π 2 ),y =f (x )的部分图象如 图,则f (π 24)=________. 答案 3 解析 由题中图象可知,此正切函数的半周期等于3π8-π8=π4,即最小正周期为π 2, 所以ω=2.由题意可知,图象过定点(3π 8,0), 所以0=A tan(2×3π8+φ),即3π 4 +φ=k π(k ∈Z ), 所以φ=k π-3π 4(k ∈Z ), 又|φ|<π2,所以φ=π4 . 又图象过定点(0,1),所以A =1. 综上可知,f (x )=tan(2x +π4 ), 故有f (π24)=tan(2×π24+π4)=tan π 3= 3. 三、解答题 9. 设函数f (x )=sin ()2x +φ (-π<φ<0),y =f (x )图象的一条对称轴是直线x =π 8 . (1)求φ; (2)求函数y =f (x )的单调增区间. 解 (1)令2×π8+φ=k π+π 2,k ∈Z , ∴φ=k π+π 4,k ∈Z , 又-π<φ<0,则φ=-3π 4. (2)由(1)得:f (x )=sin ????2x -3π4, 令-π2+2k π≤2x -3π4≤π 2+2k π,k ∈Z , 可解得π8+k π≤x ≤5π 8+k π,k ∈Z , 因此y =f (x )的单调增区间为 ??? ?π8+k π,5π8+k π,k ∈Z . 10.设函数f (x )=sin(πx 4-π6)-2cos 2πx 8 +1. (1)求f (x )的最小正周期. (2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,4 3]时,y =g (x )的最大值. 解 (1)f (x )=sin πx 4cos π6-cos πx 4sin π6-cos πx 4 = 32sin πx 4-32cos πx 4 =3sin(πx 4-π3 ), 故f (x )的最小正周期为T =2π π4 =8. (2)方法一 在y =g (x )的图象上任取一点(x ,g (x )), 它关于x =1的对称点(2-x ,g (x )). 由题设条件,知点(2-x ,g (x ))在y =f (x )的图象上, 从而g (x )=f (2-x )=3sin[π4(2-x )-π 3] =3sin[π2-πx 4-π 3] =3cos(πx 4+π 3 ). 当0≤x ≤43时,π3≤πx 4+π3≤2π 3, 因此y =g (x )在区间[0,4 3]上的最大值为 g (x )max =3cos π3=3 2 . 方法二 区间[0,43]关于x =1的对称区间为[2 3,2], 且y =g (x )与y =f (x )的图象关于直线x =1对称, 故y =g (x )在[0,4 3]上的最大值是 y =f (x )在[2 3,2]上的最大值. 由(1)知f (x )=3sin(πx 4-π 3), 当23≤x ≤2时,-π6≤πx 4-π3≤π6. 因此y =g (x )在[0,4 3]上的最大值为 g (x )max =3sin π6=3 2 . B 组 专项能力提升 (时间:30分钟) 1. 函数y =|sin x +cos x |-1的定义域是 ( ) A .[k π,k π+π 2](k ∈Z ) B .[2k π,2k π+π 2](k ∈Z ) C .[-π 2+k π,k π](k ∈Z ) D .[-π 2 +2k π,2k π](k ∈Z ) 答案 A 解析 |sin x +cos x |-1≥0?(sin x +cos x )2≥ 1?sin 2x ≥0, ∴2k π≤2x ≤2k π+π,k ∈Z , 故原函数的定义域是[k π,k π+π 2 ](k ∈Z ). 2. 设函数f (x )=3sin(π2x +π 4 ),若存在这样的实数x 1,x 2,对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2) 成立,则|x 1-x 2|的最小值为________. 答案 2 解析 f (x )=3sin(π2x +π4)的周期T =2π×2 π=4, f (x 1),f (x 2)应分别为函数f (x )的最小值和最大值, 故|x 1-x 2|的最小值为T 2 =2. 3. 已知函数f (x )=cos x sin x (x ∈R ),给出下列四个命题: ①若f (x 1)=-f (x 2),则x 1=-x 2; ②f (x )的最小正周期是2π; ③f (x )在区间[-π4,π 4]上是增函数; ④f (x )的图象关于直线x =3π 4对称. 其中真命题是________. 答案 ③④ 解析 f (x )=12sin 2x ,当x 1=0,x 2=π 2时, f (x 1)=-f (x 2),但x 1≠-x 2,故①是假命题; f (x )的最小正周期为π,故②是假命题; 当x ∈[-π4,π4]时,2x ∈[-π2,π 2],故③是真命题; 因为f (3π4)=12sin 32π=-1 2 , 故f (x )的图象关于直线x =3 4π对称,故④是真命题. 4. 已知函数f (x )=sin 2x -3cos 2x +1. (1)当x ∈[π4,π 2]时,求f (x )的最大值和最小值; (2)求f (x )的单调区间. 解 (1)f (x )=sin 2x -3cos 2x +1=2sin(2x -π 3 )+1. ∵π4≤x ≤π2,∴π2≤2x ≤π,∴π6≤2x -π3≤2π3, ∴12≤sin(2x -π3)≤1,∴1≤2sin(2x -π 3)≤2, 于是2≤2sin(2x -π 3)+1≤3, ∴f (x )的最大值是3,最小值是2. (2)由2k π-π2≤2x -π3≤2k π+π 2,k ∈Z , 得2k π-π6≤2x ≤2k π+5π 6,k ∈Z , ∴k π-π12≤x ≤k π+5π 12 ,k ∈Z , 即f (x )的单调递增区间为[k π-π12,k π+5π 12],k ∈Z , 同理由2k π+π2≤2x -π3≤2k π+3π 2,k ∈Z , 得f (x )的单调递减区间为[k π+ 5π12,k π+11π 12 ],k ∈Z . 5. 已知a >0,函数f (x )=-2a sin ????2x +π6+2a +b ,当x ∈??? ?0,π 2时,-5≤f (x )≤1. (1)求常数a ,b 的值; (2)设g (x )=f ????x +π 2且lg g (x )>0,求g (x )的单调区间. 解 (1)∵x ∈????0,π2,∴2x +π6∈????π6,7π6. ∴sin ????2x +π6∈????-1 2,1, ∴-2a sin ????2x +π 6∈[-2a ,a ]. ∴f (x )∈[b,3a +b ],又∵-5≤f (x )≤1, ∴b =-5,3a +b =1,因此a =2,b =-5. (2)由(1)得,f (x )=-4sin ????2x +π 6-1, g (x )=f ????x +π2=-4sin ????2x +7π 6-1 =4sin ????2x +π 6-1, 又由lg g (x )>0,得g (x )>1, ∴4sin ????2x +π6-1>1,∴sin ? ???2x +π6>12, ∴2k π+π6<2x +π6<2k π+5π 6,k ∈Z , 其中当2k π+π6<2x +π6≤2k π+π 2,k ∈Z 时, g (x )单调递增,即k π 6,k ∈Z , ∴g (x )的单调增区间为????k π,k π+π 6,k ∈Z . 又∵当2k π+π2<2x +π6<2k π+5π 6,k ∈Z 时, g (x )单调递减,即k π+π6 3,k ∈Z . ∴g (x )的单调减区间为? ???k π+π6,k π+π 3,k ∈Z . 【高中数学】数学《三角函数与解三角形》复习资料 一、选择题 1.函数()1sin cos 1sin cos 1tan 01sin cos 1sin cos 32x x x x f x x x x x x x π+-++? ?=++<< ?+++-? ?的最小值为 ( ) A B C D 【答案】B 【解析】 【分析】 利用二倍角公式化简函数()f x ,求导数,利用导数求函数的最小值即可. 【详解】 2 2222sin 2sin cos 2cos 2sin cos 1sin cos 1sin cos 2222221sin cos 1sin cos 2cos 2sin cos 2sin 2sin cos 222222 x x x x x x x x x x x x x x x x x x x x +++-+++= ++++-++ 2sin sin cos 2cos sin cos sin cos 222222222sin cos sin 2cos sin cos 2sin sin cos 22222222x x x x x x x x x x x x x x x x x ???? ++ ? ?????=+= +=???? ++ ? ? ???? , 则()21tan 0sin 32f x x x x π? ?= +<< ?? ?, 322222 21sin 2cos 16cos cos 1()sin 3cos sin 3cos 3sin cos x x x x f x x x x x x x ' ' ' --+????=+=-+= ? ????? . 令()cos 0,1t x =∈,() 32 61g t t t =--+为减函数,且102g ??= ??? , 所以当03 x π <<时, ()1 1,02 t g t <<<,从而()'0f x <; 当 3 2 x π π << 时,()1 0,02 t g t << >,从而()'0f x >. 故( )min 33f x f π??== ??? . 故选:A 【点睛】 本题主要考查了三角函数的恒等变换,利用导数求函数的最小值,换元法,属于中档题. 2.在ABC ?中,角,,A B C 所对的边分别为,,a b c 满足,222b c a bc +-=, 高中数学三角函数基础知识点及答案 1、角的概念的推广:平面内一条射线绕着端点从一个位置旋转到另一个位置所的图形。按逆时针方向旋转所形成的角叫正角,按顺时针方向旋转所形成的角叫负角,一条射线没有作任何旋转时,称它形成一个零角。射线的起始位置称为始边,终止位置称为终边。 2、象限角的概念:在直角坐标系中,使角的顶点与原点重合,角的始边与x 轴的非负半轴重合,角的终边在第几象限,就说这个角是第几象限的角。如果角的终边在坐标轴上,就认为这个角不属于任何象限。 3. 终边相同的角的表示: (1)α终边与θ终边相同(α的终边在θ终边所在射线上)?2()k k αθπ=+∈Z , 注意:相等的角的终边一定相同,终边相同的角不一定相等.如与角 1825-的终边相同,且绝对值最小的角的度数是___,合___弧度。 弧度:一周的弧度数为2πr/r=2π,360°角=2π弧度,因此,1弧度约为57.3°,即57°17'44.806'', 1°为π/180弧度,近似值为0.01745弧度,周角为2π弧度,平角(即180°角)为π弧度, 直角为π/2弧度。(答:25-;5 36 π- ) (2)α终边与θ终边共线(α的终边在θ终边所在直线上) ?()k k αθπ=+∈Z . (3)α终边与θ终边关于x 轴对称?2()k k αθπ=-+∈Z . (4)α终边与θ终边关于y 轴对称?2()k k απθπ=-+∈Z . (5)α终边与θ终边关于原点对称?2()k k απθπ=++∈Z . (6)α终边在x 轴上的角可表示为:,k k Z απ=∈; α终边在y 轴上的角可表示为:,2k k Z παπ=+∈;α终边在坐标轴上的角可表示为:,2 k k Z π α=∈. 如α的终边与 6 π 的终边关于直线x y =对称,则α=____________。 (答:Z k k ∈+ ,3 2π π) 4、α与2α的终边关系:由“两等分各象限、一二三四”确定.如若α是第 二象限角,则2 α 是第_____象限角 (答:一、三) 5.弧长公式:||l R α=,扇形面积公式:211||22 S lR R α==,1弧度 (1rad)57.3≈. 如已知扇形AOB 的周长是6cm ,该扇形的中心角是1弧度,求该扇形的面积。 (答:22cm ) 6、任意角的三角函数的定义:设α是任意一个角,P (,)x y 是α的终边上的任意一点(异于原点),它与原点的距离是220r x y =+>,那么 s i n ,c o s y x r r αα==,()tan ,0y x x α=≠,cot x y α=(0)y ≠,sec r x α=()0x ≠, ()csc 0r y y α=≠。三角函数值只与角的大小有关,而与终边上点P 的位置无关。 高中数学三角函数复习专题 (附参考答案) 一、知识点整理: 1、角的概念的推广: 正负,范围,象限角,坐标轴上的角; 2、角的集合的表示: ①终边为一射线的角的集合:?{}Z k k x x ∈+=,2απ={ } |360,k k Z ββα=+?∈ ②终边为一直线的角的集合:?{}Z k k x x ∈+=,απ; ③两射线介定的区域上的角的集合:?{ } Z k k x k x ∈+≤<+,22απβπ ④两直线介定的区域上的角的集合:?{}Z k k x k x ∈+≤<+,απβπ; 3、任意角的三角函数: (1) 弧长公式:R a l = R 为圆弧的半径,a 为圆心角弧度数,l 为弧长。 (2) 扇形的面积公式:lR S 2 1 = R 为圆弧的半径,l 为弧长。 (3) 三角函数定义:角α中边上任意一点P 为),(y x ,设r OP =||则: ,cos ,sin r x r y ==αα x y =αtan r= 22b a + 反过来,角α的终边上到原点的距离为r 的点P 的坐标可写为: ()cos ,sin P r r αα比如:公式βαβαβαsin sin cos cos )cos(+=- 的证明 (4)特殊角的三角函数值 α 0 6π 4π 3π 2π π 2 3π 2π sin α 2 1 2 2 2 3 1 -1 cos α 1 23 22 2 1 0 -1 0 1 tan α 0 3 3 1 3 不存在 0 不存在 (5)三角函数符号规律:第一象限全正,二正三切四余弦。 (6)三角函数线:(判断正负、比较大小,解方程或不等式等) 如图,角α的终边与单位圆交于点P ,过点P 作x 轴的垂线, 垂足为M ,则 过点A(1,0)作x 轴的切线,交角终边OP 于点T ,则 。 (7)同角三角函数关系式: ①倒数关系: 1cot tan =a a ②商数关系:a a a cos sin tan = ③平方关系:1cos sin 22=+a a (8)诱导公试 三角函数值等于α的同名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看象限 三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号; 即:函数名改变,符号看象限: 比如sin cos cos 444x x x πππ????? ?+=-=- ? ? ? ?? ???? cos sin 44x x ππ???? +=- ? ? ???? sin cos tan -α -αsin +αcos -αtan π-α +αsin -αcos -αtan π+α -αsin -αcos +αtan 2π-α -αsin +αcos -αtan 2k π+α +αsin +αcos +αtan sin con tan απ -2 +αcos +αsin +αcot απ +2 +αcos -αsin -αcot απ -23 -αcos -αsin +αcot απ +2 3 -αcos +αsin -αcot x y o M T P A 三角函数专题训练 19.(本小题满分12分) 在△ABC 中角A 、B 、C 的对边分别为a b c 、、,设向量(,cos ),(,cos )//.m a B n b A m n m n ==≠u r r u r r u r r 且, (Ⅰ)若sin sin A B +=6,求A ; (Ⅱ)若ABC ?的外接圆半径为1,且,abx a b =+试确定x 的取值范围. 17.(本小题共12分) 已知函数()sin()(0,||)2f x M x M πω??=+>< 的部分图象如图所示. (I )求函数()f x 的解析式; (II )在△ABC 中,角C B A 、、的对边分别是c b a 、、若(2)cos cos ,()2 A a c B b C f -=求的取值范围. 17.(本小题满分12分)已知向量231444x x x m (sin ,),n (cos ,cos )==.记()n m x f ?= (I )若32f ()α=,求23 cos()πα-的值; (Ⅱ)在?ABC 中,角A 、B 、C 的对边分别是a 、b 、c ,且满足 ()2cos cos a c B b C -=,若13f (A )+= ,试判断?ABC 的形状. 17、海岛B 上有一座高为10米的塔,塔顶的一个观测站A ,上午11时测得一游船位于岛北偏东15°方向上,且俯角为30°的C 处,一分钟后测得该游船位于岛北偏西75°方向上,且俯角45°的D 处。(假设游船匀速行驶) (1)求该船行使的速度(单位:米/分钟)(5分) (2)又经过一段时间后,游船到达海岛B 的正西方向E 处,问此时游船距离海岛B 多远。(7分) 19.解:因为(,cos ),(,cos )//m a B n b A m n ==u r r u r r 且, 所以cos cos a A b B =,-------------------------------------------1分 由正弦定理,得sin cos sin cos A A B B =, 《三角函数》 【知识网络】 一、任意角的概念与弧度制 1、将沿x 轴正向的射线,围绕原点旋转所形成的图形称作角. 逆时针旋转为正角,顺时针旋转为负角,不旋转为零角 2、同终边的角可表示为 {}()360k k Z ααβ? =+∈g x 轴上角:{}()180k k Z αα=∈o g y 轴上角:{}()90180k k Z αα=+∈o o g 3、第一象限角:{}()036090360k k k Z αα? ?+<<+∈o g g 第二象限角:{}()90 360180360k k k Z αα??+<<+∈o o g g 第三象限角:{}()180360270360k k k Z αα? ?+<<+∈o o g g 第四象限角: {}()270 360360360k k k Z αα??+<<+∈o o g g 4、区分第一象限角、锐角以及小于90o 的角 第一象限角:{}()0360 90360k k k Z αα? ?+<<+∈o g g 锐角: {}090αα< ,2 4 , 0π απ ≤ ≤=k ,2 345, 1παπ≤≤=k 所以 2 α 在第一、三象限 6、弧度制:弧长等于半径时,所对的圆心角为1弧度的圆心角,记作1rad . 7、角度与弧度的转化:01745.0180 1≈=?π 815730.571801'?=?≈? = π 9、弧长与面积计算公式 弧长:l R α=?;面积:211 22 S l R R α=?=?,注意:这里的α均为弧度制. 二、任意角的三角函数 1、正弦:sin y r α=;余弦cos x r α=;正切tan y x α= 其中(),x y 为角α终边上任意点坐标,r = 2、三角函数值对应表: 3、三角函数在各象限中的符号 高中数学必修4知识点总结 第一章 三角函数(初等函数二) ?? ?? ?正角:按逆时针方向旋转形成的角1、任意角负角:按顺时针方向旋转形成的角零角:不作任何旋转形成的角 2、角α的顶点与原点重合,角的始边与x 轴的非负半轴重合,终边落在第几象限,则称α为第几象限角. 第一象限角的集合为{} 36036090,k k k αα?<, 则sin y r α= ,cos x r α= ,()tan 0y x x α= ≠. 10、三角函数在各象限的符号:第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正. 11、三角函数线:sin α=M P ,cos α=O M ,tan α=AT . 12、同角三角函数的基本关系:()2 2 1sin cos 1αα+= 三角函数大题压轴题练习 1.已知函数()cos(2)2sin()sin()344 f x x x x π ππ =- +-+ (Ⅰ)求函数()f x 的最小正周期和图象的对称轴方程 (Ⅱ)求函数()f x 在区间[,]122 ππ -上的值域 解:(1) ()cos(2)2sin()sin()344 f x x x x πππ =-+-+ 1cos 22(sin cos )(sin cos )2x x x x x x = ++-+ 221cos 22sin cos 2x x x x = ++- 1cos 22cos 222 x x x = +- s i n (2) 6 x π =- 2T 2 π π= =周期∴ 由2(),()6 2 23 k x k k Z x k Z π π ππ π- =+ ∈= +∈得 ∴函数图象的对称轴方程为 ()3 x k k Z π π=+ ∈ (2) 5[,],2[,]122636 x x ππ πππ ∈- ∴-∈- 因为()sin(2)6 f x x π =- 在区间[,]123ππ- 上单调递增,在区间[,]32 ππ 上单调 递减, 所以 当3 x π= 时,()f x 取最大值 1 又 1()()12 222f f π π- =- <=,当12 x π =-时,()f x 取最小值2- 所以 函数 ()f x 在区间[,]122 ππ - 上的值域为[ 2.已知函数2 π()sin sin 2f x x x x ωωω?? =+ ?? ? (0ω>)的最小正周期为π. (Ⅰ)求ω的值; (Ⅱ)求函数()f x 在区间2π03 ?????? ,上的取值范围. 解:(Ⅰ)1cos 2()22x f x x ωω-= +112cos 222 x x ωω=-+ π1sin 262x ω? ?=-+ ?? ?. 因为函数()f x 的最小正周期为π,且0ω>, 所以 2π π2ω =,解得1ω=. (Ⅱ)由(Ⅰ)得π1()sin 262 f x x ??=- + ?? ?. 因为2π03 x ≤≤, 所以ππ7π2666 x --≤≤, 所以1πsin 2126x ??- - ?? ?≤≤, 因此π130sin 2622x ? ?- + ?? ?≤≤,即()f x 的取值范围为302?????? ,. 3. 已知向量m =(sin A ,cos A ),n =1)-,m ·n =1,且A 为锐角. (Ⅰ)求角A 的大小; (Ⅱ)求函数()cos 24cos sin ()f x x A x x R =+∈的值域. 解:(Ⅰ) 由题意得3sin cos 1,m n A A =-= 1 2sin()1,sin().662 A A ππ-=-= 由A 为锐角得 ,6 6 3 A A π π π - = = (Ⅱ) 由(Ⅰ)知1 cos ,2 A = 所以2 2 1 3()cos 22sin 12sin 2sin 2(sin ).2 2 f x x x x s x =+=-+=--+ 因为x ∈R ,所以[]sin 1,1x ∈-,因此,当1sin 2x =时,f (x )有最大值3 2 . 当sin 1x =-时,()f x 有最小值-3,所以所求函数()f x 的值域是332??-???? , 三角函数总结及统练 一. 教学内容: 三角函数总结及统练 (一)基础知识 1. 与角α终边相同的角的集合},2{Z k k S ∈+==απβ 2. 三角函数的定义(六种)——三角函数是x 、y 、r 三个量的比值 3. 三角函数的符号——口诀:一正二弦,三切四余弦。 4. 三角函数线 正弦线MP=αsin 余弦线OM=αcos 正切线AT=αtan 5. 同角三角函数的关系 平方关系:商数关系: 倒数关系:1cot tan =?αα 1c s c s i n =?αα 1s e c c o s =?αα 口诀:凑一拆一;切割化弦;化异为同。 6. 诱导公式——口诀:奇变偶不变,符号看象限。 α απ+k 2 α- απ- απ+ απ-2 α π -2 α π +2 正弦 αsin αsin - αsin αsin - αsin - αcos αcos 余弦 αcos αcos αcos - αcos - αcos αsin αsin - 正切 αtan αtan - αtan - αtan αtan - αcot αcot - 余切 αcot αcot - αcot - αcot αcot - αtan αtan - 7. 两角和与差的三角函数 ?????? ? ?+-=-?-+=+?????????+?=-?-?=+?-?=-?+?=+βαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαβαt a n t a n 1t a n t a n )t a n (t a n t a n 1t a n t a n )t a n (s i n s i n c o s c o s )c o s (s i n s i n c o s c o s )c o s (s i n c o s c o s s i n )s i n (s i n c o s c o s s i n )s i n ( 8. 二倍角公式——代换:令αβ= ??????? -= -=-=-=?=ααααααααααα22222tan 1tan 22tan sin cos sin 211cos 22cos cos sin 22sin 降幂公式?????? ?+=-=22cos 1cos 22cos 1sin 22αααα 半角公式: 2cos 12 sin αα -± =;2cos 12cos αα+±=; αα αcos 1cos 12tan +-± = αα ααα cos 1sin sin cos 12 tan += -= 9. 三角函数的图象和性质 函数 x y sin = x y cos = x y tan = 任意角 一、知识概述 1、角的分类:正角、负角、零角. 2、象限角:(1)象限角. (2)非象限角(也称象限间角、轴线角). 3、终边相同的角的集合:所有与角终边相同的角,连同α角自身在内,都可以写成α+k·360°(k∈Z)的形式;反之,所有形如α+k·360°(k∈Z)的角都与α角的终边相同. 4、准确区分几种角 锐角:0°<α<90°; 0°~90°:0°≤α<90°; 第一象限角:. 5、弧度角:弧长等于半径的弧所对应的角称为1弧度角(1 rad). 1 rad=,1°=rad. 6、弧长公式:l=αR. 7、扇形面积公式:. 二、例题讲解 例1、写出下列终边相同的角的集合S,并把S中适合不等式的元素写出来: (1)60°;(2)-21°;(3)363°14′. 解: (1), S中满足的元素是 (2), S中满足的元素是 (3), S中满足的元素是 例2、写出终边在y轴上的角的集合. 解析: ∴. 注: 终边在x轴非负半轴:. 终边在x轴上:. 终边在y=x上:. 终边在坐标轴上:. 变式:角α与β的终边关于x轴对称,则β=_______. 答案:. 角α与β的终边关于y轴对称,则β=_______. 答案: 任意角的三角函数 一、知识概述 1、定义:在直角坐标系中,设α是一个任意角,α的终边与圆心在坐标原点的单位圆交于点P(x,y),那么sinα=y,cosα=x,tan α=. 注:①对于确定的角α,其终边上取点,令, 则. ②α的终边没有表明α一定是正角或负角,以及α的大小,只表明与α的终边相同的角所在的位置. 2、公式一:, , ,其中. 3、三角函数线 角α的终边与单位圆交于P点,过P作PM⊥x轴于M,则sinα=MP(正弦线),cosα=OM(余弦线).过A作单位圆的切线,则α的终边或其反向延长线交此切线于点T,则tanα=AT(正切线). 三角函数专题复习 在三角函数复习过程中,认真研究考纲是必须做的重要工作。三角函数可以当成函数内容中的重要一支,要注意与其它知识的联系。 一、研究考题,探求规律 1. 从表中可以看出:三角函数题在试卷中所处的位置基本上是第一或第二题,本章高考重点考查基础知识,仍将以容易题及中档为主,题目的难度保持稳定,估计这种情况会继续保持下去 2. 特点:由于三角函数中,和差化积与积化和差公式的淡出,考查主体亦发生了变化。偏重化简求值,三角函数的图象和性质。考查运算和图形变换也成为了一个趋势。三角函数试题更加注重立足于课本,注重考查基本知识、基本公式及学生的运算能力和合理变形能力,对三角变换的要求有所降低。三角化简、求值、恒等式证明。图象。最值。 3、对三角函数的考查主要来自于:①课本是试题的基本来源,是高考命题的主要依据,大多数试题的产生是在课本题的基础上组合、加工和发展的结果。②历年高考题成为新高考题的借鉴,有先例可循。 二、典例剖析 例1:函数22()cos 2cos 2x f x x =-的一个单调增区间是 A .2(,)33ππ B .(,)62ππ C .(0,)3π D .(,)66 ππ- 【解析】函数22()cos 2cos 2 x f x x =-=2cos cos 1x x --,从复合函数的角度看,原函数看作2()1g t t t =--,cos t x =,对于2()1g t t t =--,当1[1,]2t ∈-时,()g t 为减函数,当1[,1]2 t ∈时,()g t 为增函数,当2(,)33x ππ∈时,cos t x =减函数,且11(,)22 t ∈-, ∴ 原函数此时是单调增,选A 【温馨提示】求复合函数的单调区间时,需掌握复合函数的性质,以及注意定义域、自变量系数的正负.求复合函数的单调区间一般思路是:①求定义域;②确定复合过程;③根据外层函数f(μ)的单调性,确定φ(x)的单调性;④写出满足φ(x)的单调性的含有x 的式子,并解出x 的范围;⑤得到原函数的单调区间(与定义域求交).求解时切勿盲目判断. 例2、已知tan 2θ=. (Ⅰ)求tan 4πθ??+ ??? 的值; (Ⅱ)求cos2θ的值. 【解析】 (Ⅰ)∵tan 2θ=, tan tan 4tan 41tan tan 4π θπθπθ+??∴+= ???- 高一数学第一次月考试题 一. 选择题(每题5分,共60分) 1.函数)6 2sin(2π +=x y 的最小正周期是( ) A .π4 B .π2 C .π D .2 π 2.0sin300=( ) A .1 2 B . 32 C .-12 D .-32 3.如图,在直角坐标系xOy 中,射线OP 交单位圆O 于点P ,若∠ AOP =θ,则点P 的坐标是( ) A .(cos θ,sin θ) B .(-cos θ,sin θ) C .(sin θ,cos θ) D .(-sin θ,cos θ) 4.如果sin α-2cos α 3sin α+5cos α =-5,那么tan α的值为( ) A .-2 B .2 D .-2316 5.函数)2 52sin(π+=x y 的图象的一条对称轴方程是( ) A .2 π-=x B .4 π-=x C .8 π = x D .4 5π= x 6.将函数y =sin(x -π 3)的图象上所有点的横坐标伸长到原来的2 倍(纵坐标不变),再将所得的图象向右平移π 3个单位,得到的图象 对应的解析式是( ) A .y =sin 1 2x B .y =sin(12x -π 2) C .y =sin(12x -π 6 ) D .y =sin(2x -π 6 ) 7.已知α是第二象限角,且4tan =-3 α,则( ) A .4sin =-5α B .4sin =5α C .3cos =5α D .4cos =-5 α 8.已知3 cos +=25πθ?? ???,且3,22 ππθ? ? ∈ ??? ,则tan θ=( ) A .43 B .-43 C .34 D .-34 9.已知函数f (x )=2sin(ωx +φ)(ω>0,|φ|< π 2 )的部分图象如 人教版初中数学锐角三角函数的知识点复习 一、选择题 1.南洞庭大桥是南益高速公路上的重要桥梁,小芳同学在校外实践活动中对此开展测量活动.如图,在桥外一点A 测得大桥主架与水面的交汇点C 的俯角为α,大桥主架的顶端D 的仰角为β,已知测量点与大桥主架的水平距离AB =a ,则此时大桥主架顶端离水面的高CD 为( ) A .asinα+asinβ B .acosα+acosβ C .atanα+atanβ D .tan tan a a αβ + 【答案】C 【解析】 【分析】 在Rt △ABD 和Rt △ABC 中,由三角函数得出BC =atanα,BD =atanβ,得出CD =BC+BD =atanα+atanβ即可. 【详解】 在Rt △ABD 和Rt △ABC 中,AB =a ,tanα= BC AB ,tanβ=BD AB , ∴BC =atanα,BD =atanβ, ∴CD =BC+BD =atanα+atanβ, 故选C . 【点睛】 本题考查了解直角三角形﹣仰角俯角问题;由三角函数得出BC 和BD 是解题的关键. 2.如图,△ABC 内接于半径为5的⊙O ,圆心O 到弦BC 的距离等于3,则∠A 的正切值等于( ) A .35 B .45 C .34 D .43 【答案】C 【解析】 试题分析:如答图,过点O作OD⊥BC,垂足为D,连接OB,OC,∵OB=5,OD=3,∴根据勾股定理得BD=4. ∵∠A=1 2 ∠BOC,∴∠A=∠BOD. ∴tanA=tan∠BOD= 4 3 BD OD . 故选D. 考点:1.垂径定理;2.圆周角定理;3.勾股定理;4.锐角三角函数定义. 3.同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图: (1)作线段AB,分别以点A,B为圆心,AB长为半径作弧,两弧交于点C; (2)以点C为圆心,仍以AB长为半径作弧交AC的延长线于点D; (3)连接BD,BC. 根据以上作图过程及所作图形,下列结论中错误的是() A.∠ABD=90°B.CA=CB=CD C.sinA= 3 2 D.cosD= 1 2 【答案】D 【解析】 【分析】 由作法得CA=CB=CD=AB,根据圆周角定理得到∠ABD=90°,点C是△ABD的外心,根据三角函数的定义计算出∠D=30°,则∠A=60°,利用特殊角的三角函数值即可得到结论. 【详解】 由作法得CA=CB=CD=AB,故B正确; ∴点B在以AD为直径的圆上, ∴∠ABD=90°,故A正确; ∴点C是△ABD的外心, 高中数学三角函数复习专题 一、知识点整理 1角的概念的推广: 正负,范围,象限角,坐标轴上的角; 2、角的集合的表示: ① 终边为一射线的角的集合: x|x 2k ② 终边为一直线的角的集合: xx k 3、任意角的三角函数: (1) 弧长公式:1 aR R 为圆弧的半径,a 为圆心角弧度数,1为弧长 (2) 扇形的面积公式 :S 1 -IR R 为圆弧的半径,1为弧长。 2 (3) 三角函数定义: 角 中边上任意一点P 为(x,y),设|OP| r 则: sin — ,cos r x J r tan y r=寸孑圧 x 女口:公式 cos( ) cos cos sin sin 的证明 (4)特殊角的三角函数值 ③两射线介定的区域上的角的集合: x2k ④两直线介定的区域上的角的集合: x k x k ,k Z ? k 360', k Z ,k Z = | ,k Z ; 反过来,角 的终边上到原点的距离为 r 的点P 的坐标可写为:P r cos ,r sin 4 x 4 4 sin cos tan - -si n + cos -ta n - + si n -cos -ta n + -si n -cos + tan 2 . -si n + cos -ta n 2k + + si n + cos + tan sin con tan 2 + cos + sin + cot 2 + cos -si n -cot 3 2 -cos -si n + cot 3_ 2 -cos + sin -cot 三角函数值等于 的同名三角函数值,前面 加 上一个把 看作锐角时,原三角函数值的 符 号;即:函数名不变,符号看象限 三角函数值等于 的异名三角函数值,前面 加 上一个把 看作锐角时,原三角函数值的 符号; 即:函数名改变,符号看象限: sin x 比如 cos 一 x 4 cos x cos x sin 一 (6)三角函数线:(判断正负、比较大小,解方程或不等式等) 如图,角 的终边与单位圆交于点P ,过点P 作x 轴的垂线, 垂足为M ,则 过点A(1,0)作x 轴的切线,交角终边0P 于点T ,贝U (7)同角三角函数关系式: ③ 平方关系:sin 2 a cos 2 a 1 ①倒数关系: tan acota 1 ②商数关系: tana ^ina cosa (8)诱导公试 三角函数及数列大题训练 1.设数列{}n a 满足21112,32n n n a a a -+=-= (1) 求数列{}n a 的通项公式;令n n b na =,求数列的前n 项和n S 2.等比数列{}n a 的各项均为正数,且212326231,9.a a a a a +== (1)求数列{}n a 的通项公式.(2)设 31323log log ......log ,n n b a a a =+++ 求数列1n b ?? ???? 的前项和. 3.已知,,a b c 分别为ABC ?三个内角,,A B C 的对边,cos 3sin 0a C a C b c +--= (1)求A (2)若2a =,ABC ?的面积为3;求,b c 。 4.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a =b cos C +c sin B . (1)求B ;(2)若b =2,求△ABC 面积的最大值. 5.已知数列{}n a 满足11a =,131n n a a +=+. ⑴证明1{}2 n a +是等比数列,并求{}n a 的通项公式;(2)证明:1231112 n a a a ++<…+. 6.ABC ?的内角A 、B 、C 的对边分别为a 、b 、c ,已知cos()cos 1A C B -+=,2a c =,求C 。 7.ABC ?的内角A 、B 、C 的对边分别为,,a b c 。已知90,2A C a c b -=+= ,求C 8.如图,在△ABC 中,∠ABC =90°,AB= 3 ,BC=1,P 为△ABC 内一点,∠BPC =90° (1)若PB=1 2,求PA ;(2)若∠APB =150°,求tan ∠PBA 9.在△ABC 中,a, b, c 分别为内角A, B, C 的对边, 且2sin (2)sin (2)sin .a A a c B c b C =+++ (Ⅰ)求A 的大小;(Ⅱ)求sin sin B C +的最大值. 10.已知等差数列{a n }满足a 2=0,a 6+a 8= -10 (I )求数列{a n }的通项公式;(II )求数列? ? ????-1 2 n n a 的前n 项和。 11. 在ABC ?中,角A 、B 、C 的对边分别为a ,b ,c 。角A ,B ,C 成等差数列。 (Ⅰ)求cos B 的值;(Ⅱ)边a ,b ,c 成等比数列,求sin sin A C 的值。 12.设向量a =(3sin x ,sin x ),b =(cos x ,sin x ),x ∈π0,2 ?? ???? . (1)若|a |=|b |,求x 的值;(2)设函数f (x )=a ·b ,求f (x )的最大值. 13.在△ABC 中,内角A 、B 、C 的对边分别为a ,b ,c ,且a >c ,已知? =2,cosB=, b=3,求:(Ⅰ)a 和c 的值;(Ⅱ)cos (B ﹣C )的值. A B C P 高三数学三角函数专题训练 1.为得到函数πcos 23y x ?? =+ ?? ? 的图像,只需将函数sin 2y x =的图像( ) A .向左平移5π12个长度单位 B .向右平移5π12 个长度单位 C .向左平移 5π6 个长度单位 D .向右平移 5π6 个长度单位 2.若动直线x a =与函数()sin f x x =和()cos g x x =的图像分别交于M N ,两点,则M N 的最大值为( ) A .1 B . 2 C . 3 D .2 3.把函数sin y x =(x R ∈)的图象上所有点向左平行移动3 π 个单位长度,再把所得图象上所有点的横坐标缩短到原来的1 2倍(纵坐标不变),得到的图 象所表示的函数是( ) A .sin(2)3 y x π =-,x R ∈ B.sin( ) 2 6 x y π =+ ,x R ∈ C.s in (2)3 y x π =+,x R ∈ D.sin(2) 3 2y x π=+ ,x R ∈ 4.设5sin 7 a π=,2cos 7 b π=,2tan 7 c π=,则( ) A.c b a << B.a c b << C.a c b << D.b a c << 5.将函数sin(2)3 y x π =+ 的图象按向量α 平移后所得的图象关于点(,0) 12 π - 中 心对称,则向量α的坐标可能为( ) A .(,0)12π - B .(,0)6 π - C .( ,0)12 π D .( ,0)6 π 6.函数2 ()sin 3sin cos f x x x x =+ 在区间 ,42ππ?? ???? 上的最大值是( ) A.1 B.13 2 + C. 3 2 D.1+ 3 7.若,5sin 2cos -=+a a 则a tan =( ) A.2 1 B. 2 C.2 1- D.2- 人教版高中数学三角函数 全部教案 This model paper was revised by the Standardization Office on December 10, 2020 三角函数 第一教时 教材:角的概念的推广 目的:要求学生掌握用“旋转”定义角的概念,并进而理解“正角”“负角”“象限角” “终边相同的角”的含义。 过程:一、提出课题:“三角函数” 回忆初中学过的“锐角三角函数”——它是利用直角三角形中两边的比值来定义 的。相对于现在,我们研究的三角函数是“任意角的三角函数”,它对我们今后的学习和研究都起着十分重要的作用,并且在各门学科技术中都有广泛应用。 二、角的概念的推广 1.回忆:初中是任何定义角的(从一个点出发引出的两条射线构成的几何图形)这种概念的优点是形象、直观、容易理解,但它的弊端在于“狭隘” 2.讲解:“旋转”形成角(P4) 突出“旋转”注意:“顶点”“始边”“终边” “始边”往往合于x轴正半轴 3.“正角”与“负角”——这是由旋转的方向所决定的。 记法:角α或α ∠可以简记成α 4.由于用“旋转”定义角之后,角的范围大大地扩大了。 1角有正负之分如:=210=150=660 2角可以任意大 实例:体操动作:旋转2周(360×2=720)3周(360×3=1080) 3还有零角一条射线,没有旋转 三、关于“象限角” 为了研究方便,我们往往在平面直角坐标系中来讨论角 角的顶点合于坐标原点,角的始边合于x轴的正半轴,这样一来,角的终边落在第几象限,我们就说这个角是第几象限的角(角的终边落在坐标轴上,则此角不属于任何一个象限) 例如:是第Ⅰ象限角30060是第Ⅳ象限角 5851180是第Ⅲ象限角2000是第Ⅱ象限角等 四、关于终边相同的角 1.观察:390,330角,它们的终边都与30角的终边相同 2.终边相同的角都可以表示成一个0到360的角与) k∈个周角的和 k (Z 390=30+360)1 k (= 330=30360)1 (= k = (- k30=30+0×360)0 三角函数复习专题 一、核心知识点归纳: ★★★1、正弦函数、余弦函数和正切函数的图象与性质: sin y x = cos y x = tan y x = 图象 定义域 R R ,2x x k k ππ?? ≠+∈Z ???? 值域 []1,1- []1,1- R 最值 当22 x k π π=+ () k ∈Z 时,max 1y =; 当22 x k π π=- ()k ∈Z 时,min 1y =-. 当()2x k k π=∈Z 时, max 1y =; 当2x k ππ=+ ()k ∈Z 时,min 1y =-. 既无最大值也无最小值 周期性 2π 2π π 奇偶性 奇函数 偶函数 奇函数 单调性 在2,22 2k k π πππ? ? - + ??? ? ()k ∈Z 上是增函数;在 32,222k k ππππ??++??? ? ()k ∈Z 上是减函数. 在[]()2,2k k k πππ-∈Z 上是增函数;在 []2,2k k πππ+ ()k ∈Z 上是减函数. 在,2 2k k π πππ? ? - + ?? ? ()k ∈Z 上是增函数. 对称性 对称中心()(),0k k π∈Z 对称轴 ()2 x k k π π=+ ∈Z 对称中心 (),02k k ππ? ?+∈Z ?? ? 对称轴()x k k π=∈Z 对称中心 (),02k k π?? ∈Z ??? 无对称轴 ★★2.正、余弦定理:在ABC ?中有: 函 数 性 质 ①正弦定理: 2sin sin sin a b c R A B C ===(R 为ABC ?外接圆半径) 2sin 2sin 2sin a R A b R B c R C =??=??=? ? sin 2sin 2sin 2a A R b B R c C R ? =?? ? =?? ? =?? 注意变形应用 ②面积公式:111 sin sin sin 222 ABC S abs C ac B bc A ?= == ③余弦定理: 222222 2222cos 2cos 2cos a b c bc A b a c ac B c a b ab C ?=+-?=+-??=+-? ? 222 222222 cos 2cos 2cos 2b c a A bc a c b B ac a b c C ab ?+-=?? +-?=???+-= ?? 二、练习题 1、角α的终边过点 b b 则且(,5 3 cos ),4,--=α的值( ) A 、3 B 、-3 C 、3± D 、5 2、已知2π θπ<<,3 sin()25 πθ+=-,则tan(π-θ)的值为( ) A .34 B .43 C .34- D .4 3 - 3、2(sin cos )1y x x =--是 ( ) A .最小正周期为2π的偶函数 B .最小正周期为2π的奇函数 4、为得到函数πcos 3y x ? ?=+ ?? ?的图象,只需将函数sin y x =的图像( ) A .向左平移π 6个长度单位 B .向右平移 π 6 个长度单位 C .向左平移5π 6 个长度单位 D .向右平移 5π 6 个长度单位 5、()sin()(0,0,||)2 f x A x A ωφωφπ =+>>< 是( ) A. y = 2sin(x -4π) B. y = 2sin(x +4π) C. y = 2sin (2x -8π) D. y = 2sin (2x +8 π ) A .30° B .45° C .60° D .90° 2.在△ABC 中,已知A =75°,B =45°,b =4,则c =( ) B .2 6 C .4 3 D .2 3.在△ABC 中,若∠A=60°,∠B =45°,BC =32,则AC =( ) A .4 3 B .2 3 在△ABC 中,AC sin B =BC sin A ,∴AC =BC ·sin B sin A =32× 22 3 2=2 3. 4.在△ABC 中,若∠A=30°,∠B =60°,则a∶b∶c=( ) A .1∶3∶2 B .1∶2∶4 C .2∶3∶4 D .1∶2∶2 5.在△ABC 中,若sin A>sin B ,则A 与B 的大小关系为( ) A .A> B B .A
高考数学压轴专题2020-2021备战高考《三角函数与解三角形》技巧及练习题附答案
高中数学三角函数基础知识点及答案
人教版高中数学三角函数复习专题及参考答案
高三数学 三角函数专题训练(含解析)
高中数学三角函数知识点归纳总结
人教版 高中数学必修4 三角函数知识点
最新上海高中数学三角函数大题压轴题练习
高考数学三角函数知识点总结及练习
人教版高中数学必修4三角函数
2020年高考数学三角函数专题解题技巧
高中数学三角函数练习题
人教版初中数学锐角三角函数的知识点复习
高中数学三角函数复习专题(2)
高考全国卷三角函数大题训练
高三数学三角函数专题训练
人教版高中数学三角函数全部教案
高考数学三角函数复习专题
高三文科数学三角函数专题测试题