
勾股定理的十种证法
初二(8)班
祁芳铭
证法1(梅文鼎证明)
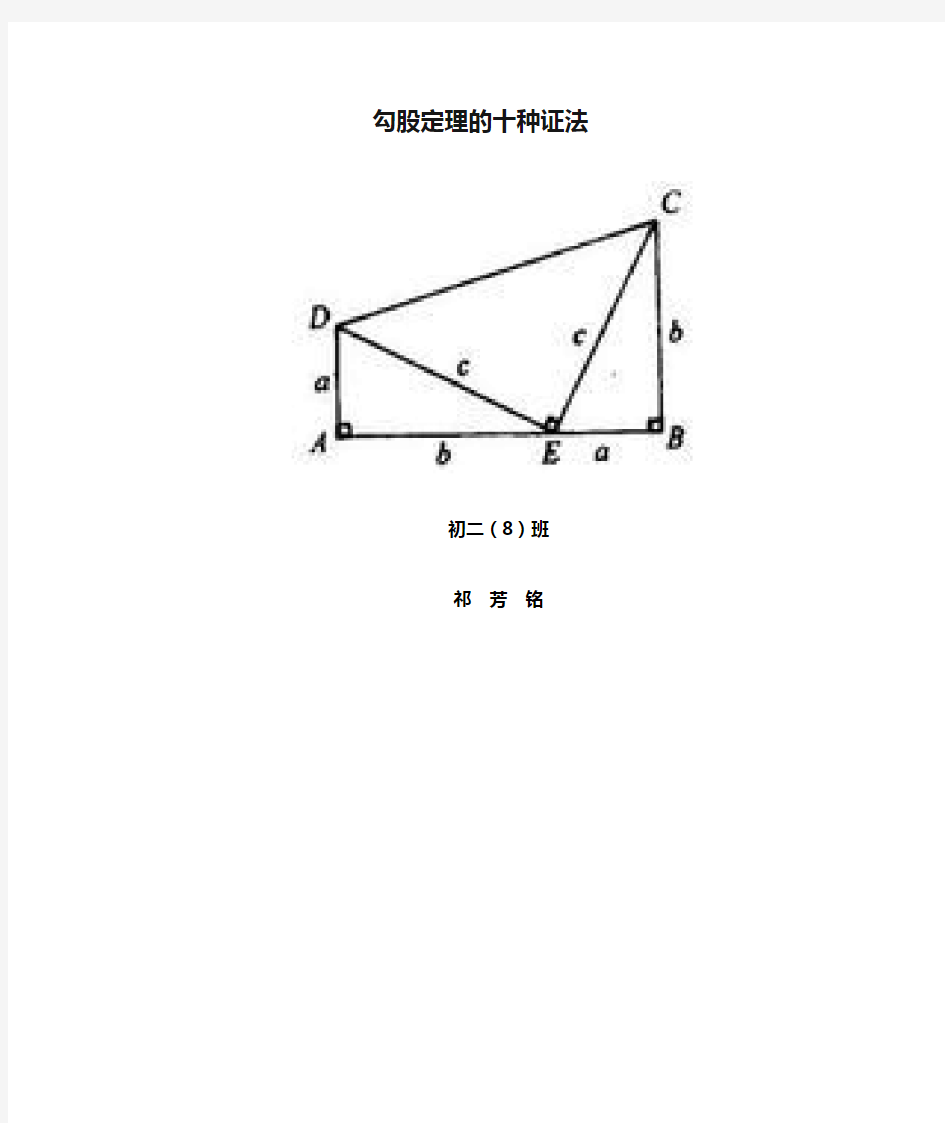
作四个全等的直角三角形,设它们的两条直角边长分别为a、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D、E、F在一条直线上. 过C作AC的延长线交DF于点P.
∵D、E、F在一条直线上, 且RtΔGEF ≌RtΔEBD,
∴∠EGF = ∠BED,
∵∠EGF + ∠GEF = 90°,
∴∠BED + ∠GEF = 90°,
∴∠BEG =180°―90°= 90°
又∵AB = BE = EG = GA = c,
∴ABEG是一个边长为c的正方形.
∴∠ABC + ∠CBE = 90°
∵RtΔABC ≌RtΔEBD,
∴∠ABC = ∠EBD.
∴∠EBD + ∠CBE = 90°
即∠CBD= 90°
又∵∠BDE = 90°,∠BCP = 90°,
BC = BD = a.
∴BDPC是一个边长为a的正方形.
同理,HPFG是一个边长为b的正方形.
设多边形GHCBE的面积为S,则
,
∴BDPC的面积也为S,HPFG的面积也为S由此可推出:a^2+b^2=c^2
证法2(项明达证明)
作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形,使E、A、C三点在一条直线上.
过点Q作QP∥BC,交AC于点P.
过点B作BM⊥PQ,垂足为M;再过点
F作FN⊥PQ,垂足为N.
∵∠BCA = 90°,QP∥BC,
∴∠MPC = 90°,
∵BM⊥PQ,
∴∠BMP = 90°,
∴BCPM是一个矩形,即∠MBC = 90°.
∵∠QBM + ∠MBA = ∠QBA = °,
∠ABC + ∠MBA = ∠MBC = 90°,
∴∠QBM = ∠ABC,
又∵∠BMP = 90°,∠BCA = 90°,BQ = BA = c,
∴RtΔBMQ ≌RtΔBCA.
同理可证RtΔQNF ≌RtΔAEF.即a^2+b^2=c^2
证法3(赵浩杰证明)
作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),斜边长为c. 再做一个边长为c的正方形. 把它们拼成如图所示的多边形.
分别以CF,AE为边长做正方形FCJI和AEIG,
∵EF=DF-DE=b-a,EI=b,
∴FI=a,
∴G,I,J在同一直线上,
∵CJ=CF=a,CB=CD=c,
∠CJB = ∠CFD = 90°,
∴RtΔCJB ≌RtΔCFD ,
同理,RtΔABG ≌RtΔADE,
∴RtΔCJB ≌RtΔCFD ≌RtΔABG ≌RtΔADE
∴∠ABG = ∠BCJ,
∵∠BCJ +∠CBJ= 90°,
∴∠ABG +∠CBJ= 90°,
∵∠ABC= 90°,
∴G,B,I,J在同一直线上,
所以a^2+b^2=c^2
证法4(欧几里得证明)
作三个边长分别为a、b、c的三角形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结
BF、CD. 过C作CL⊥DE,
交AB于点M,交DE于点L.
∵AF = AC,AB = AD,
∠FAB = ∠GAD,
∴ΔFAB ≌ΔGAD,
∵ΔFAB的面积等于,
ΔGAD的面积等于矩形ADLM
的面积的一半,
∴矩形ADLM的面积=.
同理可证,矩形MLEB的面积=.
∵正方形ADEB的面积
= 矩形ADLM的面积+ 矩形MLEB的面积
∴即a的平方+b的平方=c的平方
证法5(欧几里得的证法)
《几何原本》中的证明
在欧几里得的《几何原本》一书中提出勾股定理由以下证明后可成立。设△ABC为一直角三角形,其中A为直角。从A点划一直线至对边,使其垂直于对边上的正方形。此线把对边上的正方形一分为二,其面积分别与其余两个正方形相等。
在正式的证明中,我们需要四个辅助定理如下:
如果两个三角形有两组对应边和这两组边所夹的角相等,则两三角形全等。(SAS定理)三角形面积是任一同底同高之平行四边形面积的一半。任意一个正方形的面积等于其二边长的乘积。任意一个四方形的面积等于其二边长的乘积(据辅助定理3)。证明的概念为:把上方的两个正方形转换成两个同等面积的平行四边形,再旋转并转换成下方的两个同等面积的长方形。
其证明如下:
设△ABC为一直角三角形,其直角为CAB。其边为BC、AB、和CA,依序绘成四方形CBDE、BAGF和ACIH。画出过点A之BD、CE的平行线。此线将分别与BC和DE直角相交于K、L。分别连接CF、AD,形成两个三角形BCF、BDA。∠CAB和∠BAG都是直角,因此C、A 和G 都是线性对应的,同理可证B、A和H。∠CBD和∠FBA皆为直角,所以∠ABD等于∠FBC。因为AB 和BD 分别等于FB 和BC,所以△ABD 必须相等于△FBC。因为 A 与K 和L是线性对应的,所以四方形BDLK 必须二倍面积于△ABD。因为C、A和G有共同线性,所以正方形BAGF必须二倍面积于△FBC。因此四边形BDLK 必须有相同的面积BAGF = AB^2。同理可证,四边形CKLE 必须有相同的面积ACIH = AC^2。把这两个结果相加,AB^2+ AC^2; = BD×BK + KL×KC 由于BD=KL,BD×BK + KL×KC = BD(BK + KC) = BD×BC 由于CBDE是个正方形,因此AB^2 + AC^2= BC^2。此证明是于欧几里得《几何原本》一书第1.47节所提出的。
证法6(欧几里德(Euclid)射影定理证法)
如图,Rt△ABC中,∠ABC=90°,AD是斜边BC上的高,通过证明三角形相似则有射影定理如下:
(1)(BD)^2;=AD·DC (2)(AB)^2;=AD·AC (3)(BC)^2;=CD·AC
由公式(2)+(3)得:
(AB)^2;+(BC)^2;=AD·AC+CD·AC =(AD+CD)·AC=(AC)^2;,
即(AB)^2;+(BC)^2;=(AC)^2,这就是勾股定理的结论。
三角形为直角三角形,以勾a为边的正方形为朱方,以股b为边的正方形为青方。以盈补虚,将朱方、青方并成弦方。依其面积关系有a^2+b^2=c^2.由于朱方、青方各有一部分在玄方内,那一部分就不动了。以勾为边的的正方形为朱方,以股为边的正方形为青方。以盈补虚,只要把图中朱方(a2)的I移至I′,青方的II移至II′,III移至III′,则刚好拼好一个以弦为边长的正方形(c……2 ).由此便可证得a^+b^2=c^2; 如下:
解:在网格内,以两个直角边为边长的小正方形面积和,等于以斜边为边长的的正方形面积。勾股定理的内容:直角三角形两直角边a、b的平方和等于斜边c的平方,a的平方+b的平方=c的平方; 说明:我国古代学者把直角三角形的较短直角边称为“勾”,较长直角边为“股”,斜边称为“弦”,所以把这个定理称为“勾股定理”。勾股定理揭示了直角三角形边之间的关系。举例:如直角三角形的两个直角边分别为3、4,则斜边c的平方;= a的平方+b的平方=9+16=25即c=5 则说明斜边为5。
这个定理有许多证明的方法,其证明的方法可能是数学众多定理中最多的。路明思(Elisha Scott Loomis)的Pythagorean Proposition(《毕达哥拉斯命题》)一书中总共提到367种证明方式。有人会尝试以三角恒等式(例如:正弦和余弦函数的泰勒级数)来证明勾股定理,但是,因为所有的基本三角恒等式都是建基于勾股定理,所以不能作为勾股定理的证明。
证法8(美国第二十任总统伽菲尔德证法)
如图,
S梯形ABCD= (a+b)2
= (a2+2ab+b2),①
又S梯形ABCD=S△AED+S△EBC+S△CED
= ab+ ba+ c2
= (2ab+c2)。②
比较以上二式,便得
a2+b2=c2。
这一证明由于用了梯形面积公式和三角形面积公式,从而使证明相当简洁。
1876年4月1日,伽菲尔德在《新英格兰教育日志》上发表了他对勾股定理的这一证明。5年后,伽菲尔德就任美国第二十任总统。后来,人们为了纪念他对勾股定理直观、简捷、易懂、明了的证明,就把这一证法称为勾股定理的“总统”证法,这在数学史上被传为佳话。
在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个直角三角形与原三角形相似。
如图,Rt△ABC中,∠ACB=90°。作CD⊥BC,垂足为D。则
△BCD∽△BAC,△CAD∽△BAC。
由△BCD∽△BAC可得BC2=BD ? BA,①
由△CAD∽△BAC可得AC2=AD ? AB。②
我们发现,把①、②两式相加可得
BC2+AC2=AB(AD+BD),
而AD+BD=AB,
因此有BC2+AC2=AB2,这就是
a2+b2=c2。
证法9(利用相似三角形证明法)
有许多勾股定理的证明方式,都是基于相似三角形中两边长的比例。
设ABC为一直角三角形, 直角于角C(看附图). 从点C画上三角形的高,并将此高与AB的交叉点称之为H。此新三角形ACH和原本的三角形ABC相似,因为在两个三角形中都有一个直角(这又是由于“高”的定义),而两个三角形都有A这个共同角,由此可知第三只角都是相等的。同样道理,三角形CBH 和三角形ABC也是相似的。这些相似关系衍生出以下的比率关系:
因为BC=a,AC=b,AB=c
所以a/c=HB/a and b/c=AH/b
可以写成a*a=c*HB and b*b=C*AH
综合这两个方程式,我们得到a*a+b*b=c*HB+c*AH=c*(HB+AH)=c*c
换句话说:a*a+b*b=c*c
证法10(邹元治证明法)
以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于 . 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D 三点在一条直线上.
∵RtΔHAE ≌RtΔEBF,
∴∠AHE = ∠BEF.
∵∠AEH + ∠AHE = 90o,
∴∠AEH + ∠BEF = 90o.
∴∠HEF = 180o―90o= 90o.
∴四边形EFGH是一个边长为c的
正方形. 它的面积等于c2.
∵RtΔGDH ≌RtΔHAE,
∴∠HGD = ∠EHA.
∵∠HGD + ∠GHD = 90o,
∴∠EHA + ∠GHD = 90o.
又∵∠GHE = 90o,
∴∠DHA = 90o+ 90o= 180o.
∴ABCD是一个边长为a + b的正方形,它的面积等于 .
勾股定理的证明 【证法1】(课本的证明) a 、 b ,斜边长为 c ,再做三 个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++,整理得222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE = ∠BEF . ∵∠AEH + ∠AHE = 90o, ∴∠AEH + ∠BEF = 90o. ∴∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵Rt ΔGDH ≌Rt ΔHAE, ∴∠HGD = ∠EHA . ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 22 14c ab b a +?=+. ∴2 2 2 c b a =+.
以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21. 把这四个直角三 角形拼成如图所示形状. ∵Rt ΔDAH ≌ Rt ΔABE, ∴∠HDA = ∠EAB . ∵∠HAD + ∠HAD = 90o, ∴∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵EF = FG =GH =HE = b ―a , ∠HEF = 90o. ∴EFGH 是一个边长为b ―a 的正方形,它的面积等于()2 a b -. ∴()22 214c a b ab =-+?. ∴2 2 2 c b a =+. 【证法4】(1876年美国总统Garfiel d 证明) 以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面 积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵Rt ΔEAD ≌Rt ΔCBE, ∴∠ADE = ∠BEC . ∵∠AED + ∠ADE = 90o, ∴∠AED + ∠BEC = 90o. ∴∠DEC = 180o―90o= 90o. ∴ΔDEC 是一个等腰直角三角形, 它的面积等于221c . 又∵∠DAE = 90o, ∠EBC = 90o, ∴ AD ∥BC . ∴ABCD 是一个直角梯形,它的面积等于()2 21 b a +. ∴()2 2212122 1 c ab b a +?=+. ∴2 22c b a =+.
勾股定理的证明 【证法1】 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形 的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使 A 、E 、 B 三点在一条 直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .
∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 2214c ab b a +?=+. ∴ 2 2 2 c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21. 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB . ∵ ∠HAD + ∠HAD = 90o, ∴ ∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90o. ∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2 a b -. ∴ ()2 2 214c a b ab =-+?. ∴ 2 22c b a =+. 【证法4】(1876年美国总统Garfield 证明) 以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形 的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使 A 、E 、 B 三点在一条 直线上. ∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC . ∵ ∠AED + ∠ADE = 90o, ∴ ∠AED + ∠BEC = 90o.
勾股定理五种证明方法 【证法1】 ? ? ? ? ? ? ? ? ? ? 做8 个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 214214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角 形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点 在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o . ∴ ∠HEF = 180o ―90o= 90o . ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o . 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o . ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴ ()2 2214c ab b a +?=+. ∴ 222c b a =+. 【证法3】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为
勾股定理的不同证法 证法1:设三角形较短的两边长度分别为a和b,较长的边为c, 如果a的二次方与b的二次方的和等于c的二次方,最长边对 应的角为直角,则已证明勾股定理:a2+b2=c2 证法2:以三角形三边延伸做三个正方形,边长分别为a,b, c,如果正方形(a边长)加正方形(b边长)面积和等于正方 形(c边长),则a2+b2=c2,已证明勾股定理。 证法3:以a,b为直角边,以c为斜边做两个全等的三角形, 则每个直角三角三角形的面积等于?ab,把这两个直角三 角形如图所示,使A,E,B三点在一条直线上。 ∵Rt△EAD≌RT△CBE, ∴∠ADE=∠BEC, ∵∠AED+∠ADE=90° ∴∠AED+∠BEC=90° ∴∠DEC=180°—90°=90° ∴△DEC是一个等腰直角三角形 它的面积等于?c2 又因为∠DAE=90°,∠EBC=90°, ∴AD∥BC ∴ABCD是一个直角梯形,它的面积等于?(a+b)2 ∴?(a+b)2=2·?ab+?c2 ∴a2+b2=c2 证法4:做8个全等的直角三角形设它们的两条直 角边长为a,b,斜边长为c,在做三个边长为a,b, c的正方形,把它们像左图那样拼成两个正方形,从 左图可以看到,这两个正方形的边长都是a+b,所 以面积相等,即: a2+b2+4·?ab等于c2+4·?ab,整理便得a2+b2=c2 证法5:以a,b为直角边(b>a),以c为斜边做四 个全等的直角三角形,则每个直角三角形的面积等于?ab,把这 四个直角三角形拼成如图所示形状。 ∵RtDAH≌Rt△ABE, ∴∠HDA=∠EAB ∵∠HAD+∠HAD=90° ∴∠EAB+∠HAD=90° ∴ABCD是一个边长为c的正方形,它的面积等于c2 ∵EF=FG=GH=HE=b—a ∠HEF=90° ∴EFGH是一个边长为b—a的正方形,它的面积等于(b—a)2 4·?ab+(b—a)2等于c2 ∴a2+b2=c2 证法6:从这张图可以得到一个矩形和三个三角形,推导公式如下:
勾股定理五种证明方法 1证法】【abba aacaabc c ab bccbbb ca b 个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为做8c,再做三个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b,所以面积相等. 即 ,整理得.
证法2证明)(】【 以a、b 为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角1ab 2形的面积等于. 把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上. ∵RtΔHAE ≌RtΔEBF, CGDab∴∠AHE = ∠BEF. , o∠AHE = 90∵∠AEH + abc. o∠BEF = 90∴∠AEH + c. = 90o HEF = 180o―90o∴∠H c的四边形EFGH是一个边长为F它的面积等于
c2. 正方形.b HAE, RtΔ≌∵RtΔGDH .HGD = ∠EHA∴A, o∠GHD = 90∵∠HGD + . GHD = 90∠o∴∠EHA + , GHE = 90o又∵∠. o= 180o+ 90o∴∠DHA = 90. 是一个边长为a + b的正方形,它的面积等于∴ABCD .∴∴. 证法3证明)(】【做四个全等的直角三角形,设它们的两条直角边长分别为a、b ,斜边长为c. 把它们拼成如图那样的一个多边形,使D、E、F在一条直线上. 过C作AC的延长线交DF于点P. ∵D、E、F在一条直线上, 且RtΔGEF ≌RtΔEBD, ∴∠EGF = ∠BED,
证法1 一种借助面积完成的演绎证明(愚草提供),双击右侧图片可以清楚阅读: 另附:《对勾股定理及其逆定理教育价值的深层挖掘》[3]一文。 证法1 作四个全等的直角三角形,设它们的两条直角边长分别为a、b ;,斜边长为c. ;把它们拼成如图那样的一个多边形,使D、E、F在一条直线上。过点C作AC的延长线交DF于点P. ∵ D、E、F在一条直线上,;且RtΔGEF ;≌ RtΔEBD, ∴;∠EGF = ;∠BED, ∵;∠EGF + ;∠GEF = 90°, ∴;∠BED + ;∠GEF = 90°, ∴;∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形。 ∴;∠ABC + ;∠CBE = 90° ∵ RtΔABC ;≌ RtΔEBD, ∴;∠ABC = ;∠EBD. ∴;∠EBD + ;∠CBE = 90° 即;∠CBD= 90° 又∵;∠BDE = 90°,∠BCP = 90°, BC = BD = a. ∴ BDPC是一个边长为a的正方形。 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则 A+B=C 证法2
作两个全等的直角三角形,设它们的直角边长分别为a、b(b>a);,斜边长为c. ;再做一个边长为c的正方形。把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点 F作FN⊥PQ,垂足为N. ∵;∠BCA = 90°,QP∥BC, ∴;∠MPC = 90°, ∵ BM⊥PQ, ∴;∠BMP = 90°, ∴ BCPM是一个矩形,即∠MBC = 90°。 ∵;∠QBM + ;∠MBA = ;∠QBA = 90°, ∠ABC + ;∠MBA = ;∠MBC = 90°, ∴;∠QBM = ;∠ABC, 又∵;∠BMP = 90°,∠BCA = 90°,BQ = BA = c, ∴ RtΔBMQ ;≌ RtΔBCA. 同理可证RtΔQNF ;≌ RtΔAEF.即A2+B2=C2 证法3 作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a);,斜边长为c. ;再作一个边长为c的正方形。把它们拼成如图所示的多边形. 分别以CF,AE为边长做正方形FCJI和AEIG, ∵EF=DF-DE=b-a,EI=b, ∴FI=a, ∴G,I,J在同一直线上, ∵CJ=CF=a,CB=CD=c, ∠CJB = ;∠CFD = 90°, ∴RtΔCJB ;≌ RtΔCFD ;, 同理,RtΔABG ;≌ RtΔADE, ∴RtΔCJB ;≌ RtΔCFD ;≌ RtΔABG ;≌ RtΔADE ∴∠ABG = ;∠BCJ, ∵∠BCJ +∠CBJ= 90°, ∴∠ABG +∠CBJ= 90°, ∵∠ABC= 90°, ∴G,B,I,J在同一直线上, A2+B2=C2。 证法4 作三个边长分别为a、b、c的三角形,把它们拼成如图所示形状,使H、C、B三点在一条直线上,连结 BF、CD. ;过C作CL⊥DE, 交AB于点M,交DE于点L. ∵ AF = AC,AB = AD, ∠FAB = ;∠GAD, ∴;ΔFAB ;≌;ΔGAD, ∵;ΔFAB的面积等于, ΔGAD的面积等于矩形ADLM
勾股定理五种证明方法 【证法1】 做 8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 214214222?+=?++, 整理得 222c b a =+. 【 证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角 形的面积等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点 在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +. ∴ ()2 2214c ab b a +?=+. ∴ 222c b a =+. 【证法3】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为
v1.0 可编辑可修改 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2.
v1.0 可编辑可修改 ∴∠HGD = ∠EHA. ∵∠HGD + ∠GHD = 90o, ∴∠EHA + ∠GHD = 90o. 又∵∠GHE = 90o, ∴∠DHA = 90o+ 90o= 180o. ∴ ABCD是一个边长为a + b的正方形,它的面积等于()2b a+. ∴()2 2 2 1 4c ab b a+ ? = + . ∴2 2 2c b a= +. 【证法3】(赵爽证明) 以a、b 为直角边(b>a),以c为斜边作四个全等的直角三角形,则每个直角 三角形的面积等于 ab 2 1 . 把这四个直角三 角形拼成如图所示形状. ∵ RtΔDAH ≌ RtΔABE, ∴∠HDA = ∠EAB. ∵∠HAD + ∠HAD = 90o, ∴∠EAB + ∠HAD = 90o, ∴ ABCD是一个边长为c的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a , ∠HEF = 90o. ∴ EFGH是一个边长为b―a的正方形,它的面积等于()2a b-. ∴ ()2 2 2 1 4c a b ab= - + ? .
勾股定理五种证明方法 This manuscript was revised on November 28, 2020
勾股定理五种证明方法 【证法1】 做 c ,再. .即 b a 22+【证法以 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵Rt ΔHAE ≌Rt ΔEBF, ∴∠AHE=∠BEF . ∵∠AEH+∠AHE=90o, ∴∠AEH+∠BEF=90o . ∴∠HEF=180o ―90o=90o . ∴四边形EFGH 是一个边长为c 的 正方形.它的面积等于c2. ∵Rt ΔGDH ≌Rt ΔHAE, ∴∠HGD=∠EHA . ∵∠HGD+∠GHD=90o, ∴∠EHA+∠GHD=90o . 又∵∠GHE=90o, ∴∠DHA=90o+90o=180o . ∴ABCD 是一个边长为a+b 的正方形,它的面积等于()2b a +. ∴()2 2214c ab b a +?=+.∴222c b a =+. 【证法3】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c .把它们拼成如图那样的一个多边形,使D 、E 、F 在一条直线上.过C 作AC 的延长线交DF 于点P . ∵D 、E 、F 在一条直线上,且Rt ΔGEF ≌Rt ΔEBD, ∴∠EGF=∠BED , ∵∠EGF+∠GEF=90°, ∴∠BED+∠GEF=90°, ∴∠BEG=180o ―90o=90o . 又∵AB=BE=EG=GA=c , ∴ABEG 是一个边长为c 的正方形. ∴∠ABC+∠CBE=90o . ∵Rt ΔABC ≌Rt ΔEBD,
勾股定理的9种证明(有图) 【证法1】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形, 则每个直角三角形的面积 等于2ab .把这四个直角三角形拼成如图所示形状, 使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C G D 三点在一条直线上. v Rt △ HAE 坐 Rt △ EBF, ??? / AHE = / BEF. v / AEH + / AHE = 90o, ? / AEH + / BEF = 90o. ? / HEF = 180o — 90o= 90o. ?四边形EFGH 是一个边长为c 的 正方形.它的面积等于c 2. v Rt △ GDH 坐 Rt △ HAE, ? / HGD = / EHA. v / HGD + / GHD = 90o, ? / EHA + / GHD = 90o. 又v / GHE = 90o, ? / DHA = 90o+ 90o= 180o. 2 ? ABCD 是一个边长为a + b 的正方形,它的面积等于(a + b ). 2 1 2 a b 4 ab c 222 ? 2 . ? a b = c . 【证法2】(梅文鼎证明) 做四个全等的直角三角形,设它们的两条直角边长分别为 a 、b ,斜边长为c.把它 们拼成如图那样的一个多边形,使 D E 、F 在一条直线上.过C 作AC 的延长线交DF 于 / EGF + / GEF = 90°, / BED + / GEF = 90 ° , / BEG =18(b — 90o= 90 o. 又 v AB = BE = EG = GA = c ? / ABC + / CBE = 90o. v Rt △ ABC 坐 Rt △ EBD, ? / ABC = / EBD. ? / EBD + / CBE = 90o. 即 / CBD= 9Gb. 又 v / BDE = 90o ,Z BCP = 90o , D 、 E 、 F 在一条直线上,且Rt △ GEF 幻Rt △ EBD, ABE G 是一个边长为c 的正方形. a b H H 匕 D A F b a P b C
勾股定理的十六种证明方法 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上, B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHA E ≌ Rt ΔEBF, ∴ ∠AHE = ∠BE F . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ 2 2 2 c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角
勾股定理几种证明方法 勾股定理的证明 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为c,再做三 个边长分别为a、b、c的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a+b,所以面积相等.即 11 a2+b2+4×ab=c2+4×ab 22,整理得 a2+b2=c2. 【证法2】(邹元治证明) 以a、b为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积 1ab2等于.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、 C三点在一条直线上,C、G、D三点在一条直线 上.∵RtΔHAE≌RtΔEBF,∴∠AHE=∠BEF. ∵∠AEH+∠AHE=90o,∴∠AEH+∠BEF=90o.∴∠HEF=180o―90o=90o.∴四边形EFGH是 一个边长为c的正方形.它的面积等于c2.∵RtΔGDH≌RtΔHAE,∴∠HGD=∠EHA. ∵∠HGD+∠GHD=90o,∴∠EHA+∠GHD=90o.又∵∠GHE=90o, ∴∠DHA=90o+90o=180o. 2∴.∴a+b=c. 【证法3】(赵爽证明)以a、b为直角边(b>a),以c为斜边作四个全等的直角三 角形,则每个直角 ( a+∴ABCD是一个边长为a+b的正方形,它的面积等于(a+b)2=4×1ab+c2 222
1ab2三角形的面积等于.把这四个直角三 角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB. ∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o, 2 ∴ABCD是一个边长为c的正方形,它的面积等于c.∵EF=FG=GH=HE=b―a,∠HEF=90o. 2 (b?a)∴EFGH是一个边长为b―a的正方形,它的面积等于. 1 4×ab+(b?a)2=c2 2∴.222 ∴a+b=c.【证法4】(1876年美国总统Garfield证明) 以a、b为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面 1ab2积等于.把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线 上.∵∴∵∴∴∴RtΔEAD≌RtΔCBE,∠ADE=∠BEC. ∠AED+∠ADE=90o, ∠AED+∠BEC=90o.∠DEC=180o―90o=90o.ΔDEC是一个等腰直角三角形, 12c2它的面积等于. 又∵∠DAE=90o,∠EBC=90o, ∴AD∥BC. 1 (a+b)2 ∴ABCD是一个直角梯形,它的面积等于2. 1 (a+b)2=2×1ab+1c2
1文档来源为:从网络收集整理.word 版本可编辑. 勾股定理的证明 【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHA E ≌ Rt ΔEBF, ∴ ∠AHE = ∠BE F . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 22 14c ab b a +?=+. ∴ 2 22c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21. 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB . ∵ ∠HAD + ∠HAD = 90o, ∴ ∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2.
证法1 作四个全等的直角三角形,把它们拼成如图那样的一个多边形,使D、E、F在一条直线上(设它们的两条直角边长分别为a、b ,斜边长为c.)。过点C作AC 的延长线交DF于点P. ∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD, ∴∠EGF = ∠BED, ∵ ∠EGF + ∠GEF = 90°, ∴ ∠BED + ∠GEF = 90°, ∴ ∠BEG =180°―90°= 90° 又∵ AB = BE = EG = GA = c, ∴ ABEG是一个边长为c的正方形。 ∴ ∠ABC + ∠CBE = 90° ∵ RtΔABC ≌ RtΔEBD, ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90° 即∠CBD= 90° 又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a. ∴ BDPC是一个边长为a的正方形。 同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则 证法2 作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),做一个边长为c的正方形。斜边长为c. 再把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N. ∵ ∠BCA = 90°,QP∥BC, ∴ ∠MPC = 90°, ∵ BM⊥PQ, ∴ ∠BMP = 90°, ∴ BCPM是一个矩形,即∠MBC = 90°。 ∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°, ∴ ∠, 又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c, ∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF.即 证法3 作两个全等的直角三角形,同证法2,再作一个边长为c的正方形。把它们拼成如图所示的多边形. 分别以CF,AE为边长做正方形FCJI和AEIG, ∵EF=DF-DE=b-a,EI=b, ∴FI=a, ∴G,I,J在同一直线上,
v1.0可编辑可修改 勾股定理五种证明方法 【证法 1】 a b b a a a c a a c b a b c b cb b b c c a a b a b 做 8 个全等的直角三角形,设它们的两条直角边长分别为a、b,斜边长为 c,再做三个边长分别为 a、b、c 的正方形,把它们像上图那样拼成两个正方形 . 从图上可以看到,这两个正方形的边长都是 a + b ,所以面积相等 .即 a 2b241 ab c24 1 ab ,整理得 a 2b2c2. 22 【证法 2】(邹元治证明) 以 a、b 为直角边,以 c 为斜边做四个全等的直角三角形,则每个直角三角1 ab 形的面积等于 2 .把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上, B、F、C三点在一条直线上, C、G、 D 三点在一条直线上 . ∵ Rt HAE ≌ Rt EBF, C DbGa ∴ ∠ AHE = ∠BEF. ∵ ∠AEH + ∠AHE = 90o , ∴ ∠AEH + ∠BEF = 90 o . ∴ ∠HEF = 180o ― 90o = 90 o . ∴四边形 EFGH是一个边长为 c 的正方形 . 它的面积等于 c2. ∵ Rt GDH≌ Rt HAE,a c c b H F b c c a A a E b B
∴ ∠HGD = ∠EHA. ∵ ∠HGD + ∠GHD = 90o , ∴ ∠EHA + ∠GHD = 90o . 又∵ ∠GHE = 90o , ∴ ∠DHA = 90o + 90 o = 180 o . ∴ ABCD 是一个边长为 a + b 的正方形,它的面积等于 a b 2 . a b 2 4 1 ab c 2 b 2 c 2 . ∴ 2 .∴ a 2 【证法 3】( 梅文鼎证明 ) 做四个全等的直角三角形,设它们的两条直角边长分别为 a 、 b ,斜边长为 c. 把它们拼成如图那样的一个多边形,使 D 、E 、F 在一条直线上 . 过 C 作 AC 的延长线交 DF 于点 P. ∵ D 、E 、F 在一条直线上 , 且 Rt GEF ≌ Rt EBD, ∴ ∠EGF = ∠BED , ∵ ∠EGF + ∠ GEF = 90°, ∴ ∠BED + ∠GEF = 90°, F b a ∴ ∠BEG =180o ―90o = 90 o . G c E 又∵ AB = BE = EG = GA = c , P ∴ ABEG 是一个边长为 c 的正方形 . b C b c c ∴ ∠ABC + ∠CBE = 90o . a H D b a ∵ Rt ABC ≌ Rt EBD, a A c B ∴ ∠ABC = ∠EBD. ∴ ∠EBD + ∠CBE = 90o . 即 ∠CBD= 90o . 又∵ ∠BDE = 90o ,∠ BCP = 90o , BC = BD = a .
勾股定理的证明 【证法1】 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 ab c ab b a 21 4214222?+=?++, 整理得 222c b a =+. 【证法2】 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积 等于ab 21. 把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、 F 、 C 三点在一条直线上,C 、G 、 D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 2 21 4c ab b a +?=+. ∴ 2 22c b a =+.【证法3】
以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21. 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB . ∵ ∠HAD + ∠HAD = 90o, ∴ ∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90o. ∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2 a b -. ∴ ()2 2 214c a b ab =-+?. ∴ 2 22c b a =+. 【证法4】(1876年美国总统Garfield 证明) 以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面 积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵ Rt ΔEAD ≌ Rt ΔCBE, ∴ ∠ADE = ∠BEC . ∵ ∠AED + ∠ADE = 90o, ∴ ∠AED + ∠BEC = 90o. ∴ ∠DEC = 180o―90o= 90o. ∴ ΔDEC 是一个等腰直角三角形, 它的面积等于221c . 又∵ ∠DAE = 90o, ∠EBC = 90o, ∴ AD ∥BC . ∴ ABCD 是一个直角梯形,它的面积等于()2 21 b a +. ∴ ()2 2212122 1 c ab b a +?=+. ∴ 2 22c b a =+. 【证法5】(利用反证法证明) 如图,在Rt ΔABC 中,设直角边AC 、BC 的长度分别为a 、b ,斜边AB 的长为c ,过点C 作CD ⊥AB ,垂足是D .
第 1 页,共 1页 证明勾股定理的几种常用方法 勾股定理是几何中最重要的定理之一,它揭示了直角三角形三边之间的数量关系,即 直角三角形两直角边的平方和等于斜边的平方.探究勾股定理的证明,可以加深学生对勾 股定理的理解、丰富研究数学问题的方法、激发学习数学的兴趣. 证明勾股定理的方法有很多种,最常见的是通过构造一些含有直角三角形的特殊图形, 利用面积相等来证明,现举例说明如下: 已知R t △ABC 的斜边长为c ,两直角边的边长分别为a 、b ,求证:a 2 +b 2=c 2. 证法1: 如图1所示,以R t △ABC 的三条边作边 长分别向外作三个正方形,则正方形CDEF 与正方形 GHMN 的面积相等,即S 正方形CDEF =S 正方形GHMN . 因为S 正方形GHMN =(a +b)2, S 正方形CDEF =c 2+4×12 ab . 所以(a +b)2=c 2+4×12 ab ,故a 2 +b 2=c 2. 证法2:用四个R t △ABC 拼成图2所示的图形,则四个直角三角形的直角顶点构成了一个小正方形的四个顶点.观察图形可得出等 量关系:两个正方形的面积之差等于四个直角 三角形的面积之和,即c 2-(b -a)2=4×12 ab , ∴a 2 +b 2=c 2. 说明:用四个R t △ABC 拼成图3所示的图形,借助等量关系:两个正方形的面积之差 等于四个直角三角形的面积之和,同样可得出a 2 +b 2=c 2. 证法3:如图4所示,两个全等直角三角形的直角边a 、b 在同一条直线上,则两直角 三角形的斜边相互垂直.由图形可以看出,直角梯形的面积 等于三个直角三角形的面积之和. 则S 梯形=12(a +b)(a +b)=2×12ab +12c 2, ∴a 2 +b 2=c 2. C B A a b c G H N D F E M 图1 图2 图3 a a b b c c 图4
ab c ab b a 21421422 2 ?+=?++【证法1】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形. 从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即 整理得 222c b a =+. 【证法2】(邹元治证明) 以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21 . 把这四个直角三 角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上. ∵ Rt ΔHAE ≌ Rt ΔEBF, ∴ ∠AHE = ∠BEF . ∵ ∠AEH + ∠AHE = 90o, ∴ ∠AEH + ∠BEF = 90o. ∴ ∠HEF = 180o―90o= 90o. ∴ 四边形EFGH 是一个边长为c 的 正方形. 它的面积等于c 2. ∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA . ∵ ∠HGD + ∠GHD = 90o, ∴ ∠EHA + ∠GHD = 90o. 又∵ ∠GHE = 90o, ∴ ∠DHA = 90o+ 90o= 180o. ∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2 b a +. ∴ ()2 2214c ab b a +?=+. ∴ 2 22c b a =+. 【证法3】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜 边作四个全等的直角三角形,则每个直角 三角形的面积等于ab 21. 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB . ∵ ∠HAD + ∠HAD = 90o, ∴ ∠EAB + ∠HAD = 90o, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2 . ∵ EF = FG =GH =HE = b ―a ,
勾股定理的九种证明方法 附图 Modified by JEEP on December 26th, 2020.
勾股定理的证明方法 一、传说中毕达哥拉斯的证法(图1) 左边的正方形是由1个边长为的正方形和1个边长为的正方形以及4个直角边分别为、,斜边为的直角三角形拼成的。右边的正方形是由1个边长为的正方形和4个直角边分别为、,斜边为的直角三角形拼成的。因为这两个正方形的面积相等(边长都是),所以可以列出等式,化简得。 二、美国第20任总统茄菲尔德的证法(图3) 这个直角梯形是由2个直角边分别为、,斜边为 的直角三角形和1个直角边为 的等腰直角三角形拼成的。因为3个直角三角形的面积之和等于梯形的面积,所以可以列出等式,化简得。 三、相似三角形的证法: 4.相似三角形的方法:在学习了相似三角形以后,我们知道在直角三角形中,斜边上的高把这个直角三角形所分成的两个三直角角形与原三角形相似。 如图,Rt △ABC 中,∠ACB=90°。作CD ⊥AB ,垂足为D 。则 △BCD ∽△BAC ,△CAD ∽△BAC 。 由△BCD ∽△BAC 可得BC 2=BD × BA , ① 由△CAD ∽△BAC 可得AC 2=AD × AB 。 ② 我们发现,把①、②两式相加可得 BC 2+AC 2=AB (AD+BD ), 而AD+BD=AB , 因此有 BC 2+AC 2=AB 2,这就是 a 2+ b 2= c 2。 这也是一种证明勾股定理的方法,而且也很简洁。它利用了相似三角形的知识。 四、古人的证法: 如图,将图中的四个直角三角形涂上深红色,把中间小正方形涂上白色,,以弦为边的正方形称为弦实,然后经过拼补搭配,“令出入相补,各从其类”,他肯定了勾股弦三者的关系是符合勾股定理的。即“勾股各自乘,并之为弦实,开C A B D