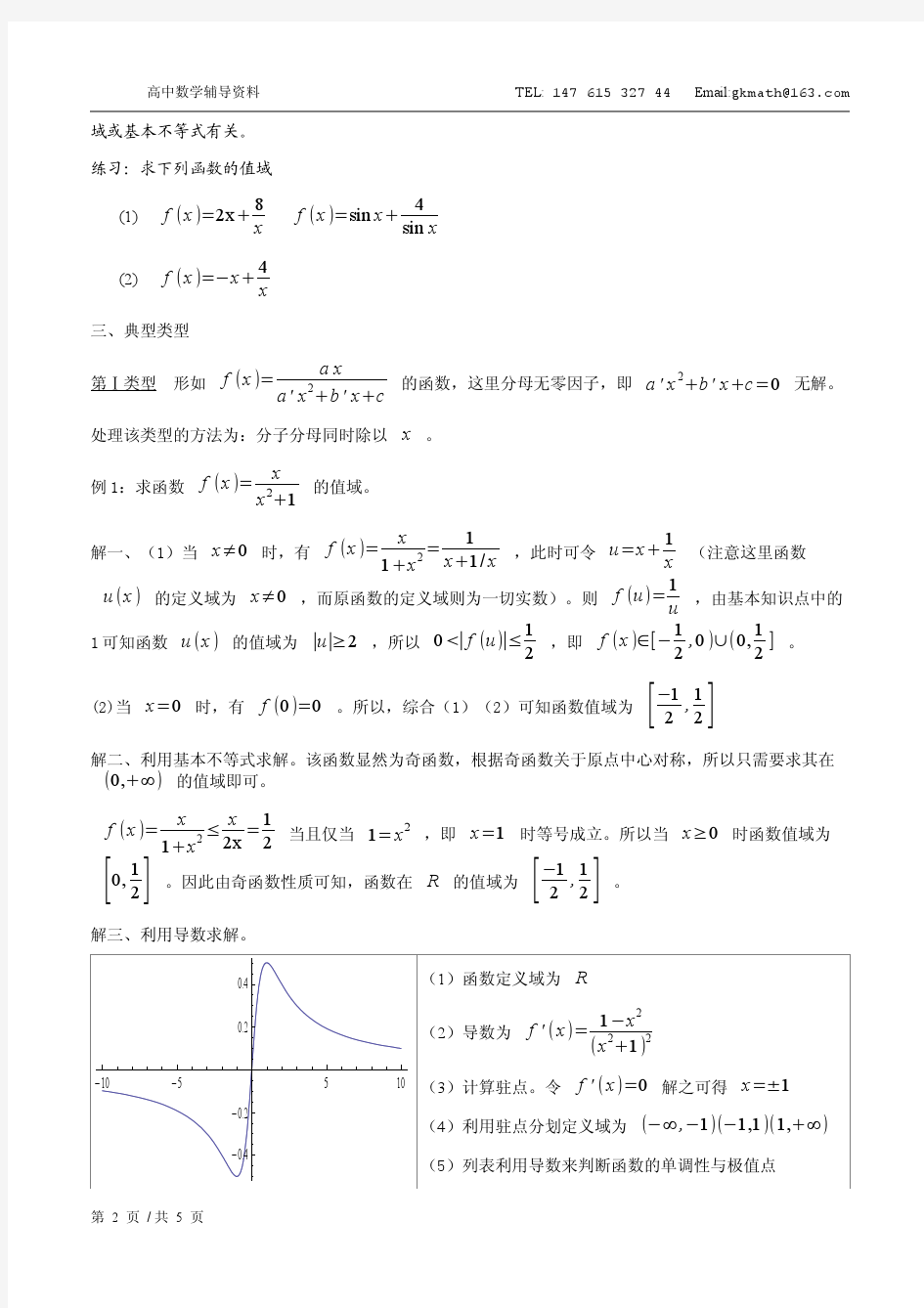
当前位置：文档之家› 有理分式函数值域1.0

有理分式函数值域1.0

附录2(分式函数求值域方法总结)

分式型函数求值域的方法总结一、形如()ax b f x cx d += + (,0a o b ≠≠)（一次式比一次式）在定义域内求值域。例1：求21()32 x f x x +=+（2)3x ≠-的值域。解：242()133()2323()3x f x x x +-=-++=123332 x -+∵1122330,323323x x -≠∴-≠++ ∴其值域为}2/3y y ?≠?? 一般性结论，()ax b f x cx d += + (,0a o b ≠≠)如果定义域为{x /d x c ≠-},则值域}/a y y c ?≠?? 注：本题所用方法即为分离常数法，分离常数之后，分子便不含有x 项，使计算变得简便。例2：求21()32x f x x += +，()1,2x ∈的值域。分析：由于此类函数图像可以经过反比列函数图像平移得出，所以解决在给定区间内的值域问题，我们可以画出函数图像，求出其值域。解：21()32x f x x +=+=123332x -+，是由1 3y x =-向左平移23，向上平移23得出，通过图像观察，其值域为35,58?? ??? 小结：函数关系式是一次式比一次式的时候，我们发现在此类函数的实质是反比例函数通过平时得出的，因此我们可以作出其图像，去求函数的值域。

x 分析：此类函数中，当0a <，函数为单调函数，较简单，在此我们不做讨论，当0a >时，对函数求导，'2()1,a f x x =-'()0f x > 时，(x ∈-∞? +∞），'()0f x <时， (x ∈?，根据函数单调性，我们可以做出此类函数的大致图像，其我们常其图像例3：求4()2,((1,4)f x x x x =+ ∈上的值域。解：将函数整理成2()2()f x x x =+，根据双钩函数的性质，我们可以判断此函数在单调递减，在)+∞1，4出的函数值，我们可以知道在1处取的最大值，所以其值域为) ?? 三、用双钩函数解决形如2()mx n f x ax bx c +=++（0,0m a ≠≠），2()ax bx c f x mx n ++=+（0,0m a ≠≠）在定义内求值域的问题。例3：已知0t >，则则函数241t t y t -+=的最小值为_______. 解：24114t t y t t t -+==+-，t o >∴由基本不等式地2y ≥-

分数函数的值域

分数函数的值域这里说的是二次即二次以下分式函数的值域，由于高二学了一阶导数，笔者见到不少学生学了导数之后，看到分式函数想都不想就直接求导做，毫无疑问是可以做出来的，但是，对于分式的导数，比原函数还要麻烦，如果函数很简单，用导数似乎有些大材小用，如果函数很复杂，求导之后就更加复杂，做起来也比较麻烦，因此，对于此类分式函数题目求最值，轻易莫求导！！！下面进入正题，这里说的分式函数大致以下几种形式：y=， y=，y=，y=其中y=与y= 基本一致对于这个问题，一般来说可能会用到三个方法：分离常数、均值不等式、几何法（构造斜率）、反函数法、判别式法。反函数法和判别式法这里不再赘述，以下我们分别讨论首先，对于最简单的分式线性函数y=，反函数法在此不再赘述，即是反解出x，利用定义域求值域，这里说下分离常数法，这个方法很重要，要谨记例1：若x∈[-1,2)求函数y=的值域解一（分离常数法）：y= =

=2+ 由x∈[-1,2)则y∈(-∞，1] 分离常数的目的是为了将自变量“挤”到分母或分子，则函数单调性、值域显而易见解二（构造斜率法）：原式可看作点A（2,1）到点P（x，2x）的斜率，其中P在直线y=2x(x∈[-1,2))上，作出图像即可得到答案构造斜率法运用时要注意，若定点与动点连线中有x轴的垂线，则垂线应画成虚线，它是正、负无穷的分界线（斜率k=tanθ）反函数法略然后是分子或分母中出现二次，无论是在分子还是在分母，处理方法基本一致。同样用到类似分离常数的配凑方法，对于功底不好的同学，可以对一次式换元，例2求函数y==，x∈[0，2] 解一：令t=x+2（t∈[2，4]），则x=t-2 则y== 分子分母同除以t后得，y=t+-6≥2-6（当且仅当t=时“=”成立）

分式函数值域的求法

分式函数值域的求法 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】

分式函数22221121c x b x a c x b x a y ++++=的值域函数值域是函数三要素之一，求函数值域无定法，且方法灵活，是中学数学的一个难点。今天我们主要讨论分式函数2 2221121c x b x a c x b x a y ++++=的值域求法。一、若21a a ，同时为零，则函数2 2221121c x b x a c x b x a y ++++=就变为形如2211c x b c x b y ++=（22b b ，不同时为零）的函数，可以用分离常数法或求反函数法来求函数的值域。例１求函数3 12+-=x x y 的值域解法１：（分离常数法）利用恒等变形可化为：3 7237)3(2+-=+-+=x x x y 所以，该函数的值域为)2()2(∞+-∞∈，， y ：解法２：（求反函数法）函数312+-=x x y 的反函数为132 x y x -=-所以原函数值域为{}2≠∈y y y （即反函数定义域为原函数值域）。二、若21a a ，不同时为零，但分子与分母有公因式子，可先约分再求值域。如果不约分，直接采用下面三的方法，将加大运算量（如例6）。例２求函数2 312+--=x x x y 的值域解：可先将函数变为)2)(1(1)(---= =x x x x f y 。约分后函数变为2 1)(-= x x g 。所以0)(≠x g

约分后函数)(x g 的定义域扩大了（严格来说()g x 与原函数)(x f 不是同一个函数，但在不引起混淆的情况下也可直接约分），)(x g 在１处所对应的函数值1-，也是)(x f 不能取到的值，所以函数2 312+--=x x x y 的值域是）（０，０）１（１），（∞+∞- ,--。例３求函数2 652-+-=x x x y 的值域解：函数可变形为32 )3)(2(-=---=x x x x y ，所以该函数的值域是{}1-≠∈y y y 。三、若21a a ，不同时为零，分子与分母没有公因式子，可以通过判别式法、分离常数法、基本不等式法求函数的值域。例４函数221 x x y x x -=-+的值域．解法1：(判别式法) 将221 x x y x x -=-+转化为关于x 的一元二次方程（y 看作参数）： (这是一个必有解的方程。讨论使上方程有解的参数y 的范围，恰为函数221 x x y x x -=-+的值域） ①若1=y ，则10=矛盾 ②由1≠y ，这时由0≥?解得1113y y -≤≤≠且；13y =-时，12 x =。 ∴综上所述知原函数的值域为1[,1)3 -．解法2：(分离常数法) 221x x y x x -=-+＝2111x x --+＝21113()24 x --+ 设213()()24g x x =-+，则()g x 的值域是3[,)4 +∞ 所以，原函数值域为1[,1)3 -。

高中函数值域的12种求法

高中函数值域的12种求法一．观察法通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域。例1求函数y=3+√(2－3x)的值域。点拨：根据算术平方根的性质，先求出√(2－3x)的值域。解：由算术平方根的性质，知√(2－3x)≥0，故3+√(2－3x)≥3。 ∴函数的知域为. 点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。练习：求函数y=[x](0≤x≤5)的值域。（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法当函数的反函数存在时，则其反函数的定义域就是原函数的值域。例2求函数y=(x+1)/(x+2)的值域。点拨：先求出原函数的反函数，再求出其定义域。解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数,故函数y的值域为｛y∣y≠1,y∈R｝。

点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。这种方法体现逆向思维的思想，是数学解题的重要方法之一。练习：求函数y=(10x+10-x)/(10x－10-x)的值域。（答案：函数的值域为｛y∣y－1或y1｝）三．配方法当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域例3：求函数y=√(－x2+x+2)的值域。点拨：将被开方数配方成完全平方数，利用二次函数的最值求。解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4] ∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2] 点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。配方法是数学的一种重要的思想方法。练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为 {y∣y≤3}) 四．判别式法若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。

次分式函数值域的求法

二次分式函数值域的求法甘肃王新宏一定义域为R 的二次分式函数用“判别式”法解题步骤：1 把函数转化为关于x 的二次方程 2 方程有实根，△≥0 3 求的函数值域 1：求y =2 2222+++-x x x x 的值域解：∵x 2+x+2>0恒成立由y =2 2222+++-x x x x 得，（y -2）x 2+(y+1)x+y-2=0 ①当y-2=0时，即y=2时，方程为x=0∈R ②当y-2≠0时，即y ≠2时, ∵x ∈R ∴方程（y -2）x 2+(y+1)x+y-2=0有实根 ∴△=(y+1)2 -(y-2) ×(y-2) ≥0 ∴3y 2-18y+15≤0 ∴1≤y ≤5 ∴函数值域为[]5,1 练习1：求y =432+x x 的值域 ?? ????-43,43 二分母最高次幂为一次的二次分式函数值域常转化为“√”函数或用“均值不等式”来做。先来学习“√”函数。形如y =x+ x k (x>0 ,k>0)的函数，叫“√”函数图像

单调性：在x ∈[] k ,0时，单调递减。在x ∈[] +∞,k 时，单调递减。值域：[]+∞,2k 解题步骤：①令分母为t,求出t 的范围 ②把原函数化为关于t 的函数 ③利用“√”函数的单调性或均值不等式来求值域例2 求y =12122-+-x x x （32 1≤

高考求函数值域及最值得方法及例题_训练题

函数专题之值域与最值问题一．观察法:通过对函数定义域、性质的观察，结合函数的解析式，求得函数的值域. 例1:求函数) + =的值域. y- 3x 3 2( 点拨：根据算术平方根的性质，先求出) -的值域. 3 2(x 解：由算术平方根的性质，知) 2(x -≥3。∴函数的值域为) 3 -≥0，故3+) 2(x 3 ,3[+∞ . 点评：算术平方根具有双重非负性，即：（1）被开方数的非负性，（2）值的非负性。本题通过直接观察算术平方根的性质而获解，这种方法对于一类函数的值域的求法，简捷明了，不失为一种巧法。练习：求函数y=[x](0≤x≤5)的值域。（答案：值域为：｛0，1，2，3，4，5｝）二．反函数法:当函数的反函数存在时，则其反函数的定义域就是原函数的值域. 例2:求函数y=(x+1)/(x+2)的值域. 点拨：先求出原函数的反函数，再求出其定义域。解：显然函数y=(x+1)/(x+2)的反函数为:x=(1－2y)/（y－1）,其定义域为y≠1的实数, 故函数y的值域为｛y∣y≠1,y∈R｝。点评：利用反函数法求原函数的定义域的前提条件是原函数存在反函数。这种方法体现逆向思维的思想，是数学解题的重要方法之一。练习：求函数y=(10x+10-x)/(10x－10-x)的值域。（答案：函数的值域为｛y∣y<－1或y>1｝）三．配方法:当所给函数是二次函数或可化为二次函数的复合函数时,可以利用配方法求函数值域. 例3：求函数y=√(－x2+x+2)的值域. 点拨：将被开方数配方成完全平方数，利用二次函数的最值求。解：由－x2+x+2≥0,可知函数的定义域为x∈[－1，2]。此时－x2+x+2=－（x－1/2）2＋9/4∈[0，9/4] ∴0≤√－x2+x+2≤3/2,函数的值域是[0,3/2] 点评：求函数的值域不但要重视对应关系的应用,而且要特别注意定义域对值域的制约作用。配方法是数学的一种重要的思想方法。练习：求函数y=2x－5＋√15－4x的值域.(答案:值域为{y∣y≤3}) 四.判别式法:若可化为关于某变量的二次方程的分式函数或无理函数,可用判别式法求函数的值域。例4:求函数y=(2x2－2x+3)/(x2－x+1)的值域. 点拨：将原函数转化为自变量的二次方程，应用二次方程根的判别式，从而确定出原函数的值域。

函数值域的13种求法

函数值域十三种求法 1. 直接观察法对于一些比较简单的函数，其值域可通过观察得到。例1. 求函数 x 1 y =的值域解：∵0x ≠ ∴0x 1≠ 显然函数的值域是：),0()0,(+∞-∞ 例2. 求函数x 3y -=的值域解：∵0x ≥ 3x 3,0x ≤-≤-∴ 故函数的值域是：]3,[-∞ 2. 配方法配方法是求二次函数值域最基本的方法之一。例3. 求函数 ]2,1[x ,5x 2x y 2-∈+-=的值域解：将函数配方得： 4)1x (y 2+-= ∵]2,1[x -∈ 由二次函数的性质可知：当x=1时，4y min =，当1x -=时，8y max = 故函数的值域是：[4，8] 3. 判别式法(只有定义域为整个实数集R 时才可直接用) 例4. 求函数 22 x 1x x 1y +++=的值域解：原函数化为关于x 的一元二次方程 0x )1y (x )1y (2=-+- （1）当1y ≠时，R x ∈ 0)1y )(1y (4)1(2≥----=? 解得：23y 21≤≤ （2）当y=1时，0x =，而??????∈23,211 故函数的值域为????? ?23,21

例5. 求函数)x 2(x x y -+=的值域解：两边平方整理得： 0y x )1y (2x 222=++-（1） ∵R x ∈ ∴ 0y 8)1y (42≥-+=? 解得：21y 21+≤≤- 但此时的函数的定义域由0)x 2(x ≥-，得2x 0≤≤ 由0≥?，仅保证关于x 的方程： 0y x )1y (2x 222=++-在实数集R 有实根，而不能确保其实根在区间[0，2]上，即不能确保方程（1）有实根，由 0≥?求出的范围可能比y 的实际范围大，故不能确定此函数的值域为????? ?23,21。可以采取如下方法进一步确定原函数的值域。 ∵2x 0≤≤ 0)x 2(x x y ≥-+=∴ 21y ,0y min +==∴代入方程（1）解得：] 2,0[22 222x 41∈-+= 即当22222x 41-+=时，原函数的值域为：]21,0[+ 注：由判别式法来判断函数的值域时，若原函数的定义域不是实数集时，应综合函数的定义域，将扩大的部分剔除。 4. 反函数法直接求函数的值域困难时，可以通过求其原函数的定义域来确定原函数的值域。例6. 求函数6x 54 x 3++值域解：由原函数式可得： 3y 5y 64x --= 则其反函数为：3x 5y 64y --=，其定义域为：53x ≠ 故所求函数的值域为：33(,)(,)55 -∞?+∞

分式函数求值域

分式型函数求值域的方法探讨在教学中，笔者常常遇到一类函数求值域问题，此类函数是以分式函数形式出现，有一次式比一次式，二次式比一次式，一次式比二次式，二次式比二次，现在对这类问题进行探讨。一、形如d cx b ax x f ++= )((0,≠≠b o a )（一次式比一次式）在定义域内求值域。例1：求2 312)(++=x x x f （)32-≠x 的值域。解：23134)32(3)32(2)(+--++=x x x x f =233132+-x 32233132,02331≠+-∴≠+-x x ∴其值域为}? ??≠32/y y 一般性结论，d cx b ax x f ++=)((0,≠≠b o a )如果定义域为{/x c d x -≠},则值域 }? ??≠c a y y / 例2：求2 312)(++=x x x f ，()2,1∈x 的值域。分析：由于此类函数图像可以经过反比列函数图像平移得出，所以解决在给定区间内的值域问题，我们可以画出函数图像，求出其值域。解：2312)(++=x x x f =233132+-x ，是由x y 31 -=向左平移32，向上平移32得出，通过图像观察，其值域为?? ? ??85,53 小结：函数关系式是一次式比一次式的时候，我们发现在此类函数的实质是反比例函数通过平时得出的，因此我们可以作出其图像，去求函数的值域。

二、形如求x a x x f + =)(（)0≠a 的值域。分析：此类函数中，当0a 时，对函数求导，,1)(2'x a x f -=0)('>x f 时，),(a x -∞∈?+∞,a ），0)('，则则函数241t t y t -+=的最小值为_______. 解：41142-+=+-=t t t t t y ，∴>o t 由基本不等式地2-≥y