
一、概念
混合同余法:
用一常数与已产生的伪随机数之积的同余式做递推公式,产生均匀伪随机数的方法。 即:
第一步:递推式 其中: M=2^k,k>2整数;A=1(mod4),即 为正整数,初值
x
*
为非负整数。
第二步:
可以证明,
是周期为2k 的伪随机数。 1、混合同余法(0,1)均匀分布的随机数 L=60,取k=2,c=1,n=5,l=60,x *
=1
公式原理:
见上第一第二步。 程序: clear clc k=8; c=1; n=5; x=1; M=2^k; A=2^n+1; store=[ ]; for i=1:60 ee=x/M; store(i)=ee;
x=mod(A*x+c,M); end
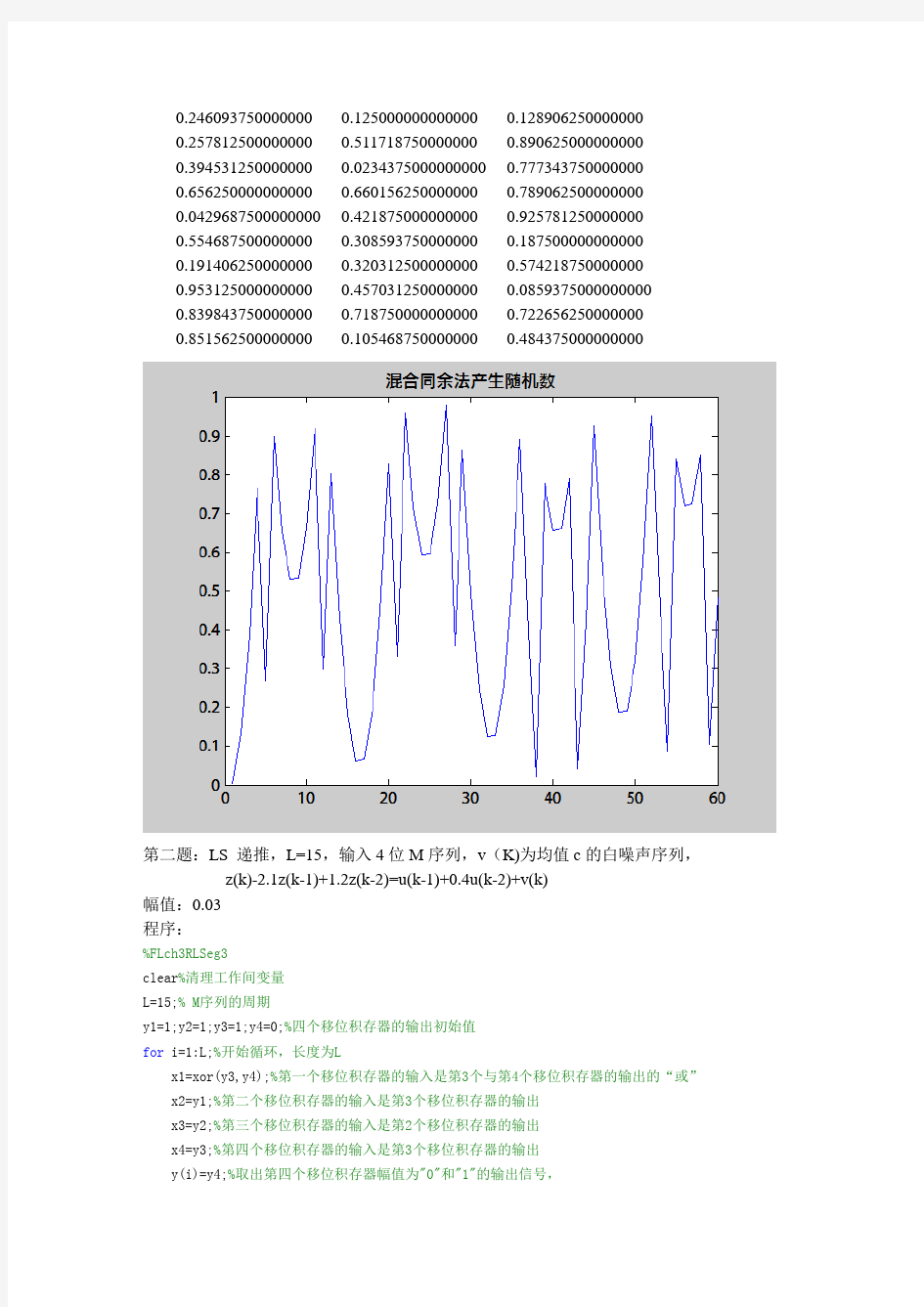
plot(1:60,store)
title('混合同余法产生随机数') store=
0.00390625000000000 0.132812500000000 0.386718750000000 0.765625000000000 0.269531250000000 0.898437500000000 0.652343750000000 0.531250000000000 0.535156250000000 0.664062500000000 0.917968750000000 0.296875000000000 0.800781250000000 0.429687500000000 0.183593750000000 0.0625000000000000 0.0664062500000000 0.195312500000000 0.449218750000000 0.828125000000000 0.332031250000000 0.960937500000000 0.714843750000000 0.593750000000000 0.597656250000000 0.726562500000000 0.980468750000000 0.359375000000000 0.863281250000000
0.492187500000000
3,2,1),(m
od 1=+≡*
-*i M c Ax x i i 342,12≤≤+=n A n M
x i i
**
=
ξ
}{*
i ξ
0.246093750000000 0.125000000000000 0.128906250000000
0.257812500000000 0.511718750000000 0.890625000000000
0.394531250000000 0.0234375000000000 0.777343750000000
0.656250000000000 0.660156250000000 0.789062500000000
0.0429687500000000 0.421875000000000 0.925781250000000
0.554687500000000 0.308593750000000 0.187500000000000
0.191406250000000 0.320312500000000 0.574218750000000
0.953125000000000 0.457031250000000 0.0859375000000000
0.839843750000000 0.718750000000000 0.722656250000000
0.851562500000000 0.105468750000000 0.484375000000000
第二题:LS 递推,L=15,输入4位M序列,v(K)为均值c的白噪声序列,z(k)-2.1z(k-1)+1.2z(k-2)=u(k-1)+0.4u(k-2)+v(k)
幅值:0.03
程序:
%FLch3RLSeg3
clear%清理工作间变量
L=15;% M序列的周期
y1=1;y2=1;y3=1;y4=0;%四个移位积存器的输出初始值
for i=1:L;%开始循环,长度为L
x1=xor(y3,y4);%第一个移位积存器的输入是第3个与第4个移位积存器的输出的“或” x2=y1;%第二个移位积存器的输入是第3个移位积存器的输出
x3=y2;%第三个移位积存器的输入是第2个移位积存器的输出
x4=y3;%第四个移位积存器的输入是第3个移位积存器的输出
y(i)=y4;%取出第四个移位积存器幅值为"0"和"1"的输出信号,
if y(i)>0.5,u(i)=-0.03;%如果M序列的值为"1"时,辨识的输入信号取“-0.03”
else u(i)=0.03;%当M序列的值为"0"时,辨识的输入信号取“0.03”
end%小循环结束
y1=x1;y2=x2;y3=x3;y4=x4;%为下一次的输入信号做准备
end%大循环结束,产生输入信号u
figure(1);%第1个图形
stem(u),grid on%以径的形式显示出输入信号并给图形加上网格
z(2)=0;z(1)=0;%取z的前两个初始值为零
for k=3:15;%循环变量从3到15
z(k)=2.1*z(k-1)-1.2*z(k-2)+u(k-1)+0.4*u(k-2);%给出理想的辨识输出采样信号
end
%RLS递推最小二乘辨识
c0=[0.001 0.001 0.001 0.001]';%直接给出被辨识参数的初始值,即一个充分小的实向量
p0=10^6*eye(4,4);%直接给出初始状态P0,即一个充分大的实数单位矩阵
E=0.000000005;%相对误差E=0.000000005
c=[c0,zeros(4,14)];%被辨识参数矩阵的初始值及大小
e=zeros(4,15);%相对误差的初始值及大小
for k=3:15; %开始求K
h1=[-z(k-1),-z(k-2),u(k-1),u(k-2)]'; x=h1'*p0*h1+1; x1=inv(x); %开始求K(k)
k1=p0*h1*x1;%求出K的值
d1=z(k)-h1'*c0; c1=c0+k1*d1;%求被辨识参数c
e1=c1-c0;%求参数当前值与上一次的值的差值
e2=e1./c0;%求参数的相对变化
e(:,k)=e2; %把当前相对变化的列向量加入误差矩阵的最后一列
c0=c1;%新获得的参数作为下一次递推的旧参数
c(:,k)=c1;%把辨识参数c 列向量加入辨识参数矩阵的最后一列
p1=p0-k1*k1'*[h1'*p0*h1+1];%求出 p(k)的值
p0=p1;%给下次用
if e2<=E break;%若参数收敛满足要求,终止计算
end%小循环结束
end%大循环结束
c%显示被辨识参数
e%显示辨识结果的收敛情况
%分离参数
a1=c(1,:); a2=c(2,:); b1=c(3,:); b2=c(4,:); ea1=e(1,:); ea2=e(2,:); eb1=e(3,:); eb2=e(4,:); figure(2);%第2个图形
i=1:15;%横坐标从1到15
plot(i,a1,'r',i,a2,':',i,b1,'g',i,b2,':') %画出a1,a2,b1,b2的各次辨识结果
title('Parameter Identification with Recursive Least Squares Method')%图形标题
figure(3); %第3个图形
i=1:15; %横坐标从1到15
plot(i,ea1,'r',i,ea2,'g',i,eb1,'b',i,eb2,'r:') %画出a1,a2,b1,b2的各次辨识结果的收敛情况title('Identification Precision') %图形标题
结果:
表二:
c =
Columns 1 through 10
0.0010 0 0.0010 -0.6746 -1.6527 -2.0886 -2.0927 -2.0987 -2.0997 -2.0998
0.0010 0 0.0010 0.0010 -0.3351 1.1763 1.1865 1.1980
1.1997 1.1998
0.0010 0 0.3008 1.4268 1.1339 1.0049 1.0045 1.0004 0.9998 0.9997
0.0010 0 -0.2988 0.8272 0.5342 0.4052 0.4037 0.4015 0.4004 0.4003
Columns 11 through 15
-2.0999 -2.1000 -2.1000 -2.1000 -2.1000
1.1999 1.2000 1.2000 1.2000 1.2000
0.9999 0.9999 0.9999 0.9999 0.9999
0.4000 0.4000 0.4000 0.4000 0.4000
e =
Columns 1 through 10
0 0 0 -675.5972 1.4500 0.2637 0.0020 0.0029 0.0005 0.0000
0 0 0 0 -336.0913 -4.5104 0.0087 0.0097 0.0014 0.0001
0 0 299.8334 3.7429 -0.2053 -0.1137 -0.0004 -0.0041 -0.0005 -0.0001
0 0 -299.8334 -3.7680 -0.3542 -0.2414 -0.0039 -0.0053 -0.0028 -0.0003
Columns 11 through 15
0.0000 0.0000 0.0000 0.0000 0.0000
0.0001 0.0000 0.0000 0.0000 0.0000
0.0001 0.0000 -0.0000 -0.0000 0.0000
-0.0007 0.0000 0.0000 -0.0000 -0.0001
MATLAB产生各种分布的随机数 1,均匀分布U(a,b): 产生m*n阶[a,b]均匀分布U(a,b)的随机数矩阵:unifrnd (a,b,m, n) 产生一个[a,b]均匀分布的随机数:unifrnd (a,b) 2,0-1分布U(0,1) 产生m*n阶[0,1]均匀分布的随机数矩阵:rand (m, n) 产生一个[0,1]均匀分布的随机数:rand 4,二类分布binornd(N,P,mm,nn)如binornd(10,,mm,nn) 即产生mm*nn均值为N*P的矩阵 binornd(N,p)则产生一个。而binornd(10,,mm)则产生mm*mm的方阵,军阵为N*p。5,产生m*n阶离散均匀分布的随机数矩阵: unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵 6,产生mm nn阶期望值为的指数分布的随机数矩阵: exprnd( ,mm, nn) 此外,常用逆累积分布函数表?
函数名调用格式函数注释? norminvX=norminv(P,mu,sigma)正态逆累积分布函数? expinvX=expinv(P,mu)指数逆累积分布函数? weibinvX=weibinv(P,A,B)威布尔逆累积分布函数? logninvX=logninv(P,mu,sigma)对数正态逆累积分布函数? Chi2invX=chi2inv(P,A,B)卡方逆累积分布函数? BetainvX=betainv(P,A,B)β分布逆累积分布函数 随机数的产生 4.1.1 二项分布的随机数据的产生 命令参数为N,P的二项随机数据 函数 binornd 格式 R = binornd(N,P) %N、P为二项分布的两个参数,返回服从参数为N、P的二项分布的随机数,N、P大小相同。 R = binornd(N,P,m) %m指定随机数的个数,与R同维数。 R = binornd(N,P,m,n) %m,n分别表示R的行数和列数 例4-1
概率论与数理统计课程设计 题目:正态分布随机数生成算法 要编程得到服从均匀分布的伪随机数是容易的。C语言、Java语言等都提供了相应的函
数。但是要想生成服从正态分布的随机数就没那么容易了。 得到服从正态分布的随机数的基本思想是先得到服从均匀分布的随机数,再将服从均匀分布的随机数转变为服从正态分布。接下来就先分析三个从均匀分布到正态分布转变的方法。然后编程实现其中的两个方法并对程序实现运作的效果进行统计分析。 1、 方法分析 (1) 利用分布函数的反函数 若要得到分布函数为F(x)的随机变量Y 。 可令1()Y F u -=, 其中u 是服从均匀分布的随机变量,有 1 ()(())() P Y y P U F y F y -≤=≤= 因而,对于任意的分布函数,只要求出它的反函数,就可以由服从均匀分布的随机变量实例来生成服从该分布函数的随机变量实例。 现在来看正态分布的分布函数,对于2 ~(,)X N μσ,其分布函数为: 2 2()21 ()t x F x e μσ ---∞ = ? 显然,要想求其反函数是相当困难的,同时要想编程实现也很复杂。可见,用此种方法来生成服从正态分布的随机变量实例并不可取。 (2) 利用中心极限定理 第二种方法利用林德伯格—莱维(Lindeberg —Levi)中心极限定理:如果随机变量序列 12,,,,n X X X 独立同分布,并且具有有限的数学期望和方差 ()()2 ,0(1,2,),i i E X D X i μσ ==>= 则对一切x R ∈有 2 2 1lim t n x i n i P X n x dt μ- -∞ →∞ =? ?? -≤= ????? ∑? 因此,对于服从均匀分布的随机变量i X ,只要n 充分大, 11 n i i X n μ=? -? ?∑就服从()0,1N 。我们将实现这一方法。 (3) 使用Box Muller 方法 先证明2 2 2x e dx π-∞-∞ =? : 令2 2 x I e dx -∞-∞ = ? ,则
C语言中产生随机数的方法 引例:产生10个[100-200]区间内的随机整数。 #include
3.3.2 均匀随机数的产生 教材分析 本节内容是数学必修三第三章 概率 3.3.2均匀随机数的产生, 本节课在学生已经掌握几何概型的基础上,来学习解决几何概型问题的又一方法,本节课的教学对全面系统地理解掌握概率知识,对于培养学生自觉动手、动脑的习惯,对于学生辩证思想的进一步形成,具有良好的作用. 通过对本节课例题的模拟试验,认识用计算机模拟试验解决概率问题的方法,体会到用计算机产生随机数,可以产生大量的随机数,又可以自动统计试验的结果,同时可以在短时间内多次重复试验,可以对试验结果的随机性和规律性有更深刻的认识。 课时分配 本节内容用1课时的时间完成,主要讲解利用计算器(计算机)产生均匀随机数的方法;利用均匀随机数解决具体的有关概率的问题。 教学目标 重 点: 掌握[0,1]上均匀随机数的产生及[a,b ]上均匀随机数的产生。学会采用适当的随机模拟法去估算几何概率。 难 点:利用计算器或计算机产生均匀随机数并运用到概率的实际应用中。 知识点:通过模拟试验,感知应用数字解决问题的方法,了解均匀随机数的概念;掌握利用计算器(计算机)产生均匀随机数的方法。 能力点:利用均匀随机数解决具体的有关概率的问题,理解随机模拟的基本思想是用频率估计概率。 教育点:通过随机模拟试验,感知应用数字解决问题的方法,自觉养成动手、动脑的良好习惯,培养逻辑 思维能力和探索创新能力。 自主探究点:在信息技术环境下,通过算法解决大量重复模拟试验中的数据统计问题,得出问题的解的估计值,并由此进一步体会随机模拟方法、算法思想以及从特殊到一般的数学研究过程。 易错易混点:在计算器上用rand()产生(0,1)之间的随机数不是什么难事,但产生任意区间(a,b )上的 随机数涉及线性变换,这是学生不易处理的问题,容易出错。 教具准备 多媒体课件 一、引入新课 复习提问: (1)什么是几何概型?(2)几何概型的概率公式是怎样的?(3)几何概型的特点是什么?(4)列举几个简单的几何概型例子? 【师生活动】 (1)几何概率模型:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型; (2)几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等. (3)几何概型的概率公式: P (A )=积) 的区域长度(面积或体试验的全部结果所构成积)的区域长度(面积或体构成事件A (4)几何概型例子:长3米的绳子被剪刀随机剪一次,问两段长度都不小于1米的概率?在这个几何概型中,随机剪绳子可以抽象成数学模型:从区间(0,3)中随机取一个数,由此引出今天的学习的内容,均匀随机数。
《概率论与随机信号分析》实验报告 实验名称:随机数的产生和特性曲线指导教师: 张正明 成绩: 姓名:陈新班级:10通信A班学号:67 一、实验目的与任务 1.了解随机数的产生方法; 2.了解常用随机数的概率分布函数、分布律和概率密度函数。 二、实验原理 随机数的产生有好多方法,可以利用乘积法和同余法产生【0,1】之间的均匀分布,然后利用函数变换法产生所需不同分布的随机数。可以按照所产生的随机数,对落在不同区间的数据进行统计,从而画出所产生的随机数的统计特性。所有这些工作我们可以自己动手用matlab,VC 或VB等语言进行编程实现。 在现代系统仿真中,大量地使用matlab工具,而且它也提供了非常丰富的函数来产生经常使用的分布的随机数,比如rand,randn就是用来产生均匀分布随机数和高斯分布随机数的。 本实验充分利用matlab提供的工具来产生随机数,验证和观察其统计特性。 1.disttool:分布函数和密度函数的可视化工具 分布函数和密度函数的工具能够产生22种常用分布的概率分布曲线和概率密度曲线,并通过图形方式显示。我们还可以通过修改参数产生同一种分布不同参数的概率分布曲线和概率密度曲线。 2.randtool:随机变量模拟工具 随机变量模拟工具能够模拟产生22种常用分布的随机数,并可以通过修改它们的参数产生同一种分布不同参数的随机数,并通过图形方式显示它们的概率密度统计。 三、实验内容与结果 1.绘制正态分布密度函数曲线 建立normal.m脚本文件,并运行 x=-10:0.1:10; u=0,c2=4; c1=sqrt(c2); f=1/(sqrt(2*pi)*d)*exp(-(x-u)^2/2/c2);正态概率密度
伪随机数的产生,现在用得较多的是“线性同余法" 就是下面这个式子 R(n+1) = [R(n) * a + b] mod c 为使随机数分布尽量均匀,a、b 均为质数, c 一般取值域内的最大值(mod 是求余数) 从这个式了可以看出,每次产生的随机数都跟上一次产生的数有关系,那么,第一个数是怎么来的呢?这就是线性同余法中必须用的的”种子",也就是说,给定某个种子后,所产生的随机数序列是固定的,在计算机编程中,一般使用系统时间来初始化种子,就是前面代码中的 srand((unsigned)time(NULL)); 这一句了。因为每次运行程序的时间肯定不一样,所以产生散列肯定也不一样,从而达到“随机”的目的。 a,b,c 的取值我用的是 a=3373, b=1, c=32768 下面的两个子程序是我在我的项目(S7-200 226)中产生随机的系统编号用的,因为我的编号中只有4位数采用了随机数,所以下面的程序中用的是整型,最大范围为32767。如果需要更宽范围的随机数,可以采用双字类型,并适当修改程序,代码很简单,就是将上面那个表达式用 S7-200 的指令表示出来就行了。 这两个子程序是从 MicroWIN V4.0 中导出来的,可以将它们用文本编辑器保存为 AW L 文件后直接导入 MicroWIN。 使用时在第一个扫描周期调用 Srand 初始种子,需要随机数的地方调用 Random Random 有了个最大范围参数,可以限制生成的随机数的最大范围,比如我只需要4位随机数,所以一般这样调用 CALL Random, 10000, vw0,生成的数就在 0-9999 范围内 下面是代码: SUBROUTINE_BLOCK Srand:SBR17 TITLE=初始化随机数种子 // // 直接使用系统时钟的分秒来作为种子 VAR_OUTPUT seed:WORD; END_VAR
数学模型: 设连续型随机变量X 的高斯分布的概率密度为 ( )22 ()2,x f x μσ-= -∞<x <+∞ (3-1) 其中μ,σ(σ>0)为常数,则称X 服从参数为μ,σ的正态分布或高斯(Gauss)分布,记为X ~N (μ,2σ)。均值和方差的计算见公式3-2和公式3-3所示,可得到正态分布随机变量X 的均值E(X)=μ和方差D(X)=2σ。 ()()E X xf x dx +∞ -∞ =? (3-2) 2()()D X x f x dx +∞ -∞ =? (3-3) ()()E X xf x dx +∞ -∞ =? 22 ()2x dx μσ-- +∞ -∞ =? 令 x t μ σ -=,则 2 2()()t E X t dt σμσ+∞ --∞ =+?? 2 2 22t t dt dt σ μ+∞ +∞---∞ -∞ =+?? ? 0μμ=+= 根据方差的定义可知: 2 (){[()]} D X E X E X =- 所以,2 (){[()]}D X E X E X =- 2()22()x x dt μσμ-- +∞ -∞ = -? 2222 t t dt σσ+∞ --∞ =?? 2 22 2t t dt σ+∞ --∞ =?
2 σ= 即知正态分布的两个参数分别是该分布的数学期望和方差。 中心极限定理: 设随机变量12,,,n X X X ???相互独立,服从同一分布,且具有相同的均值和方差:()k E X μ=,2()0(1,2,,)k D X k n σ=≠=???,则随机变量 () n n n k k k n X E X X n Y μ --= = ∑∑∑ (3-4) 的分布函数()n F x 对于任意x 都满足 2 2 lim ()lim }n t k x n n n X n F x P x dt μ →∞ →∞ -=≤=∑? (3-5) 即当n 趋向于无穷大时,随机变量n Y 近似的服从标准正态分布N(0,l)。在实际应用中当。大于等于30时,可以把1n i i Y X ==∑当作服从均值为n μ,方差为n 2σ的 正态分布,那么变量'Y = 近似服从标准正态分布N ~(0,l)。 Box-Muller 变换法: 变换法是通过一个变换将一个分布的随机数变换成一个不同分布的随机数。高斯分布的密度函数见公式3-1所示,通过Box-Muller 变换,它可以产生精确的正态分布的随机变量。其变换式如下 : 1)y v π (3-6) 2)y v π (3-7) 式中u ,v 是在区间[0,1]上服从均匀分布,且相互独立的随机变量,所以得到的随机变量1y ,2y 也应该是相互独立的,且服从N ~(0,1)的标准正态分布。 Box-Muller 变换的推导过程如下: 由公式3-6和公式3-7可得: 221212 2 1 ,()2y y y u e v arctg y π+- == (3-8)
M A T L A B产生各种分布 的随机数 The final revision was on November 23, 2020
MATLAB产生各种分布的随机数 1,均匀分布U(a,b): 产生m*n阶[a,b]均匀分布U(a,b)的随机数矩阵:unifrnd (a,b,m, n) 产生一个[a,b]均匀分布的随机数:unifrnd (a,b) 2,0-1分布U(0,1) 产生m*n阶[0,1]均匀分布的随机数矩阵:rand (m, n) 产生一个[0,1]均匀分布的随机数:rand 4,二类分布binornd(N,P,mm,nn)如binornd(10,,mm,nn) 即产生mm*nn均值为N*P的矩阵 binornd(N,p)则产生一个。而binornd(10,,mm)则产生mm*mm的方阵,军阵为N*p。 5,产生m*n阶离散均匀分布的随机数矩阵: unidrnd(N,mm,nn)产生一个数值在1-N区间的mm*nn矩阵 6,产生mm nn阶期望值为的指数分布的随机数矩阵: exprnd( ,mm, nn) 此外,常用逆累积分布函数表 函数名调用格式函数注释 norminv X=norminv(P,mu,sigma) 正态逆累积分布函数 expinv X=expinv(P,mu) 指数逆累积分布函数 weibinv X=weibinv(P,A,B) 威布尔逆累积分布函数 logninv X=logninv(P,mu,sigma) 对数正态逆累积分布函数
Chi2inv X=chi2inv(P,A,B) 卡方逆累积分布函数 Betainv X=betainv(P,A,B) β分布逆累积分布函数 随机数的产生 4.1.1 二项分布的随机数据的产生 命令参数为N,P的二项随机数据 函数 binornd 格式 R = binornd(N,P) %N、P为二项分布的两个参数,返回服从参数为N、P的二项分布的随机数,N、P大小相同。 R = binornd(N,P,m) %m指定随机数的个数,与R同维数。 R = binornd(N,P,m,n) %m,n分别表示R的行数和列数 例4-1 >> R=binornd(10, R = 3 >> R=binornd(10,,1,6) R = 8 1 3 7 6 4 >> R=binornd(10,,[1,10]) R = 6 8 4 6 7 5 3 5 6 2 >> R=binornd(10,,[2,3]) R = 7 5 8 6 5 6 >>n = 10:10:60; >>r1 = binornd(n,1./n) r1 = 2 1 0 1 1 2 >>r2 = binornd(n,1./n,[1 6]) r2 = 0 1 2 1 3 1 4.1.2 正态分布的随机数据的产生
例2.1 用乘同余法产生随机数(见光盘FLch2sjxleg1.m) ①编程如下: A=6; N=100; %初始化; x0=1; M=255; for k=1:N %乘同余法递推100次; x2=A*x0; %x2和x0分别表示x i和x i-1; x1=mod (x2,M); %将x2存储器的数除以M,取余数放x1(x i)中; v1=x1/256; %将x1存储器的数除以256得到小于1的随机数放v1中; )存放在矩阵存储器v的第k列中,v(:,k) v(:,k)=v1; % 将v1中的数( i %表示行不变、列随递推循环次数变化; x0=x1; %x i-1= x i; v0=v1; end %递推100次结束; v2=v %该语句末无‘;’,实现矩阵存储器v中随机数放在v2中,% 且可直接显示在MA TLAB的window中; k1=k; %grapher %以下是绘图程序; k=1:k1; plot(k,v,k,v,'r'); xlabel('k'), ylabel('v');tktle('(0-1)均匀分布的随机序列') ②程序运行结果如图2.5所示。 图2.5 采用MA TLAB产生的(0,1)均匀分布的随机序列图
③产生的(0-1)均匀分布的随机序列 在程序运行结束后,产生的(0,1)均匀分布的随机序列,直接从MATLAB的window 界面中copy出来如下(v2中每行存6个随机数): v2 = 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 第二章的白噪声产生程序 例2.2 用乘同余法产生(见光盘FLch2bzsheg2.m) ①编程如下: A=6; x0=1; M=255; f=2; N=100;%初始化; x0=1; M=255; for k=1: N %乘同余法递推100次; x2=A*x0; %分别用x2和x0表示x i+1和x i-1; x1=mod (x2,M); %取x2存储器的数除以M的余数放x1(x i)中; v1=x1/256; %将x1存储器中的数除以256得到小于1的随机数放v1中; )减去0.5再乘以存储器f中的系数,存放v(:,k)=(v1-0.5 )*f; %将v1中的数( i 在矩阵存储器v的第k列中,v(:,k)表示行不变、列随递推 循环次数变化;
求教:我的电子表格中rand()函数的取值范围是-1到1,如何改回1到0 回答:有两种修改办法: 是[1-rand()]/2, 或[1+rand()]/2。 效果是一样的,都可生成0到1之间的随机数 电子表格中RAND()函数的取值范围是0到1,公式如下: =RAND() 如果取值范围是1到2,公式如下: =RAND()*(2-1)+1 RAND( ) 注解: 若要生成a 与b 之间的随机实数: =RAND()*(b-a)+a 如果要使用函数RAND 生成一随机数,并且使之不随单元格计算而改变,可以在编辑栏中输入“=RAND()”,保持编辑状态,然后按F9,将公式永久性地改为随机数。 示例 RAND() 介于0 到1 之间的一个随机数(变量) =RAND()*100 大于等于0 但小于100 的一个随机数(变量) excel产生60-70随机数公式 =RAND()*10+60 要取整可以用=int(RAND()*10+60) 我想用excel在B1单元个里创建一个50-80的随机数且这个随机数要大于A1单元个里的数值,请教大家如何编写公式! 整数:=ROUND(RAND()*(80-MAX(50,A1+1))+MAX(50,A1+1),0) 无需取整数:=RAND()*(80-MAX(50,A1))+MAX(50,A1)
要求: 1,小数保留0.1 2,1000-1100范围 3,不要出现重复 =LEFT(RAND()*100+1000,6) 至于不许重复 你可以设置数据有效性 在数据-有效性设 =countif(a:a,a1)=1 选中a列设有效性就好了 其他列耶可以 急求excel随机生成数字的公式,取值要在38.90-44.03之间,不允许重复出现,保留两位小数,不允许变藏 =round(RAND()*5+38.9,2) 公式下拉 Excel随机数 Excel具有强大的函数功能,使用Excel函数,可以轻松在Excel表格产生一系列随机数。 1、产生一个小于100的两位数的整数,输入公式=ROUNDUP(RAND()*100,0)。 RAND()这是一个随机函数,它的返回值是一个大于0且小于1的随机小数。ROUNDUP 函数是向上舍入数字,公式的意义就是将小数向上舍入到最接近的整数,再扩大100倍。 2、产生一个四位数N到M的随机数,输入公式=INT(RAND()*(M-N+1))+N。 这个公式中,INT函数是将数值向下取整为最接近的整数;因为四位数的随机数就是指从1000到9999之间的任一随机数,所以M为9999,N为1000。RAND()的值是一个大于0且小于1的随机小数,M-N+1是9000,乘以这个数就是将RAND()的值对其放大,用INT 函数取整后,再加上1000就可以得到这个范围内的随机数。[公式=INT(RAND()*(9999-1000+1))+1000] 3、Excel函数RANDBETWEEN是返回位于两个指定数之间的一个随机数。使用这一个函数来完成上面的问题就更为简单了。要使用这个函数,可能出现函数不可用,并返回错误值#NAME?。 选择"工具"菜单,单击"加载宏",在"可用加载宏"列表中,勾选"分析工具库",再单击"确定"。接下来系统将会安装并加载,可能会弹出提示需要安装源,也就是office安装盘。放入光盘,点击"确定",完成安装。 现在可以在单元格输入公式=RANDBETWEEN(1000,9999)。 最后,你可以将公式复制到所有需要产生随机数的单元格,每一次打开工作表,数据都会自动随机更新。在打开的工作表,也可以执行功能键F9,每按下一次,数据就会自动随机更新了。
四院四队 正态分布随机数的产生 实验报告 2014年5月26日
正态分布随机数的产生 一、 实验简述 通过matlab 实现正态分布N(0,1)随机数的产生。 二、 历史背景 正态分布是最重要的一种概率分布。正态分布概念是由德国的数学家和天文学家Moivre 于1733年首次提出的,但由于德国数学家Gauss 率先将其应用于天文学家研究,故正态分布又叫高斯分布,高斯这项工作对后世的影响极大,他使正态分布同时有了“高斯分布”的名称,后世之所以多将最小二乘法的发明权归之于他,也是出于这一工作。高斯是一个伟大的数学家,重要的贡献不胜枚举。但现今德国10马克的印有高斯头像的钞票,其上还印有正态分布的密度曲线。这传达了一种想法:在高斯的一切科学贡献中,其对人类文明影响最大者,就是这一项。在高斯刚作出这个发现之初,也许人们还只能从其理论的简化上来评价其优越性,其全部影响还不能充分看出来。这要到20世纪正态小样本理论充分发展起来以后。拉普拉斯很快得知高斯的工作,并马上将其与他发现的中心极限定理联系起来,为此,他在即将发表的一篇文章(发表于1810年)上加上了一点补充,指出如若误差可看成许多量的叠加,根据他的中心极限定理,误差理应有高斯分布。这是历史上第一次提到所谓“元误差学说”——误差是由大量的、由种种原因产生的元误差叠加而成。后来到1837年,海根(G.Hagen )在一篇论文中正式提出了这个学说。 其实,他提出的形式有相当大的局限性:海根把误差设想成个数很多的、独立同分布的“元误差” 之和,每只取两值,其概率都是1/2,由此出发,按狄莫佛的中心极限定理,立即就得出误差(近似地)服从正态分布。拉普拉斯所指出的这一点有重大的意义,在于他给误差的正态理论一个更自然合理、更令人信服的解释。因为,高斯的说法有一点循环论证的气味:由于算术平均是优良的,推出误差必须服从正态分布;反过来,由后一结论又推出算术平均及最小二乘估计的优良性,故必须认定这二者之一(算术平均的优良性,误差的正态性) 为出发点。但算术平均到底并没有自行成立的理由,以它作为理论中一个预设的出发点,终觉有其不足之处。拉普拉斯的理论把这断裂的一环连接起来,使之成为一个和谐的整体,实有着极重大的意义。 三、 实验步骤 设U 1,U 2相互独立同服从U(0,1),令 1 2 112(2lnU )cos(2U )X π=-
均匀随机数的产生 教学目标: 1.通过模拟试验,感知应用数字解决问题的方法,了解均匀随机数的概念;掌握利用计算器(计算机)产生均匀随机数的方法;自觉养成动手、动脑的良好习惯. 2.会利用均匀随机数解决具体的有关概率的问题,理解随机模拟的基本思想是用频率估计概率.学习时养成勤学严谨的学习习惯,培养逻辑思维能力和探索创新能力. 教学重点: 掌握[0,1]上均匀随机数的产生及[a,b]上均匀随机数的产生.学会采用适当的随机模拟法去估算几何概率. 教学难点: 利用计算器或计算机产生均匀随机数并运用到概率的实际应用中. 教学方法: 讲授法 课时安排 1课时 教学过程: 一、导入新课 1、复习提问:(1)什么是几何概型?(2)几何概型的概率公式是怎样的?(3)几何概型的特点是什么? 2、在古典概型中我们可以利用(整数值)随机数来模拟古典概型的问题,那么在几何概型中我们能不能通过随机数来模拟试验呢?如果能够我们如何产生随机数?又如何利用随机数来模拟几何概型的试验呢?引出本节课题:均匀随机数的产生. 二、新课讲授: 提出问题 (1)请说出古典概型的概念、特点和概率的计算公式? (2)请说出几何概型的概念、特点和概率的计算公式? (3)给出一个古典概型的问题,我们除了用概率的计算公式计算概率外,还可用什么方法得到概率?对于几何概型我们是否也能有同样的处理方法呢? (4)请你根据整数值随机数的产生,用计算器模拟产生[0,1]上的均匀随机数. (5)请你根据整数值随机数的产生,用计算机模拟产生[0,1]上的均匀随机数. (6)[a,b]上均匀随机数的产生. 活动:学生回顾所学知识,相互交流,在教师的指导下,类比前面的试验,一一作出回答,教师及时提示引导. 讨论结果: (1)在一个试验中如果 a.试验中所有可能出现的基本事件只有有限个;(有限性) b.每个基本事件出现的可能性相等.(等可能性) 我们将具有这两个特点的概率模型称为古典概率模型(classical models of probability),简称古典概型. 古典概型计算任何事件的概率计算公式为:P(A)= 基本事件的总数数 所包含的基本事件的个 A . (2)对于一个随机试验,我们将每个基本事件理解为从某个特定的几何区域内随机地取一点,
各型分布随机数的产生算法 随机序列主要用概率密度函数(PDF〃Probability Density Function)来描述。 一、均匀分布U(a,b) ?1x∈[a,b]? PDF为f(x)=?b?a?0〃其他? 生成算法:x=a+(b?a)u〃式中u为[0,1]区间均匀分布的随机数(下同)。 二、指数分布e(β) x?1?exp(?x∈[0,∞)βPDF为f(x)=?β ?0〃其他? 生成算法:x=?βln(1?u)或x=?βln(u)。由于(1?u)与u同为[0,1]均匀分布〃所以可用u 替换(1?u)。下面凡涉及到(1?u)的地方均可用u替换。 三、瑞利分布R(μ) ?xx2 exp[?x≥0?回波振幅的PDF为f(x)=?μ2 2μ2 ?0〃其他? 生成算法:x=?2μ2ln(1?u)。 四、韦布尔分布Weibull(α,β) xα??αα?1?αβxexp[?(]x∈(0,∞)βPDF为f(x)=? ?0〃其他? 生成算法:x=β[?ln(1?u)]1/α 五、高斯(正态)分布N(μ,σ2) ?1(x?μ)2 exp[?]x∈?2PDF为f(x)=?2πσ 2σ ?0〃其他? 生成算法: 1?y=?2lnu1sin(2πu2)生成标准正态分布N(0,1)〃式中u1和u2是相互独立的[0,1]区间
均匀分布的随机序列。 2?x=μ+σy产生N(μ,σ2)分布随机序列。 六、对数正态分布Ln(μ,σ2) ?1(lnx?μ)2 exp[?x>0PDF为f(x)=?2πσx 2σ2 ?0〃其他? 生成算法: 1?产生高斯随机序列y=N(μ,σ2)。 2?由于y=g(x)=lnx〃所以x=g?1(y)=exp(y)。 七、斯威林(Swerling)分布 7.1 SwerlingⅠ、Ⅱ型 7.1.1 截面积起伏 σ?1?exp[σ≥0?σ0截面积的PDF为f(σ)=?σ0〃【指数分布e(σ0)】 ?0〃其他? 生成算法:σ=?σ0ln(1?u)。 7.1.2 回波振幅起伏 ?AA2 ?exp[?2]A≥0〃式中A2=σ〃2A02=σ0。回波振幅的PDF为f(A)=?A02【瑞利分布R(A0)】2A0?0〃其他? 生成算法:A=?2A02ln(1?u)=σ0ln(1?u)。也可由A2=σ得A==?0ln(1?u) 7.2 SwerlingⅢ、Ⅳ型 7.2.1 截面积起伏 2σ?4σ]σ≥0?2exp[?σσ截面积的PDF为f(σ)=?0〃 0?0〃其他? 生成算法:σ=?式中u1和u2是相互独立的[0,1]区间均匀分布随机序列。 [ln(1?u1)+ln(1?u2)]〃2
用乘同余法产生随机数
1 例2.1 用乘同余法产生随机数 (见光盘 FLch2sjxleg1.m) ①编程如下: A=6; N=100; %初始化; x0=1; M=255; for k=1:N %乘同余法递推100次; x2=A*x0; %x2和x0分别表示x i 和x i-1; x1=mod (x2,M); %将x2存储器的数除以M ,取余数放x1(x i )中; v1=x1/256; %将x1存储器的数除以256得到小于1的随机数放v1中; v(:,k)=v1; % 将v1中的数 (i )存放在 矩阵存储器v 的第k 列中,v(:,k)
%表示行不变、 列随递推循 环次数变化; x0=x1; %x i-1= x i; v0=v1; end %递推100次结束; v2=v %该语句末无 ‘;’,实现矩 阵存储器v中 随机数放在 v2中,%且可 直接显示在 MATLAB的 window中;k1=k; %grapher %以下是绘图程序; k=1:k1; plot(k,v,k,v,'r'); 2
xlabel('k'), ylabel('v');tktle('(0-1)均匀分布 的随机序列') ②程序运行结果如图2.5所示。 图2.5 采用MATLAB产生的(0,1)均匀分布的随机序列图 ③产生的(0-1)均匀分布的随机序列 在程序运行结束后,产生的(0,1)均匀分布的随机序列,直接从MATLAB的window界面中copy出来如下(v2中每行存6个随机数):v2 = 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 0.3750 0.2578 0.5508 0.3164 0.9023 0.4336 0.6094 0.6680 0.0234 0.1406 0.8438 0.0820 0.4922 0.9609 0.7852 0.7266 3
一维正态分布随机数序列的产生方法 一、文献综述 1.随机数的定义及产生方法 1).随机数的定义及性质 在连续型随机变量的分布中,最简单而且最基本的分布是单位均匀分布。由该分布抽取的简单子样称,随机数序列,其中每一个体称为随机数。 单位均匀分布也称为[0,1]上的均匀分布。 由于随机数在蒙特卡罗方法中占有极其重要的位置,我们用专门的符号ξ表示。由随机数序列的定义可知,ξ1,ξ2,…是相互独立且具有相同单位均匀分布的随机数序列。也就是说,独立性、均匀性是随机数必备的两个特点。 随机数具有非常重要的性质:对于任意自然数s,由s个随机数组成的 s维空间上的点(ξn+1,ξn+2,…ξn+s)在s维空间的单位立方体Gs上 均匀分布,即对任意的ai,如下等式成立: 其中P(·)表示事件·发生的概率。反之,如果随机变量序列ξ1, ξ2…对于任意自然数s,由s个元素所组成的s维空间上的点(ξn+1,…ξn+s)在Gs上均匀分布,则它们是随机数序列。 由于随机数在蒙特卡罗方法中所处的特殊地位,它们虽然也属于由具有已知分布的总体中产生简单子样的问题,但就产生方法而言,却有着本质上的差别。 2).随机数表 为了产生随机数,可以使用随机数表。随机数表是由0,1,…,9十个数字组成,每个数字以0.1的等概率出现,数字之间相互独立。这些数字序列叫作随机数字序列。如果要得到n位有效数字的随机数,只需将表中每n 个相邻的随机数字合并在一起,且在最高位的前边加上小数点即可。例如,某随机数表的第一行数字为7634258910…,要想得到三位有效数字的随机数依次为0.763,0.425,0.891。因为随机数表需在计算机中占有很大内存, 而且也难以满足蒙特卡罗方法对随机数需要量非常大的要求,因此,该方法不适于在计算机上使用。 3).物理方法
编写一个产生符合高斯分布的随机数函数信号检测与估计课程作业作业要求 1、利用计算机内部函数产生高斯分布的随机数,分别画出500,10000,100000点的波形,并进行统计分析(分别画出概率密度曲线,计算均值与方差) 2、利用计算机自己编写一个产生符合高斯分布的随机数函数,画出100000点的波形,并进行统计分析(同一) 提示:这一问分两步做,第一步先产生一个均匀分布的随机数序列(乘同余法、混合同余法等,可以用自己的方法),第二步通过适当变换得到符合高斯分布概率模型的随机数列 3、对随机数产生函数和高斯分布进行性能分析,并写出自己对于此次作业和上课的学习体会 一、利用内部函数产生高斯分布 首先利用matlab自带的内部函数randn()就可以方便的生成所需要的高斯分布随机数,然后画出概率密度曲线并计算出均值与方差即可。程序代码如下: A=randn(500,1); B=randn(10000,1);
C=randn(100000,1); subplot(2,3,1); bar(A); subplot(2,3,2); bar(B); subplot(2,3,3); bar(C); [f1,x1]=ksdensity(A); subplot(2,3,4); plot(x1,f1); title('500点高斯分布概率密度函数'); [f2,x2]=ksdensity(B); subplot(2,3,5); plot(x2,f2); title('10000点高斯分布概率密度函数'); [f3,x3]=ksdensity(C); subplot(2,3,6); plot(x3,f3); title('100000点高斯分布概率密度函数'); JZ500=mean(A) JZ1000=mean(B) JZ100000=mean(C) FC500=var(A) FC10000=var(B)
[核心必知] 1.预习教材,问题导入 根据以下提纲,预习教材P135~P136,回答下列问题. (1)教材问题中甲获胜的概率与什么因素有关? 提示:与两图中标注B的扇形区域的圆弧的长度有关. (2)教材问题中试验的结果有多少个?其发生的概率相等吗? 提示:试验结果有无穷个,但每个试验结果发生的概率相等. 2.归纳总结,核心必记 (1)几何概型的定义与特点 ①定义:如果每个事件发生的概率只与构成该事件区域的长度(面积或体积)成比例,则称这样的概率模型为几何概率模型,简称为几何概型. ②特点:(ⅰ)可能出现的结果有无限多个;(ⅱ)每个结果发生的可能性相等. (2)几何概型中事件A的概率的计算公式 P(A)= 构成事件A的区域长度(面积或体积) 试验的全部结果所构成的区域长度(面积或体积) . [问题思考] (1)几何概型有何特点? 提示:几何概型的特点有: ①试验中所有可能出现的结果(基本事件)有无限多个; ②每个基本事件出现的可能性相等. (2)古典概型与几何概型有何区别? 提示:几何概型也是一种概率模型,它与古典概型的区别是:古典概型的试验结果是有限的,而几何概型的试验结果是无限的. [课前反思] 通过以上预习,必须掌握的几个知识点: (1)几何概型的定义:;
(2)几何概型的特点: ; (3)几何概型的计算公式: . 某班公交车到终点站的时间可能是11∶30-12∶00之间的任何一个时刻. 往方格中投一粒芝麻,芝麻可能落在方格中的任何一点上. [思考1] 这两个试验可能出现的结果是有限个,还是无限个? 提示:无限多个. [思考2] 古典概型和几何概型的异同是什么? 名师指津:古典概型和几何概型的异同 如表所示: 名称 古典概型 几何概型 相同点 基本事件发生的可能性相等 不同点 ①基本事件有限个 ①基本事件无限个 ②P (A )=0?A 为不可能事件 ②P (A )=0A 为不可能事件 ③P (B )=1?B 为必然事件 ③P (B )=1 B 为必然事件 讲一讲 1.取一根长为5 m 的绳子,拉直后在任意位置剪断,那么剪得两段的长都不小于2 m 的概率有多大? [尝试解答] 如图所示. 记“剪得两段绳长都不小于2 m ”为事件A .把绳子五等分,当剪断位置处在中间一段上 时,事件A 发生.由于中间一段的长度等于绳长的15 , 所以事件A 发生的概率P (A )=15 . 求解与长度有关的几何概型的关键点 在求解与长度有关的几何概型时,首先找到试验的全部结果构成的区域D ,这时区域D
第三章随机数的产生与模拟目录 ?随机数的产生与模拟 ?§3.1均匀随机数的产生 ? 3.1.1线性同余法(LCG)的递推公式 ? 3.1.2反馈位移寄存器法(FSR) ? 3.1.3组合发生器 ?§3.2非均匀随机数的产生 ?§3.3 Monte Carlo方法在解确定性问题中的应用 ? 3.3.1计算定积分 ? 3.3.1.1随机投点法 ? 3.3.1.2平均值估计法 ? 3.3.1.3重要抽样法 ? 3.3.1.4分层抽样法 ? 3.3.2 计算多重积分 ? 3.3.2.1 随机投点法 ? 3.3.2.2 平均值估计法 ? 3.3.3应用实例 ?§3.4 随机模拟方法在随机服务系统中的应用 ?§3.5 随机模拟方法在理论研究中的应用
随机数的产生与模拟 用随机模拟方法解决实际问题时,首先要解决的是随机数的产生方法,或称随机变量的抽样方法。
随机数的产生与模拟 伪随机数: 在计算机上用数学方法产生均匀随机数是指按照一定的计算方法而产生的数列,它们具有类似于均匀随机变量的独立抽样序列的性质,这些数既然是依照确定算法产生的,便不可能是真正的随机数,因此常把用数学方法产生的随机数称为伪随机数。
随机数的产生与模拟 均匀分布随机数: 定理:设)(x F是连续且严格单调上升的分布函数,它的反函数存在,且记为)(1x F-, 1、若随机变量ξ的分布函数为)(x F,则)1,0(~)(U Fξ; 2、若随机变量)1,0(~U F-的分布函数为)(x F R,则)(1R
随机数的产生与模拟 均匀分布随机数: 该定理说明了任意分布的随机数均可由均匀分布的随机数变换得到。常简称的随机数为均匀分布随机数。 )1,0(U )1,0(U